Abstract
Accurately forecasting power generation in photovoltaic (PV) installations is a challenging task, due to the volatile and highly intermittent nature of solar-based renewable energy sources. In recent years, several PV power generation forecasting models have been proposed in the relevant literature. However, there is no consensus regarding which models perform better in which cases. Moreover, literature lacks of works presenting detailed experimental evaluations of different types of models on the same data and forecasting conditions. This paper attempts to fill in this gap by presenting a comprehensive benchmarking framework for several analytical, data-based and hybrid models for multi-step short-term PV power generation forecasting. All models were evaluated on the same real PV power generation data, gathered from the realisation of a small scale pilot site in Thessaloniki, Greece. The models predicted PV power generation on multiple horizons, namely for 15 min, 30 min, 60 min, 120 min and 180 min ahead of time. Based on the analysis of the experimental results we identify the cases, in which specific models (or types of models) perform better compared to others, and explain the rationale behind those model performances.
1. Introduction
Photovoltaic (PV) power generation is constantly gaining ground as a renewable energy source (RES) within the energy market. In 2018, a capacity over 500 GW providing around 600 TWh (roughly of the global electricity production) has been documented [1]. By 2019, the current estimation is that the PV capacity will reach 650 GW providing for the of the global production [2]. Additionally, future scenarios for RES systems penetration in the market are even more optimistic, with some countries aiming to reach [3] in the next decades, towards complete decarbonization. Therefore, it is evident that PV systems, are expected to be a key player in this rapidly evolving energy landscape.
Nevertheless, PV production is volatile and intermittent, due to its direct dependency on weather conditions. This introduces considerable uncertainty to the system operation, which is translated into significant risks to the stability and reliability of both the transmission and distribution networks [4]. The challenge is further exacerbated by the distribution of PV penetration. Several small and medium installations are appearing around the world, making such PV plants the most commonly accessed RES-based distributed energy resource (DER) [5]. This popularity creates the challenge of efficiently managing PV power generation. Unexpected shortage or excess can lead to severe imbalance between supply and demand, requiring mitigation actions from the system operator towards avoiding penalties or more severe consequences to the network operation. From a financial perspective, other market entities like aggregators and flexibility traders, have also invested in the optimal management of such resources for maximising their profits through a more efficient market participation.
An important factor in addressing these challenges is the ability to forecast the power generated by the PV systems as accurately as possible. A lot of effort has been invested in this direction as indicated by the relevant literature. Depending on the application, the time horizon for forecasting PV power generation varies from a few minutes (short-term) to days (long-term). The former is usually employed for improving control schemes as well as the participation to intra-day and ancillary markets, while the latter is applied mainly for maintenance and planning [6]. In both cases, the several PV power generation forecasting models can be classified into three categories:
- Analytical: These methods do not require any prior knowledge regarding the power generation measurements. They deliver the required results using well-known analytical equations that incorporate the technical characteristics of the PV installation along with weather forecasts derived by typical numerical weather prediction (NWP) models.
- Data-based: These models are data-driven, meaning that they are solely dependent on the historical PV power generation data, without any knowledge regarding the PV system itself. The basis of these models is the discovery of patterns and relations within the provided data. This category includes statistical time series models (e.g., autoregressive integrated moving average model—ARIMA), traditional machine learning (ML) models (e.g., artificial neural networks—ANNs) and deep learning (DL) models.
- Hybrid: These models attempt to combine the best characteristics of the other two categories in order to achieve higher forecasting accuracy. Different data-based models merged as one, or data-based models on top of analytical models, or even data-based models using NWP techniques, are some of the combinations identified in the literature. Interestingly enough, hybrid models seem to hold quite the potential in delivering the most accurate forecasting results.
In each of the above categories, quite interesting results have been presented over the last few years, with forecasting errors reaching below [7,8]. Nevertheless, in most cases, those results are limited and fragmented, due to lack of a common evaluation framework. Some of the factors limiting their scalability and replicability include: (a) forecasting over clear sky scenarios only, (b) limited amount of data, (c) presentation of results over very specific time frames, (c) inclusion of non-productive time slots (i.e., night hours) to the error metrics calculations, (d) elucidation of results from different locations, datasets and PV plants sizes [6,9]. Due to such factors, it has become quite difficult to thoroughly evaluate the predictive ability of a specific model. Therefore, a comprehensive benchmarking framework that will take into account a variety of factors during the evaluation of a multitude of PV power generation forecasting models from different categories is of great significance. On top of that, it is important to critically compare different types of methods in order to identify the objectively strong points of each type. To the best of our knowledge, very few efforts have been invested towards this direction (e.g., [10]) and even in those, the outcomes were not fully aligned with the rest of the literature [9].
This paper presents a comprehensive benchmarking framework for several analytical, data-based and hybrid models for multi-step short-term PV power generation forecasting. All models were evaluated on the same real-world power data and forecasting conditions (i.e., forecasting objectives, horizons, evaluation metrics, etc.). The main contributions of the work presented in this paper include:
- A comprehensive benchmark comparison between analytical, data-driven and hybrid direct PV power generation forecasting models.
- Extensive experimentation on real-world PV power generation data.
- A novel hybrid short-term PV power generation forecasting model, which outperforms in most cases several well-established analytical and data-based methods.
- Introduction of a new metric designed to accurately quantify the divergence error for the PV power generation forecasting problem.
The rest of this paper is organised as follows. Section 2 reviews current research efforts associated with the PV power generation forecasting problem. Section 3 presents the real-world power data on which the PV power generation forecasting models were evaluated, provides a short mathematical formulation for each model, and describes the overall setup of the evaluation framework. In Section 4, the experimental results of the evaluation process are presented and thoroughly discussed. Finally, Section 5 concludes the paper by reviewing its main contributions and suggesting future research directions.
2. Related Work
The last two decades have produced a significant number of solutions for the complex problem of PV power generation forecasting, employing analytical (or physical), data-based and hybrid models in order to predict the power output of PV installations of different sizes. Several comprehensive reviews have been published in the last couple of years [6,9,11,12,13]. PV power generation can be predicted directly (i.e., active power output) [14] or indirectly (via forecasting the solar irradiance) [15], while weather data are used either united or separated in groups with different conditions (e.g., sunny, cloudy and rainy days) [16]. For all the above approaches, analytical, data-based and hybrid models have been proposed.
2.1. Analytical Models
Analytical PV power generation forecasting models try to mimic the way in which the entire PV system operates. They are described by partial differential equations (PDEs) and are configured according to the installed infrastructure (e.g., the type of solar cells and their corresponding setup). Analytical models can be applied to both direct and indirect forecasting scenarios. In the former case, the models predict the active power output in a single iteration after being fed by NWP, while in the latter they first predict the value of a weather variable (usually the solar irradiance), and then they use this prediction to predict the PV power generation [17,18]. Additionally, there are some analytical models that directly convert the incoming meteorological data into electrical power [19]. Essentially, all analytical models are based on the production of an I-V curve for the PV installation using both the manufacturer data and experimentation under different exposure conditions.
The several analytical models are different from each other with respect to their parametrisation, ranging from two up to seven parameters [20,21,22,23,24]. The most prevalent models are (a) the simple current source and diode model, (b) the current source, diode, shunt and series resistor model and (c) the current source, double diode plus shunt and series models. It is noteworthy that more parameters do not imply better results. As demonstrated by Dolara et al. [19], in temperate climates simple three-parameter models exhibit similar, if not better, accuracy than higher order models. Moreover, in order to improve the accuracy of an analytical model, the thermal properties of the PV must be taken into account. In this case, two models prevail: the Sandia model [25] and Nominal Operating Cell Temperature (NOCT) [26] models. The former outperforms the latter for the majority of PV cell types (i.e., c-Si, CdTe, a-Si:H and organic polymeric cells) [27].
The accuracy of the direct analytical models depends on the accuracy of the NWP models used. Hence, the NWP model propagates error to the analytical PV power generation model due to its (in most cases) low spatio-temporal accuracy [19]. Irradiance is the variable that impacts the most the PV output power, with a Pearson coefficient exceeding [28]. Thus, high-accuracy irradiance forecasting is required when purely analytical PV power generation forecasting models are used. Irradiance forecasting models (or their equivalent cloud coverage forecasting models) can achieve acceptable accuracies in cases where the geographical areas of interest are of the order of tens of square kilometers [29]. Finally, the analytical direct and indirect models are proven superior in long-term forecasting scenarios (i.e., from one day to few months) and for large PV installations (order of magnitude MW), but they present inferior performance in short-term forecasting scenarios and for small PV arrays (order of magnitude kW) [30,31].
2.2. Data-Based Models
The poor performance of analytical models in short-term forecasting scenarios, led the researchers to investigate the potential of data-based models. These models depend solely on the available PV power data when they predict PV power generation directly, while they process both PV power and weather data when they predict PV power generation indirectly [6]. In this category fall the typical statistical time series models (e.g., autoregressive integrated moving average model—ARIMA), the traditional machine learning models (e.g., support vector machines - SVM), and the deep learning models (e.g., deep neural networks—DNN). A comparative analysis of these data-based approaches is difficult since each published work presenting such a model uses a completely different evaluation frameworks (hour-ahead versus day-ahead forecasts, small versus large PV plants, etc.).
In the case of day-ahead PV power generation forecasting for small-scale PV installations, the majority of published works uses the day-ahead prediction of a weather variable (generated by a typical NWP model) to feed a data-based model. This explains the non-linearities of the generated PV power under different weather conditions [32]. In these works, the reported accuracy of the models varies significantly since there are multiple variables that may impact accuracy. Therefore, it can be stated that no particular model, published in PV power generation forecasting literature, is proven to be consistently superior over others [33]. Some data-based models proven to yield acceptable accuracy for day-ahead PV power generation forecasting are the Extreme Learning Machines (ELM) [34] and the Self-Organizing Maps (SOM) [35].
As already mentioned, the data-based models contain both direct and indirect approaches. The indirect approaches combine historical measurements of PV output power and weather variables (e.g., irradiance, temperature and humidity) in order to build a model that produces highly accurate predictions. For example, Das et al. [36] proposed a support vector regression (SVR) model for hourly and day-ahead PV power generation forecasting. Though results were promising, only sunny days were used for demonstration, thus omitting covering the problem of forecasting in cloudy and rainy days. In cases where limited historical PV power data exist, iterative multi-task learning can be utilized by sharing the PV information from multiple similar solar panels [37]. Moreover, the importance of integrating weather information into data-driven models is highlighted by De Giorgi et al. [38], who proposed an Elman neural network model for direct day-ahead PV power generation forecasting. The outcome of this work is the significantly improved prediction accuracy when both temperature and irradiance historical measurements are added in the input vectors of the network. Finally, weather data can also be used for data pre-processing tasks instead of being directly integrated into the data-based prediction model [39]. For example, Yang et al. [40] divided the historical PV power data into weather-based subsets for sunny, cloudy and rainy days.
2.2.1. Statistical Time Series Models
Statistical time series models are the first data-based models employed for direct PV power generation forecasting. Some of the first models used were based on the linear regression model [41,42,43], the ARIMA model [44,45] and its variants [44,46]. In many studies, these models (along with the naive persistence model) are used for benchmarking purposes [41,44,47,48,49,50]. Additionally, such statistical models with several input variables are used to estimate the correlation between the PV power generation and weather variables [48,51]. However, these models are linear with respect to both their regressors and parameters, which results in poor performance due to the fact that the PV power generation process is, in general, a nonlinear phenomenon [42].
2.2.2. Traditional Machine Learning Models
The second type of data-based PV power generation forecasting models is the traditional machine learning models [52], namely k-nearest neighbors (kNN) [33], support vector machines (SVM) [14,49,53] and artificial neural networks (ANN). kNN models appear to yield acceptable performance [53]. For example, Fernandez-Jimenez et al. [47] proposed kNN and weighted kNN models for direct PV power generation forecasting with quite accurate results. On the other hand, SVM models present mediocre results in terms of forecasting accuracy, even in case of very short-term direct forecasting (i.e., up to 30 min ahead). Shi et al. [14] presented an SVM-based PV power generation forecasting model that approximately estimated PV power generation using day-ahead weather predictions.
ANNs have grown in popularity due to their ability to accurately represent the highly nonlinear mapping between PV power generation and its related variables [54]. Fernandez-Jimenez et al. [47] proposed five different ANN architectures, which achieved superior performance compared to ARIMA, kNN and adaptive neuro-fuzzy inference systems (ANFIS). Chen et al. [35] used radial basis function networks (RBFN) to forecast the day ahead PV power generation, having initially clustered the predictions of the weather variables. This model presented mediocre forecasting accuracy in cloudy and rainy days. Similarly, Sideratos and Hatziargyriou [55] proposed an RBFN-based PV power generation forecasting model demonstrating high accuracy in long-term forecasting scenarios (e.g., 24 h forecasting horizons) and sunny periods. However, a critical limitation of the ANNs is that they require large amount of data (and, subsequently, long training times) in order to achieve high forecasting accuracy [56].
2.2.3. Deep Learning Models
Deep learning (DL) is a sub-field of machine learning, which includes complex ANN architectures that automatically identify and extract useful features from raw data. Deep learning models have been extensively used for time series forecasting tasks ([48,56,57,58]), due to their ability to learn complex relationships from the data and use them to provide accurate forecasting results. There are (roughly) three main categories of deep learning models used for time series forecasting: deep neural networks (DNN), convolutional neural networks (CNN) and recurrent neural networks (RNN). Among RNN architectures, long short-term memory (LSTM) network is the most widely used architecture for time series forecasting. Recently, several DL architectures have been proposed in the PV power generation forecasting literature. For example, Qing and Niu [43] proposed an LSTM architecture to predict the hour-ahead solar irradiance, which is then used for estimating the PV power generation. This model was claimed to yield higher forecasting accuracy compared to traditional ANNs.
For example, Ouyang et al. [59] proposed an RNN-based PV power generation forecasting model, which was combined with clustering algorithms. The model exhibited good forecasting results in sunny days. Additionally, Ghimire et al. [60] introduced an indirect PV power generation forecasting approach in which a CNN extracts features of solar irradiation, which in turn are used by an LSTM to predict the hour-ahead irradiance. Kim and Lee [61] proposed an LSTM model with multiple inputs that include meteorological factors, seasonal factors and preceding power output information in order to predict PV power generation in the peak zone. Vidisha De et al. [62] proposed an LSTM-based model that yielded small forecasting error (i.e., approximately even though it was trained with limited data. Several other LSTM-based power generation forecasting models have been proposed in the relevant literature [42,44,48,49,57]. These models present superior forecasting performance compared to conventional models like ARIMA and DNN, especially in the case of short-term PV power generation forecasting. However, these models have limitations like the requirement for large amounts of available data in order to produce highly accurate predictions and the long training times [49].
2.3. Hybrid Models
Apart from the analytical and data-based models, there are also other PV power generation forecasting models that attempt to combine the best characteristics of these categories in order to achieve higher forecasting accuracy. These are the hybrid models. The hybrid models either combine characteristics from models of the same category (i.e., multiple analytical or multiple data-based models) or from models from different categories (i.e., analytical and data-based models). The hybrid approaches make up only of the published PV power generation forecasting models [9]. In this context, Bracale et al. [63] proposed a probabilistic direct forecasting model based on Bayesian inference and Monte Carlo simulation. The model used an analytical function in order to connect the hourly sky clearness index to the maximum power point production of a PV plant. Despite its ability to identify the probability distribution function of power generation, the model underperformed in the one step-ahead prediction case. In general, the unstable meteorological conditions usually result in inferior performance of the hybrid analytical-data-based models [38,56]. Another hybrid approach for day-ahead direct PV power generation forecasting was proposed by Mosaico and Saviozzi [54]. The authors proposed a decision system that selects between an analytical and an ANN model based on the current cloud coverage percentage. The model presents acceptable performance in clear sky days and poor in cloudy days. Additionally, Luyao et al. [64] proposed a hybrid PV power generation forecasting model that combines three ANN architectures with genetic algorithms (GA). Finally, Wang et al. [8] presented a hybrid model that fused a CNN with an LSTM architecture.
3. Materials & Methods
In this section, the real-world power generation data used for the evaluation of the several PV power generation forecasting models are presented. Additionally, a small mathematical description of each of the nine PV power generation forecasting models is provided. Finally, the configuration parameters of the overall experimental framework are presented.
3.1. Field Data
In this section, the real-world power generation data used for the evaluation of the several PV power generation forecasting models are presented and the several preprocessing methods applied on them are described.
3.1.1. Data Description
The dataset used in this study is collected from a real-world small-scale PV installation, which is located on the roof of a two-floor family house emulating building. This building is one of the official European Commission Digital Innovation Hubs (DIH) located within the campus of the Centre for Research and Technology Hellas (CERTH), 6 km away from the metropolitan area of Thessaloniki, Greece. This “smart house” is part of the research and experimental infrastructure of CERTH. Its current installation consists of 58 CIS (copper, indium, and selenium) solar panels with 165 Wp nominal power each. The solar panels are divided into 9 strings that form in total kWp, and they are facing 255° south-west with a tilt angle of 18° (Figure 1). The PV installation has a very brief shading due to hill located on the northeast of the building during early morning hours. Finally, the climatic conditions according to the Köppen Climate Classification Map (https://www.plantmaps.com/koppen-climate-classification-map-europe.php) is considered Cold Semi-Arid Climate (BSk). The exact longitude and latitude of the installation are and , respectively.

Figure 1.
CERTH/ITI Smart House and the roof-based PV Installation (only the rooftop PVs are used for the current study).
The dataset contains the power generation values of the above PV installation for each 15-min interval of a total period of 11 months, namely from 24 March 2019 to 29 February 2020. This is a total period of 343 days. However, 38 days in this period had no available data. Hence, the total number of days with available PV power generation data is 305. Based on the data granularity (i.e., one value per 15-min interval) and the total time period covered by the data (i.e., 305 days), the dataset contains 29,280 PV power generation values in total. These values are organised in time series, with one time series for each day of the dataset. Each time series contains 96 PV power generation values, one for each 15-min interval of a day.
Apart from the dataset of the PV power generation values, a dataset of weather data has also been assembled. In particular, measurements for three weather variables, namely temperature, wind speed and cloud coverage, have been collected for the location of the aforementioned PV installation. This data was collected from the online weather data aggregation service Weatherbit (https://www.weatherbit.io/), which provides weather information in 15-min intervals (same as the granularity of the PV power generation dataset) for several locations anywhere on the globe. The total period covered by this data is the same as the period covered by the PV power generation dataset. Again, the data is organised into time series. A complementary source of weather information, namely the weather data aggregation service Darksky (https://darksky.net/dev), was particularly used for cloud coverage data. Predictions are also given in time series format, in 15-min intervals. Finally, it should be mentioned that the above weather services have been used in order to collect both actual and forecasted values of the weather variables. The forecasted values are generated using typical NWP models.
3.1.2. Data Segmentation
As identified in similar works found in literature (e.g., [36,40]), it is considered a good practice to divide the available PV power generation data into periods with stable weather conditions (e.g., sunny days period and cloudy days period), and build different forecasting models for each period. This approach was followed in the present study. In particular, the PV power generation dataset was initially split into spring, summer, autumn and winter periods containing PV power generation values from the following time periods:
- Spring: from 24 March 2019 to 31 May 2019
- Summer: from 1 June 2019 to 31 August 2019
- Autumn: from 1 September 2019 to 30 November 2019
- Winter: from 1 December 2019 to 29 February 2020
Within each period, the data were re-divided based on the corresponding cloud coverage values. Specifically, the days were separated into high and low cloud coverage days based on whether the corresponding average cloud coverage of the day exceeded a specific cloud coverage threshold. This threshold was set to after experimentation. Finally, it should be mentioned that most of the PV power generation measurements from the time intervals before 5:00 A.M. UTC and 17:00 P.M. UTC were zero and therefore they were discarded.
3.1.3. Data Transformation for Supervised Learning
The data-based and hybrid models presented in this work are trained in a supervised-learning way. This means that in order to train these models, first a set of training samples of the form is required, where and . The vectors and the values should then be applied to the input and output of the models, respectively. However, as mentioned above, the data is organised as a set of time series of size n each. In order to transform a time series of data into a set of training samples appropriate for training a model in a supervised way, a window of fixed size p and a forecasting horizon h should be selected. Then, the window passes over the time series one step at a time and matches the time series values it covers to a training sample. This transformation technique is called sliding window. Having a fixed window length assists in the creation of input-output pairs. In particular, the first step is to select the values as the first training vector and the value as the first training output . Next, the values formulate the second training vector and the value the second training output , and so on. In this way, a set of training samples is generated from a time series of size n. For a set of m time series of size n the number of generated training examples is .
3.2. PV Power Generation Forecasting Models
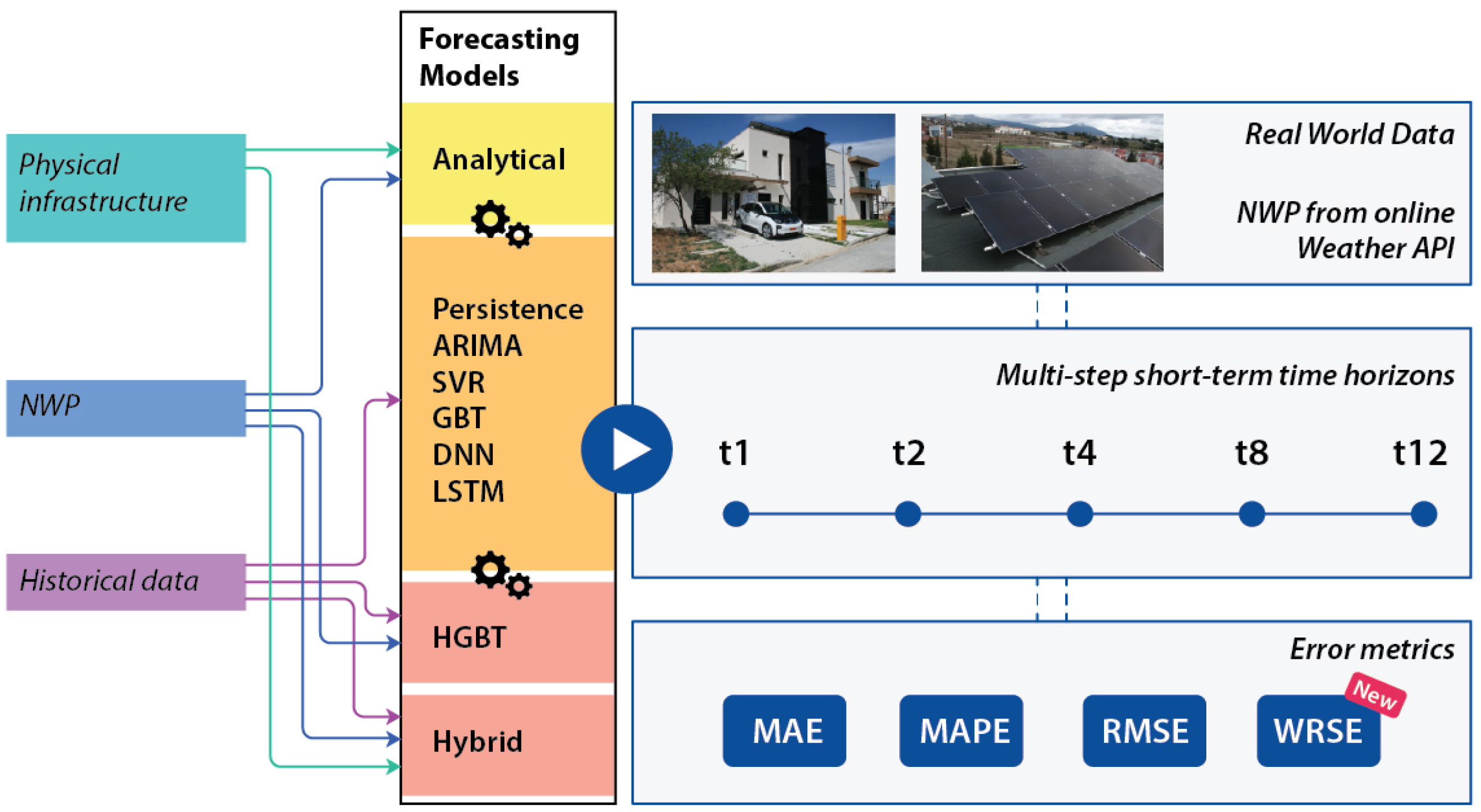
The objective of this work is to present a comprehensive evaluation framework of several analytical, data-based and hybrid models for multi-step short-term PV power generation forecasting. Extending previous research findings [8,10], this paper aims to evaluate a wider range of models over the same dataset and forecasting parameters, towards presenting a more holistic overview over their performance on multi-step short-term PV power generation forecasting, as presented in Figure 2. In this subsection, a short mathematical description of each model evaluated in this study is provided.
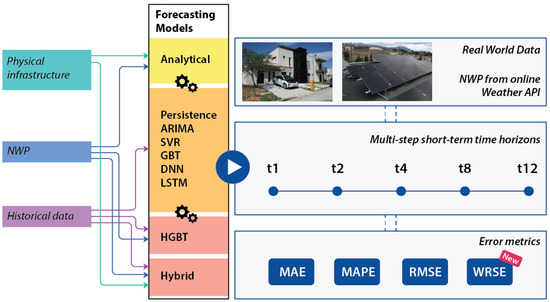
Figure 2.
Overview of the methodology explored (each t corresponds to 15’ interval).
3.2.1. Analytical Model
The first PV power generation forecasting model used in this study is a physical model. As explained, the physical models emulate both the electrical and thermal properties of the PV cell and demonstrate highly accurate forecasting performance. The physical model was implemented using the open source software PVLIB [65]. PVLIB is widely used in the PV power generation forecasting literature as it implements a simple electrical model that exhibits forecasting performance equivalent to a higher-order model, and also it incorporates the Sandia thermal model [66]. The model requires the accurate definition of the following variables:
- Location and time: The solar irradiance values, which are used for the calculation of the actual PV power generation values, are calculated by a component of the physical model that estimates the exact position of the sun in terms of installation location and time. Hence, it is important to know the exact location (i.e., latitude and longitude) of the PV installation and to have accurate time measurements in the lowest granularity possible (i.e., hh:mm).
- PV configuration: PV construction details such as type/number of modules, type of inverter, the installation’s tilt and azimuth angle should be defined.
- Weather data: Cloud coverage and temperature forecasts should also be provided as input to the physical model.
3.2.2. Statistical Models
As already mentioned, the statistical models are the first data-based models used for direct PV power generation forecasting. In this section, the details of the statistical models used in this study, namely the persistence (or random walk) model and the ARIMA model, are provided.
- Persistence model
In every time series forecasting task, it is useful to have as a basic benchmarking model, a simplistic model like the persistence model (also referred to in the forecasting literature as random walk or naive model). In the persistence model, the forecasted value for the dependent variable is equal to the current value of the variable, regardless of the forecasting horizon. The prediction equation of the persistence model is as follows:
where h is the forecasting horizon. If the forecasting accuracy of a new model is not higher than the accuracy of the persistence model, then the new model cannot be considered as useful.
- Autoregressive integrated moving average
The ARIMA model is one of the most widely used statistical models for time series forecasting tasks in general, and for power PV generation forecasting, in particular. The method was popularised by the work of Box and Jenkins [67] in the 1970s. In short, an model is described by the following equation:
where p is the autoregressive order, q is the moving average order, d is the order of differencing (i.e., how many times to apply the first differences method in order to make a time series stationary), are the autoregressive parameters of the model, are the moving average parameters of the model, is the lag operator (i.e., ) and is white noise with zero mean and constant variance. The parameters of the ARIMA model are generally estimated using either the non-linear least squares method or the maximum likelihood estimation method. When the ARIMA model does not include the moving average component, its autoregressive parameters can be estimated using the ordinary least squares (OLS) method.
3.2.3. Traditional Machine Learning Models
This subsection provides the details of the traditional machine learning models used in this study, namely the support vector regression (SVR) and the gradient boosted trees (GBT).
- Support vector regression
SVR is the version of the support vector machine (SVM) model for regression problems. Considering is the input vector of the SVR model, its prediction is given by the following equation:
where is the prediction for the input vector , is the parameter vector of the SVR model, b is the bias of the SVR model and denotes dot product. Given a set of training samples , the training process of the SVR model (i.e., the process of estimating its parameter vector ) can be expressed by the following optimisation problem:
where is a hyperparameter of the SVR model that serves as a threshold. In particular, all predictions have to be within an range of the true predictions. In addition, slack variables may be introduced to the problem in order to allow prediction errors to flow out of the range boundaries. The above optimisation problem is usually solved using quadratic programming methods like the method of Lagrange multipliers.
- Gradient boosted trees
GBT is a model based on gradient boosting, a technique used for both regression and classification problems. A gradient-boosting-based model produces predictions as ensembles of multiple predictions generated by weak prediction models called weak learners. The weak learners are trained sequentially, each one correcting the errors made by its predecessor. In the case of GBT, the weak learners are decision trees. GBT aims to minimise an objective function that combines a convex loss function and a penalty term for model complexity. The training process proceeds iteratively, adding new trees that predict the residuals of errors of prior trees that are then combined with previous trees to make the final prediction. The simplified form of the objective function for the new tree is [68]:
where and are the first and second order gradient statistics of the loss function, which are defined as follows:
The second term of the objective function represents a regularization term in charge of seeking the appropriate final weights to avoid overfitting.
3.2.4. Deep Learning Models
This section provides the details of the deep learning models used in this study, namely a DNN architecture and an LSTM network architecture.
- Deep neural networks
A DNN is a typical feed-forward ANN, which consists of at least four layers of nodes, namely the input layer, the output layer and at least two hidden layers. Except for the input layer, all other layers contain neurons with arbitrary activation functions. These activation functions may be either linear or nonlinear, but in the majority of the cases, they are nonlinear (e.g., hyperbolic tangent function, logistic function, rectifier linear unit - ReLU, etc.). The input layer of the DNN just receives the input vectors. The DNNs are trained using the backpropagation technique in a supervised learning way. Finally, DNNs are considered as universal function approximators [69], and therefore they can be used for regression tasks. Moreover, as classification can be considered as a special case of regression in which the target variable is categorical, the DNNs can also be used for classification tasks.
- Long short-term memory networks
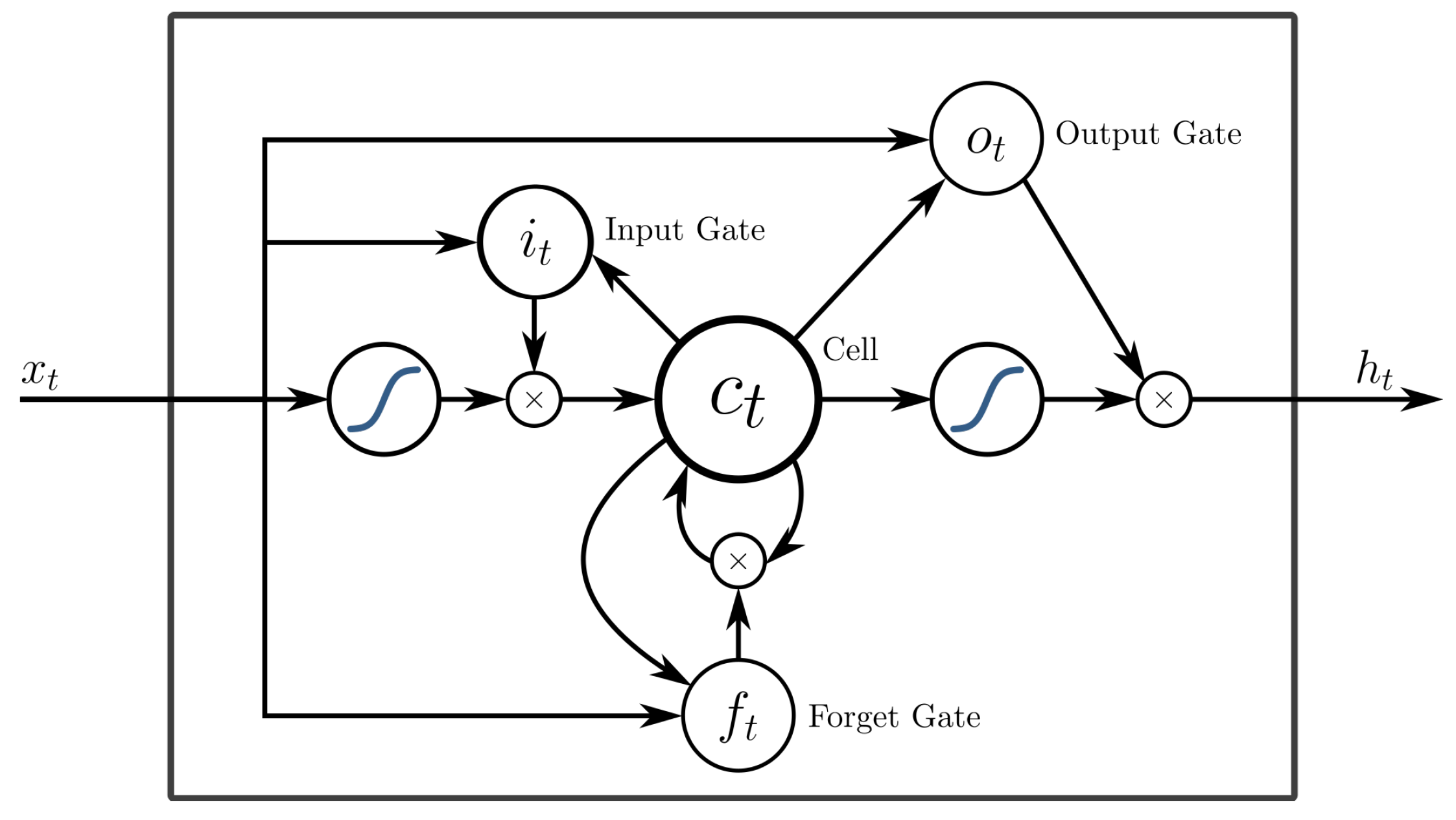
An LSTM network [70] is an RNN architecture which copes with the vanishing gradient problem (Error gradients tend to become very small or even vanished in very deep neural network models preventing the weights from changing values and thus the models to be trained) by allowing gradients to back-propagate unchanged through the network (however, an LSTM can still suffer from the exploding gradient problem). A common LSTM architecture consists of a cell, which is the memory of the LSTM unit, and three gates that control the information flow inside the LSTM. In particular, the input gate controls the extent to which new values flow into the cell, the forget gate controls the extent to which a value remains to the cell, and the output gate controls the extent to which the values in the cell are used to compute the output of the LSTM. An overview of a typical LSTM unit is presented in Figure 3.
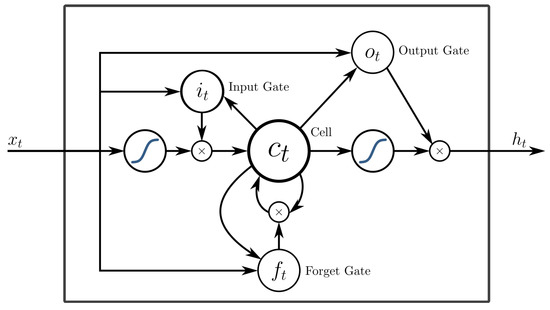
Figure 3.
LSTM unit.
A forward pass of information (i.e., of a vector of values ) through an LSTM network is described by the following equations:
where is the input vector of the LSTM network, are the activation vectors of the forget, input and output gates of the LSTM units, respectively, is the state vector of the cells of the LSTM units, and is the hidden state vector (or activation vector) of the LSTM units. Additionally, is the weight matrix of the input connections between the input vector and an LSTM element q, where q can be either the input gate i, the forget gate f, the output gate o or the cell c. Moreover, is the weight matrix of the recurrent connections between the hidden state vector (or more accurately ) and an LSTM element q. Finally, is the bias vector of an LSTM element q. The functions are activation functions. In particular, is the sigmoid activation function of the input, forget and output gates, is the hyperbolic tangent activation function of the cell and is the hyperbolic tangent activation function of the LSTM unit. The ⊙ symbol represents the Hadamard product (or element-wise product).
The initial state vectors and are usually set equal to the zero vector . The training process of an LSTM network lies in the estimation of the values of the and matrices and the vectors for all h units of the network, and it is usually performed using the backpropagation through time (BPTT) algorithm [71]. Unlike typical RNNs, the training process of an LSTM network does not suffer from the vanishing gradient problem, because while the error values are back-propagated to the input they remain unchanged inside the cells of the LSTM units and they do not exponentially degrade. In addition, as understood from the previous description, the cell of an LSTM unit decides what to store and what to leave using element-wise operations of sigmoids, which are differentiable and therefore suitable for backpropagation.
3.2.5. Hybrid Models
As presented in Section 2.3, there are a lot of different approaches for combining methods in order to build a hybrid model with increased forecasting performance. This section provides the details of the two hybrid models used in this study, namely a data-based model that utilises NWP and a combination of the presented analytical with a data-based model.
- Hybrid GBT mode—NWP-enriched GBT model
This model extends the GBT model described in Section 3.2.3 by fusing into it NWP historical data. As already mentioned, cloud coverage is the weather variable that predominantly affects PV power generation, and therefore cloud coverage data is utilized by this model. In particular, the historical cloud coverage data is initially organized as a set of time series, and then they are transformed into a set of training samples as described in Section 3.1.3. The main difference here is the fact that the existing training vector expands to a new vector , where is the cloud coverage vector.
- AI-Corrected NWP for Enriched Analytical PV Forecast
The AI-Corrected NWP for Enriched Analytical PV Forecast (AI-PVF) model is a combination of the analytical model described in Section 3.2.1 and an error correction method based on data obtained from the PV plant. The error is divided into clear sky error and cloud coverage error, a separation routinely found in the literature [14,40]. In the context of this study, clear sky error is associated with inaccuracies of the PV parameters, such as solar angles, installation angles and PV module/inverter types. This error exists at all times and it can be isolated on clear sky days.
On the other hand, the cloud coverage error exists only on cloudy days and it essentially represents the error introduced by inaccurate weather forecasts. Weather stochasticity makes it impossible to achieve cloud coverage forecast with satisfyingly high accuracy. By investigating the power generation data of the PV plant, it was found that the weather forecast errors follow specific patterns each time of the day. When those patterns are taken into consideration, the accuracy of the initial weather forecast is improved locally, resulting into a more accurate prediction of the PV power output.
In both cases, the error is corrected using the extremely randomised tree regression (EXTRA trees) [72] model. EXTRA trees is a computationally efficient ensemble method that builds unpruned trees with the classical top-down process. Its main distinctive characteristics from other tree-based ensemble methods are: (a) node splitting is done by choosing cut-points completely at random and (b) the algorithm uses the whole learning sample to grow the trees and not just a bootstrap replica. Concerning the feature extraction process, the PV power output derived from the analytical model along with NWP data and the solar azimuth/elevation angles are fed as features into the regression model. The actual PV power output is the model’s target variable. Thus, the models essentially learn the error patterns that occur under specific weather conditions (NWP forecasts) on each time of the day (sun angles). The AI-PVF method is thoroughly analysed in [73].
3.3. General Experimental Settings
This paper presents a comprehensive evaluation framework of different types of PV power generation forecasting models. In this section, the configuration details of this framework are provided. In this experimental framework, the main objective is to forecast the value of the PV power generation in multiple forecasting horizons ahead in time using all the aforementioned models, and then compare them in terms of forecasting accuracy. Five different forecasting horizons were evaluated, namely 1, 2, 4, 8 and 12 steps ahead. Given the 15-minute data granularity, these steps correspond to 15 min, 30 min, 1 h, 2 h and 3 h ahead of time. After the data has been transformed into a supervised-learning-compatible form (see Section 3.1.3) with and according to the chosen forecasting horizons, they are split into training, validation and test sets. In particular, of the data samples were used for training, for validation and for testing. Finally, since the problem investigated is essentially a multi-step time series forecasting problem, an appropriate forecasting strategy was selected, namely the direct strategy [74,75]. In this, each step is forecasted independently from each other. This means that if forecasts should be computed for k steps ahead in total, then k different models should be built. Hence, this strategy can lead to higher training times. It should be noted that, in all data-based model only the PV power generation values were used as inputs. Cloud coverage was only utilised for splitting the original dataset into different sub-datasets according to the forecasting period (e.g., spring).
3.3.1. Model Configuration and Hyperparameter Tuning
As mentioned above, of the available data was used for validation of the models, namely hyperparameter tuning. This process is required by the data-based and the hybrid models. Regarding the ARIMA, SVR and GBT models, the same hyperparameters have been selected for all data partitions. In particular, for all data partitions and forecasting horizons ARIMA(3, 1, 0) models were implemented (the term ‘models’ here refers to different instances of the ARIMA model based on the different data used for its training). Additionally, the hyperparameters of the SVR models were , , , and . Moreover, the optimal hyperparameters of the GBT model were for the maximum depth of the decision trees and for the number of trees used by the GBT. The hyperparameter tuning process for these models was performed using the grid search method. Regarding the AI-PVF approach, which utilises EXTRA trees for the error correction process, grid search was also conducted in order to find the optimal model hyperparameters. Through this process, the best parameters found were: , and .
In contrast with the above models, for each data partition and forecasting horizon different DNN and LSTM architectures, with different structure (e.g., number of neurons per hidden layer) and hyperparameters, were implemented. These configurations are presented in Table 1 ( stands for number of units, where units refer to either input units or computational neurons) for the DNNs and in Table 2 for the LSTMs. These configurations were estimated using the grid search method.

Table 1.
DNN architectures.

Table 2.
LSTM architectures.
The PV power generation forecasting models presented in this work were implemented using well-known Python statistical, machine learning and deep learning libraries. In particular, as already mentioned, the analytical model was implemented using PVLIB. The statistical models were implemented using the statsmodels library [76], SVR and AI-PVF using the scikit-learn library [77], the GBT models (i.e., both GBT and HGBT) using the XGBoost library [68], and the neural network architectures (i.e., DNN and LSTM) using the TensorFlow [78] and Keras [79] libraries.
3.3.2. Forecasting Evaluation Metrics
In order to evaluate the accuracy of the presented PV power generation forecasting models, three main error metrics were used, namely the mean absolute error (MAE), the mean absolute percentage error (MAPE) and the root mean squared error (RMSE). These metrics are defined by the following equations:
where the actual PV power generation value, is the predicted value and n is the total number of predictions. These metrics are widely used for evaluating the accuracy of PV power generation forecasting models. MAE and RMSE are expressed in the units of the predicted variable, in this case kilowatts (kW). On the other hand, MAPE is expressed as a percentage and so it is more easily interpretable.
In addition to these well-known metrics, a new metric, namely the weighted relative squared error (WRSE), is introduced. This metric is defined by the following equation:
where is the actual PV power generation value, is the predicted value and h is the forecasting horizon. WRSE expresses the relative forecasting error in terms of the magnitude of the evaluated PV power generation. It also takes into account the direction of the error and provides a uniform weighting for all errors. Finally, the metric disregards zero PV power generation values.
4. Results
The forecasting accuracy results of all PV power generation forecasting models studied in this work, for all forecasting horizons and data partitions, are presented in Table 3, Table 4, Table 5 and Table 6 for the spring, summer, autumn and winter period, respectively. In these tables, the models demonstrating the highest performance (in terms of MAPE) in each case are highlighted with their respective performance metrics in bold letters.

Table 3.
Forecasting accuracy results for the spring period.

Table 4.
Forecasting accuracy results for the summer period.

Table 5.
Forecasting accuracy results for the autumn period.

Table 6.
Forecasting accuracy results for the winter period.
4.1. Results According to Season
With regard to the spring season, in the sunny days subperiod, the AI-PVF model presents consistently the best forecasting accuracy across all forecasting horizons. On the contrary, in the cloudy days subperiod, there is no single model yielding the best performance across all forecasting horizons. In particular, the LSTM model has the best performance for 1 step ahead, the DNN model for 2, the HGBT model for 4 and the AI-PVF model for 8 and 12. It is important to highlight that, as expected [57], the forecasting errors in the cloudy days subperiod are much higher than the corresponding errors of the sunny days subperiod. For example, the MAPE value of the best performing model (i.e., AI-PVF) forecasting for 1 step ahead in the sunny days subperiod is , while the corresponding value of the best performing model (i.e., LSTM) in the cloudy days subperiod is . This is also demonstrated by the order of magnitude of the errors, where in the sunny days subperiod it is at the level of at most while in the cloudy days is at the level of .
Regarding the summer season, in the sunny days subperiod, the LSTM model presents the best forecasting accuracy for 1, 2 and 4 steps ahead, while the analytical model has the best accuracy for 8 and 12 steps ahead. However, this is not an outcome that can or should be generalised, because according to both available literature (e.g., [9,38]) and also, the hands-on experience of the authors, the plain analytical model almost never outperforms data-based or hybrid models when tested over an extended period of time. The reason for this result here may be the small size of the testing set, which occurred by the limitation of maximum cloud coverage and the size of the forecasting horizons, i.e., the more the forecasting horizon increases, the smaller the testing set becomes. Thus, the authors cannot support the statement that the analytical model outperforms any of the other forecasting models (and more importantly, the LSTM and the AI-PVF models). Therefore, this particular finding requires additional experimentation in order to reach a definite conclusion. In the cloudy days subperiod, the AI-PVF model presents the best forecasting accuracy across all forecasting horizons. Notably, in some cases, the forecasting error of the AI-PVF model is one or two orders of magnitude smaller compared to the other models (e.g., for 8 steps ahead). Additionally, as in the case of the spring period, the forecasting errors in the cloudy days subperiod are much higher than the corresponding errors of the sunny days subperiod.
With respect to the autumn season, in the sunny days subperiod, the analytical model yields the best forecasting accuracy for 1 and 2 steps ahead, the GBT model for 4 steps ahead and the AI-PVF model for 8 and 12 steps ahead. On the other hand, in the cloudy days period, the persistence model yields the best forecasting accuracy for 1 and 2 steps ahead and the analytical model for 4, 8 and 12 steps ahead. The fact that the naive persistence model outperforms all the other advanced models for two forecasting horizons is indicative of the inability of the advanced models to cope with the variations in the PV power generation variable introduced by the harsh autumn weather. Additionally, the analytical model that incorporates weather information (in the form NWP predictions) presents the best forecasting accuracy for the forecasting scenarios of 4, 8 and 12 steps ahead. In this season, the days in the sunny days subperiod when the cloud coverage is below are very few, which leads to small available datasets for training the data-based models and the HGBT model. This fact can explain the very low forecasting performance of both the data-based models and the HGBT model, and especially that of the traditional statistical model ARIMA and the traditional machine learning model SVR. The AI-PVF model is more robust in this case due to its error-correction capabilities. On the other hand, the high cloud coverage values during the autumn’s cloudy days lead to an intermittent pattern for the PV power generation variable, which cannot easily be captured even by the complex nonlinear DL models. The integration of the PV installation’s characteristics along with weather information in the DL models may possibly help them to better capture the complex distribution of the PV power generation variable during the autumn’s cloudy days.
Finally, in the sunny days subperiod of the winter season, the GBT model presents the best forecasting accuracy for 1 step ahead, the HGBT model for 2 steps ahead and the analytical model for 4, 8 and 12 steps ahead. On the other hand, in the cloudy days subperiod, the GBT model is still the best performing model for 1-step ahead forecasting, while the analytical model in the best for the other forecasting horizons. In this season, the problems reported for the autumn season have been greatly amplified. In particular, for the sunny day subperiod, the forecasting error (in terms of MAPE) of most of the models becomes greater than after the forecasting horizon of 1 step ahead. Only the analytical and the AI-PVF model with the error-correction capabilities maintain their performance at relatively acceptable levels. The problem escalates in the cloudy days subperiod when most of the models yield forecasting error greater than after the 1-step ahead forecasting scenario. This finding is consistent across all data-based models (statistical, ML or DL) which can support the argument that in cases with highly intermittent pattern of the PV power generation variable the data-based models that utilize only past values of the variable in order to predict its future values, cannot be considered as accurate and cannot be used for forecasting tasks in real RES systems. One way to mitigate this behaviour is to integrate to the models the PV installation’s characteristics along with weather information, as in the case of the analytical model.
In order to examine if the forecasting accuracy results of the several models differ from each other in a statistically significant way, we performed statistical tests on the residuals of the best performing models from each model category (i.e., analytical, data-based and hybrid) for all data partitions and forecasting horizons using the Kruskal-Wallis statistical test. This non-parametric test is used for estimating if two or more independent samples of equal or different sample sizes are drawn from the same distribution with similar mean and variance (null hypothesis). The results indicate that, in the majority of cases, the null hypothesis can be rejected. Hence, the forecasting accuracy of the best performing model in each case is different from the accuracy of the best performing models of the remaining categories in a statistically significant way. Such a result is illustrated in Table 7, which contains the results of the Kruskal–Wallis statistical test for the best performing models for the sunny days subperiod of the summer season and the cloudy days subperiod of the winter season for all forecasting horizons. In all cases apart from one, the null hypothesis is rejected (highlighted by green color). The best performing model in each case is highlighted by bold letters.

Table 7.
Results of Kruskal-Wallis statistical test performed for the sunny days subperiod of the summer season and the cloudy days subperiod of the winter season for all forecasting horizons. The rejection of the null hypothesis is highlighted by green color, while its acceptance by red. The best performing model in each case in highlighted by bold letters.
4.2. Generalized Results
Moving forward to generalize some of the aforementioned findings, it is observed that the AI-PVF model consistently outperforms all others in spring sunny days and summer cloudy days subperiods. Although it is not very clear as to why this occurs in these two particular scenarios, there are similarities that could potentially lead to a reasonable justification. Both subperiods have similar ambient conditions in terms of external temperature and humidity. In that regard, and taking account the high dependency of PV power generation on temperature, it would be safe to assume that the hybrid model that takes both physical characteristics and historical performance into account, presents the best results in close to optimal temperature conditions (not too hot nor too cold).
Another interesting finding is that the data-based models outperform the analytical and the hybrid models in very short-term forecasting scenarios, namely in 1 step ahead. From the second step ahead, the integration of weather information to the models (i.e., hybrid approaches) seems to improve the overall performance. As reported in the relevant literature [44,49], the data-based models are very precise in very short-term PV power generation forecasting scenarios.
Regarding the long-term forecasting scenarios (i.e., 12 steps or 3 hours ahead), no generalized finding can be fully justified given the incidental nature of best performance of the analytical model in the summer sunny days subperiod for 8 and 12 steps ahead forecasts. Nonetheless, given the consistent best performance of the AI-PVF model in similar spring sunny days subperiod and the relative similar performance during the summer sunny days, with reservation, the authors support that the AI-PVF model exhibits overall good behaviour. However this does not apply to PV installations and systems that have existed for long periods of time, as it does not take into account the material degradation and the physical corruption of the various physical components. As such, for old PV installations this finding might not be applicable. However, the AI-PVF model takes into account this factor and also seems to have good performance in long-term scenarios.
An almost expected outcome is that out of all data-based models, the LSTM architectures present the best and most consistent forecasting results for forecasting horizons of 2 steps-ahead onwards in all examined scenarios. This result can be attributed to the ability of the LSTM models to capture the complex nonlinear long-term dependencies in the PV power generation time series, and exploit them in order to produce accurate predictions [48,62]. What is not so expected concerning the behaviour of the data-based models is that the integration of weather data does not improve their accuracy [42]. For example, the GBT and the HGBT models present quite close performance across all forecasting horizons and for most of the data partitions.
Another interesting finding is the the abruptly decrease of the forecasting accuracy in the autumn season in sunny days subperiod. On the opposite side, in the cloudy days subperiod there is a stable high forecasting error. This result is frequently discussed in literature as a barrier towards accurate PV power generation forecasting [39,44,56,57]. Additionally, another interesting outcome refers to the winter season. In particular, for all forecasting horizons and models, the forecasting errors in the cloudy days subperiod are approximately twice the forecasting errors of the sunny days subperiod.
From the perspective of the several weather-based data partitions, a first finding is that the models in cloudy days in summer present smaller forecasting errors than in cloudy days in spring across all forecasting horizons. This behaviour can be justified by the fact that cloudy days in spring are more often and with higher cloud coverage than the respective ones in summer for the examined test data. Average cloud coverage and ratio of days with more than cloud coverage in spring is and , whereas in summer and , respectively.
Another interesting result is that in spring cloudy days and in summer clear sky days a different model has the best performance for each forecasting horizon. This is a rather difficult finding to explain. However, it seems that there are some similar patterns. Up to 2 steps ahead, it is evident that the data-based models present the best results. However, from 4 step onwards, it appears that hybrid models (i.e., models that take into account weather forecast) start outperforming the data-based models. Finally, from 8 steps ahead and beyond, the analytical model and hybrid ones present better results compared to the data-based models.
Out of all the scenarios examined, the best forecasting accuracy achieved per metric is observed on sunny days (expected), but not always on the same season (not expected), as shown below:
- MAE: kWh - GBT - 8 steps ahead - Sunny Days - Summer
- MAPE: - Hybrid - 12 steps ahead - Sunny Days - Spring
- RMSE: kWh - GBT - 4 steps ahead - Sunny Days - Summer
- WRSE: - Hybrid - 12 steps ahead - Sunny Days - Spring
Based on the above findings, it would appear that the examined models provide more accurate results when predicting long-term rather than short-term time horizons. When examined the cloudy days however, the results are slightly different:
- MAE: kWh - Hybrid - 12 steps ahead - Cloudy Days - Summer
- MAPE: - Hybrid - 8 steps ahead - Cloudy Days - Summer
- RMSE: kWh - Hybrid - 12 steps ahead - Cloudy Days - Summer
- WRSE: - Hybrid - 8 steps ahead - Cloudy Days - Summer
It is evident that for cloudy days the best performance in all metrics is for long-term predictions and through the AI-PVF model. Interestingly enough, there is an opposite pattern between clear sky days and cloudy days. In the former, absolute error metrics (i.e., MAE and RMSE) have good results in less than 12 steps ahead, with relative ones (i.e., MAPE and WRSE) having their good ones on 12 steps ahead. The exact opposite is observed for the cloudy days. Optimal results are extracted for the relative metrics for 8 steps ahead, whereas for the absolute ones for 12 steps ahead.
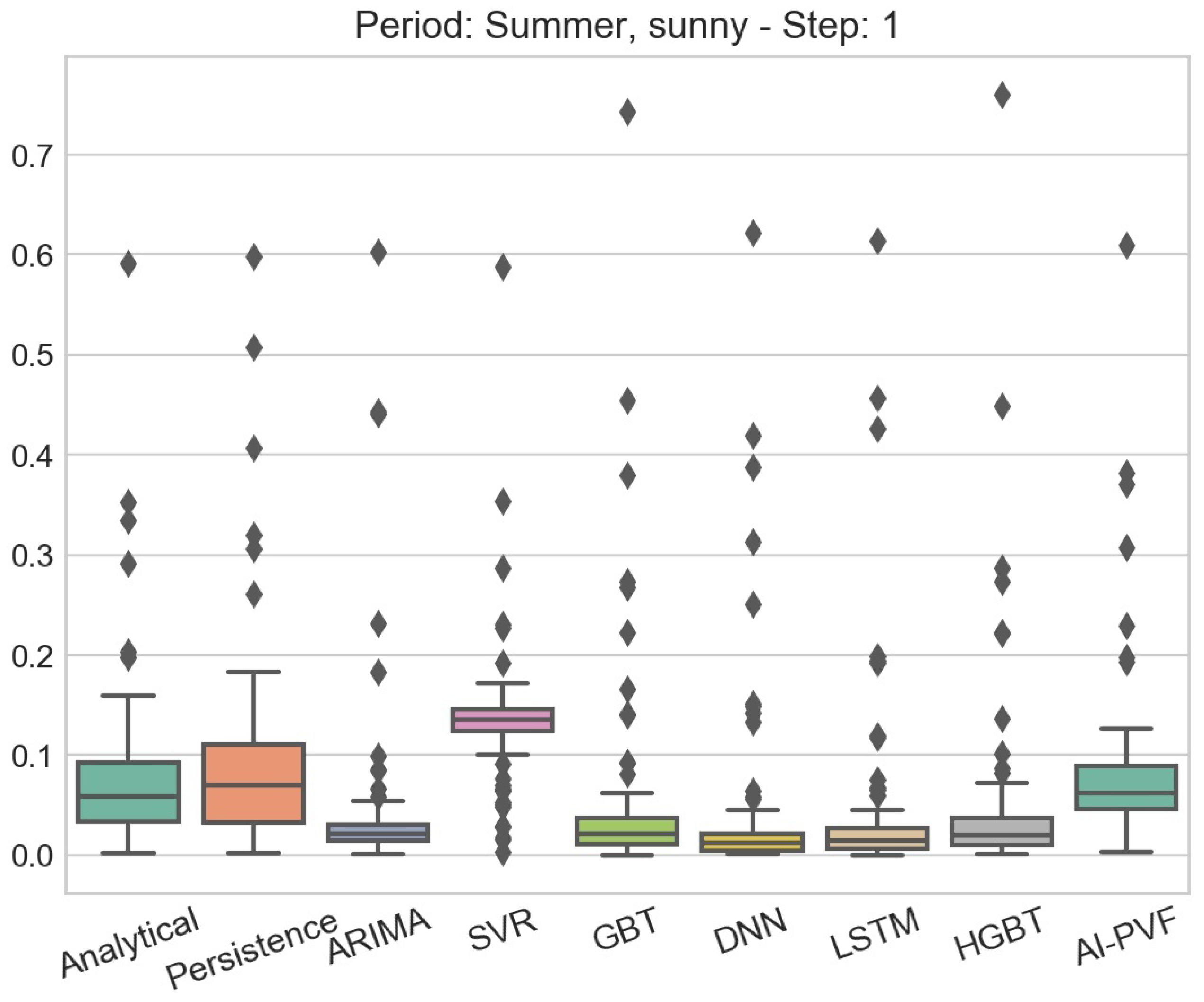
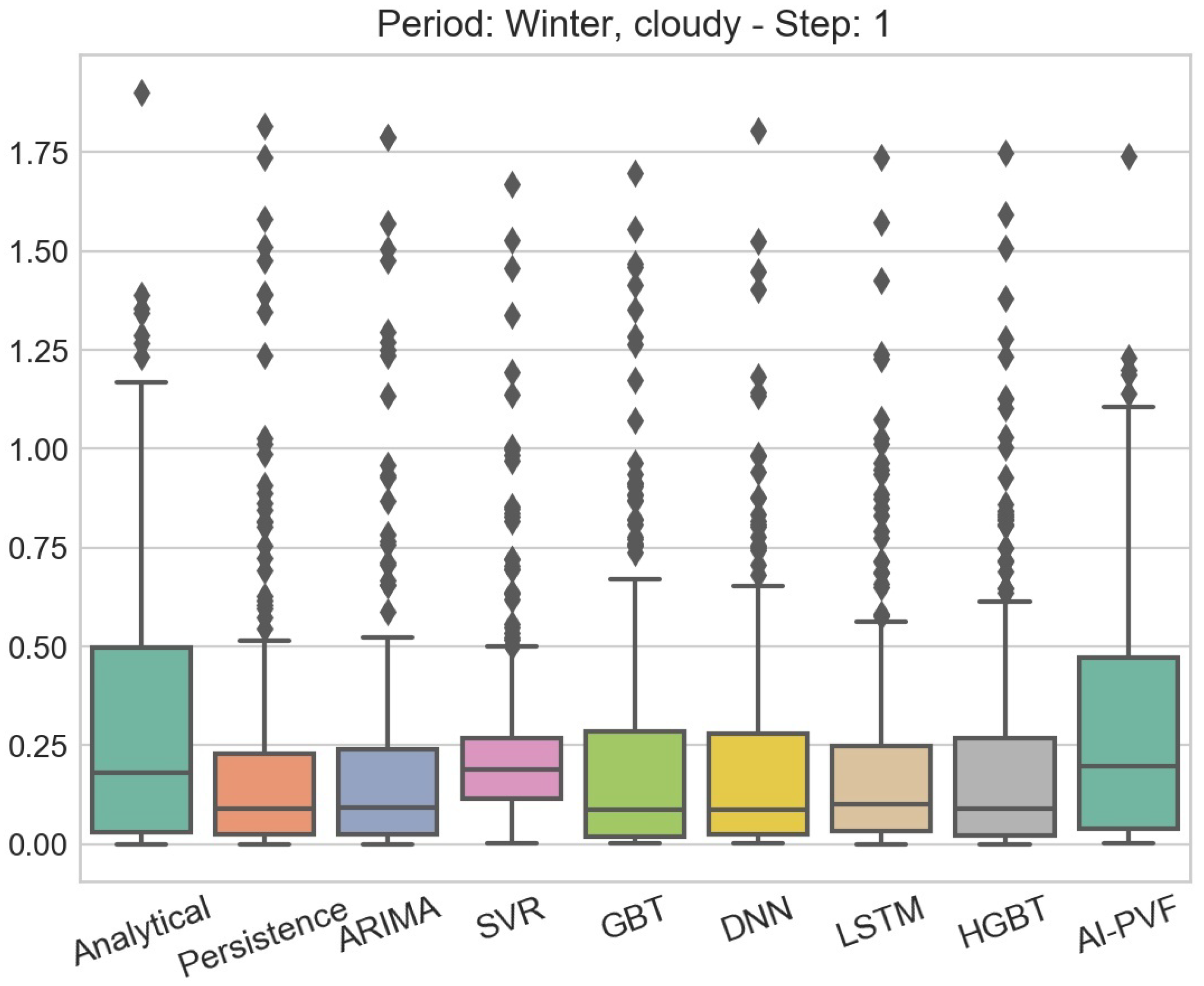
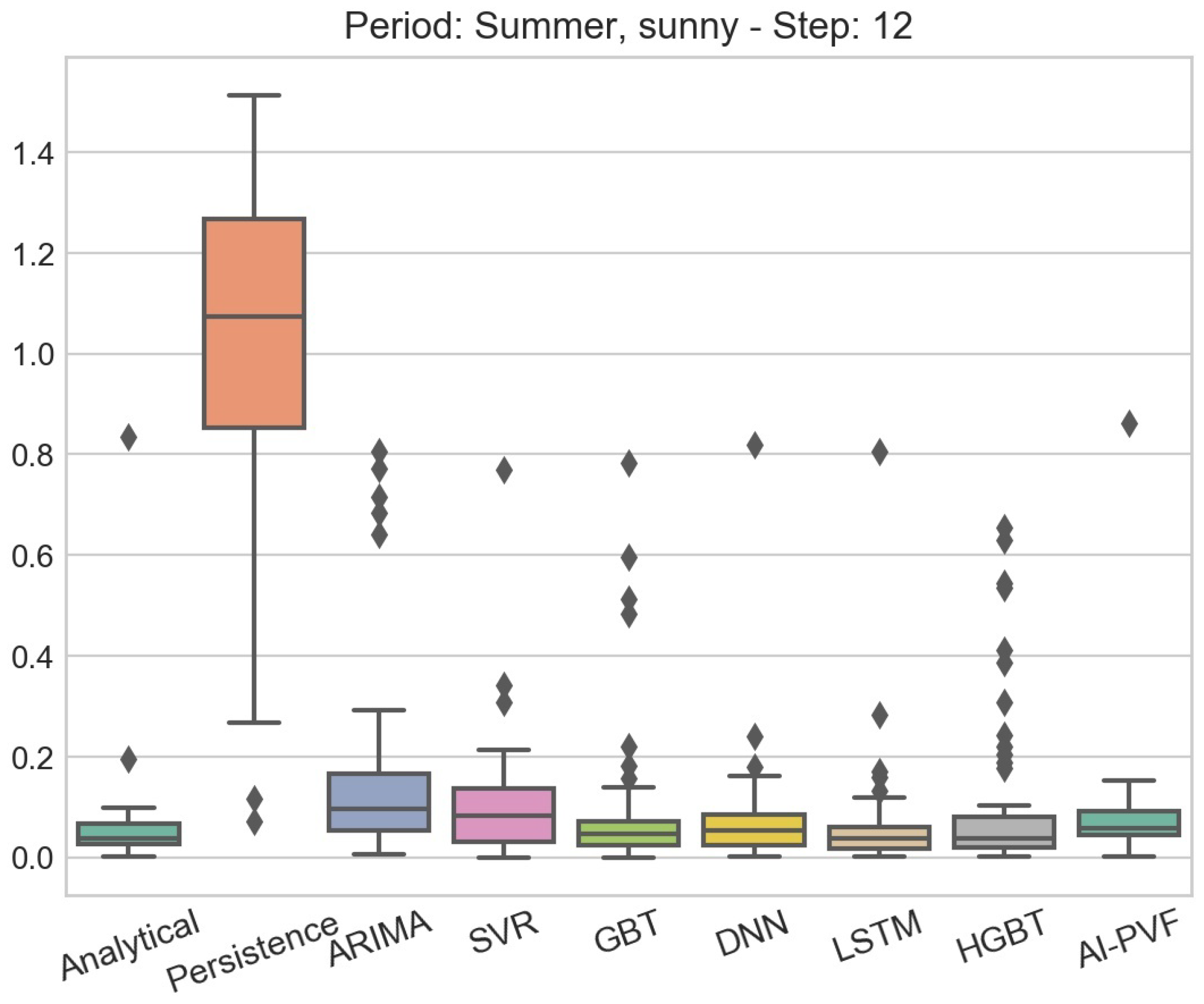
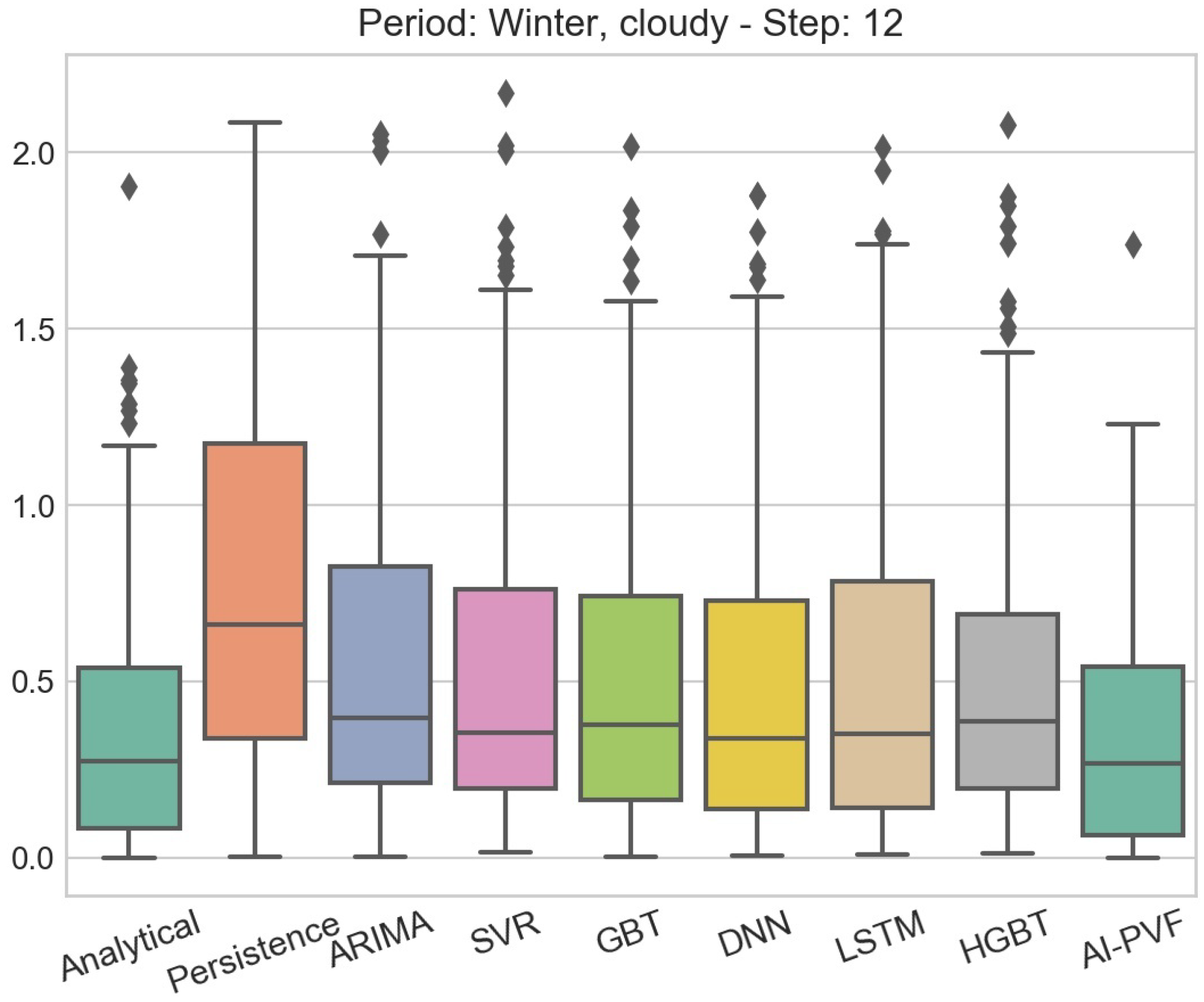
Throughout the present study, the need for further investigation of how weather data affect the performance of PV power generation forecasting models, is evident. Although errors for clear sky days remain quite low (i.e., for all examined horizons and models, the maximum average errors are below kWh, , kWh and for MAE, MAPE, RMSE and WRSE, respectively) this is not the case for cloudy days (i.e., for all examined horizons and models, the maximum average errors are below kWh, , kWh and for MAE, MAPE, RMSE and WRSE, respectively). This effect of the weather conditions on the accuracy of the PV power generation forecasting models is highlighted in the boxplots presented in Figure 4, Figure 5, Figure 6 and Figure 7, in which the distributions of the residuals of the several forecasting models for the two most extreme cases in terms of weather conditions are presented. In particular, Figure 4 presents the the residuals’ distributions of all forecasting models in the sunny days subperiod of the summer season for 1 step ahead, while Figure 5 presents the corresponding residuals’ distributions of the models for the same forecasting horizon in the cloudy days subperiod of the winter season. It is evident, by both the height of the boxes and the range of the outliers, that most of the models face difficulties when trying to predict the PV power generation under severe weather conditions. The same result applies for larger forecasting horizons, as shown in Figure 6 and Figure 7, which present the residuals’ distribution for 12 steps ahead in the sunny days subperiod of the summer season and the cloudy days subperiod of the winter season, respectively. Hence, it is apparent that there is a great need for more accurate models on diverse weather conditions. Hybrid or DL models that integrate both PV installation’s characteristics and NWP, may hold the key for accurate and generic PV power generation forecasting.
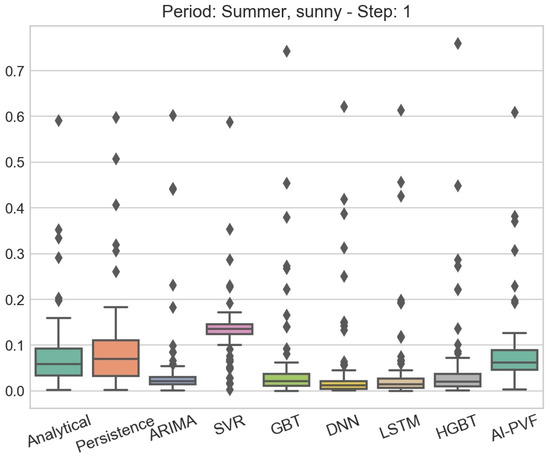
Figure 4.
Boxplot of residuals for all PV power generation forecasting models. The data partition examined in this case is the sunny days subperiod of the summer season and the forecasting horizon is 1 step ahead.
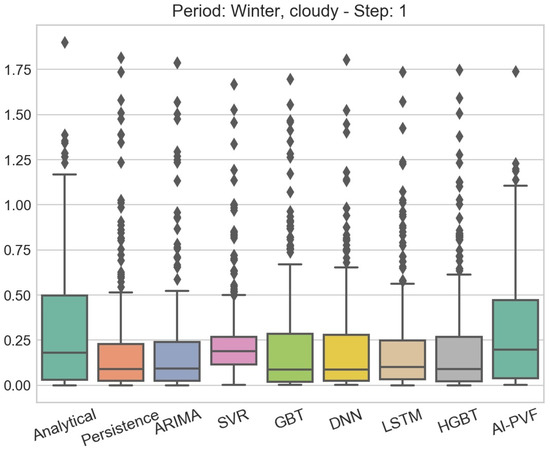
Figure 5.
Boxplot of residuals for all PV power generation forecasting models. The data partition examined in this case is the cloudy days subperiod of the winter season and the forecasting horizon is 1 step ahead.
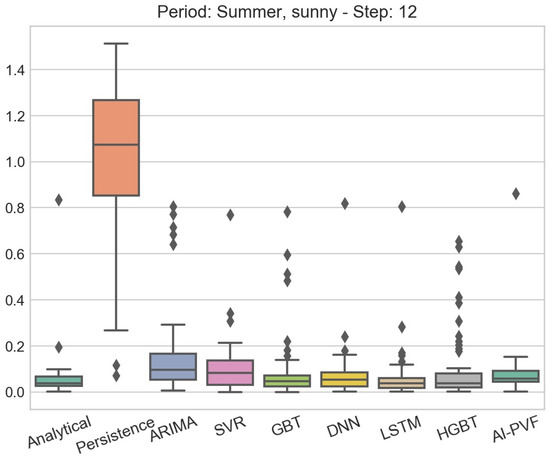
Figure 6.
Boxplot of residuals for all PV power generation forecasting models. The data partition examined in this case is the sunny days subperiod of the summer season and the forecasting horizon is 12 steps ahead.
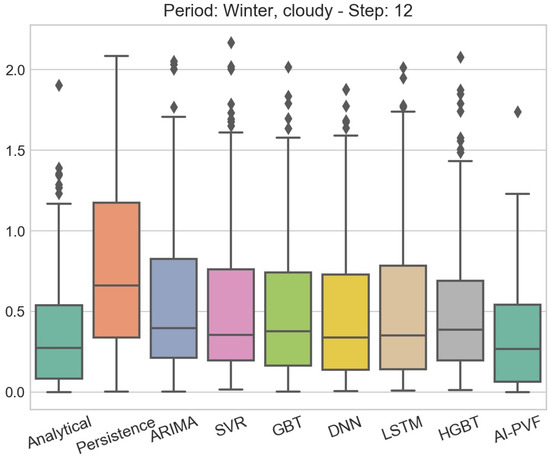
Figure 7.
Boxplot of residuals for all PV power generation forecasting models. The data partition examined in this case is the cloudy days subperiod of the winter season and the forecasting horizon is 12 steps ahead.
Finally, the results provided by different evaluation metrics are not consistent. There are cases where MAE and RMSE are reduced, while MAPE and WRSE are increased, and vise versa. This highlights the need to identify the exact evaluation metric under which such studies need to be performed towards presenting meaningful and comparable results. The most troubling part is that even though it would be expected to have more consistent results along all metrics in clear sky conditions, the most ambiguous ones have instead been observed. This could be due to the smaller errors observed compared to those of cloudy days. In particular, RMSE seems to be the metric that deviates the most from all other three, highlighting that this metric may not be suitable for such evaluation frameworks.
5. Conclusions
This paper presents a comprehensive evaluation framework for the comparison of different PV power generation forecasting models on the same forecasting conditions. In particular, a dataset has been assembled, containing PV power generation values from a real-world PV installation, along with weather data gathered from a well-known online weather data aggregation services. The experiments have specific characteristics in terms of the objectives, forecasting horizons, model configuration processes and evaluation metrics. More importantly, the authors designed and implemented a set of 9 PV power generation forecasting models from the three different categories identified in the relevant literature, namely analytical, data-based and hybrid. Specifically, one analytical, six data-based and two hybrid models were designed, implemented and evaluated. The extracted findings are considered useful for both researchers who design new PV power generation forecasting models and managers of PV installations who want to employ the best forecasting models for each situation in order to optimize the overall power generation and delivery pipeline. Future directions of our research include the evaluation of the models on bigger datasets (e.g., from larger PV installations), the design and implementation of new forecasting models, and the integration of the implemented models into more generic PV power management pipelines.
Author Contributions
For this manuscript the individual contribution is as follows: Conceptualisation, A.I.S., G.X., N.B., C.T., A.D.B., L.Z. and A.C.T.; Data curation, G.X. and N.B.; Formal analysis, A.I.S., G.X., N.B.s, C.T., A.D.B., L.Z. and A.C.T.; Funding acquisition, D.I., D.K. and D.T.; Investigation, G.X. and A.D.B.; Methodology, A.I.S., G.X., N.B., C.T., A.D.B., L.Z. and A.C.T.; Project administration, D.I., D.K. and D.T.; Resources, D.T.; Software, A.I.S., G.X., N.B. and C.T.; Supervision, A.I.S. and A.C.T.; Validation, A.I.S., G.X., N.B., C.T., A.D.B., L.Z. and A.C.T.; Writing—original draft, A.I.S., G.X., N.B., C.T., A.D.B., L.Z. and A.C.T.; Writing—review & editing, A.I.S., A.D.B. and A.C.T. All authors have read and agreed to the published version of the manuscript.
Funding
This work is partially funded by the European Union’s Horizon 2020 Innovation Action Programme through the RENAISSANCE project under Grant Agreement No. 824342 and by the European Union’s Horizon 2020 Research and Innovation Action Programme through the DELTA project under Grant Agreement No. 773960.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| Wp | watt-peak |
| DNN | Deep Neural Network |
| LSTM | Long Short-Term Memory |
| PV | Photovoltaic |
| NWP | Numerical Weather Prediction |
| RMSE | Root Mean Square Error |
| MAPE | Mean Absolute Percentage Error |
| WRSE | Weighted Relative Square Error |
| RES | Renewable Energy Source |
| DER | Distributed Energy Resource |
| ML | Machine Learning |
| NOCT | Nominal Operating Cell Temperature |
| ANN | Artificial Neural Networks |
| SVR | Support Vector Regression |
| ARIMA | Autoregressive Integrated Moving Average |
| DL | Deep Learning |
| ANFIS | Adaptive Neuro-Fuzzy Inference Systems |
| RBFN | Radial Basis Function Network |
| CNN | Convolutional Neural Networks |
| RNN | Recurrent Neural Networks |
| SVM | Support Vector Machines |
| kNN | k-Nearest Neighbors |
| DIH | Digital Innovation Hubs |
| CERTH | Centre for Research and Technology Hellas |
| API | Application Programming Interface |
| UTC | Coordinated Universal Time |
| OLS | Ordinary Least Squares |
| GBT | Gradient Boosted Trees |
| ReLU | Rectified Linear Unit |
| EXTRA | Extremely Randomised Tree Regression |
| kW | Kilowatts |
| GW | Gigawatt |
| TWh | Terawatt-hours |
| MW | Megawatt |
| Wp | Watt-peak |
| AI-PVF | AI-Corrected NWP for Enriched Analytical PV Forecast Hellas |
| PDE | Partial Differential Equation |
| ELM | Extreme Learning Machines |
| SOM | Self-Organizing Map |
| GA | Genetic Algorithms |
| MAE | Mean Absolute Error |
References
- Taylor, A.J.W. Low Carbon Energy Observatory Photovoltaics Technology Market Report 2018—Public Version, EUR 29935 EN, European Commission. 2019. Available online: https://publications.jrc.ec.europa.eu/repository/bitstream/JRC118307/jrc118307_1.pdf (accessed on 10 September 2020).
- Jäger-Waldau, A. PV Status Report 2019, EUR 29938EN, Publications Office of the European Union, Luxembourg. 2019. Available online: https://ec.europa.eu/jrc/sites/jrcsh/files/kjna29938enn_1.pdf (accessed on 10 September 2020).
- European Commission. Energy Roadmap 2050. 2012. Available online: https://ec.europa.eu/energy/sites/ener/files/documents/2012_energy_roadmap_2050_en_0.pdf (accessed on 24 August 2020).
- Qi, B.; Hasan, K.N.; Milanović, J.V. Identification of Critical Parameters Affecting Voltage and Angular Stability Considering Load-Renewable Generation Correlations. IEEE Trans. Power Syst. 2019, 34, 2859–2869. [Google Scholar] [CrossRef] [Green Version]
- IRENA. Future of Solar Photovoltaic: Deployment, Investment, Technology, Grid Integration and Socio-Economic Aspects (A Global Energy Transformation: Paper). 2019. Available online: https://www.irena.org/-/media/Files/IRENA/Agency/Publication/2019/Nov/IRENA_Future_of_Solar_PV_2019.pdf (accessed on 24 August 2020).
- Mellit, A.; Massi Pavan, A.; Ogliari, E.; Leva, S.; Lughi, V. Advanced Methods for Photovoltaic Output Power Forecasting: A Review. Appl. Sci. 2020, 10, 487. [Google Scholar] [CrossRef] [Green Version]
- Han, Y.; Wang, N.; Ma, M.; Zhou, H.; Dai, S.; Zhu, H. A PV power interval forecasting based on seasonal model and nonparametric estimation algorithm. Sol. Energy 2019, 184, 515–526. [Google Scholar] [CrossRef]
- Wang, K.; Qi, X.; Liu, H. A comparison of day-ahead photovoltaic power forecasting models based on deep learning neural network. Appl. Energy 2019, 251, 113315. [Google Scholar] [CrossRef]
- Antonanzas, J.; Osorio, N.; Escobar, R.; Urraca, R.; Martinez-de Pison, F.J.; Antonanzas-Torres, F. Review of photovoltaic power forecasting. Sol. Energy 2016, 136, 78–111. [Google Scholar] [CrossRef]
- Graditi, G.; Ferlito, S.; Adinolfi, G. Comparison of Photovoltaic plant power production prediction methods using a large measured dataset. Renew. Energy 2016, 90, 513–519. [Google Scholar] [CrossRef]
- Das, U.K.; Tey, K.S.; Seyedmahmoudian, M.; Mekhilef, S.; Idris, M.Y.I.; Van Deventer, W.; Horan, B.; Stojcevski, A. Forecasting of photovoltaic power generation and model optimization: A review. Renew. Sustain. Energy Rev. 2018, 81, 912–928. [Google Scholar] [CrossRef]
- Akhter, M.N.; Mekhilef, S.; Mokhlis, H.; Shah, N.M. Review on forecasting of photovoltaic power generation based on machine learning and metaheuristic techniques. IET Renew. Power Gener. 2019, 13, 1009–1023. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Lei, Z.; Zhang, X.; Zhou, B.; Peng, J. A review of deep learning for renewable energy forecasting. Energy Convers. Manag. 2019, 198, 111799. [Google Scholar] [CrossRef]
- Shi, J.; Lee, W.J.; Liu, Y.; Yang, Y.; Wang, P. Forecasting power output of photovoltaic systems based on weather classification and support vector machines. IEEE Trans. Ind. Appl. 2012, 48, 1064–1069. [Google Scholar] [CrossRef]
- Alessandrini, S.; Delle Monache, L.; Sperati, S.; Cervone, G. An analog ensemble for short-term probabilistic solar power forecast. Appl. Energy 2015, 157, 95–110. [Google Scholar] [CrossRef] [Green Version]
- Lingwei, Z.; Zhaokun, L.; Junnan, S.; Chenxi, W. Very short-term maximum Lyapunov exponent forecasting tool for distributed photovoltaic output. Appl. Energy 2018, 229, 1128–1139. [Google Scholar]
- Pelland, S.; Galanis, G.; Kallos, G. Solar and photovoltaic forecasting through post-processing of the Global Environmental Multiscale numerical weather prediction model. Prog. Photovoltaics Res. Appl. 2013, 21, 284–296. [Google Scholar] [CrossRef]
- Masa-Bote, D.; Castillo-Cagigal, M.; Matallanas, E.; Caamaño-Martín, E.; Gutiérrez, A.; Monasterio-Huelín, F.; Jiménez-Leube, J. Improving photovoltaics grid integration through short time forecasting and self-consumption. Appl. Energy 2014, 125, 103–113. [Google Scholar] [CrossRef] [Green Version]
- Dolara, A.; Grimaccia, F.; Leva, S.; Mussetta, M.; Ogliari, E. A physical hybrid artificial neural network for short term forecasting of PV plant power output. Energies 2015, 8, 1138–1153. [Google Scholar] [CrossRef] [Green Version]
- Celik, A.N.; Acikgoz, N. Modelling and experimental verification of the operating current of mono-crystalline photovoltaic modules using four- and five-parameter models. Appl. Energy 2007, 84, 1–15. [Google Scholar] [CrossRef]
- Tossa, A.K.; Soro, Y.; Azoumah, Y.; Yamegueu, D. A new approach to estimate the performance and energy productivity of photovoltaic modules in real operating conditions. Sol. Energy 2014, 110, 543–560. [Google Scholar] [CrossRef]
- Ma, T.; Yang, H.; Lu, L. Development of a model to simulate the performance characteristics of crystalline silicon photovoltaic modules/strings/arrays. Sol. Energy 2014, 100, 31–41. [Google Scholar] [CrossRef]
- Ciulla, G.; Brano, V.L.; Di Dio, V.; Cipriani, G. A comparison of different one-diode models for the representation of I–V characteristic of a PV cell. Renew. Sustain. Energy Rev. 2014, 32, 684–696. [Google Scholar] [CrossRef]
- Brano, V.L.; Orioli, A.; Ciulla, G.; Di Gangi, A. An improved five-parameter model for photovoltaic modules. Sol. Energy Mater. Sol. Cells 2010, 94, 1358–1370. [Google Scholar] [CrossRef]
- Fuentes, M. A simplified thermal model of photovoltaic modules. In Sandia National Laboratories Report, SAND85-0330; Sandia National Labs.: Albuquerque, NM, USA, 1985. [Google Scholar]
- International Electrotechnical Commission. Terrestrial Photovoltaic (PV) Modules—Design Qualification and Type Approva—Part 1: Test Requirements; Standard IEC 61215-1:2016; International Organization for Standardization: Geneva, Switzerland, 2016. [Google Scholar]
- Toledo, C.; López-Vicente, R.; Abad, J.; Urbina, A. Thermal performance of PV modules as building elements: Analysis under real operating conditions of different technologies. Energy Build. 2020, 223, 110087. [Google Scholar] [CrossRef]
- De Leone, R.; Pietrini, M.; Giovannelli, A. Photovoltaic energy production forecast using support vector regression. Neural Comput. Appl. 2015, 26, 1955–1962. [Google Scholar] [CrossRef] [Green Version]
- Stengel, M.; Lindskog, M.; Undén, P.; Gustafsson, N. The impact of cloud-affected IR radiances on forecast accuracy of a limited-area NWP model. Q. J. R. Meteorol. Soc. 2013, 139, 2081–2096. [Google Scholar] [CrossRef]
- Voyant, C.; Motte, F.; Notton, G.; Fouilloy, A.; Nivet, M.L.; Duchaud, J.L. Prediction intervals for global solar irradiation forecasting using regression trees methods. Renew. Energy 2018, 126, 332–340. [Google Scholar] [CrossRef] [Green Version]
- Perez, R.; Lorenz, E.; Pelland, S.; Beauharnois, M.; Van Knowe, G.; Hemker, K., Jr.; Heinemann, D.; Remund, J.; Müller, S.C.; Traunmüller, W.; et al. Comparison of numerical weather prediction solar irradiance forecasts in the US, Canada and Europe. Sol. Energy 2013, 94, 305–326. [Google Scholar] [CrossRef]
- Pierro, M.; Bucci, F.; De Felice, M.; Maggioni, E.; Moser, D.; Perotto, A.; Spada, F.; Cornaro, C. Multi-Model Ensemble for day ahead prediction of photovoltaic power generation. Sol. Energy 2016, 134, 132–146. [Google Scholar] [CrossRef]
- Zhang, Y.; Beaudin, M.; Taheri, R.; Zareipour, H.; Wood, D. Day-ahead power output forecasting for small-scale solar photovoltaic electricity generators. IEEE Trans. Smart Grid 2015, 6, 2253–2262. [Google Scholar] [CrossRef]
- Al-Dahidi, S.; Ayadi, O.; Adeeb, J.; Alrbai, M.; Qawasmeh, B.R. Extreme learning machines for solar photovoltaic power predictions. Energies 2018, 11, 2725. [Google Scholar] [CrossRef] [Green Version]
- Chen, C.; Duan, S.; Cai, T.; Liu, B. Online 24-h solar power forecasting based on weather type classification using artificial neural network. Sol. Energy 2011, 85, 2856–2870. [Google Scholar] [CrossRef]
- Das, U.K.; Tey, K.S.; Seyedmahmoudian, M.; Idris, I.; Yamani, M.; Mekhilef, S.; Horan, B.; Stojcevski, A. SVR-based model to forecast PV power generation under different weather conditions. Energies 2017, 10, 876. [Google Scholar] [CrossRef]
- Tahasin, S.; Chenhui, S.; Hui, W.; Jingjing, L.; Xi, Z.; Mingyang, L. Iterative multi-task learning for time-series modeling of solar panel PV outputs. Appl. Energy 2018, 212, 654–662. [Google Scholar]
- De Giorgi, M.G.; Congedo, P.M.; Malvoni, M. Photovoltaic power forecasting using statistical methods: Impact of weather data. IET Sci. Meas. Technol. 2014, 8, 90–97. [Google Scholar] [CrossRef]
- Ogliari, E.; Grimaccia, F.; Leva, S.; Mussetta, M. Hybrid predictive models for accurate forecasting in PV systems. Energies 2013, 6, 1918–1929. [Google Scholar] [CrossRef] [Green Version]
- Yang, H.T.; Huang, C.M.; Huang, Y.C.; Pai, Y.S. A weather-based hybrid method for 1-day ahead hourly forecasting of PV power output. IEEE Trans. Sustain. Energy 2014, 5, 917–926. [Google Scholar] [CrossRef]
- Landelius, T.; Andersson, S.; Abrahamsson, R. Modelling and forecasting PV production in the absence of behind-the-meter measurements. Prog. Photovoltaics Res. Appl. 2019, 27, 990–998. [Google Scholar] [CrossRef] [Green Version]
- Lee, W.; Kim, K.; Park, J.; Kim, J.; Kim, Y. Forecasting Solar Power Using Long-Short Term Memory and Convolutional Neural Networks. IEEE Access 2018, 6, 73068–73080. [Google Scholar] [CrossRef]
- Qing, X.; Niu, Y. Hourly day-ahead solar irradiance prediction using weather forecasts by LSTM. Energy 2018, 148, 461–468. [Google Scholar] [CrossRef]
- Zhou, H.; Zhang, Y.; Yang, L.; Liu, Q.; Yan, K.; Du, Y. Short-Term Photovoltaic Power Forecasting Based on Long Short Term Memory Neural Network and Attention Mechanism. IEEE Access 2019, 7, 78063–78074. [Google Scholar] [CrossRef]
- Colak, I.; Yesilbudak, M.; Genc, N.; Bayindir, R. Multi-period Prediction of Solar Radiation Using ARMA and ARIMA Models. In Proceedings of the 2015 IEEE 14th International Conference on Machine Learning and Applications (ICMLA), Miami, FL, USA, 9–11 December 2015; pp. 1045–1049. [Google Scholar]
- Raza, M.Q.; Nadarajah, M.; Ekanayake, C. On recent advances in PV output power forecast. Sol. Energy 2016, 136, 125–144. [Google Scholar] [CrossRef]
- Fernandez-Jimenez, L.A.; Muñoz-Jimenez, A.; Falces, A.; Mendoza-Villena, M.; Garcia-Garrido, E.; Lara-Santillan, P.M.; Zorzano-Alba, E.; Zorzano-Santamaria, P.J. Short-term power forecasting system for photovoltaic plants. Renew. Energy 2012, 44, 311–317. [Google Scholar] [CrossRef]
- Han, S.; Qiao, Y.H.; Yan, J.; Liu, Y.Q.; Li, L.; Wang, Z. Mid-to-long term wind and photovoltaic power generation prediction based on copula function and long short term memory network. Appl. Energy 2019, 239, 181–191. [Google Scholar] [CrossRef]
- Li, G.; Wang, H.; Zhang, S.; Xin, J.; Liu, H. Recurrent Neural Networks Based Photovoltaic Power Forecasting Approach. 2019, pp. 1–17. Available online: https://www.researchgate.net/publication/334157021_Recurrent_Neural_Networks_Based_Photovoltaic_Power_Forecasting_Approach (accessed on 16 November 2020).
- Qian, L.; Wu, X.X. Estimate and characterize PV power at demand-side hybrid system. Appl. Energy 2018, 218, 66–77. [Google Scholar]
- Yanting, L.; Yong, H.; Yan, S.; Shu, L. Forecasting the daily power output of a grid-connected photovoltaic system based on multivariate adaptive regression splines. Appl. Energy 2016, 180, 392–401. [Google Scholar]
- Liu, H.; Cocea, M. Traditional Machine Learning. In Granular Computing Based Machine Learning: A Big Data Processing Approach; Springer International Publishing: Cham, Switzerland, 2018; pp. 11–22. [Google Scholar]
- Barbieri, F.; Rajakaruna, S.; Ghosh, A. Very short-term photovoltaic power forecasting with cloud modeling: A review. Renew. Sustain. Energy Rev. 2017, 75, 242–263. [Google Scholar] [CrossRef] [Green Version]
- Mosaico, G.; Saviozzi, M. A hybrid methodology for the day-ahead PV forecasting exploiting a Clear Sky Model or Artificial Neural Networks. In Proceedings of the IEEE EUROCON 2019-18th International Conference on Smart Technologies, Novi Sad, Serbia, 1–4 July 2019; pp. 1–6. [Google Scholar]
- Sideratos, G.; Hatziargyriou, N.D. A distributed memory RBF-based model for variable generation forecasting. Int. J. Electr. Power Energy Syst. 2020, 120, 106041. [Google Scholar] [CrossRef]
- Nespoli, A.; Ogliari, E.; Leva, S.; Pavan, A.M.; Mellit, A.; Lughi, V.; Dolara, A. Day-ahead photovoltaic forecasting: A comparison of the most effective techniques. Energies 2019, 12, 1621. [Google Scholar] [CrossRef] [Green Version]
- Gao, M.; Li, J.; Hong, F.; Long, D. Day-ahead power forecasting in a large-scale photovoltaic plant based on weather classification using LSTM. Energy 2019, 187, 115838. [Google Scholar] [CrossRef]
- Abdel-Nasser, M.; Mahmoud, K. Accurate photovoltaic power forecasting models using deep LSTM-RNN. Neural Comput. Appl. 2019, 31, 2727–2740. [Google Scholar] [CrossRef]
- Ouyang, W.; Yu, K.M.; Sodsong, N.; Chuang, K.H. Short-term solar PV forecasting based on recurrent neural network and clustering. In Proceedings of the 2019 International Conference on Image and Video Processing, and Artificial Intelligence, International Society for Optics and Photonics, Shanghai, China, 23–25 August 2019; Volume 11321, p. 113212U. [Google Scholar]
- Ghimire, S.; Deo, R.C.; Raj, N.; Mi, J. Deep solar radiation forecasting with convolutional neural network and long short-term memory network algorithms. Appl. Energy 2019, 253, 113541. [Google Scholar] [CrossRef]
- Kim, K.; Lee, D. Photovoltaic (PV) Power Output Prediction Using LSTM Based Deep Learning. Adv. Nat. Appl. Sci. 2019, 13, 25–31. [Google Scholar]
- De, V. Photovoltaic Power Forecasting using LSTM on Limited Dataset. In Proceedings of the 2018 IEEE Innovative Smart Grid Technologies—Asia (ISGT Asia), Singapore, 22–25 May 2018; pp. 710–715. [Google Scholar]
- Bracale, A.; Caramia, P.; Carpinelli, G.; Di Fazio, A.R.; Ferruzzi, G. A Bayesian method for short-term probabilistic forecasting of photovoltaic generation in smart grid operation and control. Energies 2013, 6, 733–747. [Google Scholar] [CrossRef] [Green Version]
- Luyao, L.; Yi, Z.; Dongliang, C.; Jiyang, X.; Zhanyu, M.; Qie, S.; Hongyi, Y.; Ronald, W. Prediction of short-term PV power output and uncertainty analysis. Appl. Energy 2018, 228, 700–711. [Google Scholar]
- Holmgren, W.; Hansen, C.; Mikofski, M. pvlib python: A python package for modeling solar energy systems. J. Open Source Softw. 2018, 3, 884. [Google Scholar] [CrossRef] [Green Version]
- King, D.L.; Kratochvil, J.A.; Boyson, W.E. Photovoltaic Array Performance Model; United States Department of Energy, Sandia National Labs.: Albuquerque, NM, USA, 2004.
- Box, G.E.P.; Jenkins, G. Time Series Analysis, Forecasting and Control; Holden-Day, Inc.: San Francisco, CA, USA, 1990. [Google Scholar]
- Chen, T.; Guestrin, C. XGBoost. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016. [Google Scholar] [CrossRef] [Green Version]
- Cybenko, G. Approximation by superpositions of a sigmoidal function. Math. Control Signals Syst. (MCSS) 1989, 2, 303–314. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural. Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Williams, R.J.; Zipser, D. Gradient-Based Learning Algorithms for Recurrent Networks and Their Computational Complexity. In Backpropagation: Theory, Architectures, and Applications; Psychology Press, Taylor & Francis Group: London, UK, 1995; pp. 433–486. [Google Scholar]
- Geurts, P.; Ernst, D.; Wehenkel, L. Extremely randomized trees. Mach. Learn. 2006, 63, 3–42. [Google Scholar] [CrossRef] [Green Version]
- Timplalexis, C.; Bezas, N.; Bintoudi, A.; Zyglakis, L.; Pavlopoulos, V.; Tsolakis, A.; Krinidis, S.; Tzovaras, D. In Proceedings of the 12th Mediterranean Conference on Power Generation, Transmission, Distribution and Energy Conversion, Dubrovnik, Croatia, 12–15 December 2018; Available online: https://www.iti.gr/iti/publications/MedPower_2020_01.html (accessed on 25 August 2020).
- Sorjamaa, A.; Hao, J.; Reyhani, N.; Ji, Y.; Lendasse, A. Methodology for long-term prediction of time series. Neurocomputing 2007, 70, 286–2869. [Google Scholar] [CrossRef] [Green Version]
- Hamzacebi, C.; Akay, D.; Kutay, F. Comparison of direct and iterative artificial neural network forecast approaches in multi-periodic time series forecasting. Expert Syst. Appl. 2009, 36, 3839–3844. [Google Scholar] [CrossRef]
- Seabold, S.; Perktold, J. statsmodels: Econometric and statistical modeling with python. In Proceedings of the 9th Python in Science Conference, Austin, TX, USA, 28 June–3 July 2010. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. TensorFlow: Large-Scale Machine Learning on Heterogeneous Distributed Systems. arXiv 2016, arXiv:1603.04467. [Google Scholar]
- Chollet, F. Keras. 2015. Available online: https://keras.io (accessed on 10 October 2020).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).