Determination of the Theoretical and Actual Working Volume of a Hydraulic Motor

Abstract

A new methodology of determination of the theoretical and actual working volume of a hydraulic motor based on the characteristics of the delivered flow rate into hydraulic motor vs. the rotational speed at a constant pressure drop in the working chambers is described in this paper. A new method of describing the delivered flow rate into a motor per one shaft revolution as a nonlinear function of the pressure drop in the motor working chamber is proposed. The influence of the flowmeter location in the measurement system on the result of the theoretical and actual working volume calculation is described. It is shown that, in order to assess the energy losses (volumetric and mechanical) in the motor, the actual working volume must be a polynomial function (third degree) of its pressure drop in the working chambers. The result of the experimental tests of the satellite hydraulic motor confirmed the validity of the proposed method. The result of the calculation of the theoretical working volume of the motor according to the proposed method was compared with the results of calculations according to known methods.

1. Introduction

A hydraulic motor is a principal component of a hydraulic system, and the steady-state behavior of this motor plays an important role in the overall performance of the hydraulic system. The knowledge of the basic characteristics of the motor, such as its volumetric losses efficiency and mechanical-pressure efficiency, is essential for both users and designers of a hydraulic system. So far, the so-called theoretical working volume q_t has been used to assess the losses in the motor and its partial efficiency, that is:

(a)

the volumetric efficiency:

$${\eta }_v=\frac{q_t·n}{q_t·n+Q_v}$$

(1)

(b)

the hydraulic-mechanical efficiency:

$${\eta }_{hm}=2\pi ·\frac{M}{q_t·\Delta p}$$

(2)

where:

• Q_v—the volumetric losses in the motor;
• n—rotational speed of the motor shaft;
• M—load of the motor;
• Δp—pressure drop measured in the motor ports.

The literature describing the method of determining the theoretical working volume of a displacement machine is relatively scarce. The first method of determining the theoretical working volume was described by Wilson (1950), Schlosser and Hilbrands in 1963 [1,2,3,4]. This method was improved and described by Toet in 1970 [5]. The same method, but supplemented, was described by Toet once again in 2019 [6]. Nevertheless, Balawender’s method from 1974 is commonly used in research and development centers. This method is described in detail in [7,8]. Nevertheless, it is Toet’s method from 1970 that is referred to or used in the other available literature [9,10,11,12]. Toet’s and Balawender’s methods are described in the next section.

The simplest of all the known methods of determining the theoretical working volume is presented in the ISO standard [13] (also described in the next section).

Another original method is proposed by Kim in [14]. Kim has attempted to calculate the theoretical working volume by a flow rate analysis for a single displacement chamber of the pump. This method becomes problematic to use when dealing with multiple working chambers, i.e., in real pumps or hydraulic motors. Therefore, this method will not be described in detail.

The value of q_t is constant in the whole range of the motor operating parameters, that is, the speed n and the pressure drop Δp measured in the motor ports. In practice, the theoretical working volume q_t is determined in a simplified way. The location of a flow meter (in the high-pressure line or in the low-pressure line of the motor) is not taken into account and it is assumed that the pressure drop Δp in a motor is equal to the pressure drop Δp_i in the working mechanism of this motor. Hence, the influence of liquid compressibility is neglected, as is the pressure drop Δp_ich in the internal channels of the motor.

The theoretical working volume q_t is not the same as the geometric working volume q_g. The q_t is obtained from experiment data (for Δp tending to zero), but q_g is mainly obtained (or calculated) from drawing documentations of the motor. The mathematical formulas for describing the geometric working volume q_g are different for various types of positive displacement machines [9,15]. In addition, these formulas are derived with some simplifications for some types of pumps and motors. For example, the simplifications result in an error of up to 3% for gear machines [7,15].

In addition, in the working mechanism of positive displacement machines, there are looseness and machining errors of the working mechanism components, assembly errors, changes in the machine temperature, etc. Furthermore, the pressure drop Δp in the hydraulic motor is mainly a result of its torque load. In effect, the working chambers are resiliently deformed. Thus, in a loaded motor, the geometric working volume q_g is different from the actual working volume q_r. Therefore, the geometric volume q_g is not recommended for use to assess losses in positive displacement machines. It would be better to assume that the actual working volume q_r assesses the volumetric and mechanical losses in a hydraulic motor. Then, q_r should be expressed as a function of the pressure drop Δp_i in the working chambers of the motor. Furthermore, the theoretical working volume q_t and the geometric working volume q_r should be determined taking into account the liquid compressibility. In addition to the precise determination of volumetric and mechanical losses with this approach, it is possible to more precisely assess the clearances of the components in the working mechanism of a hydraulic motor. Therefore, the development of a new methodology of determination of the theoretical working volume q_t and the actual working volume q_r of a hydraulic motor is appropriate and justified from the scientific and cognitive point of view. For this purpose, described in the following sections of the article are:

(a)

known methods to determine the theoretical working volume;

(b)

the proposed method of determining the theoretical q_t and actual working volume q_r (taking into account the effect of the flow meter position in the measurement system, the compressibility of liquid, and the pressure drop Δp_ich in the internal channel of a motor).

In this article the practical implementation of new methods is also presented. In order to confirm the correctness of the proposed new method of determining the q_t and q_r, experimental tests of a hydraulic satellite motor were carried out, described and compared with Toet’s and Balawender’s methods.

2. Known Method to Determine the Theoretical Working Volume

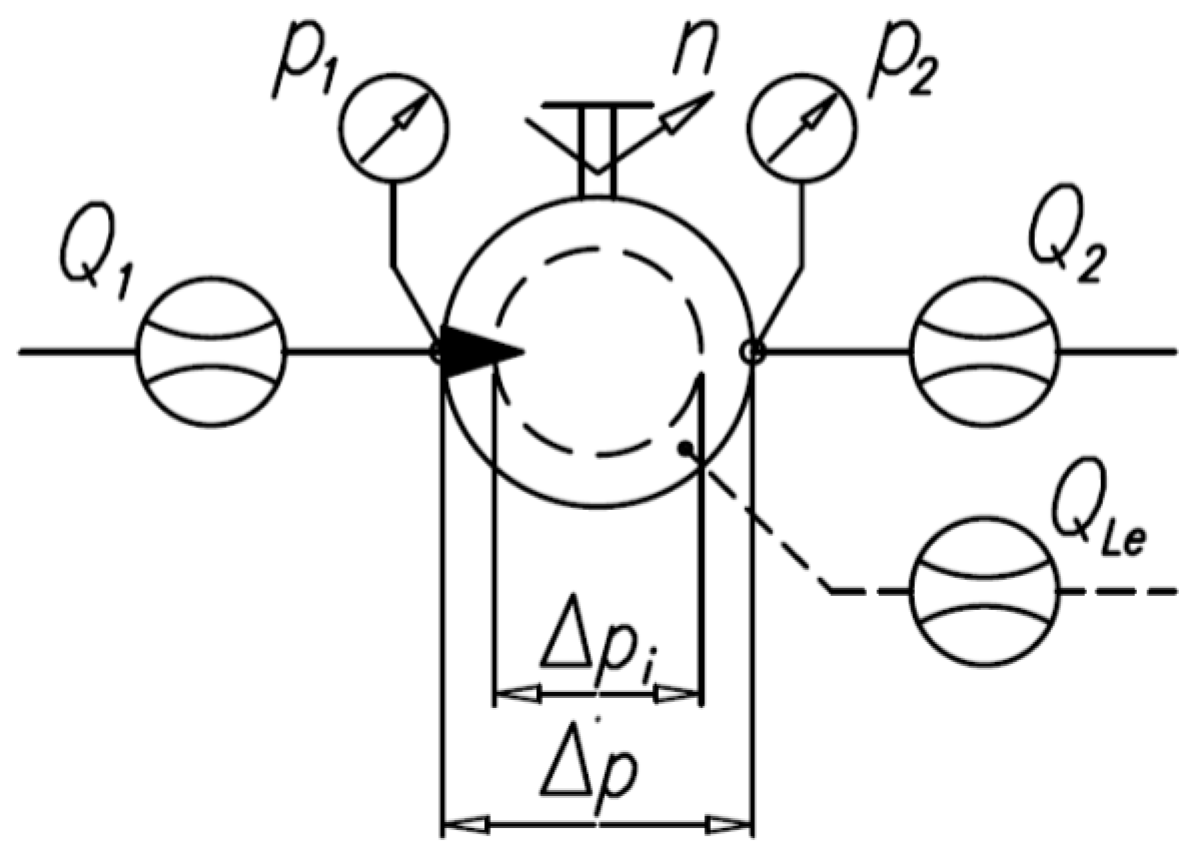
2.1. Flow Rate in Hydraulic Motor

Balawender and Toet have developed a practical method of determining the theoretical working volume q_t of a hydraulic motor by using measurements of the liquid flow rate in the motor (Figure 1). According to them, making separate measurements for determining q_t would unnecessarily extend the time of research and increase the costs [5,6,7].

According to Toet [6], the hydraulic motor input flow rate Q₁ is the volume flow delivered to the inlet port calculated at the inlet pressure p₁ and it uses the fluid temperature T₁ at the inlet port. Furthermore, the volume flow Q₁ through an averaging unit with a pressure difference Δp at an inlet temperature T₁ and for a particular hydraulic oil is [6]:

$$Q_1=Q_g+Q_u+Q_C+Q_L$$

(3)

where:

• Q_g—the positive displacement component:

$$Q_g=\underset{q_{g\left(\Delta p,T_1\right)}}{\underbrace{q_{g\left(\Delta p=0,T_1\right)}·\left(1+K_1·\Delta p\right)}}·n$$

(4)

• Q_u—the liquid lifted in the gaps:

$$Q_u=q_{u\left(\Delta p=0,T_1\right)}·\left(n+K_2·\Delta p\right)$$

(5)

• q_u—the liquid flow rate Q_u per one revolution of the shaft at Δp = 0;
• Q_C—the expansion/compression component (taken into account when the flow meter is located at the low-pressure side and the liquid is not aerated):

$$Q_C=q_{g\left(\Delta p=0,T_1\right)}·\left(\frac{{\rho }_o}{\rho }-1\right)·n$$

(6)

$$\frac{{\rho }_o}{\rho }-1=K_3·\Delta p-K_4·{\left(\Delta p\right)}^2+K_5·{\left(\Delta p\right)}^3$$

(7)

• Q_L—leakage in the working mechanism gaps;
• ρ_o—density at atmospheric pressure;
• ρ—density of liquid at pressure p;
• K₁, K₂, K₃, K₄, K₅—constants.

According to Balawender, the flow rate in a hydraulic motor should be described by the following formulas [7,8]:

$$Q_1=Q_g+Q_u+Q_k+Q_{C,1}+Q_{Li,1}+Q_{Le,1}$$

(8)

$$Q_2=Q_g+Q_u+Q_k+Q_{C,2}+Q_{Li,2}+Q_{Le,2}$$

(9)

where [7,8]:

$$Q_g=\underset{q_{g\left(\Delta p_i,T_1\right)}}{\underbrace{q_{g\left(\Delta p_i=0,T_1\right)}·\left(1\pm K_6·\Delta p_i\right)}}·\left(1+3·\alpha ·\Delta T\right)·n$$

(10)

$$Q_u=q_{u\left(\Delta p_i=0,T_1\right)}·\left(1\pm K_7·\Delta p_i\right)·n$$

(11)

• Q_k—the liquid flow rate caused by the cyclic elastic deformation of the working chambers [7,8]:

$$Q_k=\underset{q_{k\left(\Delta p_i,T_1\right)}}{\underbrace{K_8·\Delta p_i·q_{g\left(\Delta p_1=0,T_1\right)}}}·n$$

(12)

• Q_C,1—the flow rate caused by liquid compressibility at the moment of the working chamber transition from the emptying cycle to the filling cycle [7,8]:

$$Q_{C,1}=\underset{q_{c,1}}{\underbrace{\lambda ·\frac{\Delta p_i}{K_{s\left(\Delta p_i\right)}}·q_{g(\Delta p_i>0,T_1)}}}·n$$

(13)

• Q_C,2—the flow rate caused by liquid compressibility at the moment of the working chamber transition from the filling cycle to the emptying cycle [7,8]:

$$Q_{C,2}=\underset{q_{c,2}}{\underbrace{\left(1+\lambda \right)·\frac{\Delta p_i}{K_{s\left(\Delta p_i\right)}}·q_{g(\Delta p_i>0,T_1)}}}·n$$

(14)

• Q_Li,1 and Q_Li,2—the leakage from the high-pressure working chambers to the low-pressure working chambers (internal leakage) [7,8]:

$$Q_{Li,1}+Q_{Li,2}=Q_{Li}$$

(15)

• Q_Le,1 and Q_Le,2—the leakage from the working chambers on the outside of the motor (external leakage from the motor body by the third hose) and [7,8]:

$$Q_{Le,1}+Q_{Le,2}=Q_{Le}$$

(16)

• Δp_i—the pressure drop in the motor working chambers;
• α—the coefficient of linear expansion of materials of the motor working mechanism;
• ΔT—the increase in the motor temperature;
• K₆, K₇, K₈—constants;
• K_s—the isentropic secant modulus of liquid compressibility;
• λ—the relative harmful volume.

2.2. Theoretical Working Volume from the Method Defined in ISO 8426

The method defined in ISO 8426 uses measurement of the flow rate Q₁ at different speeds n at a constant pressure and a constant input fluid temperature. The theoretical working volume can be determined by [13]:

$$q_t=\frac{Q_{1\left(2\right)}-Q_{1\left(1\right)}}{n_{\left(2\right)}-n_{\left(1\right)}}$$

(17)

The q_t determined according to the above formula changes while measuring along multiple pressure differences. This makes the theoretical working volume calculation inaccurate.

2.3. Toet’s Method

After analysis of the partial derivative of the flow Q₁ (expressed by the Formula (1)) after the speed n ($\frac{\partial Q_1}{\partial n}$), Toet concluded that the theoretical working volume q_t of the motor should be described in the following form [6]:

$$q_t={\left(\frac{\partial Q_1}{\partial n}\right)}_{\left(\Delta p=0, T_1\right)}={\left(\frac{Q_1}{n}\right)}_{\left(\Delta p=0, T_1\right)}=q_{g\left(\Delta p=0, T_1\right)}+q_{u\left(\Delta p=0, T_1\right)}$$

(18)

where q_u is the volume of liquid per one revolution of the shaft caused by the relative velocities between two surfaces of clearances in the working mechanism.

According to Toet [6]:

(a)

q_t is independent of n and Δp;

(b)

besides $q_{g\left(\Delta p=0, T_1\right)}$ and $q_{u\left(\Delta p=0, T_1\right)}$ the other effects (not expressed by formulas) have influence on the leakage Q_L;

(c)

there is no way for separation of q_g and q_u;

(d)

if the volumetric efficiency is greater than 100% then only the q_g was applied (omitting the q_u);

(e)

for some types of positive displacement machines (screw pumps and motors), where q_g is very precisely determinable and q_u ≈ 0 is $q_{g\left(\Delta p=0, T_1\right)}$ ≈ q_t (for the same of T₁).

According to Toet, the flow rate Q in a hydraulic motor is described by the linear function [6]:

$$Q_{\left(\Delta p=const\right)}=A_i·n+B_i$$

(19)

where

$$A_i={\left(\frac{\partial Q}{\partial n}\right)}_{\left(\Delta p=const\right)}$$

(20)

and B is the leakage flow in the motor for Δp = 0. The characteristics of Q for different constant values of Δp are shown in Figure 2. However, the relationship

$$A=a·\Delta p+q_t$$

(21)

is determined from the values A₁, A₂, A₃,…, A_n (Figure 3). Hence, q_t is the theoretical working volume of the hydraulic motor supplied with oil at temperature T₁ measured in the inflow port of the motor [6].

Furthermore, Toet claims that the linear relationship between A and Δp is recommended with the correlation coefficient of at least 0.9. Nonlinear fitting is recommended for smaller values of correlation coefficient [6].

2.4. Balawender’s Method

In 1974, Balawender noticed the shortcomings of Toet’s method and described them in [7]. Balawender’s notes are still valid, although they were omitted by Toet in [6]. Balawender claimed that the method indicated by Toet is inaccurate, because [7]:

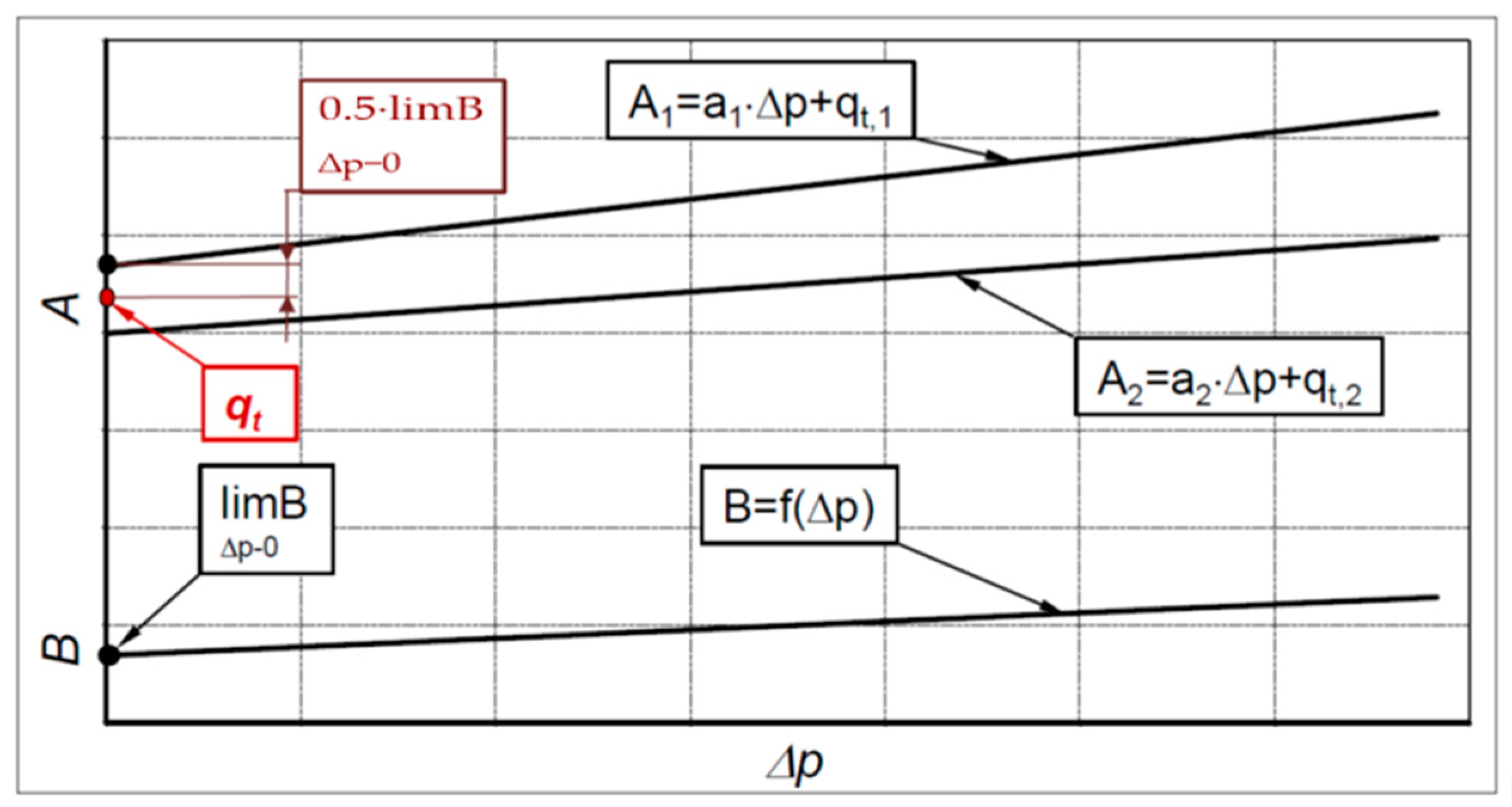
• The notation of the theoretical working volume given by Equation (16) is incorrect as it suggests a measurement at Δp = 0. In real conditions, the motor does not run at Δp = 0;
• In fact, in order to determine the theoretical working volume q_t the limit values of the working volume for the internal pressure drop Δp_i going to zero should be taken into account;
• The function $\frac{\partial Q}{\partial n}$ can be unspecified in the mathematical sense at Δp = 0 due to the unspecified displacements of the motor working mechanism elements;
• The flow component caused by the compressibility of liquid was incorrectly interpreted.

Balawender concluded that the theoretical working volume q_t of the motor should be described in the following form [7,8]:

$$q_t=\underset{\Delta p_i\to 0}{\lim }{q}_{g\left(\Delta p_i\right)}+\underset{\Delta p_i\to 0}{\lim }{q}_{u\left(\Delta p_i\right)}$$

(22)

Balawender, similarly to Toet, claims that:

(a)

qt is independent of n and Δp;

(b)

the temperature of liquid can have influence on qt,

(c)

there is no way for of qg and qu.

Furthermore, Balawender simplifies the problem by taking Δp_i ≈ Δp_. The linear relationship between A and Δp and between B and Δp is recommended (Figure 4) [7,8].

According to Balawender, the theoretical working volume is described as [7,8]:

$$q_{t,1}=\underset{\Delta p\to 0}{\lim }{A}_{1\left(\Delta p\right)}-\frac{1}{2}·\underset{\Delta p\to 0}{\lim }{Q}_{Le\left(\Delta p\right)}$$

(23)

or

$$q_{t,2}=\underset{\Delta p\to 0}{\lim }{A}_{2\left(\Delta p\right)}+\frac{1}{2}·\underset{\Delta p\to 0}{\lim }{Q}_{Le\left(\Delta p\right)}$$

(24)

Finally, the theoretical working volume should be calculated as [7,8]:

$$q_{t,1}=\frac{q_{t,1}+q_{t,2}}{2}$$

(25)

Balawender recommends to test the motor in the following speed range:

$$n_{max}\le 3·n_{min}$$

(26)

where the n_min is the minimum speed at which the motor can work stably. The limitation of the maximum speed results from the assumption Δp_i ≈ Δp.

3. New Method of Determining the Theoretical and Actual Working Volume

3.1. The Flow Rate Caused by Liquid Lifting in Gaps

Both Toet and Balawender point to the component Q_u of the flow rate. According to them Q_u has an impact on the theoretical working volume q_t. However, it should be noted that this does not apply to all displacement machines. For example, in the working mechanism of piston machines, the walls of the gaps move with a reciprocating movement. However, in satellite and gear machines, they move in a rotational movement. Thus, in piston machines the direction of flow Q_u in the gap between the piston and the cylinder varies with the direction of the piston movement. In satellite machines, the satellite rotates and there is a flow from the low-pressure chamber into the high-pressure chamber on one side, and there is also a flow of the same value but in the opposite direction on the other side. Thus, the flow Q_u should not occur in the overall balance [16]. Nevertheless, it is proposed to include the flow per one revolution of shaft q_u in the theoretical working volume according to Formula (22).

3.2. The Actual Working Volume q_r

During the tests on a prototype of an axial piston pump, Osiecki noted that the value of the mechanical-pressure efficiency exceeded 100% (with correct pressure and torque measurements). Obviously, he considered it absurd [17]. After an in-depth analysis of the pump structure, Osiecki showed that the pump was characterized by low stiffness of elements, especially the shaft. As a result, with increasing the load of the pump the working volume of the pump also increased. Thus, it can be seen that the adoption of the theoretical working volume q_t can introduce a significant error in the evaluation of the losses in displacement machines. Therefore, it is necessary to take the actual working volume q_r (as a function of pressure in working chambers) to calculate the losses in the machine.

Both Balawender and Toet in their considerations assumed that the geometric working volume q_g(Δp,T1) is a linear function of pressure (see Formulas (4) and (10)). This is a simplification, of course. It should be noted that the working chambers of displacement machines have a finite volume V. This volume can be described in the general form with three dimensions x, y, z (at p = 0):

$$V_{\left(p=0\right)}=x·y·z$$

(27)

As a result of increasing the pressure (i.e., for p > 0) the values of these dimensions change by Δx, Δy and Δz, respectively, and the actual volume V_(p) is a non-linear function of pressure:

$$V_{\left(p\right)}=V_{\left(p=0\right)}+\underset{\Delta V_{\left(p\right)}}{\underbrace{f\left(p^3\right)+f\left(p^2\right)+f\left(p\right)}}$$

(28)

The above dependence can be referred to as a displacement machine, which is a hydraulic motor. It should be noted that the deformation values Δx, Δy and Δz can be positive or negative. For example, in gear hydraulic motors not equipped with an axial clearance compensation unit, the distance between the closing plates of the toothed gear increases with the increasing of Δp_i, that is, Δz > 0. However, in such a motor with an axial clearance compensation unit, there may be a reduction in the clearance value, that is, Δz < 0. Another phenomenon is the cyclic elastic deformation of the gears cooperating with each other. This causes a cyclic change in the volume of the working chamber. Due to the same nature of the phenomenon, volumes q_g and q_k, described by Balawender with Formulas (10) and (12), are proposed to be presented by one mathematical formula with a structure such as (28):

$$q_{g\left(\Delta p_i\right)}+q_{k\left(\Delta p_i\right)}=q_{g\left(\Delta p_i=0\right)}\underset{\Delta q_{g\left(\Delta p_i\right)}}{\underbrace{\pm f\left(\Delta p_i{}^3\right)\pm f\left(\Delta {p_i}^2\right)\pm f\left(\Delta p_i\right)}}=q_r$$

(29)

where q_r is the actual working volume of a loaded motor. The value of q_r can be determined experimentally, provided that the component flow rate Q_C caused by liquid compressibility is eliminated. This can be done by taking into account the influence of compressibility of the liquid on the flow rate measured by the flow meter.

3.3. The Effect of the Flow Meter Position in the Measurement System on the Actual Working Volume Value

In his method, Toet recommends the placing of a flow meter in the inlet line to a hydraulic motor. In this arrangement, the flow meter measures the total flow including external leakage. However, Toet has omitted the effect of outside leakage on the theoretical working volume.

However, for the case of placing the flow meter in the low-pressure line, Toet introduces the influence of the liquid compressibility on the flow rate, expressed by Formula (4). Therefore, it is only the influence of the liquid compressibility related to the geometric working volume q_g. Thus, Toet neglects the influence of liquid compressibility on the leakage flow rate Q_L. This is a serious inaccuracy. Hence, according to Toet, for a flow meter located in the outflow line, the calculation of the theoretical working volume should be made according to the following formula:

$$Q_{\left(p_1\right)}=Q_2+Q_C$$

(30)

where Q_c is expressed by Formula (4). Therefore, the theoretical working volume q_t will be calculated with an error.

According to Balawender, the compressibility of the liquid has an effect on the value of the flow rate in a motor measured by a flow meter. Namely, the location of the flow meter in the measuring system is important. If the flow meter is located in a high-pressure line of the motor, then [7]:

$$Q_{\left(p_1\right)}\approx Q_1$$

(31)

However, if the flow meter is located in the low-pressure line of the motor, then [7]:

$$Q_{\left(p_1\right)}=\kappa ·Q_2$$

(32)

In the above equations, ĸ is the correction coefficient that removes the systematic error in measuring the flow rate caused by the liquid compressibility and its thermal expansion. The coefficient ĸ is a function of the liquid temperature, the content of air not dissolved in liquid (X_o) and the increase in the liquid pressure Δp. For oil and for X_o = 0.01 and t = 40 °C the coefficient is:

$$\kappa =0.97-75·{10}^{-5}·\Delta p$$

(33)

where Δp is expressed in [MPa].

In both cases, Balawender used an additional flow meter for measuring the external leakage (like in Figure 1).

Therefore, in both Toet’s and Balawender’s methods, the effect of the flow meter location in the measuring system is simplified. In order to more accurately calculate the flow rate related to the pressure in the high-pressure working chamber, the following method is proposed. The flow meter located in the inlet line to the motor measures the flow rate Q₁ of the liquid compressed to the pressure p₁ (Figure 1). The working chamber filling process is from the chamber minimum volume V_min to the chamber maximum volume V_max. The pressure in this chamber is lower than the pressure p₁ by the pressure drop Δp_ich1 in the internal inflow channel (Figure 5). Therefore, taking into consideration the compressibility of the liquid, the flow rate Q_(pH) related to the pressure p_H in the high-pressure working chamber will be:

$$Q_{\left(p_H\right)}=Q_1+\Delta Q_1$$

(34)

where ΔQ₁ is an additional flow rate resulting from the expansion from pressure p₁ to pressure p_H. It is necessary to add, that in this case the calculated value of Q_(pH) is the sum of the theoretical flow rate Q_t in the motor and the internal Q_Li and external Q_Le leakages. Thus, this method of measurement does not allow calculating the actual working volume q_r of the motor.

The flow meter located in the outflow line of the motor measures the flow rate Q₂ of liquid decompressed from pressure p_H to pressure p₂ (Figure 1). Thus, the flow meter measures the following flow rate:

$$Q_2=Q_{\left(p_H\right)}+\Delta Q_2$$

(35)

where ΔQ₂ is an additional flow rate caused by liquid decompression from pressure p_H to pressure p₂. It is necessary to add, that in this case the calculated value of Q_(pH) is the sum of the theoretical flow rate Q_t and the internal leakage Q_Li.

The value of Q_(pH), calculated from Formula (34) or (35) should be taken for the correct calculation of the theoretical working volume q_t. It is possible to calculate both ΔQ₁ and ΔQ₂ if the bulk modulus K of the liquid is known. In real conditions, the working fluid is somewhat aerated. Thus, the content of the non-dissolved air in the oil affects the bulk modulus K. The tangential isentropic bulk modulus K_Z(p) is very well described by the Zaluski formula [18]:

$$K_{Z\left(p\right)}=\frac{e^{\left(\frac{p_o-p}{K}\right)}·\lfloor 1+m·\frac{p-p_o}{K}{\rfloor }^{\left(-\frac{1}{m}\right)}+\frac{X_o}{1-X_o}·{\left(\frac{p_o}{p}\right)}^{\left(\frac{1}{n}\right)}}{\frac{e^{\left(\frac{p_o-p}{K}\right)}}{K}·\lfloor 1+m·\frac{p-p_o}{K}{\rfloor }^{\left(\frac{1-m}{m}\right)}+\frac{X_o}{n·p_o·\left(1-X_o\right)}·{\left(\frac{p_o}{p}\right)}^{\left(\frac{1+n}{n}\right)}}$$

(36)

where:

• K—the bulk modulus of non-aerated oil at atmospheric pressure p_o;
• X_o—the amount of non-dissolved air in the oil at atmospheric pressure p_o;
• p—the absolute pressure;
• n—the polytrophic exponent;
• m—the coefficient of the influence of pressure p on the bulk modulus K.

It follows from the basic definition of the bulk modulus that the change in the volume ΔV_(p2) of liquid from pressure p_o to p₂ is:

$$\Delta V_{\left(p_2\right)}=-{{\displaystyle \int }}_{p_o}^{p_2}\frac{V_o}{K_{Z\left(p\right)}}·\partial p$$

(37)

where V_o is the initial volume. Similarly, the change of the volume ΔV_(pH) of the liquid from pressure p_o to pressure p_H in the filled working chamber will be:

$$\Delta V_{\left(p_H\right)}=-{{\displaystyle \int }}_{p_o}^{p_H}\frac{V_o}{K_{Z\left(p\right)}}·\partial p$$

(38)

From the practical point of view, the volume of the flow meter chamber can be assumed as the initial volume V_o. Thus, the volume of liquid measured by the flow meter at a pressure p₂ and related to pressure p_o is:

$$Q_o=Q_2+\frac{\Delta V_{\left(p_2\right)}}{\Delta t}$$

(39)

where Δt is the time of the flow meter chamber filling at the flow rate Q₂. However, the flow rate related to the pressure p_H is:

$$Q_{\left(p_H\right)}=Q_o-\frac{\Delta V_{\left(p_H\right)}}{\Delta t}=Q_2+\frac{\Delta V_{\left(p_2\right)}-\Delta V_{\left(p_H\right)}}{\Delta t}$$

(40)

The values of Q_(pH) calculated according to Formula (40) are required for determining the characteristics Q_(pH) = f(Δp_i). It is assumed that these characteristics are linear and therefore it is proposed to describe them with a linear equation, as in Formula (19).

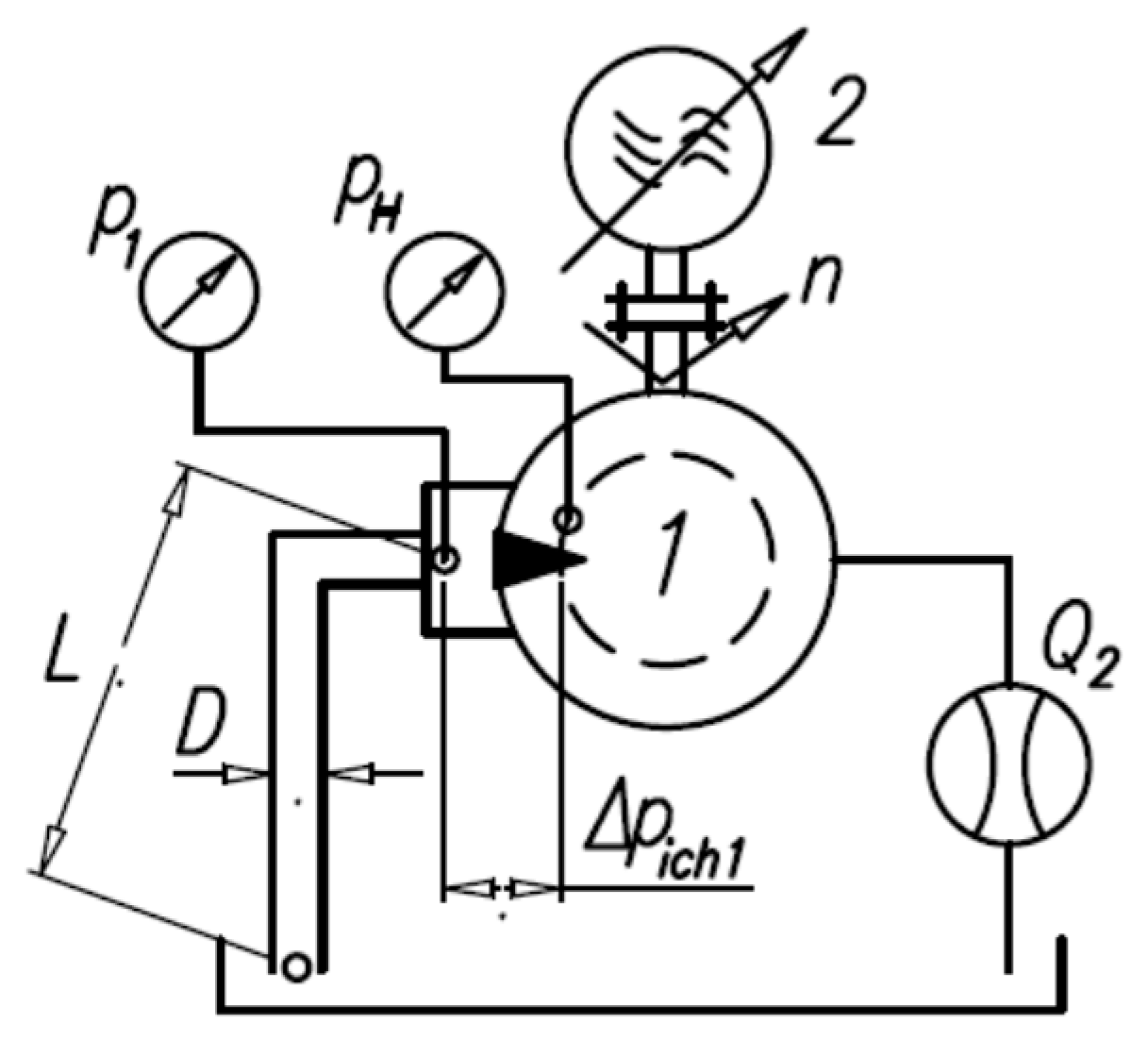
3.4. Method of Pressure Drop Measurement in Motor Internal Channels

In a hydraulic motor with variable shaft rotation directions, the inflow and outflow internal channels have the same shape and dimensions. Thus, it is only necessary to measure the pressure drop Δp_ic1 in the inflow internal channel and the pressure drop Δp_ich in the motor, which are calculated according to the formula [16]:

$$\Delta p_{ich}=2·\Delta p_{ich1}$$

(41)

where:

$$\Delta p_{ich1}=p_1- p_H$$

(42)

The idea of the measured system is shown in Figure 5. The tested hydraulic motor 1 works as a pump and is driven by an electric motor 2. The speed n of the electric motor 2 and machine 1 is set via a frequency converter. In this method, the measurement data acquisition system records:

(a)

the pressure p₁ in the motor port;

(b)

the pressure p_H in the motor working chamber;

(c)

the motor output flow rate Q₂;

(d)

the rotational speed n of the motor shaft.

The pressure losses in the motor internal channels can be described by [16]:

$$\Delta p_{ich}=C_t·\rho ·Q_2{}^2+C_l·\nu ·\rho ·Q_2$$

(43)

where:

• C_t—the constant of the turbulent flow component;
• C_l—the constant of the laminar flow component;
• ν—the kinematic viscosity;
• ρ—the density of liquid.

3.5. Model of Flow Rate in Hydraulic Motor

Taking into account the liquid compressibility (the influence of the flow meter location in the measurement system) and the fact that the leakages in the motor and the deformation of the working chamber are determined by the pressure drop Δp_i in the working chambers, the flow rate Q_(pH) in the motor should be described by the following formula:

$$Q_{\left(p_H,\Delta p_i=const\right)}=A_{\left(p_H\right)}·n+B_{\left(p_H\right)}$$

(44)

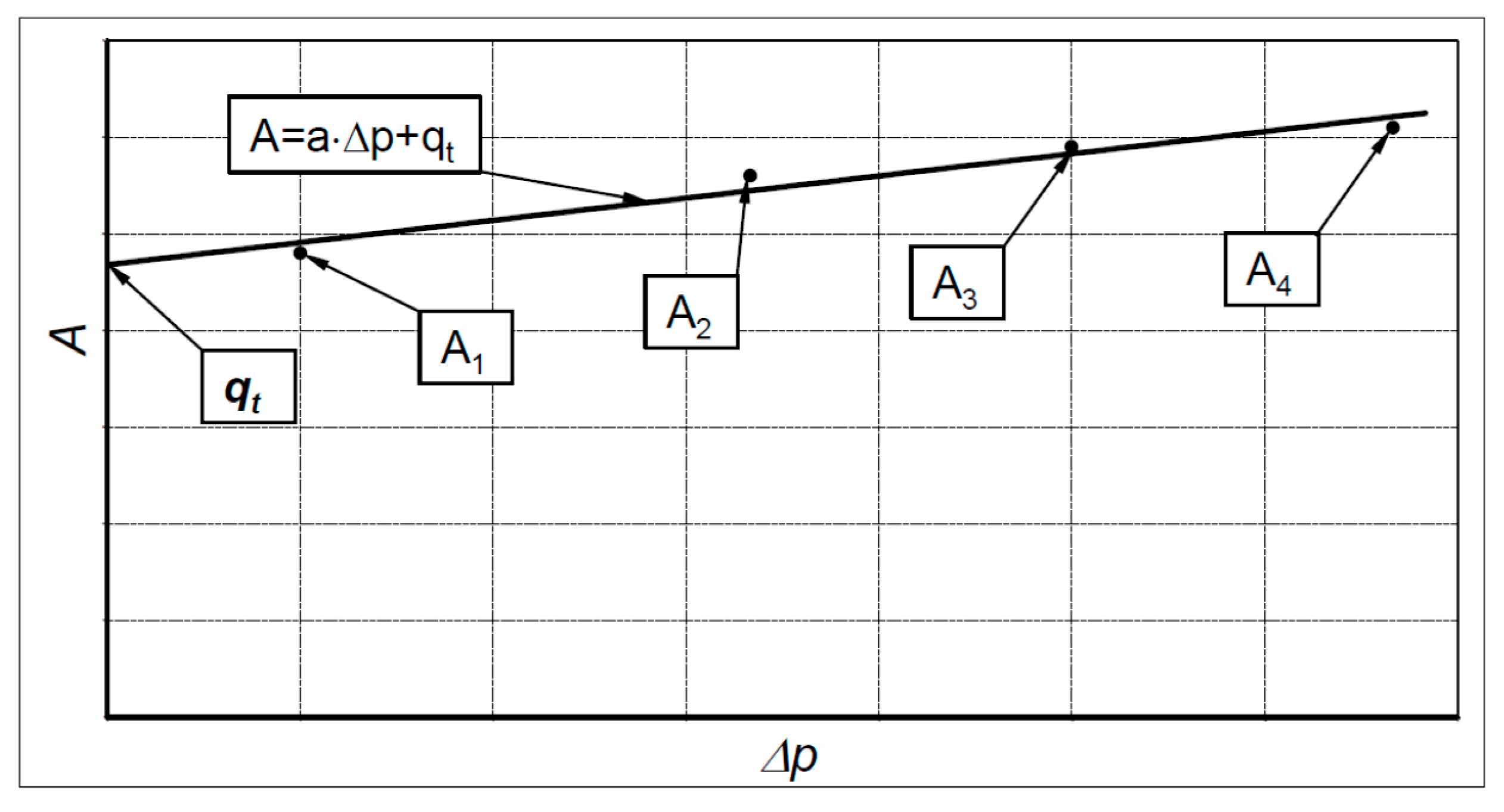
3.6. Practical Implementation of the Method

In order to determine the theoretical and actual working volume, it is necessary (step by step):

(a)

To measure the flow Q₁ or Q₂ at a constant inlet temperature T₁ and a constant pressure drop Δp for several values of n (no less than five). The measurement has to be taken once again using at least five different pressure drops Δp;

(b)

To measure the pressure drop Δp_ich in the internal channel of the motor according to the method described in Section 3.4;

(c)

To calculate the pressure drop Δp_i in the working chamber of the motor for data from item (a);

(d)

If the flow meter is located in the low-pressure line, the influence of the liquid compressibility should be taken into account and the flow rate Q_(pH) corresponding the value of high-pressure p_H in the working chamber should be calculated;

(e)

To plot the characteristics Q_(pH) = f(n)_Δpi=const and calculate the coefficients A in the Formula (17).

4. Results of Experimental Research

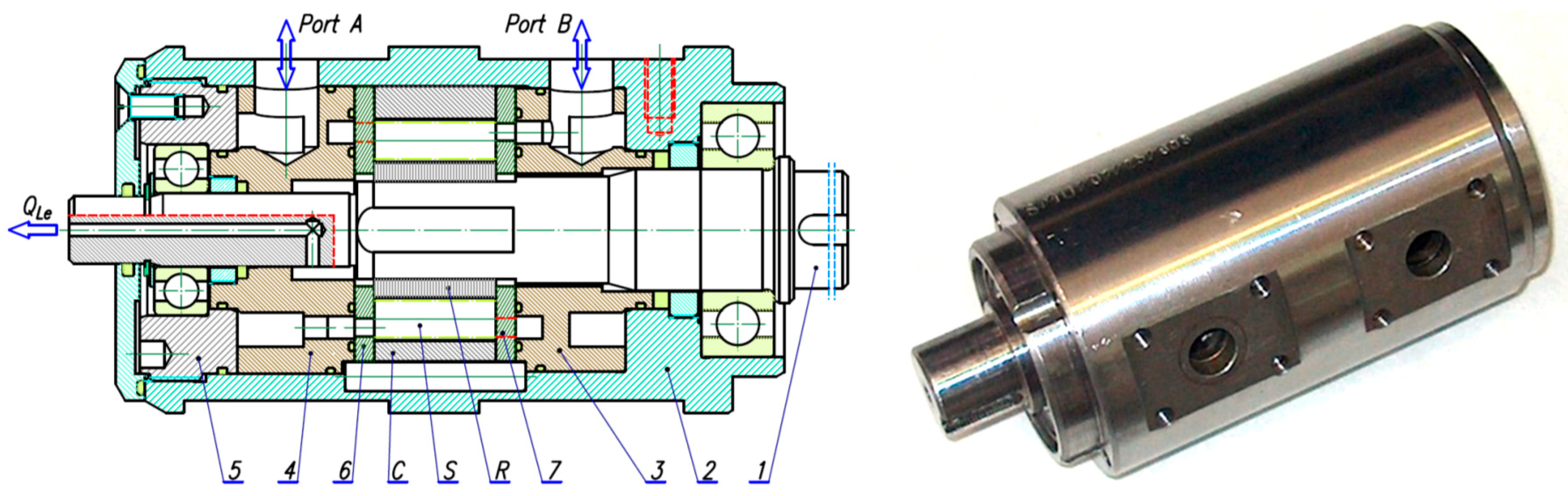
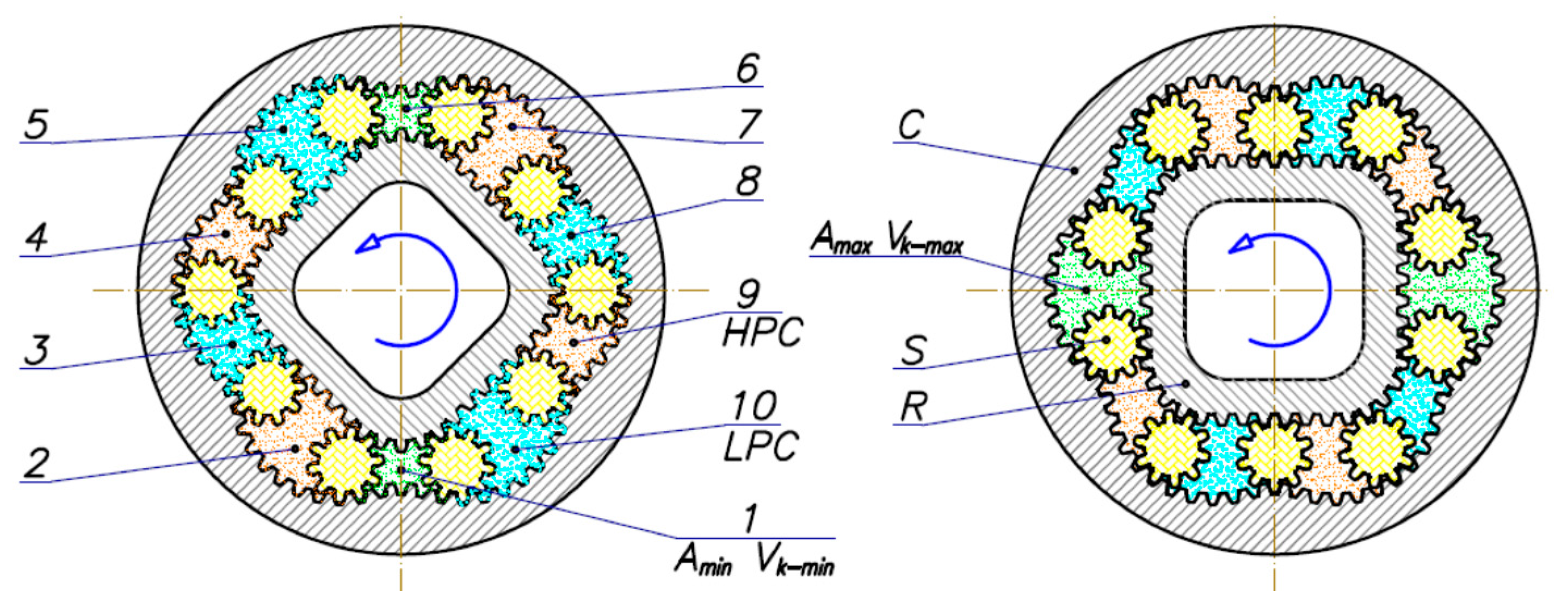
4.1. Tested Motor

The general view and design of the prototype of hydraulics satellite motor (used in the experimental tests) is presented in Figure 6. The working mechanism of the satellite motor is presented in Figure 7. The revolving motion of rotor R is done by satellites S. The satellites S are in gear with the curvature C and the rotor R and, in the same, form the working chambers (numbers from 1 to 10 in Figure 7).

During rotation of the rotor R, the volume of working chamber increases from minimum V_k-min to maximum V_k-max (the chamber is filled and is called the high-pressure chamber HPC), and next the volume of the working chamber decreases from V_k-max to V_k-min and then the chamber is emptied (and is called a low-pressure chamber LPC).

In the presented satellite mechanism, 24 cycles of filling and emptying of the working chambers occur per one rotation of the shaft, that is $n_C·n_R=24$, where n_R and n_C are the number of humps of the rotor and the curvature, respectively [16].

The compensation plates (Figure 6—elements 6 and 7), which are also called distribution plates, distribute the liquid to the working chambers and limit the leak in the gaps on the satellites and rotor faces, i.e., the plates deform elastically and thus limit the axial clearance of the rotor and the satellites. It is assumed that a reduction in the clearance can affect the theoretical working volume.

The geometric working volume q_g of the satellite mechanism is calculated according to the following formula [16]:

$$q_g=n_C·n_R·H·\left(A_{max}-A_{min}\right)$$

(45)

The satellite motor used for the test had the following geometrical parameters (from CAD documentation):

• the height of the working mechanism H = 25 mm;
• the minimum area of the working chamber A_min = 26.11 mm²;
• the maximum area of the working chamber A_max = 83.51 mm².
• Thus, the geometric working volume of the satellite mechanism was q_g = 34.44 cm³/rev. Other motor parameters were:
• the tooth module m = 0.75 mm;
• the difference in the height of the satellites and the rotor in relations to the curvature was Δh = 5 μm.

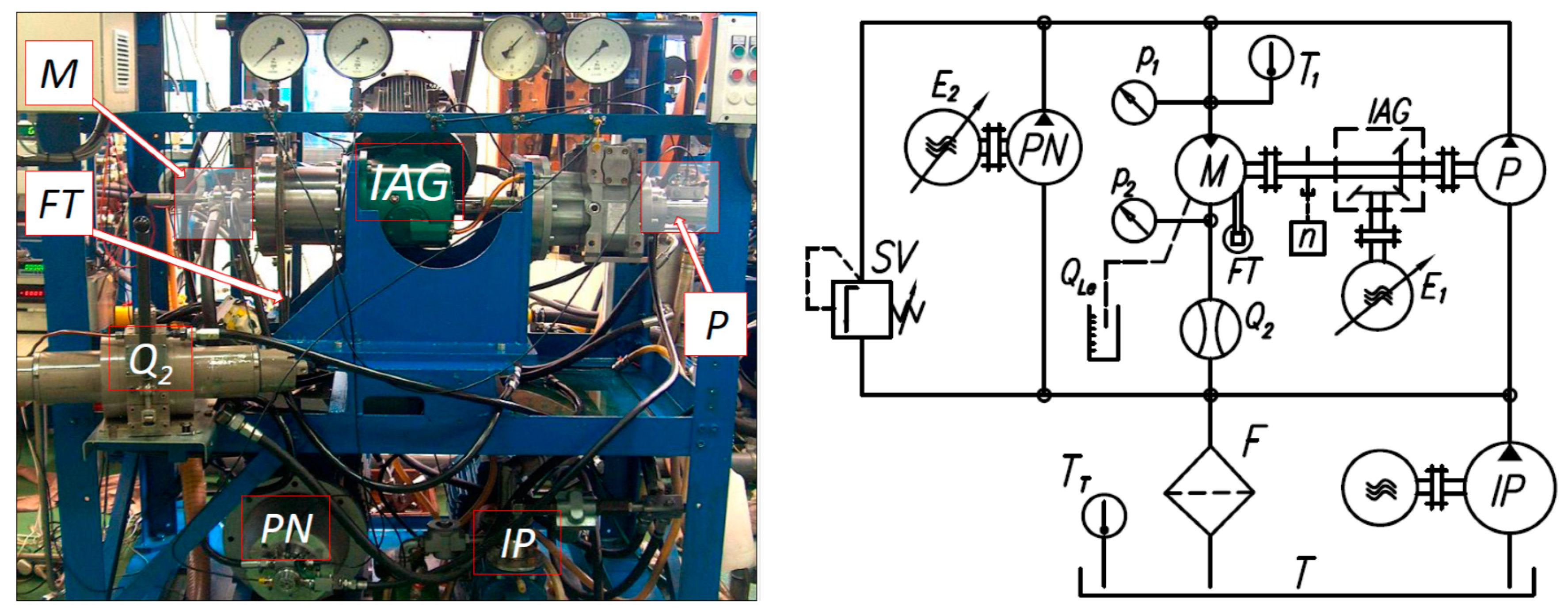
4.2. The Test Stand and Measuring Apparatus

The general view of the test stand and the diagram of the measurement system of this test stand is shown in Figure 8. The test stand was set up with power recuperation.

During the test of the motor, the following parameters were measured:

• pressure p₁ in the inflow port (strain gauge pressure transducer, range 0–10 MPa and 0–40MPa, class 0.3);
• pressure p₂ in the outflow port (strain gauge pressure transducers, range 0–2.5 MPa, class 0.3);
• flow rate Q₂ (piston flowmeter, the flowmeter chamber volume 0.63 dm³, range 0–200 L/min, class 0.2, accuracy of reading 0.01 L/min, maximum measurement error 0.41 L/min);
• torque M (strain gauge force transducer FT mounted on the arm 0.5 m (the arm attached to the motor body), range 0–100 N, class 0.1);
• rotational speed of shaft n (inductive sensor, accuracy of measurement ±0.01 rpm);
• temperature T₁ of liquid in the inflow port of the motor (RTD temperature sensor, class A, max. measurement error 0.5 °C).

In order to determine the working volume of the motor from the experimental data with the smallest possible error, it was very important to maintain the setting of speed n, pressure drop Δp and liquid temperature T₁ with the least possible deviation. Thus:

• the rotational speed n was maintained with a deviation of ±0.1 rpm;
• the pressure drop Δp was maintained with a deviation of ±0.05 MPa;
• the temperature in inflow port T₁ was maintained with a deviation of ±1.0 °C.

Due to the large chamber of the piston flowmeter (0.63 dm³), the shaft of the tested motor had to make about 18 rotations in order to obtain the flow rate measurement result. The piston flowmeter installed in the system measured the average value of the flow rate. This is a doubtless advantage. Furthermore, each recorded flow measurement result is the average of three measurements.

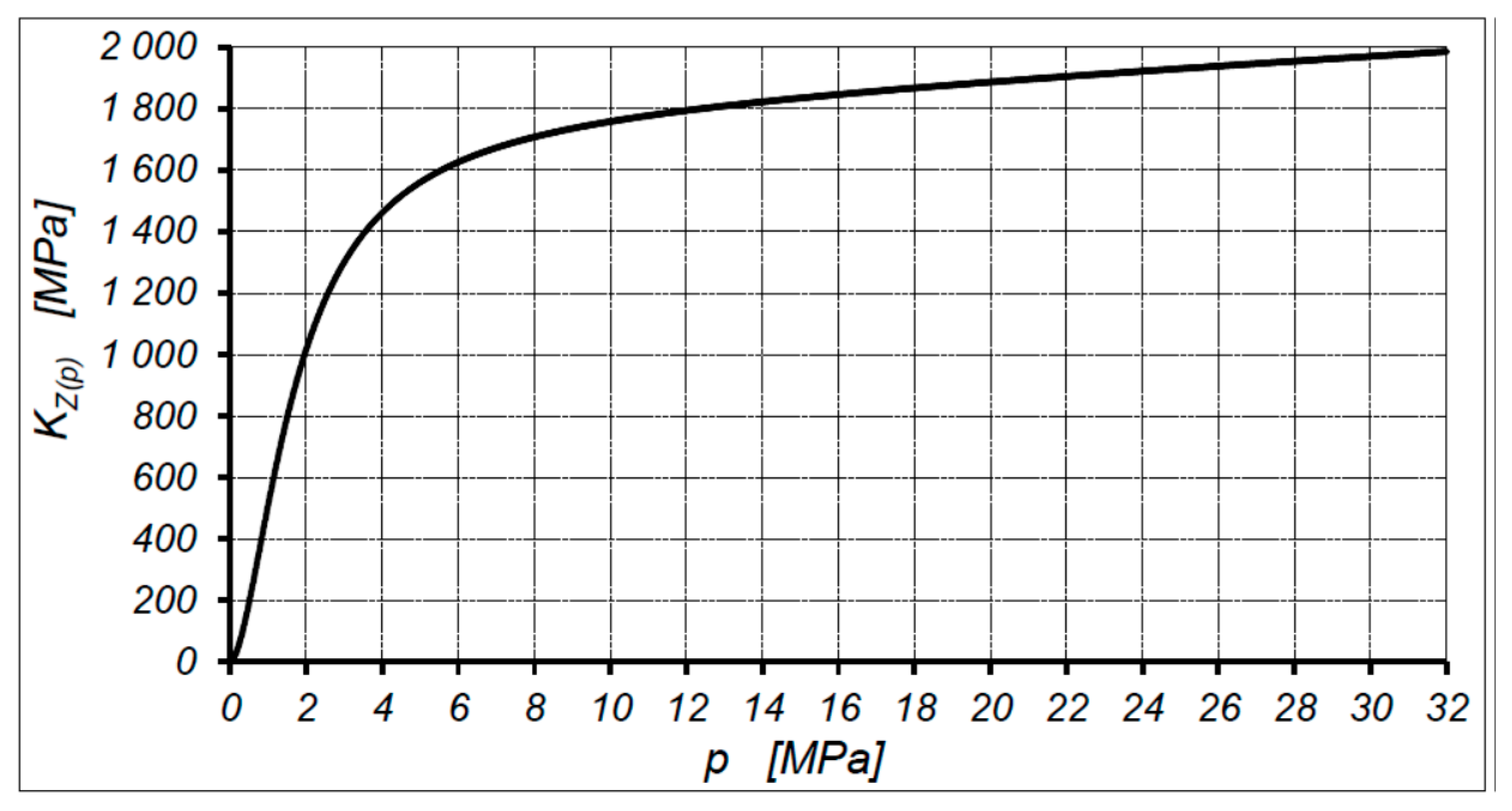
4.3. Working Liquid Parameters

The satellite motor was tested using the Total Azolla 46 oil with the temperature in the inflow port T₁ = 43 °C (kinematic viscosity ν = 40 cSt, density ρ = 873 kg/m³). Knowledge of the characteristics of the tangential isentropic bulk modulus K_Z(p) of mineral oil is required for the proper determination of theoretical and actual working volume of a hydraulic motor (Figure 9). These characteristics were set by Załuski according to Formula (46) for the following data [17]:

• the bulk modulus of non-aerated oil at atmospheric pressure K = 1775 MPa;
• the content in oil of non-dissolved air at atmospheric pressure X_o = 0.01;
• the politrophic exponent n = 1.4;
• the coefficient of the effect of pressure p on the bulk modulus m = 9.19;
• the atmospheric pressure p_o = 0.1 MPa.

For oil in the test stand and for p > 2 MPa:

$$\frac{{\rho }_o}{\rho }-1=-704.65·{10}^{-6}·\Delta p+726.32·{10}^{-8}·{\left(\Delta p\right)}^2-818.59·{10}^{-10}·{\left(\Delta p\right)}^3-826.5·{10}^{-5}$$

(46)

4.4. Pressure Drop in Motor Internal Channels

Based on the results of the experimental research carried out according to the method described in Section 3.4, the pressure drop Δp_ich in the motor internal channels can be described by the following empirical formula (according to (43)):

$$\Delta p_{ich}=0.003224·Q^2+0.02183·Q$$

(47)

where Q is measured in [L/min] and Δp_ich in [MPa].

4.5. Motor Output Flow Rate Characteristics

The experimental test of the satellite motor was carried out in the rotational speed range n = 50 –1500 rpm. The characteristics Q₂ = f(n) at Δp = const. were determined in the entire speed range and in the speed range n = 50–150 rpm (Figure 10). In order to maintain the clarity of the graphs, the characteristics are shown only for two extreme pressure drops in the motor, that is, for Δp = 2 MPa and Δp = 32 MPa. The characteristics of Q₂ = f(n) at other values of Δp are described by equations and are presented in the Appendix A in

Table A1. Equations Q₂ = A·n + B of motor output flow rate at Δp = const. (Toet’s method).

No.	Δp [MPa]	Q2 = A n + B	A [cm3/rev]	R2
1	2	Q2 = 0.033120·n + 0.245496	33.120	0.999984
2	4	Q2 = 0.033369·n + 0.379312	33.369	0.999982
3	6	Q2 = 0.033590·n + 0.441141	33.590	0.999974
4	8	Q2 = 0.033762·n + 0.462461	33.762	0.999988
5	10	Q2 = 0.033973·n + 0.476327	33.973	0.999979
6	12	Q2 = 0.034124·n + 0.498480	34.124	0.999990
7	14	Q2 = 0.034256·n + 0.518116	34.256	0.999970
8	16	Q2 = 0.034411·n + 0.566370	34.411	0.999989
9	20	Q2 = 0.034689·n + 0.649842	34.689	0.999989
10	24	Q2 = 0.034968·n + 0.735564	34.968	0.999992
11	28	Q2 = 0.035170·n + 0.800050	35.170	0.999986
12	32	Q2 = 0.035349·n + 0.852268	35.349	0.999966

and

Table A2. Equations Q₂ = A·n + B of motor output flow rate at Δp = const. (Balawender’s method).

No.	Δp [MPa]	Q2 = A·n + B	A [cm3/rev]	R2
1	2	Q2 = 0.033715·n + 0.145474	33.715	0.999960
2	4	Q2 = 0.033844·n + 0.256944	33.844	0.999785
3	6	Q2 = 0.034086·n + 0.327206	34.086	0.999926
4	8	Q2 = 0.034232·n + 0.372550	34.232	0.999909
5	10	Q2 = 0.034517·n + 0.388903	34.517	0.999904
6	12	Q2 = 0.034577·n + 0.429866	34.577	0.999537
7	14	Q2 = 0.034732·n + 0.430350	34.732	0.999907
8	16	Q2 = 0.034931·n + 0.486725	34.931	0.999677
9	20	Q2 = 0.035275·n + 0.540842	35.275	0.999824
10	24	Q2 = 0.035629·n + 0.664698	35.629	0.999920
11	28	Q2 = 0.035868·n + 0.742994	35.868	0.999823
12	32	Q2 = 0.036213·n + 0.801073	36.213	0.999438

.

The characteristics of external leakage Q_Le in the tested motor are shown in Figure 11. It is the average value of leakages for the whole range of rotational speed n.

After taking into account the pressure drop Δp_ich in the internal channels of the motor, the characteristics of output flow rate Q₂ take the form like in Figure 12 (for Δp_i = 2 MPa and Δp_i = 32 MPa). The influence of liquid compressibility was omitted. The characteristics for other Δp_i, omitting the liquid compressibility, are described by equations and presented in the Appendix A in

Table A3. Equations Q₂ = A·n + B of motor output flow rate at Δp_i = const. (new method without the influence of the oil compressibility).

No.	Δp [MPa]	Q2 = A·n + B	A [cm3/rev]	R2
1	2	Q2 = 0.033251·n + 0.226334	33.251	0.999992
2	4	Q2 = 0.033513·n + 0.291487	33.513	0.999989
3	6	Q2 = 0.033714·n + 0.347383	33.714	0.999992
4	8	Q2 = 0.033881·n + 0.397161	33.881	0.999995
5	10	Q2 = 0.034034·n + 0.442995	34.034	0.999996
6	12	Q2 = 0.034183·n + 0.486303	34.183	0.999995
7	14	Q2 = 0.034333·n + 0.527925	34.333	0.999994
8	16	Q2 = 0.034484·n + 0.568284	34.484	0.999995
9	20	Q2 = 0.034778·n + 0.645530	34.778	0.999996
10	24	Q2 = 0.035035·n + 0.717189	35.035	0.999992
11	28	Q2 = 0.035235·n + 0.781090	35.235	0.999979
12	32	Q2 = 0.035408·n + 0.834000	35.408	0.999957

.

The results of the flow rate measurements Q₂ (Figure 10) were corrected for the difference resulting from the compression of the oil to the supply pressure p₁—according to Formula (40) (Toet’s method) and Formula (42) (Balawender’s method). The characteristics presented in Figure 13 were obtained as a result. The characteristics of Q_(p1) for other Δp are described by equations and presented in the Appendix A in

Table A4. Equations Q_(p1) = A·n + B of motor output flow rate at Δp = const. (Toet’s metod).

No.	Δp [MPa]	Q(p1) = A·n + B	A [cm3/rev]	R2
1	2	Q(p1) = 0.032787·n + 0.245497	32.788	0.999984
2	4	Q(p1) = 0.032991·n + 0.379312	32.991	0.999983
3	6	Q(p1) = 0.033168·n + 0.441141	33.168	0.999974
4	8	Q(p1) = 0.033298·n + 0.462462	33.298	0.999988
5	10	Q(p1) = 0.033468·n + 0.476328	33.468	0.999978
6	12	Q(p1) = 0.033580·n + 0.498481	33.580	0.999991
7	14	Q(p1) = 0.033674·n + 0.518116	33.674	0.999969
8	16	Q(p1) = 0.033791·n + 0.566370	33.791	0.999989
9	20	Q(p1) = 0.033996·n + 0.649842	33.996	0.999989
10	24	Q(p1) = 0.034207·n + 0.735564	34.207	0.999992
11	28	Q(p1) = 0.034340·n + 0.800050	34.340	0.999986
12	32	Q(p1) = 0.034452·n + 0.852269	34.452	0.999965

and

Table A5. Equations Q_(p1) = A·n + B of motor output flow rate at Δp = const. (Balawender’s metod).

No.	Δp [MPa]	Q(p1) = A·n + B	A [cm3/rev]	R2
1	2	Q(p1) = 0.032566·n + 0.137926	32.566	0.999848
2	4	Q(p1) = 0.032770·n + 0.248459	32.770	0.999924
3	6	Q(p1) = 0.032906·n + 0.316588	32.906	0.999977
4	8	Q(p1) = 0.032797·n + 0.373599	32.797	0.999991
5	10	Q(p1) = 0.032923·n + 0.404549	32.923	0.999977
6	12	Q(p1) = 0.032867·n + 0.452474	32.867	0.999993
7	14	Q(p1) = 0.033010·n + 0.443626	33.010	0.999967
8	16	Q(p1) = 0.033279·n + 0.452977	33.279	0.999982
9	20	Q(p1) = 0.033603·n + 0.509748	33.603	0.999537
10	24	Q(p1) = 0.033501·n + 0.682885	33.501	0.999856
11	28	Q(p1) = 0.033663·n + 0.722821	33.663	0.999790
12	32	Q(p1) = 0.033824·n + 0.791678	33.824	0.999661

.

Using the method described in Section 3.3, the flow rate Q_(pH) related to the pressure p_H in the high-pressure chamber of the motor was calculated, and the liquid compressibility was taken into account. The characteristics of Q_{(pH,Δpi=const.)} = f(n) for Δp_i = 2 MPa and Δp_i = 32 MPa are shown in Figure 14. The characteristics for other Δp_i are described by equations and presented in the Appendix A in

Table A6. Equations Q_(pH) = A·n + B of motor output flow rate at Δp_i = const. (new method).

No.	Δpi [MPa]	Q(pH) = A·n + B	A [cm3/rev]	R2
1	2	Q(pH) = 0.033095·n + 0.223310	33.095	0.999982
2	4	Q(pH) = 0.033308·n + 0.346180	33.308	0.999991
3	6	Q(pH) = 0.033487·n + 0.404302	33.487	0.999993
4	8	Q(pH) = 0.033638·n + 0.431194	33.638	0.999992
5	10	Q(pH) = 0.033769·n + 0.448067	33.769	0.999990
6	12	Q(pH) = 0.033886·n + 0.466857	33.886	0.999988
7	14	Q(pH) = 0.033997·n + 0.492843	33.997	0.999988
8	16	Q(pH) = 0.034105·n + 0.526875	34.105	0.999989
9	20	Q(pH) = 0.034315·n + 0.610846	34.315	0.999990
10	24	Q(pH) = 0.034497·n + 0.696203	34.497	0.999988
11	28	Q(pH) = 0.034626·n + 0.764548	34.626	0.999979
12	32	Q(pH) = 0.034744·n + 0.802372	34.744	0.999947

.

4.6. Motor Theoretical Working Volume According to Known Methods

The working volume A was calculated for two cases, omitting and including the influence of oil compressibility. The characteristics of A = f(Δp) determined according to Toet’s and Balawender’s method for both cases are presented in Figure 15. The characteristics of external leakage in the motor show, that $\underset{·p\to 0}{\lim }{Q}_{Le\left(·p\right)}=0$ (Figure 11). Thus, in Balawender’s method, the external leakage does not affect the theoretical working volume q_t.

4.7. Motor Theoretical Working Volume According to Proposed Method

In Figure 16 are shown the characteristics A = f(Δp_i) of the working volume A per one revolution of the shaft:

(a)

determined taking into account the influence of oil compressibility;

(b)

determined omitting the influence of oil compressibility.

The theoretical working volume q_t of the motor determined by all the methods described above is shown in

Table 1. Theoretical working volume q_t of a satellie motor.

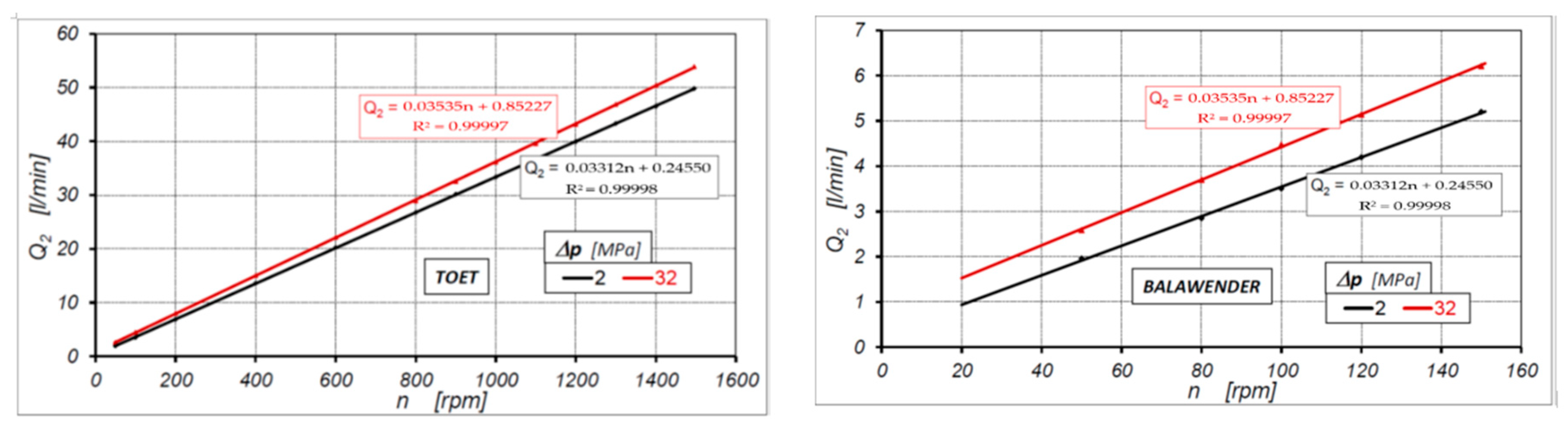
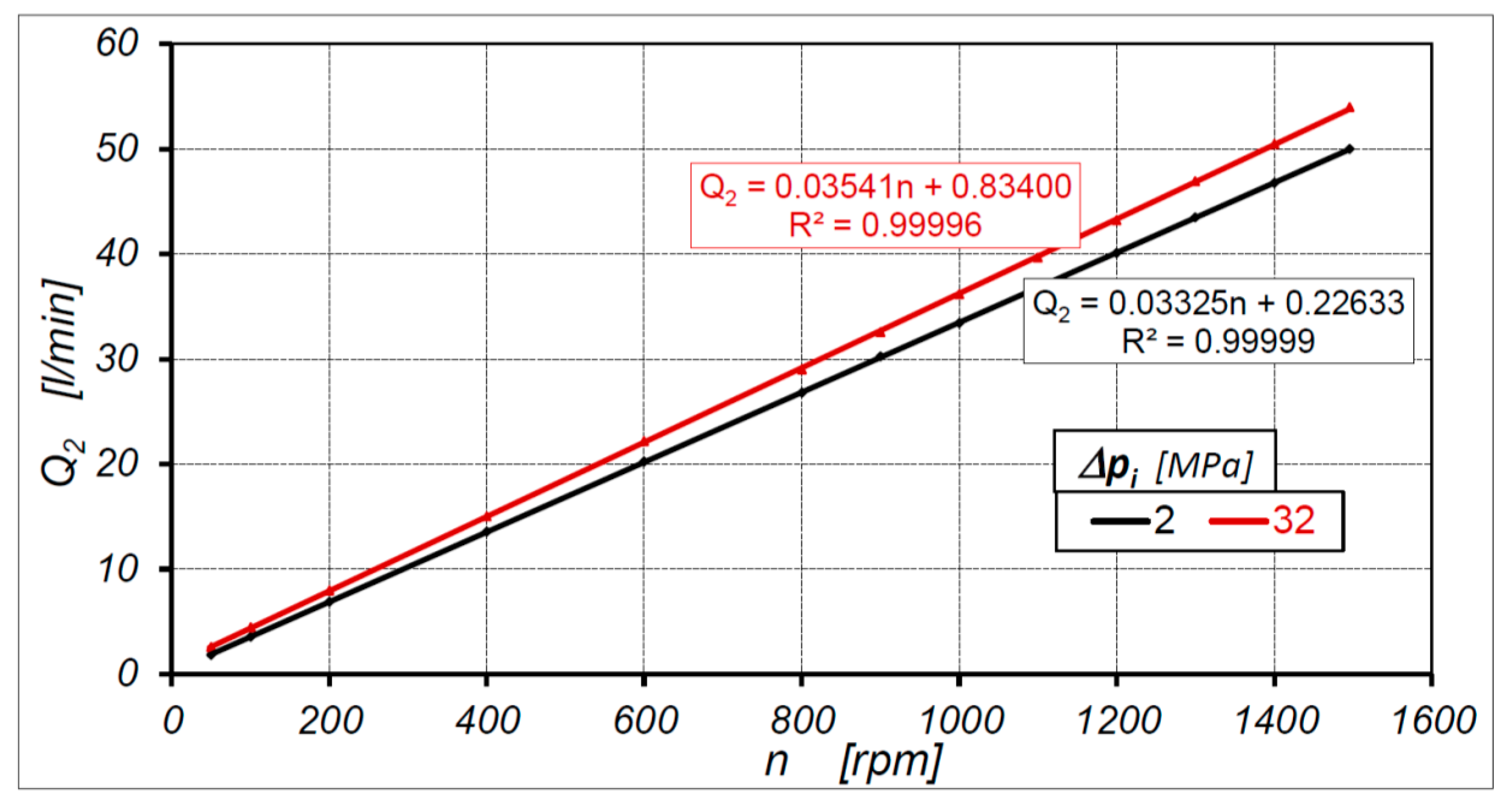
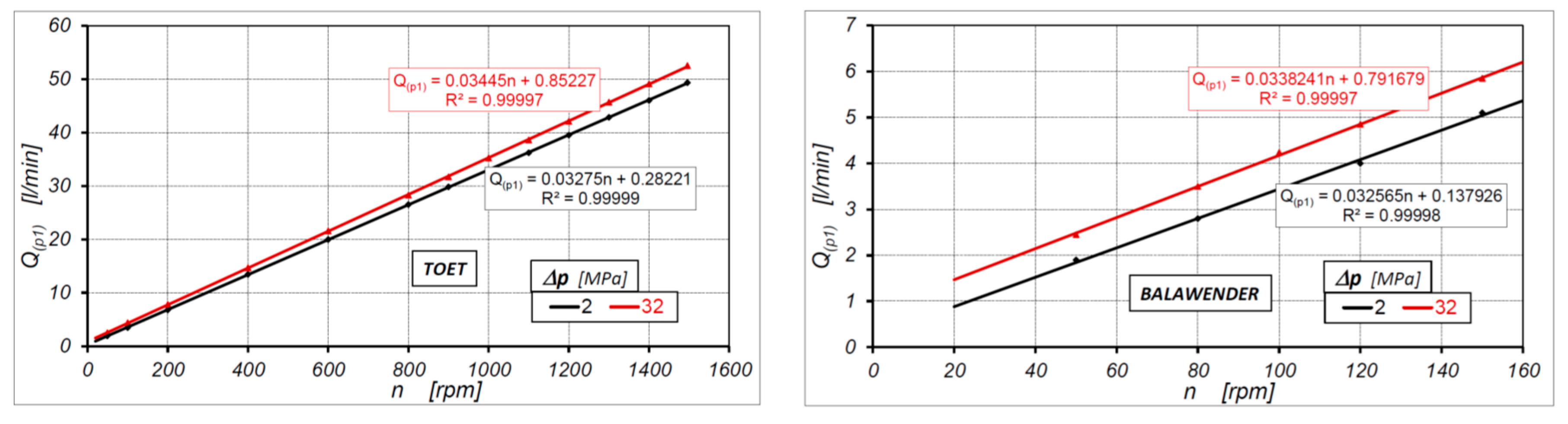
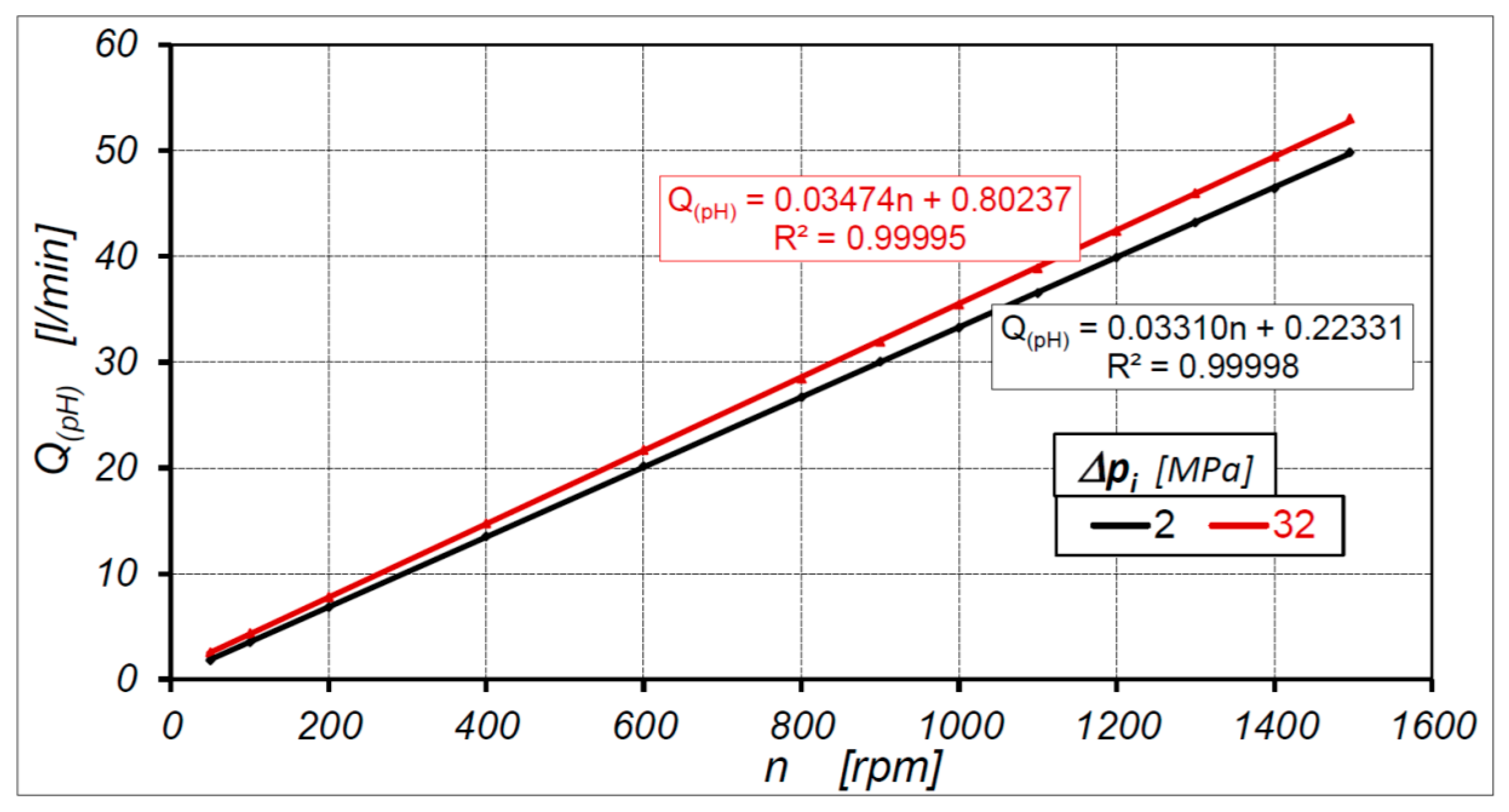
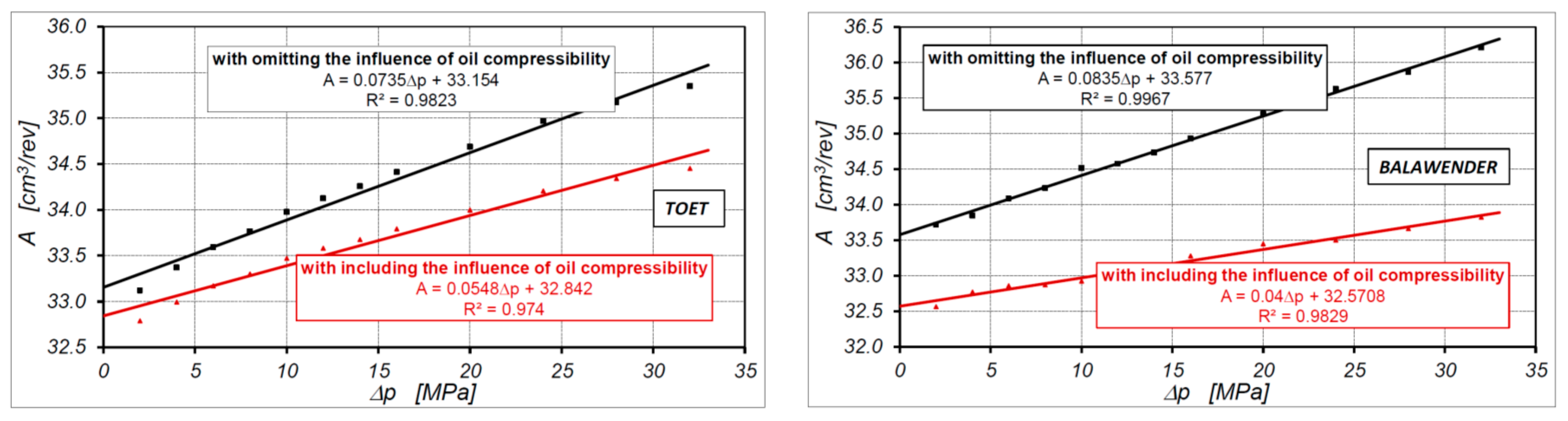
	Method	qt [cm3/rev]
	From project—qg	34.440
Omitting the influence of oil compressibility	Toet	33.105
	Balawender	33.577
	Proposed method	33.076
Including the influence of oil compressibility	Toet	32.842
	Balawender	32.571
	proposed method	32.916

.

5. Discussion

The results of the experimental research confirm that the following characteristics can be described by a linear function of the rotational speed n:

(a)

Q₂ = f(n)_Δp=const (Figure 10);

(b)

Q₂ = f(n)_Δpi=const (Figure 12);

(c)

Q_(pH) = f(n)_Δpi=const (Figure 14).

The value of the correlation coefficient R² of the above-mentioned linear function is close to one (R² > 0.999). Hence, the equations accurately describe the process of the fluid flow in the motor. Undoubtedly, the small scatter of the measurement results was mainly influenced by the piston flow meter. This flow meter measured the average flow rate corresponding to more than 18 revolutions of the motor shaft. Thus, the result indicated by the flow meter is the result of over 432 cycles of filling and emptying of the working chambers. Furthermore, very precise parameters were maintained during the tests, as described in Section 4.2.

The results of the experimental research confirm that, regardless of the method used, the theoretical working volume q_t of a hydraulic motor is independent of its rotational speed n. However, the value of q_t depends on the method used to calculate it (Table 1). Theoretical working volume q_t calculated using Balawender’s method differs up to 1.43% from q_t calculated using Toet’s method. This difference is not big. Nevertheless, it is difficult to indicate a more reliable result because both Toet’s method and Balawender’s method contain simplifications (described in Section 3.3 and Section 3.4).

Nonetheless, q_t calculated using the new method (taking into account the pressure drop in the motor internal channels, the flowmeter position in the measurement system and the influence of oil compressibility) is about 1.06% larger than q_t calculated using Balawender’s method and is about 0.22% larger than q_t calculated using Toet’s method (Table 1). These differences are also not big. It is assumed that one of the main reasons for such small differences in the results may be the low pressure drop Δp_i in the motor internal channels. In addition, for this motor, simplified calculations of the effect of liquid compressibility on the flow rate (according to Toet’s and Balawender’s methods) do not have, as can be seen, any greater impact on the theoretical working volume q_t.

Omitting the influence of liquid compressibility in the proposed method overstates the theoretical working volume by about 0.5%. Is this value small or large? From the point of view of the motor user, a difference of 0.5% is negligibly small. Bigger differences are observed in the known methods, i.e., they are 0.8% and 3.1% in Toet’s and Balawender’s methods, respectively. A difference in the order of 1% and above, however, should not be underestimated, especially by designers and researchers of positive displacement machines. From their point of view, each difference in the theoretical working volume is important because it directly influences the assessment of mechanical and volumetric efficiency.

The theoretical working volume q_t is constant in all ranges of speed n and load M of the motor. It has been shown above that with the change in the motor load (and thus the pressure drop in the motor) the working volume of the motor changes. Thus, the efficiencies defined according to Formulas (1) and (2) are subject to error. Therefore, the efficiencies should be calculated taking into account the actual working volume q_r:

$${\eta }_m=2\pi ·\frac{M}{q_r·\Delta p_i}$$

(48)

$${\eta }_v=\frac{q_r·n}{Q_1}$$

(49)

where if Δp_i = 0 then q_r = q_t.

For example, if the theoretical working volume calculated according to the simplified (omitting the influence of oil compressibility) Balawender’s method is accepted for calculations of losses, the volumetric efficiency of the motor for Δp_i < 4 MPa is larger than one (η_v > 1) (Figure 17). This makes no physical sense, of course.

The theoretical working volume q_t in all ranges of pressure drops Δp_i in the motor has commonly been accepted for assessment of losses in a hydraulic motor and its efficiencies, whereby it causes (Figure 17):

• an overestimation of volumetric losses and an underestimation of volumetric efficiency η_v;
• an underestimation of mechanical losses and an overestimation of mechanical efficiency η_m.

The results of the experimental research (Figure 16) confirm that the actual working volume q_r is a nonlinear function of pressure drop Δp_i in working chambers of the motor and can be described by a third order polynomial (expressed by Formula (29)). It should be clearly emphasized that the actual working volume q_r is determined including the influence of oil compressibility and the pressure drop Δp_ich in the motor internal channels. Then q_r = A = f(Δp_i) and q_r > q_t for Δp_i > 0. Therefore, the values of q_r according to Formula (29) should be taken into account to calculate the volumetric and mechanical losses in a hydraulic motor. In the tested satellite motor, this is:

$$q_r=0.00002054·\Delta p_i{}^3-0.00211551·\Delta p_i{}^2+0.10404691·\Delta p_i+32.91602674$$

(50)

From a practical point of view, it may seem a bit problematic to measure the pressure drop Δp_ich in internal channels of a hydraulic motor according to the method described in Section 3.4. For example, according to this method Δp_ich in an axial piston motor cannot be measured. Nevertheless, this measurement can be made using other methods, described in detail in [16].

Another issue requiring discussion is the value of geometric working volume q_g of the motor resulting from the CAD drawing documentation. Thus, this geometric working volume q_g is as much as 4.6% larger than the theoretical working volume q_t calculated according to the proposed new method. Why such a big difference? Components of the working mechanism are made by electrical cutting with wire. Obviously, this cut is made with certain allowance for the finishing treatment (lapping). The manufacturer of the motor does not reveal the size of the allowance and the final geometrical dimensions after lapping. As a result, the geometrical working volume of a satellite motor is definitely smaller than that of the drawing documentation. In addition, there are teeth tip clearances in a satellite working mechanism, the effect of which is a certain volume included in the geometric working volume. It can be assumed that the impact of this volume on the process of pumping liquid through the working mechanism is small or negligible. However, this thesis would require proof.