Integrating Bidirectionally Chargeable Electric Vehicles into the Electricity Markets
Abstract
1. Introduction
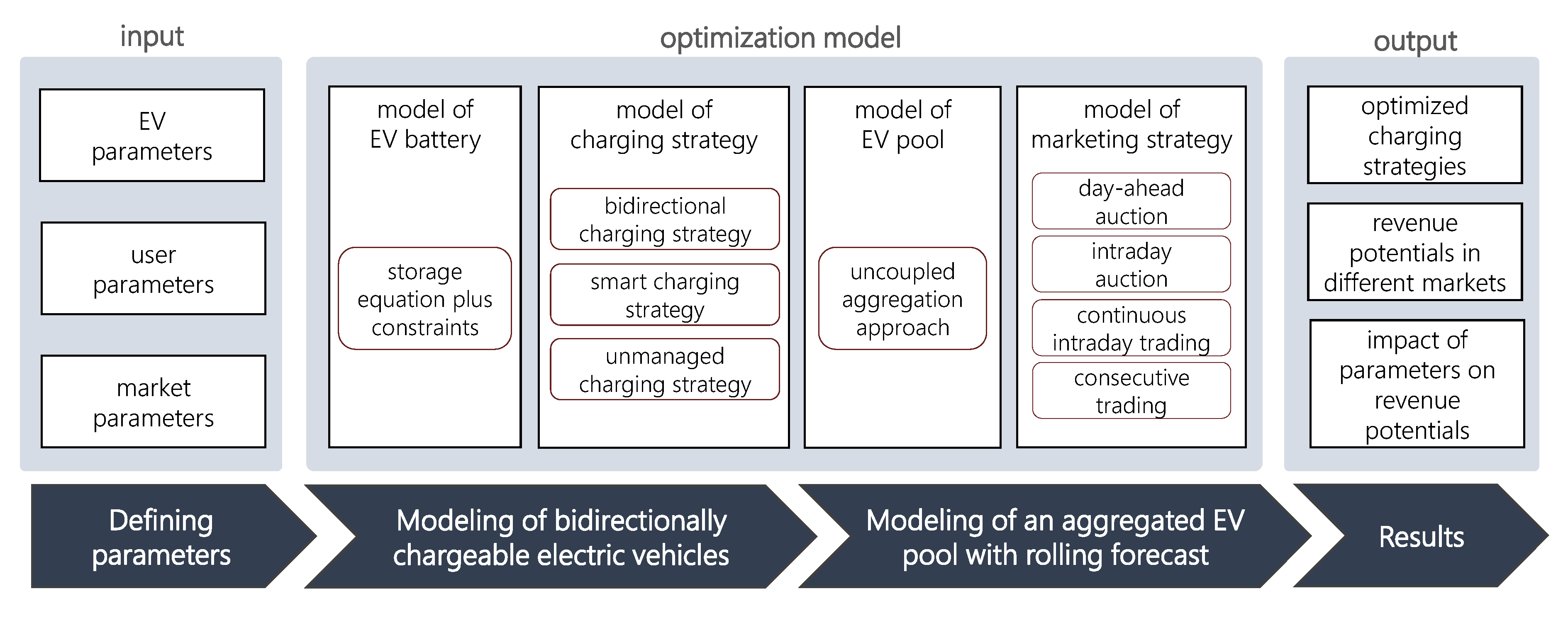
2. Methods
2.1. Modeling of Bidirectionally Chargeable Electric Vehicles
2.1.1. State of Charge
2.1.2. Charging/ Discharging Power and Already Traded Energy
2.1.3. Countertrades
2.1.4. Electricity Consumption and Fast Charging
2.2. Formulation of Optimization Model
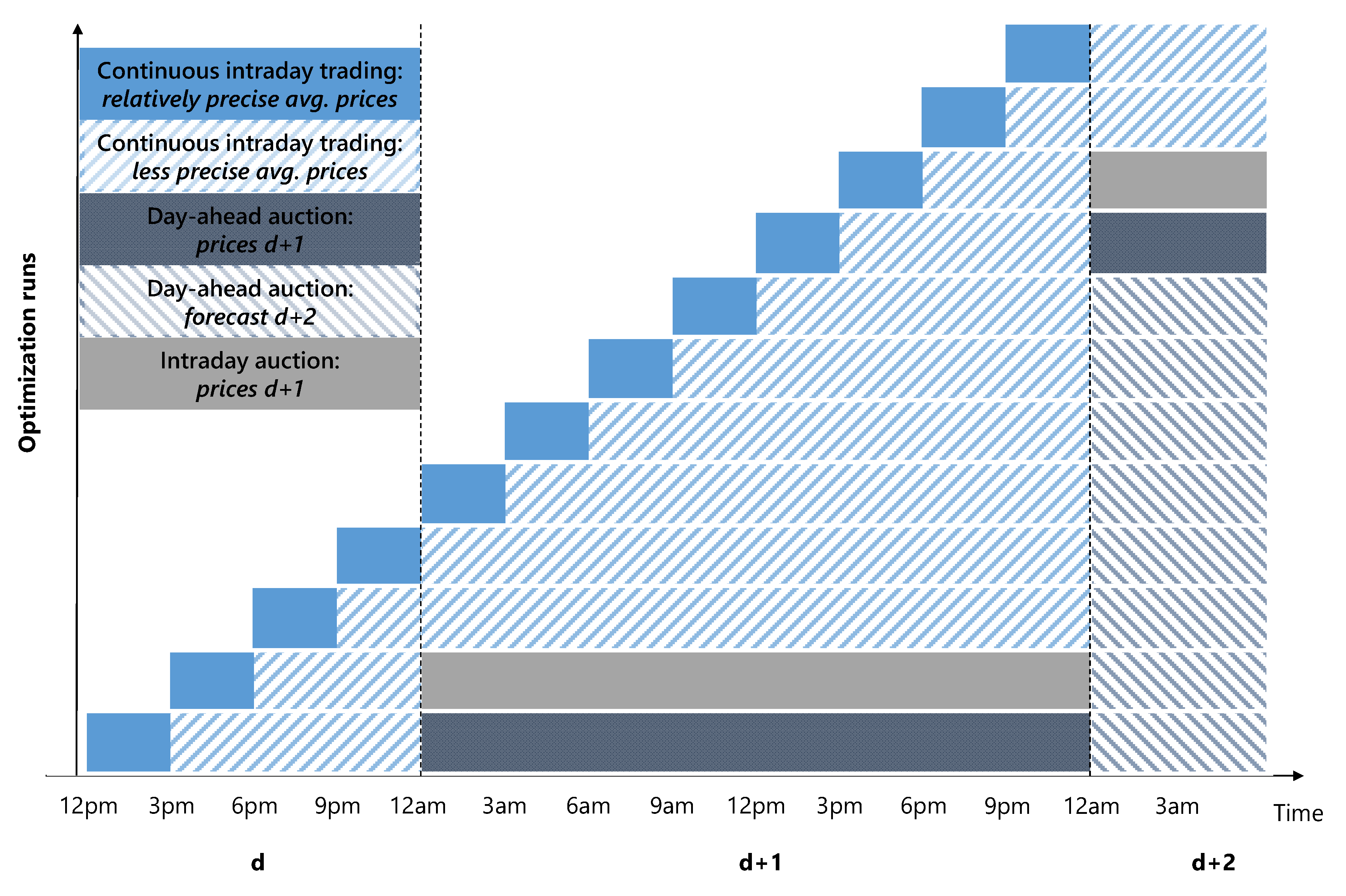
2.3. Optimization with Limited Forecast in Consecutive Spot Markets
2.4. Input Data and Parameterization of Electric Vehicle (EV) Pool Scenarios
- A change of location is always accompanied by a driving phase.
- During each driving phase, the EV has discrete consumption, which leads to a reduction of the storage level.
- The EV can be located and connected either at the place of residence, the place of work or the public space
- a commuter pool consisting of representatives of all 12 commuter groups;
- a non-commuter pool consisting of representatives of all 3 non-commuter groups.
3. Results
3.1. Revenue Potentials for Vehicle-to-Grid (V2G) Use Cases
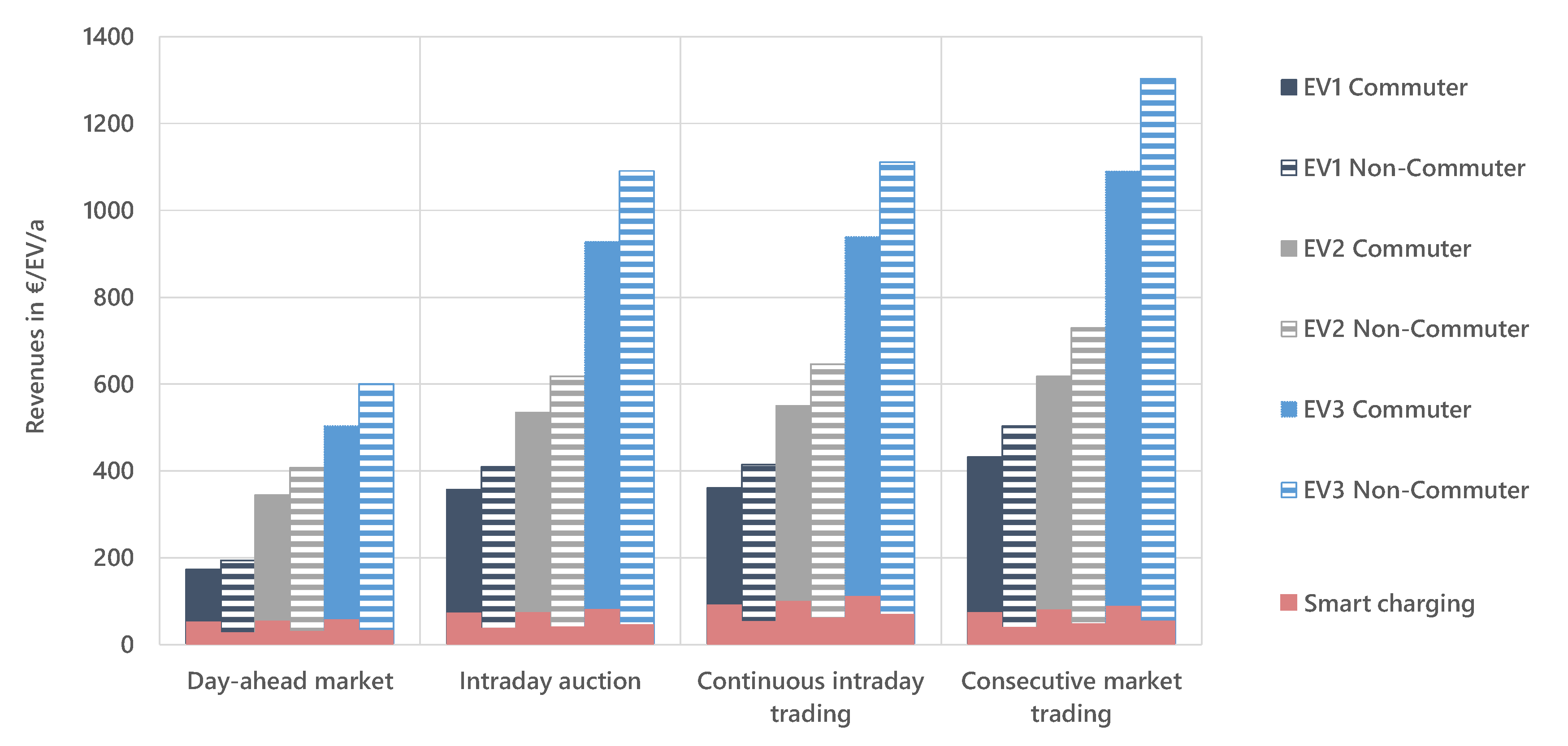
3.1.1. Revenue Potential in the German Spot Market
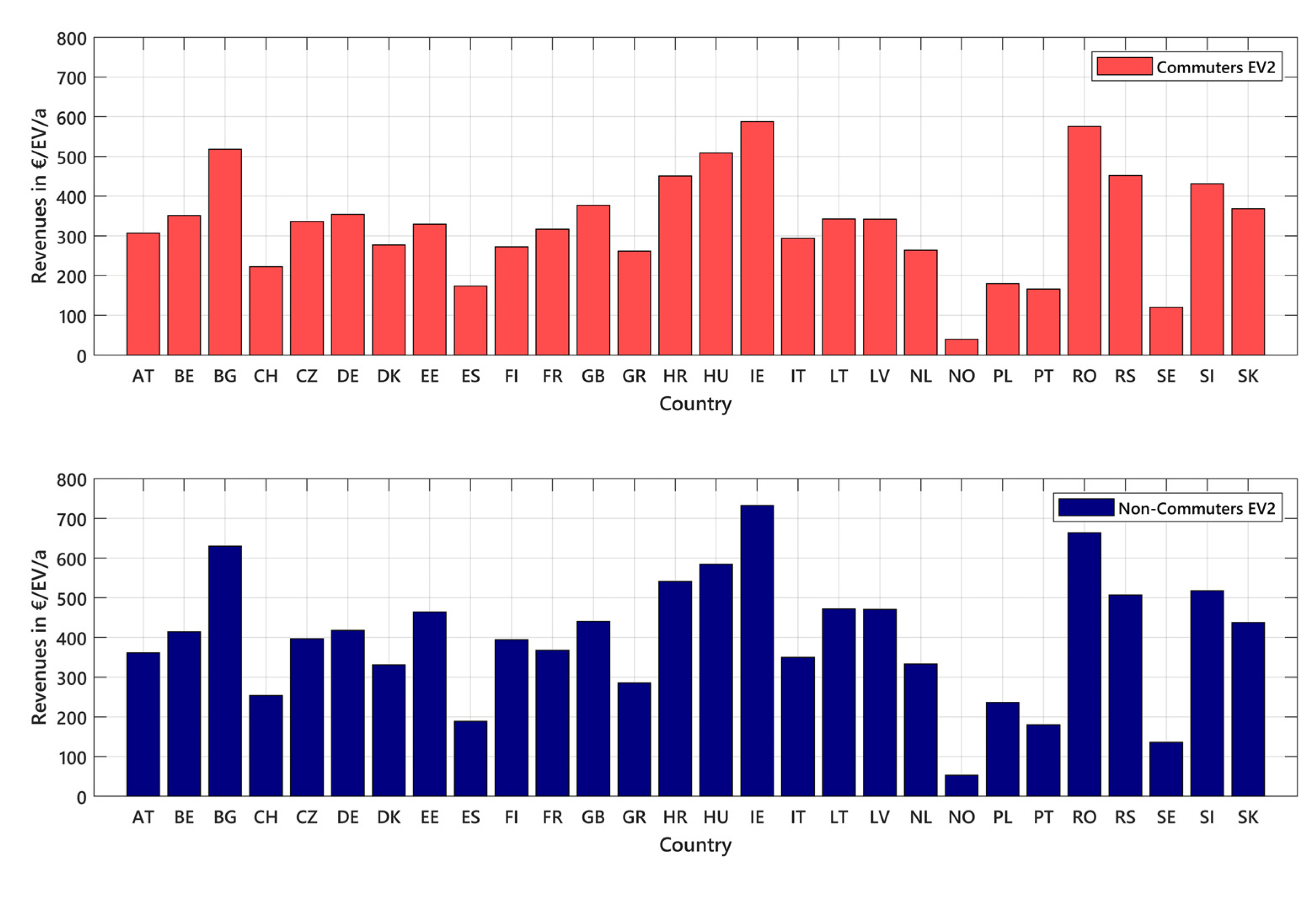
3.1.2. Revenue Potential in European Markets
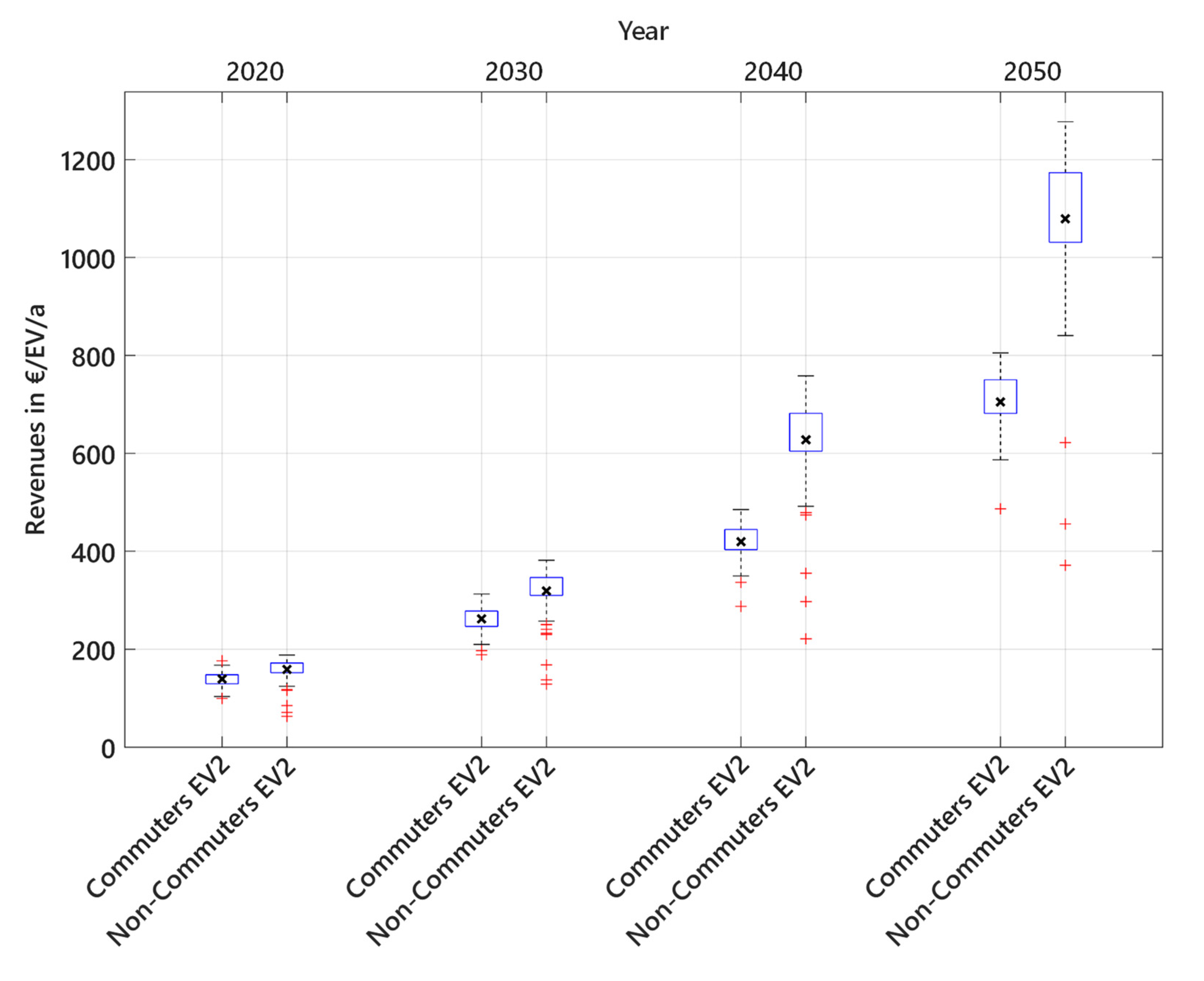
3.1.3. Revenue Potential for Future Day-Ahead Market Prices
3.2. Effect of V2G Use Cases on Full Cycles and Operating Hours
3.2.1. Effect of Unrestricted Trading in the Electricity Markets
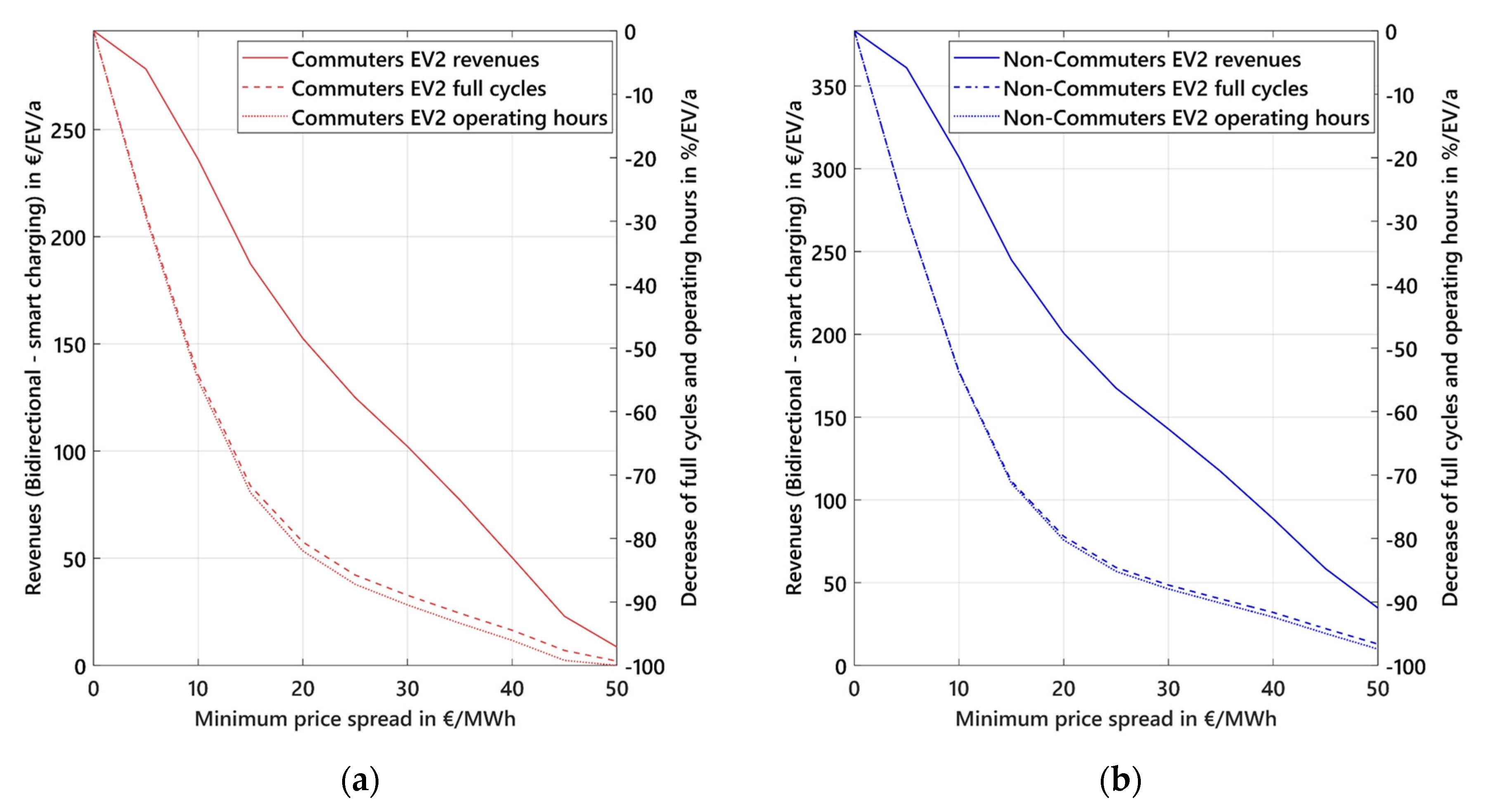
3.2.2. Effect of Restricted Trading in the Electricity Markets
3.3. Analysis of User Parameters and Regulatory Framework on Revenue Potentials of V2G Use Cases
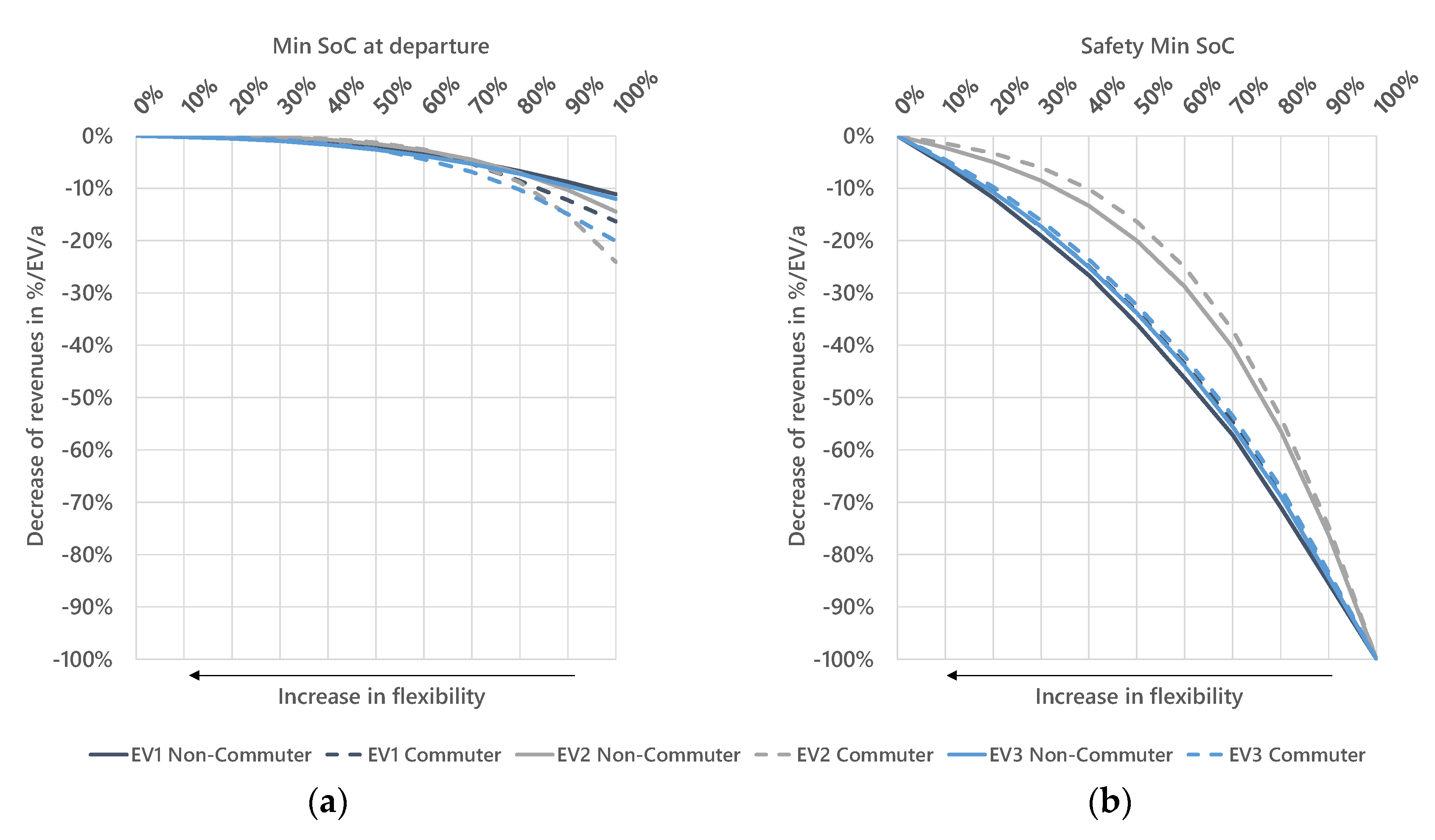
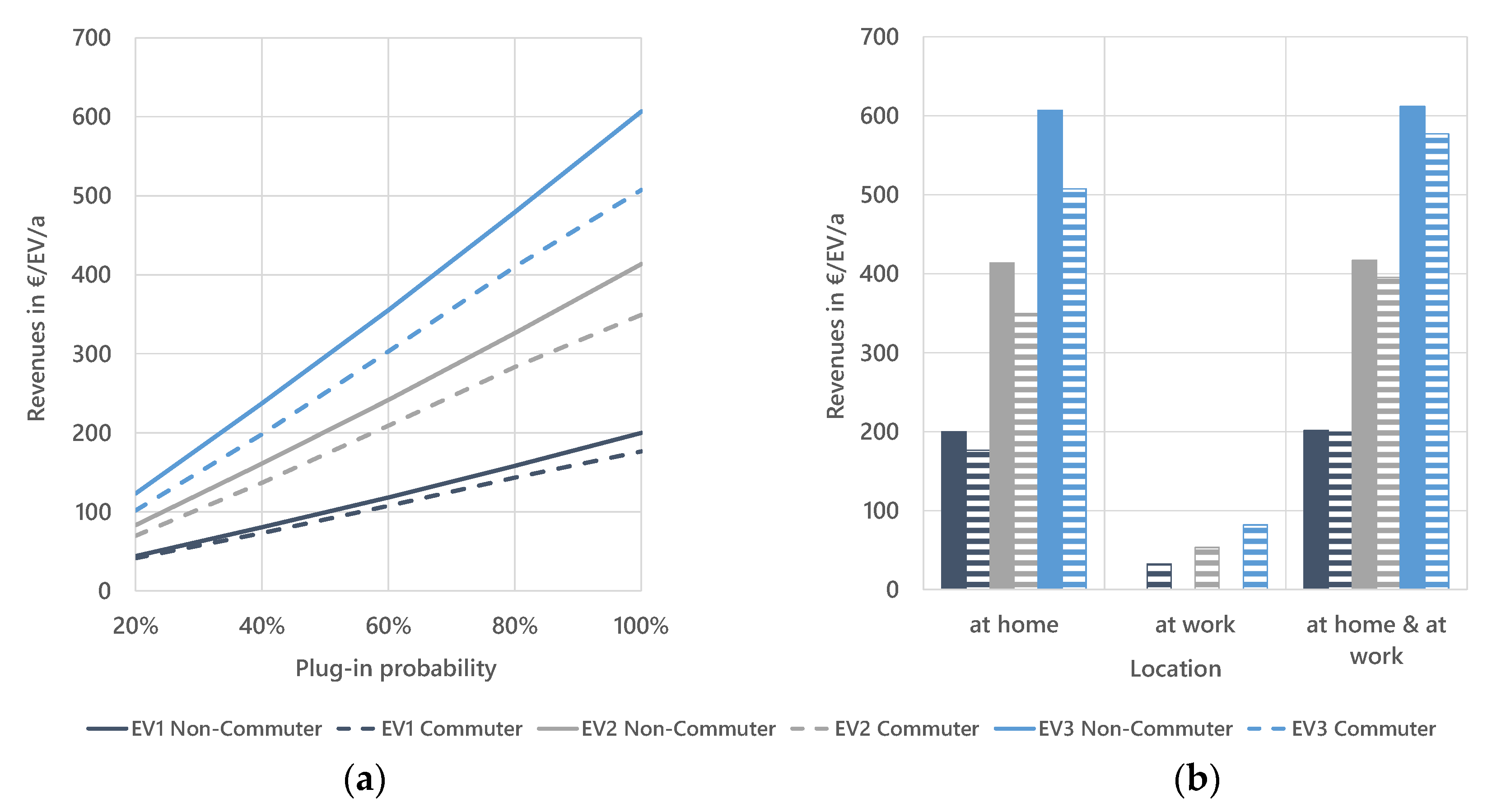
3.3.1. Influence of User Parameters
Minimum SoC at Departure
Minimum Safety SoC
Plug-in Probability
Charging Point Location
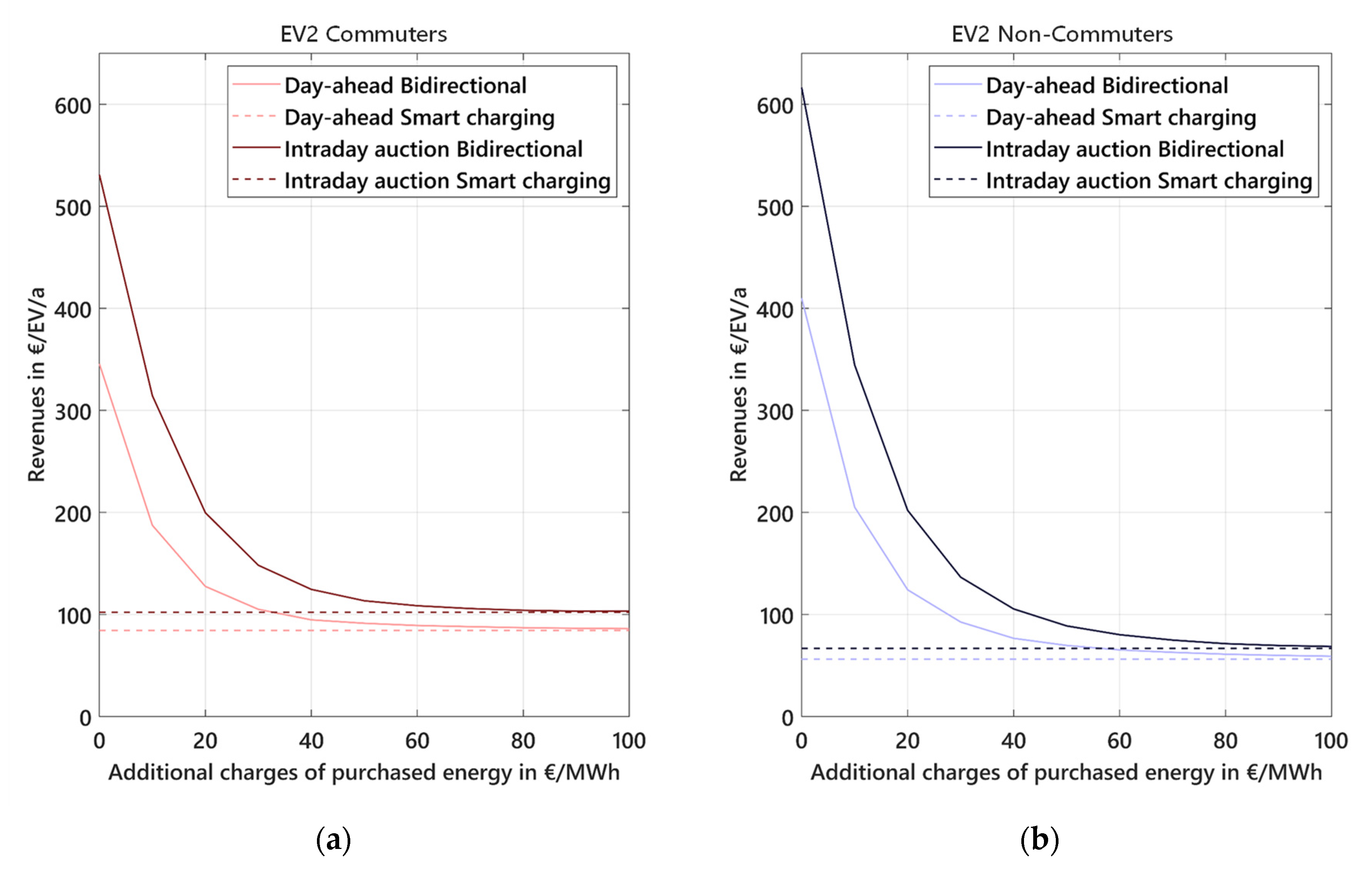
3.3.2. Impact of Regulatory Framework on Revenue Potentials
4. Discussion
5. Conclusions
- We developed a rolling optimization model that regards real trading times of European spot markets and allows countertrading in consecutive traded markets while considering user behavior parameters leading to a realistic representation of revenue potentials of bidirectionally chargeable EVs using arbitrage trading.
- Revenues of bidirectionally chargeable EVs are dependent on user parameters. An increase of the safety minimum SoC at the place of residence or the minimum SoC at departure leads to an exponential decrease of revenues for bidirectionally chargeable EVs.
- For a participation of bidirectionally chargeable EVs in the German spot markets in 2019, potential revenues range from 200 to 1300 €/EV/a depending on the modeled EV pool scenario under the assumption of no additional charges for purchased electricity.
- Revenues of currently available EV models participating in the day-ahead market are comparable to findings of other literature, while our research shows a significant increase in revenues for consecutive trading in all spot markets.
- The regulatory framework concerning additional charges of purchased energy is the most decisive parameter for the potential revenues of bidirectionally chargeable EVs.
- Considering additional charges amounting for example to the payments of a pumped storage facility for bidirectionally chargeable EVs results in a decrease of revenues by 50% to 60%. Thus, if V2G arbitrage trading is supposed to give flexibility to the future energy system, the market regulator will have to exempt bidirectionally chargeable EVs from the major part of additional charges.
- Unrestricted arbitrage trading of bidirectionally chargeable EVs results in a sharp increase of full cycles and operating hours by 200 to 600 full cycles/a, respectively, by 2000 to 6000 h/a resulting in much faster battery degradation. Restricted arbitrage trading with a minimum price spread can lower this additional load for EV and EVSE. For a minimum price spread of 10 €/MWh, operating hours and full cycles decrease by 50% while revenues only decrease by 20%.
- Revenues of bidirectionally chargeable EVs differ widely depending on the electricity production structure of the energy system. European day-ahead market revenues for EV2 in 2019 range from 50 €/EV/a in Norway to 700 €/EV/a in Ireland. Modeled potential future revenues are 2 times higher in 2030 and 5 to 6 times higher in 2050 than modeled revenues in 2020.
6. Data Availability
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Time-Dependent Variables | Minimum Value | Maximum Value | |
|---|---|---|---|
| State of charge | |||
| Charging power | |||
| Discharging power | |||
| Discharging boolean | 0 | 1 | |
| Charging boolean | 0 | 1 | |
| Counter purchase power | 0 | ||
| Counter sale power | 0 | ||
| Counter purchase boolean | 0 | 1 | |
| Counter sale boolean | 0 | 1 | |
| Supplementary power | 0 | ∞ | |
| Fast charging power | 0 | ∞ | |
Appendix B
Influence of Forecast Period
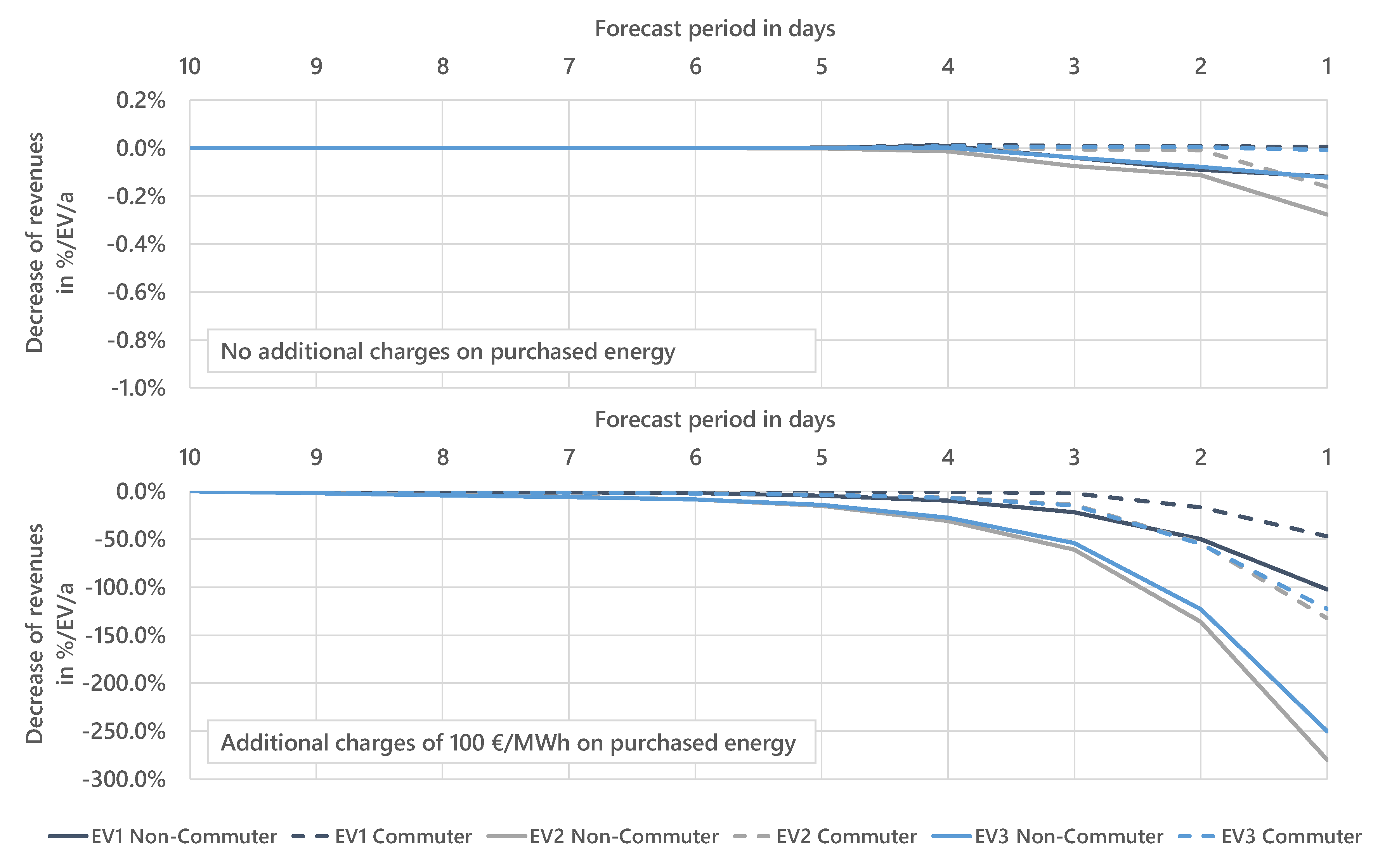
Appendix C
Determination of a Realistic Pool Size
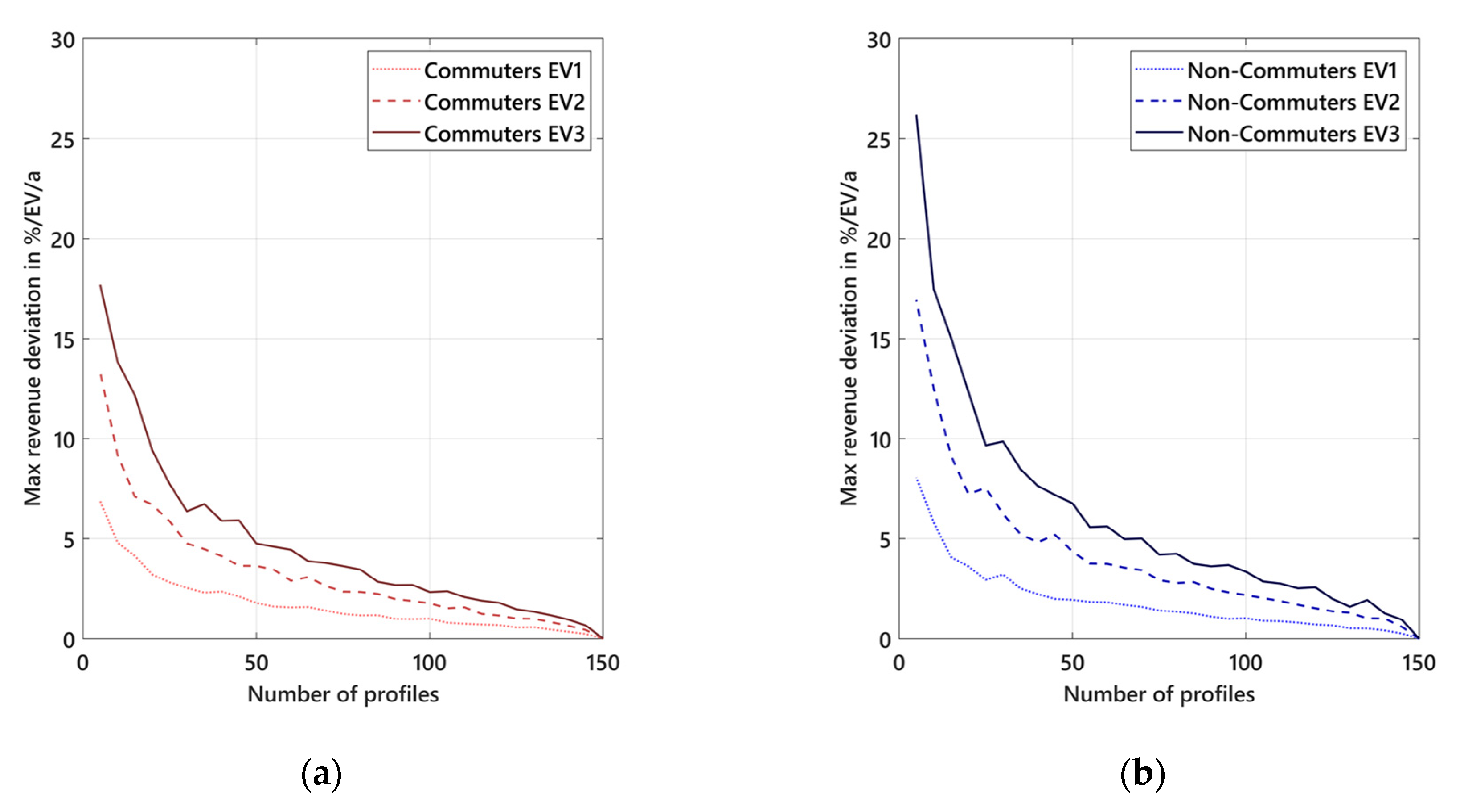
Appendix D
| EV1—Commuter | ||||||
|---|---|---|---|---|---|---|
| Minimum Price spread in €/MWh | Revenues in €/EV/a | Full Cycles per Year | Operating Hours per Year | Average Price Spread in €/MWh | Revenue/ Full Cycle in €/Full Cycle | Revenue/ Operating Hour in €/Operating Hour |
| 0 | 125.1 | 231.0 | 1898 | 14.2 | 0.54 | 0.07 |
| 5 | 117.7 | 166.7 | 1363 | 18.6 | 0.71 | 0.09 |
| 10 | 97.8 | 102.9 | 841 | 25.0 | 0.95 | 0.12 |
| 15 | 75.5 | 60.4 | 494 | 32.9 | 1.25 | 0.15 |
| 20 | 59.7 | 38.7 | 319 | 40.6 | 1.54 | 0.19 |
| 25 | 46.2 | 25.6 | 210 | 47.4 | 1.80 | 0.22 |
| 30 | 37.1 | 18.6 | 153 | 52.6 | 2.00 | 0.24 |
| 35 | 27.7 | 13.1 | 109 | 55.7 | 2.12 | 0.25 |
| 40 | 17.2 | 8.0 | 67 | 56.8 | 2.16 | 0.26 |
| 45 | 6.6 | 2.8 | 24 | 62.9 | 2.39 | 0.27 |
| 50 | 2.7 | 0.9 | 7 | 77.2 | 2.93 | 0.35 |
| EV1—Non-Commuter | ||||||
| Minimum Price Spread in €/MWh | Revenues in €/EV/a | Full Cycles per Year | Operating Hours per Year | Average Price Spread in €/MWh | Revenue/ Full Cycle in €/Full Cycle | Revenue/ Operating Hour in €/Operating Hour |
| 0 | 173.3 | 324.2 | 2737 | 14.1 | 0.53 | 0.06 |
| 5 | 162.5 | 226.7 | 1911 | 18.9 | 0.72 | 0.08 |
| 10 | 135.6 | 139.5 | 1173 | 25.6 | 0.97 | 0.12 |
| 15 | 107.1 | 85.0 | 712 | 33.2 | 1.26 | 0.15 |
| 20 | 86.1 | 56.1 | 472 | 40.4 | 1.54 | 0.18 |
| 25 | 68.7 | 38.8 | 327 | 46.6 | 1.77 | 0.21 |
| 30 | 56.5 | 29.0 | 245 | 51.3 | 1.95 | 0.23 |
| 35 | 44.2 | 22.1 | 189 | 52.7 | 2.00 | 0.23 |
| 40 | 33.7 | 16.5 | 140 | 53.9 | 2.05 | 0.24 |
| 45 | 19.9 | 10.1 | 87 | 51.9 | 1.97 | 0.23 |
| 50 | 10.8 | 5.5 | 48 | 51.4 | 1.95 | 0.23 |
| EV2—Commuter | ||||||
| Minimum Price Spread in €/MWh | Revenues in €/EV/a | Full Cycles per Year | Operating Hours per Year | Average Price Spread in €/MWh | Revenue/ Full Cycle in €/Full Cycle | Revenue/ Operating Hour in €/Operating Hour |
| 0 | 296.1 | 211.4 | 3963 | 14.0 | 1.40 | 0.07 |
| 5 | 278.2 | 150.5 | 2819 | 18.5 | 1.85 | 0.10 |
| 10 | 236.1 | 96.8 | 1815 | 24.4 | 2.44 | 0.13 |
| 15 | 187.3 | 59.9 | 1123 | 31.3 | 3.13 | 0.17 |
| 20 | 152.5 | 41.3 | 766 | 37.0 | 3.70 | 0.20 |
| 25 | 125.0 | 30.3 | 561 | 41.3 | 4.13 | 0.22 |
| 30 | 102.1 | 23.5 | 434 | 43.4 | 4.34 | 0.24 |
| 35 | 77.2 | 17.5 | 322 | 44.0 | 4.40 | 0.24 |
| 40 | 50.3 | 11.9 | 216 | 42.3 | 4.23 | 0.23 |
| 45 | 22.9 | 5.2 | 93 | 44.3 | 4.43 | 0.25 |
| 50 | 8.6 | 1.6 | 30 | 52.9 | 5.29 | 0.29 |
| EV2—Non-Commuter | ||||||
| Minimum Price Spread in €/MWh | Revenues in €/EV/a | Full Cycles per Year | Operating Hours per Year | Average Price Spread in €/MWh | Revenue/ Full Cycle in €/Full Cycle | Revenue/ Operating Hour in €/Operating Hour |
| 0 | 383.4 | 270.7 | 5113 | 14.2 | 1.42 | 0.07 |
| 5 | 361.0 | 192.5 | 3645 | 18.8 | 1.88 | 0.10 |
| 10 | 307.0 | 125.4 | 2383 | 24.5 | 2.45 | 0.13 |
| 15 | 245.0 | 78.7 | 1498 | 31.1 | 3.11 | 0.16 |
| 20 | 200.7 | 55.2 | 1045 | 36.4 | 3.64 | 0.19 |
| 25 | 167.5 | 41.9 | 795 | 40.0 | 4.00 | 0.21 |
| 30 | 142.8 | 34.5 | 654 | 41.5 | 4.15 | 0.22 |
| 35 | 117.1 | 28.5 | 541 | 41.0 | 4.10 | 0.22 |
| 40 | 88.6 | 22.8 | 429 | 38.9 | 3.89 | 0.21 |
| 45 | 58.5 | 15.9 | 299 | 36.8 | 3.68 | 0.20 |
| 50 | 34.7 | 9.3 | 174 | 37.3 | 3.73 | 0.20 |
| EV3—Commuter | ||||||
| Minimum Price Spread in €/MWh | Revenues in €/EV/a | Full Cycles per Year | Operating Hours per Year | Average Price Spread in €/MWh | Revenue/ Full Cycle in €/Full Cycle | Revenue/ Operating Hour in €/Operating Hour |
| 0 | 451.2 | 301.4 | 2994 | 15.0 | 1.50 | 0.15 |
| 5 | 430.6 | 227.5 | 2243 | 18.9 | 1.89 | 0.19 |
| 10 | 369.2 | 151.5 | 1487 | 24.4 | 2.44 | 0.25 |
| 15 | 290.4 | 92.4 | 898 | 31.4 | 3.14 | 0.32 |
| 20 | 231.8 | 60.6 | 582 | 38.3 | 3.83 | 0.40 |
| 25 | 187.6 | 42.6 | 402 | 44.0 | 4.40 | 0.47 |
| 30 | 152.0 | 31.9 | 297 | 47.7 | 4.77 | 0.51 |
| 35 | 123.6 | 24.5 | 227 | 50.4 | 5.04 | 0.54 |
| 40 | 85.1 | 17.1 | 156 | 49.8 | 4.98 | 0.55 |
| 45 | 41.7 | 8.5 | 75 | 49.2 | 4.92 | 0.55 |
| 50 | 16.7 | 2.8 | 25 | 59.1 | 5.91 | 0.66 |
| EV3—Non-Commuter | ||||||
| Minimum Price Spread in €/MWh | Revenues in €/EV/a | Full Cycles per Year | Operating Hours per Year | Average Price Spread in €/MWh | Revenue/ Full Cycle in €/Full Cycle | Revenue/ Operating Hour in €/Operating Hour |
| 0 | 574.6 | 397.5 | 3979 | 14.5 | 1.45 | 0.14 |
| 5 | 545.8 | 291.1 | 2913 | 18.8 | 1.88 | 0.19 |
| 10 | 466.9 | 191.4 | 1916 | 24.4 | 2.44 | 0.24 |
| 15 | 370.3 | 118.3 | 1188 | 31.3 | 3.13 | 0.31 |
| 20 | 298.4 | 79.2 | 795 | 37.7 | 3.77 | 0.38 |
| 25 | 243.9 | 56.8 | 568 | 42.9 | 4.29 | 0.43 |
| 30 | 202.6 | 44.2 | 444 | 45.9 | 4.59 | 0.46 |
| 35 | 171.8 | 36.2 | 365 | 47.5 | 4.75 | 0.47 |
| 40 | 132.8 | 28.4 | 287 | 46.7 | 4.67 | 0.46 |
| 45 | 92.3 | 20.7 | 211 | 44.6 | 4.46 | 0.44 |
| 50 | 56.0 | 12.7 | 128 | 44.1 | 4.41 | 0.44 |
References
- BMU. Klimaschutz in Zahlen—Fakten, Trends und Impulse deutscher Klimapolitik; BMU: Berlin, Germany, 2018.
- Fattler, S.; Regett, A. Environmental Impact of Electric Vehicles: Influence of Intelligent Charging Strategies. In Grid Integration of Electric Mobility 2019; Forschungsstelle für Energiewirtschafte e.V: München, Germany, 2019. [Google Scholar]
- European Comission. A Clean Planet for All –A European Strategic Long-Term Vision for A Prosperous, Modern, Competitive and Climate Neutral Economy; European Commission: Brussels, Belgium, 2018. [Google Scholar]
- Hinterstocker, M.; Ostermann, A.; Muller, M.; Dossow, P.; von Roon, S.; Kern, T.; Pellinger, C. Bidirectional Charging Management—Field Trial and Measurement Concept for Assessment of Novel Charging Strategies; Forschungsstelle für Energiewirtschaft e.V.: München, Germany, 2019. [Google Scholar]
- Pham, T. Do German renewable energy resources affect prices and mitigate market power in the French electricity market? Appl. Econ. 2019, 51, 1–14. [Google Scholar] [CrossRef]
- EPEX SPOT SE. Trading on EPEX SPOT; EPEX SPOT SE: Paris, France, 2019. [Google Scholar]
- Illing, B.; Warweg, O. Analysis of international approaches to integrate electric vehicles into energy market. In Proceedings of the 12th International Conference on the European Energy Market (EEM), Lisbon, Portugal, 19–22 May 2015. [Google Scholar]
- Shafiullah, M.; Al-Awami, A.T. Maximizing the profit of a load aggregator by optimal scheduling of day ahead load with EVs. In Proceedings of the 2015 IEEE International Conference on Industrial Technology (ICIT), Seville, Spain, 17–19 March 2015. [Google Scholar]
- Illing, B.; Warweg, O. Achievable revenues for electric vehicles according to current and future energy market conditions. In Proceedings of the 13th International Conference on the European Energy Market (EEM), Porto, Portugal, 6–9 June 2016. [Google Scholar]
- Bessa, R.J.; Matos, M.A.; Soares, F.J.; Lopes, J.A.P. Optimized Bidding of a EV Aggregation Agent in the Electricity Market. IEEE Trans. Smart Grid 2011, 3, 443–452. [Google Scholar] [CrossRef]
- Rominger, J.; Losch, M.; Steuer, S.; Koper, K.; Schmeck, H. Analysis of the German Continuous Intraday Market and the Revenue Potential for Flexibility Options; IEEE: Piscataway, NJ, USA, 2019. [Google Scholar]
- Schmidt, R.; Schnittmann, E.; Meese, J.; Dahlmann, B.; Zdrallek, M.; Armoneit, T. Revenue-Optimized Marketing of Electric Vehicles’ Flexibility Options; IEEE: Piscataway, NJ, USA, 2019. [Google Scholar]
- Peterson, S.B.; Whitacre, J.; Apt, J. The Economics of Using Plug-In Hybrid Electric Vehicle Battery Packs for Grid Storage; RELX Group: London, UK, 2009. [Google Scholar]
- Pelzer, D.; Ciechanowicz, D.; Knoll, A. Energy arbitrage through smart scheduling of battery energy storage considering battery degradation and electricity price forecasts. In Proceedings of the IEEE Innovative Smart Grid Technologies Asia (ISGT-Asia), Melbroune, Australia, 28 November–1 December 2016. [Google Scholar]
- Hanemann, P.; Bruckner, T. Effects of electric vehicles on the spot market price. Energy 2018, 162, 255–266. [Google Scholar] [CrossRef]
- Rodriguez, C.D.B.; Segura, J.A.J.; Ruiz, M.C.C.; Estevez, G.A.J.; Araya, P.A.M. Evaluating the Impact of a V2G Scheme on the Demand Curve; IEEE: Piscataway, NJ, USA, 2019. [Google Scholar]
- Kern, T.; Hintersrocker, M.; von Roon, S. Rückwirkungen von Batterie-Vermarktungsoptionen auf den Strommarkt. In Proceedings of the 11 Internationale Energiewirtschaftstagung an der TU Wien (IEWT 2019), Vienna, Austria, 13–15 February 2019. [Google Scholar]
- Technical Specifications BMW i3 (120 Ah). Available online: https://www.press.bmwgroup.com/global/article/attachment/T0284828EN/415571 (accessed on 7 October 2020).
- New Renault Zoe 2017. Available online: https://www.renault.com.au/sites/default/files/pdf/brochure/ZOE-Brochure-Desktop_0.pdf (accessed on 7 October 2020).
- infas Institut für angewandte Sozialwissenschaft GmbH. Mobilität in Deutschland 2017–Datensatz; infas Institut für angewandte Sozialwissenschaft GmbH: Bonn, Germany, 2019. [Google Scholar]
- Pellinger, C.; Schmid, T. Merit Order der Energiespeicherung im Jahr 2030—Hauptbericht; Forschungsstelle für Energiewirtschaft e.V. (FfE): München, Germany, 2016. [Google Scholar]
- Fattler, S.; Böing, F.; Pellinger, C. Ladesteuerung von Elektrofahrzeugen und deren Einfluss auf betriebsbedingte Emissionen. In Proceedings of the IEWT 2017, 10 Internationale Energiewirtschaftstagung Wien, Vienna, Austria, 15–17 February 2017. [Google Scholar]
- Power Market Data. Available online: https://www.epexspot.com/en/market-data/ (accessed on 26 August 2020).
- Day-Ahead Prices. Available online: https://transparency.entsoe.eu/transmission-domain/r2/dayAheadPrices/show (accessed on 31 August 2020).
- BDEW. BDEW-Strompreisbestandteile Januar 2020—Haushalte und Industrie; BDEW Bundesverband der Energie-und Wasserwirtschaft e.V.: Berlin, Germany, 2020. [Google Scholar]
- Platts. WEPP Database (Europe); Platts: Washington, DC, USA, 2018. [Google Scholar]
- International Energy Agency. Energy Policies of IEA Countries France 2016 Review; International Energy Agency: Paris, France, 2017. [Google Scholar]
- FfE. Hourly CO2 Emission Factors and Marginal Costs of Energy Carriers in Future Multi-Energy Systems (Germany); Forschungsstelle für Energiewirtschaft e. V. (FfE): München, Germany, 2019; Available online: http://opendata.ffe.de/dataset/dynamis-emission-factors/ (accessed on 28 August 2020).
- Böing, F.; Regett, A. Hourly CO2 Emission Factors and Marginal Costs of Energy Carriers in Future Multi-Energy Systems. Energies 2019, 12, 2260. [Google Scholar] [CrossRef]
- Beran, P.; Pape, C.; Weber, C. Modelling German Electricity Wholesale Spot Prices with a Parsimonious Fundamental Model—Validation and Application; House of Energy Markets and Finance: Duisburg-Essen, Germany, 2018. [Google Scholar]
- BYD Company Limited. Battery Box 2.5. Available online: https://www.climaverd.com/sites/default/files/2019-06/ft_sb_byd_b-box_2.5-10.0_b-plus_2.5_en.pdf (accessed on 27 August 2020).
- BMZ Energy Storage Systems. Maximum Performance for Your Independence. Available online: https://bmz-group.com/images/PDF-Downloads/Broschuere-ESS_EN_with_ESSX.pdf (accessed on 27 August 2020).
- Ma, K.; Yang, Y.; Wang, H.; Blaabjerg, F. Design for Reliability of Power Electronics in Renewable Energy Systems. In Use, Operation and Maintenance of Renewable Energy Systems; Sanz-Bobi, M.A., Ed.; Springer: Basel, Switerzland, 2014. [Google Scholar]
- EASE. Energy Storage: A Key Enabler for the Decarbonisation of the Transport Sector; EASE—European Association for Storage of Energy: Brussels, Belgium, 2019. [Google Scholar]
- Conrad, J.; Pellinger, C.; Hinterstocker, M. Gutachten zur Rentabilität von Pumpspeicherkraftwerken; Forschungsstelle für Energiewirtschaft e.V. (FfE): München, Germany, 2014. [Google Scholar]
- Bundesnetzagentur für Elektrizität, Gas, Telekommunikation, Post und Eisenbahnen. Regelungen zu Stromspeichern im deutschen Strommarkt; Bundesnetzagentur für Elektrizität, Gas, Telekommunikation, Post und Eisenbahnen: Bonn, Germany, 2020.
- Sandelic, M.; Stroe, D.-I.; Iov, F. Battery Storage-Based Frequency Containment Reserves in Large Wind Penetrated Scenarios: A Practical Approach to Sizing. Energies 2018, 11, 3065. [Google Scholar] [CrossRef]
- Ciechanowicz, D.; Knoll, A.; Osswald, P.; Pelzer, D. Towards a Business Case for Vehicle-to-Grid—Maximizing Profits in Ancillary Service Markets; Springer: Singapore, 2015. [Google Scholar]
- Clairand, J.M. Participation of electric vehicle aggregators in ancillary services considering users’ preferences. Sustainability 2020, 12, 8. [Google Scholar] [CrossRef]
- Szinai, J.K.; Sheppard, C.J.; Abhyankar, N.; Gopal, A.R. Reduced grid operating costs and renewable energy curtailment with electric vehicle charge management. Energy Policy 2020, 136, 111051. [Google Scholar] [CrossRef]
- Geske, J.; Schumann, D. Willing to participate in vehicle-to-grid (V2G)? Why not! Energy Policy 2018, 120, 392–401. [Google Scholar] [CrossRef]
- BDEW. Energy Market Germany 2020; Bundesverband der Energie- und Wasserwirtschaft (BDEW): Berlin, Germany, 2020. [Google Scholar]
- Besserladen. Wallbox Quasar—Bidirektionale Ladestation. Available online: https://besserladen.de/produkt/wallbox-quasar-bidirektionale-ladestation/ (accessed on 28 August 2020).
| Parameter | EV1 | EV2 | EV 3 | |
|---|---|---|---|---|
| Storage capacity | 38 kWh | 100 kWh | 100 kWh | |
| Charging power | 11 kW | 11 kW | 22 kW | |
| Discharging power | 10 kW | 11 kW | 22 kW | |
| Charging efficiency (AC-DC) | 92.5% | 94.5% | 95.0% | |
| Discharging efficiency (DC-AC) | 92.0% | 94.5% | 95.0% | |
| Roundtrip efficiency (AC-AC) | 85.1% | 89.3% | 90.3% | |
| Pools of Driving Profiles | Probability of Whereabouts | Averaged Consumption (kWh/100 km) | Averaged Driving Distance (km/a) | |||
|---|---|---|---|---|---|---|
| Place of Residence | Place of Work | Public Space | Driving Phase | |||
| Commuter Pool | 68.8% | 22.1% | 3.6% | 5.5% | 17.4 | 13,600 |
| Non-commuter Pool | 87.5% | 1.4% | 7.9% | 3.2% | 17.4 | 8300 |
| Parameter | Value | Type | Further Discussion of Parameters’ Influence on Revenue Potentials |
|---|---|---|---|
| Minimum SoC at departure | 70% | User | Section 3.3.1 |
| Minimum safety SoC | 20% (EV1 and EV2) 30% (EV3) | User | Section 3.3.1 |
| Plug-in probability | 100% | User | Section 3.3.1 |
| Charging point location | At place of residence | User | Section 3.3.1 |
| Additional charges of purchased energy | 0 €/MWh | Regulatory | Section 3.3.2 |
| Forecast period | 1 day | Model | Appendix B |
| EV pool size | Commuter: 50 Non-commuter: 75 | Model | Appendix C |
| Year | 2020 (Modeled) | 2030 (Modeled) | 2040 (Modeled) | 2050 (Modeled) | 2019 (Real Prices) |
|---|---|---|---|---|---|
| Mean day-ahead price in €/MWh | 46.3 | 61.2 | 63.8 | 80.4 | 37.7 |
| Daily standard deviation of day-ahead price in €/MWh | 5.0 | 8.7 | 15.8 | 25.9 | 9.0 |
| Market Modeling | Affected EV Parameter | Commuters | Non-Commuters | ||||
|---|---|---|---|---|---|---|---|
| EV1 | EV2 | EV3 | EV1 | EV2 | EV3 | ||
| Reference Unmanaged charge | Full cycles | 60 | 25 | 25 | 35 | 15 | 15 |
| Operating Hours | 400 | 400 | 340 | 250 | 250 | 190 | |
| Arbitrage: Day-ahead market | Full cycles | 230 | 210 | 300 | 320 | 270 | 400 |
| Revenues/Full cycle | 0.8 | 1.7 | 1.7 | 0.6 | 1.5 | 1.5 | |
| Operating Hours | 1860 | 3900 | 2920 | 2710 | 5070 | 3930 | |
| Arbitrage: Intraday auction | Full cycles | 490 | 270 | 490 | 640 | 340 | 630 |
| Revenues/Full cycle | 0.7 | 2.0 | 1.9 | 0.7 | 1.9 | 1.7 | |
| Operating Hours | 3760 | 4880 | 4660 | 4890 | 6180 | 5970 | |
| Arbitrage: Continuous intraday trading | Full cycles | 450 | 250 | 470 | 590 | 320 | 600 |
| Revenues/Full cycle | 0.8 | 2.2 | 2.0 | 0.7 | 2.0 | 1.9 | |
| Operating Hours | 3450 | 4670 | 4450 | 4490 | 5950 | 5680 | |
| Arbitrage: Consecutive trading | Full cycles | 440 | 240 | 450 | 570 | 300 | 570 |
| Revenues/Full cycle | 1.0 | 2.6 | 2.5 | 0.9 | 2.4 | 2.3 | |
| Operating Hours | 3280 | 4350 | 4110 | 4340 | 5590 | 5310 | |
| Market | Average Market Volume in Germany 2019 | EVs with 10 kW Charging Station to Completely Cover the Market |
|---|---|---|
| Day-ahead market | 26,000 MW (EPEX Spot) 1 58,000 MW (German demand) 2 | 2.6 mil (EPEX Spot) 5.8 mil (German demand) |
| Quarter hourly intraday auction | 800 MW 1 | 80,000 |
| Hourly continuous intraday trading | 4500 MW 1 | 450,000 |
| Quarter hourly continuous intraday trading | 800 MW 1 | 80,000 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kern, T.; Dossow, P.; von Roon, S. Integrating Bidirectionally Chargeable Electric Vehicles into the Electricity Markets. Energies 2020, 13, 5812. https://doi.org/10.3390/en13215812
Kern T, Dossow P, von Roon S. Integrating Bidirectionally Chargeable Electric Vehicles into the Electricity Markets. Energies. 2020; 13(21):5812. https://doi.org/10.3390/en13215812
Chicago/Turabian StyleKern, Timo, Patrick Dossow, and Serafin von Roon. 2020. "Integrating Bidirectionally Chargeable Electric Vehicles into the Electricity Markets" Energies 13, no. 21: 5812. https://doi.org/10.3390/en13215812
APA StyleKern, T., Dossow, P., & von Roon, S. (2020). Integrating Bidirectionally Chargeable Electric Vehicles into the Electricity Markets. Energies, 13(21), 5812. https://doi.org/10.3390/en13215812





