Statistical Methodology for the Definition of Standard Model for Energy Analysis of Residential Buildings in Korea

Abstract

This study was conducted to propose an optimal methodology for deriving a standard model from existing residential buildings. To strategically improve existing residential buildings, it is necessary to identify standard models that can be used as quantitative standards. In this study, a total of six methods were established for different algorithms in the dimensionality reduction and clustering stage of the data preprocessing stage. In addition, a total of 22,342 households’ data were analyzed, and a total of 26 variables were used to perform cluster analysis. The process of method 6 (data pre-processing, principal components analysis, clustering [K-medoids], verification) was proposed as a way to derive the standard model from the existing Korean housing. The method proposed in this study is capable of deriving a number of standard models considering all variables (n) in a single analysis. The representative building derived in this study contains a lot of building data, so it can be effectively used for planning and research related to buildings on a regional and national scale. In addition, this process can be applied to various buildings to derive representative buildings.

1. Introduction

According to the Climate Change 2014 Synthesis Report, the number of anthropogenic greenhouse gases recently released is the highest since observations, and several extreme weather and climate events have been observed since 1950 [1]. Korea participated in international efforts to respond to climate change and decided in 2015 to aim to “reduce 37% of greenhouse gas emissions forecast by 2030”. Among them, the building sector aims to reduce its emission forecast by 64.5 million tons through strengthening the energy standards of new buildings, improving energy performance of existing buildings, improving facility efficiency, and expanding supply of new and renewable energy, building energy information infrastructure, and others [2]. Accordingly, the government has revised and implemented the subdivision of regional classification and strengthening of the heat permeation rate (W/(m²·K)) of buildings in each region since September 2018 to expand the distribution of energy-saving buildings, but it is limited to new buildings [3]. To achieve the GHG emission forecast for the building sector, which was aimed at by 2030, it is time to try to improve energy efficiency not only for new construction but also for existing buildings [4,5]. For energy efficiency, high efficiency of equipment in existing buildings is also important, but first, it is necessary to improve the energy efficiency of the building itself so as to minimize the energy demand (kWh/(m²·a)) of the building [6,7,8]. For the strategic improvement of existing buildings, a standard model that can be used as a quantitative standard must be prepared [9,10,11]. This is because the optimal improvement process established by the standard model is easy to efficiently improve a large amount of buildings [12,13,14].

In order to define a standard model, it is necessary to consider various variables (features) affecting building energy. The cluster analysis (clustering) is a multivariate analysis method that classifies groups with similar characteristics when there is no external criterion to determine which group each individual belongs to. This method forms specialized clusters among individuals with similar patterns, and in this process, a representative point that is the center of each cluster is derived. A cluster is composed of two or more clusters with different characteristics, and it is possible to create a virtual object central to each cluster or to designate a central one among existing objects [15].

In previous studies involving standard models, studies using cluster analysis have been conducted. Schaefer et al. [16] used cluster analysis to find the standard buildings of low-income housing considering the features related to the geometry of the building. Two standard buildings were derived by cluster analysis of 120 houses, and simulations proved that the results obtained by cluster analysis were significant. In this paper, cluster analysis has proven to be a useful technique for obtaining reference buildings. However, the authors emphasize that to be very careful in choosing the variables in the analysis.

Tardioli et al. [17] presented a new methodology for identifying building groups and standard models in urban data sets. This methodology uses a combination of building classification, building clustering, and predictive modeling. The analysis was performed with Geneva’s dataset and included building type, construction period, location, and geometric information. Sixty-seven representative buildings [18] were identified in about 13,600 buildings, and five normalizations and GIS linkages were performed. There are some limitations to the approach presented, the most important of which is that clustering requires a complete set of data. In this study, the problem of lack of data and completeness of the data set was partially overcome (achieved an average accuracy of 89.6%) by using a random forest predictive modeling method.

Li et al. [19] presented a methodology for developing residential representative buildings at the district level for the purpose of bottom-up energy modeling. A satellite image of China’s Yuzhong district was used to create a 3D building information database for 575 residential buildings and to perform cluster analysis. As a result of analyzing the relative errors by simulating the energy consumption of the two representative buildings and the corresponding district, the result was 1.55%. However, this result has a limitation that the error rate of the simulation program and the actual building energy consumption are not considered in addition to the error rate of the energy consumption simulation result of the representative building and the district.

Kim et al. [20] developed a standard model for low-income housing to propose a remodeling optimization plan to improve energy efficiency [21]. The sample was extracted by sampling stratification for 2571 households of low-income housing and then analyzed by applying the Neyman allocation method. The average value of the flat type (living room, kitchen, bathroom, two rooms), building-oriented, floor area (44.5 m²), and window area ratio (three-way window) was set as the standard model. When comparing the annual energy consumption requirements of the Energy Census Report with the standard model, it showed a difference of 5.78% and 12.1% when compared to buildings of the same size.

Previous research has been conducted to derive the standard model. The model was able to see the importance of standards in carrying out an assessment of the energy use of a building or group of individual buildings. It can be confirmed that the cluster analysis [22,23,24,25,26,27,28,29] technique has been used as a tool for deriving a standard model, and its usefulness has been proven. However, the problem of data collection and incompleteness was the limit. Geometric characteristics were mainly considered in deriving the standard model, and a separate simulation was performed for verification. The verification method is different for each study, but it can be confirmed that the energy use was used as an indicator.

In this study, the cluster analysis technique was performed as the main analysis technique. Due to the nature of the building data, multivariate analysis was required, and it was judged that the techniques of finding representative points with different characteristics were appropriate in the process of deriving the standard model. In order to solve the incompleteness of the data based on the previous studies, we tried to improve the accuracy and reliability by varying the detailed methodology. In addition, various building characteristics used in the analysis of building energy were considered in the derivation of standard models to improve the limitations of existing research. Therefore, this study aims to propose an optimal methodology for deriving a standard model that reflects various characteristics of existing residential buildings.

2. Methodology

As shown in Figure 1, different methods were used in the preprocessing and clustering steps, and a total of six methods were set to perform the analysis. The analysis was conducted on existing housing in Korea that were improved by the energy efficiency improvement project in 2016–2018. The optimal method was suggested by evaluating the finally derived standard model. Details of the step-by-step method are covered in the subsections.

Figure 1. The study process.

2.1. Preparation

2.1.1. Data for Deriving a Standard Model

This study utilized a part of the database collected through “Energy Efficiency Improvement Project” from 2016 to 2018. The purpose of the study was to propose a methodology, and it was limited to existing homes with improved subject matters in the verification stage. So, the database used to derive the standard model used the improved housing data as the “Energy Efficiency Improvement Project”.

The collection data was collected based on ISO 52016-1:2017 (Energy performance of buildings—Energy needs for heating and cooling, internal temperatures, and sensible and latent heat loads—Part 1: Calculation procedures). The 8 items of categorical data for buildings, 18 items of numerical data related to building heat loss and gain, and a total of 26 items were used for analysis (Table 1).

Table 1. List of collected.

ID		Variables (Unit)	Note
Factor	F01	Identification number	Unique number for object identification
	F02	Region	Classification according to Energy saving design standards (Central/Southern/Jeju island)
	F03	City	-
	F04	Orientation	-
	F05	Structure	Classification by structure (light weight/heavy weight)
	F06	Building type	Types of residential buildings (Detached house, multi-family house, apartment unit in a house, row house, apartment, etc.)
	F07	Building construction	Classification by building material (Masonry, reinforced concrete, prefabricated panel, wood, etc.)
	F08	Boiler type	Classification by fuel
Independent variables	X01	Year of completion (year)	-
	X02	Heating area (m2)	The area heated in the house (≠X12)
	X03	Volume (m3)	-
	X04	Total area of wall (m2)	-
	X05	Averaged wall U-value (W/(m2∙K))	-
	X06	Total area of window (m2)	-
	X07	Averaged window U-value (W/(m2∙K))	-
	X08	Total area of door (m2)	-
	X09	Averaged door U-value (W/(m2∙K))	-
	X10	Total area of roof (m2)	-
	X11	Averaged roof U-value (W/(m2∙K))	-
	X12	Total area of Floor (m2)	-
	X13	Averaged floor U-value (W/(m2∙K))	-
	X14	Solar heat gain (W)	-
	X15	Averaged SC 1 (-)	1SC is shading coefficient
	X16	Averaged SHGC 2 (-)	2SHGC is solar heat gain coefficient
	X17	Efficiency of heating system (%)	Boiler energy efficiency
Dependent variable	Y01	E3 per unit area (kWh/(m2∙a))	3E is annual heating energy need

2.1.2. In-Situ Measurement Data for Standard Model Verification

The field measurement data (measured data) to be used to verify the accuracy of the methodology and standard model (simulated data) were collected by field measurement. For 50 of the target households (households that have implemented Energy Efficiency Improvement Project) from which the standard model was derived, it was carried out so that actual data could be constructed for the same items as in Table 1. From December 2018 to February 2019, we visited the target households, installed the measurement equipment in Table 2, and measured data for one week.

Table 2. Measurement detail.

	Measurement Item	Measurement Equipment
Floor plan and photo	Wall, floor, windows dimensions (m) and ceiling height	Laser distance meter
	Indoor and outdoor photo	camera
Thermal environment and thermal insulation performance	Indoor air temperature (°C)	Living environment measurement module Infrared camera
	Outdoor air temperature (°C)
	Indoor wall surface temperature (°C)
	Indoor Relative Humidity (%)
	Heat flow (W/m2)	G. Inc Heat flux sensor
	Air tightness (ACH50)	Blow door test

2.2. Preprocessing

Before performing the clustering algorithm, it is necessary to go through the process of processing data into a suitable form. The raw data may contain missing and outliers, and incomplete data hinders good results. In addition, the longer the number of objects (d) in the data, the longer it takes, and as the number of variables (x) and clusters (k) increases, the calculation time increases. It is necessary to process with high-quality data so that clustering can be achieved according to the purpose, and if necessary, to select key variables.

2.2.1. Data Preprocessing

The clustering algorithm finds a pattern based on the characteristics of the data. When the scale of the data is significantly different, the result is completely changed by the variable with the larger scale. Therefore, a standardization process is required so that all data is reflected in the analysis on the same scale.

Since the clustering algorithm is sensitive to outliers, z-score (Equation (1)) is applied to minimize the effect of outliers in preprocessing. The z-score does not generate standardized data on the exact same scale, but has the advantage of handling outliers well [16,17].

After standardization, Mahalanobis [30] distance was used for outlier detection (Equation (2)). Mahalanobis distance is a distance in the probability distribution and is useful for detecting outliers in multivariate data. Objects with outliers and missing values were removed to improve the accuracy of the clustering algorithm.

$$\mathrm{Z}=\frac{\left(x-m\right)}{\sigma }$$

(1)

where $\mathrm{Z}$: z-score, $x$: a row data, $m$: mean, $\sigma$: standard deviation.

$$D^2={\left(x-\mu \right)}^{\mathsf{{\rm T}}}{\mathrm{C}}^{-1}\left(x-\mu \right)$$

(2)

where $D^2$: Mahalanobis distance, $x$: vector of data, $\mu$: vector of mean value of independent variables, $\mathsf{{\rm T}}$: Indicates vector should be transpond, ${\mathrm{C}}^{-1}$: inverse covariance matrix of independent variables.

Objects with outliers and missing values were removed to improve the accuracy of the clustering algorithm.

2.2.2. Dimensionality Reduction

As the dimension in the data increases, the amount of data to express it increases exponentially (curse of dimensionality, increase of storage space, and processing time). In addition, if there is a high correlation between the variables, the clustering performance deteriorates or the model becomes unstable [27,31,32]. Therefore, if there is a high correlation between variables before clustering, it is necessary to process it and reduce the high-dimensional data to a lower one. The method of reducing the dimension in the data is largely divided into the selection and extraction of variables.

This study considered correlation analysis, which is a method of selecting variables, and principal component analysis, which is a method of extracting variables. Correlation analysis is a method of removing only variables with a high correlation coefficient from existing variables and using only the remaining variables. Principal component analysis is a method of linearly combining existing variables and extracting them as mutually independent principal components.

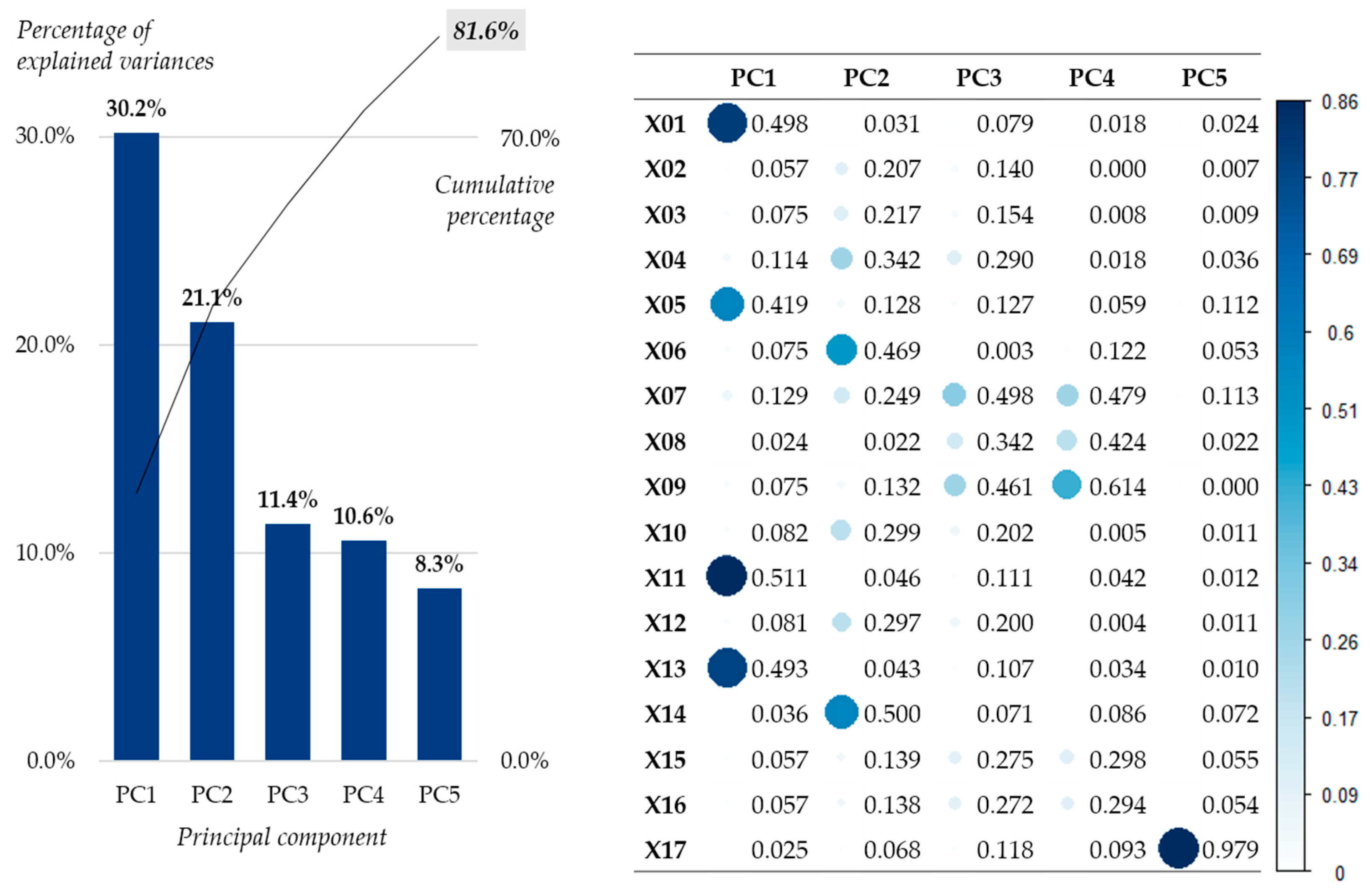
Equation (3) was applied to determine the number of dimensions to be reduced. In this study, the sum of the cumulative eigenvalues of Equation (3) was extracted as n main components with 0.8 or more (It has explanatory power up to 80% of the data before it is reduced).

$$\frac{{{\displaystyle \sum }}_{j=1}^n{\mathsf{\lambda }}_j}{{{\displaystyle \sum }}_{i=1}^d{\mathsf{\lambda }}_i}\ge \beta$$

(3)

where $\lambda$: Eigen value, $d$: Number of dimensions before reduction, $n$: Reduced number of dimensions (d > n), principal component, $\beta$: decision boundary.

In this study, clustering was performed by constructing three datasets separately according to the pre-processing process.

Data pre-processing was performed in the same way. Dataset ① did not perform dimension reduction, dataset ② performed dimension reduction by correlation analysis, and dataset ③ performed dimension reduction by principal component analysis.

2.3. Clustering

In this study, a non-hierarchical cluster analysis method was used for large-scale data analysis.

Hierarchical clustering induces clustering by sequentially classifying objects with high similarity without assumptions about the number or structure of clusters. However, once an object belongs to a cluster, it becomes impossible to move to another cluster, resulting in a problem that outliers are not removed. Additionally, when the size of the data increases, it becomes very difficult to express the resulting dendrogram (tree diagram), and a lot of difficulties arise in calculation. In this case, a non-hierarchical clustering method was developed as a method to apply cluster analysis.

Non-hierarchical cluster analysis is a method of forming an optimized cluster by examining all methods that can be divided into k clusters. It can be applied to various types of data. Compared to hierarchical analysis, computational complexity is low, so it can be used for large-scale data analysis. However, the algorithm cannot be executed until the number of clusters is determined in advance [22,23]. The number of clusters k is determined by determining the optimal point by examining the sum of squared errors (SSE) in the cluster while sequentially increasing the number of clusters. That is, the point at which the decrease in the SSE value reaches the limit becomes the number of clusters (elbow method).

Clustering was performed by two algorithms: a k-means algorithm that derives a virtual center point from a non-hierarchical analysis method and a k-medoids algorithm that derives a center point among objects. The standard model derived by the k-means algorithm is a non-existent building derived to be the central point for all variables of all objects in the cluster. The standard model derived by the k-medoids algorithm is a building that exists as the central object among the objects in the cluster [21].

The performance information (variables) of the finally obtained standard model is the same, and in the case of the standard model derived by the k-medoids algorithm, the object identification number is recognized and the performance information of the building is obtained.

2.4. Verification

In case of cluster analysis, which is case-based unsupervised learning, it is difficult to accurately evaluate numerically. To maximize reliability, significance, and accuracy for this study, RMSE (root mean square error) techniques were used to analyze the error rate of the measured data, methodology, and standard model [33]. RMSE is a commonly used measure when dealing with the difference between a predicted value and an actual observed value, and represents the overall uncertainty of the variable. The lower the RMSE value, the better, and always has a positive value.

$$\mathrm{RMSE}=\frac{\sqrt{\mathsf{\Sigma }{\left(S-M\right)}^2}}{N},$$

(4)

where S = simulated data, M = measured data, N = number of variables.

After calculating the RMSE of the observed (field measurement data, 50 households) and predicted values (derived standard model, methodology), the lower the average value of the RMSE, the better the accuracy. When there was no significant difference in the mean value (Kruskal–Wallis h-test), the standard deviation was evaluated.

3. Results

3.1. Data Preparation and Description

In this study, 22,342 households of statistically valid data were collected and analyzed. Additionally, in this paper, among the 26 variables collected, a single database was constructed with 18 variables corresponding to the performance information of the building among continuous variables excluding categorical variables. After data standardization, 2443 outliers, including missing values, were removed and the analysis was performed with 19,899 data. Table 3 shows the descriptive statistics after data preprocessing is performed.

Table 3. Descriptive statistic.

ID	Variable Name (Unit)	Min	Q1	Median	Q3	Max	Mean	Standard Deviation
X01	Year of completion (year)	4.00	32.00	40.00	49.00	73.00	41.66	56.24
X02	Heating area (m2)	4.00	30.00	43.00	57.00	195.00	44.81	66.59
X03	Volume (m3)	9.60	66.00	95.00	130.00	467.99	101.39	154.16
X04	Total area of wall (m2)	2.25	41.17	51.38	61.50	124.34	51.36	66.94
X05	Averaged wall U-value (W/(m2∙K))	0.18	0.58	1.00	1.35	2.48	0.99	1.42
X06	Total area of window (m2)	0.66	2.95	5.80	9.79	29.11	6.82	11.81
X07	Averaged window U-value (W/(m2∙K))	1.19	2.69	3.58	5.00	6.63	3.77	5.15
X08	Total area of door (m2)	0.85	1.52	2.00	3.40	13.38	2.64	4.73
X09	Averaged door U-value (W/(m2∙K))	1.19	2.40	2.70	2.70	5.50	2.52	3.43
X10	Total area of roof (m2)	1.00	30.00	43.00	57.00	164.00	44.65	65.95
X11	Averaged roof U-value (W/(m2∙K))	0.10	0.58	1.31	1.54	1.54	1.09	1.59
X12	Total area of Floor (m2)	2.10	30.00	43.00	56.98	164.00	44.62	65.92
X13	Averaged floor U-value (W/(m2∙K))	0.10	0.76	1.54	1.54	1.90	1.18	1.61
X14	Solar heat gain (W)	69	2447	5322	9469	28,351	6506	11,707
X15	Averaged SC (-)	0.36	0.75	0.80	0.88	1.30	0.80	0.87
X16	Averaged SHGC (-)	0.31	0.65	0.69	0.75	1.12	0.69	0.75
X17	Efficiency of heating system (%)	13.00	69.30	79.00	88.50	100.00	76.91	89.47
Y01	E per unit area (kWh/(m2∙a))	16.97	133.13	214.97	290.57	490.27	217.18	319.04

3.2. Clustering Results

3.2.1. Number of Clusters

Figure 2 shows the results of the SSE review by increasing the number to k = 10 to determine the number of clusters (k).

Figure 2. SSE changes with increasing number of clusters.

The analysis results showed a rapid decrease in SSE until all three data sets had two clusters, followed by a trend of gradual decline (Elbow point = 2).

In conclusion, the number of clusters was determined to be two and analyzed because there was not much difference in the result values when there were more than three clusters.

3.2.2. Results of Clustering without Dimensionality Reduction

In Methods 1 and 2, after pre-processing the data, a dataset (①) was formed without a dimensionality reduction process, and clustering (A, B) was performed. RBs 1 and 2 derived by method 1 showed more than average differences in the variables X01, X05, X11, X13, and Y01, and showed the most opposite values in the construction year and U-value. RBs 3 and 4 of Method 2 showed more than average differences in the variables X01, X05, X06, X11, X13, X14, and Y01, and showed the most opposite values in the construction year, U-value, and solar heat gain. The results are shown in the RB (representative buildings) 1 to 4 in Table 4.

Table 4. Standard model derived through methods 1 and 2.

	Methodology		Method 1		Method 2
Dimensionality Reduction Process			-		-
	Clustering Method		K-Means		K-Medoids
		Number	RB 01	RB 02	RB 03	RB 04
	Variable (Unit)
X01	Year of completion (year)		52	30	57	30
X02	Heating area (m2)		42.28	47.66	43.12	47.00
X03	Volume (m3)		92.90	110.98	90.60	112.80
X04	Total area of wall (m2)		49.25	53.74	48.48	58.80
X05	Averaged wall U-value (W/(m2∙K))		1.29	0.66	1.28	0.64
X06	Total area of window (m2)		6.41	7.28	6.80	9.87
X07	Averaged window U-value (W/(m2∙K))		4.02	3.49	3.30	3.62
X08	Total area of door (m2)		2.73	2.53	2.26	1.89
X09	Averaged door U-value (W/(m2∙K))		2.42	2.62	2.58	2.70
X10	Total area of roof (m2)		42.12	47.50	43.12	47.00
X11	Averaged roof U-value (W/(m2∙K))		1.51	0.60	1.54	0.52
X12	Total area of Floor (m2)		42.09	47.49	43.12	47.00
X13	Averaged floor U-value (W/(m2∙K))		1.52	0.79	1.54	0.76
X14	Solar heat gain(W)		6411.4	6612.5	6307.0	8939.0
X15	Averaged SC 1 (-)		0.81	0.79	0.80	0.79
X16	Averaged SHGC 2 (-)		0.70	0.68	0.69	0.68
X17	Efficiency of heating system (%)		76.3	77.6	76.5	71.5
Y01	E 3 per unit area (kWh/(m2∙a))		289.49	135.45	307.77	107.04

■: opposite patterns.

Figure 3 shows the variables of representative buildings derived by Methods 1 and 2. RB 01, 02 and RB 03, 04 have similar values for each variable, but are located in opposite directions, indicating opposite patterns.

Figure 3. Cluster profile based on variables (left: method 1, right: method 2).

In addition, the patterns of RB 01 and RB 03, RB 02 and RB 04 showed similar patterns. RB 01 and RB 03 showed an average difference of 4.9%p, and RB 02 and RB 04 showed an average difference of 9.17%p.

3.2.3. Clustering Result after Dimension Reduction (Correlation Analysis)

Methods 3 and 4 used correlation analysis to find the variables that overlap during the dimensionality reduction process and excluded variables with correlation coefficients. This was configured as a dataset (2) to perform clustering.

As a result of performing a correlation analysis on 17 independent variables excluding the dependent variable, it was found that they had correlations as shown in Table 5.

Table 5. Results of correlation analysis (■ strongly correlated variables, cutoff = 0.9).

	X01	X02	X03	X04	X05	X06	X07	X08	X09	X10	X11	X12	X13	X14	X15	X16	X17
X01	1.000	−0.145	−0.203	−0.170	0.692	−0.099	0.178	0.064	−0.094	−0.147	0.833	−0.147	0.825	−0.021	0.115	0.114	−0.058
X02	−0.145	1.000	0.983	0.767	−0.001	0.543	0.057	0.091	−0.001	0.965	−0.135	0.964	−0.136	0.498	0.084	0.085	0.044
X03	−0.203	0.983	1.000	0.793	−0.053	0.559	0.016	0.080	0.014	0.950	−0.187	0.949	−0.186	0.500	0.051	0.052	0.047
X04	−0.170	0.767	0.793	1.000	0.000	0.393	−0.004	0.054	0.006	0.781	−0.149	0.781	−0.147	0.345	0.044	0.045	0.041
X05	0.692	−0.001	−0.053	0.000	1.000	0.042	0.159	0.045	−0.115	−0.003	0.851	−0.002	0.809	0.093	0.114	0.113	0.049
X06	−0.099	0.543	0.559	0.393	0.042	1.000	0.167	−0.085	−0.136	0.547	−0.090	0.547	−0.087	0.954	0.115	0.117	0.047
X07	0.178	0.057	0.016	−0.004	0.159	0.167	1.000	0.013	−0.082	0.066	0.164	0.066	0.167	0.273	0.695	0.690	0.053
X08	0.064	0.091	0.080	0.054	0.045	−0.085	0.013	1.000	0.359	0.096	0.059	0.095	0.066	−0.100	0.021	0.021	−0.022
X09	−0.094	−0.001	0.014	0.006	−0.115	−0.136	−0.082	0.359	1.000	0.004	−0.101	0.004	−0.096	−0.163	−0.046	−0.046	−0.011
X10	−0.147	0.965	0.950	0.781	−0.003	0.547	0.066	0.096	0.004	1.000	−0.138	0.999	−0.138	0.501	0.087	0.087	0.048
X11	0.833	−0.135	−0.187	−0.149	0.851	−0.090	0.164	0.059	−0.101	−0.138	1.000	−0.139	0.942	−0.019	0.111	0.110	−0.050
X12	−0.147	0.964	0.949	0.781	−0.002	0.547	0.066	0.095	0.004	0.999	−0.139	1.000	−0.138	0.501	0.087	0.087	0.048
X13	0.825	−0.136	−0.186	−0.147	0.809	−0.087	0.167	0.066	−0.096	−0.138	0.942	−0.138	1.000	−0.017	0.109	0.109	−0.047
X14	−0.021	0.498	0.500	0.345	0.093	0.954	0.273	−0.100	−0.163	0.501	−0.019	0.501	−0.017	1.000	0.219	0.221	0.046
X15	0.115	0.084	0.051	0.044	0.114	0.115	0.695	0.021	−0.046	0.087	0.111	0.087	0.109	0.219	1.000	0.999	0.059
X16	0.114	0.085	0.052	0.045	0.113	0.117	0.690	0.021	−0.046	0.087	0.110	0.087	0.109	0.221	0.999	1.000	0.060
X17	−0.058	0.044	0.047	0.041	0.049	0.047	0.053	−0.022	−0.011	0.048	−0.050	0.048	−0.047	0.046	0.059	0.060	1.000

In these methods, 6 variables (X03, X06, X10, X11, X12, X16) were removed by removing variables with a larger correlation coefficient with other variables, and a dataset with a total of 12 variables was constructed. As a result of analyzing by applying the clustering algorithm to the dataset ② (A,B), representative buildings 5 to 8 were derived as shown in Table 6.

Table 6. Standard model derived through methods 3 and 4.

	Methodology		Method 3		Method 4
Dimensionality Reduction Process			Correlation Analysis		Correlation Analysis
	Clustering Method		K-Means		K-Medoids
		Number	RB 05	RB 06	RB 07	RB 08
	Variable (Unit)
X01	Year of completion (year)		52	30	49	29
X02	Heating area (m2)		43.09	46.71	39.26	49.38
X03	Volume (m3)		NA	NA	86.4	108.6
X04	Total area of wall (m2)		49.92	52.94	48.14	54.8
X05	Averaged wall U-value (W/(m2∙K))		1.30	0.65	1.25	0.76
X06	Total area of window (m2)		NA	NA	4.8	12.83
X07	Averaged window U-value (W/(m2∙K))		4.05	3.46	4.45	3.06
X08	Total area of door (m2)		2.74	2.52	2.94	2.97
X09	Averaged door U-value (W/(m2∙K))		2.41	2.63	2.53	2.7
X10	Total area of roof (m2)		NA	NA	39.26	49.38
X11	Averaged roof U-value (W/(m2∙K))		NA	NA	1.54	0.52
X12	Total area of Floor (m2)		NA	NA	39.26	49.38
X13	Averaged floor U-value (W/(m2∙K))		1.52	0.80	1.54	0.76
X14	Solar heat gain(W)		6592.24	6410.24	5111	5453
X15	Averaged SC 1 (-)		0.81	0.79	0.85	0.76
X16	Averaged SHGC 2 (-)		NA	NA	0.73	0.65
X17	Efficiency of heating system (%)		76.37	77.51	78	78
Y01	E 3 per unit area (kWh/(m2∙a))		290.65	135.94	299.42	155.04

■: opposite patterns.

In the case of K-means in method 3, an algorithm to generate the center coordinates was applied, so values were omitted for some variables. Figure 4 shows the variables of representative buildings derived by methods 3 and 4. RB 05, 06 and RB 07, 08 have similar values for each variable, but they are located in opposite directions, indicating opposite patterns. In addition, the patterns of RB 05 and RB 07, RB 06 and RB 08 showed similar patterns. RB 05 and RB 07 showed an average difference of 7.05%p, and RB 06 and RB 08 showed an average difference of 8.08%p.

Figure 4. Cluster profile based on variables (left: method 3, right: method 4).

3.2.4. Clustering Result after Dimension Reduction (Principal Component Analysis)

Methods 5 and 6 performed clustering by constructing a dataset (③) from which variables were extracted by principal component analysis in the dimensionality reduction process after data preprocessing. As a result of performing principal component analysis, it appeared as shown in Figure 5. The first main component (PC1) explains the existing variable by 30.2% and PC2 by 21.1%, and up to PC5, 81.63% of the existing variable can be explained and summarized into five independent variables.

Figure 5. Scree plot: plot of eigenvalues ordered from PC1 to PC5 and contributions of all variables to PCs.

The PC1 through PC5 were named as Building envelop U-value (30.23%), solar heat gain (21.13%), heat loss (window) (11.39%), heat loss (door) (10.55%), and heating system efficiency (8.33%). As a result of clustering (A,B) of the data set (③) in which variables were extracted by principal component analysis in the dimensionality reduction process in the pre-processing step, it was derived as shown in the representative buildings 9–12 in Table 7.

Table 7. Standard model derived through methods 5 and 6.

	Methodology		Method 5		Method 6
Dimensionality Reduction Process			Principal Component Analysis		Principal Component Analysis
	Clustering Method		K-Means		K-Medoids
		Number	RB 09	RB 10	RB 11	RB 12
	Variable (Unit)
X01	Year of completion (year)		NA	NA	45	25
X02	Heating area (m2)		NA	NA	38.15	52.8
X03	Volume (m3)		NA	NA	80.1	127.2
X04	Total area of wall (m2)		NA	NA	36.85	51.46
X05	Averaged wall U-value (W/(m2∙K))		NA	NA	1.37	0.65
X06	Total area of window (m2)		NA	NA	6.41	7.37
X07	Averaged window U-value (W/(m2∙K))		NA	NA	3.46	3
X08	Total area of door (m2)		NA	NA	2.24	1.71
X09	Averaged door U-value (W/(m2∙K))		NA	NA	2.7	2.7
X10	Total area of roof (m2)		NA	NA	38.15	52.8
X11	Averaged roof U-value (W/(m2∙K))		NA	NA	1.54	0.52
X12	Total area of Floor (m2)		NA	NA	38.15	52.8
X13	Averaged floor U-value (W/(m2∙K))		NA	NA	1.54	0.76
X14	Solar heat gain (W)		NA	NA	6455	5777
X15	Averaged SC 1 (-)		NA	NA	0.82	0.81
X16	Averaged SHGC 2 (-)		NA	NA	0.71	0.7
X17	Efficiency of heating system (%)	NA		NA	75	79.5
Y01	E 3 per unit area (kWh/(m2∙a))		289.54	135.51	275.63	110.74

■: opposite patterns.

In the case of Method 5, which creates an imaginary center point, values are omitted for the existing variables used for principal component extraction In both methods, the difference is clearly revealed in the variables PC1 and Y01, and representative buildings with particularly opposite values in the building envelope U-value, which is the first main component containing the most information on the existing variables, were derived. Figure 6 shows the parameters of representative buildings derived by methods 5 and 6. RB 09, 10 and RB 11, 12 have similar values for each variable, but they are located in opposite directions, indicating opposite patterns. In addition, the patterns of RB 09 and RB 11, RB 10 and RB 12 have similar patterns. When comparing only the dependent variable, RB 09 and RB 11 show a difference of 5.05%p, and RB 10 and RB 12 show a difference of 22.37%p.

Figure 6. Cluster profile based on variables (left: method 5, right: method 6).

3.3. Verification; RMSE

In this section, RMSE (root mean square error) is used to analyze the difference between the predicted value of the methodologies proposed in the study and the value measured in the actual environment. As for the analysis results, when the observations and methodology (predicted values) were analyzed, Method 6 was found to be the most accurate (Table 8).

Table 8. Results of root mean square error (RMSE), by methods.

	Method 1	Method 2	Method 4	Method 6
Average	1097.68	1408.94	1006.19	951.56
Standard deviation	524.15	526.48	490.47	472.29

■: min, ■: max, ■: minimum difference. Kruskal–Wallis h-test; p-value = 2.347 × 10⁻¹⁰.

First, the difference was analyzed using RMSE for 50 households (=actual value, M) and 8 representative buildings (=predicted value, S) that conducted actual field surveys. When analyzed by representative buildings, RB 08 of Method 4 was analyzed to be the most accurate (Table 9).

Table 9. Results of RMSE, by representative buildings.

	RB 01	RB 02	RB 03	RB 04	RB 07	RB 08	RB 11	RB 12
Average	1362.19	833.18	1581.62	1236.26	1260.50	751.89	1111.45	791.68
Standard deviation	416.44	485.92	429.42	557.06	416.05	422.70	382.63	498.58

■: min, ■: max, ■: minimum difference. Kruskal–Wallis h-test; p-value < 2.2 × 10⁻¹⁶.

The RB 08 having the minimum average value and RB 12 having the minimum difference show a difference of about 5.29%p, and a difference of 52.46%p from RB 03 having the maximum average value. As a result of performing the Kruskal–Wallis h-test, whether this RMSE verification value represents a significant difference, reject the null hypothesis (H0; RMSE values are the same; there is no significant difference) at the 0.05 significance level.

4. Discussion

The detailed method of the cluster analysis process was used differently, and the analysis was performed in a total of six methods. The variables of the two representative buildings derived by each method show opposite patterns, and this shows the characteristics of clustering in which the center points of each cluster are separated from each other as much as possible. In addition, it suggests that it meets the purpose of this study to define a specialized representative building that reflects the performance pattern of the variables as much as possible.

Among the methodologies, method 6, which performed dimensionality reduction process by principal component analysis and applied the K-medoids algorithm, was found to be the best in deriving representative buildings. Among the derived representative buildings, RB 08, which performed dimensional reduction through correlation analysis and applied K-medoids algorithm, was the most excellent.

In the methodology presented in this study, a number of models in which various variables have opposite values are presented. Therefore, it is judged appropriate that one model does not represent the whole, but the derived multiple models represent the whole. In addition, in the RMSE results for each building in Table 8, RB 12 shows a slight difference from RB 08 and 5.29%p in the average, and in the standard deviation, it can be confirmed that RB 11 is superior to RB 08 with a difference of 10.47%p.

Therefore, method 6 applying principal component analysis and K-medoids algorithm is proposed as a methodology for defining representative buildings in existing residential buildings as shown in Figure 7.

Figure 7. Process of deriving representative buildings of existing domestic houses.

In this study, two representative buildings were derived from about 20,000 existing residential buildings by applying the clustering technique, and the derived two representative buildings show the performance as shown in Table 10 below. RB 1 is an older building than RB2, has a small area, and has a high U-value. In addition, RB1 showed opposite patterns with annual heating energy demand per unit area of about 275 KWh/(m²·a), and RB 2 of annual heating energy demand per unit area of about 110 KWh/(m²·a).

Table 10. Data on existing residential representative buildings in Korea.

ID	Variables	Representative Building 1	Representative Building 2
F01	Identification number	28,681	8170
F02	Region	Southern area	Southern area
F03	City	Jeonju	Gwangju
F04	Orientation	West	East
F05	Structure	Heavy construction	Heavy construction
F06	Building type	Detached house	Detached house
F07	Building construction	Etc.	Ferroconcrete
F08	Boiler type	Oil fired boiler	Oil fired boiler
X01	Year of completion (year)	45	25
X02	Heating area (m2)	38.15	52.8
X03	Volume (m3)	80.1	127.2
X04	Total area of wall (m2)	36.85	51.46
X05	Averaged wall U-value (W/(m2∙K))	1.37	0.65
X06	Total area of window (m2)	6.41	7.37
X07	Averaged window U-value (W/(m2∙K))	3.46	3
X08	Total area of door (m2)	2.24	1.71
X09	Averaged door U-value (W/(m2∙K))	2.7	2.7
X10	Total area of roof (m2)	38.15	52.8
X11	Averaged roof U-value (W/(m2∙K))	1.54	0.52
X12	Total area of Floor (m2)	38.15	52.8
X13	Averaged floor U-value (W/(m2∙K))	1.54	0.76
X14	Solar heat gain (W)	6455	5777
X15	Averaged SC (-)	0.82	0.81
X16	Averaged SHGC (-)	0.71	0.7
X17	Efficiency of heating system (%)	75	79.5
Y01	E per unit area (kWh/(m2∙a))	275.63	110.74

In addition, since this method uses the K-medoids algorithm, it is possible to recognize the object’s unique number and check all the qualitative building data of the building.

5. Conclusions

In this study, in deriving representative buildings, a methodology was studied that includes various information of buildings as much as possible and reflects their characteristics. In the case of previous studies, the usefulness of the cluster analysis technique was proved, but limitations and imperfections of data collection appeared, and geometric characteristics were mainly considered in deriving the standard model.

In this paper, a representative building derivation methodology based on multivariate building data used for building energy analysis was proposed. Additionally, a total of six methods were established for different algorithms in the dimensionality reduction and clustering stage of the data preprocessing stage. In addition, to verify the established methodology, data collected on existing domestic houses were used for analysis, and a total of 22,342 households and 26 building variables were used for analysis. Among the six methods, method 6, which consists of data preprocessing, principal component analysis, clustering (K-medoids), and verification, is presented as a method of deriving representative buildings from existing domestic houses, and through this, two representative buildings of existing houses were derived.

The method proposed in this study is capable of deriving a number of standard models considering all variables (n) in a single analysis. In other words, the representative building contains information on n variables used for analysis, and becomes the center of the n-dimensional. The representative building derived in this study contains a lot of building data, so it can be effectively used for planning and research related to buildings on a regional and national scale. In addition, this process can be applied to various buildings to derive representative buildings. Depending on the data, a more optimized method should be applied by performing the process presented, and understanding and proficiency of the process is required to perform this series of processes. If the process is built as a program, accessibility is expected to be secured. As a representative building derived later, a study on establishing a standard improvement strategy for the existing building will be conducted.