A New Bi-Level Optimisation Framework for Optimising a Multi-Mode Wave Energy Converter Design: A Case Study for the Marettimo Island, Mediterranean Sea
Abstract
1. Introduction
2. Modelling
2.1. Wave Energy Converter
2.2. Wave Climate
2.3. Equations of Motion
- Step 1.
- Define the sea state and corresponding incident wave spectrum .
- Step 2.
- Compute the power spectral density (PSD) matrix of the excitation force:where is the vector of excitation force coefficients, and denotes the conjugate transpose of a vector/matrix.
- Step 3.
- Calculate the WEC response matrix assuming in the first iteration:
- Step 4.
- Establish the power spectral density matrix of the buoy motion:
- Step 5.
- Calculate the covariance matrix of the WEC velocity:
- Step 6.
- Estimate the equivalent damping matrix using the analytical expression from [38]:
- Step 7.
- Check the convergence criteria:where n corresponds to the iteration number, and the threshold is set to . If this condition is not satisfied, go to Step 3.
2.4. Economic Model
- -
- The mass of the buoy is calculated based on a given geometry as ;
- -
- The needed mass of the anchoring system (three piles) relays on the tether tension associated with buoyancy and the wave force, and can be approximated by using case presented in [47] as a reference. The tether peak force () is estimated from the spectral-domain model.
2.5. Implementation
3. Optimisation Configuration Models
- (i)
- The average annual produce power output computed utilising Equation (14), that is maximised as
- (ii)
- The LCoE is minimised using the below equation that is specified in Equation (16):
4. Optimisation Algorithms
4.1. All-at-Once Optimisation
4.1.1. L-SHADE with an Ensemble Pool of Sinusoidal Parameter Adaptation (LSHADE-EpSin)
Mutation Strategy with External Archive
Ensemble of Parameter Adaptation
Local Search
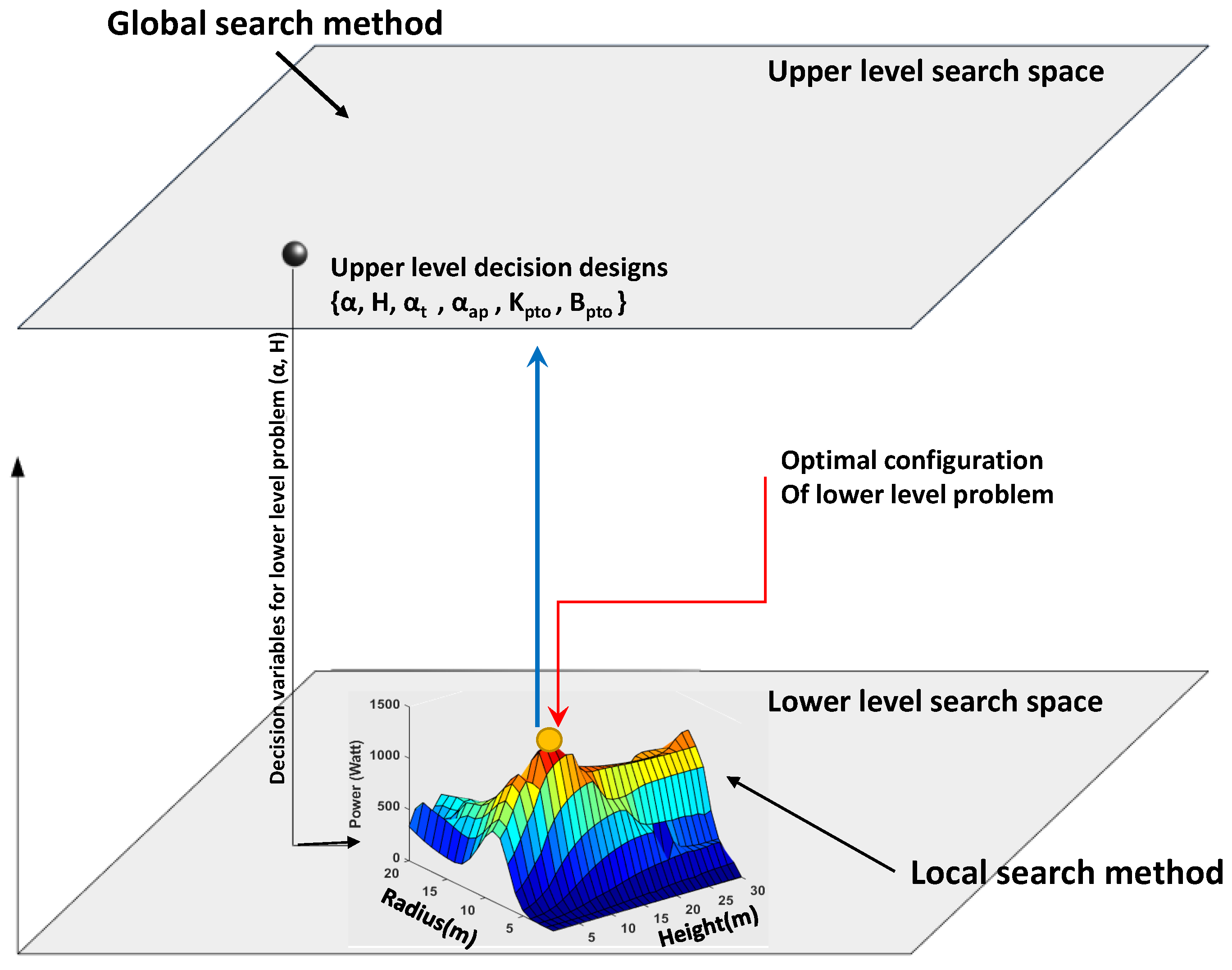
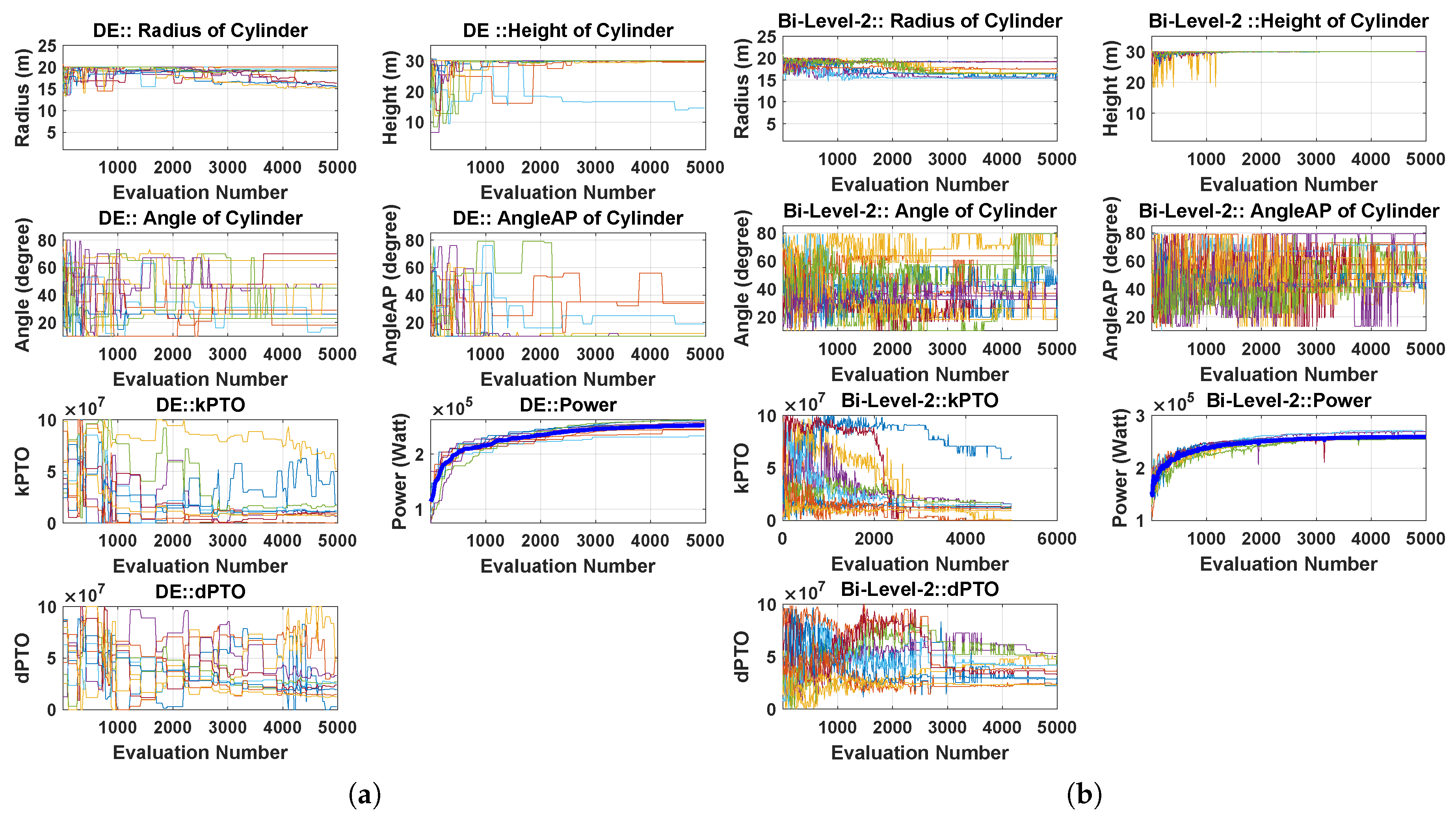
4.2. Bi-Level Optimisation
Tuning the Local Search
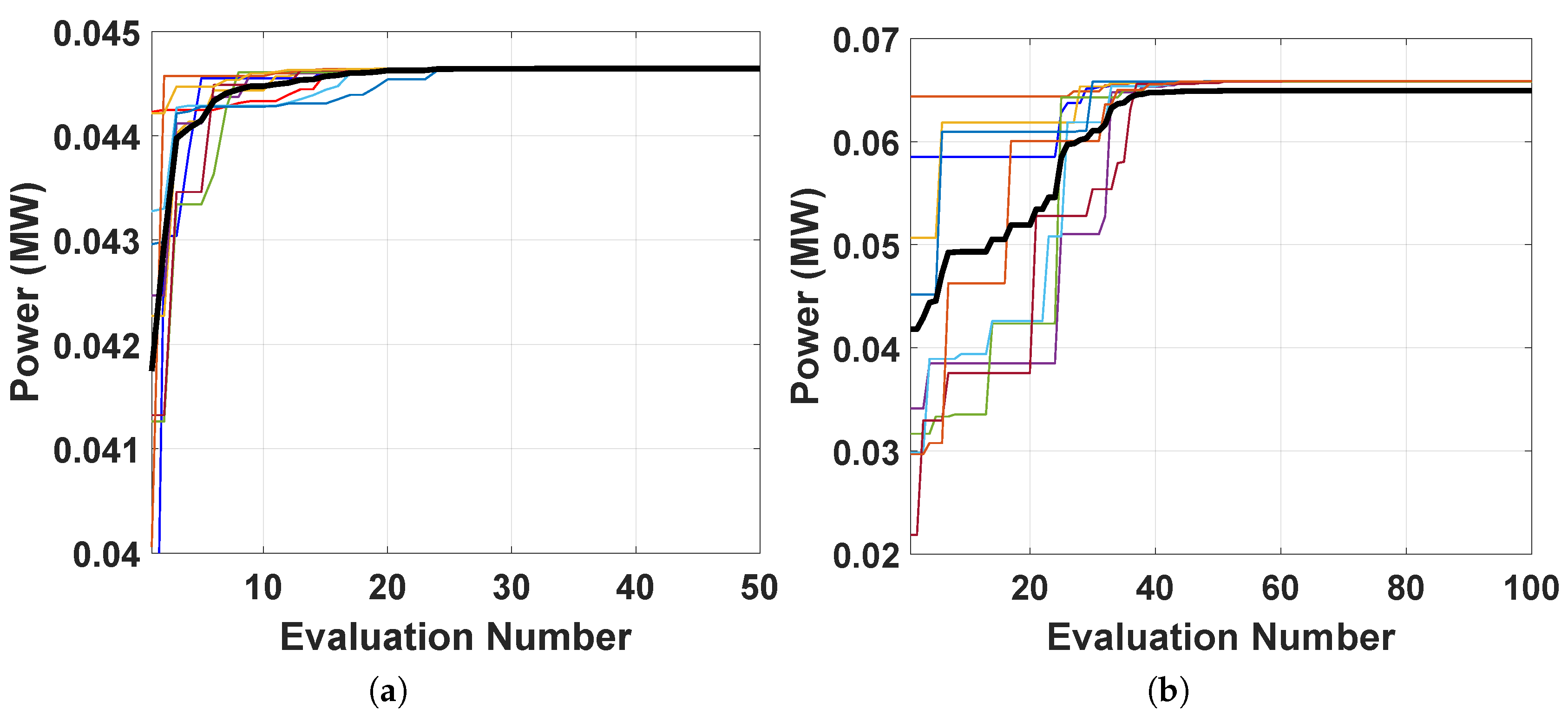
5. Optimisation Results and Discussions
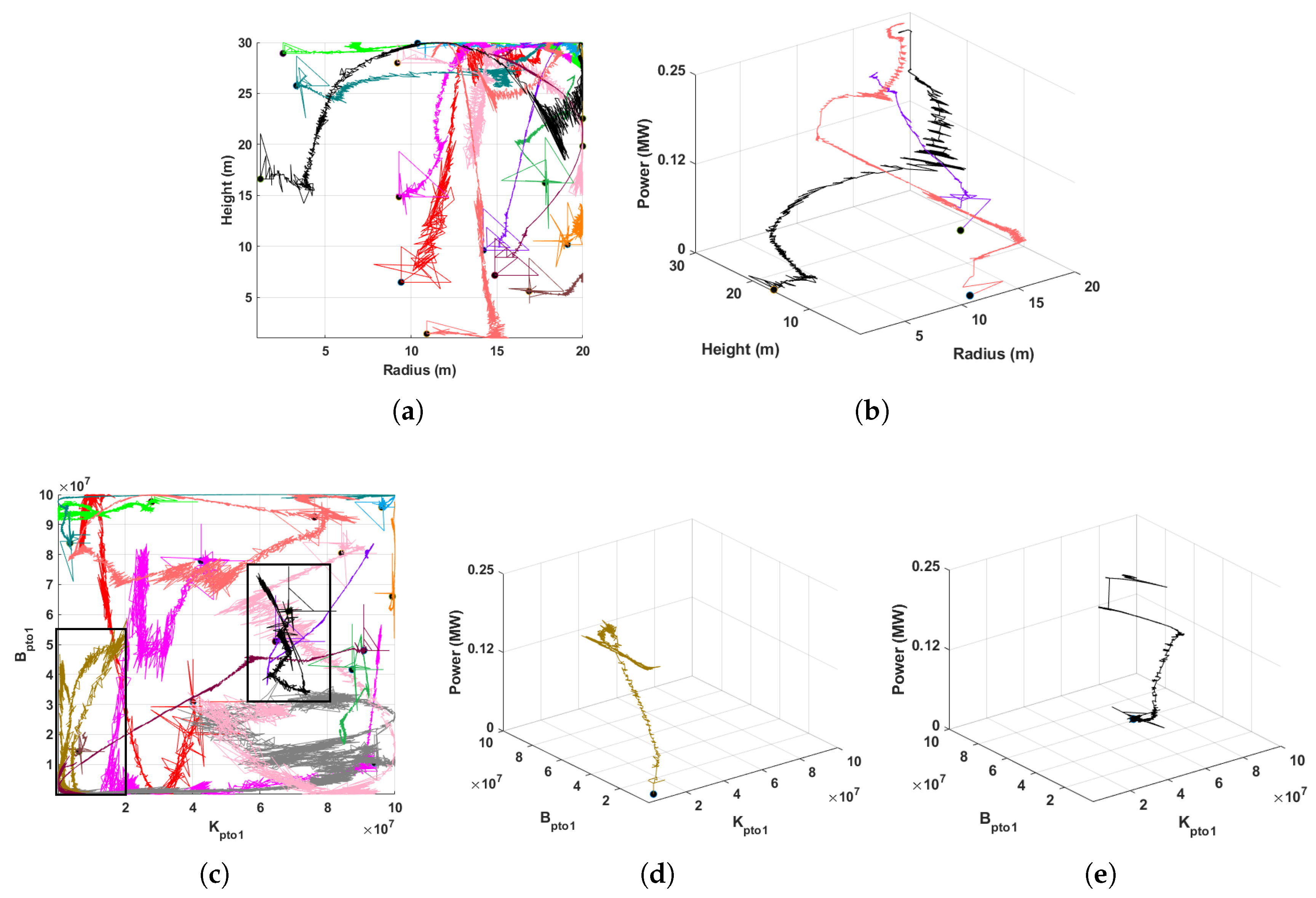
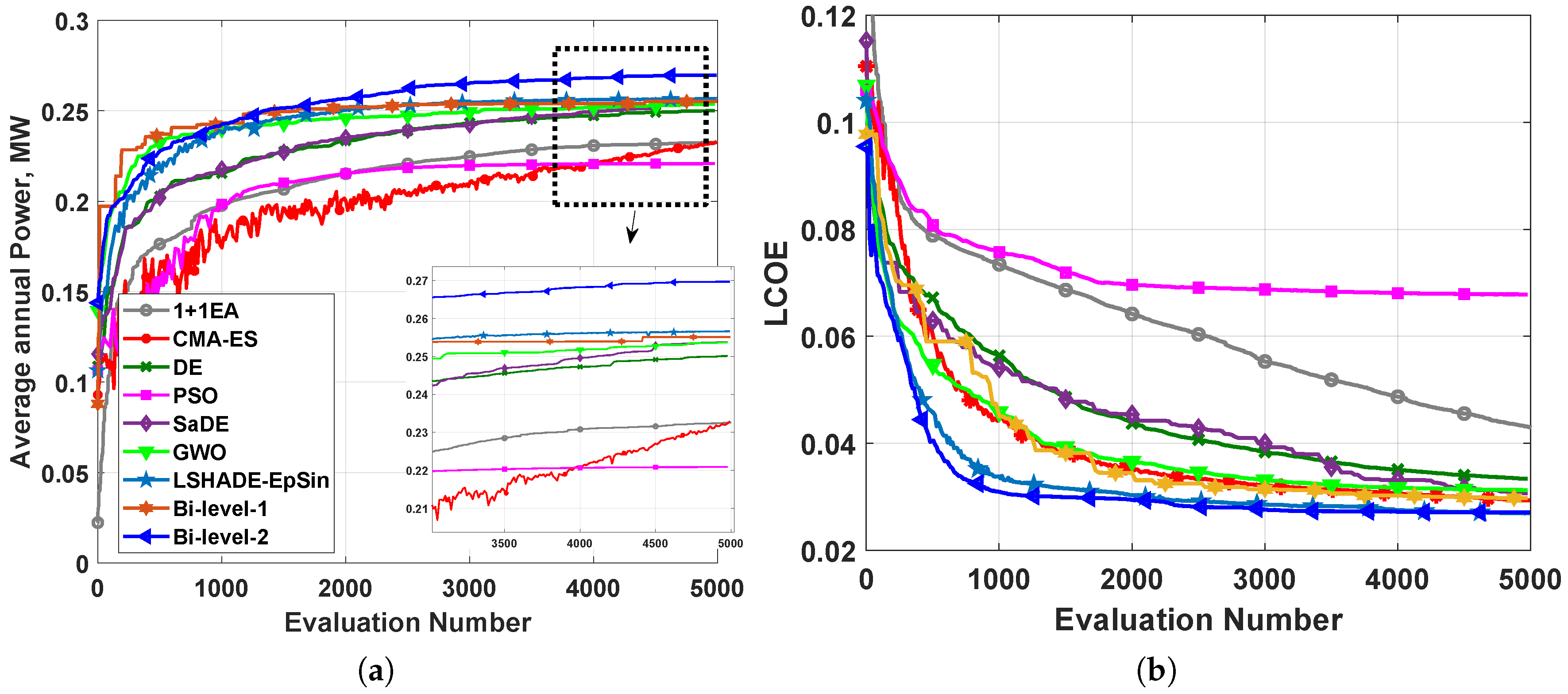
5.1. Multi-Modality of Search Space
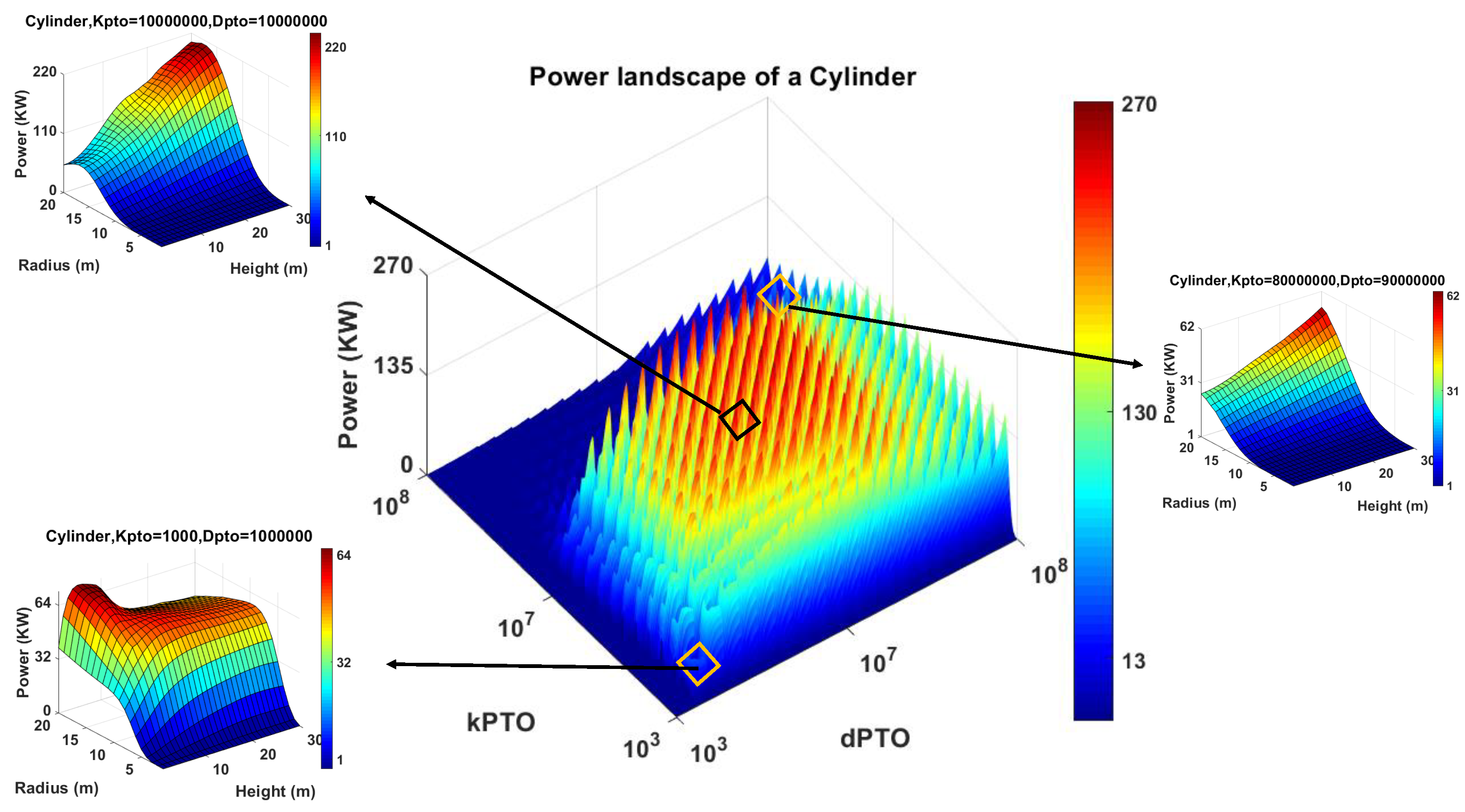
5.2. Power Landscape Analysis
| Algorithm 1 Bi-level Optimisation method (LSHADE-EpSin+NM) | |
| procedureBi-level Optimisation method | |
| Initialization | |
| ▹ initial population | |
| M:F =CR=0.5 | ▹ initialise memory of first control settings |
| M:freq = 0.5, | ▹ initialise memory of second control settings |
| Upper-Level (Global search method) | |
| for in do | ▹ termination criteria |
| if then | |
| Call second control parameter settings | |
| ▹ Reset successful mean vectors | |
| ▹ Generate a random index, H is memory size | |
| , | |
| end if | |
| if then | |
| Call first control parameter settings | |
| if then | |
| else | |
| end if | |
| Generate same as first control parameters (Equation 23) | |
| end if | |
| for to N do | |
| Generate , | |
| ▹ Mutation -- | |
| ▹ Binomial Crossover | |
| ▹ Selection | |
| Store successful and | |
| end for Update the memory according to used settings Update the population size by Equation (28) Sort based on the fitness function Remove worst solutions from AND Select the best solution | |
| Lower-Level (Local search method) | |
| if > 0.001% then | ▹ Optimise Cylinder dimension |
| Compute improvement rate end if | |
| if > 0.001% then | ▹ Optimise tether angles |
| Compute improvement rate | |
| end if | |
| Update by the best-found NM configurations | |
| end for | |
| end procedure | |
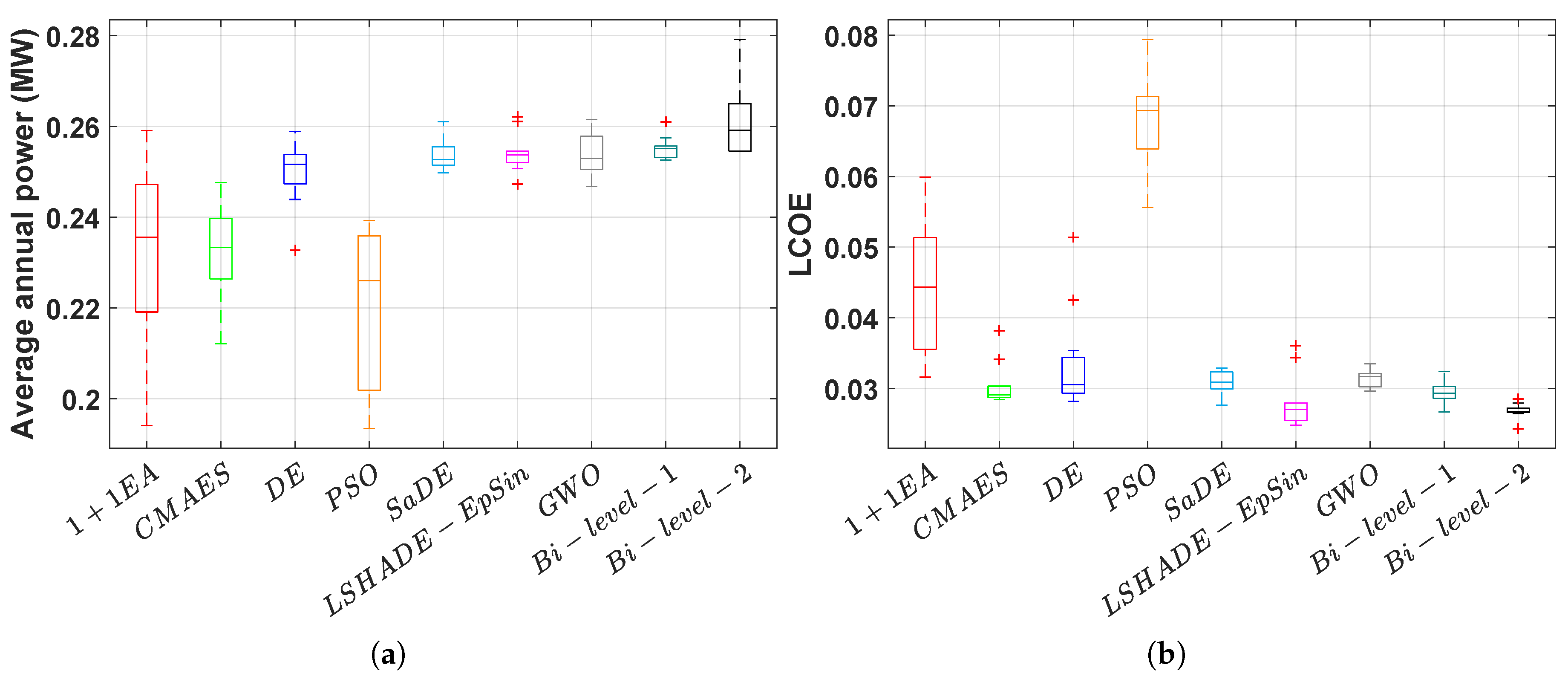
5.3. The Annual Average Power Output Maximisation
5.4. LCoE Minimisation
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| WEC | Wave Energy Converter |
| PTO | Power Take-off system |
| PSO | Particle Swarm Optimisation |
| DE | Differential Evolution |
| SaDE | Self adaptive Differential Evolution |
| CMA-ES | Covariance Matrix Adaptation Evolution Strategy |
| LSHADE | Local Success-history Adaptive Differential Evolution |
References
- Murdock, H.E.; Gibb, D.; André, T.; Appavou, F.; Brown, A.; Epp, B.; Kondev, B.; McCrone, A.; Musolino, E.; Ranalder, L.; et al. Renewables 2019 Global Status Report; United Nations Environment Programme: Nairobi, Republic of Kenya, 2019; Available online: http://hdl.handle.net/20.500.11822/28496 (accessed on 19 September 2020).
- Tronchin, L.; Manfren, M.; Nastasi, B. Energy analytics for supporting built environment decarbonisation. Energy Procedia 2019, 157, 1486–1493. [Google Scholar] [CrossRef]
- Mazzoni, S.; Ooi, S.; Nastasi, B.; Romagnoli, A. Energy storage technologies as techno-economic parameters for master-planning and optimal dispatch in smart multi energy systems. Appl. Energy 2019, 254, 113682. [Google Scholar] [CrossRef]
- Aderinto, T.; Li, H. Ocean wave energy converters: Status and challenges. Energies 2018, 11, 1250. [Google Scholar] [CrossRef]
- Falnes, J. A review of wave-energy extraction. Mar. Struct. 2007, 20, 185–201. [Google Scholar] [CrossRef]
- Astariz, S.; Iglesias, G. Wave energy vs. other energy sources: A reassessment of the economics. Int. J. Green Energy 2016, 13, 747–755. [Google Scholar] [CrossRef]
- Wen, Y.; Wang, W.; Liu, H.; Mao, L.; Mi, H.; Wang, W.; Zhang, G. A Shape Optimization Method of a Specified Point Absorber Wave Energy Converter for the South China Sea. Energies 2018, 11, 2645. [Google Scholar] [CrossRef]
- Alamian, R.; Shafaghat, R.; Safaei, M.R. Multi-Objective Optimization of a Pitch Point Absorber Wave Energy Converter. Water 2019, 11, 969. [Google Scholar] [CrossRef]
- Esmaeilzadeh, S.; Alam, M.R. Shape optimization of wave energy converters for broadband directional incident waves. Ocean Eng. 2019, 174, 186–200. [Google Scholar] [CrossRef]
- Wang, L.; Ringwood, J.V. Geometric optimization of a hinge-barge wave energy converter. In Proceedings of the 13th European Wave and Tidal Energy Conference, Napoli, Italy, 1–6 September 2019; p. 1389. [Google Scholar]
- Garcia-Teruel, A.; Forehand, D.I.M.; Jeffrey, H. Metrics for wave energy converter hull geometry optimisation. In Proceedings of the 13th European Wave and Tidal Energy Conference EWTEC, Napoli, Italy, 1–6 September 2019. [Google Scholar]
- Sergiienko, N.Y.; Neshat, M.; da Silva, L.S.; Alexander, B.; Wagner, M. Design optimisation of a multi-mode wave energy converter. In Proceedings of the ASME 2020 39th International Conference on Ocean, Offshore and Arctic Engineering (OMAE2020), Fort Lauderdale, FL, USA, 28 June–3 July 2020. [Google Scholar]
- Abdelkhalik, O.; Zou, S.; Robinett, R.D.; Bacelli, G.; Wilson, D.; Coe, R.G.; Korde, U.A. Multiresonant Feedback Control of a Three-Degree-of-Freedom Wave Energy Converter. IEEE Trans. Sustain. Energy 2017, 8, 1518–1527. [Google Scholar] [CrossRef]
- Neshat, M.; Alexander, B.; Sergiienko, N.; Wagner, M. A Hybrid Evolutionary Algorithm Framework for Optimising Power Take Off and Placements of Wave Energy Converters. arXiv 2019, arXiv:1904.07043. [Google Scholar]
- Sharp, C.; DuPont, B. Wave energy converter array optimization: A genetic algorithm approach and minimum separation distance study. Ocean Eng. 2018, 163, 148–156. [Google Scholar] [CrossRef]
- Fang, H.W.; Feng, Y.Z.; Li, G.P. Optimization of Wave Energy Converter Arrays by an Improved Differential Evolution Algorithm. Energies 2018, 11, 3522. [Google Scholar] [CrossRef]
- Neshat, M.; Alexander, B.; Wagner, M.; Xia, Y. A detailed comparison of meta-heuristic methods for optimising wave energy converter placements. In Proceedings of the Genetic and Evolutionary Computation Conference. ACM, Kyoto, Japan, 15–19 July 2018; pp. 1318–1325. [Google Scholar]
- Neshat, M.; Alexander, B.; Sergiienko, N.Y.; Wagner, M. Optimisation of Large Wave Farms Using a Multi-Strategy Evolutionary Framework. In Proceedings of the 2020 Genetic and Evolutionary Computation Conference; Association for Computing Machinery: New York, NY, USA, 2020; pp. 1150–1158. [Google Scholar] [CrossRef]
- Giassi, M.; Castellucci, V.; Göteman, M. Economical layout optimization of wave energy parks clustered in electrical subsystems. Appl. Ocean Res. 2020, 101, 102274. [Google Scholar] [CrossRef]
- Fairley, I.; Lewis, M.; Robertson, B.; Hemer, M.; Masters, I.; Horrillo-Caraballo, J.; Karunarathna, H.; Reeve, D.E. A classification system for global wave energy resources based on multivariate clustering. Appl. Energy 2020, 262, 114515. [Google Scholar] [CrossRef]
- Franzitta, V.; Rizzo, G. Renewable energy sources: A mediterranean perspective. In Proceedings of the 2010 2nd International Conference on Chemical, Biological and Environmental Engineering, Cairo, Egypt, 2–4 November 2010; pp. 48–51. [Google Scholar]
- Rusu, E.; Onea, F. Estimation of the wave energy conversion efficiency in the Atlantic Ocean close to the European islands. Renew. Energy 2016, 85, 687–703. [Google Scholar] [CrossRef]
- Rusu, E. Wave energy assessments in the Black Sea. J. Mar. Sci. Technol. 2009, 14, 359–372. [Google Scholar] [CrossRef]
- Bouali, B.; Larbi, S. Contribution to the geometry optimization of an oscillating water column wave energy converter. Energy Procedia 2013, 36, 565–573. [Google Scholar] [CrossRef]
- Kramer, M.V.; Frigaard, P. Efficient wave energy amplification with wave reflectors. In The Twelfth International Offshore and Polar Engineering Conference. International Society of Offshore and Polar Engineers; International Society of Offshore and Polar Engineers: Mountain View, CA, USA, 2002. [Google Scholar]
- Vantorre, M.; Banasiak, R.; Verhoeven, R. Modelling of hydraulic performance and wave energy extraction by a point absorber in heave. Appl. Ocean Res. 2004, 26, 61–72. [Google Scholar] [CrossRef]
- Goggins, J.; Finnegan, W. Shape optimisation of floating wave energy converters for a specified wave energy spectrum. Renew. Energy 2014, 71, 208–220. [Google Scholar] [CrossRef]
- Hager, R.; Fernandez, N.; Teng, M.H. Experimental study seeking optimal geometry of a heaving body for improved power absorption efficiency. In the Twenty-second International Offshore and Polar Engineering Conference. International Society of Offshore and Polar Engineers; International Society of Offshore and Polar Engineers: Mountain View, CA, USA, 2012. [Google Scholar]
- McCabe, A. Constrained optimization of the shape of a wave energy collector by genetic algorithm. Renew. Energy 2013, 51, 274–284. [Google Scholar] [CrossRef]
- De Andres, A.; MacGillivray, A.; Roberts, O.; Guanche, R.; Jeffrey, H. Beyond LCOE: A study of ocean energy technology development and deployment attractiveness. Sustain. Energy Technol. Assessments 2017, 19, 1–16. [Google Scholar] [CrossRef]
- Piscopo, V.; Benassai, G.; Della Morte, R.; Scamardella, A. Cost-based design and selection of point absorber devices for the mediterranean sea. Energies 2018, 11, 946. [Google Scholar] [CrossRef]
- Piscopo, V.; Benassai, G.; Cozzolino, L.; Della Morte, R.; Scamardella, A. A new optimization procedure of heaving point absorber hydrodynamic performances. Ocean Eng. 2016, 116, 242–259. [Google Scholar] [CrossRef]
- Piscopo, V.; Benassai, G.; Della Morte, R.; Scamardella, A. Towards a cost-based design of heaving point absorbers. Int. J. Mar. Energy 2017, 18, 15–29. [Google Scholar] [CrossRef]
- Sergiienko, N.Y.; Cazzolato, B.S.; Ding, B.; Arjomandi, M. An optimal arrangement of mooring lines for the three-tether submerged point-absorbing wave energy converter. Renew. Energy 2016, 93, 27–37. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Awad, N.H.; Ali, M.Z.; Suganthan, P.N.; Reynolds, R.G. An ensemble sinusoidal parameter adaptation incorporated with L-SHADE for solving CEC2014 benchmark problems. In Proceedings of the 2016 IEEE Congress on Evolutionary Computation (CEC), Vancouver, BC, Canada, 24–29 July 2016. [Google Scholar]
- Iuppa, C.; Cavallaro, L.; Vicinanza, D.; Foti, E. Investigation of suitable sites for Wave Energy Converters around Sicily (Italy). Ocean Sci. Discuss. 2015, 12, 315–354. [Google Scholar] [CrossRef]
- Silva, L.; Sergiienko, N.; Pesce, C.; Ding, B.; Cazzolato, B.; Morishita, H. Stochastic analysis of nonlinear wave energy converters via statistical linearization. Appl. Ocean Res. 2020, 95, 102023. [Google Scholar] [CrossRef]
- Silva, L.S.P. Nonlinear Stochastic Analysis of Wave Energy Converters Via Statistical Linearization. Master’s Thesis, University of São Paulo, São Paulo, Brazil, 2019. [Google Scholar]
- Folley, M. Numerical Modelling of Wave Energy Converters: State-of-the-Art Techniques for Single Devices and Arrays; Elsevier Science: Saint Louis, MI, USA, 2016. [Google Scholar]
- Spanos, P.D.; Arena, F.; Richichi, A.; Malara, G. Efficient dynamic analysis of a nonlinear wave energy harvester model. J. Offshore Mech. Arct. Eng. 2016, 138, 041901. [Google Scholar] [CrossRef]
- Silva, L.S.P.; Morishita, H.M.; Pesce, C.P.; Gonçalves, R.T. Nonlinear analysis of a heaving point absorber in frequency domain via statistical linearization. In Proceedings of the ASME 2019 38th International Conference on Ocean, Offshore and Arctic Engineering. American Society of Mechanical Engineers, Glasgow, Scotland, 9–14 June 2019. [Google Scholar]
- Penalba, M.; Giorgi, G.; Ringwood, J.V. Mathematical modelling of wave energy converters: A review of nonlinear approaches. Renew. Sustain. Energy Rev. 2017, 78, 1188–1207. [Google Scholar] [CrossRef]
- Scruggs, J.T.; Lattanzio, S.M.; Taflanidis, A.A.; Cassidy, I.L. Optimal causal control of a wave energy converter in a random sea. Appl. Ocean Res. 2013, 42, 1–15. [Google Scholar] [CrossRef]
- Da Silva, L.S.P.; Cazzolato, B.S.; Sergiienko, N.Y.; Ding, B.; Morishita, H.M.; Pesce, C.P. Statistical linearization of the Morison’s equation applied to wave energy converters. J. Ocean. Eng. Mar. Energy 2020, 6, 1–13. [Google Scholar] [CrossRef]
- De Andres, A.; Maillet, J.; Hals Todalshaug, J.; Möller, P.; Bould, D.; Jeffrey, H. Techno-Economic Related Metrics for a Wave Energy Converters Feasibility Assessment. Sustainability 2016, 8, 1109. [Google Scholar] [CrossRef]
- Sergiienko, N.Y.; Rafiee, A.; Cazzolato, B.S.; Ding, B.; Arjomandi, M. Feasibility study of the three-tether axisymmetric wave energy converter. Ocean Eng. 2018, 150, 221–233. [Google Scholar] [CrossRef]
- Jiang, S.C.; Gou, Y.; Teng, B. Water wave radiation problem by a submerged cylinder. J. Eng. Mech. 2014, 140, 6014003. [Google Scholar] [CrossRef]
- Jiang, S.C.; Gou, Y.; Teng, B.; Ning, D.Z. Analytical solution of a wave diffraction problem on a submerged cylinder. J. Eng. Mech. 2014, 140, 225–232. [Google Scholar] [CrossRef]
- Hoerner, S. Fluid-Dynamic Drag: Practical Information on Aerodynamic Drag and Hydrodynamic Resistance; Hoerner Fluid Dynamics: Midland Park, NJ, USA, 1965. [Google Scholar]
- The Specialist Committee on Waves. Final Report and Recommendations to the 23rd ITTC. In Proceedings of the 23rd International Towing Tank Conference, Venice, Italy, 8–14 September 2002; Volume II, pp. 505–736. [Google Scholar]
- Sinha, A.; Malo, P.; Deb, K. A review on bilevel optimization: From classical to evolutionary approaches and applications. IEEE Trans. Evol. Comput. 2017, 22, 276–295. [Google Scholar] [CrossRef]
- McKinnon, K.I. Convergence of the Nelder–Mead Simplex Method to a Nonstationary Point. SIAM J. Optim. 1998, 9, 148–158. [Google Scholar] [CrossRef]
- Jansen, T.; Wegener, I. On the choice of the mutation probability for the (1+ 1) EA. In International Conference on Parallel Problem Solving from Nature; Springer: Cham, Switzerland, 2000; pp. 89–98. [Google Scholar]
- Hansen, N. The CMA evolution strategy: A comparing review. Towards a New Evolutionary Computation; Springer: Berlin/Heidelberg, Germany, 2006; pp. 75–102. [Google Scholar]
- Eberhart, R.; Kennedy, J. A new optimizer using particle swarm theory. In Proceedings of the Symposium on Micro Machine and Human Science (MHS), Nagoya, Japan, 4–6 October 1995; pp. 39–43. [Google Scholar]
- Storn, R.; Price, K. Differential evolution–a simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Qin, A.K.; Huang, V.L.; Suganthan, P.N. Differential evolution algorithm with strategy adaptation for global numerical optimization. IEEE Trans. Evol. Comput. 2008, 13, 398–417. [Google Scholar] [CrossRef]
- Neumann, F.; Wegener, I. Randomized local search, evolutionary algorithms, and the minimum spanning tree problem. Theor. Comput. Sci. 2007, 378, 32–40. [Google Scholar] [CrossRef]
- Goudos, S.K.; Deruyck, M.; Plets, D.; Martens, L.; Joseph, W. Optimization of power consumption in 4G LTE networks using a novel barebones self-adaptive differential evolution algorithm. Telecommun. Syst. 2017, 66, 109–120. [Google Scholar] [CrossRef]
- Ramli, M.A.; Bouchekara, H.; Alghamdi, A.S. Optimal sizing of PV/wind/diesel hybrid microgrid system using multi-objective self-adaptive differential evolution algorithm. Renew. Energy 2018, 121, 400–411. [Google Scholar] [CrossRef]
- Tanabe, R.; Fukunaga, A.S. Improving the search performance of SHADE using linear population size reduction. In Proceedings of the 2014 IEEE Congress on Evolutionary Computation (CEC), Beijing, China, 6–11 July 2014; pp. 1658–1665. [Google Scholar]
- Tanabe, R.; Fukunaga, A. Success-history based parameter adaptation for differential evolution. In Proceedings of the 2013 IEEE Congress on Evolutionary Computation, Cancun, Mexico, 20–23 June 2013; pp. 71–78. [Google Scholar]
- Zhang, J.; Sanderson, A.C. JADE: Adaptive differential evolution with optional external archive. IEEE Trans. Evol. Comput. 2009, 13, 945–958. [Google Scholar] [CrossRef]
- Bullen, P.S. Handbook of Means and Their Inequalities; Springer Science & Business Media: Cham, Swtzerland, 2013; Volume 560. [Google Scholar]
- Goudos, S.K.; Siakavara, K.; Samaras, T.; Vafiadis, E.E.; Sahalos, J.N. Self-adaptive differential evolution applied to real-valued antenna and microwave design problems. IEEE Trans. Antennas Propag. 2011, 59, 1286–1298. [Google Scholar] [CrossRef]
- Rajagopalan, A.; Sengoden, V.; Govindasamy, R. Solving economic load dispatch problems using chaotic self-adaptive differential harmony search algorithm. Int. Trans. Electr. Energy Syst. 2015, 25, 845–858. [Google Scholar] [CrossRef]
- Nelder, J.A.; Mead, R. A simplex method for function minimization. Comput. J. 1965, 7, 308–313. [Google Scholar] [CrossRef]
- Ghasemi, M.; Ghavidel, S.; Ghanbarian, M.M.; Habibi, A. A new hybrid algorithm for optimal reactive power dispatch problem with discrete and continuous control variables. Appl. Soft Comput. 2014, 22, 126–140. [Google Scholar] [CrossRef]
- Rajan, A.; Malakar, T. Optimal reactive power dispatch using hybrid Nelder–Mead simplex based firefly algorithm. Int. J. Electr. Power Energy Syst. 2015, 66, 9–24. [Google Scholar] [CrossRef]
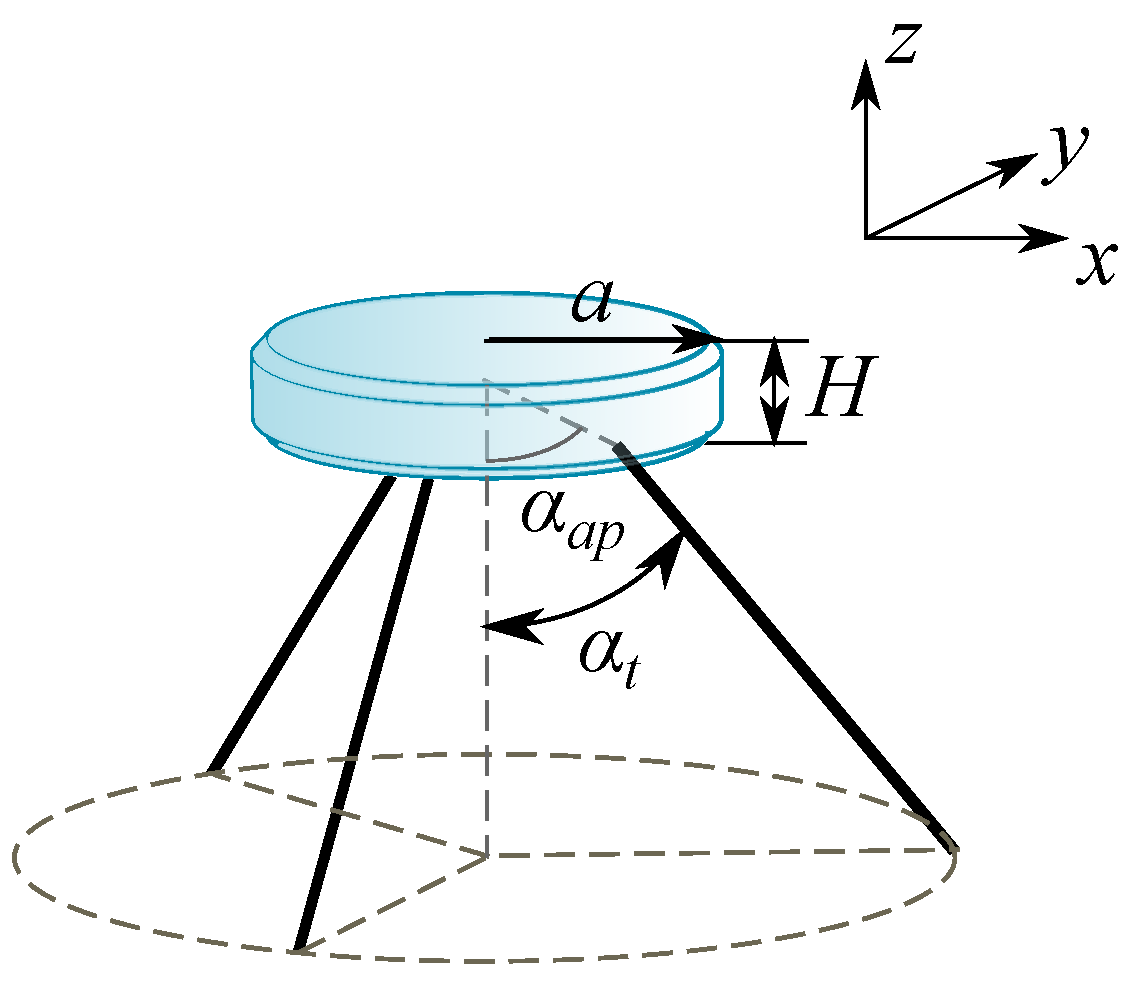
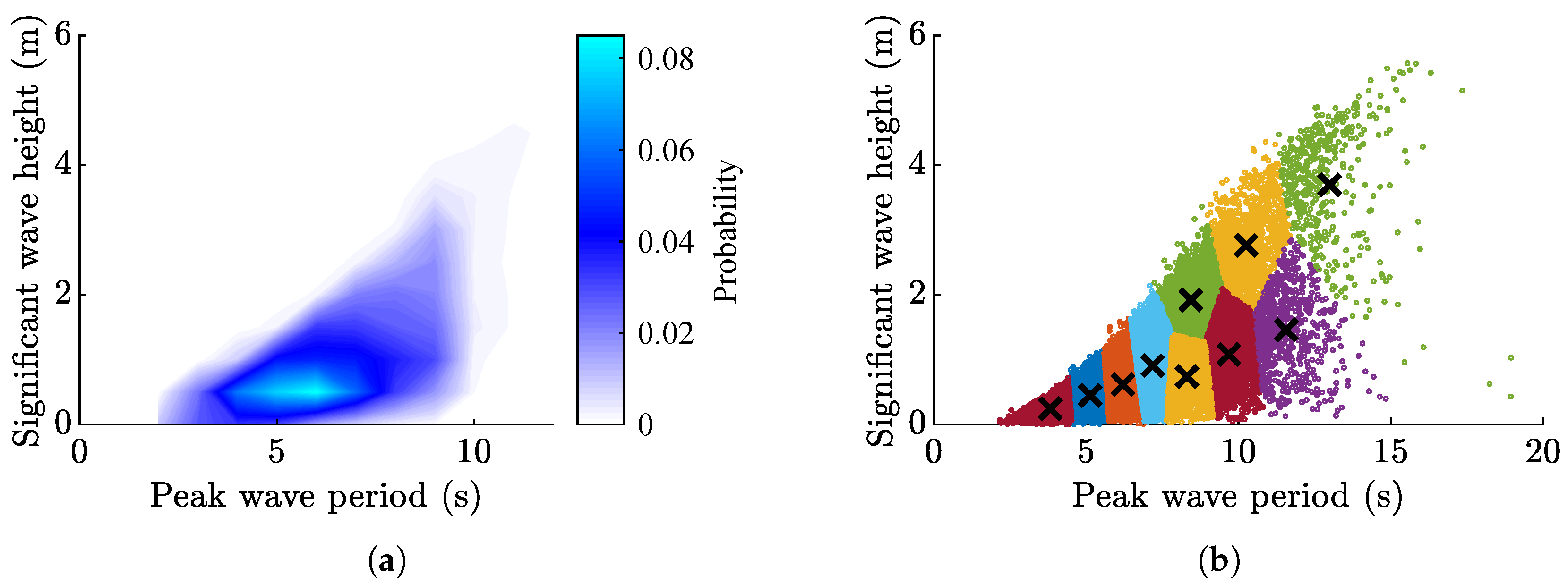
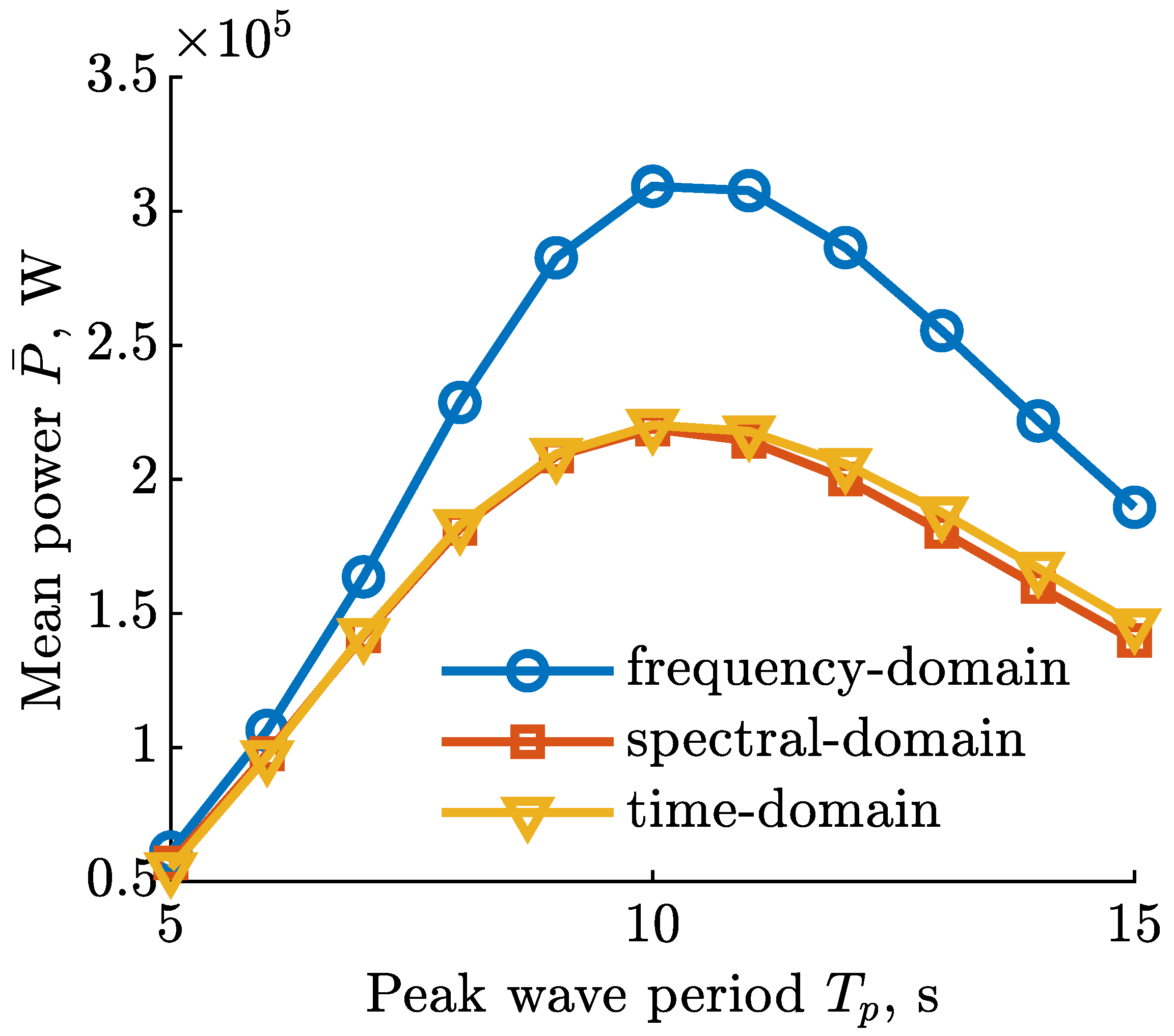
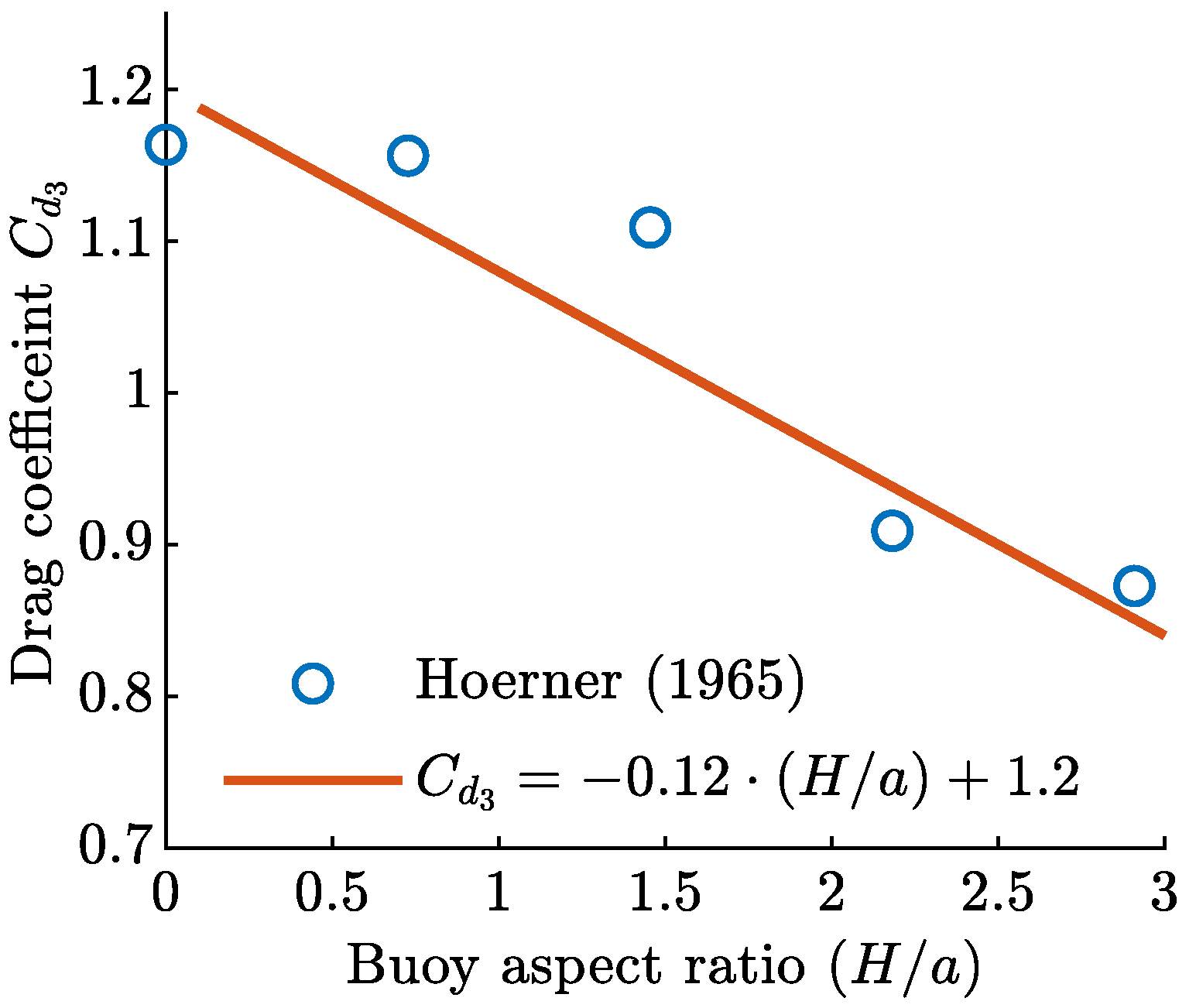
| Sea State | , s | , m | Probability O, % |
|---|---|---|---|
| 1 | 3.82 | 0.24 | 8.06 |
| 2 | 5.13 | 0.44 | 14.62 |
| 3 | 6.20 | 0.61 | 17.80 |
| 4 | 7.18 | 0.90 | 18.01 |
| 5 | 8.30 | 0.73 | 12.10 |
| 6 | 8.43 | 1.92 | 9.58 |
| 7 | 9.68 | 1.08 | 8.68 |
| 8 | 10.24 | 2.76 | 5.78 |
| 9 | 11.56 | 1.46 | 3.30 |
| 10 | 12.99 | 3.69 | 2.07 |
| Parameter | Unit | Min | Max | Length |
|---|---|---|---|---|
| radius, a | m | 1 | 20 | 1 |
| height, H | m | 1 | 30 | 1 |
| aspect ratio, | 0.4 | 2 | 1 | |
| Tether inclination angle, | deg | 10 | 80 | 1 |
| Tether attachment angle, | deg | 10 | 80 | 1 |
| PTO stiffness, | N/m | 10 | ||
| PTO damping, | N/(m/s) | 10 |
| Methods | Settings |
|---|---|
| Nelder–Mead [53] | Nelder–Mead simplex direct search (NM) |
| 1+1EA [54] | mutation step sizes are , ,, , and Probability mutation rate=, |
| CMA-ES [55] | with the default settings and ; |
| PSO [56] | with , , , ( decreased with a damping ratio exponentially); |
| GWO [35] | with = 25, (linearly decreased to zero) |
| DE [57] | with , , |
| SaDE [58] | with , , |
| LSHADE-EpSin [36] | , historical memory size , |
| Bi-level-1 | SaDE +NM, WEC’s dimensions and tether angles are optimised in the lower-level, default settings of SaDE |
| Bi-level-2 | LSHADE-EpSin + NM, WEC’s dimensions and tether angles are optimised in the lower-level, default settings of LSHADE-EpSin |
| Parameter | 1+1EA | CMA-ES | PSO | GWO | DE | SaDE | LSHADE-EpSin | Bi-Level-1 | Bi-Level-2 |
|---|---|---|---|---|---|---|---|---|---|
| a [m] | 16.62 | 16.10 | 19.99 | 16.68 | 15.46 | 15.50 | 15.49 | 15.61 | 14.51 |
| H [m] | 30 | 30 | 14.80 | 30 | 30 | 30 | 30 | 30 | 30 |
| [deg] | 70 | 26 | 60 | 14 | 48 | 26 | 39 | 50 | 10 |
| [deg] | 10 | 13 | 63 | 28 | 10 | 11 | 29 | 40 | 67 |
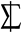 | 0.665 | 0.863 | 3.796 | 1.51 | 1.894 | 2.883 | 0.882 | 0.665 | 0.514 |
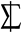 | 2.765 | 9.928 | 4.676 | 1.51 | 3.775 | 4.036 | 2.479 | 2.095 | 1.129 |
| 259 | 248 | 239 | 261 | 259 | 261 | 262 | 265 | 279 |
| Power [MW] | ||||||||
| 1+1EA | CMA-ES | PSO | GWO DE | SaDE | LSHADE-EpSin | Bi-Level-1 | Bi-Level-2 | |
| Mean | 0.2325 | 0.2329 | 0.2208 | 0.2537 0.2501 | 0.2537 | 0.2541 | 0.2551 | 0.2612 |
| Min | 0.1941 | 0.2121 | 0.1934 | 0.2467 0.2327 | 0.2498 | 0.2473 | 0.2526 | 0.2544 |
| Max | 0.2590 | 0.2476 | 0.2392 | 0.2615 0.2589 | 0.261 | 0.2621 | 0.261 | 0.2792 |
| STD | 0.0234 | 0.0117 | 0.0181 | 0.0049 0.0087 | 0.0036 | 0.0046 | 0.0032 | 0.0088 |
| LCoE | ||||||||
| 1+1EA | CMA-ES | PSO | GWO DE | SaDE | LSHADE-EpSin | Bi-Level-1 | Bi-Level-2 | |
| Mean | 0.0443 | 0.0303 | 0.0678 | 0.0315 0.0334 | 0.0309 | 0.028 | 0.0295 | 0.0268 |
| Min | 0.0316 | 0.0284 | 0.0556 | 0.0297 0.0282 | 0.0277 | 0.0248 | 0.0267 | 0.0243 |
| Max | 0.0599 | 0.0382 | 0.0794 | 0.0335 0.0514 | 0.0329 | 0.0361 | 0.0324 | 0.0285 |
| STD | 0.0109 | 0.0036 | 0.0071 | 0.0014 0.0079 | 0.0019 | 0.0041 | 0.0019 | 0.0012 |
| Parameter | 1+1EA | CMA-ES | PSO | GWO | DE | SaDE | LSHADE-EpSin | Bi-Level-1 | Bi-Level-2 |
|---|---|---|---|---|---|---|---|---|---|
| a [m] | 7.31 | 6.40 | 14.32 | 7.00 | 7.38 | 6.57 | 5.00 | 6.15 | 5.00 |
| H/a | 0.40 | 0.40 | 0.40 | 0.4 | 0.40 | 0.40 | 0.40 | 0.40 | 0.40 |
| αt [deg] | 28 | 29 | 10 | 10 | 31 | 25 | 35 | 31 | 34 |
| αap [deg] | 10 | 11 | 10 | 31 | 14 | 11 | 10 | 12 | 10 |
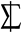 | 0.647 | 0.919 | 3.90 | 0.651 | 3.50 | 0.383 | 2.094 | 0.77 | 2.071 |
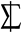 | 0.577 | 0.332 | 3.52 | 0.847 | 1.15 | 1.481 | 1.350 | 0.256 | 1.914 |
| LCoE | 0.0316 | 0.0284 | 0.0556 | 0.0297 | 0.0287 | 0.0277 | 0.0248 | 0.0267 | 0.0243 |
| PAAP [kW] | 53.1 | 43.6 | 131 | 51.4 | 64.8 | 50.6 | 27.1 | 43.5 | 28.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Neshat, M.; Sergiienko, N.Y.; Amini, E.; Majidi Nezhad, M.; Astiaso Garcia, D.; Alexander, B.; Wagner, M. A New Bi-Level Optimisation Framework for Optimising a Multi-Mode Wave Energy Converter Design: A Case Study for the Marettimo Island, Mediterranean Sea. Energies 2020, 13, 5498. https://doi.org/10.3390/en13205498
Neshat M, Sergiienko NY, Amini E, Majidi Nezhad M, Astiaso Garcia D, Alexander B, Wagner M. A New Bi-Level Optimisation Framework for Optimising a Multi-Mode Wave Energy Converter Design: A Case Study for the Marettimo Island, Mediterranean Sea. Energies. 2020; 13(20):5498. https://doi.org/10.3390/en13205498
Chicago/Turabian StyleNeshat, Mehdi, Nataliia Y. Sergiienko, Erfan Amini, Meysam Majidi Nezhad, Davide Astiaso Garcia, Bradley Alexander, and Markus Wagner. 2020. "A New Bi-Level Optimisation Framework for Optimising a Multi-Mode Wave Energy Converter Design: A Case Study for the Marettimo Island, Mediterranean Sea" Energies 13, no. 20: 5498. https://doi.org/10.3390/en13205498
APA StyleNeshat, M., Sergiienko, N. Y., Amini, E., Majidi Nezhad, M., Astiaso Garcia, D., Alexander, B., & Wagner, M. (2020). A New Bi-Level Optimisation Framework for Optimising a Multi-Mode Wave Energy Converter Design: A Case Study for the Marettimo Island, Mediterranean Sea. Energies, 13(20), 5498. https://doi.org/10.3390/en13205498









