1. Introduction
The power sector constitutes one of the most significant emitters of CO
, which thus contributes substantially to global warming [
1]. Therefore, significant measures are required to render the sector fossil-free. The traditional evolution of most power systems has resulted in a generation mix that typically combines thermal and hydro generation, where, depending on the available resources and socio-political constraints, thermal generation typically comprises of nuclear, coal or natural gas as the primary energy fuels. Decarbonizing the power supply would require the replacement of thermal generators based on fossil fuels with technologies that exploit renewable energy sources (RES), primarily wind and solar power [
2]. Unlike fossil fuels, however, whose primary energy sources can be stored and transferred, these technologies can only generate electricity exactly where and when the corresponding resources are available. This introduced inflexibility in supply can pose challenges to the integration of RES and increase the significance of energy storage [
3] as well as the role of the transmission grid [
4]. In addition, further electrification is expected by other energy consumers, e.g., in the transportation sector, which outweigh any energy efficiency measures and thus increase the total electricity demand. On the other hand, the new consumer types may also offer options for higher flexibility on the demand side. Under such expected large-scale changes in the power system’s landscape, an extensive examination of the future system’s behavior is necessary.
The term integration of variable renewable energy sources (VRES) may refer to either the engineering perspective or the system perspective. From the engineering perspective, compliance, and harmonization with network codes are necessary for the proper, technical operation of the power system, such power quality, and frequency restoration. In this paper, the focus consists of the system perspective, i.e., the techno-economic parameters contributing in the long-term stability and reliability of the system’s operation at broad scale. The intermittent nature of VRES generation may compromise the ability of the system to maintain balanced operation and provide uninterruptible power to consumers. Therefore, storage and load shifting operation should be considered. In addition, the dependency on weather conditions, which are highly unpredictable in the long-term, may cause issues regarding security of supply that would require additional investments in back-up systems and oversizing of renewable generation capacity. On the other hand, the domination of power electronics may reduce the system’s inertia significantly, hence requiring additional rotating machines in operation. Finally, the spatial limitations of the availability of the primary source, especially for wind power, may put significant strain on an electricity grid that has not been designed for such spatial patterns of supply and demand and the necessary power flows respectively. Technical grid constraints may substantially restrict the integration of VRES generation into the system, potentially reducing the economic value of investing in an otherwise resources-rich area.
This paper investigates the integration of VRES, in particular wind and solar energy, into the future power system of Europe from the system perspective but only with respect to energy volumes and balancing, excluding security of supply or short-term stability considerations. Curtailments of otherwise available wind or solar energy caused by temporal imbalance and power transfer constraints are expected to grow with a higher presence of VRES in the system, as additional measures for their integration may not be economically beneficial. Nevertheless, it is considered important to investigate whether such curtailments can also be further exploited by converting them into alternative energy carriers besides electricity, e.g., via so-called power-to-x technologies [
5,
6] that can be more easily stored and transferred. In this way, part of the demand of other energy sectors, e.g., transportation, may become possible to be supplied by VRES as well. The goal of this work is to examine the behavior of the future power system and the spatio-temporal properties of the respective curtailments under this prism.
The future European power system has been examined by a variety of studies incorporating either low [
7,
8], medium [
9,
10,
11,
12] or high [
13,
14] spatial resolution. However, the investigation of VRES curtailments does not typically constitute the primary focus and, although often considered, they tend to remain outside the analysis and discussion. On the other hand, studies where curtailments are reported [
15,
16,
17,
18,
19] typically employ a form of spatial aggregation that may result in underestimating their total amount. Similarly, employing temporal aggregation in energy systems, as analyzed by Hoffmann et al. [
20], can also lead to analogous conclusions. This becomes more prevalent for the long-term analysis of power systems, where the majority of the respective studies involve investment models. Such studies primarily focus on designing the system and not merely analyzing its operation. However, in order to reduce the high complexity imposed by the broad geographical scope and the concomitant uncertainties, a combination of spatial and temporal aggregation is usually applied to the system that may underestimate the amount of VRES curtailment as well. Power system models providing pan-European coverage at high spatial resolution, although not very common in the past, have been receiving increasing attention due to the challenges associated with the increasing penetration of VRES, as well as the coupling of European markets [
21,
22,
23,
24]. Nevertheless, such models are only rarely applied in a long-term context.
In this paper, a novel approach is introduced, aspiring to cover the afore-mentioned gaps in the literature. A methodology to estimate VRES curtailments in a high amount of detail for future contexts is developed. This methodology simultaneously incorporates both the main sources as well as alleviating factors related to renewable curtailments. The main causes include the temporal and spatial imbalances that are addressed by modeling the system in high spatio-temporal resolution. On the other hand, system flexibilities such as load shifting, storage, and inclusion of weather patterns spanning continental scales are also taken into account. Such a holistic approach can rarely be found in the literature, especially for future contexts, where it becomes even more necessary due to the expected increase in VRES shares. To that end, a detailed description of the European power system of the future is also introduced, where existing aggregated designs are translated into a highly resolved system in both spatial and temporal dimensions. With this work, a better estimation and deeper understanding of VRES curtailments in future system designs can be obtained.
The remainder of this paper is divided into four sections. In
Section 2, the fundamentals of the applied methodology are described.
Section 3 introduces the implemented scenarios, while the corresponding results are presented and analyzed in
Section 4. Finally, the main conclusions of this work are derived in
Section 5.
2. Methodology
Due to the high complexity and size of the European power system, its operation is characterized by a hierarchical structure in terms of both time and space. This principle therefore carries direct implications for the modeling of the system as well. As this paper focuses on measuring VRES integration in terms of energy volume, the temporal resolution is selected to be one hour, such that the system can be analyzed as a sequence of static states but still capture the main intra-day dynamics. A finer temporal resolution does not necessarily translate into a higher accuracy in results for future scenarios, since the quality of the time series of the generation and demand forecasts is limited. Moreover, time steps below 15 min would compromise the steady-state assumption. On the other hand, a coarser temporal resolution would be possible; nevertheless, averaging over long time periods may significantly underestimate the amount of VRES curtailments caused by both temporal and spatial imbalances. In addition, due to the broad geographical scope under investigation, only the bulk transfer of energy across the continent is examined, and so only the transmission level (i.e., ≥220 kV) is taken into consideration. Although for some countries lower voltage levels such as 150 kV may also be considered part of their transmission system, 220 kV was selected as consistent value across all countries to account for long-distance, bulk energy transfer. Further granularity on the spatial representation may become increasingly useful for systems exhibiting high degree of distributed generation like photovoltaic (PV) systems, since more balancing will need to be accomplished locally, before the transmission level. Nevertheless, such an approach would additionally pose challenges in modeling the grid based on the existing topology data, additional computational load due to the increasing number of grid nodes, as well as challenges regarding the spatial distribution of generation and demand. Moreover, including lines that do not directly belong to transmission system operators (TSO) may require more complex methods for congestion management, a topic that still remains under heavy research. On the other hand, as VRES curtailments may exhibit high sensitivity to the power flow constraints posed by the network, no further spatial aggregation beyond the 220 kV level is considered. Such a high level of spatial resolution becomes prohibitive for investment models, and therefore the system will only be analyzed with regard to its operation via a dispatch model.
Syranidis et al. [
25] discuss the fundamentals of modeling static power flows over transmission networks as well as electricity markets and congestion management schemes in the modern European context. Moreover, they review the corresponding literature, where it is found that the majority of the studies using a highly resolved representation of the transmission grid employ a variation of either the DC optimal power flow (DC OPF) or the power transfer distribution factors (PTDF) method. Both of these methods rely on the principles of the DC flow approximation to linearize the power flow equations, such that linear optimization problems can be formulated that can offer higher scalability and computational performance. The approximation assumes small differences in voltage angles, similar voltage magnitudes in all nodes and high X/R ratios (i.e., reactance to resistance) in all lines, all of which may be considered valid for steady state operation of transmission grids.
2.1. The DC Optimal Power Flow
For these reasons, the methodology developed for the current analysis also relies on the principles of the DC OPF formulation. Such principles include a perfect market competition environment and a centralized congestion management scheme, where social welfare maximization is sought and no cost penalties are associated with curtailing VRES generation. When a deterministic and partly inflexible demand curve is additionally considered, a linear optimization formulation can be obtained, where the objective can be translated into the minimization of the system’s operational cost. Moreover, due to the perfect market conditions, each generator can be simply represented by their marginal cost of operation.
The only constraints in the classical DC OPF formulation consist of the generation capacity and line flow limits described by Equation (1c,1h), respectively, as well as the energy balance constraint on each node (see Equation (1b)), where the positive sign indicates the injection of power into the node and
K is the network’s incidence matrix. The DC flow approximation is expressed by Equation (1i) where the power flow over a line depends linearly on the voltage angle difference of the adjacent nodes. A direct extension of this formulation consists of the inclusion of storage units, which can be described by a charging and discharging rate as well as a state of charge (SOC) variable, all with their respective capacities (see Equation (1d–1f)). The energy contained in each storage unit’s inventory is updated via an energy balance equation (Equation (1g)) that follows a forward Euler scheme:
where
| i | generator index |
| n | grid node index |
| t | time index |
| g | generation in MW |
| storage unit discharge rate in MW |
| generation cost in €/MWh |
| storage unit discharge cost in €/MWh |
| storage charge rate in MW |
| K | incidence matrix |
| l | line index |
| f | power flow in MW |
| d | electricity load in MW |
| minimum generation in MW |
| maximum generation in MW |
| maximum discharge rate in MW |
| maximum charge rate in MW |
| state of charge in MWh |
| maximum state of charge in MWh |
| charging efficiency |
| external power inflow in MW |
| inflow curtailments in MW |
| minimum power flow in MW |
| maximum power flow in MW |
| voltage angle in radians |
| “departing” node of line l |
| “arriving” node of line l |
| x | reactance in Ohm |
The modeling of different types of power generation with respect to their primary energy source characteristics can be accomplished by appropriately adjusting the described formulation. Thermal power plants can essentially be modeled via fixed marginal costs and capacities, hence assuming unlimited and unbounded fuel provision, whereas VRES generators are modeled with variable maximum capacities that depend on the available primary energy and, consequently, on the weather conditions. Unlike thermal power plants, hydro power plants are assumed to have a limited storage capacity of their primary fuel (water), which is also time-dependent and therefore they are modeled as storage units with variable but deterministic inflows.
2.2. Linear Unit Commitment
The classical DC OPF formulation has the advantage of a linear description; however, it may overestimate the flexibility of steam turbines as well as their respective cycling costs. Such costs refer to the additional costs of starting up or stopping the turbines, which may become significant for a system with a high shares of VRES. In such a system, the high variability of wind and solar power can lead to a highly intermittent positive residual load that cannot be easily addressed by existing turbine technology due to its relatively high minimum operational load requirements, i.e., its requirements for minimum generation output. These limitations can be described through the introduction of additional binary variables for each generator and time step, indicating the online status of the respective unit; however, such an approach would substantially increase the computational requirements. A linear unit commitment (LUC) approximation for power plant aggregates that can better estimate the thermal cycling costs than the simple DC OPF formulation is introduced by Göransson et al. [
26] and described by Equation (2a–2c):
where
| effective generator index |
| N | minimum load of generator relative to the nominal capacity |
| k | time index |
| K | start-up time in hours |
Values for
N and
K for the different types of thermal generation can be found in
Table 1.
2.3. The Four Level Approach
Despite the simplifications that lead to a linear formulation of the DC OPF problem, considering the complete transmission grid at an hourly resolution can still become computationally prohibitive when an entire year is considered. Although specific decomposition methods for the typical structures of energy system problems have been developed in order to exploit parallelization possibilities that could improve computational performance [
27], in this work, a less mathematically rigorous approach is selected wherein the original problem is split into four consecutive modeling levels. Developing such an approach achieves a general methodology that does not depend on the particular generation, demand or grid topology conditions of each problem. However, the guarantee of reaching the optimal solution of the original problem is sacrificed, since the sequence of the part-problems does not constitute a mathematically equivalent problem to the original problem. The primary complexity sought to be reduced concerns the coupling of time steps via storage units operation, load shifting, and thermal generation constraints. To that end, the main rationale consists of developing a generic way to reduce the dimensionality of the original problem by solving a large amount of smaller problems. This process, however, results in an overall feasible space that is different and smaller than the original one. This essentially means that the final solution is not guaranteed to also solve the original problem and most likely it merely finds a sub-optimal solution. Hence, the various flexibility options of the system, such as storage units, are probably not utilized in a globally optimal way, leading to higher VRES curtailments. Moreover, since the methodology does not follow a mathematically rigorous procedure, a prediction of the discrepancy to the original optimal value of the objective function can only be estimated by empirically comparing its application in smaller problems. The developed methodology constitutes an extension of the model that was introduced by Syranidis et al. [
28] and, together with the respective pan-European power system data, will be referred to as ’Europower’.
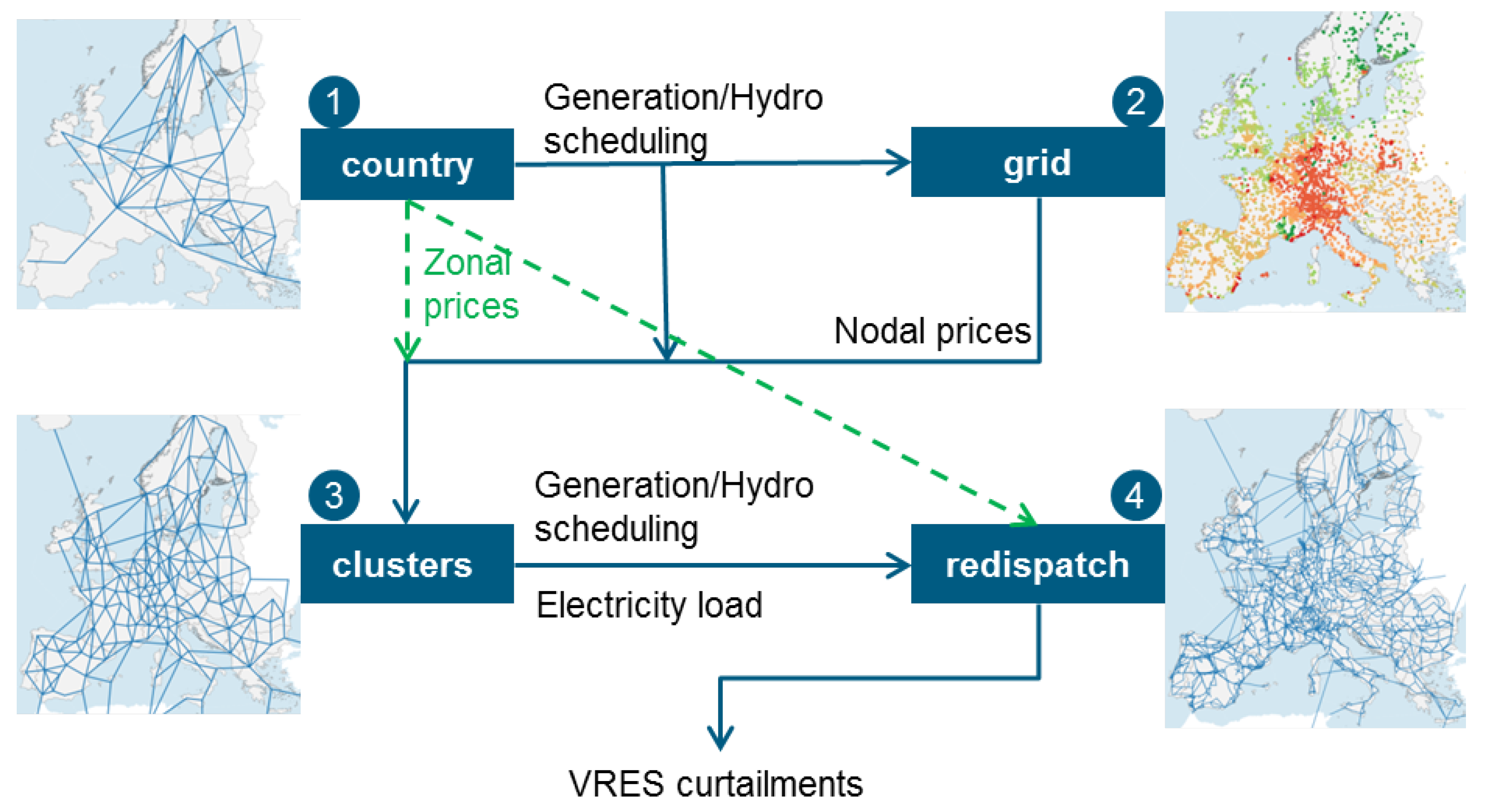
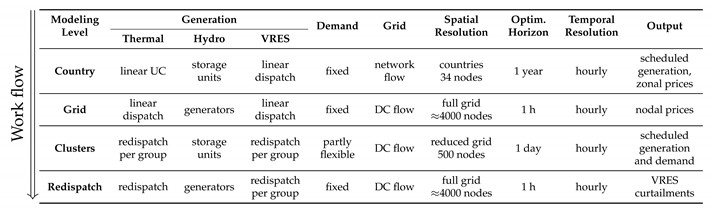
The complete modeling chain is summarized in
Figure 1, where the soft linking between the different levels is depicted schematically. The country level constitutes the initial dispatch problem with the lowest spatial resolution (i.e., one node per country) and provides the generation scheduling information to the cluster level, as well as the hydro scheduling information at both the grid and cluster levels. In addition, the final two models further consider the zonal prices obtained at the country level to formulate their problems. The second modeling level estimates the nodal prices for the complete representation of the transmission grid, which are then used in order to reduce it into a lower number of representative nodes for the cluster level. At this level, the demand is considered flexible, hence updated generation, hydro power, and load scheduling are obtained and passed to the final redispatch level. Finally, the redispatch level can yield the VRES curtailments for the complete transmission grid at hourly resolution. Aside from the data flows,
Table 2 further summarizes the most significant modeling aspects for each of the four levels with respect to generation dispatch and demand flexibility modeling, as well as the spatial resolution and temporal horizon used. By observing this table, the trade-offs between the various introduced modeling complexities from each aspect can become clearer. Nevertheless, despite the comprehensive overview, a more detailed description of each modeling level is deemed necessary.
2.3.1. Country Level
The first level of Europower’s methodology consists of the “country” level, where power plants are aggregated by technology and country while the grid is represented via simple market interconnections with the corresponding net transfer capacity (NTC) values as flow constraints. In addition to these flow constraints, however, the power flows over the various links are independent from each other (i.e., Equation (1i) is not included in the set of constraints described by Equation (3e)), and hence the corresponding formulation takes the form of a classical “network flow” formulation. The problem is described by Equation (3b–3e), where yearly perfect foresight is assumed for the operation of both thermal and hydro power plants:
where
and
| nominal generation capacity in MW |
such that nuclear power plant aggregates are forced to never shut down completely.
To avoid generating infeasible problems when such minimum generation constraints are applied as well as when demand cannot be covered by the available supply, additional variables are introduced at each node to correspondingly represent positive and negative balancing. The respective costs are set to 10,000 €/MWh for withdrawing any must-run excess energy and 1000 €/MWh [
29] for curtailing demand, and hence these options will only be activated when the system cannot maintain the energy balance with its available resources. The negative balancing price is selected such that it is more expensive than the corresponding positive balancing procurement. Aside from the country level, these backup flexibility options are applied to all other modeling levels as well.
2.3.2. Grid Level
The second modeling level in Europower consists of the grid level, where the system is operated using the full transmission grid information in order to obtain information about the main grid bottlenecks. This problem is described by the classical DC OPF formulation shown in Equation (5b–5f), where the reservoir and pumped hydro storage (PHS) power plants are operated merely as dispatchable generators (hence the replacement of
with
variables), while the PHS pumping schedule is added to the rest of the electrical load of the respective transmission node. The inequality constraints in Equation (5e) correspond to the reservoir power plants’ operation since, due to the lack of available data, only total storage capacities per country are used and therefore individual power plants cannot be distinguished from each other in the country-level formulation. To this end, only the cumulative generation of all the reservoir power plants within a country is limited by the scheduled generation of the corresponding group that is represented by
G. The goal of this level consists of merely identifying the main grid congestion:
where
| storage unit generation in MW |
| G | group or reservoir power plants |
| generation of reservoir power plant i in MW |
| total scheduled generation of group G in MW |
| generation of PHS power plant i in MW. |
2.3.3. Clusters Level
At the third modeling level, the “clusters” level, demand flexibility is introduced into the system. However, due to the considerable size of the overall problem, two additional simplifications are introduced. The first simplification consists of reducing the size of the grid to 500 representative nodes out of the roughly 4000 original, where this number is selected as an adequate compromise between computational complexity and grid representation. As it is desirable to retain the main bottlenecks of the initial system, the nodes are clustered on the basis of their average nodal prices obtained at the grid level. These nodal prices correspond to the Langrangian coefficients of Equation (1b) and indicate the additional system costs induced by a marginal increase in the demand at the specific node and time step. The reason for selecting this metric relates to its comprehensive way of measuring congestion while considering all aspects of the system simultaneously, as in the absence of transfer losses, differences in nodal prices can only occur due to the transfer capacity limitations of the network. The clustering uses the k-means algorithm as described and implemented by Hörsch et al. [
30].
The second simplification consists of decoupling the total amount of time steps into smaller chunks, hence producing a number of smaller but independent problems that can be independently solved. The chunk size is selected to be 24 h, where the flexible load can be freely shifted, i.e., without additional energy losses or costs. This flexible part of the load is considered technology-agnostic, in that it behaves as a load aggregator whose strategy and underlying technologies are not necessarily known to the system operator. Decoupling of time chunks can lead to unrealistic load ramps between two days. This can be avoided by limiting the load values of the initial time step for each time frame based on the corresponding values of the last time step determined by the previous time frame as expressed by Equation (6l). This soft coupling is introduced to avoid high load ramps at the discontinuity points, where the maximum ramps are selected to be 1% of the maximum instance of the initial demand, a typical value for aggregated loads.
Unlike the two previous modeling levels, the clusters level is formulated as a re-dispatch problem, thus retaining the information of thermal generation inflexibility. Therefore, demand shifting is primarily intended to relieve congestion rather than replace expensive fossil generation with cheaper alternatives. This new formulation is reflected in the objective function, as shown in Equation (6b), where each dispatch variable is replaced by a redispatch up and redispatch down pair, as well as the constraints (6h–6j), which indicate that injecting the scheduled generation is accompanied with zero costs, while any deviation from it may only increase the value of the objective function. The corresponding costs for upwards and downwards redispatch are selected to consist of the marginal operational cost and the zonal system price obtained at the country level respectively, and hence the generators are remunerated by the initially scheduled plan regardless of their final generation, which might be restricted due to grid limitations. Moreover, as the time steps within each daily horizon are coupled, the reservoir and PHS hydro plants can be operated as storage units, thus providing additional flexibility to the system. Nevertheless, the individual SOC for each hydro plant must respect the long-term scheduling for each country. This constraint is expressed in Equation (6f), where a small tolerance is also introduced for the handling of potential numerical errors.
The final part of the clusters level, demand flexibility, is modeled as a generic shiftable load, wherein the specifics of the underlying technologies that could result in the final behavior are ignored. In particular, for each cluster, a part of the total initial demand (e.g., 10%) is considered to be flexible and hence uniformly deduced by the initial load over all the time steps. This part is then modeled as a virtual storage device where power injection back into the system is prohibited, while the power (or “charging”) capacity is limited by the initial maximum load occurrence. Finally, the SOC of the virtual storage unit is set via Equation (6k) such that, at the end of each time frame, the load recovery is guaranteed:
where
| upwards redispatch in MW |
| downwards redispatch in MW |
| T | time chunk size in hours |
| zonal price in €/MWh |
| small tolerance accounting for numerical errors, e.g., 0.001 |
| time chunk index |
| scheduled generation in MW |
| state of charge for the DSM storage in MWh |
| total electricity load that can be shifted within one time chunk in MWh |
| charge rate of DSM storage in MW |
| r | maximum ramp of charge rate between time chunks in MW. |
2.3.4. Redispatch Level
As the primary aim of this work consists of estimating the VRES curtailments and clustering the grid necessarily ignores any congestion that occurs within the clusters, a fourth modeling level, the “redispatch” level, is introduced, in which the transmission grid is represented in its original form. The problem, described by Equation (7b–7h), is formulated again as a redispatch problem, where in this case the scheduled generation is dictated by the outcome of the clusters level. The only difference to the previous level in terms of the formulation consists of the hydro power plants being modeled as generators similarly to the grid level approach and the existence of non-grouped thermal power plants, for which the redispatch constraints are applied to individual generators, as shown in Equation (7e). Finally, the scheduled demand, after the application of flexibility, is applied as fixed profiles to all nodes corresponding to each cluster via grouped equality constraints, described by Equation (7h):
2.4. Implementation and Validation
The implementation of the entire modeling chain, which is comprehensively summarized by
Figure 1 and
Table 2, is implemented in Python using the PyPSA modeling framework [
31], which utilizes the Pyomo algebraic modeling language for building optimization problems. Solving the generated models is carried out with the Gurobi solver on a 2x Intel
Xeon
Gold 6154 CPU 3.00 GHz machine with 18 cores per CPU and 512 GB memory. As for the country and redispatch modeling levels, the individual time steps are decoupled and the yearly system operational cost is minimized if—and only if—the corresponding hourly costs are minimized, the respective sub-problems can be trivially parallelized and hence considerably increase the total computational performance. The parallelization is implemented using the mpi4py package [
32], which provides the bindings of the MPI standard for Python.
As mentioned before, a mathematical prediction of the accuracy of the developed methodology cannot be obtained and only empirical comparisons to the original problem by considering adequately small system are possible. The requirement for adequately small problems requires that the original coupled problem can be solved in reasonable time. This would mean that the involved transmission systems should be selected to be small enough—however not so small that the modeling of cross-border connections via NTC values loses its validity. Moreover, the reduction of the size of time steps should not be such that the needs for seasonal storage become irrelevant. In addition to the small size of the test cases, an adequately large number of different conditions and scenarios should be examined in order to estimate the extent of the introduced error for larger systems that cannot be tested.
3. The European Power System of the Future
Analyzing power systems through dispatch models requires knowledge of the system’s boundaries, including power plant and transmission grid infrastructure, as well as electricity demand. Although these boundaries can be reproduced with a relative confidence for historical system states, future configurations necessarily rely on estimates or investment models. However, due to the increased complexity and high uncertainties involved in long-term planning, such investment models primarily rely on low spatial resolution. As estimating or designing the future power system of Europe would lie beyond the scope of this study, efforts from the Ten Year Network Development Plan (TYNDP) 2016 [
33] and e-Highway 2050 project [
34] are considered for the years 2030, 2040, and 2050.
As a power system’s evolution depends on factors that are difficult to predict with confidence, such as political decisions and economic development, future planning typically involves more than a single scenario for each target year. For the year 2030, the TYNDP 2016, published by the European Network of Transmission System Operators for Electricity (ENTSO-E), consists of four distinct scenarios (visions 1, 2, 3, and 4) as a result of the combination of two separate axes, namely the strength of a common European framework and the level of advancement with respect to the Energy Roadmap 2050 [
2], as depicted in
Appendix A. Based on these four visions, the e-Highway 2050 project develops five scenarios for 2040 and 2050, with rationales briefly described in
Appendix A. As is stated by the authors of the respective reports, the various scenarios do not aspire to constitute a forecast of how the system will evolve, but rather provide a set of possible future system conditions that meet specific design criteria, while remaining sufficiently distinguishable from each other. Moreover, the aim of this work is not to evaluate the scenarios themselves but rather, on the basis of them, to estimate and analyze the integration of VRES into the European power system of the future.
3.1. Spatial Disaggregation of System Boundaries
The available system information from the TYNDP and e-Highway 2050 reports are provided at an aggregated level over extended regions; therefore, the translation of such information to a higher spatial resolution becomes essential. Considering the lack of additional sources, the existing infrastructure is selected to constitute the primary source for the spatial disaggregation of the regional system boundaries. Thereby, a representation of the European power system for the year 2015 is used as the basis for implementing the future scenarios, as introduced by Syranidis et al. [
28], while the wind generation potential is calculated as described by Ryberg et al. [
35,
36].
With respect to generation, the corresponding spatial disaggregation distinguishes between VRES, thermal and hydro generation, where hydro power plants do not follow the development suggested by the respective studies but are instead always considered as of the year 2015. Concerning VRES generation, when provided at the country level, it is further distributed to the e-Highway clusters based on the average capacity factor and electricity demand of each region, where each factor weighs differently in accordance with the scenario’s rationale relating to the degree of decentralization. Furthermore, the additional distribution within each cluster region merely follows the average capacity factor, and hence constitute the locations with the highest generation potential. Finally, thermal generation follows a similar logic to the VRES disaggregation, where the total capacity per fuel type is first distributed to the e-Highway clusters with respect to already existing capacity, and so the existing spatial balance is maintained. Within each cluster, the existing individual power plants are either replaced, extended, or dismantled according to each scenario, with the shutdown or replacement of the least efficient power plants prioritized. Any new generators follow the existing locations when possible due to their accessibility to existing infrastructure. Moreover, the scaling is performed in discrete steps by assuming a maximum generation unit of 300 MW.
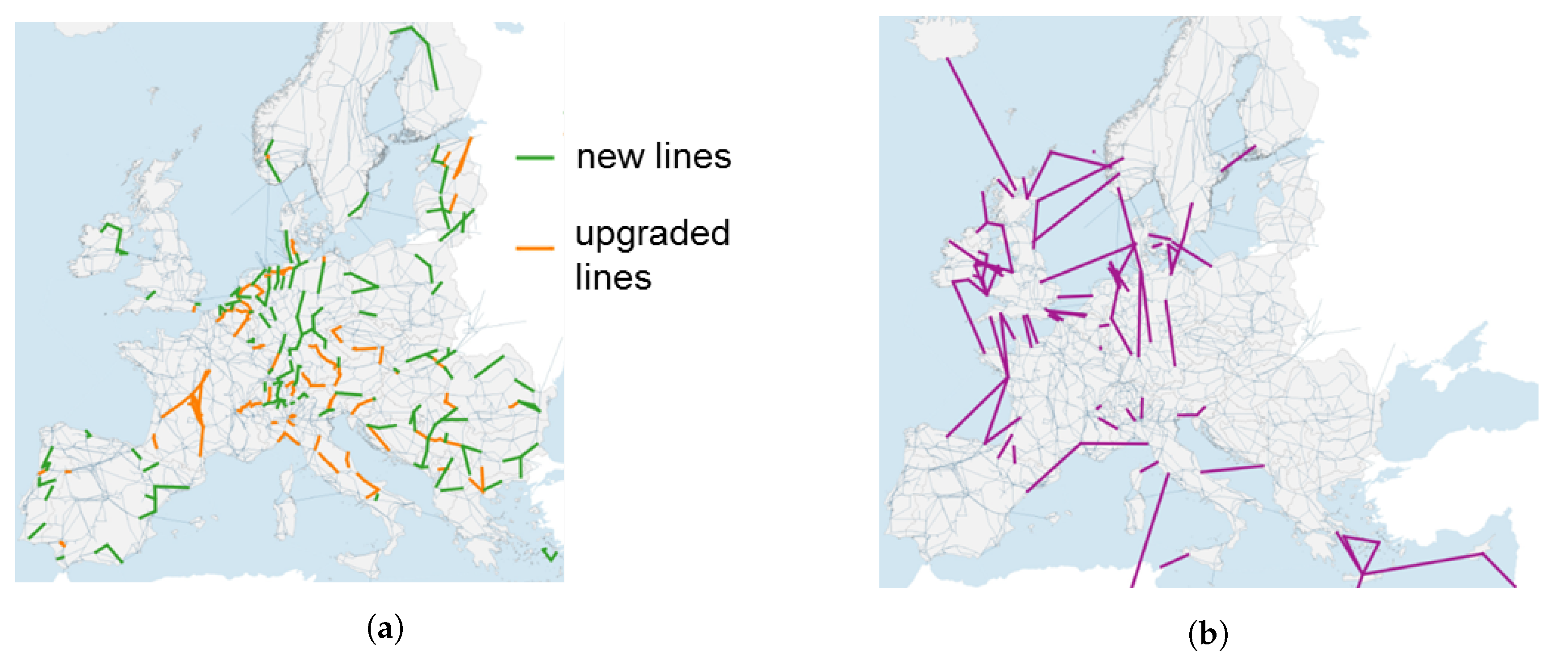
Unlike generation and demand, disaggregating the inter-regional transmission expansion requirements to individual lines cannot be accomplished in a straightforward manner. Therefore, any grid expansion beyond the year 2030 is not considered here. However, it is considered that all projects included in the TYNDP 2016 will be completed by 2030. The respective upgraded and new AC and DC lines are shown in
Figure 2.
Finally, with regard to electricity demand, a top-down approach is opted for. The national profiles are created according to the respective assumptions for each scenario, and these are then spatially distributed using the existing population density and consequently are assigned to the nearest substation. Although distributing by a single indicator can be regarded as oversimplification [
37], the difficulty in obtaining data, especially regarding industrial demand, on the European scale has driven many researchers to such an approach [
13,
14,
23,
38]. The total electricity consumption follows the e-Highway assumptions and is split into three components, namely battery-electric vehicles with different charging profiles depending on their controllability, heat pumps for industrial processes, water and space heating, and the remaining conventional load that follows historical profile shapes.
3.2. The “Large-Scale RES” Scenario
A more detailed description of all of the scenarios and their components can be found in the corresponding report [
39]. Nevertheless, further insight can be obtained by examining the capacity mix and total electrical energy consumption for the “large-scale RES” 2050 scenario, which is selected for the analysis of this paper. This scenario was chosen due to its centralized generation rationale that is expected to result in significant challenges in terms of integration of VRES.
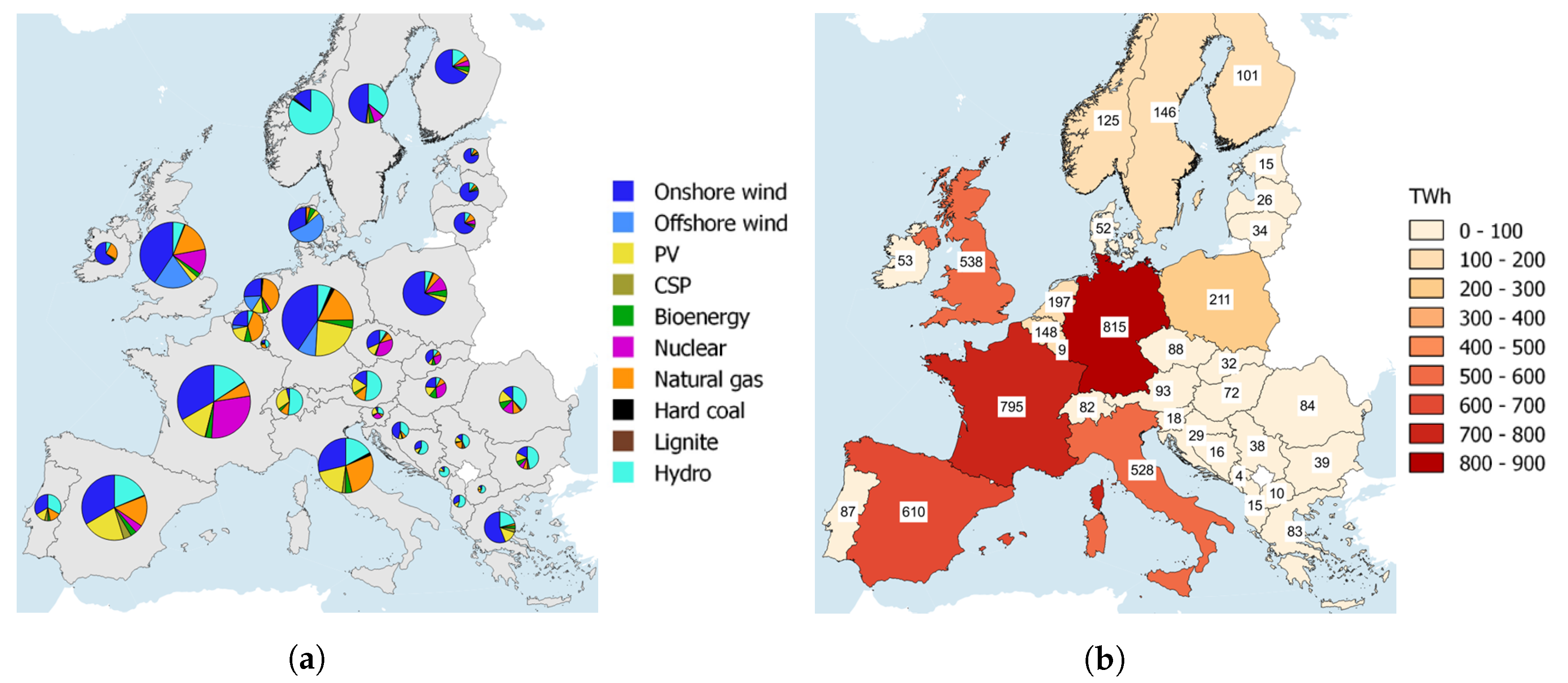
Figure 3 shows the capacity mix per country as defined by the e-Highway report [
38], as well as the total corresponding electricity consumption. It can be noticed that nuclear and natural gas still play a significant role in the countries that traditionally relied on them, while coal power plants are overall negligible. With respect to RES, the centralized rationale of the selected scenario translates to the most dominant source across Europe consisting of wind energy with 813 GW of total installed capacity (including a significant amount of offshore capacity), while the more distributed solar generation remains low (256 GW). As of electricity demand, the “large-scale RES” scenario has the highest total consumption amongst all scenarios, approximately 66% higher than today’s values, due to the assumed passive public attitude towards efficiency measures.
4. Results and Discussion
As the primary research focus is on the integration of VRES into the European power system of the future, investigating the system’s operation can provide valuable insight into the causes of VRES curtailments and the corresponding impact of the transmission grid. Therefore, in addition to analyzing these curtailments, the outcomes of the intermediate modeling levels are also examined, as they can increase understanding of the system’s behavior.
Figure 4 shows the energy mix per country as calculated by the country level, where the total imports and exports are included as well, thus signifying the influence of energy exchanges amongst the countries in the individual energy supply. As anticipated by the scenario’s definition, where the respective national capacity mix is depicted in
Figure 3, nuclear and natural gas are still noticeably present with respect to conventional power sources, while wind is by far the most dominant source amongst all RES technologies. The inclusion of exchanges illustrates the significance of the interconnections, as they typically constitute a considerable part of the national energy mixes, while it can also assist in identifying particular tendencies when observing the net positions of each country. For instance, it can be noticed that most eastern European countries are closer to a balanced net position, in contrast to the western part of Europe where, for example, it can be observed that Germany behaves as a net importer in this scenario, supplied by cheap nuclear and wind electricity from the neighboring systems of France, Denmark, and Czechia.
A closer look at the behavior of power transmission and the impact of grid constraints can be obtained by observing the results of the grid modeling level.
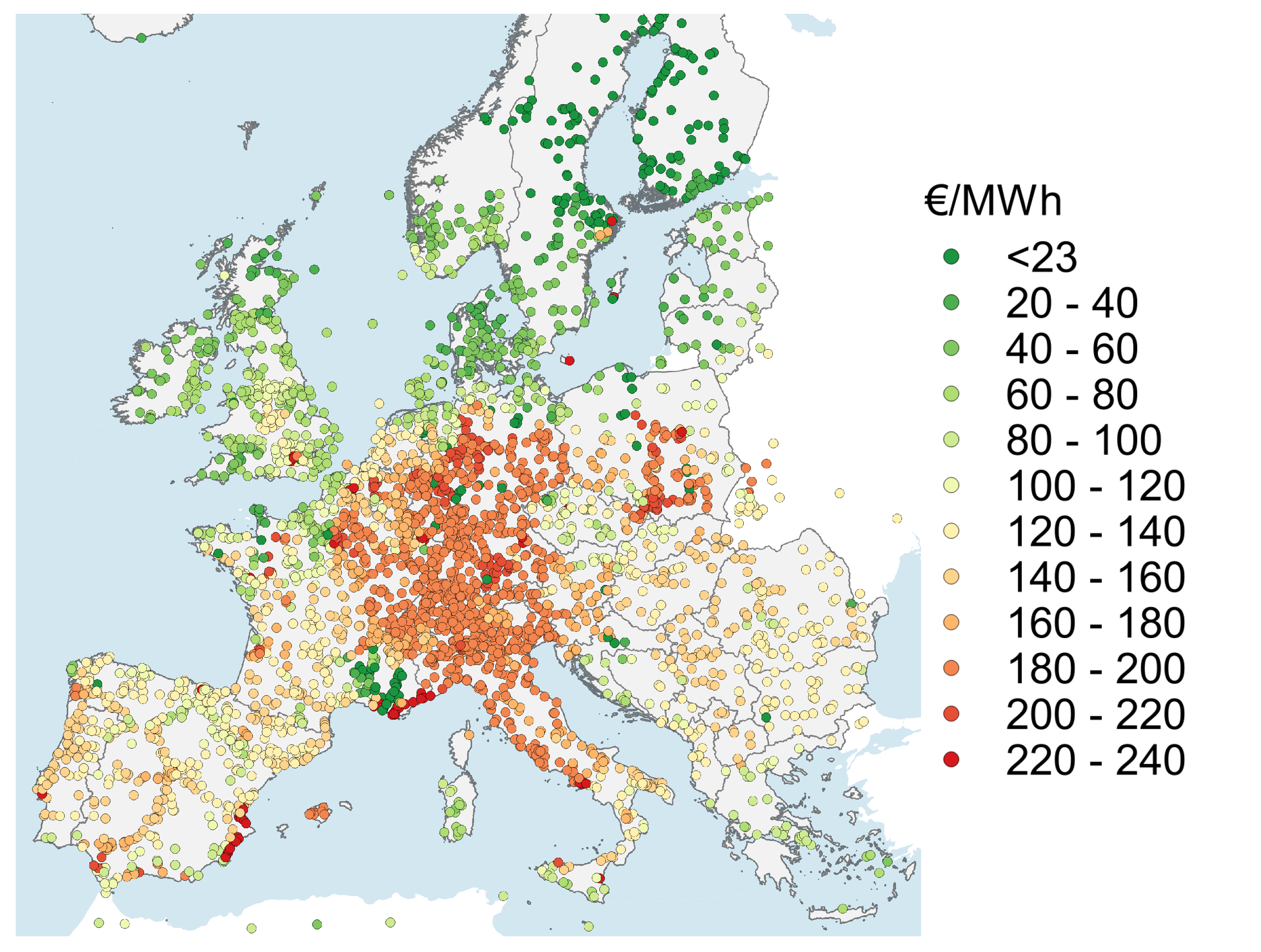
Figure 5 shows the average nodal prices for each transmission node for the selected scenario in 2050. It can be noticed that these prices disregard the national borders to a much higher degree than in the present system, and hence the separation of market zones in accordance with the administrative borders further loses its proximity to the original physical system and its validity as a reasonable means of zonal partitioning. Similar findings have also been shown by Breuer et al. [
40] for Europe even earlier than 2050. Nevertheless, it can be also observed that distinct clusters of similar average prices can be identified. For instance, one such cluster consists of the northern part of Europe, including the coasts of the North and Baltic Seas and the British Isles. Due to the scenario’s preference for locations with high potential, the cheap hydro power from Scandinavia and the significant presence of wind generation concentrated near the coastline lead to average prices that are considerably lower than inland Europe. A similar zone of low average nodal prices can be observed around southern Europe and northern Africa, where cheap solar generation, predicated on PV and concentrated solar power (CSP) technologies, predominate. However, between both zones and inland Europe, where the demand centers of central Europe are located, prices rise rapidly. It can be seen that, although relatively uniform, the prices in central Europe are significantly higher, reaching up to 200 €/MWh. Nevertheless, one exception to this behavior is Czechia, where nuclear generation keeps prices lower than its neighbors, which in turn however also illustrates the congestion along these interconnections. A second island of very low prices can also be observed in southern France, which indicates considerable grid bottlenecks around this region.
At the next modeling level, the clusters level, demand flexibility is applied in order to accommodate the spatio-temporal imbalances between generation and load in the system, as described in
Section 2. For this scenario, it was decided to apply 10% of demand flexibility, deferrable by 24 h. The impact of demand flexibility can be seen when comparing the average daily curves before and after their application to VRES generation potential, as is shown in
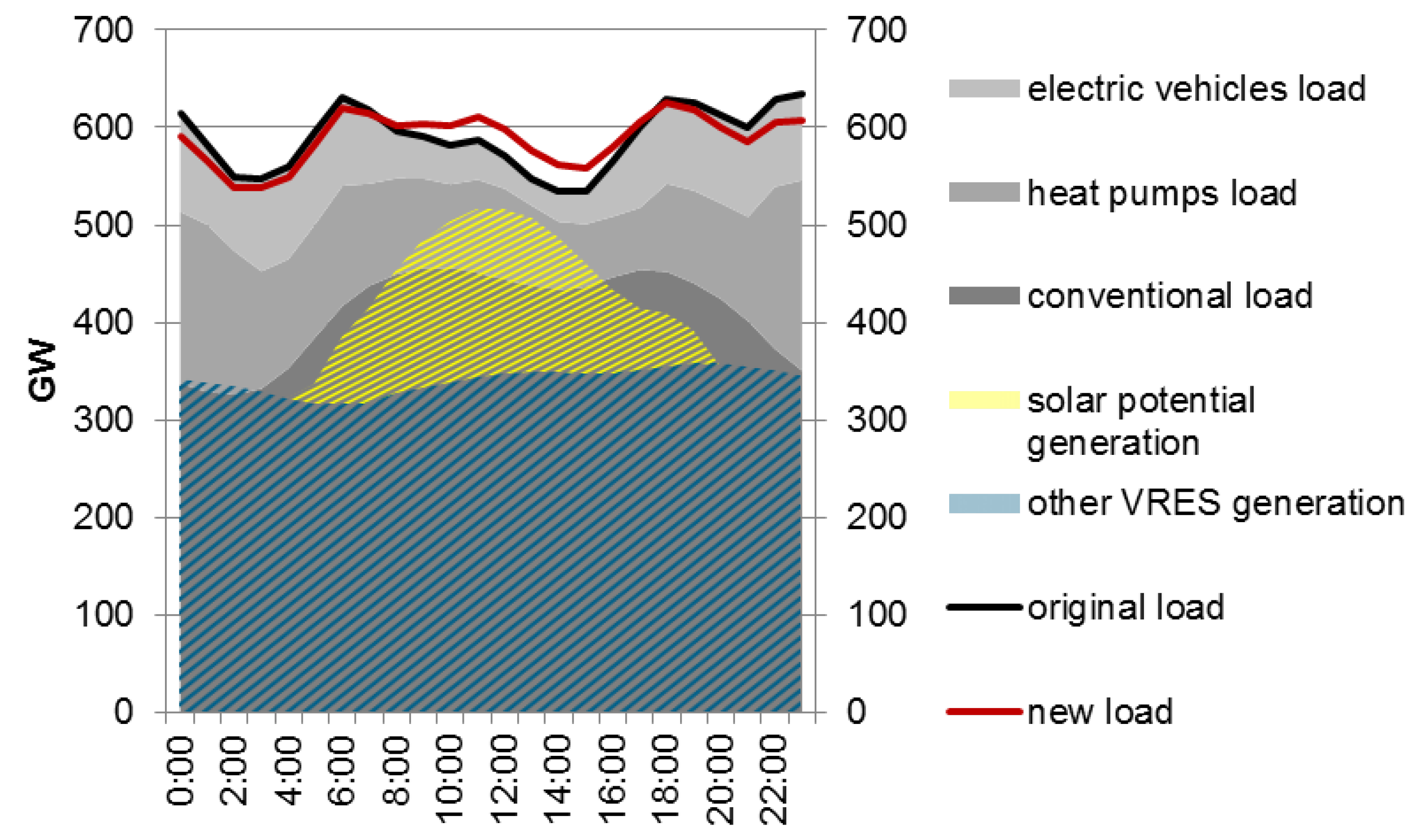
Figure 6. Unlike today’s situation, depicted by the conventional load, where the demand starts dropping early at night, the new consumers of electric vehicles and heat pumps delay this drop further during the night, which also leads to a deeper afternoon valley that intensifies the positive evening ramp. With regard to VRES variation during the day, it can be observed that solar potential shows strong dependency on the hour of the day, where the maximum generation is concentrated at midday. On the other hand, wind and hydro potential do not seem to show any significant preference during the day, as the frequencies of the corresponding profiles are typically lower and span multiple hours or days. The load and solar potential profile shapes, along with the maximum load shifting being limited to 24 h, result in a net load shift from the night hours towards midday after applying demand flexibility, as depicted in
Figure 6. This behavior stands in contrast to what would be expected to be the impact of applying demand flexibility in today’s power system.
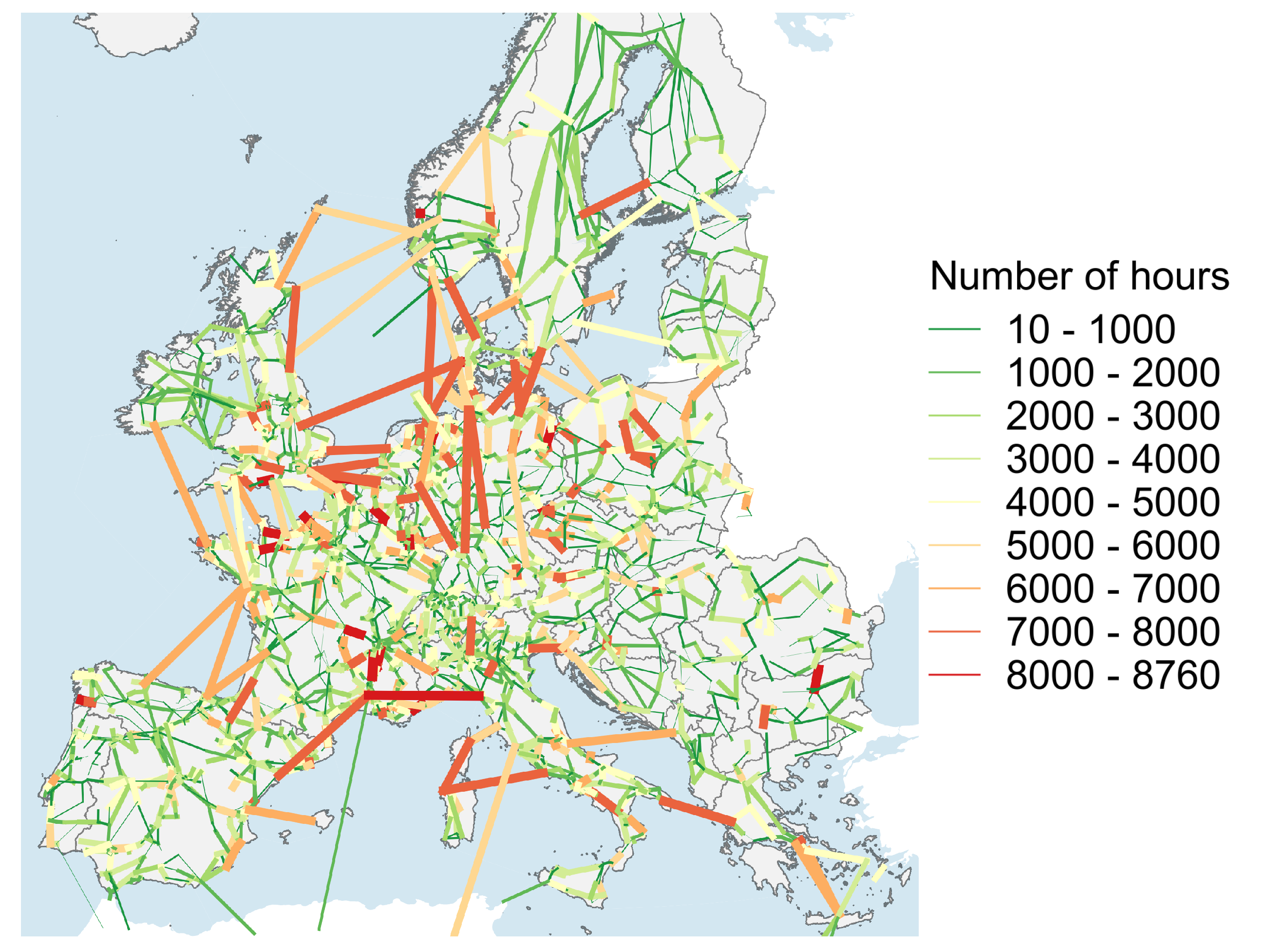
Applying the results of the clusters modeling level to the redispatch level, where the full transmission grid is used, the final VRES curtailments can be obtained. The behavior of the system can be illustrated through the utilization of the individual power lines, depicted in
Figure 7. Despite the application of demand flexibility, the picture resembles
Figure 5 at the grid level, although different system variables are used to depict grid congestion. Here, the frequency of lines’ loading over 50% of their nominal capacity is depicted over the year, as overloading beyond the 65% level [
41] that is used to represent the N-1 security criterion, is already strictly prohibited by the respective optimization constraints. As in
Figure 5, the main congestion areas can be identified between the zones with high wind and solar concentrations, in the north and south, respectively, as well as central Europe. Therefore, it is expected that the majority of VRES curtailments to be found within these two zones.
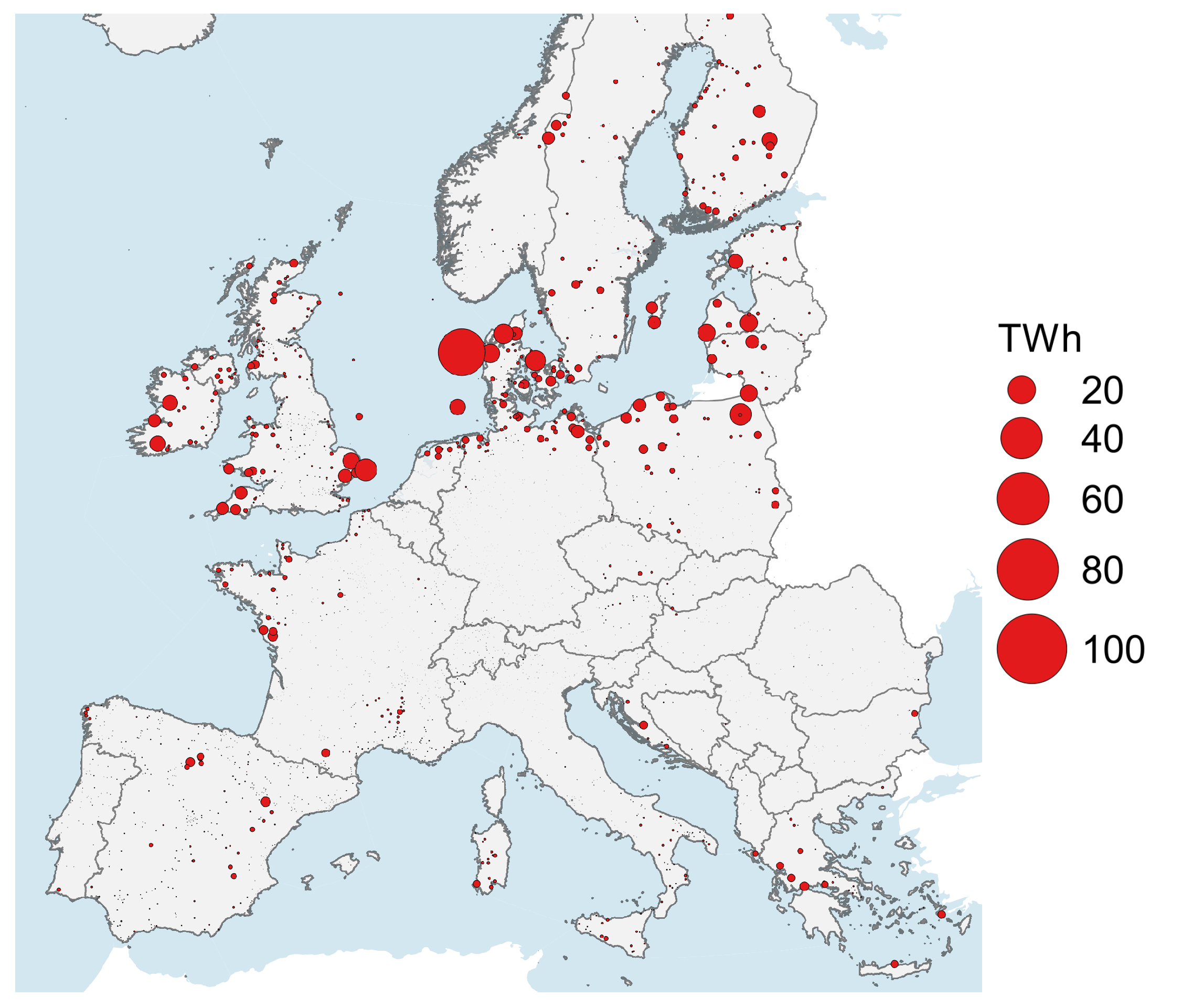
In the context of this paper, VRES curtailments refer to the amount of energy from VRES that is available but cannot be consumed, stored or transmitted and therefore cannot enter the system. This definition only includes the wind, solar, and run-off-river hydro sources, as these technologies cannot store their respective primary energy source. Considering the relatively high presence of wind energy in comparison to the other VRES sources, as depicted in
Figure 3, as well as the preference of load shifting in the direction of integrating solar energy, it is expected that the primary source related to curtailments would be wind energy. This can be verified by
Figure 8, where the total amount of curtailments per node is shown, and it can be noticed that the locations with the highest curtailments coincide with nodes that contain primarily wind generation. Moreover, it can be observed that these locations are also in agreement with
Figure 5 and
Figure 7 which depict grid congestion, as expected. Thereby, it can be concluded that the spatial imbalance and limitations posed by the transmission grid constitute the primary drivers preventing further VRES integration into the system.
A reduction of the resulting curtailments can be achieved through a combination of transmission grid reinforcement and the addition of further storage options. However, the decision to invest in such options depends on the frequency and intensity of the curtailments, as this may not be economically beneficial. In addition, taking measures to further integrate these curtailments into the power system, power-to-X applications can also be used to exploit the energy collected by transforming into different carriers like hydrogen or heat. In this way, more green energy from RES can be integrated into the overall energy system, which includes more energy sectors additional to electricity that must also be decarbonized.
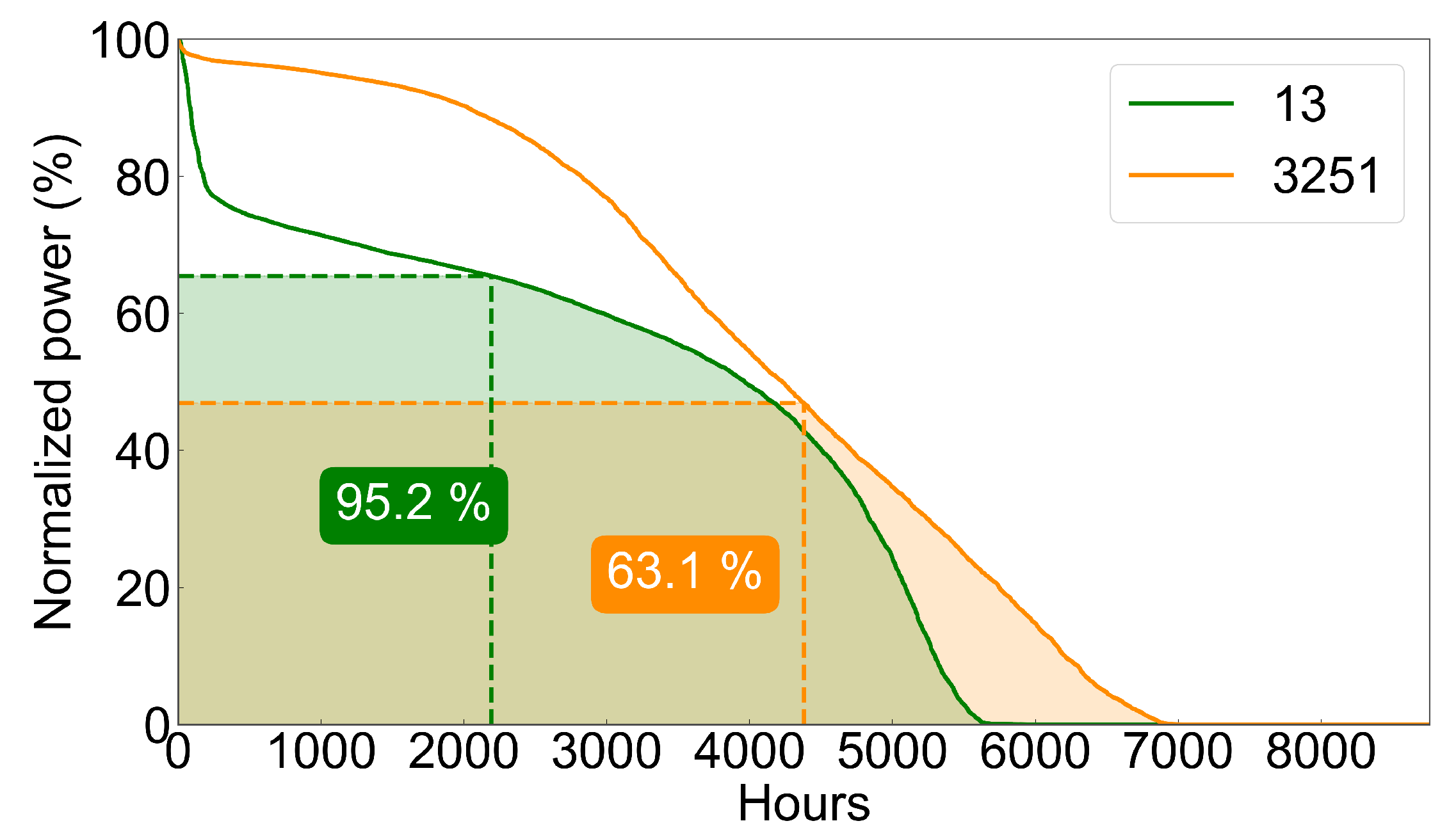
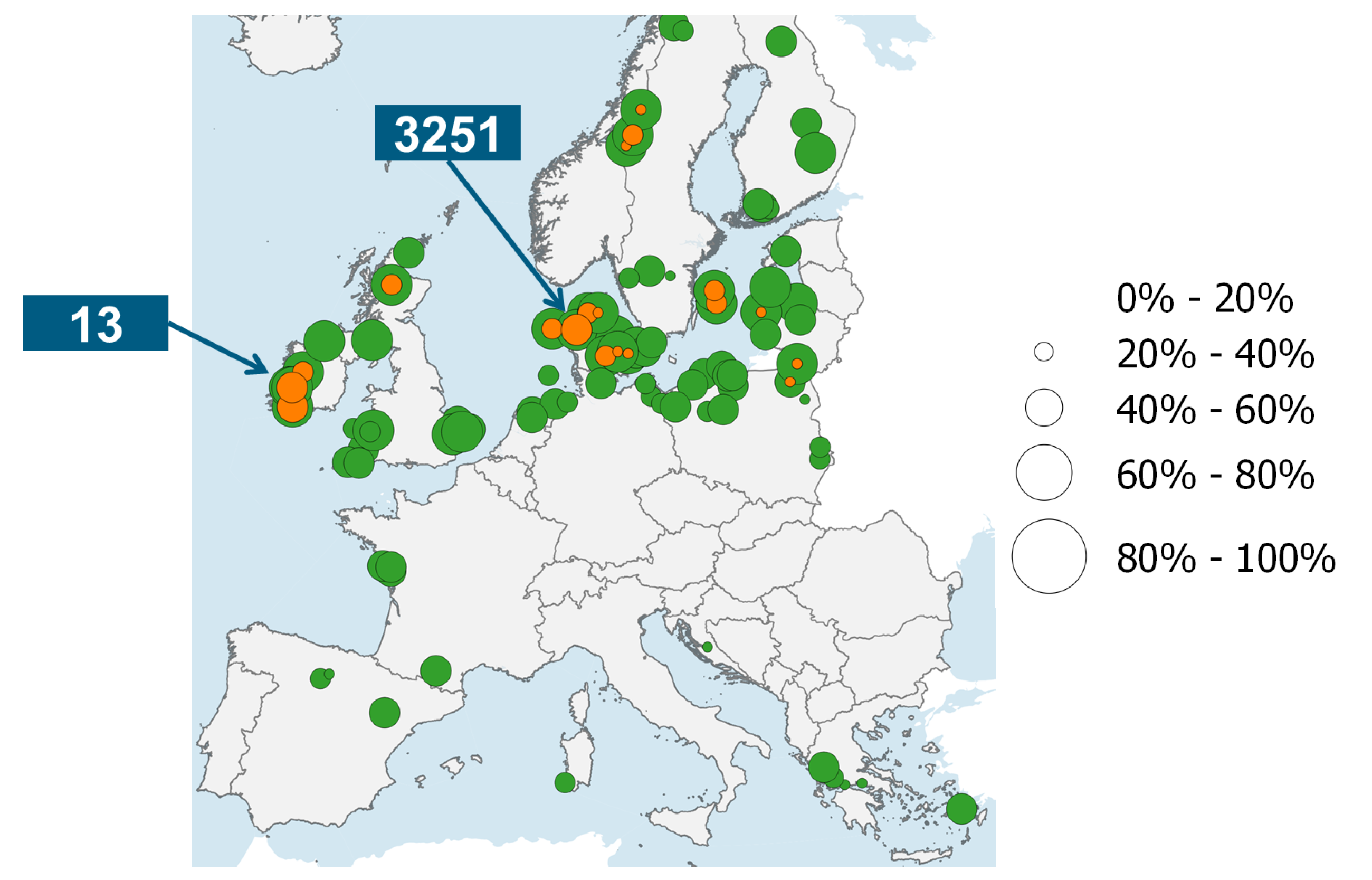
Investigating all of the different technological options lies beyond the scope of this paper; however, analyzing the obtained curtailments via ideal converters, i.e., with 100% efficiency, can provide valuable insight into their spatio-temporal properties. In order to better compare these properties between the different transmission nodes, all of the profiles are normalized. However, to avoid including insignificant profiles with low energy content, the transmission nodes are filtered such that only the first 100 with the highest amount of total curtailments are considered. The filtered set corresponds to approximately 73% of total European curtailments. Considering that, regardless of the installed technology, frequent operation is desired, two ideal converters are placed in each node. Their capacity depends on the frequency of full-load operation over the year, hence functioning as a metric of the gradient and curvature of the respective curtailment duration curve. A narrow, convex duration curve would mean that the installed capacity can be utilized in only a few instances whereas a flatter, concave duration curve would allow for better utilization of the installed capacity. A corresponding example is shown in
Figure 9 for nodes “13” and “3251”, which are located in Ireland and Denmark, respectively, as depicted in
Figure 10. It can be seen that, in the case of node “13”, a converter with a capacity equal to the 75th percentile of the corresponding curtailment distribution (i.e., 65.4% of the maximum occurring curtailment) can yield 95.2% of the available curtailment energy while, in the same fashion, a converter at node “3251” with a capacity equal to the 50th percentile (i.e., 46.9% of the maximum occurrence) can yield 63.1% of the available energy. The corresponding normalized converted energies of all of the filtered nodes are shown for the 50th and 75th capacity percentiles with orange and green colors, respectively. A high value for the 50th percentile is desired, as this translates into a flatter, more concave duration curve where the energy content of the respective curtailments are distributed more uniformly over the year. Consequently, it can be derived from
Figure 10 that the best nodes in that regard are located in western Ireland and western Denmark.
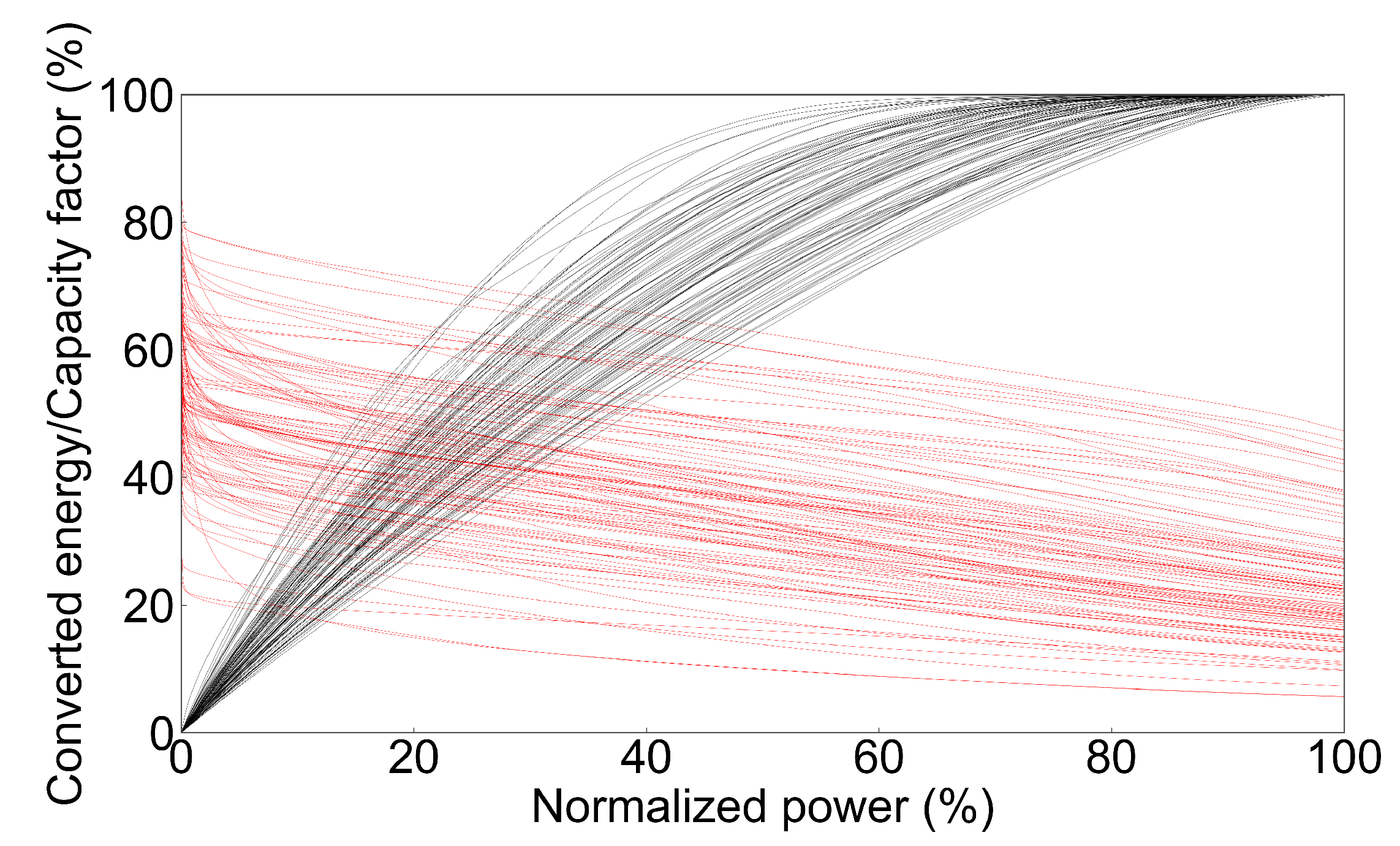
Further insight on how the available curtailment energy can be extracted for different converter capacities is depicted in
Figure 11. The black lines illustrate the converted energy as a function of the converter capacity which are concave for all nodes; however, the individual curvatures can differ significantly. This difference becomes more prominent when comparing the resulting capacity factor as a function of the installed capacity, which is depicted by the red lines. Although all of them decrease in similar rates, the spread in absolute values is considerable. Additional understanding of this behavior can be better obtained by applying cost parameters or curves for the energy curtailments and converters; however, such an analysis would exceed the scope of this work.
5. Conclusions
In this paper, a novel pan-European dispatch model with high spatio-temporal resolution and consideration of demand flexibility was introduced in order to investigate the integration of VRES into the future European power system. The developed model can be used for obtaining detailed estimations of renewable curtailments in both spatial and temporal dimensions. Such information can be proven useful to researchers, system operators or utilities to evaluate different system designs with regard to VRES integration, investigate options of system expansion in congested areas or invest in power-to-X applications such as power-to-gas.
The application of the model showed that, for the investigated scenario in 2050, the majority of the VRES curtailments are concentrated near the coastlines of the North and Baltic Seas, as well as the British Isles. These curtailments originate from wind energy that cannot be transferred to inland Europe due to power transfer restrictions posed by the transmission grid. Therefore, centralized pathways based on wind generation will also require significant investments in grid reinforcements but may also offer profitable options for power-to-X technologies.
Due to the limitation in demand shifting to 24 h, it was shown that this tends to follow the solar generation pattern, hence shift load from the night towards midday, hence its significance decreases for wind-based systems. Further analysis of the time series properties of the VRES curtailments, with respect to the distribution of their energy content over the year, showed that the best candidates are located in western Ireland and western Denmark. In these locations, installing converters with capacities equal to both the 75th and 50th percentiles of the corresponding curtailments distribution can be utilized more frequently over the year, hence rendering them more suitable for exploiting the respective curtailments than in different locations. Such behavior cannot be easily deduced by merely analyzing the weather conditions or by using reduced models. However, the application of the introduced methodology can directly identify specific locations not only in terms of curtailments volume, but also in terms of quality of curtailment profiles suitable for energy conversion.