Short-Term Electricity Price Forecasting with Recurrent Regimes and Structural Breaks

Abstract

This paper develops a new approach to short-term electricity forecasting by focusing upon the dynamic specification of an appropriate calibration dataset prior to model specification. It challenges the conventional forecasting principles which argue that adaptive methods should place most emphasis upon recent data and that regime-switching should likewise model transitions from the latest regime. The approach in this paper recognises that the most relevant dataset in the episodic, recurrent nature of electricity dynamics may not be the most recent. This methodology provides a dynamic calibration dataset approach that is based on cluster analysis applied to fundamental market regime indicators, as well as structural time series breakpoint analyses. Forecasting is based upon applying a hybrid fundamental optimisation model with a neural network to the appropriate calibration data. The results outperform other benchmark models in backtesting on data from the Iberian electricity market of 2017, which presents a considerable number of market structural breaks and evolving market price drivers.

1. Introduction

Price forecasting in electricity markets is facing frequent, and perhaps increasing, structural changes in the market. Apart from new entrants and corporate restructuring affecting market conduct, the technology mix is going through a transition to intermittent renewables and end-user engagement is becoming substantial. In addition, policy interventions are increasing as governments seek to achieve a balance of decarbonisation, security and affordability. All of this creates a modelling challenge for price forecasting. Time series estimation, therefore, has to take account of structural breaks and evolving parameters as market circumstances change. A simple response is to work with short time series to reflect only recent conditions that may be representative of the intended forecast horizon, but that limits the complexity of model estimation. In contrast, econometric methods often seek to include estimated structural break terms. These, however, tend to be limited to a few distinct interventions and do not capture more complex evolutions. Hybrid methods, alternatively, that link time series analyses to underlying market simulation models can be more effective [1], but even with a hybrid method, the choice of an appropriate time series calibration length still remains.

Surprisingly, despite its crucial role, research on how to select the appropriate data window for model estimation is an under-researched topic in forecasting. Whilst we have seen time series methods increase in complexity to capture the distinctive features of power price formation, going from ARIMA and its variants [2,3,4], neural network and other AI approaches [5,6,7,8,9,10] to wavelets [11,12,13] and various combinations, these procedures all rely on the presumption that the time series model, as estimated, can be projected forward, which may not be so appropriate in the more evolving power systems of today. In one of the few research papers to look at this aspect, the sensitivity of forecast errors to the estimation window has been analysed in [14] and based upon this, the research in [15] presented a pragmatic averaging of forecasts of individual ARX models estimated upon different data calibration windows. However, only heuristic suggestions were made for the choice of windows for calibration.

To complicate the specification further, apart from permanent abrupt and gradual structural changes affecting the window of relevant history, power price formation is known to manifest recurrent regime changes and exhibit multi-seasonal behaviour [16], according to the interactions of periods of scarcity, input prices, weather conditions and behavioural dynamics. Thus we have seen Markov and factor-based regime-switching methods outperform single regime models in several comparative studies [17,18]. The implication of this is that there are recurrent episodes in the time series when one specification is more relevant than another. So, if we are seeking to find the most relevant window of data for model calibration, it may not be the most recent. For instance, if the power system is expected to experience a sharp and sudden increase in wind generation based on weather forecasts, it may prove advantageous to disregard for predictive estimation any periods in the past that do not present significant wind outputs. Our research, therefore, seeks to make a contribution by developing a methodology to select the appropriate calibration window for a hybrid fundamental/timeseries forecasting approach based upon considerations of structural breaks and recurrent regimes. It is evidently important to have an integrated method to select the calibration window both with respect to considerations of recurrent regimes as well as respecting structural changes, and we are not aware of this joint specification being considered in previous research. This is therefore the focus and main contribution of this research.

Various aspects of calibration window selection have appeared in previous research but without the full specification being sought in this paper. For example, in neural networks, [11] uses a training set involving the seven days prior to the forecasting day and adds three extra days based on the similarity with respect to the day immediately prior to the forecasting day in terms of daily price patterns. In contrast, [19] utilises a modified version of the similar days method proposed in [20] in order to select the 12 most similar days in a predefined 4-month calibration period according to exogenous variables available at the moment of the forecast, such as expected demand and temperature. However, these methods are motivated more by considerations of neural network overfitting issues rather than by market regime changes.

In providing a more formal method for calibration window selection, according to robust criteria for identifying both recurrent regimes and structural changes, we undertake this in the context of advocating a hybrid fundamental/econometric approach. We consider the inclusion of a fundamental market simulation model crucial for forecasting with structural changes since it can explicitly represent price formation under new market conditions. For example, the impending decarbonisation of power systems is not a recurring event that econometric approaches can interpret and project in the future. Indeed, that is why hybrid methods have become widely applied in medium-term applications [21,22,23]. But only a few researchers have considered applying them to the short term [19,24], perhaps because of the high computational requirement of running hourly fundamental models. Nevertheless, this issue can be dealt with by means of simplification methods, such as aggregating similar generation units [24,25]. Furthermore, given that these hybrid models explore most of the drivers of electricity prices, an immense volume of information must be handled by the models. For accuracy, however, this is worthwhile, but only if the time series calibration window is appropriately chosen.

In summary, therefore, this work attempts to provide a novel forecasting method that properly addresses the joint problem of recurrent regimes and market structural breaks in selecting the calibration window, in order to support a state-of-the-art hybrid model. The hybrid model is similar to one of the models proposed in [19] and involves a short-term model that is composed of an hourly cost-production optimisation model whose outputs provide market-related information to a neural network (NN) model. However, there are several distinctive modelling features of this new work that add to its novel research contributions:

• Prior to the NN forecast, the NN training period, which is initially set to a very large window, is filtered by means of a structural break analysis method and periods where prices significantly differ from those prior to the forecasting period (i.e., most recent prices) are discarded.
• Furthermore, the hourly trends in the actual forecasting period according to market regime related variables are evaluated via a K-means clustering procedure. The hours of the initial NN calibration period where the assigned cluster coincides with that of the hours in the forecasting period are included in the previously filtered calibration period by the structural break analysis method. This combination of training window selection techniques is carried out ex-ante and therefore provides a dynamic calibration dataset.
• The proposed set of methodologies is backtested on the real and full-scale Iberian electricity market of 2017. The performance of this approach is compared with that of other well-recognised forecasting models.

The remainder of this manuscript is organised as follows: the methodology is described in Section 2; Section 3 presents the case studies in which the proposed forecasting method, as well as other comparative forecasting methods, have been tested; and Section 4 contains the conclusions, including suggestions for potential extensions.

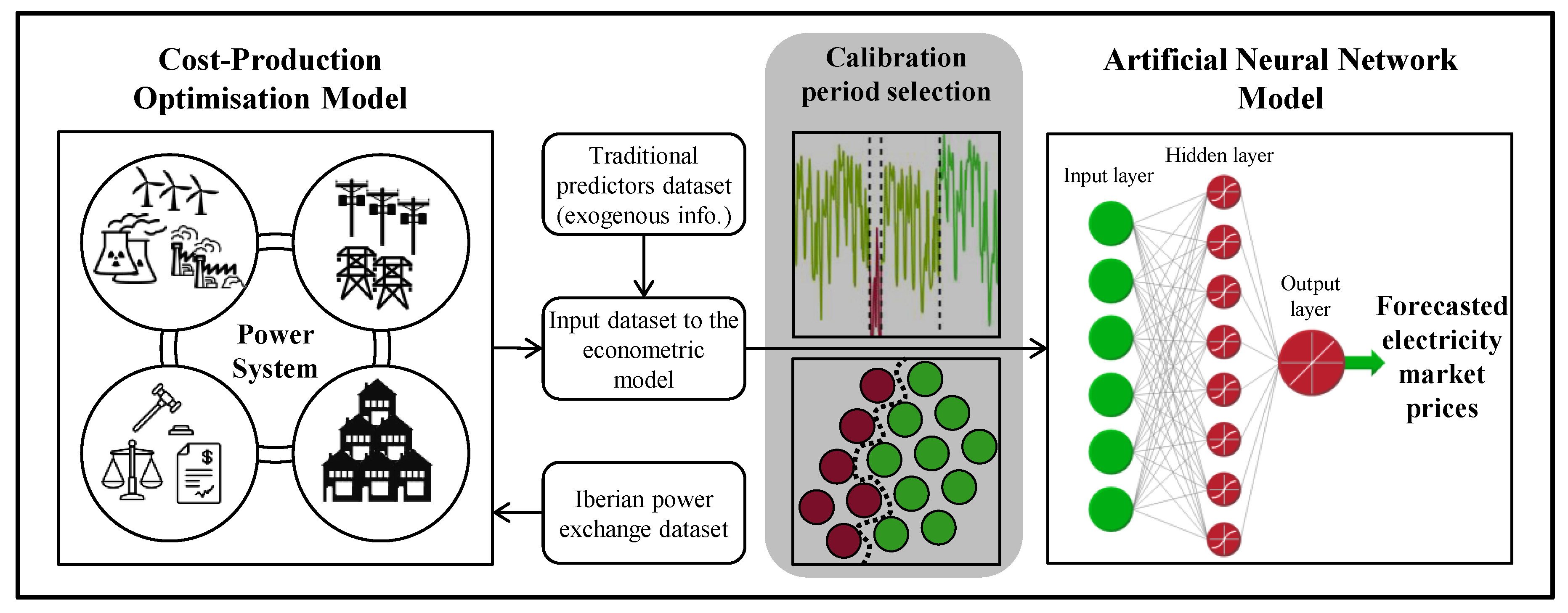
2. Proposed Methodology

Essentially, this work’s proposed methodology is comprised of the methods displayed in Figure 1, all of which have been tested on a real-size power exchange with complex price dynamics: the Iberian (Spain and Portugal) electricity market. The first phase of the methodology represents its fundamental component, the cost-production optimisation model. The next stage involves several data pre-processing approaches that aim to enhance the final step of the methodology, which is an artificial neural network model. Each element of the proposed methodology is explained below.

2.1. Cost-Production Optimisation Model

In order to consider physical elements, regulatory limits and the operation of the market, a cost-production optimisation model, which is based on the Iberian power exchange, is specified. The required information is obtainable from the transparency platforms of the Spanish System Operator [26] and of the ENTSO-E [27]. This fundamental model seeks to reduce total system costs under perfect competition assumptions by setting the production outputs of the system’s power units to optimal values. The mathematical formulation of this optimisation model is similar to the one presented in [19,25] and estimates the electricity market price as a result of the market-clearing according to competitive fundamentals. These prices are known as system marginal prices, and they are derived from the dual variables of the demand and generation balance constraints. Furthermore, it was observed in [19] that considering thermal units separately is worthwhile in terms of accuracy. Specifically, although a week is solved by minimising system costs simultaneously throughout the 168 h in 7.4 s (up from 3.91 if the thermal units are aggregated), the forecasting error is reduced by approximately 33% when compared to the optimisation model of [25]. The optimisation is solved via relaxed mixed-integer programming (RMIP) in order to consider all units’ variable costs and not only those of the committed units.

2.2. Period Selection

The main contribution of the work, however, is an improvement in model performance by achieving an appropriate calibration data selection procedure. The calibration period selection methodology provides a suitable and novel solution to this issue, allowing the subsequent NN model to handle only the necessary data by focusing upon the relevant circumstances or regimes present in the power system at the moment of the forecast. This methodology is split into three steps.

2.2.1. Structural Breaks

Before applying any filtering method, the initial dataset period needs to be oversized in order to find an appropriate subset. In this case, 13 months prior to the forecasting period are taken (i.e., a 13-month rolling window dataset), which is too large a calibration dataset for NN models if hourly precision is considered. The fact that structural patterns change throughout a 13-month period is not in question. Not only due to several seasonal effects that occur in the system but also abrupt market condition fluctuations or other structural breaks. An example can be seen in Figure 2, which shows the evolution of the Iberian electricity market prices during the autumn of 2016. It can be observed that early autumn is significantly different from late autumn. When it comes to forecasting late autumn prices (e.g., shortly after 6 December), it is evident that one should consider discarding the previous periods with the lowest prices, as they clearly correspond to other market circumstances. It should be noted that the structural breaks depicted in Figure 2 serve as an illustrative example and this work’s case study does not involve forecasting prices during late 2016. The different market circumstances are separated by the vertical lines, which correspond to the structural breaks. These structural breaks have been computed by means of the “strucchange” package in R that is based on the work presented in [28].

In theory, structural breaks split a time series into several segments that feature significantly different coefficients and perhaps different model specifications. In this application, we test the baseline model that the electricity price equals a constant. Thus, the “constant” becomes the varying element in the segments that are separated by the structural breakpoints. The purpose of the methodology presented in [28] is the determination of these breakpoints whose corresponding segments provide the least total residual sum of squares of the models associated with each segment.

Evaluating a 13-month hourly dataset is cumbersome if high precision is desired and therefore, the number of candidate breaks should be limited. In order to capture most of the structural breaks in the 13-month price dataset, the breakpoints were computed in two sequential runs. The first run involves a daily arrangement of the 13-month dataset with a minimum breakpoint distance of one week. The second run involves an hourly arrangement of the remaining days as a result of the first run. After computing the breakpoints in a run, the input dataset is divided into periods, which are compared to the most recent period in terms of the average price. In order to discard sufficiently dissimilar periods that belong to other market circumstances, the periods where the price average falls outside the interval $\mu \pm \sigma$, where $\mu$ and $\sigma$ represent the most recent period’s price average and standard deviation respectively, are discarded. While larger thresholds than $\mu \pm \sigma$ (e.g., $\mu \pm 2\sigma$, $\mu \pm 3\sigma$, etc.) are chosen in other contexts to discard outliers, two periods in time may belong to different market conditions even with a difference of one standard deviation. As a result, this unique manner of performing the methodology of [28] provides an efficient way of detecting structural breaks in a 13-month dataset with hourly precision, as well as discarding significantly different periods as per price behaviours.

Figure 3 depicts the resulting calibration period selection according to the structural break analysis. Whilst the left y-axis is related to Iberian electricity market prices from December 2015 up to December 2017, the shaded shape indicates the calibration periods (x-axis) selected for a certain forecasting day (right y-axis). For example, if the first day of 2017 is selected by drawing an imaginary horizontal line that crosses said day in the right y-axis (which, in this case, the line coincides with the upper border of the graph), the shaded area overlaps this imaginary line during 3 months in late 2016 and part of December 2015 according to the x-axis, which represents the calibration periods that are selected if the forecasting day is the first day of 2017. Given that early 2017 was characterised by uncommonly high prices, the selected calibration periods were much shorter than those of late 2017. Furthermore, January’s peak is generally discarded from calibration datasets when forecasting days later in that year. Moreover, summer 2016 is considered while forecasting summer 2017. Therefore, the result of this algorithm eliminates periods in the past that are expected to be highly dissimilar to the forecasting period.

2.2.2. Hourly Clustering

This stage seeks to determine the most relevant factors regarding the market conditions during the forecasting period. The variable with the most predictive content is the estimation of the actual price from the fundamental model, which reflects several aspects of the operations and the dynamics of the market. Although futures prices are often used as predictive variables, they were less useful here than the market-clearing prices, since they do not specify intraday effects. A variable that responds well to sudden market condition disruptions is the expected thermal gap, which represents the difference between the expected demand and the expected renewable generation from wind and solar facilities. Prices are bound to fall if the gap is low. Although the expected market-clearing prices also capture this effect, the expected thermal gap contains a higher level of short-term dynamic information and thus indicates intraday effects with higher definition. The expected temperature is also useful in order to remove periods with significantly different temperature effects.

A K-means clustering method was applied to take these three exogenous variables into account (estimated market-clearing prices, expected thermal gap and expected temperature) and relate the hours in the forecasting period to those of the training period. Given that these exogenous variables are expressed in different units and orders of magnitude, they were standardized before applying the clustering procedure. The K-means clustering application involves the identification of centroids of the values of those three variables throughout the 13-month initial dataset. Consequently, each hour in the dataset belongs to the closest centroid in terms of squared Euclidean distances in the 3D plane formed by the three variables. Depending on the predefined number of clusters, the centroids are placed so as to minimise the total quantisation error or the sum of squared Euclidean distances. Thus, a greater number of clusters lead to lower quantisation errors and higher complexity levels. In order to appropriately set the number of clusters, the K-means algorithm is computed for several numbers of clusters and, by means of a Pareto optimal frontier procedure [29], a suitable compromise between complexity level and total quantisation error is obtained. Finally, the clusters that include the hours of the forecasting period are deemed relevant and thus the hours of the input dataset that do not belong to said clusters are discarded.

The combination of these period selection algorithms is intended to discard the information pertaining to dissimilar market regimes, according to recent price behaviours and forecasted market regime indicators. Therefore, the hours that were not discarded by the structural breaks method were combined with those included by the K-means procedure, as displayed in Figure 4. The difference in Figure 4’s shape with respect to that of Figure 3 is related to the hours that are only selected by the K-means method (i.e., there are hours that were chosen by both techniques). This new shaded shape is somewhat hollow given that the clustering has been performed hourly. This provides useful information as to what intraday patterns in the past are the most similar to that of the forecasting period.

The resulting calibration dataset that is shown in Figure 4 contains two sets of information: the recent dynamics such as agent strategic behaviours provided by the structural breaks method and the patterns that are driven by market fundamentals yielded by the hourly clustering technique. All in all, this combined dataset discards the information pertaining to dissimilar market regimes according to recent price behaviours and forecasted market regime indicators in an automated fashion.

2.2.3. Neural Network Validation Set

Considering the length of the filtered dataset, a validation set is obtained following the similar days method performed in [19], which selects the top 20% of days in the most recent segment (i.e., between the most recent structural break and immediately prior to the forecasting period) as per their similarity with respect to the forecasting period in terms of daily patterns regarding exogenous variables such as expected demand.

2.3. Artificial Neural Network Model

As displayed in Figure 1, four outputs of the fundamental model are combined with common predictors to form the set of input variables for the NN model. This set consists of the following factors:

• Expected values of demand, wind and solar generation
• Expected mean temperature in the Iberian Peninsula
• Two dummy variables corresponding to working days or a Sunday/holiday, thus Saturdays would correspond to both dummy variables being false
• Actual electricity market prices with the following lags: one day, two days, one week and two weeks
• Commodity related month-ahead forward prices: API2 coal, NBP natural gas and European CO₂ emission allowances
• Day-ahead Iberian electricity market futures
• Fundamental model output variables: market-clearing prices; and coal, CCGT and hydro production levels.

This set of variables has been obtained and validated by means of a variable selection procedure based on mutual information and partial mutual information in order to analyse their dependency with respect to electricity prices and their redundancy with respect to the other explanatory variables when used to predict electricity prices. However, it is worth noting that this work’s contributions are centred on the period selection methods.

Once the proposed period filtering methods have been carried out, the remaining data are used as training inputs to a NN forecasting method. The literature suggests that the most suitable NN configuration is a single hidden and output layer architecture, as stated in [30]. Another well-established choice in the literature is the Levenberg-Marquardt training algorithm. The hyperbolic tangent sigmoid activation function was utilised for the hidden layer’s neurons and a pure linear activation function has been resorted to for the output layer. However, due to the lack of consensus in the literature with regards to the number of neurons to be set in the hidden layer, several variations were tested (a range from 10 to 60 with a step of 5 neurons). The validation set mean-square error MSE of the neural networks was used in order to choose the optimal number of the hidden layer’s neurons. Moreover, in order to consider the random initialisation of the weights of the NN training algorithm, a high number of replications of the NN forecasting procedure were carried out. This is also done in order to improve the likelihood of the NN training algorithm going from local to global minima.

2.4. Model Performance Metrics and Evaluation Criteria

Consistent with most forecasting research, the models are evaluated using three error metrics: mean absolute percentage error (MAPE), mean absolute error (MAE) and root-mean-square error (RMSE). Note that electricity prices can sometimes approach zero and in such cases, MAPE may approach infinite values. Nevertheless, the case study utilised in this work does not include any actual zero-price occurrences. In order to assess performance comparisons in a statistically significant manner, the Diebold-Mariano (DM) test has been carried out with a 5% significance level [31].

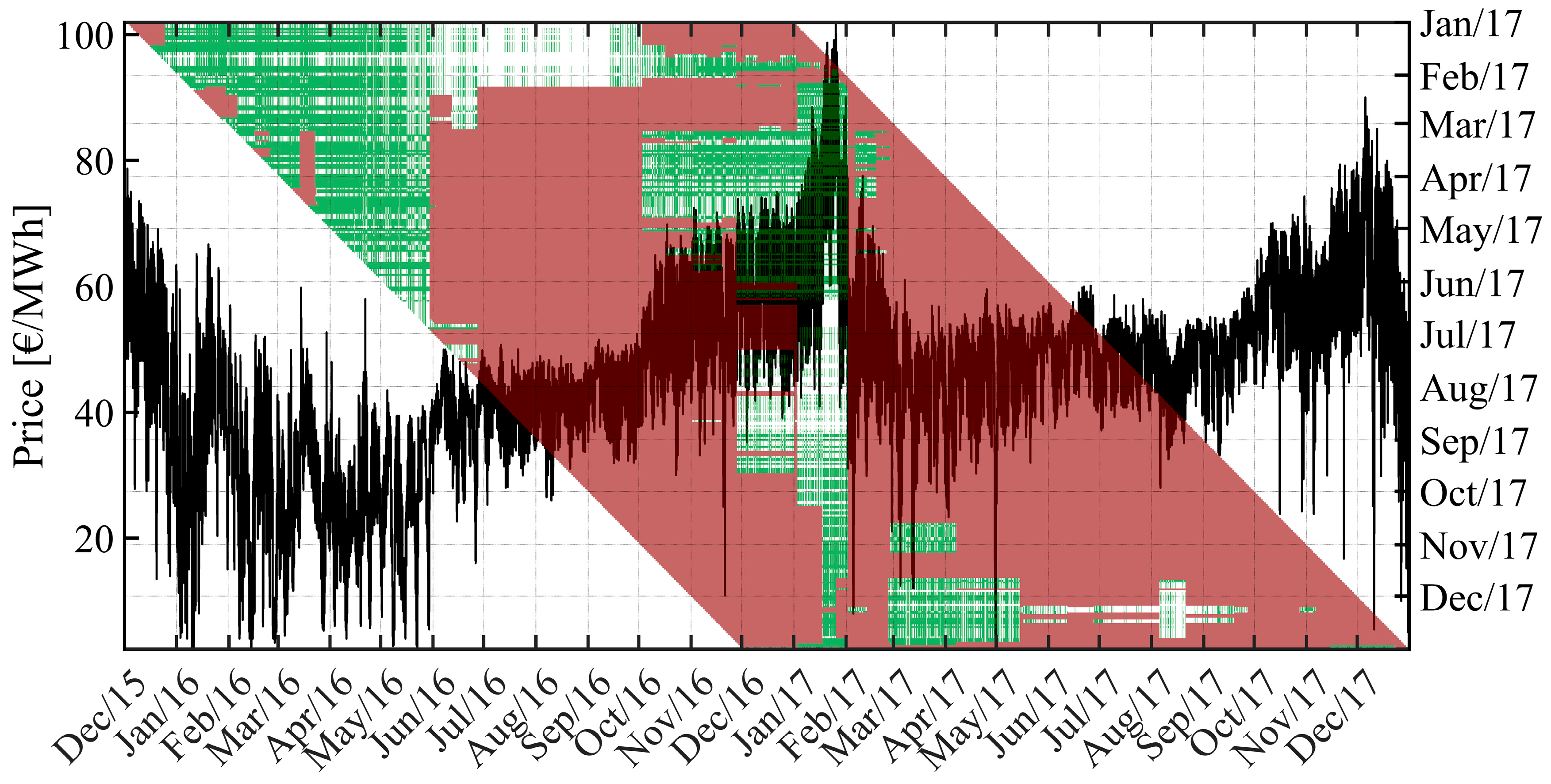
3. Case Studies, Results and Discussion

The case study for this work is the Iberian electricity system throughout the entire year of 2017. Early 2017 was characterised by very cold weather, low renewable energy generation, high natural gas prices and external disruptions originated by the decommissioning of nuclear power plants in France. This caused the price surge that is seen in Figure 3, which represents the 2017 maximum price of 101.99 €/MWh (up from 2016’s peak of 75 €/MWh). Furthermore, a steady increase in the European CO₂ emission allowance prices began in the late summer of 2017. More specifically, these prices rose by approximately 25% throughout the year of 2017. Therefore, this case study poses a highly challenging task with disruptions and evolving changes and is, therefore, a suitable test of the methodology proposed in this paper.

First of all and as per Figure 1, the cost production model is run so as to obtain the necessary information to carry out the remaining stages of the proposed methodology. This provides the fundamental model output variables: market clearing prices as well as CCGT, hydro and coal unit generation output levels. Furthermore, given that the aim of this work is to provide forecasts for the entire year of 2017 and that the NN model’s initial training dataset is of 13 months, all input variables must be made available from December 2015 up to December 2017. Once these 13 months are filtered according to the methodologies presented in the previous section, the NN model is run to provide rolling forecasts for every day of the year in 2017. Therefore, the actual forecasting horizon is of one day.

In order to specifically assess the ingredients of this methodology, the proposed hybrid forecasting model is split into stages, where each stage adds one of the techniques detailed in the previous subsection as follows:

• Stage 0: A base hybrid fundamental-econometric model without filtering any periods and variables and using 120 days of calibration data, although a limited filtering procedure in winter 2017 reduced this data length by roughly 70%. This coincides with the Proposed Model 2 that was presented in [19].
• Stage 1: 13 months of calibration data are used and these are filtered via the structural breaks technique.
• Stage 2: The K-means hourly clustering procedure is added to the calibration period selection method.

These models will be referred to as PMS_i, i.e., the Proposed Model at its Stage i. As in other works, for instance [11], the performance of these models has been analysed for every season of the year and compared with that of six other electricity price forecasting models, some of which correspond to well-established methodologies in the literature. The first chosen benchmark model (Benchmark 1 or BM₁) consists of the proposed simple average of [19] between the forecasts of a pure NN model and the base hybrid fundamental-econometric model (PMS₀). Benchmark two (BM₂) only involves this pure NN model that utilises the same input variables as BM₁/PMS₀ (except those pertaining to the fundamental model) and the same calibration window. This 120-day window includes four months within the 13-month window established in this work, more specifically, the 13th, 12th, 2nd and 1st month prior to the forecasting day [19].

The third benchmark model (BM₃) is related to a linear regression model with several autoregressive terms and exogenous components. This ARX model, introduced in [32] and recently utilised in [15], includes a logarithmic transform that was modified so as to account for the lower price cap of zero in the Iberian electricity market:

$$\begin{array}{c}{p}_{d,h}={\beta }_{h,1}{p}_{d-1,h}+{\beta }_{h,2}{p}_{d-2,h}+{\beta }_{h,3}{p}_{d-7,h}+{\beta }_{h,4}{p}_{d-1}^{min}+{\beta }_{h,5}{z}_{d,h}\\ +{\beta }_{h,6}{D}_{Sat}+{\beta }_{h,7}{D}_{Sun}+{\beta }_{h,8}{D}_{Mon}+{\epsilon }_{d,h}\end{array}$$

(1)

$$n_{d,h}=\frac{\left(P_{d,h}-{\mu }_T\right)}{{\sigma }_T}$$

(2)

$$p_{d,h}=sgn\left(n_{d,h}\right)\left[log\left(n_{d,h}+\frac{1}{c}\right)+log\left(c\right)\right]$$

(3)

According to Equation (1), the log-price at day d and hour h, $p_{d,h}$, depends upon: lagged prices, such as $p_{d-1,h}$; the minimum log-price during the 24 h of day d minus one (i.e., $p_{d-1}^{min}$); the load forecast ($z_{d,h}$); and three dummy variables that specify if day d is a Saturday, Sunday or Monday. The logarithmic transform of Equation (3) is the mirror-log transform, where prices, $P_{d,h}$, are first normalised in Equation (2) across the training period T, and the parameter c was set to 1/3 according to the application presented in [33]. The transformations that have been applied to the explanatory variables regarding past electricity prices stabilise their variance and ensure stationarity, as observed in [33]. Three months prior to the forecasting day were used as calibration data. The next benchmark (BM₄) is the extension of BM₃ as per the work presented in [15], which performs a weighted average of forecasts from the ARX model of Equation (1) across the following calibration windows (in terms of days prior to the forecast day): 56, 84, 112, 714, 721 and 728 days. The weights of these six forecasts are computed by means of an inverse MAE weighting procedure when testing the ARX models on the day prior to the forecast day.

Benchmark five (BM₅) is related to a SARIMAX model, whose SARIMA noise presents the following notation: SARIMA(1,0,0)₁₆₈(1,0,2)₂₄(1,0,0)₁. A daily and weekly seasonality was considered, as well as the expected demand as an exogenous variable. This model was created following [34,35], with the Box-Jenkins methodology. Furthermore, the Box-Cox transformation was used to stabilise the price variance [36]. The final benchmark (BM₆) is related to a simple naïve approach that sets the forecast to the actual electricity price value corresponding to the previous week.

The proposed model, in all of its stages as well as the six benchmark models, have been tested for every day of the year in 2017 and their error measures across the four seasons of 2017 are shown in

Table 1. Forecast error measures for the proposed and benchmark models: MAPE (%), MAE & RMSE (€/MWh).

Model	Winter			Spring			Summer			Autumn			Entire 2017
	MAPE	MAE	RMSE	MAPE	MAE	RMSE	MAPE	MAE	RMSE	MAPE	MAE	RMSE	MAPE	MAE	RMSE
PMS0—Base model [19]	11.68	4.756	5.479	8.106	2.882	3.407	4.450	2.070	2.517	6.812	3.453	4.129	7.744	3.282	3.874
PMS1—Structural breaks	11.02	4.266	4.917	7.706	2.487	2.960	4.501	2.063	2.509	6.237	3.150	3.820	7.348	2.984	3.543
PMS2—Hourly clustering	10.05	4.133	4.785	7.303	2.433	2.892	4.467	2.045	2.504	6.284	3.139	3.818	7.012	2.930	3.492
BM1—½(PMS0 + BM2) [19]	11.30	4.610	5.334	7.902	2.832	3.349	4.477	2.079	2.525	6.756	3.409	4.069	7.591	3.224	3.810
BM2—Pure NN [19]	11.12	4.562	5.308	7.804	2.826	3.342	4.605	2.136	2.588	6.834	3.440	4.089	7.575	3.233	3.823
BM3—ARX [32]	16.79	6.838	7.809	13.58	4.765	5.552	7.153	3.262	3.885	10.51	5.066	6.055	11.99	4.972	5.814
BM4—W. ARX [15]	16.27	6.390	7.314	13.21	4.500	5.268	7.015	3.211	3.857	10.14	4.880	5.874	11.64	4.736	5.568
BM5—SARIMAX	15.06	8.113	10.84	9.293	4.150	5.585	5.097	2.473	4.531	7.654	4.454	4.959	9.248	4.780	6.460
BM6—Naïve approach	25.93	10.53	11.48	17.55	6.225	7.092	9.343	4.266	5.030	12.82	6.387	7.567	16.37	6.828	7.773

. Furthermore, the average calibration dataset windows for each of the models involving a NN forecasting technique are displayed in

Table 2. Average calibration length window of the NN models (days).

Model	Winter	Spring	Summer	Autumn	Overall
PMS0, BM1 & BM2 [19]	36.67	120.0	120.0	120.0	99.17
PMS1 (Figure 3)	152.9	237.0	324.7	300.5	254.2
PMS2 (Figure 4)	288.8	324.5	344.7	348.1	326.7

.

Compared with the base model of PMS₀, the implementation of the structural breaks technique increased the NN training set by well beyond the predefined number of 120 days that was established in [19]. The reason behind the reduced dataset during the 2017 winter is due to its high instability, and it was observed in [19] that a reduction of the 120-day dataset provided useful results. This agrees with the rationale that consists of increasing adaptability on unstable periods by reducing the calibration window in order to remove structural breaks from the input dataset. However, in this work, an average dataset of 152.9 days yields lower forecasting errors. Furthermore, PMS₁ discards most of the previous winter, which is considerably different from the 2017 winter as depicted in Figure 3. This also seems to be the case for spring, as the 2016 spring yielded approximately twice as much hydro generation as the 2017 spring. In general, the structural breaks algorithm provides a generally lower error throughout 2017. However, summer 2017 appears to be the exception, where prices are relatively stable and thus, it lacks room for improvement, as proven by the generally low errors yielded by most models.

Furthermore, the lengthening of PMS₁’s calibration dataset with the hourly clustering technique of PMS₂ further reduces the overall forecasting error. This is more notable during winter, where the average calibration dataset is greatly increased to 288.8 days. As for the other seasons, a calibration dataset of approximately one year proves to be beneficial for electricity price forecasting with NN models even with the hourly arrangement and does not seem to cause any overfitting issues. Although PMS₂ yields a lower error overall, the statistical significance of these error measures must be verified in order to confirm its superiority against its competitors, especially the highest-ranked models according to Table 1. Therefore, a DM test was carried out for PMS₂ against every other model. The DM test statistic is evaluated with a 5% significance level, such that a DM statistic < −1.96 implies significant outperformance. The results of the DM test statistic are shown in

Table 3. DM statistic values of PMS2 against every other model.

Model Comparison	Winter	Spring	Summer	Autumn	Entire 2017
PMS2 vs. PMS0	−8.834	−12.31	−0.975	−6.787	−14.75
PMS2 vs. PMS1	−2.903	−3.199	−1.833	−0.436	−3.917
PMS2 vs. BM1	−6.528	−8.042	−2.883	−5.726	−11.29
PMS2 vs. BM2	−6.316	−11.36	−3.262	−6.877	−13.18
PMS2 vs. BM3	−21.54	−28.70	−22.94	−21.69	−44.76
PMS2 vs. BM4	−18.78	−26.37	−21.18	−19.59	−40.67
PMS2 vs. BM5	−21.21	−17.96	−4.454	−16.85	−29.70
PMS2 vs. BM6	−34.44	−33.17	−27.75	−28.66	−58.82

.

The three values in bold indicate the three occasions that PMS₂ was unable to significantly outperform. The comparison with PMS₀ suggests that the increase in calibration data window lengths does not significantly contribute to summer forecasts, albeit not detrimental to the accuracy. This may also imply that a robust calibration period selection is not highly crucial in such a stable market regime. Therefore, the same conclusion can be drawn from the summer comparison with PMS₁. Furthermore, the DM statistic value in autumn when compared with PMS₁ may indicate that the information provided by the hourly clustering method is not significantly different than that provided by the structural breaks technique. However, these values indicate that PMS₂ is significantly outperforming all other models throughout the year in 2017.

4. Conclusions

This research presents a novel short-term hybrid electricity price forecasting methodology which is comprised of three main elements: a cost-production optimisation model, a sophisticated period filtering approach and a neural network (NN) model. These three elements were utilised sequentially with the calibration selection procedure as the main focus of this work. Given a forecasting day, the structural patterns in actual prices corresponding to the 13 months prior to that day are analysed and those deemed unimportant were discarded. A K-means clustering method was also applied to relate the moments in the prior 13 months to the forecasting day in terms of the estimated fundamental market-clearing prices, expected thermal gap and expected mean temperatures in the Iberian Peninsula. The key innovation of this approach is to move beyond the conventional forecasting principles which suggest that adaptive methods should place most emphasis upon recent data and that regime-switching should likewise model transitions from the latest regime. The approach recognises that the most relevant dataset in the episodic, recurrent nature of electricity dynamics may not be the most recent. Another unique feature of this methodology is the definition of a calibration period that is not driven by heuristic assumptions or any other specific predefinitions.

The results and analyses indicate the following. The combination of structural break analysis and hourly clustering provides a dynamic calibration period appropriate for the forecasting model estimation. In validation, this sophisticated training window selection for the NN model yields appealing results in every market circumstance present in the relatively challenging case study of the Iberian electricity market of 2017. The period selection technique is more selective in volatile market conditions, such as early 2017, albeit providing a considerably longer training window length than other works which claim that employing much shorter calibration windows is most suitable in these situations. In addition, the proposed methodology proves most useful during volatile periods, whilst the accuracy is marginally increased in stable market regimes, such as summer 2017.

Overall, this short-term fundamental-econometric electricity price forecasting model, which features a unique hybridisation approach, has yielded appropriate results when applied to a real-size electricity system with complex price dynamics, such as the Iberian power exchange of 2017. Furthermore, the performance of this proposal is superior to that of other benchmark models. Although only one market has been chosen as the case study, the results may be generalised for other markets due to the high number of special circumstances that the Iberian power system experienced throughout the year 2017. However, there seems to be room for improvement regarding the utilised structural breaks period selection algorithm, as it is highly challenging to ascertain a convenient compromise between accuracy and computational burden. Transient spikes for example cannot all be considered structural breaks, yet it may be beneficial if these are more adequately considered in a computationally feasible manner. Furthermore, more complex neural network topologies may be tested in conjunction with this calibration period selection methodology, such as convoluted or LSTM neural networks.