In this section, we first present the original CPs for the 32 reviewed papers, followed by the validation of the extraction and characterization processes. Subsequently, we describe the calculation of the CPs and EPs for the 40 LDCs. Finally, we study the relations between the CPs and the EPs.
3.1. Original Characteristic Parameters for Local Driving Cycles
Table 4 lists the original CPs (CP
ORIG) for the 36 LDCs developed for passenger cars, and
Table 5 lists CP
ORIG for the 41 LDCs for the other vehicle classes (buses, trucks, and motorcycles). The occasional appearance of dashes in both the tables corresponds to the cases in which the authors did not inform the CP value. We emphasize that each author uses a specific formula to calculate the CPs. The last columns of
Table 4 and
Table 5 list the number of local driving cycles (NCs) considered in each paper.
Table 4 lists the results for the CPs presented in the original papers (only for the passenger cars). The relatively large standard deviations for the average speed (
V = 27.2 ± 7.5 km/h) and acceleration (
a = 0.53 ± 0.23 m/s
2) reconfirm numerically that the LDCs worldwide are distinct, thus justifying their differences. In relation to the comparison of the LDCs with SDCs, FTP-75 cycle, and WLTC (class 3) present an average speed of 34.1 km/h and 46.5 km/h, respectively, both being higher than the mean average speed of the LDCs (27.2 km/h).
Comparing the results of the passenger cars and other vehicles, we can see that the mean average speed decreases (
Table 4:
V = 27.2 ± 7.5 km/h;
Table 5:
V = 23.3 ± 10.3 km/h) and the acceleration increases (
Table 4:
a = 0.53 ± 0.23 m/s
2;
Table 5:
a = 0.56 ± 0.28 m/s
2). To understand these results, we divided
Table 5 based on the vehicle category, obtaining a greater speed for trucks (
V = 24.3 ± 12.4 km/h), then motorcycles (
V = 23.9 ± 8.5 km/h), and then buses (
V = 20.6 ± 10.3 km/h). Motorcycles cycles have lower average speeds, probably because trucks cycles have more highway stretches. In terms of acceleration, the higher values were for the motorcycles (
a = 0.75 ± 0.27 m/s
2), as expected from their lower masses, followed by those for the trucks (
a = 0.38 ± 0.15 m/s
2). There is no acceleration information for buses. Another interesting result is found by analyzing the modes of movement. For trucks, we calculated a very short cruising time (
CT = 3% ± 3%), whereas the motorcycles interestingly presented a longer time for the cruising speed (
CT = 21% ± 8%); because they are nimble, one would expect motorcycles to spend more time accelerating.
3.2. Validation
The numerical vectors of well-known SDCs for the type—approval tests, such as FTP-75 cycle and WLTC, are easily available online [
48,
49]. LDC papers typically present only the figure showing the speed as a function of time, whereas the numerical vector is not specified. In addition, they do not generally present all of the CPs considered in this study.
To obtain the CPs from the figures, we used a method comprising two steps: extraction and characterization. The extraction step refers to obtaining the numerical vector from the figure, and the characterization step refers to the process of obtaining the CPs from the extracted numerical vector (ENV). The last step, the simulation, is the process to obtain the EPs from the numerical vector.
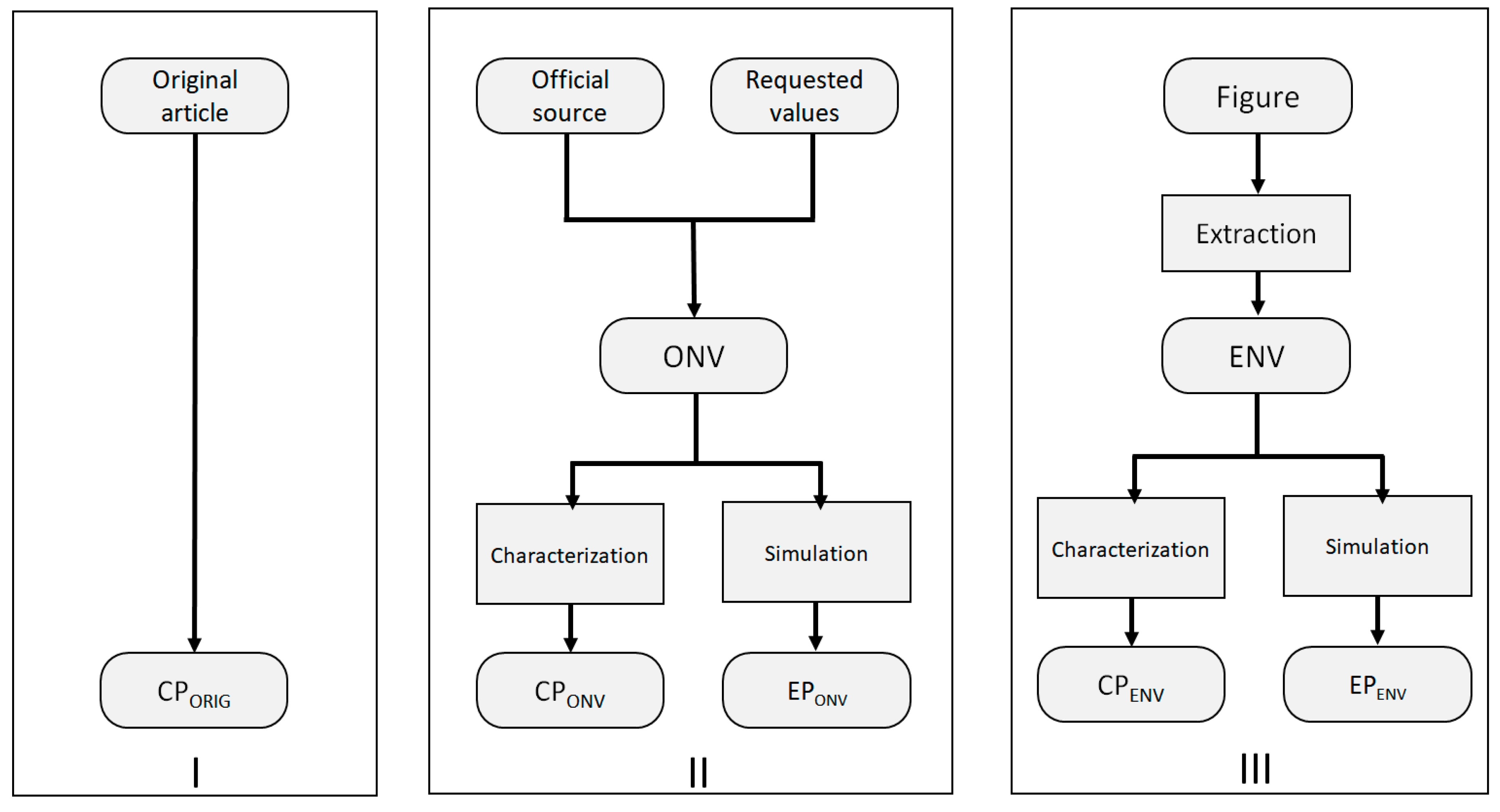
Figure 3 presents a flowchart explaining the methodology to obtain the CPs and EPs investigated in this study. In group I, CP
ORIG refers to the CPs obtained directly from the papers, as informed by their authors. In group II, the original numerical vector (ONV) is obtained from agencies (in the case of SDCs) or authors (in the case of LDCs). CP
ONV refers to our standardized characterization (calculation) of the CPs using the ONV. In Group III, the ENV is the numerical vector we extracted from the figures presented in the papers studied and CP
ENV and EP
ENV refer to our calculation of the CPs and EPs obtained from the ENV.
We used six driving cycles to validate the extraction and characterization methods: two SDCs (FTP-75 cycle and WLTC) and four LDCs (Athens, Toronto, and two from Chennai). The LDC data were obtained directly from the authors.
Table 6 contains CP
ORIG (as presented by the authors), CP
ONV (calculated by us from the ONVs), and CP
ENV (calculated by us from the ENVs).
To validate the characterization step, we compared CP
ORIG [
50] and CP
ONV for FTP-75 cycle and WLTC. From
Table 6, we can verify that the characterization is effective, because there is no considerable difference between the values of CP
ORIG and CP
ONV, for both the SDCs.
To validate the extraction step, CPONV (calculated from the ONV) is compared to the CPENV (calculated from the ENV). For FTP-75 cycle, the results for the average speed, distance, time, acceleration, and deceleration were virtually equal. There was a little difference in the time proportion for each driving mode (CT, IT, AT, and DT), because the CPs were more sensitive to the acceleration and speed fluctuations. The validation using the WLTC data presented similar results.
For the four LDCs listed in
Table 6, we compared CP
ENV (characterized following the extraction of the numerical vector from the figure) to CP
ONV (from the vectors shared by the authors). For all the cycles, the speed difference was under 0.1 km/h, and the distance difference was shorter than 0.2 km. For the acceleration and deceleration, the difference was less than 0.2 m/s
2. There are some differences between the CP
ENV and CP
ONV in
Table 6, but with little effect on the energy consumption. For example, the relative error for the acceleration in Athens could be considered high (20%). However, the acceleration difference was 0.14 m/s
2, equivalent to a speed variation of 0.5 km/h per second. This is low, because, for example, in the Brazilian law for driving cycle tests, there is a tolerance of 3.2 km/h in relation to the instantaneous velocity, in the type approval test [
51]. Therefore, in general, we can deduce that our extraction process is also validated.
3.4. Results for Energy
For comparison purposes, all the EPs for the LDCs (
Table 9 and
Table 10) are calculated for the reference car, defined in
Table 3, using Equations (1)–(6). The same car is also used for the LDCs originally developed for motorcycles and trucks (
Table 10). The average energy consumption for the passenger cars was
EC = 2.1 ± 0.3 MJ/km (
FE = 13.5 ± 2.3 km/L,
Table 9), whereas for FTP-75 cycle, it was
EC = 2.4 MJ/km (
FE = 12.0 km/L), and for WLTC was
EC = 2.8 MJ/km (
FE = 10.5 km/L). In this paper, if not stated otherwise, the economy is expressed in km per liter of E22.
In
Table 9, EC is the energy consumption of the whole cycle, in MJ/km, comprising all the modes of energy (drag, inertia, rolling, and idling). It is important to emphasize that these values are in MJ of the fuel, and already consider the engine and transmission efficiency. The gravitational force is not included, because we simulated the reference vehicle considering a plain road, and the wind speed was 0 km/h. Comparing the average values of the LDCs in
Table 9 with those with FTP-75 cycle and WLTC, we see that WLTC has a higher drag power (LDCs average: 0.3 MJ/km; WLTC: 1.1 MJ/km; FTP-75 cycle: 0.5 MJ/km) owing to its higher speed. In comparison, FTP-75 cycle has the higher inertial power (LDCs average: 1.0 MJ/km; WLTC: 1.0 MJ/km; FTP-75 cycle: 1.1 MJ/km), owing to its higher acceleration.
In
Table 9, on average, the highest energy spent during a driving cycle is to overcome the inertia (46%), followed by for the rolling resistance (32%), aerodynamic drag (15%), and idling (7%). The drag is not extremely important, owing to the low average speed. Focusing on specific driving cycles, WLTC has a high drag energy percentage (38%), owing to its high speed, whereas Hong Kong has a low drag (4%), owing to its low speed. Athens has a high inertial energy percentage (59%), owing to its high acceleration allied to low speed, and Hong Kong has a high idling energy percentage (22%), because it has a long idling time. WLTC has a high (2.8 MJ/km) overall fuel energy, owing to its high speed, whereas Santa Maria has a low value (1.4 MJ/km), owing to its low acceleration.
From
Table 9, it also possible to obtain an estimation of the CO
2 emitted using stoichiometric calculation. The energy consumption (MJ/km) can be converted to CO
2 emitted when multiplying it by a factor of 0.072 kg CO
2/MJ of E22.
Table 10 summarizes the energy splitting considering the cycles developed for other vehicles (trucks and motorcycles). We emphasize that although the cycles are developed for distinct vehicles, for comparison, all of the energy calculations were conducted for the same reference vehicle (
Table 3). In fact, in these calculations, the differences in the masses of the motorcycles and the trucks were not considered (our aim here was to compare cycles, not vehicles). The cycles developed for motorcycles (simulated with the reference car) present lower energy consumption (2.1 MJ/km), owing to their lower speed (21.3 km/h), and for trucks (also simulated with the reference car), the values are 2.3 MJ/km and 29.8 km/h. The inertial resistance percentage is higher for the cycles developed for motorcycles (50%), because of their higher acceleration (0.44 m/s
2), than that for the cycles for trucks (38%;
a = 0.33 m/s
2). For comparison, by changing the characteristics of the vehicles (e.g., drag, mass, and power peak), if we simulated FTP-75 cycle with a motorcycle, then we would obtain
FE = 32.1 km/L (E22) and
EC = 0.9 MJ/kg; and for a truck,
FE = 3.7 km/L (diesel) and
EC = 9.6 MJ/kg.
The simulations provided in
Table 9 (cycles for the passenger cars) point to the gains one could obtain with each technological improvement. The major consumption is by the inertial resistance (46%), thus the improvement should point primarily to mass reduction. One should remember (Equation (1)) that the mass also influences the rolling and gravitational resistances; thus, mass gains would have a higher impact than only reducing the inertial resistance. The second major consumption is by the rolling resistance (32%), which can be decreased with a higher tire pressure, stiffer dampers, and lowering the mass. However, such ameliorations do not depend only on the vehicle itself, because they depend on the quality of the roads as well. The aerodynamic drag is not extremely important (15%) owing to the lower speeds (recalling that aerodynamic improvements in general increase the price of a vehicles). The use of a start–stop strategy could decrease the energy consumed during idling (7%). Our simulations did not consider the road inclination, because the cycles did not yield this variable. However, certainly the gravitational resistance is also a major factor in energy consumption.
Indeed, the general recommendations continue to be valid, e.g., the adoption of hybrid and electric vehicles and regenerative braking. These modifications can be considered in the reference vehicle/engine model of this study, changing the total mass and maximal engine efficiency of the vehicle in
Table 3.
Table 11 summarizes the values of the
EC and
FE in the case of technology improvements or under other road conditions. For example, if the car mass was to be reduced by 50%, the energy consumption would decrease by 17%. The use of ethanol as a fuel instead of E22 would decrease the energy consumption in 2% (owing to its higher-octane number, compression ratio, and engine efficiency). The effect of the wind is small (4% for a 5 km/h wind). A slope of 2° would increase the energy consumption by 72%, from 2.39 to 4.11 MJ/km. With road inclination, 43% of the energy is spent to overcome the gravitational resistance, whereas drag, inertia, rolling, and idle contributes with 14%, 21%, 19%, and 3%, respectively.
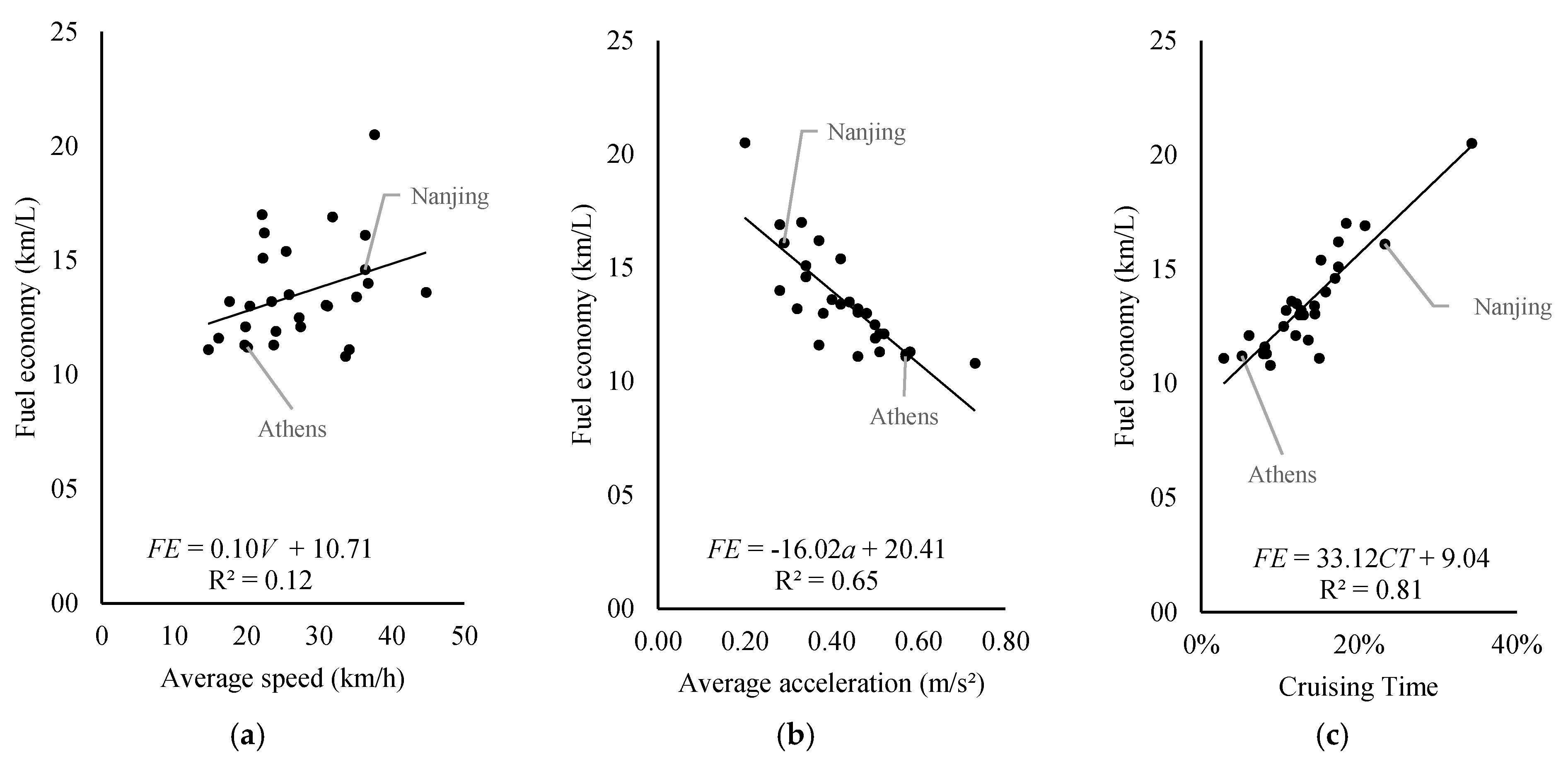
Returning to
Table 7 (the LDCs developed for cars), the last row presents the correlation between the
FE and the CPs. For cars, the highest correlation was for the cruising time (
r = 0.90), followed by for deceleration (
r = 0.84) and acceleration (
r = −0.81). It might seem surprising to find the cruising time as the most important factor influencing the
FE, because according to
Table 9, inertia (thus acceleration) is the most important energy fraction in the consumption. The explanation is that there is a correlation between the cruising time and the acceleration (
r = −0.71): the longer the cruising time (constant speed), the lower the acceleration. There is also a strong correlation between the deceleration and the acceleration (
r = −0.89), because each time a car brakes, it has to subsequently accelerate, which also explains the influence of deceleration on the
FE. Unexpectedly, there is no correlation between the time percentage a car accelerates and its energy consumption; this occurs because there is no correlation between
a and
AT (
r = −0.11).
No good correlation is found between the
FE and the average speed of the car (
r = 0.35); therefore, it is possible to conclude that the average speed is not a good alternative to estimate fuel economy. This conclusion is similar to that of Ho et al. [
19]. Obviously, in general, the energy consumption varies with the average speed, because the drag energy varies with V
3. We did not find this correlation because the average speed for the studied LDCs (for cars) was low, 27.1 (±7.6) km/h. This is listed in
Table 9, in which only 15% of the energy is owing to the aerodynamic drag.
Figure 4 illustrates the variation of the
FE with the average speed (
Figure 4a), average acceleration (
Figure 4b), and cruising time (
Figure 4c), illustrating the correlation coefficients (
r) discussed above. Equation (11) provides a good estimation of the
FE using only the CPs, without the necessity of simulating the car as conducted in this study. The mean deviation of Equation (11) is ±0.7 km/L (i.e., 6% of the average
FE)
Recalling, all the calculations until now were conducted for a 1 ton car. For example, if the car was 1.4 ton, the FE would be decreased by 2.7 km/L.
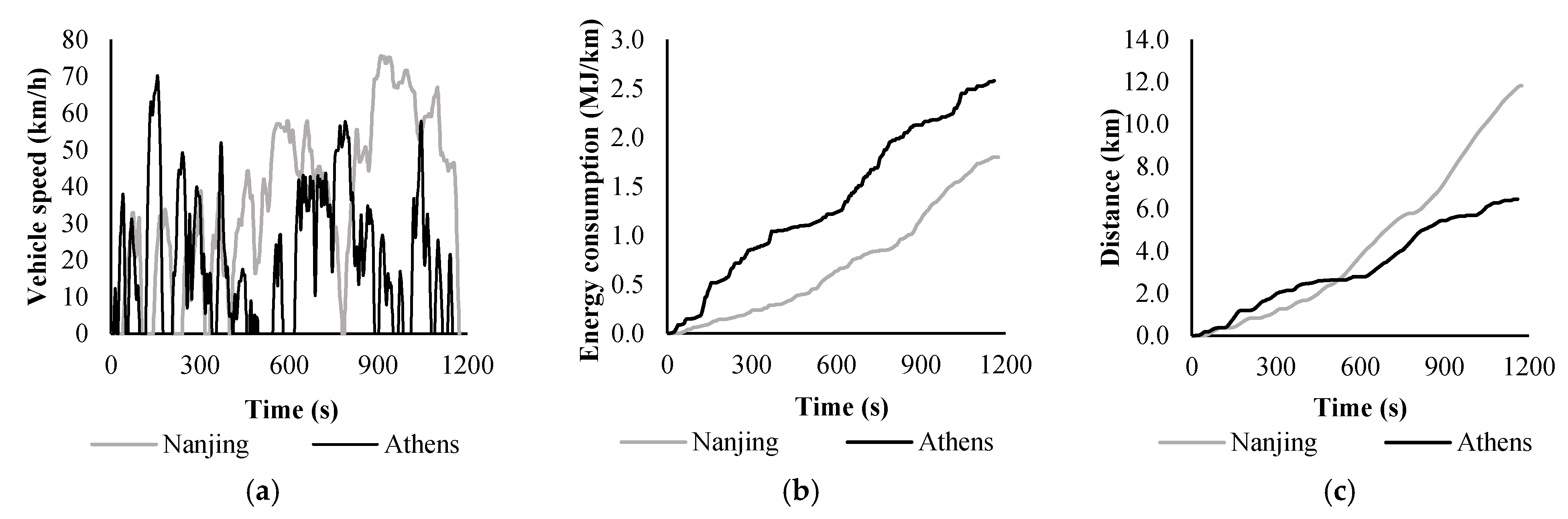
To understand the importance of acceleration (or cruising time) for the energy consumption (or
FE), we chose two cycles from
Figure 4 with distinct values of the
FE: Athens and Nanjing. Both were selected because they were in the main cluster of
Figure 4c and near the regression curve. From the data for Athens (
V = 20.1 km/h,
a = 0.57 m/s
2,
FE = 11.2 km/L,
EC = 2.6 MJ/km,
CT = 5%,
D = 6.5 km,
t = 1160 s) and Nanjing (
V = 36.3 km/h,
a = 0.29 m/s
2,
FE = 16.1 km/L,
EC = 1.8 MJ/km,
CT = 23%,
D = 11.8 km,
t = 1174 s), we again confirm that acceleration (reflected in cruising time,
CT, as discussed above) is the main parameter influencing the energy consumption.
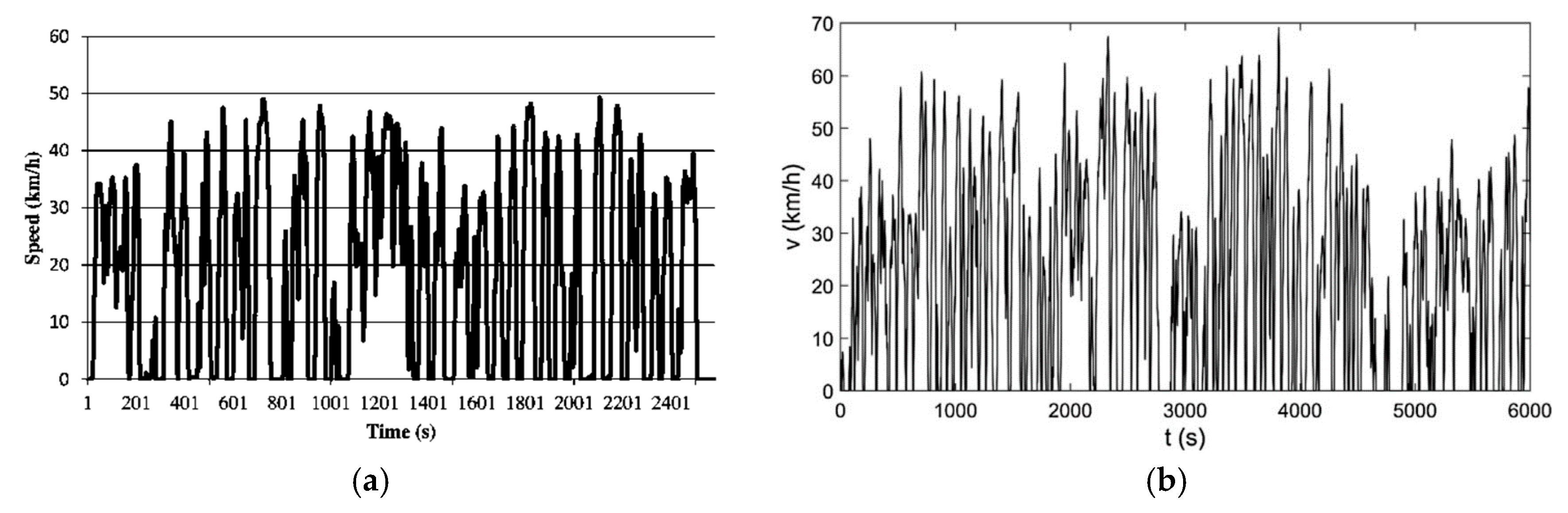
Figure 5a presents the speed vectors of the two cities (Athens and Nanjing), from which it is noticeable that in Nanjing, the average speed is higher than in Athens.
Figure 5b presents the evolution of the energy consumption (accumulated energy per total cycle distance, MJ/km) for both the cycles.
Figure 5c displays the traveled distances for both the cities (it should be noted that the Athens cycle is half the distance of Nanjing, although requiring approximately the same total time).
By analyzing the energy simulations for the LDCs in
Table 9 (passenger car), we calculated that 75% of the energy consumption (when the car is accelerating) occurs with accelerations under 38% of the maximal acceleration of each cycle. Approximately ¼ of the total consumption occurs when the acceleration is in each of the ranges of 0–11%, 12–21%, 22–38%, and 39–100% of the maximum acceleration of the vehicle. Returning to Equation (1), we note that inertia contributes with a term
aV; therefore, higher accelerations should be expected to be more important than lower accelerations, for the energy consumption. However, lower accelerations, regardless of their lower values, are more frequent in the cycles (median acceleration of the cycles is 0.31 m/s
2 and the mean acceleration is 0.44 m/s
2), contributing more to the energy consumption in the integral of Equation (5) than the higher accelerations.