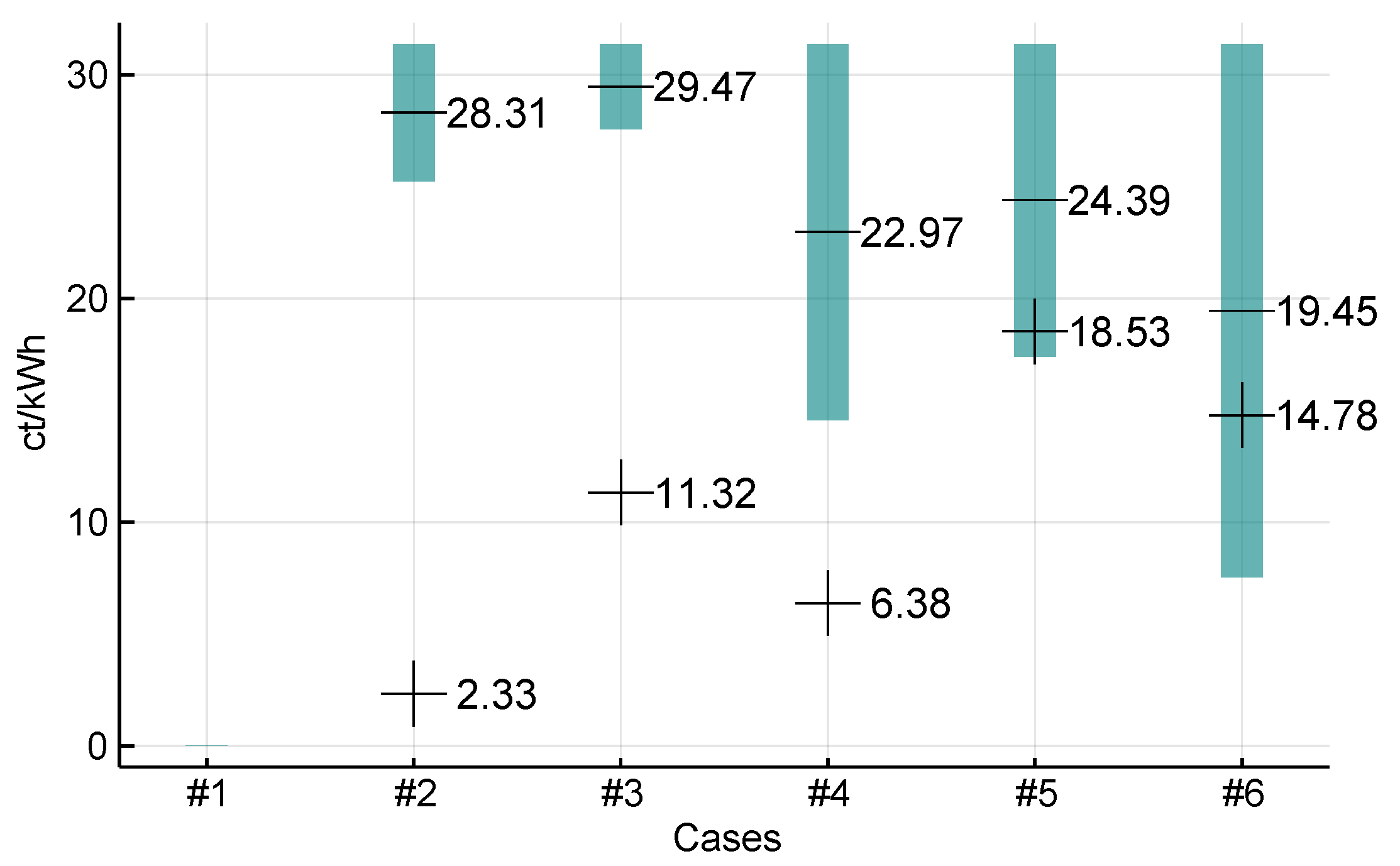1. Introduction
Starting with the liberalization of the electricity markets, gradually a more and more competitive market environment was established. Recently, the European Commission’s clean energy package [
1] pushed for a new disruption—now, even more and much smaller players are encouraged to actively participate in the energy value chain (e.g., share their energy with fellow citizens). Distributed renewable energy sources (RES), as well as sector coupling and storage technologies such as electric vehicles (EV), battery energy storage systems (BESS), and heat pumps (HP), could introduce more flexibility. The potential is promising due to diverse generation and demand patterns [
2]. With smart meters, energy management systems, and communication and control technologies, even the smallest assets can profit from the integration into the energy markets [
3]. The challenge at hand is to transform a system formerly relying on large centralized power plants—whose economies of scale are increasingly challenged with grid parity of RES [
4]—to a system based on distributed renewable energy sources. Existing market arrangements, however, are not quite up for the task; system design and tariff incentive structures still vastly assume limited flexibility and passive price-taking consumers [
3]. Lower and diminishing tariff-based incentives will increase the pressure for alternative revenue streams [
4,
5].
For these new consumers, energy is not a homogeneous product but a diverse set of energy classes [
3] (e.g., based on geographical vicinity, preferred energy sources by time, or preference for only trading with close friends and family). The necessary communication, automation, and price negotiation is provided by peer-to-peer (P2P) and other market platforms. Their functionality can range from a simple match-maker like
Enyway (see
https://www.enyway.com/de/power) to more complex energy community or virtual power plant setups like
sonnenCommunity (see
https://sonnengroup.com/sonnencommunity) or
NextKraftwerke (see
https://www.next-kraftwerke.com/vpp/next-box). Complexity increases with the regional distance of market participants and control powers of the intermediary. Nowadays, most of these setups build workarounds due to prevailing regulatory and technical limitations, but have courageous aspirations to engage in a sustainable manner. In addition, the Global Observatory on Peer-to-Peer, Community Self-Consumption and Transactive Energy Models (GO-P2P) coordinates global efforts, not only from an academic, but also a business and societal perspective.
Optimally, a P2P platform incentivizes the cooperative integration of distributed energy resources and pro-active consumers in an approach compatible with the present system. Oftentimes, however, they are predominantly self-centered cost-optimizers. For a system-supporting operation—potentially matching supply and demand locally [
5]—further design and regulation efforts are needed [
3]. A diverse set of viable business models has been identified [
3] and pilot projects are already underway (see overviews in [
2,
6]). Most of these setups include some kind of intermediary [
4] to operate the P2P market, exercise the rights, but also perform the duties of an electric utility company (e.g., handling trade, billing, balancing, or other administrative obligations).
Yet, the challenge remains to select a suitable business model and system design for a specific setup [
3,
5,
7]. For example, Zepter et al. (2019) [
8] propose a two-stage stochastic program in order to integrate a local energy community with PV, BESS, and small-scale wind turbines into the German wholesale market. In addition to the business and regulatory aspects, the technological challenges of bidirectional power and information flows, as well as intermittence and uncertain RES generation have to be addressed in order to plan, operate, and provide energy security [
2]. Local distribution network conditions (e.g., local power flow and voltage constraints) have to be taken into account. While the system operators had traditionally been incentivized to invest in long-term physical network reinforcement, a shift to more active management is needed [
3]. This might become easier with further advances in metering, control devices, information and communication technology, as well as distributed ledger technology, which will simplify metering and billing [
5] and hopefully reduce transaction costs sufficiently. Privacy and data protection regulations introduce new challenges.
The immediate goal is to efficiently match supply and demand, deliver low cost electrification of the heat and transport sector, while at the same time guaranteeing transparency, autonomy, and scalability. P2P solutions are suitable to address these issues when low economies of scale, demand variability and diversity, as well as the ability to efficiently match small-scale buyers and sellers, are given [
3]. This is increasingly also the case in the electricity sector.
The objective of this study is to evaluate if the current German market conditions are sufficient to introduce a working P2P market. We derive agreeable market price ranges based on the current levy regime and reservation prices of the market participants. We consider an illustrative market setup with consumers, producers (with RES generation), and prosumagers (with additional BESS). The representative buildings are equipped with heat pumps and thermal storage systems. We implement a mixed-integer linear program (MILP), minimizing overall costs while considering thermal comforts. Over the course of a whole year, with a time resolution of one hour, we analyze the seasonal effects on the market operations. In order to evaluate the current and two proposed market designs, we present market splits, cost distribution, and self-sufficiency rates. We provide our input data, as well as our model implementation, in an open-source manner, to enhance reproducibility.
The remainder of this paper is structured as follows.
Section 2 relates the given problem to the literature.
Section 3 introduces the context of the numerical study, and derives the market designs, as well as associated levies and prices. In
Section 4, we introduce the model formulation of the P2P market.
Section 5 presents the results of our analysis.
Section 6 concludes the study and proposes further research directions.
Appendix A presents the nomenclature of the decision variables and parameters, as well as the technical specifications.
2. Related Work
In the following section, we analyze market studies incorporating RES into residential microgrids. Thereby, we focus on studies that evaluate tariff structures in the context of P2P markets (see
Table 1 for details).
One of the key configurations of market design are prices for P2P trading. In most market studies, first traded loads are optimized and market prices are only fixed appropriately afterwards. Long et al. (2017) [
9] compare different methods to determine prices: the bill sharing method (to split costs between peers in retrospect), the mid-market rate (between retail purchasing and selling prices), and auction-based pricing (where participants bid). In their study, they evaluate the influence of PV penetration on cost reductions. Yet, all their prices are determined in retrospect. This way, the prices do not affect market operations—demand response is not considered. In a subsequent work, Long et al. (2018) [
10] introduce a BESS, they plan based on past data, and incorporate a rule-based control for real-time adjustments. They evaluate the impact of battery size, time delay, and participation rates. The prices are set based on the supply and demand ratio of the past 24 h. Neves et al. (2020) [
4] deliver a comprehensive overview of market studies in the field. In addition, they conduct a Portuguese case study where they evaluate the influence of PV penetration, while setting a midmarket rate. Similarly, Huang et al. (2020) [
11] fix the loads based on forecasts while only net loads are traded, evaluating a range of midmarket rates (see also a similar Korean case in [
12]).
In order to guarantee fair cost distribution, Alam et al. (2017) [
13] optimize loads minimizing costs and disutility of delayed consumption; afterwards, they allocate pareto-optimal midmarket rates. Subsequently, Alam et al. (2019) [
14] propose a near optimal algorithm ECO-trade, evaluating the impact of PV and storage penetration with lower computational effort. The only study we found that endogenously sets P2P prices is that of Lüth et al. (2020) [
15]. By comparing to levelized costs of energy (LCOE), they study different market designs and propose a setup where consumers can actively engage and profit from shared asset investments.
Fridgen et al. (2018) [
7] give an overview of potential tariff designs and evaluate the impact on market operations in a residential microgrid considering PV, EV, and BESS. In order to do so, they simulate 100 random weeks with different tariff-parameter combinations. Meena et al. (2019) [
16] analyze time-of-use (ToU), feed-in-tariffs (FiT), and fixed tariffs. Similarly, de la Hoz et al. (2020) [
17] evaluate the Iberian economic and regulatory structures with regard to economic performance and market operation. Nguyen et al. (2018) [
5] evaluate the impact of PV system scaling, margin of the intermediary, PV penetration, and FiT. They evaluate storage sizes based on levelized costs of storage (LCOS). Their peer price is calculated in retrospect based on the reservation prices of the market participants.
The interaction of P2P markets and BESS, as well as the impact of central versus decentral storage systems is evaluated in [
18]. Joo and Choi (2017) [
19] model the interaction in a local and a global home energy management system, where first the loads are scheduled locally, and afterwards the BESS and trade are optimized globally. However, they do not set P2P prices. Relatively little research has been conducted with regard to sector coupling in the context of P2P markets. The combination with EVs is studied in [
20]. The only studies incorporating HPs in a P2P setting are [
21,
22]. Here, a double-sided auction market with simple non-predictive constant bidding strategies of each device is simulated; the overall integrated system is not optimized.
Therefore, we observe—in line with [
21]—a lack of studies investigating the integration of thermal and electrical assets in combination with P2P flexibility. We found no study covering the detailed operational flexibility of heat pumps and thermal storage systems with regard to P2P markets. Moreover, the focus oftentimes is on overall market implications; little attention is paid to the optimization of and impact on single end-users’ operation, see also [
5]. Policy makers, however, should gain insights into the role of P2P markets and distributed RES to evoke high participation rates in the energy transition [
4]. Prices and market design should increase economic benefits for all participants, while allocating costs fairly. In addition to that, to our knowledge, no study analyses the German tariff regime and its single components with regard to P2P markets. The evaluation of policy proposals in a realistic setting could, however, be valuable in order to draw conclusions for efficient market design and regulation.
We therefore propose a MILP, taking into account the detailed German levy regime. We evaluate three tariff structures of varying support for P2P markets. We analyze the optimal operation of three different players (consumers, prosumers, and prosumagers) and derive policy recommendations. Meanwhile, we use a representative residential building incorporating PV and BESS, but also an HP in combination with thermal storage systems. We chose a tariff-appropriately scaled PV and BESS system to gain insights into the policy impact for a representative German RES owner. In line with the literature, we derive a fair exogenous midmarket P2P trading price and evaluate the performance over a whole year using a rolling horizon approach, given a time resolution of one hour, in order to analyze seasonal effects.
3. Numerical Study: Market Design
In this section, the numerical study is introduced. In
Section 3.1, we describe the components of the current retail prices in Germany. Subsequently, in
Section 3.2, we present the current levy regime. In
Section 3.3, we propose a market design for P2P markets based on the regime. In
Section 3.4, we briefly elaborate on the levy structure for BESS in the given case. Finally, in
Section 3.5, we derive market prices based on the introduced regimes considering the reservation prices of the producers and consumers participating in the market.
In
Table 2 columns 3–5, the retail price components have been adapted for P2P markets based on the regimes of our numerical study. Each regime (column) represents two cases, one with and one without FiT; only the value-added tax (VAT) might differ based on the P2P market price of the respective case (see further
Section 3.5 and
Table 3). In the following, the columns of
Table 2 will be explained one at a time.
3.1. Current Retail Price Components in Germany
The German retail electricity price paid by a residential consumer consists of a diverse set of price components. Surcharges, fees, and taxes make up most of the price; only about 23% account for electricity acquisition and sale. Customers are free to choose their provider; offers do however not differ significantly and almost all residential consumers face fixed tariffs not considering; for example, ToU or other flexibility incentives. The presented mean retail price components (
Table 2 column 1–2) are based on the periodical electricity price analysis conducted by the BDEW (German Association of Energy and Water Industries) as of January 2020 [
23]. The updated report as of July 2020 shows slightly higher costs for acquisition and sale, the other price components, however, remained constant. In
Table A6, we briefly describe the price components from a residential perspective, based on the definitions provided by the BNetzA (Federal Network Agency) [
24] and the BMWi (Federal Ministry for Economic Affairs and Energy) [
25]. In our model, those costs are incurred when sourcing from the grid.
3.2. Current Levy Regime
So far, there exists no tariff regulation covering the specific use case of P2P trading. Yet, one can build on some proposals [
26,
27], also with a focus on shared electricity storage systems in energy communities [
28,
29]. Since the application is similar—after all, in the latter case, the producer feeds into a battery and the battery forwards electricity to another user—at least the regulatory intentions ought to be coherent. This is why we will base our current and proposed levy regimes on a combination of these proposals. In general, the current levy regime includes all levies from
Table 2 to the full extent. They have to be paid by the final consumer. This states the most pessimistic case when it comes to supporting P2P markets.
3.3. Proposed Levy Regimes for P2P Trading
In order to derive an appropriate levy structure to support P2P markets, the circumstances of the German regulatory system and the current levy regime have to be taken into account. The goal is to derive a fair cost allocation to incentivize market participation without burdening non-market participants disproportionately. The most important factors directing the level of surcharges in the electricity market are [
26,
28]:
the self-consumption case or whether producer and consumer are identical,
spacial distance between them,
whether we face final consumption or intermediate transmission,
whether renewable energy only or also fossil energy is transferred, and
whether the market is located before or after the point of common coupling (PCC).
In our proposed regime in
Table 2 column 4, producer and consumer are not identical, yet are located in close vicinity. Purchasing from the P2P network is considered final consumption. We assume a renewable energy-only community. We argue that for feeding into the P2P network, no additional costs should apply and all surcharges have to be paid by the final consumer. We propose a reduced grid fee (−2 ct/kWh) in accordance with [
27], because of the close vicinity and potential resulting grid relief. The EEG surcharge could be charged at a reduced rate of 40% (normally used for renewable energy systems larger 10 kW or kWp), as a measure to compensate for saved feed-in tariff or to supersede it [
26]. Because of close vicinity and the use of EEG assets smaller 2 MW only, additionally, the electricity tax might be waived [
27]. These suggestions sum up to the rather conservative but realistic market design illustrated in
Table 2 column 4.
The last proposed area regime (
Table 2 column 5) of our numerical study is located in an area network. All trade is assumed to happen before the grid connection point (PCC). In this case, no levies apply; the community, however, still faces the value-added tax, which is calculated based on a common retail price, see
Table 2. The behavioral patterns resulting from the three designs will be analyzed in
Section 5.
3.4. Battery Levies
The prosumagers face two economically viable use cases for their battery: they could self-consume the energy therein or feed into the P2P market. Feeding into the grid is sub-optimal because of the constant prices in combination with conversion losses. Because of the close vicinity of the users—resulting in similar PV production patterns—charging the battery from the P2P market is also not economically viable. This way, the battery is only charged by the owner (and not other peers). Consequently, no levies apply for charging the BESS [
29]. All case-specific levies have to be paid by the final consumer sourcing from the P2P market—independent of whether the market was fed from the battery or from PV.
3.5. Market Prices
In the following section, we will derive the market prices for the numerical study based on the reservation prices of the market participants. The results can be considered as the suitable range of prices that would facilitate P2P trade. Within this range, producers could set individual prices like it is done in the business case of Enyway, a matchmaking platform operating in Germany. Here, individual producers decide on the fixed unit price they want to offer their RES generation for. Consumers can choose from a wide range of producers all over Germany. The consumer experience is similar to sourcing from traditional electric utility companies, as Enyway provides the additional services. In our numerical study, we assume a uniform market price, for all times-of-use, but also for the different producers. In the following, these prices are derived based on the introduced regimes.
3.5.1. Reservation Purchase Price
The reservation purchase price (RPP) is defined as the maximum price consumers are willing to pay for a kWh of electricity [
5]. This price is based on the opportunity costs of the customer—in our case the electricity retail price of 31.373 EUR/kWh presented in
Table 2. In order to derive the yield of the producer for the price the customer is paying, all additional price components have to be subtracted. This includes a margin of 5% for the coordinating intermediary (trader) of the P2P market based on Nguyen et al. (2018) [
5], the German value-added tax of 19%, as well as the levies introduced in
Table 2.
Table 4 presents the maximum yields of the producers based on the introduced retail price and levies (
Table 2). The producer could gain a margin of about 23.84 ct/kWh in the area regime, 12.77 ct/kWh in the proposed regime, and 4.66 ct/kWh in the current regime. Subsequently, in the latter case with a FiT of currently 9.87 ct/kWh, selling at the P2P market is sub-optimal for the producer. Without a FiT, and in general for the other regimes, both the producer and the consumer might gain from P2P trading. The resulting yields are the maximum values a producer can collect in the given cases. A higher market price would exceed the reservation purchase price—the consumer’s willingness to pay—and would result in a lack of demand.
3.5.2. Reservation Sales Price
The reservation sales price (RSP) is the minimum price that the producers are willing to sell their electricity for [
5]. This lower bound is based on alternative potential revenue streams like a FiT. This is why, in
Table 3, six cases are derived, one case with and one without a FiT for each of the three regimes, respectively. We regard investments as sunk costs, and therefore do not consider levelized costs of electricity (LCOE) or storage (LCOS). The main focus of our study is on operational decisions of already installed assets under subsiding FiTs. Determining optimal investment decisions is beyond the scope of our study.
Table 3 presents the potential P2P retail prices, based on the lower bound of the reservation sales price of the producer and the levies to be paid. In the current regime case with a FiT of 9.87 ct/kWh (column 2), the resulting market price of 38.23 ct/kWh would exceed the willingness to pay of the consumer (the reservation purchase price)—the market price would exceed the electric utility price. In this case, purchasing from the P2P market would be sub-optimal. In all other cases, the resulting P2P price is lower than the retail price offered by the utility. The prices indicate lower bounds—lower prices would lead to a lack of supply.
In
Figure 1, the upper and lower bounds of the potential market price—derived in the previous sections—are illustrated by bars. In case #1, no price satisfies the RSP and RPP. In our numerical study, we chose the mean price of the price ranges as the uniform market prices (indicated by the horizontal lines), similar to the midmarket rate. The according yields of the producer are indicated by the crosses. We notice that from left to right (considering whether we have a FiT or not), the prices for the consumer decrease, but also the yields for the producer increase. Both are better off in our introduced market designs.
The price has to be determined within the energy community. A uniform price based only on the RSP and RPP is a strong assumption that is commonly made in these market studies, see
Section 2. A uniform price within an energy community, not influenced by individual producers or by technology used, might increase transparency, social acceptance, and participation rates. In the following section, the formulation of the energy management system models of the users is described in further detail.
4. Model Formulation
In this study, we consider a network of three user types, see
Figure 2. The underlying home energy management systems are based on the study of Langer and Volling (2020) [
30]. We model identical representative residential buildings with modulating air-sourced heat pumps (
), as well as thermal storage systems for floor heating (
) and hot water (
). The floor heating temperature and the hot water volume must be maintained within a certain comfort range. We consider two kinds of thermal energy buffers: the built-in thermal mass of the floor heating system and a domestic hot water tank. The details of the technical configuration can be found in
Appendix A.
Buildings of producers (prosumager and prosumer) are additionally equipped with a PV system (
or
). Prosumager buildings also contain a BESS (
b). Energy flows not included in the technical setup and omitted in
Figure 2 (e.g.,
) are fixed at zero in the model, see
Table A1 for an overview of decision variables used in the model. Since we assume close vicinity, PV generation of prosumager and producer are identical. All market participants have the same exogenous electricity, floor heating, and hot water demand (see dotted frames in
Figure 2). The demand is modeled based on a representative German household, see details in [
30]. Additional endogenous demand is introduced by the BESS (in case of the prosumager) and thermal storage devices (for all participants). Considering identical (exogenous) demand is a strong assumption that is introduced in order to eliminate one influencing factor for the analysis of the market operations. This can be considered the worst case of a P2P market setup; diverse demand and generation patterns would improve market participation.
Both the electrical and the thermal storage systems suffer from dissipation losses. The buildings are connected to the power grid (
), enabling unlimited supply in addition to the P2P trading volume. Technical specifications are explained in greater detail in [
30]. However, in this study, we chose a slightly smaller BESS, which is more common in Germany, because of the regulatory upper bound of 10 kWh battery capacity—smaller units avoid the EEG surcharge. Technical specifications can be found in
Table A2 for the PV system,
Table A3 for the HP and thermal storage systems, and in
Table A4 for the BESS.
Parameters known to the model include outside temperature (
), PV generation (
), as well as demand for floor heating (
), hot water (
), and electricity (
). Considering perfect information is a strong but common assumption in these kind of market models. Fischer et al. (2017) [
31] show, however, that especially short term demand and generation—in our case 36 h—can be predicted with high accuracy, due to the strong correlation between succeeding days. Data sources are given in
Table A5 and explained in greater detail in [
30]. Tariff and price components are known to the model and explained in greater detail in
Section 4.1. Prices are assumed to be constant. This is why, redirecting flows via the battery—resulting in conversion losses—has to be sub-optimal. This is why we omit all interaction between battery and grid. The battery can feed into the P2P market, however.
This study intends to determine the cost-optimal market operation for the overall P2P network, as well as individual users with an hourly resolution. We allow violations of ranges of comfort for floor heating temperature and hot water volume to prevent infeasibilities. We do however impose virtual violation costs for discomfort, see
Section 4.1.
We formulate the problem as a mixed-integer linear program (MILP). To solve the problem, we use a rolling horizon approach setting a prediction horizon of 36 h and a control horizon of 12 h with an hourly time resolution. Binary variables are needed to switch between the floor heating and hot water mode of the HP, to set the plus/minus sign of the floor heating loss term, to switch dis-/charging modes of the battery, as well as selling/purchasing mode for P2P market participants. We describe the model components in detail in the following sections. Data inputs, parameter settings, and technical specifications are detailed in [
30].
4.1. Objective Function
The net profit of the model is maximized by balancing the revenues obtained by selling to the grid and peer market with the cost of purchasing from the grid and peer market (Equation (
1)). In addition to that, we penalize violations of the comfort ranges of the floor heating temperatures and hot water volumes. Comfort violations occur when the state of charge (SoC) exceeds the upper or lower bound of the respective comfort range; further details in
Section 4.4. Following a weighted sum approach, we add comfort violations weighted by a parameter cost factor at 100 ct/violation to the objective function, see [
30] for details. The common tariff values derived in
Section 3 are formalized in the vector tariffs; see
Table 5 column 2. The cases are factorized by the matrix
indicated in
Table 5 and
Table 6. This way, the first element of the objective function represents overall costs associated with energy flows
of a peer
n in time period
h—all profits and costs of selling to or buying from the peer market (
pm) or grid—including tariffs defined by the case used.
Table 5 illustrates the common columns of the case matrices (row 1 differs by whether a FiT is implemented or not). All energy flows that are not related to the
pm are included here; see
Figure 2. This is why they are constant over all cases—which only alters P2P tariffs. Columns 1–2 present the name and value of the costs introduced in
Section 3; the columns to the right present the multipliers that the price component is multiplied with when a certain flow (column header) occurs. For example, the flow
(from the PV system to the grid) adds 9.87 ct/kWh × 1 = 9.87 ct/kWh profit in the FiT case (row 1) and 9.87 ct/kWh × 0 = 0 ct/kWh in the case without FiT (row 2) to the objective function. Costs to be paid have negative multipliers (red) and profits have positive multipliers (green). Via matrix multiplication all tariffs are assigned to model flows appropriately. For all flows within a single building, no costs are induced, which is why most factors are zero.
Table 6 presents the factors related to the peer market (
) by regime. The first column for each regime always indicates the yield of the producers feeding into the
pm (→
); the second column indicates the price paid by the customers sourcing from the
pm (
→) consisting of the peer price and the levies depending on the regime. The difference between peer price paid and yield received results from the additional costs of the trader’s margin and the VAT. So, for example, in case #5 (area regime with FiT), the consumers pay 24.39 ct/kWh × (−0.999) = 24.39 ct/kWh and the producers receive 24.39 × 0.7599 = 18.53 ct/kWh, also shown in
Figure 1. The difference of 24% consists of 19% VAT and 5% trader margin.
4.2. Flow Constraints
Equation (
2) ensures that electricity demand (
) is fulfilled for all market participants
n at all times
h. Demand is identical for all users, which constitutes a worst case scenario. This is done in order to eliminate another influencing factor and concentrate the analysis on the chosen market design. The P2P market would benefit from a more diverse demand. Equation (
3) makes sure that the sum of electricity provided by the PV system of a user (taking into account the inverter efficiency
) is equal to the overall electricity generated by the PV system (
). Equation (
4) clears the peer market.
4.3. Battery Constraints
Equation (
5) maintains the energy balance of the battery. We introduce a small dissipation loss (
) proportional to the state of charge of the battery (
) and consider the battery efficiency
.
is bounded by
and
, which are obtained based on the specified usable battery capacity (Equation (
6)). Equations (
7) and (
8) prevent charging and discharging at the same time and limit both to the maximum charging–discharging rate (
). This rate is determined by the specified nominal power of the inverter
. The technical specifications of the installed battery are presented in
Table A4.
4.4. Heat Pump Constraints
Equation (
9) maintains the energy balance of the heat pump. Equations (
10) and (
11) ensure that only one mode, the floor heating or the hot water mode, can be active at any given time. The modulation degrees of floor heating and hot water modes (denoted by
and
) are continuous variables between zero and one. Equations (
12) and (
13) restrict the load of the heat pump to its maximum power (
).
4.5. Floor Heating Constraints
Floor heating SoC is modeled with respect to building mass and is represented by floor heating temperature
[
30,
32]. The floor heating energy balance is maintained using Equations (
14)–(
16). The next
is equal to the sum of the current
and energy supplied by the heat pump to the floor heating
multiplied by coefficient of performance
, minus heating demand
and dissipation losses of the floor heating system
. Coefficient of performance
describes the ratio of thermal power output to electrical power input and is determined by source and sink temperatures of the floor heating system (see [
30] for details). All factors influencing
must be multiplied by a conversion factor
converting kWh to
C and implementing the hourly resolution. This conversion factor, which is set by Equation (
15), is determined using volume
and material specification associated with the floor heating (see [
32] for details). Equations (
19) and (
20) model comfort-range violations associated with the floor heating system (see [
30] for details).
4.6. Hot Water Constraints
Hot water constraints (Equations (
21)–(
24)) are governed by the same principles as floor heating constraints. The factor
converting kWh to liters and hourly resolution, set by Equation (
22), requires supply temperature
and material configuration of the hot water tank (see [
32] for details). Comfort violations (Equations (
23) and (
24)) are given in liters not in
C.
The model formulated in Equations (
1)–(
24) is an extended variant of a multiperiod capacitated transshipment problem. The used binary decision variables ensure single-mode operation of heat pump (
or
), battery (dis-/charging), and P2P participation (selling/purchasing), as well as sign adjustment of
. Thus, the problem is formulated as a MILP that can be efficiently solved under the given problem size. All cases solve a whole year with an hourly aggregation in under 100 s. We use an Intel Core i7-8550U with an 1.8 GHz processor, four cores, and 16 GB RAM. The model is written in the mathematical optimization language
JuMP (version 0.21.2, see
https://github.com/JuliaOpt/JuMP.jl) [
33]. The package is embedded in the
Julia programming language (version 1.4.0, see
https://julialang.org). Both these software packages are provided open-source and are available free of charge. For solving the model, we use the
Gurobi solver with an academic license (see
https://www.gurobi.com/). Model implementation and data as well as an interactive visualization of results can be found in the
Supplementary Material on
GitHub (see
https://github.com/lilanger/PEERS/tree/master/peer-to-peer).
5. Results and Discussion
P2P market participants represent three user groups: prosumagers, prosumers, and consumers. The configuration of the associated buildings represents a typical German household. The technical configuration is a common RES setup. Capacity of the PV system is 10 kWp and maximum usable capacity of the BESS are 10 kWh, and maximum power of the heat pump is 3 kW. For larger RES systems (>10 KWp or kWh), EEG surcharges apply.
In the following numerical study, we will analyze the resulting P2P trade, as well as energy flows determined by a central home energy management system over the course of a year assuming full information. This idealized case minimizes total costs and discomfort of all users. The way we designed market prices nobody can be worse off when introducing P2P trade. In
Section 5.1 and
Section 5.2, market operations will be explained on the basis of a set of exemplary days. In
Section 5.3, we will analyze resulting market splits. In
Section 5.4, we present annual KPIs of the numerical study. Finally, in
Section 5.5, resulting levies will be analyzed. Illustrations of the system behavior used for the exemplary days are available online for the reader to explore in an interactive manner and examine other days, cases, and users (see
Supplementary Material https://github.com/lilanger/PEERS).
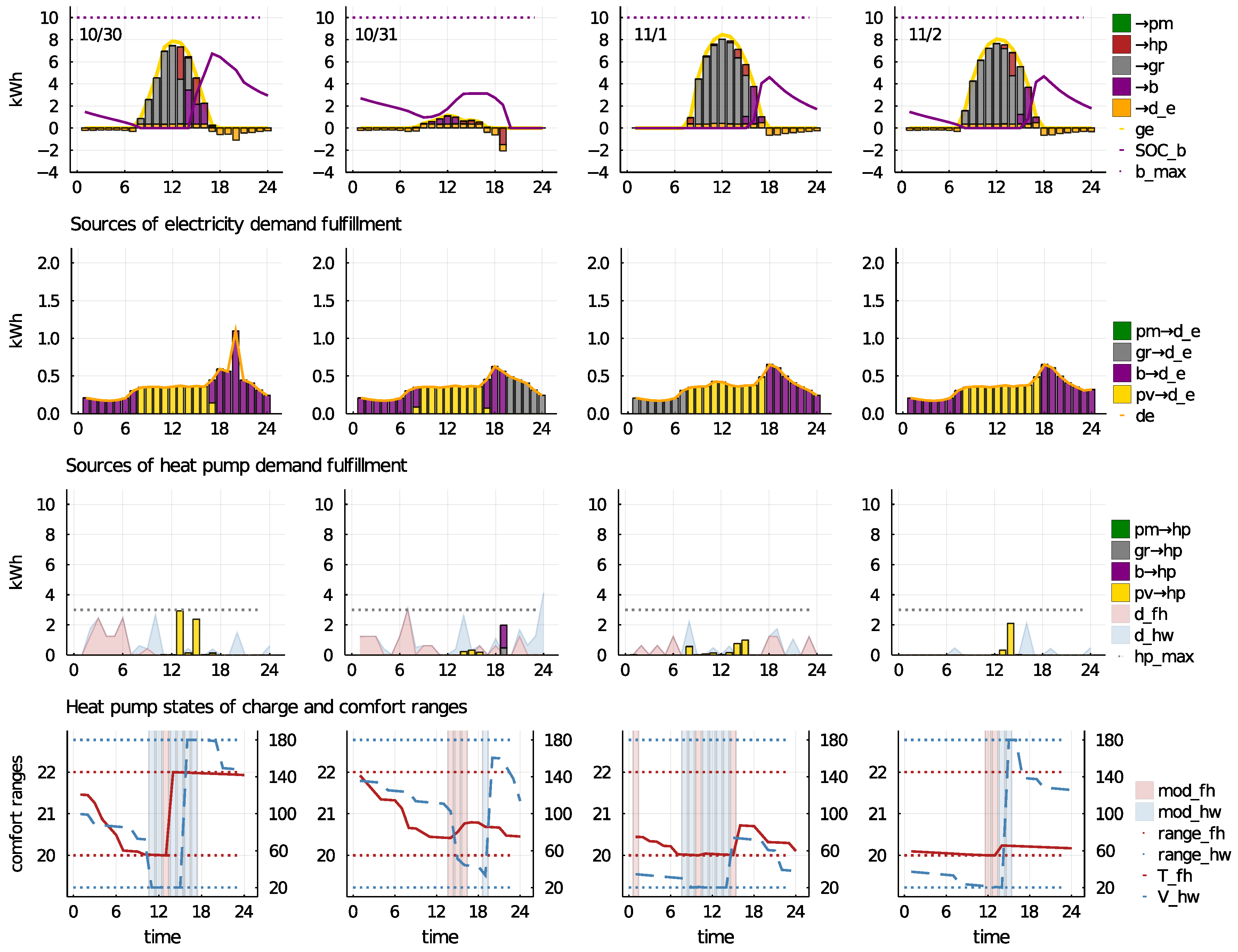
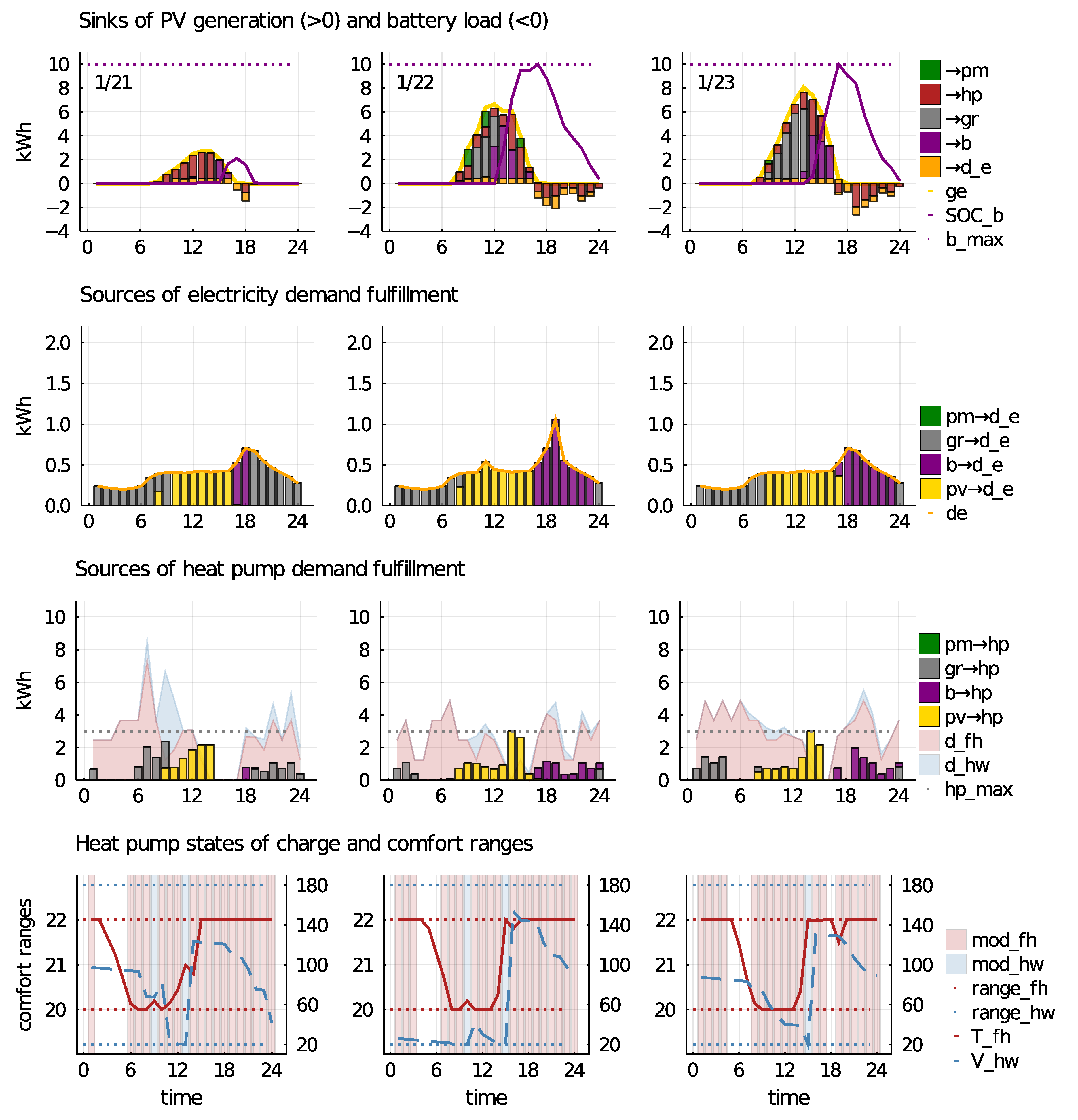
5.1. Exemplary Autumn Days
In the following parts of the comprehensive graph in
Figure 3 are used to describe the behavior of specific market participants on explanatory days in a year. The color code is standardized throughout the paper: purple represents the battery (
b), gray the grid (
), green the P2P market (
), orange the electricity demand (
d_e), yellow the PV generation (
g_e), and red the heat pump (
). Heat pump operation is further differentiated between floor heating (
) in red and hot water (
) in blue.
The first row of
Figure 3 illustrates PV and BESS operation: positive stacked bars indicate sinks of PV generation, negative bars indicate sinks for BESS discharging. Overall PV generation is shown by the yellow line, the purple line indicates the battery SoC. BESS capacity (
b_max) is illustrated by the dotted purple line. The second row illustrates demand fulfillment, electricity demand is shown by the orange line, the stacked bars illustrate the sources used for demand fulfillment. In the third row thermal demand (area plot), as well as energy sources for the HP operation (stacked bars) are presented. Floor heating demand is shown by the red, hot water demand by the blue areas, respectively. The dotted line indicates maximum power of the HP. Finally, the last row illustrates HP operation and thermal SoCs. The bars indicate whether the HP is in floor heating (red), hot water (blue), or off mode (transparent). The red line indicates floor heating SoCs, the red dotted lines, indicated on the left axis, show lower and upper bounds of the floor heating comfort range, 20
C and 22
C, respectively. The blue dotted lines on the right axis show lower and upper bounds of the comfort range of the hot water SoC (blue line), 20 and 180 L, respectively.
5.1.1. Case #1—No P2P Trading
Figure 3 presents the case of the current regime with a FiT (Case #1) for the prosumager. As explained in
Section 3, the tariff structure of this case makes trading at the P2P market unattractive for a producer. Profit from the FiT is higher than potential gains from the P2P market. Accordingly, the P2P market is not used, the consumer’s demand is fulfilled solely using the grid (see also
Figure 4).
On 30 October, in
Figure 3 Row 1, electricity generated by the PV system is used to fulfill electricity (positive orange bars) and thermal demand (red bars) of the prosumager. Both demands are fully covered during PV hours. In Row 2, electricity demand is covered by PV (yellow bars) and after PV hours by the BESS (purple bars) up to the PV generation of the next day. In Row 3, heat pump demand is also supplied by PV (yellow bars). This is sufficient to charge both thermal SoCs to the upper bound (Row 4). CoP of the HP increases when the outside temperatures are high, therefore main HP operations are conducted in the hottest time periods in Row 3 (see further [
30]). PV surplus (Row 1) is fed into battery (purple bars) and grid (gray bars). Even though on October 31, nightly demand cannot be fully covered, the battery is deliberately not fully charged on October 30—instead the FiT is collected. Hence, oftentimes the battery is not fully utilized—except for winter days, when demand up to the next PV hour succeeds BESS capacity.
On 31 October, PV generation does not allow one to charge the battery enough to fulfill all demand up to the next PV hour. This is also oftentimes the case in winter when floor heating demands are high and more days with little PV occur. Consequently, nothing is fed into the grid.
On 1 November, the battery is charged with exactly the amount needed to cover the prosumager’s demand up to the next PV hour. Surplus is fed into the grid. This is the most common operation from around April up to November. Prosumagers can neither consume all PV generated during the day, nor can they store all energy efficiently (neither in the BESS nor thermal storage systems) to consume it later—they collect the FiT. This is also reflected in the annual self-consumption rate of 39% and the annual self-sufficiency rate of 75%. The BESS is not fully utilized for most of the year, demand is spread between winter and the rest of the year leads to unbalanced utilization.
5.1.2. Other Cases—With P2P Trading
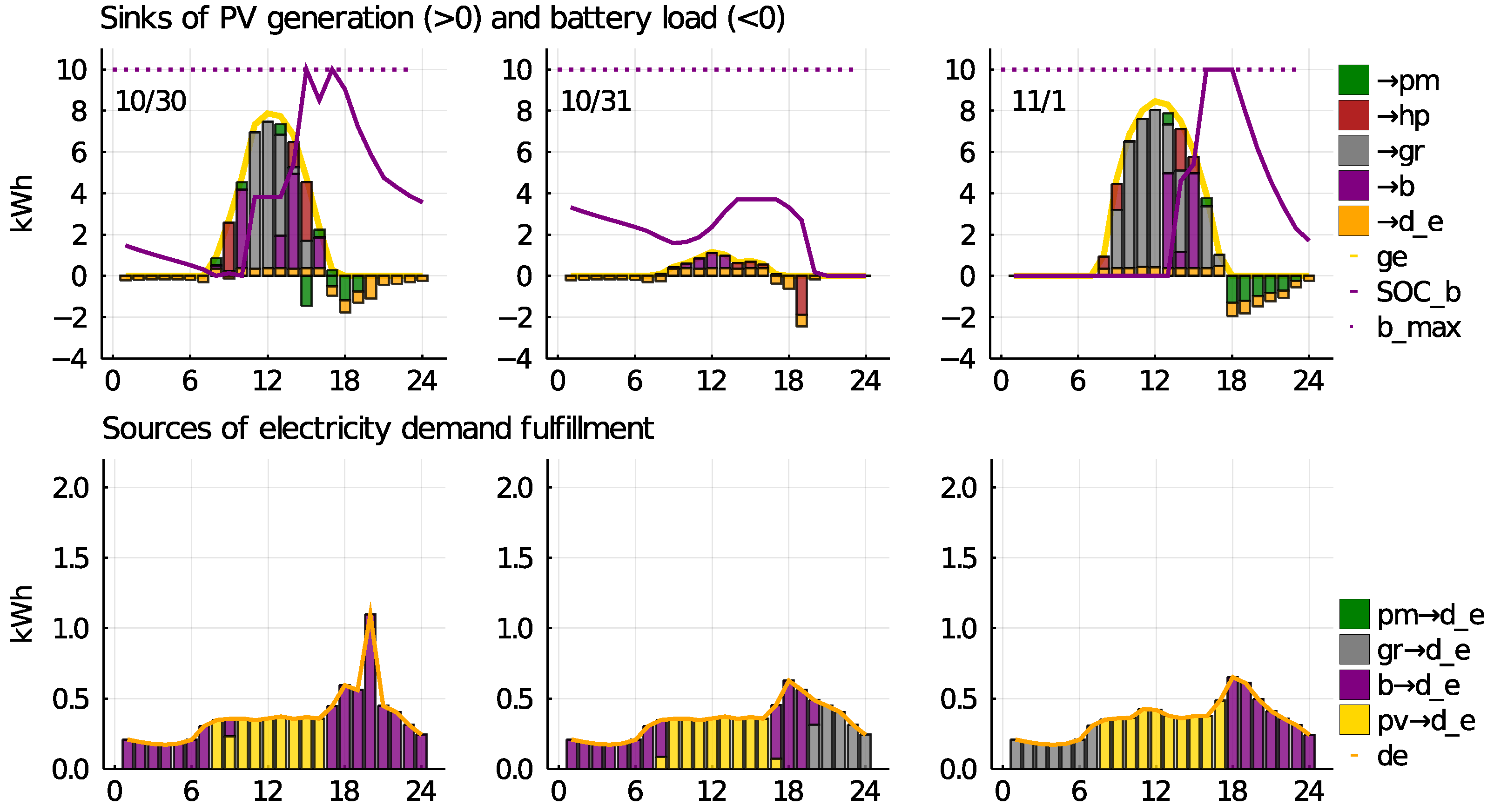
Figure 5 presents the same autumn days for one of the cases where feeding into the P2P market is attractive for the producer, but FiT still applies (Cases #3 or #5). In both these cases, the battery is fully charged whenever PV generation is sufficient (purple bars). The prosumager feeds into the P2P market directly from PV during the day (positive green bars), but also from the BESS in the afternoon (negative green bars).
In Cases #2, #4, and #6, the FiT is zero and the prosumager does not benefit from feeding into the grid.
Figure 6 shows that, even without compensated grid feed-in, oftentimes not all PV generation can be used efficiently, and the gray bars (row 1) show PV that has to be curtailed (or fed into the grid without compensation). This is why inefficient charging and discharging operations of the BESS on 30 October at 15 h can be observed. The P2P market is supplied by the battery (with conversion losses), even though PV would also be available. PV surplus in this case leads to inefficient processing.
In all cases, the demand of the prosumager is always fulfilled first (see Row 2). Only in summer, BESS capacity is sufficient to cover all demand for all the peers (in our small example). Most often, especially during winter and with low PV, prosumer and consumer have to cover their nightly demand using the grid (see
Figure 7). During the day, in addition to the prosumager, the prosumer also feeds into the P2P network. This way, during PV hours, oftentimes, all demand for all users can be fulfilled. Sometimes however, as is the case on 31 October, PV is not sufficient (see
Figure 6 and
Figure 7).
5.2. Exemplary Winter Days
In winter, in all cases except for Case #1, the prosumager still fully charges the battery whenever PV is sufficient. In
Figure 8, on 21 January, this is not the case. On 22 and 23 January, during PV hours, prosumer and prosumager jointly provide P2P energy to fulfill demand of the consumer and charge the BESS (prosumager). PV surplus is fed into the grid. Depending on the ratio of producers to consumers and PV generation on a specific day, during the day, all or only part of the demand of all market participants can be fulfilled.
Figure 8 Row 3 shows that floor heating demand in winter is much higher. Therefore, during the night BESS capacity does not cover all nightly demand of the prosumager. This is why the BESS does not feed into the P2P market. All demand of prosumer and consumer after sunset has to be provided by the grid. In these cases BESS capacity is not sufficient to supply all demand. BESS utilization is high throughout the year.
To conclude, we find that the P2P market helps to increase the utilization of the BESS, especially in summer, leading to a more balanced utilization. Without compromising self-consumption and self-sufficiency rates, which stay at 39% and 75% for the prosumager and at 28% and 52% for the prosumer, respectively, PV surplus can be consumed locally. Even higher rates would be possible for larger BESS (or shared BESS), or more diverse demand or generation profiles. The FiT leads to lower BESS utilization in summer, but at the same time prevents conversion losses, inefficient operation and curtailment. We can conclude that a complete abolition of FiTs might require a precise scaling of BESS, in order to prevent inefficient processing. Thermal storages will not suffice, since oversupply of PV mostly occurs during summer when heat demand is low.
5.3. Market Splits
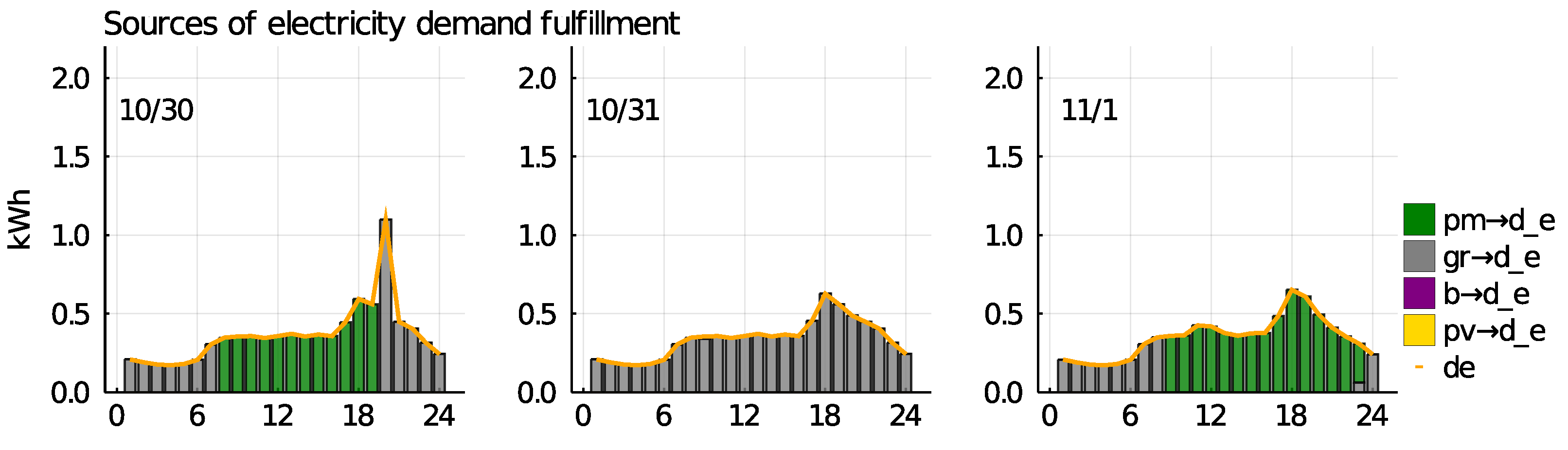
Figure 4 presents market splits—the discrimination of energy sources to fulfill demand by user and case—of the numerical study. We distinguish between produced electricity by PV (self-consumption), electricity sourced from the grid at retail prices, and electricity sourced from the P2P market.
Again, we notice that, in Case #1, the P2P market is not used. This is due to the fact that producers collect the FiT instead of supplying the P2P market. In general, in none of the cases, the prosumager sources from the P2P market. Only the prosumer is both seller and buyer at the P2P market, yet never in the same time period. The consumer is the main customer of the P2P market. This indicates that the consumer is most affected by levy regimes introduced in
Section 3. Proposed regimes only alter levies relating to the P2P market. Interestingly, market splits (and flows) differ very little between proposed cases. This was already indicated by the exemplary days. Operational behavior of the players is not affected much. This results from the prices, which are all set in the acceptable range (except for Case #1).
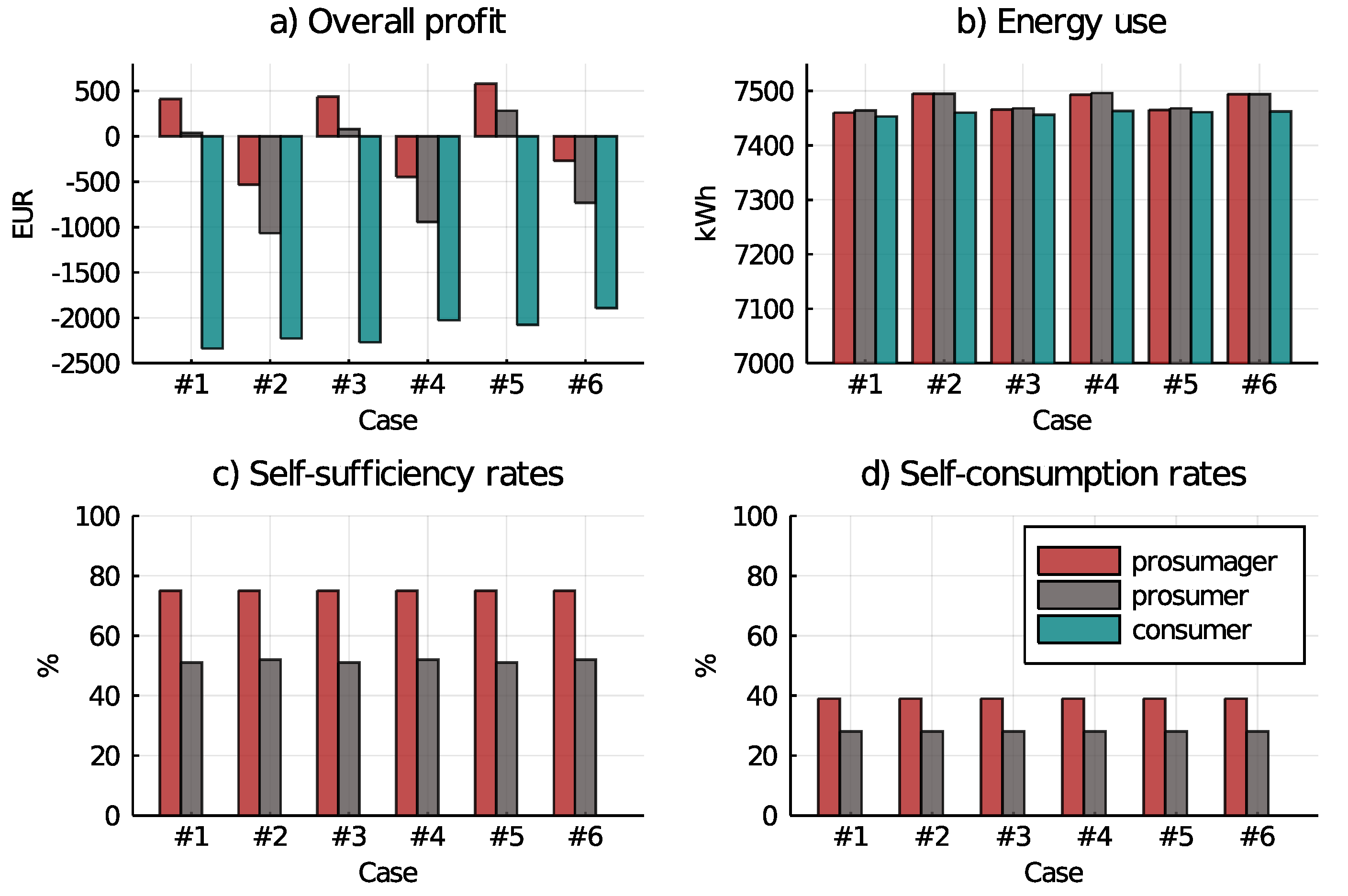
5.4. Key Performance Indicators
Figure 9 presents key performance indicators for the six cases and three user types. We examine annual overall profits, electricity consumption, as well as the self-sufficiency and self-consumption rates. The latter is the share of energy produced that is consumed on-site, whereas self-sufficiency rate is the share of demand that is produced on-site.
Figure 9 a presents overall annual profits from selling and sourcing electricity for each user. Cases #1, #3, and #5 (with FiT) are the only ones generating positive overall annual profits for the prosumager (EUR 409, EUR 435, and EUR 578) and the prosumer (EUR 35, EUR 79, and EUR 281).
Figure 10 shows that the main source of income is the FiT. This indicates that nowadays benefits of the RES expansion are predominantly claimed by producers (who also bear the investments).
Without the FiT (in Cases #2, #4, and #6), all users make a negative profit because the paid surcharges overweight profits made on the P2P market (prosumager: −533/−447/−271, prosumer: −1068/−945/−733, consumer: −2227/−2027/EUR−1893). Even in Case #6, where levies only apply for sourcing from the grid, this is the case. Quite intuitively, the more the levies are reduced, the higher the profit for all users. Compared to the FiT case, consumers face slightly lower overall costs, as they profit from lower peer prices compared to the retail price.
Figure 9 b shows that, in all cases without FiT, energy use is slightly increased. This is because when incentivized to self-consume energy instead of feeding it into the grid, delayed consumption using storage systems leads to depreciation losses.
Figure 9c,d show that self-consumption and self-sufficiency rates are neither influenced by levy regimes nor by the FiT. This is due to the fact that cost minimization promotes self-sufficiency, because of the margin between costs for self-consumption and retail price. Promoting self-sufficiency leads to high self-consumption as well (not necessarily the other way round).
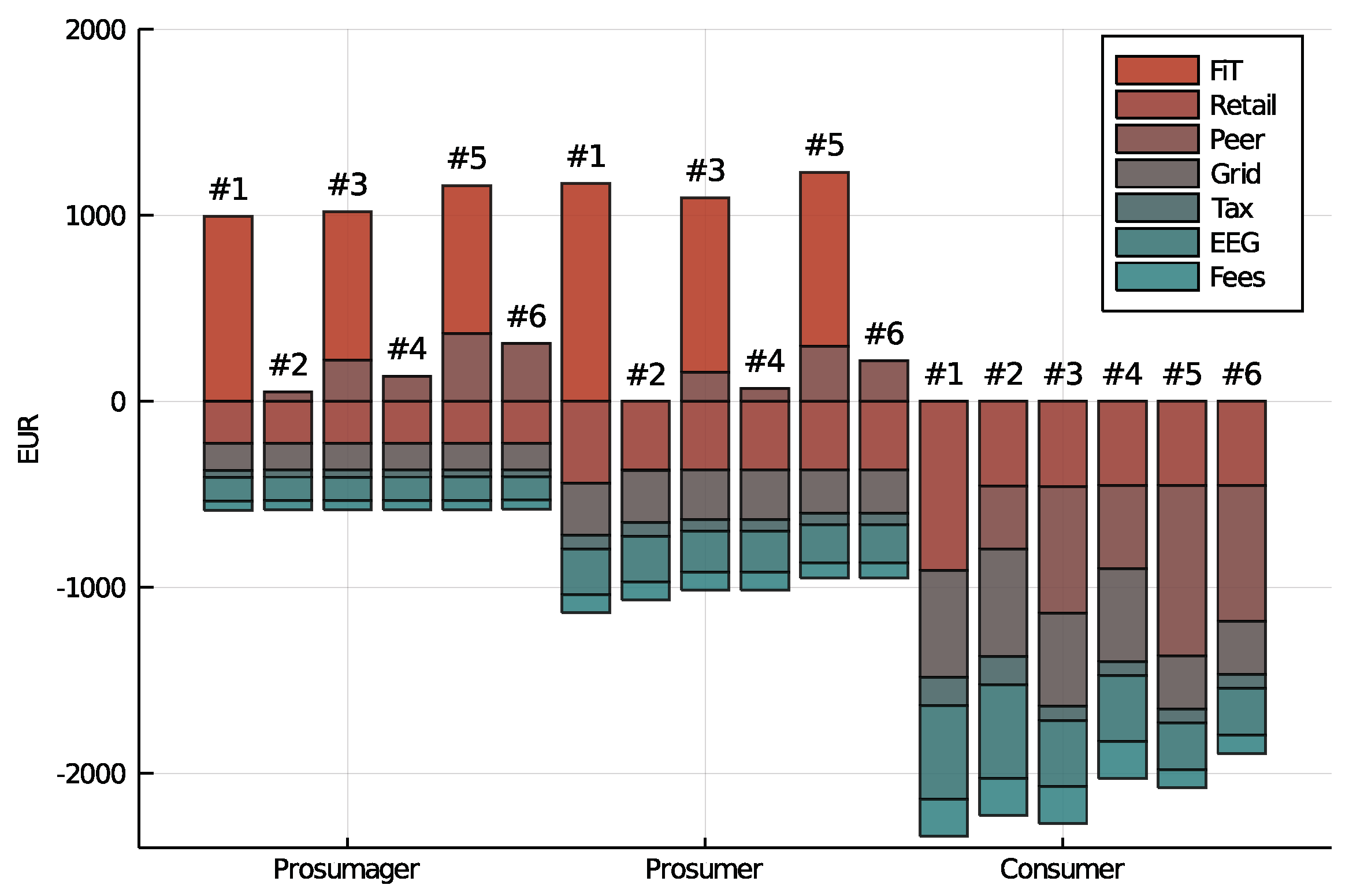
5.5. Levy Structure
Figure 10 presents the distribution of costs and benefits in greater detail for all cases and users. The negative part of the first six stacked bars for the prosumager clearly indicate that they source a constant amount from the grid—do not alter their operations by case—and do not source from the P2P market. The prosumager is merely a supplier to the P2P market. This way, their profits are determined by profit margins dominated by the FiT. In the FiT Cases (#1, #3, and #5), peer prices increase due to the higher reservation sales price. Hence, prosumager’s costs are predominantly determined by the self-sufficiency rate (which is also constant).
The prosumer sells and buys from the P2P market; annual net peer costs are presented in
Figure 10. Costs of the cases vary with the amount of P2P energy consumed—in contrast to the prosumager. Even though, without a P2P market in Case #1, profits from FiTs are higher than the sum of profits from FiTs and net peer gains in case #3, the reduced levies compensate for the difference. The prosumer is better in Case #3 when P2P trade is introduced. This is also due to the fact that the prosumer also profits from the P2P market as a customer; benefits are indicated by lower retail costs (plus associated levies) of Cases #2–6. Costs of Cases #5 and #6 are again only determined by the self-sufficiency rate. The income difference between the two producers is not very large (considering that one owns a BESS); the significant difference in profits is driven by the higher self-sufficiency rate of the prosumager.
The consumer in
Figure 10 is the only one profiting from the elimination of the FiT in all cases. While producers loose a significant share of their revenue, consumers (in Cases #2, #4, and #6) profit from lower P2P market price (based on lower RSP of producers). The share of grid sourcing (in Cases #2–6) is constant and determined by BESS availability, not price. As the consumers do not profit from reduced tariffs for self-consumption, they are more exposed to levies and bear more of the system costs.
Overall, we can conclude that all users are better when the current levy regime is adapted. Under the current regime with a FiT, the P2P market does not form, because grid feed-in is more profitable for producers. Eliminating the FiT reduces profits of producers significantly. Consumers gain from the reduced market price, but producers cannot be compensated sufficiently for the lost profit. When introducing a more P2P-supporting levy regime, costs for the prosumager are only slightly affected due to their high self-sufficiency rate. Mainly, consumers benefit from reduced levies. The prosumager, however, also profits from higher margins of the P2P market. The FiT paid by the state is reduced due to the P2P trading of producers. These savings might partly be used to mitigate the lower EEG surcharge paid by the consumer.
Given that the gradual reduction of tariff-based incentives seems inevitable, the challenge will be how to replace the subsidy with a more balanced cost distribution policy, in order to increase the participation rate in RES expansion, also for consumers who might not be able to bear the investments. Without the FiT in Cases #2, #4, and #6, again, the consumer profits twice, once from the reduced peer price and again from lower levies. We can conclude that the altered levy regimes are primarily a policy measure to support consumers who so far do not profit significantly from the energy transition. As indicated in
Figure 1, however, there is also some flexibility to increase P2P prices towards the reservation purchase price of the consumer, in order to incentivize further RES investments.
6. Conclusions
In this study, we propose six different market designs for an illustrative P2P market consisting of three user types: a prosumager, a prosumer, and a consumer. The proposed levy regimes are based on current surcharges in Germany, as well as the recent discussion on levy alterations. In line with the literature, we derive fair exogenous mid-market peer prices and evaluate the performance over a whole year using a rolling horizon approach with a time resolution of one hour. In the numerical study, we propose an MILP to model home energy management systems of market participants based on a representative residential building incorporating PV and BESS, as well as a HP in combination with thermal storage systems. We choose tariff-appropriate PV and BESS scaling to gain insights into the policy impact for a representative German RES prosumager. We evaluate three tariff regimes of varying support for P2P markets. Analyzing the optimal operation of market participants, we derive policy recommendations.
We find that, under the current regime with a FiT, the P2P market is not economically viable, because grid feed-in is more profitable for the producer. Eliminating the FiT reduces profits of producers significantly. Consumers gain from reduced P2P price and increased availability, but for producers, the P2P market cannot compensate for lost FiT profits. The prosumager is merely a supplier to the P2P market and therefore not affected by lower P2P levies. The prosumer is slightly, the consumer most affected by cost reductions and availability. Market splits, however, remain almost unchanged by specific details of the market design. If a P2P market is formed, it is used to the fullest extent (limited by demand and BESS availability). This is the case when P2P prices are set fairly, following reservation prices of producers and consumers. Following this conclusion, policy makers, but also energy communities and individual market participants, face some freedom to choose their P2P price within the range determined by reservation prices. Alterations of the market regime within this range primarily affect the costs of the consumer. The regimes could be used to shift the distribution of RES benefits more towards this user group, in order to increase social cohesion.
In our numerical study, we find that matching supply and demand will not only be determined by appropriate tariff design in order to foster demand response, but also by the utilization of storage systems. The imbalance between demand in summer and winter, as well as PV and non-PV hours, make scaling of individual storage devices hard. FiT lead to inefficient under-utilization of prosumager BESS. With a P2P market, these devices can be utilized more efficiently, especially during summer. Shared devices—and their appropriate regulations—might make even better use of diverse demand and generation patterns. Further research should be conducted investigating the impact of penetration and tariff regulations of shared BESS—also since [
5] point out that high investments make installation still economically non-viable for single users. In addition to this, a more diverse set of demand and generation patterns, as well as different technical specifications of the buildings and their influence on market KPIs, might be an interesting research prospect. In line with literature, we find that the appropriate scaling of RES and storage systems [
4], as well as appropriate tariff regimes [
7], are needed in order for P2P markets to work most effectively.
Further investigations should focus on the influence of uncertainty regarding forecasts of loads, RES generation, and potentially prices. In addition, we did not consider game-theoretic aspects, non-cooperative behavior, as well as restrictions on data availability of decentralized decision systems. Incorporating these aspects, algorithms need to become smarter. Traditional solution approaches like MILPs might reach their limits considering the complex intertwined non-linear nature of these problems. Especially, deriving endogenous peer prices based on asset utilization, seasonality of demand and generation, and potentially grid congestion, as well as support regarding investment decisions in such energy communities, are promising research paths. Multi-agent reinforcement learning methods might be a promising supplement in order to bridge the gap between exogenous prices and endogenous learning [
34]. A shift from volumetric tariffs to capacity charges might encourage more risk-averse customers to invest in RES or storage systems and help to stabilize loads [
7].