Predictive Trajectory Control with Online MTPA Calculation and Minimization of the Inner Torque Ripple for Permanent-Magnet Synchronous Machines
Abstract
1. Introduction
1.1. Motivation
1.2. Preliminary Work
1.3. Outline of the Paper
2. Machine Model
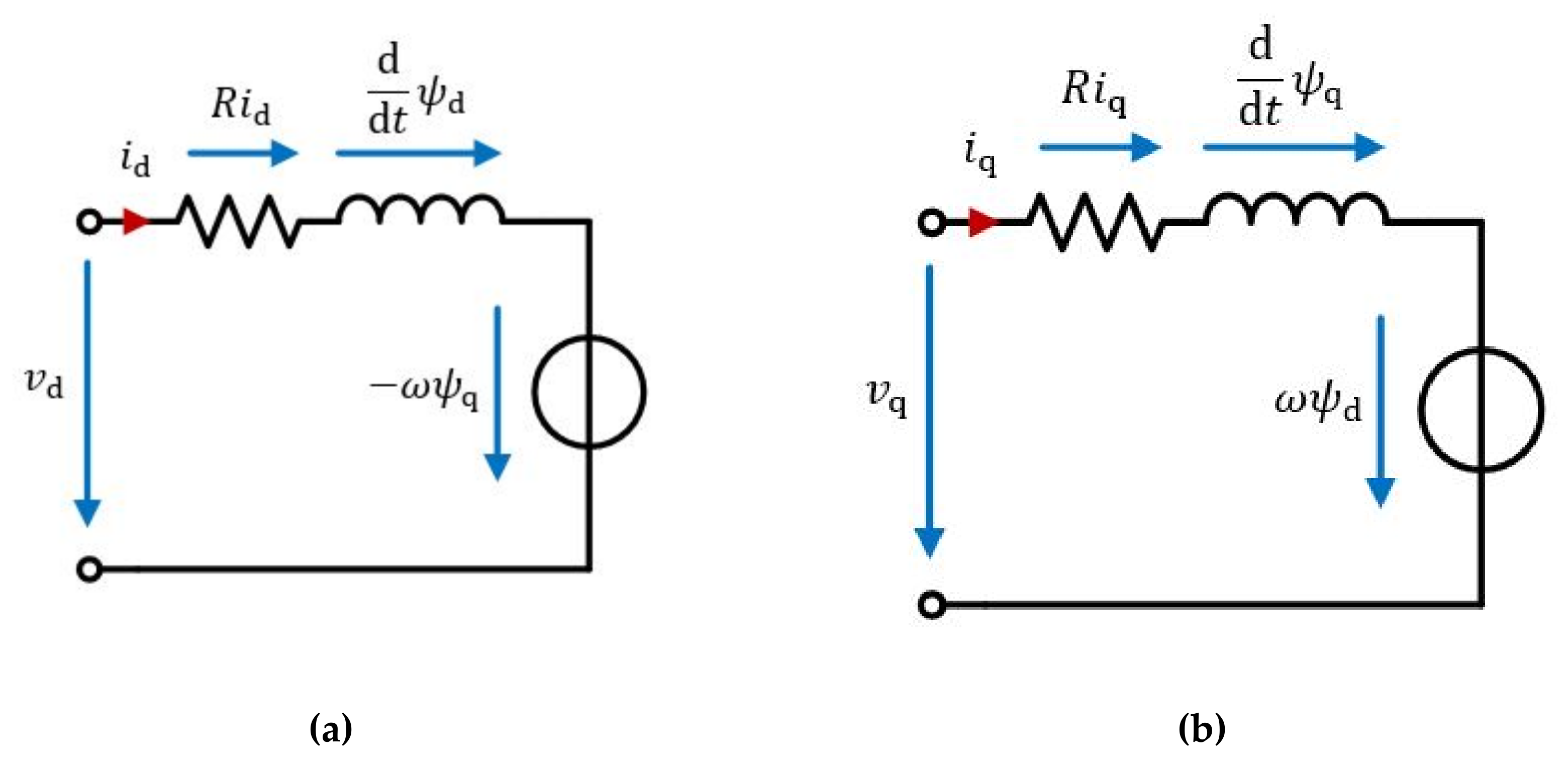
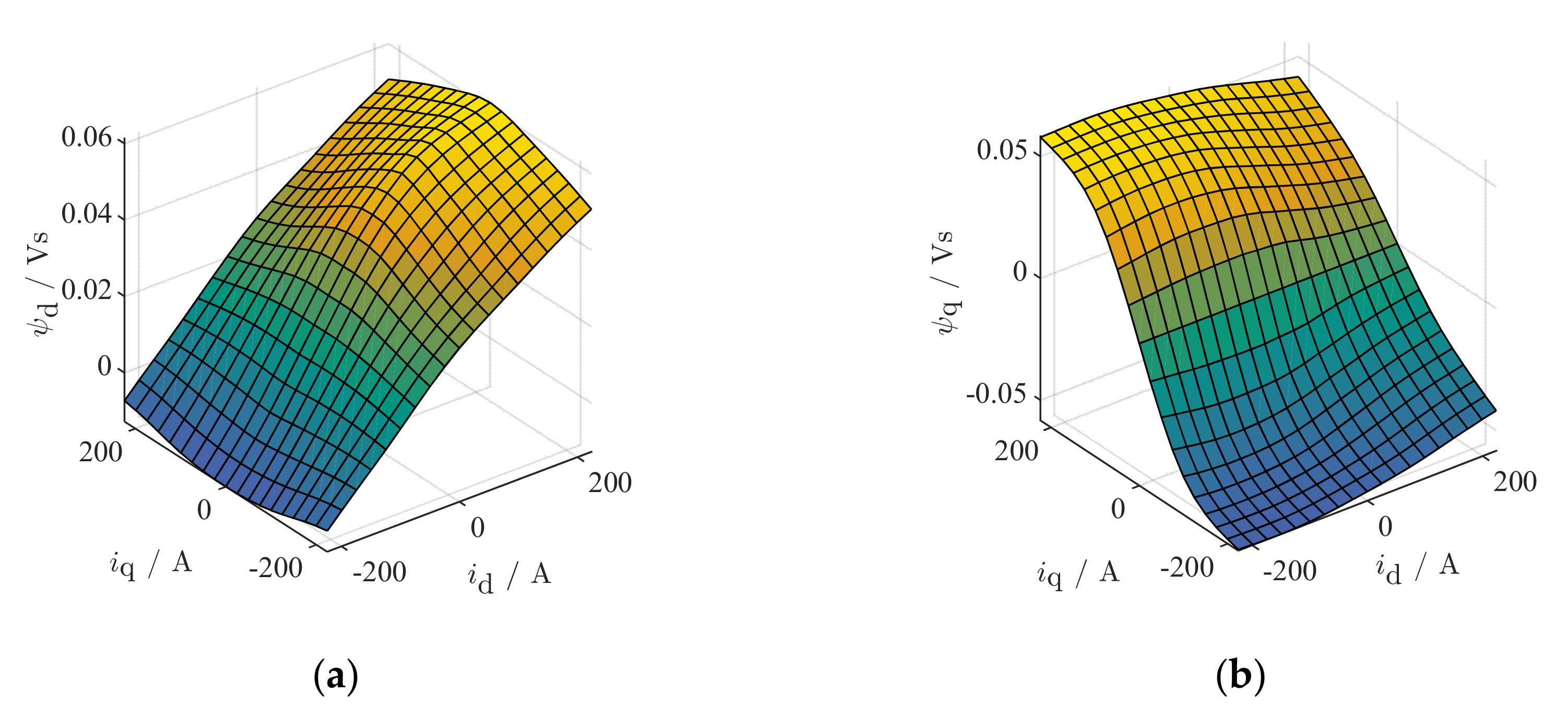
2.1. Permanent Magnet Synchonous Machine Model
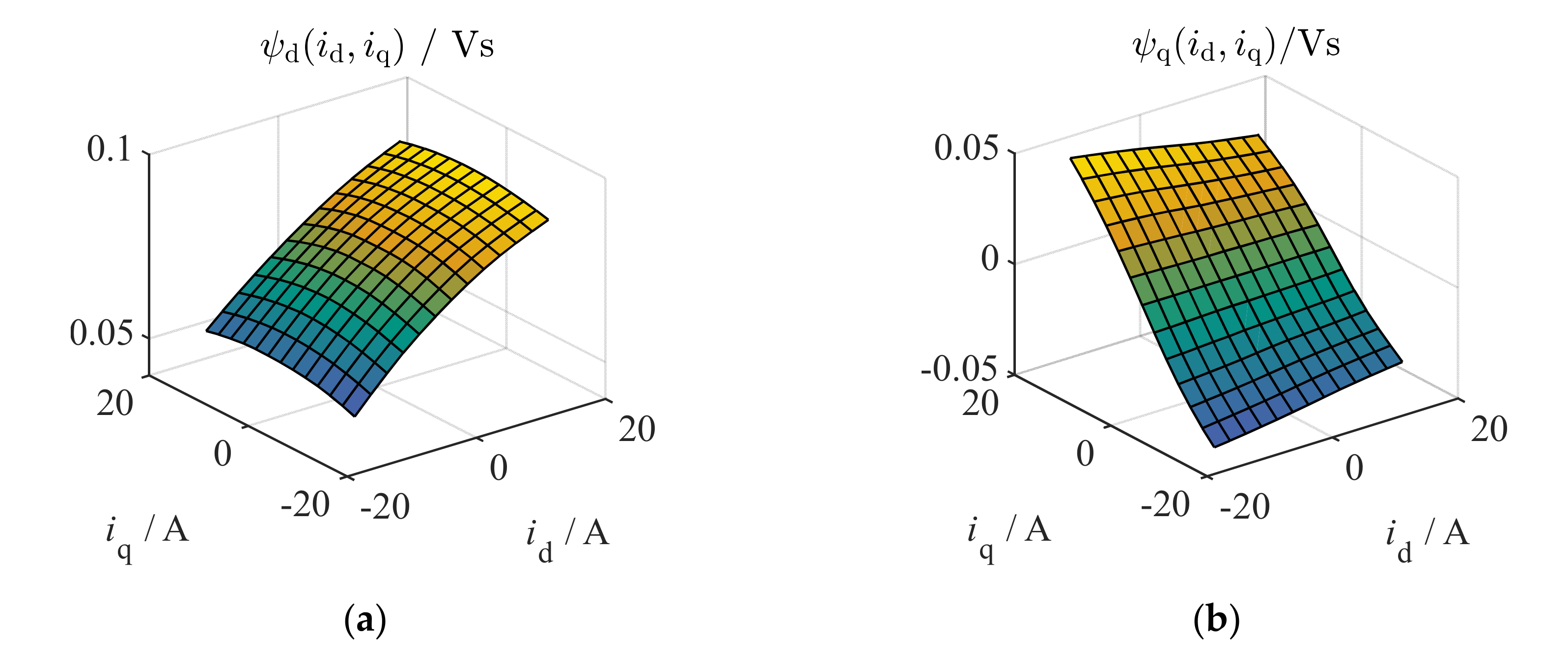
2.2. Parameter Identification
2.3. Time-Discrete Model Equations
2.4. Inverter- and Iron-Losses
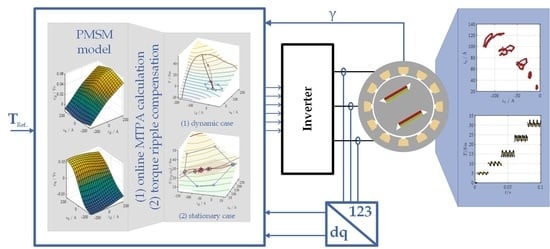
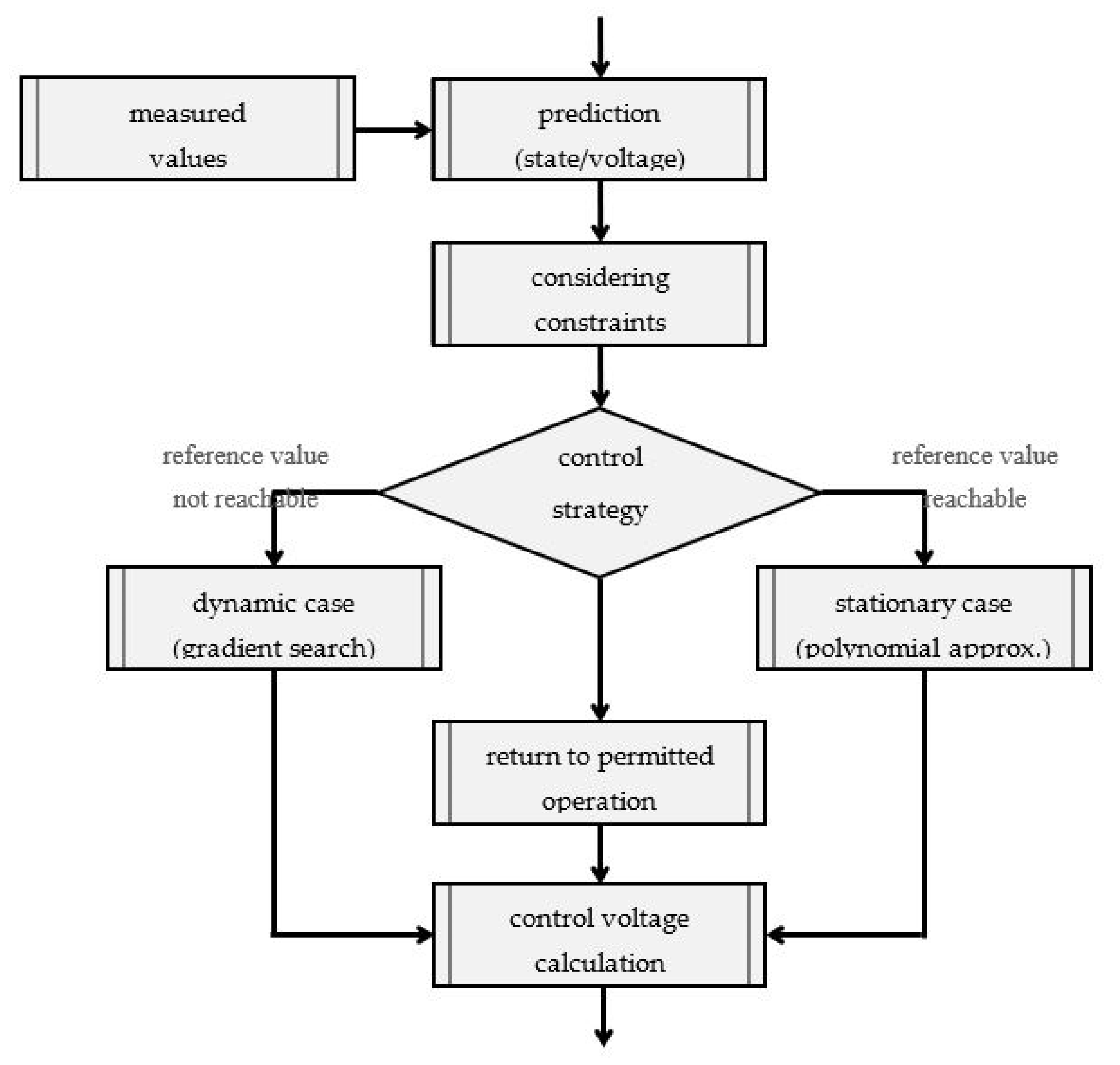
3. Control Algorithm
3.1. Simulation Environment
3.2. Basic Principle of the Predictive Current Control
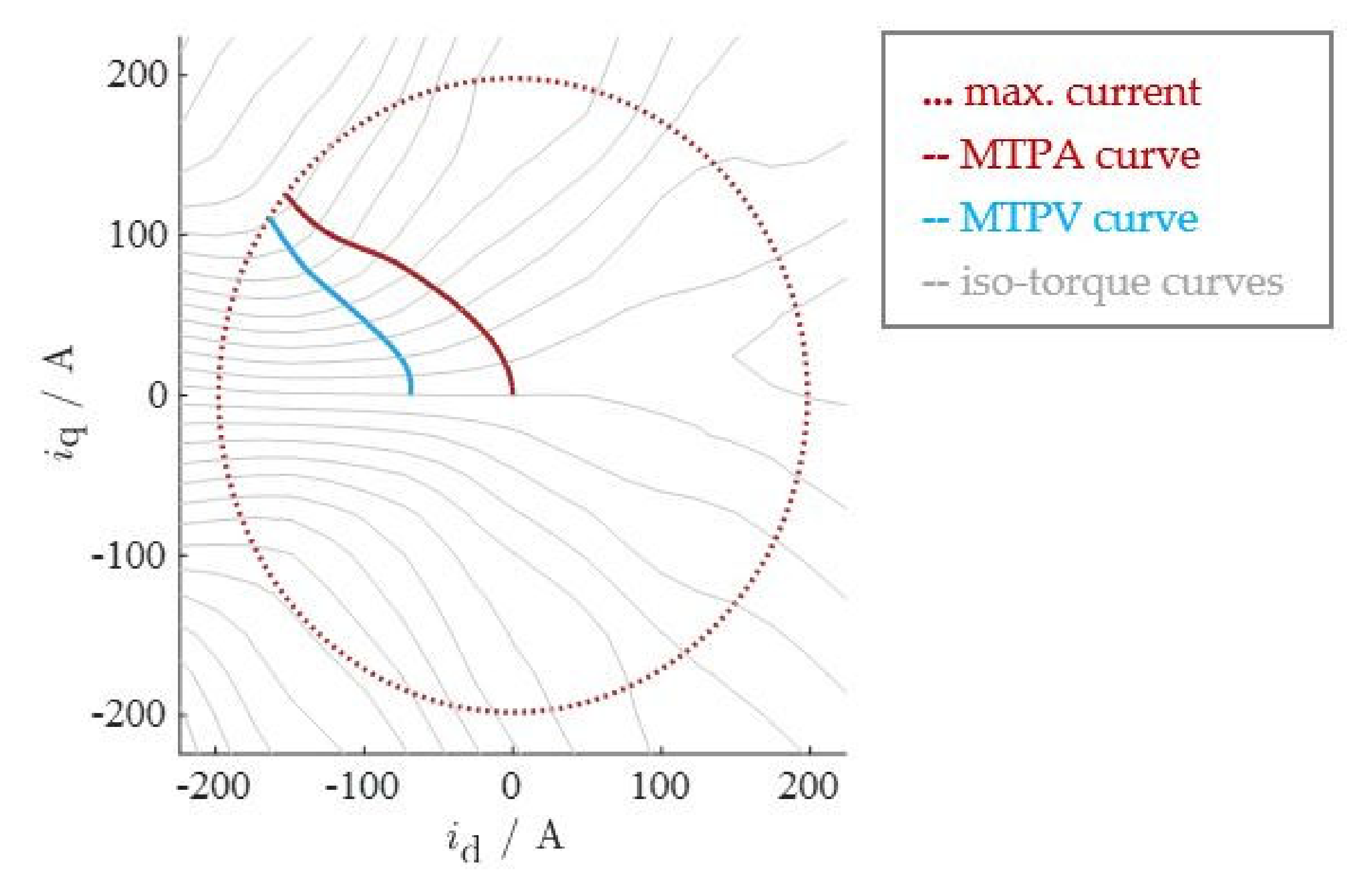
3.2.1. Operation Area Constraints
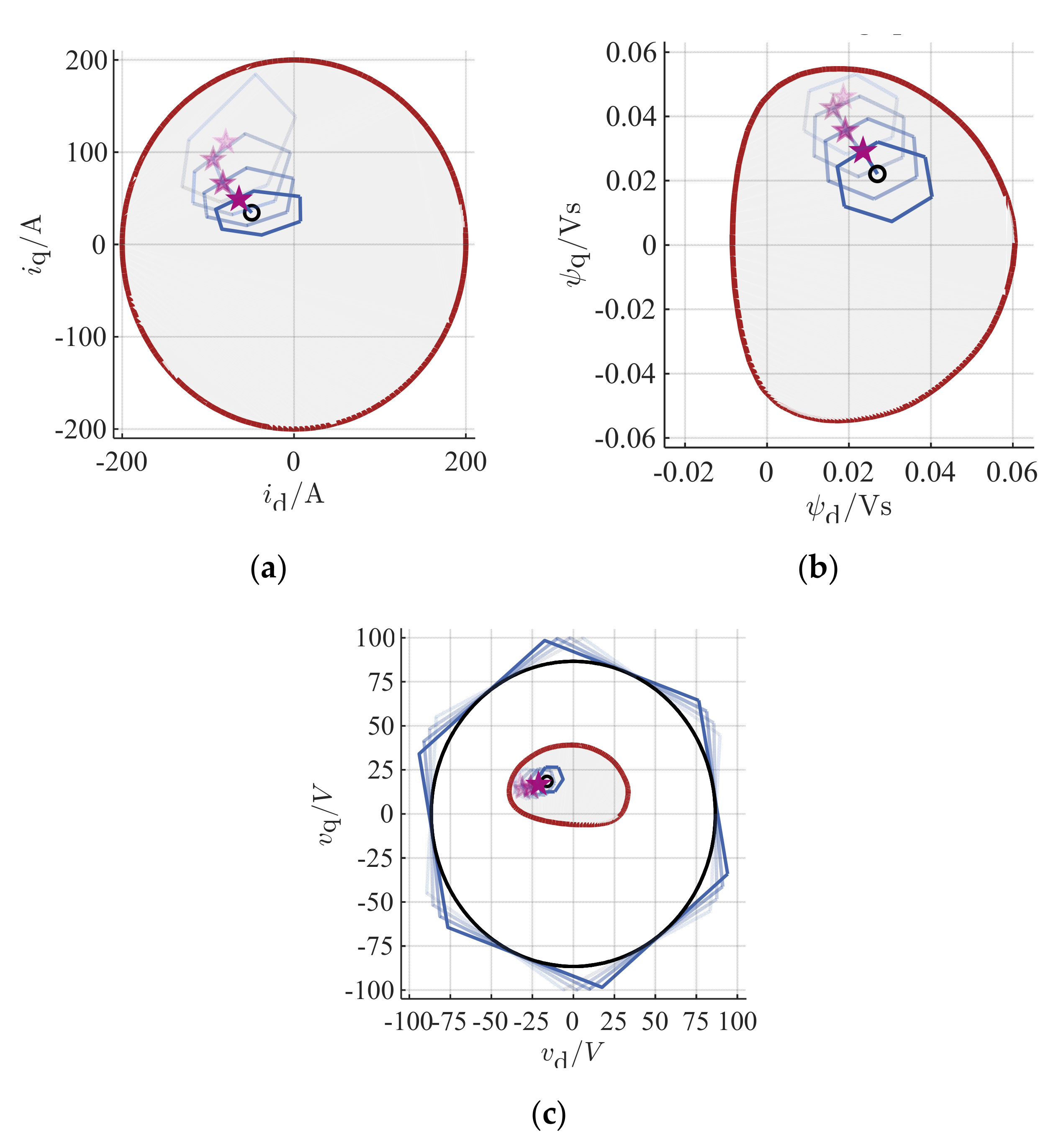
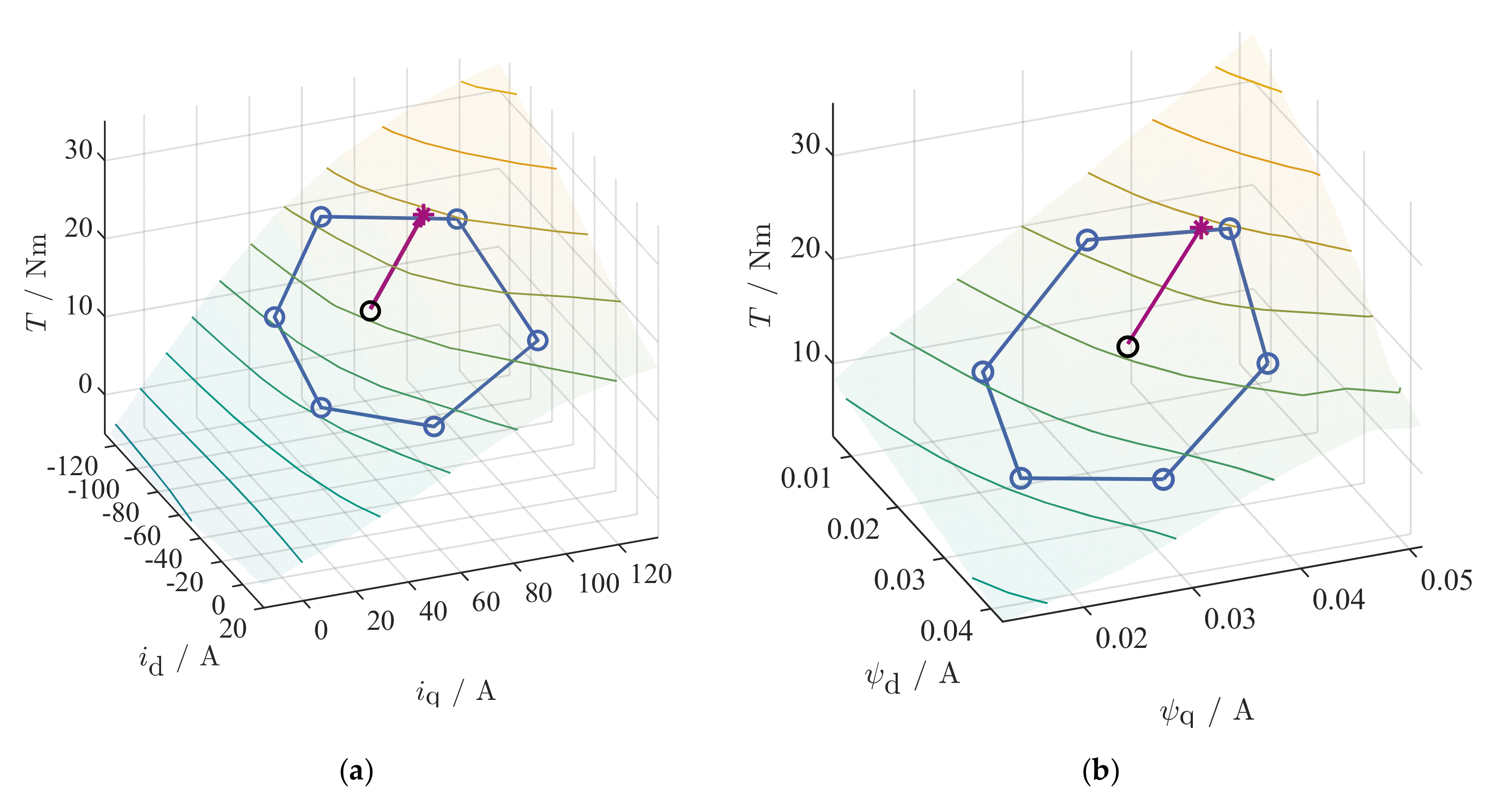
3.2.2. Current-, Flux-Linkage-, and Voltage-Planes
3.2.3. Timing of the Digital Control
3.2.4. Prediction of the Reachable Operational Area
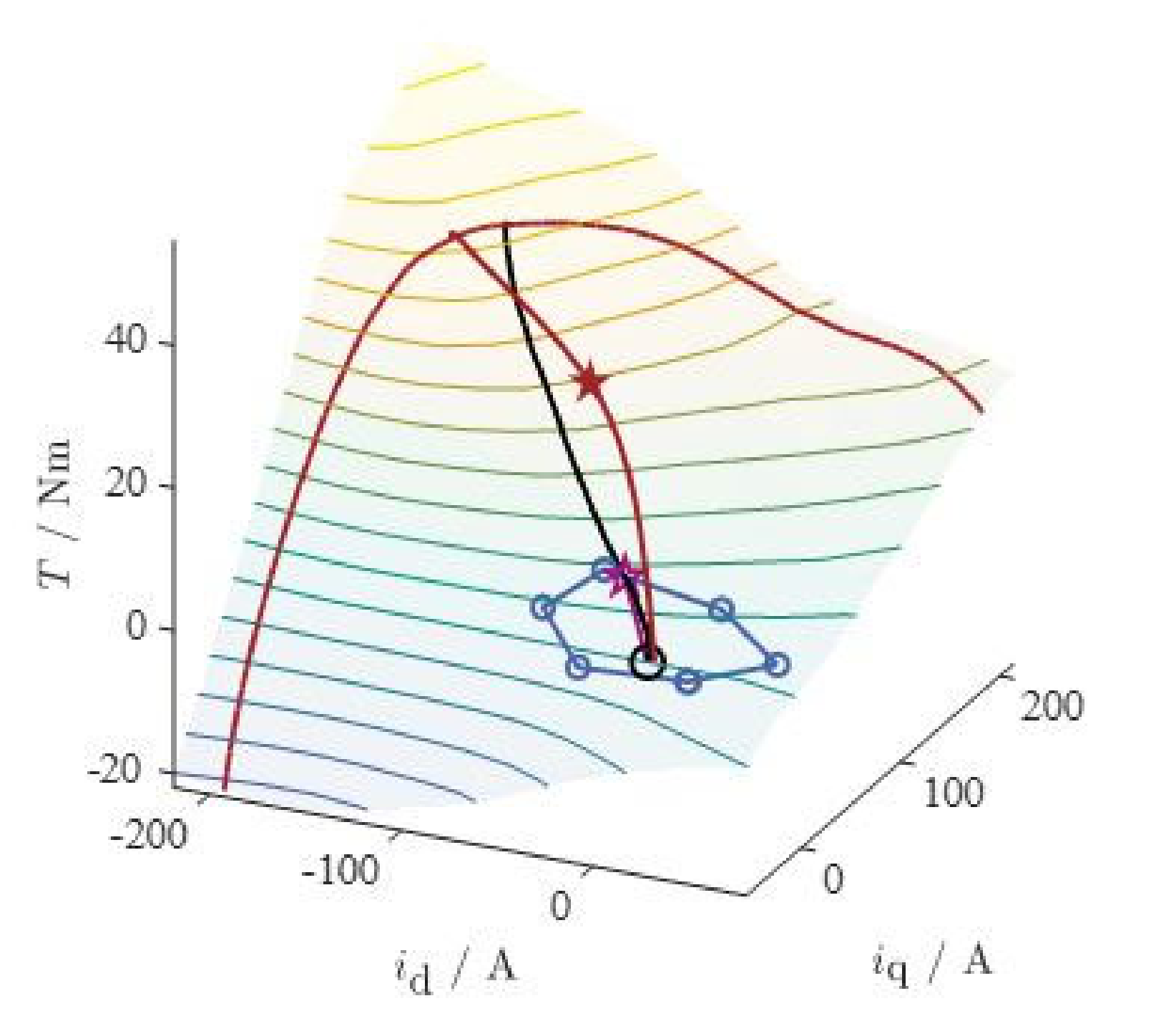
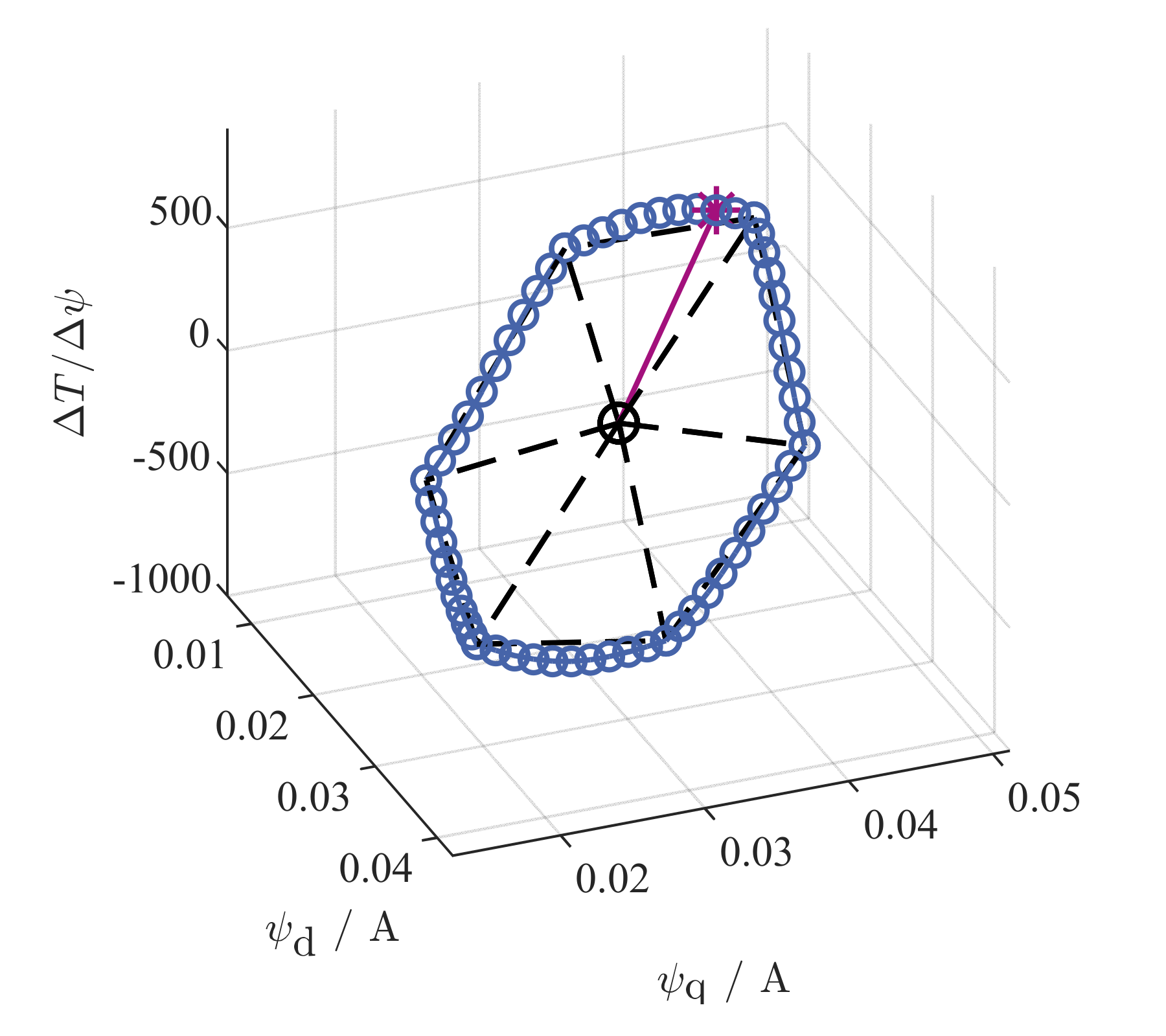
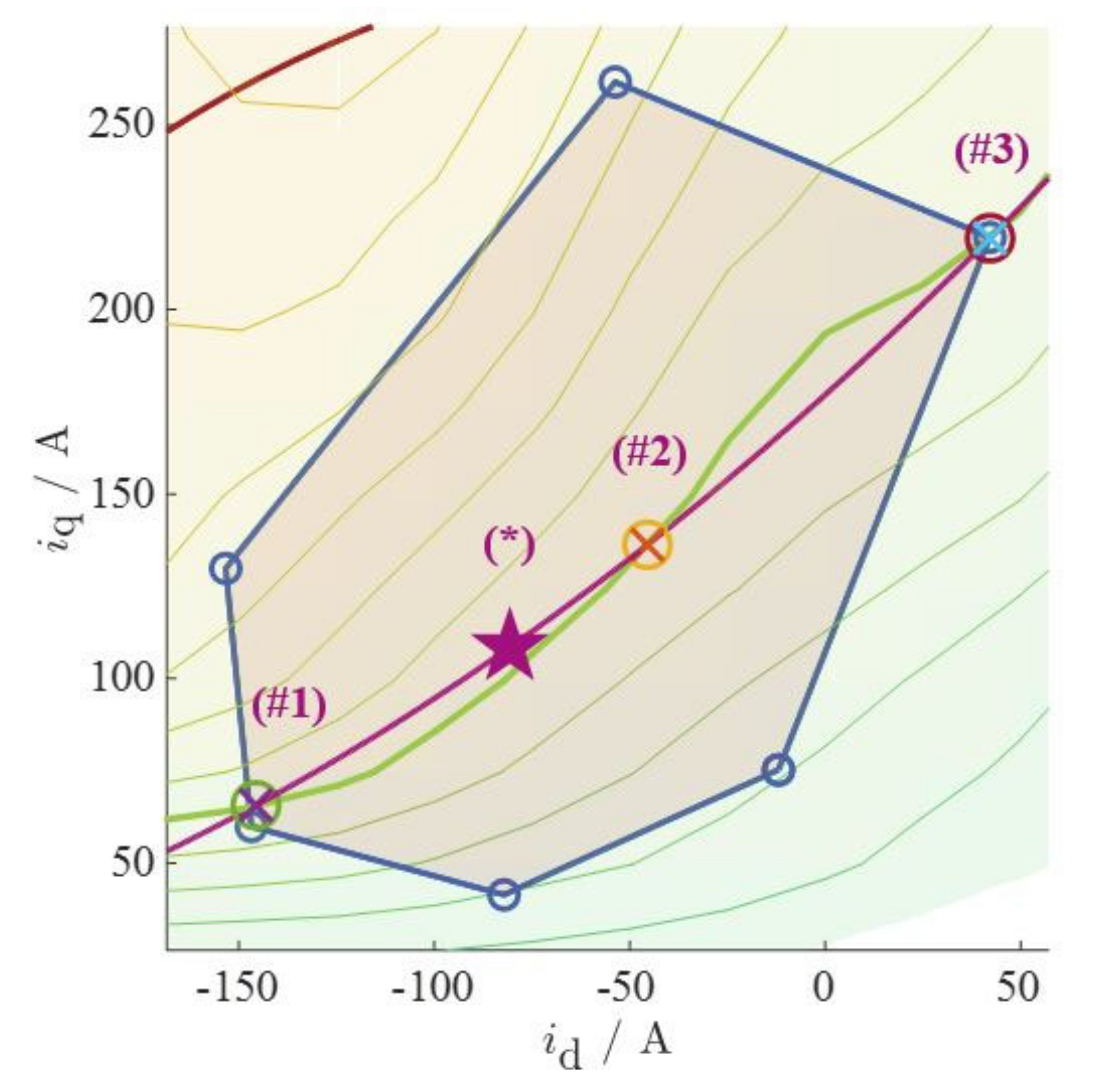
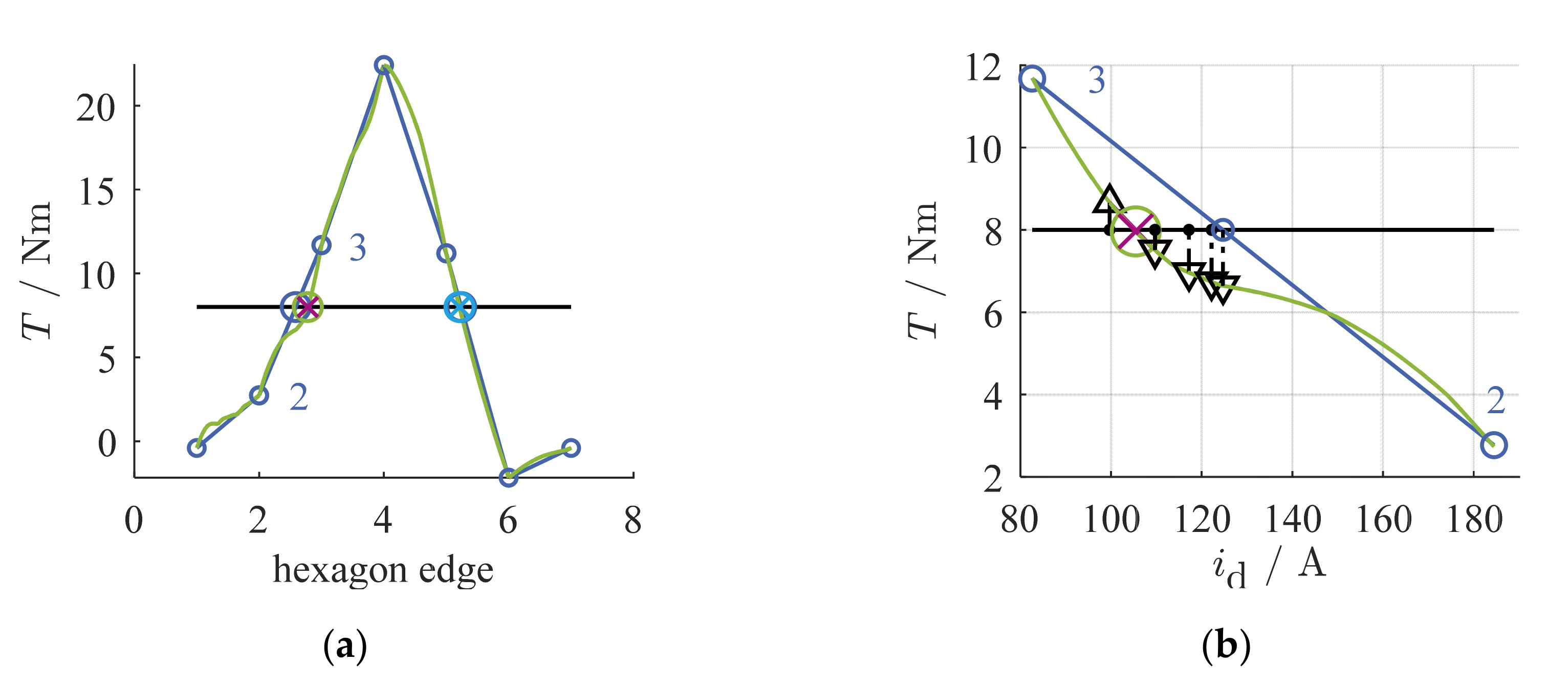
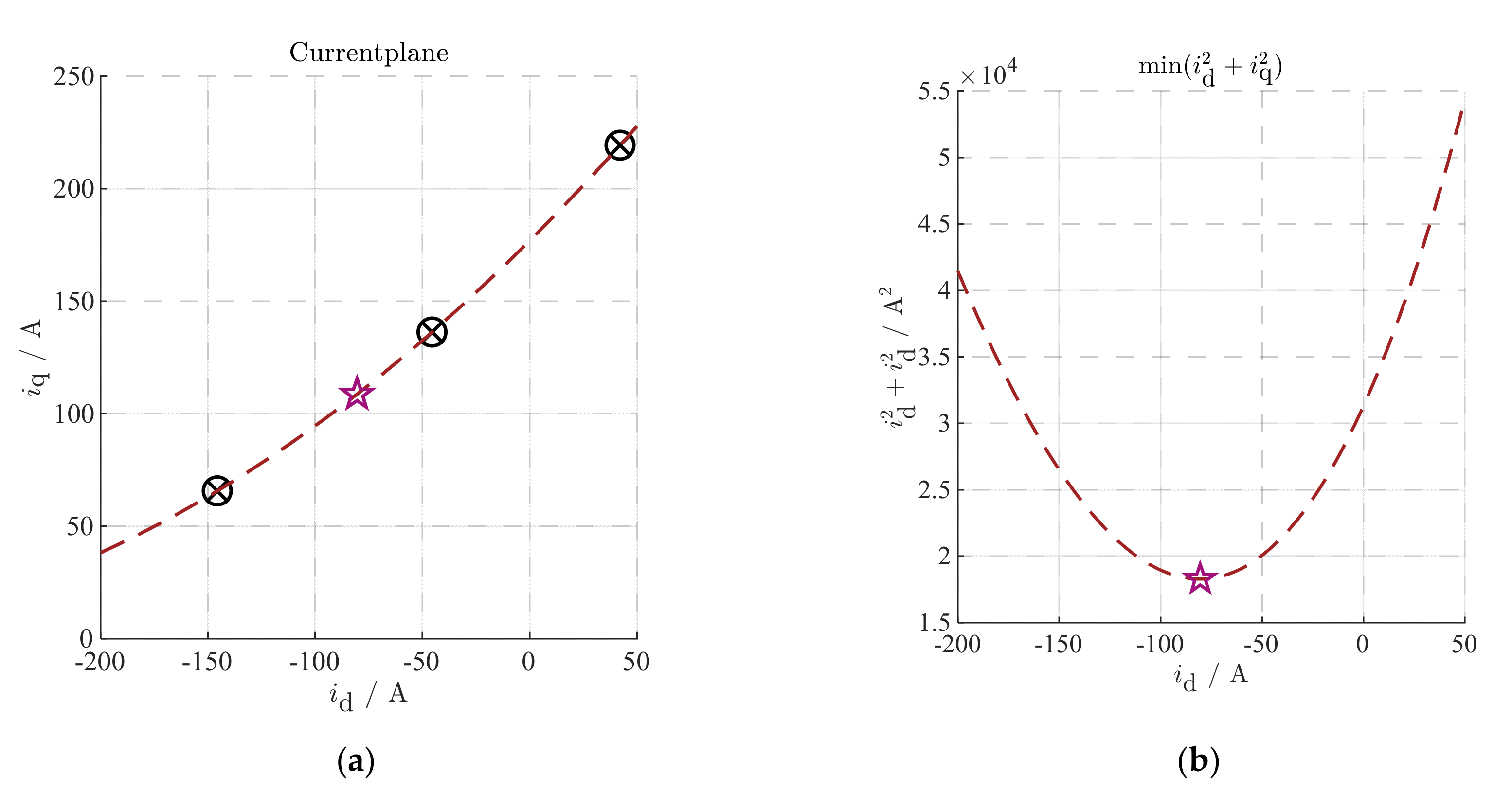
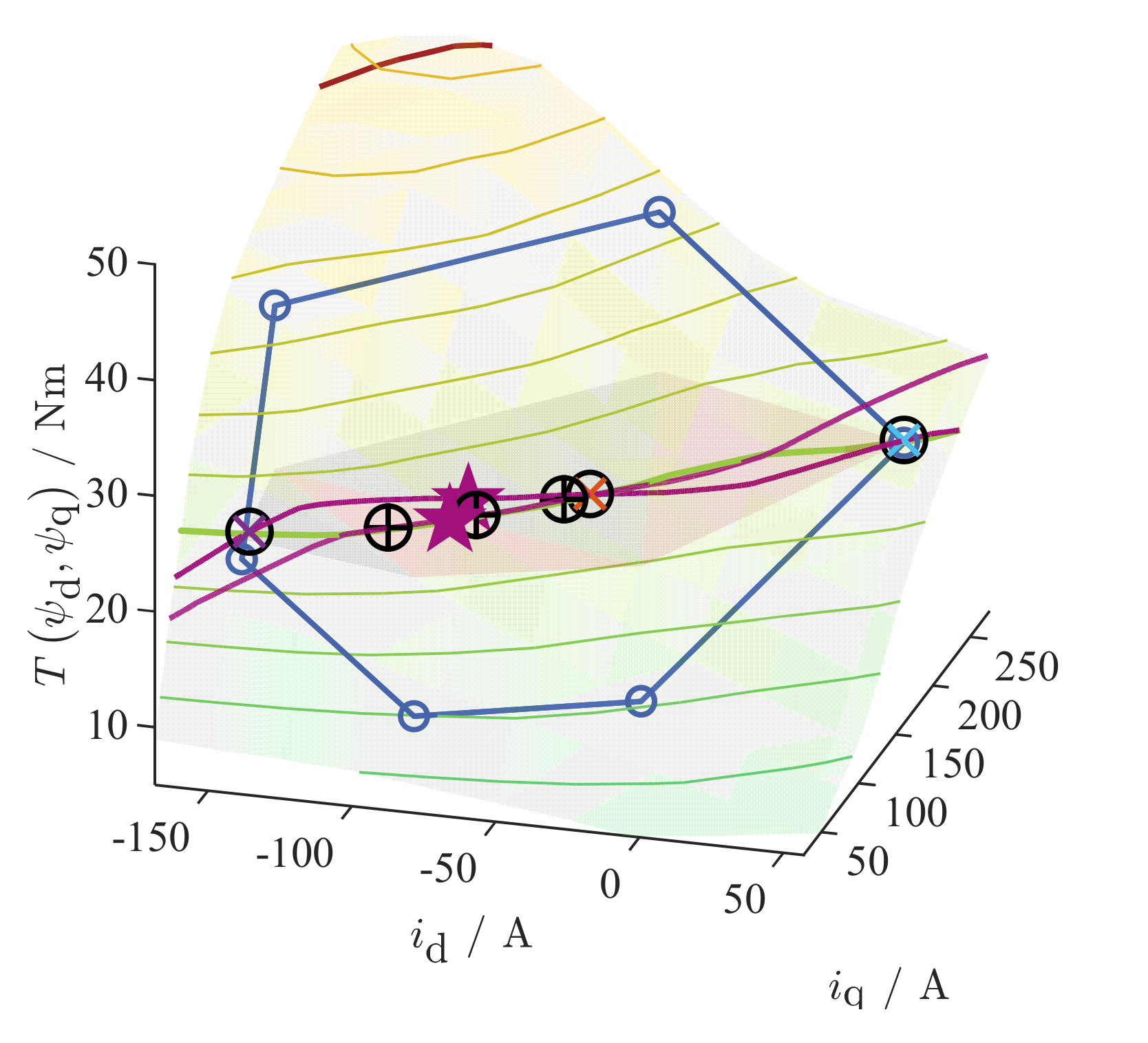
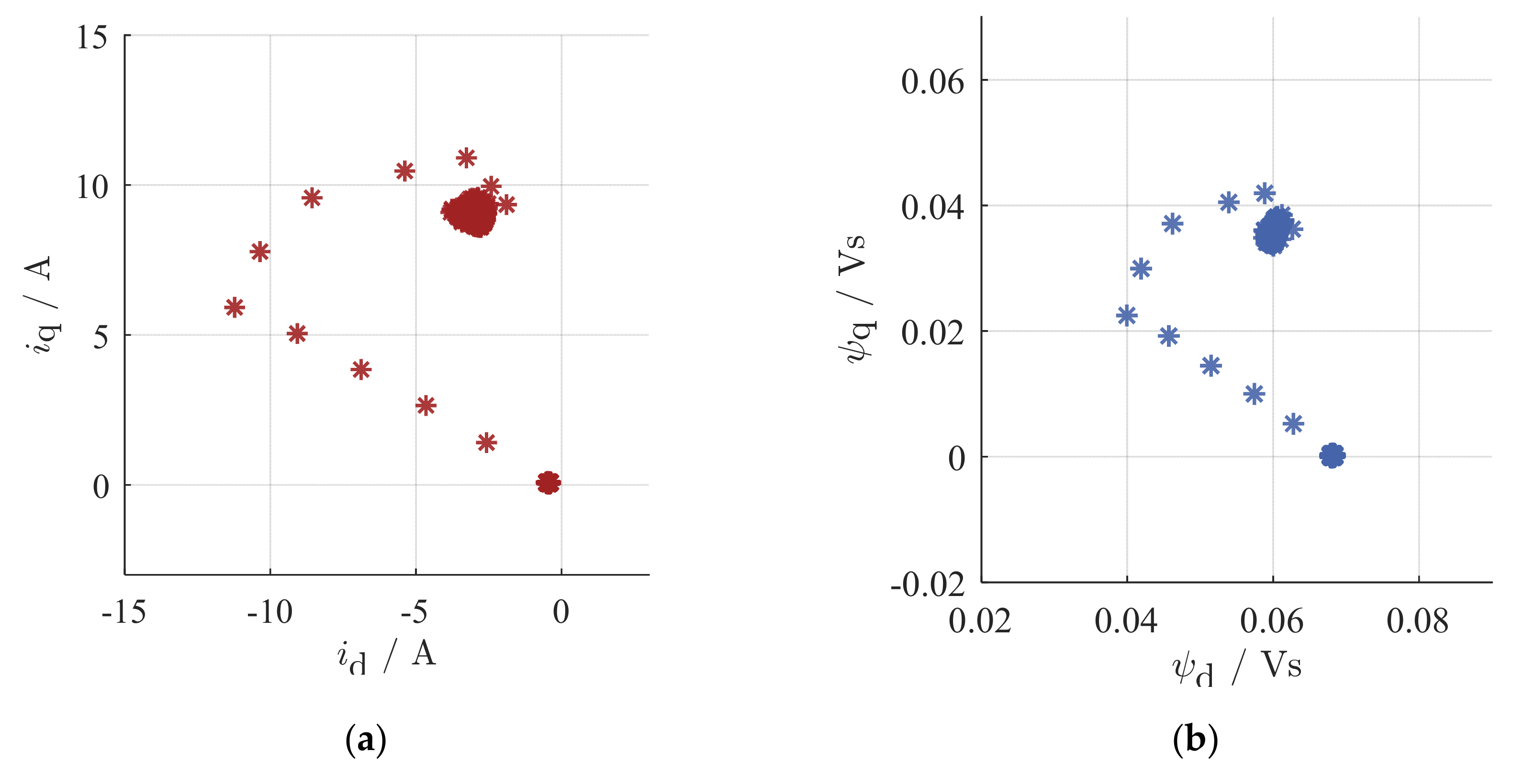
3.3. Online Torque Reference Calculation and Control
3.3.1. Dynamic Operation
3.3.2. Stationary Operation
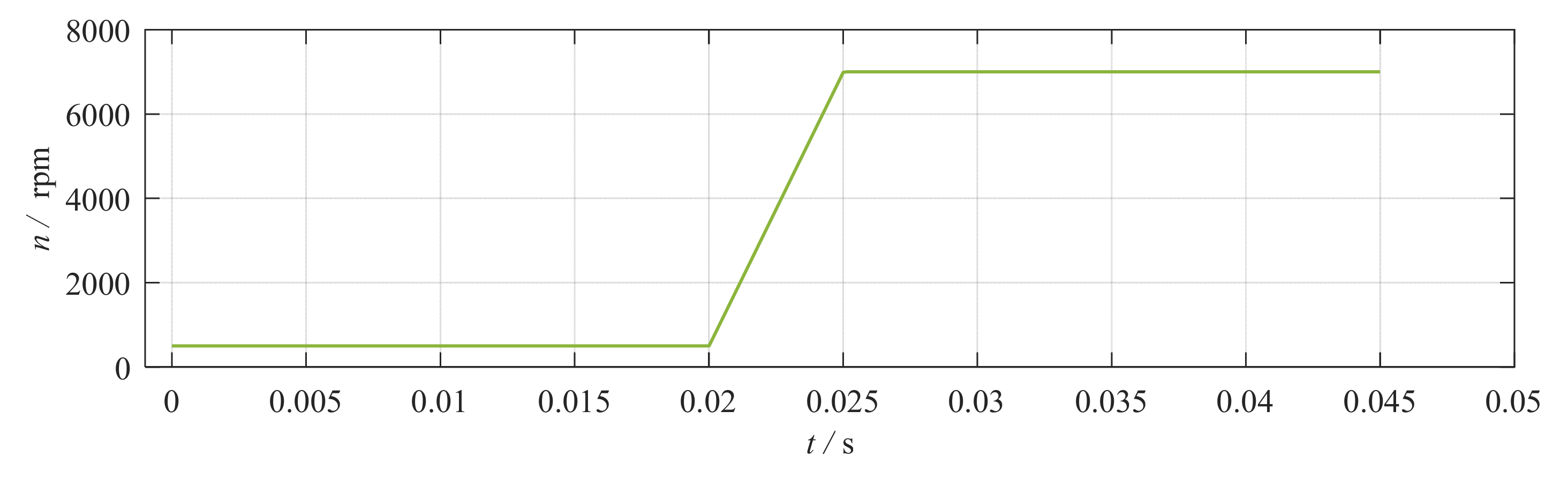
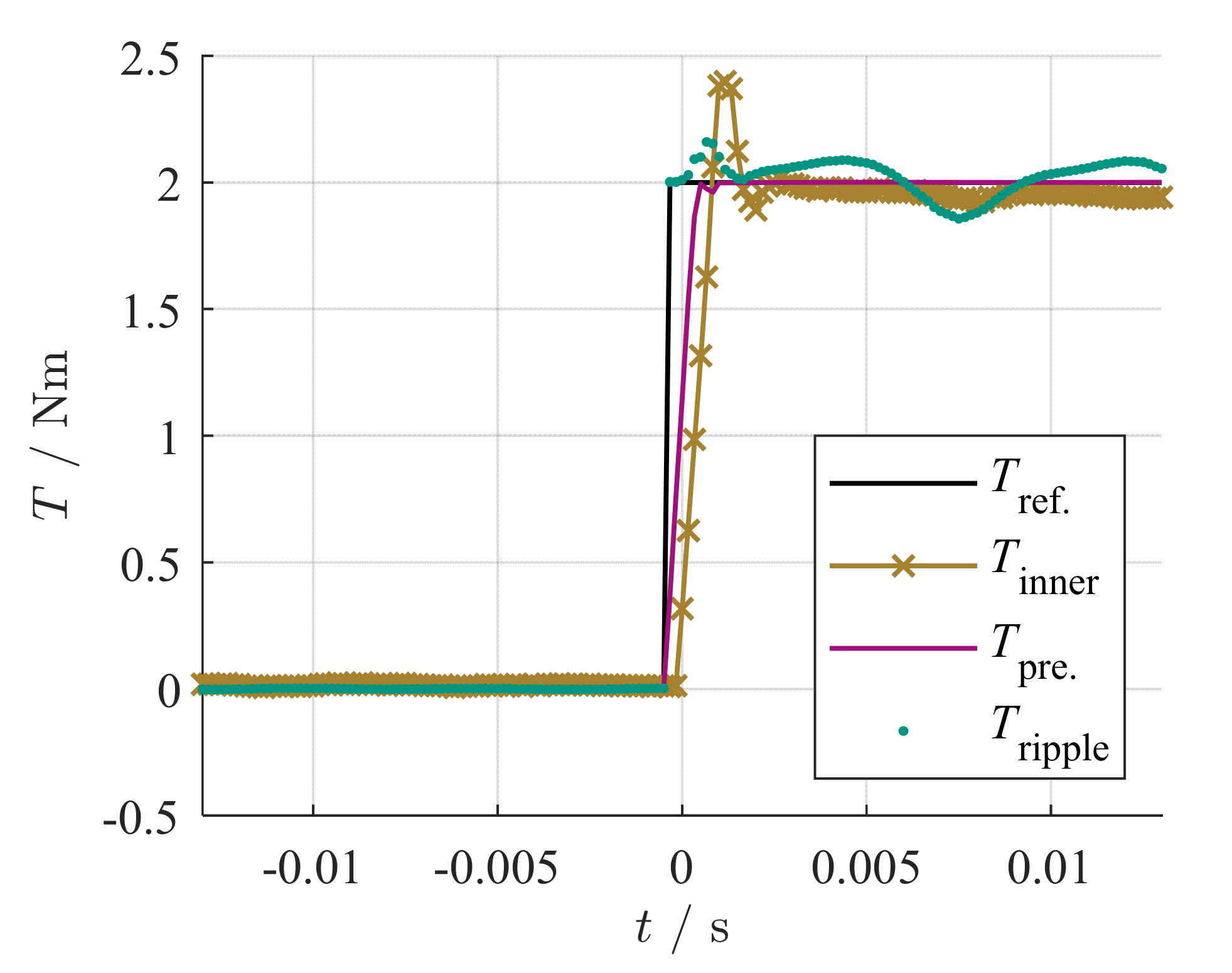
3.4. Simulation Results
4. Test-Setup
4.1. Device-Under-Test
4.2. Test-Bench Setup
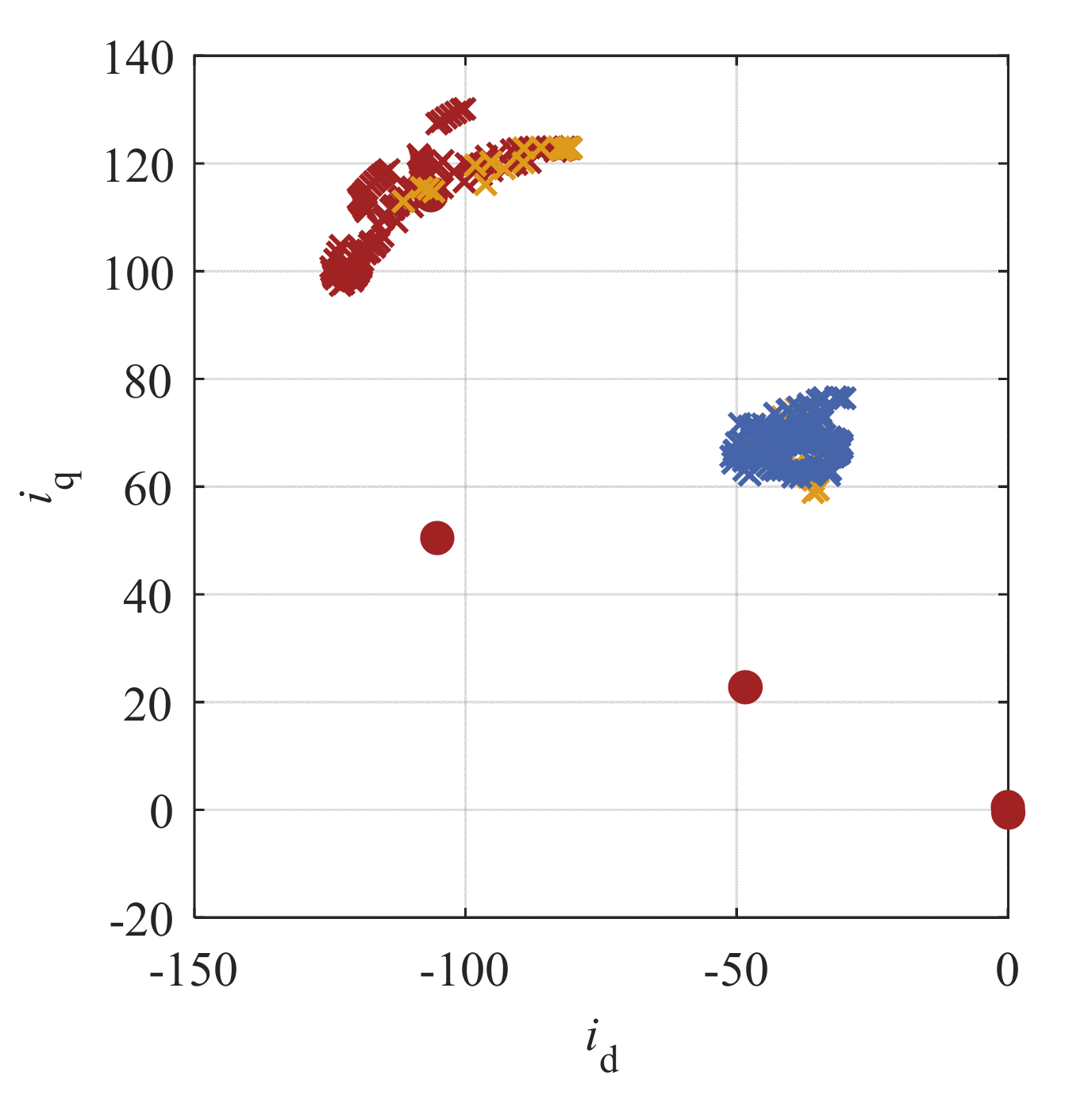
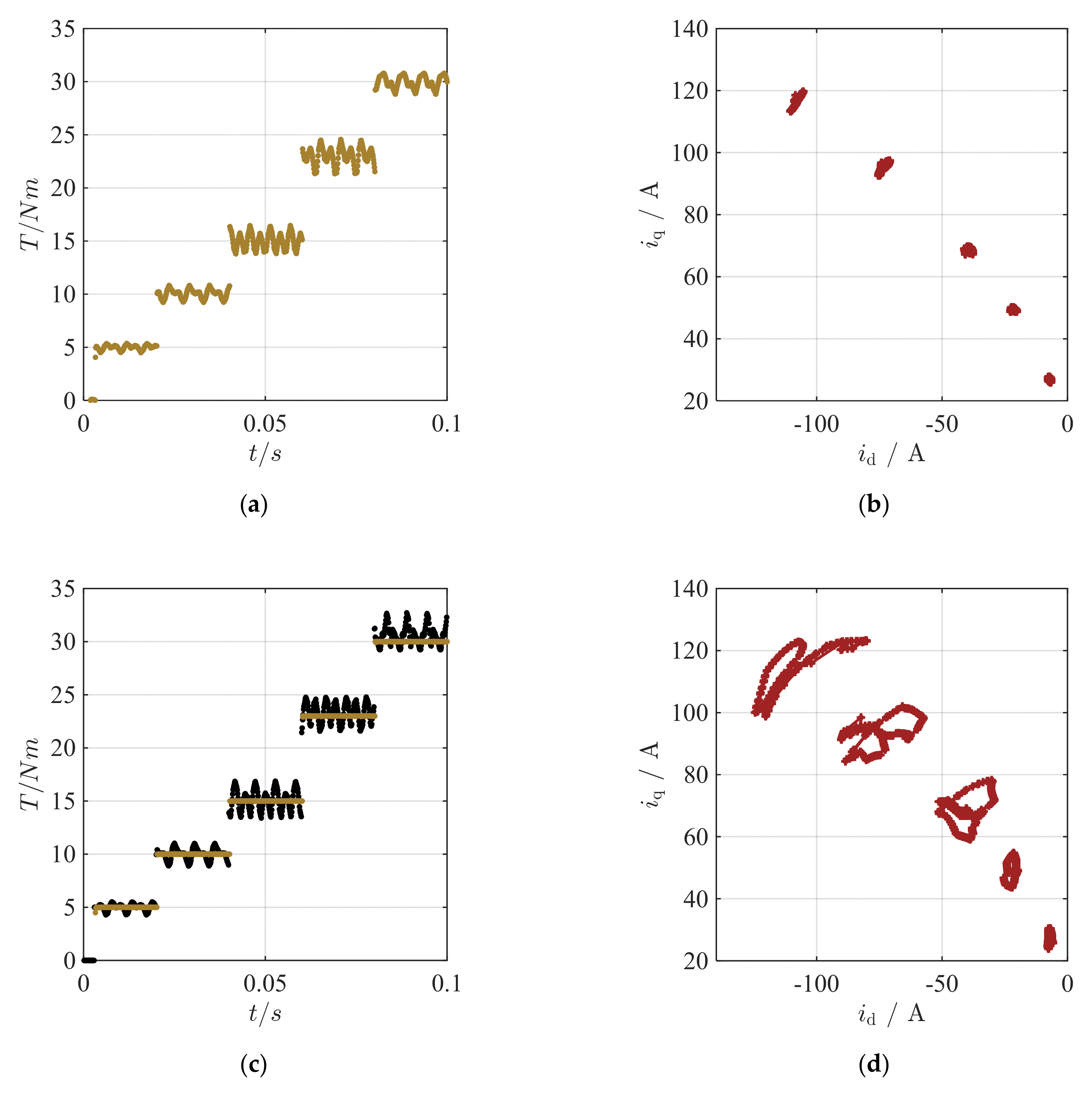
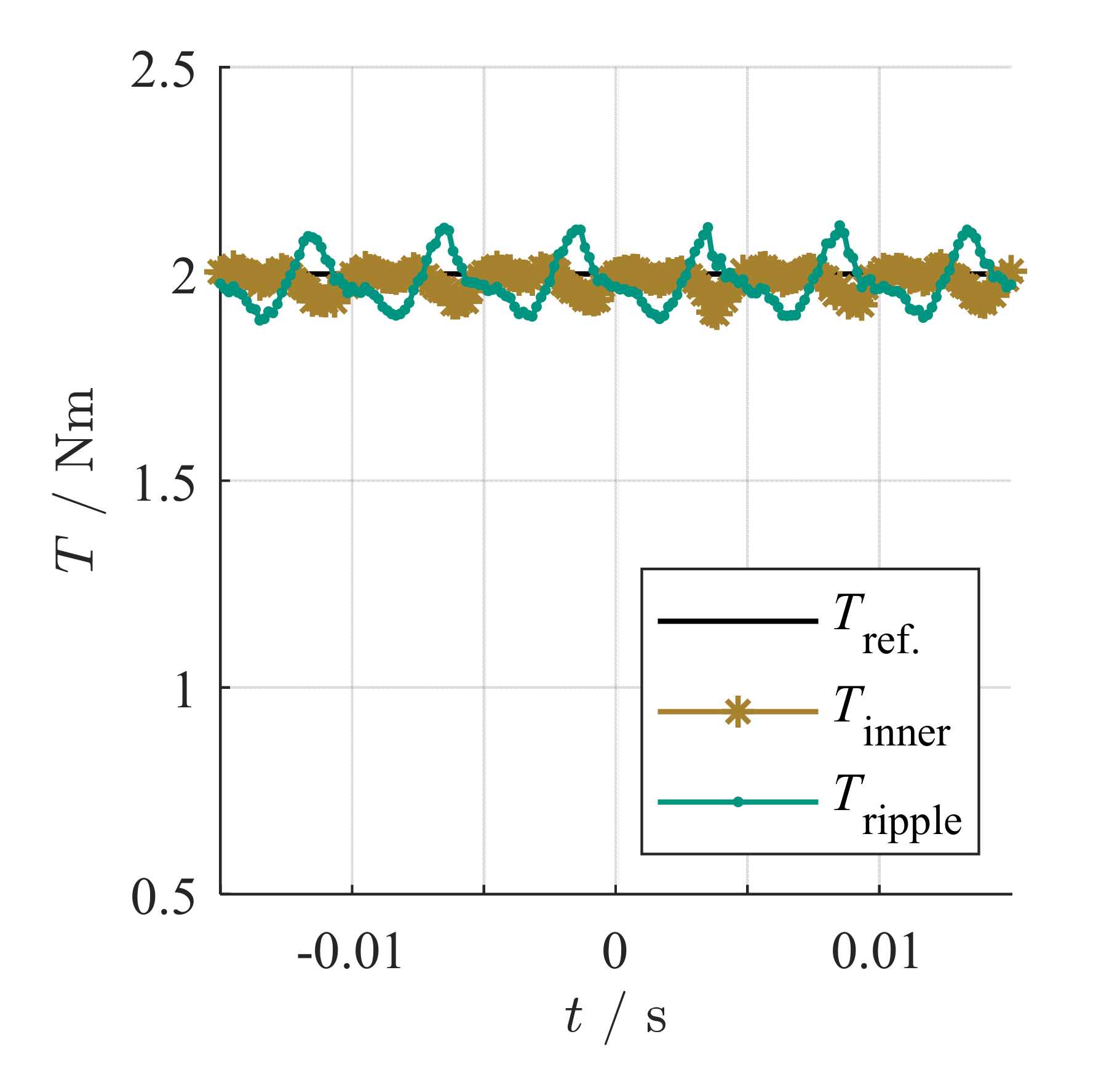
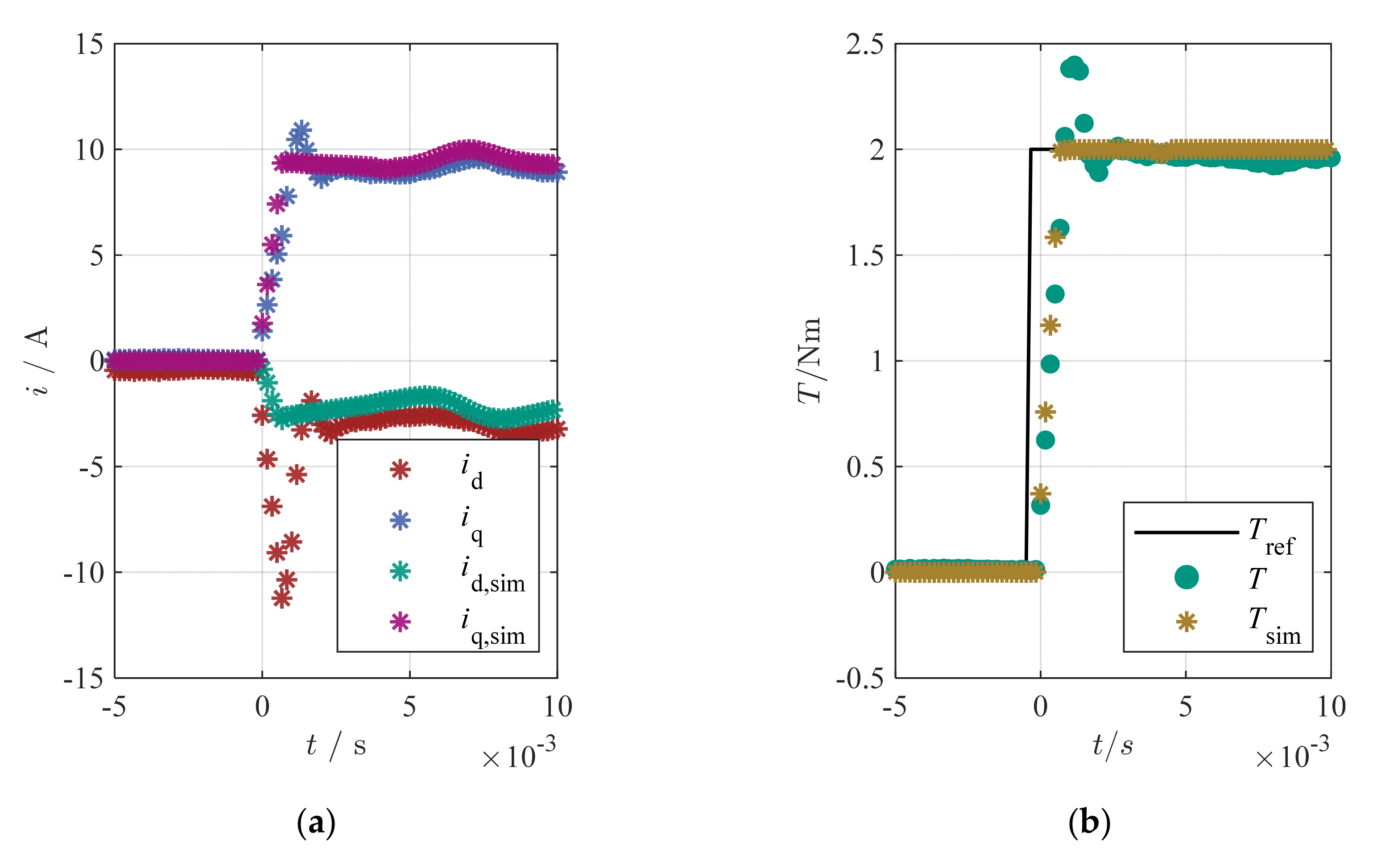
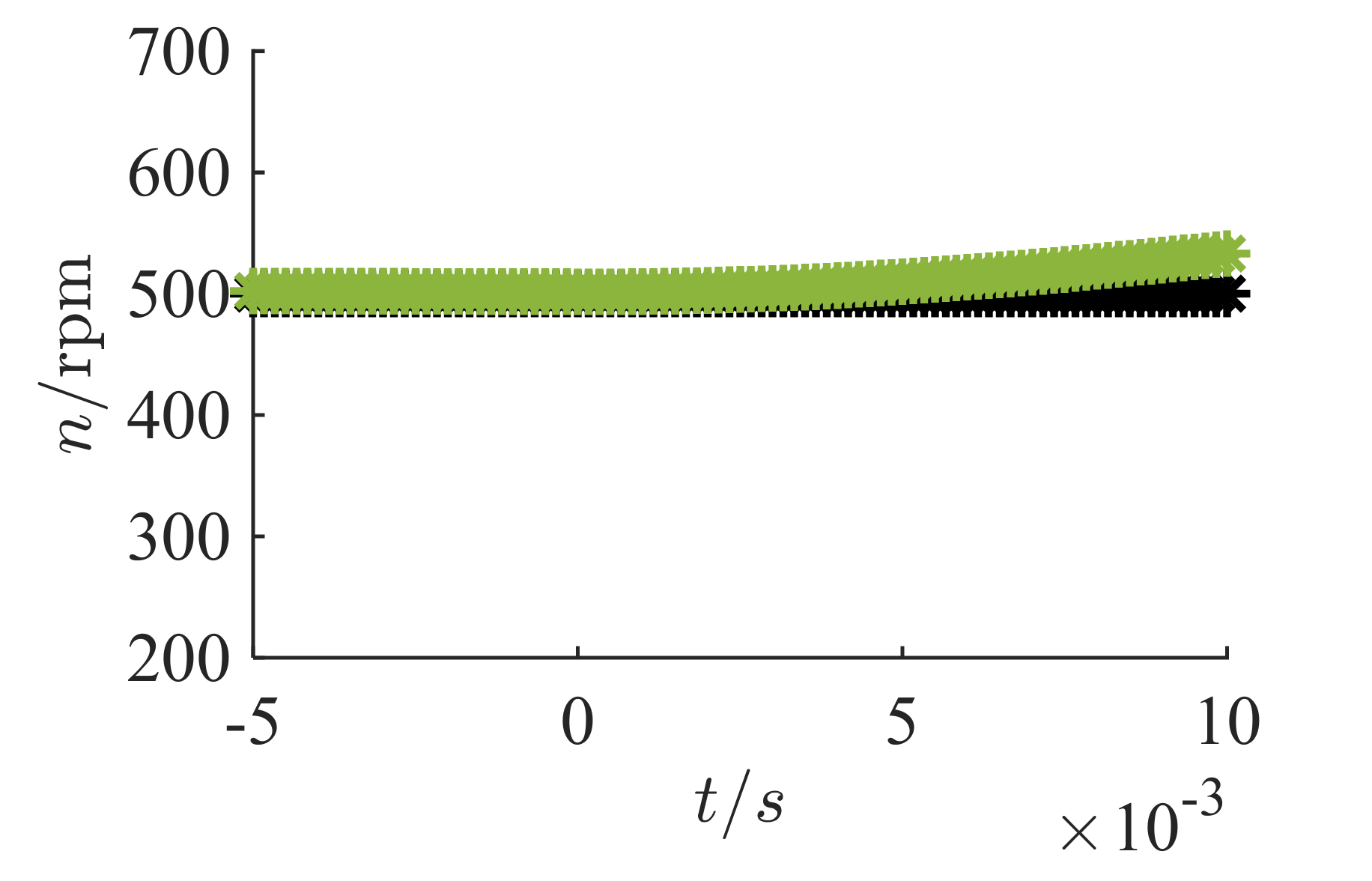
5. Measurement Results
Test-Bench Measurement
6. Discussion and Conclusions
6.1. Parameteridentification and Modelling
6.2. Introduced Control Algorithm
6.3. Results
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Han, Z.; Liu, J.; Yang, W.; Pinhal, D.B.; Reiland, N.; Gerling, D. Improved Online Maximum-Torque-Per-Ampere Algorithm for Speed Controlled Interior Permanent Magnet Synchronous Machine. IEEE Trans. Ind. Electron. 2020, 67, 3398–3408. [Google Scholar] [CrossRef]
- Tinazzi, F.; Bolognani, S.; Calligaro, S.; Kumar, P.; Petrella, R.; Zigliotto, M. Classification and review of MTPA algorithms for synchronous reluctance and interior permanent magnet motor drives. In Proceedings of the 2019 21st European Conference on Power Electronics and Applications (EPE ’19 ECCE Europe), Genova, Italy, 3–5 September 2019; pp. 1–10. [Google Scholar]
- Wang, J.; Huang, X.; Yu, D.; Chen, Y.; Zhang, Y.; Niu, F.; Fang, Y.; Cao, W.; Zhang, H. An Accurate Virtual Signal Injection Control of MTPA for an IPMSM With Fast Dynamic Response. IEEE Trans. Power Electron. 2018, 33, 7916–7926. [Google Scholar] [CrossRef]
- Lee, G.-H.; Kim, S.-I.; Hong, J.-P.; Bahn, J.-H. Torque Ripple Reduction of Interior Permanent Magnet Synchronous Motor Using Harmonic Injected Current. IEEE Trans. Magn. 2008, 44, 1582–1585. [Google Scholar] [CrossRef]
- Nishio, T.; Ryosuke, Y.; Masahiko, K.; Akatsu, K. A Method of Torque Ripple Reduction by Using Harmonic Current Injection in PMSM. In Proceedings of the 2019 IEEE 4th International Future Energy Electronics Conference (IFEEC), Singapore, 25–28 November 2019; pp. 1–5. [Google Scholar]
- Li, S.; Han, D.; Sarlioglu, B. Modeling of Interior Permanent Magnet Machine Considering Saturation, Cross Coupling, Spatial Harmonics, and Temperature Effects. IEEE Trans. Transp. Electrific. 2017, 3, 682–693. [Google Scholar] [CrossRef]
- Cho, H.-J.; Kwon, Y.-C.; Sul, S.-K. Optimal Current Trajectory Control of IPMSM for Minimized Torque Ripple. In Proceedings of the 2019 IEEE Transportation Electrification Conference and Expo (ITEC), Detroit, MI, USA, 19–21 June 2019; pp. 1–6. [Google Scholar]
- Farshadnia, M.; Cheema, M.A.M.; Dutta, R.; Fletcher, J.E.; Rahman, M.F. Detailed Analytical Modeling of Fractional-Slot Concentrated-Wound Interior Permanent Magnet Machines for Prediction of Torque Ripple. IEEE Trans. Ind. Applicat. 2017, 53, 5272–5283. [Google Scholar] [CrossRef]
- Richter, J.; Doppelbauer, M. Predictive Trajectory Control of Permanent-Magnet Synchronous Machines with Nonlinear Magnetics. IEEE Trans. Ind. Electron. 2016, 63, 3915–3924. [Google Scholar] [CrossRef]
- Krause, P.C.; Wasynczuk, O.; Sudhoff, S.D. Analysis of Electric Machinery and Drive Systems; Wiley-Interscience: Hoboken, NJ, USA; IEEE Press: New York, NY, USA, 2002. [Google Scholar]
- Pinto, D.E.; Pop, A.-C.; Kempkes, J.; Gyselinck, J. Dq0-modeling of interior permanent-magnet synchronous machines for high-fidelity model order reduction. In Proceedings of the 2017 International Conference on Optimization of Electrical and Electronic Equipment (OPTIM) & 2017 Intl Aegean Conference on Electrical Machines and Power Electronics (ACEMP), Brasov, Romania, 25–27 May 2017; pp. 357–363. [Google Scholar]
- Štumberge0r, G.; Štumberger, B.; Marčič, T. Magnetically Nonlinear Dynamic Models of Synchronous Machines and Experimental Methods for Determining their Parameters. Energies 2019, 12, 3519. [Google Scholar] [CrossRef]
- Richter, J.; Doppelbauer, M. Control and mitigation of current harmonics in inverter-fed permanent magnet synchronous machines with non-linear magnetics. IET Power Electron. 2016, 9, 2019–2026. [Google Scholar] [CrossRef]
- Decker, S.; Rollbühler, C.; Rehm, F.; Brodatzki, M.; Oerder, A.; Liske, A.; Kolb, J.; Braun, M. Dq0-modelling and parametrization approaches for small delta connected permanent magnet synchronous machines. In Proceedings of the 2020 International Conference on Power Electronics, Machines and Drives (PEMD 2020), Nottingham, UK, 15–17 December 2020. [Google Scholar]
- Decker, S.; Foitzik, S.; Rehm, F.; Brodatzki, M.; Rollbühler, C.; Kolb, J.; Braun, M. DQ0 Modelling and Parameterization of small Delta connected PM Synchronous Machines. In Proceedings of the 2020 International Conference on Electrical Machines (ICEM), Göteborg, Sweden, 23–26 August 2020. [Google Scholar]
- Richter, J.; Dollinger, A.; Doppelbauer, M. Iron loss and parameter measurement of permanent magnet synchronous machines. In Proceedings of the 2014 International Conference on Electrical Machines (ICEM), Berlin, Germany, 2–5 September 2014; pp. 1635–1641. [Google Scholar]
- Richter, J.; Winzer, P.; Doppelbauer, M. Einsatz Virtueller Prototypen bei der Akausalen Modellierung und Simulation von Permanenterregten Synchronmaschinen. Application of Virtual Prototypes of Permanent Magnet Synchronous Machines by Acausal Modeling and Simulation; VDE-Verlag: Berlin, Germany, 2013. [Google Scholar]
- Axtmann, C.; Boxriker, M.; Braun, M. A custom, high-performance real time measurement and control system for arbitrary power electronic systems in academic research and education. In Proceedings of the 2016 18th European Conference on Power Electronics and Applications (EPE’16 ECCE Europe), Karlsruhe, Germany, 5–9 September 2016; pp. 1–7. [Google Scholar]
- Schwendemann, R.; Decker, S.; Hiller, M.; Braun, M. A Modular Converter- and Signal-Processing-Platform for Academic Research in the Field of Power Electronics. In Proceedings of the 2018 International Power Electronics Conference (IPEC-Niigata 2018 -ECCE Asia), Niigata, Japan, 20–24 May 2018; pp. 3074–3080. [Google Scholar]



| Quantities | Symbol | Value |
|---|---|---|
| Maximum voltage | ||
| Maximum current | ||
| Nominal speed | ||
| Nominal torque | ||
| Permanent magnet flux-linkage | ||
| Stator resistance |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Decker, S.; Brodatzki, M.; Bachowsky, B.; Schmitz-Rode, B.; Liske, A.; Braun, M.; Hiller, M. Predictive Trajectory Control with Online MTPA Calculation and Minimization of the Inner Torque Ripple for Permanent-Magnet Synchronous Machines. Energies 2020, 13, 5327. https://doi.org/10.3390/en13205327
Decker S, Brodatzki M, Bachowsky B, Schmitz-Rode B, Liske A, Braun M, Hiller M. Predictive Trajectory Control with Online MTPA Calculation and Minimization of the Inner Torque Ripple for Permanent-Magnet Synchronous Machines. Energies. 2020; 13(20):5327. https://doi.org/10.3390/en13205327
Chicago/Turabian StyleDecker, Simon, Matthias Brodatzki, Benjamin Bachowsky, Benedikt Schmitz-Rode, Andreas Liske, Michael Braun, and Marc Hiller. 2020. "Predictive Trajectory Control with Online MTPA Calculation and Minimization of the Inner Torque Ripple for Permanent-Magnet Synchronous Machines" Energies 13, no. 20: 5327. https://doi.org/10.3390/en13205327
APA StyleDecker, S., Brodatzki, M., Bachowsky, B., Schmitz-Rode, B., Liske, A., Braun, M., & Hiller, M. (2020). Predictive Trajectory Control with Online MTPA Calculation and Minimization of the Inner Torque Ripple for Permanent-Magnet Synchronous Machines. Energies, 13(20), 5327. https://doi.org/10.3390/en13205327