Computer Simulation of Stochastic Energy Fluctuations in Tensile Test of Elasto-Plastic Porous Metallic Material

Abstract

The main aim of this work is the computational implementation and numerical simulation of a metal porous plasticity model with an uncertain initial microdefects’ volume fraction using the Stochastic Finite Element Method (SFEM) based on the semi-analytical probabilistic technique. The metal porous plasticity model applied here is based on Gurson–Tvergaard–Needleman theory and is included in the ABAQUS finite element system, while the external probabilistic procedures were programmed in the computer algebra system MAPLE 2017. Hybrid usage of these two computer systems enabled the determination of fluctuations in elastic and plastic energies due to initial variations in the ratio of the metal micro-voids, and the calculation of the first four probabilistic moments and coefficients of these energies due to Gaussian distribution of this ratio. A comparison with the Monte-Carlo simulation validated the numerical efficiency of the proposed approach for any level of input uncertainty and for the first four probabilistic characteristics traditionally seen in the experimental series.

1. Introduction

Porous plasticity in metals is a significant engineering problem that frequently leads to ductile fracture [1,2]. According to the literature, this type of plastic behavior was initially modeled mathematically by Gurson [2,3,4], Gurson–Tvergaard [5,6] and was then extended by the Gurson–Tvergaard–Needleman approach [7,8] implemented in many Finite Element Method (FEM) systems. It is based on assumptions regarding the spherical shape of the micro-voids distributed in the metal volume and accounts for micro-pore nucleation and coalescence [9]. This constitutive theory has been employed to analyze the fracture of structural elements [10], to model metal alloys [11], to include interface phenomena [12] and has also been used in the context of homogenization theory [13]. Further, according to engineering intuition and supported by experimental research, uncertainty in various parameters of this model plays a role in the overall randomness of the porous metal deformation process at the macro scale. This problem is significant in the context of the available probabilistic methods as well as computer usage and was initially studied by Strąkowski and Kamiński [14] while randomizing Tvergaard coefficients. Their statistical treatment uses experimental measurements and least squares fitting procedures that are necessary for the determination of these coefficients. Nevertheless, it does not answer the research question, that is, how does the initial micro-porosity of a given metal affect its deformation process.

The main objective of this work is to numerically investigate the role of the initial metal porosity in the overall deformation process of a material in a classical strength tension test. For this purpose, we validated a probabilistic semi-analytical method to determine the basic stochastic structural response [15] to the given plasticity problem. This provided an efficient numerical tool, which offers time and computer power savings compared to the traditional Monte-Carlo simulation [16]. This was done for the displacement formulation of the FEM, because precise analyses of the elastic and plastic deformation energies, which are fundamental for FEM convergence, is of paramount importance.

The semi-analytical approach is based on cyclic FEM usage with a fluctuating parameter (or a few of them) for the numerical recovery of an analytical polynomial function that relates the resulting deformation increments and the given uncertain initial porosity of the metal specimen. Then, the probabilistic moments of such a structural response can be calculated using analytical integrals from probability theory, especially in their truncated forms. According to central limit theorem the initial porosity has a Gaussian distribution but this limitation can be removed by applying one of the many existing continuous distributions.

2. Governing Equations of the Model

The main aim of this study is to determine the probabilistic moments of the deformation energy U for the given material continuum in the presence of some uncertain Gaussian parameter b uniquely defined by its expected value E[b] and standard deviation σ(b). This material continuum is subjected to large deformations in the following boundary value problem:

$$\mathsf{\Delta }{\sigma }_{kl,l}+\rho \mathsf{\Delta }{f}_k=0;x\in \mathsf{\Omega }$$

(1)

$$\mathsf{\Delta }{\sigma }_{kl}=C_{klmn}\mathsf{\Delta }{\epsilon }_{mn};x\in \mathsf{\Omega }$$

(2)

$$\mathsf{\Delta }{\epsilon }_{kl}=\frac{1}{2}\left(\mathsf{\Delta }{u}_{k,l}+\mathsf{\Delta }{u}_{l,k}+u_{i,k}\mathsf{\Delta }{u}_{i,l}+\mathsf{\Delta }{u}_{i,k}{u}_{i,l}+\mathsf{\Delta }{u}_{i,k}\mathsf{\Delta }{u}_{i,l}\right);x\in \mathsf{\Omega }$$

(3)

for i, j, k, l = 1, 2, 3 with the following boundary conditions:

$$\mathsf{\Delta }{\sigma }_{kl}{n}_l=\mathsf{\Delta }{t}_k;x\in \partial {\mathsf{\Omega }}_{\sigma },k=1,2,3$$

(4)

$$\mathsf{\Delta }{u}_k=\mathsf{\Delta }{\widehat{u}}_k;x\in \partial {\mathsf{\Omega }}_u,k=1,2,3$$

(5)

Here $\mathsf{\Delta }{u}_k$ denotes the displacement field components increments, $\mathsf{\Delta }{\epsilon }_{mn}$ and $\mathsf{\Delta }{\sigma }_{kl}$ stand for the strain and stress tensors components, $\mathsf{\Delta }{t}_k$ and $\mathsf{\Delta }{\widehat{u}}_k$ correspond to Neumann and Dirichlet boundary conditions. Traditionally, notation $u_{i,k}$ denotes the first order partial derivative of the vector $u_i$ with respect to the spatial coordinate $x_j$, while C_klmn is a constitutive tensor adopted specifically for porous metal plasticity. According to the Gurson–Tvergaard–Needleman model, the elastoplastic behavior of the given continuum includes micro-scale structural defects (spherical imperfections), and is constituted by the following equation [4,6]:

$${\left(\frac{{\sigma }_e}{{\sigma }_0}\right)}^2+2q_{1}f\cosh \left(\frac{3q_2{\sigma }_m}{2{\sigma }_0}\right)-\left(1+q_3{f}^2\right)=0,$$

(6)

where ${\sigma }_e$ is the reduced stress according to the Huber–Mises–Hencky hypothesis, ${\sigma }_0$ is the yield stress of virgin metallic material, ${\sigma }_m$ denotes the hydrostatic stress, while $f$ represents the volume fraction of the material voids. It is assumed that the micro-pores under consideration are uniformly distributed throughout a solid volume. The constants $q_i$ were originally introduced by Tvergaard to obtain better agreement with the localized shear band bifurcations than those predicted by the initial Gurson model. The best predictions of the growth and coalescence of the voids were obtained with $q_1=1.5$, $q_2=1$ and $q_3=q_1{}^2=2.25$.

The incremental equilibrium problem given by Equations (1)–(5) is solved by construction of the potential energy functional, its minimization in addition to the nodal displacement vector, and the final application of the FEM discretization and solution procedure [17].

The semi-analytical probabilistic and the stochastic perturbation approaches employed in this work are based on polynomial approximation of the displacement increment vector ∆u with respect to the input uncertain Gaussian variable b parametrized by its mean E[b] and standard deviation σ(b) as follows [18]

$$\mathsf{\Delta }{u}_i^{\left(m\right)}=N_{i\alpha }\mathsf{\Delta }{q}_{\alpha }^{\left(m\right)}=N_{i\alpha }{D}_{\alpha j}^{\left(m\right)}{b}^j$$

(7)

where $N_{i\alpha }$ represents the FEM shape functions, $D_{\alpha j}^{\left(m\right)}$ are the deterministic coefficients of the polynomial basis corresponding to the αth degree of freedom, jth power of input random variable and the mth increment during nonlinear analysis. These coefficients are initially determined thanks to the Least Squares Method fitting to the FEM experiments series while deterministically varying parameter b in the interval $\left[E\left[b\right]-3\sigma \left(b\right),E\left[b\right]+3\sigma \left(b\right)\right]$. Having determined the nodal polynomial bases, one may determine the analytically expected values of the structural response as

$$E\left[\mathsf{\Delta }{u}_i^{\left(m\right)}\right]=E\left[N_{i\alpha }\mathsf{\Delta }{q}_{\alpha }^{\left(m\right)}\right]=N_{i\alpha }E\left[D_{\alpha j}^{\left(m\right)}{b}^j\right]=N_{i\alpha }{\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}{D}_{\alpha j}^{\left(m\right)}{b}^j{p}_b}\left(x\right)dx$$

(8)

and the variance function as

$$Var\left(\mathsf{\Delta }{u}_i^{\left(m\right)}\right)={\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}{\left(N_{i\alpha }{D}_{\alpha j}^{\left(m\right)}{b}^j-N_{i\alpha }E\left[D_{\alpha j}^{\left(m\right)}{b}^j\right]\right)}^2{p}_b}\left(x\right)dx$$

(9)

The aforementioned formulas include the probability density function $p_b\left(x\right)$ of the variable b. Higher order central probabilistic moments are also available and can be determined from the following formula which is suitable for the lth order one:

$${\mu }_l\left(\mathsf{\Delta }{u}_i^{\left(m\right)}\right)={\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}{\left(N_{i\alpha }{D}_{\alpha j}^{\left(m\right)}{b}^j-N_{i\alpha }E\left[D_{\alpha j}^{\left(m\right)}{b}^j\right]\right)}^l{p}_b}\left(x\right)dx$$

(10)

Elastic and plastic energies as well as their probabilistic characteristics are the main purpose of this numerical study and were determined by using their traditional definitions rewritten as:

$$U_{el}=\frac{1}{2}{\displaystyle \underset{\mathsf{\Omega }}{\int }{\sigma }_{ij}^c{\epsilon }_{ij}^{(el)}d\mathsf{\Omega },}{U}_{pl}=\frac{1}{2}{\displaystyle \underset{\mathsf{\Omega }}{\int }{\sigma }_{ij}^c{\epsilon }_{ij}^{(pl)}d\mathsf{\Omega },}$$

(11)

where ${\sigma }_{ij}^c$ denotes the stress tensor components derived from the user-specified constitutive equation, while ${\epsilon }_{ij}^{(el)},{\epsilon }_{ij}^{(pl)}$ represent the components of elastic and plastic strain tensors, respectively. It should be mentioned that all probabilistic characteristics of elastoplastic response in the given problem have been determined as the function of the input statistical scattering level represented by the coefficient of variation α(b). A validation of the proposed method was carried out with a Monte-Carlo simulation, which was implemented in the MAPLE 2017 computer system.

3. Numerical Analysis

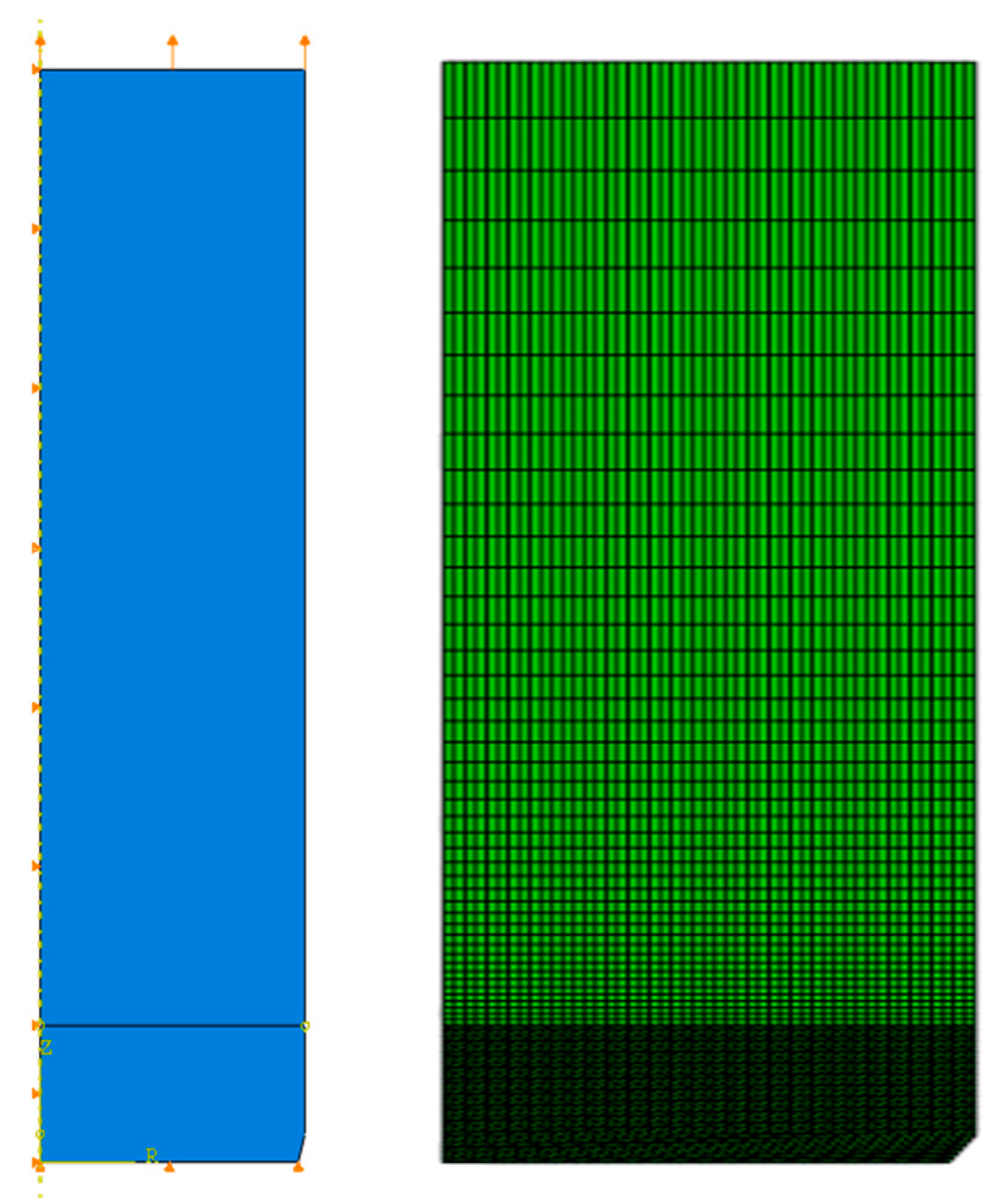
An axisymmetric cylindrical steel specimen, 10 mm wide and 40 mm long, was discretized in the ABAQUS Standard finite element system using CAX3, which are t3-node axisymmetric triangle elements and CAX4R, which are 4-node bilinear axisymmetric quadrilateral, reduced integration, hourglass control elements. Quadrilaterals were used to mesh the upper part of computational domain, where relatively smaller deformations are expected, whereas the lower part is discretized with the triangular finite elements to avoid possible error of rectangular elements’ distortion. Further, a small cutout of one corner was provided (Figure 1) to ensure proper localization of the expected necking phenomenon at the horizontal symmetry axis. The Young modulus of the specimen was set as E = 210 GPa, the Poisson ratio as ν = 0.30, and the mass density as ρ = 7.85 t/m³, while its yield stress was set as f_y = 235 MPa. The final deformed configuration of this steel specimen is shown in Figure 2 and it agrees well with a number of experimental strength tests [7]. The finite element size was assumed as 0.2 mm for triangular elements and in the range of 0.2–2.0 mm for the rectangular elements, so that the entire mesh includes 2548 triangular and 2156 rectangular FEM elements (with 3550 nodal points). An incremental analysis was carried out with the initial increment equal to 0.0001, the maximum increment equals 1.0, while the minimum is 0.01. The deterministic incremental solution was obtained with the Full Newton technique, where the total number of increments varies together with the input value of the volumetric ratio of the micro-voids, i.e., f₀ = 0.0000 needs 117, while f₀ = 0.0024 demands only 82 increments. Boundary conditions imposed on the extended material specimen are shown in Figure 1 and include symmetrical conditions along the left vertical edge as well as along the lower horizontal one, while upper surface of this element has been subjected to tensile deformation.

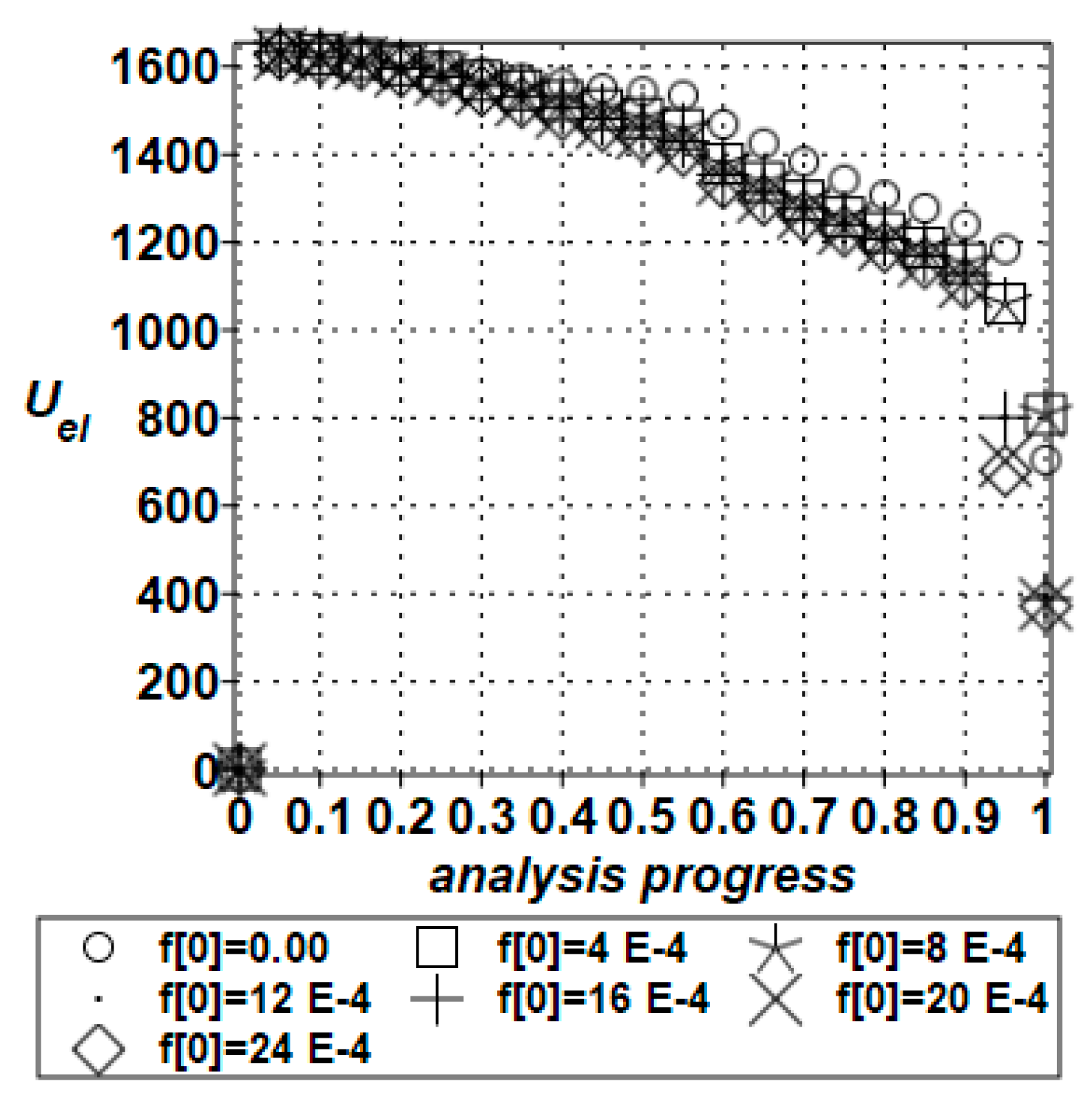
The interrelation between total elastic energy and the initial micro-voids’ volumetric ratio was modeled; the same was done in respect to the energy dissipated by rate-independent and rate-dependent plastic deformation with respect to the same input parameter. The discrete values of the input micro-void parameter f₀ were chosen from the following set: {0.0,2.0,4.0,6.0,8.0,10.0,12.0,14.0,16.0,18.0,20.0,22.0,24.0} × E − 4. A huge difference was noticed between the elastic Figure 3 and plastic Figure 4 energies, with the latter being more than a hundred times larger. Plastic energy increases constantly as the analysis progresses, in the same way as all void ratios. Elastic analysis increases rapidly at the very beginning of a deformation process and then decreases moderately until the end of the process. It is greatly affected by the input random parameter f₀, especially at the end of the FEM incremental analysis.

Probabilistic numerical analysis was completed thanks to the interoperability of the ABAQUS and MAPLE 2017 systems. The fourth order polynomials were chosen to model the response functions of both the elastic and plastic energies with respect to the volumetric ratio of the micro-voids. These functions enabled the final determination of the expected values (Figure 5 and Figure 6), coefficients of variation (Figure 7 and Figure 8), skewness (asymmetry measure of the output distribution, Figure 9 and Figure 10) as well as the kurtosis ( a concentration measure, Figure 11 and Figure 12) of these two energies using the technique proposed (semi-analytical method, abbreviated as SAM in the legends) and Monte-Carlo simulation (MCS) for a population size equal to 10⁶. The computational effort of the SAM approach is very close to that of the stochastic perturbation method. However, thanks to the application of the computer algebra program, where integrals of any order polynomials are evaluated automatically, the time required for this procedure is almost the same as the time needed to process of all perturbation-based formulas. Contrary to these two methods, MCS analysis (even for a single input coefficient of variation) uses a time proportional to the population size, so, computations can be extremely long due to the higher order statistics involved. These characteristics were all collected as functions of the input uncertainty dispersion for a few increments (25, 50, 75 and 100) in the nonlinear FEM analysis.

Numerical analysis proved that the expected values of both energies are totally independent of the coefficient of variation α(f₀), and this result was observed frequently in many elastic systems under reversible deformation processes. This holds true for any increment of nonlinear FEM analysis. The values returned by the semi-analytical approach agree perfectly with these estimated by the Monte-Carlo simulation. Figure 7 and Figure 8 show clearly that input uncertainty affects elastic energy, whereas its impact on plastic energy is rather marginal. Nevertheless, the interrelation between the output and input uncertainties is almost linear for both energies, whereas the largest values are seen at the end of the deformation; the coincidence of two probabilistic techniques was also documented in this case. Very similar patterns can be observed in Figure 9 and Figure 10 for the skewness, and the absolute values increase in almost linear mode together with an increase in the parameter α(f₀). The plastic energy distribution has very little asymmetry in contrast to its elastic counterpart. For both, skewness increases up until the middle stage of the deformation process and then decreases to 0 or even to a small negative value. The agreement between the two probabilistic techniques is perfect in the case of the elastic energy, while it is a little less so for plastic energy skewness. Kurtosis of elastic energy (Figure 11) also increases with input uncertainty, while the trends showing extreme values can be seen in the middle of the extension process. These extremes show some remarkable differences between the SAM and MCS series. Kurtosis of plastic energy (Figure 12) exhibits similar trends to those in Figure 11 but the extreme values are many times smaller and a negative concentration is obtained at the end of deformation. It can also be seen that both the skewness and kurtosis of elastic energy equal almost 0 for the last increment, thus its probability density is very close to the Gaussian one; the plastic energy distribution in this context is quite far from this probability density function.

4. Conclusions

First, by using numerical simulation we demonstrated that the initial metal porosity greatly affects the deformation energy of the extended specimen, especially at the end of this incremental process; interestingly, the overall elastic energy is also affected. Secondly, it was demonstrated that the semi-analytical probabilistic method implemented in conjunction with the finite element method is an efficient computational methodology that allows for the reliable determination of the first four probabilistic moments and coefficients for elasto-plastic behavior of materials containing micro-voids. The agreement between the probabilistic moments of structural response determined with this technique and the reference Monte-Carlo simulation is perfect for the first two moments and very good for higher order statistics, and it is also independent of the input coefficient of variation for the micro-voids’ volumetric ratio α(f₀). This agreement shows that response statistics can be efficiently computed by the generalized stochastic perturbation technique, which offers large time and computer power savings compared to the Monte-Carlo approach and it may be implemented in any computer program, contrary to the semi-analytical technique, which demands computer algebra programs. Further stochastic finite element method analyses in this area will include the influence of the yield stress, nucleation as well as coalescence parameters (and eventually their statistical parameters) on the elastic and plastic energies accumulated in elasto-plastic porous metal. Probabilistic analysis should focus on other probability distributions that characterize the material characteristics of porous metals.