Abstract
Pipe design is one of the most significant research lines in the area of parabolic semi-cylindrical solar collectors. The main idea behind pipe design is to increase the capillarity angle by expanding the total area being heated, therefore boosting the work capacity of the device. Such capillarity depends on several factors, whose numerical calculations are highly complex. Moreover, some of those variables are integers, whereas some others are real; hence, it is necessary to use optimization techniques that are capable of searching in those numerical spaces. There are several optimization tools that allow individual codification as binary strings, granting the coding of integer, real, or any other, as part of the same individual. Consequently, in this paper we propose the comparison of four metaheuristics when they are utilized to maximize the capillarity angle of the pipe in a parabolic trough. Experimental results show a better performance of binary particle swarm optimization when compared against the other techniques, achieving improvements in the capillarity angle of on average in comparison with a similar study.
1. Introduction
The use of fossil fuels for energy production has been the origin of many improvements to human life. However, it is also the cause of several problems, such as pollution and climate change. For that reason, research efforts have been focused on the utilization of alternative energy sources, like wind [1], geo-thermal [2], sun-based [3], biomass [4], hydrogen [5], bio-fuels [6], or even tidal [7]. Contrary to fossil fuels, these are considered renewable because they are sustainable, cost-effective, and environmentally friendly [8,9]. Because of its abundance and availability in many places around the world, the sun is the most critical source. Therefore, much research has focused on improvements to the associated technologies to extract its energy, such as photo-voltaic and concentrated solar power (CSP) systems [10].
In CSP systems of the parabolic trough collector (PTC) type, heat pipes (HPs) receive the concentrated solar power to transfer the temperature into a heat transfer fluid (HTF) that is later utilized to perform mechanical work. Among all the components of PTCs, HPs are considered the most crucial element to increase the efficiency in energy harvesting [11,12] by boosting the transformation of sunlight to heat. One way to improve the receiver efficiency is by modifying its parameters. Thus, the optimal design of HPs is an essential need to be covered by research endeavors [13]. This work proposes a comparison of four metaheuristic methods when they are used to increase the capillarity angle of micro-grooved pipes.
Various components of CSP systems are feasible for optimization, such as (1) the reflector, (2) the collector, (3) the heat receiver, (4) heat transport, (5) power production, and (6) thermal storage. The use of metaheuristic algorithms is a relatively recent trend in research related to CSP improvements. In that sense, several studies have been made, particularly in the last four decades. There are two optimization methods that can be used: classical and evolutionary. The second class of techniques are the main focus of this work. For example, Wang and Yang [14] proposed the optimization a prism-based solar concentrator via genetic algorithm, achieving improvements in brightness of around 400% when compared with a similar approach. In this case, the main idea is to find the optimal combination of prismatic crystals to enhance sunlight energy transmission via optic fiber. Nazemi and Boroushaki describe the optimal design of a dish/stirling system in [15]. The model considers the parabolic dish and the cavity receiver as the optimization problem, and the metaheuristic used was particle swarm optimization. The obtained design and a real system were compared, finding that the approach gave a good approximation of real devices. In the same venue, authors in [16] optimized the coefficients of a photovoltaic/thermal system through a genetic algorithm, finding improvements in the thermal addition to its exergetic efficiency.
The mentioned articles pay attention mainly to the collector; however, the heat transmission between the collector and the HTF is another vital aspect of CSP research. In that sense, Petersont began studies related to pipes with V-shaped micro-grooves [17], although other kinds of improvements to pipes have been put forth. For instance, authors in [18] propose the insertion of twisted tapes in that kind of exchanger, with the idea of increasing the heat transfer by modifying the Reynolds and Nusselt numbers. In [19], the pipe optimization considered two criteria: (1) the investment costs, and (2) the coupling between the CSP system and the steam turbine discharge. The authors found that the use of finned hexagonal tubes is the best option to reduce cost in commercial production, packing, and storage. Another proposal is the use of helically finned tubes; for example, authors in [20] made numerical simulations for the utilization of those pipes in the design of a CSP, and they found that the whole system’s efficiency could be increased with their use. A recent attempt to optimize the design of an HP using evolutionary algorithms was made in [21]. Here, the use of genetic algorithms was proposed [22] to improve the design of the absorber in a parabolic trough. Several variables were examined and used to improve the capillarity. Additionally, an adiabatic model was proposed to calculate the liquid front, as well as its establishment velocity. The authors made improvements of around 10% in comparison with another study [23].
Our proposal improves upon the results shown in [21], with different metaheuristic algorithms: discrete binary differential evolution (DBDE), clonal selection algorithm (CSA), binary particle swarm optimization (BPSO), and genetic algorithm (GA). Because of their configuration, these metaheuristic algorithms are capable of searching in mixed numerical spaces. In that sense, this work contributes, on the one hand, to the search for better algorithms [24] to solve the capillarity problem in the design of micro-grooved pipes in CSP systems. On the other hand, it contributes to the use of the capillary-driven two-phase flow model proposed by [21]. The approach obtained improved upon HP designs by maximizing the capillarity angle. Even though other fluids (e.g., vegetable oils, synthetic oil) are used frequently as HTFs for CSPs [25], in the present study only four commonly utilized fluids are considered for the design optimization of CSP systems: liquid sodium, water, and two molten salts [26]. From the compared techniques, BPSO achieved improvements in the wet front, via the capillarity angle, from around 11% against the study reported in [21]. The results suggest that metaheuristic algorithms are a good option for the optimal design of micro-grooved HPs in CSP systems. The rest of the article is structured as follows: Section 2 explains the details concerning the micro-groove pipe design, particularly its governing equations. Section 3 deals with the details regarding the utilized metaheuristic algorithms, whereas Section 4 describes the experimental part. Section 5 provides some conclusions of the present work.
2. Design of Micro-Grooved Pipe
The study made in [21,27] considered the capillarity angle and the velocity of a heat transfer fluid (HTF) inside a heat pipe (HP) in the model. This work used the same design and held the same assumptions. The mathematical explanation of the model is in the next subsection, and the other paragraph describes its solution methodology.
Governing Equations
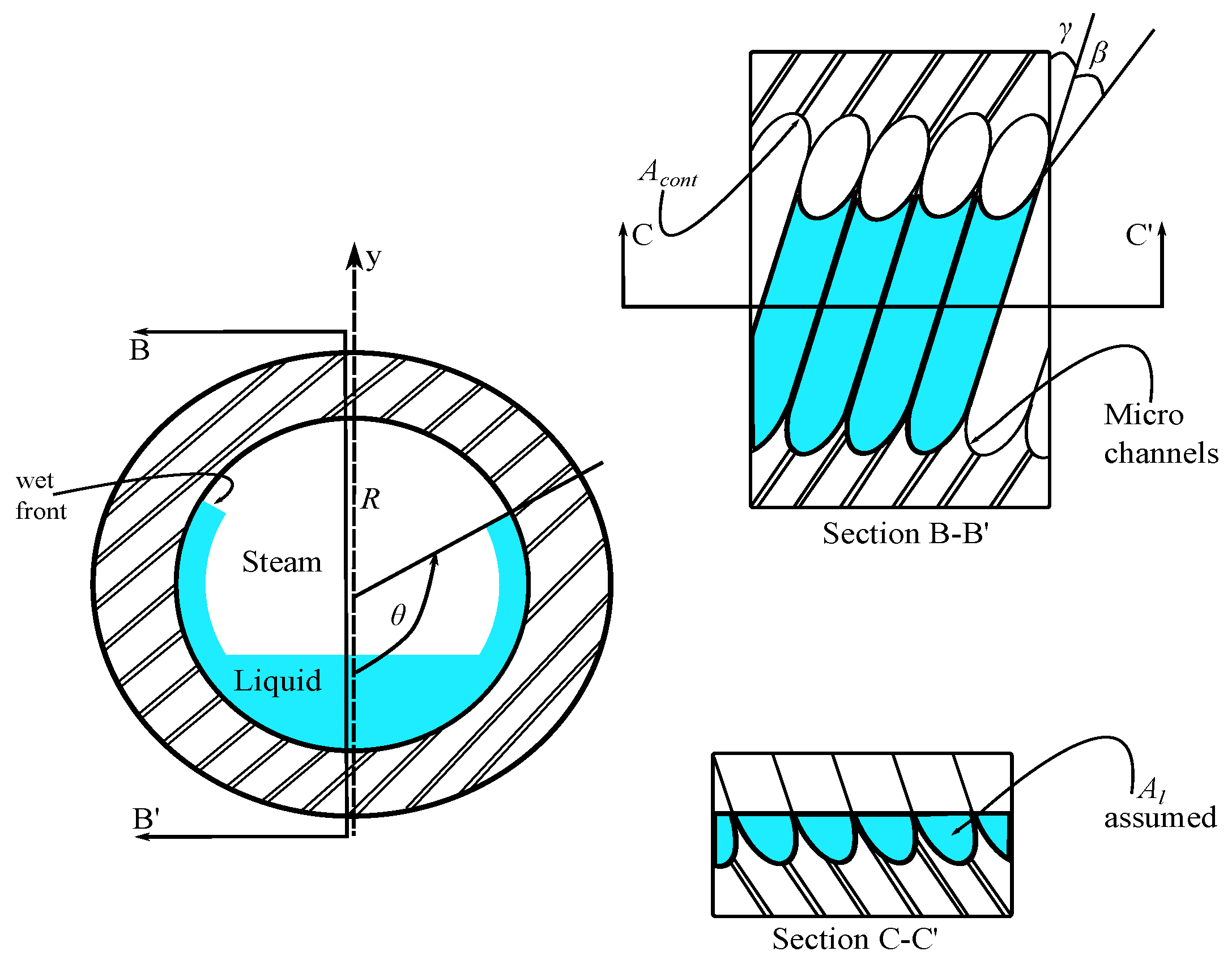
The use of micro-grooved pipes as a heat receiver is frequent in CSP systems. Authors in [27] developed a capillary-driven two-phase model with several design variables. In the first phase, it is assumed, that there is no heat flux for the calculus of the liquid front velocity. The second stage establishes two relationships: heat flux vs. liquid front velocity, and mass of liquid vs. liquid front velocity. Those relations are crucial to calculate the fluid supply to a micro-grooved pipe (Figure 1) under the CSP working conditions.
Figure 1.
Pipe with micro-grooves (adapted from [21]).
It is important to remark that the model only predicts the behavior of saturated liquids with different operating temperatures. Additionally, the steam being displaced by the moving fluid in the micro-grooves is non-negligible. By considering those situations, the flow behavior in this kind of pipe is influenced only by the momentum balance of the liquid in the direction of the capillarity angle, , as shown in Figure 1. The momentum balance is given by:
where are the inertial forces over the liquid layer, are the capillarity-driven forces, are the gravitational forces, and are the viscous forces. Other assumptions are:
- Laminar and Newtonian flux in the micro-groove;
- Isothermal layer of fluid, therefore its internal friction is negligible; and
- The thickness of the liquid layer advancing on the micro-groove insignificant.
If we consider a mass for the liquid that flows in the direction of the capillarity angle, with a liquid front velocity, then Equation (1) becomes [23]:
where the meaning of every variable and constant is in Appendix A. In this work, the objective is to maximize the capillarity angle (e.g., liquid front position). Equation (2) is prone to errors if used to calculate , the maximum capillarity angle. Therefore, authors in [23] proposed its reformulation using time as the independent variable:
Methodology to Solve the Governing Equations
Equation (3) can be re-formulated as a system of differential algebraic equations:
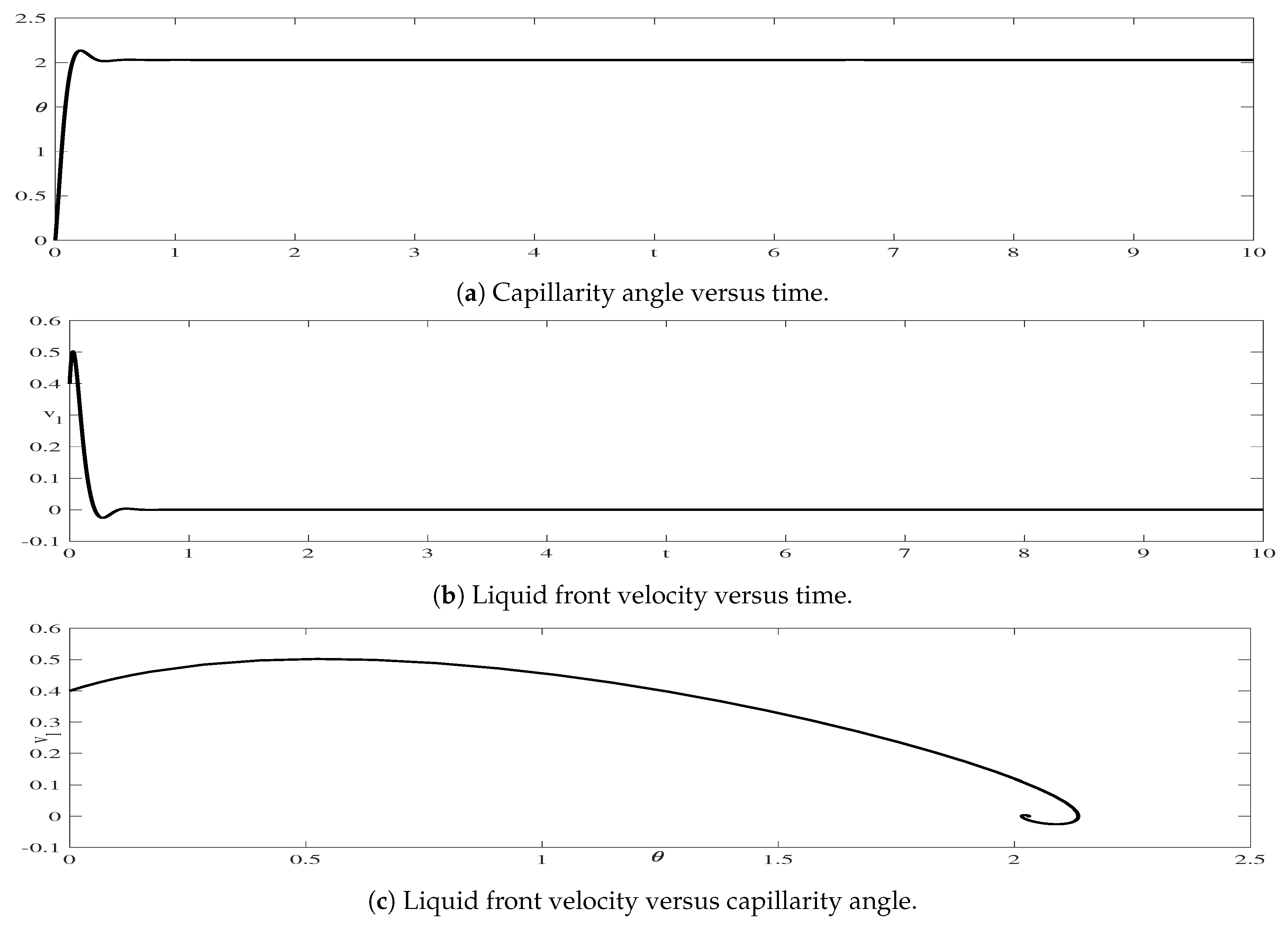
with initial conditions and . In the experimental part, Equation (4) is evaluated in 10 seconds by using the Matlab solver , to find the stable values of and . An illustrative example of the evaluation of Equation (4) is in Figure 2, where the initial conditions are and . This Figure also depicts the dynamics of the capillarity angle and the velocity of the liquid front. Concerning the angle, it surpasses the stable point around the first second, with a tendency to stability after around s. We consider maximizing the value of the capillarity angle in the stable state of the simulation.
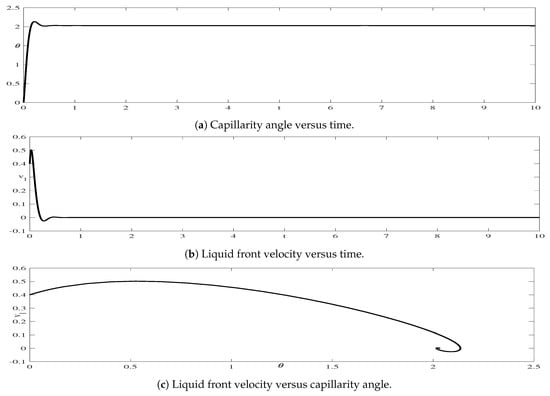
Figure 2.
A simulation of Equation (4), solved with the ode45 Matlab solver.
The optimization process produces an increase in the capillarity angle, which enhances the heat transfer to the micro-grooved pipe. Then, the objective function can be described as the maximization of the capillarity angle:
The value is function of several variables that are defined in Appendix A. In this work, four fluids (Appendix B) are used in the optimization of the capillarity angle; while some parameters depend on the kind of fluid (), such as liquid density, viscosity and dynamic density (Appendix C, Appendix D, Appendix E and Appendix F), other are independent of such variable, e.g. the micro-groove geometry (Appendix G).
3. Metaheuristic Algorithms
This section briefly explains the four selected metaheuristic algorithms utilized to solve the problem of pipe design in the parabolic trough. In each technique, the individual codification was as binary strings, because they are capable of encoding the two kinds of variables optimized in this article: integers and real values. Another critical remark is the fact that in every algorithm, the initialization of the population is performed by considering a uniform probability distribution [28].
3.1. Discrete Binary Differential Evolution
This motivation of this metaheuristic is the evolutionary process, similar to the genetic algorithms. Nevertheless, and even though the operators’ names are the same, they function in a slightly different manner. Such operators explore the search space efficiently, allowing the algorithm to achieve the right balance between exploration and exploitation [29]. The algorithm was first proposed to minimize nonlinear and non-differentiable functions. In their seminal paper, Storn and Price considered some essential features of this optimization technique: few control variables, easily parallelizable, and excellent convergence properties, among others [28]. The basic algorithm for real candidate solutions utilizes three operators, which modify the whole population of vectors: (1) mutation, (2) crossover, and (3) re-selection of the best individual, which are mostly the same operators used in the discrete binary differential evolution (DBDE) [30] utilized in this work. A detailed description of those mathematical operators is given in the following.
Mutation
For DBDE, this operator must select three random parents from the original population with the restriction that , where i is the actual individual and and are three randomly generated integers from a uniform distribution. Once selected, the mutated vector is calculated by
where represents the step size, and the binarization is achieved by
with being a uniform random number.
Crossover
The mutated vector, as well as the actual candidate solution, serve to construct a trial vector:
where is a uniform random number, is the crossover rate, is an integer number generated from a uniform distribution. This value is to ensure that at least one bit is mutated.
Selection
The final step of the algorithm consists of a greedy re-selection of the objective function value of the actual candidate solution, and the fitness value of the trial vector:
3.2. Clonal Selection Algorithm
The environment is a source of many health imbalances to many living beings, particularly mammals. To counteract that situation, those individuals have several internal systems, one of them being the immune system. This system has compelling attributes, such as learning capability, pattern recognition, and memory [31]. A theory formulated by immunologists is called the clonal selection theory; in this theory, the immune system’s elements (antibodies) are continually monitoring for external substances which attacked the body in the past. If a component of that kind appears (e.g., an antigen), then an immune response is triggered, with the following steps: cloning, mutation, destruction of the foreign agent, re-selection, and memory. Those characteristics have served as an inspiration to computer scientists to create an area of soft computing called artificial immune systems, which has several variants. The version utilized in this paper is the clonal selection algorithm [32], whose steps are: (1) cloning, (2) hyper-mutation, (3) re-selection, and (4) diversity introduction.
Cloning and Hyper-Mutation
Even though there are other schemes, this paper uses the one related to the simple cloning of the individuals, considering a certain percentage, . First, it generates a cloned population, , which has clones
and then mutation is carried out with a probability to every bit in the population, to get a new cloned and mutated population,
It is essential to say that those individuals will compete against the original parents from B. Consequently, the evaluation of clones will be in groups: the fitness value of every parent will be contrasted against the fitness of its mutated clones, repeating the procedure for each parent of the original population.
Re-Selection and Diversity Introduction
In order to evaluate each individual from , it is necessary to transform those binary strings to real and integer values, obtaining :
where f is the objective function, is the real version of , are the real version of the clones corresponding to individual i, and is the best binary candidate solution extracted from the clones corresponding to individual i. Once the re-selection between and is complete, the last phase of the CSA is a diversity introduction consisting of replacing a percentage of the worst individuals in with random individuals created with Equation (22). As in other evolutionary metaheuristics, all the steps repeat until a criterion is reached, usually until a maximum iteration number.
3.3. Binary Particle Swarm Optimization
This metaheuristic takes as inspiration the behavior of flocks of bird flocks and schools of fish. It was initially proposed as an optimizer by Kennedy and Eberhart in 1995 [33]. The algorithm considers a population of individuals called particles, which represent candidate solutions for a problem (usually an optimization problem); this set also describes a swarm from the analogous point of view. In the algorithmic implementation, the particles evolve by moving around the space of solutions, considering the velocity of each particle around itself and the best global particle found so far. In that sense, the original technique has two operators: (1) the velocity calculus, which considers the global and the local social behavior of each particle, and (2) position upgrade. The next lines describe the operators mathematically for the binary particle swarm optimization (BPSO) used in this paper [34].
Velocity Calculus
In BPSO, the global velocity change utilizes two vectors which hold the probability that every bit changes either to zero or to one; the respective equations to calculate these vectors are
where w represents the inertia weight, and , , , and are temporary values calculated with the following conditions:
- if = 1 then = and = ,
- if = 0 then = and = ,
- if = 1 then = and = ,
- if = 0 then = and = ,
with the indexes i and j representing the actual individual and the bit, respectively; are the constriction factors taken from the original PSO; and are random numbers drawn from a uniform distribution; and are the bits that belong to the local and global best individuals, respectively. After calculating and , the next step consists of transforming those probabilities into the velocity change of the actual particle:
Position Upgrade and Selection
The position calculus of the actual particle in the next iteration is
where is the 2 complement of , and is a uniform random number. The last stage in the BPSO is the comparison of the generated candidate solution against the local best as well as the global best:
- iff(xi) > f(xibest) then f(xibest) = f(xi) and bibest = bi,
- iff(xi) > f(xgbest) then f(xgbest) = f(xi) and bgbest = bi,
where , , and are the real versions of the binary , , and , respectively.
3.4. Genetic Algorithms
Considered as an evolutionary algorithm [22,35], this metaheuristic was proposed in the 1960s. This algorithm is based on Darwin’s theory of evolution, where individuals are represented by bit strings; similar to the previous algorithms, this description is useful to codify simple data structures. As an optimizer, this technique is capable of finding competitive solutions to complex optimization problems [35]. Therefore, it has been extensively used to solve problems from different domains (machine learning, operations research, image processing, etc.), and it was even utilized in a similar study to the one presented in this article [21]. The operators used in the canonical version of the genetic algorithm (GA) are (1) interchange of genetic material, (2) a mutation scheme, and (3) re-selection of the fittest. Below is the mathematical description of these operators.
Crossover
One method to achieve crossover in GA is the roulette technique, in which it is necessary to calculate the fitness of every individual, and then the cumulative fitness as
where is the real representation of the binary individual . Later, the selection probability as well as the cumulative selection probability of every individual are computed according to their fitness (Equations (17) and (18)):
Two random numbers, and , from a uniform distribution are generated after the previous calculus, and the selection applies to the parents that meet and . After the selection of two parents in the prior step of the GA, the next step corresponds to the crossover, which is the crossover of one point in this paper. This method works by choosing, with a given probability , a point of the selected parents to generate two new individuals by an interchange of genetic information. The crossover points are calculated with and .
Mutation and Reselection
The mutation considers the change of every bit in the binary individual by taking the mutation probability :
where is the binary and mutated child number 1; the same procedure applies for child number 2. Finally, the last step in GA is the competence between the two parents and the two children:
3.5. Population Initialization
As mentioned previously, the optimization tool utilized in the problem of pipe design in a parabolic trough must be capable of searching in two numerical spaces, namely, real, and integer. For that reason we use binary versions of the aforementioned algorithms, which allow the management of those codifications. In that sense, the conformation of each individual both as real and as integer values is
whose binary representation—denoted by —is a string of 150 bits. A more detailed explanation of each variable, their limits, as well as the number of bits used for a particular codification, is given in Table 1.

Table 1.
Variables in the individual codification.
In the four compared algorithms, the population is created by
where is the population size, is the total number of bits in each string, is a row vector of uniformly generated random numbers, is a positive limiting function, and l, u are respectively the lower and upper limits of the search space. Finally, Equation (5) representing the objective function can be written as:
4. Experimental Setup and Results
In the methodology applied in this paper, the optimization problem consists of maximizing the capillarity angle described by Equations (24) and (5). A virtual pipe was constructed to evaluate the objective function, and its behavior was simulated until 10 s (Figure 2). Once the optimization problem was defined, the next step was tuning the specific parameters that belong to every algorithm utilized in this work. To adjust the settings, we used a hyper-optimization scheme, where a statistical adjustment was employed. Finally, all the algorithms were compared under different criteria when they were utilized to solve the problem considered in this work.
4.1. Tuning
In order to make fair comparisons among the metaheuristic algorithms, we used the framework presented in [36], in which a higher-level algorithm (in this case, differential evolution) is utilized to tune every algorithm. This scheme is known as a hyper-optimization problem, where the main idea is to minimize the computational effort (represented by the number of iterations) of a given algorithm:
considering that is the iteration number achieved under the restriction , is the best result achieved by a similar study [21], and is the best outcome achieved by the algorithm being tuned. Additionally, the value of the threshold is set to as used in [36], is the candidate solution for the problem being optimized, and is the candidate parameter tuning for the algorithm A. The tuning algorithm was run 30 times for every metaheuristic reported in this work to get the statistics of the best parameters. Results are shown in Table 2 and following the format . It is important to note that the vector is composed of the parameters of every algorithm, and .

Table 2.
Statistical results of the parameter tuning, in the format mean(standard deviation). CSA: clonal selection algorithm; GA: genetic algorithm; BPSO: binary particle swarm optimization; DBDE: discrete binary differential evolution.
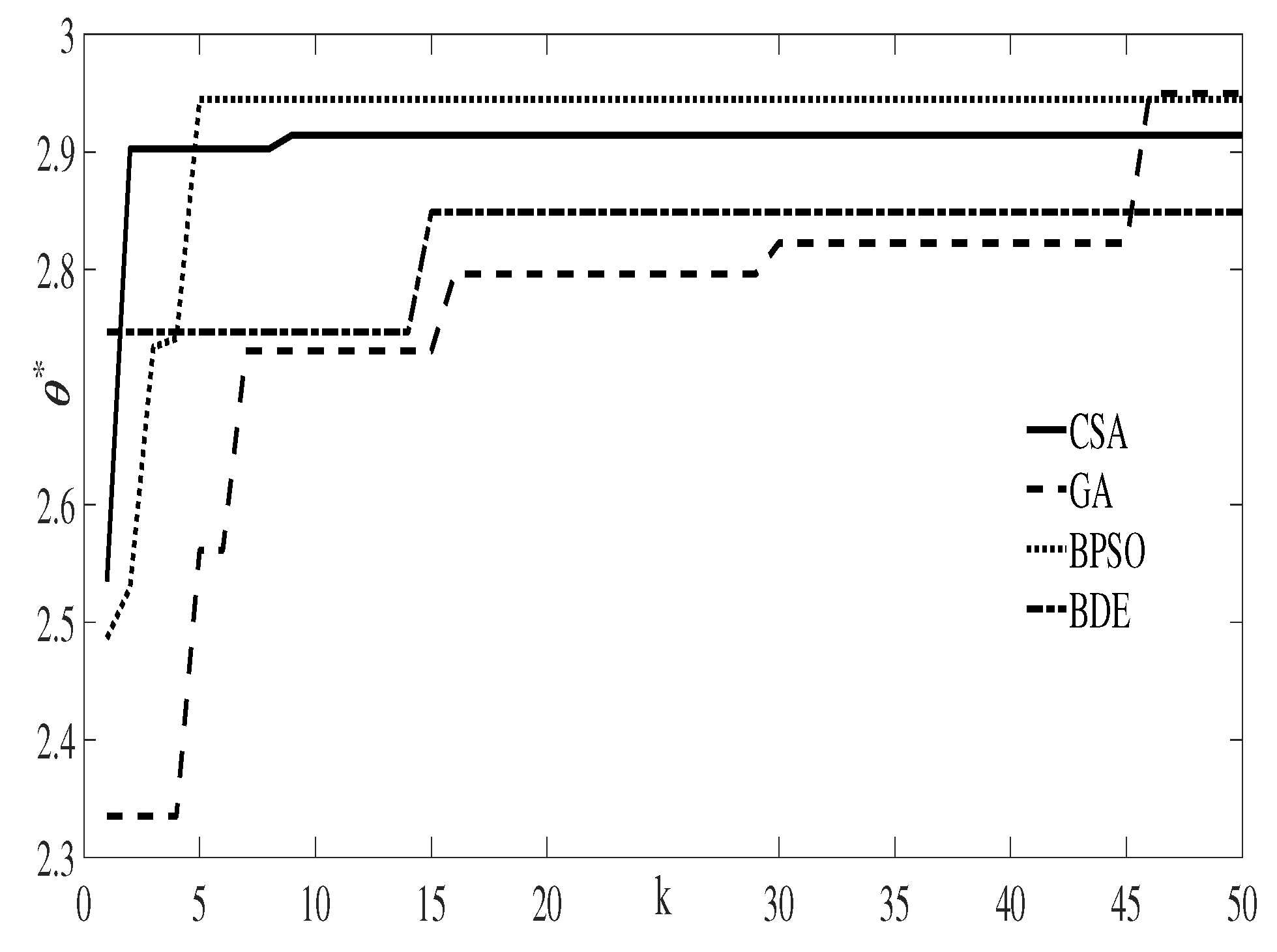
As mentioned in [36], in general terms the parameter tuning depends on the problem being solved. In that sense, after reviewing the results shown in Table 2, and based on the standard deviation, it can be considered that the most sensitive parameters—at least for the problem of the parabolic trough—are , , w, and . A single run of every algorithm with the tuning parameters of Table 2 gave the results shown in Table 3 and Figure 3.

Table 3.
Best individuals found after one run.
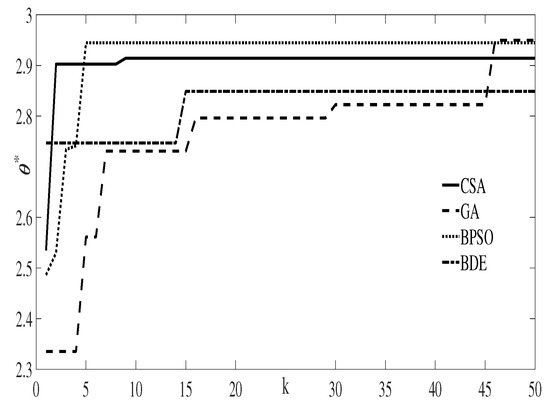
Figure 3.
Convergence of capillarity angles after one run, with k being the actual iteration.
4.2. A General Comparison
The first experimental set consisted of completing 100 tests per algorithm, for statistical purposes. The main idea was to compare their performance by considering the best design solution discovered at every run, and by acknowledging that every metaheuristic is searching in the entire design space of nine variables (Table 3). Every run had 50 iterations and the same initial population, to make a fair comparison among the techniques. The first 30 results after every trial are in Table 4, with the best result of the four metaheuristics in bold letters.

Table 4.
Best capillarity angles of 30 runs. The best results of the four metaheuristics are in bold.
A brief review of Table 4 shows that BPSO was capable of finding the best result in the majority of cases, in comparison with the other metaheuristics. The second best algorithm was GA, which acquired the best results in fewer runs, and the third-best algorithm was the DBDE with only two hits, whereas CSA showed the worst performance of all. To statistically validate the mentioned observations, we used the nonparametric Wilcoxon test over the 100 runs of the complete experiment.
In the Wilcoxon paired test, the null hypothesis is that two independent data samples come from continuous distributions with equal medians. In contrast, the alternative hypothesis is that those samples are different in that regard. Usually, either the rejection or the failure to reject the null hypothesis considers a significance level of . The test mentioned above was applied to the experimental data, thus obtaining the results shown in Table 5. After reviewing those values, we can conclude that the best algorithm was BPSO, which was capable of finding better values in the majority of the runs. According to the p-values obtained from the experiment, it is clear that the results acquired by every algorithm came from different medians; therefore, the following arrangement of metaheuristics can be given, from best to worst performance in this task, as BPSO, GA, DBDE, and CSA.

Table 5.
p-Values of the Wilcoxon test.
The average and standard deviation of the 100 runs are given in Table 6. The information confirms that BPSO was, on average, the best metaheuristic to solve the design of pipe with micro-grooves. Additionally, the algorithm achieved improvements in the capillarity angle of around 11% in comparison with a similar study [21].

Table 6.
Average and standard deviation of the best individuals found after 100 runs.
4.3. A Time-Based Comparison
The required time in seconds to complete every trial is in Table 7, given in the format mean and standard deviation of the 30 runs. In this experiment, the comparison did not need a statistical validation because the mean values were different for every metaheuristic. In that sense, the best metaheuristic for the micro-groove design was the genetic algorithm (GA), which had the minimum execution time. The second and third best algorithms were discrete binary differential evolution and binary particle swarm optimization, with very similar average times, with a slightly lower standard deviation of the DBDE. In terms of execution time, the clonal selection algorithm had the worst performance, due mainly to the fact that the fitness evaluation of the mutated clones is computationally expensive.

Table 7.
Mean and standard deviation of execution times after 30 runs.
5. Conclusions
In this article, were used four metaheuristic algorithms to optimize the pipe design in a parabolic trough: genetic algorithms, binary particle swarm optimization, binary differential evolution, and clonal selection algorithm. In the proposal, we used two differential equations to simulate the dynamic behavior of several fluids contained in a pipe with two kinds of micro-grooves. The experimental results show an averaged improved performance (11%) of the binary particle swarm optimization in comparison with a similar study that explored the design of micro-grooved pipes. After several runs of the algorithm, it is clear that the best tube must have semi-circular micro-grooves, with water as the best working fluid when compared with liquid sodium and two different molten salts. This study also considers the values of angles and to calculate the wet front, producing a better pipe design in a concentrated solar power system than a previous study [21].
Author Contributions
Conceptualization, V.O.-E.; Methodology, M.P.-C.; Software, D.Z.-N.; Validation, V.O.-E., M.P.-C. and D.Z.-N.; Formal Analysis, M.P.-C.; Investigation, V.O.-E.; Resources, M.P.-C.; Data Curation, V.O.-E.; Writing—Original Draft Preparation, V.O.-E.; Writing—Review & Editing, D.Z.-N., M.P.-C.; Visualization, M.P.-C.; Supervision, V.O.-E.; Project Administration, V.O.-E.; Funding Acquisition, M.P.-C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by PRODEP-SEP with the grant number DSA/103.5/15/10814.
Acknowledgments
We appreciate the comments of anonymous reviewers to improve early versions of this document.
Conflicts of Interest
The author declares no conflict of interest.
Appendix A. Nomenclature
| Symbol | Description | Units |
| Wetting cross section of the micro-channel | m | |
| Surface in contact with the liquid layer | m | |
| R | Pipe inner radius | m |
| Contact angle of the liquid steam solid interface | rad | |
| Micro-channel angle to the vertical | rad | |
| Saturated temperature | K | |
| p | Groove’s depth in triangular micro-groove | m |
| Apex angle in triangular micro-groove | rad | |
| Angular liquid front position | rad | |
| Radius of semicircular groove | m | |
| Hydraulic radius of the micro-channel | m | |
| Effective of equivalent capillary radius in the direction of interest | m | |
| t | Time | s |
| Liquid density | kg/m | |
| Dynamic liquid viscosity | mPa s | |
| Surface tension | mN/m | |
| g | Gravitational acceleration | m/s |
| Kind of fluid: liquid sodium, HITEC salt, molten salt | none | |
| Liquid front velocity | m/s | |
| Type of groove: triangular, semi-circular | none |
Appendix B. Fluid Characteristics
This paper reports the utilization of four fluids of common use in the design of concentrated solar power systems [37,38,39]. Some useful features of those liquids are in Table A1.

Table A1.
Fluids utilized.
Table A1.
Fluids utilized.
| Fluid | Chemical Name | Temperature Range (K) | |
|---|---|---|---|
| 0 | Liquid Sodium | Na | |
| 1 | Water | HO | |
| 2 | HITEC Salt | NaNO-NaNO-KNO | |
| 3 | Molten Salt | KCl-MgCl |
Appendix C. Calculus of Variables for Liquid Sodium
Appendix D. Calculus of Variables for Water
Appendix E. Calculus of Variables for HITEC Salt
Appendix F. Calculus of Variables for Molten Salt
Appendix G. Micro-Groove Geometry
The calculus of the variables connected with the micro-groove geometry are in Table A2.

Table A2.
Micro-groove parameters (Source: [21]).
Table A2.
Micro-groove parameters (Source: [21]).
| Micro-Groove | |||||
|---|---|---|---|---|---|
| 0 | Semicircular | ||||
| 1 | Triangular |
References
- Ackermann, T. Wind Power in Power Systems; John Wiley: Chichester, UK, 2005; pp. 1–692. [Google Scholar]
- Chennouf, N.; Negrou, B.; Dokkar, B.; Settou, N. Valuation and estimation of geothermal electricity production using carbon dioxide as working fluid in the south of Algeria. Energy Procedia 2013, 36, 967–976. [Google Scholar] [CrossRef][Green Version]
- Brabec, C.; Sariciftci, N.; Hummelen, J. Plastic solar cells. Adv. Funct. Mater. 2001, 11, 15–26. [Google Scholar] [CrossRef]
- Demirbas, A. Progress and recent trends in biofuels. Prog. Energy Combust. Sci. 2007, 33, 1–18. [Google Scholar] [CrossRef]
- Hoffert, M.; Caldeira, K.; Benford, G.; Criswell, D.; Green, C.; Herzog, H.; Jain, A.; Kheshgi, H.; Lackner, K.; Lewis, J.; et al. Engineering: Advanced technology paths to global climate stability: Energy for a greenhouse planet. Science 2002, 298, 981–987. [Google Scholar] [CrossRef]
- Gupta, K.; Rehman, A.; Sarviya, R. Bio-fuels for the gas turbine: A review. Renew. Sustain. Energy Rev. 2010, 14, 2946–2955. [Google Scholar] [CrossRef]
- Pelc, R.; Fujita, R. Renewable energy from the ocean. Mar. Policy 2002, 26, 471–479. [Google Scholar] [CrossRef]
- Bajpai, P.; Dash, V. Hybrid renewable energy systems for power generation in stand-alone applications: A review. Renew. Sustain. Energy Rev. 2012, 16, 2926–2939. [Google Scholar] [CrossRef]
- Chu, S.; Majumdar, A. Opportunities and challenges for a sustainable energy future. Nature 2012, 488, 294–303. [Google Scholar] [CrossRef]
- Odeh, S.; Morrison, G.; Behnia, M. Modelling of parabolic trough direct steam generation solar collectors. Sol. Energy 1998, 62, 395–406. [Google Scholar] [CrossRef]
- Shen, Y.; Zhang, H.; Xu, H.; Yu, P.; Bai, T. Maximum heat transfer capacity of high temperature heat pipe with triangular grooved wick. J. Cent. South Univ. 2015, 22, 386–391. [Google Scholar] [CrossRef]
- Lu, J.; Ding, J.; Yu, T.; Shen, X. Enhanced heat transfer performances of molten salt receiver with spirally grooved pipe. Appl. Therm. Eng. 2015, 88, 491–498. [Google Scholar] [CrossRef]
- Weinstein, L.A.; Loomis, J.; Bhatia, B.; Bierman, D.M.; Wang, E.N.; Chen, G. Concentrating Solar Power. Chem. Rev. 2015, 115, 12797–12838. [Google Scholar] [CrossRef] [PubMed]
- Wang, K.J.; Yang, J.W. Sunlight concentrator design using a revised genetic algorithm. Renew. Energy 2014, 72, 322–335. [Google Scholar] [CrossRef]
- Nazemi, S.; Boroushaki, M. Design, Analysis and Optimization of a Solar Dish/Stirling System. Int. J. Renew. Energy Dev. 2016, 5, 33–42. [Google Scholar] [CrossRef]
- Zhao, J.; Song, Y.; Lam, W.H.; Liu, W.; Liu, Y.; Zhang, Y.; Wang, D. Solar radiation transfer and performance analysis of an optimum photovoltaic/thermal system. Energy Convers. Manag. 2011, 52, 1343–1353. [Google Scholar] [CrossRef]
- Petersont, G.; Lu, X.; Peng, X.; Wang, B. Analytical and experimental investigation of the rewetting of circular channels with internal V-grooves. Int. J. Heat Mass Transf. 1992, 35, 3085–3093. [Google Scholar] [CrossRef]
- Jaramillo, O.; Borunda, M.; Velazquez-Lucho, K.; Robles, M. Parabolic trough solar collector for low enthalpy processes: An analysis of the efficiency enhancement by using twisted tape inserts. Renew. Energy 2016, 93, 125–141. [Google Scholar] [CrossRef]
- Hübner, S.; Eck, M.; Stiller, C.; Seitz, M. Techno-economic heat transfer optimization of large scale latent heat energy storage systems in solar thermal power plants. Appl. Therm. Eng. 2016, 98, 483–491. [Google Scholar] [CrossRef]
- Muñoz, J.; Abánades, A. Analysis of internal helically finned tubes for parabolic trough design by CFD tools. Appl. Energy 2011, 88, 4139–4149. [Google Scholar] [CrossRef]
- Dung, N.D.T.; Wang, K.J.; Chuang, F.S.; Kung, K.Y. Optimizing the design of receiver in parabolic trough by using genetic algorithm. Eur. J. Mech. B/Fluids 2015, 49 Pt A, 146–152. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control and Artificial Intelligence; MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Rojas, M.; de Andrés, M. Theoretical and experimental study of two-phase flow in micro-channels grooved into horizontal pipes. Int. J. Multiph. Flow 2006, 32, 517–526. [Google Scholar] [CrossRef]
- Wolpert, D.; Macready, W. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef]
- Hoffmann, J.F.; Henry, J.F.; Vaitilingom, G.; Olives, R.; Chirtoc, M.; Caron, D.; Py, X. Temperature dependence of thermal conductivity of vegetable oils for use in concentrated solar power plants, measured by 3omega hot wire method. Int. J. Therm. Sci. 2016, 107, 105–110. [Google Scholar] [CrossRef]
- Benoit, H.; Spreafico, L.; Gauthier, D.; Flamant, G. Review of heat transfer fluids in tube-receivers used in concentrating solar thermal systems: Properties and heat transfer coefficients. Renew. Sustain. Energy Rev. 2016, 55, 298–315. [Google Scholar] [CrossRef]
- Dung, N.; Chuang, F.S.; Wang, K.J. Capillary-driven flow analysis of a micro-grooved pipe. Contin. Mech. Thermodyn. 2014, 26, 423–435. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential Evolution—A Simple and Efficient Heuristic for Global Optimization over Continuous Spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Das, S.; Suganthan, P. Differential evolution: A survey of the state-of-the-art. IEEE Trans. Evol. Comput. 2011, 15, 4–31. [Google Scholar] [CrossRef]
- Chen, P.; Li, J.; Liu, Z. Solving 0-1 knapsack problems by a discrete binary version of differential evolution. In Proceedings of the 2008 Second International Symposium on Intelligent Information Technology Application, Shanghai, China, 20–22 December 2008; Volume 2, pp. 513–516. [Google Scholar]
- Farmer, J.; Packard, N.; Perelson, A. The immune system, adaptation, and machine learning. Phys. D Nonlinear Phenom. 1986, 22, 187–204. [Google Scholar] [CrossRef]
- De Castro, L.; Von Zuben, F. Learning and optimization using the clonal selection principle. IEEE Trans. Evol. Comput. 2002, 6, 239–251. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the IEEE International Conference on Neural Networks, Western Australia, Perth, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Khanesar, M.; Teshnehlab, M.; Shoorehdeli, M. A novel binary particle swarm optimization. In Proceedings of the 2007 Mediterranean Conference on Control and Automation, MED, Athens, Greece, 27–29 June 2007; pp. 1–6. [Google Scholar]
- Whitley, D. An overview of evolutionary algorithms: Practical issues and common pitfalls. Inf. Softw. Technol. 2001, 43, 817–831. [Google Scholar] [CrossRef]
- Yang, X.S.; Deb, S.; Loomes, M.; Karamanoglu, M. A framework for self-tuning optimization algorithm. Neural Comput. Appl. 2013, 23, 2051–2057. [Google Scholar] [CrossRef]
- Fink, J.; Leibowitz, L. Thermodynamic and Transport Properties of Sodium Liquid and Vapor; Argonne National Lab.: Argonn, IL, USA, 1995. [Google Scholar] [CrossRef]
- GmbH, D. Saturated Liquid Density. 2016. Available online: http://ddbonline.ddbst.de/DIPPR105DensityCalculation/DIPPR105CalculationCGI.exe?component=Methanol (accessed on 1 December 2019).
- Sohal, M.S.; Ebner, M.A.; Sabharwall, P.; Sharpe, P. Engineering Database of Liquid Salt Thermophysical and Thermochemical Properties; Idaho National Laboratory: Idaho Falls, ID, USA, 2010. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).