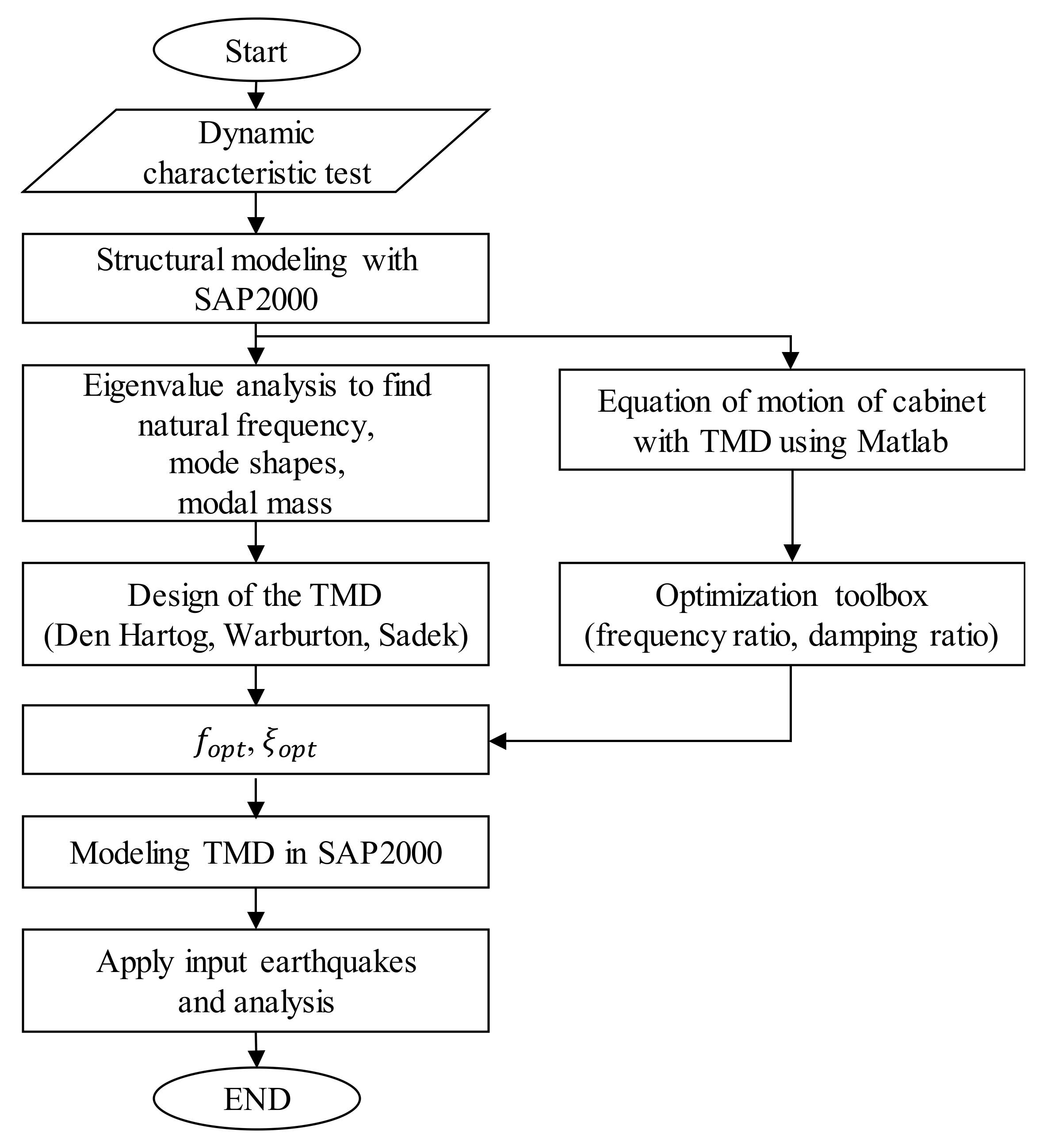
Figure 1.
Tuned mass damper (TMD) design and analysis process in this study.
Figure 1.
Tuned mass damper (TMD) design and analysis process in this study.
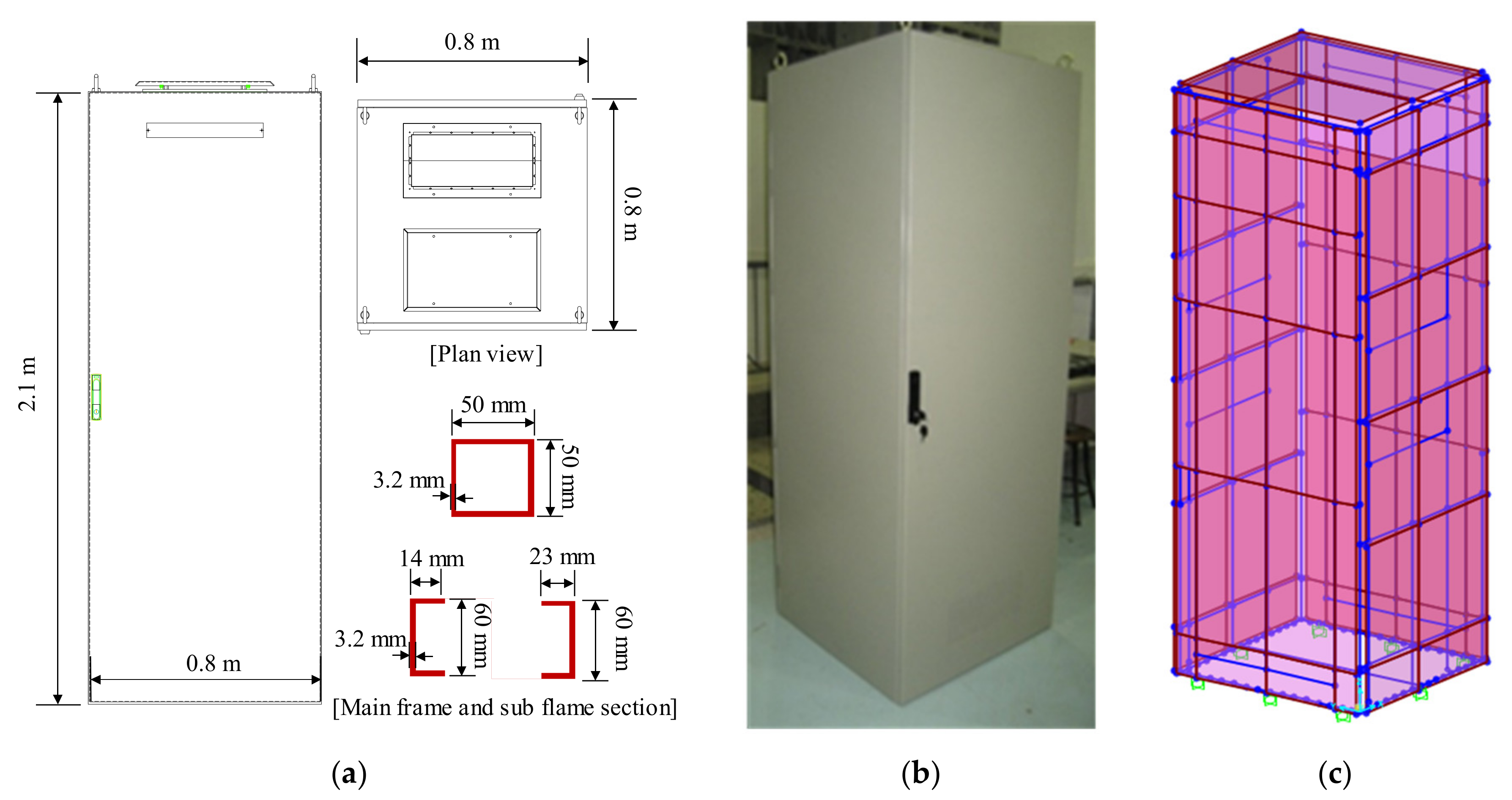
Figure 2.
Electrical cabinet model: (a) Dimensions of the electrical cabinet; (b) Prototype of the electrical cabinet; and, (c) Finite element model.
Figure 2.
Electrical cabinet model: (a) Dimensions of the electrical cabinet; (b) Prototype of the electrical cabinet; and, (c) Finite element model.
Figure 3.
Shaking table test of the electrical cabinet: (a) Cabinet and sensors; and, (b) Shaking table and servo motor.
Figure 3.
Shaking table test of the electrical cabinet: (a) Cabinet and sensors; and, (b) Shaking table and servo motor.
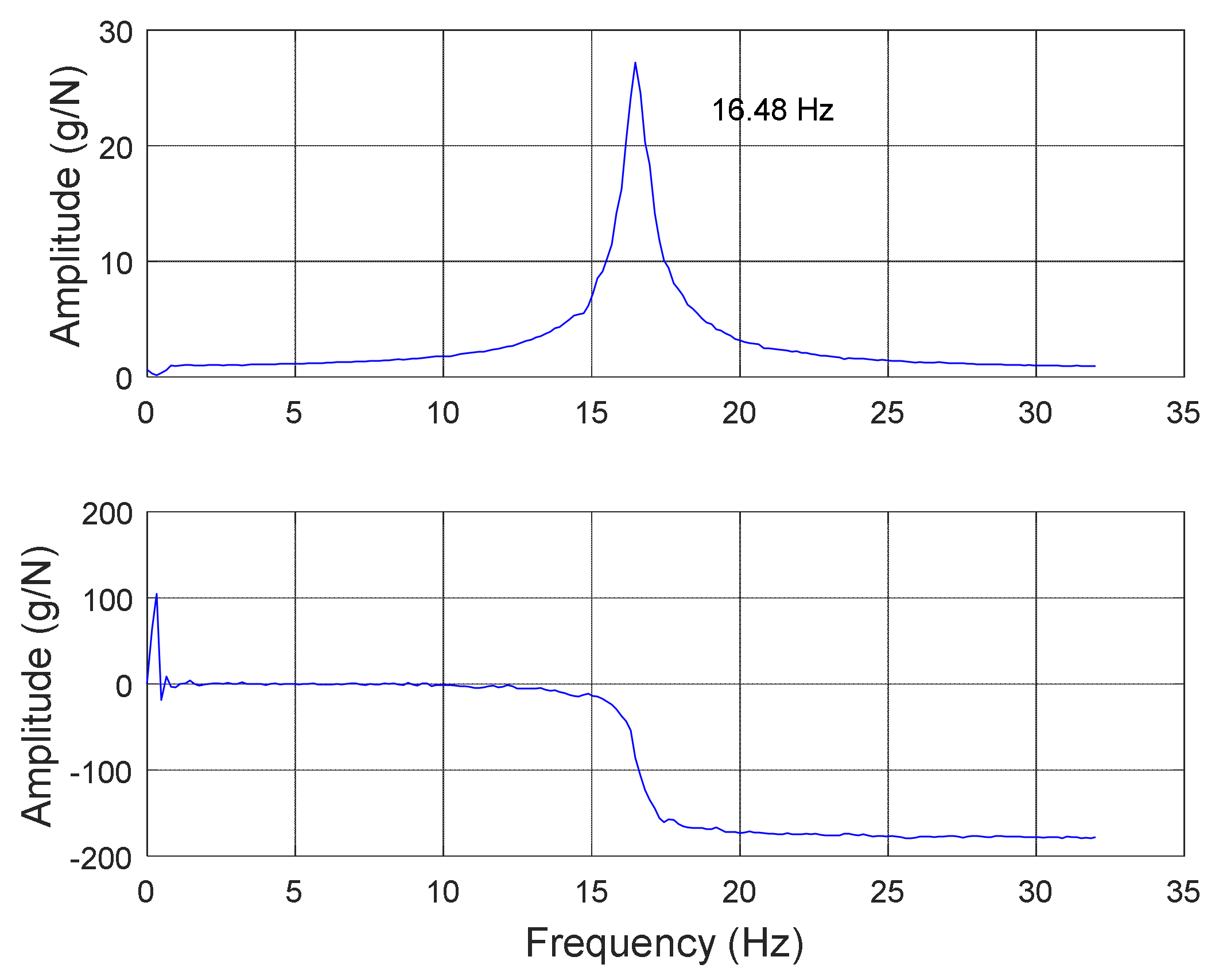
Figure 4.
Transfer function of the electrical cabinet obtained from shaking table test.
Figure 4.
Transfer function of the electrical cabinet obtained from shaking table test.
Figure 5.
Mode shapes of the electrical cabinet: (a) First mode (x-direction); (b) Second mode (x-direction); (c) Third mode (y-direction); and (d) Fourth mode (x-direction).
Figure 5.
Mode shapes of the electrical cabinet: (a) First mode (x-direction); (b) Second mode (x-direction); (c) Third mode (y-direction); and (d) Fourth mode (x-direction).
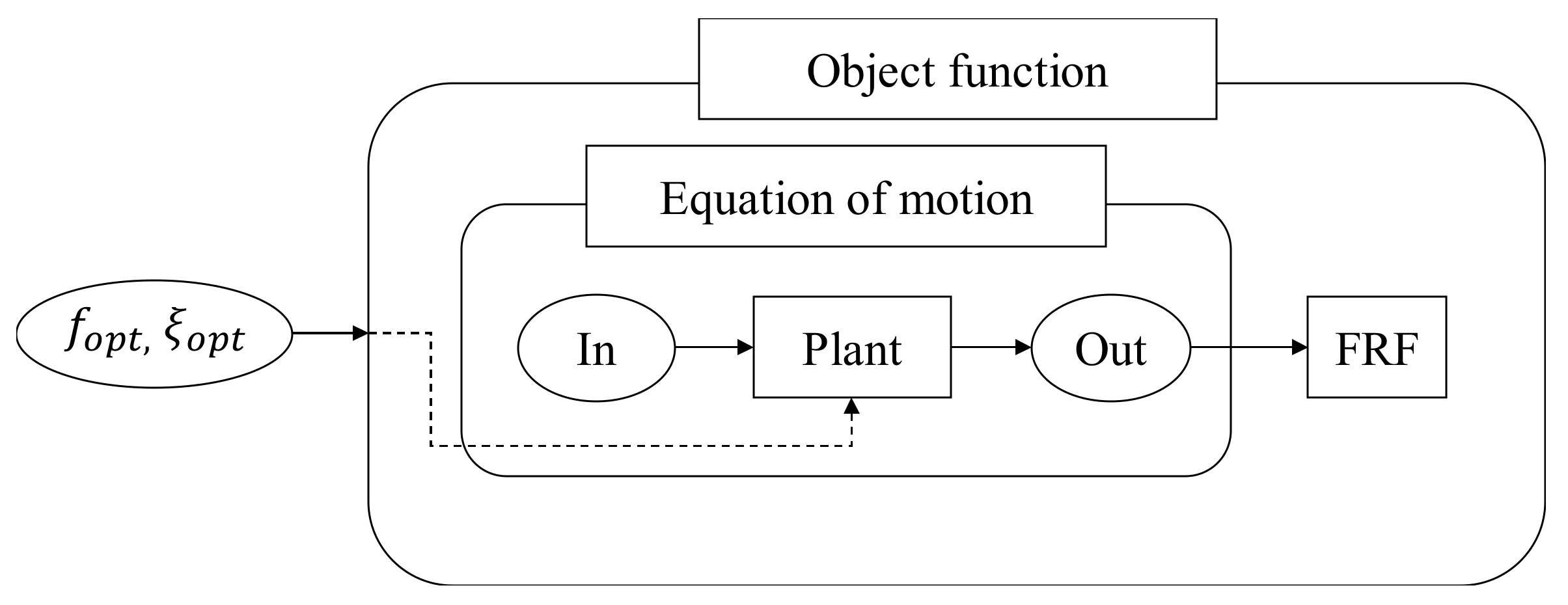
Figure 6.
Block diagram of the objective function.
Figure 6.
Block diagram of the objective function.
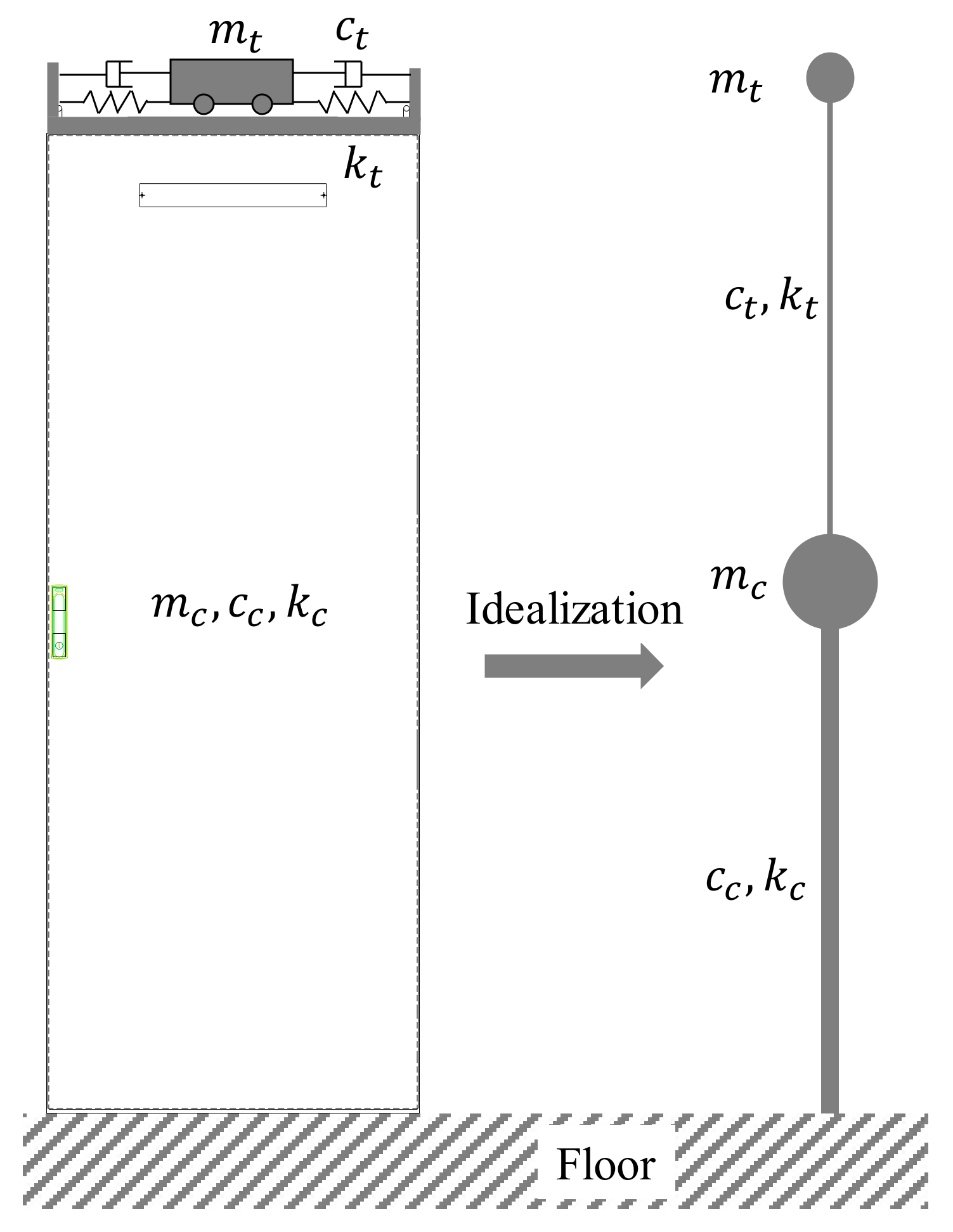
Figure 7.
TMD installation concept and idealization.
Figure 7.
TMD installation concept and idealization.
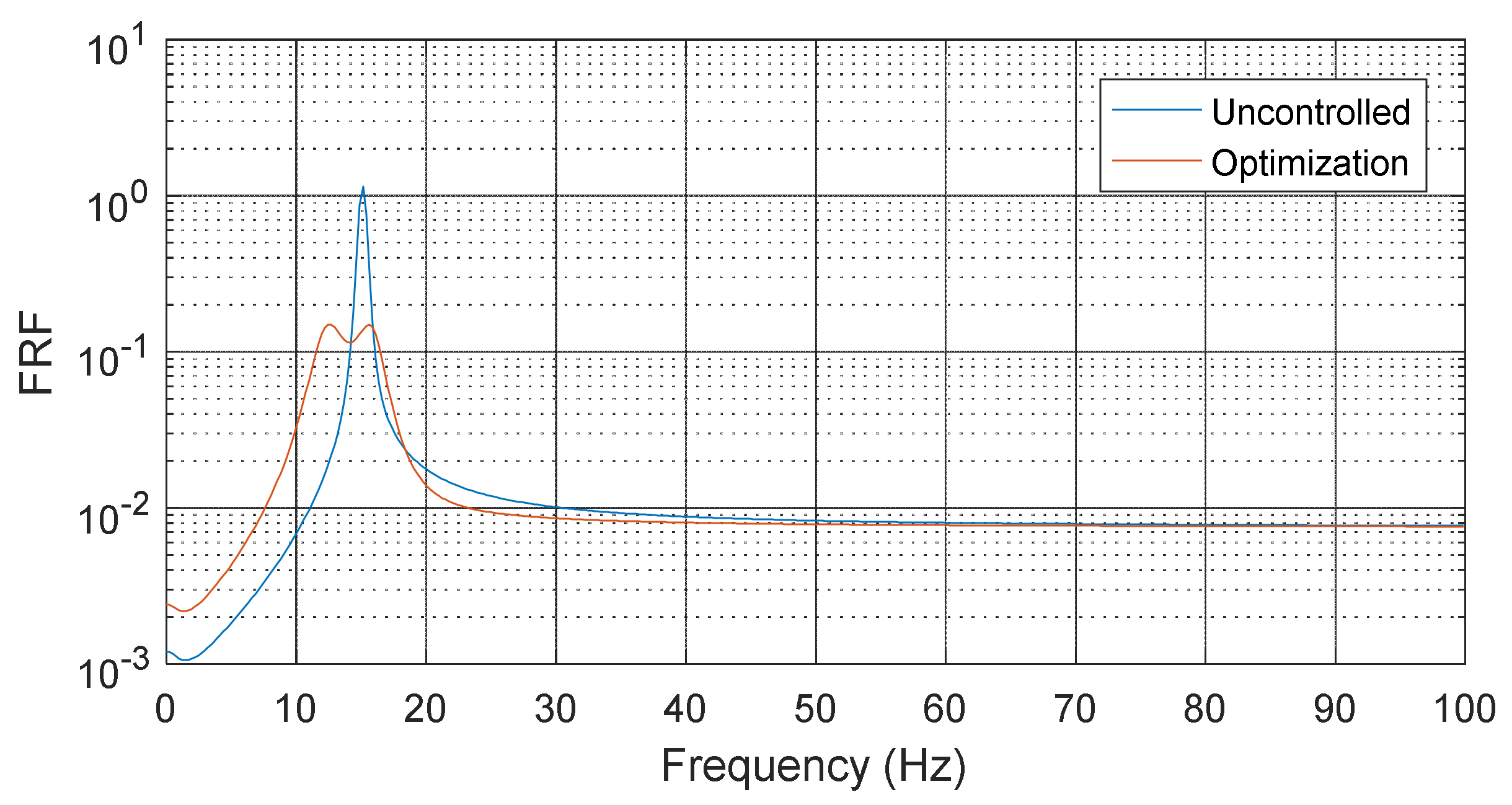
Figure 8.
Frequency response function (FRF) of electrical cabinet before and after optimization under sinusoidal sweep wave.
Figure 8.
Frequency response function (FRF) of electrical cabinet before and after optimization under sinusoidal sweep wave.
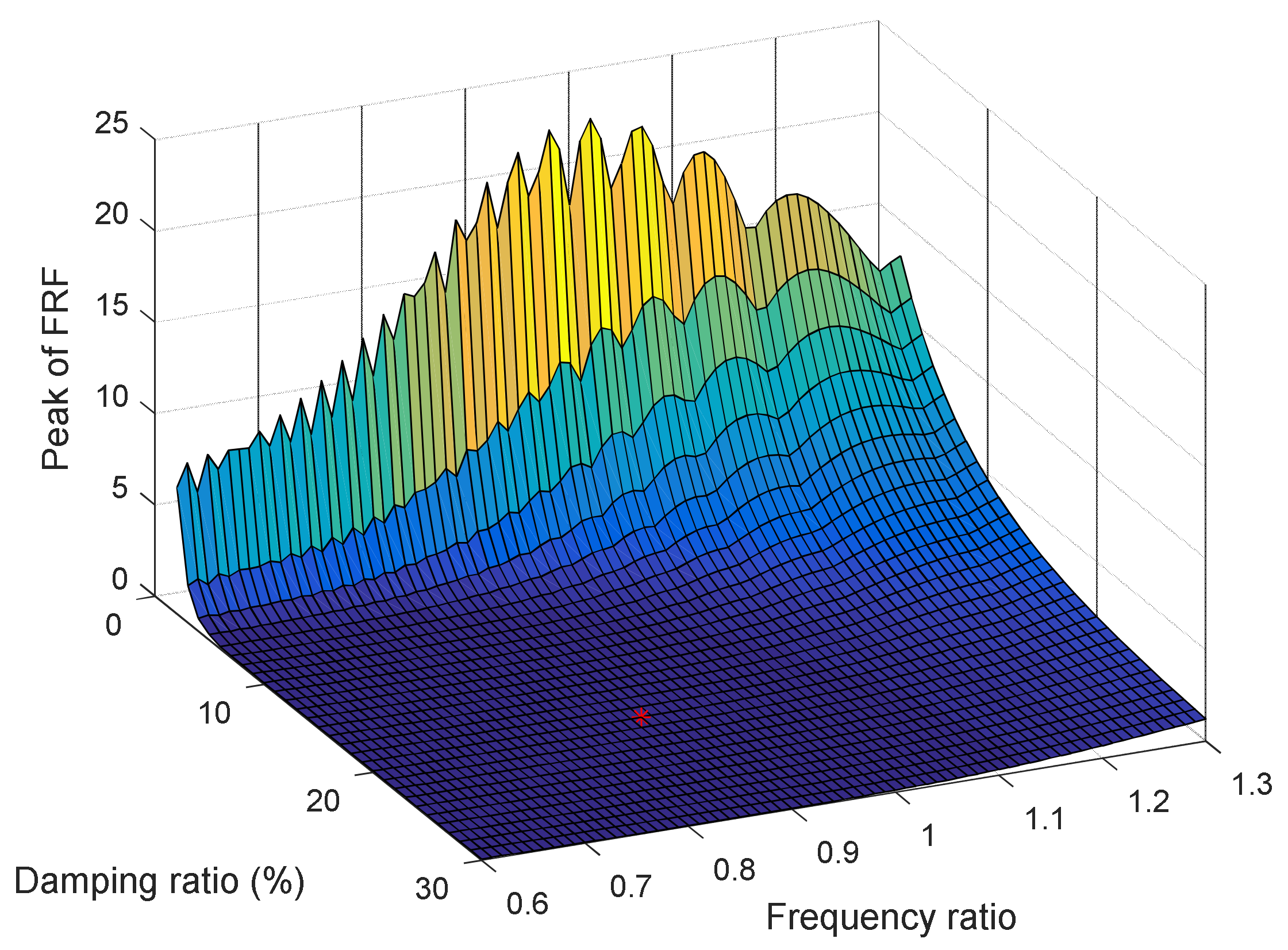
Figure 9.
FRF peak surface depending on TMD parameters.
Figure 9.
FRF peak surface depending on TMD parameters.
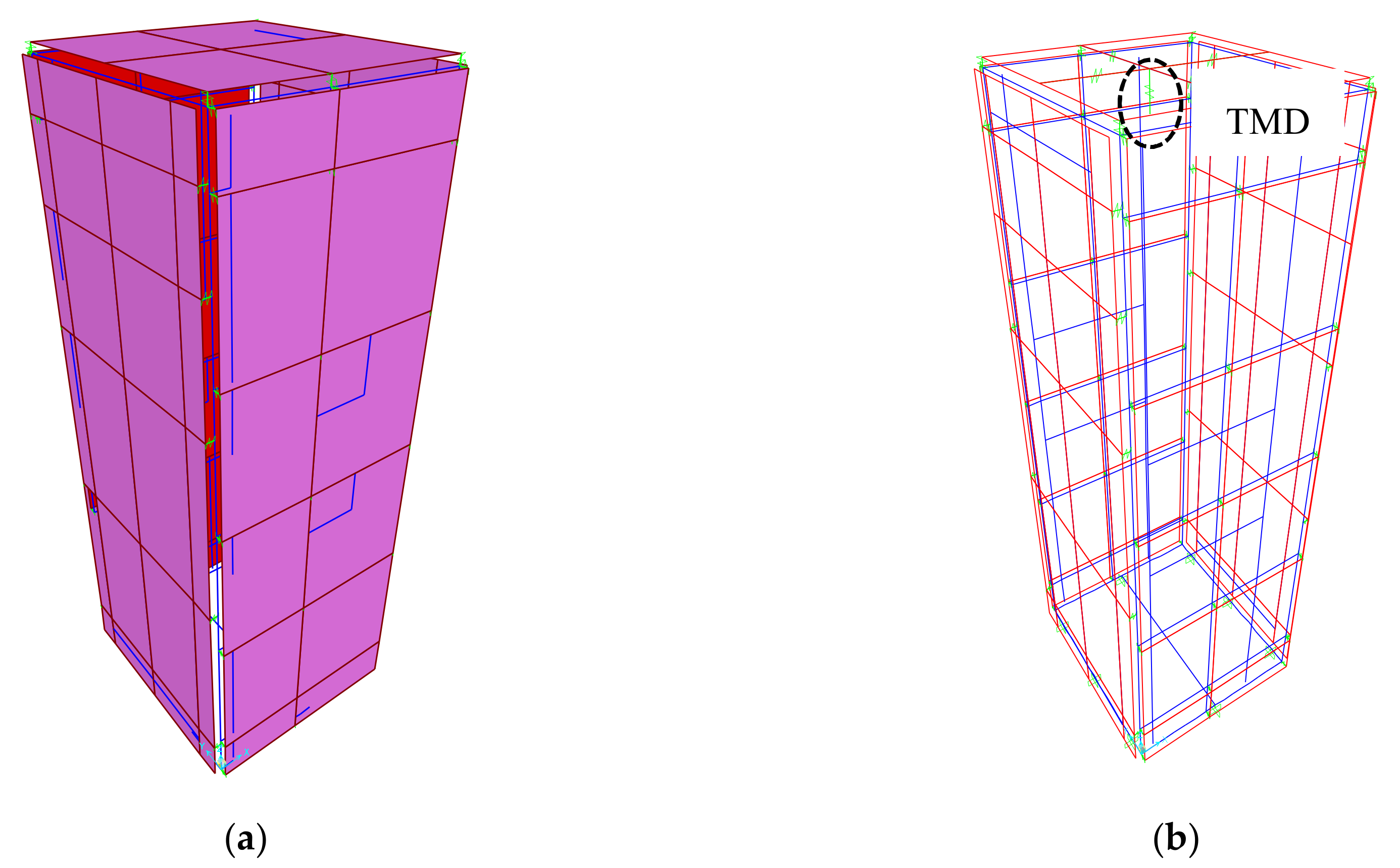
Figure 10.
Numerical models of electrical cabinet: (a) Without a TMD; and, (b) With a TMD.
Figure 10.
Numerical models of electrical cabinet: (a) Without a TMD; and, (b) With a TMD.
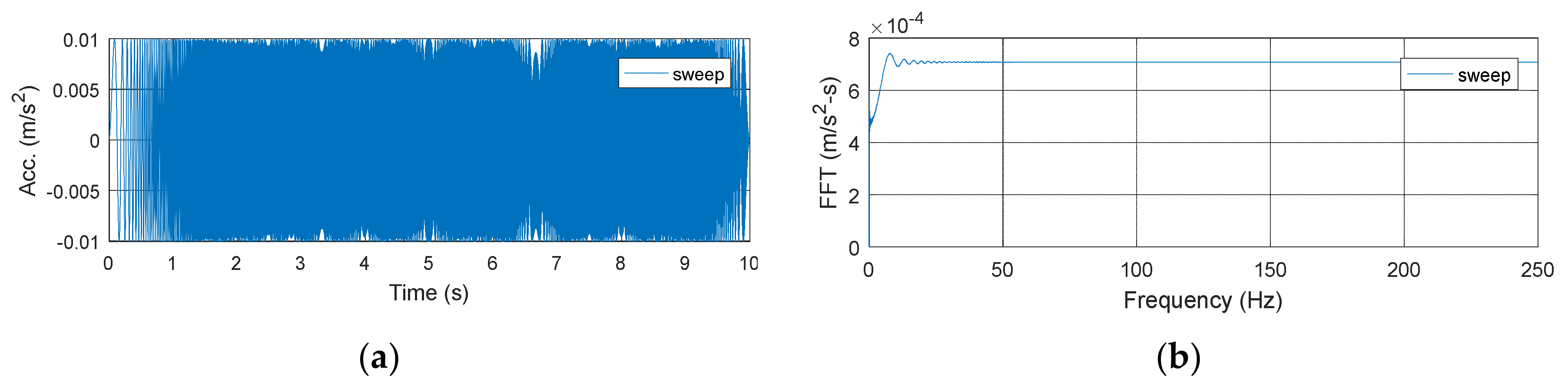
Figure 11.
Sinusoidal sweep wave and its fast Fourier transform (FFT): (a) Sweep wave; (b) FFT.
Figure 11.
Sinusoidal sweep wave and its fast Fourier transform (FFT): (a) Sweep wave; (b) FFT.
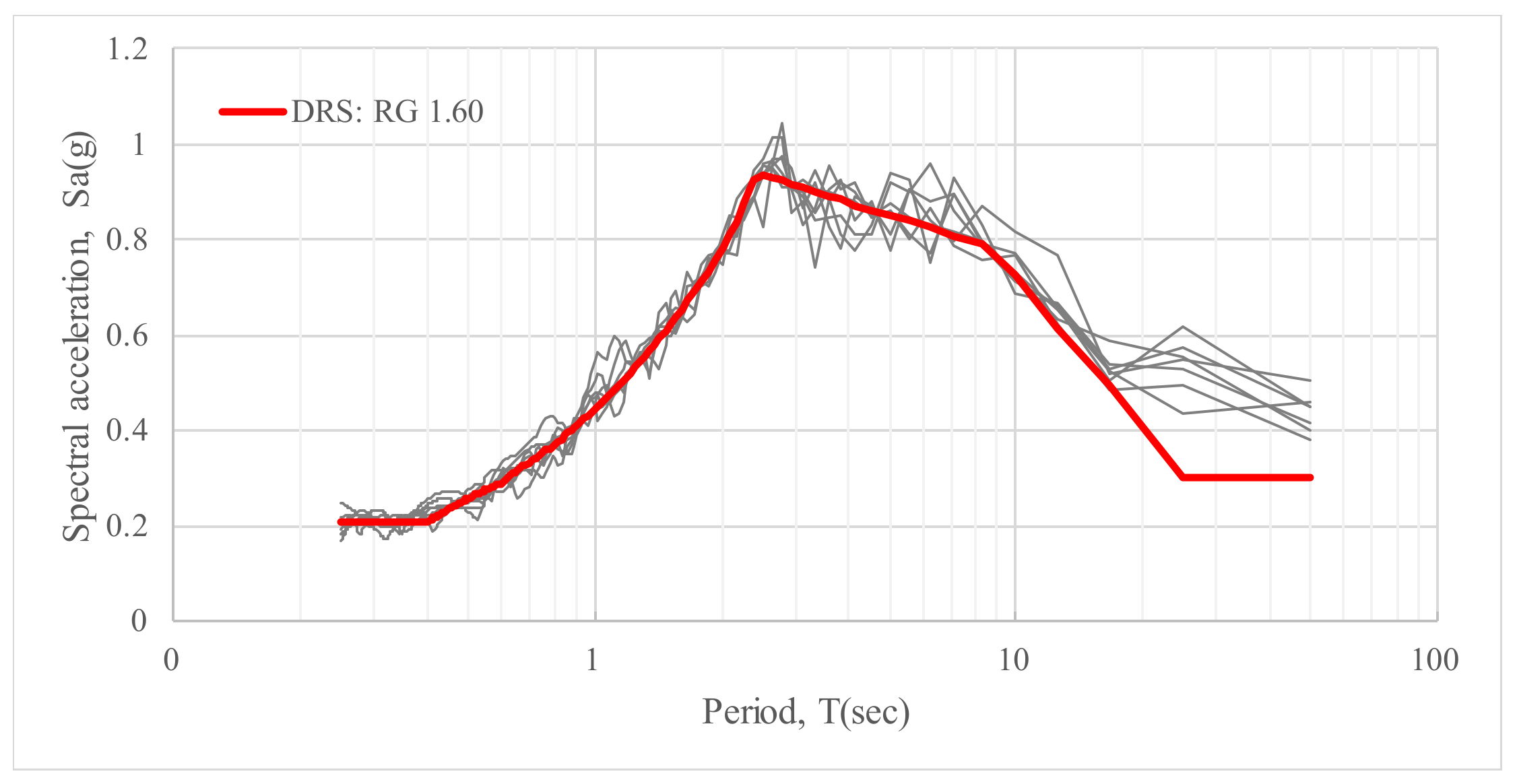
Figure 12.
Horizontal design response spectrum (DRS) of RG 1.60 spectrum (5% damping).
Figure 12.
Horizontal design response spectrum (DRS) of RG 1.60 spectrum (5% damping).
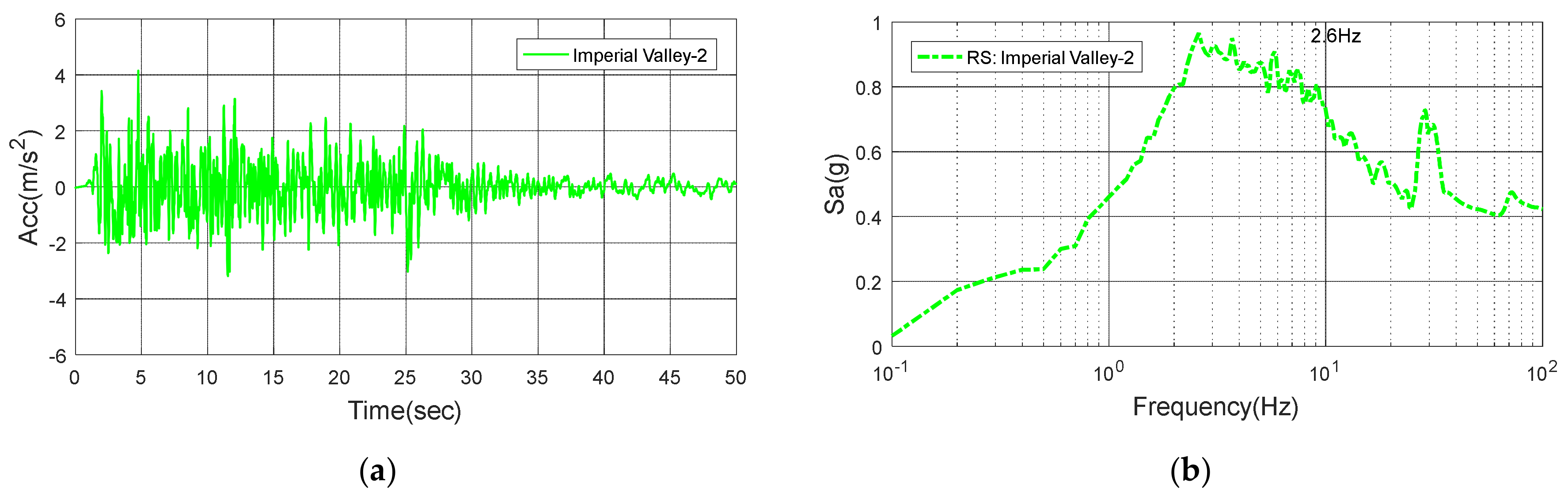
Figure 13.
Imperial Valley-2: (a) Time history; (b) Response spectrum.
Figure 13.
Imperial Valley-2: (a) Time history; (b) Response spectrum.
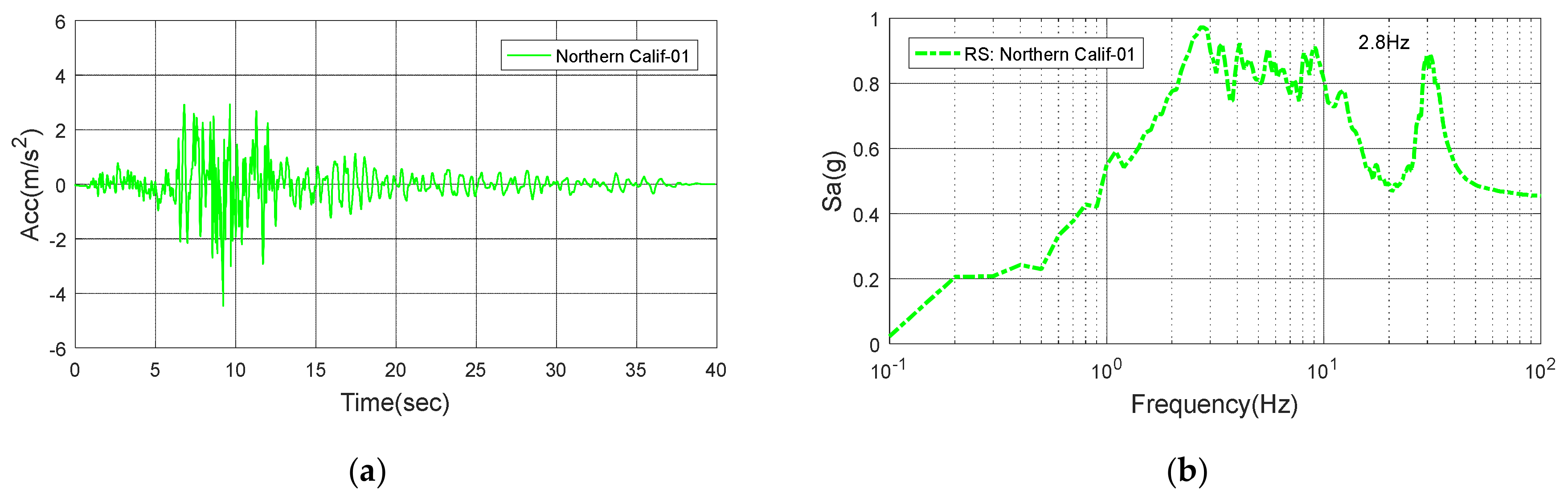
Figure 14.
Northern Calif-01: (a) Time history; (b) Response spectrum.
Figure 14.
Northern Calif-01: (a) Time history; (b) Response spectrum.
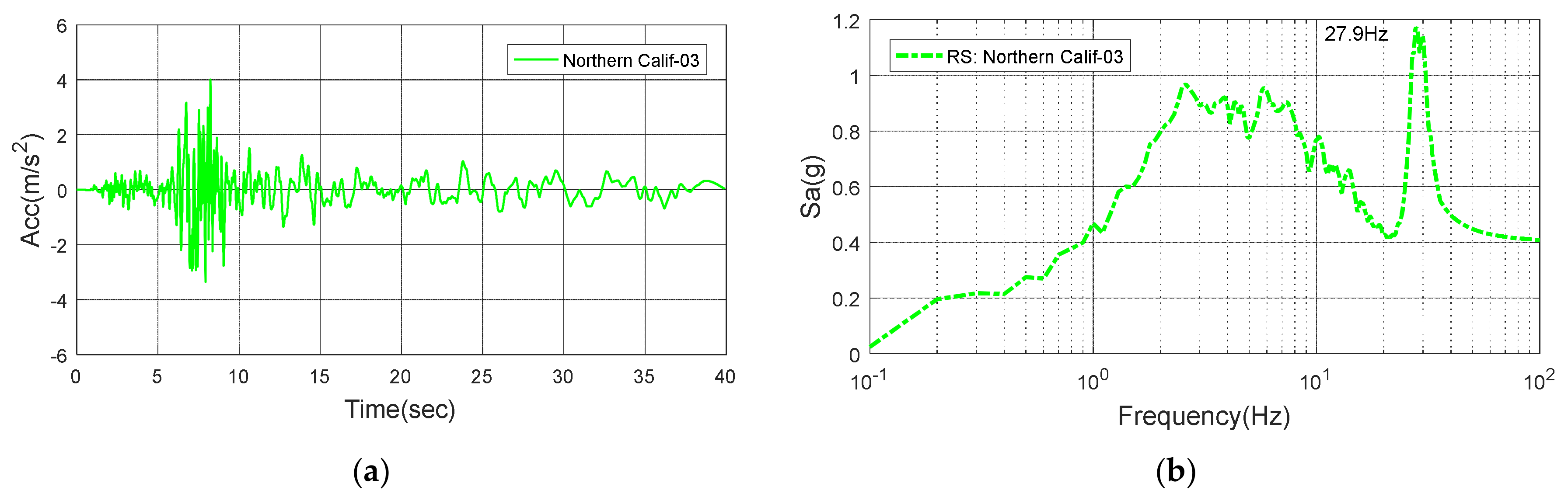
Figure 15.
Northern Calif-03: (a) Time history; (b) Response spectrum.
Figure 15.
Northern Calif-03: (a) Time history; (b) Response spectrum.
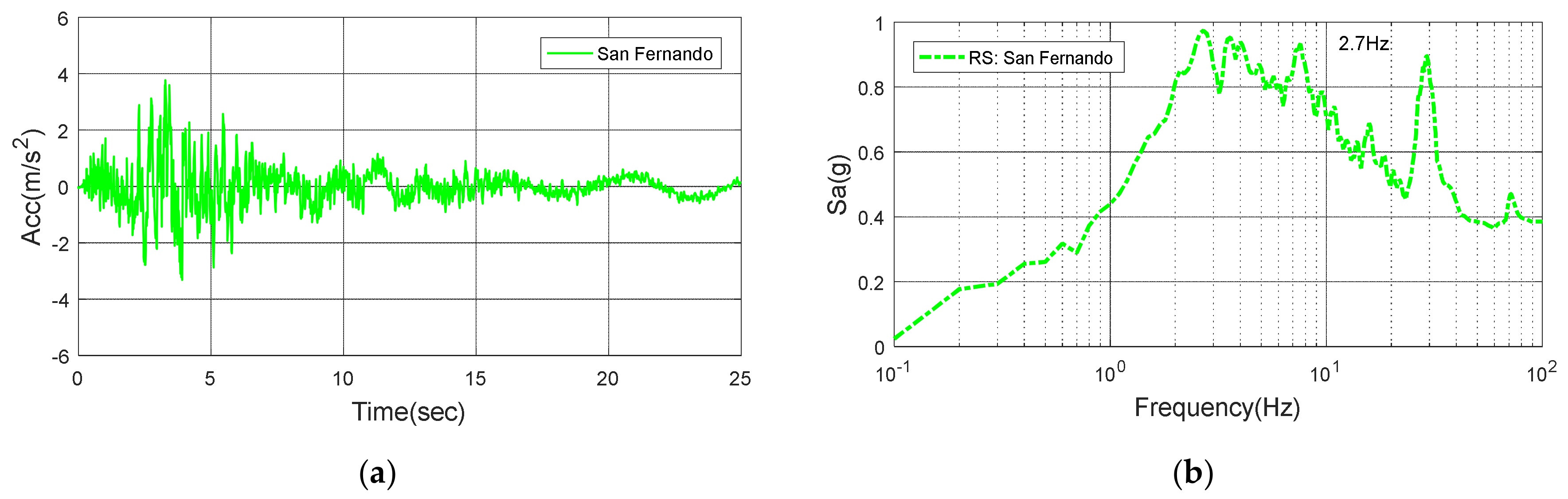
Figure 16.
San Fernando: (a) Time history; (b) Response spectrum.
Figure 16.
San Fernando: (a) Time history; (b) Response spectrum.
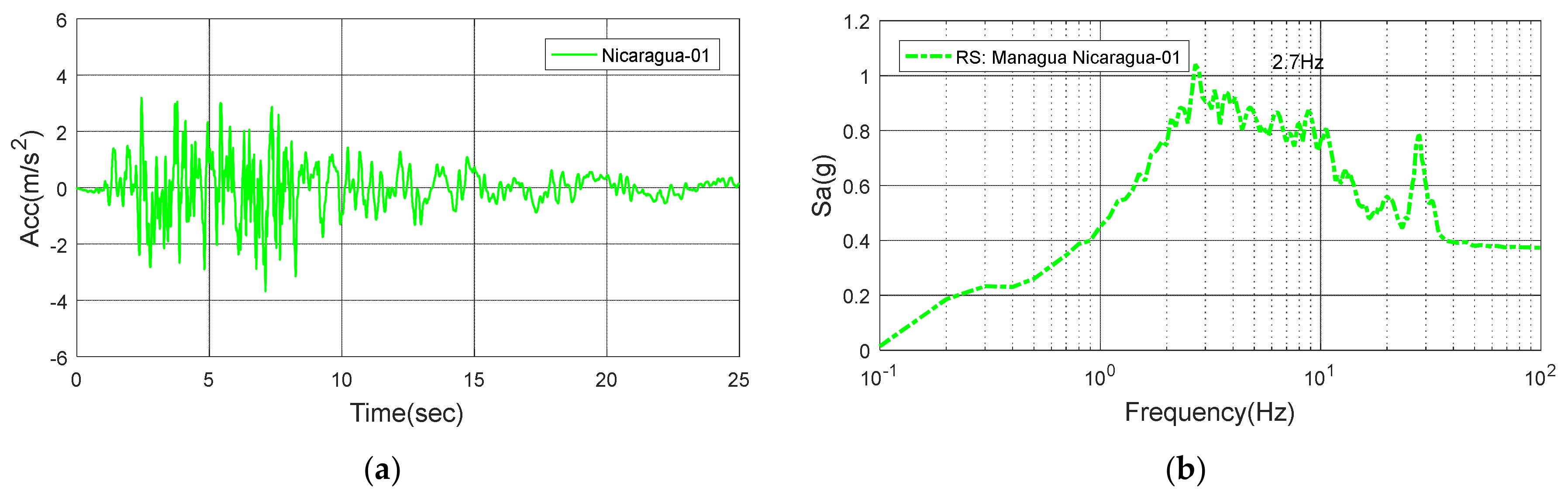
Figure 17.
Nicaragua-01: (a) Time history; (b) Response spectrum.
Figure 17.
Nicaragua-01: (a) Time history; (b) Response spectrum.
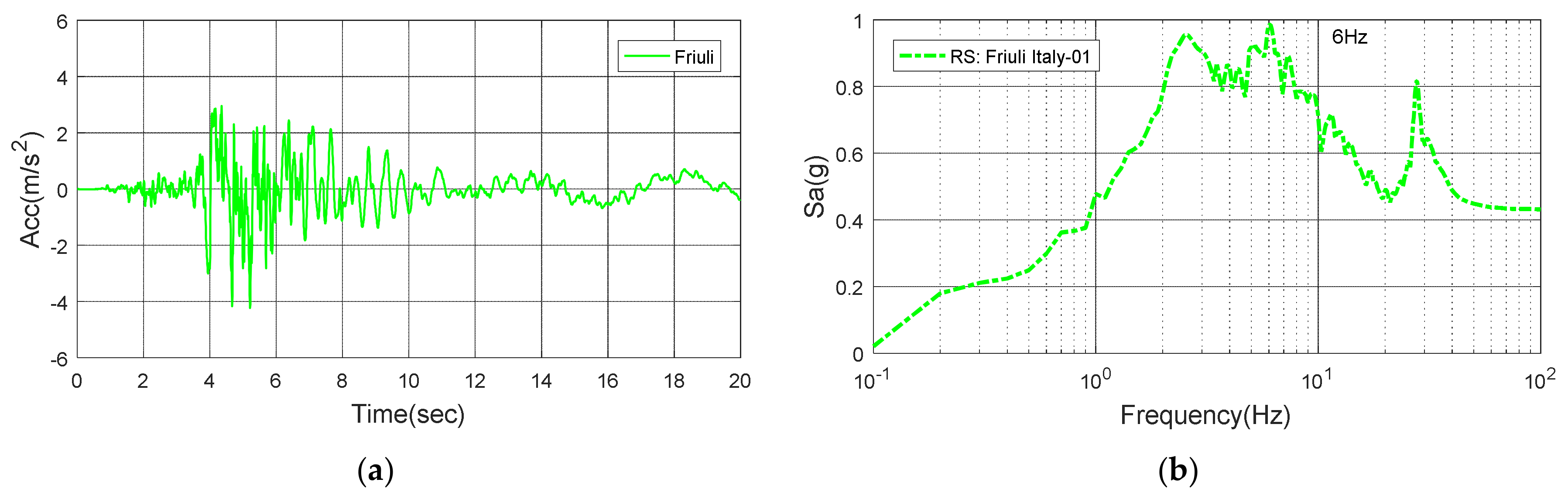
Figure 18.
Friuli: (a) Time history; (b) Response spectrum.
Figure 18.
Friuli: (a) Time history; (b) Response spectrum.
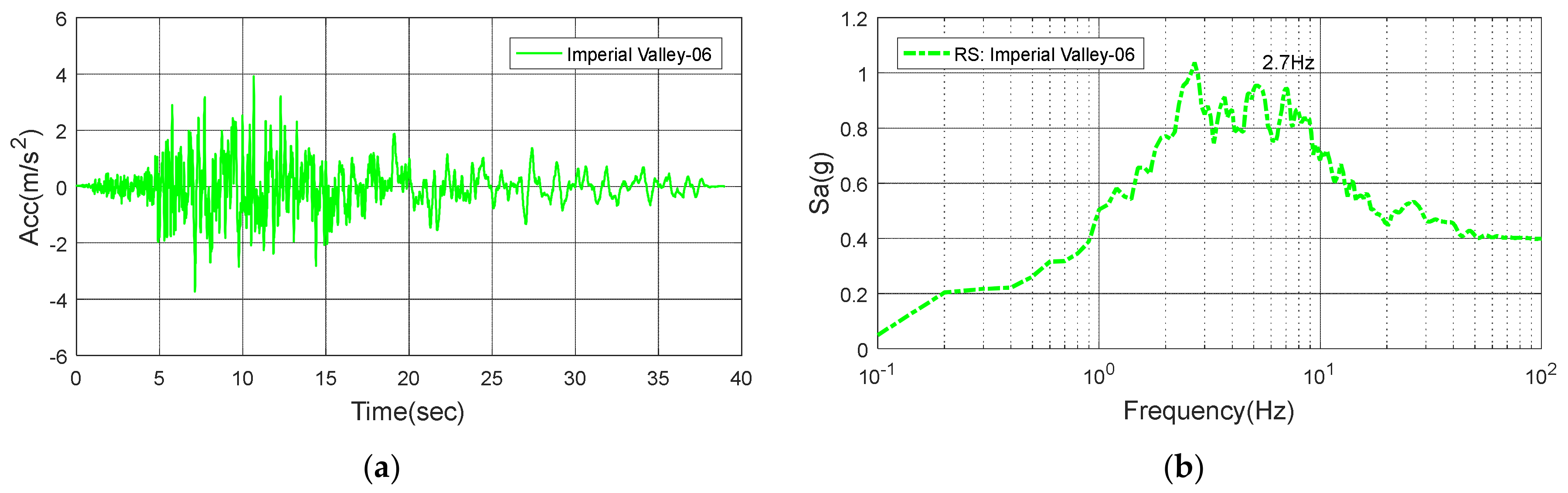
Figure 19.
Imperial Valley-06: (a) Time history; (b) Response spectrum.
Figure 19.
Imperial Valley-06: (a) Time history; (b) Response spectrum.
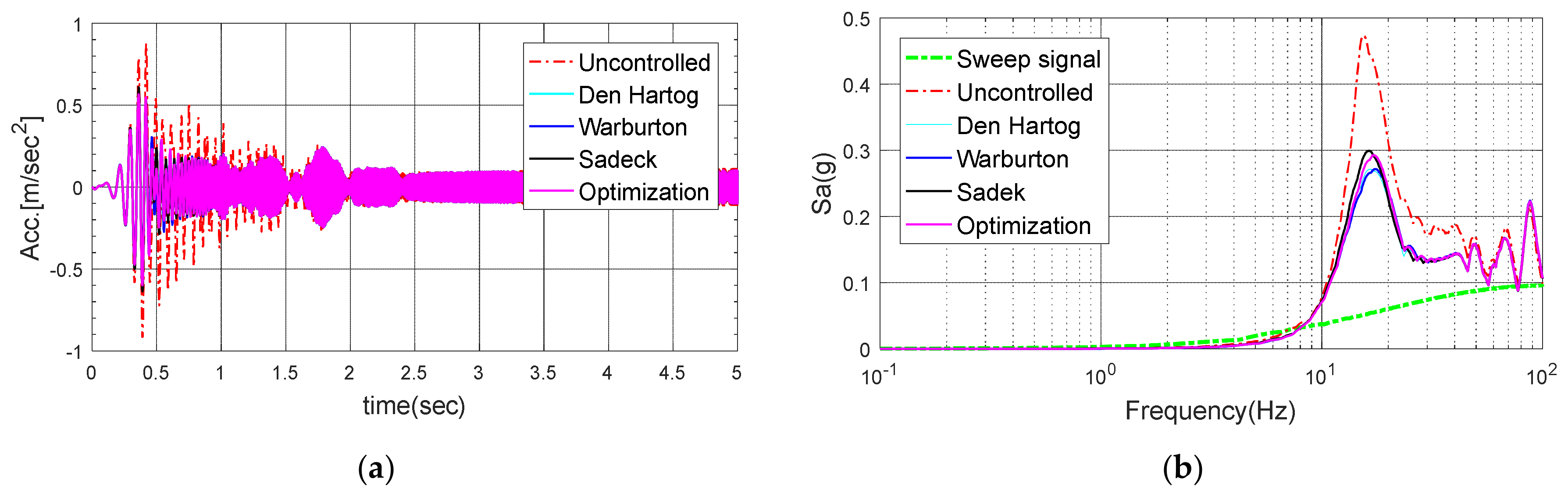
Figure 20.
Acceleration response at the top of the electrical cabinet when subjected to a sinusoidal sweep wave: (a) Time history; (b) Response spectrum.
Figure 20.
Acceleration response at the top of the electrical cabinet when subjected to a sinusoidal sweep wave: (a) Time history; (b) Response spectrum.
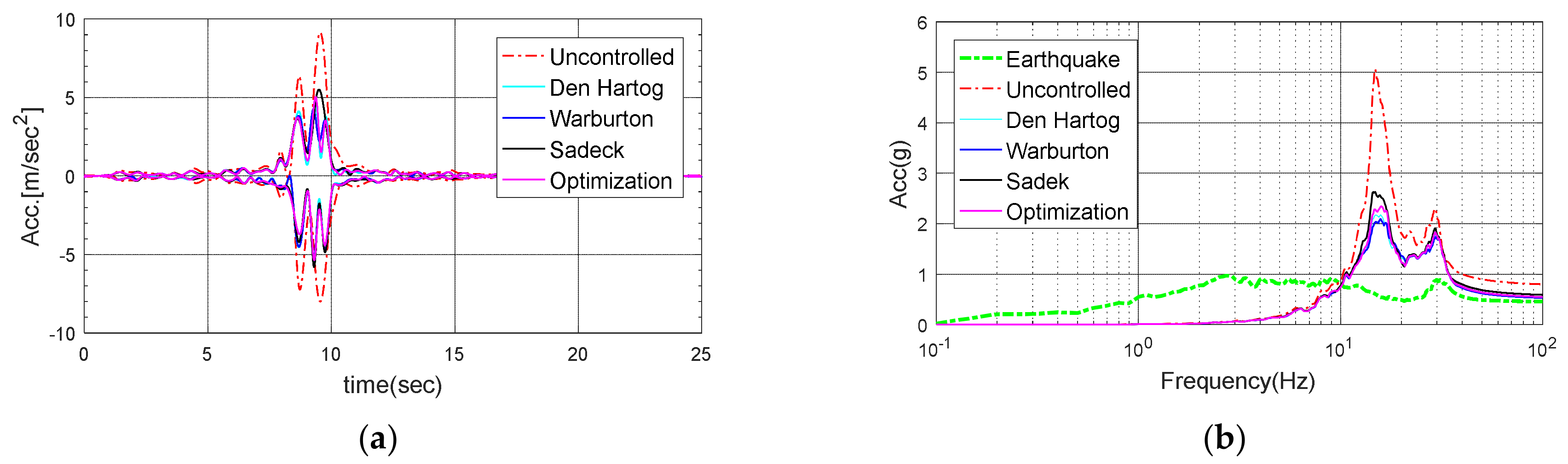
Figure 21.
Response of the electrical cabinet subjected to Imperial Valley-2: (a) Time history; (b) Response spectrum.
Figure 21.
Response of the electrical cabinet subjected to Imperial Valley-2: (a) Time history; (b) Response spectrum.
Figure 22.
Response of the electrical cabinet subjected to Northern Calif-01: (a) Time history; (b) Response spectrum.
Figure 22.
Response of the electrical cabinet subjected to Northern Calif-01: (a) Time history; (b) Response spectrum.
Figure 23.
Response of the electrical cabinet subjected to Northern Calif-03: (a) Time history; (b) Response spectrum.
Figure 23.
Response of the electrical cabinet subjected to Northern Calif-03: (a) Time history; (b) Response spectrum.
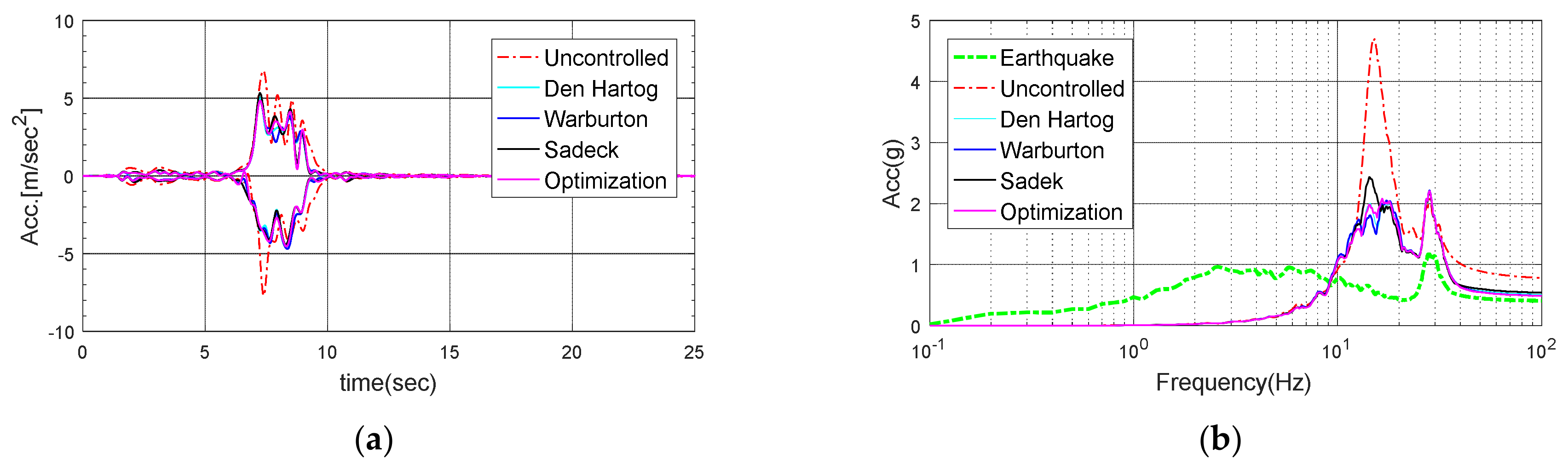
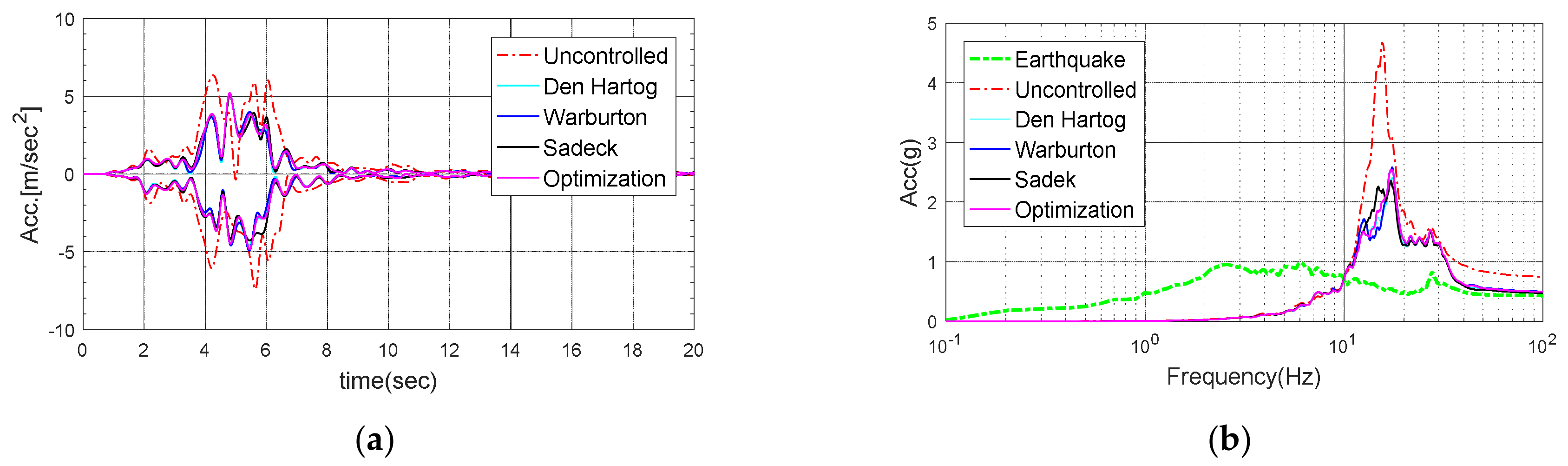
Figure 24.
Response of the electrical cabinet subjected to San Fernando: (a) Time history; (b) Response spectrum.
Figure 24.
Response of the electrical cabinet subjected to San Fernando: (a) Time history; (b) Response spectrum.
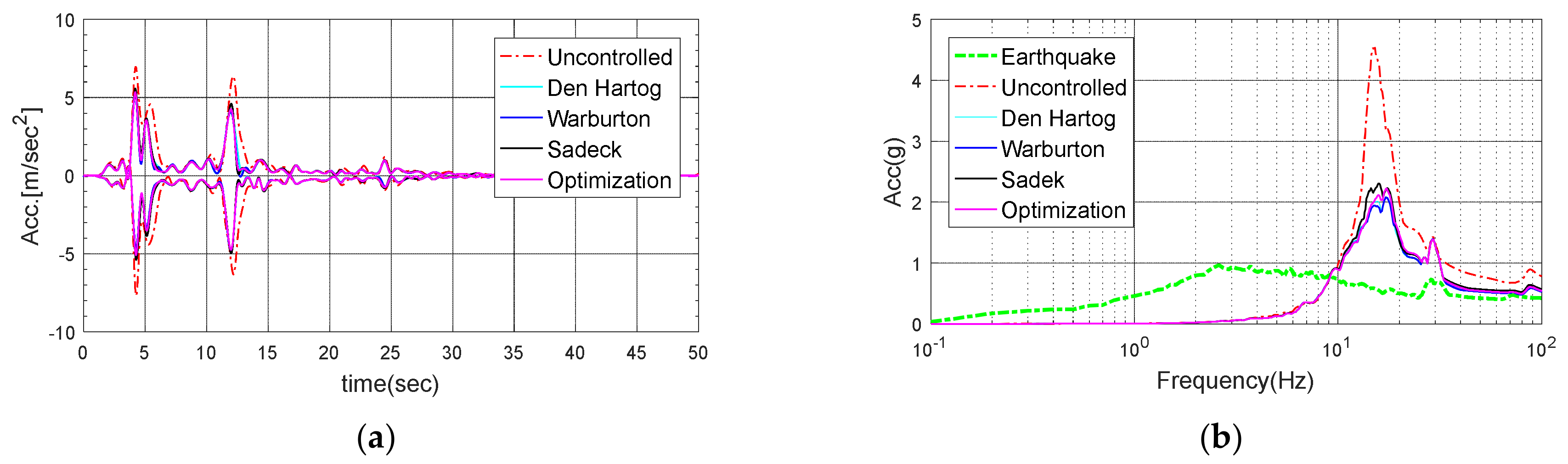
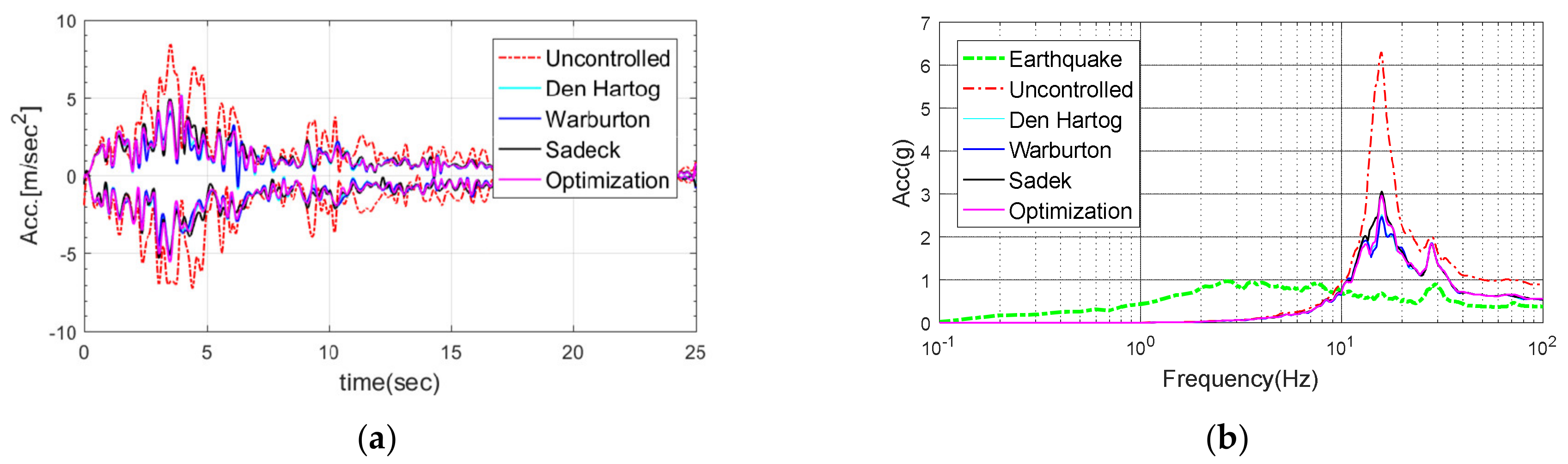
Figure 25.
Response of the electrical cabinet subjected to Nicaragua-01: (a) Time history; (b) Response spectrum.
Figure 25.
Response of the electrical cabinet subjected to Nicaragua-01: (a) Time history; (b) Response spectrum.
Figure 26.
Response of the electrical cabinet subjected to Friuli: (a) Time history; (b) Response spectrum.
Figure 26.
Response of the electrical cabinet subjected to Friuli: (a) Time history; (b) Response spectrum.
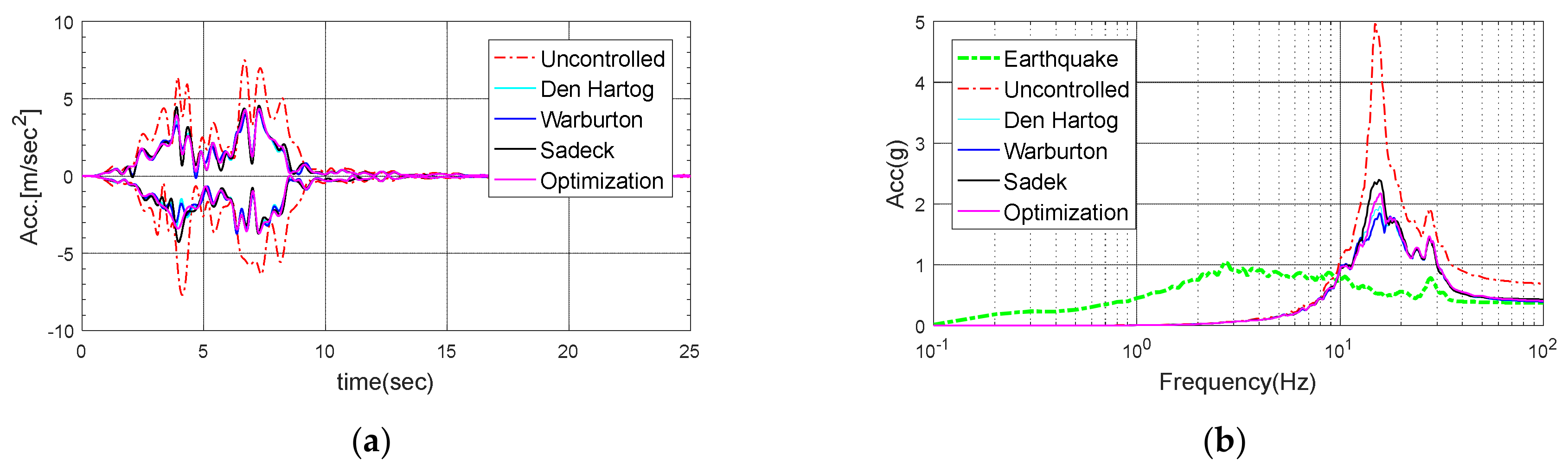
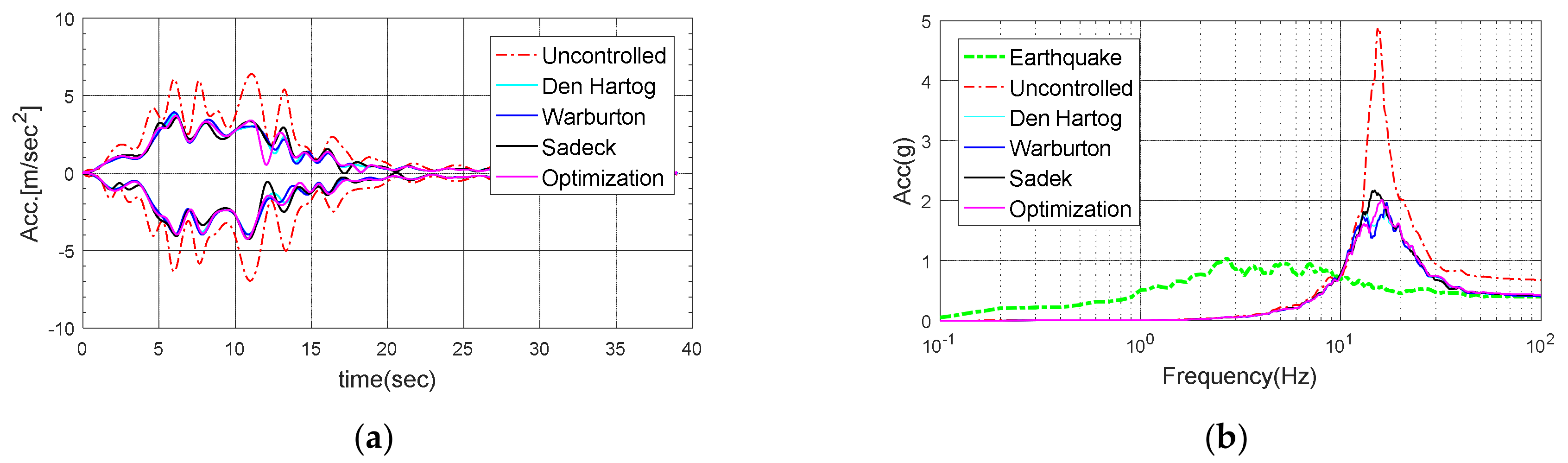
Figure 27.
Response of the electrical cabinet subjected to Imperial Valley-06: (a) Time history; (b) Response spectrum.
Figure 27.
Response of the electrical cabinet subjected to Imperial Valley-06: (a) Time history; (b) Response spectrum.
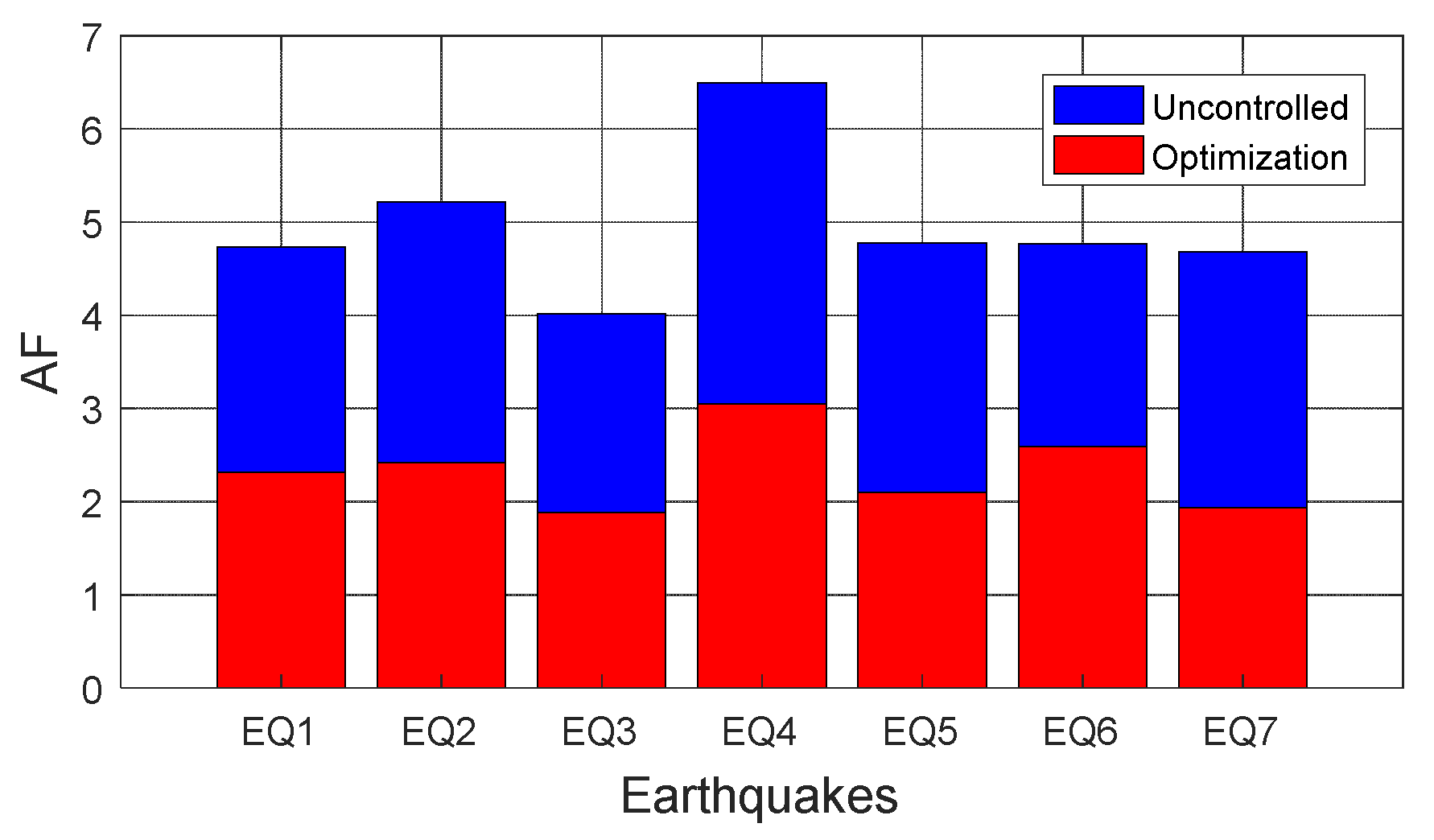
Figure 28.
Amplification factor (AF) due to seismic loads of the electrical cabinet with and without a TMD.
Figure 28.
Amplification factor (AF) due to seismic loads of the electrical cabinet with and without a TMD.
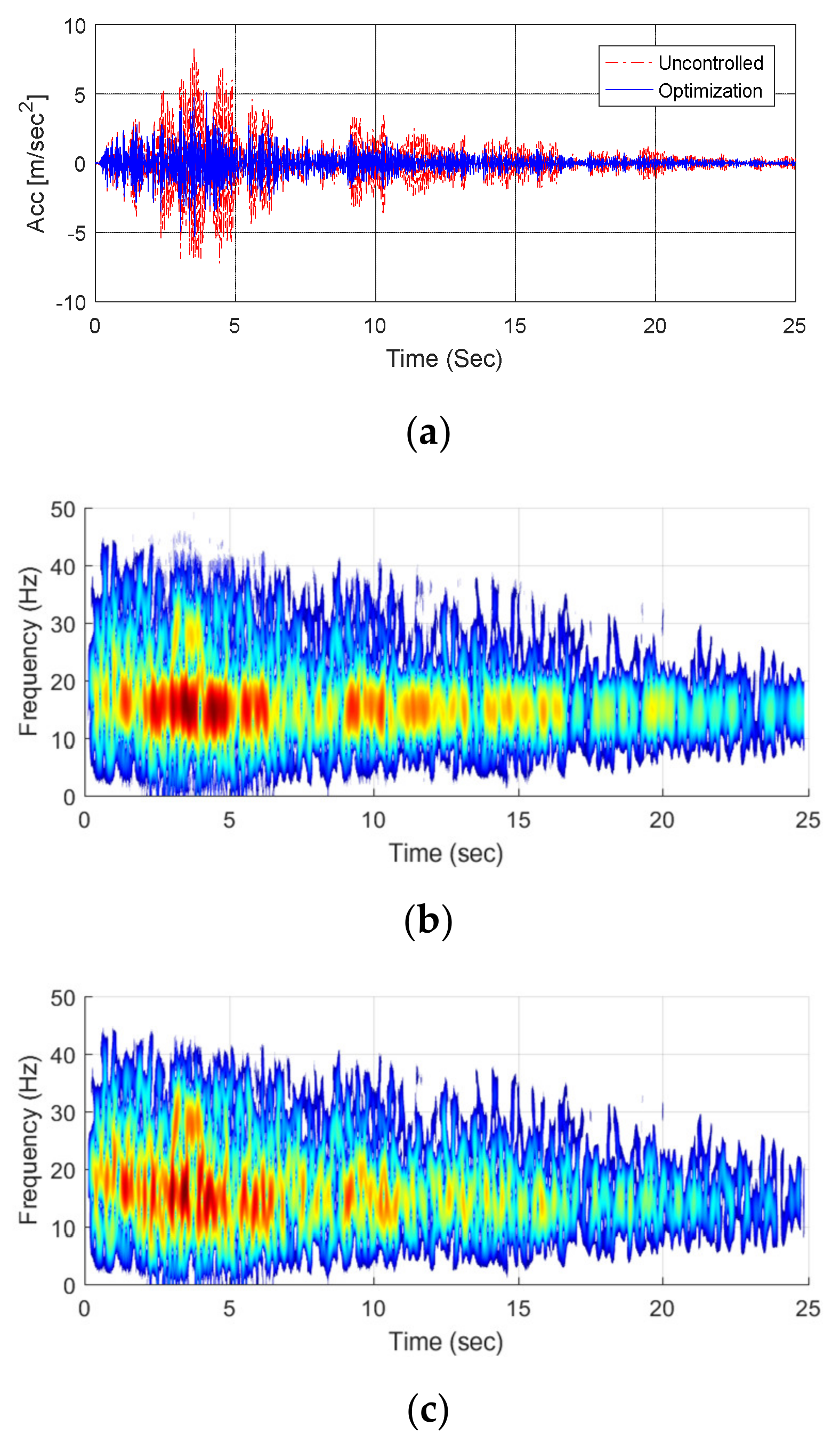
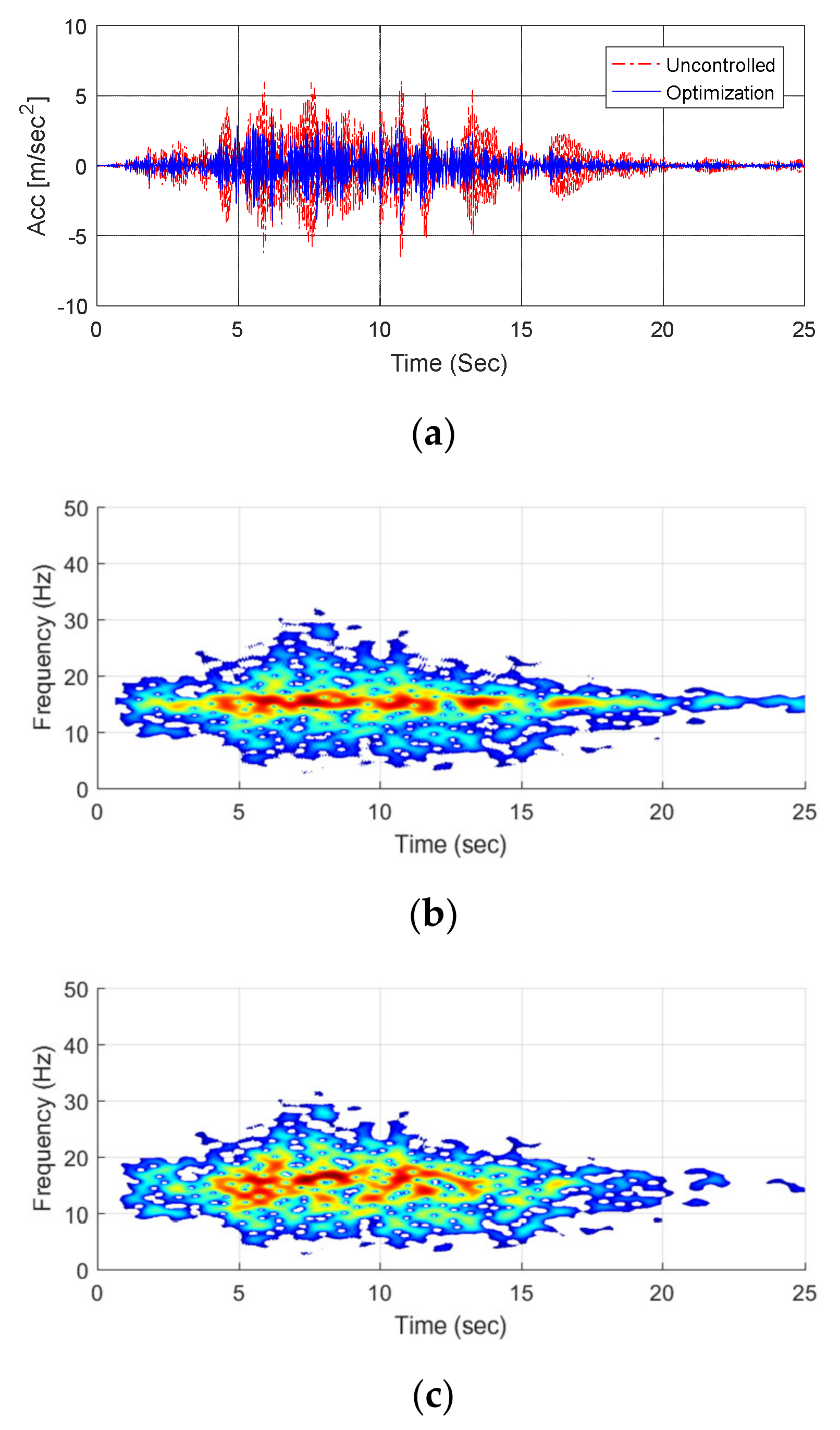
Figure 29.
Results of time–frequency analysis of the electrical cabinet subjected to San Fernando: (a) Time history; (b) Uncontrolled response; and, (c) Controlled response.
Figure 29.
Results of time–frequency analysis of the electrical cabinet subjected to San Fernando: (a) Time history; (b) Uncontrolled response; and, (c) Controlled response.
Figure 30.
Results of time–frequency analysis of the electrical cabinet subjected to Imperial Valley-06: (a) Time history; (b) Uncontrolled response; and, (c) Controlled response.
Figure 30.
Results of time–frequency analysis of the electrical cabinet subjected to Imperial Valley-06: (a) Time history; (b) Uncontrolled response; and, (c) Controlled response.
Table 1.
Material properties of the electrical cabinet.
Table 1.
Material properties of the electrical cabinet.
| Item | Value | Unit |
|---|
| Young’s modulus | 2.14 × 105 | MPa |
| Poisson’s ratio | 0.30 | - |
| Steel density | 7851 | kg/m3 |
Table 2.
Results of shaking table test.
Table 2.
Results of shaking table test.
| Contents | Values |
|---|
| Natural frequency (Hz) | 16.48 |
| Damping ratio (%) | 2.16 |
Table 3.
Dynamic properties of the electrical cabinet.
Table 3.
Dynamic properties of the electrical cabinet.
| | First Mode | Second Mode | Third Mode |
|---|
| Frequency (Hz) | 14.42 | 14.56 | 15.13 |
| Modal mass (kg) | 12 | 12 | 133 |
| Structural damping (%) | 2.16 | 2.16 | 2.16 |
Table 4.
Optimum parameters suggested for the TMD design.
Table 4.
Optimum parameters suggested for the TMD design.
| | Frequency Ratio | Damping Ratio |
|---|
| Den Hartog | | |
| Warburton | | |
| Sadek | | |
Table 5.
Properties of TMDs designed while using optimum methods.
Table 5.
Properties of TMDs designed while using optimum methods.
| Parameters | Den Hartog | Warburton | Sadek | Optimization |
|---|
| Mass (kg) | 10 | 10 | 10 | 10 |
| Mass ratio | 0.075 | 0.075 | 0.075 | 0.075 |
| Frequency ratio | 0.930 | 0.912 | 0.925 | 0.874 |
| Stiffness (N/m) | 78,134 | 75,196 | 78,134 | 68,997 |
| Damping ratio (%) | 16.2 | 13.4 | 28.5 | 18.9 |
| Damping (N/m∙s) | 286 | 231 | 500 | 313 |
Table 6.
Characteristics of seismic loads.
Table 6.
Characteristics of seismic loads.
| Earthquakes | Year | PGA (g) | Sampling Time (s) | Max. Frequency (Hz) |
|---|
| Imperial Valley-2 | 1940 | 0.423 | 0.01 | 2.6 |
| Northern Calif-01 | 1941 | 0.454 | 0.01 | 2.8 |
| Northern Calif-03 | 1954 | 0.408 | 0.01 | 27.9 |
| San Fernando | 1971 | 0.385 | 0.01 | 2.7 |
| Nicaragua-01 | 1972 | 0.374 | 0.01 | 2.7 |
| Friuli | 1976 | 0.431 | 0.01 | 6.0 |
| Imperial Valley-06 | 1979 | 0.380 | 0.01 | 2.7 |
Table 7.
Maximum acceleration in each earthquake case.
Table 7.
Maximum acceleration in each earthquake case.
| Earthquake | Unit | Uncontrolled | Control Method |
|---|
| Den Hartog | Warburton | Sadek | Optimization |
|---|
| Imperial Valley-2 | | 7.64 | 5.27 | 5.17 | 5.57 | 5.31 |
| % | - | 31.0 | 32.3 | 27.1 | 30.5 |
| Northern Calif-01 | | 7.82 | 5.35 | 5.19 | 5.78 | 5.36 |
| % | - | 31.6 | 33.6 | 26.1 | 31.5 |
| Northern Calif-03 | | 7.67 | 5.03 | 4.81 | 5.30 | 4.79 |
| % | - | 34.4 | 37.3 | 31.0 | 37.6 |
| San Fernando | | 8.42 | 5.20 | 5.13 | 5.22 | 5.29 |
| % | - | 38.2 | 39.1 | 38.0 | 37.2 |
| Nicaragua-01 | | 6.75 | 3.79 | 3.83 | 4.21 | 3.98 |
| % | - | 43.9 | 43.2 | 37.6 | 41.0 |
| Friuli | | 7.29 | 4.71 | 4.89 | 4.64 | 4.85 |
| % | - | 35.4 | 32.9 | 36.3 | 33.5 |
| Imperial Valley-06 | | 6.65 | 3.99 | 3.95 | 4.18 | 4.22 |
| % | - | 40.0 | 40.6 | 37.1 | 36.5 |
Table 8.
Peak spectral acceleration for each earthquake.
Table 8.
Peak spectral acceleration for each earthquake.
| Earthquake | Unit | Uncontrolled | Control Method |
| Den Hartog | Warburton | Sadek | Optimization |
| Imperial Valley-2 | | 4.54 | 2.08 | 2.08 | 2.30 | 2.22 |
| % | - | 54.2 | 54.3 | 49.3 | 51.1 |
| Northern Calif-01 | | 5.06 | 2.17 | 2.09 | 2.63 | 2.35 |
| % | - | 57.1 | 58.8 | 48.0 | 53.7 |
| Northern Calif-03 | | 4.70 | 2.20 | 2.21 | 2.43 | 2.20 |
| % | - | 53.1 | 52.9 | 48.2 | 53.1 |
| San Fernando | | 6.30 | 2.52 | 2.47 | 3.05 | 2.96 |
| % | - | 60.0 | 60.9 | 51.6 | 53.0 |
| Nicaragua-01 | | 4.97 | 1.96 | 1.85 | 2.40 | 2.18 |
| % | - | 60.5 | 62.8 | 51.7 | 56.2 |
| Friuli | | 4.67 | 2.41 | 2.58 | 2.35 | 2.54 |
| % | - | 48.3 | 44.7 | 49.6 | 45.5 |
| Imperial Valley-06 | | 4.87 | 1.81 | 1.96 | 2.17 | 2.01 |
| % | - | 62.9 | 59.7 | 55.5 | 58.8 |
Table 9.
AF and rate of decrease due to seismic loading of the electrical cabinet with and without a TMD.
Table 9.
AF and rate of decrease due to seismic loading of the electrical cabinet with and without a TMD.
| Earthquake | AF | Rate of Decrease (%) |
|---|
| Uncontrolled | Optimization Method |
|---|
| Imperial Valley-2 | 4.7 | 2.3 | 51.1 |
| Northern Calif-01 | 5.2 | 2.4 | 53.6 |
| Northern Calif-03 | 4.0 | 1.9 | 53.2 |
| San Fernando | 6.5 | 3.1 | 53.0 |
| Nicaragua-01 | 4.8 | 2.1 | 56.1 |
| Friuli | 4.8 | 2.6 | 45.6 |
| Imperial Valley-06 | 4.7 | 1.9 | 58.7 |