Abstract
The vertical inline pump is a single-suction single-stage centrifugal pump with a curved inlet pipe before the impeller, which usually causes a significant increase of hydraulic losses in the inline pump. Considering the matching relationship between the inlet pipe and impeller, a multi-objective direct optimization based on the MOPSO of the inlet pipe and impeller was carried out to broaden the efficient operating area of the vertical inline pump. Bezier curves were adopted to control the profiles of the inlet pipe and impeller and 39 coordinates of the control points and the blade number were selected as the optimization variables. The efficiencies of the inline pump at the part-load and nominal conditions were chosen as the objective functions, which were obtained by the automatic simulation program. A dramatic improvement in pump performance was found after optimization. In the set of Pareto solutions, the maximum increases of efficiency at part-load and nominal conditions were 8.06% and 7.33% respectively. It also reported that the inlet pipe with longer horizontal length and lower bend curvature could reduce the hydraulic losses of the inlet pipe and increase the pump performance.
1. Introduction
1.1. Background
The vertical inline pump is a single-suction single-stage centrifugal pump with a curved inlet pipe before the impeller. This type of pump is widely applied where installation space is a constraint, such as urban water supply [1]. However, it is characterized by a non-uniform and complex inflow phenomenon which results in a significant decrease in the pump performance [2,3,4,5,6]. Hence, it is necessary to optimize the vertical inline pump to improve the performance and save energy.
1.2. Literature Review
The investigation of optimization methods for fluid machinery has a long tradition. In recent years, the application of surrogate models to optimize a single hydraulic component has gained much recognition [7] and there have been several studies focusing on optimizing pumps [8,9,10,11,12,13]. Nourbakhsh [14] compared the performance of the multi-objective genetic algorithm and multi-objective particle swarm optimization algorithm in pump optimization design. In the study, the artificial neural network was used to optimize a centrifugal pump with efficiency and cavitation performance as the objective functions. Zhang [15] used the artificial neural network and multi-objective genetic algorithm to optimize a helical axial impeller. Takayama [16] combined the three-dimensional inverse design method, numerical simulation, design of experiment, response surface model and multi-objective genetic algorithm to optimize a high specific speed mixed-flow pump with the objective functions of pump efficiency, the maximum slope of the head curve and cut-off power.
However, the approach based on surrogate models will no more be efficient when the number of decision variables is large, or the objective functions are very complex. Nowadays, along with the development of computational resources, the direct optimization method that is based on intelligent algorithms has received attention [17]. This approach directly uses the simulation results as the objective values and has no requirement for the properties of the objective functions (such as continuous, differentiable, and so on), and the design parameters of the target model that could comprehensively determine the objectives are usually set as decision variables. However, the performance of this method directly depends on the algorithm. There are several multi-objective stochastic algorithms widely applied in the field of fluid machinery optimization. Multi-objective Particle Swarm Optimization (MOPSO), Multi-objective Genetic Algorithm (MOGA), and Multi-objective Evolutionary Algorithm (MOEA) are the most commonly used multi-objective algorithms in this field.
As direct optimization of fluid machinery usually cost a lot of computational resources and PSO generally shows a faster convergence speed than traditional evolutionary algorithms (EA), it has gradually been introduced into the complex optimization problem of fluid machinery in recent years. Many studies also reported the improvement of the PSO algorithms [18,19,20,21,22,23,24]. Safari et al. [25] proposed a metamodel guided particle swarm optimization (MGPSO) algorithm, which could obtain more accurate results with a relative smaller computational resource. Song et al. [26] applied adaptive control strategies into the improvement of PSO, and the results showed a significant decrease in the optimization cost.
In 2018, a multi-objective optimization on the inlet pipe of a vertical inline pump was carried out based on a multi-objective genetic algorithm and artificial neural network by Pei Ji [27]. The performance at different operating conditions improved after optimization, and it also reported that the design of the inlet pipe has a slight influence on the performance of the inline pump under the overload condition. However, this approach ignored the matching relationship between the different subassemblies.
1.3. Paper Organization
In this research, an industrial vertical inline pump with a suboptimal design was applied in the optimization. While considering the match relationship between the impeller and the inlet pipe of a vertical inline pump, the profiles of these two parts were redesigned to obtain better performance. Specifically, 40 design variables of these two components were selected, and the efficiencies under part-load and nominal conditions were set as objective functions. As the number of variables was large, the optimization approach that was based on surrogate models was no longer applicable. Hence, the direct optimization method based on an intelligent algorithm was applied.
2. Computational Model
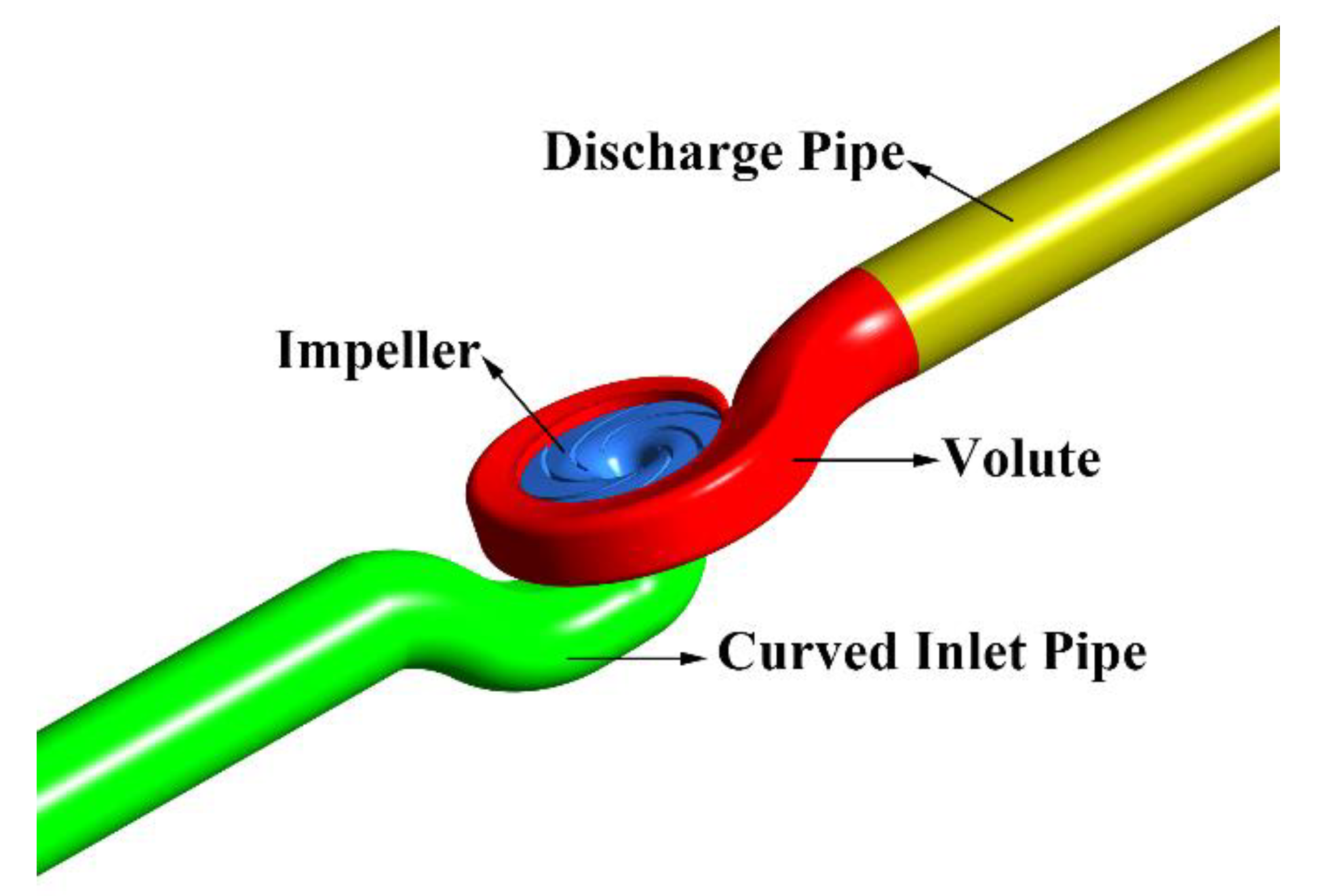
Figure 1 shows the original model, and Table 1 lists the main parameters. As shown in Figure 1, the flow domain was divided into four parts: inlet pipe, impeller, volute, and discharge pipe, which could simplify the meshing process. The specific speed of the original vertical inline pump is 132.36 rpm, and the definition is given as follows:
where:
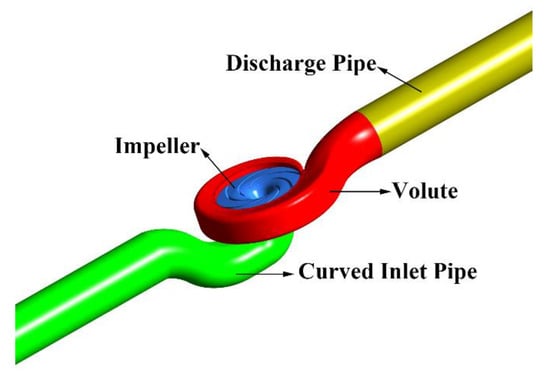
Figure 1.
Flow Domains of the Original Case.

Table 1.
Design Parameters of the Original Case.
- : specific speed, rpm;
- : rotation speed of the impeller, rpm;
- : design volume flow rate, m3/s; and,
- : head, m.
3. Numerical Methodology
3.1. Computational Grids
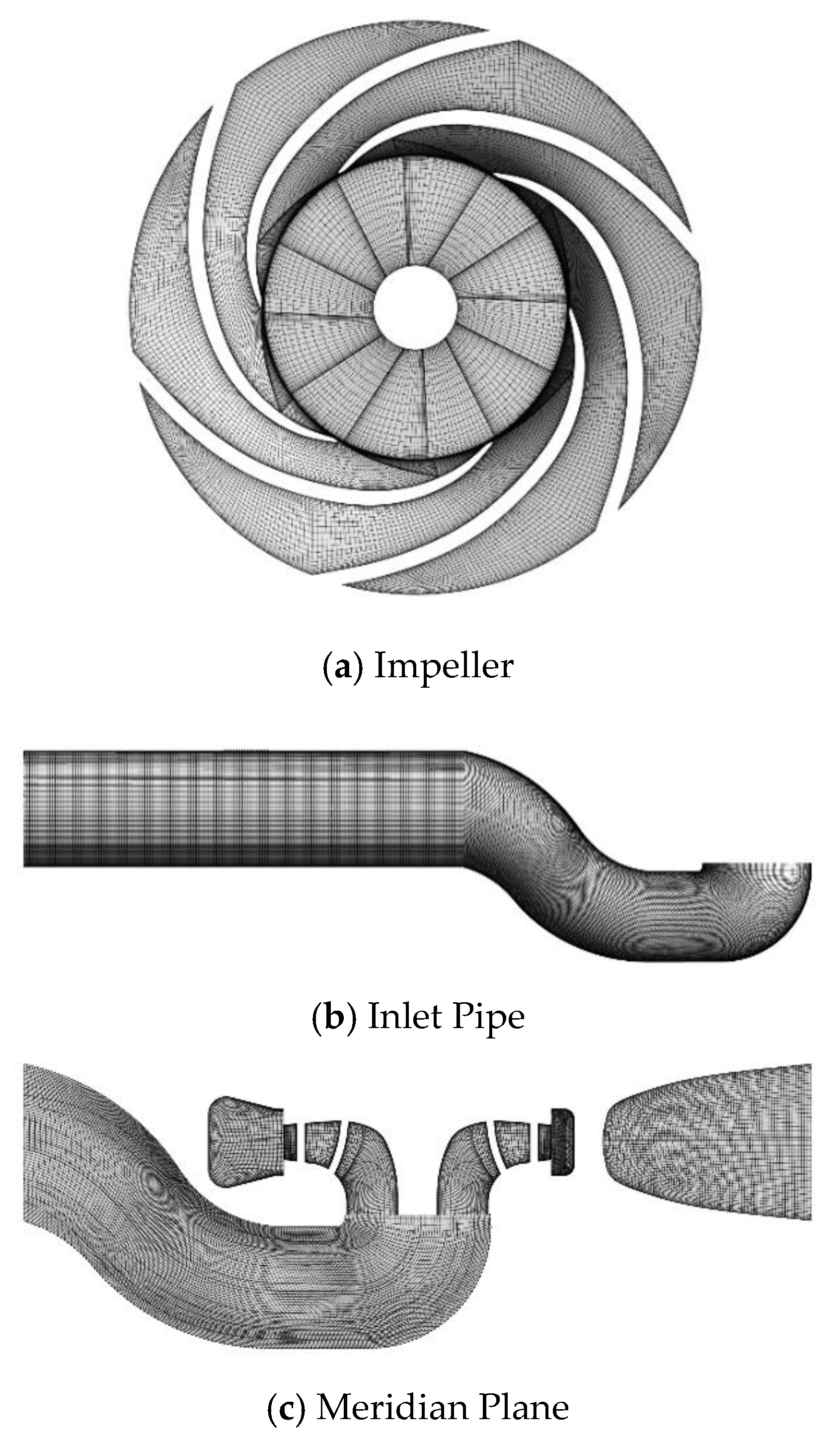
In the process of numerical simulation, it is widely known that the quantity and quality of grids has great influence on the computational speed and accuracy. In this research, the flow domain was divided into four parts (see Figure 1). As shown in Figure 2, the structural cells and multi-block strategies were applied to mesh each part using the commercial pretreatment software ANSYS ICEM. Meanwhile, the grids near walls were refined to achieve the accurate results near the boundaries. The non-dimensional wall distance (y+) was applied in the evaluation of the grids. The figure for the significant surfaces, such as the leading edge of the impeller, was from 5 to 10, and the max value in the whole passage was less than 80. Hence, the grids condition was enough for the characteristic calculation.
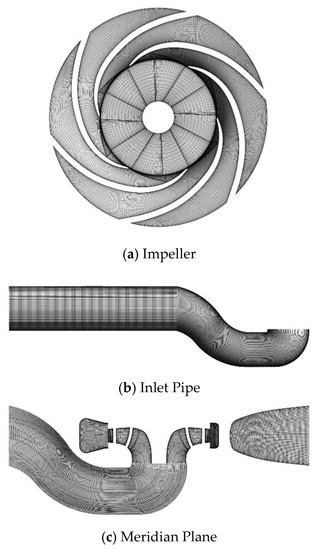
Figure 2.
Computational Grids.
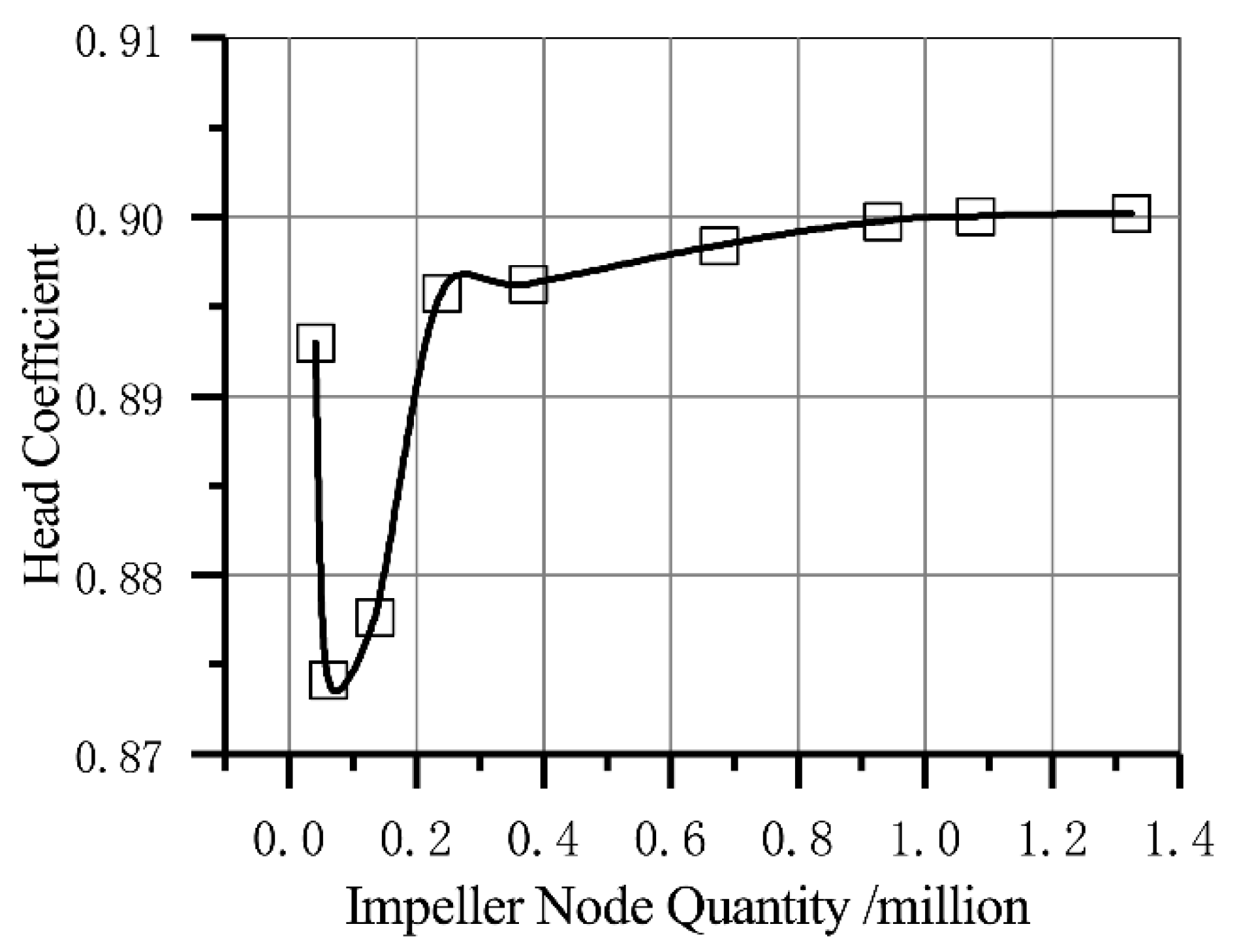
A grid sensitivity study was also carried out to improve the reliability of the computational grids. Figure 3 gives the results of this study. Formula (2) shows the definition of the head coefficient . The figures for the head coefficient of the vertical inline pump was going to be stable when the impeller node quantity was greater than 0.9 million. Therefore, the final grid size of each component was set to this figure during the optimization process and the final calculational grid number of the inlet pipe, the impeller, the volute, and the discharge pipe were 1.36 million, 0.93 million, 1.21 million and 0.78 million, respectively.
where:
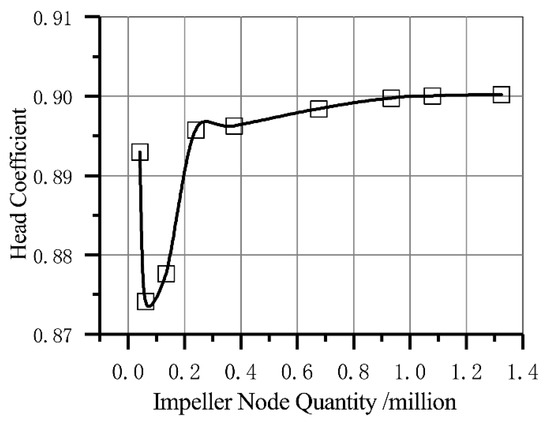
Figure 3.
Mesh Sensitivity Study.
- : gravity coefficient, 9.81 m/s2; and,
- : tangential velocity of impeller outflow, m/s.
3.2. Computational Setup
In this research, the three-dimensional steady Reynolds averaged Naiver–Stokes equation system with shear stress transport turbulence model (SST), which could give accurate result in the near-wall regions and better predictions for flow separation [28], were solved by commercial CFD code ANSYS CFX to obtain the characteristics and inner flow features of original case and optimized cases.
The inlet and outlet condition in the calculation were set as “total pressure” and “mass flow rate”, respectively. The no slip wall condition and a roughness of 25 μm were utilized for describing the solid walls. The value of reference pressure was 101.325 kPa and the “Frozen Rotor” was set in the interface condition between the rotor and stator. The residual and the maximum step of the simulation was 10−4 and 500, respectively.
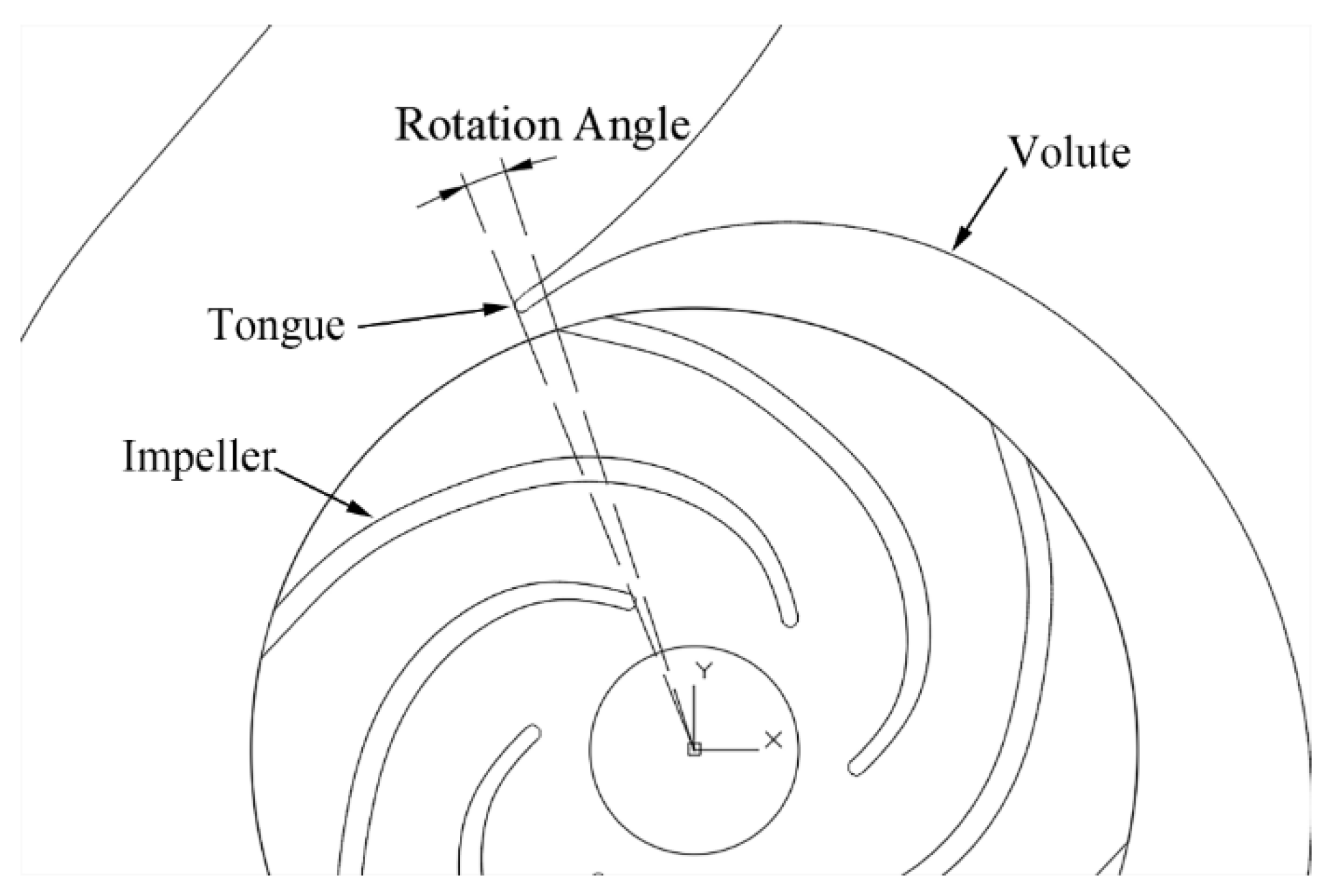
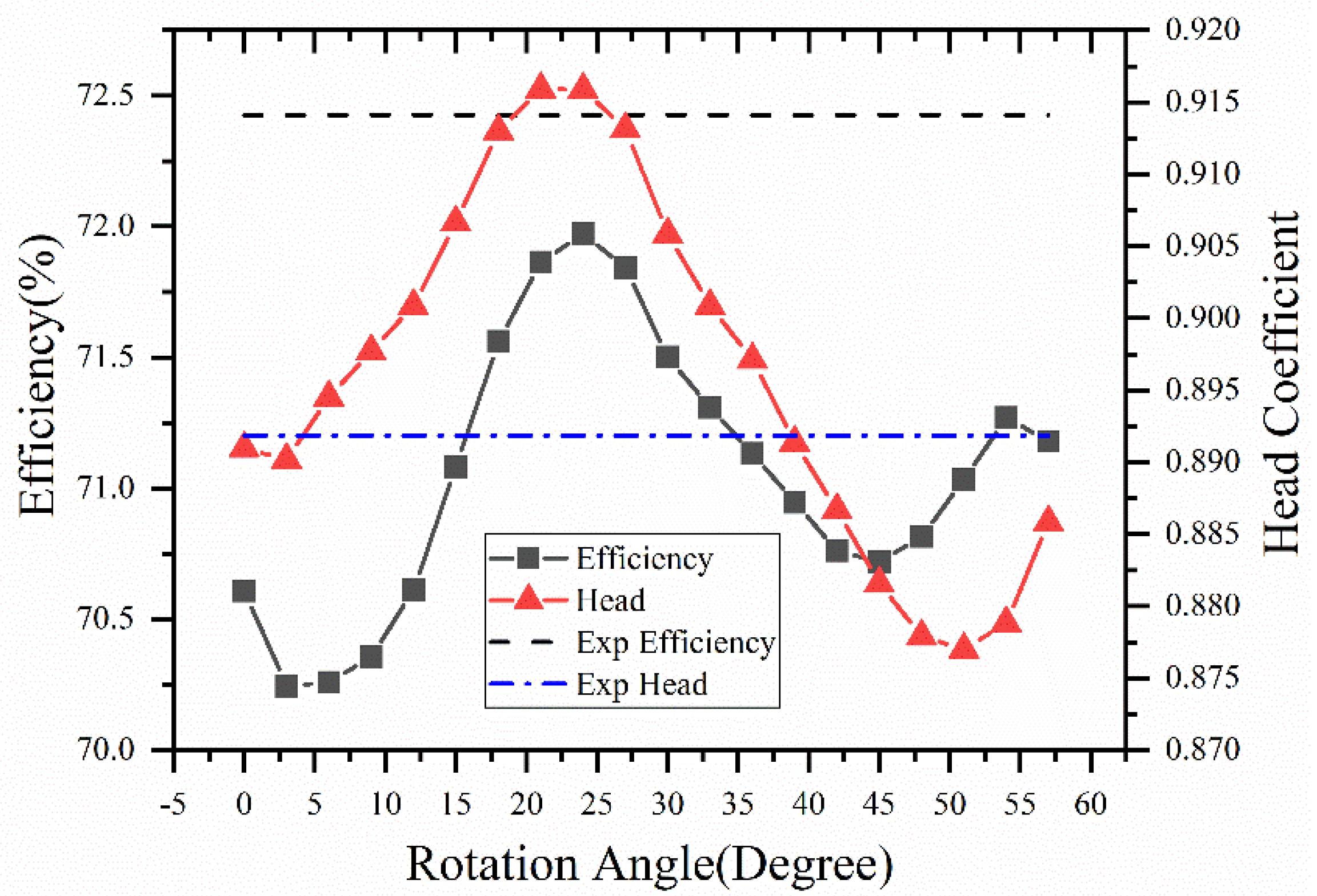
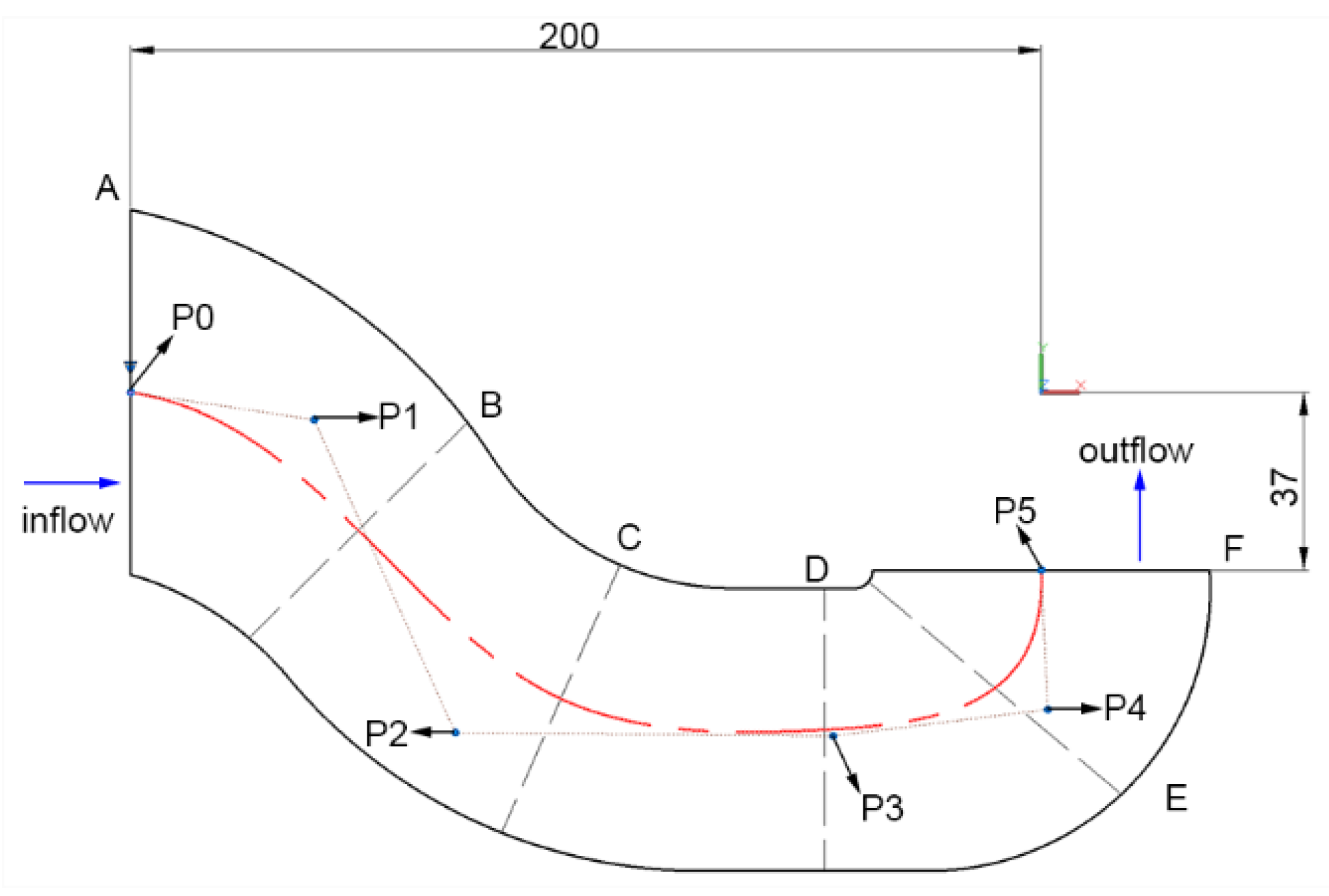
Additionally, the influence of different impeller position on the characteristic of the inline pump was studied in order to ensure the reliability of the computational results. The relative position between impeller and volute is defined as Figure 4, and the computational results are given in Figure 5. When compared with the experimental results, the case with the impeller rotating 37 degrees showed better performance. Hence, this relative position was applied in the optimization process.
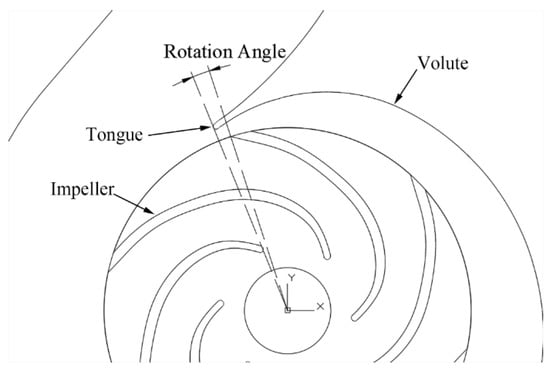
Figure 4.
Impeller Rotation Angle.
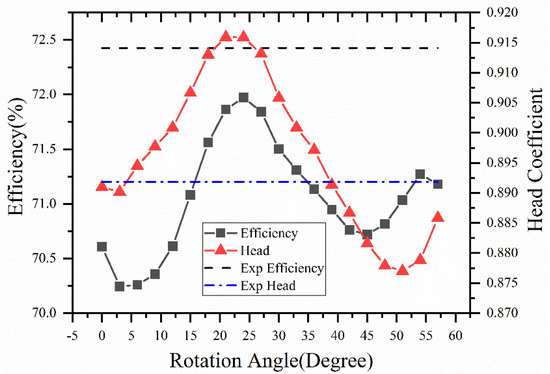
Figure 5.
Characteristic Comparison of Different Impeller Rotation Angle.
4. Optimization Process
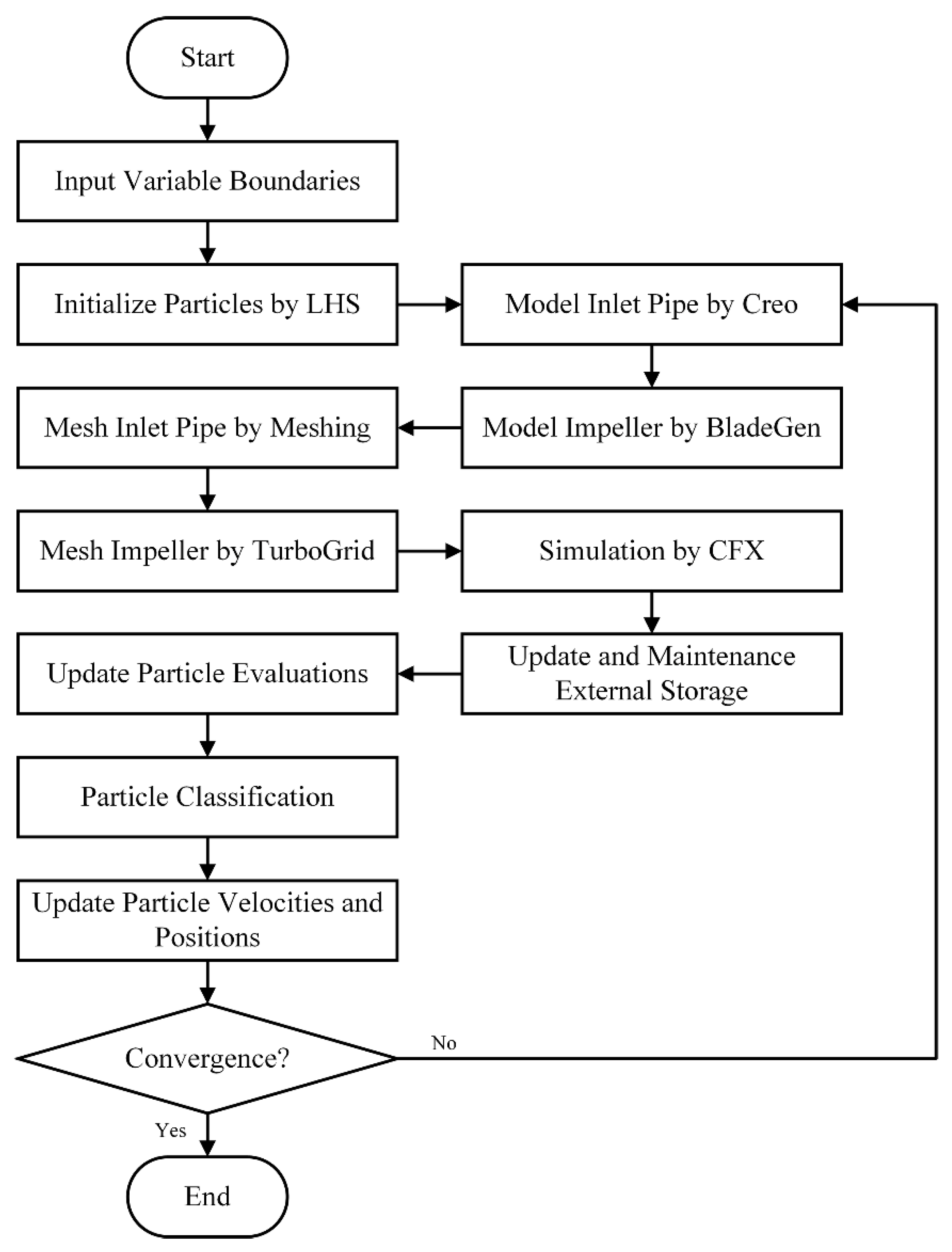
As the number of design variables was large, it will cost too much to optimize the impeller and the inlet pipe using surrogate model. In this research, an optimization procedure based on a modified multi-objective particle swarm optimization algorithm was proposed to solve this problem. Figure 6 gives the flow chart of the optimization process.
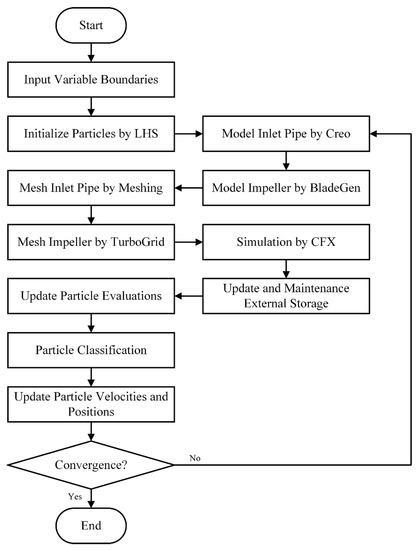
Figure 6.
Procedure of Multi-component Optimization on the Vertical Inline Pump.
Latin hypercube sampling was applied to initialize the particles of the modified MOPSO algorithm, and the objective functions were set as an automatic simulation program which includes modeling, meshing, and calculation process. The commercial three-dimensional (3D) modeling software Creo and ANSYS BladeGen were adopted to create the inlet pipe and impeller, respectively. ANSYS Meshing and TurboGrid were used to mesh inlet pipe and impeller, and then the grids files were then imported to CFX for the simulation process.
4.1. Objective Functions
As Ji Pei [27] reported that the design of the inlet pipe has little effect on the performance at the over-load condition of the vertical inline pump, therefore, the efficiencies at part-load and nominal conditions were selected to be the objective functions of the optimization process. The mathematical descriptions of the objective functions are given as follows:
where:
- : the efficiency under 0.5 times design flow rate condition;
- : the efficiency under design flow rate condition;
- : the head of optimized cases under 0.5 times design flow rate condition;
- : the head of the original case under 0.5 times design flow rate condition;
- : the head of optimized cases under design flow rate condition; and,
- : the head of original cases under design flow rate condition.
4.2. Design Variables
A multi-objective optimization on these two components was carried out while considering the matching relationship between impeller and curved inlet pipe in order to further widen the high-efficiency operation period of the vertical inline pump. The Bezier curves were adopted to control the profiles of the inlet pipe and the impeller, and the coordinates of the control points for these Bezier curves were set as the design variables of the optimization.
4.2.1. Inlet Pipe
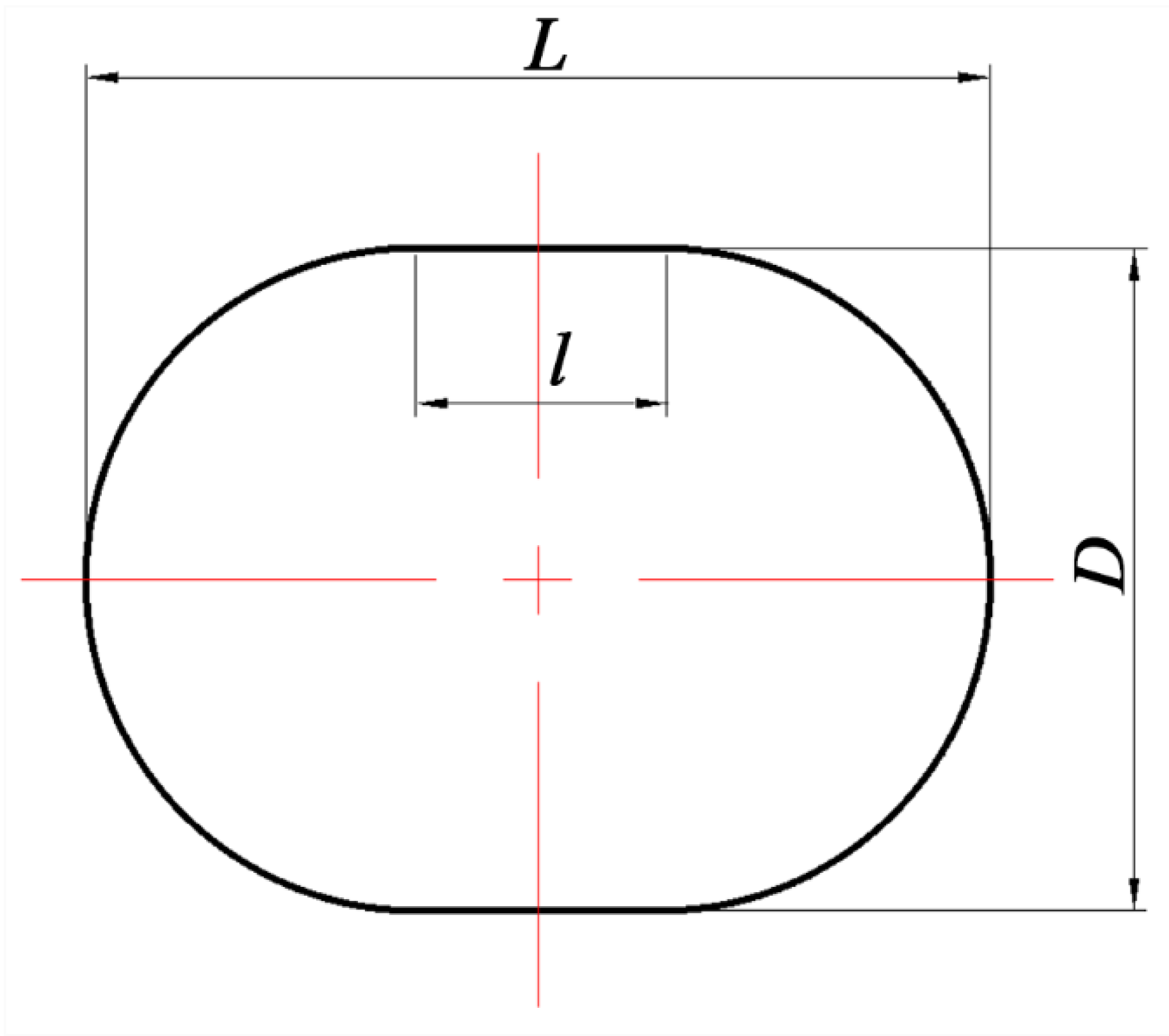
As shown in Figure 7 and Figure 8, the profile of the curved inlet pipe could be described while using the mid curve and the shape of cross-sections. There were totally three parameters controlling the shape of cross-sections (see Figure 8). In this study, the cross-sectional area linearly decreased from the inlet to the outlet to realize the steady change of the velocity and pressure. Hence, the parameter L can be computed by the formula below.
where:
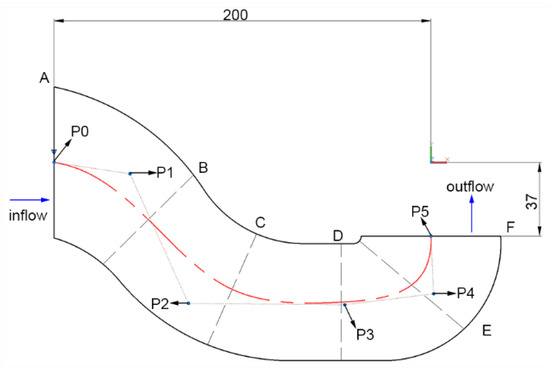
Figure 7.
Mid Curve of the Curved Inlet Pipe.
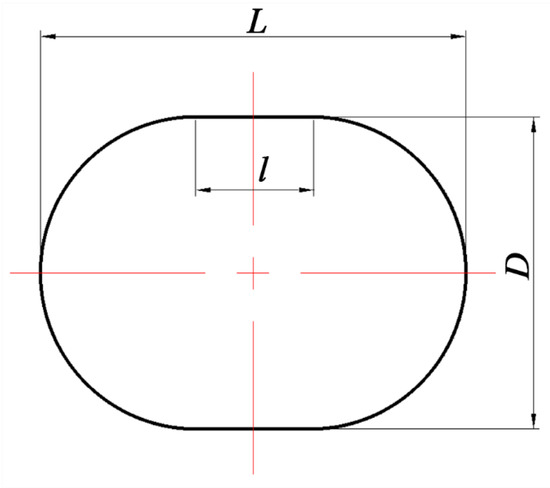
Figure 8.
Cross Section of the Curved Inlet Pipe.
- : cross-sectional area;
- : diameter of suction pipe;
- : diameter of impeller inlet;
- : relative position of the cross section; and,
- : design parameters of cross sections (see Figure 8).
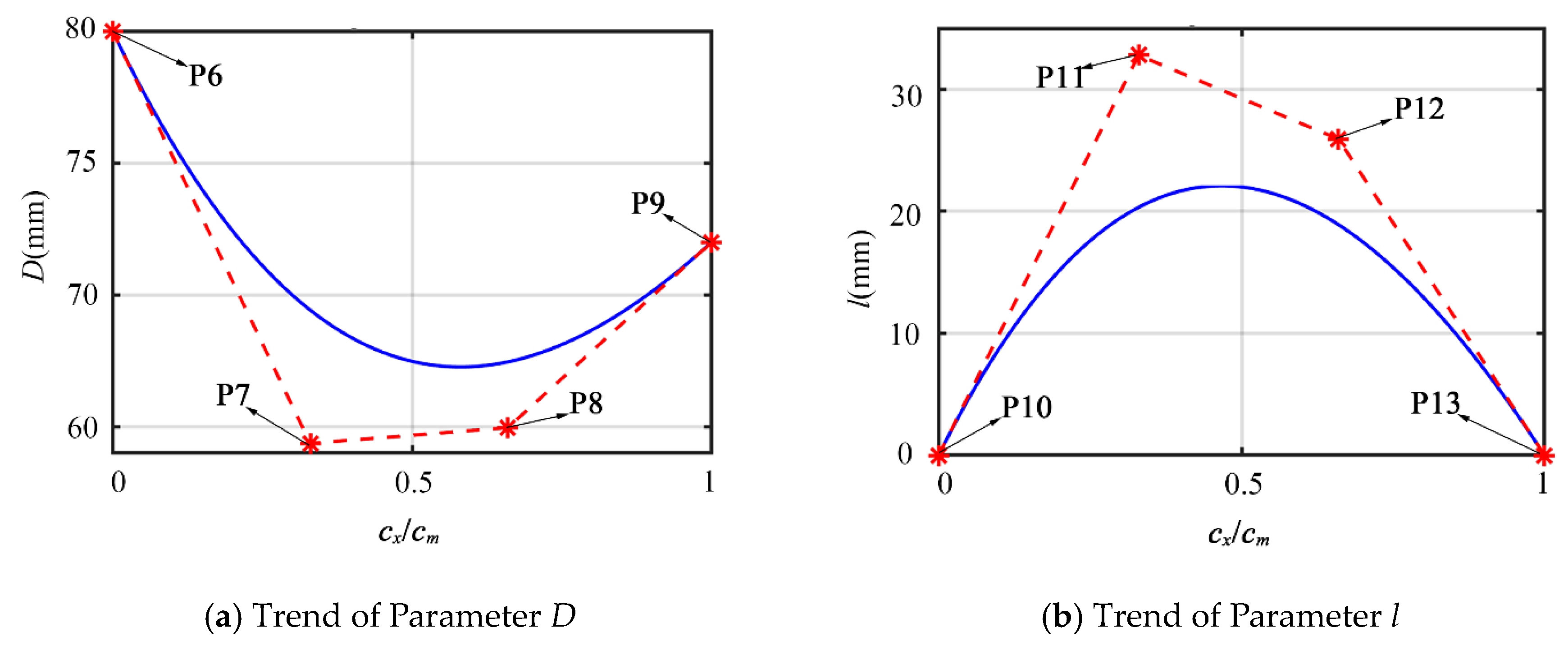
As shown in Figure 9, third order Bezier curves were applied to fit the trend of design parameters of cross-sections from the inlet to the outlet. A fifth order Bezier curve was adopted to fit the mid curve (see Figure 7). There are totally 14 points controlling the shape of the inlet pipe.
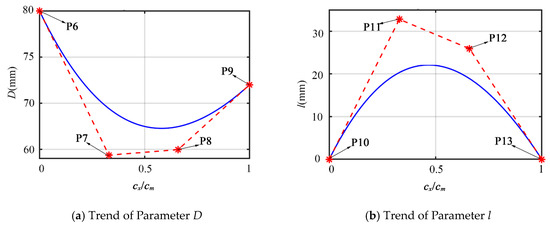
Figure 9.
The trend of Design Parameters of Cross Sections.
4.2.2. Impeller
The geometry of the impeller flow domain can be determined by axis shape, blade shape, and blade number. Therefore, the parameters of these elements were set as variables for the impeller.
Blade Shape
The blade shape of the impeller is mainly controlled by blade angles and blade thickness. A fifth order Bezier curve was used to fit the trend of blade angle, and a third-order Bezier curve was applied to fit the trend of blade thickness, in order to simplify the trend of blade angle and blade thickness from impeller inlet to impeller outlet.
The horizontal coordinates are relative positions and the longitudinal coordinates are the control objects. The control points of the Bezier curve of blade thickness are evenly distributed in the transverse direction, that is, the transverse coordinates of the control points are 0, 33.33, 66.66 and 100, respectively, in order to reduce the number of design variables. The coordinates of each control point were used as the design variables in the optimization process.
Meridional View
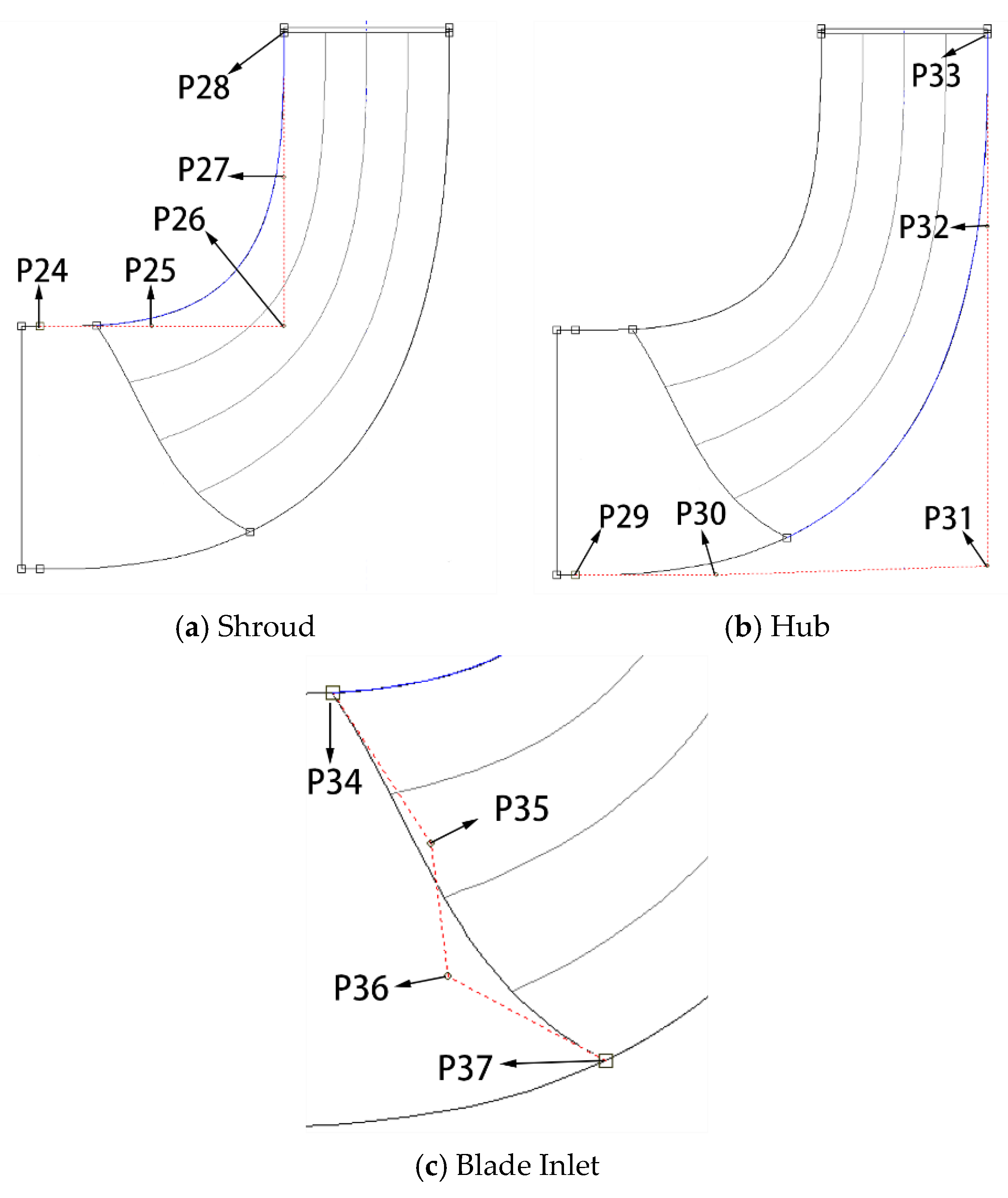
The axial projection diagram of the impeller is mainly composed of three elements, namely, the shroud, the hub, and the blade inlet. To realize the parametric control of the impeller axial shape, two fourth order Bezier curves were used to fit the shroud and the hub of the impeller, and a third order Bezier curve is used to fit the blade inlet shape, as shown in Figure 10.
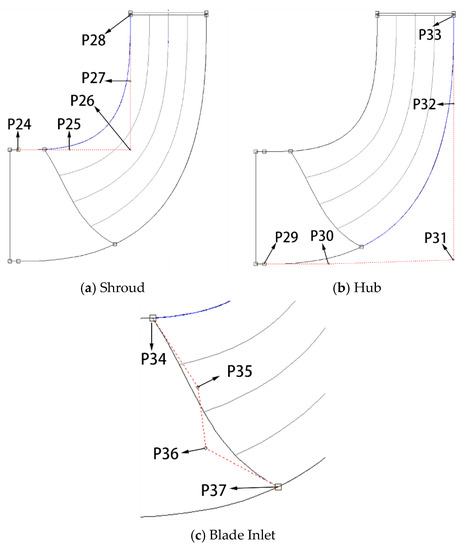
Figure 10.
Control Points for Meridional View of Impeller.
Blade Number
It is well known that the number of blades plays an important role in the performance of the pump. More blades have better workability, but their passing performance will become worse. Therefore, the selection of blade number often needs to adopt different schemes for different applications in the process of impeller design. The vertical inline pump is a special single-stage single-suction centrifugal pump with the working fluid of clear water. According to the relevant literature [29], the number of its blades generally takes 5–7.
In this research, the blade number was set as Variable 40, it is taken as an integral variable in the optimization. The range was {5,6,7,8}.
4.3. Algorithm Setup
Particle swarm optimization (PSO) is a random algorithm inspired by social behaviors [30] and was first proposed by Kennedy, Eberhart, and Shi in 1995 [31,32]. The fundamental position and velocity update strategies of particles are given as following [32]:
For the optimization process, the population size and maximum iteration applied in the MOPSO were 70 and 100, respectively.
5. Result and Discussion
5.1. Validation Experiment
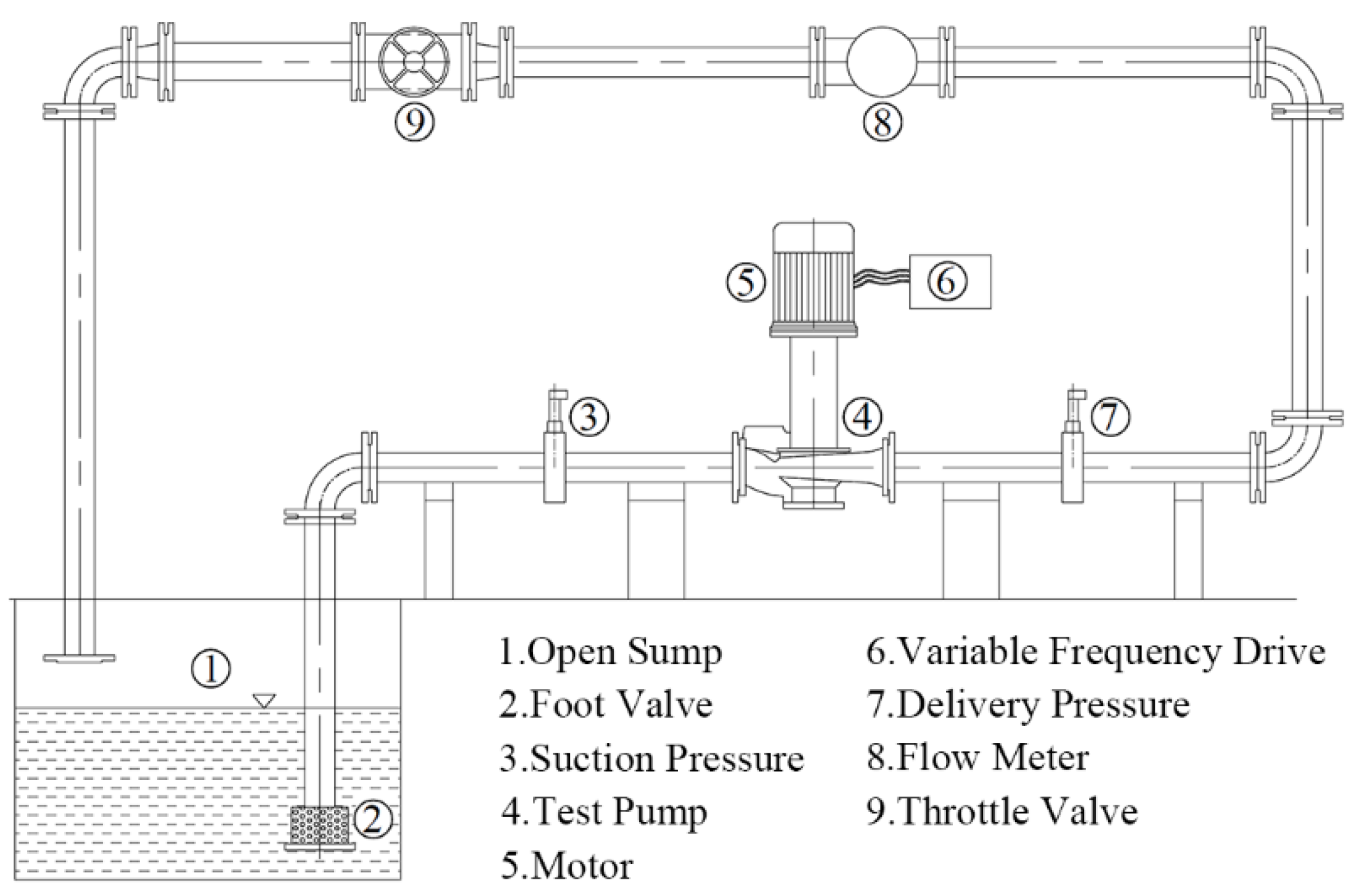
A validation experiment was carried out to ensure the reliability of the numerical results. Figure 11 shows the experimental pump, and Figure 12 shows the test rig. The characteristic test of the original vertical inline pump was carried out on the open-loop in National Research Center of Pumps, Jiangsu University. The measurement errors of head and efficiency were less than ±2%, and the figure for flowrate was less than ±2%. The WIKA pressure sensor was used to measure the inlet and outlet pressure of the pump, with the range of 0–1.6 bar and 0–4 bar respectively. The flow rate of the pump was obtained by the electromagnetic Flowmeter (KROHNE-UFM 3030), and the input power of the pump was recorded by the power meter. In the experiment, the variable frequency drive controlled the rotational speed of the motor, and the flow rate was adjusted by adjusting the throttle valve. At the same time, repeated tests were carried out to ensure the reliability of the results.

Figure 11.
Experimental Pump.
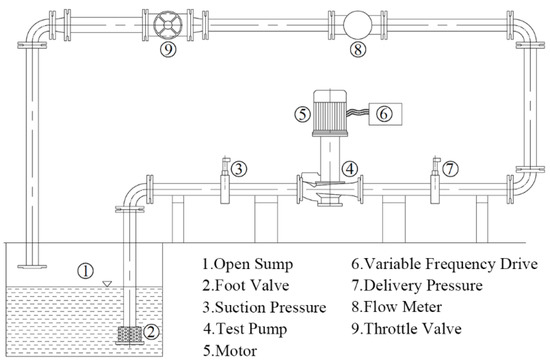
Figure 12.
Test Rig.
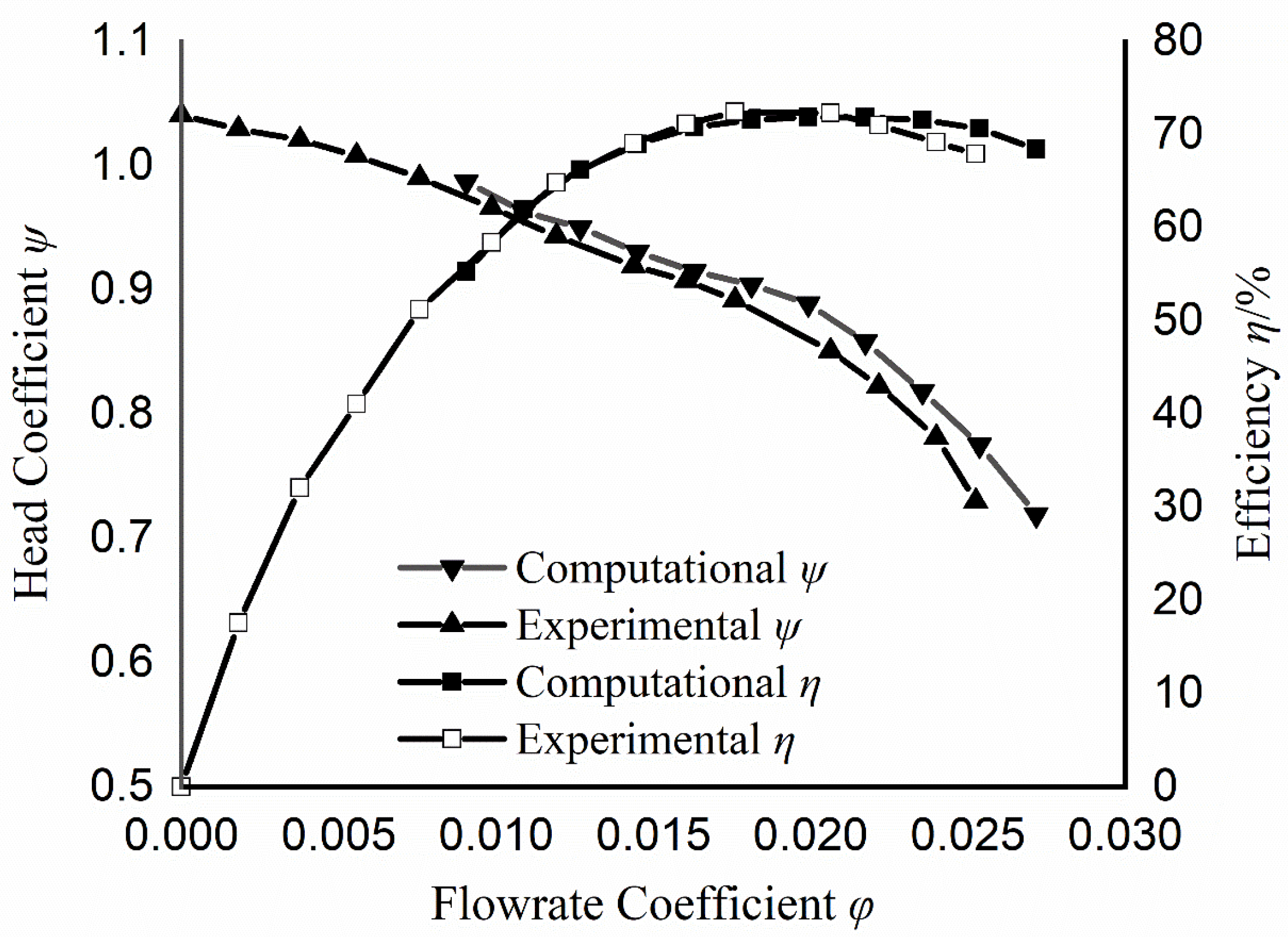
As shown in Figure 13, dimensionless parameters show both the test results and the calculated results. The computational results showed good agreement with the experimental results. The head coefficient is defined as Formula (2), and the flow coefficient used in the diagram is defined, as follows:
where:
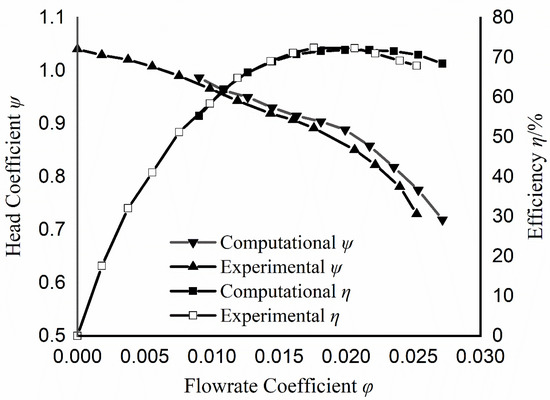
Figure 13.
Comparison between Computational and Experimental Results.
- : volume flow rate, ;
- : impeller outlet diameter, m;
- : impeller outlet width, m; and,
- : tangential velocity at impeller outlet, m/s.
5.2. Data Mining Analysis
The cases generated in the optimization process were adopted in order to analyze the correlation between these 40 variables and the objective functions. A data mining analysis based on multiple linear regression was carried out. The regressions for models of efficiencies at the part-load condition and nominal condition are 0.96 and 0.934, respectively, indicating that the results had great reliability.
The data were sorted in descending order with reference to the absolute sum of standardized coefficients for models of efficiency at the part-load condition and nominal condition. It was found that the blade angle and the blade number have great influence on the performance of the vertical inline pump. Specifically, the outlet blade angle (y19) has the greatest effect on pump performance and the increase of this value has a negative influence on the efficiencies of both operating conditions. The increase of the blade number (z) has a slight positive effect on the performance under the part-load condition, while it has a strong negative effect on the performance under the nominal flow condition.
5.3. Pareto Frontiers Analysis
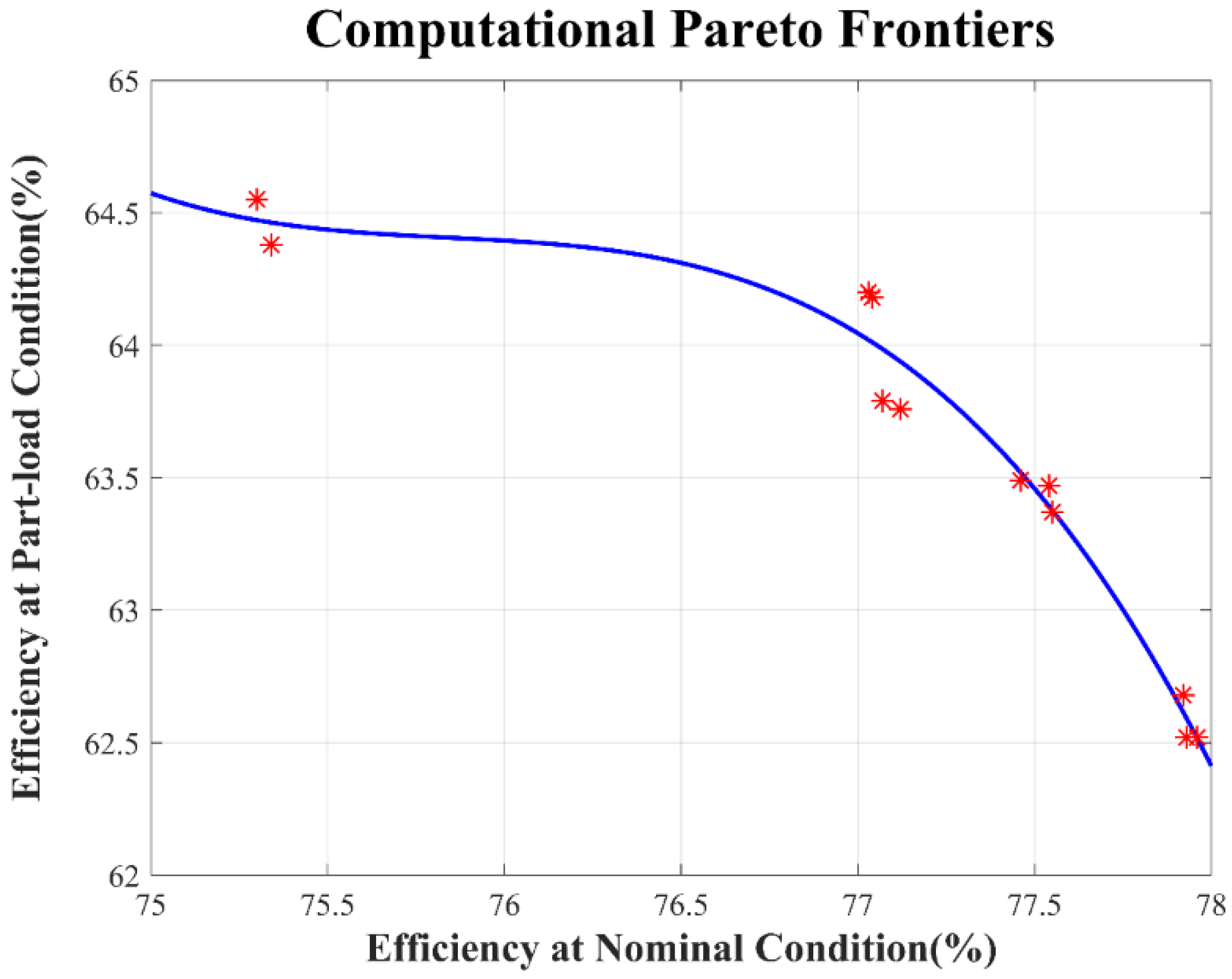
The calculated Pareto frontiers are shown in Figure 14, and the performance data is given in Table 2, and the main design parameters are shown in Table 3. When compared with the original model, the optimized cases have higher efficiency and the heads can also satisfy the design conditions. For the part-load condition, the maximum efficiency increase after optimization is 8.06%. When compared with the original model, the optimized cases have obvious decreases in terms of input power, and the heads do not have obvious fluctuation. For nominal flow conditions, the maximum efficiency increase after optimization is 7.33%. In terms of input power and head, there is a great difference between different results.
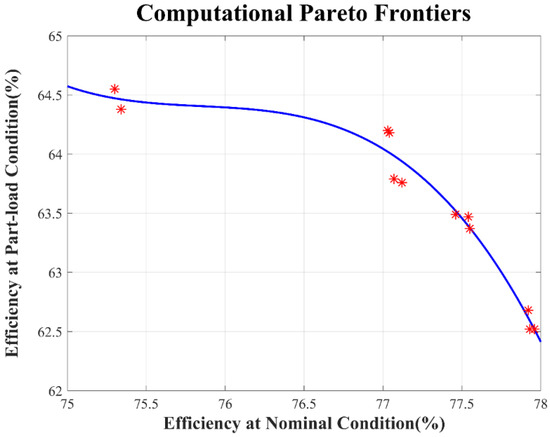
Figure 14.
Computational Pareto Frontiers.

Table 2.
Computational Pareto Frontiers.

Table 3.
Main Parameters of Pareto Solutions.
As shown in Figure 14, the efficiency of the part-load condition decreases with the increase of efficiency for the nominal flow rate. When the efficiency of is less than 76%, there is a slight decrease in efficiency at part-load conditions. However, when the efficiency of the design flow rate is higher than 76%, the efficiency at part-load rapidly decreases with the increase of the efficiency at the nominal condition.
According to the design parameters of the Pareto solutions in Table 3, the case with higher efficiency at part-load condition usually has an inlet pipe with a relatively longer transverse length (x0 in the table indicates the transverse length of the inlet bend, the same as below), an impeller with smaller inlet blade angle, and a larger outlet blade angle (y14 indicates inlet blade angle and y19 indicates outlet blade angle, the same below). The case with better performance at nominal flow condition shows that it generally has an inlet pipe with smaller transverse length and the impeller outlet angle is smaller. The design schemes with more blades (the number of blades is more than six) commonly have better comprehensive performance.
Three representative cases were selected and compared with the original case in order to further study the reasons for the performance improvement of the vertical inline pump after optimization, and their numbers were 1, 8, 12 respectively.
5.4. Performance Comparison
A performance comparison between the three selected optimized cases and the original case based on transient calculation was carried out. The time step was set as s, which is the time that is required for the impeller to rotate three degrees, and the mean value of the last 20 positions was utilized in the analysis. Table 4 lists the main design variables of these four cases and the Table 5 gives the performance characteristics (where Optimized Case (1), (2), (3) refer to Pareto solutions 1, 8, and 12 in Table 2 respectively).

Table 4.
Main Parameters Comparison between Optimized and Original Cases.

Table 5.
Performance Comparison between Optimized and Original Cases.
As shown in Table 5, the optimized cases show better performance and stability than the original model from 0.5 to 1.5 times design flow rate conditions. However, with the further increase of the flow, the stability of the optimized cases is poor, and the optimization model (1) has a steep drop in efficiency.
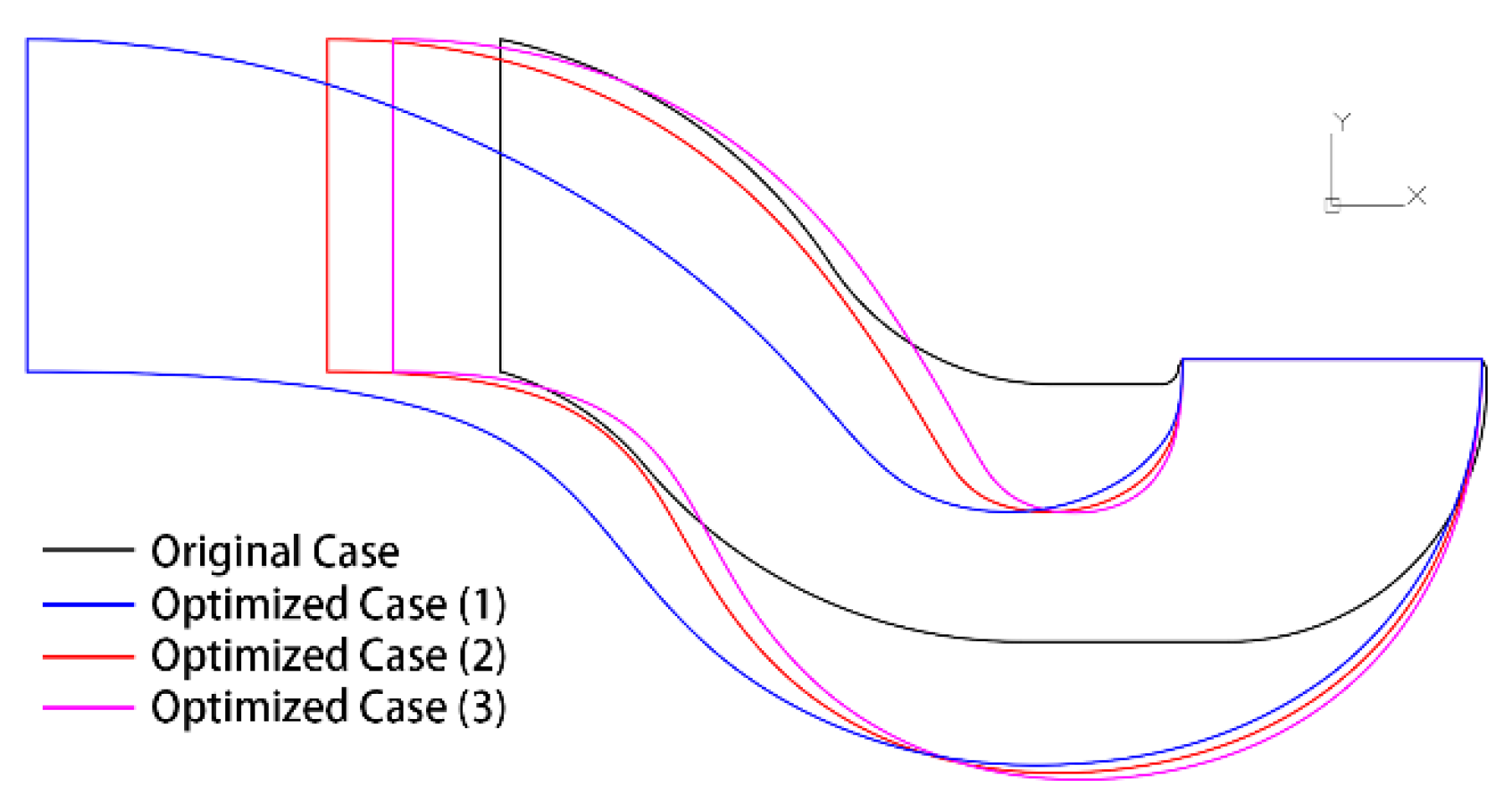
Figure 15 shows a comparison of profiles for inlet pipe between the three selected models and the original case. The black line represents the original model, blue represents the optimized case (1), red represents the optimized case (2), and pink represents the optimized case (3). As shown in the diagram, the transverse length of the inlet pipe of the optimized models is longer, and the relative position of the second bend is further away from the outlet. Specifically, the transverse lengths of the three optimization models decrease in turn, with optimized case (1) being the longest, whereas optimized case (3) is the shortest. The curvature of the first bend of the optimized case (1) is relatively smaller, and the transition section between the first bend and the second bend is longer.
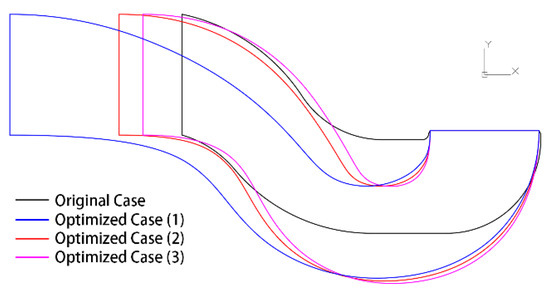
Figure 15.
Inlet Pipe Shape Comparison between Optimized and Original Cases.
5.5. Hydraulic Head Distribution
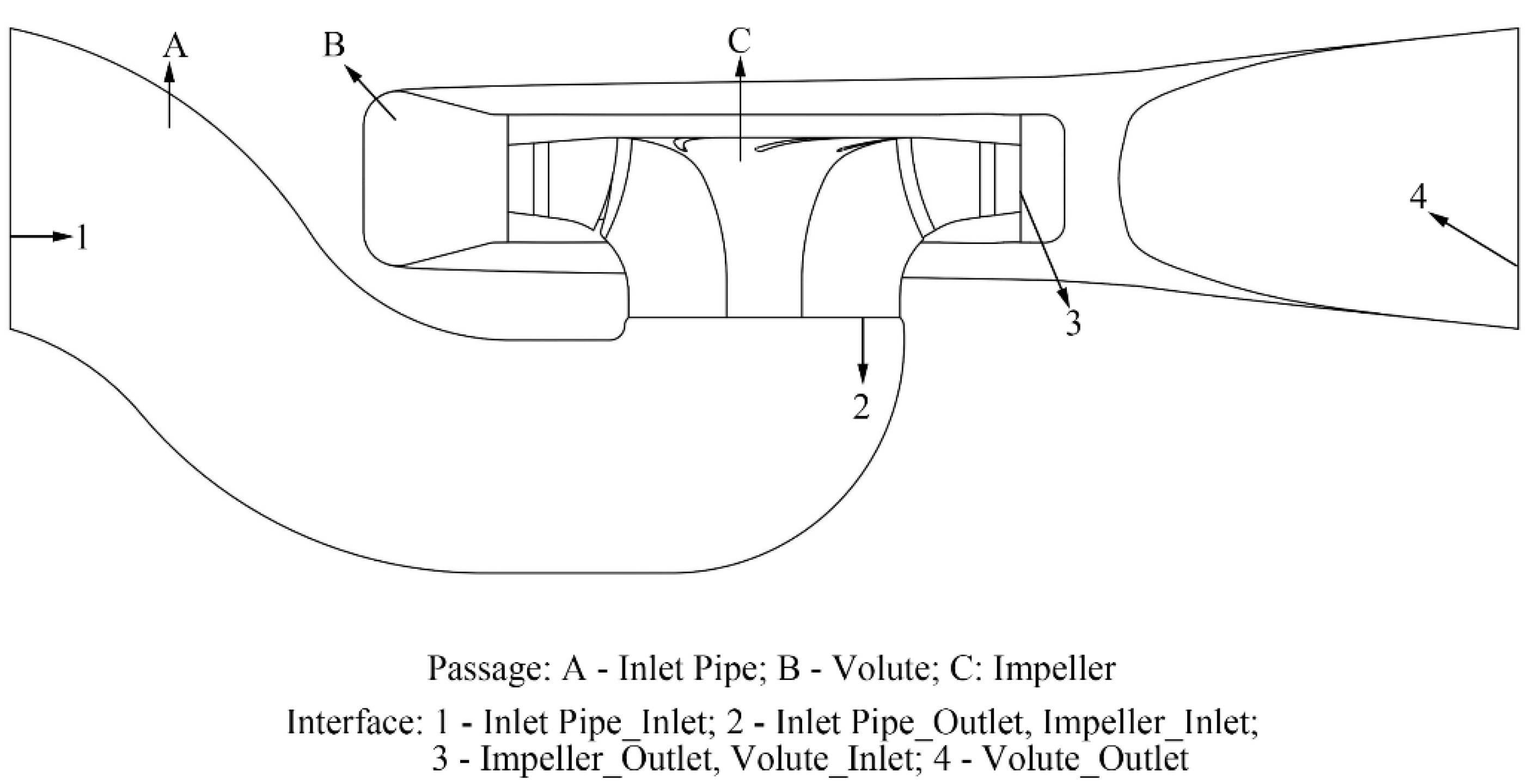
The head distributions of the original model and the optimized cases were analyzed in order to study the flow losses in different parts, and the results are shown in Table 6. The head value was calculated using the formula below:
where, subtitle 1, 2 represent the inlet and the outlet of each component (as shown in Figure 16), respectively.

Table 6.
Hydraulic Head Distribution of Optimized and Original Cases.
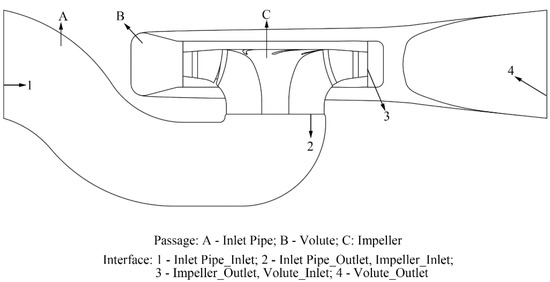
Figure 16.
Interface of each component.
For the overload condition, the input power for the three optimized cases is significantly reduced. The workability of the impeller for optimized case (1) under the over-load condition is poor and, therefore, the input power of this case is obviously lower than the others. For the inlet pipe, the hydraulic losses are mainly composed of the impact losses and the friction losses under the design flow and the large flow condition. The optimized cases have more hydraulic losses in the inlet pipes, as the length of the inlet pipe of the optimized case is longer than the original one. The data for other parts is not much different (in addition to the optimization model (1)), but the input power is significantly reduced, so that the efficiency of the optimized cases (2) and (3) is better than the original model under large flow conditions.
In the same way, under the design flow condition, the input power of the three optimized cases is lower than that of the original case, and the hydraulic losses inside the volute and the delivery pipe are reduced, so the performance of the optimized model under the nominal condition is superior to the original model.
Under the part-load condition, the working ability of the optimized impeller had a slight decrease, but, at the same time, the losses in other flow channels reduce for different degrees, so the total head still meets the design requirements. For the optimized case (1), the hydraulic losses in the inlet pipe are significantly reduced when compared with the original model, and the figure for the volute is also lower than the original one. For the optimized cases (2) and (3), the hydraulic losses in the volute have a significant decrease, and the figures for inlet pipe are similar to the original case. Meanwhile, the input power of the three optimized cases under the small flow condition is obviously lower than that of the original model, so the efficiencies of the three optimized cases at the part-load condition are improved.
6. Conclusions
In this research, a multi-objective particle swarm optimization algorithm was proposed to reduce the costs of the pump direct optimization problem. The MOPSO algorithm was applied for optimizing the inlet pipe and impeller of a vertical inline pump. Based on the Bezier curves, 40 design variables were selected for the optimization process, and the efficiencies of the inline pump under the part-load and nominal flow conditions were chosen as the objective functions.
Three Pareto solutions were selected after optimization for further study. The maximum increase of efficiency under part-load and nominal conditions were 8.06% and 7.33%, respectively. The horizontal length of the inlet pipe was longer when the design had better performance at part-load conditions, while the design with better performance at nominal condition had shorter inlet pipe and impeller with smaller outlet blade angle, and the design schemes with large blade number (which is greater than 6) usually had better comprehensive performance. The inlet pipe with longer horizontal length and lower bend curvature could effectively reduce the hydraulic losses of the inlet pipe and increase the pump performance.
Author Contributions
X.G. proposed this research, performed the simulation and optimization, analyzed the results and wrote the original draft. W.W. proposed the methodology and helped to revise the paper. J.P. and S.Y. supervised this work. M.K.O. and Y.T. helped to outline the manuscript and improve the language. All authors have read and agreed to the published version of the manuscript.
Funding
This research and the APC was funded by the National Natural Science Foundation of China (Grant No. 51879121), Natural Science Foundation of Jiangsu Province (Grant No. BK20190851), China Postdoctoral Science Foundation funded project (Grant No. 2019M651736), Primary Research & Development Plan of Jiangsu Province (Grant No. BE2019009-1), Open Research Subject of Key Laboratory of Fluid and Power Machinery (Xihua University), Ministry of Education (szjj2019-007).
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Ax | Area of cross-section, mm2 |
| b1 | Impeller inlet width, mm |
| b2 | Impeller outlet width, mm |
| cx | Length along the mid curve, mm |
| cm | The total length of the mid curve, mm |
| Cp | The pressure coefficient |
| D | Parameter D of cross-section, mm |
| D1 | The diameter of impeller inlet, mm |
| Ds | The diameter of section pipe, mm |
| Dd | The diameter of the delivery pipe, mm |
| H | Pump head, m |
| l | Parameter l of cross-section, mm |
| L | Parameter L of cross-section, mm |
| n | Rotating speed of impeller, rpm |
| ns | Specific speed of the pump, rpm |
| Q | Flow rate, m3/s |
| Qd | The volume flow rate of design flow condition, m3/h |
| u2 | Impeller peripheral velocity at the outlet, m/s |
| xi | Horizonal coordinate of control point i, mm |
| yi | Vertical coordinate of control point i, mm |
| z | Number of blades |
| β1 | Impeller inlet vane angle, degree |
| β2 | Impeller outlet vane angle, degree |
| The efficiency of the pump | |
| Flow coefficient | |
| Head coefficient |
References
- Lazarkiewicz, S.; Troskolanski, A. Impeller Pumps; Pergamon: Oxford, UK, 1965. [Google Scholar]
- Stephen, C.; Yuan, S.; Pei, J.; Gan, X. Numerical Flow Prediction in Inlet Pipe of Vertical Inline Pump. J. Fluids Eng. 2018, 140, 051201. [Google Scholar] [CrossRef]
- Pei, J.; Osman, M.K.; Wang, W.; Yuan, J.; Yin, T.; Appiah, D. Unsteady flow characteristics and cavitation prediction in the double-suction centrifugal pump using a novel approach. Proc. Inst. Mech. Eng. Part A J. Power Energy 2019. [Google Scholar] [CrossRef]
- Wang, W.; Pavesi, G.; Pei, J.; Yuan, S. Transient simulation on closure of wicket gates in a high-head Francis-type reversible turbine operating in pump mode. Renew. Energy 2020, 145, 1817–1830. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Y.; Wu, Y.L. A review of rotating stall in reversible pump turbine. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2017, 231, 1181–1204. [Google Scholar] [CrossRef]
- Pei, J.; Zhang, F.; Appiah, D.; Hu, B.; Yuan, S.; Chen, K.; Asomani, S. Performance prediction based on effects of wrapping angle of a side channel pump. Energies 2019, 12, 139. [Google Scholar] [CrossRef]
- Wang, G.G.; Shan, S. Review of metamodeling techniques in support of engineering design optimization. J. Mech. Des. 2007, 129, 370–380. [Google Scholar] [CrossRef]
- Liu, M.; Tan, L.; Cao, S. Design method of controllable blade angle and orthogonal optimization of pressure rise for a multiphase pump. Energies 2018, 11, 1048. [Google Scholar] [CrossRef]
- Jeon, S.Y.; Yoon, J.Y.; Jang, C.M. Optimal design of a novel ‘s-shape’ impeller blade for a microbubble pump. Energies 2019, 12, 1793. [Google Scholar] [CrossRef]
- Kim, J.H.; Kim, K.Y. Analysis and optimization of a vaned diffuser in a mixed flow pump to improve hydrodynamic performance. J. Fluids Eng. 2012, 134, 071104. [Google Scholar] [CrossRef]
- Kim, J.H.; Choi, J.H.; Kim, K.Y. Design optimization of a centrifugal compressor impeller using radial basis neural network method. In Proceedings of the ASME Turbo Expo 2009: Power for Land, Sea, and Air, American Society of Mechanical Engineers Digital Collection, Orlando, FL, USA, 8–12 June 2009; pp. 443–451. [Google Scholar]
- Derakhshan, S.; Pourmahdavi, M.; Abdolahnejad, E.; Reihani, A.; Ojaghi, A. Numerical shape optimization of a centrifugal pump impeller using artificial bee colony algorithm. Comput. Fluids 2013, 81, 145–151. [Google Scholar] [CrossRef]
- Wang, W.; Osman, M.K.; Pei, J.; Gan, X.; Yin, T. Artificial Neural Networks Approach for a Multi-Objective Cavitation Optimization Design in a Double-Suction Centrifugal Pump. Processes 2019, 7, 246. [Google Scholar] [CrossRef]
- Nourbakhsh, A.; Safikhani, H.; Derakhshan, S. The comparison of multi-objective particle swarm optimization and NSGA II algorithm: Applications in centrifugal pumps. Eng. Optim. 2011, 43, 1095–1113. [Google Scholar] [CrossRef]
- Zhang, J.; Zhu, H.; Yang, C.; Li, Y.; Wei, H. Multi-objective shape optimization of helico-axial multiphase pump impeller based on NSGA-II and ANN. Energy Convers. Manag. 2011, 52, 538–546. [Google Scholar] [CrossRef]
- Takayama, Y.; Watanabe, H. Multi-objective design optimization of a mixed-flow pump. In Proceedings of the ASME 2009 Fluids Engineering Division Summer Meeting, American Society of Mechanical Engineers, Vail, CO, USA, 2–6 August 2009; pp. 371–379. [Google Scholar]
- Benturki, M.; Dizene, R.; Ghenaiet, A. Multi-Objective Optimization of Two-Stage Centrifugal Pump using NSGA-II Algorithm. J. Appl. Fluid Mech. 2018, 11, 929–943. [Google Scholar] [CrossRef]
- Shi, Y.; Eberhart, R.C. Parameter selection in particle swarm optimization. In Proceedings of the International Conference on Evolutionary Programming, San Diego, CA, USA, 25–27 March 1998; Springer: Berlin/Heidelberg, Germany, 1998. [Google Scholar]
- Fourie, P.C.; Groenwold, A.A. The particle swarm optimization algorithm in size and shape optimization. Struct. Multidiscip. Optim. 2002, 23, 259–267. [Google Scholar] [CrossRef]
- Clerc, M.; Kennedy, J. The particle swarm-explosion, stability, and convergence in a multidimensional complex space. IEEE Trans. Evol. Comput. 2002, 6, 58–73. [Google Scholar] [CrossRef]
- Yang, B.; Xu, Q.; He, L.; Zhao, L.H.; Gu, C.G.; Ren, P. A novel global optimization algorithm and its application to airfoil optimization. ASME J. Turbomach. 2015, 137, 041011. [Google Scholar] [CrossRef]
- Chao, D.; Qiu, Z. Particle swarm optimization algorithm based on the idea of simulated annealing. Int. J. Comput. Sci. Netw. Secur. 2006, 6, 152–157. [Google Scholar]
- Wu, X.; Wang, Y.; Zhang, T. An improved GAPSO hybrid programming algorithm. In Proceedings of the International Conference on Information Engineering and Computer Science, Wuhan, China, 19–20 December 2009. [Google Scholar]
- Xie, X.; Wu, P. Research on the optimal combination of ACO parameters based on PSO. In Proceedings of the 2010 International Conference on Networking and Digital Society, Wenzhou, China, 30–31 May 2010. [Google Scholar]
- Safari, A.; Hajikolaei, K.H.; Lemu, H.G.; Wang, G.G. A high-dimensional model representation guided PSOmethodology with application on compressor airfoil shape optimization. In Proceedings of the ASME Turbo Expo 2016: Turbomachinery Technical Conference and Exposition, Seoul, Korea, 13–17 June 2016. [Google Scholar]
- Song, Z.; Liu, B.; Mao, X.; Lu, X. Optimization of tandem blade based on improved particle swarm algorithm. In Proceedings of the ASME Turbo Expo 2016: Turbomachinery Technical Conference and Exposition, Seoul, Korea, 13–17 June 2016. [Google Scholar]
- Pei, J.; Gan, X.; Wang, W.; Yuan, S.; Tang, Y. Multi-objective Shape Optimization on the Inlet Pipe of a Vertical Inline Pump. J. Fluids Eng. 2019, 141, 061108. [Google Scholar] [CrossRef]
- ANSYS. ANSYS CFX User’s Guide, Release; ANSYS: Canonsburg, PA, USA, 2019. [Google Scholar]
- Gülich, J.F. Centrifugal Pumps; Springer: Berlin, Germany, 2008; Volume 2. [Google Scholar]
- Kennedy, J. The particle swarm: Social adaptation of knowledge. In Proceedings of the 1997 IEEE International Conference on Evolutionary Computation (ICEC’97), Indianapolis, IN, USA, 13–16 April 1997. [Google Scholar]
- Eberhart, R.; Kennedy, J. Particle swarm optimization. In Proceedings of the IEEE International Conference on Neural Networks, Indianapolis, IN, USA, 27–30 November 1995; Volume 4. [Google Scholar]
- Shi, Y.; Eberhart, R. A modified particle swarm optimizer. In Proceedings of the 1998 IEEE International Conference on Evolutionary Computation Proceedings. IEEE World Congress on Computational Intelligence (Cat. No. 98TH8360), Anchorage, AK, USA, 4–9 May 1998. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).