Seismic Data Denoising Based on Sparse and Low-Rank Regularization
Abstract
1. Introduction
2. Method
| Algorithm 1 Seismic denoising based on sparsity and low-rank regularization |
|
3. Numerical Experiments
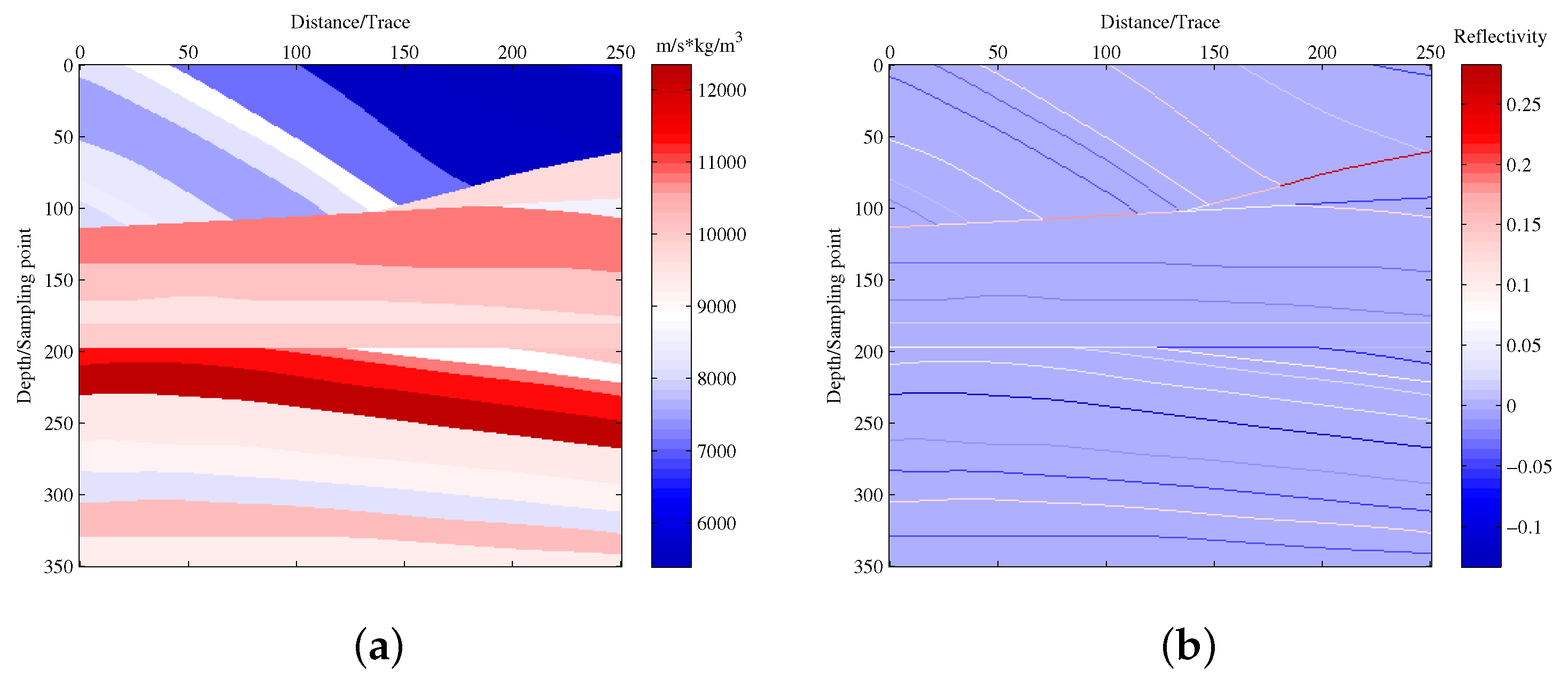
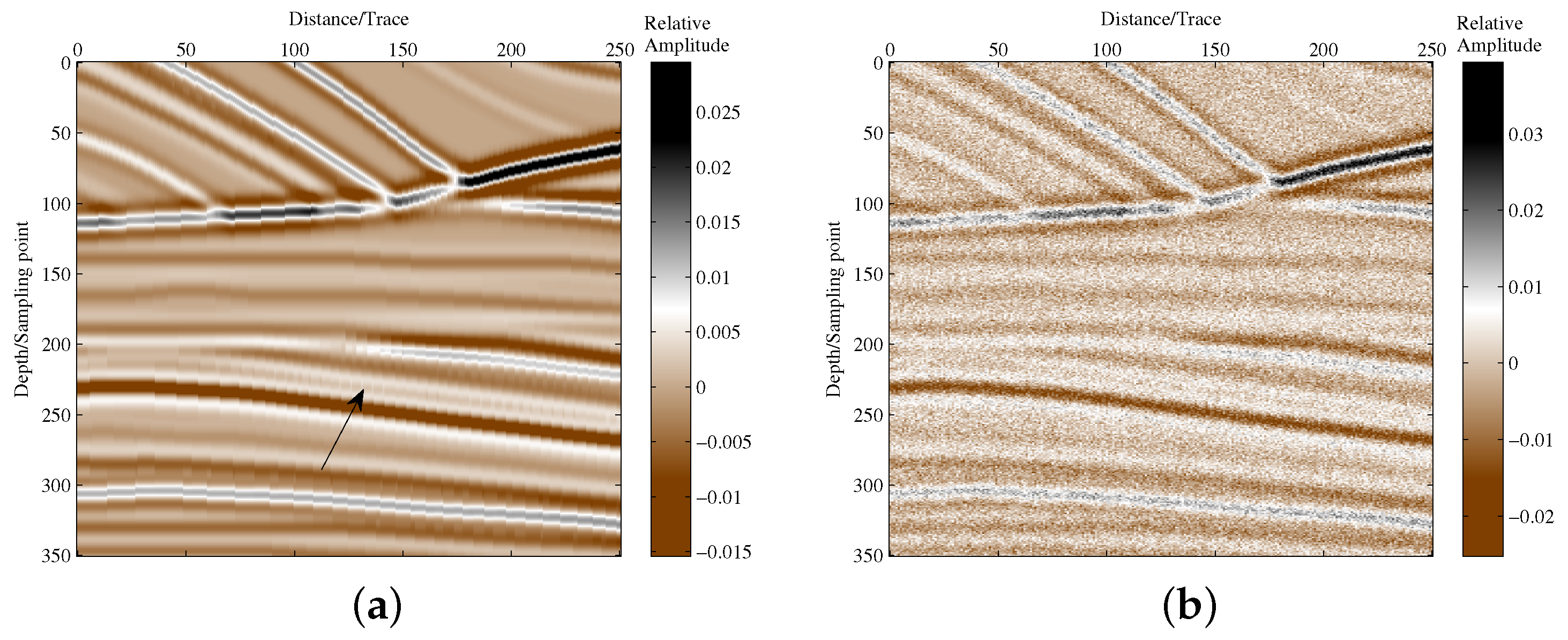
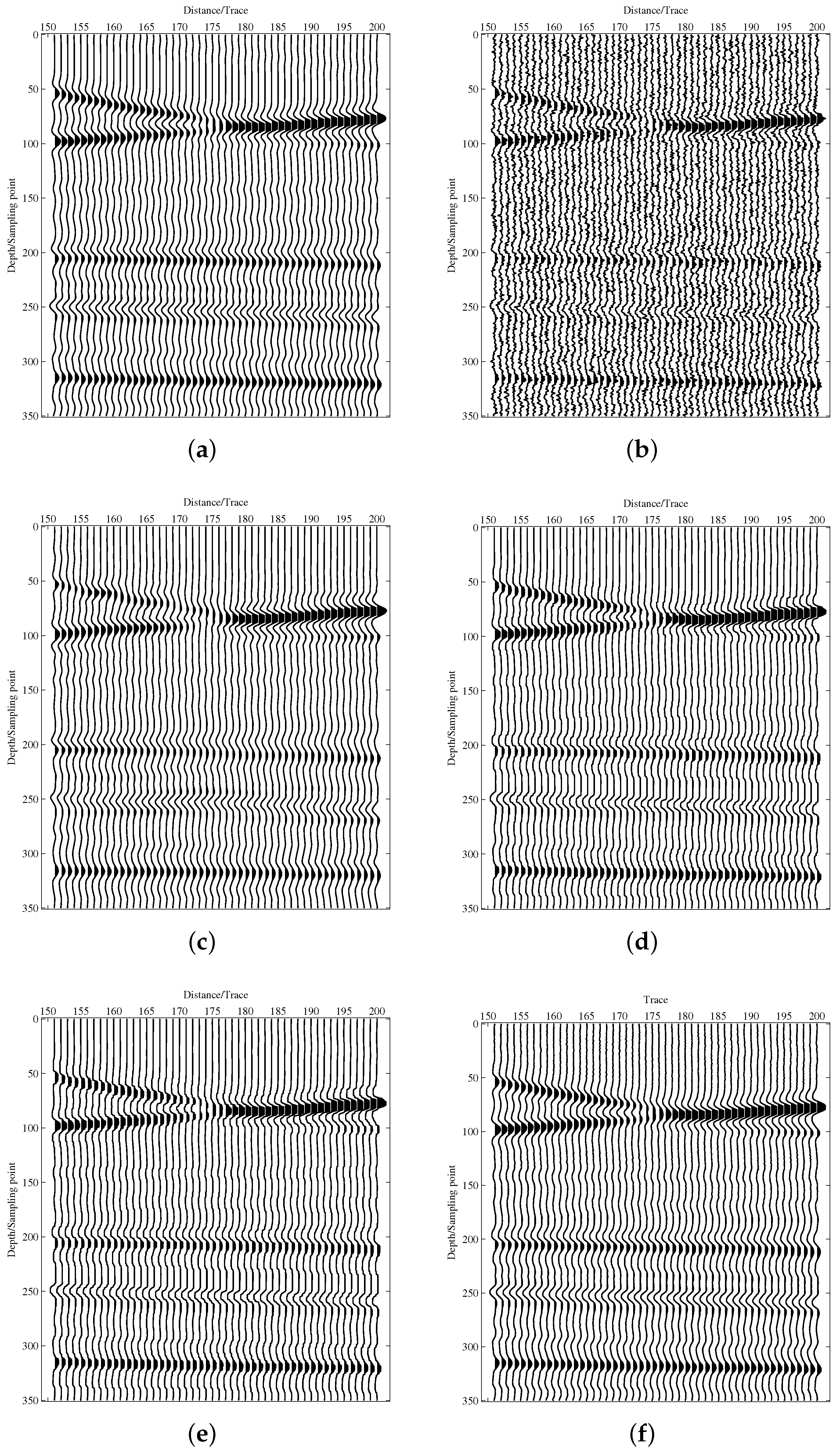
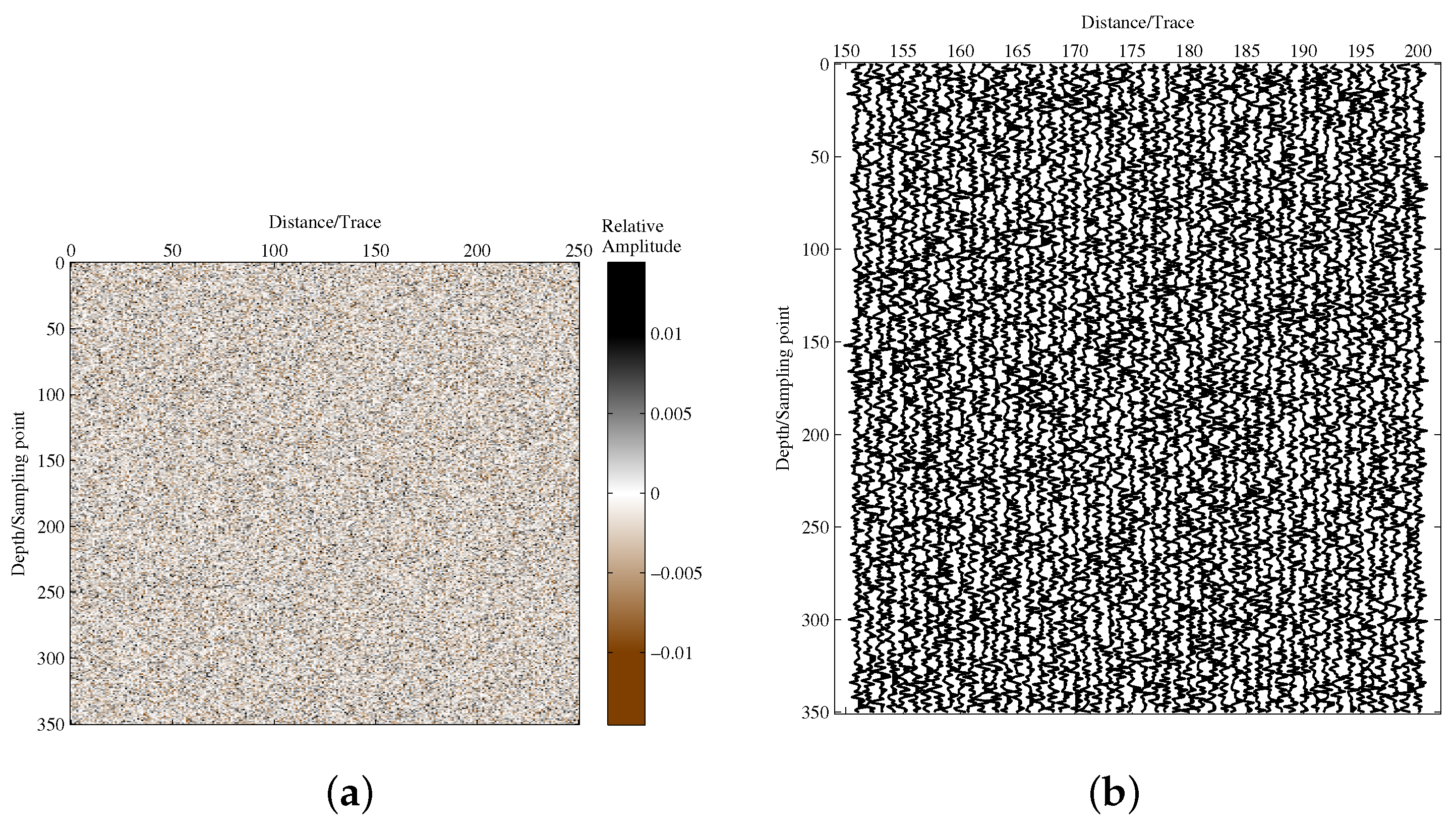
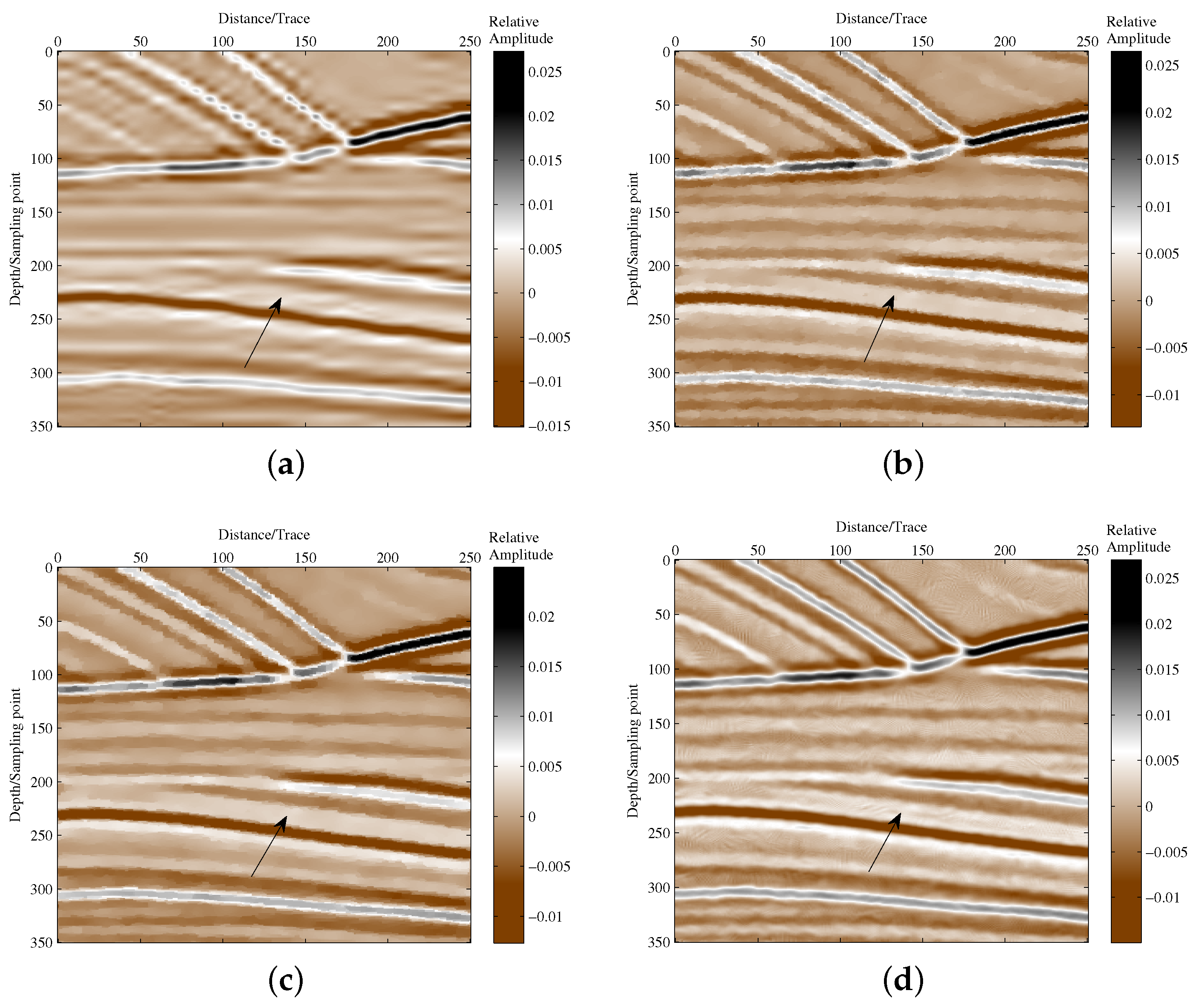
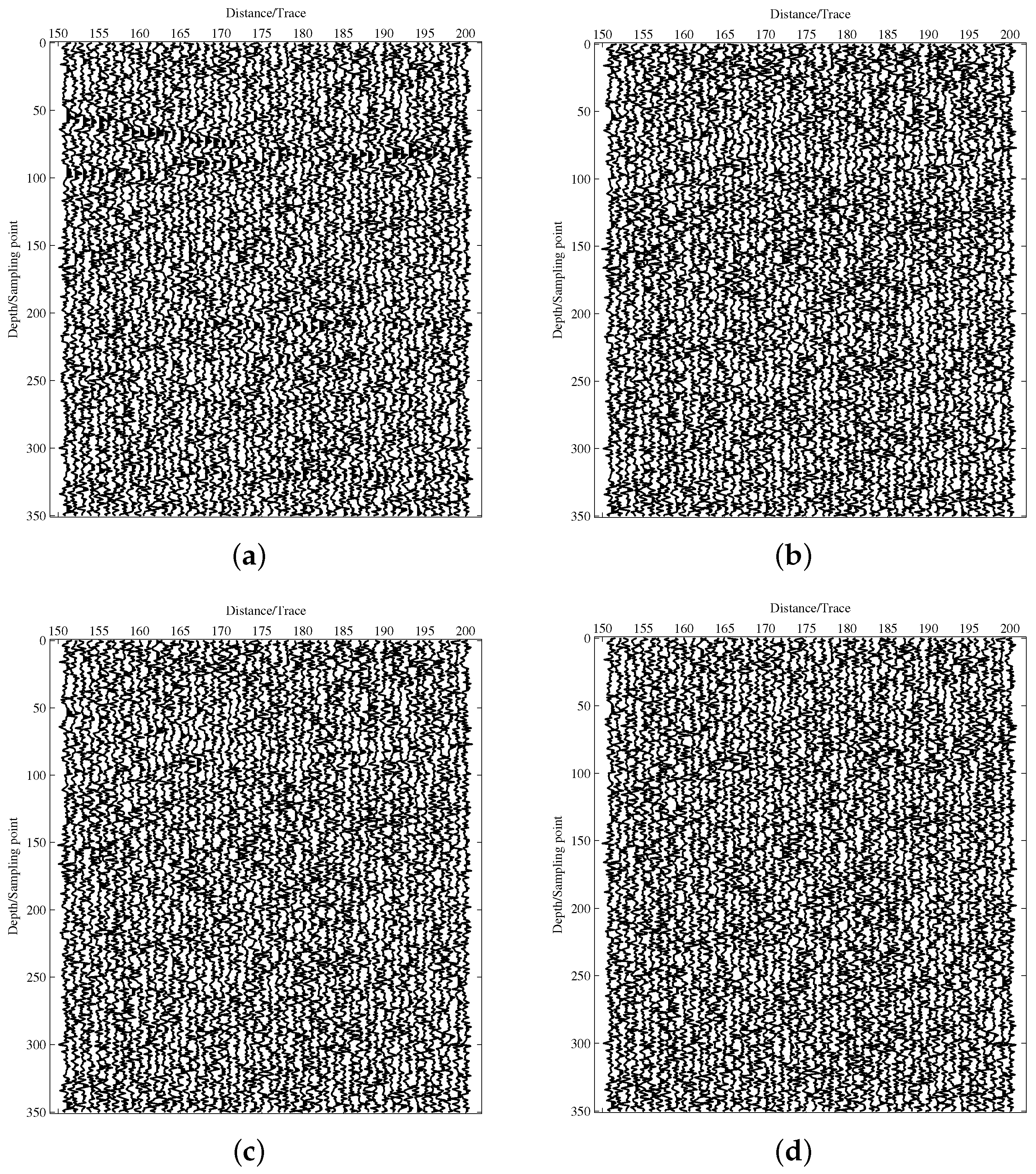
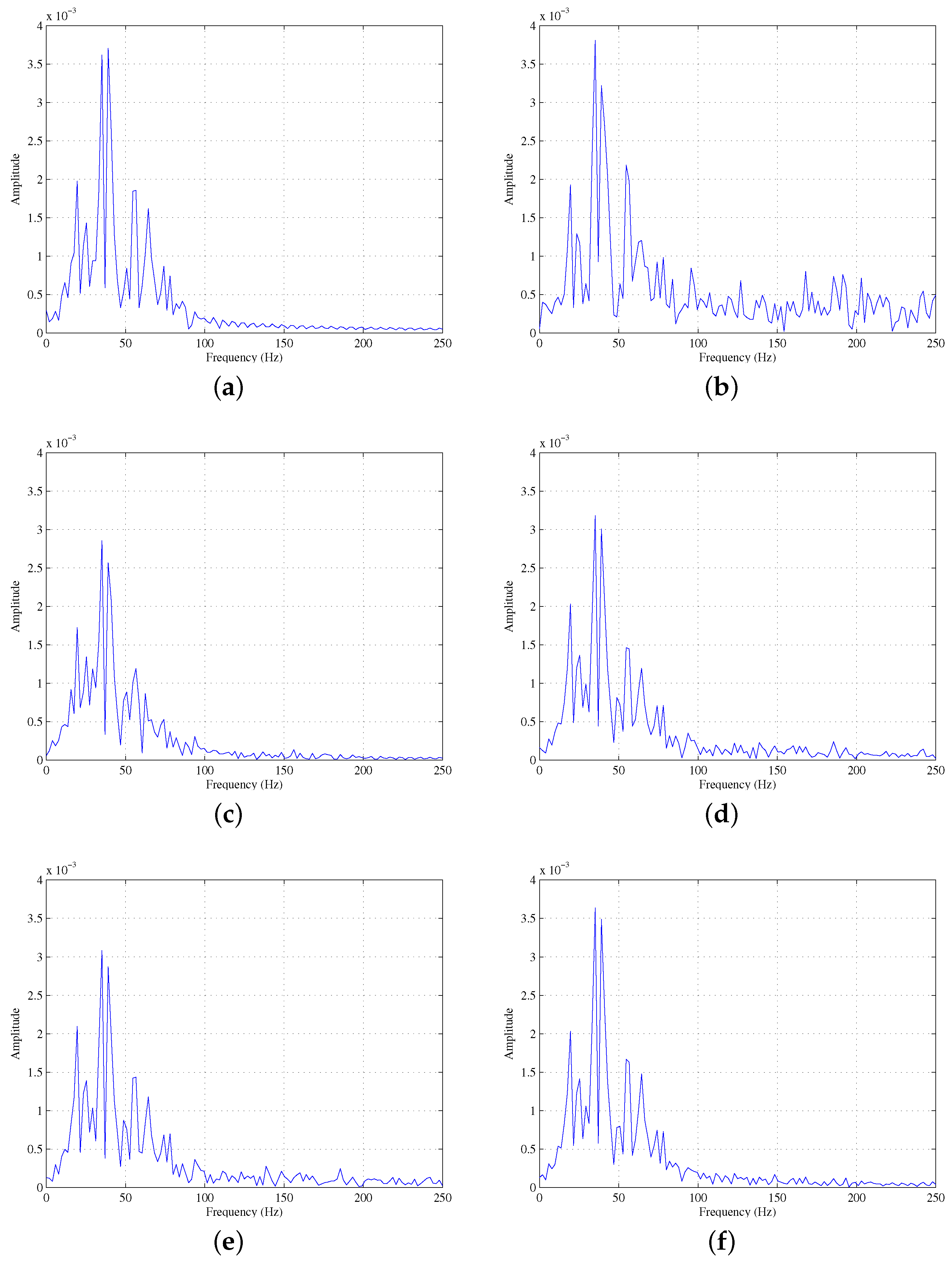
3.1. Synthetic Seismic Data Test
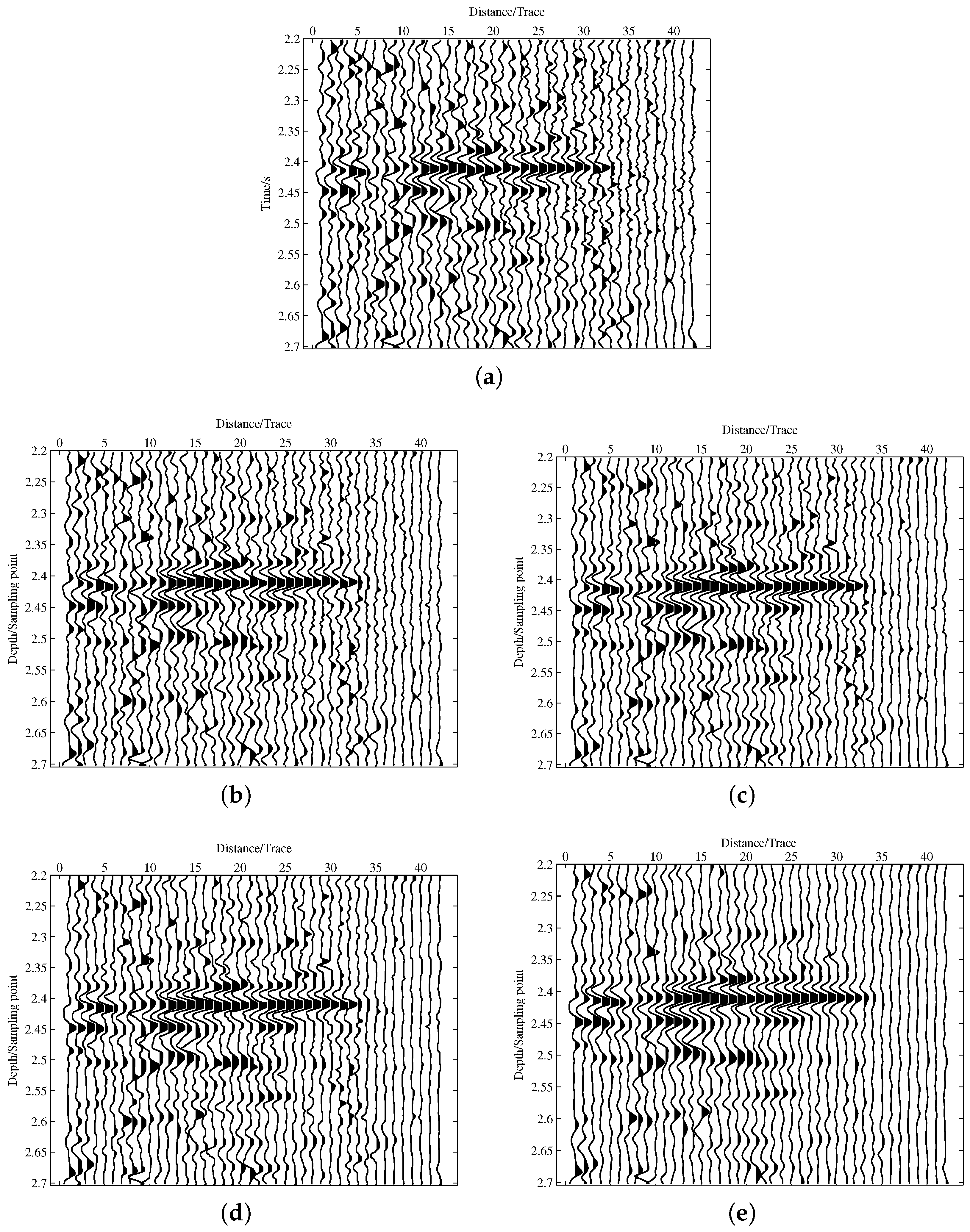
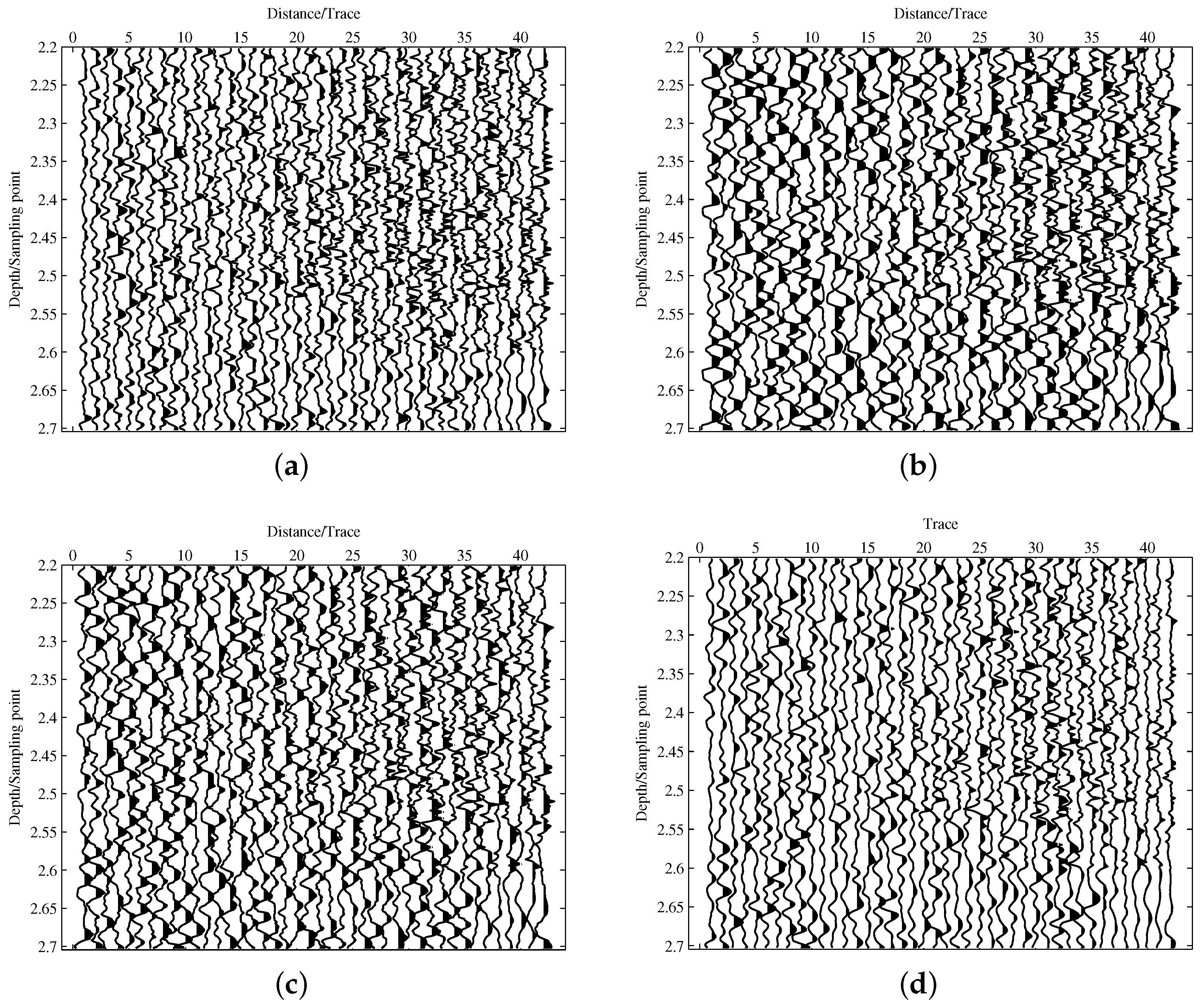
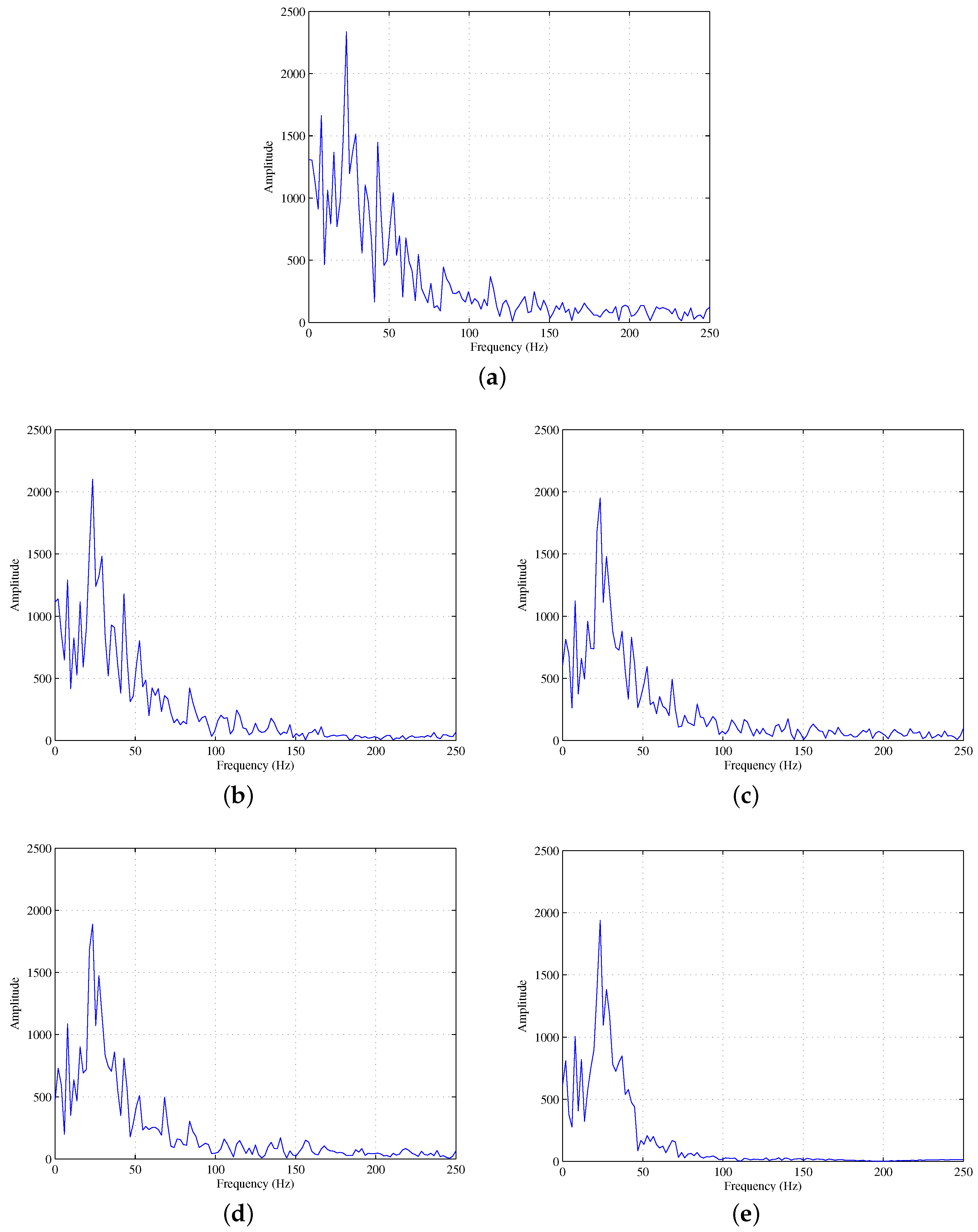
3.2. Field Seismic Data Test
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| TV | Total Variation |
| ITVD | Isotropic Total Variation Denoising |
| ATVD | Anisotropic Total Variation Denoising |
| DCT | Discrete Cosine Transform |
| SD-SpaLR | Seismic Denoising using Sparsity and Low-Rank regularization |
| SVD | Singular Value Decomposition |
| SSIM | Structural Similarity |
| BM | Block Matching |
| SNR | Signal-to-Noise Ratio |
References
- Jiang, T.; Lin, J.; Li, T.L.; Chen, Z.B.; Zhang, L.H. Boosting Signal to Noise Ratio of Seismic Signals Using the Phased-Array Vibrator System. Chin. J. Geophys. 2006, 49, 1658–1664. [Google Scholar] [CrossRef]
- Canales, L.L. Random noise reduction. In SEG Technical Program Expanded Abstracts 1984; Society of Exploration Geophysicists: Tulsa, OK, USA, 1984; pp. 525–527. [Google Scholar]
- Wang, Y. Inverse Q-filter for seismic resolution enhancement. Geophysics 2006, 71, V51–V60. [Google Scholar] [CrossRef]
- Cao, S.; Chen, X. The second-generation wavelet transform and its application in denoising of seismic data. Appl. Geophys. 2005, 2, 70–74. [Google Scholar] [CrossRef]
- Zhai, M.Y. Seismic data denoising based on the fractional Fourier transformation. J. Appl. Geophys. 2014, 109, 62–70. [Google Scholar] [CrossRef]
- Neelamani, R.; Baumstein, A.I.; Gillard, D.G.; Hadidi, M.T.; Soroka, W.L. Coherent and random noise attenuation using the curvelet transform. Lead. Edge 2008, 27, 240–248. [Google Scholar] [CrossRef]
- Kong, D.; Peng, Z. Seismic random noise attenuation using shearlet and total generalized variation. J. Geophys. Eng. 2015, 12, 1024–1035. [Google Scholar] [CrossRef]
- Tang, G.; Ma, J. Application of total-variation-based curvelet shrinkage for three-dimensional seismic data denoising. IEEE Geosci. Remote Sens. Lett. 2011, 8, 103–107. [Google Scholar] [CrossRef]
- Chen, Y.; Peng, Z.; Li, M.; Yu, F. Random noise suppression based on the improved total generalized variation with overlapping group sparsity. Oil Geophys. Prospect. 2019, 54, 24–35. (In Chinese) [Google Scholar]
- Bonar, D.; Sacchi, M. Denoising seismic data using the nonlocal means algorithm. Geophysics 2012, 77, A5–A8. [Google Scholar] [CrossRef]
- Chen, Y.; Ma, J.; Fomel, S. Double-sparsity dictionary for seismic noise attenuation. Geophysics 2016, 81, V103–V116. [Google Scholar] [CrossRef]
- Ghaderpour, E.; Liao, W.; Lamoureux, M.P. Antileakage least-squares spectral analysis for seismic data regularization and random noise attenuation. Geophysics 2018, 83, V157–V170. [Google Scholar] [CrossRef]
- Ghaderpour, E. Multichannel antileakage least-squares spectral analysis for seismic data regularization beyond aliasing. Acta Geophys. 2019, 67, 1349–1363. [Google Scholar] [CrossRef]
- Wen, B.; Li, Y.; Bresler, Y. When sparsity meets low-rankness: Transform learning with non-local low-rank constraint for image restoration. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, New Orleans, LA, USA, 5–9 March 2017; pp. 2297–2301. [Google Scholar]
- Dabov, K.; Foi, A.; Katkovnik, V.; Egiazarian, K. Image denoising by sparse 3-D transform-domain collaborative filtering. IEEE Trans. Image Process. 2007, 16, 2080–2095. [Google Scholar] [CrossRef]
- Tang, G.; Ma, J.W.; Yang, H.Z. Seismic data denoising based on learning-type overcomplete dictionaries. Appl. Geophys. 2012, 9, 27–32. [Google Scholar] [CrossRef]
- Fomel, S.; Liu, Y. Seislet transform and seislet frame. Geophysics 2010, 75, V25–V38. [Google Scholar] [CrossRef]
- Yu, G.; Sapiro, G. DCT image denoising: A simple and effective image denoising algorithm. Image Process. Line 2011, 1, 292–296. [Google Scholar] [CrossRef]
- Kumar, P.; Foufoula-Georgiou, E. Wavelet analysis for geophysical applications. Rev. Geophys. 1997, 35, 385–412. [Google Scholar] [CrossRef]
- Zhou, Y.; Li, S.; Xie, J.; Zhang, D.; Chen, Y. Sparse dictionary learning for seismic noise attenuation using a fast orthogonal matching pursuit algorithm. J. Seism. Explor. 2017, 26, 433–454. [Google Scholar]
- Elad, M.; Aharon, M. Image denoising via sparse and redundant representations over learned dictionaries. IEEE Trans. Image Process. 2006, 15, 3736–3745. [Google Scholar] [CrossRef]
- Ravishankar, S.; Bresler, Y. l0 sparsifying transform learning with efficient optimal updates and convergence guarantees. IEEE Trans. Signal Process. 2015, 63, 2389–2404. [Google Scholar] [CrossRef]
- Wen, B.; Li, Y.; Bresler, Y. The power of complementary regularizers: Image recovery via transform learning and low-rank modeling. arXiv 2018, arXiv:1808.01316. [Google Scholar]
- Martin, G.S.; Wiley, R.; Marfurt, K.J. Marmousi2: An elastic upgrade for Marmousi. Lead. Edge 2006, 25, 156–166. [Google Scholar] [CrossRef]
- Bredies, K.; Kunisch, K.; Pock, T. Total generalized variation. SIAM J. Imaging Sci. 2010, 3, 492–526. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef]
| SNR of the input seismic data (dB) | 3 | 6 | 9 | 12 | 15 |
| SNR of wavelet denoising (dB) | 8.39 | 10.92 | 12.97 | 14.95 | 16.89 |
| SNR of ITVD (dB) | 12.64 | 14.91 | 16.77 | 18.76 | 20.61 |
| SNR of ATVD (dB) | 11.90 | 14.74 | 15.51 | 18.59 | 20.97 |
| SNR of SD-SpaLR (dB) | 16.34 | 18.18 | 19.52 | 20.40 | 21.03 |
| SNR of the input data (dB) | 3 | 6 | 9 | 12 | 15 |
| SSIM of wavelet denoising | 0.68 | 0.77 | 0.84 | 0.9 | 0.93 |
| SSIM of ITVD | 0.83 | 0.89 | 0.93 | 0.95 | 0.97 |
| SSIM of ATVD | 0.81 | 0.89 | 0.93 | 0.95 | 0.97 |
| SSIM of SD-SpaLR | 0.90 | 0.94 | 0.96 | 0.98 | 0.98 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, S.; Yang, X.; Liu, H.; Cai, Y.; Peng, Z. Seismic Data Denoising Based on Sparse and Low-Rank Regularization. Energies 2020, 13, 372. https://doi.org/10.3390/en13020372
Li S, Yang X, Liu H, Cai Y, Peng Z. Seismic Data Denoising Based on Sparse and Low-Rank Regularization. Energies. 2020; 13(2):372. https://doi.org/10.3390/en13020372
Chicago/Turabian StyleLi, Shu, Xi Yang, Haonan Liu, Yuwei Cai, and Zhenming Peng. 2020. "Seismic Data Denoising Based on Sparse and Low-Rank Regularization" Energies 13, no. 2: 372. https://doi.org/10.3390/en13020372
APA StyleLi, S., Yang, X., Liu, H., Cai, Y., & Peng, Z. (2020). Seismic Data Denoising Based on Sparse and Low-Rank Regularization. Energies, 13(2), 372. https://doi.org/10.3390/en13020372





