Abstract
In a high geo-temperature environment, it is rarely reported that geo-temperature has been considered during a back analysis. This may cause the initial geo-stress field that is obtained by a back analysis to be wrong. In this study, according to the theory of elasticity, the theoretical solution of the hydraulic fracturing equation is obtained in a high geo-temperature environment. Since the vertical stress that is obtained by the hydraulic fracturing method is calculated using the density of overlying strata, this vertical stress lacks the thermal stress that is caused by geothermal gradients. Therefore, in a high geo-temperature environment, inverting the initial geo-stress field of rock masses directly using the stress that is measured by the hydraulic fracturing method can cause serious errors. We propose that the regression coefficient of a gravitational stress field should be set to one during a back analysis if stresses are measured by the hydraulic fracturing method, and this regression coefficient should not be equal to one if stresses are measured by overcoring methods. We also propose a workflow for the back analysis of the initial geo-stress field of rock masses that considers geo-temperature, and this workflow is applied to the Sangzhuling tunnel in China.
1. Introduction
With the gradual implementation of underground engineering projects in western China, such as the Sichuan–Tibet Railway and the Sichuan–Tibet Highway, deep, long, and high geo-stress tunnels have emerged in Tibetan areas [1,2,3]. In order to understand the state of in situ stresses in Tibetan areas, scholars have measured the in situ stresses of rock masses using the hydraulic fracturing and overcoring methods proposed by the International Society for Rock Mechanics (ISRM) [4,5]. The results of measurements show that maximum horizontal principal stresses are greater than vertical stresses in these areas [6,7,8,9]. That is, there is strong tectonism in rock masses due to tectonic plate movements. Therefore, in these areas, the distribution of the initial geo-stress field of rock masses is more complicated than that of the gravitational field of rock masses [10]. However, the initial geo-stress field of rock masses is the basis for calculating stresses and displacements after excavation is performed in an underground engineering project [11]. Consequently, it is of great practical significance to understand the distribution of the initial geo-stress field of rock masses [12,13]. Moreover, because of difficult downhole conditions and high costs [14], measured in situ stresses are usually insufficient, such that it is difficult to use the measured in situ stresses to express the macroscopic distribution of the initial geo-stress field of rock masses. As a result, in order to obtain the initial geo-stress field with macroscopic distribution, it is of great theoretical significance to invert the initial geo-stress field of rock masses [15,16,17]. In summary, the initial geo-stress field of rock masses is very important to underground engineering projects.
However, current studies rarely report that geo-temperature has been considered during a back analysis of the initial geo-stress field of rock masses [12,15,18,19,20,21,22,23,24,25,26,27,28,29,30,31]. Because high geo-temperature is rarely observed in practice, these studies are acceptable. However, if high geo-temperature is observed in an underground engineering project, these studies will not apply. In order to make the initial geo-stress field that is obtained by a back analysis more compatible with the actual state of rock masses, we propose a workflow for a back analysis that considers geo-temperature and is based on current studies. That is, the thermal stress of rock masses that is caused by geothermal gradients is added during the back analysis. In this study, one important hypothesis, that the geothermal gradient of the same stratum is the same, should be made. Moreover, this hypothesis has been proposed (see Equation (3)).
In this study, according to the theory of elasticity, we firstly obtain the theoretical solution of the hydraulic fracturing equation in a high geo-temperature environment. Then, we propose a workflow for a back analysis that considers geo-temperature. Finally, taking as an example the Sangzhuling tunnel, in which high geo-temperature and high geo-stress occur, we carry out a back analysis of the initial geo-stress field of rock masses.
2. The Thermal Stress of Rock Masses Caused by Geothermal Gradients
Rock masses expand due to the heat flow from the Earth’s interior, and surrounding rock masses constrain the expanded rock masses, which causes the thermal stress in rock masses (i.e., compressive stresses) [32,33]. The magnitude of this thermal stress can be approximated by Equation (1) given by Yu et al. [32] and Zheng et al. [33].
where stands for the thermal stress of rock masses in MPa; stands for the geothermal gradient in ; stands for the thermal expansion coefficient in ; stands for the elastic modulus of rock masses in MPa; and Z stands for the distance from a certain point in rock masses to the constant temperature zone in m. As can be seen from Equation (1), the thermal stress field of rock masses is in a state of hydrostatic pressure [32,33]. That is,
The geothermal gradient of the same stratum can be calculated by Equation (3) [34,35].
where stands for the virgin rock temperature at the depth of H in ; stands for the rock temperature of the constant temperature zone in ; H stands for buried depth in m; h stands for the distance from the constant temperature zone to land surfaces in m; ; and can be obtained through the regression of many sets of and H. Zhan and Cai [36] gave the definition of the constant temperature zone.
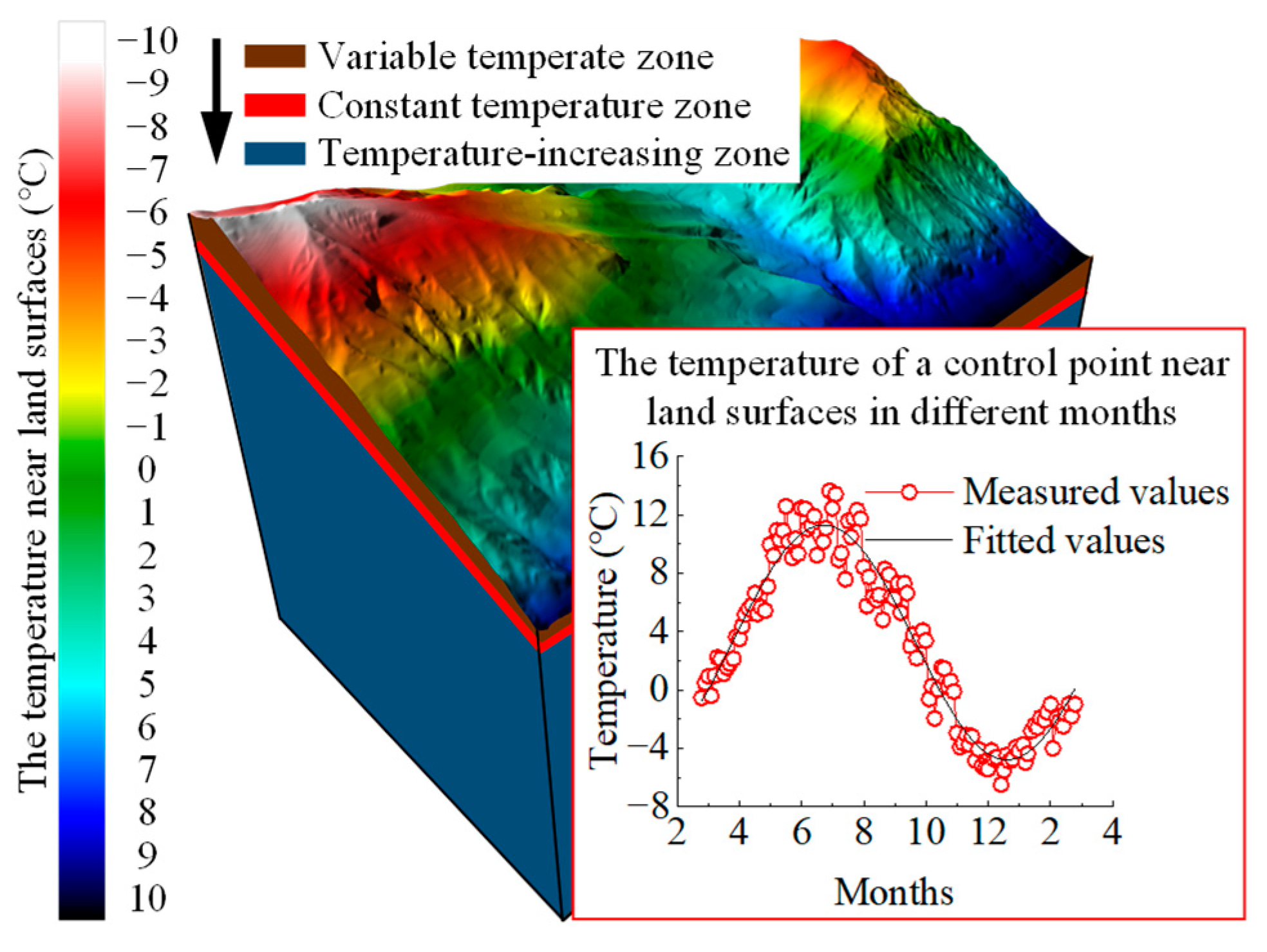
(1) The constant temperature zone is defined as the stratigraphic zone that geo-temperature does not change over time. The thickness of the strata for the constant temperature zone is about 3–5 m. The reason why geo-temperature does not change over time is that the heat flow from the Earth’s interior and the thermal radiation from the Sun are in equilibrium near the constant temperature zone. (2) The variable temperate zone is defined as the stratigraphic zone that geo-temperature changes over time. The variable temperature zone is positioned above the constant temperature zone, and is about 20–30 m away from land surfaces. The geo-temperature of the variable temperate zone changes periodically due to the thermal radiation from the Sun. Therefore, there are diurnal, monthly, and annual temperature changes in the variable temperate zone, as shown in Figure 1. (3) The temperature-increasing zone is defined as the stratigraphic zone that geo-temperature is not affected by the periodic changes in the thermal radiation from the Sun, and is only affected by the heat flow from the Earth’s interior. The temperature-increasing zone is positioned below the constant temperature zone, and the geo-temperature of the temperature-increasing zone is positively correlated with depth. The vertical distribution of the variable temperate zone, constant temperature zone, and temperature-increasing zone is shown in Figure 1.
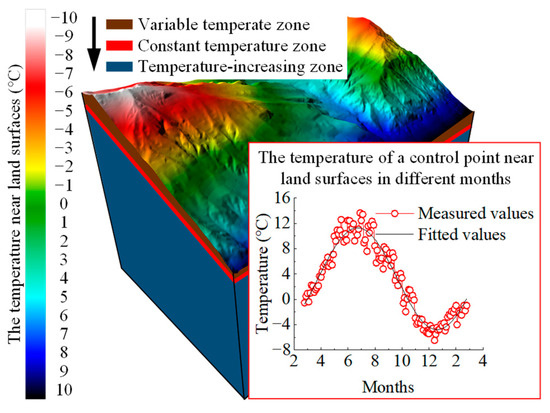
Figure 1.
The vertical distribution of the temperature zone of rock masses.
Thermal stress inside rock masses is usually considered in underground engineering. For example, in tunnel engineering, the thermal stress near tunnels needs to be determined. Moreover, tunnels are usually located in the temperature-increasing zone, and the thermal stress inside rock masses in the temperature-increasing zone can be simply and approximately expressed by Equation (1). Therefore, in this study, the geothermal gradient method (Equation (1)) was used to approximately estimate the thermal stress field of rock masses. In order to determine the state of in situ stresses, the hydraulic fracturing and overcoring methods are usually used to measure in situ stresses. The measurement principles of the hydraulic fracturing and overcoring methods are presented in Section 3.
3. The Measurement Principles of the Hydraulic Fracturing and Overcoring Methods
3.1. The Measurement Principle of the Hydraulic Fracturing Method in a Non-High Geo-Temperature Environment
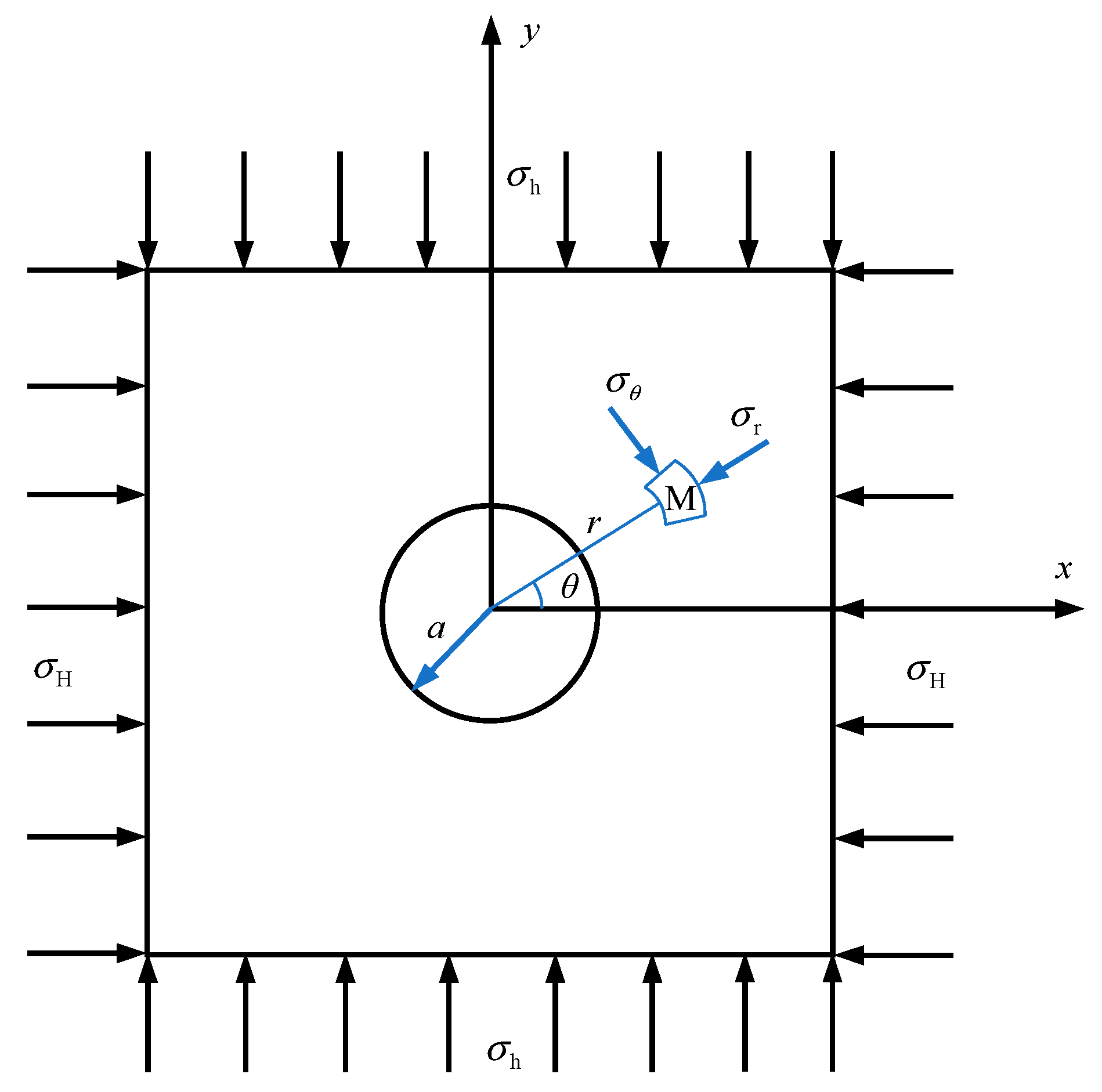
Haimson and Cornet [4] gave the measurement principle of the hydraulic fracturing method. The following two points should be noted with respect to hydraulic fracturing: (1) it is assumed that the borehole axis of hydraulic fracturing is parallel to one of principal stresses of rock masses; and (2) when maximum horizontal principal stresses are estimated, it is assumed that rock masses are linearly elastic, homogeneous, and isotropic. Further information on hydraulic fracturing stress measurements can be found in Haimson and Cornet [4]. Therefore, the mechanical model of hydraulic fracturing stress measurements can be simplified to the plane problem shown in Figure 2. That is, horizontal principal stresses are applied to a flat plate with a circular hole of radius a. According to the theory of elasticity, the stress at any point M outside the circular hole can be expressed as
where stands for the radial stress of rock masses; stands for the tangential stress of rock masses; stands for the shear stress of rock masses; and stand for the maximum and minimum horizontal principal stresses, respectively; is the radius of the borehole for hydraulic fracturing; stands for the distance from point M to the origin of coordinates; and stands for the angle between the -direction and the x-direction. When , the state of the stress on the borehole wall can be expressed as
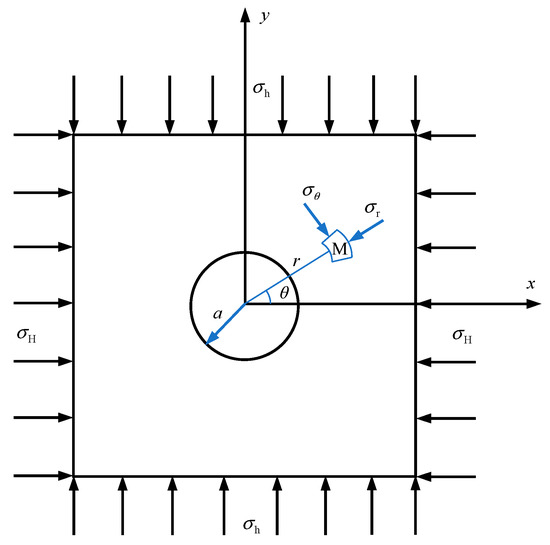
Figure 2.
The mechanical model of hydraulic fracturing stress measurements.
As can be seen from Equation (5), when , the minimum tangential stress on the borehole wall can be obtained. That is,
Therefore, when the hydraulic fluid pressure is greater than , in the direction of the maximum horizontal principal stress, a fracture is initiated on the borehole wall, and this hydraulic fluid pressure is taken to be the breakdown pressure (). stands for the tensile strength of the tested rock. can be expressed as
In saturated rocks with low permeability, the pore pressure () should be added. Therefore, the breakdown pressure can be expressed as
As the hydraulic fluid pressure increases, the induced fracture will extend further. When the depth of the induced fracture reaches three times the diameter of the borehole of hydraulic fracturing, the pressure at this time is close to the state of in situ stresses. When the pump is shut off, and the hydraulically induced fracture closes back, the reached pressure is the shut-in pressure (). Moreover, the shut-in pressure is in equilibrium with the minimum horizontal principal stress (). That is,
As can be seen from Equations (8) and (9), and can be obtained by , , , and . However, the tensile strength () is difficult to obtain. In order to overcome this problem, the fracture reopening pressure () is used. When the induced fracture that has closed completely after the initial pressure cycle reopens, the reached pressure is assumed to be the fracture reopening pressure (). Since a fracture has be induced, the tensile strength () is equal to zero, and thus Equation (8) becomes
The vertical stress of rock masses () can be calculated by the overburden weight of rock masses.
where is the mass density of the i-th rock layer; is the gravitational acceleration; and is the thickness of the i-th rock layer.
In summary, the three principal stresses that are measured by the hydraulic fracturing method can be expressed as
3.2. The Measurement Principle of the Hydraulic Fracturing Method in a High Geo-Temperature Environment
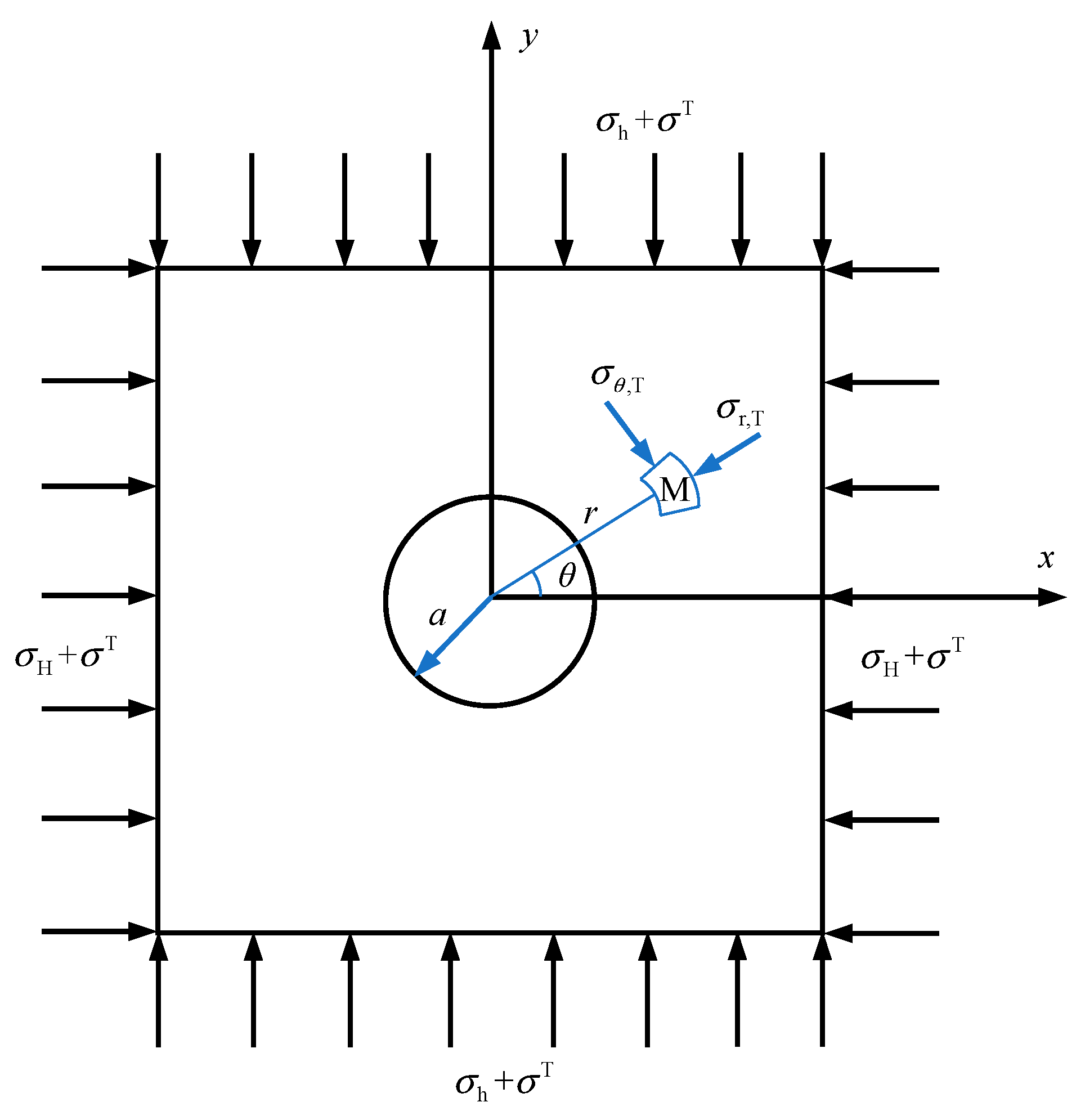
In a high geo-temperature environment, deeply buried rock masses are subject to the thermal stress described in Equation (1). Moreover, the thermal stress field of rock masses is in a state of hydrostatic pressure (see Equation (2)). Therefore, the tectonic state of rock masses is shown in Figure 3. That is, the thermal stress that is caused by geothermal gradients is added to boundary stresses. In a high geo-temperature environment, it is assumed that the temperature of water in the borehole of hydraulic fracturing is the same as the virgin rock temperature because of the good thermal conductivity of water. In other words, it is assumed that the water in the borehole of hydraulic fracturing does not cause thermal stresses. Then, the stress at any point M outside the circular hole becomes
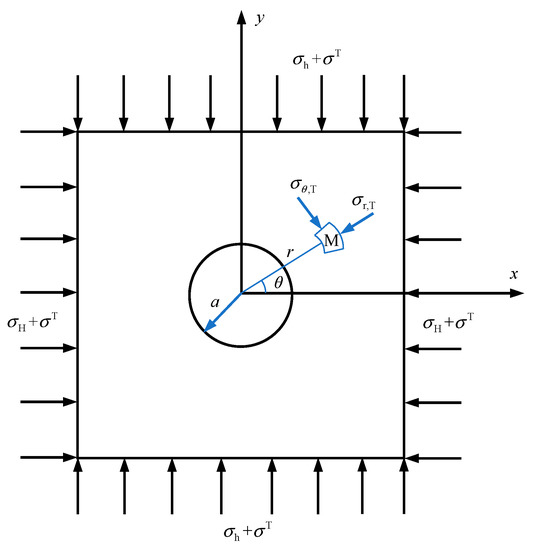
Figure 3.
The mechanical model of hydraulic fracturing stress measurements in a high geo-temperature environment.
When , the state of the stress on the borehole wall becomes
As can be seen from Equation (14), when , the minimum tangential stress on the borehole wall can be obtained. That is,
Since the shut-in pressure is in equilibrium with the minimum horizontal principal stress, and the minimum horizontal principal stress shown in Figure 3 is , the shut-in pressure in a high geo-temperature environment becomes
The fracture reopening pressure in a high geo-temperature environment becomes
Therefore, in a high geo-temperature environment, is added to the shut-in pressure, and is added to the fracture reopening pressure. Moreover, the maximum and minimum horizontal principal stresses are calculated based on the shut-in pressure, the fracture reopening pressure, and the pore pressure, as shown in Equation (12). Thus, in a high geo-temperature environment, the maximum horizontal principal stress that is measured by the hydraulic fracturing method becomes
As can be seen from Equation (18), the maximum horizontal principal stress increases as compared to a non-high geo-temperature environment. In a high geo-temperature environment, the minimum horizontal principal stress that is measured by the hydraulic fracturing method becomes
As can be seen from Equation (19), the minimum horizontal principal stress increases as compared to a non-high geo-temperature environment. However, the vertical stress of rock masses () is calculated by the overburden weight of rock masses. That is, the vertical stress of rock masses is independent of geo-temperature. Therefore, in a high geo-temperature environment, the vertical stress measured by the hydraulic fracturing method lacks the thermal stress caused by geothermal gradients, as shown in Equation (20).
As can be seen from Equation (20), in a high geo-temperature environment, since the vertical stress that is measured by the hydraulic fracturing method contains only gravitational information, inverting the initial geo-stress field of rock masses directly using the stress measured by the hydraulic fracturing method can cause serious errors.
3.3. The Measurement Principle of Overcoring Methods
After excavation is performed in an underground engineering project, in order to understand the state of in situ stresses, overcoring methods proposed by Sjöberg et al. [5] are usually used to measure in situ stresses. Further information on overcoring stress measurements can be found in Sjöberg et al. [5]. The results measured by overcoring methods comprise the complete stress tensor that can be expressed as three principal stresses (magnitudes and orientations) [5], and Leeman [37] presented the computed theory of overcoring methods. That is, in a high geo-temperature environment, the stress measured by overcoring methods contains not only gravitational information, but also the information of stresses caused by geo-temperature, weathering, deposition, erosion, or tectonism. In other words, the stress measured by overcoring methods is closest to the in situ stress of rock masses.
4. The Workflow for a Back Analysis Considering Geo-Temperature
4.1. In Situ Stresses Are Measured by the Hydraulic Fracturing Method
In a high geo-temperature environment, the vertical stress that is measured by the hydraulic fracturing method contains only gravitational information (see Equation (20)). Therefore, the regression coefficient of the gravitational stress field of rock masses should be set to 1 during a back analysis, as shown in Equation (21). In other words, gravitational and thermal stress fields are used as known stress fields, and only tectonic stress fields need to be inversely determined. As noted, when the stress that is measured by the hydraulic fracturing method is used to invert the initial geo-stress field of rock masses, the workflow for a back analysis considering geo-temperature is as follows: (1) gravitational and thermal stresses should be removed from the measured horizontal in situ stresses of rock masses; (2) the back analysis of tectonic stress fields should be carried out (i.e., the regression coefficients of tectonic stress fields should be solved); and (3) the initial geo-stress field of rock masses should be obtained by superposing the gravitational, tectonic, and thermal stress fields of rock masses. Thus, the adopted regression model of the initial geo-stress field of rock masses can be expressed as
where stands for the measured stress of rock masses; stands for the calculated stress caused by gravity; stands for the calculated stress caused by tectonic loads; and are regression coefficients; and stands for random error.
4.2. In Situ Stresses Are Measured by Overcoring Methods
As can be seen from Section 3.3, in a high geo-temperature environment, the vertical stress that is measured by overcoring methods contains not only gravitational information, but also the information of stresses that is caused by geo-temperature, weathering, deposition, erosion, or tectonism. Therefore, is introduced to reflect the information of stresses that is caused by weathering, deposition, erosion, or tectonism. In other words, only the thermal stress field of rock masses is used as a known stress field, and gravitational and tectonic stress fields need to be inversely determined. As a result, when the stress that is measured by overcoring methods is used to invert the initial geo-stress field of rock masses, the workflow for a back analysis considering geo-temperature is as follows: (1) the thermal stress of rock masses should be removed from the measured in situ stresses of rock masses; (2) the back analysis of gravitational and tectonic stress fields should be carried out (i.e., the regression coefficients of gravitational and tectonic stress fields should be solved); and (3) the initial geo-stress field of rock masses should be obtained by superposing the gravitational, tectonic, and thermal stress fields of rock masses. Thus, the adopted regression model of the initial geo-stress field of rock masses can be expressed as
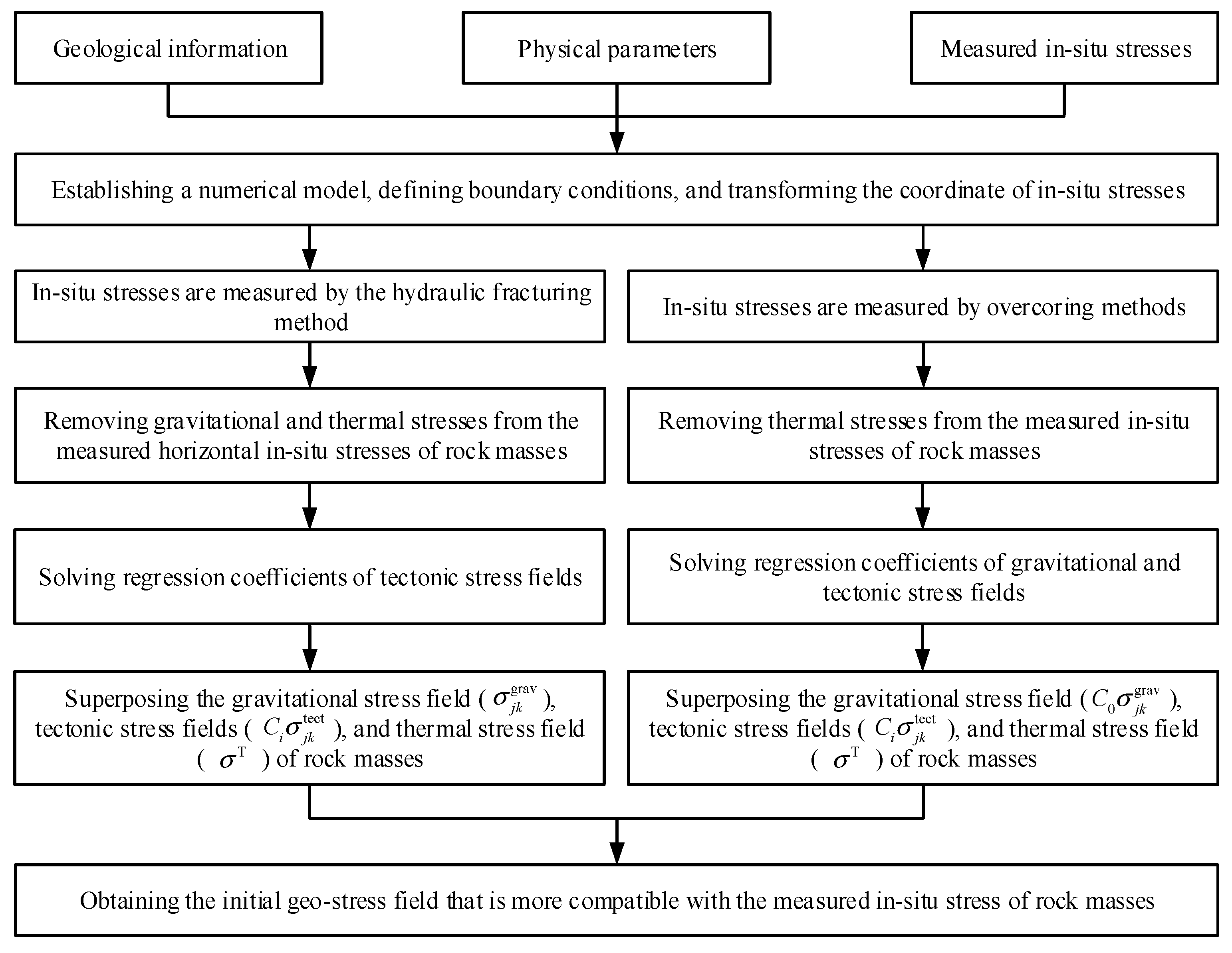
In summary, based on the information of measured vertical stresses, the proposed workflow for a back analysis considering geo-temperature is shown in Figure 4. Moreover, the advantage of the hydraulic fracturing method is that there is no theoretical limit to the depth of measurement [4]. The disadvantage of the hydraulic fracturing method is that there are difficult downhole conditions and high costs [14], and it is necessary to assume that the borehole axis is parallel to one of the principal stresses [4]. The advantage of overcoring methods is that overcoring methods can obtain a complete stress tensor [5]. The disadvantage of overcoring methods is that stresses can only be measured after excavation is performed in an underground engineering project [5].
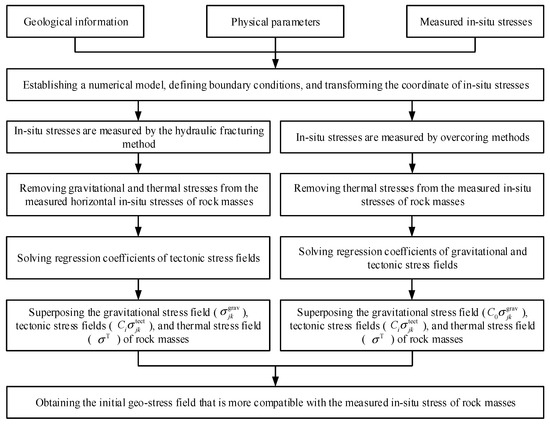
Figure 4.
The workflow for a back analysis of the initial geo-stress field of rock masses considering geo-temperature.
5. Engineering Application: A Case Study
5.1. Project Overview
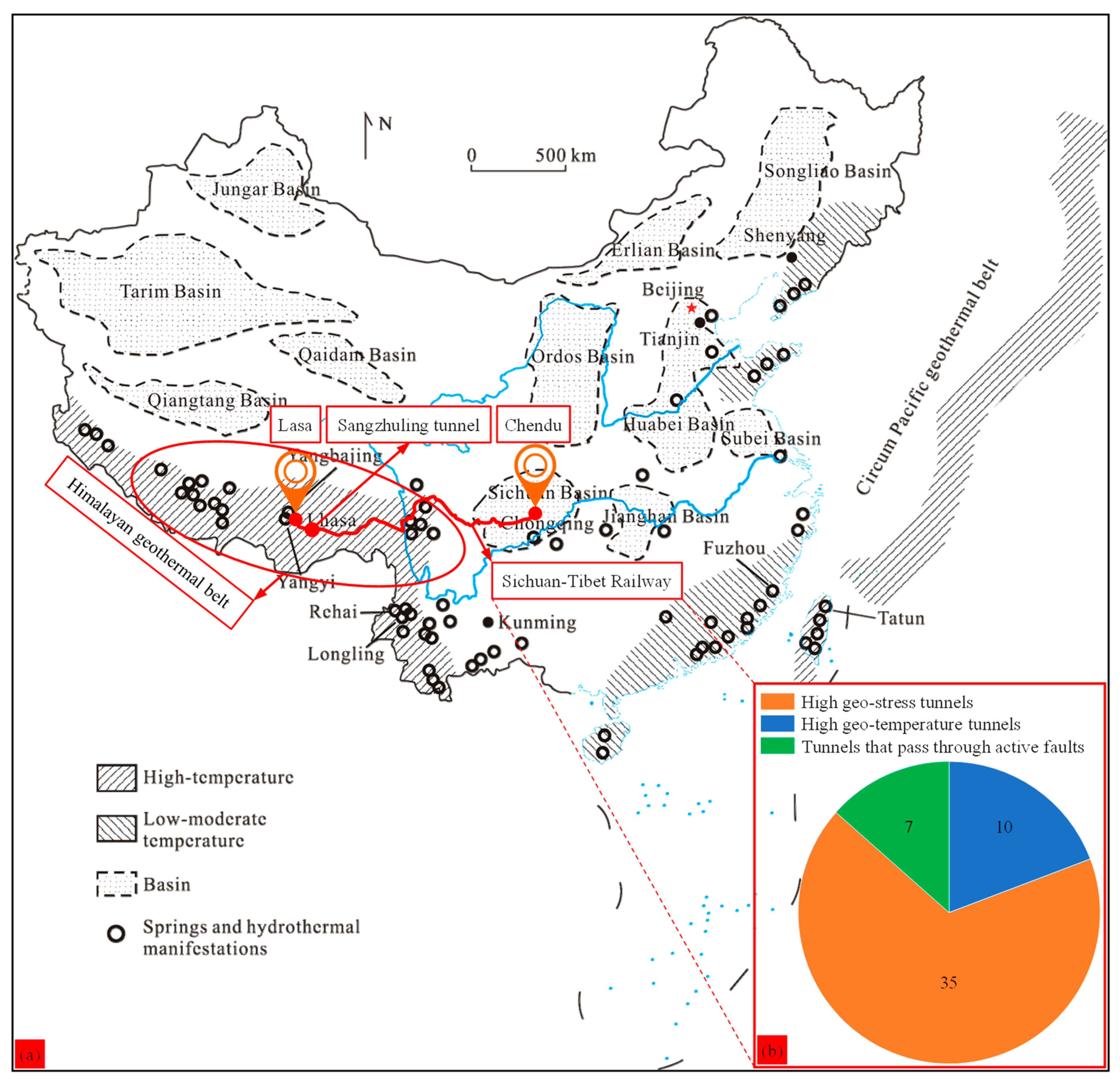
The Sichuan–Tibet Railway runs from Chengdu to Lasa, passes through Ya’an, Kangding, Changdu, Linzhi, and Shannan, and has a total length of 1742.39 km. Moreover, the Sichuan–Tibet Railway passes through the Himalayan geothermal belt [38,39], and this geothermal belt is one of the most active geothermal belts in China [40], as shown in Figure 5a. There are 10 tunnels with high geo-temperature along the Sichuan–Tibet Railway, and the geo-temperature ranges from 28.7 to 89.9 °C at a depth range of 392–1347 m [41]. Moreover, along the Sichuan–Tibet Railway, there are 35 tunnels with high geo-stress, and 7 tunnels pass through active faults [41], as shown in Figure 5b.
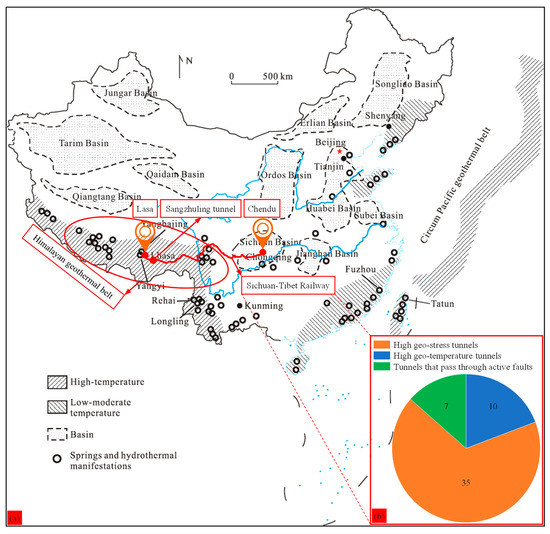
Figure 5.
The Himalayan geothermal belt: (a) the distribution of geothermal resources in China [39]; (b) the number of tunnels with high geo-stress, with high geo-temperature, and that pass through active faults.
The Sangzhuling tunnel in the Sichuan–Tibet Railway is a typical high geo-temperature and high geo-stress tunnel, and it is located in the Tibetan Plateau, as shown in Figure 6a. The Tibetan Plateau is one of the regions with the strongest tectonic movement in China [10]. The longer the length of the arrow in Figure 6a, the greater the speed of crustal movements, and the stronger the tectonism. The ground elevation of the Sangzhuling tunnel is about 3300–5100 m. The total length and the maximum buried depth of this tunnel are about 16,258 and 1347 m, respectively, as shown in Figure 6b. It can be seen that the Sangzhuling tunnel is a long and deeply buried tunnel, and it is a critical element in the Sichuan–Tibet Railway.

Figure 6.
The general situation of the Sangzhuling tunnel: (a) the GPS velocity field of Crustal Movement Observation Network of China with respect to Eurasia [43]; (b) the topography of the Sangzhuling tunnel; (c) the measured virgin rock temperatures in the Sangzhuling tunnel; (d) the longitudinal section of the Sangzhuling tunnel.
Figure 6c shows the measured virgin rock temperatures in the Sangzhuling tunnel. The highest recorded virgin rock temperature in this tunnel was [3]. The process for measuring virgin rock temperatures is as follows: (1) a 5 m deep hole is drilled using a 50 mm drill near the tunnel face or sidewalls; (2) virgin rock temperatures are measured using infrared radiation thermometers or temperature sensors (see Figure 6c). Through the regression of many sets of measured virgin rock temperatures and buried depth, the geothermal gradient in the Sangzhuling tunnel is determined (i.e., α = 5.5 °C/100 m) [41,42]. Therefore, according to the physical parameters in Table 1, the thermal and gravitational stresses of diorite can be calculated, as shown in Equations (23) and (24), respectively.

Table 1.
The physical parameters of rock masses [30,42].
In the Sangzhuling tunnel, the distance from the constant temperature zone to land surfaces () is about 20 m [41,42]. That is, . Therefore, when the buried depth of diorite exceeds 800 m, thermal stresses are more than 60% of gravitational stresses. Thus, it is necessary to consider geo-temperature during the back analysis of the initial geo-stress field of rock masses in the Sangzhuling tunnel.
In order to ensure that the initial geo-stress field obtained by a back analysis is reliable, a small area with a length of 4000 m (at the mileage location of DK184+000–DK188+000 m) is used for the back analysis. Figure 6d shows the longitudinal section of the Sangzhuling tunnel in this area, and the stratum that the Sangzhuling tunnel passes through in this area is composed of diorite. The physical parameters of the diorite and the rubble soil are shown in Table 1. In order to understand the state of in situ stresses in the Sangzhuling tunnel, at the mileage location of DK186+327 m, in situ stresses were measured by the hydraulic fracturing method proposed by ISRM [4] and are shown in Table 2.

Table 2.
The measured in situ stresses of rock masses in the DK-SZLSD-2 borehole [30].
Table 2 shows that maximum horizontal principal stresses are greater than gravitational stresses. Thus, there is a strong tectonic stress field near the Sangzhuling tunnel. Moreover, it is difficult to express the macroscopic distribution of the initial geo-stress field of rock masses using the in situ stresses of the five measuring points listed in Table 2. Therefore, it is more necessary to invert the initial geo-stress field of rock masses in the Sangzhuling tunnel.
5.2. Establishing a Three-Dimensional Numerical Model
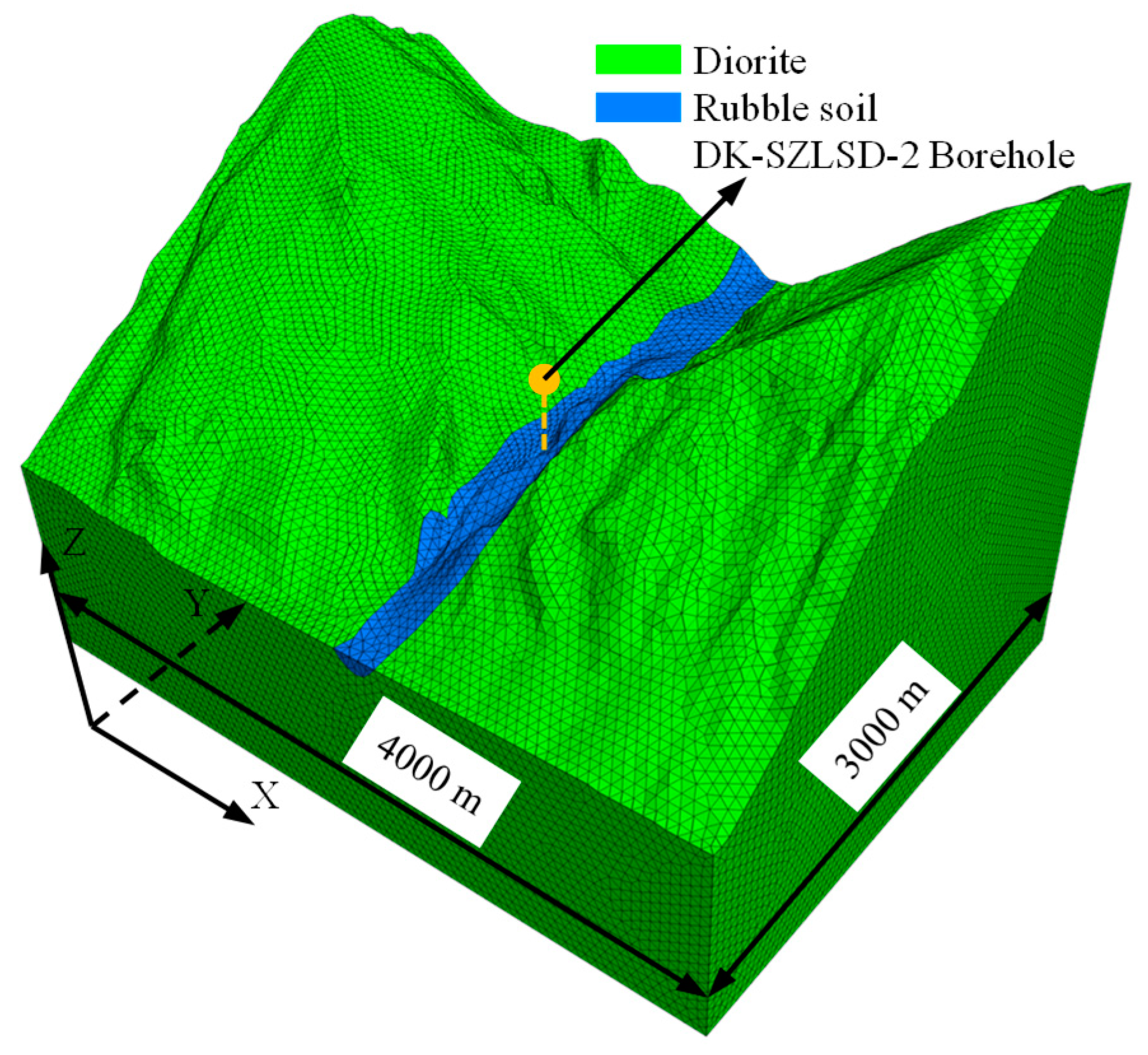
As shown in Figure 7, the calculation area of the three-dimensional numerical model is a rectangular area with a length of 4000 m and a width of 3000 m. This numerical model consists of 1,166,718 elements and 204,646 nodes. Since the elastic modulus of diorite is 36 GPa, the finite element analysis (FEA) program ANSYS was used for the calculations, and a linear elastic stress–strain criterion was adopted. ANSYS is a general-purpose finite element computer program. In order to ensure that the calculations were reliable, the bottom of this numerical model was set to 1000 m below the axis of the Sangzhuling tunnel. In order to conveniently compute the stress perpendicular to the axis of the Sangzhuling tunnel, the x-direction of this numerical model was set to the direction of the tunnel axis, and the y-direction and z-direction of this numerical model are shown in Figure 7.
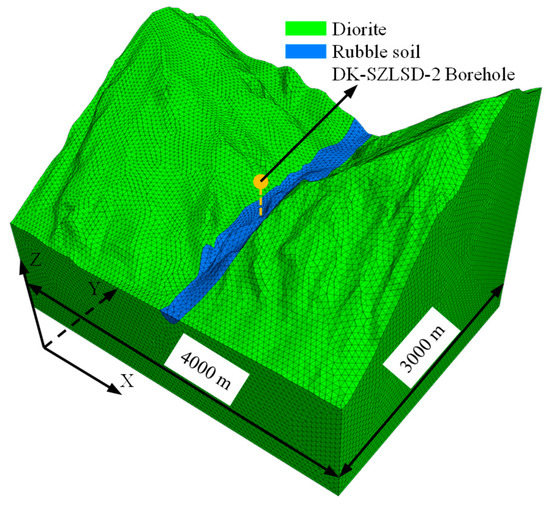
Figure 7.
The three-dimensional numerical model after meshing.
5.3. Defining Boundary Conditions
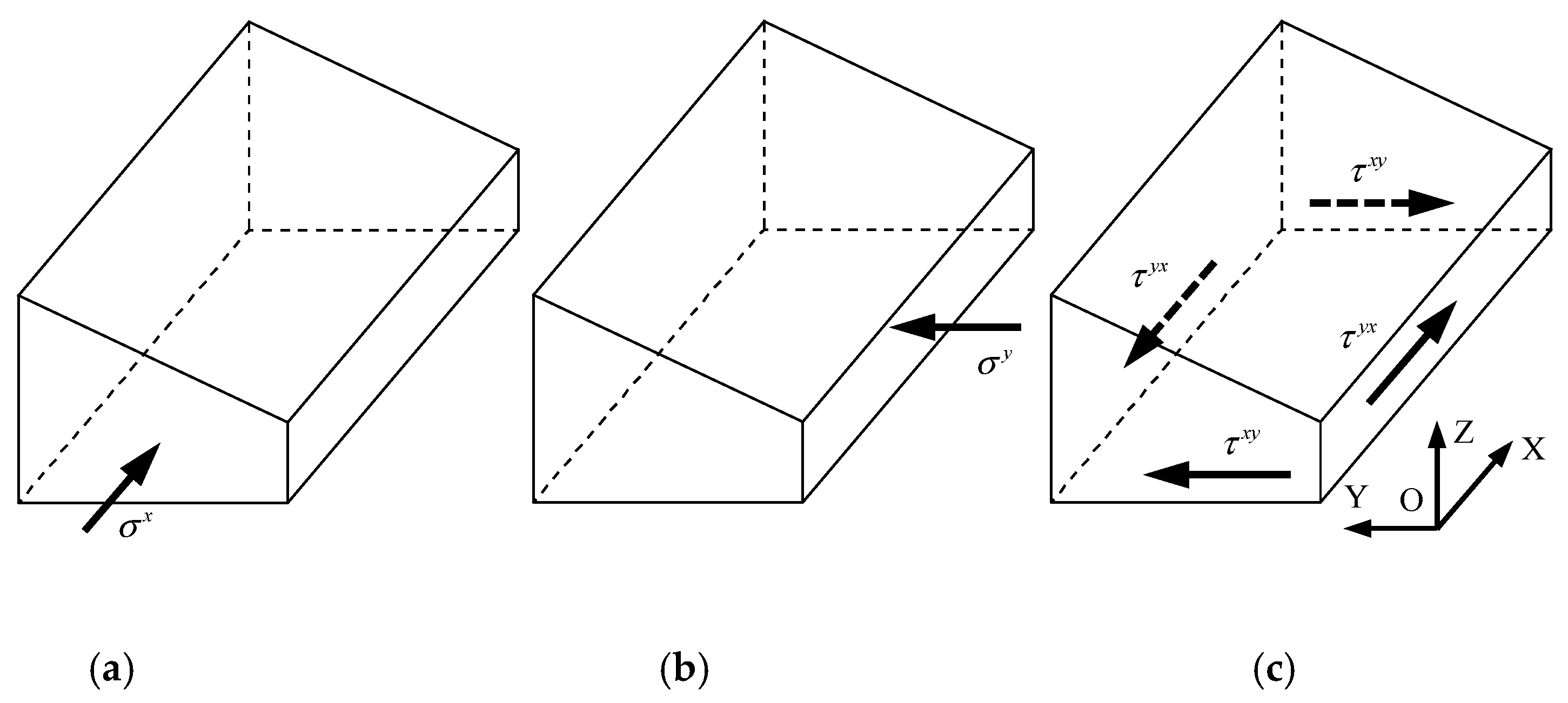
Since the in situ stresses of the Sangzhuling tunnel were measured by the hydraulic fracturing method, gravitational and thermal stresses can be calculated by and , respectively. Therefore, gravitational and thermal stress fields can be used as known stress fields, and only tectonic stress fields need to be inversely determined. Figure 8 shows the tectonic boundary loads that were applied to the numerical model shown in Figure 7.
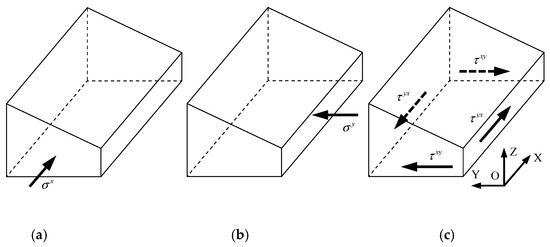
Figure 8.
Tectonic boundary loads: (a) the tectonic boundary load along the x-direction; (b) the tectonic boundary load along the y-direction; (c) the tectonic shear loads in the xy plane.
5.4. Transforming the Coordinate of in Situ Stresses
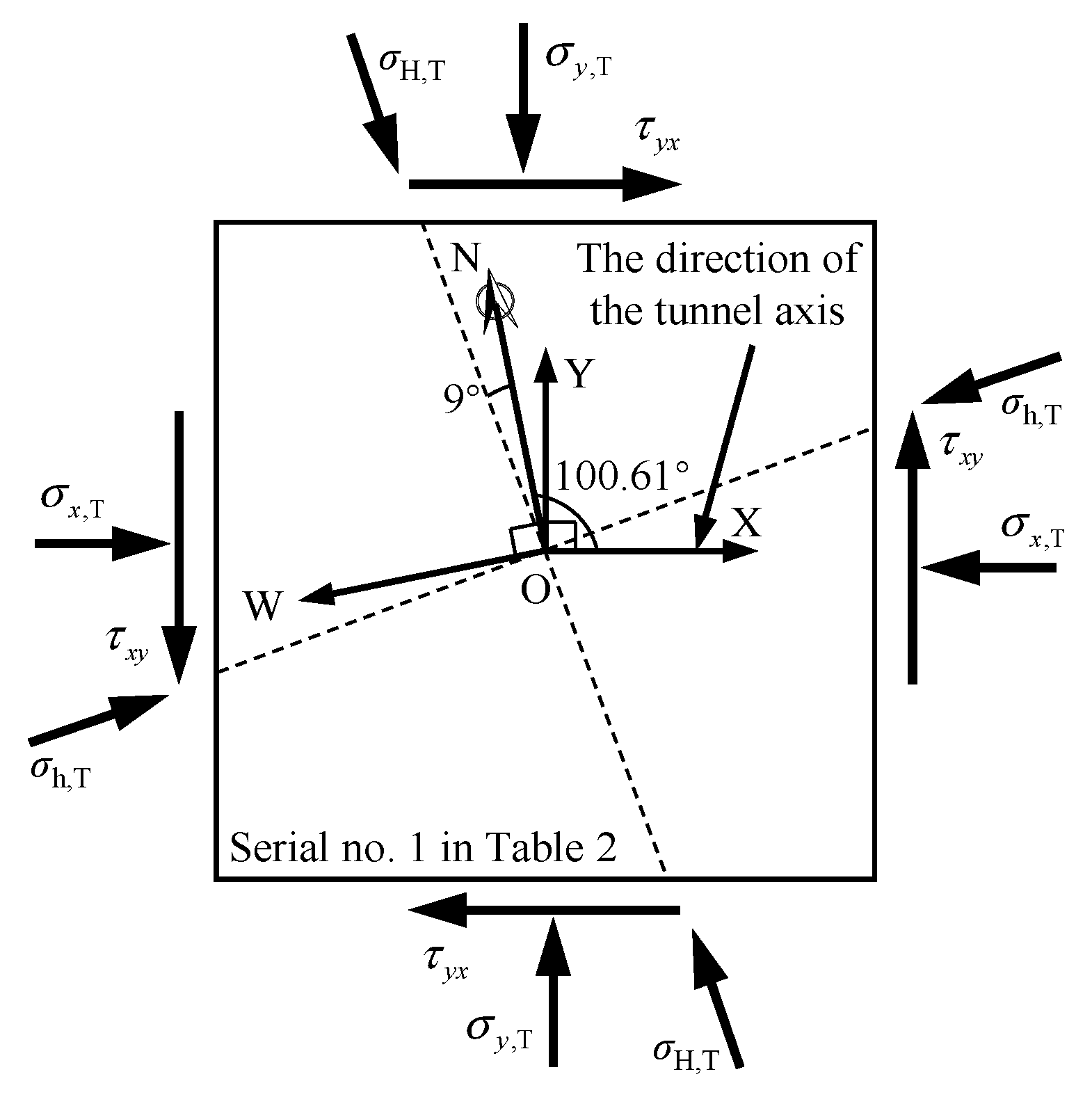
Figure 9 shows that the XOY coordinate system used in the three-dimensional numerical model is different from the NOW coordinate system used in the measured in situ stresses of rock masses. Therefore, the measured in situ stresses of rock masses need to be converted. According to the theory of elasticity, Equation (25) can be used to convert the measured in situ stresses of rock masses, and the converted in situ stresses of rock masses are shown in Table 3.
where is the stress before conversions; is the stress after conversions; and are conversion coefficients; the X direction of the XOY coordinate system is defined as the direction of the tunnel axis; and the N direction of the NOW coordinate system is defined as the direction of true north.
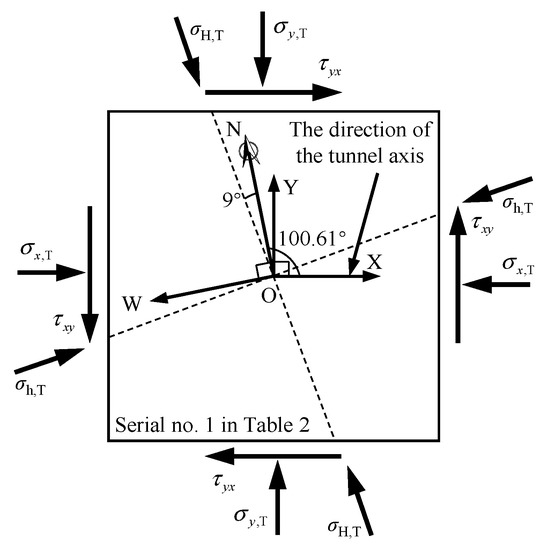
Figure 9.
The coordinate systems of the three-dimensional numerical model (XOY) and measured in-situ stresses (NOW).

Table 3.
The converted in situ stresses of rock masses.
5.5. Removing Gravitational and Thermal Stresses
According to Section 4.1, since the in situ stresses of the Sangzhuling tunnel were measured by the hydraulic fracturing method, gravitational and thermal stresses should be removed from the measured horizontal in situ stresses of rock masses shown in Table 3. Therefore, the horizontal tectonic stresses in the x-direction and y-direction can be obtained by Equations (26) and (27), respectively, and are shown in Table 4.
where is the x-direction horizontal tectonic stress after removing gravitational and thermal stresses; is the y-direction horizontal tectonic stress after removing gravitational and thermal stresses; and is Poisson’s ratio.

Table 4.
The tectonic stresses after removing gravitational and thermal stresses.
5.6. Solving Regression Coefficients and Superposing Stress Fields
Table 1 shows that the elastic modulus of diorite is high. Therefore, an elastic constitutive model can be used to approximately calculate the initial geo-stress field of rock masses. Moreover, in high geo-temperature and high geo-stress environments, it is usually assumed that the initial geo-stress field of rock masses is approximately composed of gravitational, tectonic, and thermal stress fields. As can be seen from Section 5.1, the in situ stresses of the Sangzhuling tunnel were measured by the hydraulic fracturing method. Thus, Equation (21) can be used as the regression model of the initial geo-stress field of rock masses in the Sangzhuling tunnel. Combined with the three tectonic boundary loads shown in Figure 8, the adopted regression model considering geo-temperature can be expressed as
In order to conduct a comparison with previous works, the initial geo-stress field without considering geo-temperature was added, and the adopted regression model can be expressed as
where is the calculated stress caused by the x-direction tectonic load shown in Figure 8a; is the calculated stress caused by the y-direction tectonic load shown in Figure 8b; and is the calculated stress caused by the tectonic shear loads in the xy plane shown in Figure 8c.
, , and can be solved by the least-squares method, and the least-squares method can determine the unique solution of regression coefficients. That is, this unique solution can minimize the error between calculated stresses and measured ones. If geo-temperature is considered, , , and are equal to 0.67, 4.67, and 2.88, respectively. Then, the initial geo-stress field of rock masses can be obtained by superposing the gravitational stress field (), the tectonic stress fields (, , and ), and the thermal stress field () of rock masses. The initial geo-stress field after superposition can be expressed as
If geo-temperature is not considered, the initial geo-stress field after superposition can be expressed as
5.7. Discussion
The calculated value of in situ stress magnitudes with and without considering geo-temperature can be obtained by Equations (30) and (31), respectively. For the calculated value of in situ stress orientations, horizontal principal stresses can be obtained by Equation (32) firstly. Then, the angle between the direction of maximum horizontal principal stresses and the x-direction can be obtained by Equation (33). Finally, according to the relationship between the x-direction shown in Figure 9 and true north, Equation (34) can be obtained, and the azimuth of maximum horizontal principal stresses can be obtained by Equation (34). The calculated values of in situ stress magnitudes and orientations are shown in Table 5 and Figure 10, Figure 11 and Figure 12.
where is the angle between the direction of maximum horizontal principal stresses and the x-direction; is the azimuth of maximum horizontal principal stresses, and clockwise is defined as positive.

Table 5.
Stress magnitudes, stress orientations, residuals, and the residual sum of squares.
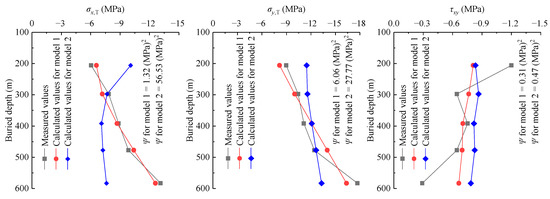
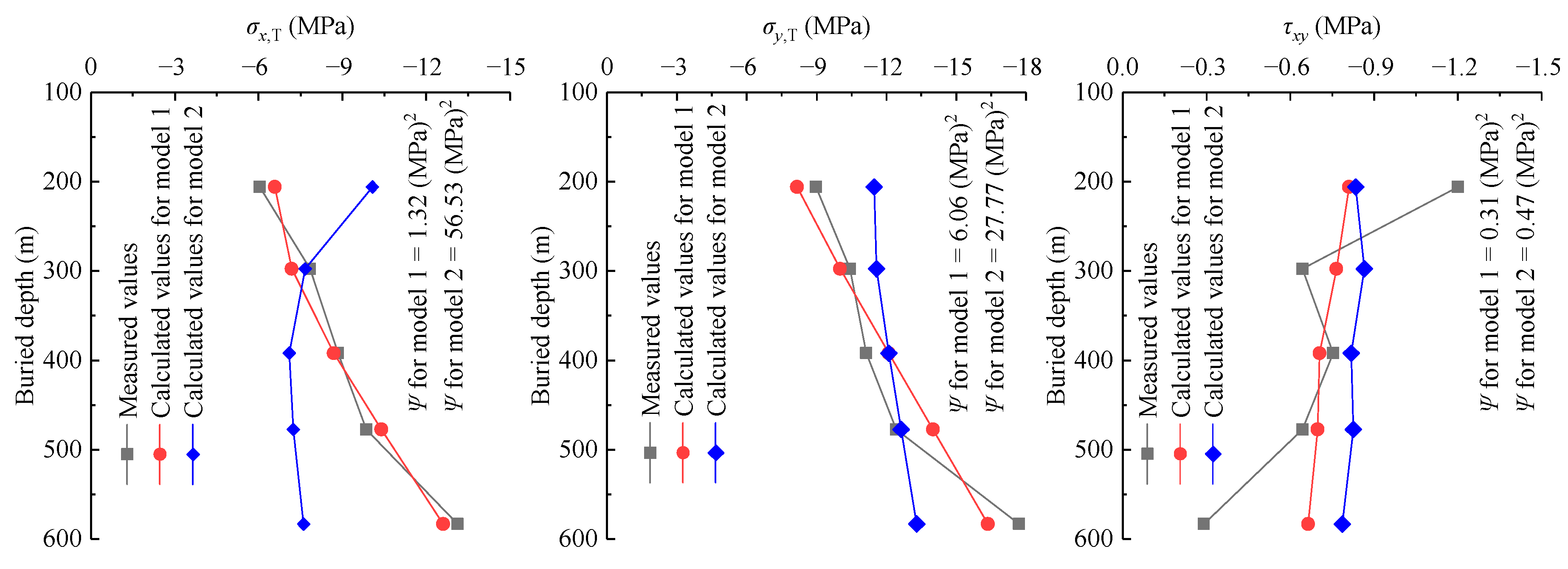
Figure 10.
The comparison of the magnitude between measured in situ stresses and calculated ones.
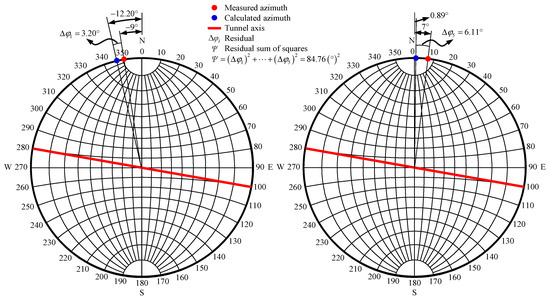
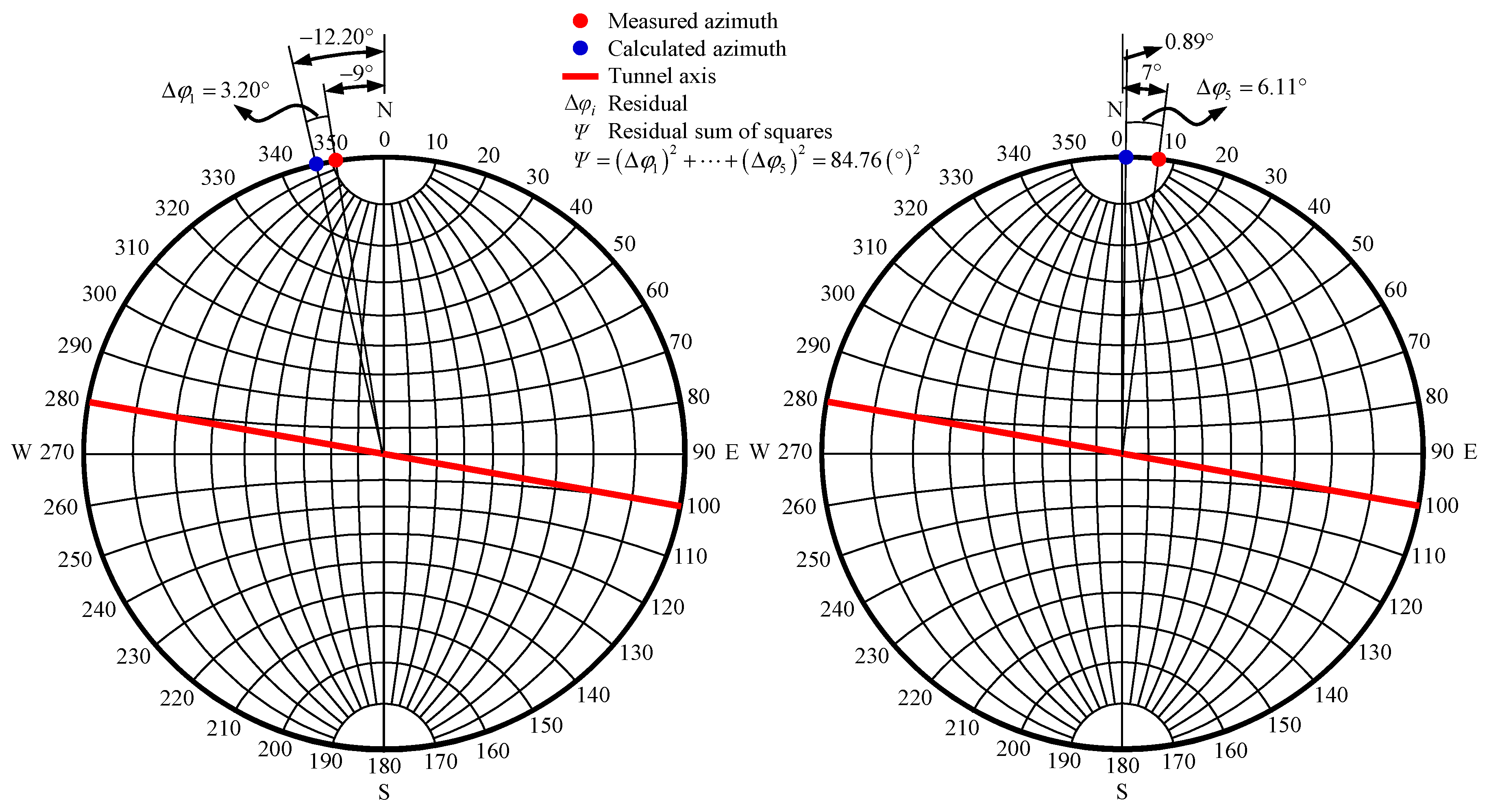
Figure 11.
The comparison of in situ stress orientations considering geo-temperature.
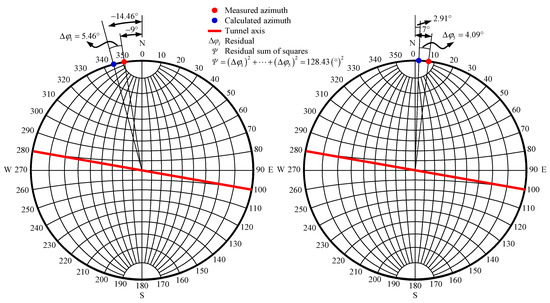
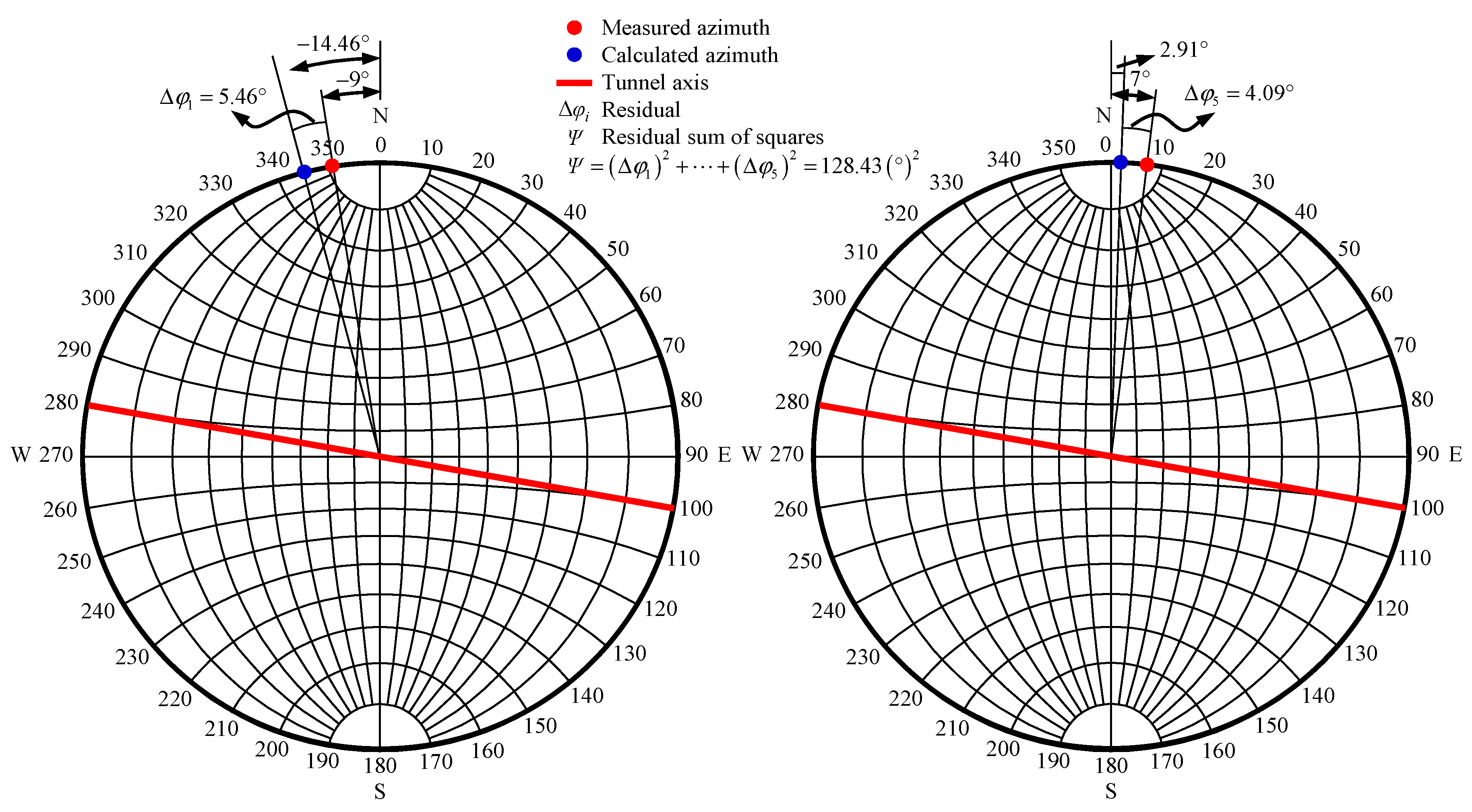
Figure 12.
The comparison of in situ stress orientations without considering geo-temperature.
Table 5 shows (1) the maximum residual of in situ stress magnitudes considering geo-temperature is 1.58 MPa, and the residual sum of squares for in situ stress magnitudes considering geo-temperature is . Similarly, the maximum residual and the residual sum of squares for in situ stress magnitudes without considering geo-temperature are −5.51 MPa and 84.77 (MPa)2, respectively. Therefore, the calculated stress magnitude considering geo-temperature is more consistent with the measured stress magnitude of rock masses. (2) The maximum residual of in situ stress orientations considering geo-temperature is 6.11°, and the residual sum of squares for in situ stress orientations considering geo-temperature is 84.76. Similarly, the maximum residual and the residual sum of squares for in situ stress orientations without considering geo-temperature are −7.59° and 128.43, respectively. Therefore, the calculated stress orientation considering geo-temperature is more identical to the measured stress orientation of rock masses. (3) Moreover, Figure 10, Figure 11 and Figure 12 show that the distribution of calculated in situ stress magnitudes and orientations considering geo-temperature is more consistent with that of measured in situ stress magnitudes and orientations. As noted, the accuracy of the initial geo-stress field obtained by a back analysis considering geo-temperature is higher than that without considering geo-temperature.
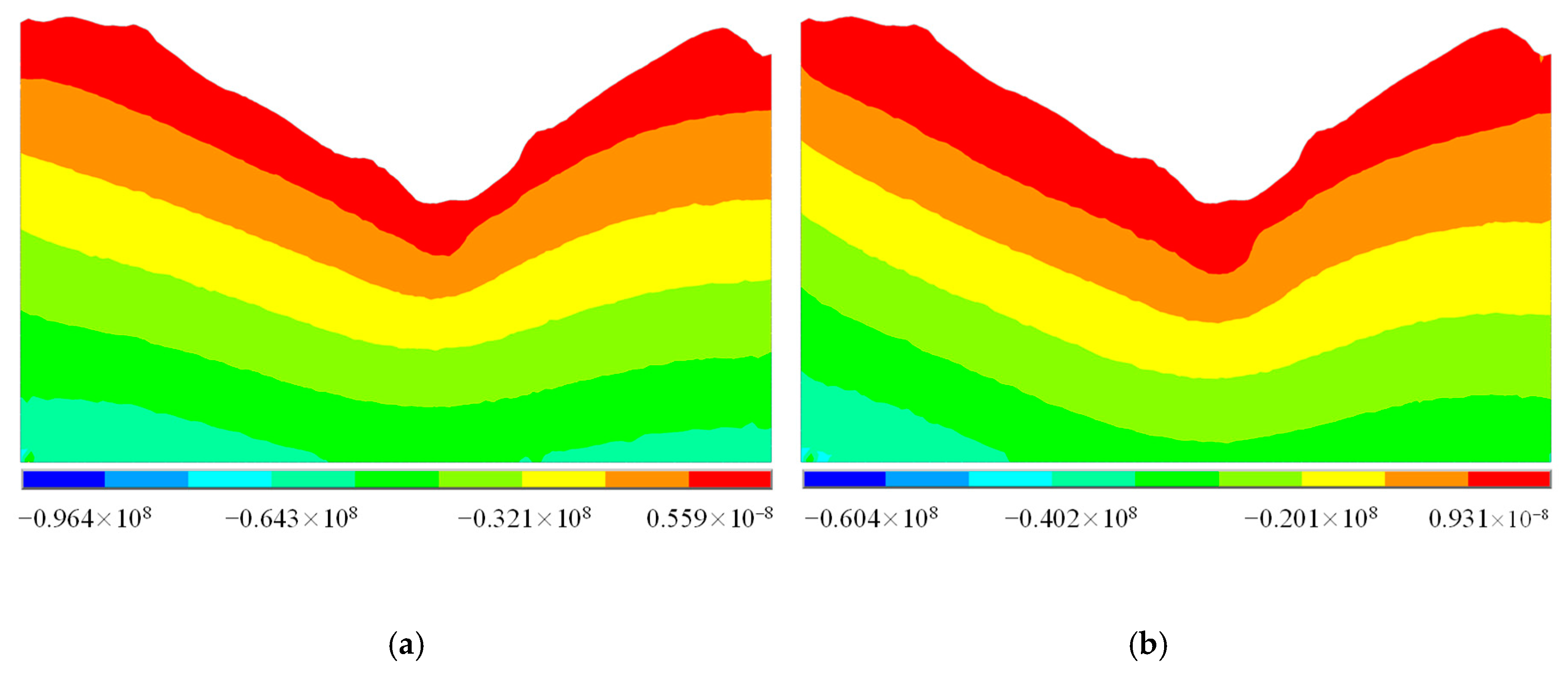
If geo-temperature is not considered, gravitational and tectonic stresses are used to superpose the thermal stress in the measured stress of rock masses. However, the thermal stress field of rock masses is in a state of hydrostatic pressure (see Equation (2)). Moreover, gravitational and tectonic stress fields are in a state of non-hydrostatic pressure. Therefore, superposing the thermal stress by gravitational and tectonic stresses will produce low accuracy. That is, if geo-temperature is not considered, the accuracy of the initial geo-stress field obtained by a back analysis will be low. Figure 13 shows the vertical stress in the longitudinal section along the tunnel axis.
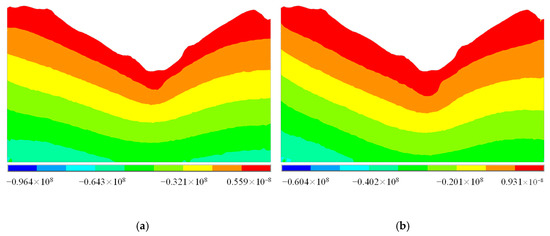
Figure 13.
The vertical stress in the longitudinal section along the tunnel axis (a) considering geo-temperature; (b) without considering geo-temperature.
If geo-temperature is not considered during a back analysis, the regression model of Equation (29) should be adopted. That is, compared with Equation (28), Equation (29) ignores the thermal stress of rock masses. Moreover, the in situ stresses of rock masses in the Sangzhuling tunnel were measured by the hydraulic fracturing method, that is, the vertical stress shown in Table 2 lacks the thermal stress of rock masses (see Equation (20)). Therefore, if geo-temperature is not considered during a back analysis, the initial geo-stress field obtained by a back analysis will lack the vertical thermal stress field of rock masses (see Figure 13b), which can cause serious errors.
6. Conclusions
- (1)
- Since the vertical stresses that are measured by the hydraulic fracturing method contain only gravitational information in a high geo-temperature environment, if stresses are measured by the hydraulic fracturing method, the regression coefficient of the gravitational stress field of rock masses should be set to one during a back analysis.
- (2)
- In a high geo-temperature environment, the vertical stresses that are measured by overcoring methods contain not only gravitational information, but also the information of stresses caused by geo-temperature, weathering, deposition, erosion, or tectonism. Therefore, is introduced to reflect the information of stresses caused by weathering, deposition, erosion, or tectonism during a back analysis. That is, if stresses are measured by overcoring methods, the regression coefficient of the gravitational stress field of rock masses will not be equal to one during a back analysis.
- (3)
- Based on the information of measured vertical stresses, a workflow for the back analysis of the initial geo-stress field of rock masses considering geo-temperature is proposed (see Figure 4), and this workflow can obtain the initial geo-stress field that is more compatible with the measured in situ stress of rock masses.
- (4)
- In the Sangzhuling tunnel, since in situ stresses were measured by the hydraulic fracturing method, only tectonic stress fields need to be inversely determined.
- (5)
- In this study, the thermal stress field of the same stratum was discussed. However, actual rock masses contain different strata. Therefore, the thermal stress field of different strata will need to be investigated in the future.
Author Contributions
W.M. wrote the paper. C.H. provided guidance for the whole work. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the High-Speed Railway and Natural Science United Foundation (Grant No. U1734205), National key research and development program of China (Grant No. 2016YFC0802201), and Doctoral Innovation Fund Program of Southwest Jiaotong University (Grant No. D-CX201802). This work utilizes data from literature which are cited in the main reference list.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Wang, M.N.; Hu, Y.P.; Wang, Q.L.; Tian, H.T.; Liu, D.G. A study on strength characteristics of concrete under variable temperature curing conditions in ultra-high geothermal tunnels. Constr. Build. Mater. 2019, 229, 116989. [Google Scholar] [CrossRef]
- Cui, S.G.; Liu, P.; Cui, E.Q.; Su, J.; Huang, B. Experimental study on mechanical property and pore structure of concrete for shotcrete use in a hot-dry environment of high geothermal tunnels. Constr. Build. Mater. 2018, 173, 124–135. [Google Scholar] [CrossRef]
- Hu, Y.P.; Wang, M.N.; Wang, Q.L.; Liu, D.G.; Tong, J.J. Field test of thermal environment and thermal adaptation of workers in high geothermal tunnel. Build. Environ. 2019, 160, 106174. [Google Scholar]
- Haimson, B.C.; Cornet, F.H. ISRM Suggested Methods for rock stress estimation—Part 3: Hydraulic fracturing (HF) and/or hydraulic testing of pre-existing fractures (HTPF). Int. J. Rock Mech. Min. Sci. 2003, 40, 1011–1020. [Google Scholar] [CrossRef]
- Sjöberg, J.; Christiansson, R.; Hudson, J.A. ISRM suggested methods for rock stress estimation—Part 2: Overcoring methods. Int. J. Rock Mech. Min. Sci. 2003, 40, 999–1010. [Google Scholar] [CrossRef]
- Yang, S.X.; Huang, L.Y.; Xie, F.R.; Cui, X.F.; Yao, R. Quantitative analysis of the shallow crustal tectonic stress field in China mainland based on in situ stress data. J. Asian Earth Sci. 2014, 85, 154–162. [Google Scholar] [CrossRef]
- Meng, W.; Chen, Q.C.; Zhao, Z.; Wu, M.L.; Qin, X.H.; Zhang, C.Y. Characteristics and implications of the stress state in the Longmen Shan fault zone, eastern margin of the Tibetan Plateau. Tectonophysics 2015, 656, 1–19. [Google Scholar] [CrossRef]
- Meng, W.; Chen, Q.C.; Wu, M.L.; Feng, C.J.; Qin, X.H. Tectonic stress state changes before and after the Wenchuan Ms 8.0 earthquake in the eastern margin of the Tibetan Plateau. Acta Geol. Sin. (Engl. Ed.) 2015, 89, 77–89. [Google Scholar]
- Meng, W.; Guo, C.B.; Zhang, Y.S.; Du, Y.B.; Zhang, M.; Bao, L.H.; Zhang, P. In Situ Stress Measurements in the Lhasa Terrane, Tibetan Plateau, China. Acta Geol. Sin. (Engl. Ed.) 2016, 90, 2022–2035. [Google Scholar]
- Ju, W.; Sun, W.F.; Ma, X.J. Tectonic stress pattern in the Chinese Mainland from the inversion of focal mechanism data. J. Earth Syst. Sci. 2017, 126, 41. [Google Scholar]
- Zhao, H.J.; Ma, F.S.; Xu, J.M.; Guo, J. In situ stress field inversion and its application in mining-induced rock mass movement. Int. J. Rock Mech. Min. Sci. 2012, 53, 120–128. [Google Scholar] [CrossRef]
- McKinnon, S.D. Analysis of stress measurements using a numerical model methodology. Int. J. Rock Mech. Min. Sci. 2001, 38, 699–709. [Google Scholar] [CrossRef]
- Wang, J.L.; Li, M.; Xu, S.C.; Qu, Z.H.; Jiang, B. Simulation of Ground Stress Field and Advanced Prediction of Gas Outburst Risks in the Non-Mining Area of Xinjing Mine, China. Energies 2018, 11, 1285. [Google Scholar] [CrossRef]
- Lee, H.; Ong, S.H. Estimation of In Situ Stresses with Hydro-Fracturing Tests and a Statistical Method. Rock Mech. Rock Eng. 2018, 51, 779–799. [Google Scholar] [CrossRef]
- Obara, Y.; Nakamura, N.; Kang, S.S.; Kaneko, K. Measurement of local stress and estimation of regional stress associated with stability assessment of an open-pit rock slope. Int. J. Rock Mech. Min. Sci. 2000, 37, 1211–1221. [Google Scholar] [CrossRef]
- Zhang, T.J.; Zhang, L.; Li, S.G.; Liu, J.L.; Pan, H.Y.; Song, S. Stress Inversion of Coal with a Gas Drilling Borehole and the Law of Crack Propagation. Energies 2017, 10, 1743. [Google Scholar] [CrossRef]
- Han, H.X.; Yin, S.D. Determination of In-Situ Stress and Geomechanical Properties from Borehole Deformation. Energies 2018, 11, 131. [Google Scholar] [CrossRef]
- McKinnon, S.D.; Garrido de la Barra, I. Stress field analysis at the El Teniente Mine: Evidence for N–S compression in the modern Andes. J. Struct. Geol. 2003, 25, 2125–2139. [Google Scholar] [CrossRef]
- Liu, C.L.; Li, G.; Kuriyama, K.; Mizuta, Y. Development of a computer program for inhomogeneous modeling using 3-D BEM with analytical integration and its application to rock slope stability evaluation. Int. J. Rock Mech. Min. Sci. 2005, 1, 137–144. [Google Scholar] [CrossRef]
- Li, G.; Mizuta, Y.; Ishida, T.; Li, H.; Nakama, S.; Sato, T. Stress field determination from local stress measurements by numerical modelling. Int. J. Rock Mech. Min. Sci. 2009, 46, 138–147. [Google Scholar] [CrossRef]
- Khademian, Z.; Shahriar, K.; Gharouni Nik, M. Developing an algorithm to estimate in situ stresses using a hybrid numerical method based on local stress measurement. Int. J. Rock Mech. Min. Sci. 2012, 55, 80–85. [Google Scholar] [CrossRef]
- Figueiredo, B.; Cornet, F.H.; Lamas, L.; Muralha, J. Determination of the stress field in a mountainous granite rock mass. Int. J. Rock Mech. Min. Sci. 2014, 72, 37–48. [Google Scholar] [CrossRef]
- Zhang, S.R.; Hu, A.K.; Wang, C. Three-dimensional inversion analysis of an in situ stress field based on a two-stage optimization algorithm. J. Zhejiang Univ.-Sci. A 2016, 17, 782–802. [Google Scholar] [CrossRef]
- Pei, Q.T.; Ding, X.L.; Liu, Y.K.; Lu, B.; Huang, S.L.; Fu, J. Optimized back analysis method for stress determination based on identification of local stress measurements and its application. Bull. Eng. Geol. Environ. 2019, 78, 375–396. [Google Scholar] [CrossRef]
- Zhang, C.Q.; Feng, X.T.; Zhou, H. Estimation of in situ stress along deep tunnels buried in complex geological conditions. Int. J. Rock Mech. Min. Sci. 2012, 52, 139–162. [Google Scholar] [CrossRef]
- Li, F.; Wang, J.A.; Brigham, J.C. Inverse calculation of insitu stress in rock mass using the Surrogate-Model Accelerated Random Search algorithm. Comput. Geotech. 2014, 61, 24–32. [Google Scholar] [CrossRef]
- Li, Y.S.; Yin, J.M.; Chen, J.P.; Xu, J. Analysis of 3D In-situ Stress Field and Query System’s Development Based on Visual BP Neural Network. Procedia Earth Planet. Sci. 2012, 5, 64–69. [Google Scholar]
- Shi, Y.L.; Marcelo, A. Genetic Algorithm-Finite Element Inversion of Stress Field of Brazil. Chin. J. Geophys. 2000, 43, 191–199. [Google Scholar] [CrossRef]
- Song, Z.F.; Sun, Y.J.; Lin, X. Research on In Situ Stress Measurement and Inversion, and its Influence on Roadway Layout in Coal Mine with Thick Coal Seam and Large Mining Height. Geotech. Geol. Eng. 2018, 36, 1907–1917. [Google Scholar]
- Wang, Q.W.; Ju, N.P.; Du, L.L.; Huang, J.; Hu, Y. Three dimensional inverse analysis of geostress field in the Sangri–Jiacha section of Lasa–Linzhi railway. Rock Soil Mech. 2018, 39, 1450–1462. [Google Scholar]
- Huang, S.L.; Ding, X.L.; Liao, C.G.; Wu, A.Q.; Yin, J.M. Initial 3D geostress field recognition of high geostress field at deep valley region and considerations on underground powerhouse layout. Chin. J. Rock Mech. Eng. 2014, 33, 2210–2224. [Google Scholar]
- Yu, X.F.; Zheng, Y.R.; Liu, H.H.; Fang, Z.C. Stability Analysis of Surrounding Rock Mass in Underground Engineering; Coal Industry Press: Beijing, China, 1983; pp. 51–52. [Google Scholar]
- Zheng, Y.R.; Zhu, H.H.; Fang, Z.C.; Liu, H.H. The Stability Analysis and Design Theory of Surrounding Rock of Underground Engineering; China Communications Press: Beijing, China, 2012; pp. 17–21. [Google Scholar]
- Zhang, Y.M.; Chang, J.; Liu, N.; Liu, J.W.; Ma, X.F.; Zhao, S.F.; Shen, F.Y.; Zhou, Y. Present-day temperature–pressure field and its implications for the geothermal resources development in the Baxian area, Jizhong Depression of the Bohai Bay Basin. Nat. Gas Ind. B 2018, 5, 226–234. [Google Scholar] [CrossRef]
- Wang, L.S.; Li, C.; Liu, S.W.; Li, H.; Xu, M.J.; Wang, Q.; Ge, R. Characteristics of Geo-Temperature Gradient Distribution in the Kuqa Foreland Basin on the North Edge of the Tarim Basin, Western China. Chin. J. Geophys. 2003, 46, 575–581. [Google Scholar] [CrossRef]
- Zhan, F.L.; Cai, M.F. Influence of Earth Temperature Gradient on Ground Stress Calculation in Underground Mines. Min. Res. Dev. 2006, 26, 24–25, 48. [Google Scholar]
- Leeman, E.R. The determination of the complete state of stress in rock in a single borehole—Laboratory and underground measurements. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1968, 5, 31–38. [Google Scholar] [CrossRef]
- Hochstein, M.P.; Regenauer-Lieb, K. Heat generation associated with collision of two plates: The Himalayan geothermal belt. J. Volcanol. Geotherm. Res. 1998, 83, 75–92. [Google Scholar] [CrossRef]
- Zhang, X.B.; Hu, Q.H. Development of Geothermal Resources in China: A Review. J. Earth Sci. 2018, 29, 452–467. [Google Scholar] [CrossRef]
- Yokoyama, T.; Nakai, S.I.; Wakita, H. Helium and carbon isotopic compositions of hot spring gases in the Tibetan Plateau. J. Volcanol. Geotherm. Res. 1999, 88, 99–107. [Google Scholar] [CrossRef]
- Yan, J.; He, C.; Wang, B.; Meng, W.; Wu, F.Y. Inoculation and characters of rockbursts in extra-long and deep-lying tunnels located on Yarlung Zangbo suture. Chin. J. Rock Mech. Eng. 2019, 38, 769–781. [Google Scholar]
- Yan, J.; He, C.; Wang, B.; Meng, W.; Yang, J.F. Prediction of Rock Bursts for Sangzhuling Tunnel Located on Lhasa-Nyingchi Railway Under Coupled Thermo-Mechanical Effects. J. Southwest Jiaotong Univ. 2018, 53, 434–441. [Google Scholar]
- Zhao, B. GPS Velocity Field of CMONOC with Respect to Eurasia. 2015. Available online: ftp://ftp.cgps.ac.cn/products/velocity/image/cmnc_vel_eura_grd_flt.png (accessed on 5 September 2019).
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).