CFD Analysis of Falling Film Hydrodynamics for a Lithium Bromide (LiBr) Solution over a Horizontal Tube
Abstract
1. Introduction
2. Problem Statement
3. CFD Model
3.1. Conservation Equations
3.2. Volume of Fluid Model (VOF) Model
3.3. Continuum Surface Force (CSF) Model
3.4. Operating and Boundary Conditions
3.5. Methodology
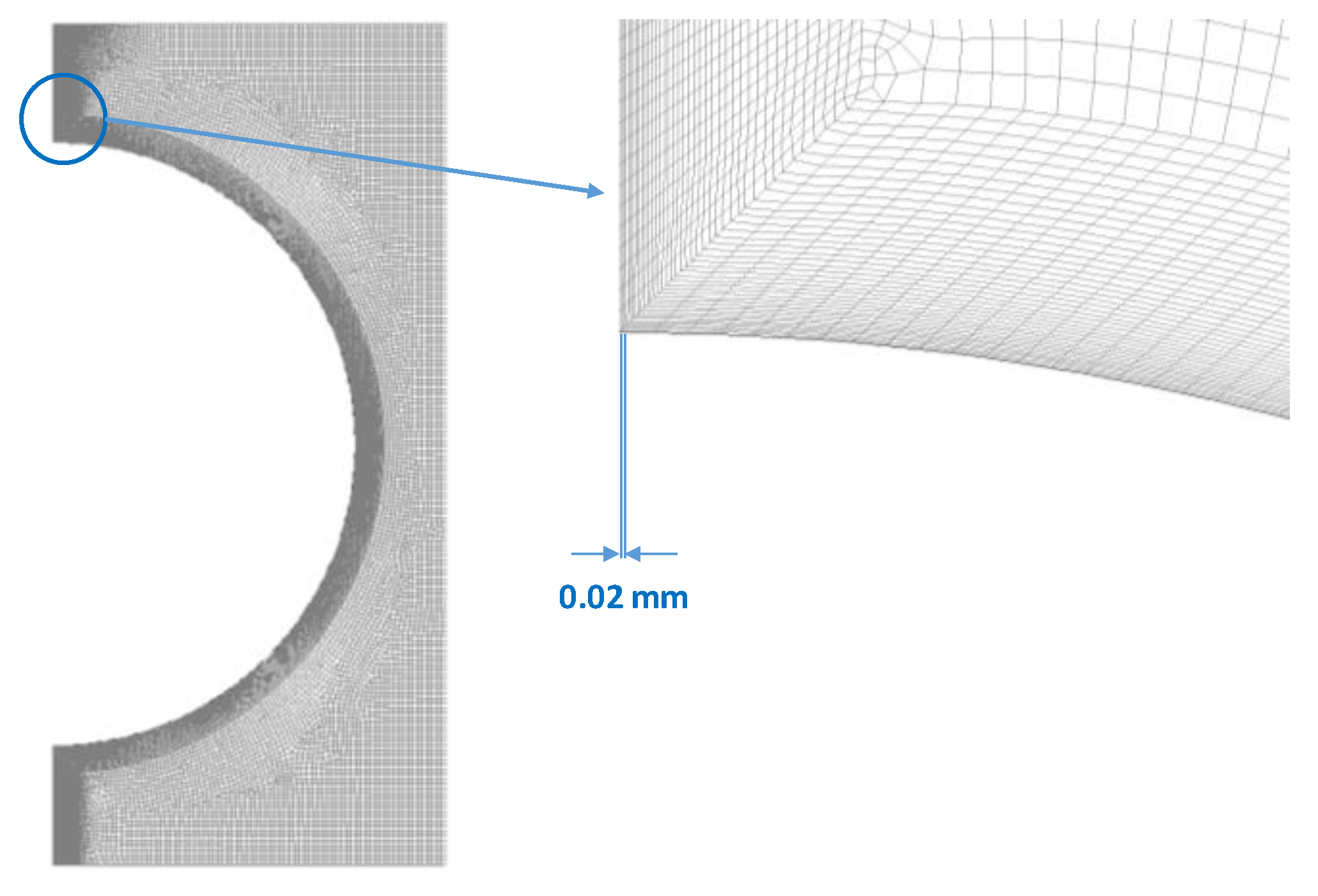
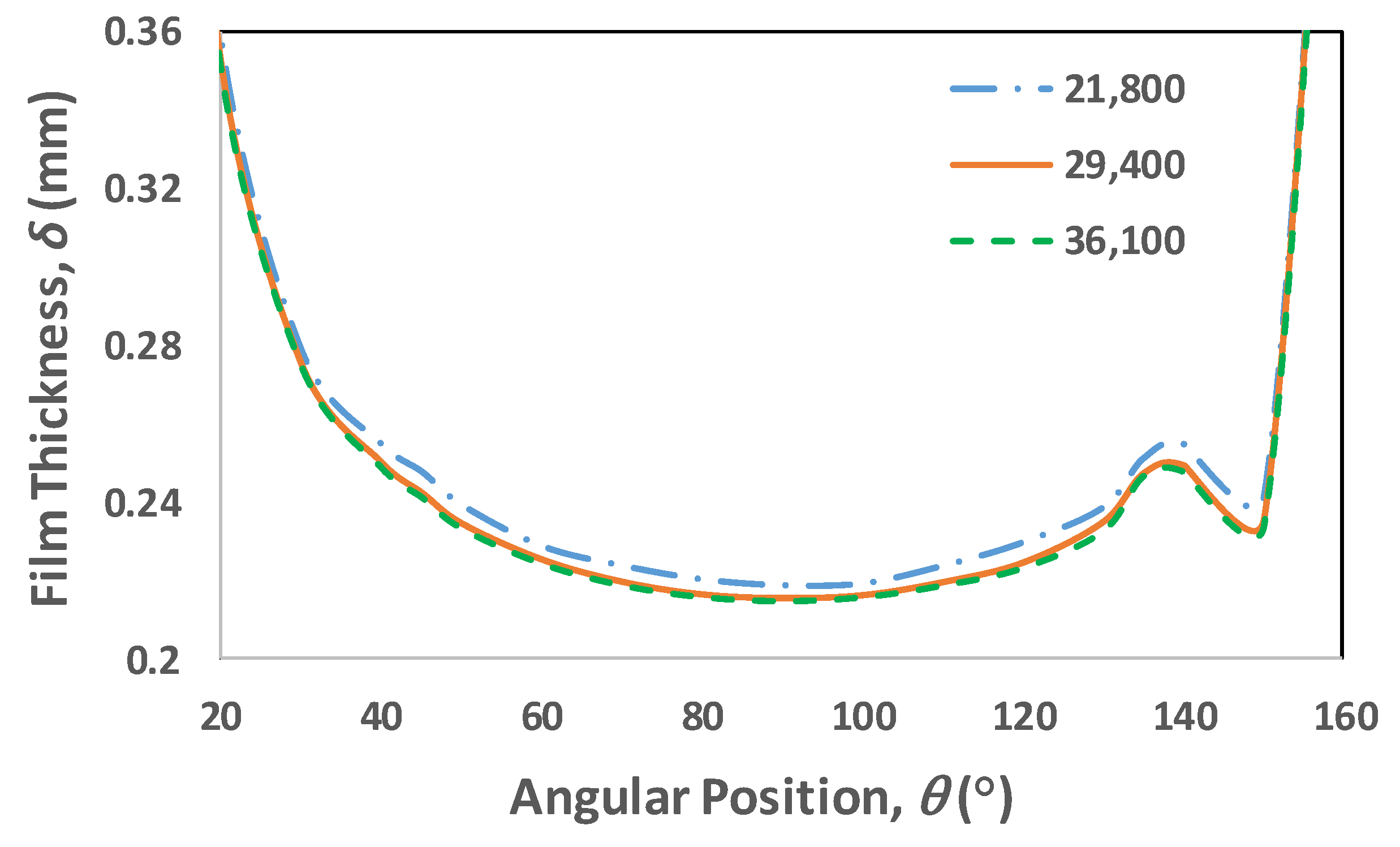
3.6. Mesh Dependency Test
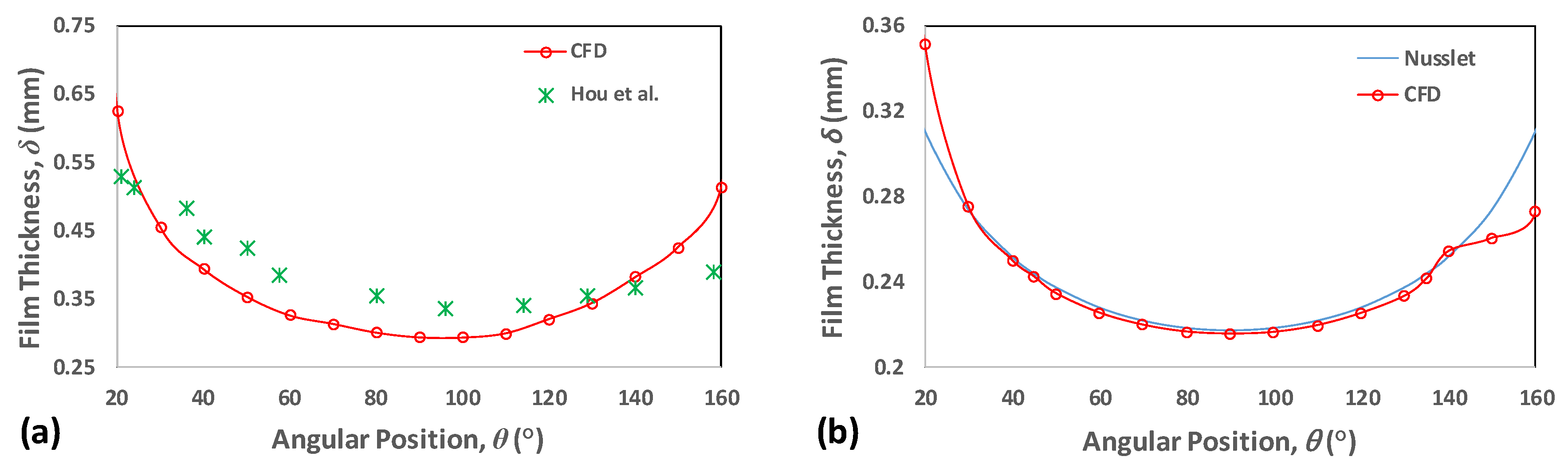
3.7. Validation
4. Results and Discussion
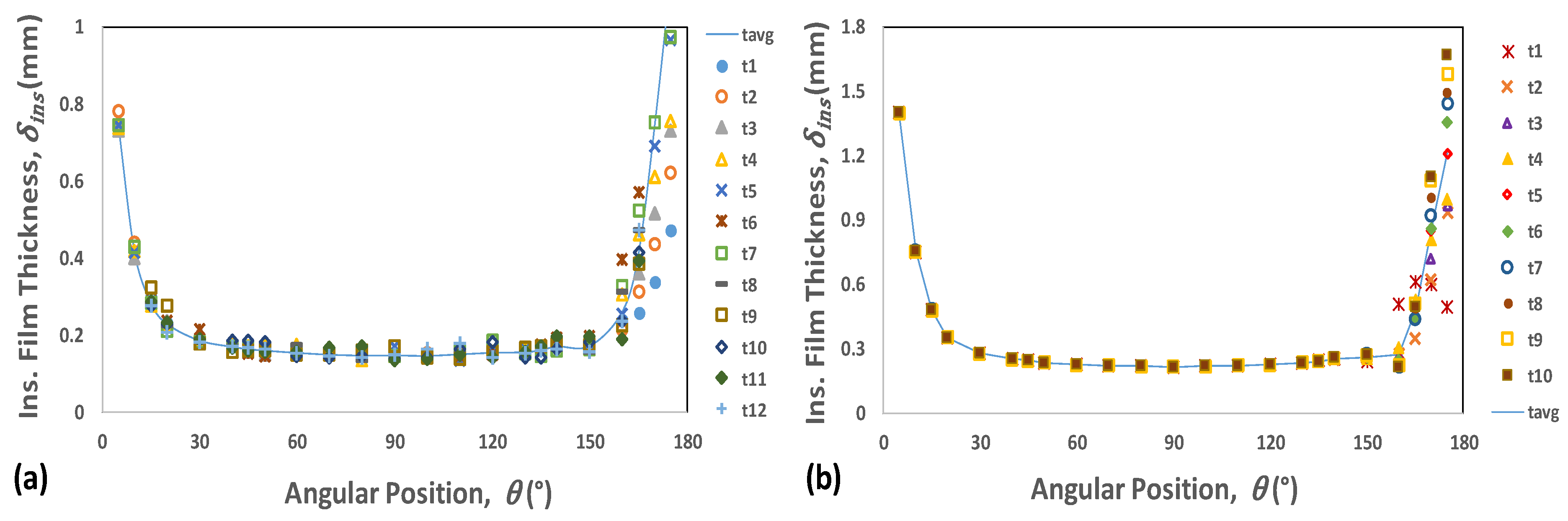
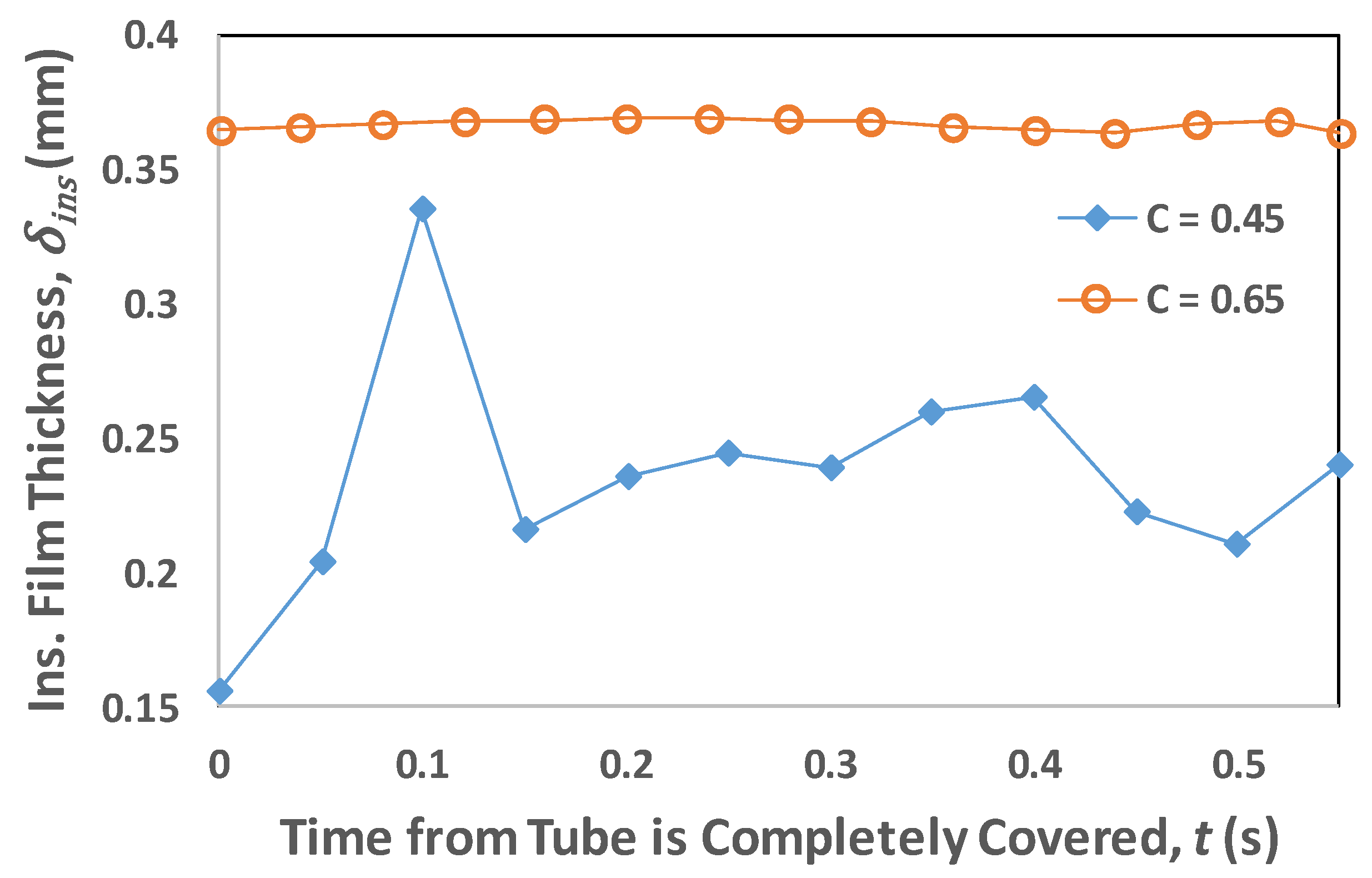
4.1. Transient Analysis
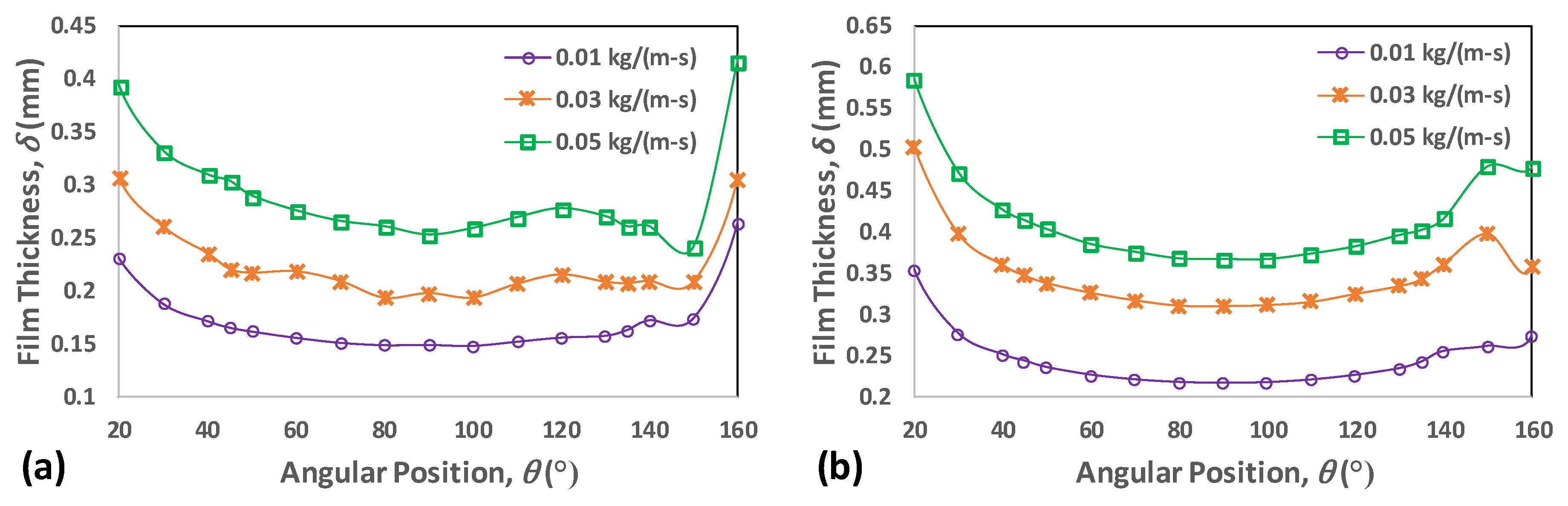
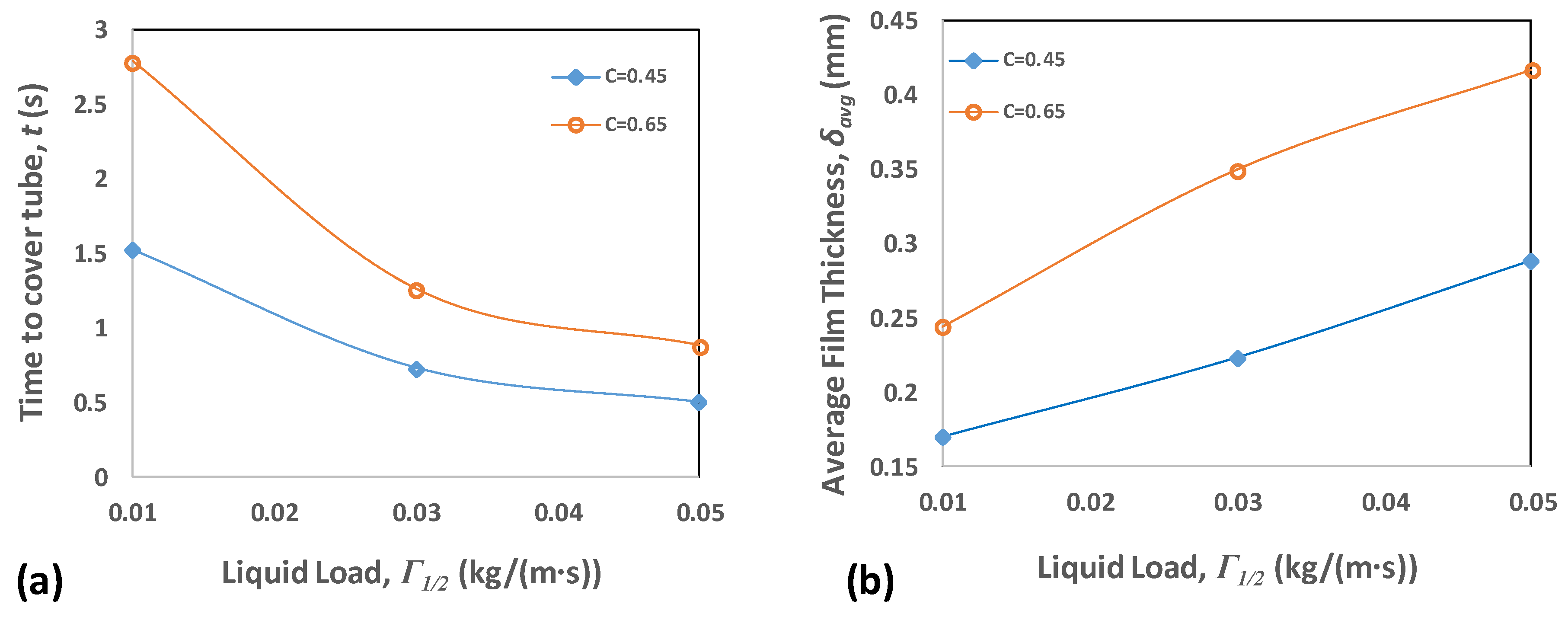
4.2. Film Thickness and Residence Time
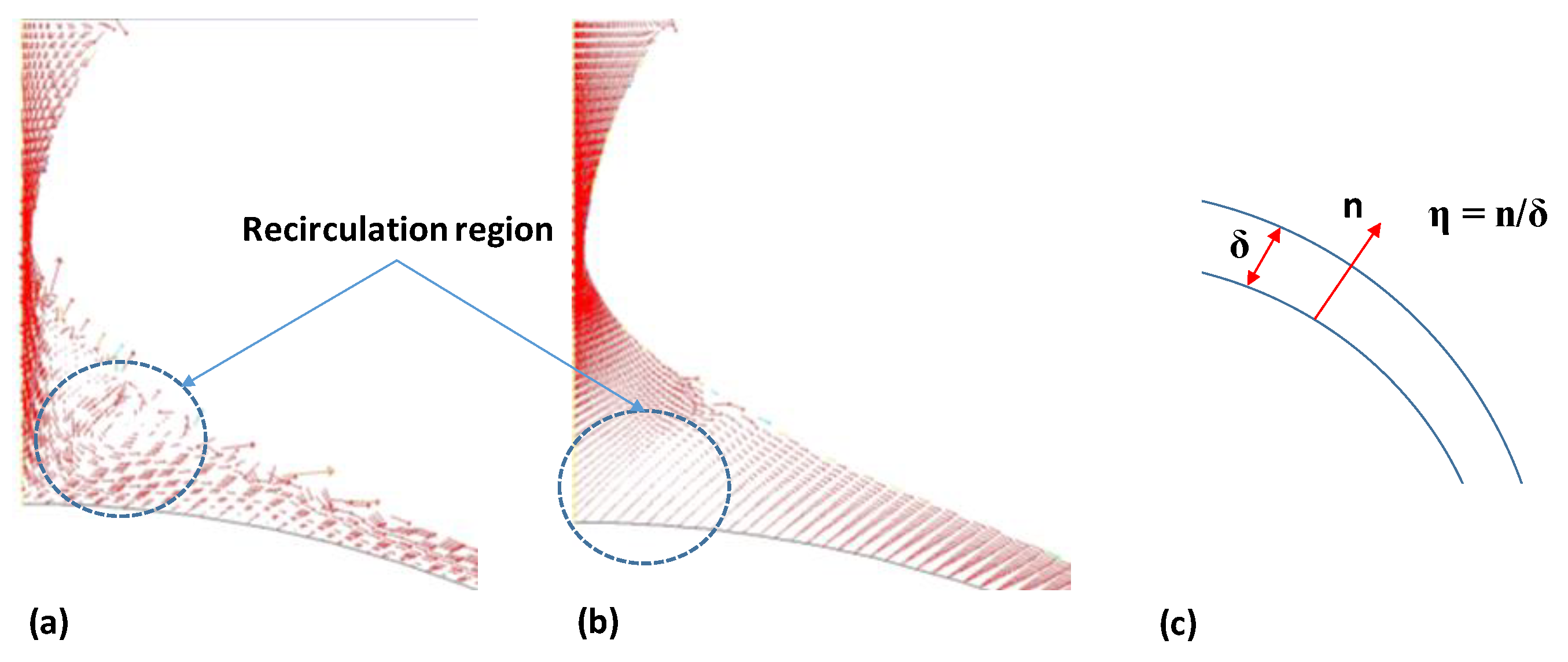
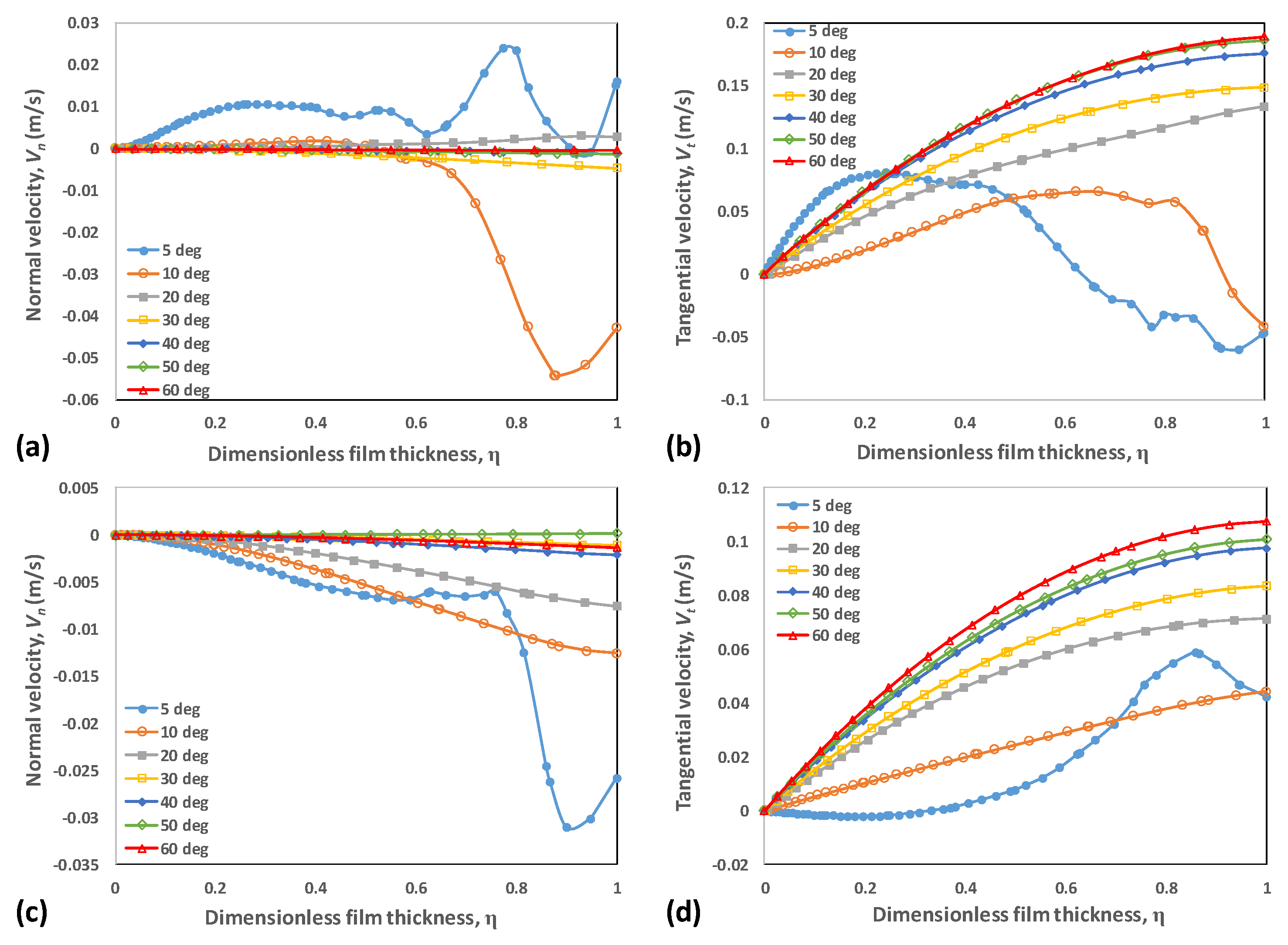
4.3. Velocity Distribution
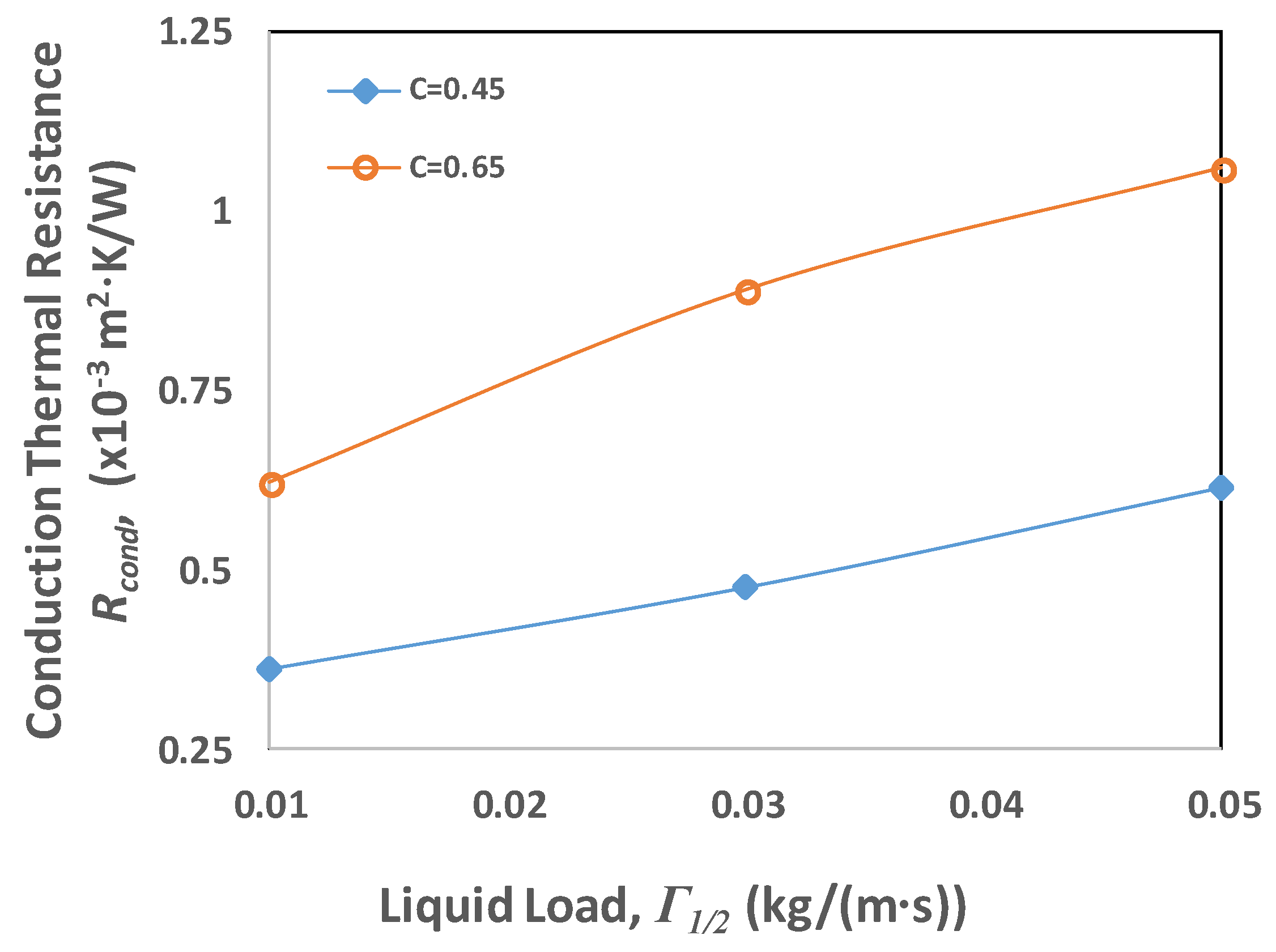
4.4. Thermal Resistance
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| C | LiBr mass concentration (%) |
| CFD | computational fluid dynamics |
| CSF | continuum surface force |
| D | tube diameter (m) |
| F | force (N) |
| g | acceleration due to gravity (m/s2) |
| Ga | modified Galileo number |
| hi | impingement height (m) |
| k | thermal conductivity (W·m/K) |
| K | curvature |
| LiBr | lithium bromide |
| PRESTO | pressure staggering option |
| R | thermal resistance (m2·K/W) |
| Ref | film Reynolds number |
| s | intertube spacing (m) |
| SIMPLE | semi-implicit method for pressure linked equations |
| t | time (s) |
| V | velocity (m/s) |
| VOF | volume of fluid |
| Greek letters | |
| α | void fraction |
| σ | surface tension (N/m) |
| μ | viscosity (Pa·s) |
| Γ1/2 | liquid load, on one side of tube (kg/(m·s)) |
| ρ | density (kg/m3) |
| δ | film thickness (m) |
| θ | angular position (°) |
| θw | wall adhesion contact angle (°) |
| η | dimensionless film thickness |
| Subscripts | |
| avg | time averaged from θ = 20–160° |
| cond | conduction |
| evap | evaporation |
| g | gaseous phase |
| int | internal |
| ins | instantaneous |
| l | liquid phase |
| n | normal |
| t | tangential |
| tot | total |
| w | wall |
| vol | volumetric |
References
- Danilova, G.N.; Burkin, V.G.; Dyundin, V.A. Heat transfer in spray-type refrigerator evaporators. Heat Transf. Res. 1976, 8, 105–113. [Google Scholar]
- Lorenz, J.J.; Yung, D. Film Breakdown and Bundle-Depth Effects in Horizontal-Tube, Falling-Film Evaporators. J. Heat Transf. 1982, 104, 569–571. [Google Scholar] [CrossRef]
- Gonzalez, G.J.M.; Jabardo, J.M.S.; Stoecker, W.F. Falling Film Ammonia Evaporators; University of Illinois: Champaign, IL, USA, 1992. [Google Scholar]
- Zeng, X.; Chyu, M.-C.; Ayub, D.Z.H. Evaporation heat transfer performance of nozzle-sprayed ammonia on a horizontal tube. ASHRAE Trans. 1995, 101, 136–149. [Google Scholar]
- Hoffmann, L.; Greiter, I.; Wagner, A.; Weiss, V.; Alefeld, G. Experimental investigation of heat transfer in a horizontal tube falling film absorber with aqueous solutions of LiBr with and without surfactants. Int. J. Refrig. 1996, 19, 331–341. [Google Scholar] [CrossRef]
- Kwon, K.; Jeong, S. Effect of vapor flow on the falling-film heat and mass transfer of the ammonia/water absorber. Int. J. Refrig. 2004, 27, 955–964. [Google Scholar] [CrossRef]
- Ribatski, G.; Jacobi, A.M. Falling-film evaporation on horizontal tubes—A critical review. Int. J. Refrig. 2005, 28, 635–653. [Google Scholar] [CrossRef]
- Fernández-Seara, J.; Pardiñas, Á.Á. Refrigerant falling film evaporation review: Description, fluid dynamics and heat transfer. Appl. Therm. Eng. 2014, 64, 155–171. [Google Scholar] [CrossRef]
- Tahir, F.; Mabrouk, A.; Koc, M. Review on CFD analysis of horizontal falling film evaporators in multi effect desalination plants. Desalin. Water Treat. 2019, 166, 296–320. [Google Scholar] [CrossRef]
- Tahir, F.; Mabrouk, A.; Koc, M. CFD Analysis of Falling Film Wettability in MED Desalination plants. In Proceedings of the Qatar Foundation Annual Research Conference Proceedings, Ar-Rayyan, Qatar, 19–20 March 2018; Volume 2018, p. EEPD650. [Google Scholar]
- Tahir, F.; Mabrouk, A.A.; Koc, M. CFD analysis of spray nozzle arrangements for multi effect desalination evaporator. In Proceedings of the 3rd Thermal Fluids Engineering Conference, Ft. Lauderdale, FL, USA, 4–7 March 2018; pp. 935–941. [Google Scholar]
- Mabrouk, A.A.; Bourouni, K.; Abdulrahim, H.K.; Darwish, M.; Sharif, A.O. Impacts of tube bundle arrangement and feed flow pattern on the scale formation in large capacity MED desalination plants. Desalination 2015, 357, 275–285. [Google Scholar] [CrossRef]
- Mitrovic, J. Flow structures of a liquid film falling on horizontal tubes. Chem. Eng. Technol. 2005, 28, 684–694. [Google Scholar] [CrossRef]
- Hu, X.; Jacobi, A.M. The Intertube Falling Film: Part 1—Flow Characteristics, Mode Transitions, and Hysteresis. J. Heat Transf. 1996, 118, 616–625. [Google Scholar] [CrossRef]
- Hu, X.; Jacobi, A.M. Flow characteristics of liquid droplets and jets falling between horizontal circular tubes. In Experimental Heat Transfer, FLuid Mechanics and Thermodynamics; PISA, Edizioni ETS: Paris, France, 1997; pp. 1295–1302. [Google Scholar]
- Roques, J.F.; Dupont, V.; Thome, J.R. Falling Film Transitions on Plain and Enhanced Tubes. J. Heat Transf. 2002, 124, 491–499. [Google Scholar] [CrossRef]
- Roques, J.-F.; Thome, J.R. Falling Film Transitions Between Droplet, Column, and Sheet Flow Modes on a Vertical Array of Horizontal 19 FPI and 40 FPI Low-Finned Tubes. Heat Transf. Eng. 2003, 24, 40–45. [Google Scholar] [CrossRef]
- Nusselt, W. Die oberflachenkondensation des wasserdamphes. VDI-Zs 1916, 60, 541–546. [Google Scholar]
- Ji, G.; Wu, J.; Chen, Y.; Ji, G. Asymmetric distribution of falling film solution flowing on hydrophilic horizontal round tube. Int. J. Refrig. 2017, 78, 83–92. [Google Scholar] [CrossRef]
- Hosseinnia, S.M.; Naghashzadegan, M.; Kouhikamali, R. CFD simulation of water vapor absorption in laminar falling film solution of water-LiBr—Drop and jet modes. Appl. Therm. Eng. 2017, 115, 860–873. [Google Scholar] [CrossRef]
- Ding, H.; Xie, P.; Ingham, D.; Ma, L.; Pourkashanian, M. Flow behaviour of drop and jet modes of a laminar falling film on horizontal tubes. Int. J. Heat Mass Transf. 2018, 124, 929–942. [Google Scholar] [CrossRef]
- Rogers, J.T.; Goindi, S.S. Experimental laminar falling film heat transfer coefficients on a large diameter horizontal tube. Can. J. Chem. Eng. 1989, 67, 560–568. [Google Scholar] [CrossRef]
- Gstoehl, D.; Roques, J.F.; Crisnel, P.; Thome, J.R. Measurement of Falling Film Thickness Around a Horizontal Tube Using a Laser Measurement Technique. Heat Transf. Eng. 2004, 25, 28–34. [Google Scholar] [CrossRef]
- Hou, H.; Bi, Q.; Ma, H.; Wu, G. Distribution characteristics of falling film thickness around a horizontal tube. Desalination 2012, 285, 393–398. [Google Scholar] [CrossRef]
- Chen, X.; Shen, S.; Wang, Y.; Chen, J.; Zhang, J. Measurement on falling film thickness distribution around horizontal tube with laser-induced fluorescence technology. Int. J. Heat Mass Transf. 2015, 89, 707–713. [Google Scholar] [CrossRef]
- Lin, S.; Liu, X.; Li, X. The spatial distribution of liquid film thickness outside the horizontal falling film tube. Int. J. Heat Mass Transf. 2019, 143, 118577. [Google Scholar] [CrossRef]
- Wang, J.; Chen, X.; Lu, T.; Chen, X.; Shen, S.; Liu, B. Three-dimensional film thickness distribution of horizontal tube falling film with column flow. Appl. Therm. Eng. 2019, 154, 140–149. [Google Scholar] [CrossRef]
- Tahir, F.; Baloch, A.A.B.; Ali, H. Resilience of Desalination Plants for Sustainable Water Supply in Middle East. In Sustainability Perspectives: Science, Policy and Practice, Strategies for Sustainability; Khaiter, P.A., Erechtchoukova, M.G., Eds.; Springer Nature Switzerland AG: Basel, Switzerland, 2020; pp. 303–329. ISBN 978-3-030-19550-2. [Google Scholar]
- Tahir, F.; Mabrouk, A.; Koc, M. Energy and exergy analysis of thermal vapor compression (TVC) and absorption vapor compression (AVC) for multi effect desalination (MED) plants. In Proceedings of the 8th Global Conference on Global Warming (GCGW), Doha, Qatar, 22–25 April 2019; p. 25. [Google Scholar]
- Mabrouk, A.; Abotaleb, A.; Abdelrehim, H.; Tahir, F.; Koc, M.; Abdelrashid, A.; Nasralla, A. High Performance MED Desalination Plants, Part II: Novel Integration MED-Absorption Vapor Compression. In Proceedings of the IDA 2017 World Congress on Water Reuse and Desalination, Sao Paulo, Brazil, 15–20 October 2017. [Google Scholar]
- Narváez-Romo, B.; Chhay, M.; Zavaleta-Aguilar, E.W.; Simões-Moreira, J.R. A critical review of heat and mass transfer correlations for LiBr-H2O and NH3-H2O absorption refrigeration machines using falling liquid film technology. Appl. Therm. Eng. 2017, 123, 1079–1095. [Google Scholar] [CrossRef]
- Pátek, J.; Klomfar, J. A computationally effective formulation of the thermodynamic properties of LiBr–H2O solutions from 273 to 500K over full composition range. Int. J. Refrig. 2006, 29, 566–578. [Google Scholar]
- Kaushik, S.C.; Arora, A. Energy and exergy analysis of single effect and series flow double effect water–lithium bromide absorption refrigeration systems. Int. J. Refrig. 2009, 32, 1247–1258. [Google Scholar] [CrossRef]
- Khan, S.A.; Tahir, F.; Baloch, A.A.B.; Koc, M. Review of Micro–Nanoscale Surface Coatings Application for Sustaining Dropwise Condensation. Coatings 2019, 9, 117. [Google Scholar] [CrossRef]
- Hirt, C.; Nichols, B. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Baloch, A.; Ali, H.; Tahir, F. Transient Analysis of Air Bubble Rise in Stagnant Water Column Using CFD. In Proceedings of the ICTEA: International Conference on Thermal Engineering, Doha, Qatar, 25–28 February 2018; Volume 2018. [Google Scholar]
- Nigim, T.H.; Eaton, J.A. CFD prediction of the flashing processes in a MSF desalination chamber. Desalination 2017, 420, 258–272. [Google Scholar] [CrossRef]
- Ozmen-Cagatay, H.; Kocaman, S. Dam-Break Flow in the Presence of Obstacle: Experiment and CFD Simulation. Eng. Appl. Comput. Fluid Mech. 2011, 5, 541–552. [Google Scholar] [CrossRef]
- Lopes, R.J.G.; Quinta-Ferreira, R.M. Assessment of CFD−VOF Method for Trickle-Bed Reactor Modeling in the Catalytic Wet Oxidation of Phenolic Wastewaters. Ind. Eng. Chem. Res. 2010, 49, 2638–2648. [Google Scholar] [CrossRef]
- Gupta, R.; Fletcher, D.F.; Haynes, B.S. On the CFD modelling of Taylor flow in microchannels. Chem. Eng. Sci. 2009, 64, 2941–2950. [Google Scholar] [CrossRef]
- Brackbill, J.; Kothe, D.; Zemach, C. A continuum method for modeling surface tension. J. Comput. Phys. 1992, 100, 335–354. [Google Scholar] [CrossRef]
- Yang, L.; Liu, Y.; Yang, Y.; Shen, S. Microscopic mechanisms of heat transfer in horizontal-tube falling film evaporation. Desalination 2016, 394, 64–71. [Google Scholar] [CrossRef]


| Fluid | Density (kg/m3) | Viscosity (Pa-s) | Surface Tension (N/m) | |
|---|---|---|---|---|
| LiBr solution | C = 0.45 | 1453 | 0.002274 | 0.08 |
| C = 0.65 | 1814 | 0.01102 | 0.085 | |
| Water Vapors | 0.0304 | 0.0000101 | ||
| C | Γ1/2 (kg/(m·s)) | Ref | Ga | Transitional Ref [16] | Mode | |
|---|---|---|---|---|---|---|
| Droplet to Droplet-Jet | Droplet-Jet to Jet | |||||
| 0.45 | 0.01 | 17.6 | 2.84 × 109 | 52.3 | 73 | Droplet |
| 0.03 | 52.8 | Droplet-Jet | ||||
| 0.05 | 87.9 | Jet | ||||
| 0.65 | 0.01 | 3.6 | 7.7 × 106 | 7.5 | 11 | Droplet |
| 0.03 | 10.9 | Droplet-Jet | ||||
| 0.05 | 18.2 | Jet | ||||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tahir, F.; Mabrouk, A.; Koç, M. CFD Analysis of Falling Film Hydrodynamics for a Lithium Bromide (LiBr) Solution over a Horizontal Tube. Energies 2020, 13, 307. https://doi.org/10.3390/en13020307
Tahir F, Mabrouk A, Koç M. CFD Analysis of Falling Film Hydrodynamics for a Lithium Bromide (LiBr) Solution over a Horizontal Tube. Energies. 2020; 13(2):307. https://doi.org/10.3390/en13020307
Chicago/Turabian StyleTahir, Furqan, Abdelnasser Mabrouk, and Muammer Koç. 2020. "CFD Analysis of Falling Film Hydrodynamics for a Lithium Bromide (LiBr) Solution over a Horizontal Tube" Energies 13, no. 2: 307. https://doi.org/10.3390/en13020307
APA StyleTahir, F., Mabrouk, A., & Koç, M. (2020). CFD Analysis of Falling Film Hydrodynamics for a Lithium Bromide (LiBr) Solution over a Horizontal Tube. Energies, 13(2), 307. https://doi.org/10.3390/en13020307





