Sensitivity Study of Greitzer Model Based on Physical System Parameters of Radial Compressing Units
Abstract
1. Introduction
1.1. Unstable Phenomena in Radial Compressing Units
1.2. Greitzer Model of the Surge Phenomenon
- The flow within pipes is incompressible, inviscid, and one dimensional
- Compression in the plenum is isentropic
- The temperature is constant in the entire system
- The pressure in the container is uniform
- Valve is quasi-static
- Gravity forces are neglected
- Non-dimensional mass flow rate coefficient:
- Non-dimensional pressure rise coefficient:
- Non-dimensional time coefficient:
- Model parameters:
- Compressor steady state pressure rise coefficient .
1.3. The Aim of the Study
2. Methods
2.1. Investigated System
2.2. Sensitivity Study Procedure
2.2.1. Two-Equation Model
2.2.2. Three-Equation Model—Compressor Response Delay
2.2.3. Three-Equation Model—Valve Modelling
2.3. Comparison with Experiment
3. Results
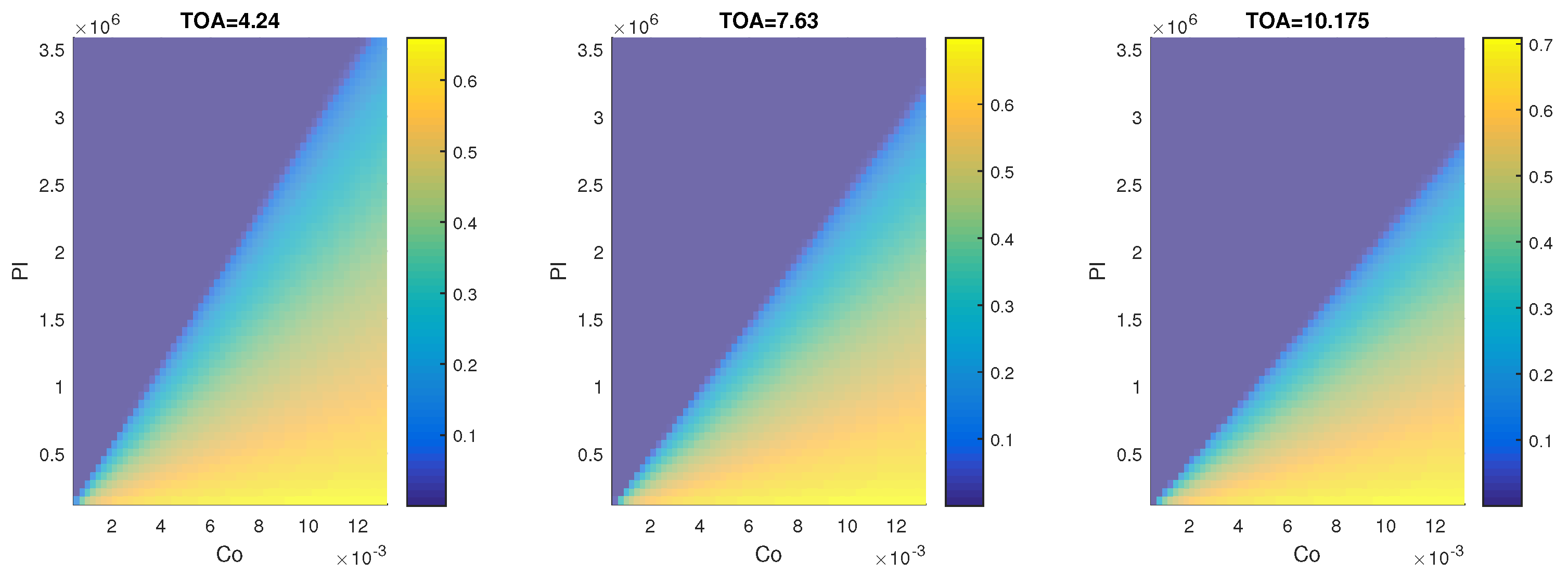
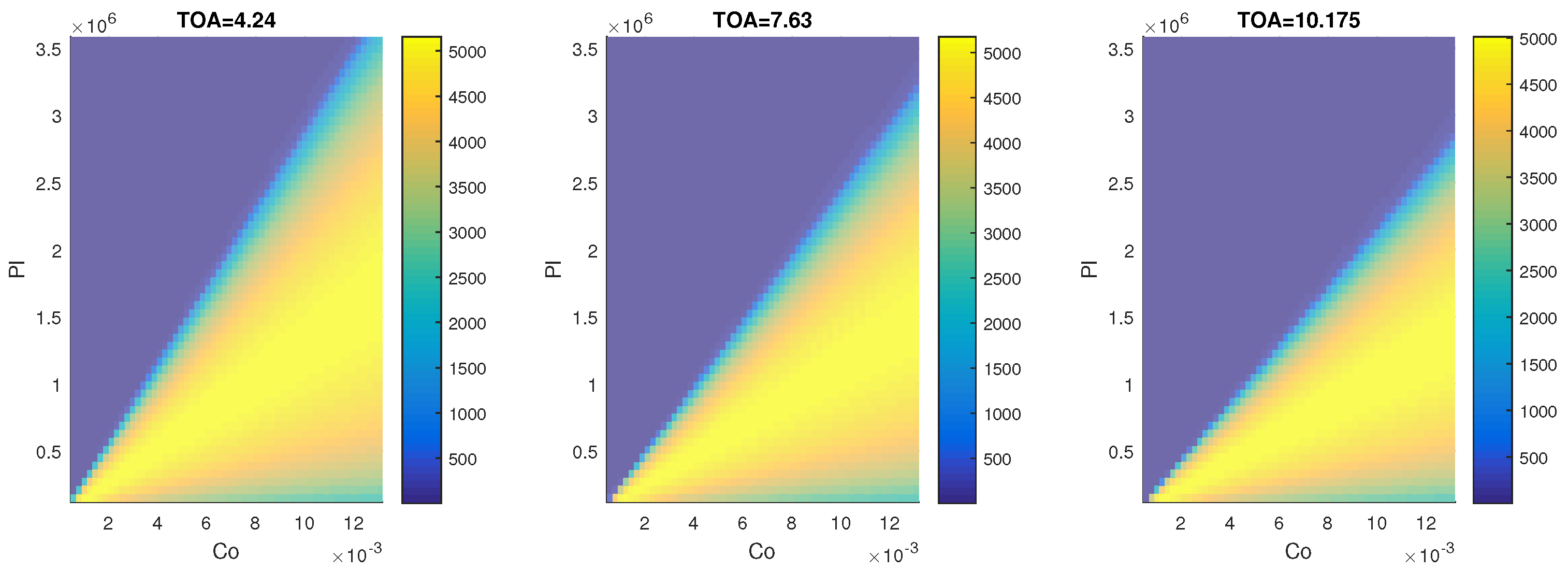
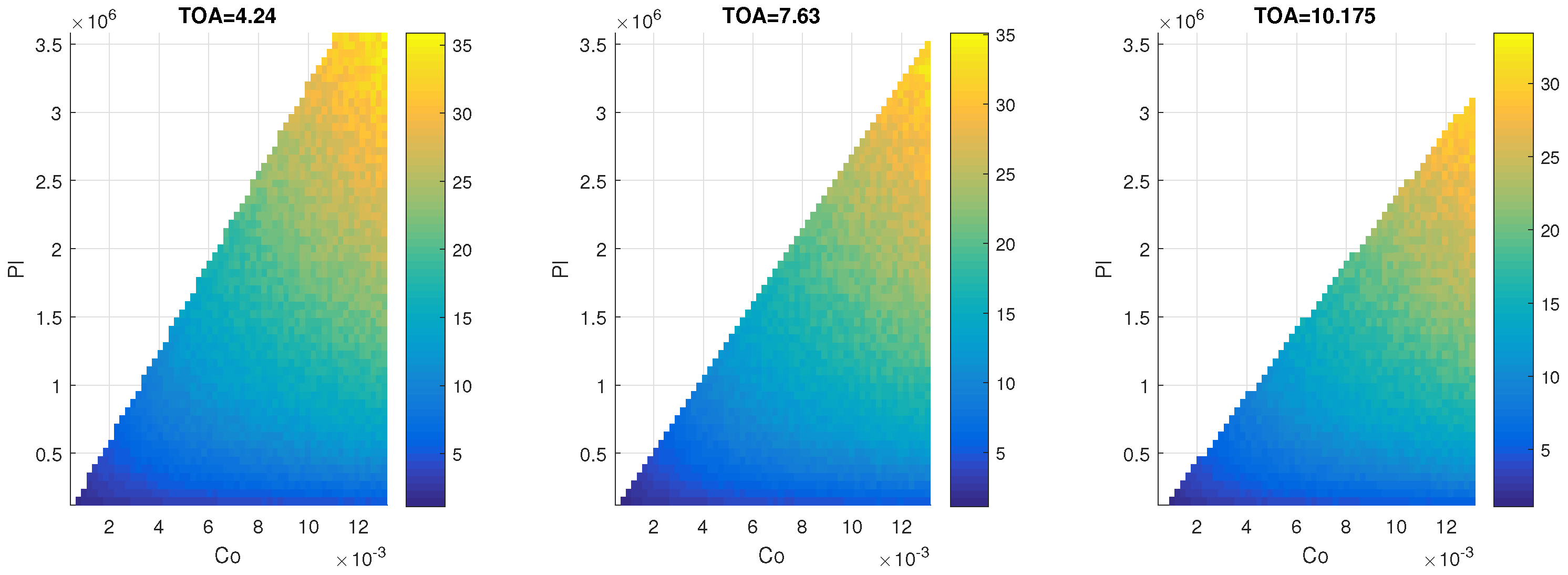
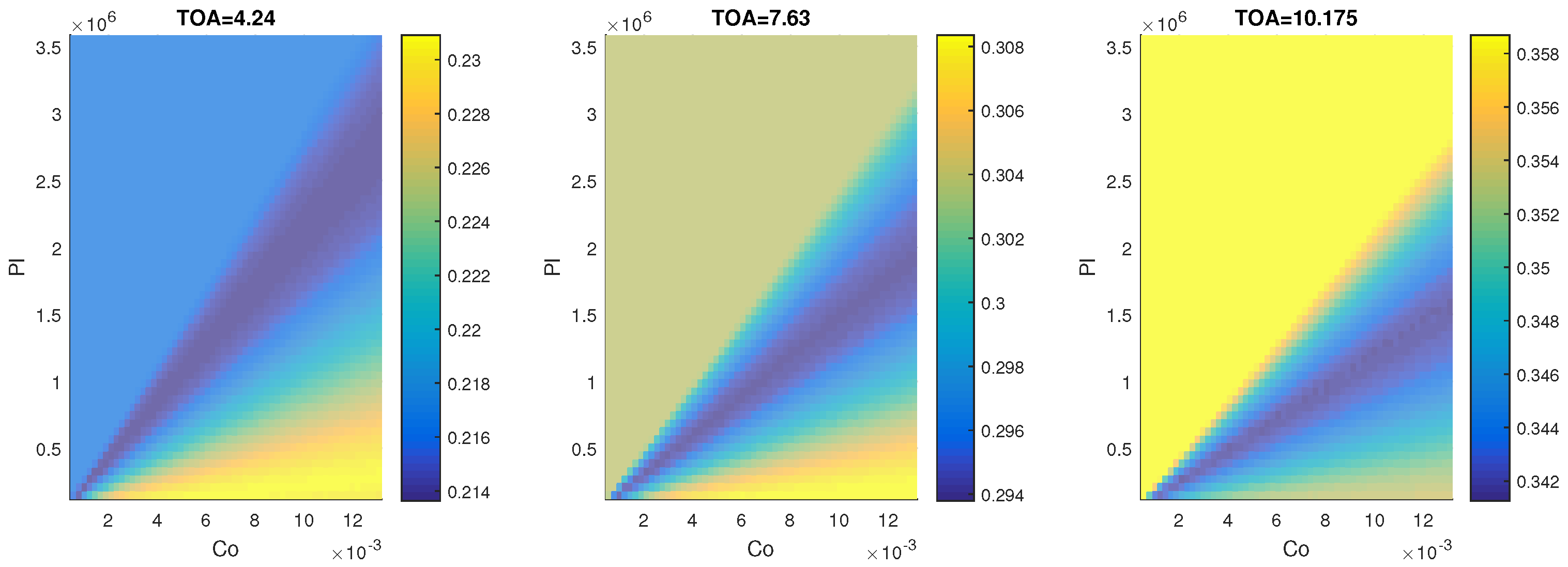
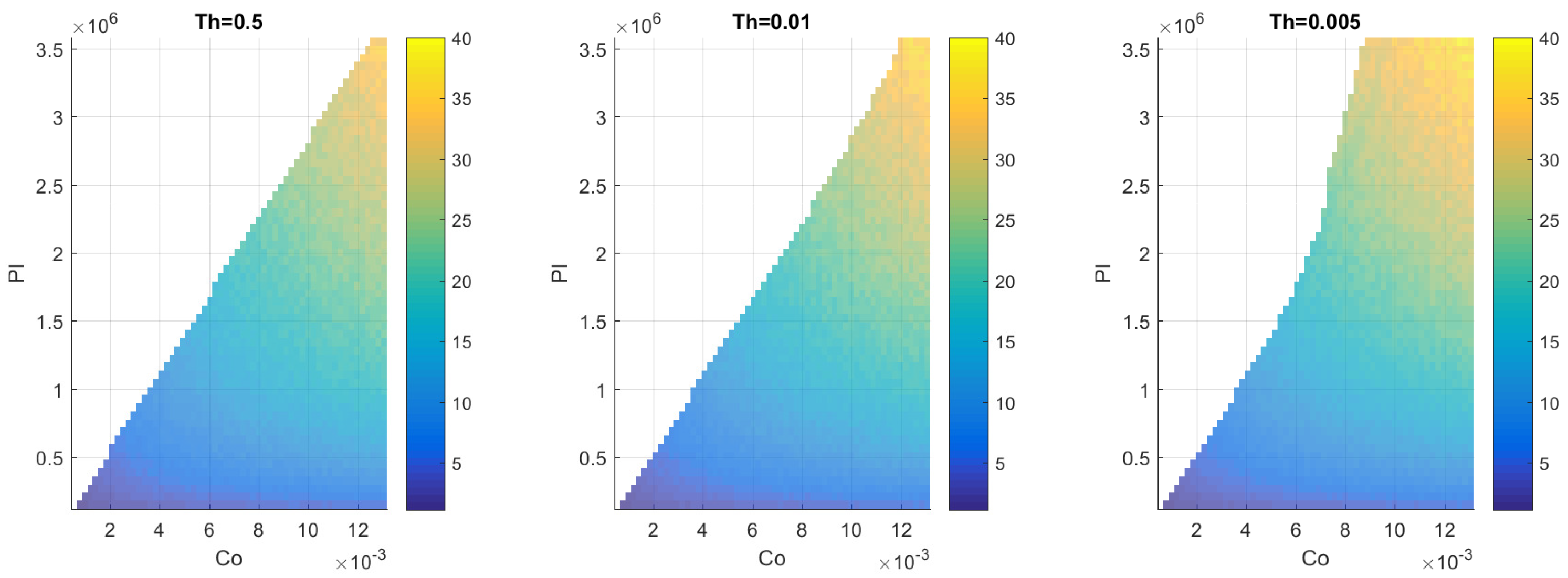
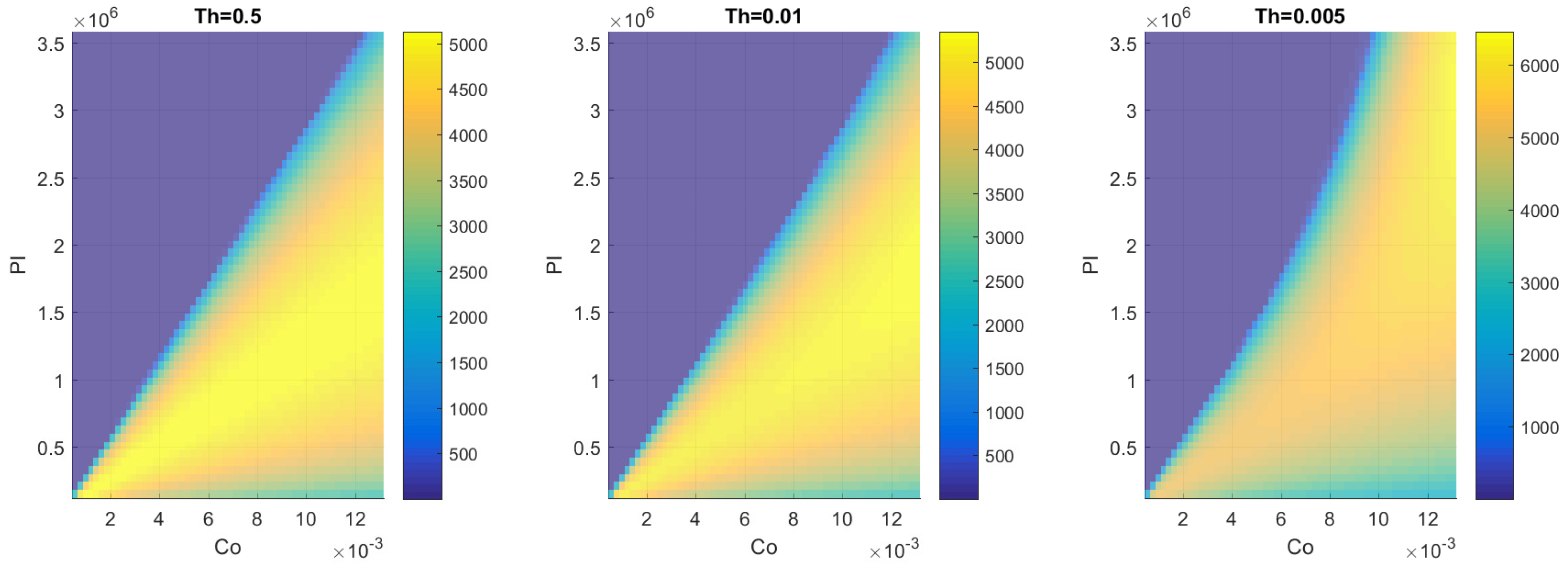
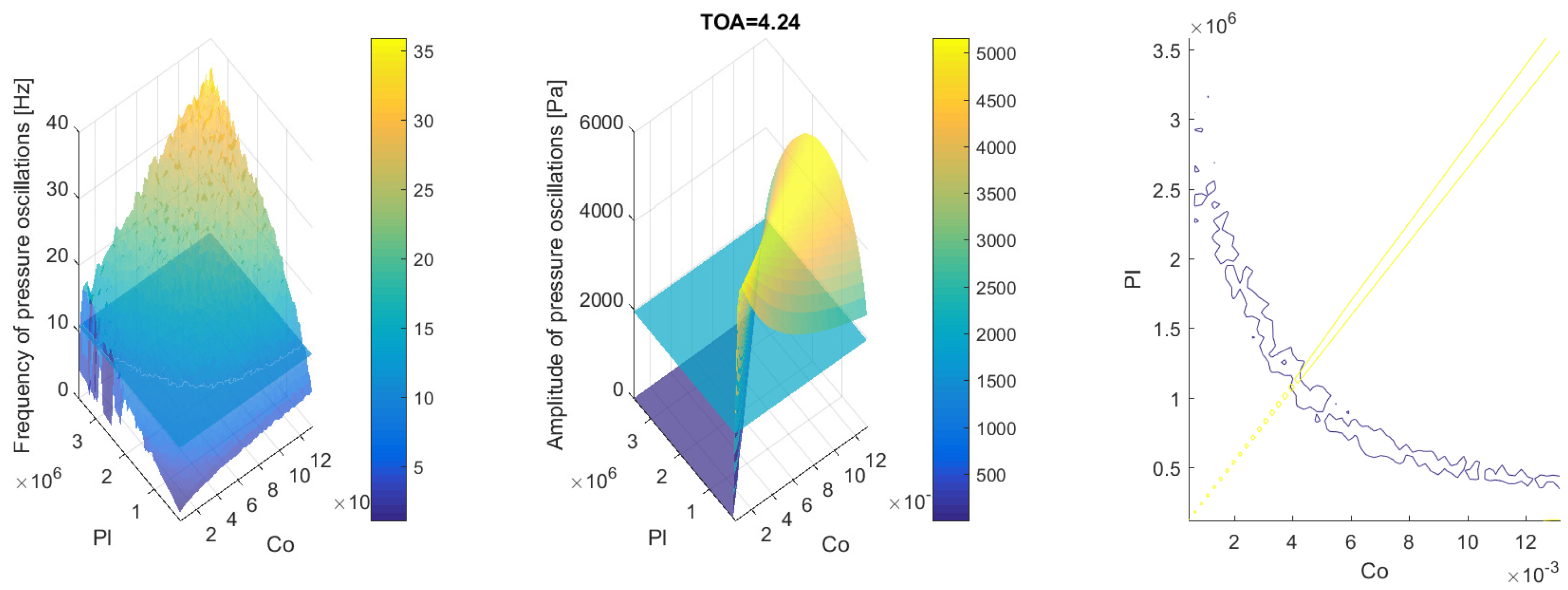
3.1. Two-Equation Model
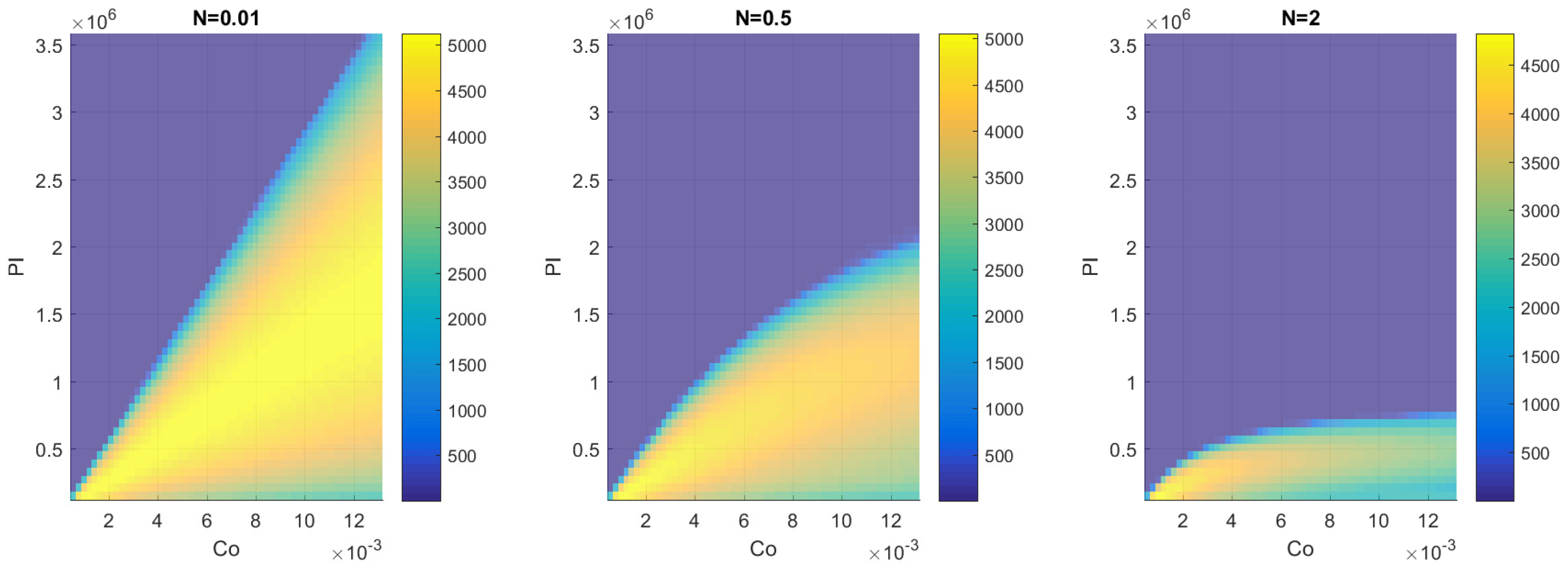
3.2. Three-Equation Model—Compressor Response Delay
3.3. Three-Equation Model—Valve Modelling
3.4. Comparison with Experiment
4. Discussion
4.1. Two-Equation Model
4.2. Three-Equation Model—Compressor Response Delay
4.3. Three-Equation Model—Valve Modelling
4.4. Comparison with Experiment
5. Summary
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bloch, H.P. A Practical Guide to Compressor Technology; John Wiley & Sons: Hoboken, NJ, USA, 2006; p. 560. [Google Scholar]
- Emmons, H.W.; Pearson, C.E.; Grant, H.P. Compressor surge and stall propagation. Trans. ASME 1955, 138, 455–467. [Google Scholar]
- Day, I. Stall, surge, and 75 years of research. J. Turbomach. 2016, 138, 011001. [Google Scholar] [CrossRef]
- Moore, F.K.; Greitzer, E.M. A theory of post-stall transients in axial compression systems: Part II Application. J. Eng. Gas Turbines Power 1986, 108, 231–239. [Google Scholar] [CrossRef]
- Abed, E.H.; Houpt, P.K.; Hosny, W.M. Bifurcation analysis of surge and rotating stall in axial flow compressions. In Proceedings of the American Control Conference, San Diego, CA, USA, 23–25 May 1990; pp. 2239–2246. [Google Scholar]
- Liaw, D.; Chang, S. Bifurcation analysis of a centrifugal compressor. In Proceedings of the IEEE International Conference on Systems, Man and Cybernetics, Anchorage, AK, USA, 9–12 October 2011; pp. 1538–1543. [Google Scholar]
- Greitzer, E. Surge and Rotating Stall in Axial Flow Compressors Part I: Theoretical Compression System Model. J. Eng. Power 1976, 98, 190–198. [Google Scholar] [CrossRef]
- Greitzer, E. Surge and Rotating Stall in Axial Flow Compressors Part II: Experimental Results and Comparison With Theory. J. Eng. Power 1976, 98, 199–211. [Google Scholar] [CrossRef]
- Hansen, K.E.; Jorgensen, P.; Larsen, P.S. Experimental and theoretical study of surge in a small centrifugal compressor. J. Fluids Eng. 1981, 103, 391–395. [Google Scholar] [CrossRef]
- Moore, F.; Greitzer, E. A theory of post-stall transients in axial compression systems: Part I Development of equations. J. Eng. Gas Turbines Power 1986, 108, 68–76. [Google Scholar] [CrossRef]
- Meuleman, C.; Willems, F.; de Lange, R.; de Jager, B. Surge in a low-speed radial compressor. In Proceedings of the 43rd International Gas Turbine and Aeroengine Congress, ASME, Stockholm, Sweden, 2–5 June 1998. [Google Scholar]
- Fink, D.A.; Cumpsty, N.A.; Greitzer, E.M. Surge dynamics in a free-spool centrifugal compressor system. In Proceedings of the ASME 1991 International Gas Turbine and Aeroengine Congress and Exposition, Orlando, FL, USA, 3–6 June 1991. [Google Scholar]
- Van Helvoirt, J.; de Jager, B.; Steinbuch, M.; Smeulers, J. Stability parameter identification for a centrifugal compression system. In Proceedings of the 2004 43rd IEEE Conference on Decision and Control (CDC) (IEEE Cat. No.04CH37601), Nassau, Bahamas, 14–17 December 2004; Volume 4, pp. 3400–3405. [Google Scholar]
- Willems, F.; Heemels, W.; De Jager, B.; Stoorvogel, A.A. Positive feedback stabilization of centrifugal compressor surge. Automatica 2002, 38, 311–318. [Google Scholar] [CrossRef]
- Yoon, S.Y.; Lin, Z.; Goyne, C.; Allaire, P.E. An enhanced Greitzer compressor model with pipeline dynamics included. In Proceedings of the American Control Conference (ACC), San Francisco, CA, USA, 29 June–1 July 2011; pp. 4731–4736. [Google Scholar]
- Van Helvoirt, J.; De Jager, B. Dynamic model including piping acoustics of a centrifugal compression system. J. Sound Vib. 2007, 302, 361–378. [Google Scholar] [CrossRef]
- Backi, C.J.; Gravdahl, J.T.; Skogestad, S. Simple method for parameter identification of a nonlinear Greitzer compressor model. IFAC-PapersOnLine 2018, 51, 198–203. [Google Scholar] [CrossRef]
- Jin, Y.; Fu, Y.; Qian, Y.; Zhang, Y. A Moore-Greitzer Model for Ducted Fans in Ground Effect. J. Appl. Fluid Mech. 2020, 13, 693–701. [Google Scholar] [CrossRef]
- Cousins, W.T.; Davis, M.W. The Influence of the Characteristics of a Centrifugal Compressor on System Stability and Distortion Response. In Proceedings of the ASME Turbo Expo 2012: Turbine Technical Conference and Exposition. American Society of Mechanical Engineers, Copenhagen, Denmark, 11–15 June 2012; pp. 37–49. [Google Scholar]
- Liu, A.; Zheng, X. Methods of surge point judgment for compressor experiments. Exp. Therm. Fluid Sci. 2013, 51, 20–213. [Google Scholar] [CrossRef]
- Sundström, E.; Semlitsch, B.; Mihăescu, M. Generation mechanisms of rotating stall and surge in centrifugal compressors. Flow Turbul. Combust. 2018, 100, 705–719. [Google Scholar] [CrossRef] [PubMed]
- Yang, Z.; Guang, X.; Zhiheng, W.; Pengfei, Z. Numerical investigation of deep surge in a centrifugal compressor with vaned diffuser and large plenum. Proc. Inst. Mech. Eng. Part A J. Power Energy 2020, 234, 143–155. [Google Scholar] [CrossRef]
- Kulak, M.; Grapow, F.; Liśkiewicz, G. Numerical analysis of centrifugal compressor operating in near-surge conditions. JPhCS 2018, 1101, 012017. [Google Scholar] [CrossRef]
- Liu, Z.; Zhao, Q.; Xiang, X.; Zhao, W.; Zhou, X. A hybrid viscous body force model for low-speed centrifugal compressors. Proc. Inst. Mech. Eng. Part A J. Power Energy 2020. [Google Scholar] [CrossRef]
- Huang, Q.; Zhang, M.; Zheng, X. Compressor surge based on a 1D-3D coupled method—Part 1: Method establishment. Aerosp. Sci. Technol. 2019, 90, 342–356. [Google Scholar] [CrossRef]
- Grapow, F.; Liśkiewicz, G. Compressor modeling using Greitzer model validated by pressure oscillations. Trans. Inst. Fluid-Flow Mach. 2016, 133, 69–89. [Google Scholar]
- Liśkiewicz, G. Numerical Model of the Flow Phenomena Preceding Surge in the Centrifugal Blower and Assessment of Its Applicability in Designing Anti-Surge Devices. Ph.D. Thesis, University of Strathclyde, Glasgow, Scotland, 2014. [Google Scholar]
- Gravdahl, J.T.; Egeland, O. Compressor Surge and Rotating Stall: Modeling and Control; Springer Science & Business Media: Berlin, Germany, 2012. [Google Scholar]
- Willems, F.; de Jager, B. Modeling and control of compressor flow instabilities. IEEE Control Syst. 1999, 19, 8–18. [Google Scholar]
- Ng, Y.E.; Liu, N. Parametric study of Greitzer’s instability flow model through compressor system using Taguchi method. In Compressor Instability with Integral Methods; Springer: Berlin, Germany, 2007; pp. 107–129. [Google Scholar]
- Liśkiewicz, G.; Horodko, L.; Stickland, M.; Kryłłowicz, W. Identification of phenomena preceding blower surge by means of pressure spectral maps. Exp. Therm. Fluid Sci. 2014, 54, 267–278. [Google Scholar] [CrossRef]
- Brigham, E.O.; Morrow, R. The fast Fourier transform. Spectr. IEEE 1967, 4, 63–70. [Google Scholar] [CrossRef]
- Hos, C.; Champneys, A.; Kullmann, L. Bifurcation analysis of surge and rotating stall in the Moore–Greitzer compression system. IMA J. Appl. Math. 2003, 68, 205–228. [Google Scholar] [CrossRef][Green Version]
- Van den Braembussche, R. Design and Analysis of Centrifugal Compressors; John Wiley & Sons: Hoboken, NJ, USA, 2019. [Google Scholar]
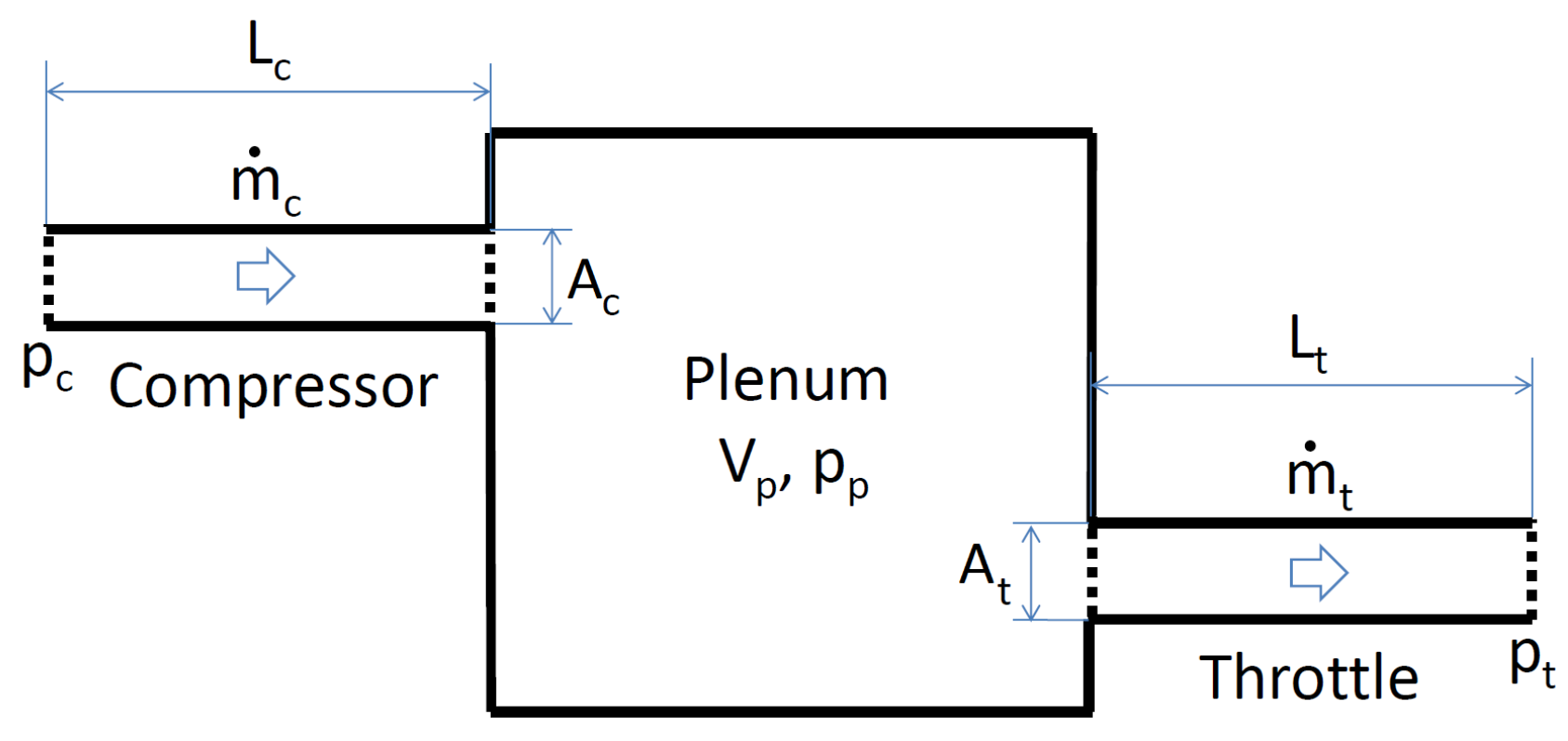
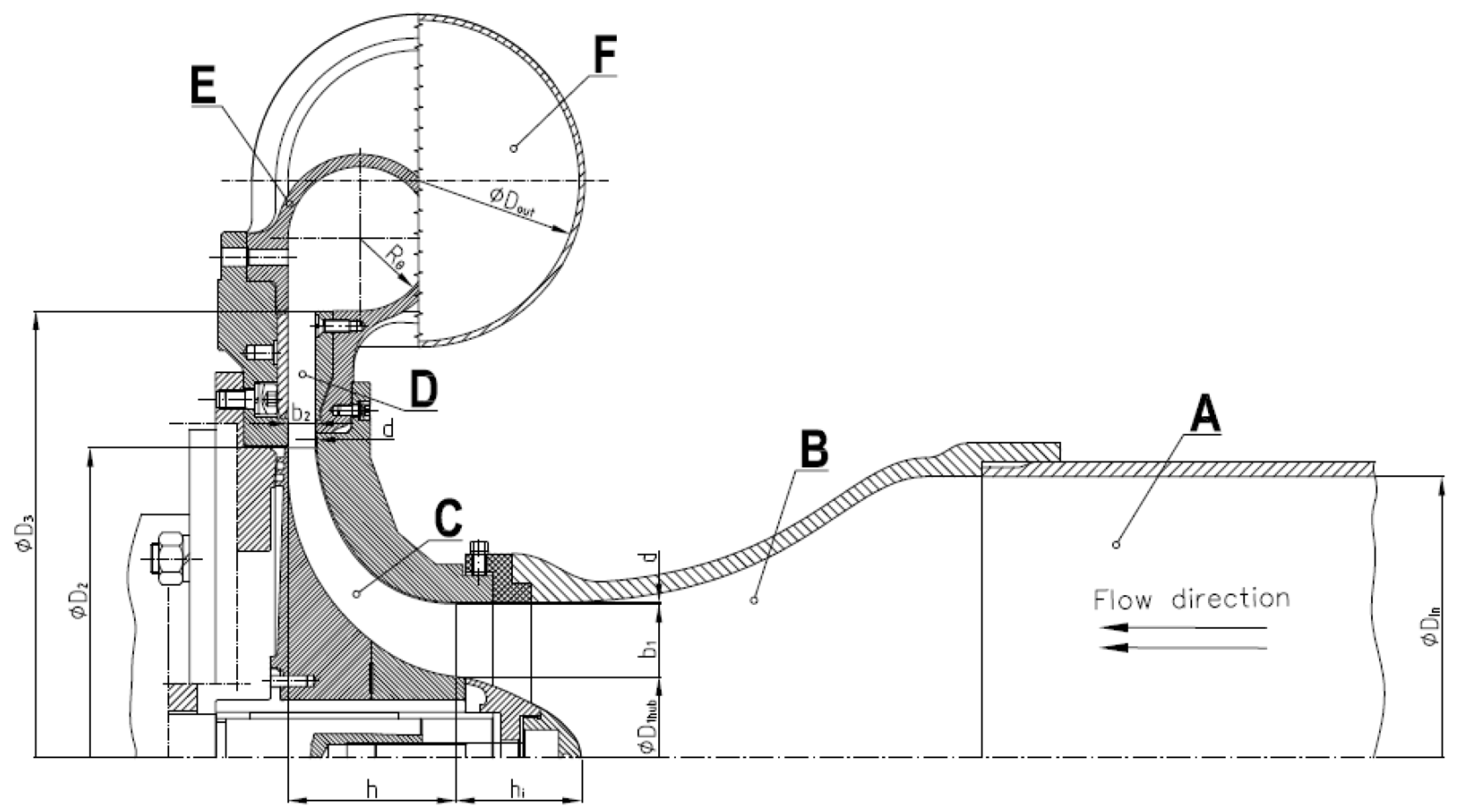
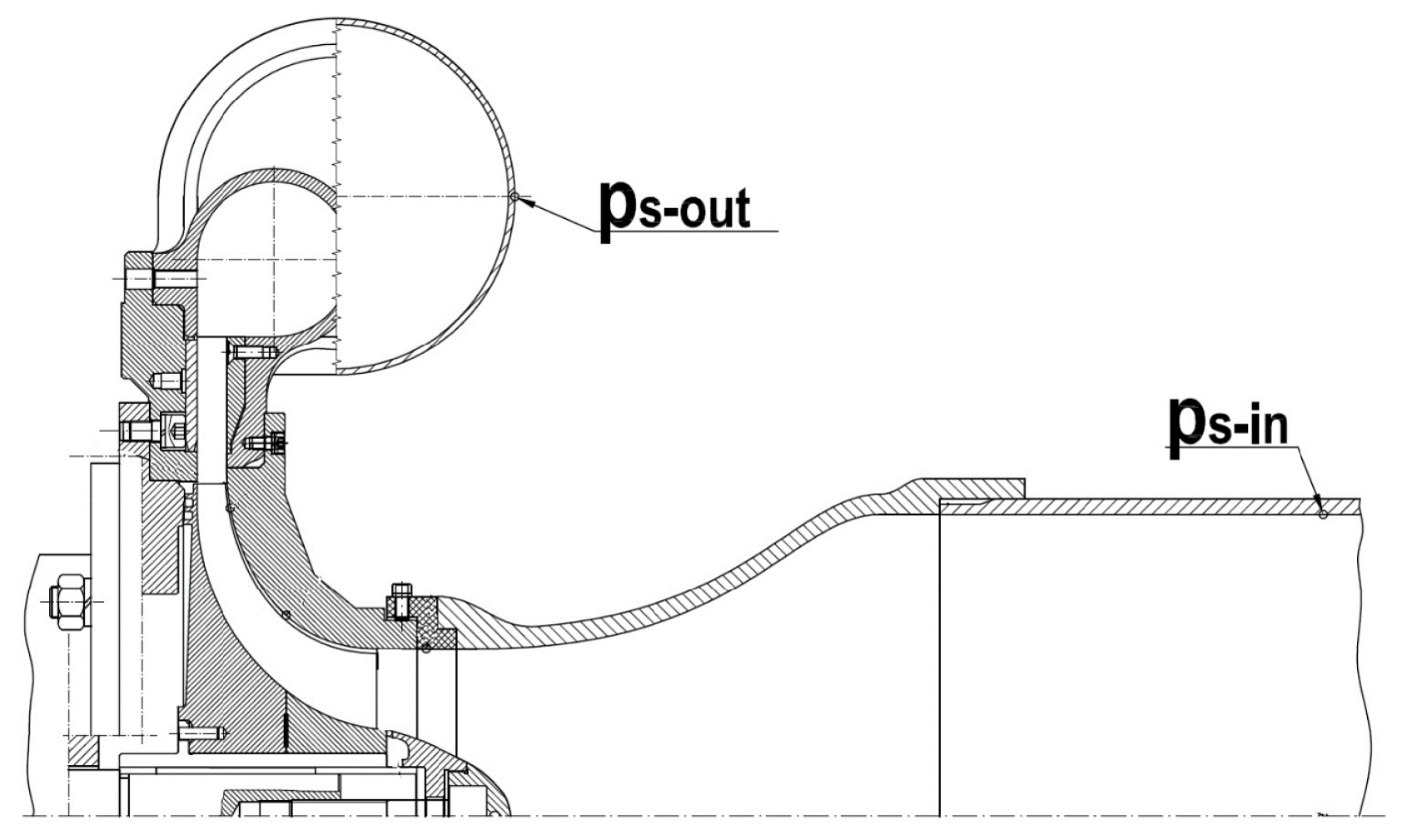


| Parameter | Notation | Value |
|---|---|---|
| Inlet pipe diameter | 300 mm | |
| Rotor inlet diameter at hub | mm | |
| Rotor inlet span | mm | |
| Rotor outlet diameter | 330 mm | |
| Rotor outlet span | mm | |
| Diffuser outlet diameter | 476 mm | |
| Volute tongue gap | 5 mm | |
| Diameter of outlet pipe | 150 mm | |
| Length of the outlet pipe | l | m |
| Volume of the outlet pipe |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jaeschke, A.; Liśkiewicz, G. Sensitivity Study of Greitzer Model Based on Physical System Parameters of Radial Compressing Units. Energies 2020, 13, 5111. https://doi.org/10.3390/en13195111
Jaeschke A, Liśkiewicz G. Sensitivity Study of Greitzer Model Based on Physical System Parameters of Radial Compressing Units. Energies. 2020; 13(19):5111. https://doi.org/10.3390/en13195111
Chicago/Turabian StyleJaeschke, Andrzej, and Grzegorz Liśkiewicz. 2020. "Sensitivity Study of Greitzer Model Based on Physical System Parameters of Radial Compressing Units" Energies 13, no. 19: 5111. https://doi.org/10.3390/en13195111
APA StyleJaeschke, A., & Liśkiewicz, G. (2020). Sensitivity Study of Greitzer Model Based on Physical System Parameters of Radial Compressing Units. Energies, 13(19), 5111. https://doi.org/10.3390/en13195111






