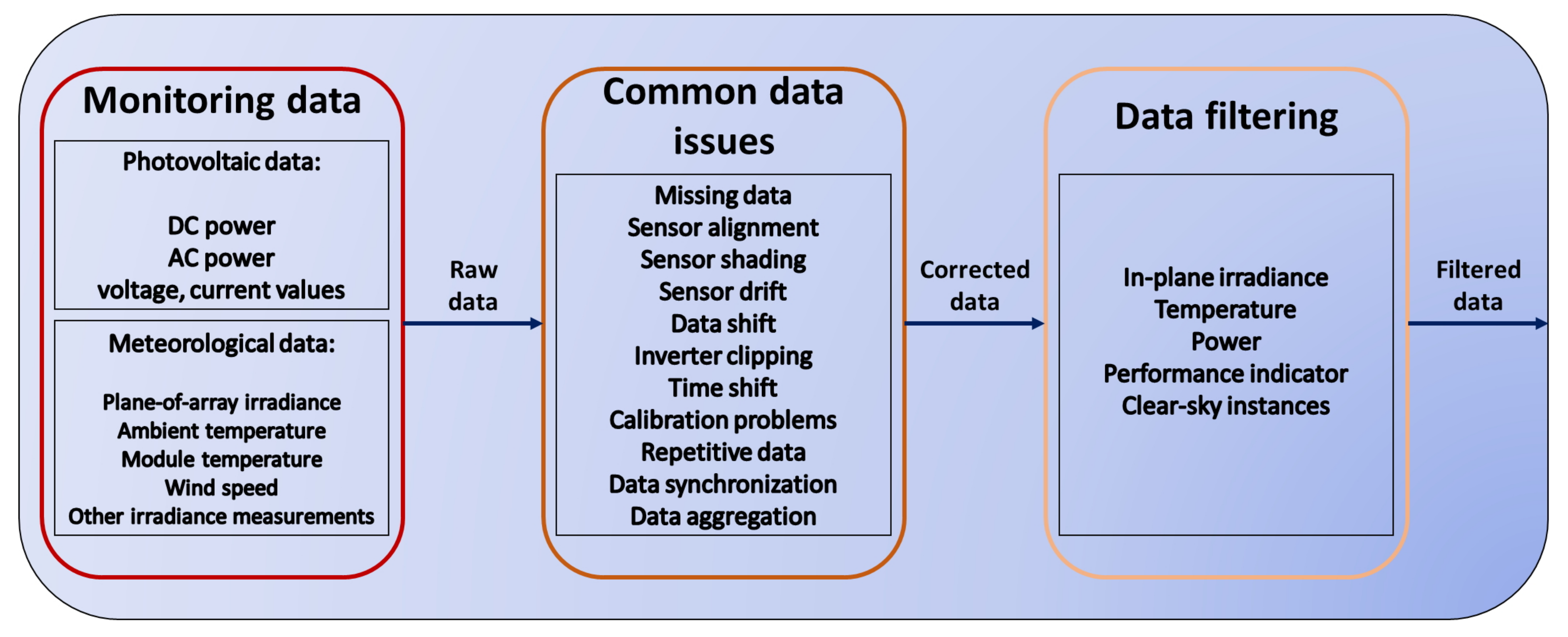
In this work, we focus on irradiance, temperature and power measurements. These are the most commonly measured and used data in performance evaluation studies of PV systems. In-plane irradiance
is measured in the same plane of the PV modules. Irradiance for PV applications is measured either with thermopile pyranometers or photovoltaic reference devices. The usage of these devices, calibration interval and guidelines as well as possible measurement corrections are stated in standard IEC 60904:2015 [
12] and in IEC 61724:2017 [
10]. If on-site measurements are difficult to realize, irradiance datasets can be acquired via clear-sky modeling or satellite-derived data. Usually, such measurements are subject to higher uncertainties and do often deviate considerably from ground measurements. Another problem when using satellite data is data consistency. Although satellite data quality consistently improves the data retrieved in the past might have a different accuracy from data used today.
Standardized quality checks include the deletion of invalid readings and treatment of missing data [
10]. Therefore, it is recommended to identify faulty data entries and to apply realistic thresholds as well as statistical outlier tests. In the case of missing data, it is recommended to assess whether filling (imputation) of missing data is reasonably possible, and what kind of approach needs to be used. Many different approaches for data imputation exist, including using different types of interpolation, Kalman filtering, auto-regression or moving averages [
13,
14]. For high-resolution data (minutely or hourly) and short gaps, interpolation is a reasonable approach, but with larger gaps or lower resolution data (daily, weekly) other approaches yield better results [
13]. Depending on the availability of other measured parameters (for instance satellite-based irradiance measurements or peered irradiance sensors in different locations), multi- or univariate regression or machine learning models can also be applied [
14,
15]. In the PV community there does not seem to be a consensus of how data filling should be performed and will often depend on the amount of data to be filled and the size of data gaps. In all situations where data has been imputed, it is recommended to label filled values to remain identifiable and to document the imputation approach applied.
In the process of data quality checking and data correction, temperature should be considered separately from irradiance and power data. Thresholds and outlier detection using statistical tests, which will be presented in the following section, are important to improve the quality of a dataset but not always sufficient to detect faulty measurements. By analyzing the time series of the raw data, significant measurement errors can already be identified. They can either be connected to faulty readings or stem from problems during measurement acquisition. Common problems are for example the shadowing of irradiance sensors by an object for a certain amount of time or the detachment of module temperature sensors from the module. Such events can easily be identified when visualizing the data at hand. If small parts of the datasets are affected data imputation can be used to recover the faulty/missing data. In case of longer data outages other sources should be used to retrieve the data, for example satellite data for irradiance or temperature models for the module temperature. In the following, temperature data on one hand, and irradiance and PV power data on the other hand are discussed with application examples in terms of data imputation. The examples stem from issues we were facing while analyzing the data for further treatment.
3.1. Temperature Data
The module temperature
is a function of several solar irradiance related parameters such as ambient temperature, wind speed and direction, mounting configuration, thermal behavior and efficiency of the module, and system level parameters such as soiling or shading conditions. Usually, plotting ambient and module temperature over time provides a fairly good estimation of the measurement quality. If multiple module temperature sensors are available an inter-comparison is suggested. With such figures, strong outliers are easy to detect and can be taken care of. If module temperature readings are showing unexpected trends, module temperature models could be applied, and the measured values be compared to modeled values. If the discrepancy between both is too high, measured values should be replaced with modeled ones. The choice of the model will depend on the availability of other climate data from that specific side. The simplest model hereby is the Nominal Operating Cell Temperature (
NOCT Model) equation [
16]:
is the normal operating cell temperature and is determined for a 45
south-facing module with incident irradiance of 800 W/m
, an ambient temperature of 20
C and a wind speed of 1 m/s.
is the measured in-plane irradiance and
the measured ambient temperature. The
variable is mostly provided in the datasheet of the respective model. The inclusion of wind speed, if available, usually improves the accuracy of the module temperature estimation. A well behaving model is the Sandia module temperature model (SMTM) [
17]:
is the measured wind speed and
a and
b empirical parameters depending on mounting configuration, module backside material as well as solar cell material. More sophisticated models including more empirical coefficients, the transmittance of the module cover and the absorption coefficient of the cell were formulated by Skoplaki et al. [
18] and Mattei et al. [
19]. The choice of the model, and therefore the accuracy of the modeled temperature, will always depend on the available input parameters.
Plotting module temperature over time already gives an impression whether the measurements are realistic. The following figure shows ambient and module temperature of the PV plant under investigation. When looking at
Figure 2 it is obvious that the module temperature readings are faulty at the beginning of recording. For roughly one year the values are very similar to the ones of the ambient temperature sensor. The module temperature sensor was detached from the module because of the usage of unsuitable tape and glue. After reattaching using adequate adhesion material in April 2012, the readings are stable throughout the time of observation.
Several regression models have been tested to replace the faulty data with modeled module temperature values. Two of them, namely multivariate regression and multivariate adaptive regression splines (MARS), are discussed further as the better performing models. Therefore, the data were subject to light outlier filters according to the third part of IEC 61724:2016 [
20], which are listed in
Section 4. The initial motivation for using a regression model was to have a simple model which does not require any metadata of the PV system. Regression models rely only on measured data. As explained before, to use the SMTM one must know the kind of mounting type and which backside material is used in the modules.
The faulty data in
Figure 2 account for 11% of the overall dataset. Therefore, the strongly correlated values of ambient temperature, in-plane irradiance and wind speed were used to model
. The remaining dataset was used to test the regression models. 20% of the remaining, trustful, data were used as test set and 80% of the data as training data. In order to rate the regression models, this and the two established models,
NOCT and SMTM, haven been tested on the test set and the results yield the model parameter presented in
Table 2.
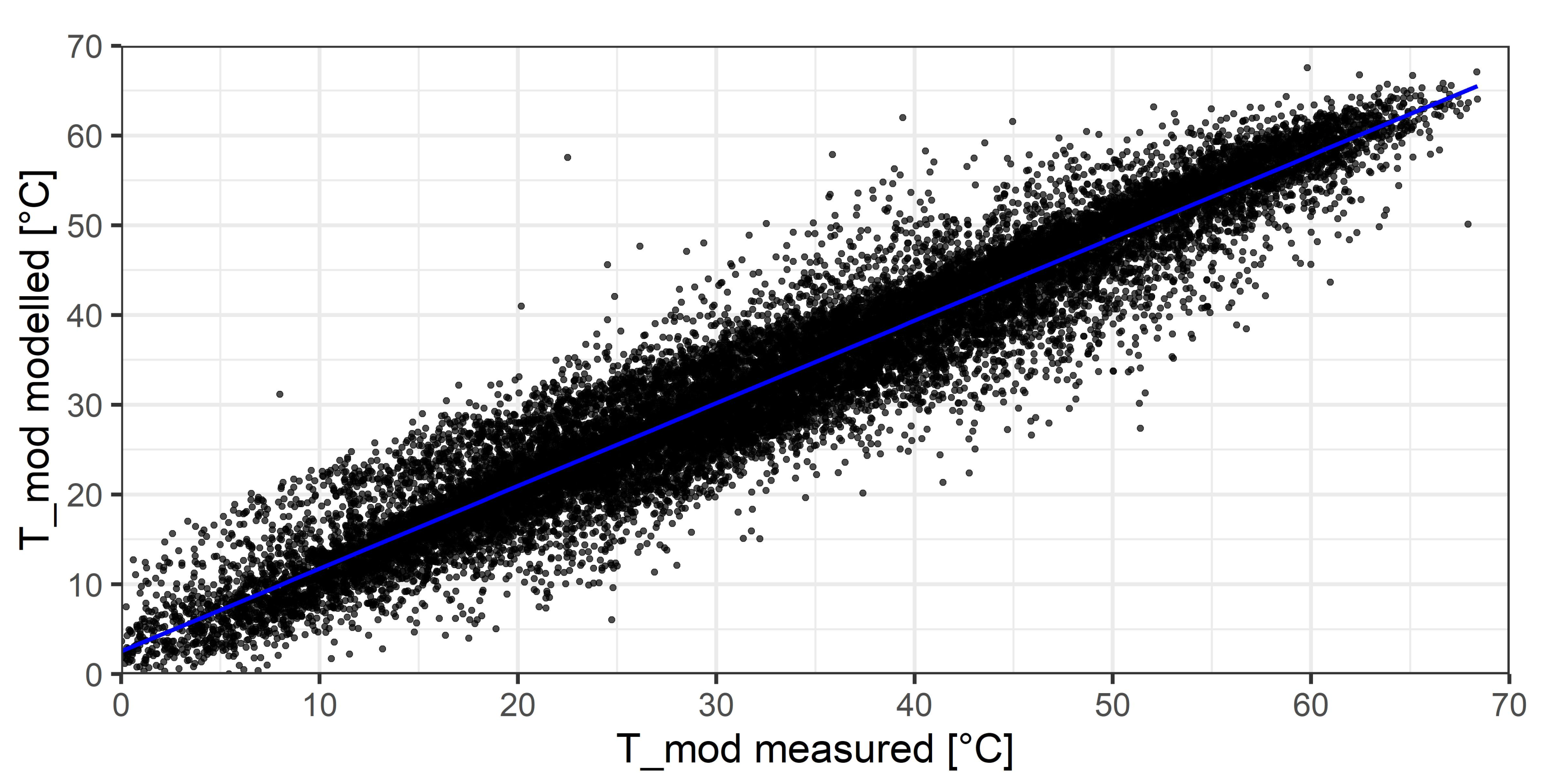
The difference between the modeled module temperature using MARS regression and the correctly measured temperature can be seen in
Figure 3. The relationship between measured and modeled data should be nearly linear. R
between model and measured values is 0.92 and the root-mean-square-error (RMSE) is 4.26
C. These values show that a trained regression model is performing slightly better compared to the SMTM, provided that a sufficient amount of the measured data is trustful and can be used as training data. Furthermore, the modeling results in
Table 2 show that the SMTM yields more accurate results compared to the
NOCT model and is always preferable if wind speed measurements and metadata are available.
3.2. In-Plane Irradiance Imputation
Irradiance determination is a very complex topic. In the best case, the in-plane irradiance (
) is measured with an irradiance measurement device installed in the same plane as the investigated PV system. If no in-plane irradiance sensor is installed, a transposition of the
from global horizontal irradiance
must be calculated. Therefore, irradiance data can be categorized into different accuracy classes based on data availability [
21]:
- (a)
High accuracy: is measured on-site
- (b)
Medium accuracy: horizontal irradiance is measured on-site and is estimated using decomposition and transposition approaches
- (c)
Low accuracy: is estimated using decomposition and transposition approaches from extracted , which is taken from one of the following sources: interpolated (weighted regression) using peered data of different weather stations in relatively close proximity to the test side, satellite or re-analysis-based datasets, clear-sky modeled datasets
The order of accuracy corresponds to increasing uncertainties in the datasets. Although measured irradiance values can have uncertainties as low as 2% [
22], the introduction of decomposition and transposition approaches as well as the estimation of
introduces additional, partially very high, uncertainties.
In general, ground measurements are always preferred because of higher accuracy, both for in-plane and horizontal irradiance. If weather stations are used the spatial resolution might be not high enough leading to high uncertainties. Datasets from satellite data might be inaccurate because of their low spatial (and possibly temporal) resolution and treatment of clouds, snow or aerosol. Many different clear-sky models are available. In the simplest case, they are based on geometrical calculations. More advanced clear-sky models take into account different measurable atmospheric parameters such as ozone, aerosols and precipitable water. The problem is that these data must be measured and provided as model inputs.
To get useful results, the best of these options must be selected for each case and carefully evaluated.
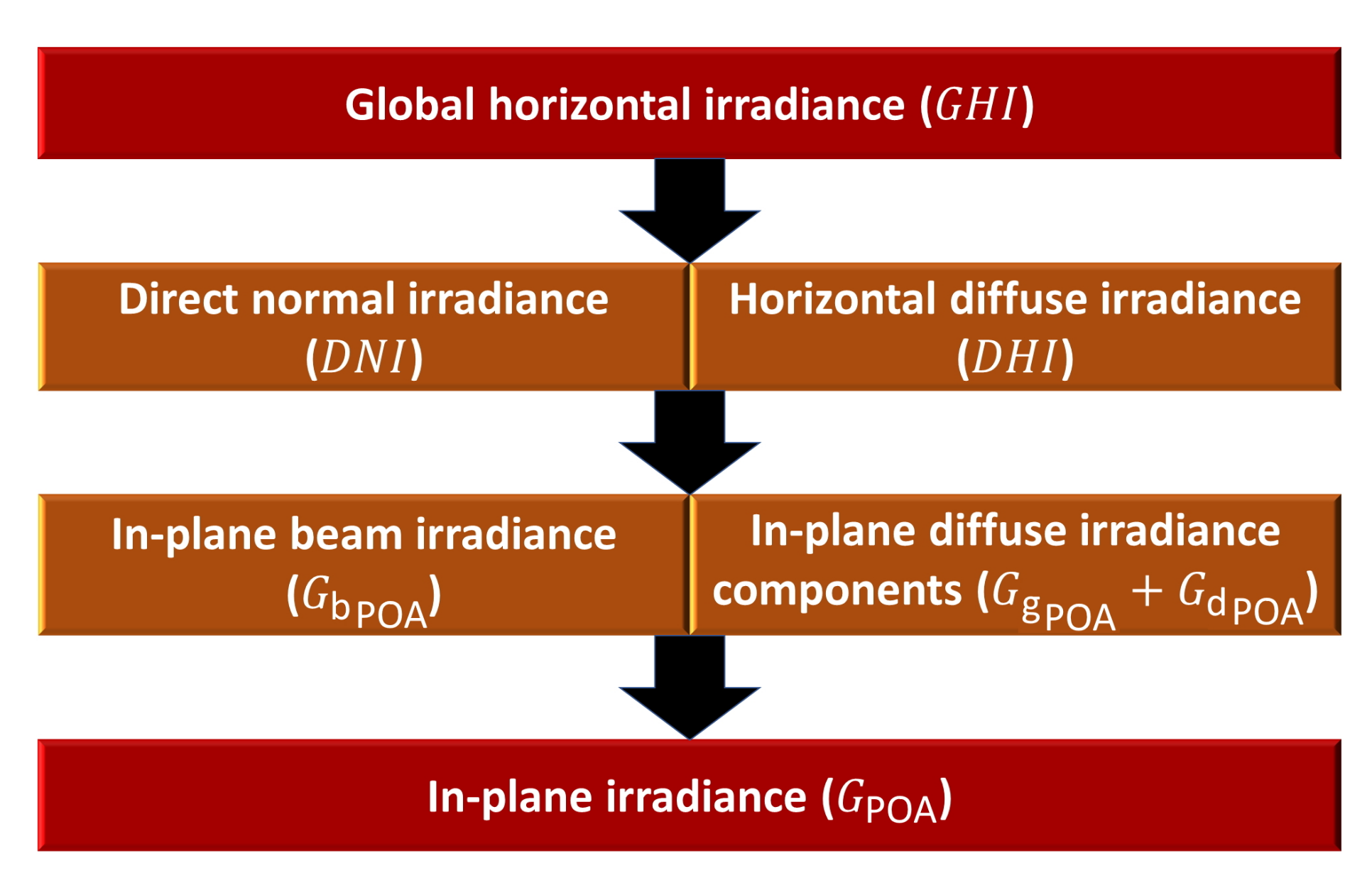
is the sum of diffuse and direct irradiance and is defined by:
Here, is the diffuse share of horizontal irradiance, which comes from all directions and is the direct normal irradiance. is the solar zenith angle.
depends on several factors such as the sun position, orientation of the system, individual irradiance components, albedo and shading. It can be expressed as the sum of the in-plane beam component of irradiance
and the in-plane diffuse irradiance components, which include an in-plane ground-reflected component
and a sky-diffuse component in the plane of array
:
If no measured in-plane irradiance is available, the individual components are calculated from
, provided through one of the scenarios mentioned above. The separation of the individual irradiance parts is necessary because the diffuse irradiance component is very complex to model. A comprehensive discussion on models can be found in [
23] and a comparison and rating of different models in [
24,
25].
Figure 4 shows a simplified model structure to calculate the in-plane irradiance [
26].
If instead
sensors are available at the side, they should be used to ensure the highest possible data accuracy. Usually, the readings are much more precise and accurate. To ensure smooth and reliable operation of the sensors, they must be systematically cleaned and calibrated in order to comply with part one of standard IEC 61724:2017 [
10]. Possible problems are measurement errors, sensor alignment issues or sensor drifts and are discussed in greater detail in the next section.
As discussed before, faulty or missing measurements for a limited amount of time could be replaced by data imputation. However, if a measurement is faulty or missing for longer periods of time, filling these values with simple approaches such as interpolation are no longer valid or possible.
In a recent study, we encountered such an issue when examining a dataset [
27] needed for PV performance loss calculations. We found that our input dataset was missing in-plane irradiance measurements for a period of four years at the beginning of the dataset, and had smaller gaps of hours to days in other years. Aside from in-plane irradiance, the dataset also contained other irradiance measurements (global horizontal irradiance
and diffuse horizontal irradiance
) and measurements of other parameters such as relative humidity
. These other measurements were not missing for the first four years of the dataset.
The aim of the study was to fill the missing
measurements using the available
,
and
measurements. To replace the missing data, we compared several classical irradiance transposition models (implemented in the python software package PVLIB [
28]) with several machine learning-based models [
29]. We compared the isotropic [
30], Klucher [
31], Hay–Davies [
32], Reindl [
33,
34], King (As discussed by the authors of PVLIB, the King model is not well documented nor is there published documentation [
28]) and Perez [
35] classical models, and random forest [
36], extra trees [
37], gradient boosting [
38] and histogram-based gradient boosting (The implementation of histogram-based gradient boosting in scikit-learn is based on the LightGBM framework [
39]) machine learning regression models as implemented in the python library scikit-learn [
29]. We added solar position parameters (solar zenith, solar azimuth and solar elevation) to our input dataset of
,
and
, and removed all measurements of solar elevation
. Using a random subsample (
n = 50,000) of our complete training dataset (
n = 275,000), we performed hyperparameter optimization to determine optimal values for the modeling parameters for both the classical transposition models as well as the machine learning models. The models were subsequently run (transposition models) and trained and run (machine learning models) using the full training dataset, and cross-validated using a 0.75/0.25 train-test split. Although testing all considered methods for modeling estimation
, we found that the machine learning-based models clearly outperformed the transposition-based models, with average RMSEs of around 30 W/m
and 70 W/m
. The highest accuracy was found for the histogram-based gradient boosting regressor (RSME of 29.8 W/m
). Using this regressor, we estimated and filled the missing
values.
In summary, ground measurements are always preferred if available, possibly with necessary corrections. For certain locations, other methods may yield good results. Retrieving accurate irradiance data of locations with complicated shading conditions and a high amount of diffuse light due to regular fog, mist or cloud cover, is still an open issue.
3.3. In-Plane Irradiance and Power
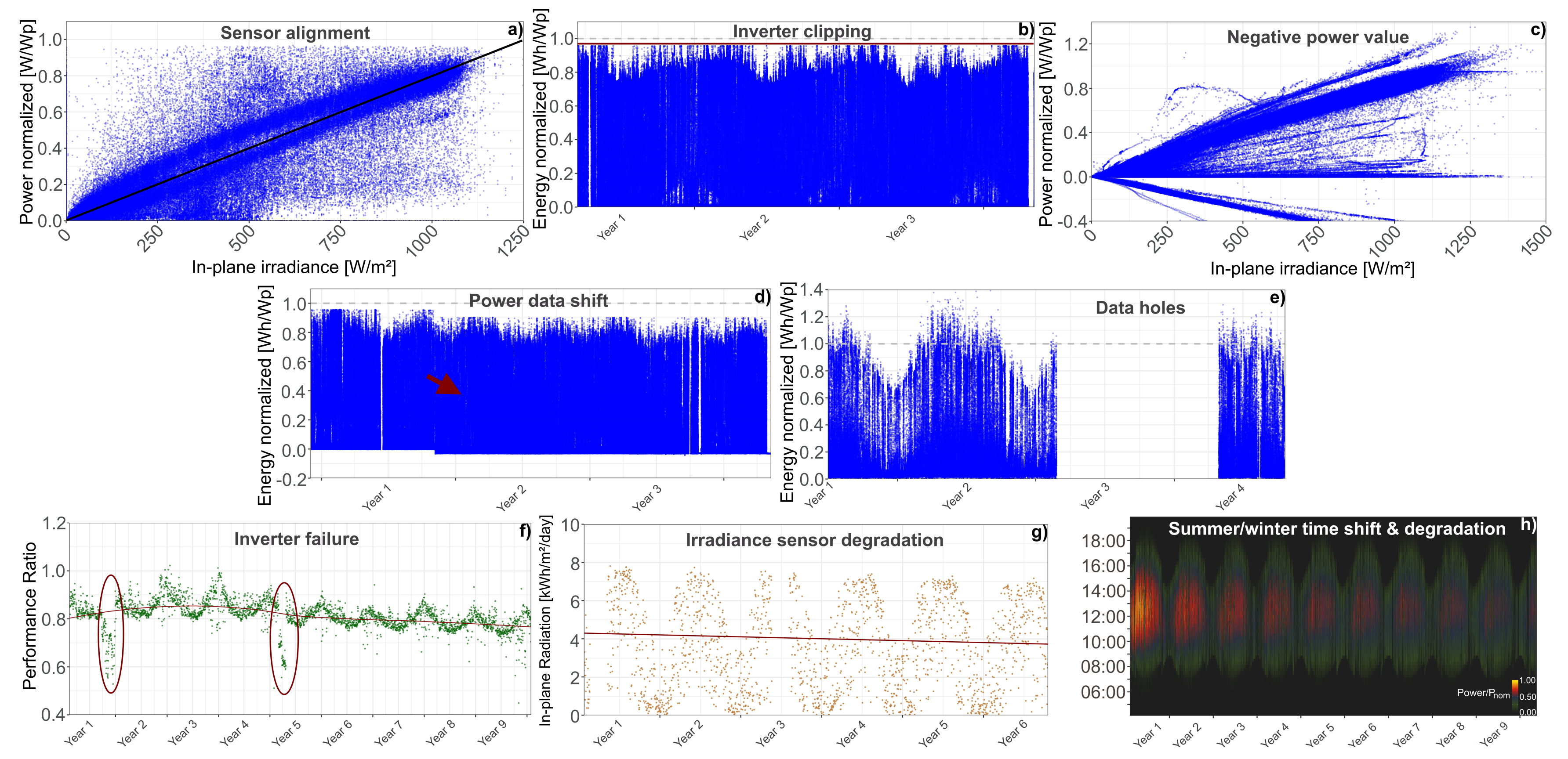
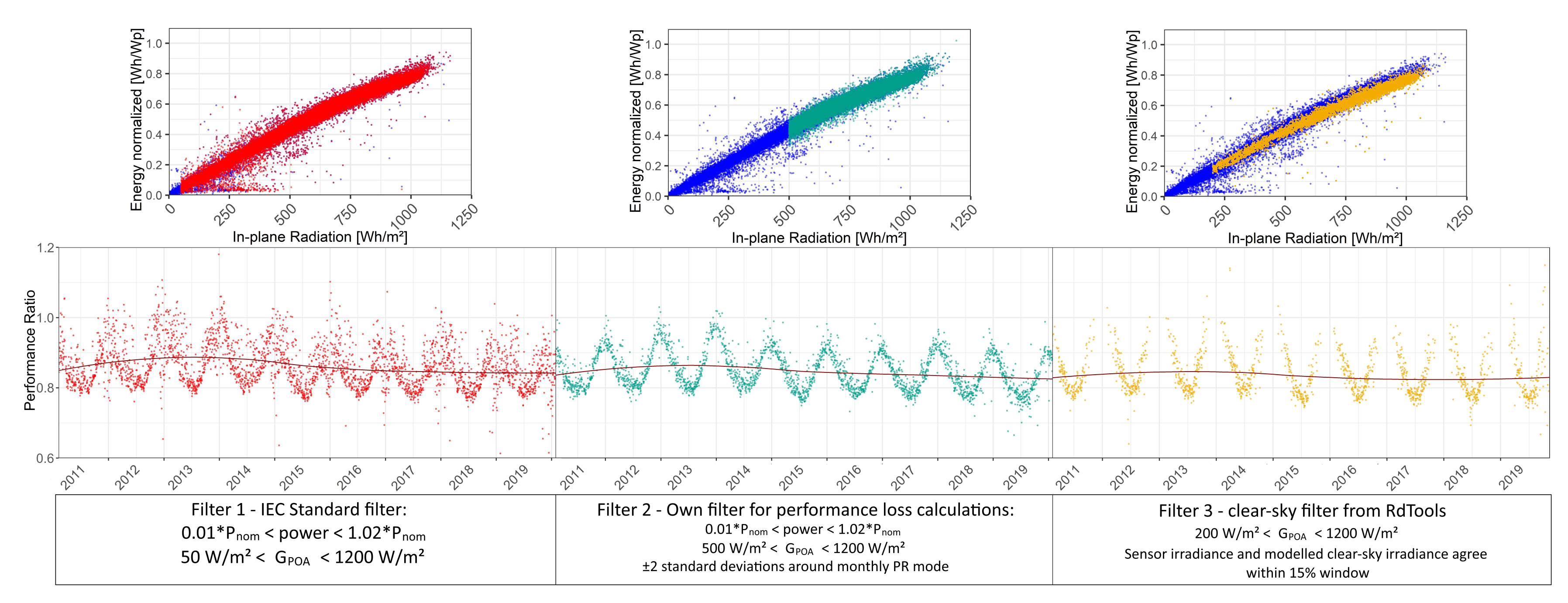
A thorough check of power and in-plane irradiance raw data is absolutely necessary to perform any kind of data analysis. The quality of the datasets depends on various factors and can be compromised for many reasons. In this section, simple visual quality checks and examples of common data issues are presented. Therefore,
Figure 5 is based on the measured data of the experimental PV system introduced in
Section 2, while
Figure 6 presents data from various other plants installed across the globe which are kept anonymous.
Since irradiance and power time series are supposed to behave in a similar fashion and are directly proportional over a large irradiance interval, similar checks can be performed.
Figure 5 shows recommended visualizations for a basic data quality check.
The following relations are depicted for the example PV plant: (a) energy vs. time, (b) power-density plot, (c) power vs. in-plane irradiance and (d) daily performance ratio (
) over time. All measured data can be evaluated in a similar fashion. The Performance Ratio describes the relation between incoming irradiation and power produced by the PV system. It is a unit-less parameter and is calculated using the following formula [
10]:
The first equation holds for AC power and the second for DC power. For AC, the final yield
is divided by the reference yield
. If DC power is evaluated,
is replaced by the array yield
. Yield values are given in [kWh/m
]. The yields itself are ratios of normalized energy
E and normalized in-plane irradiation
. Energy values are aggregated power measurements while irradiation values are aggregated irradiance instances (from W to Wh). The energy
E is normalized by the nominal power of the respective system
obtained under Standard Test Conditions [
40] (ambient temperature
= 25
C, in-plane irradiance
= 1000 W/m
, air mass AM 1.5) and
by STC irradiance
. In
Figure 5, all values have been normalized to STC. By doing this, an easier inter-comparison between different PV systems can be performed.
By examining the figures, it is apparent that this particular plant operates without any profound problems. The only visible issue is a very slight power loss over time, especially in the last two to three years, which can be seen in
Figure 5a,d. Time-dependent system performance degradation has to be expected, and is not necessarily an issue, as long as the degradation is within acceptable margins. If strong system degradation is detected, it is recommended to evaluate the performance of individual modules to trace back the root causes of the observed degradation. Aside from detecting issues with system performance,
Figure 5c,d are valuable to evaluate the alignment of the irradiance sensor in plane with the PV system and to rate the irradiance measurement quality. As said before, power and irradiance are nearly proportional. Therefore, high-quality data are characterized by a linear relationship, visualized in
Figure 5c. Here, instantaneous measurement data are depicted. A higher number of outliers might suggest certain synchronization issues. In
Figure 5c, some outlying values are visible where irradiance values of up to 500 W/m
are measured while no power is produced. That is because the system is installed in a valley of a mountainous region. Under low sun inclination in the morning, the irradiance sensor is already irradiated while the PV system is still in the shadow, and thereby not producing any power, while higher irradiance values are correctly measured.
Figure 5d could also depict other aggregation time steps (daily/weekly/monthly sums/averages) for
, power or irradiance values. Like this, time-dependent trends could be evaluated, which are assumed to be periodical and without strong degradation patterns.
Another helpful way to verify data quality is to look at a heatmap plot of instantaneous measurement values, as shown in
Figure 5b for normalized power. Here, 15 min power data of the mc-Si system are colored according to normalized power and plotted as a function of the time of the day and the day of the year. Higher power values for a longer duration of the day are detected in summer because of higher irradiation and longer days in summertime. From such a plot one can detect longer system outages, timestamp issues, shading instances or also exceptionally strong degradation. If similar plots are shown on a weekly or monthly scale, additionally cloudy days can be detected. The data of the system are converted to UTC (Universal Time Coordinated) to remove daylight-saving time shifts in the density plot. It is visible that the data follow a fairly stable pattern and can be considered being of high quality.
In general, strong outliers, missing data, sensor measurement issues, inverter clipping instances or other common data issues can be identified from the plots above. In
Figure 6, examples of such data issues are presented from several PV systems not belonging to the experimental PV installation introduced above. All data are anonymized and normalized.
In the figures, blue has been used to represent power values plotted on the y-axis, orange for irradiance values and green for values. In each subplot, the corresponding problem is depicted.
Figure 6a shows a typical sensor alignment issue. Many data points are away from the linear trend-line between power and irradiance. Furthermore, two distinct lines can be recognized. These issues can stem from various problems, Usually they are connected to an offset between timestamps, an incident which decreases the power output at some point, a change in irradiance readings or the sensor with a different tilt/orientation as the solar modules. In such situations it is recommended to investigate the power and irradiance data over smaller time scales to possibly detect certain performance impairing issues. Furthermore, the irradiance data must be thoroughly filtered or possibly replaced.
Figure 6b shows inverter clipping of a PV system, which occurs when their AC power rating is lower than the total installed PV module capacity and the output power is limited. This is actually not an error or issue, but a way to increase the reliability of PV systems. Nevertheless, it is important to be detected and taken into account for further data treatment. Using undersized inverters has the benefits of saving money for cheaper components, producing more power under low light conditions and the fact that PV systems degrade naturally over time (a high rated inverter power might not be needed anymore). Thus, inverter clipping is common practice in modern PV plants.
In
Figure 6c, the system under investigation apparently produced negative power values. From a physical standpoint, that is not possible. It is more likely that the polarity has been switched. Filtering negative values is a common procedure defined in standard IEC 61724:2016 [
20].
The system data, presented in
Figure 6d, show inverter clipping and a power data shift after one year of operation. Since the source and reason of the shift is not known, it is advisable to omit the first year of operation to ensure realistic measurement conditions.
The data holes in
Figure 6e stem from calibration activities of the sensors at the measurement site. In order to avoid these issues related to maintenance of the measurement system, it is recommended to have redundancy in sensors, and to have a proper calibration plan to avoid losing large amounts of measurements.
In
Figure 6f, the daily aggregated
of a PV system is seen. Two instances of inverter failures were recorded, marked with red ellipses. Inverter failures are preceded by distinct losses in performance. The performance drops and the
values deviate clearly from their normal patterns. Either the inverter breaks down completely or the deviation is detected beforehand, and the inverter is repaired or exchanged. Inverter failures can be categorized as reversible performance losses.
Figure 6g depicts the daily in-plane radiation measured with an irradiance sensor. A simple approach to detect possible sensor drifts or sensor degradation (if solar cell material is used) is to perform a linear regression of the irradiance time series. A clear trend change of the regression line over time would indicate a possible drift in the sensor readings. Certain trend variations could also be explained by inter-annual irradiance variability (especially for shorter time series) and appearing global brightening effects in recent year. These effects are observed since the late 1980s and are attributed to reductions in aerosol content in the atmosphere and cloud cover leading to higher transmission of sunlight [
41]. In this particular case a decrease in measured irradiance over time can be seen. If this irradiance sensor measurements were to be used for constructing
or other KPI time-series, the
would artificially increase, provided the corresponding power time series is fairly stable over time. After enquiring about this sensor, it was reported that it is an amorphous silicon reference cell. It is expected that the active solar material in the reference cell degraded, resulting in decreasing irradiance measurement values while not being re-calibrated. To evaluate the PV system performance corresponding to this irradiance sensor, it is necessary to use another source of irradiance measurement to ensure realistic readings.
Figure 6h shows a power heatmap for a thin-film PV system. The data are measured and plotted in central European time including summertime, therefore a 1-h shift in March and October every year can be seen. It is visible that this shift interrupts the periodic structure of the figure and should therefore be removed by converting the timestamp to UTC. Furthermore, this particular system is subject to an unusual high degradation, visible in the decreasing color intensity over time.