Compressed Machine Learning Models for the Uncertainty Quantification of Power Distribution Networks
Abstract
1. Introduction
2. Goal Statement
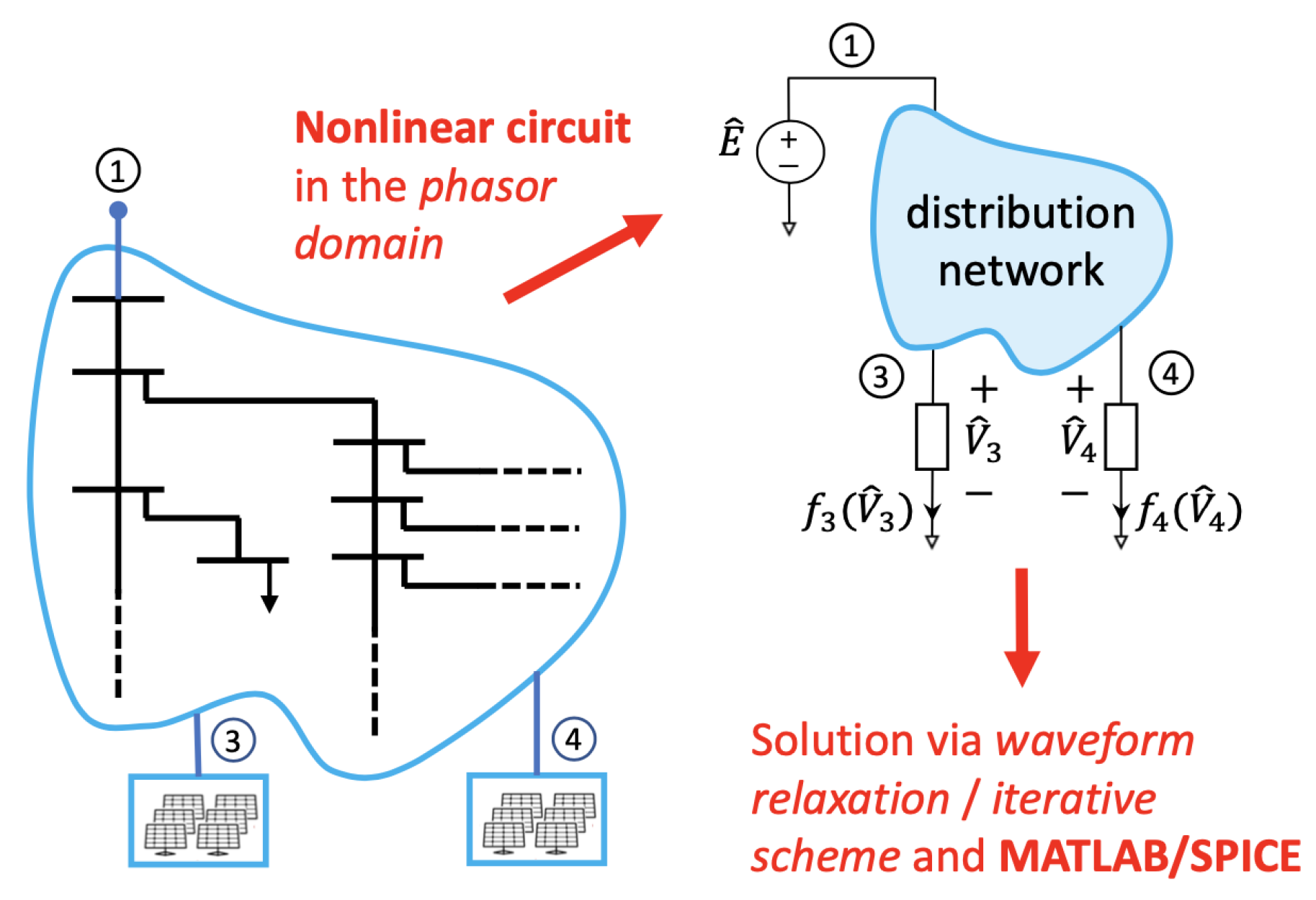
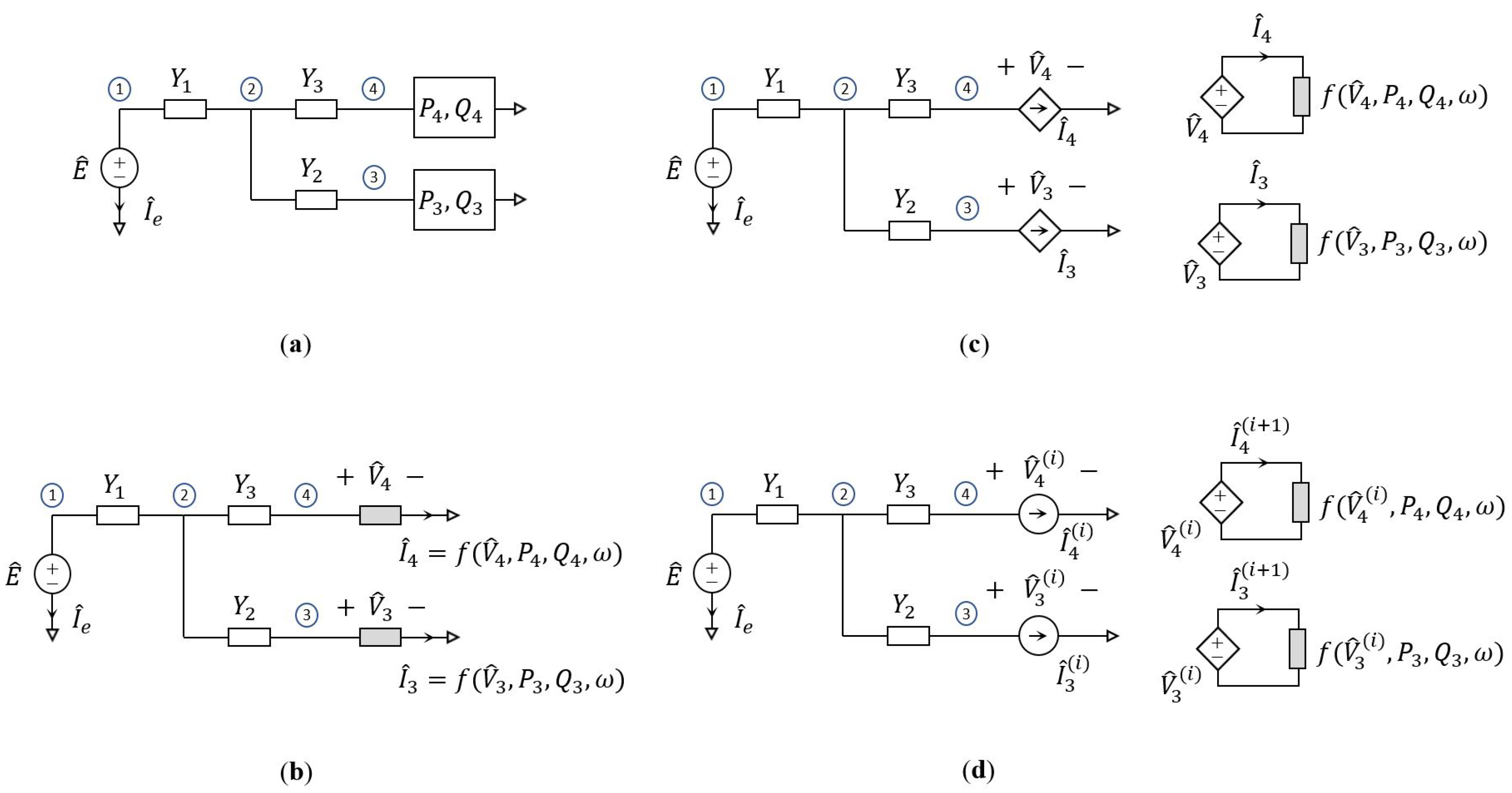
3. Power-Flow Analysis
- is the MNA matrix, which is constructed by circuit inspection and incorporates the characteristics of the circuit elements;
- is a complex vector collecting the nodal voltages ;
- is a vector collecting the amplitude of the independent current sources; and
- is a vector collecting the phasors of the currents that flow through the controlled voltage sources.
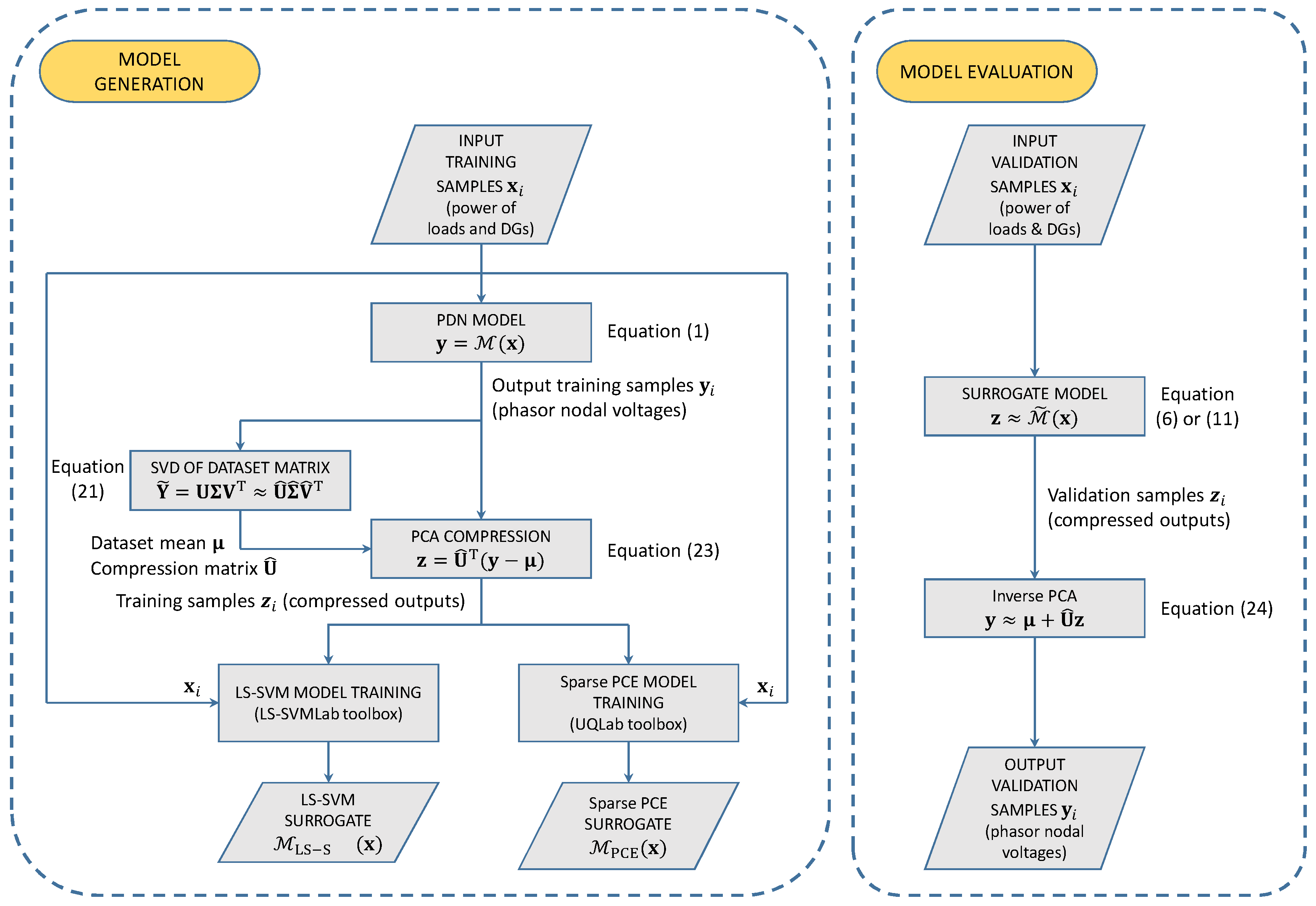
4. Surrogate Models
4.1. LS-SVM Regression
4.1.1. Primal Space Formulation
4.1.2. Dual Space Formulation
- linear kernel: ,
- polynomial kernel of order q: , and
- Gaussian radial basis function (RBF) kernel: .
4.2. Sparse PCE
- is a vectorial multi-index belonging to set , and
- k is a scalar index pointing to the elements of , which are typically assumed to be sorted according to the graded lexicographic ordering.
- Total-degree truncation (), leading to terms;
- Hyperbolic truncation (), which leads to an increasingly sparser expansion as u is decreased;
- Tensor-product truncation (), which is usually avoided because of the exorbitant number of terms.
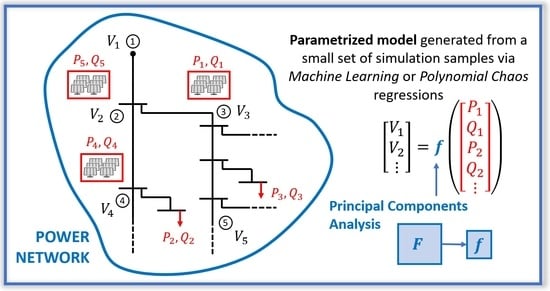
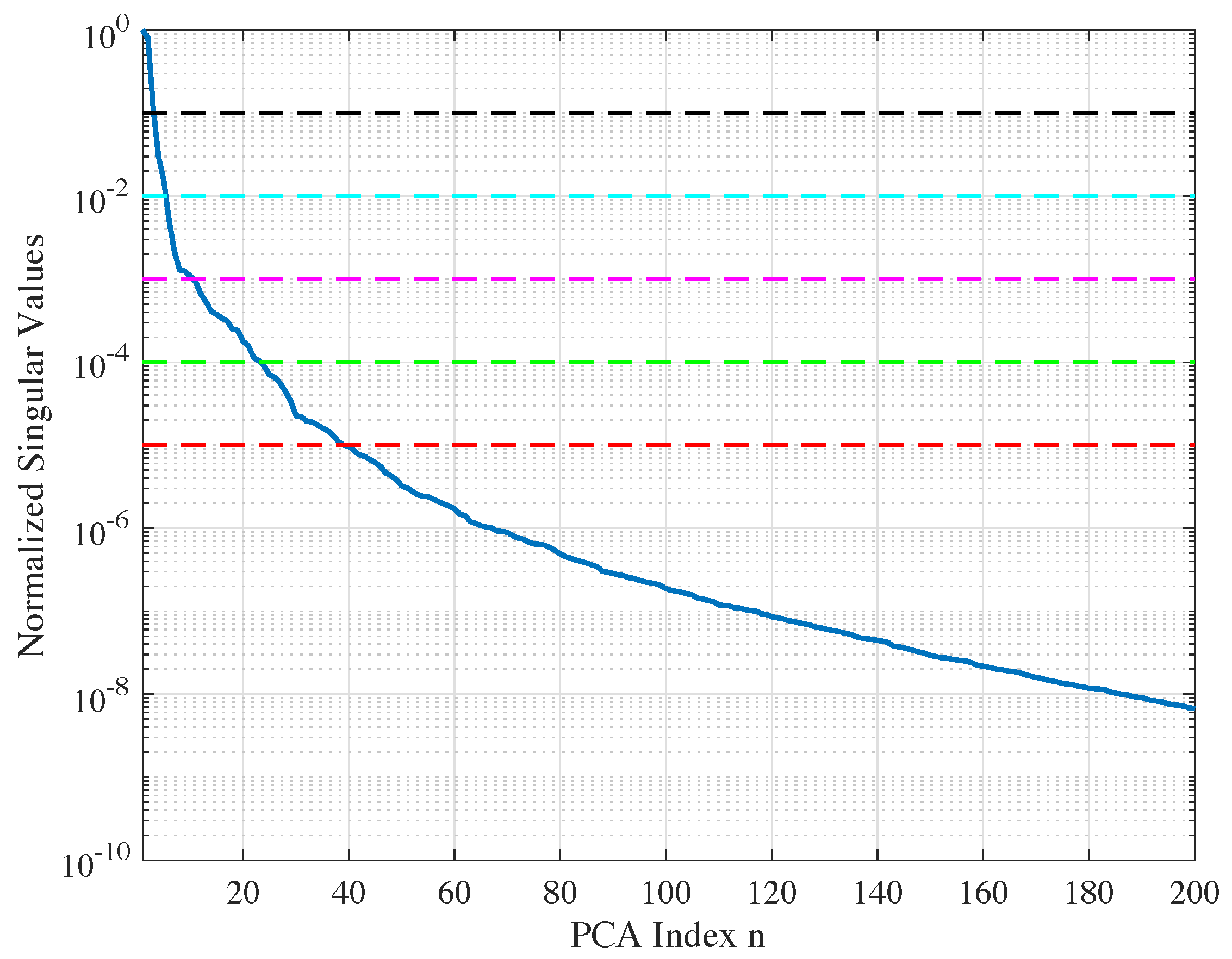
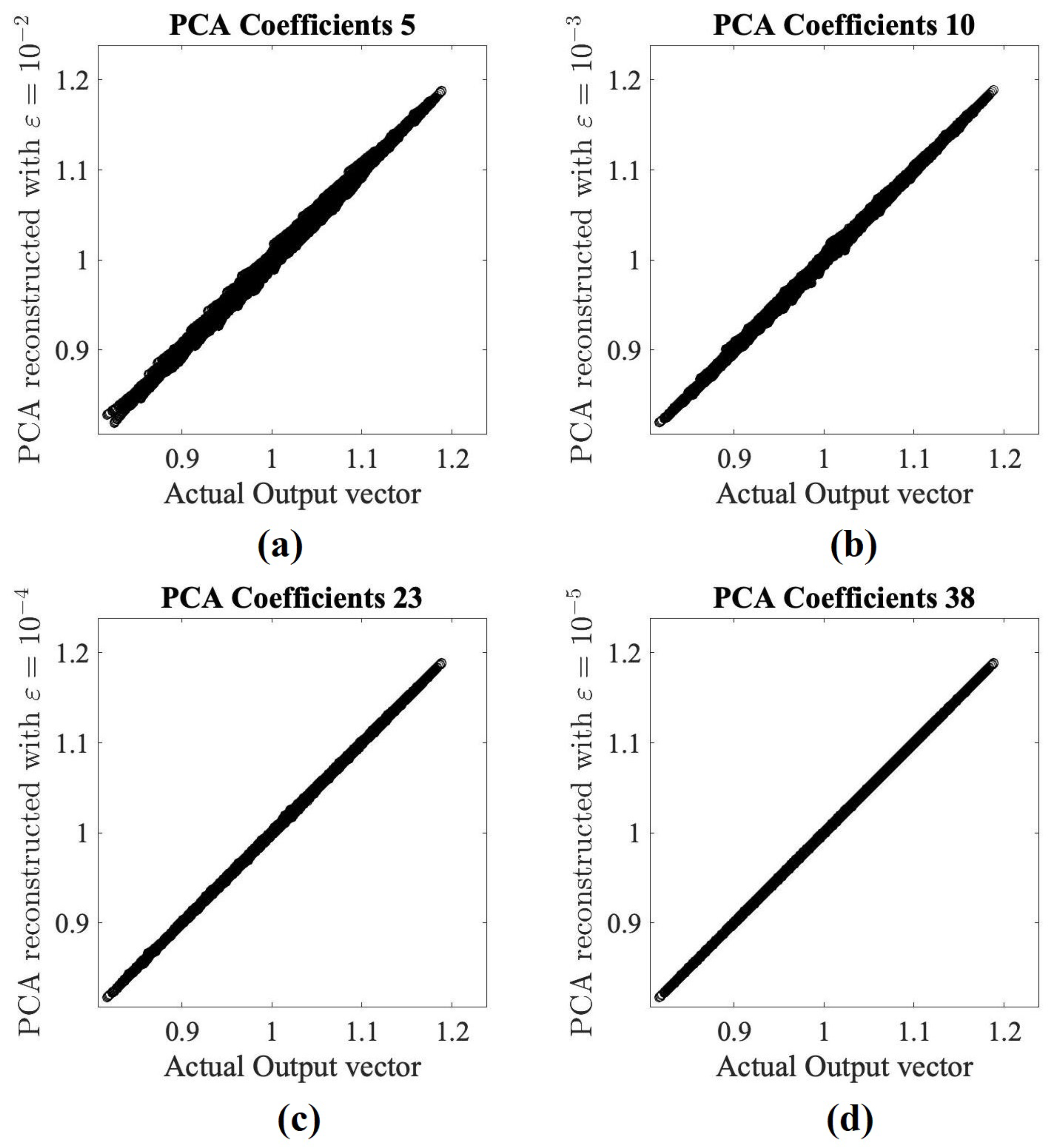
4.3. PCA Compression
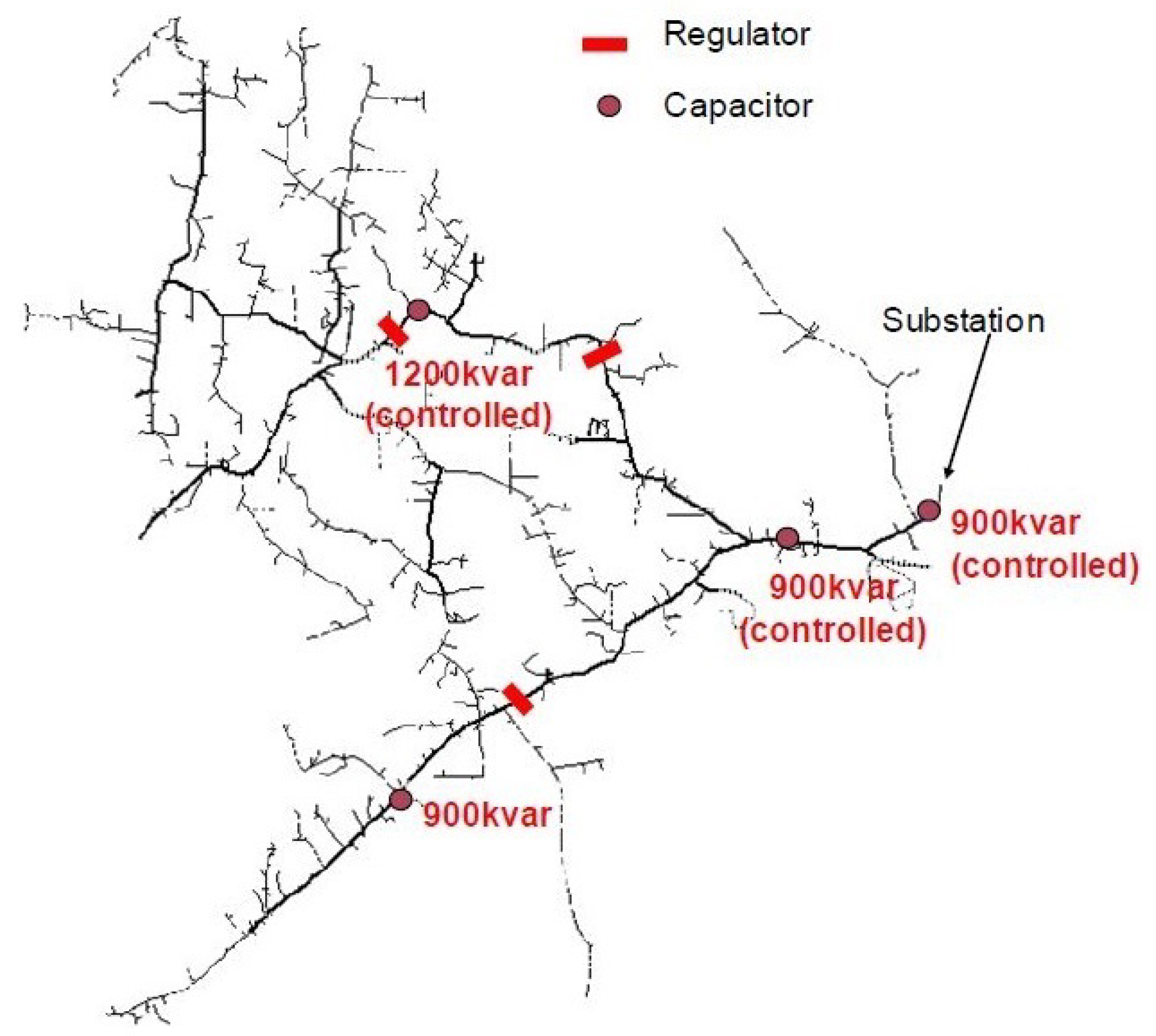
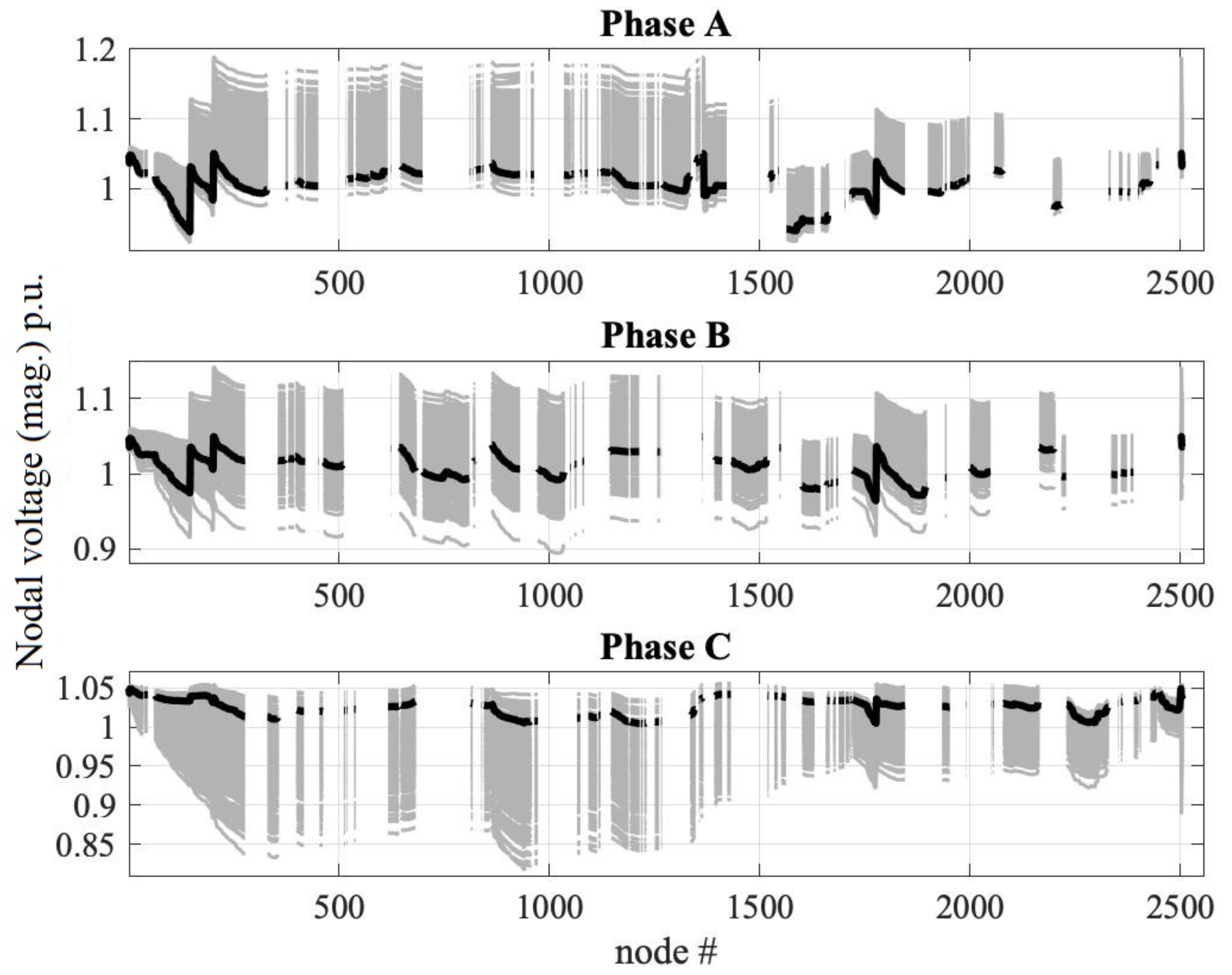
5. Application Examples
- Case 1: uncertain parameters, i.e., loads and PV generators.
- Case 2: uncertain parameters, i.e., loads and PV generators.
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| DG | Distributed Generator |
| PDN | Power Distribution Network |
| UQ | Uncertainty Quantification |
| MC | Monte Carlo |
| Probability Density Function | |
| PCE | Polynomial Chaos Expansion |
| ML | Machine Learning |
| SVM | Support Vector Machine |
| LS-SVM | Least-Square Support Vector Machine |
| PCA | Principal Component Analysis |
| IEEE | Institute of Electrical and Electronics Engineers |
| PV | Photovoltaic |
| MNA | Modified Nodal Analysis |
| RBF | Radial Basis Function |
| RMSE | Root mean squared error |
| p.u. | per unit |
References
- An, K.; Song, K.-B.; Hur, K. Incorporating charging/discharging strategy of electric vehicles into security-constrained optimal power flow to support high renewable penetration. Energies 2017, 10, 729. [Google Scholar] [CrossRef]
- Kongjeen, Y.; Krischonme, B. Modeling of electric vehicle loads for power flow analysis based on PSAT. In Proceedings of the 13th International Conference on Electrical Engineering/Electronics, Computer, Telecommunications and Information Technology (ECTI-CON), Chiang Mai, Thailand, 28 June–1 July 2016; pp. 1–6. [Google Scholar]
- Leou, R.-C.; Su, C.-L.; Lu, C.-N. Stochastic analyses of electric vehicle charging impacts on distribution network. IEEE Trans. Power Syst. 2014, 29, 1055–1063. [Google Scholar] [CrossRef]
- Samadi, P.; Mohsenian-Rad, H.; Wong, V.W.S.; Schober, R. Tackling the load uncertainty challenges for energy consumption scheduling in smart grid. IEEE Trans. Smart Grid 2013, 4, 1007–1016. [Google Scholar] [CrossRef]
- Meliopoulos, A.P.S.; Cokkinides, G.J.; Chao, X.Y. A new probabilistic power flow analysis method. IEEE Trans. Power Syst. 1990, 5, 182–190. [Google Scholar] [CrossRef]
- Li, X.; Li, Y.; Zhang, S. Analysis of probabilistic optimal power flow taking account of the variation of load power. IEEE Trans. Power Syst. 2008, 23, 992–999. [Google Scholar]
- Li, G.; Zhang, X. Modeling of plug-in hybrid electric vehicle charging demand in probabilistic power flow calculations. IEEE Trans. Smart Grid 2012, 3, 492–499. [Google Scholar] [CrossRef]
- El-Khattam, W.; Hegazy, Y.G.; Salama, M.M.A. Investigating distributed generation systems performance using Monte Carlo simulation. IEEE Trans. Power Syst. 2006, 21, 524–532. [Google Scholar] [CrossRef]
- Zhang, H.; Li, P. Probabilistic analysis for optimal power flow under uncertainty. IET Gener. Transm. Distrib. 2010, 4, 553–561. [Google Scholar] [CrossRef]
- Hajian, M.; Rosehart, W.D.; Zareipour, H. Probabilistic power flow by Monte Carlo simulation with Latin supercube sampling. IEEE Trans. Power Syst. 2013, 28, 1550–1559. [Google Scholar] [CrossRef]
- Carpinelli, G.; Caramia, P.; Varilone, P. Multi-linear Monte Carlo simulation method for probabilistic load flow of distribution systems with wind and photovoltaic generation systems. Renew. Energy 2015, 76, 283–295. [Google Scholar] [CrossRef]
- Martinez-Velasco, J.A.; Guerra, G. Reliability analysis of distribution systems with photovoltaic generation using a power flow simulator and a parallel Monte Carlo approach. Energies 2016, 9, 537. [Google Scholar] [CrossRef]
- Abdelaziz, M. GPU-OpenCL accelerated probabilistic power flow analysis using Monte-Carlo simulation. Elect. Power Syst. Res. 2017, 147, 70–72. [Google Scholar] [CrossRef]
- Constante-Flores, G.E.; Illindala, M.S. Data-driven probabilistic power flow analysis for a distribution system with renewable energy sources using Monte Carlo simulation. IEEE Trans. Ind. Appl. 2019, 55, 147–181. [Google Scholar] [CrossRef]
- Trinchero, R.; Manfredi, P.; Ding, T.; Stievano, I.S. Combined parametric and worst-case circuit analysis via Taylor models. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 2016, 63, 1067–1078. [Google Scholar] [CrossRef]
- Ding, T.; Trinchero, R.; Manfredi, P.; Stievano, I.S.; Canavero, F.G. How affine arithmetic helps beat uncertainties in electrical systems. IEEE Circuits Syst. Mag. 2015, 15, 70–79. [Google Scholar] [CrossRef]
- Femia, N.; Spagnuolo, G. True worst-case circuit tolerance analysis using genetic algorithms and affine arithmetic. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 2000, 47, 1285–1296. [Google Scholar]
- Manfredi, P.; Vande Ginste, D.; Stievano, I.S.; De Zutter, D.; Canavero, F.G. Stochastic transmission line analysis via polynomial chaos methods: An overview. IEEE Electromagn. Compat. Mag. 2017, 6, 77–84. [Google Scholar] [CrossRef]
- Kaintura, A.; Dhaene, T.; Spina, D. Review of polynomial chaos-based methods for uncertainty quantification in modern integrated circuits. Electronics 2018, 7, 30. [Google Scholar] [CrossRef]
- Xiu, D.; Karniadakis, G.E. The Wiener-Askey polynomial chaos for stochastic differential equations. SIAM J. Sci. Comput. 2002, 24, 619–644. [Google Scholar] [CrossRef]
- Blatman, G.; Sudret, B. An adaptive algorithm to build up sparse polynomial chaos expansions for stochastic finite element analysis. Probab. Eng. Mech. 2010, 25, 183–197. [Google Scholar] [CrossRef]
- Blatman, G.; Sudret, B. Adaptive sparse polynomial chaos expansion based on least angle regression. J. Comput. Phys. 2011, 230, 2345–2367. [Google Scholar] [CrossRef]
- Zhang, Z.; Weng, T.; Daniel, L. Big-data tensor recovery for high-dimensional uncertainty quantification of process variations. IEEE Trans. Compon. Packag. Manuf. Technol. 2017, 7, 687–697. [Google Scholar] [CrossRef]
- Zhang, Z.; Nguyen, H.D.; Turitsyn, K.; Daniel, L. Probabilistic power flow computation via low-rank and sparse tensor recovery. arXiv 2015, arXiv:1508.02489. [Google Scholar]
- Larbi, M.; Stievano, I.S.; Canavero, F.G.; Besnier, P. Variability impact of many design parameters: The case of a realistic electronic link. IEEE Trans. Electromagn. Compat. 2018, 60, 34–41. [Google Scholar] [CrossRef]
- Santner, T.J.; Williams, B.J.; Notz, W.I. The Design and Analysis of Computer Experiments; Springer: New York, NY, USA, 2003. [Google Scholar]
- Haykin, S.S. Neural Networks and Learning Machines, 3rd ed.; Pearson Education: Upper Saddle River, NJ, USA, 2009. [Google Scholar]
- Torun, H.M.; Yu, H.; Dasari, N.; Chekuri, V.C.K.; Singh, A.; Kim, J.; Lim, S.K.; Mukhopadhyay, S.; Swaminathan, M. A spectral convolutional net for co-optimization of integrated voltage regulators and embedded inductors. In Proceedings of the 2019 IEEE/ACM International Conference on Computer-Aided Design (ICCAD), Westminster, CO, USA, 4–7 November 2019. [Google Scholar]
- Yu, H.; Michalka, T.; Larbi, M.; Swaminathan, M. Behavioral modeling of tunable I/O drivers with preemphasis including power supply noise. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2020, 28, 233–242. [Google Scholar] [CrossRef]
- Vapnik, V.N. The Nature of Statistical Learning Theory, 2nd ed.; Springer: New York, NY, USA, 2000. [Google Scholar]
- Vapnik, V.N. Statistical Learning Theory; Wiley: New York, NY, USA, 1998. [Google Scholar]
- Suykens, J.A.K.; von Gestel, T.; Brabanter, J.D.; Moor, B.D.; Vandewalle, J. Least Squares Support Vector Machines; World Scientific: River Edge, NJ, USA, 2002. [Google Scholar]
- Rasmussen, C.E.; Williams, C.K.I. Gaussian Processes for Machine Learning; MIT Press: Cambridge, MA, USA, 2006. [Google Scholar]
- Trinchero, R.; Manfredi, P.; Stievano, I.S.; Canavero, F.G. Machine learning for the performance assessment of high-speed links. IEEE Trans. Electromagn.Compat. 2018, 60, 1627–1634. [Google Scholar] [CrossRef]
- Trinchero, R.; Dolatsara, M.A.; Roy, K.; Swaminathan, M.; Canavero, F.G. Design of high-speed links via a machine learning surrogate model for the inverse problem. In Proceedings of the 2019 Electrical Design of Advanced Packaging and Systems (EDAPS), Kaohsiung, Taiwan, 16–18 December 2019. [Google Scholar]
- Trinchero, R.; Canavero, F.G. Combining LS-SVM and GP regression for the uncertainty quantification of the EMI of power converters affected by several uncertain parameters. IEEE Trans. Electromagn. Compat. 2020. [Google Scholar] [CrossRef]
- Trinchero, R.; Larbi, M.; Torun, H.M.; Canavero, F.G.; Swaminathan, M. Machine learning and uncertainty quantification for surrogate models of integrated devices with a large number of parameters. IEEE Access 2018, 7, 4056–4066. [Google Scholar] [CrossRef]
- Gruosso, G.; Storti Gajani, G.; Zhang, Z.; Daniel, L.; Maffezzoni, P. Uncertainty-aware computational tools for power distribution networks including electrical vehicle charging and load profiles. IEEE Access 2019, 7, 9357–9367. [Google Scholar] [CrossRef]
- Manfredi, P.; Trinchero, R. A data compression strategy for the efficient uncertainty quantification of time-domain circuit responses. IEEE Access 2020, 8, 92019–92027. [Google Scholar] [CrossRef]
- Arritt, R.F.; Dugan, R.C. The IEEE 8500-node test feeder. In Proceedings of the 2010 IEEE PES T&D, New Orleans, LA, USA, 19–22 April 2010. [Google Scholar]
- Memon, Z.A.; Trinchero, R.; Xie, Y.; Canavero, F.G.; Stievano, I.S. An iterative scheme for the power-flow analysis of distribution networks based on decoupled circuit equivalents in the phasor domain. Energies 2020, 13, 386. [Google Scholar] [CrossRef]
- Ho, C.W.; Ruehli, A.; Brennan, P.A. The modified nodal approach to network analysis. IEEE Trans. Circuits Syst. 1975, 22, 504–509. [Google Scholar]
- White, J.K.; Sangiovanni-Vincentelli, A. Relaxation Techniques for the Simulation of VLSI Circuits. In The Kluwer International Series in Engineering and Computer Science, 1st ed.; Springer: New York, NY, USA, 1987; Volume 20. [Google Scholar]
- LS-SVMlab, Version 1.8; Department of Electrical Engineering (ESAT), Katholieke Universiteit Leuven: Leuven, Belgium, 2011; Available online: http://www.esat.kuleuven.be/sista/lssvmlab/ (accessed on 3 February 2020).
- Marelli, S.; Sudret, B. UQLab: A framework for uncertainty quantification in MATLAB. In Proceedings of the 2nd International Conference on Vulnerability Risk Analysis and Management, Liverpool, UK, 13–16 July 2014; 2014; pp. 2554–2563. [Google Scholar]
- Yaghoubi, V.; Marelli, S.; Sudret, B.; Abrahamsson, T. Sparse polynomial chaos expansions of frequency response functions using stochastic frequency transformation. Probab. Eng. Mech. 2017, 48, 39–58. [Google Scholar] [CrossRef]
- Karaki, S.H.; Chedid, R.B.; Ramadan, R. Probabilistic performance assessment of autonomous solar-wind energy conversion systems. IEEE Trans. Energy Convers. 1999, 14, 766–772. [Google Scholar] [CrossRef]
- Sheng, H.; Wang, X. Probabilistic power flow calculation using non-intrusive low-rank approximation method. IEEE Trans. Power Syst. 2019, 34, 3014–3025. [Google Scholar] [CrossRef]
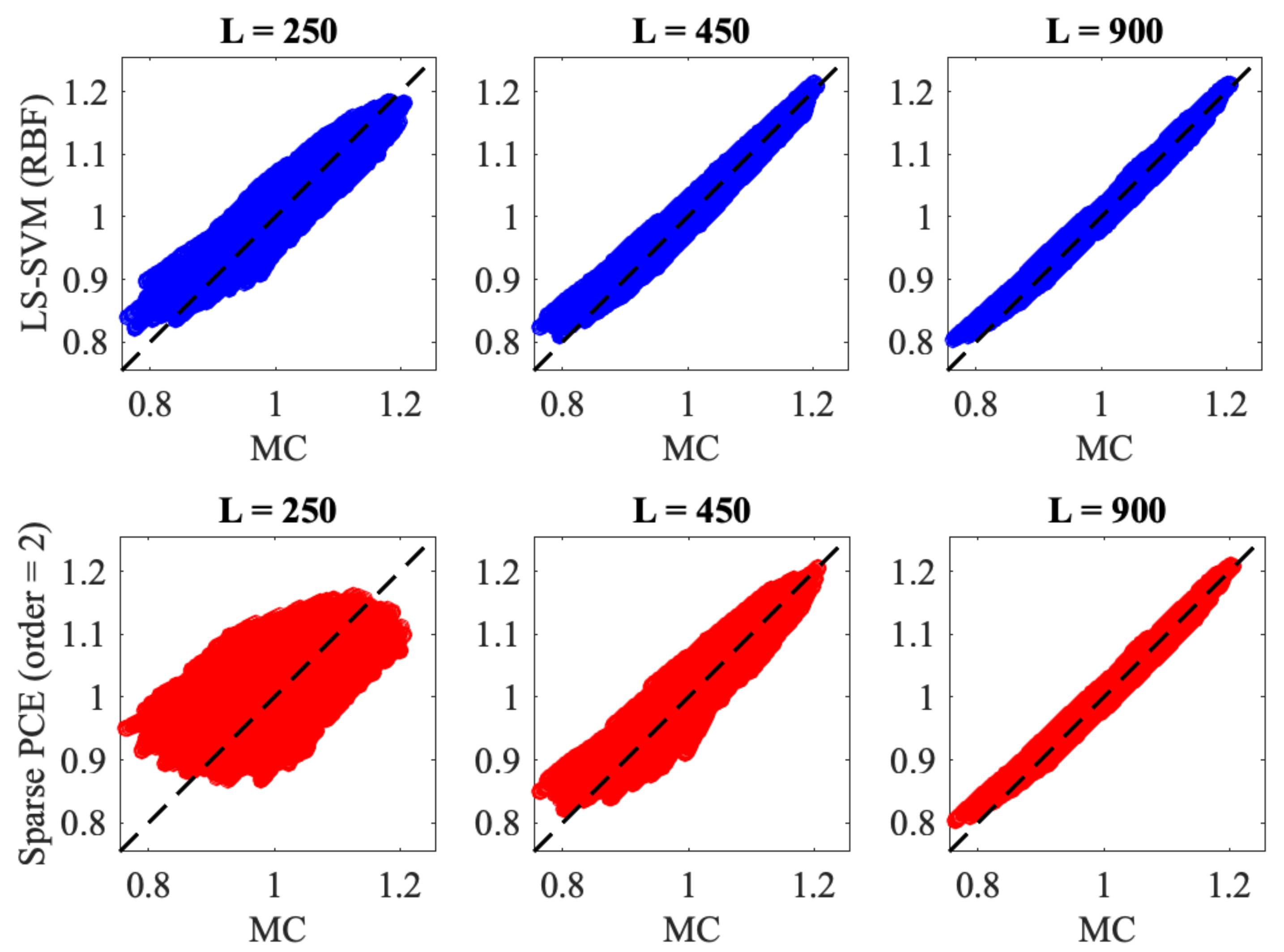



| (cost = 28.7 min) | (cost = 51.6 min) | (cost = 1.7 h) | |||||||
| Method | RMSE | RMSE | RMSE | ||||||
| MC | – | – | 19.1 h | – | – | 19.1 h | – | – | 19.1 h |
| LS-SVM (RBF) | 0.0127 | 18.8 s | 3.3 s | 0.0054 | 48.1 s | 5.1 s | 0.0028 | 3.6 min | 8.9 s |
| Sparse PCE | 0.0265 | 5.6 min | 1.6 min | 0.0124 | 8.9 min | 1.6 min | 0.0031 | 23.8 min | 1.7 min |
| (cost = 51.6 min) | (cost = 1.7 h) | (cost = 3.4 h) | |||||||
| Method | RMSE | RMSE | RMSE | ||||||
| MC | – | – | 19.1 h | – | – | 19.1 h | – | – | 19.1 h |
| LS-SVM (RBF) | 0.0166 | 55 s | 7.8 s | 0.0077 | 4 min | 12.8 s | 0.00401 | 22.7 min | 22.7 s |
| Sparse PCE | 0.0313 | 44.1 min | 3.4 min | 0.0294 | 1.7 h | 3.5 min | 0.00445 | 5.9 h | 3.8 min |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Memon, Z.A.; Trinchero, R.; Manfredi, P.; Canavero, F.; Stievano, I.S. Compressed Machine Learning Models for the Uncertainty Quantification of Power Distribution Networks. Energies 2020, 13, 4881. https://doi.org/10.3390/en13184881
Memon ZA, Trinchero R, Manfredi P, Canavero F, Stievano IS. Compressed Machine Learning Models for the Uncertainty Quantification of Power Distribution Networks. Energies. 2020; 13(18):4881. https://doi.org/10.3390/en13184881
Chicago/Turabian StyleMemon, Zain Anwer, Riccardo Trinchero, Paolo Manfredi, Flavio Canavero, and Igor S. Stievano. 2020. "Compressed Machine Learning Models for the Uncertainty Quantification of Power Distribution Networks" Energies 13, no. 18: 4881. https://doi.org/10.3390/en13184881
APA StyleMemon, Z. A., Trinchero, R., Manfredi, P., Canavero, F., & Stievano, I. S. (2020). Compressed Machine Learning Models for the Uncertainty Quantification of Power Distribution Networks. Energies, 13(18), 4881. https://doi.org/10.3390/en13184881