Abstract
Nowadays, due to the decreasing use of traditional generators in favor of renewable energy sources, power grids are facing a reduction of system inertia and primary frequency regulation capability. Such an issue is exacerbated by the continuously increasing number of electric vehicles (EVs), which results in enforcing novel approaches in the grid operations management. However, from being an issue, the increase of EVs may turn to be a solution to several power system challenges. In this context, a crucial role is played by the so-called vehicle-to-grid (V2G) mode of operation, which has the potential to provide ancillary services to the power grid, such as peak clipping, load shifting, and frequency regulation. More in detail, EVs have recently started to be effectively used for one of the most traditional frequency regulation approaches: the so-called frequency droop control (FDC). This is a primary frequency regulation, currently obtained by adjusting the active power of generators in the main grid. Because to the decommissioning of traditional power plants, EVs are thus recognized as particularly valuable solutions since they can respond to frequency deviation signals by charging or discharging their batteries. Against this background, we address frequency regulation of a power grid model including loads, traditional generators, and several EVs. The latter independently participate in the grid optimization process providing the grid with ancillary services, namely the FDC. We propose two novel control strategies for the optimal control of the batteries of EVs during the frequency regulation service. On the one hand, the control strategies ensure re-balancing the power and stabilizing the frequency of the main grid. On the other hand, the approaches are able to satisfy different types of needs of EVs during the charging process. Differently from the related literature, where the EVs perspective is generally oriented to achieve the optimal charge level, the proposed approaches aim at minimizing the degradation of battery devices. Finally, the proposed strategies are compared with other state-of-the-art V2G control approaches. The results of numerical experiments using a realistic power grid model show the effectiveness of the proposed strategies under the actual operating conditions.
1. Introduction
Nowadays, power systems around the world rely on fossil fuel-based energy generation systems, which have caused severe environmental problems. In this context, renewable energy sources (RESs) are progressively driving the transition to the production of low carbon energy [1]. At the same time, the connection to main grid of large-scale wind power systems and distributed photovoltaic (PV) panels in place of traditional synchronous generators (SGs), arise major frequency regulation problems to the power systems [2,3]. Indeed, expensive ancillary plants must operate in order to satisfy the changing power demand, with a significant environmental impact.
Ensuring the stability of the power plant frequency is a crucial problem and it is strictly associated to the balancing of power generation and demand. Stability is ensured by several frequency regulation actions, divided in primary, secondary, and tertiary. Currently, the inertia of SGs is adopted in primary frequency regulation (PFR), whose purpose is to compensate the demand and the supply of electricity in seconds. Secondary frequency regulation (SFR) is usually performed in a centralized manner; namely, a central unit restores the system nominal frequency by changing the generators’ output within 10–15 minutes. Tertiary frequency regulation (TFR) consists of an economic dispatching of energy aimed at adapting the outputs of the generators to minimize operating costs [4,5]. Nevertheless, the increased penetration of RESs leads to a deterioration in the power system inertia [6]. Moreover, the variations caused by these sources increase the frequency deviations. For instance, Italy’s total energy demand was 191.73 TWh from January 2019 to December 2019. However, over such a period, forecasts overestimated and underestimated the real demand for a cumulative amount of 3.95 TWh and 0.85 TWh, respectively [7]. In particular, in Figure 1a, we show the discrepancy between the forecasts and the real demand on a specific day, while in Figure 1b we show the hourly gap during the whole year.
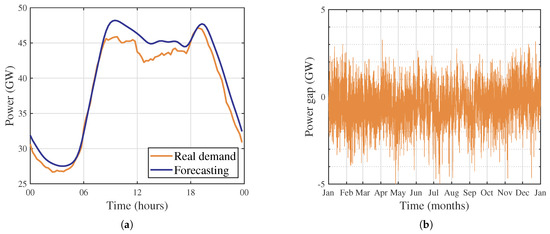
Figure 1.
Discrepancy between forecasts and real demand in Italy: (a) hourly profile of 1 March 2019; (b) hourly profile from January 1st 2019 to December 31st 2019. Data from Italian transmission system operator (Terna) [7].
Therefore, to support the power grid operations, the installation of energy storage systems (ESSs) is globally becoming even more frequent [8]. In particular, battery energy storage systems (BESSs) are effectively used for frequency regulation and voltage support activities [9]. Moreover, other innovative applications, such as load shifting, peak shaving, and renewable capacity firming, are at an early adoption stage. In this context, electric vehicles (EVs) are considered as key elements in supporting the grid operations [10]. Due to greenhouse gas emissions reduction, EVs have been preliminarily promoted as an essential technology for sustainable urban mobility and logistics [11,12]. Several research studies are focused on the so-called concept of vehicle-to-grid (V2G), where electric vehicle batteries (EVBs) are employed as valuable resources for the power grid, i.e., EVs are connected into power systems when not in use. As a result, together to the progress of Information and Communication Technology [13,14], V2G is enabling a highly distributed, fast-acting means of control for power systems [10].
It has to be highlighted that the majority of vehicles are mostly parked during their usage time, i.e., 95% on average [15], thus their batteries could be used as additional power storage systems to be connected to the main grid that maximize the advantages both for grid operator and EVs’ owners. On the one hand, for power system operators, it is possible to ensure higher supply reliability and electricity quality. On the other hand, the possible gains deriving from the retail of the accumulated electricity or the ancillary services, such as PFR, may reduce the effective life-cycle costs of EVs [16]. Utility companies are increasingly considering their customers as a promising solution to enable the system to be more responsive to intermittent renewables, thanks to their storage and eventually generation capability.
There is a considerable amount of literature on the use of ESSs to guarantee ancillary services to the grid [17]. For instance, in [18], the authors propose a model able to improve the grid voltage and frequency responses employing ESSs. Following this wave, in recent years, a growing body of literature has examined the concept of V2G focusing on the application of EVs for the load frequency regulation [19,20,21]. Several works concentrate on the benefits that EVs’ owners and power system operators can achieve by means of V2G approaches [22,23]. For instance, the authors of [24] propose an optimal dispatching strategy for a V2G aggregator, which aims at meeting the driving demand of EVs’ owners while maximizing the economic benefits of the aggregator due to the participation of EV’s to supplementary frequency regulation. Most of the existing works rely on centralized control approaches [17,25]; nevertheless, these methods are particularly valuable for the SFR [26].
Among the frequency regulation actions, the PFR is the most interesting for EVs. In effect, the frequency signal is accessible at any connection point available for the EVs. For instance, the authors of [27] present a decentralized V2G control scheme that allows the participation of EVs in PFR by taking into account the charging demands from EVs’ owners. In addition, many decentralized or distributed approaches have been proposed for the PFR when considering the increasing presence of intermittent wind power generation [28,29]. For instance, the authors of [23] present a method for PFR that consists in the optimal sizing of an ESS that is based on a lead-acid battery. Differently in [30], the PFR is guaranteed by following a standard droop characteristic, aiming at reestablishing the State of charge (SoC) of the system as soon as the grid frequency is in acceptable boundaries. In [31], the authors present an optimal scheduling algorithm that aims at determining the bidding capacity in each operational period so as to obtain the maximum advantage while guaranteeing a stable SoC interval. A control for the scheduled charging power in V2G is proposed in [32] in order to satisfy the charging demand and based on historic frequency deviation. In [33], the authors analyze the stability of an IEEE 39 bus system with 30% V2G penetration after critical contingencies. The authors compare different strategies that aim at guaranteeing ancillary services through EVs; moreover, in [34], the authors propose an optimal strategy for the charging and discharging of EVs so as to increase the frequency stability of a microgrid.
Furthermore, various studies focus on non-conventional techniques. For instance, in [35], a new modified general type-2 fuzzy proportional integral controller was proposed to minimize the system’s frequency deviations against load disturbances. In [36], a novel fuzzy logic controller based on genetic algorithms was defined for the control of the frequency, providing improved performance with respect to traditional and further more recent control methods.
The previous discussion of the literature review shows that, through participation in the PFR service, the EVs perspective is generally oriented in order to achieve the optimal charge level. To the best of the authors’ knowledge, no studies address frequency control strategies that are able to satisfy different types of needs of EVs during the charging process. Few works consider the effects of degradation in the battery, particularly on EVBs [37,38]. For instance, in [39], the authors present a degradation model for ESSs, which is able to assess the PFR impact during a period of 1.5 years. The lifetime of an ESS, which provides PFR, is estimated in [40]. In this work, the impact of different strategies on the lifetime of the batteries is evaluated and discussed. Lastly, in [41], a feasibility study of V2G frequency regulation under an economic perspective is presented, which takes into account the battery wear. However, all of the cited works [37,38,39,40,41] are mainly feasibility and assessment studies that provide an estimation of the impacts of the frequency regulation strategies on the battery lifetime. As a result, there is a lack of studies on EVs’ control approaches focused on battery degradation control instead of frequency control. To fill this gap, in this paper we firstly propose a battery degradation model that discerns from different depths of discharge cycles. Subsequently, we propose two novel control strategies for the optimal control of the batteries of EVs during the frequency regulation service. On the one hand, the proposed control strategies ensure to re-balance the power and stabilize the frequency of the main grid. On the other hand, the proposed approaches are able to satisfy a graceful degradation of the EVBs during the charging process.
Summing up, the contributions of this work can be thus summarized, as follows.
- We propose two novel frequency control strategies that aim at minimizing the EVs battery degradation. Differently from the existing contributions, which only address the need for frequency regulation service, our approach proposes a battery degradation model while ensuring the stabilization of grid frequency.
- We propose a profitability analysis to correlate the profit obtained by the EV’s user in participating in the frequency regulation service and the cost incurred by the battery degradation. Hence, we compare the proposed frequency control strategies with other related techniques in terms of energy that is exchanged with the main grid and degradation of the battery. The results obtained through numerical experiments based on a realistic power system model show the better performance of the proposed mechanisms under the actual operating conditions with respect to the reference strategies.
The remainder of this paper is organized, as follows. Section 2 recalls the basic concepts related to frequency regulation in power grids. Section 3 describes the distribution network architecture and the battery model of EVs under study. Section 4 introduces the novel control algorithms in the V2G context. Section 5 provides the description of the simulated control architecture and the experimental results on a realistic case study. Finally, Section 6 concludes this paper.
2. Preliminaries on Frequency Regulation
In power networks, the load frequency must be maintained at the nominal value even though demand or supply vary. In most cases, power grid regulations require that all of the power stations with a capacity over a certain threshold must keep a sufficient damping capability to increase their output in case of a reduction of the system frequency. In detail, each generating unit must provide additional active power (up to its nominal capacity) for under-frequency events and decrease its active power output (droop-type) for over-frequency events.
In the absence of any contingencies, the frequency of the grid must be kept within a non-critical deadband at any operating point. However, the non-critical deadband can vary among different countries due to the different power quality regulations.
Frequency control systems are mostly classified into three categories, namely the PFR, SFR, and TFR. Figure 2 shows the sequential application of these frequency control actions that are involved in the scenario of a sudden generation loss.
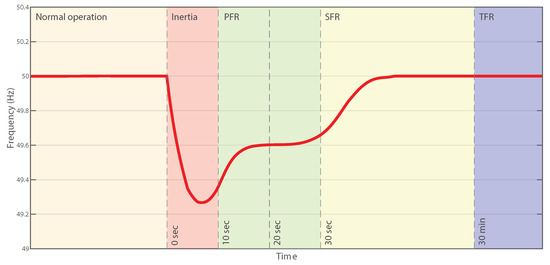
Figure 2.
The subsequent effects of primary, secondary, and tertiary frequency regulation after an unexpected loss of generation.
The PFR is usually called droop control. This is a completely distributed regulation system and operates on a timescale of a few seconds. The PFR can only stabilize the frequency; however, it is not able to reestablish the frequency to the nominal value. Conversely, the SFR operates on a larger timescale up to minutes and adjusts the generators governors’ setpoints in a control area in a centralized way to bring the frequency of the grid back to the nominal value while restoring the inter-area power flows to their prefixed values. Lastly, the TFR, usually named economic dispatch or optimal power flow works on a timescale of minutes up to hours and regulates the grid by modifying the output levels of all the power stations.
When an event that modifies the frequency occurs, the inertia of rotating masses of synchronous generators responds immediately to the change of frequency: in fact, the power imbalance is compensated by the kinetic energy stored in the rotating mass of synchronous machines in 0–10 s. PFC comes into operation at this step; in detail, the controllers of generators are activated to stabilize frequency to a new steady-state point. Indeed, inertia is essential for the power system operations: in fact, with different inertia value, the variation of frequency may have a different rate. Therefore, the PFC control system has a different impact when it operates to stabilize the frequency droop.
When frequency diverges from its nominal value, the kinetic energy stored in the rotating masses of generators (e.g., flywheels) is released. Let us define the rotational energy of the g-th generator in the grid as:
where is the moment of inertia of the SG and its rotating frequency. Moreover, let us define the inertia constant (i.e., the period in when the SG can provide its nominal power releasing barely kinetic energy) of the g-th SG as:
where is the rated power of the g-th SG. Moreover, it is useful to define the well-known swing equation [42], which describes the change in the rotational frequency of SG induced by a power variation. By disregarding the power losses and aggregating several SGs, we can write the so called swing equation of a power grid composed of n generators and d loads as:
where is the reference frequency, the power supplied by the generators, the total load, f is frequency of the center of inertia, H the system inertia constant, the total nominal power of the generators, D the inertia of the load, and:
However, the swing equation is usually linearized around the reference frequency due to the low load-frequency disturbances. By denoting the variation of frequency, of power supplied by generators, and of total load, respectively, as , , and , we thus get:
For instance, after an unexpected failure in the generation side, in the transient stage, the power is taken from the system inertia, which makes the frequency to decline at the rate of change of frequency. The latter is inversely proportional to the system inertia. The PFR control restores the power equilibrium a few seconds after the power imbalance occurs. More in detail, at a steady-state, the activation of their primary reserve is made by a specific proportional speed-droop law:
where is the change in the power output related to the g-th SG until the primary reserve is completely used, is the rated power the g-th SG, and K is the permanent droop constant.
It is evident that the frequency rate of change is inversely related to the total inertia of the system; therefore, a weaker inertia value leads to a more inadequate frequency response capability. At present, synchronous generators inertia plays a key role in reducing the variations of frequency, responding immediately by releasing kinetic energy. Conversely, photovoltaic (PV) generators and wind turbines are coupled to the power grid through a power electronics interface. Thus, intrinsically, they cannot provide an inertia response.
Hence, with the grown diffusion of renewable generation in the grid, the overall system has a weaker inertial response capability than traditional grids. Therefore, traditional frequency regulation controller may not properly counterbalance the disturbance events. In this context, EVBs may deeply contribute to the PFR mitigating the impact of RESs.
3. EV Battery Model
Let us now model the EVs in the V2G mode of operation. We consider a group of EVs with cardinality N. From the perspective of the system dynamics, without lack of generalization, we model each corresponding EVB by a first-order discrete-time system. Hence, it is useful to define for each i-th EVB with : the charging and discharging inefficiencies and , the maximum capacity , and the maximum charging rate . The charge level of the EVB at the current slot equals the charge level at the the previous slot corrected by the energy storage profile. The latter is proportional to the charging and discharging inefficiency. The SoC dynamics for the i-th EVB is thus computed as:
where:
where and are the power upstream and downstream of the inverter, respectively. Moreover, we include a constraint on the maximum power as:
Understandably, the battery efficiency can vary during the charging and discharging phases; in fact, the inverter may have a different efficiency with different charge/discharge values. However, for the sake of simplicity, we assume that the efficiencies are constant.
All of the various battery technologies suffer from degradation in terms of capacity decrease and resistance increase. Even though the literature in this field is still insufficient, many influencing factors have been identified in battery degradation, which can be broadly classified into: calendar and operational aging degradation factors.
The first category refers to the natural degradation of the battery, whose most important factor is the temperature. In our work, we neglect these degradation effects, because they are not directly dependent on the control strategy.
The second category refers to the degradation effects caused by operational factors. The actual operation of a battery determines most of its degradation. Thus, it is crucial to define an accurate control strategy that takes this effect into account. In particular, the category of operational aging degradation factors includes: state of charge and depth of discharge (DoD). The DoD is the most important stress factor and the battery degradation is an highly nonlinear function of both SoC and DoD. In the related literature, the definitions of DoD are various and contradictory. Thus, in this paper, we define the DoD as the full cycle consisting of one equal discharging and charging process.
Because the EVs are mostly equipped with common Li-ion batteries, we further refer to the life cycle, which is defined as the maximum number of the charge-discharge cycles until the capacity of the battery falls under to a specific threshold. The life degradation is usually defined as a percentage reduction of the battery life cycle. Therefore, the economic loss due to the degradation in a time slot, under the operating conditions, is defined as follows:
where is the substitution cost of the battery and the degradation percentage of the battery.
In the literature, the maximum number of cycles is calculated by performing several tests with a specific battery model. The test is performed by discharging and charging the battery from the maximum capacity to a specific state of charge. We refer to this as a standard DoD cycle (e.g., a standard DoD of 0.3 refers to a cycle varying in a SoC interval from 100% to 70%). However, in a realistic application, the battery works slightly far from a standard DoD cycle. The model available in the literature fits the experimental data with exponential, quadratic, or logarithmic functions. Given the high nonlinear dynamics, most of theworks consider the degradation by a linear or a quadratic function of the charged or discharged power. Other works neglect the difference between a standard cycle and a normal one (e.g., a cycle between 100%–70% is assumed to be equal to a cycle between 50%–20%) [43]. A more accurate model is based on an exponential function that better fits the experimental data, for instance, employing the experimental model proposed in [44], we define the deterioration that the battery undergoes during the charge or discharge between two SoC values, as follows:
Figure 3 shows the behavior of the aforementioned relation, where a prominent difference between distinct DoD cycles is evident.
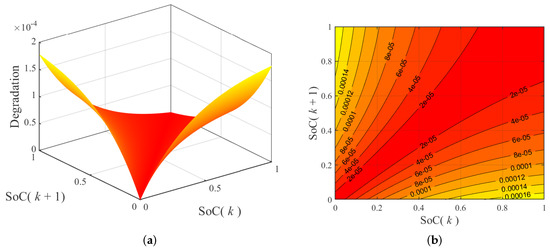
Figure 3.
Degradation of lithium-ion batteries as a function of subsequent SoC: surface plot (a) and contour plot (b).
4. V2G for Load Frequency Regulation
The V2G control approaches can reduce the frequency deviation from the nominal value by appropriately modulating the charge/discharge profile of the involved EVBs. Each battery, given the frequency deviation signal, modifies its profile proportionally. In this context, the V2G approach for frequency droop regulation equals the conventional SGs one. However, the EVs’ primary goal is to satisfy the owners’ needs, whilst frequency regulation is solely a secondary service that the EVs may provide. In fact, two important aspects must be analyzed in parallel: the battery charging process and the regulation service. For instance, when the load increases instantly or some generation faults occur (i.e., when the system frequency decreases) the battery management system may increase the power injection into the main grid or decrease the load adsorption of the EV required during the battery charging phase. Conversely, when the residual battery in the EV is not enough, the primary goal is to reach a charging level sufficient for the next trip. In general, the regulation service and the charging process influence each other: it is not straightforward to simultaneously deal with the two aspects. In the sequel, several control approaches for the management of EVBs during the PFR are presented: we preliminarily recall three main state-of-the-art control strategies namely the Elementary Control (ElCo) [45], the Balance Control (BaCo) [32], and the Smart Charging Control (SmChCo) [32]; subsequently, we propose two novel strategies aimed at reducing the impact of the PFR service on the batteries’ lifetime: the Bounded Control (BoCo) and the Low Degradation Control (LoDeCo).
4.1. Elementary Control (ElCo)
The most natural approach for the batteries that are involved in frequency regulation mechanisms is to replicate the control scheme of SGs. However, while SGs during the regulation process change their output, which must always be positive (i.e., the SGs can increase only or reduce their output), batteries may also invert the power flow. Therefore, let us define the ElCo as in [45] by the following relations:
where is the frequency deviation at time k, while and are the constant coefficients representing the EV charging/discharging droop. In general, we have that , i.e., we assume the same droop for the charging and discharging phases. Note that, given the battery power flow limits, the last two saturation conditions in (11) are added in the ElCo. In Figure 4a, we show the V2G power flow with respect to the system’s frequency. This strategy is particularly valuable from the grid stabilization point of view. In fact, by applying this approach, the batteries follow exactly the frequency deviation, without considering any degradation effects and impact on the SoC. Therefore, when the EV is plugged off, the SoC may have any value different from the initial value or the desired final SoC.
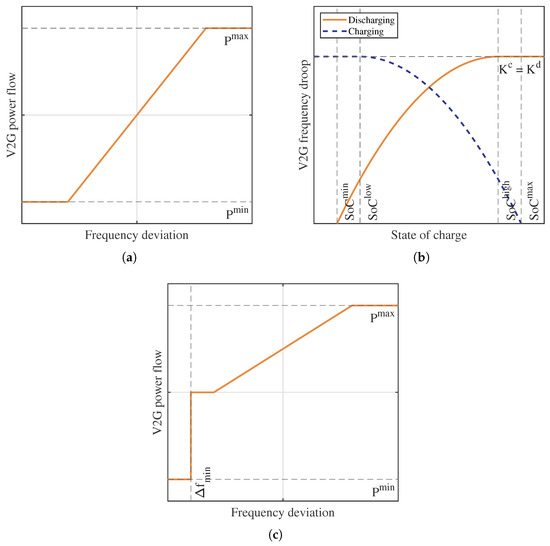
Figure 4.
(a) ElCo: V2G power flow control scheme. (b) BaCo: V2G frequency droop as a function of the SoC for the charging and discharging cases (the SoC is kept around 0.5 by using , , and [32]). (c) SmChCo: V2G power flow control scheme [32].
4.2. Balance Control (BaCo)
The authors in [32] propose the BaCo approach for batteries management in the PFR. This approach aims at keeping the SoC around a predetermined value. The power exchange by the i-th battery at the time k is:
where is the frequency deviation at the time k, while and are the coefficients representing the EV charging/discharging droop at the time k. In this strategy, the exchanged power is not only a function of the frequency deviation. In fact, and depend on the SoC of the battery as:
and
where the coefficients , , and define the values among which the SoC must be maintained, while is the maximum droop. By applying this approach, the battery always follows the frequency deviation; however, if this leads to a high distancing from the predetermined SoC value, the response of the battery is lower. The BaCo keeps the SoC around a predetermined value; however, it can increase or reduce the SoC value by a proper selection of the parameters in (13) and (14). For instance, in Figure 4b, we show the values of parameters that keep the SoC level around 50%. In particular, the figure shows how the charging and discharging droop range with respect to the EVB’s SoC.
4.3. Smart Charging Control (SmChCo)
The authors in [32] propose the SmChCo approach. The SmChCo is a fast-charging control technique that is able to charge the battery while participating in the PFR service. More in detail, the SmChCo is defined as:
The SmChCo is composed of two part: the frequency droop regulation and the battery charging. In fact, with half-maximum V2G frequency droop, the battery responds to the frequency deviation, while the other half is used to achieve the battery’s charging. If the frequency deviation goes down a given threshold , the maximum discharge policy is immediately applied to support the main grid frequency.
In Figure 4c, we show the V2G power flow with respect to the system’s frequency. From the figure, it is evident that this approach is different from the ElCo, because the battery is charging, even if the frequency is negative. This approach provides fast charging; however, it does not offer an efficient stabilization of the power grid.
4.4. Bounded Control (BoCo)
We propose a novel approach by modifying the ElCo strategy for the sake of reducing the batteries’ degradation. In particular, we introduce two thresholds on the SoC that stop the PFR services. Hence, let us define the BoCo, as follows:
where the charging and discharging droops and depend on the battery SoC as:
and
From Figure 5a, it is apparent that the droop shifts to zero both for the charging and discharging cases when the two SoC thresholds are exceeded.
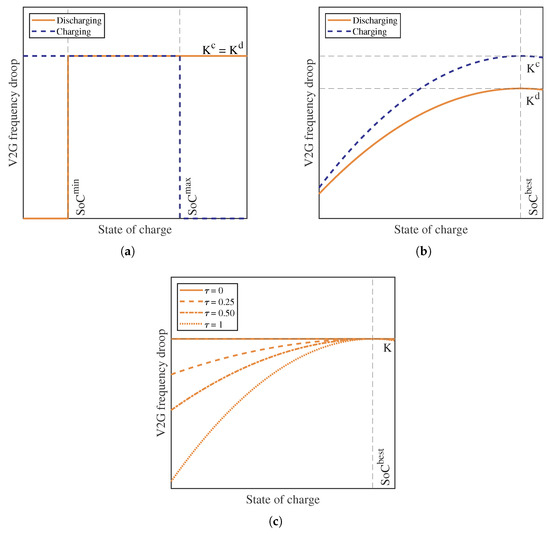
Figure 5.
V2G frequency droop as a function of the SoC for the charging and discharging cases for the BoCo approach (a). V2G frequency droop as a function of the SoC for the charging and discharging cases for the LoDeCo approach (b). V2G frequency droop as a function of the SoC for the LoDeCo for different values (c).
Similarly to the ElCo, the BoCo approach is particularly valuable from the grid stabilization point of view. In fact, by applying this approach, the batteries follow exactly the frequency deviation. However, differently from the ElCo, the batteries are forced to work at an operational point distant from the extreme SoC values that lead to higher degradation, with a beneficial effect for battery life.
4.5. Low Degradation Control (LoDeCo)
We now propose a novel control approach that can support the grid in the PFR while minimizing the degradation effects on the EVBs. The power that is exchanged by the i-th battery at the time k is:
where with this approach the charging/discharging droop and are set as:
and
is a characteristic parameter whose value is calculated from the battery degradation function, whilst is a coefficient indicating how much the approach is conservative. This approach aims at decreasing the droop gain when the battery SoC is low, as shown in Figure 5b; in fact, when the battery is poorly charged, employing the battery for a high DoD cycle will profoundly deteriorate its future performance. From the Figure, it is evident that this approach is completely different from the BaCo; when the SoC is low, the BaCo charges the battery at its maximum, causing a high degradation of the EVB. The coefficient ranges from 0 to 1. In fact, when equals to 0, the approach matches the ElCo providing no advantage in terms of degradation. Conversely, when equals to 1, the proposed approach provides higher protection against degradation. Figure 5c shows the impact of different values of . The choice of the value of both and has a strong impact on the control approach performance; in fact, a low value of or a not proper selection of may reduce the control performance. Therefore, these values must be selected according to the degradation function: in particular, from the previously presented nonlinear degradation function, considering and can be satisfactory.
5. Case Study
Different numerical experiments are conducted on a single area power grid composed by a SG, an aggregate load, and an intermittent RES, as in Figure 6. The SG is characterized by the following parameters: the governor time constant (Tg) is set to s, the turbine time constant (Tt) is set to s, the inertia (H) is 4 s, the governor speed regulation (R) is p.u., and the integral gain (Ki) is 4. The generator dead band is set to Hz. Moreover, we consider a not constant aggregate load (i.e., the power consumption varies with the frequency variation), in particular we employ a rate , i.e., the load varies by 0.9% with a variation of the frequency of 1%. The system is used to simulate the variation of the frequency that results from variable loads and RES: the variation is recreated through random time series.
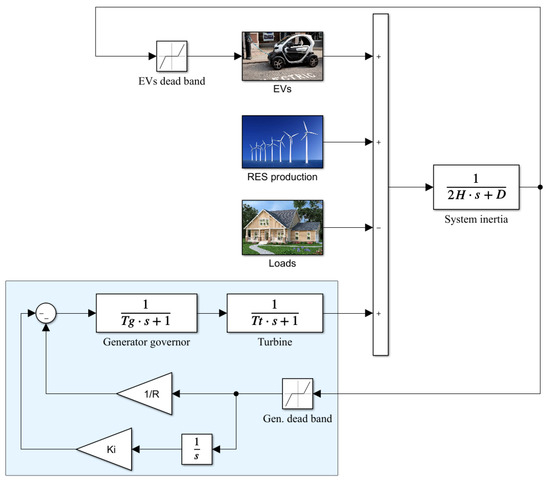
Figure 6.
Power system model scheme.
We employ a 50 kWh EVB, with charging and discharging inefficiencies equal to 0.95 and 1.05, respectively. The maximum charging rate () is set to 10 kW. The EVB dead band is set to Hz. The charging and discharging droop are set equal to the unitary value, i.e., for all of the strategies kW/Hz. The BoCo approach has and . The BaCo approach aims to maintain the SoC around 0.5 by setting , , and . Moreover, The SmChCo has a Hz. Lastly, we assume a and a for the LoDeCo strategy.
For the sake of analyzing the influence of the PFR service on the EVBs’ lifetime, a one-year simulation is considered. For each presented control strategy, the SoC profile is divided into cycles completed between two distinct values of SoC. As a first outcome, the number of cycles performed by the battery between two distinct values of SoC is presented in Figure 7 for all pf the proposed strategies. Figure 7 shows that, differently from the other approaches, the novel proposed strategy (i.e., the LoDeCo) has an operating area close to the maximum SoC. Furthermore, in Figure 8, we show the SoC profile for each control strategy. As expected, from Figure 8a–c we note that that the ElCo, BoCo, and BaCo strategies follow the frequency deviation without any control on the SoC. Moreover, from Figure 8d, the highly cyclic pattern of the SmChCo caused by its parameter selection is evident. Indeed, with the SmChCo, the batteries are always charged unless the frequency deviation reaches a minimum value. However, when a high concentration of RES is present in the main grid, a high frequency deviation occurs and therefore the parameter should be carefully chosen. In our simulations, we assume a Hz, which, also if it is small, is not sufficient to ensure the proper operation. Conversely, Figure 8e further confirms that the SoC profile settles on the maximum value.
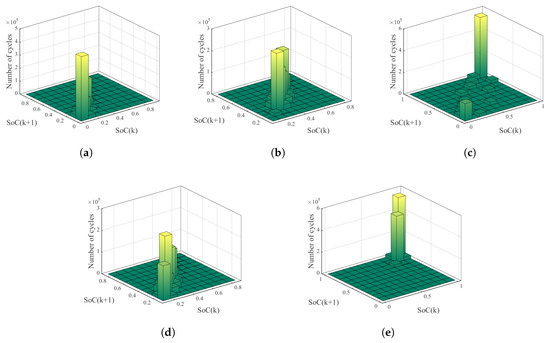
Figure 7.
Number of cycles of the battery with respect to the SoC profile for the five considered strategies: (a) ElCo; (b) BaCo; (c) SmChCo; (d) BoCo; and, (e) LoDeCo.
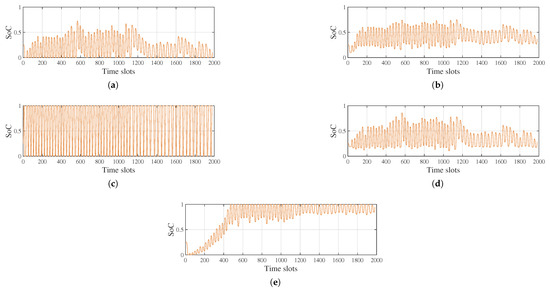
Figure 8.
Battery SoC profile for the five considered strategies: (a) ElCo; (b) BaCo; (c) SmChCo; (d) BoCo; (e) LoDeCo.
In addition, we compare the different strategies from the EVB degradation perspective. Indeed, the batteries are subject to different aging conditions based on the employed control strategy, resulting in different estimation of lifetime. By employing the degradation model described in Section 3, we first calculate the total degradation resulting from each strategy and the total exchanged energy. Table 1 shows the obtained results: it can be noticed that the SmChCo has the highest exchanged energy, imposing the most significant degradation to the battery. Conversely, the proposed LoDeCo ensures the lowest degradation while ensuring a quite high exchanged energy.

Table 1.
Degradation of the battery and energy exchanged with the power grid.
Moreover, we analyze the impact of the proposed control strategies on the system frequency. In particular, in Figure 9 the system frequency profile is shown for the different strategies and for the case when no batteries are deployed. It is evident that the profile related to the ElCo is the closest to the reference value of the system frequency, thus resulting in the best stabilizing effect. Conversely, because the SmChCo is not at all focused on frequency regulation, the corresponding profile is the farthest from the reference value, even with respect to the the case when no batteries are deployed. The remaining strategies (i.e., the BoCo, BaCo, and LoDeco) have an intermediate profile, resulting in a satisfatory grid stabilizing effect.
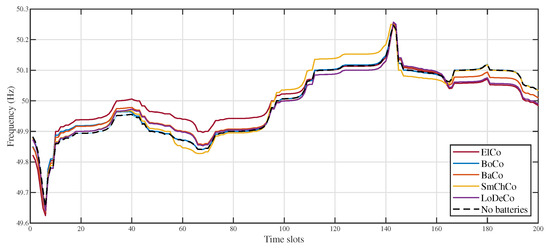
Figure 9.
Power grid frequency for the different considered control strategies: focus on the first 200 time slots.
Finally, we observe that the price paid for the frequency regulation may profoundly influence the results of the control strategy: the use of different price coefficients may lead to different findings. Therefore, let us assume a constant pricing, i.e., the price paid for the PFR service does not depend on the time or other parameters. With this assumption, we can easily correlate the price coefficient with the owners’ profit. By assuming a cost of 200 $/kWh for the battery and calculating the resulting degradation cost, we show, in Figure 10, the overall profit when the different strategies are applied. From the figure, it is evident that the LoDeCo is the first strategy to become profitable with a coefficient of 0.26 $/kWh; however, it becomes less valuable than the other strategies with a price coefficient of 1 $/kWh.
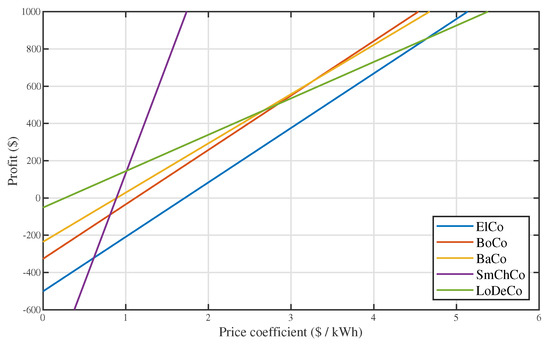
Figure 10.
Profitability analysis for the different considered control strategies.
6. Conclusions
In this work, we propose two novel control strategies for the optimal control of electric vehicle batteries (EVBs) during the primary frequency regulation (PFR) service. By optimally integrating electric vehicle batteries (EVBs) in an isolated power system, the approaches principally aim at minimizing the degradation of batteries while profitably participating in the PFR.
This work has a twofold contribution. From a theoretical perspective, it contributes to the literature on frequency droop control by EVBs, which lacks studies for identifying the optimal strategy satisfying the needs both from the regulation service and the battery lifetime. From a practical point of view, the control strategies provide both the power system operator and the electric vehicles’ owners with effective mechanisms for charging the batteries while stabilizing the grid frequency.
Numerical experiments using a realistic power system model, and including comparison with other state-of-the-art methodologies, show the effectiveness of the proposed strategies under the actual operating conditions. An additional merit of the developed approaches is its scalability to different grid size levels, since the computational complexity does not increase with the number of EVBs.
Nonetheless, this study is not without limitations, which still needs to be investigated in future works. In particular, the main limitation of the proposed strategies relies on the non-cooperative computation of the frequency control actions. The cooperation of EVBs could be encouraged to improve system-wide performance through the avoidance of individual EVBs’ uncoordinated behavior in order to improve the effectiveness of the vehicle-to-grid approach. Hence, the frequency control strategies may be preferably performed through a cooperative distributed framework. Therefore, our future work will mainly be devoted to extending the defined mechanisms in a cooperative distributed setting.
Author Contributions
All authors contributed equally to the manuscript: Conceptualization, P.S., R.C., G.C., and M.D.; methodology, P.S., R.C., G.C., and M.D.; software, P.S., R.C., G.C., and M.D.; validation, P.S., R.C., G.C., and M.D.; formal analysis, P.S., R.C., G.C., and M.D.; writing—original draft preparation, P.S., R.C., G.C., and M.D.; writing—review and editing, P.S., R.C., G.C., and M.D. All authors have read and agree to the published version of the manuscript.
Funding
This work received funding from the Italian University and Research Ministry under the National Research Program (project RAFAEL—contract No. ARS01_00305).
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| RES | Renewable energy source |
| EV | Electric vehicle |
| V2G | vehicle-to-grid |
| FDC | Frequency droop control |
| EVB | Electric-vehicle battery |
| ESS | Energy storage system |
| BESS | Battery energy storage system |
| SoC | State of charge |
| DoD | Depth of discharge |
| SG | Synchronous generator |
| PV | Photovoltaic |
| PFR | Primary frequency regulation |
| SFR | Secondary frequency regulation |
| TFR | Tertiary frequency regulation |
| ElCo | Elementary Control |
| BoCo | Bounded Control |
| BaCo | Balance Control |
| SmChCo | Smart Charging |
| LoDeCo | Low Degradation Control |
References
- Lawrenz, L.; Xiong, B.; Lorenz, L.; Krumm, A.; Hosenfeld, H.; Burandt, T.; Löffler, K.; Oei, P.Y.; Von Hirschhausen, C. Exploring energy pathways for the low-carbon transformation in India—A model-based analysis. Energies 2018, 11, 3001. [Google Scholar] [CrossRef]
- Oureilidis, K.; Malamaki, K.N.; Gallos, K.; Tsitsimelis, A.; Dikaiakos, C.; Gkavanoudis, S.; Cvetkovic, M.; Mauricio, J.M.; Maza Ortega, J.M.; Ramos, J.L.M. Ancillary Services Market Design in Distribution Networks: Review and Identification of Barriers. Energies 2020, 13, 917. [Google Scholar] [CrossRef]
- Eto, J.H.; Berkeley, L.; Undrill, J.; Mackin, P.; Daschmans, R.; Williams, B.; Haney, B.; Hunt, R.; Ellis, J.; Illian, H.; et al. Use of Frequency Response Metrics to Assess the Planning and Operating Requirements for Reliable Integration of Variable Renewable Generation; Lawrence Berkeley National Laboratory (LBNL): Berkeley, CA, USA, 2010.
- Peng, C.; Zou, J.; Lian, L. Dispatching strategies of electric vehicles participating in frequency regulation on power grid: A review. Renew. Sustain. Energy Rev. 2017, 68, 147–152. [Google Scholar] [CrossRef]
- Alsharafi, A.S.; Besheer, A.H.; Emara, H.M. Primary frequency response enhancement for future low inertia power systems using hybrid control technique. Energies 2018, 11, 699. [Google Scholar] [CrossRef]
- Adrees, A.; Papadopoulos, P.N.; Milanovic, J.V. A framework to assess the effect of reduction in inertia on system frequency response. In Proceedings of the 2016 IEEE Power and Energy Society General Meeting (PESGM), Boston, MA, USA, 17–21 July 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 1–5. [Google Scholar]
- Terna. 2020. Available online: https://www.terna.it/en (accessed on 16 July 2020).
- Lucchese, F.C.; Canha, L.N.; Brignol, W.S.; Hammerschmitt, B.K.; Da Silva, L.N.; Martins, C.C. Energy Storage Systems Role in Supporting Renewable Resources: Global Overview. In Proceedings of the 2019 54th International Universities Power Engineering Conference (UPEC), Bucharest, Romania, 3–6 September 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–6. [Google Scholar]
- Zeh, A.; Müller, M.; Naumann, M.; Hesse, H.C.; Jossen, A.; Witzmann, R. Fundamentals of using battery energy storage systems to provide primary control reserves in Germany. Batteries 2016, 2, 29. [Google Scholar] [CrossRef]
- Bellocchi, S.; Manno, M.; Noussan, M.; Vellini, M. Impact of grid-scale electricity storage and electric vehicles on renewable energy penetration: A case study for Italy. Energies 2019, 12, 1303. [Google Scholar] [CrossRef]
- Hosseini, S.M.; Carli, R.; Cavone, G.; Dotoli, M. Distributed control of electric vehicle fleets considering grid congestion and battery degradation. Internet Technol. Lett. 2020, 3, e161. [Google Scholar] [CrossRef]
- Boenzi, F.; Digiesi, S.; Facchini, F.; Mossa, G.; Mummolo, G. Sustainable warehouse logistics: A NIP model for non-road vehicles and storage configuration selection. In Proceedings of the XX Summer School Operational Excellence Experience “Francesco Turco”, Naples, Italy, 16–18 September 2015. [Google Scholar]
- Casalino, G.; Del Buono, N.; Mencar, C. Nonnegative matrix factorizations for intelligent data analysis. In Non-Negative Matrix Factorization Techniques; Springer: Berlin/Heidelberg, Germany, 2016; pp. 49–74. [Google Scholar]
- D’Amato, G.; Avitabile, G.; Coviello, G.; Talarico, C. DDS-PLL phase shifter architectures for phased arrays: Theory and techniques. IEEE Access 2019, 7, 19461–19470. [Google Scholar] [CrossRef]
- Kotb, A.O.; Shen, Y.C.; Zhu, X.; Huang, Y. iParker—A new smart car-parking system based on dynamic resource allocation and pricing. IEEE Trans. Intell. Transp. Syst. 2016, 17, 2637–2647. [Google Scholar] [CrossRef]
- Hosseini, S.S.; Badri, A.; Parvania, M. The plug-in electric vehicles for power system applications: The vehicle to grid (V2G) concept. In Proceedings of the 2012 IEEE International Energy Conference and Exhibition (ENERGYCON), Florence, Italy, 9–12 September 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 1101–1106. [Google Scholar]
- Galus, M.D.; Koch, S.; Andersson, G. Provision of load frequency control by PHEVs, controllable loads, and a cogeneration unit. IEEE Trans. Ind. Electron. 2011, 58, 4568–4582. [Google Scholar] [CrossRef]
- Datta, U.; Kalam, A.; Shi, J. Battery Energy Storage System for Aggregated Inertia-Droop Control and a Novel Frequency Dependent State-of-Charge Recovery. Energies 2020, 13, 2003. [Google Scholar] [CrossRef]
- Kempton, W.; Udo, V.; Huber, K.; Komara, K.; Letendre, S.; Baker, S.; Brunner, D.; Pearre, N. A test of vehicle-to-grid (V2G) for energy storage and frequency regulation in the PJM system. Results Ind. Univ. Res. Partnersh. 2008, 32. [Google Scholar]
- Jha, I.; Sen, S.; Tiwari, M.; Singh, M.K. Control strategy for Frequency Regulation using Battery Energy Storage with optimal utilization. In Proceedings of the 2014 IEEE 6th India International Conference on Power Electronics (IICPE), Kurukshetra, India, 8–10 December 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 1–4. [Google Scholar]
- Lopes, J.A.P.; Soares, F.J.; Almeida, P.M.R. Integration of electric vehicles in the electric power system. Proc. IEEE 2010, 99, 168–183. [Google Scholar] [CrossRef]
- Brooks, A.; Lu, E.; Reicher, D.; Spirakis, C.; Weihl, B. Demand dispatch. IEEE Power Energy Mag. 2010, 8, 20–29. [Google Scholar] [CrossRef]
- Oudalov, A.; Chartouni, D.; Ohler, C. Optimizing a battery energy storage system for primary frequency control. IEEE Trans. Power Syst. 2007, 22, 1259–1266. [Google Scholar] [CrossRef]
- Peng, C.; Zou, J.; Lian, L.; Li, L. An optimal dispatching strategy for V2G aggregator participating in supplementary frequency regulation considering EV driving demand and aggregator’s benefits. Appl. Energy 2017, 190, 591–599. [Google Scholar] [CrossRef]
- Pillai, J.R.; Bak-Jensen, B. Integration of vehicle-to-grid in the western Danish power system. IEEE Trans. Sustain. Energy 2011, 2, 12–19. [Google Scholar] [CrossRef]
- Masuta, T.; Yokoyama, A. Supplementary load frequency control by use of a number of both electric vehicles and heat pump water heaters. IEEE Trans. Smart Grid 2012, 3, 1253–1262. [Google Scholar] [CrossRef]
- Liu, H.; Hu, Z.; Song, Y.; Lin, J. Decentralized vehicle-to-grid control for primary frequency regulation considering charging demands. IEEE Trans. Power Syst. 2013, 28, 3480–3489. [Google Scholar] [CrossRef]
- Almeida, P.R.; Lopes, J.P.; Soares, F.; Seca, L. Electric vehicles participating in frequency control: Operating islanded systems with large penetration of renewable power sources. In Proceedings of the 2011 IEEE Trondheim PowerTech, Trondheim, Norway, 19–23 June 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 1–6. [Google Scholar]
- Yang, J.; Zeng, Z.; Tang, Y.; Yan, J.; He, H.; Wu, Y. Load frequency control in isolated micro-grids with electrical vehicles based on multivariable generalized predictive theory. Energies 2015, 8, 2145–2164. [Google Scholar] [CrossRef]
- Li, X.; Huang, Y.; Huang, J.; Tan, S.; Wang, M.; Xu, T.; Cheng, X. Modeling and control strategy of battery energy storage system for primary frequency regulation. In Proceedings of the 2014 International Conference on Power System Technology, Chengdu, China, 20–22 October 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 543–549. [Google Scholar]
- Yang, J.S.; Choi, J.Y.; An, G.H.; Choi, Y.J.; Kim, M.H.; Won, D.J. Optimal scheduling and real-time state-of-charge management of energy storage system for frequency regulation. Energies 2016, 9, 1010. [Google Scholar] [CrossRef]
- Ota, Y.; Taniguchi, H.; Nakajima, T.; Liyanage, K.M.; Baba, J.; Yokoyama, A. Autonomous distributed V2G (vehicle-to-grid) satisfying scheduled charging. IEEE Trans. Smart Grid 2011, 3, 559–564. [Google Scholar] [CrossRef]
- Hernández, J.C.; Sanchez-Sutil, F.; Vidal, P.; Rus-Casas, C. Primary frequency control and dynamic grid support for vehicle-to-grid in transmission systems. Int. J. Electr. Power Energy Syst. 2018, 100, 152–166. [Google Scholar] [CrossRef]
- Vahedipour-Dahraie, M.; Rashidizaheh-Kermani, H.; Najafi, H.R.; Anvari-Moghaddam, A.; Guerrero, J.M. Coordination of EVs participation for load frequency control in isolated microgrids. Appl. Sci. 2017, 7, 539. [Google Scholar] [CrossRef]
- Khooban, M.H.; Niknam, T.; Blaabjerg, F.; Dragičević, T. A new load frequency control strategy for micro-grids with considering electrical vehicles. Electr. Power Syst. Res. 2017, 143, 585–598. [Google Scholar] [CrossRef]
- Cam, E.; Gorel, G.; Mamur, H. Use of the genetic algorithm-based fuzzy logic controller for load-frequency control in a two area interconnected power system. Appl. Sci. 2017, 7, 308. [Google Scholar] [CrossRef]
- Tchagang, A.; Yoo, Y. V2B/V2G on Energy Cost and Battery Degradation under Different Driving Scenarios, Peak Shaving, and Frequency Regulations. World Electr. Veh. J. 2020, 11, 14. [Google Scholar] [CrossRef]
- Baure, G.; Dubarry, M. Durability and Reliability of EV Batteries under Electric Utility Grid Operations: Impact of Frequency Regulation Usage on Cell Degradation. Energies 2020, 13, 2494. [Google Scholar] [CrossRef]
- Świerczyński, M.; Stroe, D.I.; Lærke, R.; Stan, A.I.; Kjær, P.C.; Teodorescu, R.; Kær, S.K. Field experience from Li-ion BESS delivering primary frequency regulation in the Danish energy market. Ecs Trans. 2014, 61, 1. [Google Scholar] [CrossRef]
- Stroe, D.I.; Knap, V.; Swierczynski, M.; Stroe, A.I.; Teodorescu, R. Operation of a grid-connected lithium-ion battery energy storage system for primary frequency regulation: A battery lifetime perspective. IEEE Trans. Ind. Appl. 2016, 53, 430–438. [Google Scholar] [CrossRef]
- Han, S.; Han, S. Economic feasibility of V2G frequency regulation in consideration of battery wear. Energies 2013, 6, 748–765. [Google Scholar] [CrossRef]
- Kundur, P.; Balu, N.J.; Lauby, M.G. Power System Stability and Control; McGraw-Hill: New York, NY, USA, 1994; Volume 7. [Google Scholar]
- Maheshwari, A.; Paterakis, N.G.; Santarelli, M.; Gibescu, M. Optimizing the operation of energy storage using a non-linear lithium-ion battery degradation model. Appl. Energy 2020, 261, 114360. [Google Scholar] [CrossRef]
- Yan, G.; Liu, D.; Li, J.; Mu, G. A cost accounting method of the Li-ion battery energy storage system for frequency regulation considering the effect of life degradation. Prot. Control Mod. Power Syst. 2018, 3, 1–9. [Google Scholar] [CrossRef]
- Yan, G.; Zhu, X.; Li, J.; Mu, G.; Luo, W.; Yang, K. Control strategy design for hybrid energy storage system with intrinsic operation life measurement and calculation. Dianli Xitong Zidonghua Automation Electr. Power Syst. 2013, 37, 110–114. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).