Electro-Hydraulic Transient Regimes in Isolated Pumps Working as Turbines with Self-Excited Induction Generators
Abstract
1. Introduction
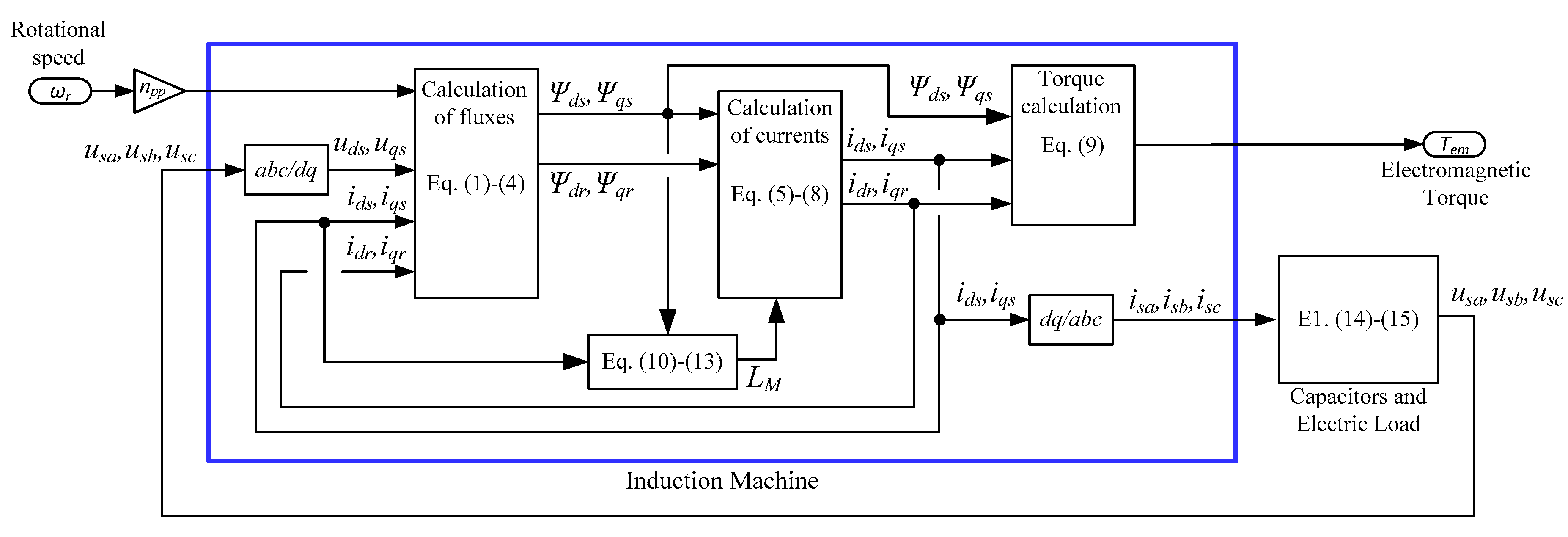
2. Self-Excited Induction Generator Model
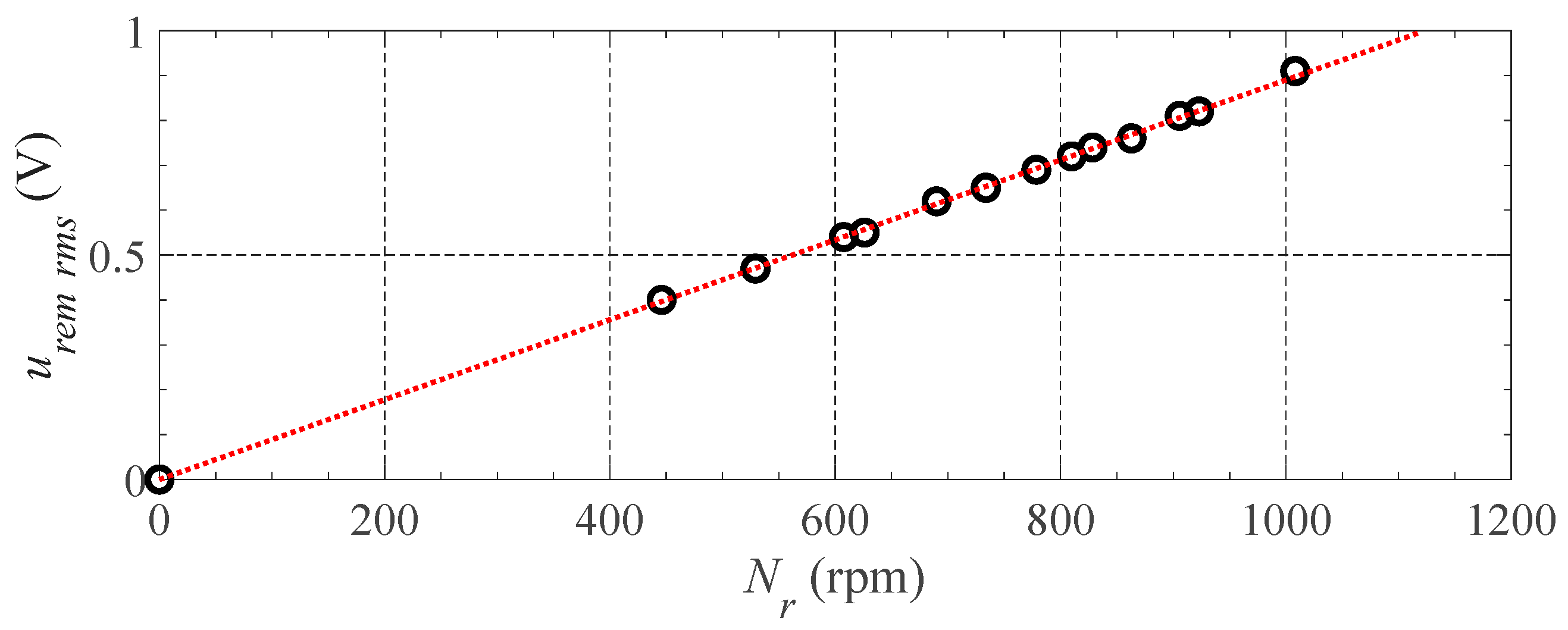
2.1. Magnetizing Inductance
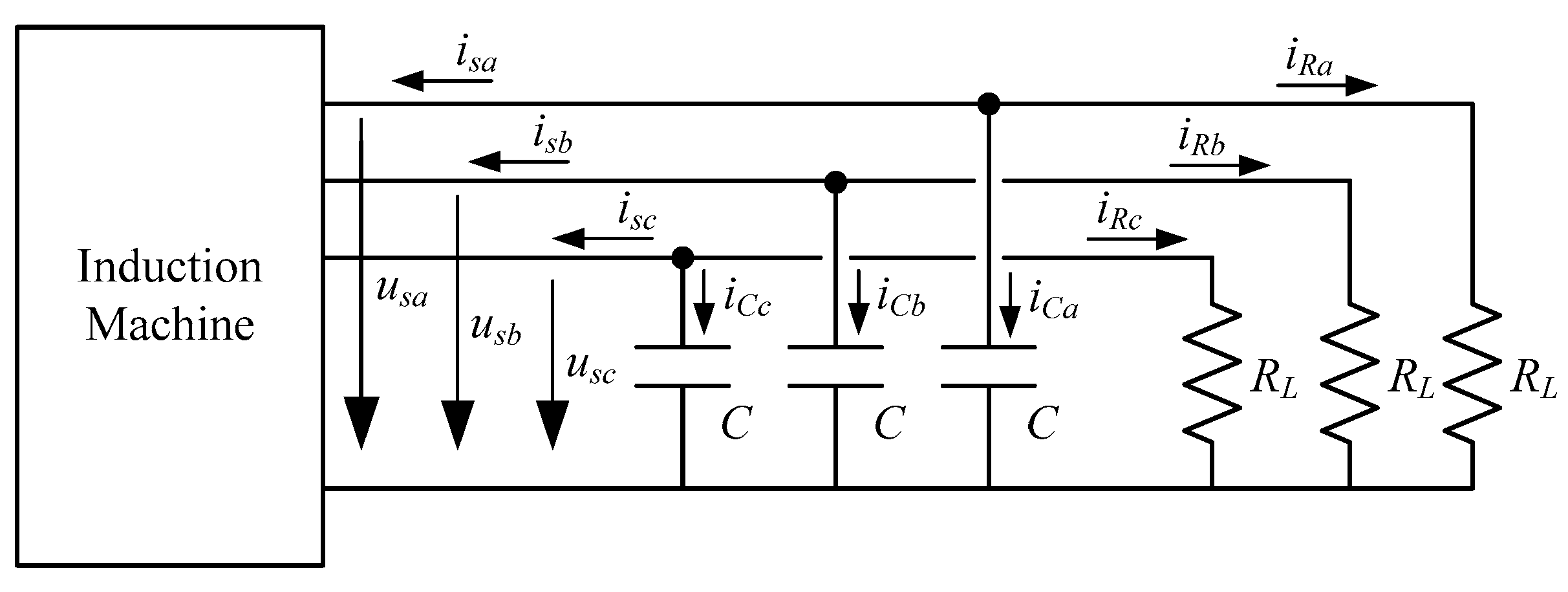
2.2. Capacitor and Electrical Load Models
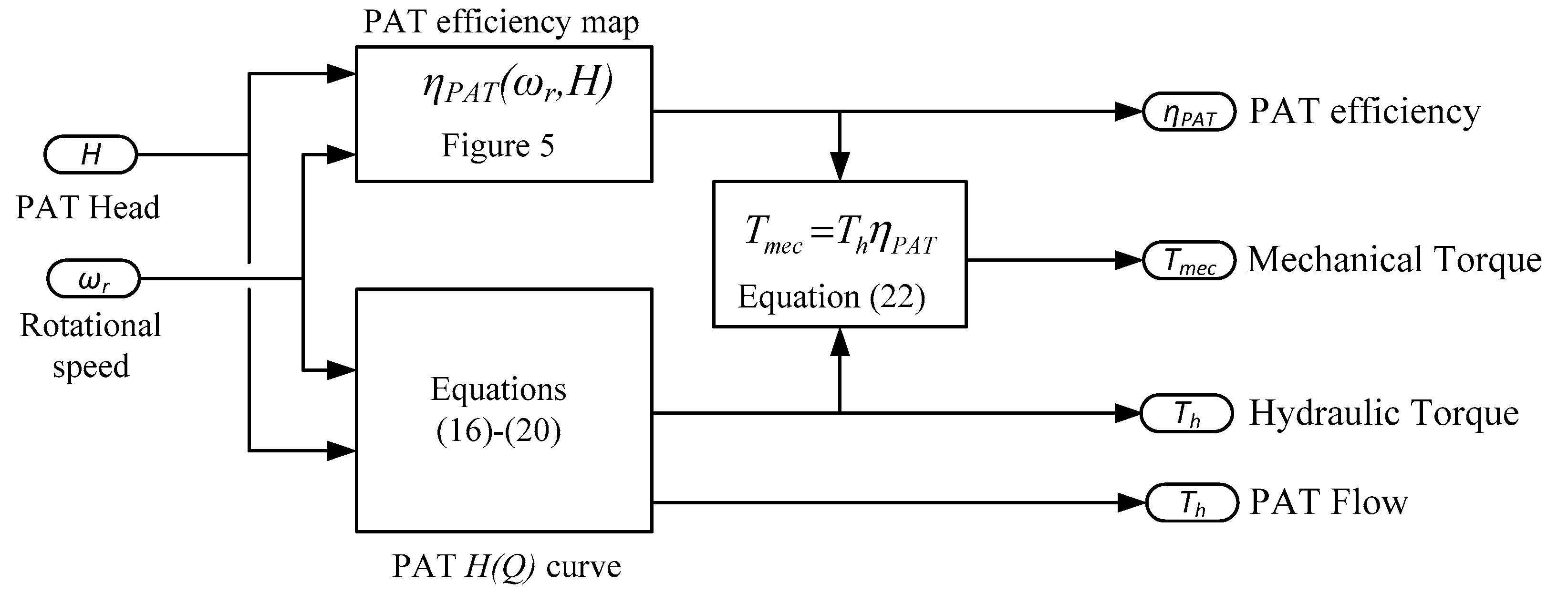
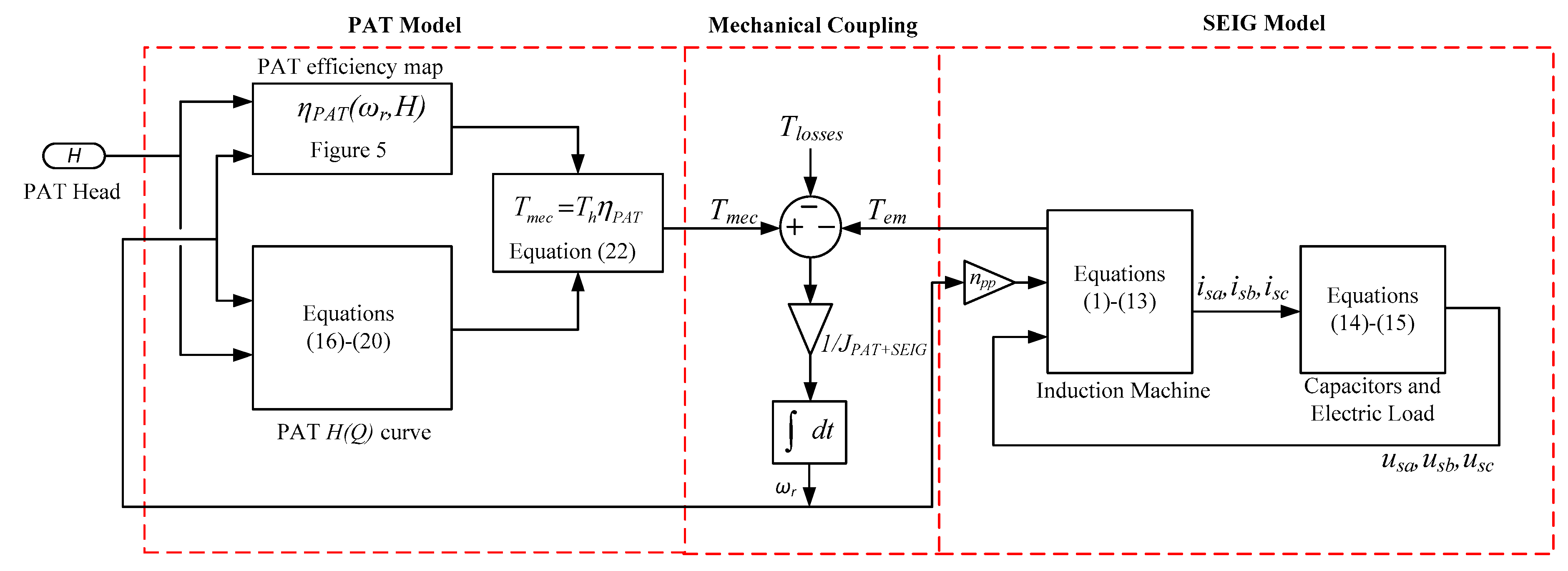
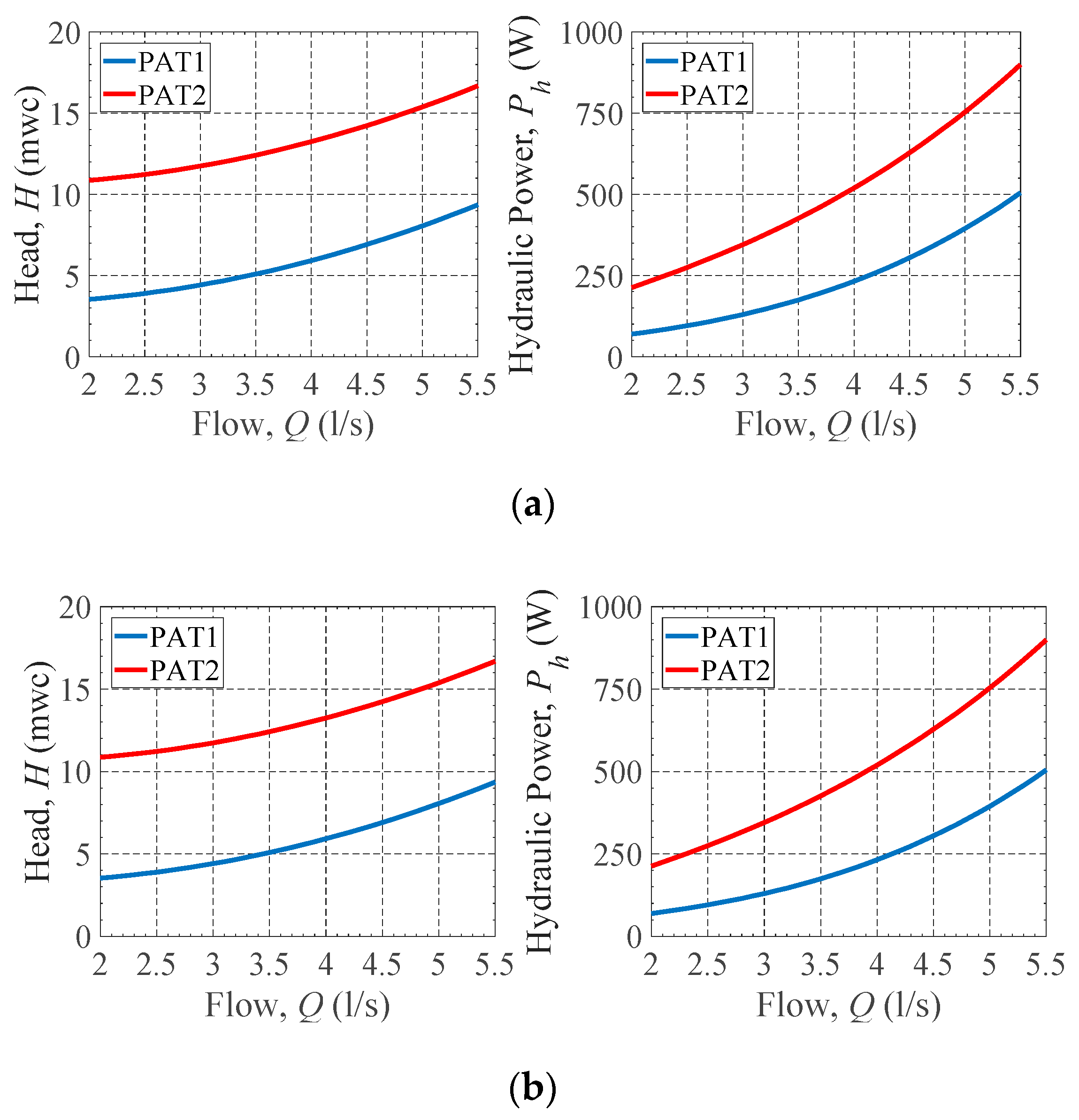
3. Pump as a Turbine (PAT) Model
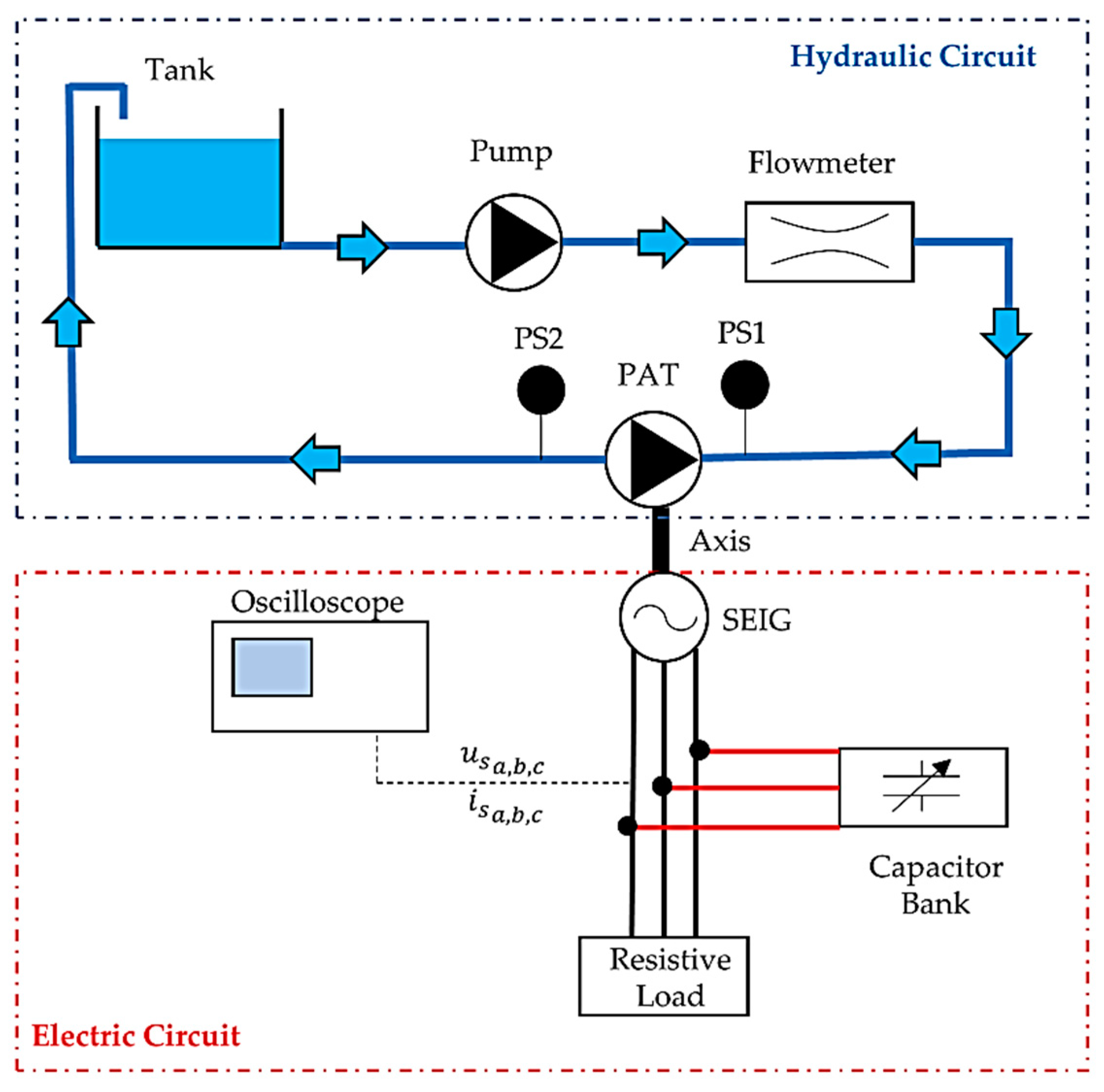
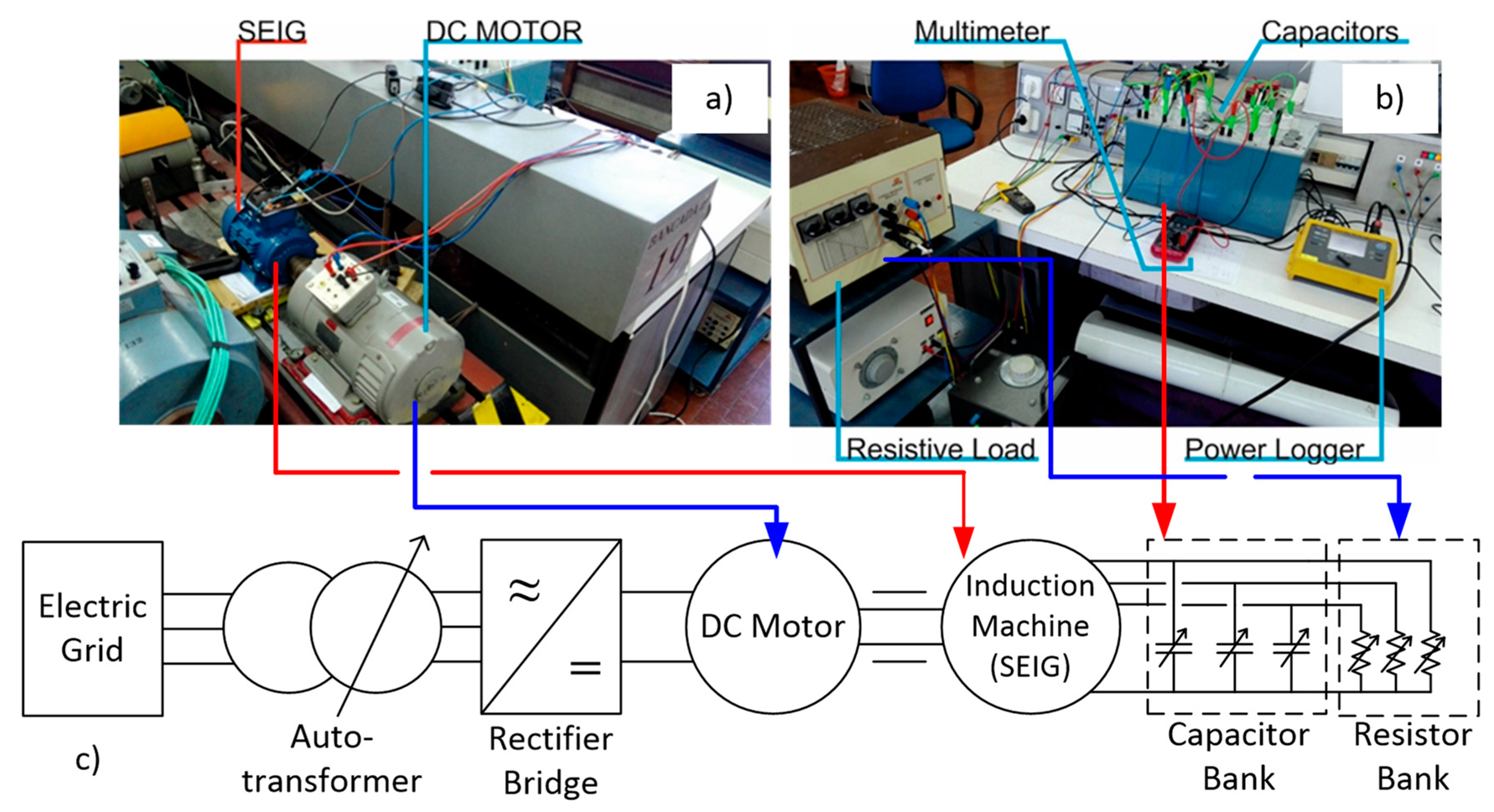
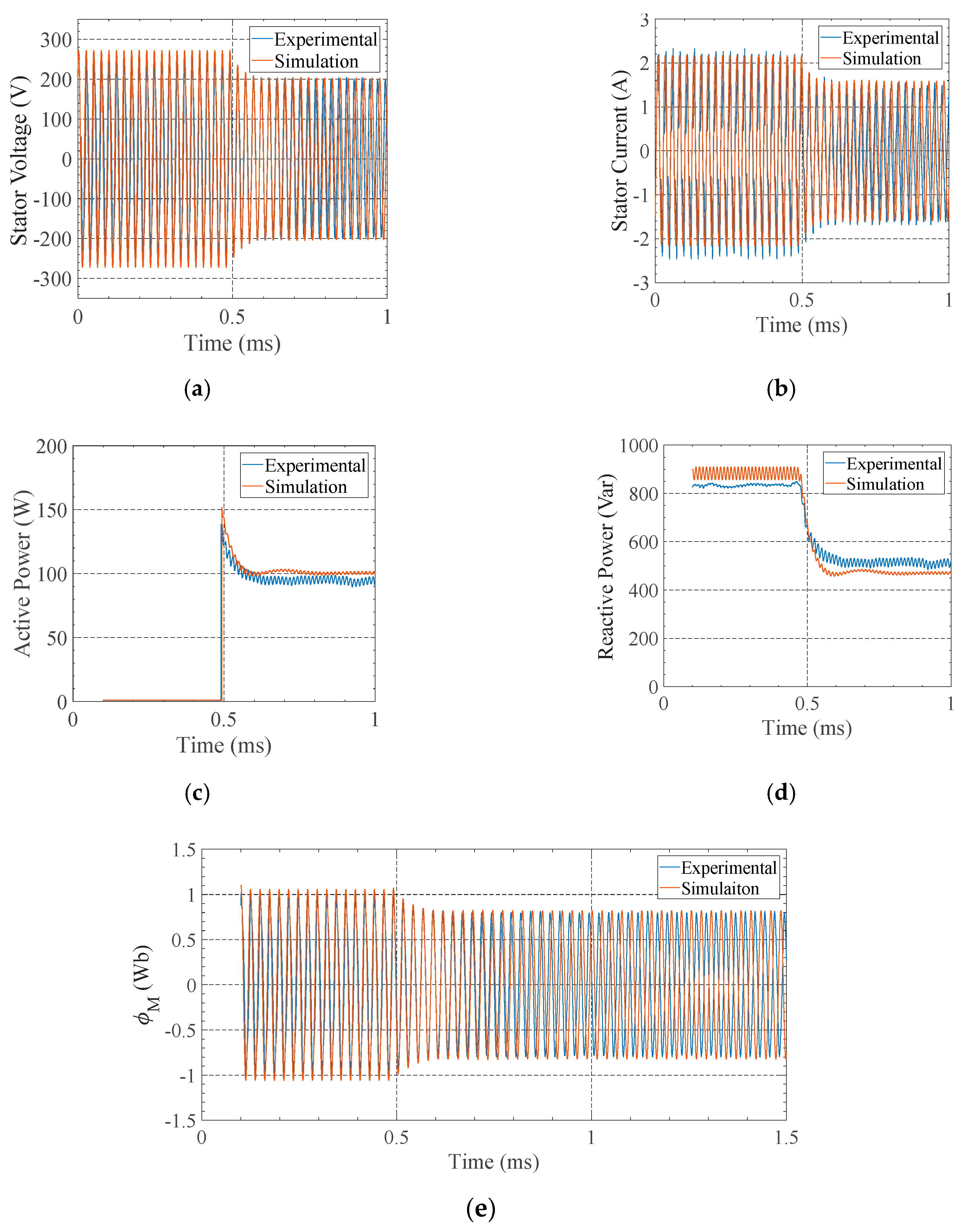
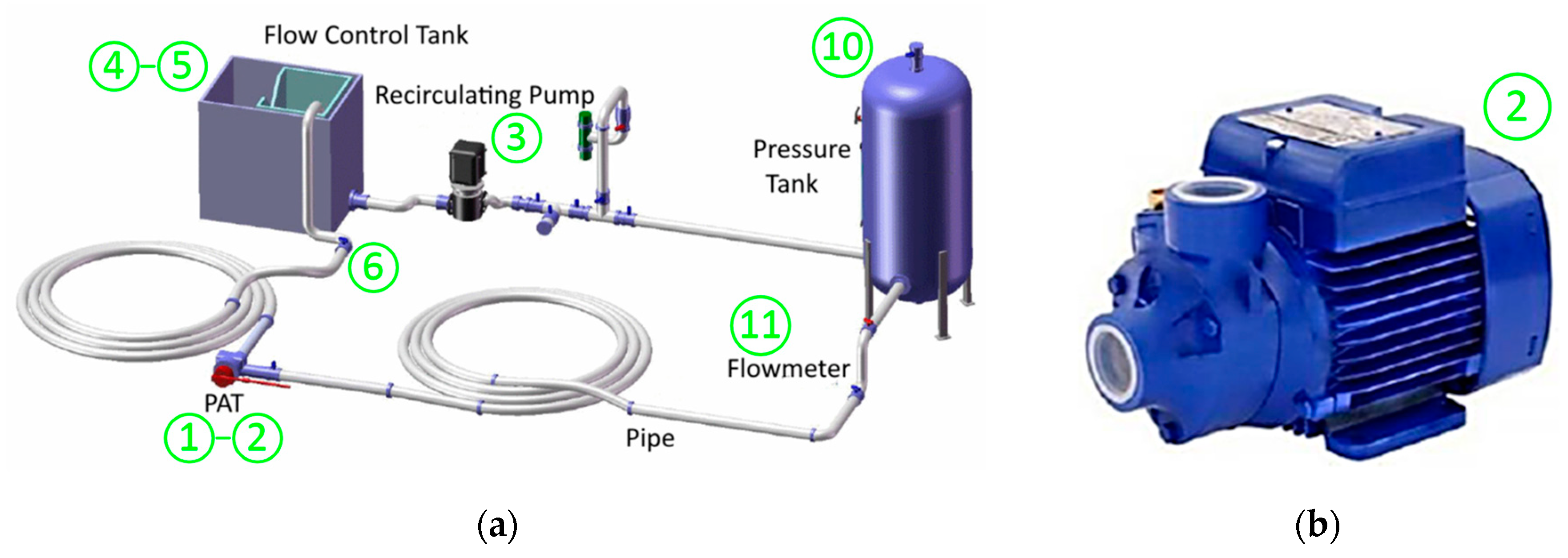
4. PAT-SEIG Model Validation
- I1. Nash–Sutcliffe index (NSI). This index is a fit indicator, which is used in temporal series. NSI value oscillates between − and 1. When values are below 0, the fit is considered poor. When the values are above 0, the model is considered good. Table 1 shows the used ranges to define the fit according to NSI values. NSI is defined by (25) where is the experimental value in each interval, is the average of the observed values and is the simulated value in each interval.
- I2. Root Relative squared error (RRSE). It measures the error of the model by normalizing the variable. Perfect fits are defined when the RRSE value is zero. The efficiency of the simulation is better when the RRSE value is low. This index is defined by (26).
- I3. Mean relative deviation (MRD). The index defines the significance of the error concerning variable value (27). The fit is good when MRD has values close to 0.
- I4. Bias (BIAS). This index compares the tendency of the simulated values, determining if the simulated values are lower or higher than experimental data (28). The model overestimates if BIAS is negative. When BIAS is positive, the variable is underestimated by the model. The optimal value is zero when BIAS is analyzed.
4.1. Self-Excited Induction Generator: d–q Model Validation
4.2. PAT Model Validation
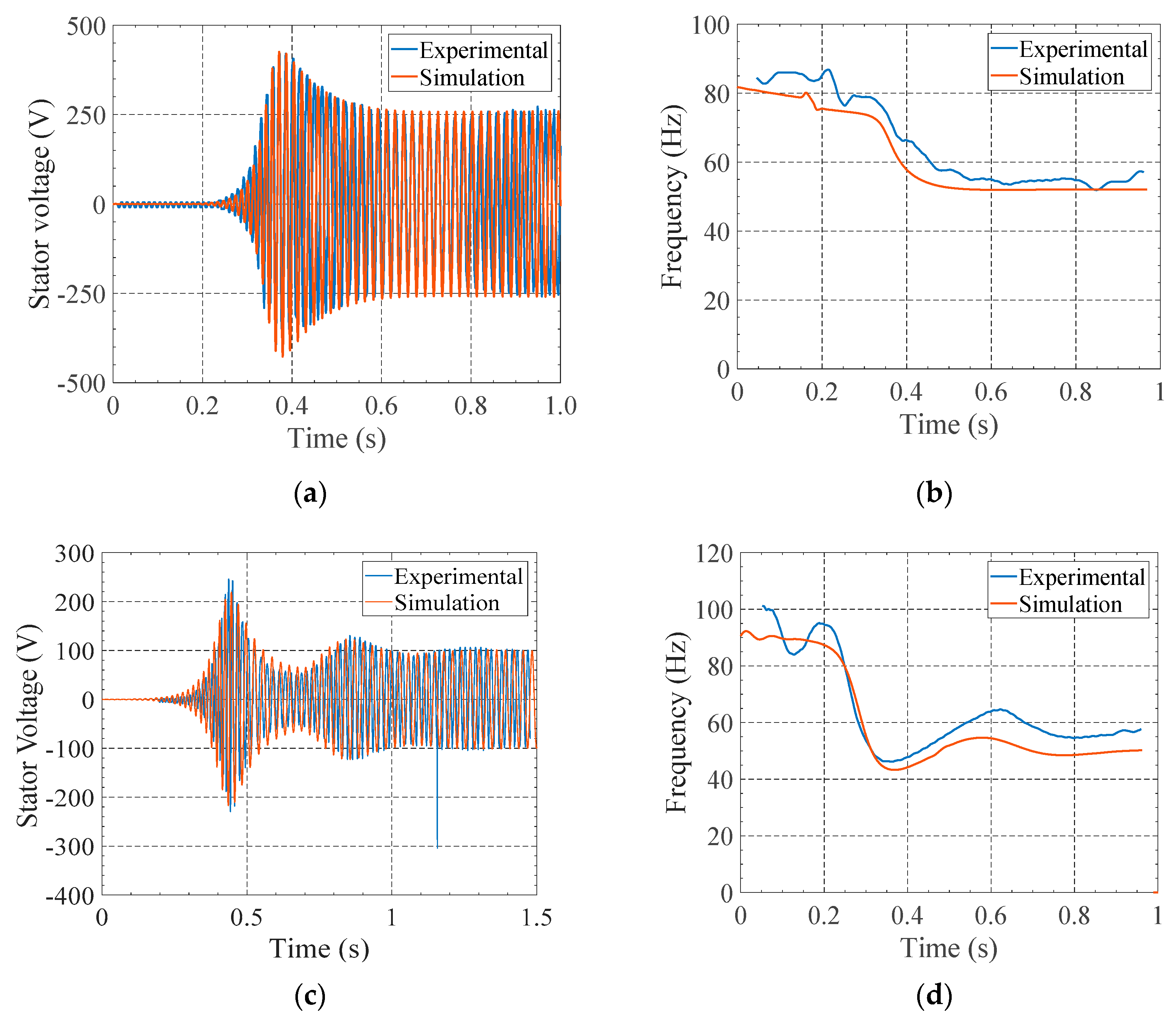
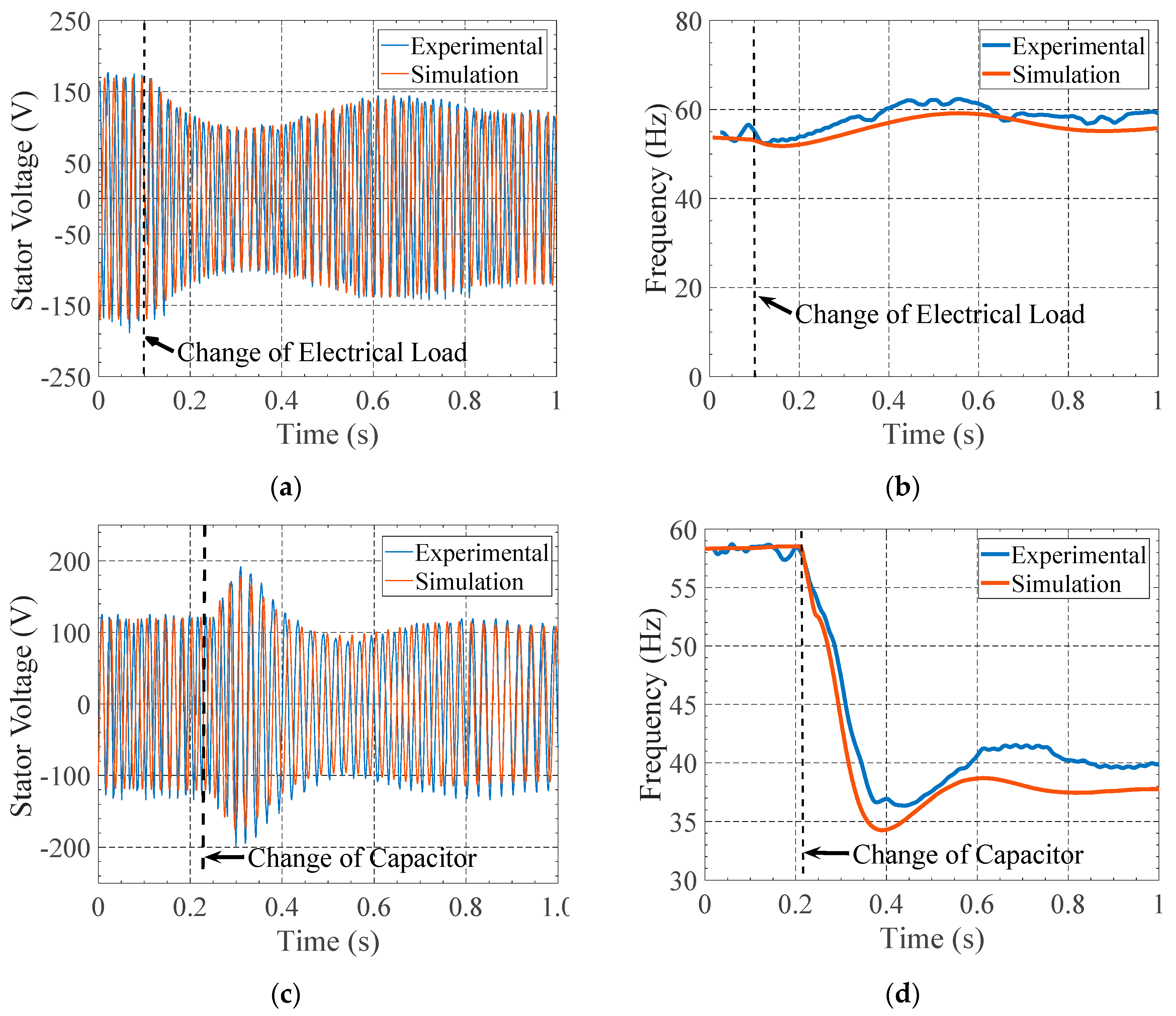
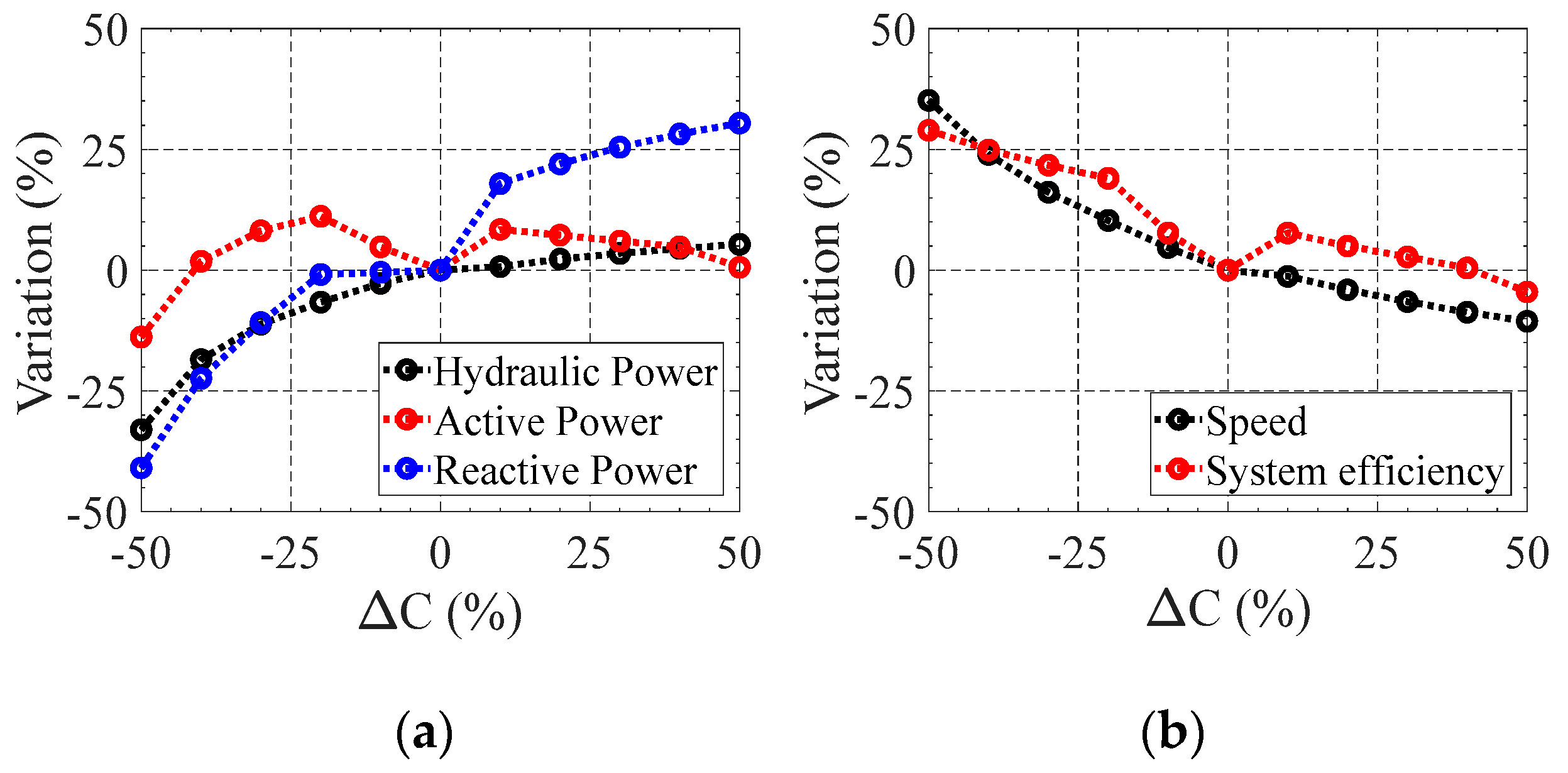
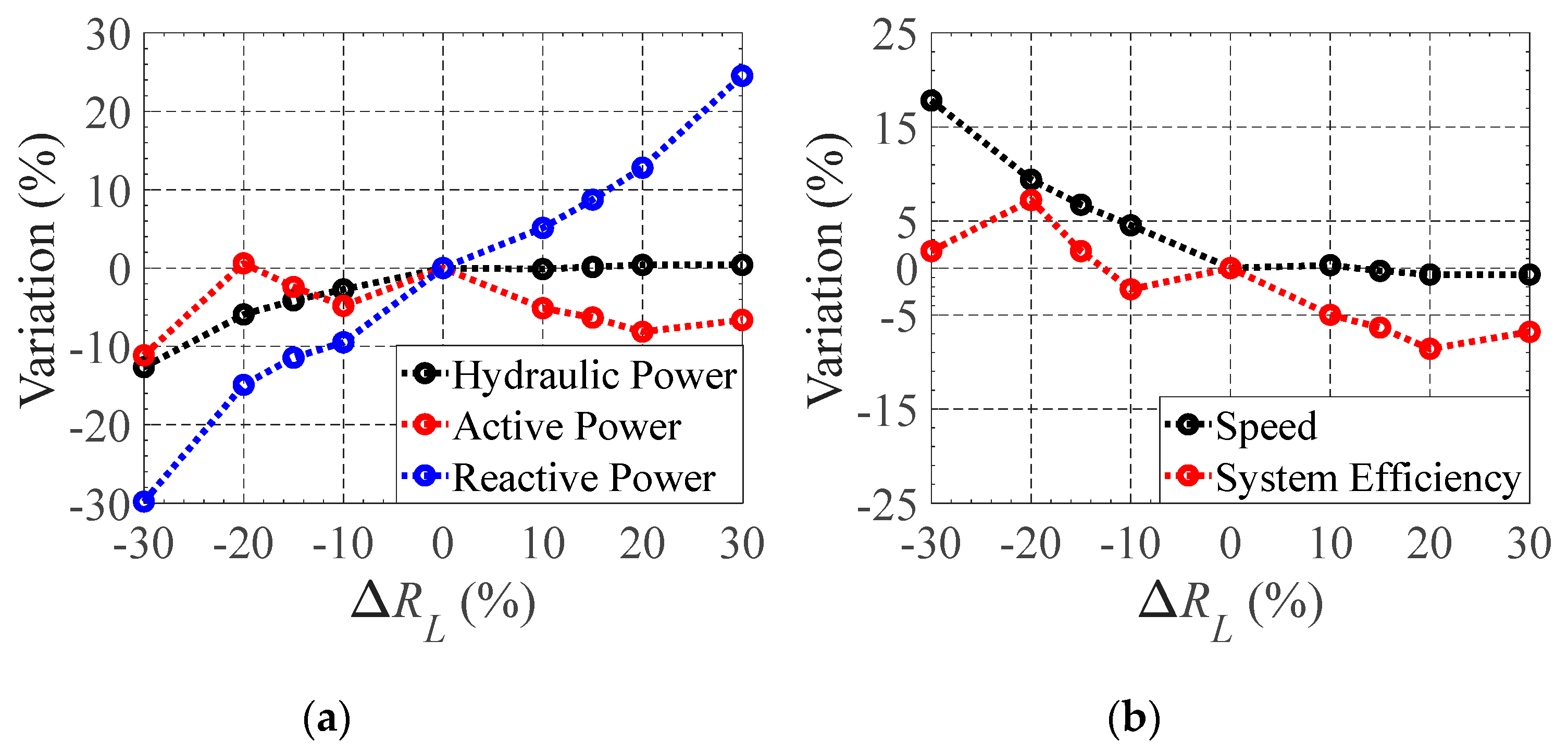
5. Impact of Electric and Hydraulic Perturbations in the PAT-SEIG Stability
5.1. Variation of Excitation Capacitance
5.2. Variation of Resistive Load
5.3. PAT Head Variation
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Postacchini, M.; Darvini, G.; Finizio, F.; Pelagalli, L.; Soldini, L.; di Giuseppe, E. Hydropower generation through pump as turbine: Experimental study and potential application to small-scale WDN. Water 2020, 12, 958. [Google Scholar] [CrossRef]
- Capelo, B.; Pérez-Sánchez, M.; Fernandes, J.F.P.; Ramos, H.M.; López-Jiménez, P.A.; Branco, P.J.C. Electrical behaviour of the pump working as turbine in off grid operation. Appl. Energy 2017, 208, 302–311. [Google Scholar] [CrossRef]
- Fecarotta, O.; Aricò, C.; Carravetta, A.; Martino, R.; Ramos, H.M. Hydropower potential in water distribution networks: Pressure control by PATs. Water Resour. Manag. 2014, 29, 699–714. [Google Scholar] [CrossRef]
- Ramos, H.; Borga, A. Pumps as turbines: An unconventional solution to energy production. Urban Water 1999, 1, 261–263. [Google Scholar] [CrossRef]
- Fernandes, J.F.P.; Pérez-Sánchez, M.; Silva, F.F.; López-Jiménez, P.A.; Ramos, H.M.; Branco, P.J.C. Optimal energy efficiency of isolated PAT systems by SEIG excitation tuning. Energy Convers. Manag. 2019, 183, 391–405. [Google Scholar] [CrossRef]
- Yi, Y.; Zhang, Z.; Chen, D.; Zhou, R.; Patelli, E.; Tolo, S. State feedback predictive control for nonlinear hydro-turbine governing system. J. Vib. Control 2018, 24, 4945–4959. [Google Scholar] [CrossRef]
- Khan, M.F.; Khan, M.R. Analysis of voltage build-up and speed disturbance ride-through capability of a self-excited induction generator for renewable energy application. Int. J. Power Energy Convers. 2016, 6, 157–177. [Google Scholar] [CrossRef]
- Carravetta, A.; del Giudice, G.; Fecarotta, O.; Ramos, H. PAT design strategy for energy recovery in water distribution networks by electrical regulation. Energies 2013, 6, 411–424. [Google Scholar] [CrossRef]
- Morani, M.C.; Carravetta, A.; del Giudice, G.; McNabola, A.; Fecarotta, O. A comparison of energy recovery by pATs against direct variable speed pumping in water distribution networks. Fluids 2018, 3, 41. [Google Scholar] [CrossRef]
- Liu, Y.; Tan, L. Tip clearance on pressure fluctuation intensity and vortex characteristic of a mixed flow pump as turbine at pump mode. Renew. Energy 2018, 129, 606–615. [Google Scholar] [CrossRef]
- Liu, Y.; Tan, L. Symmetrical and unsymmetrical tip clearances on cavitation performance and radial force of a mixed flow pump as turbine at pump mode. Renew. Energy 2018, 127, 368–376. [Google Scholar]
- Han, Y.; Tan, L. Dynamic mode decomposition and reconstruction of tip leakage vortex in a mixed flow pump as turbine at pump mode. Renew. Energy 2020, 155, 725–734. [Google Scholar] [CrossRef]
- Pérez-Sánchez, M.; Sánchez-Romero, F.J.; López-Jiménez, P.A.; Ramos, H.M. PATs selection towards sustainability in irrigation networks: Simulated annealing as a water management tool. Renew. Energy 2018, 116, 234–249. [Google Scholar] [CrossRef]
- García, I.F.; Nabola, A.M. Maximizing hydropower generation in gravity water distribution networks: Determining the optimal location and number of pumps as turbines. J. Water Resour. Plan. Manag. 2020, 146, 04019066. [Google Scholar] [CrossRef]
- Simões, M.G.; Farret, F.A. Modeling and Analysis with Induction Generators, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2014; ISBN 9781482244670. [Google Scholar]
- Mataix, C. Turbomáquinas Hidráulicas; Universidad Pontificia Comillas: Madrid, Spain, 2009. [Google Scholar]
- Pérez-Sánchez, M.; López-Jiménez, P.A.; Ramos, H.M. PATs operating in water networks under unsteady flow conditions: Control valve manoeuvre and overspeed effect. Water 2018, 10, 529. [Google Scholar] [CrossRef]
- Carravetta, A.; Houreh, S.D.; Ramos, H.M. Pumps as Turbines, Fundamentals and Applications; Springer: Cham, Switzerland, 2018. [Google Scholar] [CrossRef]
- Pérez-Sánchez, M.; Sánchez-Romero, F.J.; Ramos, H.M.; López-Jiménez, P.A. Calibrating a flow model in an irrigation network: Case study in Alicante, Spain. Span. J. Agric. Res. 2017, 15, e1202. [Google Scholar] [CrossRef]
- Moriasi, B.; Arnold, J.; van Liew, M.; Binger, R.; Harmel, R.; Veith, T. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]





| Goodness Fit | NSI | RRSE | BIAS |
|---|---|---|---|
| Very Good | NSI > 0.6 | 0.00 ≤ RRSE ≤ 0.50 | |
| Good | 0.40 < NSI ≤ 0.60 | 0.50 < RRSE ≤ 0.60 | |
| Satisfactory | 0.20 < NSI ≤ 0.40 | 0.60 < RRSE ≤ 0.70 | |
| Unsatisfactory | NSI < 0.20 | RRSE > 0.70 |
| Frequency | 50 Hz |
|---|---|
| Voltage | 400 V |
| Current | 1.6 A |
| Output Power | 0.55 kW |
| Power factor | 0.73 |
| Speed | 910 rpm |
| Experimental | Model | MRD | ||
|---|---|---|---|---|
| C = 50 μF | N (rpm) | 750 | 758 | +0.010 (1.0%) |
| (Hz) | 35.2 | 35.0 | −0.006 (0.6%) | |
| (Vrms) | 144 | 145 | +0.007 (0.7%) | |
| C = 80 μF | N (rpm) | 597 | 603 | +0.010 (1.0%) |
| (Hz) | 27.6 | 27.2 | −0.015 (1.5%) | |
| (Vrms) | 113 | 108 | −0.044 (4.4%) |
| Experimental | Model | MRD | |||||
|---|---|---|---|---|---|---|---|
| Initial | Final | Initial | Final | Initial | Final | ||
| = 600 Ω | N (rpm) | 839 | 834 | 842 | 835 | +0.004 (+0.4%) | +0.001 (+0.1%) |
| (Hz) | 41.0 | 40.0 | 40.9 | 39.3 | −0.000 (−0.0%) | −0.018 (−1.8%) | |
| (Vrms) | 183 | 141 | 191 | 141.9 | −0.044 (−4.4%) | −0.006 (−0.6%) | |
| (Arms) | 1.6 | 1.05 | 1.53 | 1.12 | −0.023 (−2.3%) | +0.023 (+2.3%) | |
| (V) | 4.46 | 3.53 | 4.67 | 3.61 | −0.005 (−0.5%) | +0.003 (+0.3%) | |
| = 300 Ω | N (rpm) | 848 | 843 | 849 | 851 | +0.001 (0.1%) | +0.010 (+1.0%) |
| (Hz) | 41.2 | 40.3 | 41.5 | 40.0 | +0.007 (+0.7%) | −0.007 (−0.7%) | |
| (Vrms) | 181 | 90 | 184.6 | 84.8 | +0.002 (+0.2%) | +0.058 (+5.8%) | |
| (Arms) | 1.6 | 0.8 | 1.62 | 0.87 | +0.013 (+1.3%) | +0.088 (+8.8%) | |
| (V) | 4.4 | 2.2 | 4.49 | 2.22 | +0.020 (+2.0%) | +0.009 (+0.9%) | |
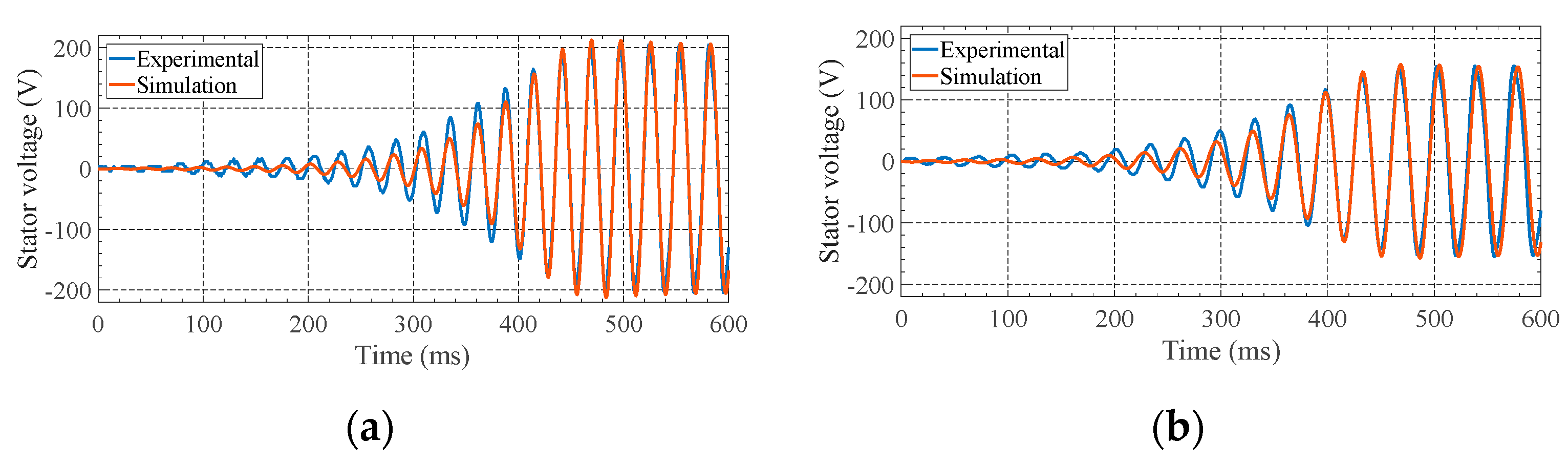
| Indexes | Stator Voltage (Figure 15a) | Frequency (Figure 15b) | Stator Voltage (Figure 15c) | Frequency (Figure 15d) |
|---|---|---|---|---|
| NSI | 0.960 (VG) | 0.797 (VG) | 0.802 (VG) | 0.841 (VG) |
| RRSE | 0.200 (VG) | 0.451 (VG) | 0.441 (VG) | 0.399 (VG) |
| BIAS | 0.039 (VG) | −0.071 (VG) | 0.095 (VG) | −0.075 (VG) |
| MRD | −0.0244 (−2.44%) | 0.062 (6.2%) | 0.010 (1.0%) | 0.0664 (6.64%) |
| Indexes | Stator Voltage (Figure 16a) | Frequency (Figure 16b) | Stator Voltage (Figure 16c) | Frequency (Figure 16d) |
|---|---|---|---|---|
| NSI | 0.569 (G) | 0.787 (VG) | 0.761 (VG) | 0.793 (VG) |
| RRSE | 0.648 (S) | 0.462 (VG) | 0.429 (VG) | 0.455 (VG) |
| BIAS | 0.063 (VG) | −0.041 (VG) | −0.034 (VG) | −0.037 (VG) |
| MRD | 0.0360 | 0.0269 | −0.054 | 0.281 |
| C. | N (rpm) | ||||||
|---|---|---|---|---|---|---|---|
| −50% | 1005 | 1365 | 139.7 | 1.16 | 331 | −392 | 33.0% |
| −40% | 1223 | 1252 | 152.6 | 1.34 | 392 | −515 | 32.0% |
| −30% | 1333 | 1173 | 157.4 | 1.47 | 416 | −592 | 31.1% |
| −20% | 1401 | 1114 | 158.8 | 1.58 | 427 | −658 | 30.5% |
| −10% | 1460 | 1057 | 155.5 | 1.60 | 403 | −661 | 27.6% |
| 0% | 1501 | 1010 | 150.2 | 1.65 | 384 | −664 | 25.6% |
| +10% | 1512 | 997 | 157.0 | 1.83 | 417 | −783 | 27.6% |
| +20% | 1535 | 969 | 155.2 | 1.90 | 412 | −810 | 26.9% |
| +30% | 1553 | 944 | 154.4 | 1.95 | 408 | −833 | 26.3% |
| +40% | 1568 | 922 | 152.1 | 2.01 | 403 | −851 | 25.7% |
| +50% | 1581 | 903 | 149.4 | 2.07 | 387 | −866 | 24.4% |
| N (rpm) | |||||||
|---|---|---|---|---|---|---|---|
| −30% | 1311 | 1190 | 119.1 | 1.54 | 342 | −466 | 26.1% |
| −20% | 1412 | 1105 | 135.6 | 1.61 | 387 | −565 | 27.5% |
| −15% | 1439 | 1078 | 139.6 | 1.60 | 375 | −588 | 26.0% |
| −10% | 1460 | 1056 | 141.5 | 1.60 | 366 | −601 | 25.0% |
| 0% | 1501 | 1010 | 150.2 | 1.65 | 384 | −664 | 25.6% |
| +10% | 1499 | 1013 | 153.5 | 1.66 | 365 | −698 | 24.3% |
| +15% | 1503 | 1007 | 157.9 | 1.66 | 360 | −722 | 24.0% |
| +20% | 1507 | 1003 | 159.2 | 1.69 | 353 | −749 | 23.4% |
| +30% | 1507 | 1003 | 168.1 | 1.75 | 359 | −827 | 23.9% |
| N (rpm) | |||||||
|---|---|---|---|---|---|---|---|
| −50% | 457 | 887 | 75.0 | 0.74 | 96 | −145 | 21.1% |
| −40% | 642 | 912 | 100.2 | 1.01 | 163 | −267 | 25.3% |
| −30% | 842 | 942 | 118.8 | 1.23 | 221 | −386 | 26.2% |
| −20% | 1057 | 970 | 132.9 | 1.41 | 277 | −499 | 26.2% |
| −10% | 1297 | 995 | 144.8 | 1.55 | 334 | −601 | 25.3% |
| 0% | 1501 | 1010 | 150.2 | 1.65 | 384 | −664 | 25.6% |
| +10% | 1782 | 1059 | 170.2 | 1.92 | 453 | −885 | 25.5% |
| +20% | 2047 | 1086 | 180.6 | 2.08 | 521 | −1017 | 25.5% |
| +30% | 2320 | 1091 | 181.3 | 2.11 | 569 | −1040 | 25.3% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Madeira, F.C.; Fernandes, J.F.P.; Pérez-Sánchez, M.; López-Jiménez, P.A.; Ramos, H.M.; Costa Branco, P.J. Electro-Hydraulic Transient Regimes in Isolated Pumps Working as Turbines with Self-Excited Induction Generators. Energies 2020, 13, 4521. https://doi.org/10.3390/en13174521
Madeira FC, Fernandes JFP, Pérez-Sánchez M, López-Jiménez PA, Ramos HM, Costa Branco PJ. Electro-Hydraulic Transient Regimes in Isolated Pumps Working as Turbines with Self-Excited Induction Generators. Energies. 2020; 13(17):4521. https://doi.org/10.3390/en13174521
Chicago/Turabian StyleMadeira, Filipe C., João F. P. Fernandes, Modesto Pérez-Sánchez, P. Amparo López-Jiménez, Helena M. Ramos, and P. J. Costa Branco. 2020. "Electro-Hydraulic Transient Regimes in Isolated Pumps Working as Turbines with Self-Excited Induction Generators" Energies 13, no. 17: 4521. https://doi.org/10.3390/en13174521
APA StyleMadeira, F. C., Fernandes, J. F. P., Pérez-Sánchez, M., López-Jiménez, P. A., Ramos, H. M., & Costa Branco, P. J. (2020). Electro-Hydraulic Transient Regimes in Isolated Pumps Working as Turbines with Self-Excited Induction Generators. Energies, 13(17), 4521. https://doi.org/10.3390/en13174521










