Mathematical Model of Thermodynamic Processes in the Intake Manifold of a Diesel Engine with Fuel and Water Injection
Abstract
1. Introduction
2. Main Part
2.1. Developed Mathematical Model
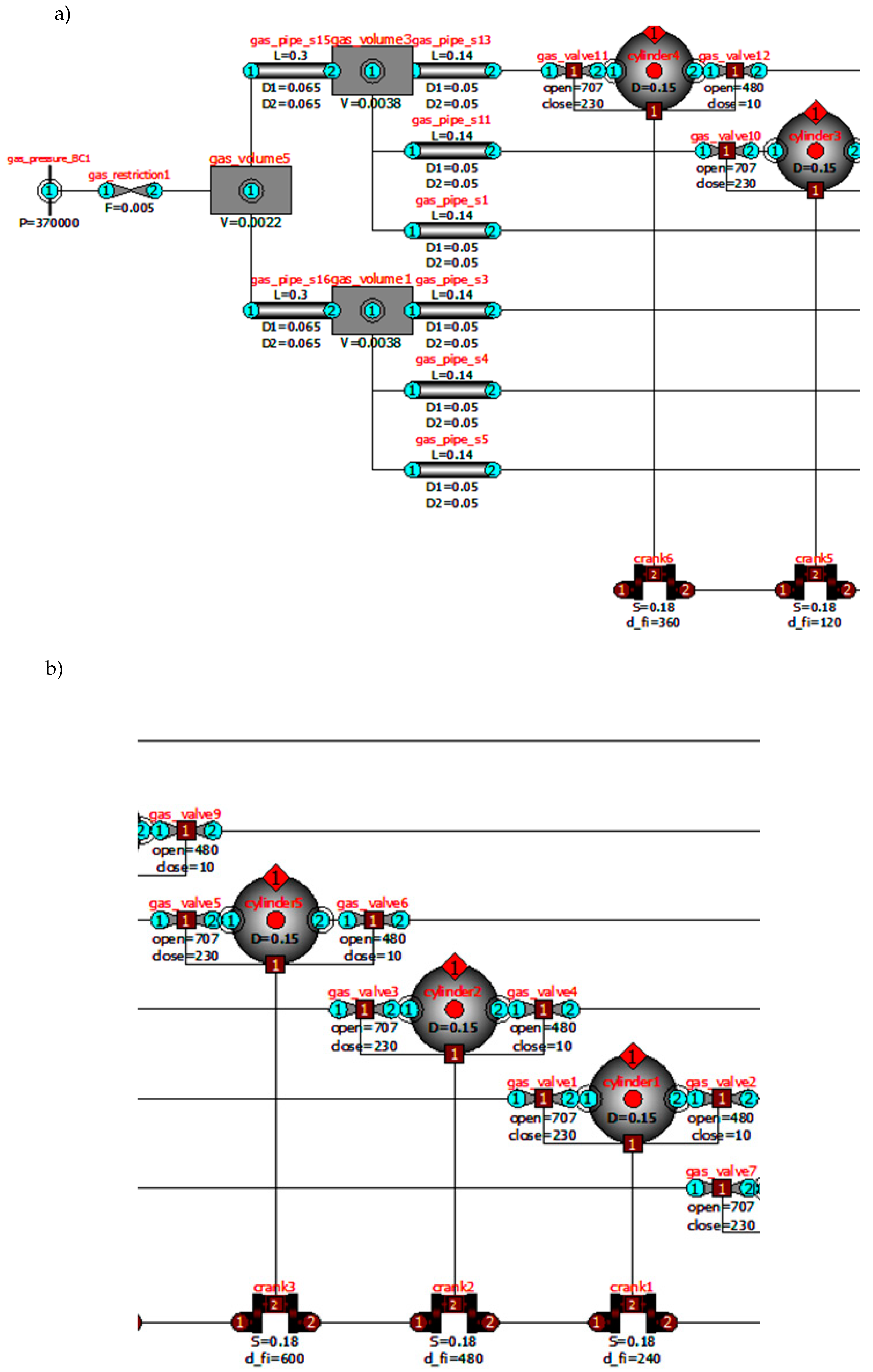
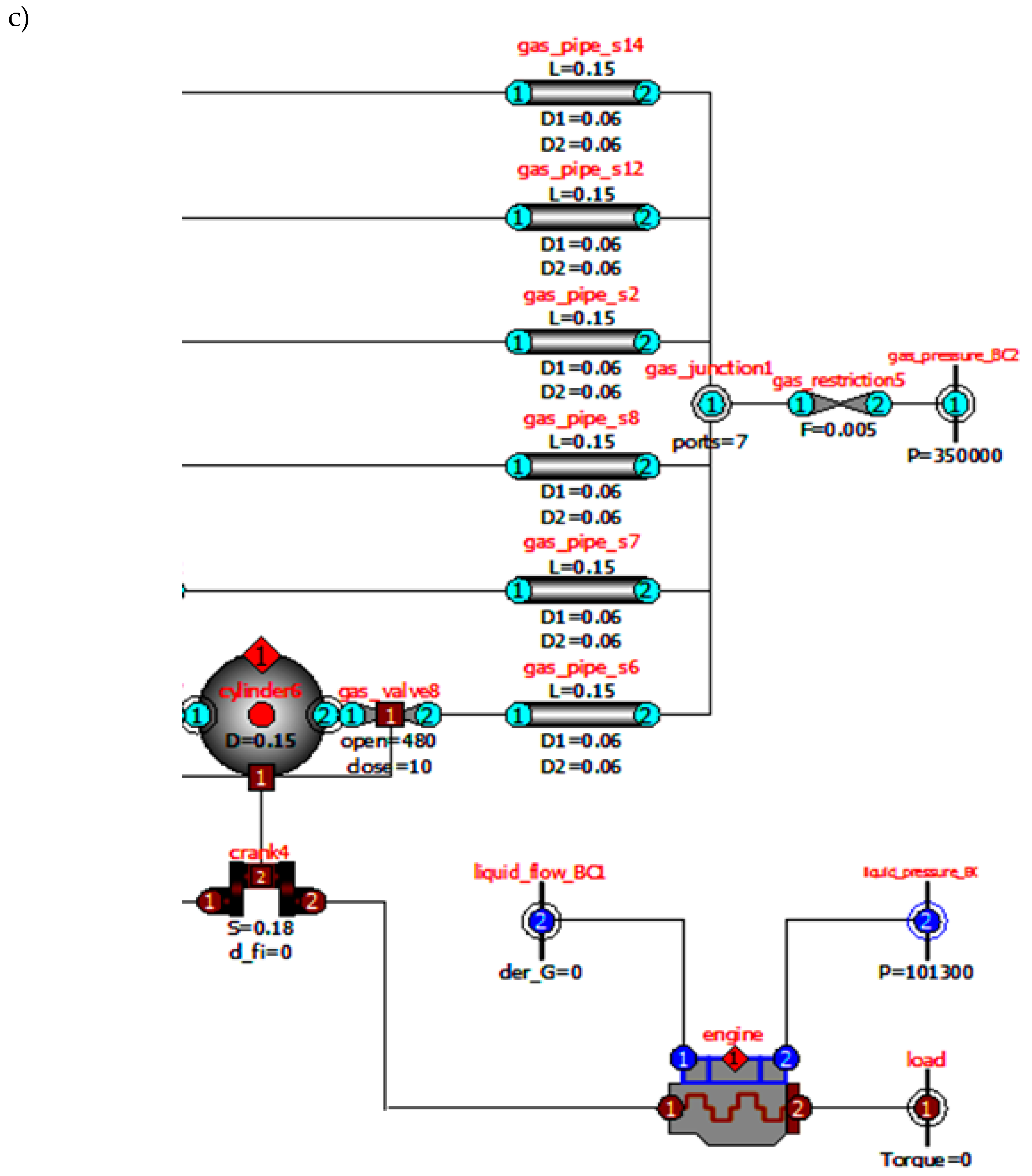
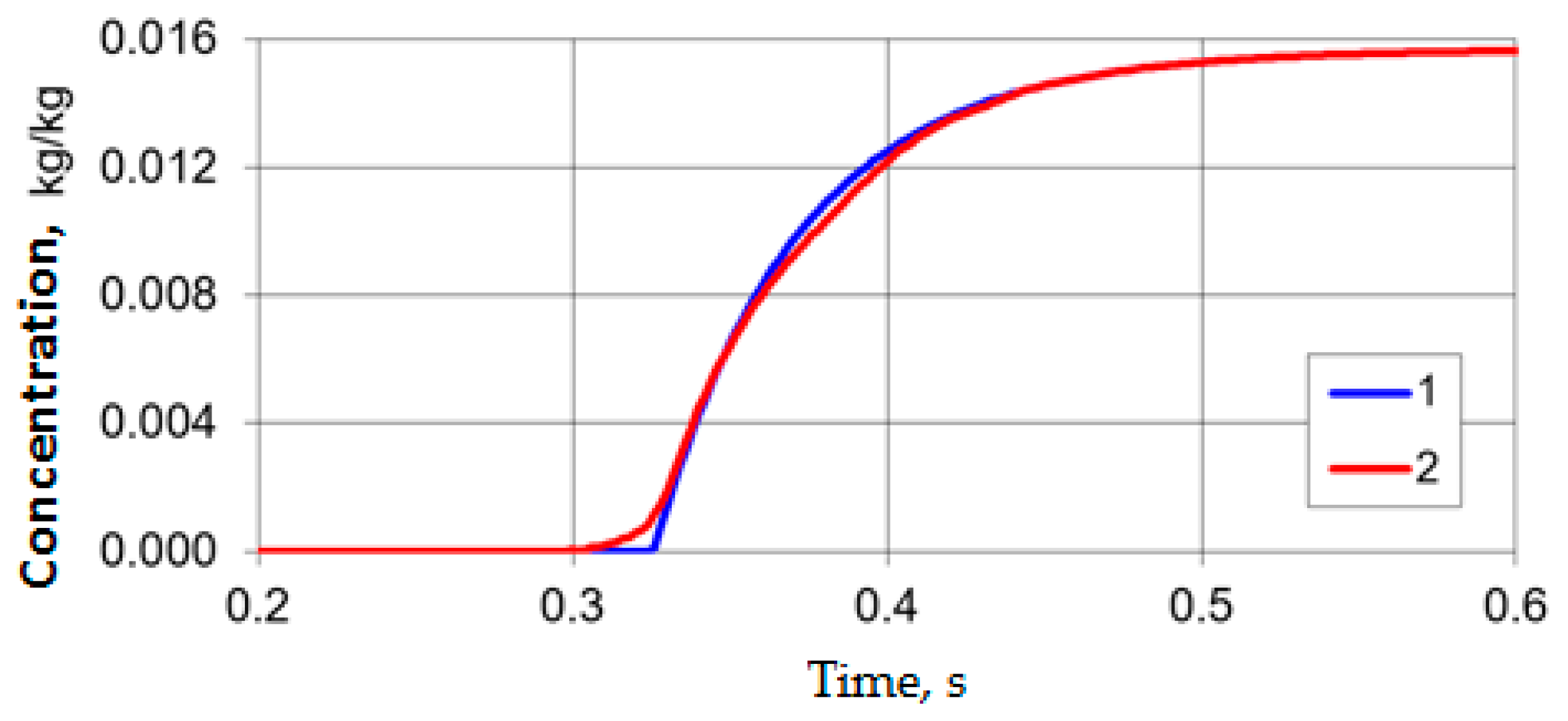
2.2. Verification of the Mathematical Model
- the base class “volume” was supplemented by a description of the process of evaporation of fuel and water and its effect on the parameters of the state of gases in the combustion chamber;
- in the remaining base classes, including component relationships, additional variables were included—the concentration of fuel and water vapor;
- the base class “cylinder” was supplemented by descriptions of the combustion process of fuel vapor coming from the intake manifold, and the effect of water vapor and combustion products of fuel vapor on the combustion performance the Vibe equation of the main portion of fuel injected into the combustion chamber [28].
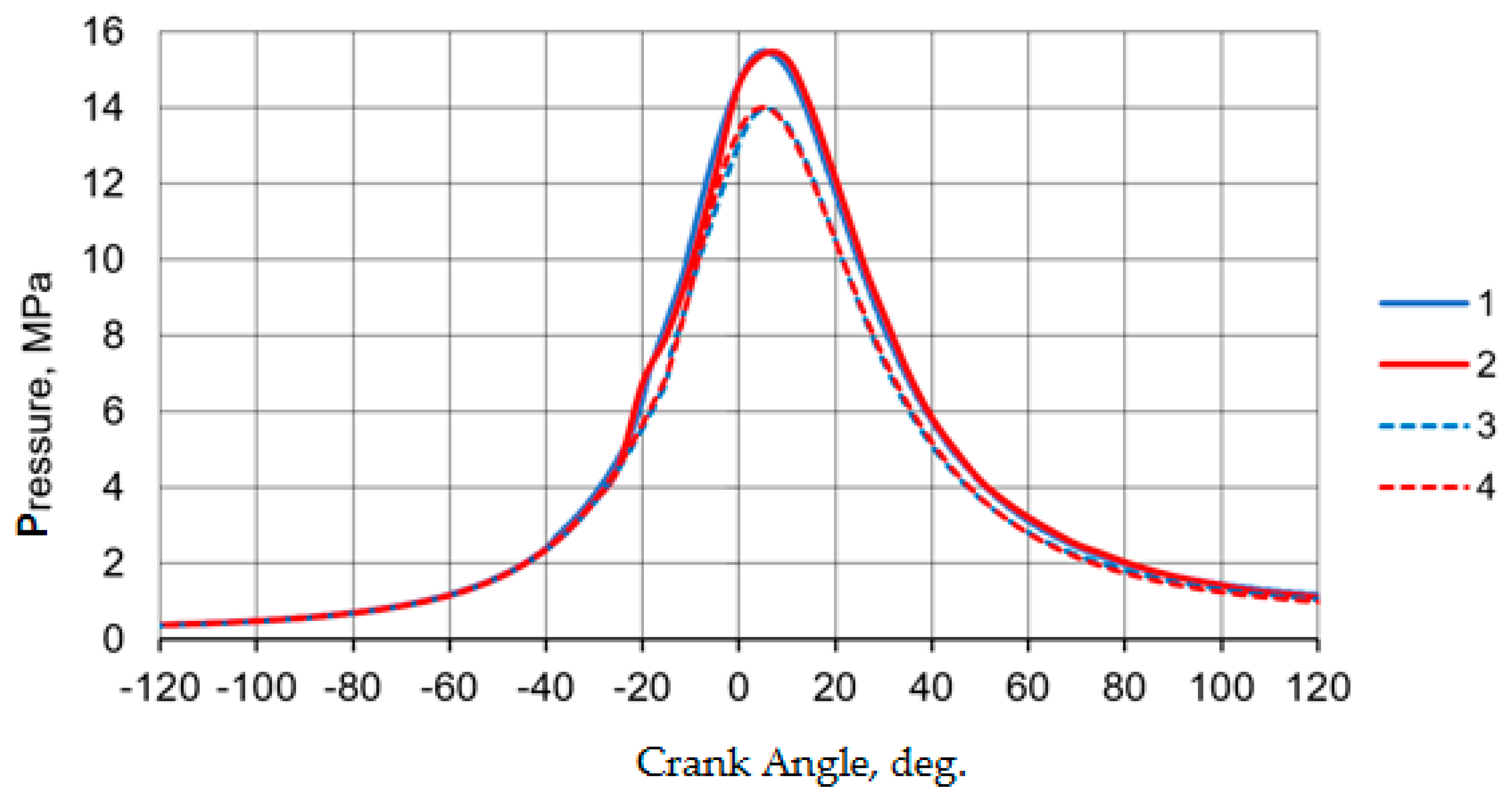
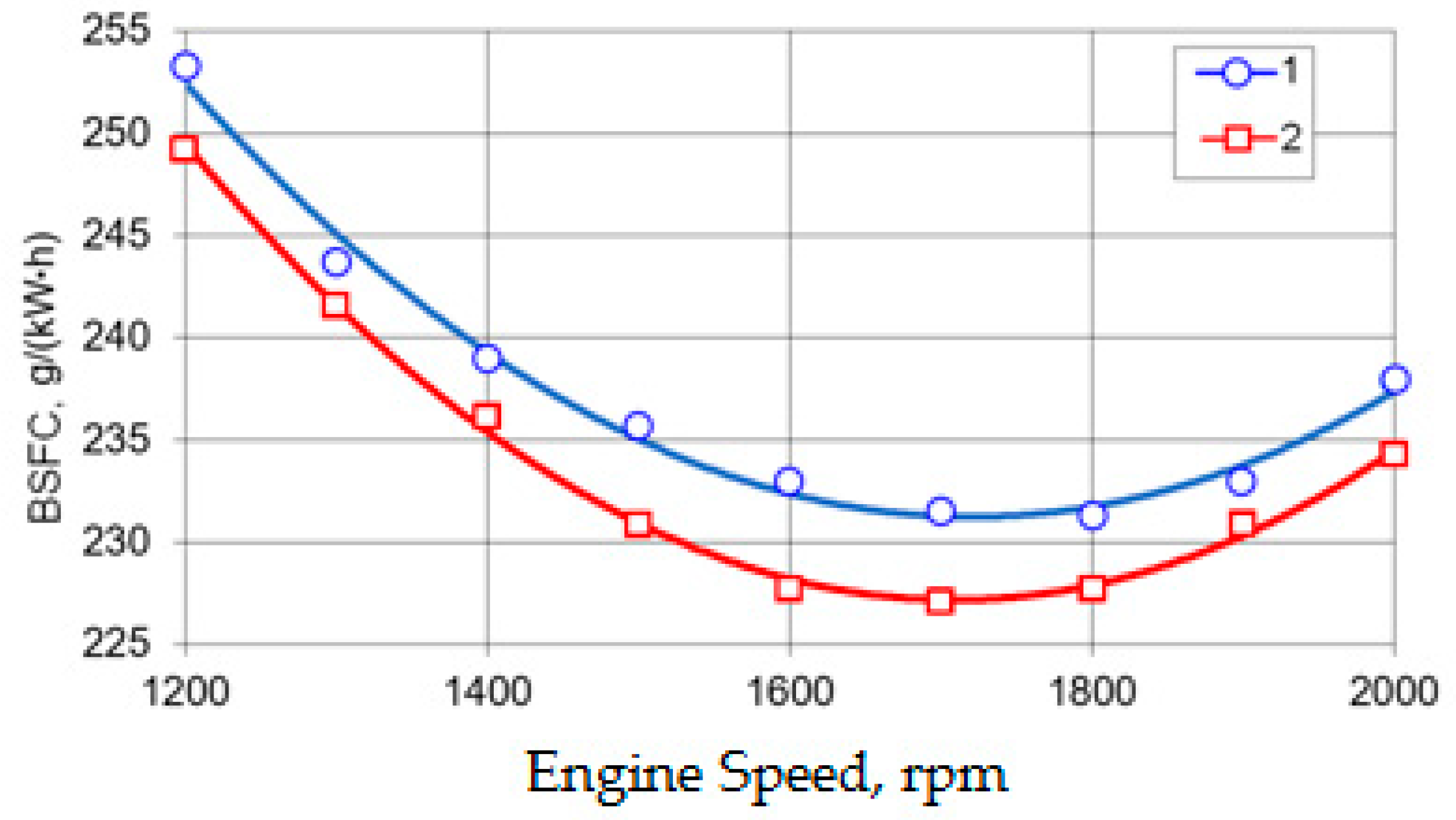
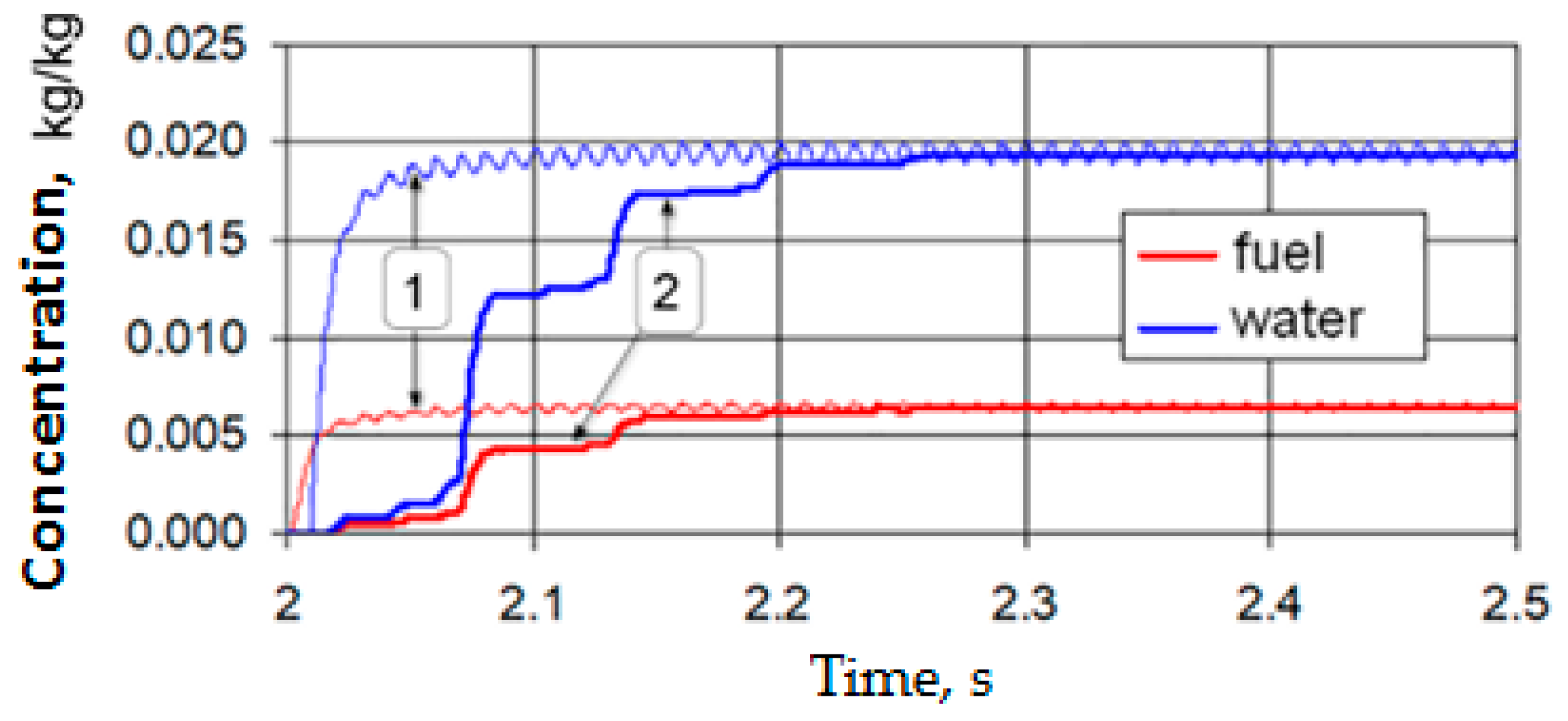
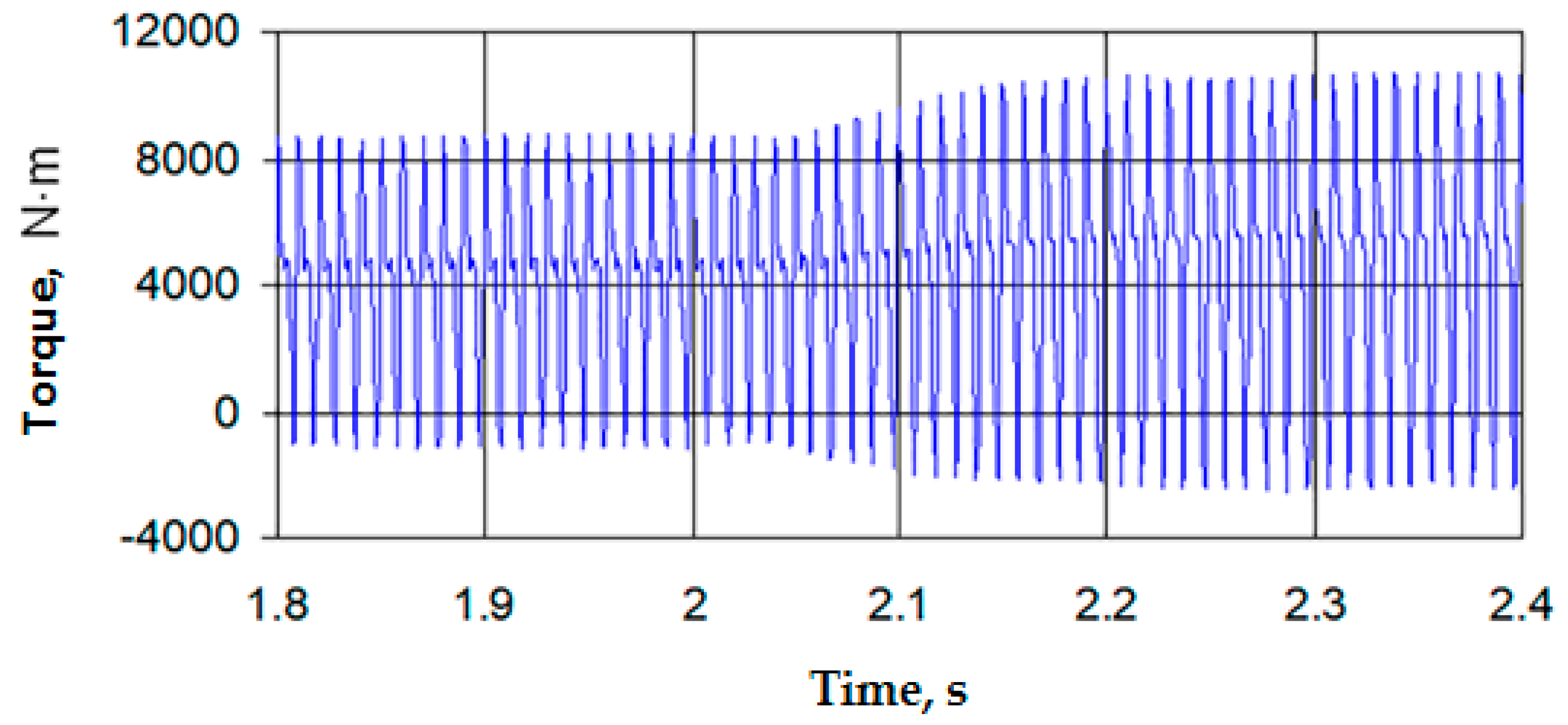
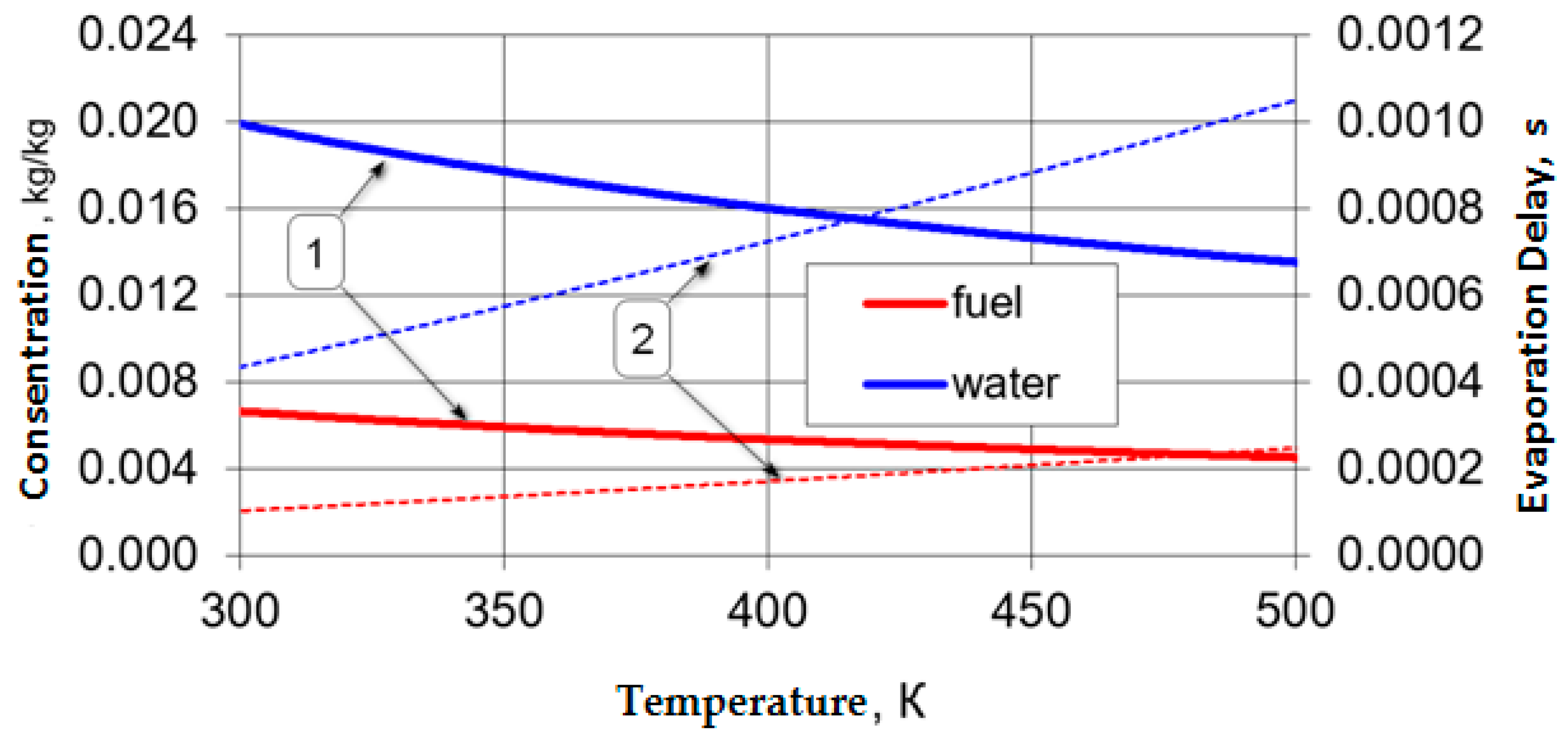
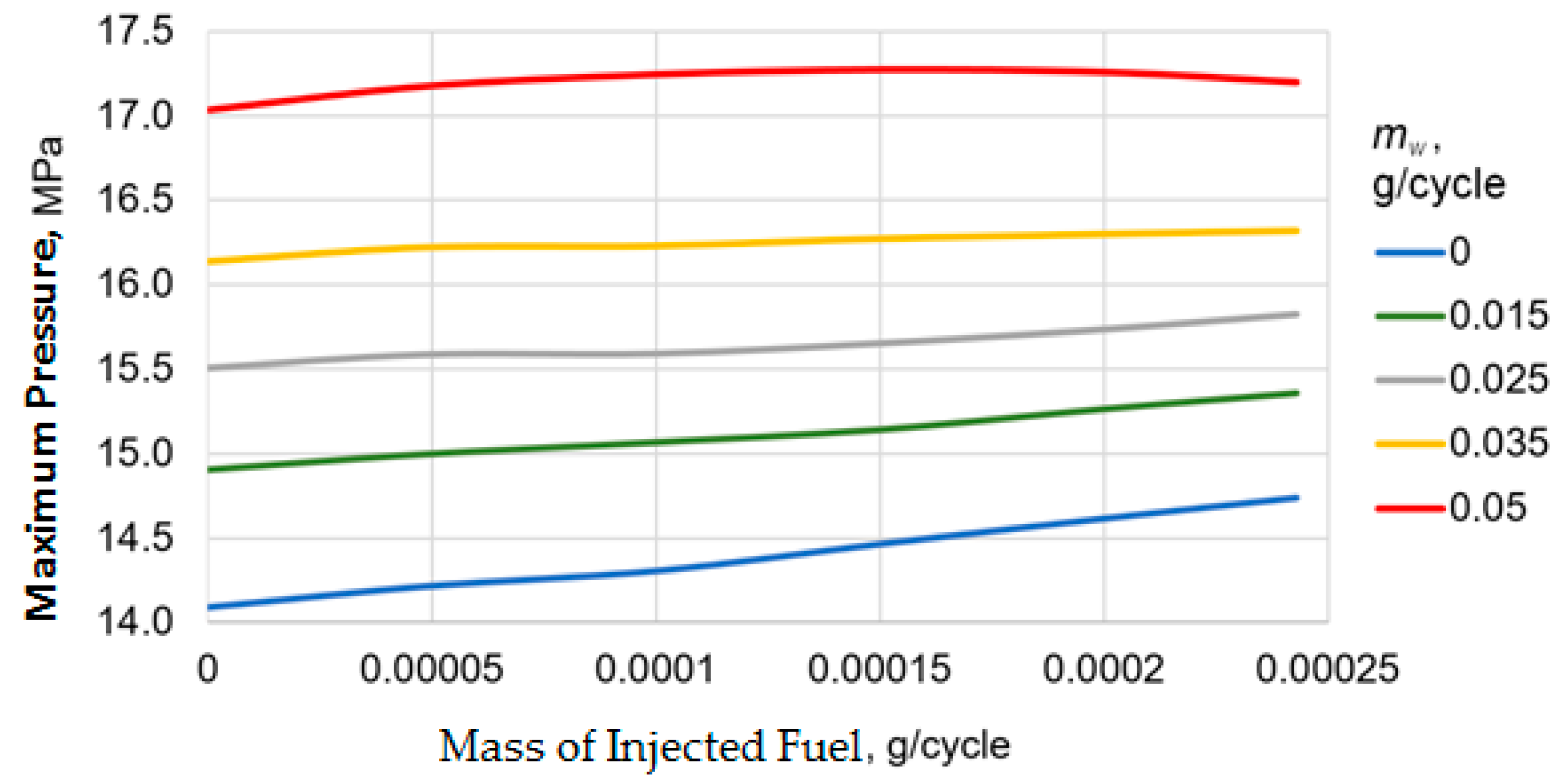
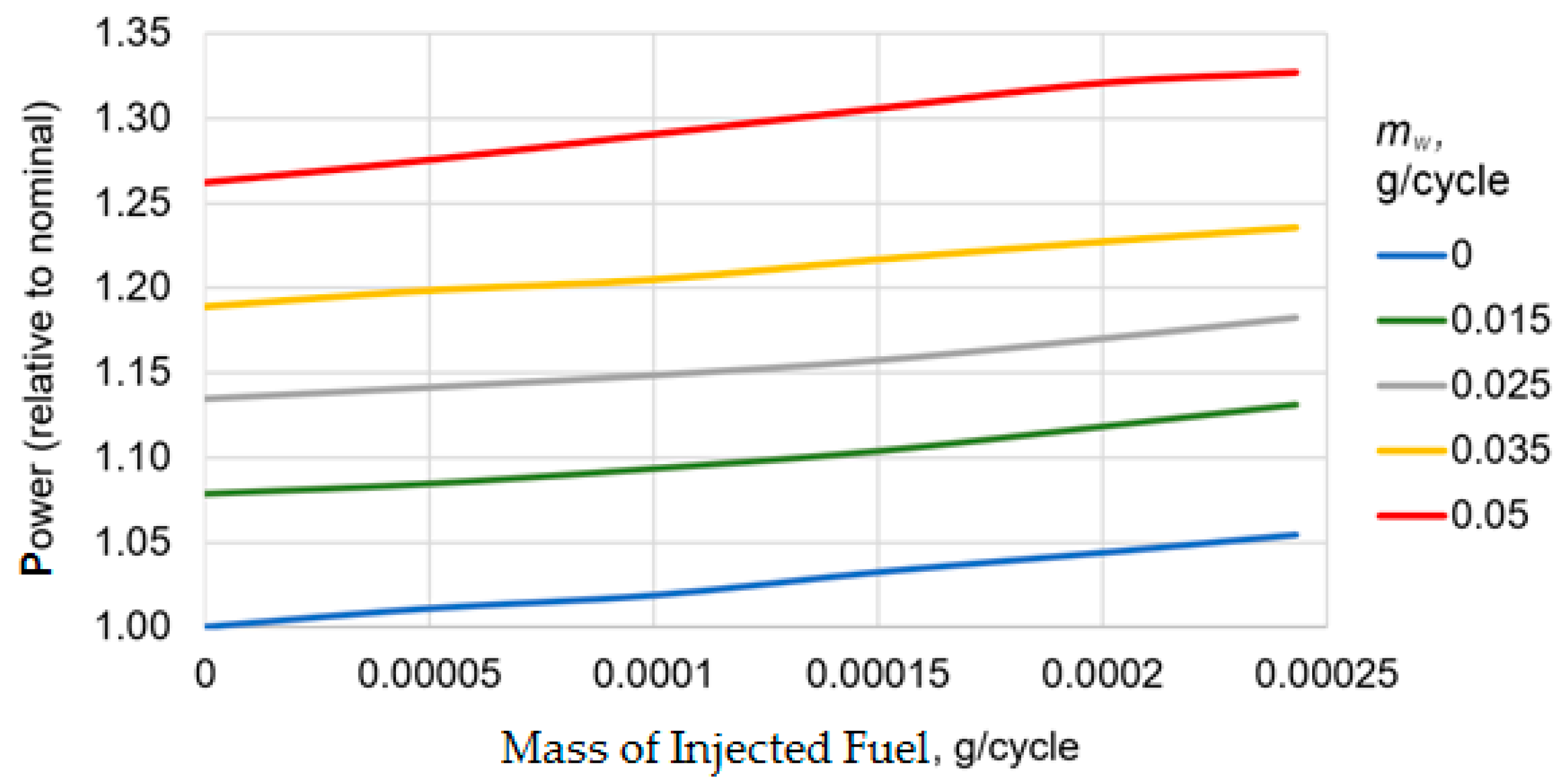
3. Calculation Results and Discussion
4. Conclusions
- includes detailed mathematical submodels of the processes of simultaneous evaporation of fuel and water in the intake manifold;
- takes into account the influence of the process of evaporation of fuel and water on the parameters of the gas state in the intake manifold;
- takes into account the influence of the parameters of the state of the working fluid in the intake manifold on the physical characteristics of fuel and water;
- complies with the principles of component modeling, since it does not contain “unnecessary” parameters that are not related to the component being modeled;
- describes the process of simultaneous transfer of vapors and non-evaporated liquids between components;
- is based on basic equations of physics, and not on empirical dependencies that require data on the dynamics of fuel evaporation under reference conditions.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Indexes | |
| Ainj | cross-sectional area of the collector at the nozzle installation site; |
| am | empirical indicator; |
| bui | relative constant of evaporation in the i-zone; |
| c | number of connections; |
| component concentration vector; | |
| clf | specific heat of liquid fuel; |
| clw | specific heat of liquid water; |
| D32 | average droplet diameter according to Sauter; |
| Dc | diameter of nozzle holes; |
| Dp | vapor diffusion coefficient; |
| Dp0 | vapor diffusion coefficient under normal conditions; |
| E32 | empirical coefficient; |
| hin | specific enthalpy of inflowing gas; |
| hout | specific enthalpy of effluent gas; |
| i | number of drops; |
| ic | number of nozzle holes; |
| k | adiabatic exponent; |
| kevap | evaporation factor; |
| Ki | evaporation constant in the i-zone; |
| mef | mass of fuel evaporated; |
| mg | manifold gas mass; |
| mlf | mass of liquid fuel; |
| mlw | mass of liquid water; |
| n | empirical indicator; |
| NuD | Nusselt criterion for the diffusion process; |
| p | current pressure; |
| pin | gas pressure before the cross-section; |
| pout | gas pressure after the section; |
| ps | saturated steam pressure; |
| qbf | specific heat of vaporization of fuel; |
| qbw | specific heat of vaporization of water; |
| Qew | heat spent on water evaporation; |
| Tin | gas temperature before cross-section; |
| Tef | boiling point of fuel; |
| Tew | boiling point of water; |
| Tκ | drop temperature; |
| Tlf | oil temperature; |
| Tlw | liquid water temperature; |
| U | internal gas energy; |
| u | specific internal energy of gas; |
| Ug | flow rate at the nozzle installation site; |
| Y | function that corrects unaccounted factors and errors of assumptions; |
| z | characteristic droplet size; |
| enthalpy flow due to mass transfer; | |
| gas flow through connection; | |
| mass flow of gas entering a manifold; | |
| change in gas mass due to evaporation of water and fuel; | |
| gas mass flowing out of the manifold; | |
| energy drain due to fuel vaporization; | |
| energy drain due to water evaporation; | |
| energy drain due to heating of fuel droplets to boiling point; | |
| energy drain due to heating of water droplets to boiling point; | |
| energy drain due to heating and evaporation of water and fuel; | |
| energy flow through the walls; | |
| σg | liquid surface tension coefficient; |
| μA | effective cross-sectional area; |
| μl | fluid dynamic viscosity coefficient; |
| σzi | share of fuel in the i-zone; |
| ρg | gas density; |
| ρl | fluid density; |
| τ | time; |
| τs | current time; |
| τs0i | time of fuel hit in i-zone; |
| τui | current time from the start of injection. |
References
- Gartner: The Use of Digital Twins is Becoming Widespread. Open Systems Publishing House. Available online: https://cio.ru/news/250219-Gartner-ispolzovanie-tsifrovyh-dvoynikov-stanovitsya-massovym (accessed on 15 June 2020).
- Malozemov, A.A.; Bondar, V.N.; Egorov, V.V.; Malozemov, G.A. Digital twins technology for internal combustion engines development. In Proceedings of the 2018 Global Smart Industry Conference (GloSIC), Chelyabinsk, Russia, 13–15 November 2018. [Google Scholar]
- Petrov, A.V. Imitation as the Basis of Technology of Digital Doubles; Irkutsk State Technical University: Irkutsk, Russia, 2018; pp. 56–66. [Google Scholar]
- Cynner, K. Theoretical Background of the Influence of Water Additives on the Working Process of Internal Combustion Engines; Forschung: Moscow, Russia, 1940; No. 5. (In Russian) [Google Scholar]
- Grankin, M.G.; Yakimushkin, R.V.; Omelchenko, A.S.; Kozlov, A.A. Analysis of ways to increase the traction properties of diesel engines. Sci. Mil. Secur. 2018, 1, 16–20. (In Russian) [Google Scholar]
- Romanov, S.V. Improving the Fuel Economy of Engines of Agricultural Machine-Tractor Units through the Use of Water Injection. Ph.D. Thesis, State Agrarian University of the North Urals, Troitsk, Russia, 2017; p. 207. (In Russian). [Google Scholar]
- Hlyupin, V.B. Method for Improving the Environmental Performance of a Vortex Chamber Diesel Engine by Injecting Water into the Intake Pipe. Ph.D. Thesis, Moscow State Technical University, Moscow, Russia, 2016; p. 142. (In Russian). [Google Scholar]
- Incropera, F.P.; DeWitt, F.; Hoboken, D.P. Fundamentals of Heat and Mass Transfer; Wiley: Hoboken, NJ, USA, 2007; pp. 490–511. (In Russian) [Google Scholar]
- Gamma Technologies LLC. Available online: https://www.gtisoft.com/ (accessed on 9 February 2020).
- AVL GmbH. Available online: https://www.avl.com (accessed on 12 July 2020).
- Ricardo plc. Available online: https://ricardo.com (accessed on 23 June 2020).
- Siemens Industry Software Inc. Available online: https://www.plm.automation.siemens.com/global/ru/products/simcenter/simcenter-amesim.html (accessed on 4 June 2020).
- Kang, Z.; Jiang, L.; Deng, J.; Wu, Z.; Li, L.; Liang, H. Simulation of intake manifold water injection in a heavy duty natural gas engine for performance and emissions enhancement. SAE Tech. Pap. 2018, 1, 1653. [Google Scholar]
- Lyshevskiy, A.S. Diesel Power Systems; Mashinostroeniye: Moscow, Russia, 1981; p. 216. (In Russian) [Google Scholar]
- Razleycev, N.F. Modeling and Optimization of the Combustion Process in Diesel Engines; Visha shkola: Harkiv, Ukraine, 1980; p. 169. (In Russian) [Google Scholar]
- Kuleshov, A.S. Development of Calculation Methods and Optimization of ICE Working Processes. Ph.D. Thesis, Moscow State Technical University, Moscow, Russia, 2012; p. 157. (In Russian). [Google Scholar]
- Hiroyasu, H.; Kadota, T.; Arai, M. Development and use of a spray combustion modeling to predict diesel engine efficiency and pollutant emissions. Bull. JSME 1983, 214, 576–583. [Google Scholar] [CrossRef]
- Voropay, P.I.; Shlenov, A.A. Improving the Reliability and Efficiency of Reciprocating Compressors; Publish House Nedra: Moscow, Russia, 1980; p. 360. (In Russian) [Google Scholar]
- Rosin, P.; Rammler, E. Die Korn zusammensetzung des Mahl—Gutes im Licht der Wahrscheinlichkeitslehre. Kolloid Z. 1934, 5, 16–26. [Google Scholar] [CrossRef]
- Razleycev, N.F. On the calculation of fuel evaporation in a diesel cylinder at a fuel supply section. ICE 1976, 23, 15–22. (In Russian) [Google Scholar]
- Volodin, A.I. Computer Simulation of Diesel Locomotive Operation; Transport: Moscow, Russia, 1985; p. 216. (In Russian) [Google Scholar]
- Tanatarov, M.A.; Ahmedshina, M.N.; Fashutdinov, R.A. Technological Calculations of Oil Refining Plants; Chemistry: Moscow, Russia, 1987; p. 352. (In Russian) [Google Scholar]
- Vargaftik, N.B. Handbook of Thermophysical Properties of Gases and Liquids; Nauka: Moscow, Russia, 1972; p. 721. (In Russian) [Google Scholar]
- Ryvkin, S.L.; Alexandrov, A.A. Thermophysical Properties of Water and Water Vapor; Energiya: Moscow, Russia, 1980; p. 424. (In Russian) [Google Scholar]
- Malozemov, A.A.; Bondar, V.N.; Malozemov, G.A. Diesel Engine Pre-Heating and Starting Simulation with Modelica Language. Available online: http://icie-rus.org/programme2018-eng.html (accessed on 13 June 2020).
- Malozyomov, A.A.; Kukis, V.S.; Gimazetdinov, R.R. Development of a Mathematical Model and Software for Simulation of Piston ICE; Engines: St. Petersburg, Russia, 2018; pp. 3–9. (In Russian) [Google Scholar]
- Modelica Association. Available online: https://www.modelica.org (accessed on 17 June 2020).
- Grankin, M.G. Modeling of Thermodynamic Processes with Enrichment of the Air Charge in the Intake Manifold of a Briefly Boosted Diesel Engine; Double Technology: Korolev, Russia, 2020; pp. 51–57. (In Russian) [Google Scholar]
- Malozemov, A.A. Development of software for calculation and optimization of diesel operating processes and fuel supply. Procedia Eng. 2015, 129, 724–730. [Google Scholar] [CrossRef]


© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bondar, V.; Aliukov, S.; Malozemov, A.; Das, A. Mathematical Model of Thermodynamic Processes in the Intake Manifold of a Diesel Engine with Fuel and Water Injection. Energies 2020, 13, 4315. https://doi.org/10.3390/en13174315
Bondar V, Aliukov S, Malozemov A, Das A. Mathematical Model of Thermodynamic Processes in the Intake Manifold of a Diesel Engine with Fuel and Water Injection. Energies. 2020; 13(17):4315. https://doi.org/10.3390/en13174315
Chicago/Turabian StyleBondar, Vladimir, Sergei Aliukov, Andrey Malozemov, and Arkaprava Das. 2020. "Mathematical Model of Thermodynamic Processes in the Intake Manifold of a Diesel Engine with Fuel and Water Injection" Energies 13, no. 17: 4315. https://doi.org/10.3390/en13174315
APA StyleBondar, V., Aliukov, S., Malozemov, A., & Das, A. (2020). Mathematical Model of Thermodynamic Processes in the Intake Manifold of a Diesel Engine with Fuel and Water Injection. Energies, 13(17), 4315. https://doi.org/10.3390/en13174315




