Abstract
Smart grid (SG) is a next-generation grid which is responsible for changing the lifestyle of modern society. It avoids the shortcomings of traditional grids by incorporating new technologies in the existing grids. In this paper, we have presented SG in detail with its features, advantages, and architecture. The demand side management techniques used in smart grid are also presented. With the wide usage of domestic appliances in homes, the residential users need to optimize the appliance scheduling strategies. These strategies require the consumer’s flexibility and awareness. Optimization of the power demand for home appliances is a challenge faced by both utility and consumers, particularly during peak hours when the consumption of electricity is on the higher side. Therefore, utility companies have introduced various time-varying incentives and dynamic pricing schemes that provides different rates of electricity at different times depending on consumption. The residential appliance scheduling problem (RASP) is the problem of scheduling appliances at appropriate periods considering the pricing schemes. The objectives of RASP are to minimize electricity cost (EC) of users, minimize the peak-to-average ratio (PAR), and improve the user satisfaction (US) level by minimizing waiting times for the appliances. Various methods have been studied for energy management in residential sectors which encourage the users to schedule their appliances efficiently. This paper aims to give an overview of optimization techniques for residential appliance scheduling. The reviewed studies are classified into classical techniques, heuristic approaches, and meta-heuristic algorithms. Based on this overview, the future research directions are proposed.
1. Introduction
Energy is one of the most important sources of socio-economic need and its growing demand is putting a lot of pressure on the traditional electric grid. Utility companies are facing challenges to fulfill this demand in residential households as well as industrial sectors. This issue can be solved either by producing new generation units or by using the available energy effectively. The first approach is expensive and time-consuming than the second one. Nowadays, information and communication technology has been evolved and various schemes have been proposed for energy consumption optimization. The increase in the energy consumption of residential sectors increases the load demand for consumers. Therefore, the burden on the existing power grid is increasing manifold. In addition, the traditional grid is not equipped for the two way communication between utility and consumers. It is unable to sense along the transmission lines which makes it unreliable and inefficient []. There is a requirement for a new architecture that will overcome these issues. Smart Grid is a future power grid that can enhance reliability, security, and control by upgrading generation, transmission, and distribution systems of the existing electric grid. This can be achieved by two-way communication between utility and end-users. By this communication, utilities can send the information and power flow to end-users and receive feedback. SG allows the utility and consumer to control electricity consumption through two-way communication between utility and consumers []. It provides opportunities for both consumers and utility companies to reduce the electricity cost. Along with minimizing electricity cost (EC), the other concerns of the smart grid include minimum peak-to-average ratio (PAR) and maximum user satisfaction (US) level. These objectives are achieved at the consumer level by effective management of electricity load profiles of appliances. The utility provides different pricing schemes: Time-of-use pricing (ToUP), critical peak pricing (CPP), real-time pricing (RTP), and inclined block rate pricing (IBR). Thus, electricity can be consumed effectively in the household appliances to optimize EC, PAR, and US according to mentioned pricing schemes. This optimization problem is called a residential appliance scheduling problem.
Residential appliance scheduling problem has been extensively studied in the literature in various ways [,,,]. Makhadmeh et al. [] have carried out an extensive survey on optimization methods for demand-side scheduling in smart homes. Jordehi [] has presented a review on optimization of demand response schemes in power systems. A review on demand response schemes based on objective functions including reduction of aggregate power consumption, maximization of social welfare, and minimization of electricity cost was conducted in []. Barbato and Capone [] presented optimization models and methods for residential and co-operative users using deterministic and stochastic approaches. Shakeri et al. [] have given an overview of demand response programs, their practices along with home energy management system (HEMS) and load management techniques. Leitão et al. [] have presented a thorough review of HEMS with insights on the household appliance management. In [], authors have explained mathematical models and heuristic optimization techniques integrated into HEMS for computing optimal appliance schedules and minimizing the energy usage by shifting the home appliances from peak to off-peak periods without hampering the user comfort. It is noted that, while the aforementioned reviews have been very valuable, they tend to be narrower in scope. They often focus either on exact methods or meta-heuristic algorithms to address the residential appliance scheduling problem (RASP). They tend to ignore the heuristic approaches for RASP due to their unavailability. In this paper, we review the most pertinent studies on RASP with focus on heuristic optimization.
The contributions of this overview are summarized as:
- We have provided an overview of smart grid with its architecture, demand side management techniques, and demand response programs used in smart grid including dynamic pricing schemes.
- Most of the existing surveys formulate RASP as a single objective problem focusing on cost optimization only. In this paper, we have presented the residential appliance scheduling problem using multi-objective optimization problem with three major optimization objectives which include electricity cost, peak-to-average ratio, and user satisfaction level. The user satisfaction parameter is formulated using the timing illustrations.
- We have presented the survey of most relevant studies done in the area of appliance scheduling with special focus on residential sector. The purpose of this overview is to give a more holistic view on RASP techniques including classical, heuristic, and meta-heuristic techniques with their objectives, contribution, and research gap.
- In this paper, we have classified the home appliances into shiftable interruptible, shiftable non-interruptible, and non-shiftable appliances on the basis of user’s comfort to provide clarity of classification. Several methods in existing literature do not consider non-shiftable category for appliance scheduling. It may lead to cross the highest allowable threshold for power consumption which can result in power failures in homes. Moreover, we have reviewed the existing methods which use more number of appliances which enhance the performance of the appliance scheduling algorithms.
The rest of the paper is structured as follows: In Section 2, smart grid, its architecture, demand side management techniques, and demand response programs are discussed. Section 3 presents the home energy management system model with classification of smart home appliances. In Section 4, a comprehensive definition of RASP is provided. In addition, the formulation of RASP is discussed with three major objective functions. Section 5 presents classical, heuristic, and meta-heuristic optimization techniques for appliance scheduling along with possible future directions. Finally, the conclusions of this overview are presented in Section 6.
2. Smart Grid
Smart grid (SG) concept is introduced at the beginning of the 2000s. It presents future power systems integrating advanced sensing and communication technologies. SG has many definitions but in short, it is an integration of Information and Communication Technology (ICT) into electric generation, transmission, and distribution networks. It increases the efficiency and sustainability of traditionally existing electric grid. The factors affecting the performance of the existing electric grid are listed below:
- Increasing demand for electricity.
- Shortfalls of generating units.
- Increasing power losses.
- Peak load management.
- Integration of renewable energy sources.
- Difficulties in meter reading.
- Customer satisfaction.
- Aging assets.
- Security of supply
2.1. Characteristics of Smart Grid
A smart grid is a modern electric infrastructure network. It is equipped with ICT that enables the grid to include renewable energy sources (RES) to manage the stability of the power system. A smart grid uses advanced ICTs and intelligent controllers to enable automated power networks [], in which the RESs are integrated into the grid based on reliability, safety, and control in distributed generation systems [].
In the smart grid, the power demands of industrial sectors, residential homes, and buildings are managed in such a way that the gap between the demand and supply is reduced. As the residential sector contributes to high load, it becomes necessary to manage appliances effectively to reduce the demand–supply gap and maintain system stability []. However, this is a challenging task as the residential appliance scheduling problem mentioned in our paper is for multiple appliances functioning at different times of the day. To achieve this task, home appliances must be scheduled based on the power supplied by the utility. Smart grids help in achieving the optimal use of appliances. Some of the functions of the smart grid are listed below:
- Efficient transmission of electricity.
- Reduced cost for utilities and thereby reducing cost for end-users.
- Faster electricity restoration after power failures.
- Reduce peak load which will help in reducing electricity rates.
- Use of RESs.
- Use of customer-owned local power generation systems like plug-in electric vehicles (PEVs).
2.2. Consumer Perspective
The SG promises several opportunities for consumers to save energy bills. In addition, it encourages consumers to install small-scaled home-based renewable energy sources. However, it depends on the consumer to act smartly on the available information. The consumers are benefited by using the smart grid in the various ways which are described in this section:
- The consumer will no longer have to wait for monthly electricity bills to know how much electricity he/she uses. Using the smart meter, a timely and clear picture can be obtained.
- The consumer can be able to see the price of electricity at a particular hour so that he/she can manage the use of electricity. It will ensure the less usage when the price is high.
- Consumers can be able to generate their own power by putting rooftop solar which will help them save money and manage the electricity well and will also be able to contribute the surplus power to main grid.
2.3. Smart Grid over Existing Grid
A systematic comparison between smart grid and existing traditional grid is covered in this subsection, that focuses on technology, metering infrastructure, communication, generation, sensors, monitoring, fault management, and restoration. Table 1 shows the advantages of the SG over the existing grid.

Table 1.
Advantages of smart grid over existing grids.
2.4. Architecture of Smart Grid
The architecture of the smart grid is shown in Figure 1. It comprises of various domains that include generation, transmission, distribution, end users, service providers, energy market, operations, and demand response. Each of these domains is discussed below:
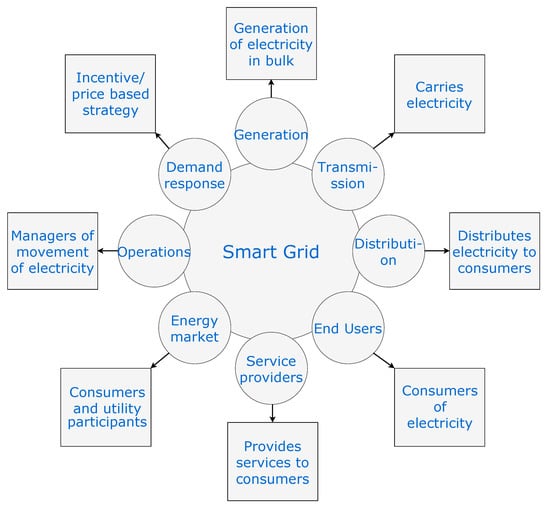
Figure 1.
Architecture of smart grid.
2.4.1. Generation
It is the domain that generates electricity from various forms of energy which includes Thermal, hydro, wind, coal, solar, biomass, RESs, etc. New requirements of generation domain include greenhouse gas emission controls, increase in RESs, electric vehicles, and provision of storage such as batteries.
2.4.2. Transmission
It acts as an interface between the generation and distribution domains. This domain transfers energy from generating sources to distribution sources via several substations. The transmission network is operated by regional transmission operator (RTO) whose goal is to balance load and supply across the network.
2.4.3. Distribution
This domain is responsible for distributing the electricity to consumers via the AC or DC network. This domain connects intelligent electronic devices (IEDs) to smart meters (SM). Also, it manages them through a bi-directional wired/wireless communication channel.
2.4.4. End Users
It is the domain where electricity is consumed. Usually, it is classified into two sub-domains which include home/building users and industrial users. The end-user domain and its functions are depicted in Figure 2.
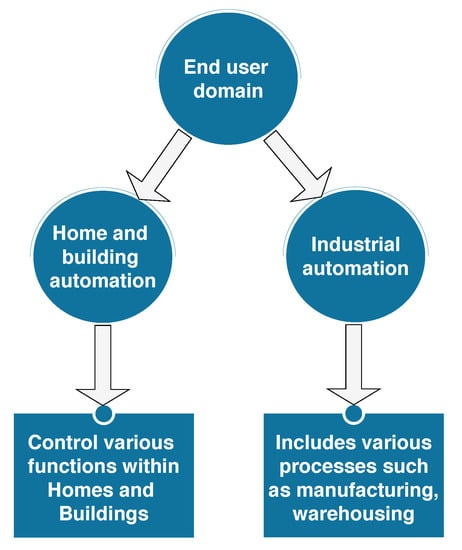
Figure 2.
End-user domain participators.
2.4.5. Service Provider
It is the domain that provides services to the distributors and end-users. These services include installation, maintenance, billing, end-user account maintenance, monitoring and controlling home energy use, managing customer relationships, etc.
2.4.6. Market
It is the domain where market assets are bought and sold. The key issues in the market domain are listed below:
- Communication mechanism for prices between markets and end-user domain.
- Interoperability among providers (supply) and consumers (demand).
- Regulation of trading, retailing, and wholesaling of energy.
- Extension of pricing signals to each end-user.
2.4.7. Operations
It helps in the smooth operation of the power system. It includes network operations, supervising network connectivity, meter reading and control, supply chain logistics, maintenance of continuous power supply, security management such as fault analysis, etc.
2.4.8. Demand Response (DR)
Demand response (DR) is a strategy by which a consumer can play a key role in the operation of the smart grid either by reducing the peak load or shifting the electricity consumption from on-peak hours to off-peak based on dynamic pricing schemes employed by the utility. The DR programs are classified into two types namely incentive-based DR programs and price-based DR programs. Demand response is discussed in detail in Section 2.6.
2.5. Demand Side Management (DSM)
Demand side management (DSM) is one of the important components in a smart grid that promises consumers to decide their electricity consumption patterns. The DSM [,] is a key feature of energy management in the smart grid. It can be defined as an alteration of consumption patterns of users to bring the desired changes in the load curves of power systems. It focuses on utilizing power-saving strategies, dynamic electric tariffs, incentive-based DR programs to reduce the peak load instead of having to install new generating capacities, or reinforcing the transmission and distribution corridor. The objectives of DSM include: utilize RESs, maximize economic benefit, minimize power from the utility, and minimize peak load.
Necessity of DSM
The DSM is necessary due to following reasons:
- Increasing usage of appliances during peak hours and peak energy deficit.
- Scarcity of fossil fuels.
- Global warming concern.
- Penetration of highly stochastic RESs.
Since power demand is regularly increasing, there could be a need of installing new generation units for the required power in the future. The DSM manages this issue by reducing peak load. Therefore, we can certainly delay the new installations for a few years. However, consumers need to act smartly by shifting their power consumption from on-peak to off-peak to maintain a balance between demand and supply []. The DSM helps utility companies in reducing the peak load and flatten the load profiles for consumers. This makes the grid more sustainable as well as helps in minimizing overall operational costs. During the on-peak consumption hours, there is a sudden spike in demand. It solves this issue by reducing power consumption during peak hours rather than burdening new installations and generation capacities to fulfil the demand [,,]. Thus, the DSM aims to balance the supply and the demand for power systems [].
The DSM techniques are deployed to overcome power consumption challenges. Several DSM techniques are used in the literature [,,,,,,]. The key objectives of these techniques are the minimization of peak load and electricity cost. Most of the techniques are system-specific strategies [,,,], and few of which are inapplicable to practical scenarios that require a large number of electric appliances. In [], dynamic programming is used to achieve DSM while the authors in [,] have used linear programming. These techniques are computationally slower and not capable to manage a large number of appliances. The SG requires handling a large number of appliances with controllable loads. Some of these appliances are required to function over a few hours (for example, refrigerator). Thus, DSM techniques need to manage all possible durations of appliance loads. In addition, there is a requirement of DSM techniques which are faster as well as effective. Logenthiran et al. [] proposed a demand-side management technique using an evolutionary heuristic algorithm. Further, a genetic algorithm-based DSM for a power optimization problem was presented in [].
Figure 3 represents six different load curves of the demands of residential users. The load curve is defined as the variation of load concerning time. There are six different DSM techniques in which load curves are altered between on-peak and off-peak duration [,,] which are listed below:
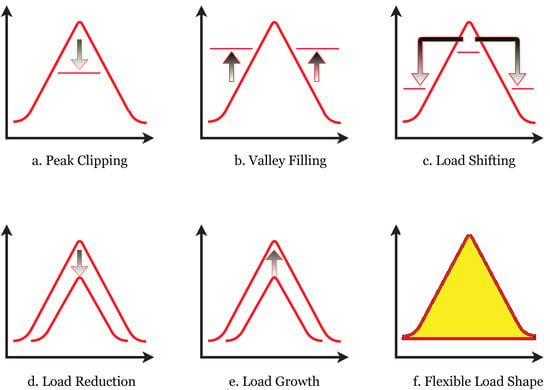
Figure 3.
Demand side management techniques.
- (a)
- Peak Clipping: [,]It is a direct load control technique which focuses on decreasing the demand during peak hours. This technique is important where there is a problem of investments to install new generation units.
- (b)
- Valley Filling: []It focuses on increasing consumption during off-peak hours. The demand in off-peak hours is achieved by encouraging end-users to consume the electricity by paying lower prices during that time.
- (c)
- Load shifting: []It is a widely used and most effective DSM technique. It is achieved by shifting the load from peak to off-peak hours. Customers are encouraged by paying cheaper tariffs during off-peak hours. This technique is the best solution from a utility point of view.
- (d)
- Load Reduction: []This technique is also called as strategic energy conservation. As shown in Figure 3d, the area under the new characteristic is reduced than the previous one. Thus, the peak can be reduced. Load reduction is achieved by using more efficient appliances which is also important at the global level.
- (e)
- Load Growth: [,,]This technique is also called as load building. It increases the power consumption of users with a certain limit. It is achieved by encouraging users to spend the electricity to maintain the power system capacities and for the smooth operation of the power system.
- (f)
- Flexible Load Shape: [,,]In this technique, there is redistribution of loads to various time slots. Here, customers with flexible loads are identified who are ready to control their consumption in exchange for various incentives.
2.6. Demand Response
Out of the total electricity produced in the world, the residential sector consumes about 30–40% of it []. As the population is growing, the demand for electricity is increasing. Thus, peak demand is also increasing. Conventionally, utility provider companies used to balance the demand and supply through traditional power units. However, with an increase in global warming and greenhouse emissions, it is not preferred. To solve this issue, utility companies increased energy generation capacities. By integrating more RESs, incorporating the energy storage systems like batteries, EVs, and deploying DR programs, the goal of demand–supply balance is achieved. Thus, DR programs provide opportunities for users to play a part in the operation of smart grids by reducing the peak load or shifting the energy consumption in response to dynamic pricing or other methods of incentives. The following are the goals of the demand response:
- To reduce total electricity consumption.
- To reduce the total required power generation.
- To promote the idea of clean and green energy.
Figure 4 depicts the classification of DSM. The DSM is used for achieving the energy efficiency of the smart grid [,]. However, the demand response is a key component in DSM [,]. In simple words, DR is the demand which is responsive to economic signals. DR is used in the smart grid to design efficient programs []. The main difference between DSM and DR is that DSM is performed at the utility side whereas DR is performed at both utility and consumer side separately/together to achieve minimum peak load and electricity cost.
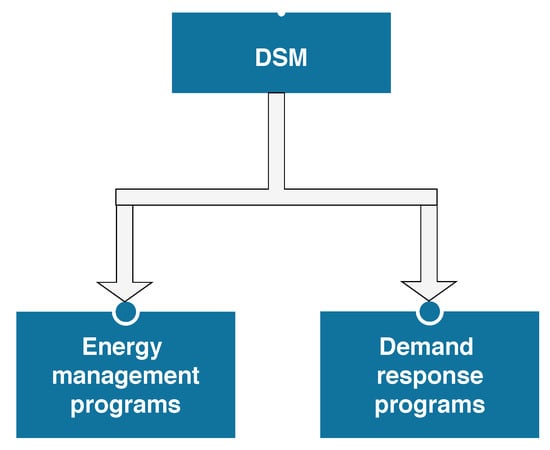
Figure 4.
Demand side management (DSM) classification.
The literature provides various definitions of DR. Authors in [,] define DR as “changes in electric usage by end-use customers from their normal consumption patterns in response to changes in the price of electricity over time, or to incentive payments designed to induce lower electricity use at times of high wholesale market prices or when system reliability is jeopardized”. This definition indicates that DR programs aim to help power systems during peak demand or contingencies. Figure 5 depicts the DR classification. DR programs are classified into incentive-based DR and price-based DR [].
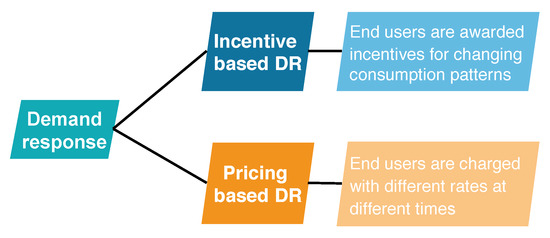
Figure 5.
Demand response classification.
2.6.1. Incentive-Based DR
Incentive-based DR (IBDR) provides incentives to the consumers for changing their consumption patterns as per the desire of the utilities. IBDR is an agreement between utility and end-users. Utility companies directly control the consumer’s electricity loads and consumers in return get the incentives from utility. It is more flexible about aiding the utilities to attain the required demand response resources. IBDR includes direct load control, emergency demand response program, demand bidding program, capacity market program, interruptible tariffs, and ancillary service markets []. For the IBDR program, there are fixed or time-varying incentives and specific constraints to administrate the consumer’s appliances remotely [,]. The consumers are expected to reduce their power consumption during the peak hours of high system stress []. For example, in direct load control-based IBDR [], heavy load appliances such as water heater and air conditioners can be remotely turned off by the utility.
2.6.2. Price-Based DR
A price-based DR (PBDR) program passes on the benefits of the wholesale electricity price market directly to consumers so that they can pay for electricity at different times of the day. In the PBDR program, the time-varying prices encourage the consumers to adjust their flexible loads to different periods to avail the facility of lower prices []. The utility companies employ dynamic pricing schemes to affect consumer behavior. The PBDR pricing schemes include time-of-use pricing (ToUP), critical peak pricing (CPP), real-time pricing (RTP), and inclined block rate (IBR) as shown in Figure 6. In ToUP, the electricity prices vary during the day. Thus, the consumers are encouraged to shift their consumption from peak hours to off-peak hours [,,]. A CPP is the scheme in which prices are very high when consumption is more than 20 kW. The price is a pre-specified for forecasted critical periods [,]. The RTP is a scheme that changes dynamically every hour or day. Utility announces the upcoming day’s predicted real-time price beforehand which is called day ahead pricing (DAP) and customers then schedule their consumption a day before the execution [,,]. In IBR, electricity pricing is divided into multiple blocks. Initially, the price of the first block is at the lowest. As the consumer purchases more electricity during a month, IBR pricing falls to the second block which is more expensive. This process is repeated until the month is over. At the end of the month, IBR is reset and next month will start again from block 1. In practical applications, the PBDR program is usually more suited for residential customers than the IBDR program []. The pricing schemes are discussed in detail below:
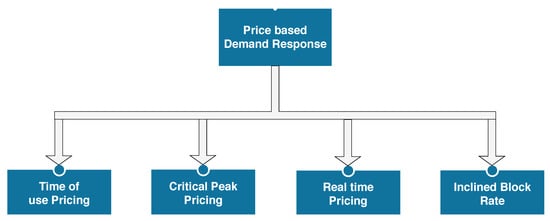
Figure 6.
Classification of price-based demand response.
- Time-Of-Use Pricing (ToUP):A ToUP is adjusted on different time blocks during a day (for example, four-hour block). The rate of ToUP is different at different blocks. Typically, a day is divided into three blocks which are peak, mid-peak, and off-peak. The price during peak periods is kept high by the utility. The cost of electricity is high when consumed during peak hours. Therefore, consumers are encouraged to minimize their usage in peak hours and shift it to mid-peak or off-peak hours to balance the load profile.
- Critical Peak Pricing (CPP):A CPP is implemented in homes only when electricity usage is more than 20 kW and where the facility of a smart meter is available which records the consumption after every fifteen minutes. If load demand is very high (more than 20 kW) during a specific period, then the period is called as critical period. The CPP is declared only when the day is forecasted as a critical period. This scheme is similar to ToUP. In a critical period, the normal peak pricing of ToUP is replaced by CPP. Thus, consumers have to shift their consumption out of the critical period to balance the power demand.
- Real-Time Pricing (RTP):The price in RTP varies depending on hours/days. This impacts the consumption of users during peak periods. A RTP can be classified into two schemes, namely, day-ahead pricing (DAP) and hourly pricing (HP). In the DAP scheme, utility publishes price details to users one day beforehand. For HP, it is provided every hour before consumption. The advantages of RTP are discussed in []. A RTP can be classified into two parts: first part records the consumer response based on real-time prices [], while the second part records the consumer response based on optimized real-time prices published by utility [].
- Inclining Block Rate (IBR):IBR scheme is adopted by pacific gas and electric, Southern California Edison, San Diego gas companies since 1980s. This pricing scheme charges more for each incremental block of consumption. For instance, first block of 50 kWh consumption costs 2 units, the second block of 50 kWh would cost 2.5 units and so on. In other words, it offers multi-level pricing. If the electricity consumption during a block exceeds a certain threshold, then price will also increase to a higher value for subsequent blocks. The motive behind IBR scheme is to encourage consumers to self-generate the electricity by using local generating resources, to conserve the energy efficiently, to distribute the load to different time periods of the day to avoid high electricity rates. Thus, this pricing scheme provides help in reducing PAR to achieve demand response.
3. Home Energy Management System (HEMS)
A DR programs can be implemented for residential, commercial, and industrial users. Among these, residential users have proved to be more responsive in DR since the residential appliances are more elastic, interruptible, and shiftable []. The amount of electricity consumed in the residential sector has increased rapidly because of the modernistic lifestyle. A recent study shows that the residential sector consumes 30% of overall electrical energy [,]. Thus, demand-side management of smart homes has become essential to meet their excessive electricity consumption. The DR programs for residential users is called as home energy management. To implement DR programs in the residential sector, advanced metering infrastructure (AMI) is installed in every home. AMI keeps the track of energy consumption usage of different appliances at different times. It determines the on-off status of home appliances at different times. For every smart home, there exists HEMS model which helps consumers by scheduling their appliances with minimum electricity consumption and maximum user comfort. In addition, it provides communication between home appliances and utility companies to shift the demand. HEMS allows consumers to automate energy use within a household. HEMS is capable of sending signals to smart home controllers to shift their appliances to avoid power blackouts during peak periods. There are various advantages of HEMS for consumers including electricity bill reduction, peak load reduction, maximum utilization of RESs, achieve energy efficiency.
Figure 7 depicts the HEMS model with its components. In this model, we have considered the central DSM controller, smart meter, energy consumption scheduler (ECS), and home appliances. HEMS comprises software and hardware devices. Central DSM controller co-ordinates communication between utility and home. Consumer preference is the ordered priority of appliances to be scheduled by the user according to their comfort. A smart meter is responsible for two-way communication between the utility and the consumer. It collects detailed information about the user’s consumption pattern. HEMS starts functioning when utility sends dynamic pricing signals to the smart meter. These signals are further sent to energy consumption scheduler. ECS is the heart of home energy management system which is capable of exchanging the information among HEMS components. Various algorithms are embedded in ECS to generate the appliance schedules of the user. Finally, the smart meter sends the user feedback to the utility. In the HEMS model below, we have categorized the home appliances into three types which are shiftable interruptible appliances, shiftable non-interruptible appliances, and non-shiftable appliances. Appliance classification is discussed in Section 3.1.
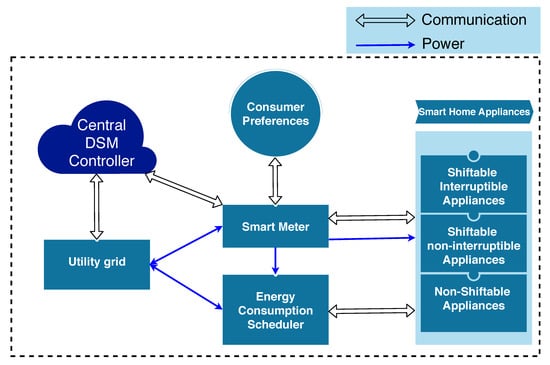
Figure 7.
Home energy system management model.
3.1. Appliance Classification
In this subsection, we have broadly classified 13 frequently operating home appliances into three categories based on the clarity of classification which are non-shiftable appliances (NS), shiftable non-interruptible appliances (SNI), and shiftable interruptible appliances (SI). The classification of the appliances varies depending on the user. Table 2 displays smart appliances along with their average power ratings (kWh) and the corresponding duration in time slots (hr).

Table 2.
Power ratings of different appliances of a single user with a length of operational time.
- Non-Shiftable (NS) appliances:These appliances cannot be shifted to other slots. They should remain ON continuously without any interruption for the entire duration for which they are scheduled. For instance, refrigerator, tube-lights.
- Shiftable Non-Interruptible (SNI) appliances:These appliances can be adjusted to any other time slots. However, these appliances cannot be interrupted during their functioning. For instance, washing machine, electric heater.
- Shiftable Interruptible (SI) appliances:These appliances are flexible and can be adjusted to other time intervals. They can be interrupted during their functioning. For instance, vacuum cleaner, dishwasher, etc.
3.2. Datasets for Appliances Classification and Their Energy Consumption
In literature, various smart home appliances are classified according to the user’s comfort and clarity of classification. Authors in the literature have used their own classification for scheduling of home appliances. Faisal et al. [] classified fifteen appliances into seven interruptible, two non-interruptible, and six base appliances. The interruptible appliances include the vacuum cleaner, sensors, PHEV, dishwasher, stove, microwave, and other occasional loads. The non-interruptible appliances are clothes washer and spin dryer while the base appliances include oven, TV, PC, laptop, radio, and coffee maker. Shuja et al. [] classified fifteen appliances into seven shiftable, two non-shiftable, and six fixed appliances. Shiftable appliances include water pump, water heater, vacuum cleaner, dishwasher, steam iron, air conditioner, and refrigerator. Non-shiftable appliances include washing machines and tumble dryer while fixed appliances include TV, oven, desktop PC, blender, laptop, and ceiling fan.
Thirteen smart home appliances were used in [] classified into eight shiftable and five non-shiftable appliances. Shiftable appliances include air conditioner, clothes dryer, washing machine, dishwasher, refrigerator, coffee maker, water heater, and space heater while the non-shiftable appliances were fan, light, iron, toaster, and microwave oven. Abbasi et al. [] used eleven appliances which were classified into three categories fixed appliances, shiftable appliances, interruptible appliances. Fixed appliances include light, oven, blender, coffee maker. Shiftable appliances include cloth dryer, washing machine, dishwasher while the interruptible appliances were water heater, iron, vacuum cleaner, space heater. Eight shiftable appliances namely dishwasher, refrigerator air conditioner, clothes dryer, water heater, coffee maker, space heater, dishwasher and six non-shiftable, namely, fan, light, blender, clothes iron, oven, and vacuum cleaner were used in []. The datasets for energy consumption profiles for different appliances of various households are given in [,,].
4. Residential Appliance Scheduling Problem (RASP)
There are many scheduling problems encountered in various fields. The main goal of scheduling any event is to perform the intended activities/tasks in an organized manner without any interruption. Some of the general scheduling problems mentioned in the literature are job scheduling [], flow shop scheduling [], and power scheduling problems [].
The day by day increase in the electricity demand for residential sectors is responsible for increasing the gap between demand and supply. To reduce this gap, there exist two possible solutions: (i) Installing new generation units. (ii) Efficient utilization of energy sources. The first approach is not feasible as it is expensive and takes more time to build new units. Hence, the second approach is preferred as it is economical and does not require installing new units. The primary objective of a smart grid is to utilize the energy sources so that it reduces the power demand during peak periods and thereby reduces the cost of power generation. To achieve this objective, the optimization of power consumption is necessary. With the development of SG, it is possible to optimize power consumption by scheduling smart home appliances effectively. The reduction of the electricity bill is the major advantage gained by consumers in optimizing their appliance consumption. Non-scheduling of appliances leads to high electricity cost, imbalance in demand and supply, high power demand during peak periods. For a smart home with multiple appliances, in peak hours, the electricity demand is higher than electricity production. Thus, HEMS can face difficulties in maintaining the balance between demand and supply. To avoid this problem, a proficient scheme is required that can distribute the load between peak hours and off-peak hours. This is called power scheduling. In the power scheduling problem, the objective of consumers is to have a minimum electricity bill, minimum consumption, minimum PAR, minimum waiting time. In smart homes, the majority of electricity is consumed by the use of various appliances. Therefore, it is required to modify their consumption pattern effectively to achieve the aforementioned objectives. Thus, we study the topic of power scheduling in smart homes.
The residential appliance scheduling problem (RASP) is a problem that considers residential home appliances and schedules them within a specific time interval provided by the consumer concerning a set of constraints. These constraints are classified into two types, namely, soft constraints and hard constraints []. Soft constraints are the constraints that are not mandatory to satisfy but it is desired to follow them. For example, the appliance can be scheduled at the beginning of its operational period to finish its working before its ending time whereas hard constraints are those which are mandatory to satisfy. For example, the appliance must be scheduled within its stipulated period of operation. Overall, RASP achieves the following objectives:
- To minimize electricity cost (EC).
- To minimize peak-to-average ratio (PAR).
- To maximize user satisfaction (US) level.
4.1. Appliance Scheduling Model
This section provides an appliance scheduling model with the help of three objective functions. For simplicity, we have formulated RASP for a single residential home. However, it can be extended to multiple homes as well. Three optimization functions required for RASP are explained with their mathematical formulations.
4.1.1. Minimization of Electricity Cost (EC)
The EC is the cost paid by consumers to the utility and is computed as power consumed by appliances weighted with the price announced by the utility in that hour. The formulae for calculation of EC over an hour and complete day are given by Equations (1) and (2).
Electricity cost for 1 h:
Electricity cost for a complete day:
where, denotes the specific appliance. is the power rating of each appliance. Here we have considered n appliances. denotes the length of operational time of each appliance and is electricity tariff price generated by the utility for corresponding hour h. .
The objective function for cost optimization can be written as:
4.1.2. Minimization of Peak to Average Ratio (PAR)
Peak to average load ratio is computed as:
is maximum load consumed by home appliances in a smart home for a particular hour and average demand is load consumed in one day.
Let us assume be the load consumed in an hour. It is calculated using Equation (5):
where, is the power rating of all the appliances which are functioning during that hour.
Similarly, is the average load for the entire day which is computed using Equation (6):
The Equation (4) for PAR can be symbolized as below:
The objective function for PAR optimization can be written as:
4.1.3. Maximization of User Satisfaction (US)
This parameter is evaluated in terms of waiting time (). Smaller the waiting time, the higher is the user satisfaction level. Thus, to improve US, we need to minimize the waiting time or delay for appliances to start. Figure 8 depicts the execution pattern of the appliance. is operational time for appliance i.e., allowable duration for the appliance to schedule which is given by the user. is length of operational time i.e., time for which appliance is running. Here, for illustration of the waiting time, we have considered one appliance. and denote starting and ending times of appliance to be scheduled. is the actual starting time when the appliance is started by HEMS and is ending time when the appliance stops running. Thus, , where denotes the length of operational time for the appliance.
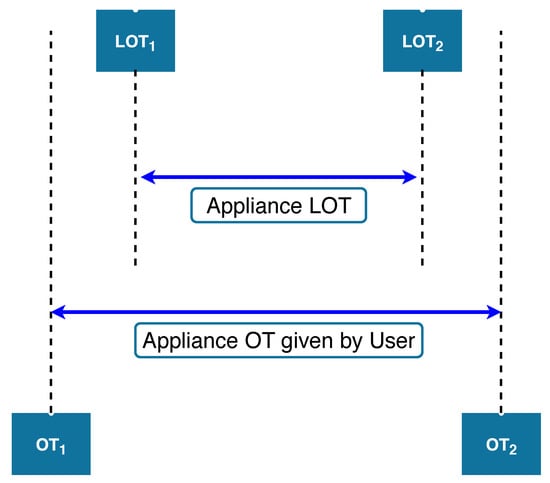
Figure 8.
Execution pattern for an appliance with timing illustrations.
Waiting time value lies between 0 and 1. The for a single appliance is computed using Equation (9).
5. Optimization Techniques for RASP
The residential appliance scheduling problem is an optimization problem for scheduling the appliances in an energy-efficient manner with minimum EC, minimum PAR, and the maximum US. Mahmood et al. [] have presented the overview of load management techniques in which the authors have described the home energy management system and optimization techniques associated with it. Beaudin and Zareipour [] have discussed the comparative analysis of literature in HEMS. They have presented a review on multi-objective appliance scheduling techniques. Schminke [] has presented an overview of the current state of research on energy management systems in buildings. Makhadmeh et al [] have carried out a comprehensive survey of power scheduling problem considering exact algorithms and meta-heuristic algorithms. However, authors have not considered heuristic approaches for RASP. In this overview of RASP, we have classified the existing research works into three categories which include classical techniques, heuristic approaches, and meta-heuristic algorithms with a focus on heuristic approach towards optimization. An overview of the aforementioned techniques has been presented in this section.
5.1. Classical Techniques
The RASP can be solved by different classical optimization techniques. Mainly, RASP can be formulated as a linear programming (LP) and non-linear programming (NLP) problem. Depending on the formulation, LP or NLP model can be used to solve RASP. To determine the on-off status of appliances, binary decision variables are required. Thus, mixed-integer linear programming (MILP) or mixed-integer non-linear programming (MINLP) techniques are used. These techniques can guarantee an optimal solution. Various LP- and NLP-based optimization techniques to solve RASP in smart homes have been studied in the literature. The following section presents an overview of the existing classical techniques for RASP.
5.1.1. LP and MILP Techniques
LP problems are the simplest forms of optimization problem where objectives and constraints are linear. In LP, a global optimum solution is guaranteed. In addition, the structure of MILP is modular and can be modified to fit into the desired optimization objectives. Some of the LP techniques for RASP are presented in this section.
Kurucz et al. [] have used a linear programming model using direct load control (DLC) for appliance scheduling. The PAR reduction has been achieved through this model. The proposed model is used for finding the optimal number of residential consumers participating in the DLC program. Chen et al. [] have proposed an LP-based appliance scheduling algorithm for smart homes to compute deterministic scheduling. The total cost for the consumer is minimized in the proposed algorithm. Authors have used the time-varying RTP pricing model. The energy-efficient stochastic scheduling algorithm has considered the uncertainties in appliance scheduling and the monetary expenses of consumers are minimized by optimally scheduling the appliances. In Mohsenian et al. [], optimal residential energy consumption model is proposed. The model attempts to minimize electricity payment of household and waiting time for the operation of household appliances. A linear programming model is proposed for the optimization of objective functions with the combination of IBR and RTP schemes. The simulation results show that there is a significant reduction in PAR as well. The results show 38% PAR and 25% bill saving. The results also show that the design can be extended for more households which helps in PAR minimization and load balancing.
In [], the appliance scheduling optimization problem is formulated as a computationally efficient mixed-integer linear programming (MILP) problem. The authors have analyzed the consumption scheduling mechanism within the home area network. The objective of this study is to minimize EC paid by the user. Six appliances each for six dwellings are considered. The results show that the cost reduction is extended to 16% from 3%. The MILP model for appliance scheduling in smart homes was proposed in []. The study has focused on the minimization of the total cost of electricity. A detailed HEM structure is proposed considering the energy storage system and distributed generation. Thermostatic and non-thermostatic control loads have been modeled using MILP to achieve total cost reduction.
Ratnam et al. [] proposed an LP-based algorithm for HEMS. The objective of the algorithm is to maximize the operational savings. The proposed algorithm has considered the data of 145 residential users. The result shows that most of them exhibit operational savings. In [], the RASP optimization problem is modeled as MILP. The authors have used the multi-objective mixed-integer linear programming (MOMILP) technique to solve RASP. The objective of the proposed model is to reduce PAR and EC. The authors have incorporated a battery storage system to save power and enhance the effectiveness of the proposed model. In [], HEMS for appliance scheduling has been proposed. The main objective of the work is to minimize the energy cost while maintaining user satisfaction level. The MILP optimization model is developed to achieve the aforementioned objectives. The authors have considered renewable local energy sources, electric vehicles, and batteries. The results show that cost saving is exhibited major change from 8% to 389%. Rafkaoui et al. [] used MILP-based optimization algorithm to minimize PAR and EC in for scheduling five home appliances. The algorithm compares EC with and without RES. The result shows that EC is reduced by 38% without RES and 47% with RES.
5.1.2. NLP and MINLP Techniques
This section presents non-linear programming-based models for solving the RASP problem. NLP techniques are used for solving optimization problems in which the relationship between objectives and decision variables is non-linear. The MINLP problems are difficult to solve. It may not guarantee a solution even if it exists. Since RASP is formulated as a linear problem in most of the existing works, very few optimization algorithms using non-linear programming techniques are published in the literature.
In [], authors have used MINLP to schedule ten home appliances to minimize EC. In the proposed design, the ToUP scheme is used with the facility of incentivizing the user during peak hours. The results show that EC is reduced by more than 25%.
Shafie-Khah et al. [] used NLP for deciding on and off status of appliances in different time slots. The objective functions considered in this method are the reduction of EC and consumer fatigue. Different price-based and incentive-based programs with CPP, ToUP, RTP are used. A stochastic-based HEMS model is proposed considering the uncertainties of EVs, energy storage systems and small-scaled RESs. The result shows that the proposed system considerably reduces EC and consumer fatigue.
In [], the MINLP model is considered for the optimization of energy hubs. The objective of the proposed approach is to reduce the total cost of an energy hub. The focus is to schedule day ahead appliances in an energy hub with an RTP scheme. The consumption of energy hub at different times with different loads are considered. The approach shows that the total cost of an energy hub and the total cost of purchased electricity from the grid is reduced.
Ampimah et al. [] proposed a constrained non linear programming (CNLP)-based scheme for optimization of residential consumption of electricity. The objective of the proposed scheme is to reduce EC and PAR. The credit function is used to enable residential users to shift their load from on-peak to off-peak periods. The consumers are encouraged to minimize peak load and increase the off-peak load to help generators reduce the overall cost and increase revenue at off-peak.
The RASP is complex and involves a large number of appliances. It involves finding the best solution to achieve the optimization objectives. The classical techniques mentioned in this section are efficient for solving low scale optimization problem where less number of appliances are involved. However, these techniques fail to solve high scale optimization problems. Moreover, classical techniques face difficulties in convergence. These techniques often converge at a local optimum solution. In addition, some of these optimization techniques are computationally expensive and difficult to solve. Thus, there is a need for optimization techniques that are efficient and faster. Heuristic approaches are often used to find the optimal solution and they are faster than classical techniques. The following section presents the overview of heuristic approaches to solve residential appliance scheduling problems.
5.2. Heuristic Approaches
Heuristic approaches are knowledge-based approaches to find an approximate solution to an optimization problem based on the specified rules. For energy scheduling, these approaches require knowledge of the energy systems in homes. They are efficient, well designed, and faster than classical techniques. In addition, they are useful for reducing the computational burden of an appliance scheduling algorithm and capable of approximating the optimal schedule. Recent literature on RASP focus on heuristic approaches. However, these approaches achieve good but not the optimal solution.
A heuristic algorithm to compute price update step size and price update interval has been proposed in []. It is noted that due to network delays and transmission errors, price update intervals may get fluctuated. The proposed algorithm indicates that the deviation of the power load can be limited for several users.
In [,], authors have proposed and partially evaluated a heuristic approach for scheduling the residential appliances. The approach uses greedy processing to schedule home appliances. The proposed approach aims to minimize EC with a set of constraints over the appliances. Initial simulation-based investigations indicated that the obtained cost was within 5% of the exact algorithm.
An aggregator-based residential demand response approach for scheduling smart home appliances has been proposed in []. The aggregator entity is responsible for scheduling the residential consumer assets that include smart appliances. The authors have introduced a new customer incentive pricing (CIP) scheme. The objective of this approach is to optimize the profit of aggregators. The simulation results of the proposed heuristic approach show that the aggregator profit is optimized.
A heuristic scheduling algorithm for residential home IDSS has presented in []. IDSS is an intelligent decision support system that enables consumers to respond to varying electricity prices during a day. RTP, ToUP, two-tier pricing (2TP) schemes have been used. The heuristic approach greedily schedules the appliances to minimize EC. The results indicate that the gap between optimal achievable costs is negligible.
Jindal et al. [] have used a heuristic approach for appliance scheduling. The appliance scheduling problem is divided into subproblems of different time slots. The heuristic solution is designed for each subproblem. The objective of the proposed approach is to manage the load requirements of the home to create a balance between supply and demand. The authors have designed a heuristic-based appliance scheduling scheme that determines the optimal appliance schedule by achieving the load balance in the system. Matallanas et al. [] described an artificial neural network (ANN) control system for active demand-side management (ADSM). The control system consists of a scheduler and coordinator. Both these modules are implemented in ANN. The system achieves the objective of maximizing the local generation, scheduling the appliances, and enhancing the local energy performance.
A residential energy management mechanism for the smart grid using markov decision process (MDP) proposed in []. The objective of the work is to minimize the energy expenses of consumers. central energy management unit layer (CEMU) interacts with home energy management unit (HEMU) to fulfill the energy demand. CEMU follows its dynamic pricing mechanism. The results show that expenses for the consumer are reduced.
Lee et al. [] have proposed backtracking-based power scheduling scheme for smart grid homes. They have designed a power scheduler capable of reducing the peak load. The proposed model aims to reduce the peak load in homes and power transmission networks. The authors have considered homes where the number of appliances is less than ten. The results show that the proposed method reduces the peak load of up to 23.1%.
Tiptipakorn and Lee [] have developed consumer-centered control strategies for a heavy load such as air conditioner and water heater as they account for the highest electricity consumption. The objective of the work is to balance user comfort and consumer price preferences. The proposed control strategy achieves the said objectives with saving in EC for consumers.
The comparative analysis of the aforementioned schemes is given in Table 3.

Table 3.
Summarized heuristic approaches for the residential appliance scheduling problem (RASP).
5.3. Meta-Heuristics Algorithms
Meta-heuristic algorithms are used to solve various optimization problems. Meta-heuristic is a concept of iterative generation process which guides the underlying heuristics to optimize the search space. These algorithms are more efficient and converging than the classical approaches because of their efficiency to explore the search space to reach a global optimum solution []. They make very few assumptions about the problem being optimized. They use a large population size that travels randomly within a search space until the solution is converged. Meta-heuristics can often find good solutions with less computational time than classical and heuristic approaches. These algorithms make complex problems like RASP solvable in an acceptable time. Several meta-heuristic algorithms for RASP are studied in the literature. Genetic algorithm (GA) [,], particle swarm optimization (PSO) [], wind-driven optimization (WDO) [], ant colony optimization (ACO) [] are some of the most prominent meta-heuristic algorithms. The existing research works in meta-heuristic algorithms involve HEMS-based appliance scheduling methods. Dynamic pricing schemes are used to evaluate the performance of the proposed schemes. These schemes schedule the appliances in such a way that EC, PAR are minimized and user satisfaction is maximized. Some of the nature-inspired meta-heuristic algorithms are discussed below:
In [], a genetic algorithm-based thermal control model is developed for optimal scheduling of inverter ACs. The authors have considered inverter-ACs specifically instead of single-speed ACs because, nowadays, inverter ACs are installed in residential buildings. The proposed model proved that EC and PAR are reduced while meeting the thermal constraints. Chui et al. [] have proposed a genetic algorithm-based support vector machine multiple-kernel approach for load monitoring with consideration of 20 appliances. Genetic algorithm helps in solving multi-objective optimization problem to achieve the overall accuracy of 91.8%.
In [], a meta-heuristic scheme named updated population scheme is proposed to minimize EC while maximizing the US level. The proposed scheme uses fifteen home appliances for scheduling. RTP signal is used to evaluate the performance of the scheme. It is compared with two meta-heuristic algorithms which are single swarm optimization (SSO) and earthworm algorithm (EWA). The simulation results show that the proposed scheme met the desired objectives. Khan et al. [] have proposed a novel scheme to schedule home appliances to minimize the waiting time for appliances and thus, improve the user satisfaction level. The proposed scheme has considered twelve home appliances for scheduling. The scheme is evaluated by comparing it with the jaya optimization algorithm (JOA) and the flower pollination algorithm (FPA). CPP is used to evaluate the performance of the scheme. It is noted that the proposed scheme outperforms both JOA and FPA. The results show that EC is reduced by 58% and PAR is reduced by 56% compared to that of an unscheduled scenario. Shuja et al. [] proposed a load shifting technique for cost reduction. The authors have employed JOA on bat algorithm (BA) to develop candidate solution updation algorithm (CSUA). Fifteen smart home appliances are considered with ToUP and CPP signals for evaluation of the proposed technique. The simulation results depicts that the load is shifted from higher price period to lower price period which in turn reduces the electricity cost.
In [], a new meta-heuristic algorithm is proposed for scheduling the consumption patterns of home appliances. This study has considered fifteen home appliances for scheduling. RTP and CPP pricing signals are incorporated into the scheme to calculate EC. The proposed algorithm named runner updation optimization algorithm (RUOA) is compared with the strawberry algorithm (SBA) and the firefly algorithm (FA) to minimize EC and PAR. It is noted that RUOA outperforms both SBA and FA to achieve the RASP objectives. However, the scheme fails to improve the US level. Rahim et al. [] proposed HEMS-based GA, binary PSO, and ACO controllers to schedule home appliances. The objectives of the proposed model are minimum EC, minimum PAR, and the maximum US. The RASP is formulated as a multiple-knapsack problem. The combined pricing model of ToUP and IBR is used. The proposed model is used for thirteen home appliances and is evaluated for 24 times slots. The simulation results show that GA-based controller performs better than BPSO and ACO controllers. EC is reduced by 48.79%, 40.43%, and 28.26% for GA, BPSO, and ACO, respectively.
Abbasi et al. [] proposed a novel meta-heuristic load shifting technique to schedule the appliances in a smart home. The objective of the proposed technique is to manage the load in such a way that EC and WT are minimized and PAR is maintained throughout the operation of appliances. Eleven home appliances are considered for scheduling with CPP and RTP signals. The proposed technique is compared with SBA and EWA. The results show that EC using the CPP scheme for SBA, EWA, and the proposed approach is reduced by 18.75%, 30.65%, and 26.99%, respectively. Thus, EWA outperforms the other two schemes while EC using RTP for SBA, EWA, and the proposed approach is reduced by 13.99%, 15.25%, and 27.05%, respectively. Here, the proposed technique outperforms the others when the RTP scheme is considered. Further results show that the proposed technique minimizes the waiting time. However, it compromises for PAR in case of CPP signal. For the RTP signal, the proposed scheme minimizes the waiting time and cost. However, it compromises for PAR.
Mohsin et al. [] have proposed a harmony search algorithm (HSA) for varying time intervals. They have considered intervals of 5, 30, and 60 min. Four objectives with the minimization of EC, PAR, WT, and maximization of the US are considered. It is noted that the simulation results show the proposed algorithm performs better than an unscheduled scenario and shorter time intervals produced better results than longer intervals. In [], the authors have adapted EWA and GA to address RASP. The objective of the proposed adaptation is to minimize EC, PAR, and WT for 16 home appliances with 14 interruptible and 2 non-interruptible appliances. The simulation results show that GA and EWA reduce the EC by 35% and 20% than the unscheduled mode. GA also outperforms EWA when PAR is considered. PAR is reduced by 50% by GA while EWA reduced PAR by 40%. Ayub et al. [] have proposed EWA- and HSA-based schemes for appliance scheduling to reduce PAR and EC by shifting home appliances from peak hours to off-peak hours. ToUP scheme is used for evaluating the EC of six appliances. It is noted that EC and PAR are reduced by 12% and 9% using HSA while EWA reduced EC and PAR by 17% and 6.8%. Thus, EWA outperforms HSA while reducing EC whereas HSA performs better than EWA in the reduction of PAR. Tariq et al. [] presented FPA- and HSA-based appliance scheduling schemes to address RASP. CPP is used to determine EC. The purpose of the scheme is to schedule 16 appliances to reduce EC and PAR and evaluate the behavior of waiting time. It is noted that FPA outperforms HSA in EC and PAR reduction. However, HSA performed better than FPA in minimizing the trade-off between the EC and the US level.
Awais et al. [] have proposed a novel algorithm by merging the best features of bacterial foraging optimization algorithm and flower pollination algorithm. The objective of the proposed algorithm is to minimize EC and PAR with affordable WT. 14 appliances are considered for the evaluation of the algorithm with RTP and CPP pricing signals. Results demonstrate that the hybrid bacterial flower pollination algorithm (HBFPA) shows reduction in EC and PAR with reasonable WT. In [], authors have proposed a GWO-based appliance scheduling scheme with the integration of smart battery to reduce EC and PAR. IBR scheme is combined with RTP to balance the power demand of 38 appliances. The results show that the RASP objectives are achieved with the use of a smart battery scheme. GWO is compared with GA to evaluate the performance of the scheme. It is noted that GWO performed better than GA to reduce EC and PAR. Iqbal et al. [] have proposed three hybrid optimization schemes for EC and PAR reduction: (1) hybrid of WDO and GWO referred as wind driven GWO (WDGWO). (2) Hybrid of WDO and BPSO named wind driven BPSO (WBPSO). (3) Wind driven GA (WDGA) which is hybrid of WDO and GA. The simulation results show that the proposed techniques outperforms the existing meta-heuristic techniques. Apart from above algorithms, a number of other nature-inspired meta-heuristic algorithms with optimization of all three major objectives are studied in literature. They are summarized in Table 4:

Table 4.
Summary of meta-heuristic algorithms.
5.4. Discussion and Directions for Future Research
Following are the discussion and future research directions of the review:
- This paper provides an overview of RASP techniques in three categories: (i) Classical techniques; (ii) heuristic approaches; (iii) meta-heuristic algorithms. Three major optimization objectives are considered which are minimization of EC, minimization of PAR, and maximization of the US level. Dynamic pricing schemes are used to evaluate the performances of these scheduling techniques.
- Classical techniques such as LP, NLP are capable of finding an exact solution to an optimization problem. RASP requires more complex computations because it involves the scheduling of multiple appliances at the same time. Thus, the classical techniques fail to solve such computationally expensive and high dimensional problems in an acceptable time.
- Heuristic approaches for RASP are used to find an approximate solution to an optimization problem. They are well designed, efficient, and faster techniques that are capable of finding a near-optimal appliances schedule for RASP. The heuristic approach used in [] proved that the difference between optimally achievable cost and heuristic-based achieved cost is negligible.
- Many meta-heuristic algorithms such as ACO [], GA [], PSO [] are inspired by natural phenomena. These algorithms explore the alternative meaning of optimizing RASP objectives and scheduling the power profile of home appliances at any hour of the day. These algorithms can be effective for a given instance of RASP. However, in some cases, because of the nature of convergence, these algorithms can take a long time without a satisfactory solution.
- Based on the conducted review, the most commonly studied optimization objectives for RASP are electricity cost, peak-to-average ratio, and user satisfaction level. Very few studies in the literature have optimized all three objectives simultaneously. In the future, there is a scope of proposing a new objective with novel fitness function which combines all the three objectives with potentially better results.
- RASP is also a scheduling problem in which appliances are required to be scheduled one after the other. The consumer prioritizes the appliances and schedules them in a time-wise fashion. The priority concept in appliance scheduling can be correlated with the scheduling of CPU in the operating system. Some of the known CPU scheduling algorithms are first-come-first-served, shortest job first, round robin, pre-emptive-based priority, non-pre-emptive-based priority algorithms. Thus, in the future, RASP can be studied concerning priority or above-mentioned scheduling algorithms.
- Since the phenomenon in nature/ecosystem exhibits optimization properties, the nature-inspired algorithms have come forward in the optimization domain. No study in the literature describes the exact simulation of meta-heuristics to appliances. Thus, there is a need for a step-by-step simulation of nature-inspired algorithms with an appliance scheduling problem.
- Demand response programs for the smart grid have been thoroughly studied in the literature. However, a detailed investigation is recommended in the demand response for the wholesale electricity market where bidding and competition for electricity are involved.
- All the heuristic approaches for RASP have not been explored in the literature. In this paper, we have reviewed heuristic approaches for appliance scheduling in detail. In the future, there is further scope of proposing a new heuristic approach for RASP with mathematical modeling.
- In literature, residential appliance scheduling is studied to a large extent. A similar overview is required in the case of the Industrial Appliance Scheduling Problem (IASP). Since very high loads are involved in industries, specific industries (For example, mining industry, printing industry) can be studied concerning appliance scheduling. Thus, there is a possible future scope in the industrial domain.
6. Conclusions
In this paper, smart grid concept is studied in detail with its characteristics and advantages over existing electric grids. The architecture of smart grid is described with its domains. We have discussed demand side management techniques along with demand response programs for RASP. DR programs are reactive solutions designed to encourage the users to change their consumption pattern. These programs achieve peak load reduction by fixed or time-varying incentives and dynamic price schemes. Home energy management system model with its components is discussed with classification of home appliances into three categories, namely shiftable interruptible, shiftable non-interruptible, and non-shiftable appliances.
A comprehensive definition of residential appliance scheduling problem is discussed. The RASP is formulated as multi-objective optimization problem with three major objectives which are EC minimization, PAR minimization and US maximization. In addition, we have presented a wide range of optimization techniques proposed to address the residential appliance scheduling problem. The state-of-the-art RASP is classified into classical, heuristic, and meta-heuristic algorithms.
In classical techniques, RASP is formulated based on mathematical optimization models like linear and non-linear programming. These techniques achieve global optimum with exact solutions. However, these techniques are computationally expensive and results in high computing times. Heuristic approaches are faster and useful for approximating the optimal schedule of appliances. The studies in this overview show that the difference between the optimal achievable solution and heuristic solution is negligible. Finally, the overview of nature-inspired meta-heuristic algorithms is presented. Meta-heuristic algorithms can solve computationally expensive problems like RASP in an acceptable time. These algorithms exhibit faster convergence to achieve optimal schedule in appliance scheduling.
Author Contributions
Conceptualization, A.S. and A.M.; methodology, A.S. and A.M.; validation, A.M. and N.D.B.; formal analysis, A.S., A.M., and N.F.; investigation, A.S., N.F., and A.M., resources, A.M. and N.D.B.; data curation, A.S.; writing—original draft preparation, A.S., A.M., and N.D.B.; writing—review and editing, A.S., A.M., N.F., and N.D.B.; visualization, A.S. and N.D.B.; supervision, A.M. and N.D.B.; project administration, A.M.; funding acquisition, A.M. and N.D.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| 2TP | Two-Tier Pricing |
| ACO | Ant Colony Optimization |
| ADSM | Active Demand Side Management |
| AMI | Advanced Metering Infrastructure |
| ANN | Artificial Neural Network |
| BFO | Bacterial Foraging Optimization |
| CEMU | Central Energy Management Unit |
| CIP | Customer Incentive Pricing |
| CPP | Critical Peak Pricing |
| CNLP | Constrained Non Linear Programming |
| CSA | Crow Search Algorithm |
| DAP | Day Ahead Price |
| DLC | Direct Load Control |
| DR | Demand Response |
| DSM | Demand Side Management |
| EC | Electricity Cost |
| ECS | Energy Consumption Scheduler |
| EDE | Enhanced Differential Evaluation |
| EV | Electric Vehicles |
| EWA | Earth Worm Algorithm |
| FA | Firefly Algorithm |
| FPA | Flower Pollination Algorithm |
| GA | Genetic Algorithm |
| GWO | Grey Wolf Optimization |
| HEMS | Home Energy Management System |
| HEMU | Home Energy Management Unit |
| HP | Hourly Pricing |
| HSA | Harmony Search Algorithm |
| IBDR | Incentive-Based Demand Response |
| IBR | Inclined Block Rate |
| ICT | Information and Communication Technology |
| IDSS | Intelligent Decision Support System |
| IED | Intelligent Electronic Vehicles |
| JOA | Jaya Optimization Algorithm |
| LOT | Length of Operational Time |
| LP | Linear Programming |
| MDP | Markov Decision Process |
| MILP | Mixed-Integer Linear Programming |
| MINLP | Mixed-Integer Non-linear Programming |
| MOMILP | Multi Objective Mixed-Integer Linear Programming |
| NLP | Non Linear Programming |
| NS | Non Shiftable Appliances |
| OT | Operational Time |
| PAR | Peak-to-Average Ratio |
| PBDR | Price-Based Demand Response |
| PEVs | Plug-in Electric Vehicles |
| PIO | Pigeon Inspired Optimization |
| PSO | Particle Swarm Optimization |
| RASP | Residential Appliance Scheduling Problem |
| RESs | Renewable Energy Sources |
| RTO | Regional Transmission Operator |
| RTP | Real Time Pricing |
| RUOA | Runner Updation Optimization Algorithm |
| SBA | Strawberry Algorithm |
| SG | Smart Grid |
| SI | Shiftable Interruptible appliances |
| SM | Smart Meter |
| SNI | Shiftable Non-interruptible appliances |
| SSO | Single Swarm Optimization |
| ToUP | Time-of-Use Pricing |
| UCM | User Comfort Maximization |
| US | User Satisfaction |
| WDO | Wind Driven Optimization |
| WT | Waiting Time |
References
- Gungor, V.C.; Sahin, D.; Kocak, T.; Ergut, S.; Buccella, C.; Cecati, C.; Hancke, G.P. Smart grid technologies: Communication technologies and standards. IEEE Trans. Ind. Inform. 2011, 7, 529–539. [Google Scholar] [CrossRef]
- Esther, B.P.; Kumar, K.S. A survey on residential demand side management architecture, approaches, optimization models and methods. Renew. Sustain. Energy Rev. 2016, 59, 342–351. [Google Scholar] [CrossRef]
- Makhadmeh, S.N.; Khader, A.T.; Al-Betar, M.A.; Naim, S.; Abasi, A.K.; Alyasseri, Z.A.A. Optimization methods for power scheduling problems in smart home: Survey. Renew. Sustain. Energy Rev. 2019, 115, 109362. [Google Scholar] [CrossRef]
- Jordehi, A.R. Optimisation of demand response in electric power systems, a review. Renew. Sustain. Energy Rev. 2019, 103, 308–319. [Google Scholar] [CrossRef]
- Vardakas, J.S.; Zorba, N.; Verikoukis, C.V. A survey on demand response programs in smart grids: Pricing methods and optimization algorithms. IEEE Commun. Surv. Tutor. 2014, 17, 152–178. [Google Scholar] [CrossRef]
- Barbato, A.; Capone, A. Optimization models and methods for demand-side management of residential users: A survey. Energies 2014, 7, 5787–5824. [Google Scholar] [CrossRef]
- Shakeri, M.; Pasupuleti, J.; Amin, N.; Rokonuzzaman, M.; Low, F.W.; Yaw, C.T.; Asim, N.; Samsudin, N.A.; Tiong, S.K.; Hen, C.K.; et al. An Overview of the Building Energy Management System Considering the Demand Response Programs, Smart Strategies and Smart Grid. Energies 2020, 13, 3299. [Google Scholar] [CrossRef]
- Leitão, J.; Gil, P.; Ribeiro, B.; Cardoso, A. A survey on home energy management. IEEE Access 2020, 8, 5699–5722. [Google Scholar] [CrossRef]
- Mahapatra, B.; Nayyar, A. Home energy management system (HEMS): Concept, architecture, infrastructure, challenges and energy management schemes. Energy Syst. 2019, 1–27. [Google Scholar] [CrossRef]
- Fang, X.; Misra, S.; Xue, G.; Yang, D. Smart grid—The new and improved power grid: A survey. IEEE Commun. Surv. Tutor. 2011, 14, 944–980. [Google Scholar] [CrossRef]
- Çelik, D.; Meral, M.E. Current control based power management strategy for distributed power generation system. Control Eng. Pract. 2019, 82, 72–85. [Google Scholar] [CrossRef]
- Safdarian, A.; Fotuhi-Firuzabad, M.; Lehtonen, M. Benefits of demand response on operation of distribution networks: A case study. IEEE Syst. J. 2014, 10, 189–197. [Google Scholar] [CrossRef]
- Rahman, S. An efficient load model for analyzing demand side management impacts. IEEE Trans. Power Syst. 1993, 8, 1219–1226. [Google Scholar] [CrossRef]
- Cohen, A.I.; Wang, C.C. An optimization method for load management scheduling. IEEE Trans. Power Syst. 1988, 3, 612–618. [Google Scholar] [CrossRef]
- Wu, Z.; Tazvinga, H.; Xia, X. Demand side management of photovoltaic-battery hybrid system. Appl. Energy 2015, 148, 294–304. [Google Scholar] [CrossRef]
- Bakker, V.; Bosman, M.; Molderink, A.; Hurink, J.L.; Smit, G.J.M. Demand side load management using a three step optimization methodology. In Proceedings of the 2010 First IEEE International Conference on Smart Grid Communications, Gaithersburg, MD, USA, 4–6 October 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 431–436. [Google Scholar]
- Mahmood, A.; Ullah, M.; Razzaq, S.; Basit, A.; Mustafa, U.; Naeem, M.; Javaid, N. A new scheme for demand side management in future smart grid networks. Procedia Comput. Sci. 2014, 32, 477–484. [Google Scholar] [CrossRef]
- Gellings, C.W. The concept of demand-side management for electric utilities. Proc. IEEE 1985, 73, 1468–1470. [Google Scholar] [CrossRef]
- Sithara, N.N.; Saminathan, V.; Saminathan, V. Optimal scheduling of ICT for demand side management in smart grid. Int. J. Adv. Res. Electr. Electron. Instrum. Eng. 2014, 3, 9187–9193. [Google Scholar]
- Ng, K.H.; Sheble, G.B. Direct load control-A profit-based load management using linear programming. IEEE Trans. Power Syst. 1998, 13, 688–694. [Google Scholar] [CrossRef]
- Schweppe, F.; Daryanian, B.; Tabors, R. Algorithms for a spot price responding residential load controller. IEEE Trans. Power Syst. 1989, 4, 507–516. [Google Scholar] [CrossRef]
- Lee, S.; Wilkins, C. A practical approach to appliance load control analysis: A water heater case study. IEEE Trans. Power Appar. Syst. 1983, 1007–1013. [Google Scholar] [CrossRef]
- Kurucz, C.; Brandt, D.; Sim, S. A linear programming model for reducing system peak through customer load control programs. IEEE Trans. Power Syst. 1996, 11, 1817–1824. [Google Scholar] [CrossRef]
- Chu, W.C.; Chen, B.K.; Fu, C.K. Scheduling of direct load control to minimize load reduction for a utility suffering from generation shortage. IEEE Trans. Power Syst. 1993, 8, 1525–1530. [Google Scholar]
- Weller, H. Managing the instantaneous load shape impacts caused by the operation of a large-scale direct load control system. IEEE Trans. Power Syst. 1988, 3, 197–199. [Google Scholar] [CrossRef]
- Hsu, Y.Y.; Su, C.C. Dispatch of direct load control using dynamic programming. IEEE Trans. Power Syst. 1991, 6, 1056–1061. [Google Scholar]
- Logenthiran, T.; Srinivasan, D.; Shun, T.Z. Demand side management in smart grid using heuristic optimization. IEEE Trans. Smart Grid 2012, 3, 1244–1252. [Google Scholar] [CrossRef]
- Bharathi, C.; Rekha, D.; Vijayakumar, V. Genetic algorithm based demand side management for smart grid. Wirel. Pers. Commun. 2017, 93, 481–502. [Google Scholar] [CrossRef]
- Maharjan, I.K. Demand Side Management: Load Management, Load Profiling, Load Shifting, Residential and Industrial Consumer, Energy Audit, Reliability, Urban, Semi-Urban and Rural Setting; LAP Lambert Academic Publ: Saarbrucken, Germany, 2010. [Google Scholar]
- Kothari, D.P.; Nagrath, I. Modern Power System Analysis; Tata McGraw-Hill Education: Noida, India, 2003. [Google Scholar]
- Gellings, C.W.; Chamberlin, J.H. Demand-Side Management: Concepts and Methods; Fairmont Press: Lilburn, GA, USA, 1987. [Google Scholar]
- Wu, Z.; Zhou, S.; Li, J.; Zhang, X.P. Real-time scheduling of residential appliances via conditional risk-at-value. IEEE Trans. Smart Grid 2014, 5, 1282–1291. [Google Scholar] [CrossRef]
- Gao, J.; Xiao, Y.; Liu, J.; Liang, W.; Chen, C.P. A survey of communication/networking in smart grids. Future Gener. Comput. Syst. 2012, 28, 391–404. [Google Scholar] [CrossRef]
- Sharifi, A.H.; Maghouli, P. Energy management of smart homes equipped with energy storage systems considering the PAR index based on real-time pricing. Sustain. Cities Soc. 2019, 45, 579–587. [Google Scholar] [CrossRef]
- Yilmaz, S.; Chambers, J.; Patel, M.K. Comparison of clustering approaches for domestic electricity load profile characterisation-Implications for demand side management. Energy 2019, 180, 665–677. [Google Scholar] [CrossRef]
- Varaiya, P.P.; Wu, F.F.; Bialek, J.W. Smart operation of smart grid: Risk-limiting dispatch. Proc. IEEE 2010, 99, 40–57. [Google Scholar] [CrossRef]
- Qdr, Q. Benefits of Demand Response in Electricity Markets and Recommendations for Achieving Them; Technical Report; US Department of Energy: Washington, DC, USA, 2006.
- Federal Energy Regulatory Commission; Lee, M.; Aslam, O.; Foster, B.; Kathan, D.; Kwok, J.; Medearis, L.; Palmer, R.; Sporborg, P.; Tita, M.; et al. Assessment of Demand Response and Advanced Metering Staff Report 2012; Technical Report; FERC: Washington, DC, USA, 2012.
- Ma, K.; Yao, T.; Yang, J.; Guan, X. Residential power scheduling for demand response in smart grid. Int. J. Electr. Power Energy Syst. 2016, 78, 320–325. [Google Scholar] [CrossRef]
- Mortaji, H.; Ow, S.H.; Moghavvemi, M.; Almurib, H.A.F. Load shedding and smart-direct load control using internet of things in smart grid demand response management. IEEE Trans. Ind. Appl. 2017, 53, 5155–5163. [Google Scholar] [CrossRef]
- Avci, M.; Erkoc, M.; Rahmani, A.; Asfour, S. Model predictive HVAC load control in buildings using real-time electricity pricing. Energy Build. 2013, 60, 199–209. [Google Scholar] [CrossRef]
- Costanzo, G.T.; Zhu, G.; Anjos, M.F.; Savard, G. A system architecture for autonomous demand side load management in smart buildings. IEEE Trans. Smart Grid 2012, 3, 2157–2165. [Google Scholar] [CrossRef]
- Tang, Q.; Yang, K.; Zhou, D.; Luo, Y.; Yu, F. A real-time dynamic pricing algorithm for smart grid with unstable energy providers and malicious users. IEEE Internet Things J. 2015, 3, 554–562. [Google Scholar] [CrossRef]
- Palensky, P.; Dietrich, D. Demand side management: Demand response, intelligent energy systems, and smart loads. IEEE Trans. Ind. Inform. 2011, 7, 381–388. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, G.; Ma, K. Matching supply with demand: A power control and real time pricing approach. Int. J. Electr. Power Energy Syst. 2014, 61, 111–117. [Google Scholar] [CrossRef]
- Zhou, K.; Wei, S.; Yang, S. Time-of-use pricing model based on power supply chain for user-side microgrid. Appl. Energy 2019, 248, 35–43. [Google Scholar] [CrossRef]
- Celebi, E.; Fuller, J.D. Time-of-use pricing in electricity markets under different market structures. IEEE Trans. Power Syst. 2012, 27, 1170–1181. [Google Scholar] [CrossRef]
- Yang, P.; Tang, G.; Nehorai, A. A game-theoretic approach for optimal time-of-use electricity pricing. IEEE Trans. Power Syst. 2012, 28, 884–892. [Google Scholar] [CrossRef]
- Schedule CPP, Critical Peak Pricing. 2015. Available online: http://www.sce.com/NR/sc3/tm2/pdf/ce300.pdf (accessed on 10 March 2020).
- Aghaei, J.; Alizadeh, M.I. Critical peak pricing with load control demand response program in unit commitment problem. IET Gener. Transm. Distrib. 2013, 7, 681–690. [Google Scholar] [CrossRef]
- Fan, Z.; Kulkarni, P.; Gormus, S.; Efthymiou, C.; Kalogridis, G.; Sooriyabandara, M.; Zhu, Z.; Lambotharan, S.; Chin, W.H. Smart grid communications: Overview of research challenges, solutions, and standardization activities. IEEE Commun. Surv. Tutor. 2012, 15, 21–38. [Google Scholar] [CrossRef]
- Samadi, P.; Mohsenian-Rad, H.; Wong, V.W.; Schober, R. Real-time pricing for demand response based on stochastic approximation. IEEE Trans. Smart Grid 2014, 5, 789–798. [Google Scholar] [CrossRef]
- Ayotamuno, M.; Kogbara, R.; Ogaji, S.; Probert, S. Petroleum contaminated ground-water: Remediation using activated carbon. Appl. Energy 2006, 83, 1258–1264. [Google Scholar] [CrossRef]
- Venkatesan, N.; Solanki, J.; Solanki, S.K. Residential demand response model and impact on voltage profile and losses of an electric distribution network. Appl. Energy 2012, 96, 84–91. [Google Scholar] [CrossRef]
- Holland, S.P.; Mansur, E.T. Is real-time pricing green? The environmental impacts of electricity demand variance. Rev. Econ. Stat. 2008, 90, 550–561. [Google Scholar] [CrossRef]
- Mohsenian-Rad, A.H.; Wong, V.W.; Jatskevich, J.; Schober, R.; Leon-Garcia, A. Autonomous demand-side management based on game-theoretic energy consumption scheduling for the future smart grid. IEEE Trans. Smart Grid 2010, 1, 320–331. [Google Scholar] [CrossRef]
- Borenstein, S.; Jaske, M.; Rosenfeld, A. Dynamic Pricing, Advanced Metering, and Demand Response in Electricity Markets; University of California Energy Institute: Berkeley, CA, USA, 2002. [Google Scholar]
- Deng, R.; Yang, Z.; Chow, M.Y.; Chen, J. A survey on demand response in smart grids: Mathematical models and approaches. IEEE Trans. Ind. Inform. 2015, 11, 570–582. [Google Scholar] [CrossRef]
- Setlhaolo, D.; Xia, X. Optimal scheduling of household appliances with a battery storage system and coordination. Energy Build. 2015, 94, 61–70. [Google Scholar] [CrossRef]
- Shakouri, H.; Kazemi, A. Multi-objective cost-load optimization for demand side management of a residential area in smart grids. Sustain. Cities Soc. 2017, 32, 171–180. [Google Scholar] [CrossRef]
- Faisal, H.M.; Javaid, N.; Qasim, U.; Habib, S.; Iqbal, Z.; Mubarak, H. An efficient scheduling of user appliances using multi objective optimization in smart grid. In Workshops of the International Conference on Advanced Information Networking and Applications; Springer: Berlin/Heidelberg, Germany, 2019; pp. 371–384. [Google Scholar]
- Shuja, S.M.; Javaid, N.; Khan, S.; Akmal, H.; Hanif, M.; Fazalullah, Q.; Khan, Z.A. Efficient Scheduling of Smart Home Appliances for Energy Management by Cost and PAR Optimization Algorithm in Smart Grid. In Workshops of the International Conference on Advanced Information Networking and Applications; Springer: Berlin/Heidelberg, Germany, 2019; pp. 398–411. [Google Scholar]
- Rahim, S.; Javaid, N.; Ahmad, A.; Khan, S.A.; Khan, Z.A.; Alrajeh, N.; Qasim, U. Exploiting heuristic algorithms to efficiently utilize energy management controllers with renewable energy sources. Energy Build. 2016, 129, 452–470. [Google Scholar] [CrossRef]
- Abbasi, R.A.; Javaid, N.; Khan, S.; ur Rehman, S.; Asif, R.M.; Ahmad, W. Minimizing Daily Cost and Maximizing User Comfort Using a New Metaheuristic Technique. In Workshops of the International Conference on Advanced Information Networking and Applications; Springer: Berlin/Heidelberg, Germany, 2019; pp. 80–92. [Google Scholar]
- Rahim, M.H.; Khalid, A.; Javaid, N.; Alhussein, M.; Aurangzeb, K.; Khan, Z.A. Energy efficient smart buildings using coordination among appliances generating large data. IEEE Access 2018, 6, 34670–34690. [Google Scholar] [CrossRef]
- Open Energy Information. Available online: https://openei.org/datasets/dataset (accessed on 15 February 2020).
- US Energy Information Administration. Available online: https://www.eia.gov/consumption/residential/ (accessed on 10 March 2020).
- Pecan Street Data for Water and Electricity Research. Available online: https://dataport.pecanstreet.org/ (accessed on 5 July 2020).
- Yamada, T.; Nakano, R. Job shop scheduling. IEE Control Eng. Ser. 1997, 134–160. [Google Scholar]
- Sadik, A.R.; Urban, B. Flow shop scheduling problem and solution in cooperative robotics—case-study: One cobot in cooperation with one worker. Future Internet 2017, 9, 48. [Google Scholar] [CrossRef]
- Zhao, Z.; Lee, W.C.; Shin, Y.; Song, K.B. An optimal power scheduling method for demand response in home energy management system. IEEE Trans. Smart Grid 2013, 4, 1391–1400. [Google Scholar] [CrossRef]
- Aycan, E.; Ayav, T. Solving the course scheduling problem using simulated annealing. In 2009 IEEE International Advance Computing Conference; IEEE: Piscataway, NJ, USA, 2009; pp. 462–466. [Google Scholar]
- Mahmood, A.; Javaid, N.; Khan, M.A.; Razzaq, S. An overview of load management techniques in smart grid. Int. J. Energy Res. 2015, 39, 1437–1450. [Google Scholar] [CrossRef]
- Beaudin, M.; Zareipour, H. Home energy management systems: A review of modelling and complexity. Renew. Sustain. Energy Rev. 2015, 45, 318–335. [Google Scholar] [CrossRef]
- Schminke, B. Overview of the current state of research on energy management systems in buildings. In Proceedings of the 2019 Advances in Science and Engineering Technology International Conferences (ASET), Dubai, UAE, 26 March–10 April 2019. [Google Scholar]
- Chen, X.; Wei, T.; Hu, S. Uncertainty-aware household appliance scheduling considering dynamic electricity pricing in smart home. IEEE Trans. Smart Grid 2013, 4, 932–941. [Google Scholar] [CrossRef]
- Mohsenian-Rad, A.H.; Leon-Garcia, A. Optimal residential load control with price prediction in real-time electricity pricing environments. IEEE Trans. Smart Grid 2010, 1, 120–133. [Google Scholar] [CrossRef]
- Bradac, Z.; Kaczmarczyk, V.; Fiedler, P. Optimal scheduling of domestic appliances via MILP. Energies 2015, 8, 217–232. [Google Scholar] [CrossRef]
- Paterakis, N.G.; Erdinc, O.; Bakirtzis, A.G.; Catalão, J.P. Optimal household appliances scheduling under day-ahead pricing and load-shaping demand response strategies. IEEE Trans. Ind. Inform. 2015, 11, 1509–1519. [Google Scholar] [CrossRef]
- Ratnam, E.L.; Weller, S.R.; Kellett, C.M. Scheduling residential battery storage with solar PV: Assessing the benefits of net metering. Appl. Energy 2015, 155, 881–891. [Google Scholar] [CrossRef]
- Lokeshgupta, B.; Sivasubramani, S. Multi-objective home energy management with battery energy storage systems. Sustain. Cities Soc. 2019, 47, 101458. [Google Scholar] [CrossRef]
- de Souza Dutra, M.D.; Anjos, M.F.; Le Digabel, S. A realistic energy optimization model for smart-home appliances. Int. J. Energy Res. 2019, 43, 3237–3262. [Google Scholar] [CrossRef]
- Rafkaoui, M.A.; Khallaayoun, A.; Lghoul, M.R. Optimal Scheduling of Smart Homes Energy Consumption in Conjunction with Solar Energy Resources; Al Akhawayn University Ifrane: Ifrane, Morocco, 2016. [Google Scholar]
- Setlhaolo, D.; Xia, X.; Zhang, J. Optimal scheduling of household appliances for demand response. Electr. Power Syst. Res. 2014, 116, 24–28. [Google Scholar] [CrossRef]
- Shafie-Khah, M.; Siano, P. A stochastic home energy management system considering satisfaction cost and response fatigue. IEEE Trans. Ind. Inform. 2017, 14, 629–638. [Google Scholar] [CrossRef]
- Alipour, M.; Zare, K.; Abapour, M. MINLP probabilistic scheduling model for demand response programs integrated energy hubs. IEEE Trans. Ind. Inform. 2017, 14, 79–88. [Google Scholar] [CrossRef]
- Ampimah, B.C.; Sun, M.; Han, D.; Wang, X. Optimizing sheddable and shiftable residential electricity consumption by incentivized peak and off-peak credit function approach. Appl. Energy 2018, 210, 1299–1309. [Google Scholar] [CrossRef]
- Kong, P.Y. Effects of communication network performance on dynamic pricing in smart power grid. IEEE Syst. J. 2013, 8, 533–541. [Google Scholar] [CrossRef]
- Ogwumike, C.; Short, M.; Denai, M. Near-optimal scheduling of residential smart home appliances using heuristic approach. In Proceedings of the 2015 IEEE International Conference on Industrial Technology (ICIT), Seville, Spain, 17–19 March 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 3128–3133. [Google Scholar]
- Ogwumike, C.; Short, M. Evaluation of a heuristic approach for efficient scheduling of residential smart home appliances. In Proceedings of the 2015 IEEE 15th International Conference on Environment and Electrical Engineering (EEEIC), Rome, Italy, 10–13 June 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 2017–2022. [Google Scholar]
- Hansen, T.M.; Roche, R.; Suryanarayanan, S.; Maciejewski, A.A.; Siegel, H.J. Heuristic optimization for an aggregator-based resource allocation in the smart grid. IEEE Trans. Smart Grid 2015, 6, 1785–1794. [Google Scholar] [CrossRef]
- Ogwumike, C.; Short, M.; Abugchem, F. Heuristic optimization of consumer electricity costs using a generic cost model. Energies 2016, 9, 6. [Google Scholar] [CrossRef]
- Jindal, A.; Bhambhu, B.S.; Singh, M.; Kumar, N.; Naik, K. A Heuristic-Based Appliance Scheduling Scheme for Smart Homes. IEEE Trans. Ind. Inform. 2019, 16, 3242–3255. [Google Scholar] [CrossRef]
- Matallanas, E.; Castillo-Cagigal, M.; Gutiérrez, A.; Monasterio-Huelin, F.; Caamaño-Martín, E.; Masa, D.; Jiménez-Leube, J. Neural network controller for active demand-side management with PV energy in the residential sector. Appl. Energy 2012, 91, 90–97. [Google Scholar] [CrossRef]
- Misra, S.; Mondal, A.; Banik, S.; Khatua, M.; Bera, S.; Obaidat, M.S. Residential energy management in smart grid: A Markov decision process-based approach. In Proceedings of the 2013 IEEE International Conference on Green Computing and Communications and IEEE Internet of things and IEEE Cyber, Physical and Social Computing, Beijing, China, 20–23 August 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 1152–1157. [Google Scholar]
- Lee, J.; Kim, H.J.; Park, G.L.; Kang, M. Energy consumption scheduler for demand response systems in the smart grid. J. Inf. Sci. Eng. 2012, 28, 955–969. [Google Scholar]
- Tiptipakorn, S.; Lee, W.J. A residential consumer-centered load control strategy in real-time electricity pricing environment. In Proceedings of the 2007 39th North American Power Symposium, Las Cruces, NM, USA, 30 September–2 October 2007; IEEE: Piscataway, NJ, USA, 2007; pp. 505–510. [Google Scholar]
- Desale, S.; Rasool, A.; Andhale, S.; Rane, P. Heuristic and meta-heuristic algorithms and their relevance to the real world: A survey. Int. J. Comput. Eng. Res. Trends 2015, 351, 2349–7084. [Google Scholar]
- Shafiq, S.; Fatima, I.; Abid, S.; Asif, S.; Ansar, S.; Abideen, Z.U.; Javaid, N. Optimization of home energy management system through application of tabu search. In International Conference on P2P, Parallel, Grid, Cloud and Internet Computing; Springer: Berlin/Heidelberg, Germany, 2017; pp. 37–49. [Google Scholar]
- Rasheed, M.B.; Javaid, N.; Ahmad, A.; Khan, Z.A.; Qasim, U.; Alrajeh, N. An efficient power scheduling scheme for residential load management in smart homes. Appl. Sci. 2015, 5, 1134–1163. [Google Scholar] [CrossRef]
- Hu, M.; Xiao, F. Price-responsive model-based optimal demand response control of inverter air conditioners using genetic algorithm. Appl. Energy 2018, 219, 151–164. [Google Scholar] [CrossRef]
- Chui, K.T.; Lytras, M.D.; Visvizi, A. Energy sustainability in smart cities: Artificial intelligence, smart monitoring, and optimization of energy consumption. Energies 2018, 11, 2869. [Google Scholar] [CrossRef]
- Khan, S.; Khan, Z.A.; Javaid, N.; Ahmad, W.; Abbasi, R.A.; Faisal, H.M. On Maximizing User Comfort Using a Novel Meta-Heuristic Technique in Smart Home. In International Conference on Advanced Information Networking and Applications; Springer: Berlin/Heidelberg, Germany, 2019; pp. 26–38. [Google Scholar]
- Shuja, S.M.; Javaid, N.; Rafique, M.Z.; Qasim, U.; Khan, R.F.M.; Butt, A.A.; Hanif, M. Towards efficient scheduling of smart appliances for energy management by candidate solution updation algorithm in smart grid. In International Conference on Advanced Information Networking and Applications; Springer: Berlin/Heidelberg, Germany, 2019; pp. 67–81. [Google Scholar]
- Mohsin, S.M.; Javaid, N.; Madani, S.A.; Abbas, S.K.; Akber, S.M.A.; Khan, Z.A. Appliance scheduling in smart homes with harmony search algorithm for different operation time intervals. In Proceedings of the 2018 32nd International Conference on Advanced Information Networking and Applications Workshops (WAINA), Krakow, Poland, 16–18 May 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 51–60. [Google Scholar]
- Khan, A.; Mushtaq, N.; Faraz, S.H.; Khan, O.A.; Sarwar, M.A.; Javaid, N. Genetic algorithm and earthworm optimization algorithm for energy management in smart grid. In International Conference on P2P, Parallel, Grid, Cloud and Internet Computing; Springer: Berlin/Heidelberg, Germany, 2017; pp. 447–459. [Google Scholar]
- Ayub, N.; Ishaq, A.; Ali, M.; Sarwar, M.A.; Amin, B.; Javaid, N. An efficient scheduling of power and appliances using metaheuristic optimization technique. In International Conference on Intelligent Networking and Collaborative Systems; Springer: Berlin/Heidelberg, Germany, 2017; pp. 178–190. [Google Scholar]
- Tariq, M.; Khalid, A.; Ahmad, I.; Khan, M.; Zaheer, B.; Javaid, N. Load scheduling in home energy management system using meta-heuristic techniques and critical peak pricing tariff. In International Conference on P2P, Parallel, Grid, Cloud and Internet Computing; Springer: Berlin/Heidelberg, Germany, 2017; pp. 50–62. [Google Scholar]
- Awais, M.; Javaid, N.; Aurangzeb, K.; Haider, S.I.; Khan, Z.A.; Mahmood, D. Towards effective and efficient energy management of single home and a smart community exploiting heuristic optimization algorithms with critical peak and real-time pricing tariffs in smart grids. Energies 2018, 11, 3125. [Google Scholar] [CrossRef]
- Makhadmeh, S.N.; Khader, A.T.; Al-Betar, M.A.; Naim, S. An optimal power scheduling for smart home appliances with smart battery using grey wolf optimizer. In Proceedings of the 2018 8th IEEE International Conference on Control System, Computing and Engineering (ICCSCE), Penang, Malaysia, 23–25 November 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 76–81. [Google Scholar]
- Iqbal, Z.; Javaid, N.; Iqbal, S.; Aslam, S.; Khan, Z.A.; Abdul, W.; Almogren, A.; Alamri, A. A domestic microgrid with optimized home energy management system. Energies 2018, 11, 1002. [Google Scholar] [CrossRef]
- Batool, S.; Khalid, A.; Amjad, Z.; Arshad, H.; Aimal, S.; Farooqi, M.; Javaid, N. Pigeon inspired optimization and bacterial foraging optimization for home energy management. In International Conference on Broadband and Wireless Computing, Communication and Applications; Springer: Berlin/Heidelberg, Germany, 2017; pp. 14–24. [Google Scholar]
- Khan, H.N.; Iftikhar, H.; Asif, S.; Maroof, R.; Ambreen, K.; Javaid, N. Demand side management using strawberry algorithm and bacterial foraging optimization algorithm in smart grid. In International Conference on Network-Based Information Systems; Springer: Berlin/Heidelberg, Germany, 2017; pp. 191–202. [Google Scholar]
- Abbasi, B.Z.; Javaid, S.; Bibi, S.; Khan, M.; Malik, M.N.; Butt, A.A.; Javaid, N. Demand side management in smart grid by using flower pollination algorithm and genetic algorithm. In International Conference on P2P, Parallel, Grid, Cloud and Internet Computing; Springer: Berlin/Heidelberg, Germany, 2017; pp. 424–436. [Google Scholar]
- Aimal, S.; Parveez, K.; Saba, A.; Batool, S.; Arshad, H.; Javaid, N. Energy optimization techniques for demand-side management in smart homes. In International Conference on Intelligent Networking and Collaborative Systems; Springer: Berlin/Heidelberg, Germany, 2017; pp. 515–524. [Google Scholar]
- Ishaq, A.; Ayub, N.; Saba, A.; Ghafar, A.; Amin, B.; Javaid, N. An efficient scheduling using meta heuristic algorithms for home demand-side management in smart grid. In International Conference on Intelligent Networking and Collaborative Systems; Springer: Berlin/Heidelberg, Germany, 2017; pp. 214–227. [Google Scholar]
- Khan, M.; Khalid, R.; Zaheer, B.; Tariq, M.; ul Abideen, Z.; Malik, H.; Javaid, N. Residential Demand Side Management in Smart Grid Using Meta-Heuristic Techniques. In International Conference on P2P, Parallel, Grid, Cloud and Internet Computing; Springer: Berlin/Heidelberg, Germany, 2017; pp. 76–88. [Google Scholar]
- Khan, M.S.; ul Hassan, C.A.; Sadiq, H.A.; Ali, I.; Rauf, A.; Javaid, N. A new meta-heuristic optimization algorithm inspired from strawberry plant for demand side management in smart grid. In International Conference on Intelligent Networking and Collaborative Systems; Springer: Berlin/Heidelberg, Germany, 2017; pp. 143–154. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).