Analytical Modeling of the Cyclic ES-SAGD Process
Abstract
1. Introduction
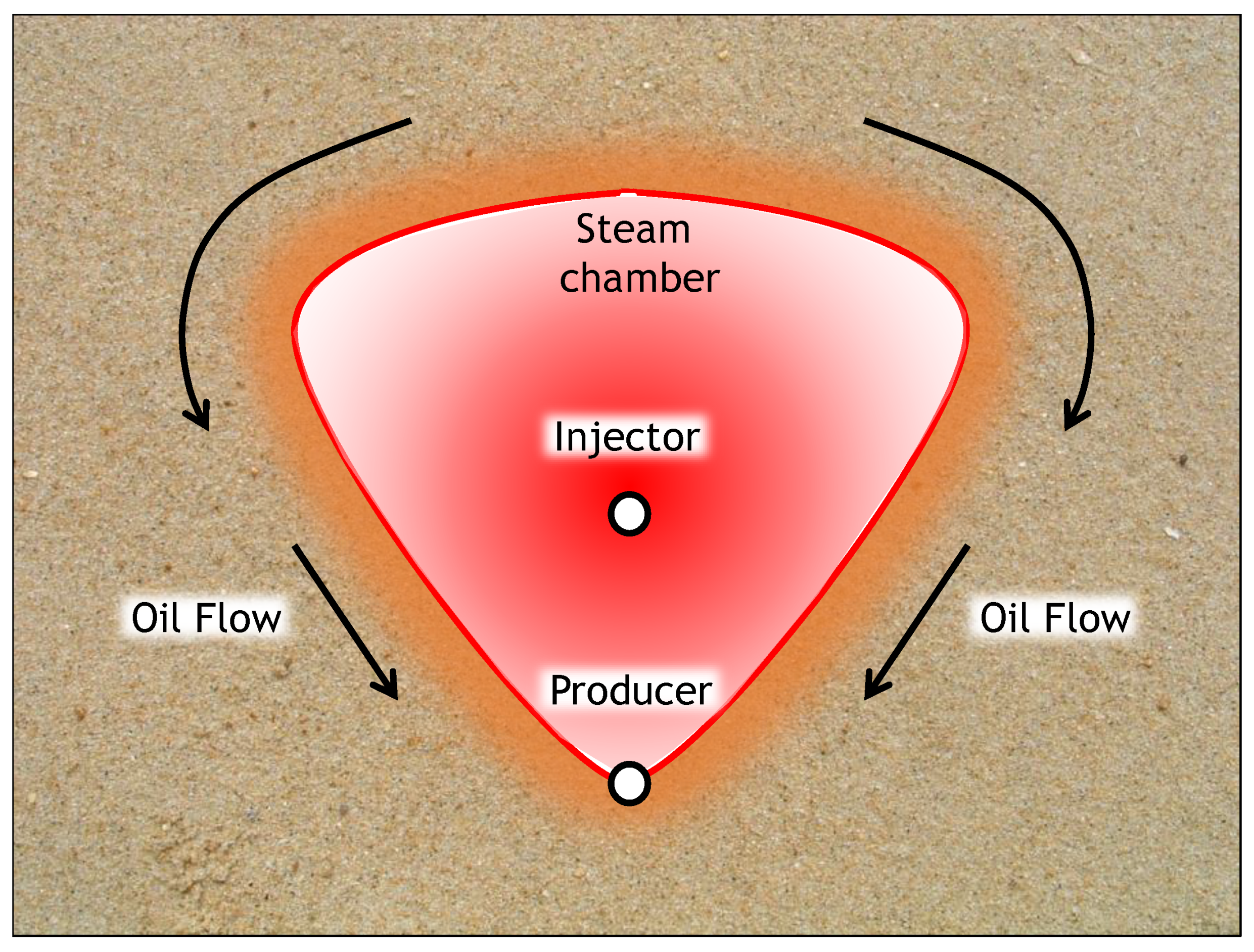
1.1. Steam Assisted Gravity Drainage (SAGD)
1.2. Vapor Extraction (VAPEX)
1.3. Expanding-Solvent Steam Assisted Gravity Drainage (ES-SAGD)
1.4. Cyclic ES-SAGD
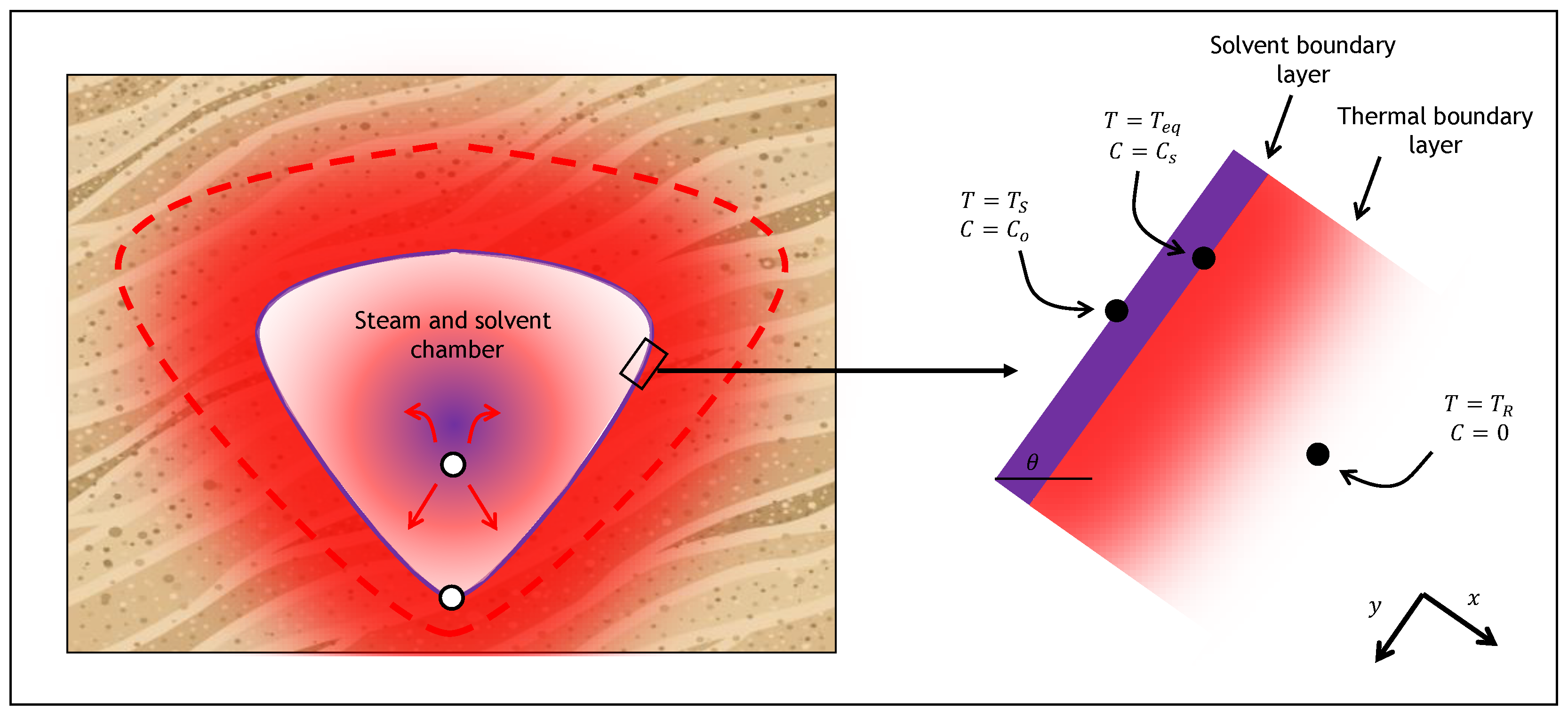
2. Theory
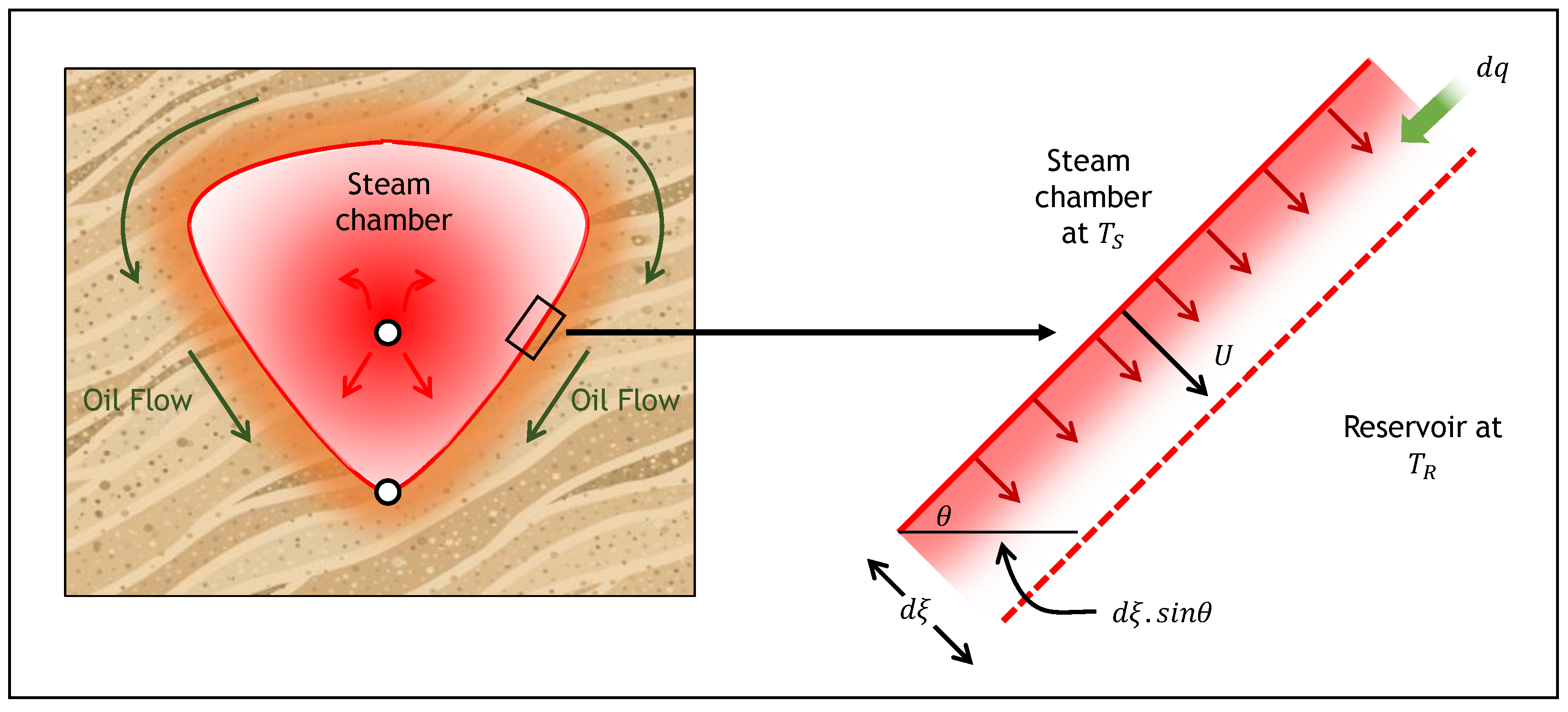
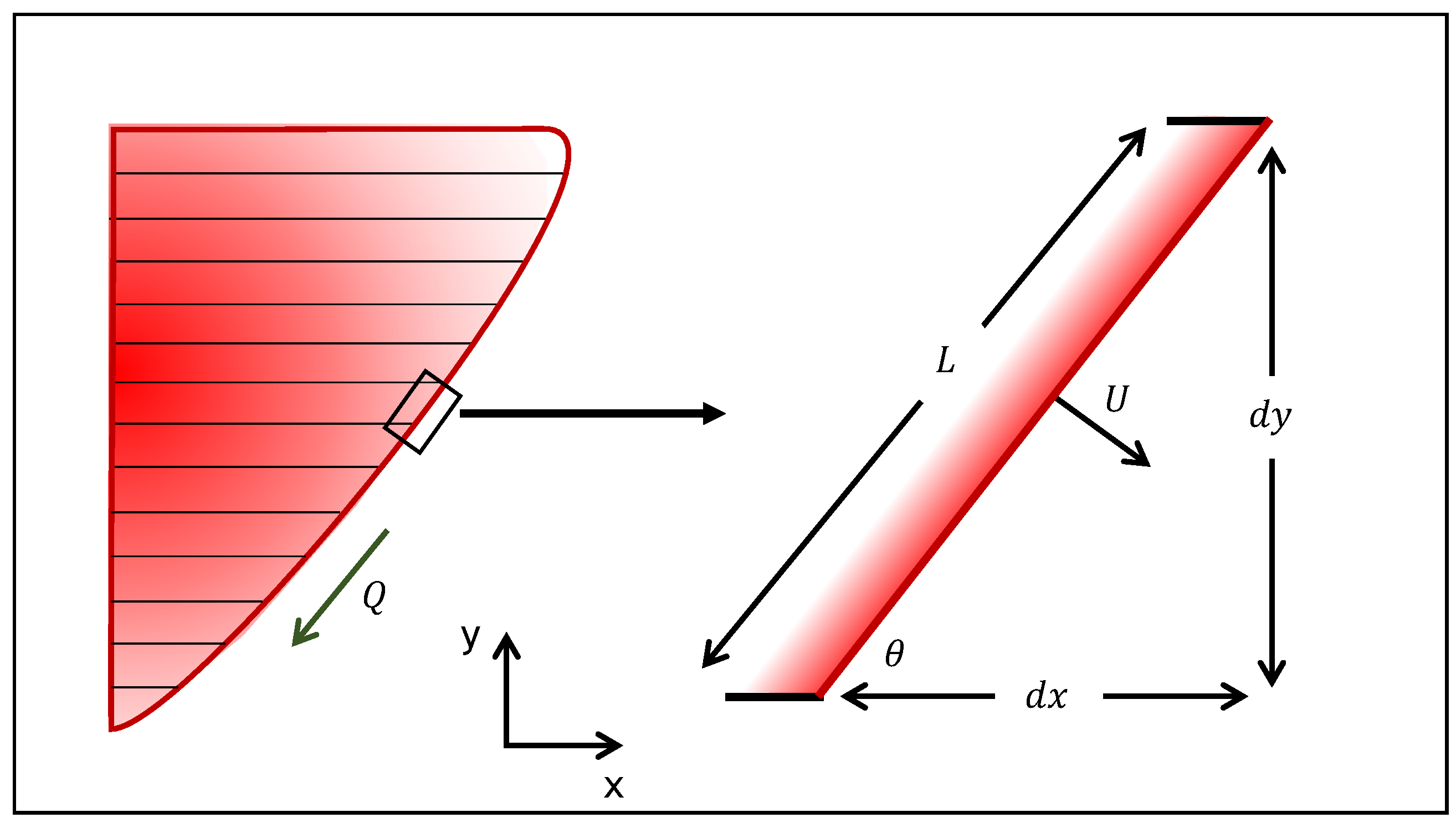
2.1. SAGD Analytical Model
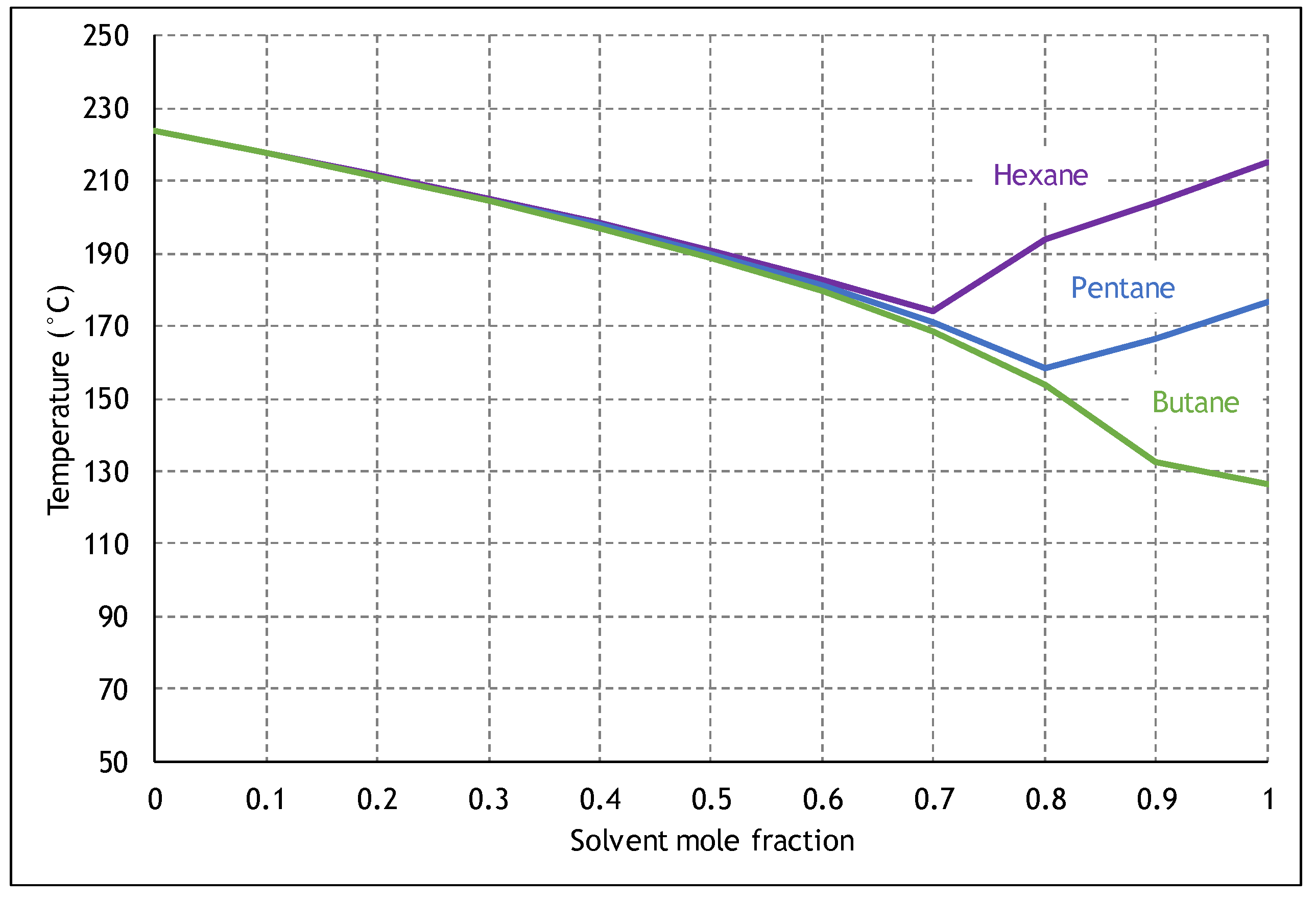
2.2. ES-SAGD Analytical Model
2.3. Cyclic ES-SAGD Analytical Model Description
3. Results
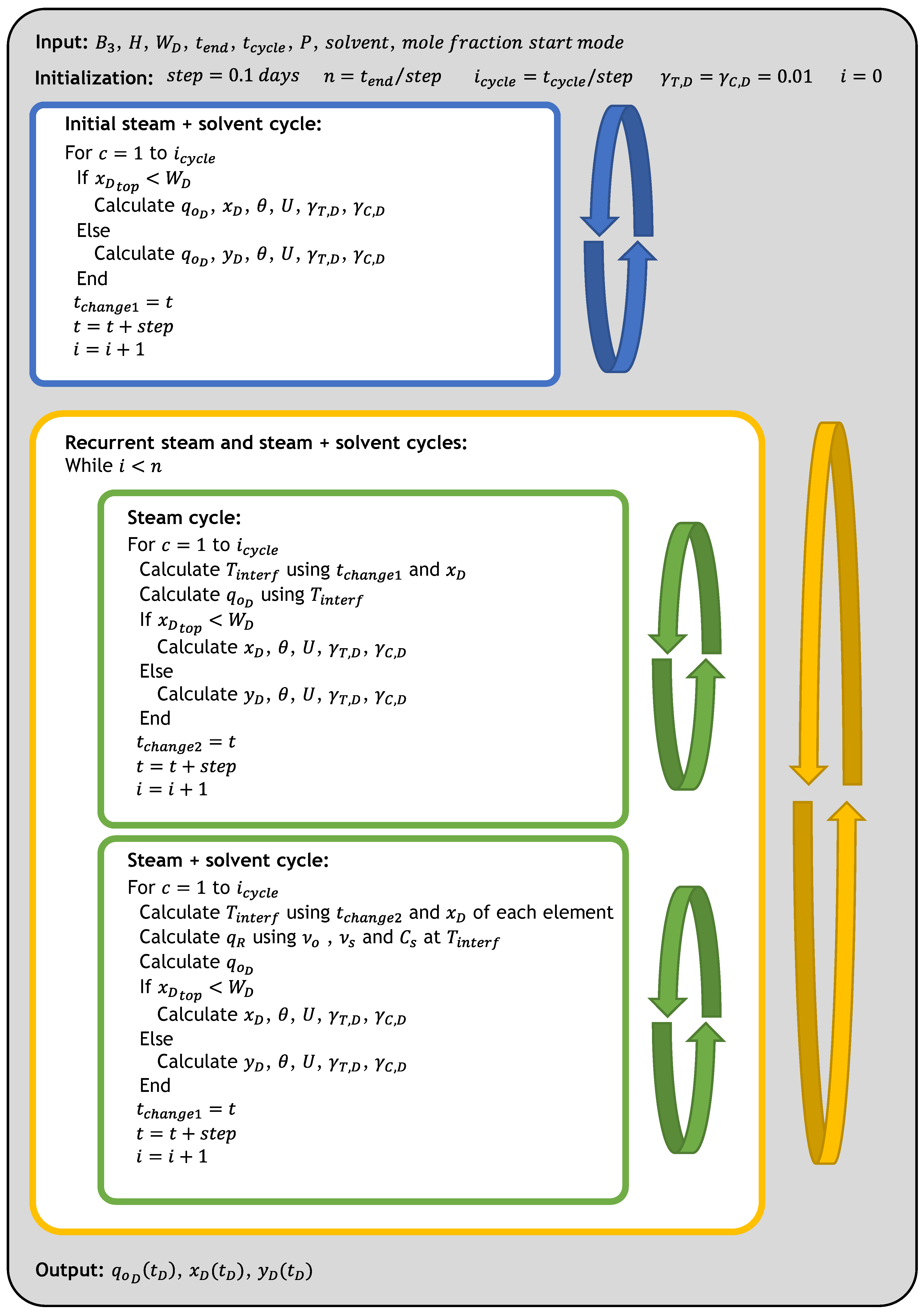
3.1. Computational Procedure
3.1.1. Input Data
- Reservoir properties: porosity, permeability, thermal diffusivity, and initial oil saturation.
- Height of the model, H, measured from the production well to the top of the model.
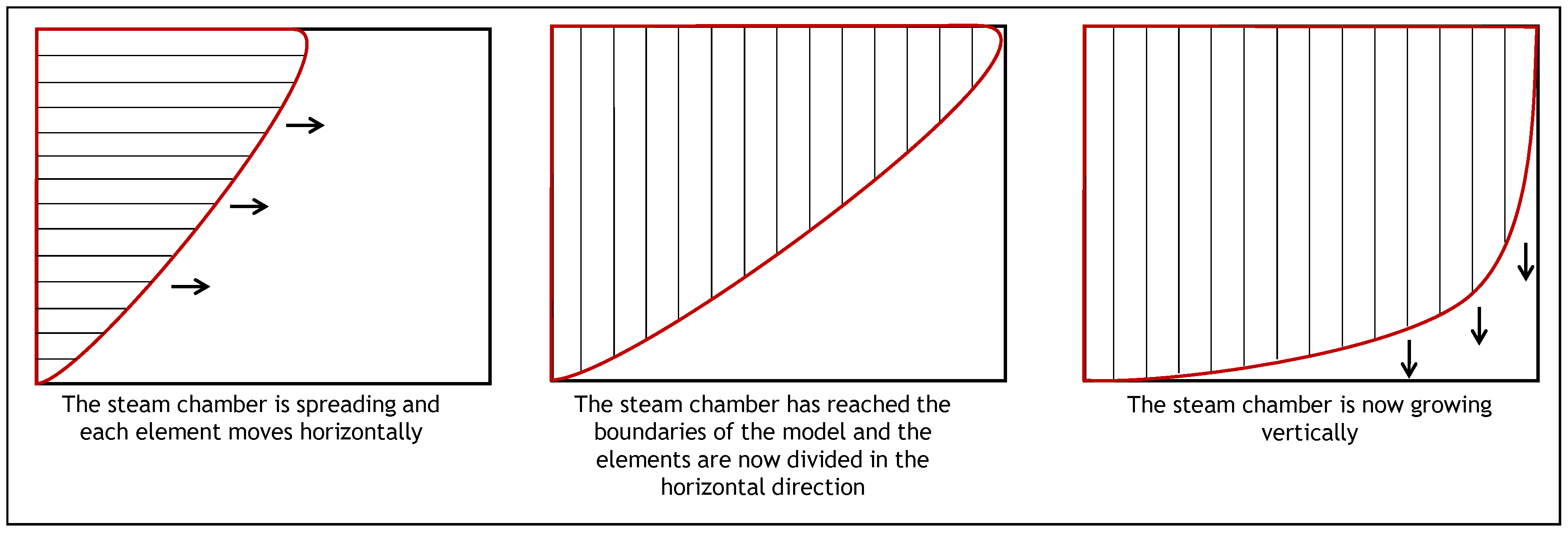
- Width of the model normalized with respect to the height, . The width of the model is considered to be half of the complete model. As it was done with the previous analytical models, the computations are performed for half of the steam chamber.
- Total duration of the proposed cyclic ES-SAGD procedures, .
- Duration of each injection cycle, .
- Injection pressure, mole fraction, and the type of solvent that is used.
- Start mode: this variable tells the algorithm if the initial cycle would be a steam or a steam–solvent cycle.
- Time step size ().
3.1.2. Initialization
- Total number of steps (): it depends on the step size and the length of the calculation. This variable is used as a stopping criterion for the whole procedure.
- Steps for each cycle (): this is the number of time steps that each cycle will take.
- Iteration counter (): this variable count each of the steps that are taken in the calculation. The procedure stops when is equal to .
- Initial heat (Equation (4)) and concentration (Equation (9)) penetration depths: both SAGD and ES-SAGD previous analytical models use an initial penetration depth in order to start the algorithm. In this case, both penetration depths were set to 0.01. This number was assigned after running multiple cases taking into account the convergence of the equations.
3.1.3. First Cycle
- This part of the procedure corresponds to the calculations that are performed for the first cycle. These calculations are repeated for the number of steps of the cycles (). During this part, each element is considered for the calculation of the oil drainage rate, the movement in the horizontal direction, the angle, the velocity, and the dimensionless penetration depths. Depending on the type of injection scheme (steam or steam + solvent), the appropriate expression from Section 2 is used to calculate the rate changes.
- At the end of each time step, the variable t stores the time at which the rest of the variables were calculated, increases with each iteration and it represents the current step, and the variable stores the time at which the change of cycle will occur. This variable is used afterwards to calculate the temperature at the interface.
3.1.4. Recurrent Steam and Solvent Cycles
- After the initial period of injection, a new cycle begins in which there is an alternate calculation of different injection schemes. The order of these calculations depends on the initial cycle. For the steam injection periods, the first step is to calculate the temperature at the interface (). This temperature will depend on the time that has elapsed since the last cycle () and the position of each element (). After that, the calculation is similar to what was explained previously; the rates are calculated taking into account the viscosity at the interface temperature using Equation (17) and then the rest of the variables are calculated considering the position of the top element.
- For the steam–solvent injection periods, the temperature at the interface () is also the first variable that is calculated using Equation (16). Subsequently, the rates are calculated considering the oil and solvent viscosity at the interface temperature and then, the remaining variables are determined in the same way that was previously explained. It is important to point out that in this cycle the temperature at the interface is calculated considering , which is the time at which the previous injection period ended.
- For each iteration that is performed, the counter increases by one unit until it reaches , and then the process comes to a stop. The change in the dimensionless oil drainage rate over time for the element at the bottom represents the dimensionless oil rate of the Cyclic ES-SAGD process.
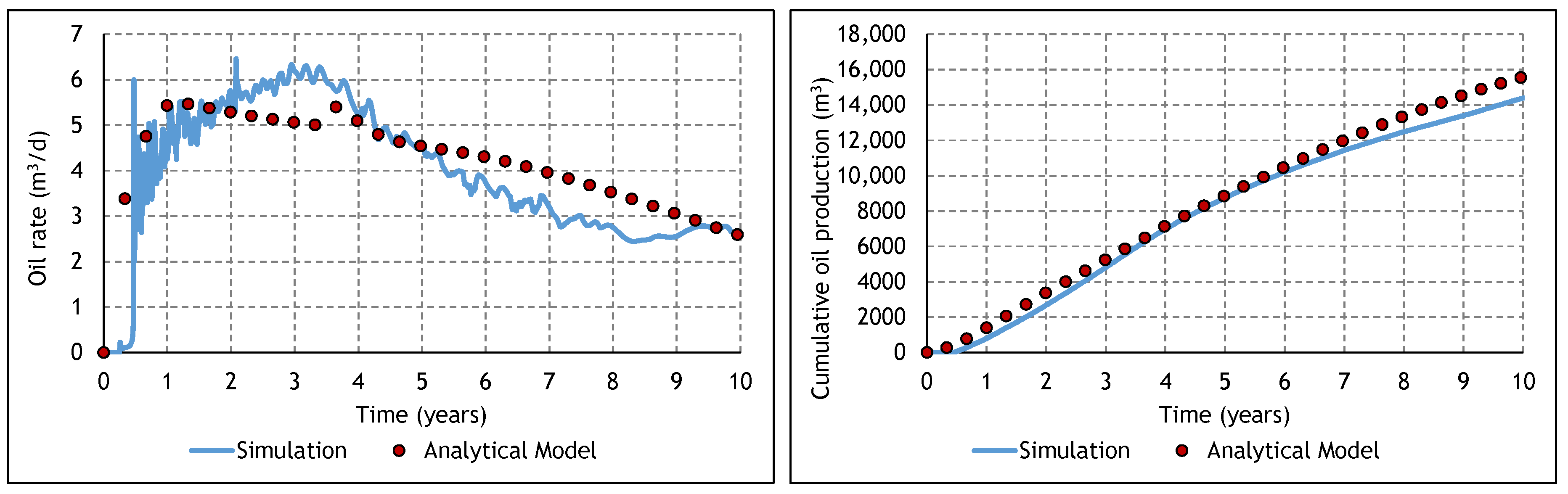
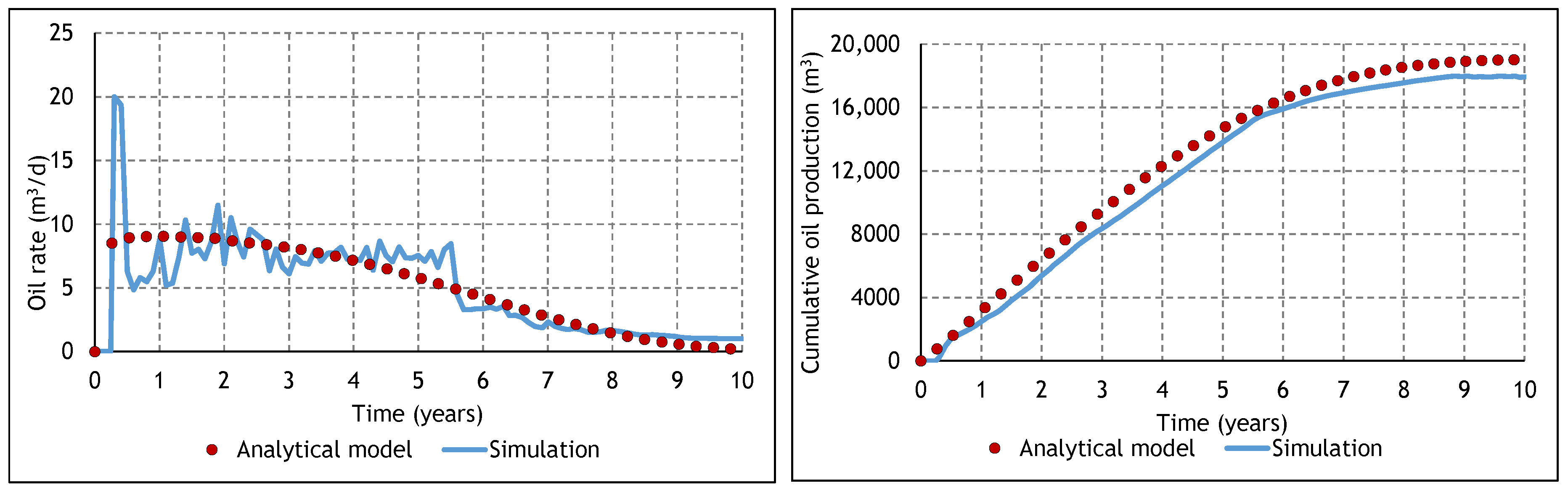
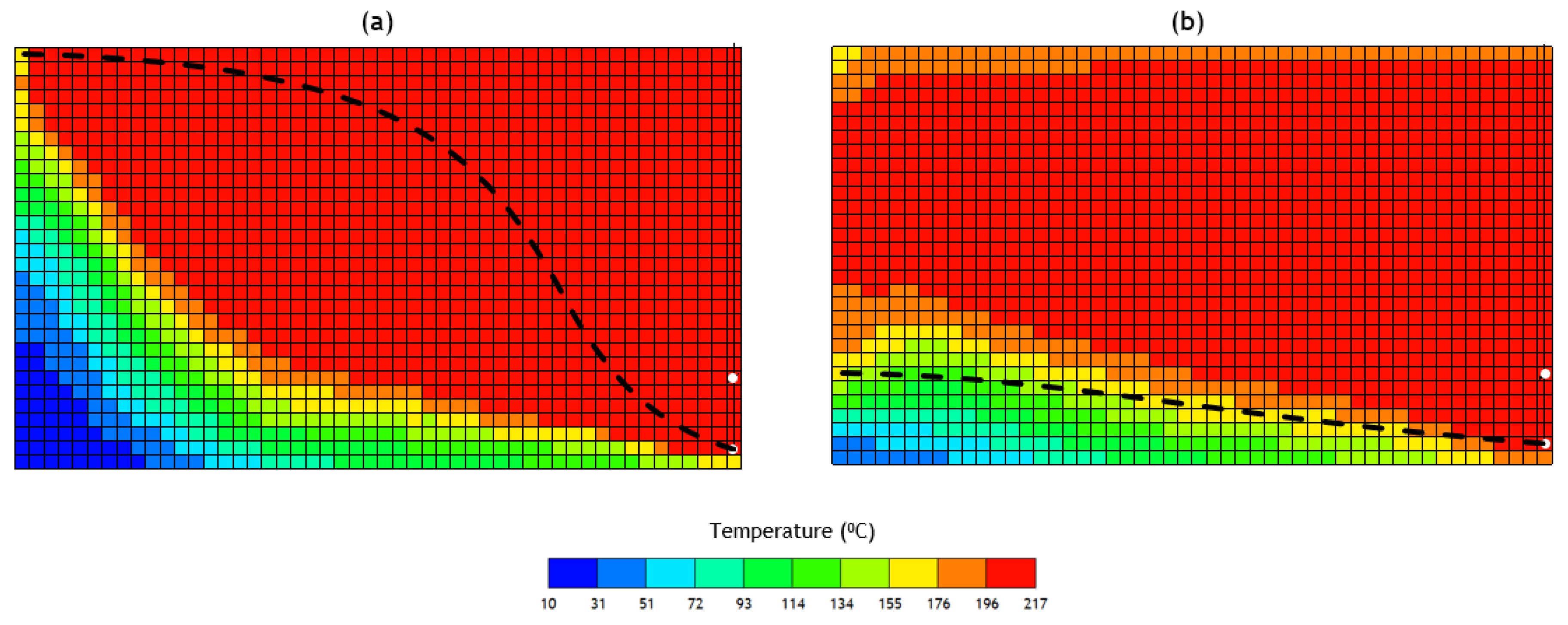
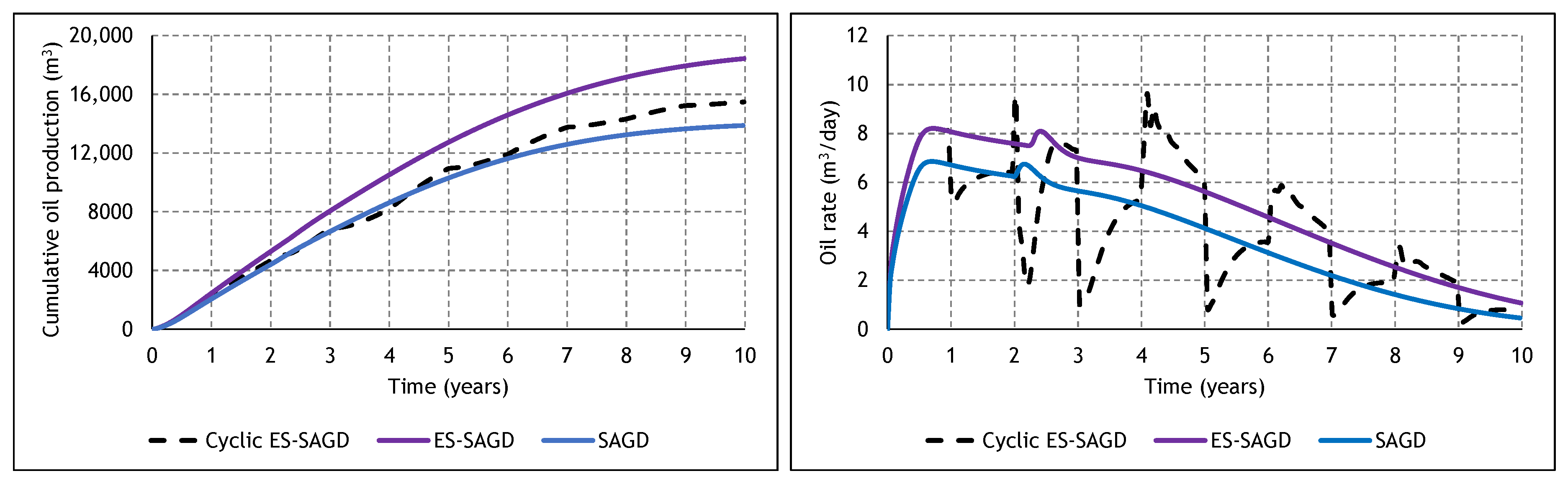
3.2. Analysis of the Constituent SAGD and ES-SAGD Models’ Performance
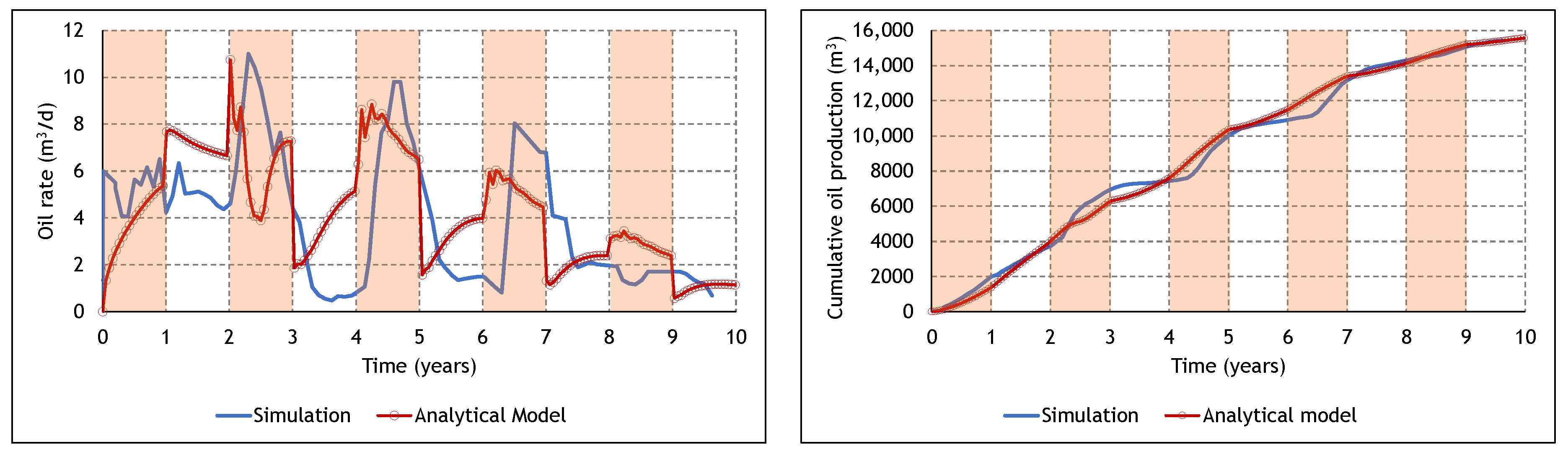
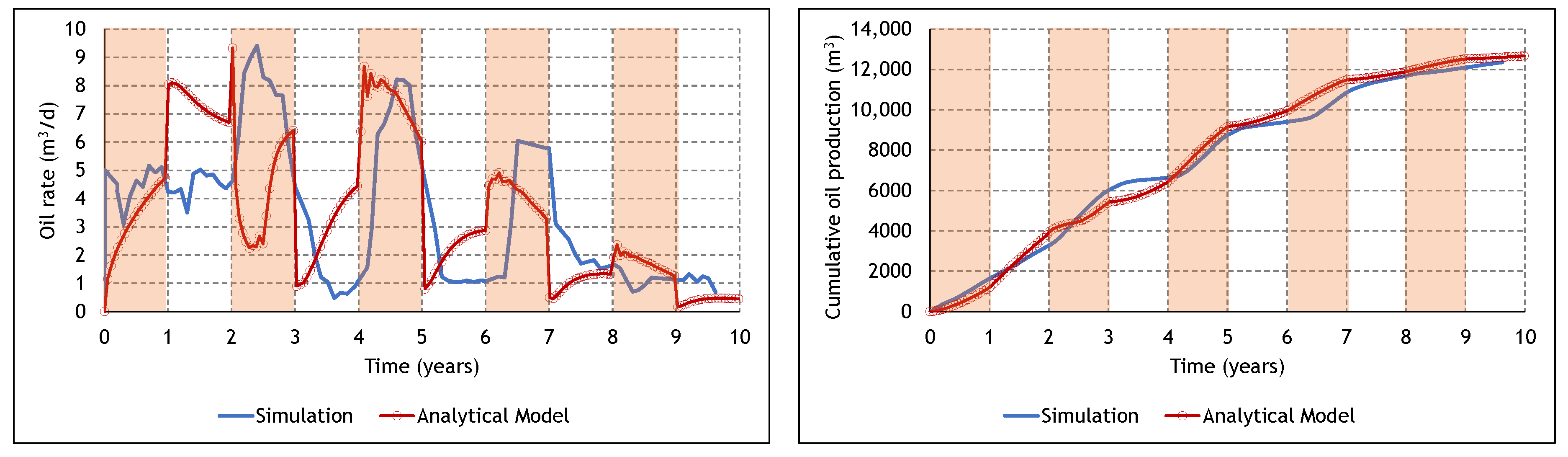
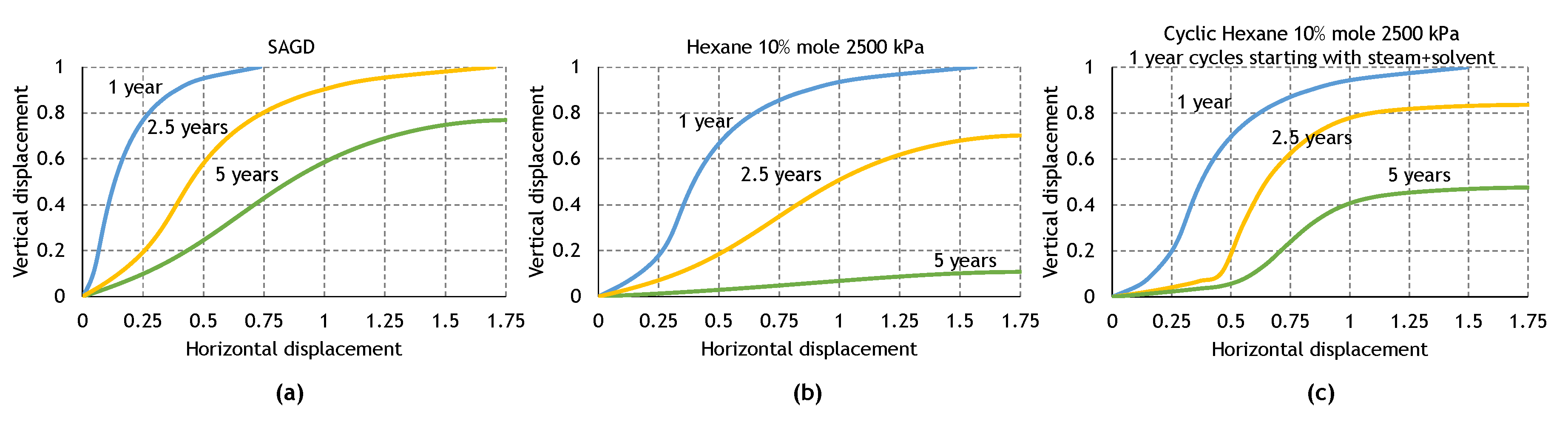
3.3. Analysis of the Cyclic ES-SAGD Model’s Performance
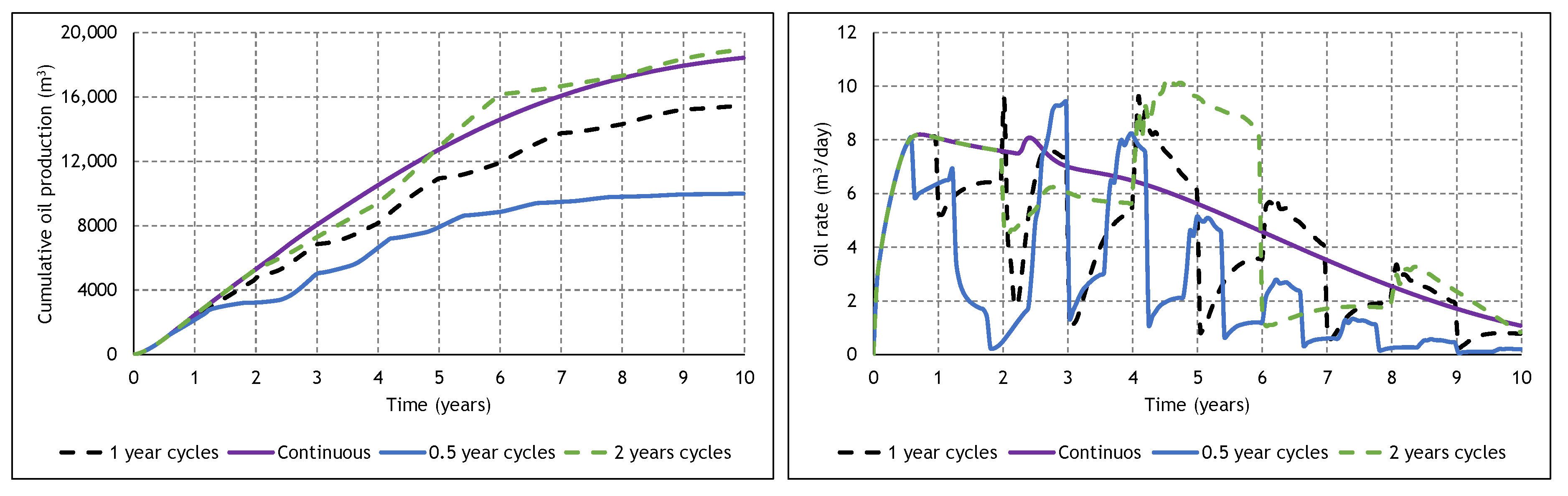
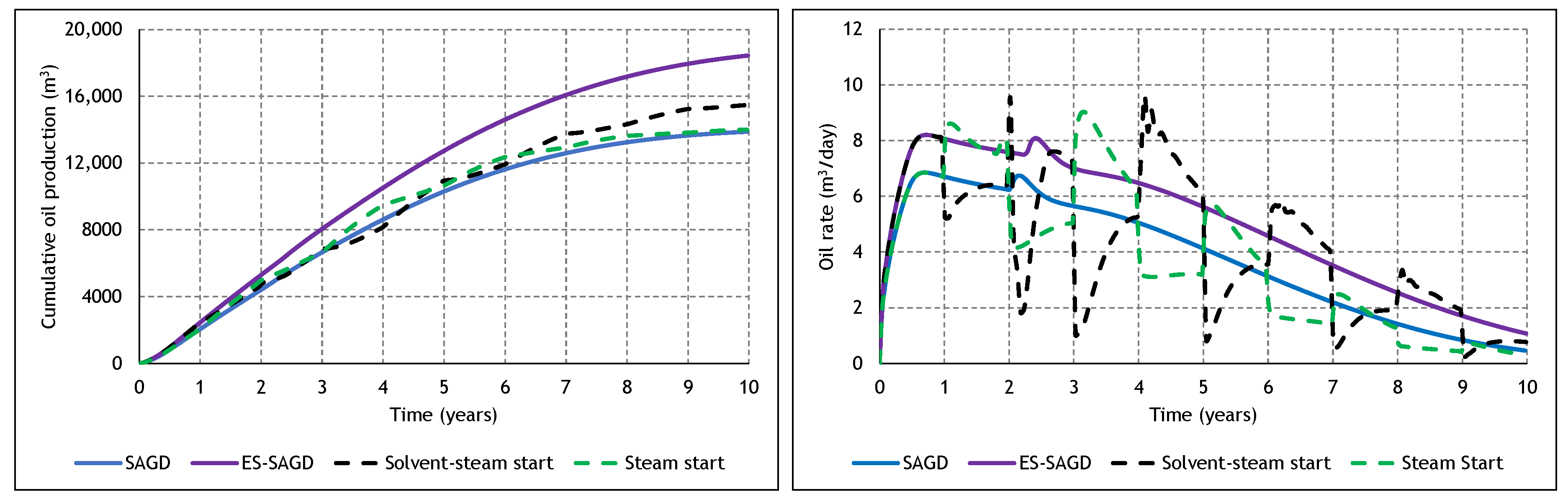
3.4. The Effect of Cycle Length and Starting Mode
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Symbols | |
| Dimensionless concentration | |
| Maximum solvent concentration in the steam | |
| ES-SAGD | Expanding Solvent Steam Assisted Gravity Drainage |
| Permeability (md) | |
| P | Pressure (kPa) |
| Dimensionless oil rate | |
| SAGD | Steam Assisted Gravity Drainage |
| Residual oil saturation to water | |
| Irreducible water saturation | |
| Residual oil saturation to gas | |
| Critical gas saturation | |
| Relative permeability of water at the residual oil saturation | |
| Relative permeability of oil at the irreducible water saturation | |
| Relative permeability of oil at the critical gas saturation | |
| Relative permeability of gas at the residual oil saturation | |
| Time (s) | |
| TS | Steam temperature (°C) |
| TR | Reservoir temperature (°C) |
| Teq | Equilibrium temperature (°C) |
| VAPEX | Vapor Extraction |
| Greek letters | |
| Thermal diffusivity (m2/s) | |
| Dimensionless solvent penetration depth | |
| Dimensionless heat penetration depth | |
| Density (kg/m3) | |
| Dynamic Viscosity (mPa.s) | |
| Kinematic Viscosity (mm2/s) | |
| Distance (m) | |
| ϕ | Porosity |
References
- Butler, R.; McNab, G.; Lo, H. Theoretical Studies on the Gravity Drainage of Heavy Oil during in-Situ Steam Heating. Can. J. Chem. Eng. 1981, 59, 455–640. [Google Scholar] [CrossRef]
- Butler, R. A new approach to the modelling of steam-assisted gravity drainage. J. Can. Pet. Technol. 1985, 3, 42–51. [Google Scholar] [CrossRef]
- Butler, R.; Mokrys, I. A New Process (VAPEX) for Recovering Heavy Oils Using Hot Water and Hydrocarbon Vapour. J. Can. Pet. Technol. 1991, 30, 97–106. [Google Scholar] [CrossRef]
- Li, W.; Mamora, D. Phase behavior of steam with solvent Co-injection under steam Assisted gravity drainage (SAGD) process. In Proceedings of the SPE EUROPEC/EAGE Annual Conference and Exhibition SPE 130807, Barcelona, Spain, 14–17 June 2010. [Google Scholar]
- Ivory, J.; Zheng, R.; Nasr, T.; Deng, X.; Beaulieu, G.; Heck, G. Investigation of low-pressure ES-SAGD. In Proceedings of the International Thermal Operations and Heavy Oil Symposium, Calgary, AB, Canada, 20–23 October 2008. [Google Scholar]
- Yazdani, A.; Alvestad, J.; Kjoensvik, D.; Gilje, E.; Kowalewski, E. A Parametric Simulation Study for Solvent-Coinjection Process in Bitumen Deposits. J. Can. Pet. Technol. 2012, 51, 244–255. [Google Scholar] [CrossRef]
- Orr, B. ES-SAGD: Past, Present and Future. In Proceedings of the SPE Annual Technical Conference and Exhibition, SPE-129518, New Orleans, LA, USA, 4–7 October 2009. [Google Scholar]
- Li, W.; Mamora, D.; Li, Y. Light- and Heavy-Solvent Impacts on Solvent-Aided-SAGD Process: A Low-Pressure Experimental Study. J. Can. Pet. Technol. 2011, 50, 19–30. [Google Scholar] [CrossRef]
- Butler, R.M.; Mokrys, I. Recovery of Heavy Oils Using Vaporized Hydrocarbon Solvents: Further Development of the Vapex Process. J. Can. Pet. Technol. 1993, 32. [Google Scholar] [CrossRef]
- Das, S.K.; Butler, R.M. Investigation of Vapex Process in a Packed Cell Using Butane as a Solvent. In Proceedings of the International Conference on Recent Advances in Horizontal Well Applications, Calgary, AB, Canada, 20–23 March 1994. [Google Scholar]
- Boustani, A.; Maini, B. The Role of Diffusion and Convective Dispersion in Vapor Extraction Process. J. Can. Pet. Technol. 2001, 40. [Google Scholar] [CrossRef]
- Haghighat, P.; Maini, B. Effect of Temperature on VAPEX Performance. J. Can. Pet. Technol. 2013, 52. [Google Scholar] [CrossRef]
- Torabi, F.; Jamaloei, B.Y.; Stengler, B.M.; Jackson, D.E. The evaluation of CO2-based vapour extraction (VAPEX) process for heavy-oil recovery. J. Pet. Explor. Prod. Technol. 2012, 2, 93–105. [Google Scholar] [CrossRef]
- Shu, W.; Hartman, K. Effect of Solvent on Steam Recovery of Heavy Oil. SPE Reserv. Eng. 1988, 3, 457–465. [Google Scholar] [CrossRef]
- Zhao, L. Steam Alternating Solvent Process. SPE Reserv. Eval. Eng. 2007, 185–190. [Google Scholar] [CrossRef]
- Nasr, T.; Beaulieu, G.; Golbeck, H.; Heck, G. Novel Expanding Solvent-SAGD Process ES-SAGD. J. Can. Pet. Technol. 2003, 13–16. [Google Scholar] [CrossRef]
- Perlau, D.; Jaafar, A.E.; Boone, T.; Dittaro, L.; Yerian, J.; Dickson, J.; Wattenbarger, C. Findings from a Solvent-Assisted SAGD Pilot at Cold Lake. In Proceedings of the SPE Heavy Oil Conference, Calgary, AB, Canada, 11–13 June 2013. [Google Scholar]
- Gates, I. Oil phase viscosity behaviour in Expanding-Solvent Steam-Assisted Gravity Drainage. J. Pet. Sci. Eng. 2007, 59, 123–134. [Google Scholar] [CrossRef]
- Gibbs, J. On the equilibrium of heterogeneous substances. Am. J. Sci. 1878, 16, 441–458. [Google Scholar] [CrossRef]
- Govind, P.; Das, S.; Srinivasan, S.; Wheeler, T. Expanding solvent SAGD in Heavy Oil Reservoirs. In Proceedings of the International Thermal Operations and Heavy Oil Symposium, Calgary, AB, Canada, 20–23 October 2008. [Google Scholar]
- Sharma, J.; Moore, R.; Mehta, R. Effect of Methane Co-Injection in SAGD—Analytical and Simulation Study. In Proceedings of the Canadian Unconventional Resources Conference, Calgary, AB, Canada, 15–17 November 2011. [Google Scholar]
- Edmunds, N. Observations on the Mechanisms of Solvent-Additive SAGD Processes. In Proceedings of the SPE Heavy Oil Conference, Calgary, AB, Canada, 11–13 June 2013. [Google Scholar]
- Khaledi, R.; Boone, T.; Motahhari, H.R.; Subramanian, G. Optimized solvent for Solvent Assisted-Steam Assisted Gravity Drainage (SA-SAGD) Recovery Process. Soc. Pet. Eng. 2015. [Google Scholar] [CrossRef]
- Rabiei Faradonbeh, M. Mathematical Modeling of Steam-Solvent Gravity Drainage of Heavy Oil and Bitumen in Porous Media. Ph.D. Thesis, University of Calgary, Calgary, AB, Canada, 2013. [Google Scholar]
- Venkatramani, A.V.; Okuno, R. Mechanistic simulation study of expanding-solvent steam-assisted gravity drainage under reservoir heterogeneity. J. Pet. Sci. Eng. 2018, 169, 146–156. [Google Scholar] [CrossRef]
- Eghbali, S.; Dehghanpour, H. A Simulation Study on Solvent-Aided Process using C3 and C4 in Clearwater Oil-Sand Formation. J. Pet. Sci. Eng. 2020, 184, 106267. [Google Scholar] [CrossRef]
- Gupta, S.; Gittins, S.; Picherack, P. Field Implementation of Solvent Aided Process. In Proceedings of the 53rd Canadian International Petroleum Conference, Calgary, AB, Canada, 11–13 June 2002. [Google Scholar]
- Gates, I.; Larter, S. Energy efficiciency and emissions intensity of SAGD. Fuel 2014, 115, 706–713. [Google Scholar] [CrossRef]
- Manfre Jaimes, D.; Gates, I.D.; Clarke, M. Reducing the Energy and Steam Consumption of SAGD through Cyclic Solvent Co-Injection. Energies 2019, 12, 3860. [Google Scholar] [CrossRef]
- Gates, I.; Chakrabarty, N. Design of the Steam and Solvent Injection Strategy in Expanding Solvent Steam-Assisted Gravity Drainage. J. Can. Pet. Technol. 2008, 47, 12–20. [Google Scholar] [CrossRef]
- Butler, R. Thermal Recovery of Oil and Bitumen; Prentice Hall: Upper Saddle River, NJ, USA, 1991. [Google Scholar]
- CMG. Winprop User Manual; Computer Modelling Group: Calgary, AB, Canada, 2017. [Google Scholar]
- Shu, W. A viscosity correlation for mixtures of heavy oil, bitumen, and petroleum fractions. Soc. Pet. Eng. 1984, 24, 277–282. [Google Scholar] [CrossRef]
- Bergman, T.; Incropera, F.; DeWitt, D.; Lavine, A. Fundamentals of Heat and Mass Transfer; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Shin, H.; Polikar, M. Fast-SAGD application in the Alberta Oil Sands Area. J. Can. Pet. Technol. 2006, 45, 46–53. [Google Scholar] [CrossRef]
- CMG. STARS User Manual; Computer Modelling Group: Calgary, AB, Canada, 2017. [Google Scholar]
- Strausz, O.; Lown, E. The Chemistry of Alberta Oil Sands, Bitumens and Heavy Oils; Alberta Energy Research Institute: Calgary, AB, Canada, 2003. [Google Scholar]
- Keshavarz, M. Analytical Modeling of Steam Injection and Steam-Solvent Co-Injection for Bitumen and Heavy Oil Recovery with Parallel Horizontal Wells. Ph.D. Thesis, University of Calgary, Calgary, AB, Canada, 2019. [Google Scholar]
- Salama, D.; Kantzas, A. Monitoring of Diffusion of Heavy Oils with Hydrocarbon Solvents in the Presence of Sand. In Proceedings of the SPE International Thermal Operations and Heavy Oil Symposium, Calgary, AB, Canada, 1–3 November 2005. [Google Scholar]

| Parameter | Value |
|---|---|
| Grid dimensions | 30 × 50 m |
| Cell dimensions | 1 × 1 m |
| Porosity () | 30% |
| Permeability () | 5000 md |
| Permeability ratio () | 0.5 |
| Initial temperature | 12 °C |
| Initial pressure | 1800 kPa |
| Initial oil saturation () | 0.8 |
| Initial water saturation () | 0.2 |
| Rock compressibility | 1 × 10−6 1/kPa |
| Rock heat capacity | 2.6 × 106 J/(m3∙C) |
| Rock thermal conductivity | 2.7 × 105 J/(m∙day∙C) |
| Oil thermal conductivity | 1.2 × 104 J/(m∙day∙C) |
| Water thermal conductivity | 5.4 × 104 J/(m∙day∙C) |
| Gas thermal conductivity | 0.4 × 104 J/(m∙day∙C) |
| Overburden Heat Capacity | 2.3 × 106 J/(m3∙C) |
| Overburden thermal conductivity | 1.5 × 105 J/(m∙day∙C) |
| 0.2 | |
| 0.15 | |
| 0.005 | |
| 0.05 | |
| 0.1 | |
| 0.992 | |
| 0.834 | |
| 1 |
| Parameter | Value |
|---|---|
| 9.7 | |
| 28 m | |
| 5 × 10−7 m2/s | |
| 1.75 | |
| 4.32 × 10−5 m2/day |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Manfre Jaimes, D.; Clarke, M. Analytical Modeling of the Cyclic ES-SAGD Process. Energies 2020, 13, 4243. https://doi.org/10.3390/en13164243
Manfre Jaimes D, Clarke M. Analytical Modeling of the Cyclic ES-SAGD Process. Energies. 2020; 13(16):4243. https://doi.org/10.3390/en13164243
Chicago/Turabian StyleManfre Jaimes, Diego, and Matthew Clarke. 2020. "Analytical Modeling of the Cyclic ES-SAGD Process" Energies 13, no. 16: 4243. https://doi.org/10.3390/en13164243
APA StyleManfre Jaimes, D., & Clarke, M. (2020). Analytical Modeling of the Cyclic ES-SAGD Process. Energies, 13(16), 4243. https://doi.org/10.3390/en13164243




