Abstract
This work aims at the economic evaluation of a semi-underground pumped hydro storage power plant erected in an abandoned open-pit mine. For the exploratory model-based analysis, we develop and apply both a simple deterministic and a stochastic net present value (NPV) approach, the latter of which uses a Monte Carlo simulation to account for revenue uncertainty from electricity price fluctuations. The analytical framework developed is applied to two promising sites in the Rheinland region in Germany, Hambach and Inden, making reasonable parameter value assumptions and considering and ignoring the lengthy duration of lower reservoir flooding. The investor’s value-at-risk is computed for alternative performance indicators (NPV, net cash recovery, profit-to-investment ratio, and specific production costs) to compare the different outcomes in terms of the project’s financial risk distribution. Calculations show that a semi-underground pumped hydro storage power plant in an abandoned open-pit mine can be constructed at reasonably low investment costs and operated at low specific production costs. However, because the investment has to be made long before the pit lake is (naturally) flooded—a process that for realistic flow rates may take up to 20 years—the project is highly uneconomical and would require substantial subsidies, as compared to a situation where flooding happens immediately.
1. Introduction
Germany is shifting its power production away from fossil fuels and nuclear power towards renewable energies [1]. With increasing wind and solar photovoltaic power supply fluctuations, security of supply, and long-term sustainability need to be managed [2]. One solution to this problem is the expansion of electricity storage capacities. The pumped hydro storage (PHS) technology is suitable for efficient electricity storage with low specific production costs [3]. To create high capacities, large areas and large height differences are required. Typically, PHS is placed in mountainous areas (e.g., in Austria, Switzerland, and Norway), often creating controversies due to their substantial socio-economic-ecological impacts. Potential locations for PHS are thus rare in Germany, but several lignite open-pit mines will cease operation in the years to come (due to the planned 100% phaseout of coal-fired power generation until 2035/2038), resulting in some areas being recultivated with large pit lakes. Due to soil extraction, height differences have been developed in the form of mine dumps. The aim of our investigation is to show whether such locations can be used profitably for the installation of what we call semi-underground PHS (semi-UPHS) power plants, in order to contrast them with UPHS built in underground coal mines (cf. [4] and references therein). Reasonable parameter values, based on future pit lakes in Germany (Hambach; Inden), are used for the empirical analysis, and boundaries for maximum head and storage volume are set. The model-based economic investigation is performed by applying the net present value (NPV) method and a sensitivity analysis, as well as a Monte Carlo simulation to account for electricity price uncertainties and a value-at-risk analysis for decision-making under uncertainty.
The literature on PHS in abandoned open-pit mines is still very scarce. Menéndez et al. [5,6,7] studied the geological potential of an area with closed open-pit coal mines in northwestern Spain. Pujades et al. [8,9] investigated the influence of groundwater exchange with reservoirs built in abandoned open-pit mines on the efficiency of UPHS. Madlener and Specht [4] analyzed the economic viability of UPHS in deep abandoned coal mines in the Rheinland area in Germany. To the best of our knowledge, our study seems to be the first to analyze the economic feasibility of semi-UPHS in open-pit mines. On the very complex and manifold interactions of the mining industry with water resources more generally, an excellent reference is Northey et al. [10], and on mine closure and pit lakes as terminal sinks see McCullough et al. [11]. To the best of our knowledge, the present study is the first detailed economic analysis on the use of abandoned coal mines for (semi-subsurface) PHS power plants.
The remainder of this article is structured as follows. In Section 2, we present and investigate the UPHS concept used in the study. Part of the concept is a cost analysis, the time flow of the pit lake flooding, revenue considerations, and relevant fees and regulations. In Section 3, the methodology is presented and relevant parameters are introduced. Section 4 presents the results of the analysis. Section 5 offers some conclusions and an outlook for further research.
2. Pumped Hydro Storage
2.1. Principles of PHS and Situation in Germany
Pumped hydro storage is utilized by storing water in an elevated basin in times of power surplus and releasing it through turbines down to a lower basin in times of power demand. Capacities of 50 GWh at a discharge time of 1000 h can be achieved. PHS is a sophisticated but well-established and mature technology, which is used all over the world. It reaches high efficiencies of up to 80% and a high flexibility due to its black-start ability [12]. PHS can participate in all three reserve markets (primary, secondary, and tertiary) and has the lowest specific production costs of 7.73 €-ct/kWh compared to other storage technologies [13]. With 1060 MW of power and a capacity of 8.5 GWh, Goldisthal is the largest PHS power plant in Germany [14]. The disadvantage in Germany is that potential natural locations with existing water reservoirs and effective heads are rare and are largely under use already. Furthermore, social acceptance must be considered. Planned projects, such as the one in Simmerath (Eifel region, Germany, 640 MW, 3.8 GWh), have encountered fierce resistance from the local citizens because of its adverse environmental, recreational, and tourism impacts; the Simmerath project was turned down in 2013.
2.2. Markets for Large-Scale Storage Operation
Electricity storage technologies draw profit by peak shaving on the spot market and with grid services, such as offering balancing energy [15]. One assignment of the German transmission system operators (TSOs) is to maintain equilibrium between electricity fed into and withdrawn from the grid. There are four TSOs in Germany: Amprion, Transnet BW, Tennet, and 50 Hertz [16]. In the case of imbalances, the TSOs are able to retrieve balancing energy from the three reserve markets. PHS power plants are able to preserve all three kinds of reserve energy; however, these are most likely to be used on the secondary reserve market, because the provision of secondary reserve capacity is technically hard to achieve for other participants, resulting in higher expected revenues in comparison with the other reserve capacity markets [17]. Since 2007, the TSOs have shared an online tendering platform to procure their weekly demand for secondary reserve capacity. Pricing distinguishes between the demand rate (€/MWh) and the energy rate (€/MWh). Tendering is performed on a weekly basis by the use of a merit order (stacked supply curve in ascending cost order). The facilities are used in line with the merit order of the demand rates and receive payment for every MWh provided within one week. The bids are again sorted according to the declining merit order of the energy rate. In the case of reserve capacity being used, the price is defined by the lowest energy rate of the merit order, and the provider is paid for every MWh used [18] (cf. Tab. A1).
2.3. Concept for an Open-Pit Mine Semi-Underground Pumped Hydro Storage Power Plant
As a consequence of open-pit (or open-cast) mining, residual mining holes are created. One reason for this is the difference between gross production and usable materials. The other reason is that not all of the produced material is refilled into the pit but some is stored as mine dumps adjacent to the pit mine on account of the high costs of refilling as well as the dip of the coal seam, the latter requiring an ever-increasing volume to be moved during extraction [19]. For example, half of the mined area of Hambach will remain a residual mining hole. Most of these holes are flooded and become pit lakes [20]. The idea of a PSH power plant in an abandoned open-pit mine is to use this artificial lake in combination with the mine dump in order to store electricity. Currently, lignite is mined on twelve different sites in Germany [21].
The best locations for PHS in an open-pit mine are located in the Rhineland, owing to deep coal layers of up to 400 m and the resulting offset of overburden. Table 1 shows the dimensions of the future pit lakes in the Rhineland, Hambach, and Inden (referred to as Scen. 1 and Scen. 2 hereafter).

Table 1.
Dimensions of future pit lakes in the German Rhineland region.
2.4. Energy Storage and Conversion
PHS stores energy in the form of potential energy, which is dependent on the flow rate, the gravitational constant, the head, the density of the medium, and the efficiency of the pumping process. It is calculated with the following equation [23]:
where denotes the number of machine units, the power of the loading process (kW), the volumetric flow rate of the loading process (m3/s), the gravitational constant (9.81 m/s2), the efficiency of the loading process (%), h the head (m), and ρ the density of water (~1000 kg/m3). The conversion of the potential energy into kinetic and electric energy is calculated as:
where represents the power of the discharging process (kW), the volumetric flow rate of discharging (m3/s), and the efficiency of the discharging process (%). The correlated capacity is also dependent on the storage volume and the flow rate and is the product of the maximum power and the duration of a complete discharge of the storage volume:
where is the discharge time (h), the capacity discharge (kWh), and
the utilizable volume (m3). The overall efficiency of PHS power plants is calculated by the product of the loading efficiency in the pumping mode ( and the discharging efficiency ( in the turbine mode.
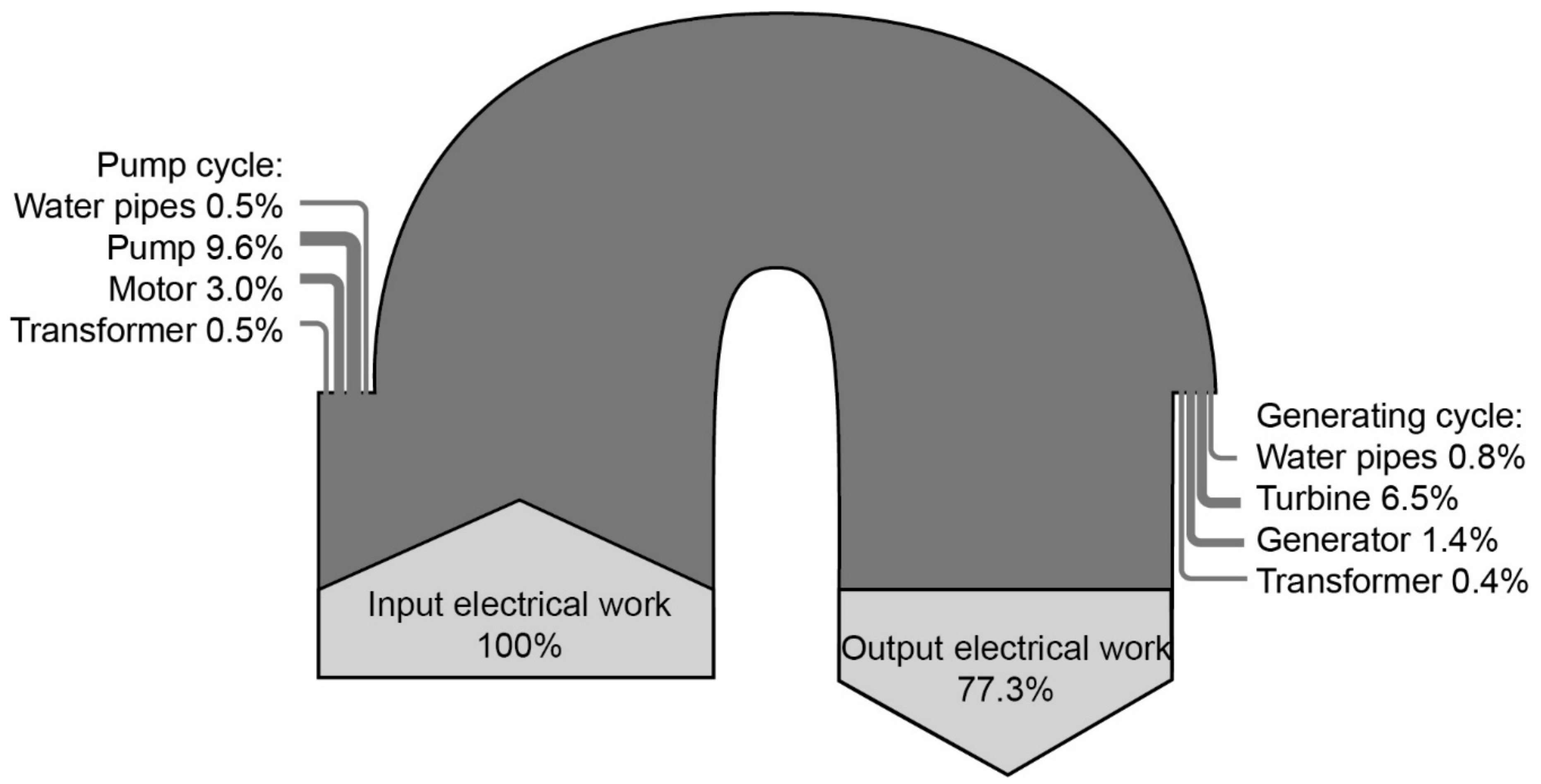
An exemplary overview of the energy losses and the resulting efficiency of PHS is provided in Figure 1.
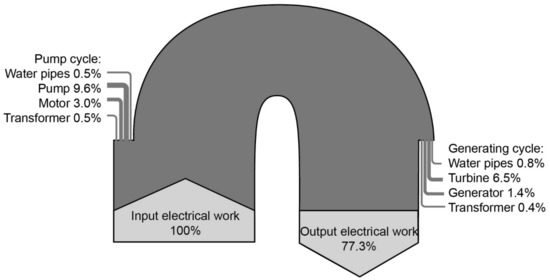
Figure 1.
Efficiency and energy losses of PHS. Source: own illustration, based on [24].
2.5. Technical Concept
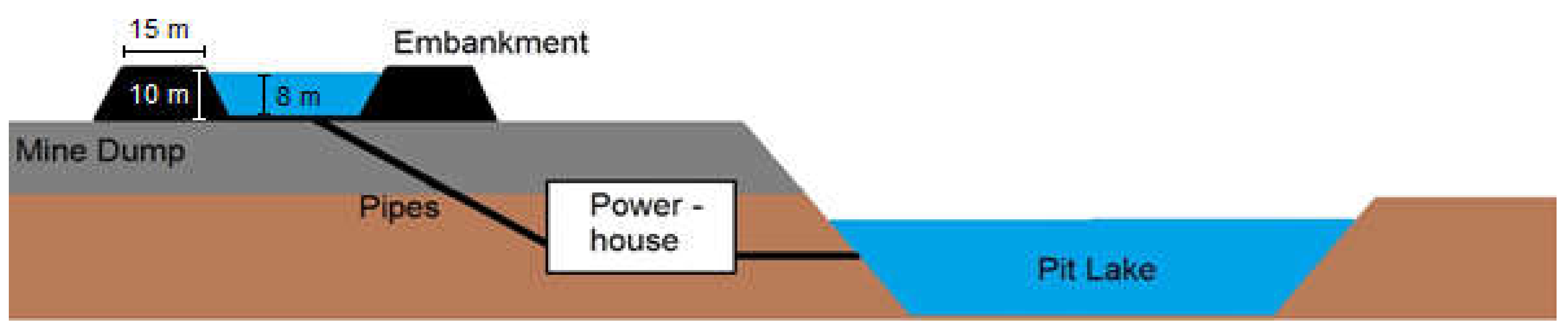
The future pit lake functions as the lower reservoir, whereas the mine dump of the abandoned pit mine functions as the bed of the upper reservoir. The two reservoirs are connected by underground pressure pipes and the powerhouse excavation with turbines, transformer, and connection to the electricity line (cf. Figure 2). In times of power surplus, water from the pit lake is pumped into the upper reservoir, where the electricity is stored as potential energy. In times of power demand, water runs down the pipes, and the potential energy is transformed into kinetic energy, running the turbine, and finally turning into electrical energy via the generator. Our semi-UPHS concept investigated uses four machine units, which can be controlled separately and are modeled after the PHS plant Goldisthal, the largest PSH plant in southern Thuringia, Germany (1060 MW, in operation since 2003, owned by Vattenfall).
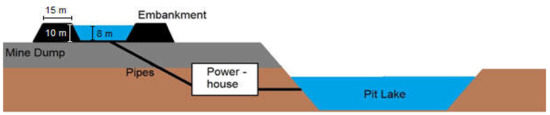
Figure 2.
Technical concept of a semi-underground pumped hydro storage plant (Hambach-like).
The upper reservoir is constructed with a kind of circular embankment. The width of the dam crest amounts to 15 m with an inclination of 32° at a height of 10 m and freeboard of 2 m (Popp, 2015 [25]; on the dimensioning and economic analysis of ringwall storage power plants see [26]. In our study, the maximum water level is limited to 8 m in order to minimize the possible subsidence of the mine dump. This value has to be individually adapted depending on the project. Another project-specific parameter is the available area on the mine dump for building the upper reservoir determining its volume. The inside of the reservoir has to be sealed with an asphalt coating. At a diameter of 1000 m, the upper reservoir has a volume of almost 6 × 106 m3. The possibility of storage on a mine dump would require geotechnical studies that are beyond the scope of this study. Maximum achievable heights are estimated to be about a 200 m (height difference between mine dump and pit lake). Ranges for the dimension of the pit lake are volumes of 25 × 106 m3 to 5.8 × 109 m3 and lake surface areas between 1 × 106 m2 to 40 × 106 m2. These values are derived from German lignite pit mines in operation. The maximum values for volume and surface area are provided by the pit lake in Hambach [27].
2.6. Cost Analysis
2.6.1. Capital Expenditures (Capex)
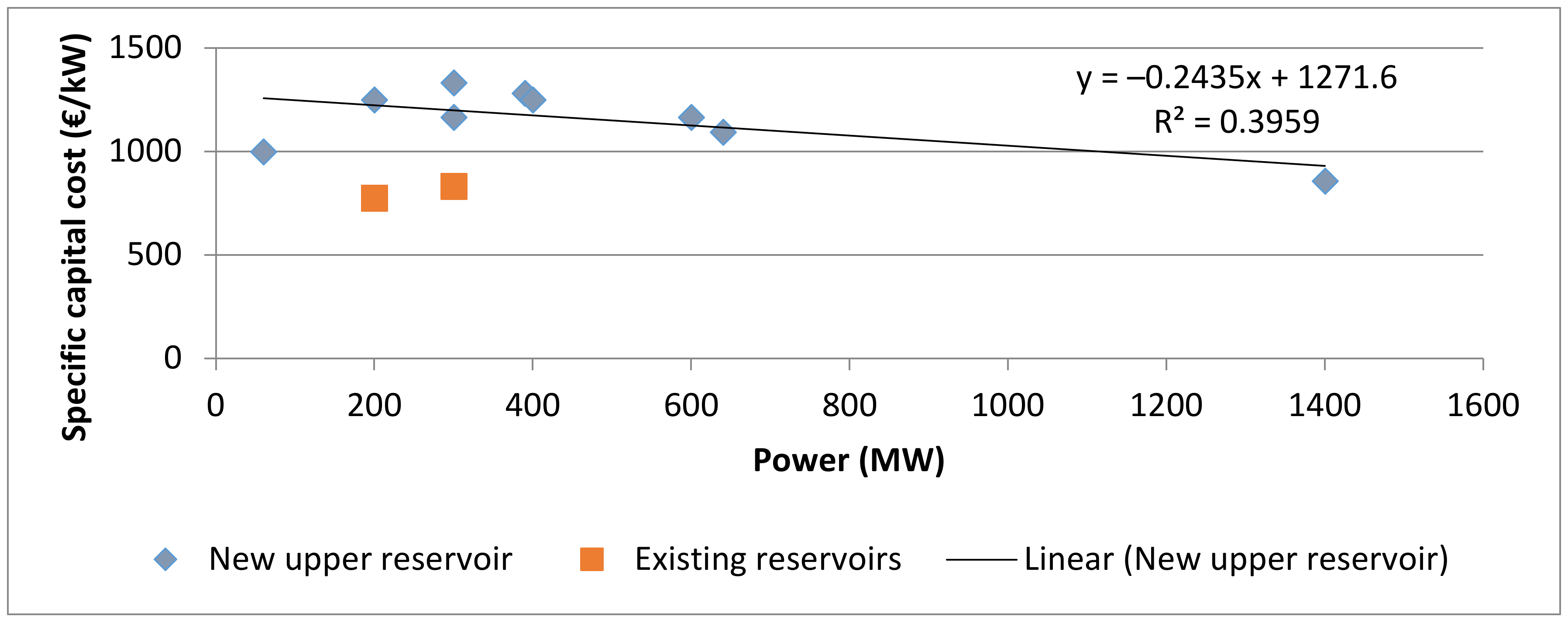
The specific investment costs of PHS can vary significantly (600–3000 €/kW) depending on the site-specific conditions [28,29]. The capital costs for the mechanical facilities of an open-pit mine PHS are comparable to the investment of other PHS power plants. The largest share is the powerhouse with 37%, followed by the upper reservoir with 19%, owner’s costs at 17% (these include paid-up royalties, preproduction costs, inventory capital, and land costs, cf. [30]), and engineering-, procurement and construction management services at another 17% [30]. It is part of a study by the U.S. National Renewable Energy Laboratory (NREL) in 2012 (figures converted using the official exchange rate of Sep 14, 2014 (US$1 = €0.7742; www.oanda.org). Summing up, the specific capital costs amounted to 1726 €/kW. The specific capital costs in a related study by [13] amount to 750 €/kW, which makes a difference of nearly 1000 €/kW. In order to obtain a reference value, the specific capital costs of a series of planned PHS projects (see Table 2) has been plotted with specific capital costs and power in Figure 3. The average of projects with only one existing reservoir is approx. 1100 €/kW. The specific capital costs for powerhouse, powerhouse excavation, tunnels and engineering, procurement, and construction management services are taken over proportionally by the values from [30] and are adapted to 1100 €/kW, which leads to power-related specific capital costs of 704 €/kW. The costs for the upper reservoir, owner’s costs, and other arising costs are assessed in this study and offer cost reduction potential. It is also reasonable to look at these two groups separately because the volume of the upper reservoir does not influence the power in kW but it does influence the capacity in kWh, and thus should be excluded for the power-related specific capital costs.

Table 2.
PHS projects in Germany.
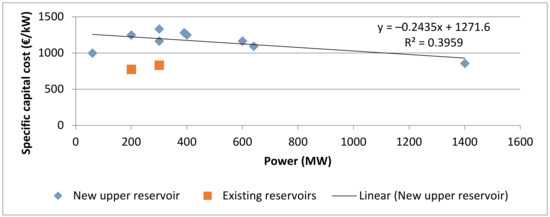
Figure 3.
Specific capital costs of PHS projects in Germany. Source: own illustration after [31].
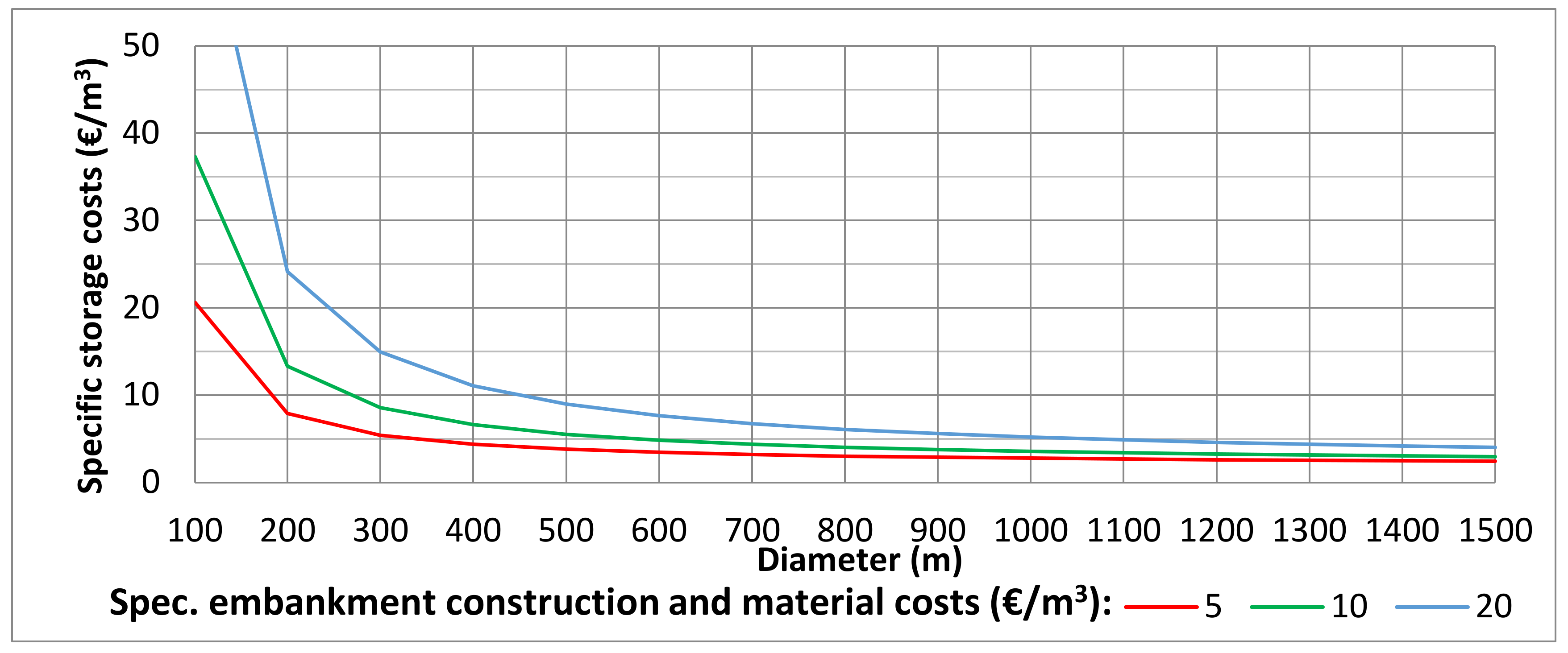
The costs of the upper reservoir are composed of owner’s costs, embankment construction, and material, as well as sealing costs [25]. As an illustration, for a diameter of 1000 m and a height of 10 m, costs of approx. €16 million arise, which is comparatively low due to the synergies between the construction project and the recultivation process. Figure 4 shows the investment costs per m3 for the upper reservoir, depending on the diameter at a constant height (=height of embankment, with freeboard of 2 m, resulting in 8 m water depth) of 10 m with varying embankment construction costs between 5 €/m3, 10 €/m3, and 20 €/m³. At a diameter of 1500 m, the costs per m³ of storage volume of the reservoir converge asymptotically to approx. 2.50 €/m3, 3 €/m3, and 4 €/m3, respectively, comprising owner’s costs of 5 €/m2, embankment construction and material costs of 5 €/m3, and sealing costs or 10 €/m2, according to [25].
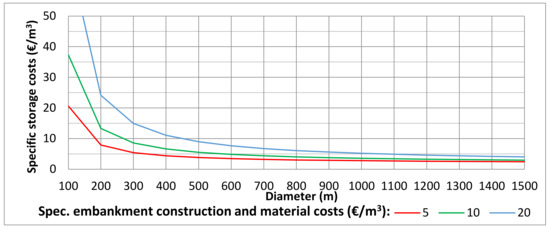
Figure 4.
Costs in € per m3 for the upper reservoir, by reservoir diameter.
Note that we deliberately restrict the costs to some embankment construction and sealing costs and ignore those for recultivation. The reason is that we assume that these costs would occur anyhow and thus there are no additional costs arising as a consequence of building the (semi-)underground PSPH plant. Neither cost data nor clear plans and legislation seem to be available for reconverting the open-pit coal mines in Germany back to some acceptable state, let alone any documentation for UPHS as an alternative recultivation scenario or risk management strategies and liabilities taking the polluter pays principle into account. Hence, it seems fair to say that as of today it is far from clear what the overall societal costs of the coal phase-out will be. Internationally, the situation does not seem to be any better, as the discussion, e.g., on the best available practice for mine closure and long-term management of pit lakes in arid regions discussed in McCullough et al. [11], indicates.
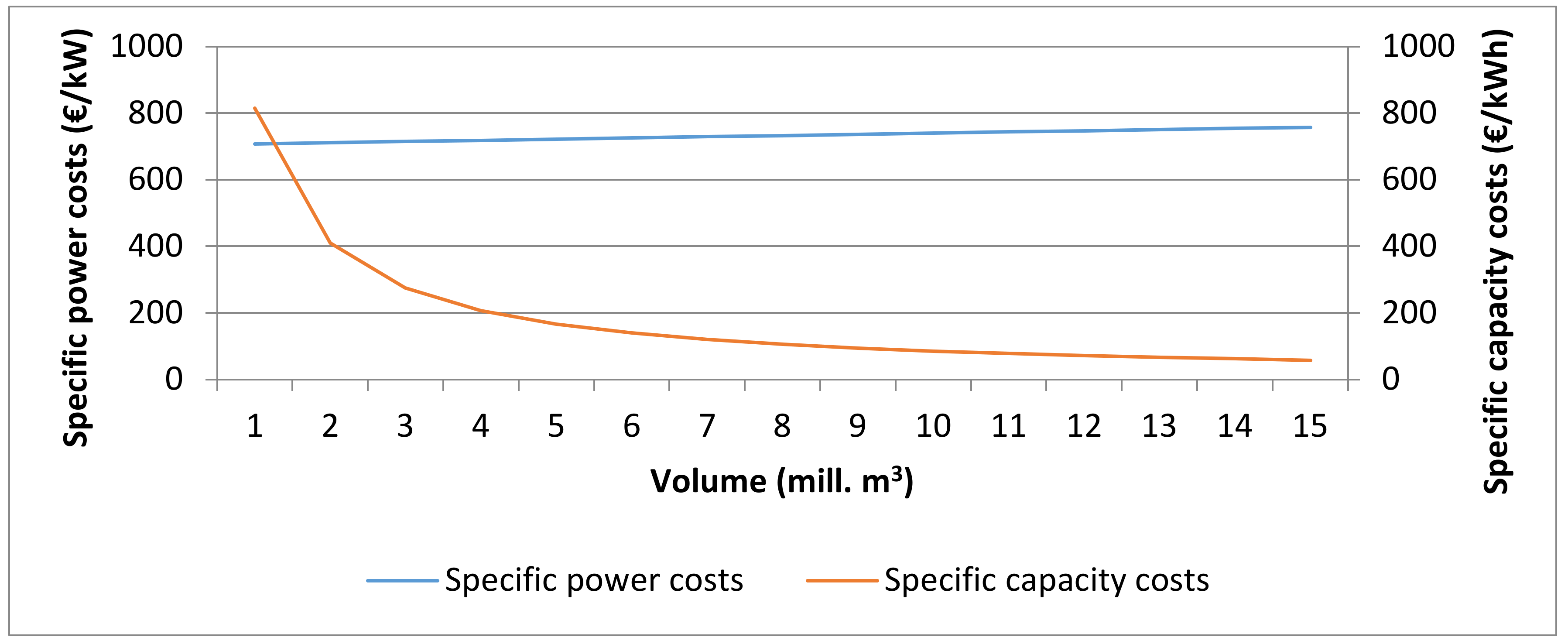
Summing up, the specific investment costs per kW and kWh depicted in Figure 5 were calculated as a function of storage volume for a construction with an installed power of 700 MW and embankment construction and material costs of 5 €/m3 (see Figure 4). The costs per installed power rise slightly with the storage volume, whereas the costs per unit of installed capacity fall rapidly. Compared to the Capex of other PHS projects reported in Table 2, the costs of an open-pit mine PHS are in the lower range.
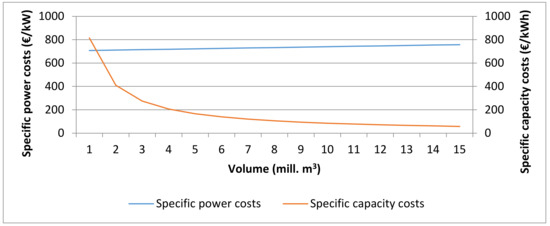
Figure 5.
Specific investment costs as a function of storage volume, both in terms of installed power (€/kW) and installed capacity (€/kWh).
2.6.2. Operational Expenditures (Opex)
The operational expenditures are split into fixed and variable expenditures. The fixed annual costs for operation and maintenance are estimated at 10,000 €/MW [13]. According to [13], the variable costs are composed of (1) costs per start load of 2 €/MW_start; (2) costs per start discharge of 2 €/MW_start; (3) other costs of 1 €/MWh; and (4) average power procurement costs at 24 €/MWh (power procurement costs are adapted for specific scenarios).
2.7. Flooding of Pit Lake
Flooding is an important impact on the technical scenarios. The PHS power plant cannot start operation until the pit lake has been filled and groundwater inflow has been prepared. The investment in and construction of the power plant will take place when the pit mine operation is over and the slope construction for the pit lake begins. The flooding is assumed to be achieved by water extraction from surrounding flowing waters, and is either cost-free for hydropower plants (see also Table A2) or paid for by the pit mine operator as part of the recultivation process (note again that we assume that no additional recultivation costs will arise due the construction of a semi-underground PSH power plant). Water losses through evaporation, seepage, discharge, or physical entrainment in the tailings materials are ignored for simplicity reasons (for a review of the manifold and complex issues related to the quantification of the water footprint of mining operations, and scarcity and site-specificity of mine site water data, we refer to [10]). Groundwater inflow will not take place until the pit lake has been filled, in order to reduce acid mine drainage (AMD). The duration of flooding is dependent on the surrounding flowing waters. Every river has a maximum extraction volume depending on its flow rate. A filling rate of 40 × 106 m3/a is assessed for the pit lake in Inden (Scen. 2) by water extraction from the Rur river [22]; 270 × 106 m3/a from the Rhine is assessed for the flooding in Hambach (Scen. 1) [27,32]. Given these filling rates, more than 20 years will elapse until a pumped-storage hydropower plant eventually goes into full operation after an investment of several hundred million Euros. During these years, obviously, such a power plant will not generate any revenues. The maintenance costs for this time are assumed to be 10% of the maintenance and operation costs during operation.
2.8. Fees and Regulations
In the following, an overview regarding the assumptions made on relevant fees and regulations for PHS is given.
2.8.1. Grid-Use Fees
Consumers of grid electricity are legally bound to pay fees to the TSO. PHS electricity in Germany is also regarded as an end customer of the grid and must, therefore, pay network charges in the form of grid-use fees in accordance with § 3 (25) EnWG (German Energy Industry Act) [33]. While they usually have to pay fees for the procurement of electricity, this does not apply to the grid feed-in (see also Section 2.8.2). Also, new electricity storage facilities that go into operation between 4 August 2011, and 3 August 2026, are excluded from grid-use fees for the first 20 years. In our calculations, such fees are not taken into account in the economic evaluation, assuming that PHS plants will continue to be exempted also in the future. This is in line with Steffen [31], who considers grid fees not to be a barrier for new PHS power plants and thus ignores them in his calculations as well, and mentions that at the time of his analysis the federal government had just doubled the exemption period from all grid-use fees from 10 to 20 years.
2.8.2. EEG Levy
In accordance with § 60 EEG (German Renewable Energy Sources Act) [34], electricity suppliers have to pay an EEG levy to the TSOs for every kWh delivered to end consumers. This is necessary to cover the difference between revenues and expenditures for the priority feed-in of renewable energy pursuant to the EEG (netztransparenz.de, 2020) [35]. Although the operator of a PHS system is regarded as an end consumer, he/she is exempted due to special regulations that the EEG stipulates for PHS [36].
2.8.3. Water Extraction Fees
The European water framework directive 2000 requires adequate pricing of water usage but allows for exceptions due to environmental, social or economic reasons, defined by the member states (European Commission 2000, § 9) [37].
While in this study we assess the possibility of a PHS plant in the state of North Rhine-Westphalia, where no fees are incurred for water extracted for generating hydropower [38], such fees may be due in other federal states (cf. Table A2). In North-Rhine Westphalia, the Water Retrieval Act 2004 (Wasserentnahmegesetz, WasEG) regulates water usage fees. Various exemptions apply (e.g., for cooling water purposes reduced rates are granted). Related other laws are the Water Household Act (Wasserhaushaltsgesetz, WHG) and the State Water Act (Landeswassergesetz, LWG); these are available online at https://recht.nrw.de (in German only). The LWG also deals with the use of water for hydropower production (§ 28); Section (1) stipulates explicitly that climate protection requirements have to be considered when granting permits, whereas Section (2) foresees exemptions from recultivating waterbodies that were used for hydropower due to their social welfare benefits (as stipulated in WHG § 6 (2)).
3. Methodology
3.1. Economic Model and Input Description
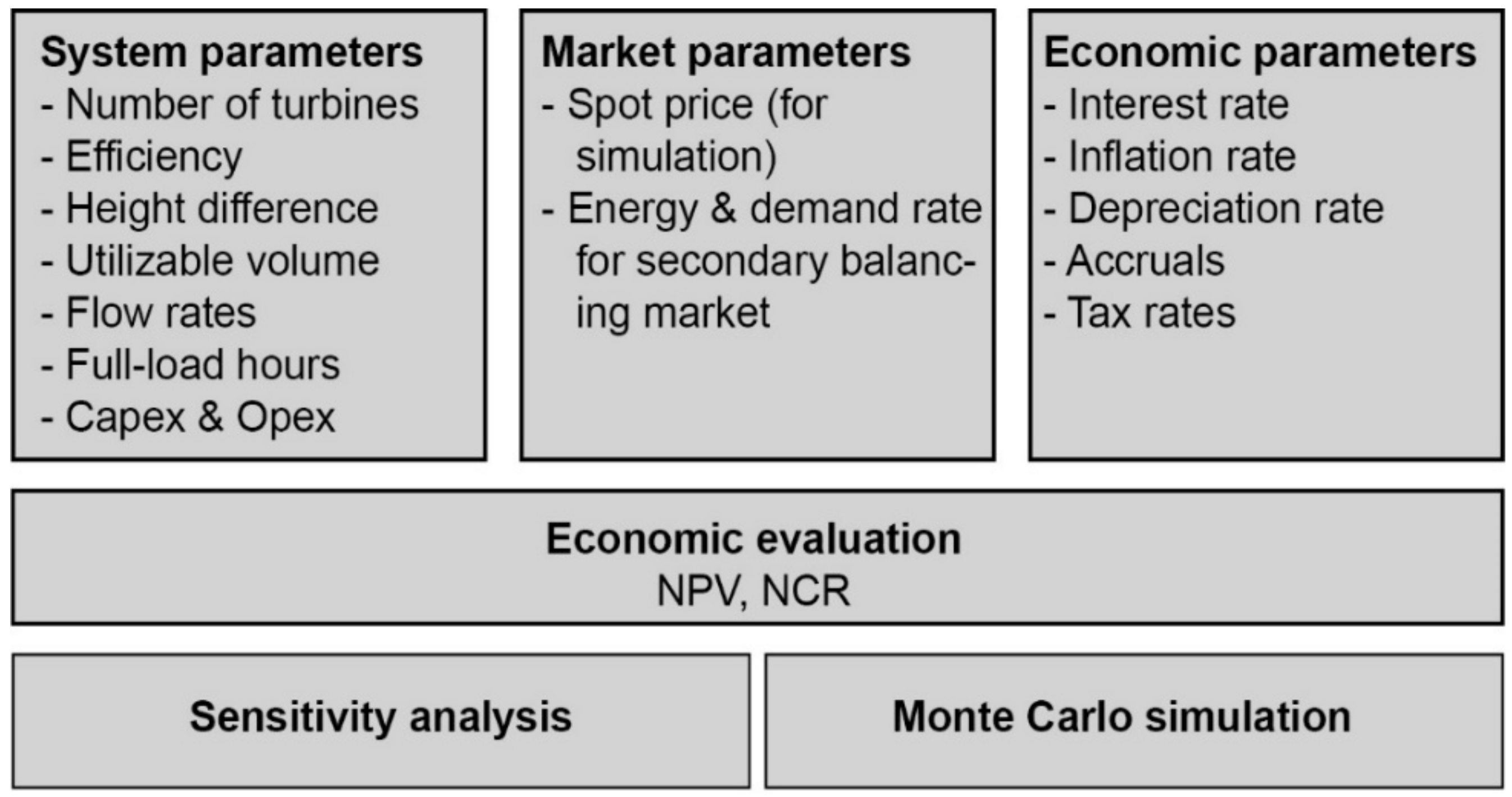
The results of the economic evaluation are presented in terms of net present value (NPV) and net cash recovery (NCR). Further, the robustness of the model results is scrutinized deterministically by means of sensitivity analysis and, probabilistically, also by running a Monte Carlo simulation. Figure 6 displays the setup of the economic model. In the following, the parameters are specified in tabular form.
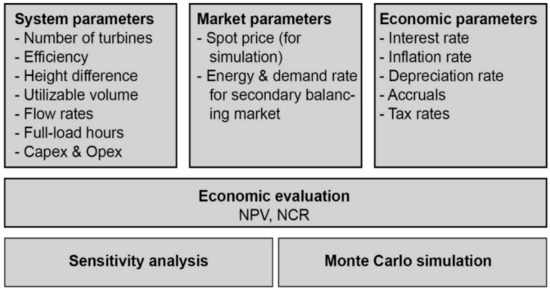
Figure 6.
Overview of the economic model.
Table 3 shows the PHS system-related parameters using Hambach as an example. The values are chosen and calculated in accordance with the underlying conditions described in Section 2.

Table 3.
System-related parameter and technical specifications exemplary for Scenario 1.
Table 4 shows the input parameters of the cost analysis undertaken in Section 2.6. On the one hand, the costs consist of Capex, which are split into power-related costs and costs for building the reservoir. On the other hand, they comprise of fixed and variable operational expenditures (Opex).

Table 4.
Cost-related parameter values assumed.
Table 5 gives representative parameters for the day-ahead spot market and the secondary reserve market. The parameters are derived from the analysis presented in Section 3.4.2 and Section 3.4.3 below.

Table 5.
Power market-related parameter values assumed.
Economic parameters and values assumed are listed in Table 6. The interest rate i and the related discounting factor (1+i) are essential for the NPV analysis, and thus detailed sensitivity analyses are undertaken in the empirical part. The former denotes the minimum return over the operational lifetime of the project. Table 7 shows the variables involved in the economic analysis presented in Section 4.1, which are discussed next.

Table 6.
Economic parameter values assumed.

Table 7.
Economic variables and symbols used.
3.2. Economic Evaluation
Calculations of the economic feasibility of a PHS plant are made with the help of the net present value (NPV) method. The NPV computes the overall value of benefits and costs of the project by summing up all time-discounted net revenues (i.e., costs and revenues ) at different points in time and comparing them with the investment at time t = 0 as the initial cost outlay [39]:
The annual cash flow is divided by the interest factor to reflect the time value of money in dependence on selected rates:
Thus, the discounting factor makes the different cash flows in time comparable [40]. In the case of an investment project with a lifetime of up to 70 years, aside from the interest rate i, it is important to also account for the inflation rate , which counteracts the former:
The NPV method without consideration of the inflation rate is called the nominal NPV (Equation (9); including the inflation rate
it is referred to as the NPV in real terms (Equation (10) (cf. [41]):
The latter can be used to calculate the dynamic amortization (or payback time) as follows:
A related, simplified economic measure is the net cash recovery (NCR). Since it does not take either of the rates into account, it simply reflects the net cash flows without any time value, i.e.:
The annuity factor is derived from the as follows:
With the annuity factor the annuity can be calculated, which gives the constant payment over periods required to provide a complete redemption of both the investment, , and the running costs, [41]:
Dividing the annuity by the expected amount of electricity generated within a year gives the maximum specific costs in €/kWh permissive to avoid any losses:
Still another often-used indicator is the profit-to-investment ratio (PIR):
which is an indicator for whether, and how fast, an investment pays off from the net cash recovered, NCR. For obvious reasons, if PIR > 1 (< 1), the project should be accepted (rejected) (see also Figure A2 in Appendix C).
3.3. Integration of Cash Flow
The cash flow consists of expenditures and revenues. The expenditures can be separated into investment costs and annual expenditures. The former comprise the power-related Capex as well as the Capex for the upper reservoir:
The annual expenditures consist of variable and fixed costs. The fixed operation and maintenance (O&M) costs are dependent on the installed power. The variable costs are dependent on installed power, number of starts per turbine, and power procurement costs, i.e.:
Revenues comprise the electricity sold within a year as well as any revenues generated from service provision in the secondary reserve market:
3.4. Monte Carlo Simulation
The economic analysis forms the basis for the Monte Carlo simulation. In a predetermined number of simulation runs, the NPV can be derived stochastically, thus allowing for the consideration of uncertainty (NPV probability distribution). Price uncertainties on the spot- and secondary reserve markets are varied by fitting alternative probability distributions assumed and forecasting the distribution of the output [42]. With these uncertainties included, it is possible to compute the value-at-risk (VaR) for different scenarios (see also Figure A3, Figure A4, Figure A5 and Figure A6 in Appendix C). The statistical testing and survey of market data are described next.
3.4.1. Statistical Testing
To simulate adequate spot prices, historical data are tested on different probability distributions. Three different goodness-of-fit tests are applied to a set of probability distributions: (1) Chi-square test; (2) Kolmogorov–Smirnov test; and (3) Anderson–Darling test (cf. Appendix B).
The distributions and the results for the peak prices in 2014 are given in Table 8. The tests suggest that preference be given to the logistical distribution, which shows the best goodness-of-fit, featuring a mean value of 37.31 €/MWh and a standard deviation of 6.94 €/MWh. Detailed explanations of the tests can be found in Appendix B.

Table 8.
Goodness-of-fit test results for EEX peak-power spot prices in 2014.
3.4.2. Empirical Analysis of Historical Spot Prices
For the illustrative analysis, data from 2009 to 2014 have been used. The data are provided in an hourly resolution. The annual means and standard deviations for base-load and peak-load times are given in Table 9. Average spot market prices vary from 30 €/MWh to 55 €/MWh. Standard deviations around the mean value range from about 8 €/MWh to 15 €/MWh and provide some evidence regarding the price volatility. While the variation of average prices is relatively high in the annual comparison, the price spreads have a more constant level with a negative trend.

Table 9.
Mean and standard deviation of EEX base- and peak-power spot prices from 2009–2014.
Supply and demand have to be in balance at any time and any place. Furthermore, electricity is needed in the daily processes of the economy and households and cannot easily be substituted by other factors. That is why electricity prices show seasonality, cyclicality, and mean-reverting [43]. On a winter day, the peak is typically at around 6 p.m. in the evening hours, while it shifts in summer days to around 12 a.m. The cyclicality and seasonality of the daily structure of spot prices are applicable to the weekly structure, where the daily cycle is relatively constant for summer and winter days on the five weekdays and decreases on weekends and public holidays. For simplicity, holidays have been neglected in the analysis. On an annual scale, the fluctuations and the volatility of spot prices are noticeable in the total grid load.
Although the power price development is exposed to short-term fluctuations and to volatility, it reverts to its mean value after a specific amount of time, instead of drifting in a random direction [43]. This shows that the cycle of load and the coherent spot prices are predictable and can be simulated with stochastic functions.
The future development of the spot prices has a large impact on the feasibility of electricity storage facilities. To generate high revenues, a wide price spread of base- and peak-load hours is necessary. One theoretical aspect is that the extension of PV capacity can be expected to lead to a smoothed peak-price curve, because of the high feed-in of PV at noon, another one that due to high wind feed-in, the volatility of spot prices will expectedly increase and generate higher price peaks.
3.4.3. Simulation of Spot Prices
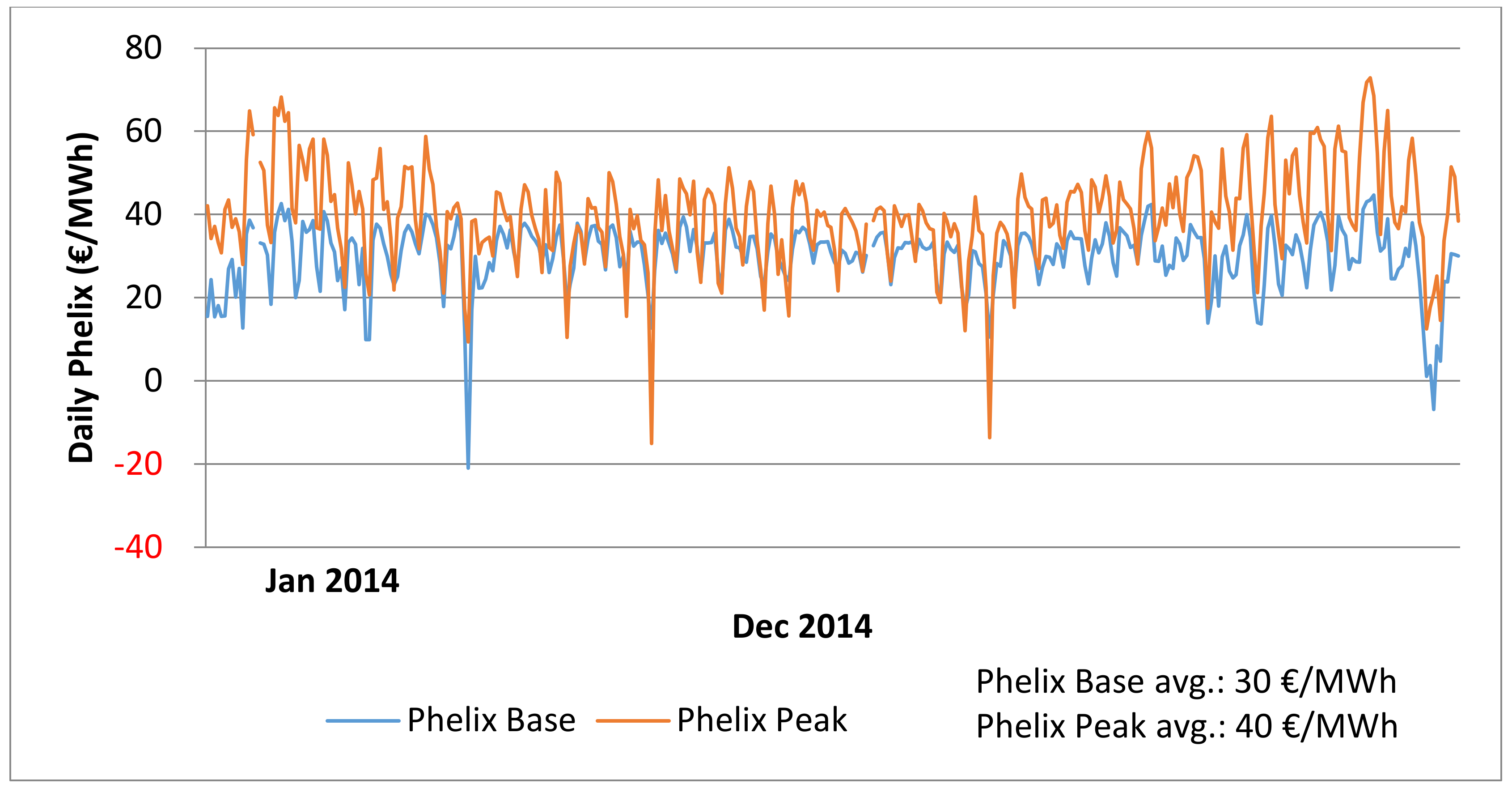
To simulate adequate spot prices, an hourly price forward curve (HPFC) is created. The HPFC is a popular tool for assessing the feasibility of power plant investments. To create the characteristic cyclicality and seasonality of spot prices, the spot price curve of 2014 is used. For simplicity, holidays are again neglected. Each peak-hour price is divided by the annual average peak price, and each base-hour price is divided by the annual average base price. These relations can be multiplied by an expected PHELIX base price and PHELIX peak price in order to create an HPFC that allows to simulate the expected spot market prices on an hourly resolution. Figure 7 shows the daily average spot price for peak and base hours with a yearly average base of 25 €/MWh and yearly average peak of 45 €/MWh, resulting in a daily average price spread of 20 €/MWh.
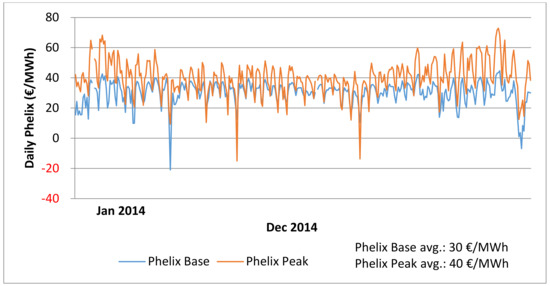
Figure 7.
Hourly price forward curve, Phelix Base, and Phelix Peak. Source: own illustration, based on EEX data for 2014 (obtained from www.eex.com).
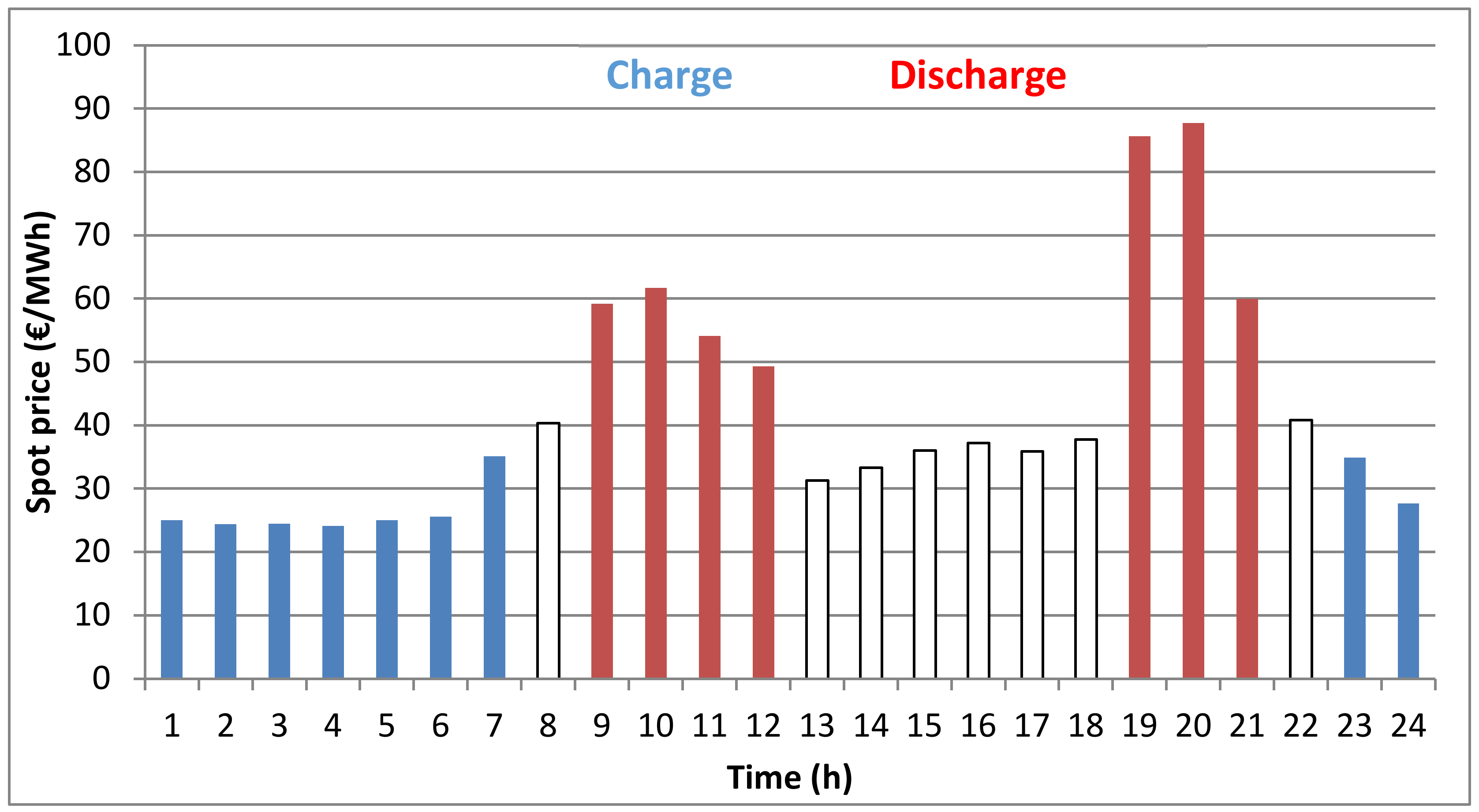
A possible operation of the PHS power plant on a daily basis is presented in Figure 8. It is aspired to drive a whole cycle in one day in order to achieve a maximum of full-load hours per year. At an installed power of 700 MW the exemplary day would create expected revenues of €185,400.
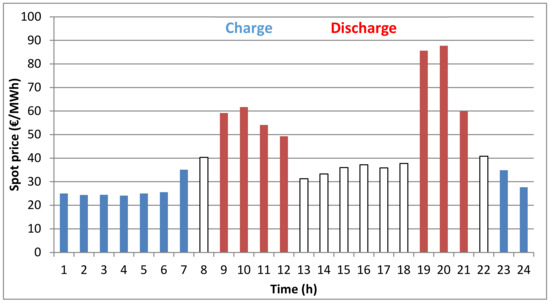
Figure 8.
Operation strategy of a PHS power plant for given spot prices on a daily basis. Notes: white bars denote inactivity (neither discharging nor charging the upper reservoir); price variation derived (downscaled) from the Phelix future prices shown in Figure 7.
3.4.4. Retrieval of Secondary Reserve Capacity
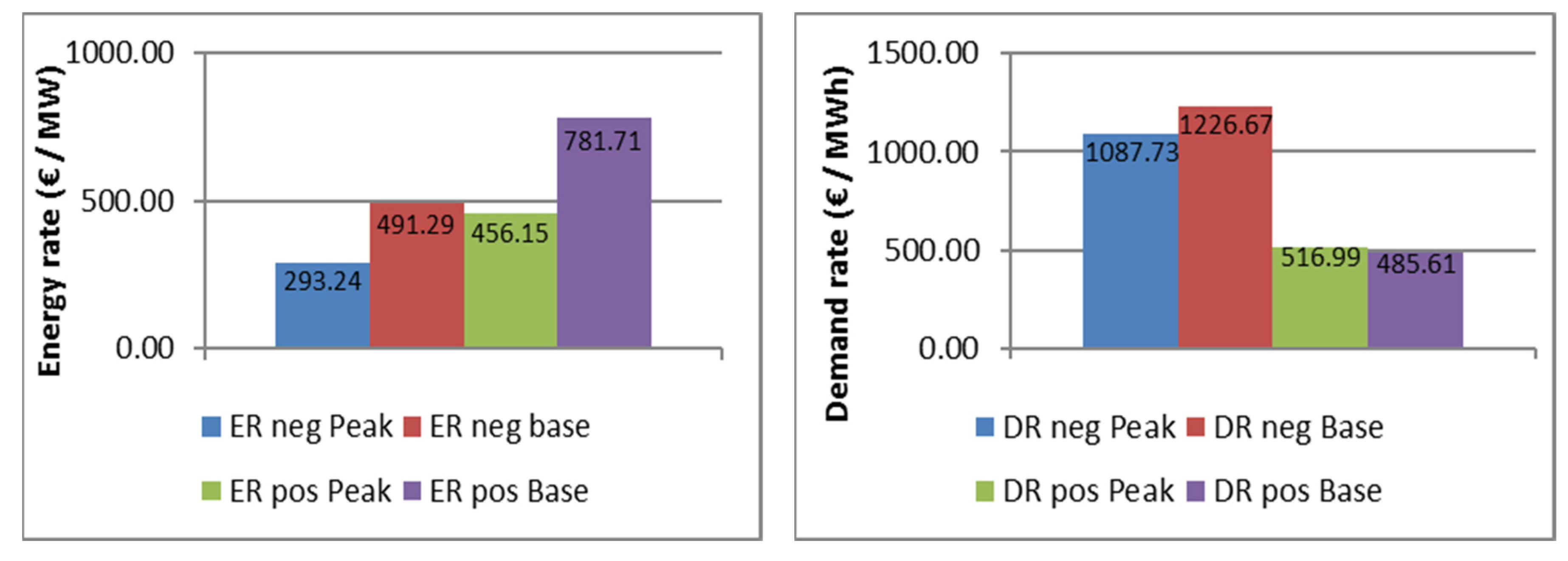
Table 10 shows the secondary reserve capacity market data for 2014 from the German tendering platform regelleistung.net (https://www.regelleistung.net/ext/data/), which are used in the economic model. Table 10 (upper part) gives an overview of the positive secondary reserve capacity used when demand exceeds the forecast. Table 10 (lower part) presents the data for the negative secondary reserve capacity, which becomes necessary in times when demand is lower than the forecasted value. The data comprise offered capacity, demand rate, and energy rate for base and peak times with mean, standard deviation, minimum, and maximum. Additionally, the mean energy rate and demand rate for 2014 are shown in Figure 9. The high standard deviations and spreads between the maximum and minimum of the demand rates are remarkable. The reason for this is the probability of successful tendering. A low demand rate bid will be successful with a high probability, whereas a high demand rate has a low probability but generates high revenues. For the economic evaluation, we assume that the PHS plant will participate in every weekly tendering and will be successful in the bidding, i.e., we assume the most optimistic outcome.

Table 10.
Prices for positive and negative secondary reserve capacity in Germany, 2014.
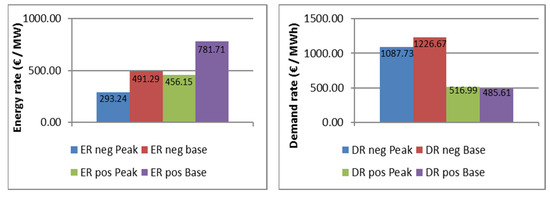
Figure 9.
Energy rate (left plot) and demand rate (right plot) for secondary reserve capacity (base/peak; pos./neg.) in Germany, 2014. Source: own illustration, based on regelleistung.net [44].
To integrate the provision of reserve capacity in the operating of the peak shaving, negative capacity is made available during base times (8 p.m.–8 a.m.) and positive capacity during peak times (8 a.m.–8 p.m).
3.5. Sensitivity Analysis
The sensitivity analysis shows the impact of key parameter variation on the NPV, varying the key parameter values by ±50% in 10% steps. The sensitivity analysis allows to check for the robustness of the results, and also to check for the relative impact of the system parameters, which can also help to make improvements to the model.
4. Results
The economic results are presented in the following. Reasonable parameters of open-pit mines are used, and limits for specific values are set in the calculations to create realistic scenarios. Market parameters are assessed according to the calculations described in Section 3.4.
Two different scenarios are calculated to show the impact of key project-related variables, such as head, storage volume, and pit lake volume. Scenario 1 reflects the conditions at the Hambach pit mine, and Scenario 2, those of the Inden pit mine. Both pit mines are located in the Rhineland, where the best conditions for PHS power plants in abandoned pit mines prevail thanks to high exploration depth and high pit lake volumes, creating sizable water storage volumes without exceeding the lake level variation of 1 m/d.
4.1. Economic Evaluation
The economic evaluation is carried out twice. First, the flooding time is excluded, assuming the PHS plant could start operation right after the investment, in order to show whether the power plant can be operated profitably at all under the parameter values and limitations assumed. In a second step, the flooding time is explicitly taken into account—as a situation of several years of fixed O&M costs but no revenues. The economic outcomes are reported in terms of NPV, NCR, specific production costs, and PIR, each before and after tax (BT, AT; we assume a corporate tax rate of 25%, which is representative for both Germany and the Rhineland region). Additionally, the NPV BT is displayed as a function of the interest rate and price spread, respectively, in order to show the impact of the two parameters and to see at which values the project would become economically viable.
4.1.1. Excluding Flooding Time
The economic evaluation is presented in Table 11. First, the scenario parameters are listed, followed by the cash flow items and the economic outcomes before and after tax. The temporal developments of NPV and NCR (BT and AT) are reported in Appendix C (Figure A2).

Table 11.
Economic evaluation for both scenarios.
Scenario 1 shows a positive NCR before tax and a PIR > 1. The SPC are, at 0.08 €/kWh, an order of magnitude lower than the value in [13] (0.77 €/kWh). According to [13], specific production costs < 0.1 €/kWh are necessary to break even. The NPV turns out to be negative even before taxation. After tax, the NCR remains positive, but the PIR is <1, and the SPC is only slightly below 0.1 €/kWh.
For Scenario 2, in contrast, we find a positive NCR as well as a positive NPV before tax. The PIR of 2.05 suggests a profitable scenario, and the specific production costs of 0.07 €/kWh are again low and retain the value of 0.07 €/kWh after tax. The NCR remains positive after tax, and the PIR is slightly greater than 1. The NPV after tax is even lower than in Scenario 1. None of the two scenarios would amortize during the technical lifetime, as the dynamic amortization calculation with a moderate interest rate of 6% shows.
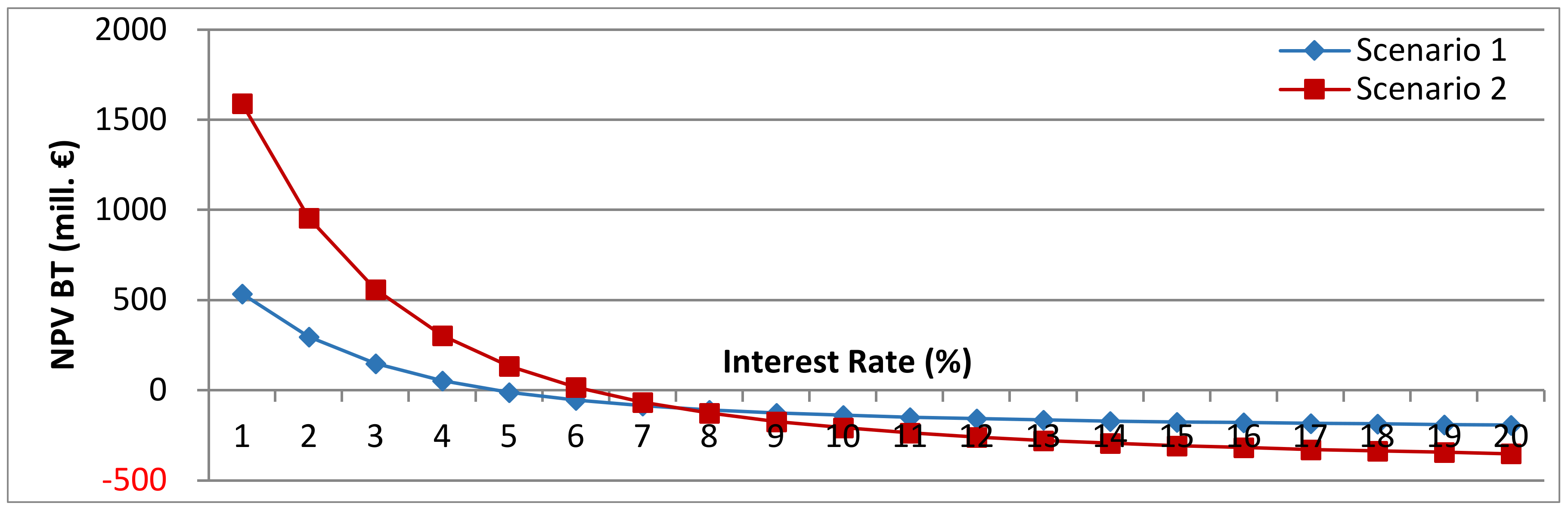
Figure 10 displays the impact of the interest rate on the NPV BT for both scenarios. The interest rate has a particularly high influence because of the long lifetime of a PHS power plant. Again, due to the lifetime, the net cash recoveries are high because they are unaffected by the interest rate. The graph shows a higher influence for Scen. 2, because of the higher cash flows that can be realized due to the higher power and capacity of the system. Scen. 1 creates a positive NPV BT at interest rates <5%, whereas for Scen. 2 this is already the case at an interest rate of <6.5%.
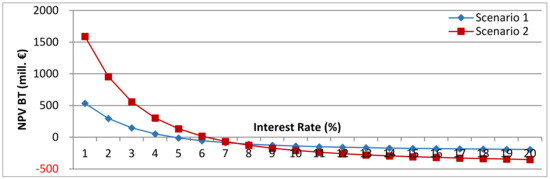
Figure 10.
Net present value before tax as a function of the interest rate, Scen. 1 and 2, excl. flooding time.
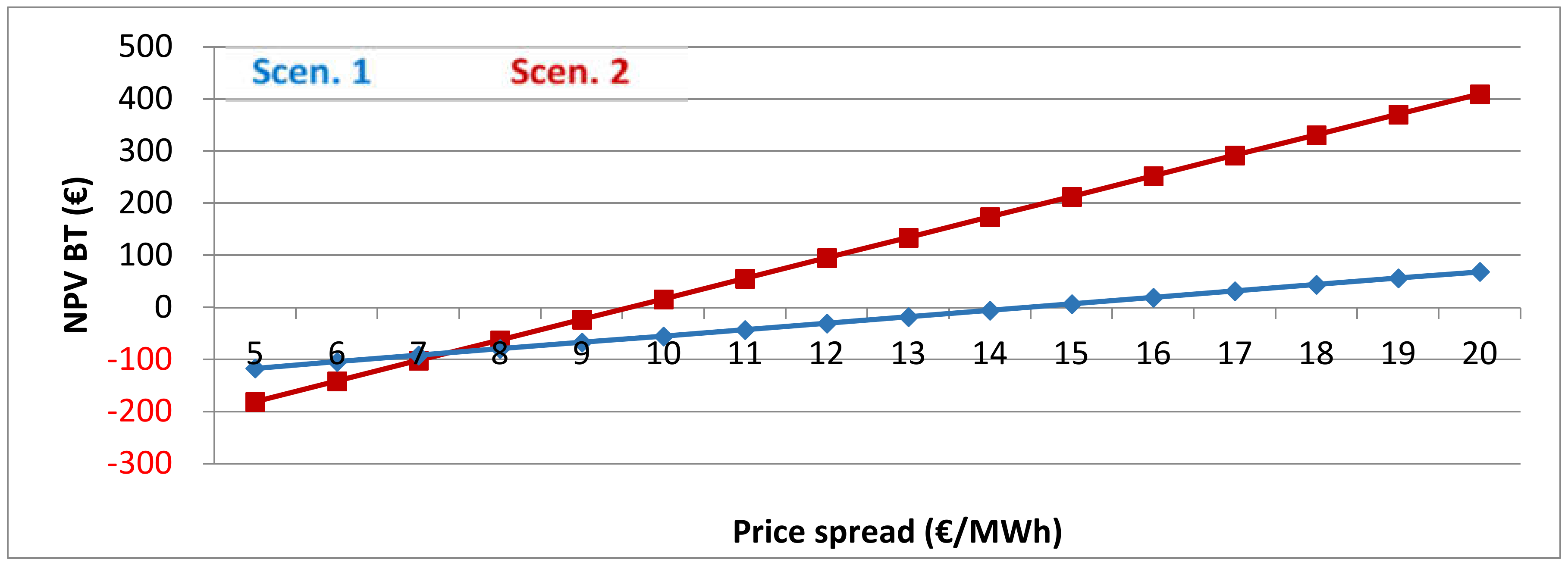
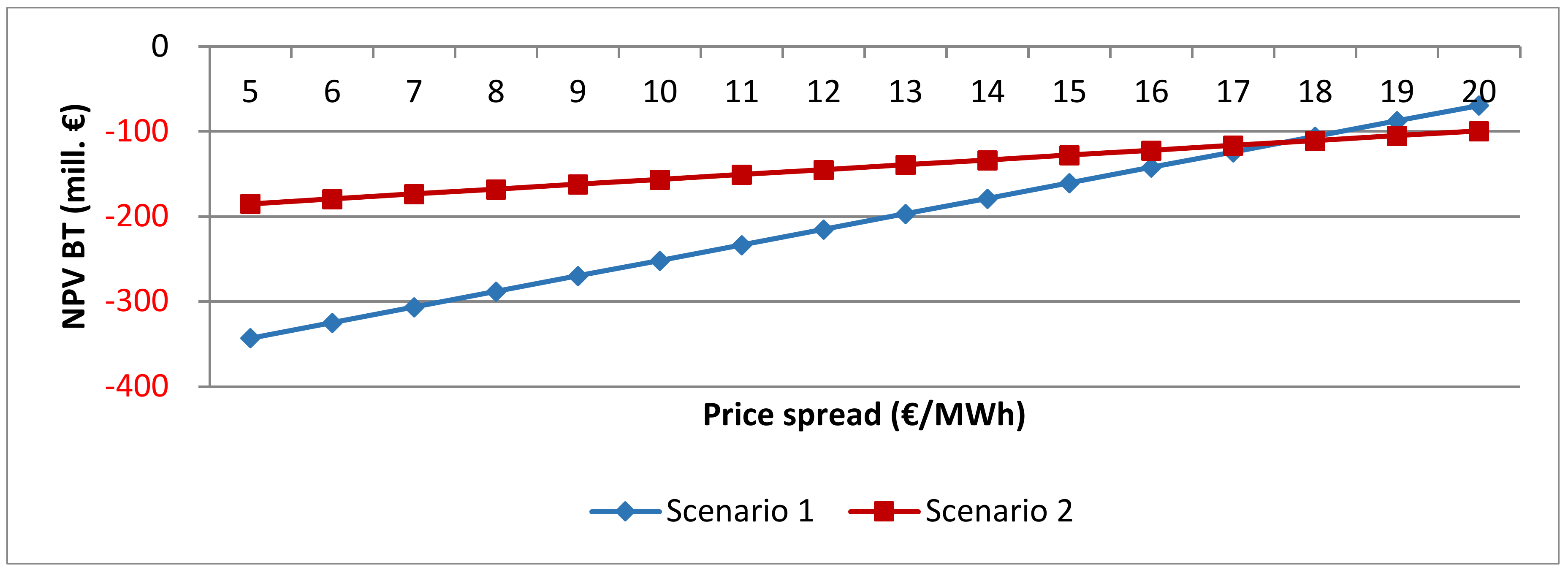
Figure 11 displays the NPV BT as a function of the daily average price spread on the spot market in €/MWh. At higher price spreads, a PHS plant is able to generate higher revenues. The development of the spot prices in the future is very important for the feasibility of electricity storage facilities. Figure 11 shows which price spreads need to be expected in order to generate revenues that allow for a profitable project. Today, the average price spread is around 10 €/MWh. Scen. 1 needs price spreads of over 14.5 €/MWh for a profitable scenario before tax. The gradient of Scen. 2 is higher because of higher power and capacity and cutting the x-axis at 9.5 €/MWh. The gradient shows the high impact of the price spread; a higher price spread of 1 €/MWh increases the NPV by approx. €40 million.
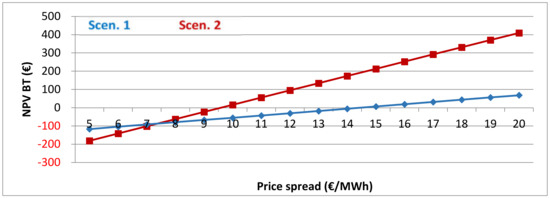
Figure 11.
Net present value before tax as a function of the price spread, Scenarios 1 and 2, excl. flooding time.
4.1.2. Including Flooding Time
If the flooding time is included in the investment calculations, fixed costs for maintenance have to be taken into account at an assumed 10% of the regular fixed operational expenditures during the time of delayed operation. The investment is made before flooding is started in order to integrate the construction into the recultivation process of the pit mine and thus to mitigate construction costs. The power plant does not create any revenues while flooding is performed. Due to the prolonged lifetime of the project, the discounting factor has a greater impact. Combined with additional costs for maintenance and market risks, the investment case is subject to uncertainty. Table 12 shows the results in terms of NCR, NPV, and PIR calculations before and after tax and for both scenarios. The temporal development of NPV and NCR (BT and AT) can again be found in Appendix C.

Table 12.
Economic evaluation for both scenarios, flooding time included.
It is still possible for each scenario to create a positive NCR before and after tax. The increased discounting factor has no influence on the NCR and, therefore, has no influence on the PIR, because it is derived from the NCR. Except for Scen. 1 and AT, all PIRs exceed unity. However, neither of the two projects are expected to yield a positive NPV, neither before nor after tax. Also, at an interest rate of 6%, none of the scenarios are found to pay back within the technical lifetime when using the dynamic amortization method.
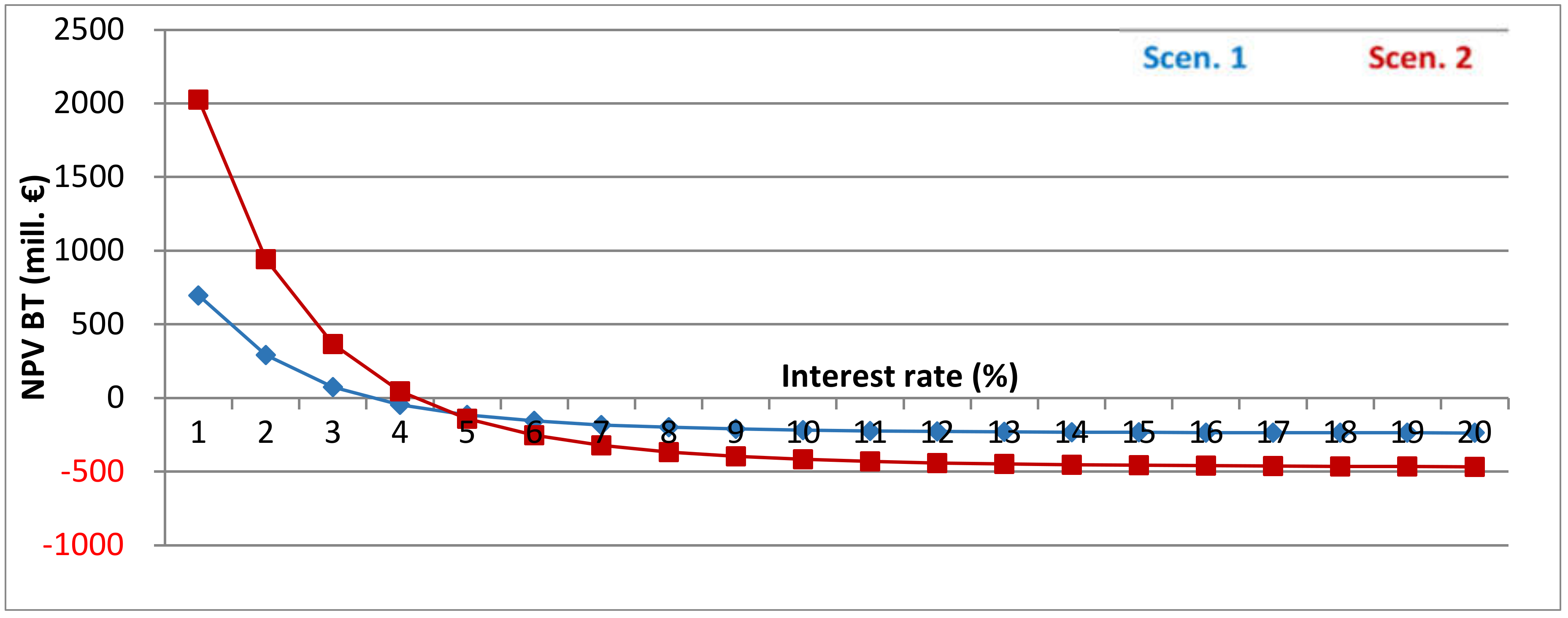
Taking flooding time into account, the impact of the interest rate and the resulting discounting factor is obviously higher, as Figure 12 shows. The NPV BT for Scen. 1 approaches 0 at an interest rate of about 4%. For Scen. 2, the NPV BT becomes positive at an interest rate of approx. 4.5%.
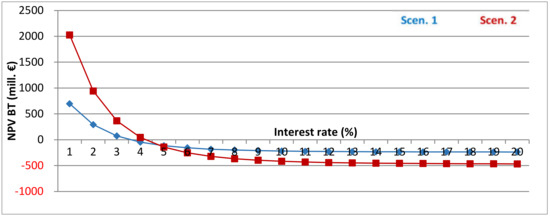
Figure 12.
Net present value before tax as a function of the interest rate, Scen. 1 and 2, incl. flooding time.
Figure 13 illustrates the price spreads that would be necessary in order to achieve a positive NPV before tax. If the flooding time is explicitly taken into account, a positive NPV BT is not reached under an average daily price spread of 22 €/MWh, which is very high compared to today’s spread of 10 €/MWh, and therefore unlikely.
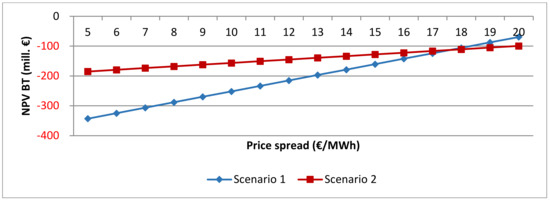
Figure 13.
Net present value before tax as a function of price spread, Scen. 1 and 2, incl. flooding time.
4.2. Sensitivity Analysis
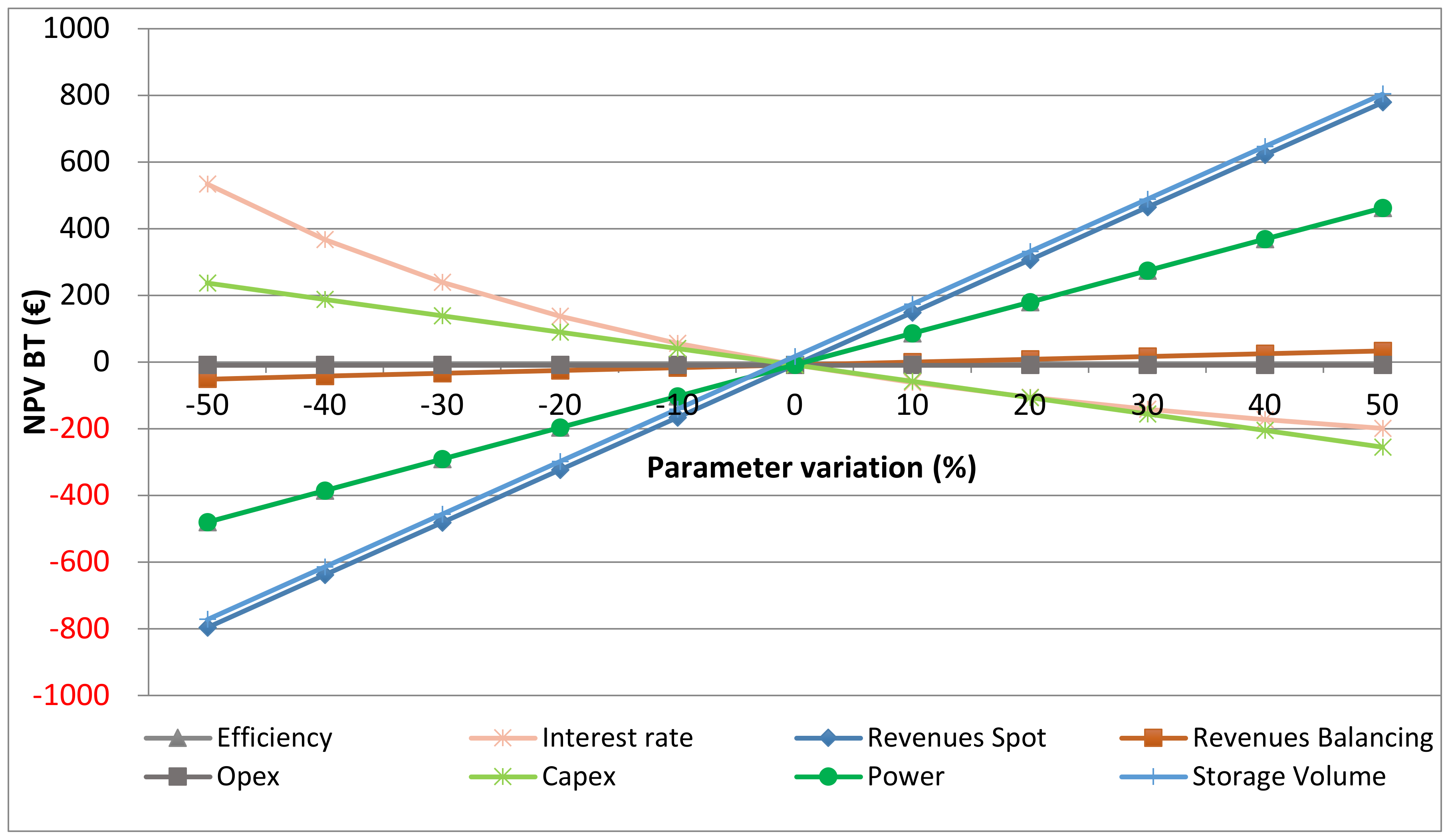
The sensitivity analysis is applied to Scen. 2 only and excludes flooding time because it is more likely to become an economically feasible project. The analysis is displayed in a spider diagram (Figure 14). The robustness of the results with regard to different key system parameters, such as cash flow elements and the interest rate, are tested for variations of +/−50%.
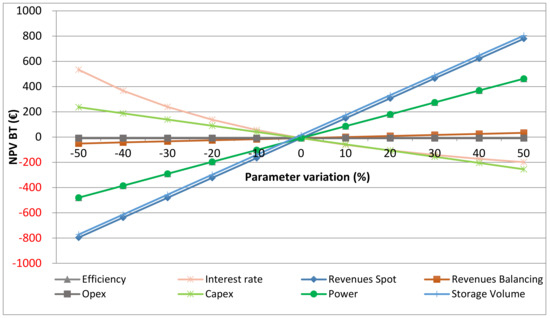
Figure 14.
Sensitivity analysis of Scen. 2 on the net present value before tax, with a variation of ± 50% of key parameter values.
The lowest sensitivity is found for the O&M expenditures and the revenues from the balancing market. The O&M expenditures for pumped hydro storage are very low, hence alteration does not have a high impact. The revenues from trading in the balancing market are low compared to the revenues that are generated on the spot market. This is why parameter variations only have a very small impact on the project’s economic viability.
A positive deviation of installed power, efficiency, storage volume, and revenues on the spot market due to a higher price spread have high impacts on profitability. Spot market revenues and storage volume are correlated, so that their impact on the NPV BT is congruent; the same can be observed for power and efficiency. Installed power and the storage volume are both limited by the location of an open-pit mine. The power would be increased by a higher head, but more than 200 m, as assumed in Scen. 2, is nowhere to be found in Germany. The space for storage, in the form of upper reservoirs, is limited by the plateau areas on the mine dumps and by the maximum water depth of the basin to minimize the subsidence. Therefore, power and storage volume do not have much potential to contribute to a better scenario. The efficiency of 80% is already very high and does not have much potential for improvement either. The revenues are dependent on the price spread on the spot market. A positive development of spot price spreads is essential for a profitable scenario. Another way to influence the NPV in a positive direction is by a negative deviation of the interest rate and the capital expenditures. The Capex were already estimated to be low at 744 €/kW, and thus further cost reductions are rather unlikely. The influence of the interest rate was already displayed and discussed in Figure 10.
4.3. Value-at-Risk
The VaR indicates the maximum loss of an investment over a predefined time period and with a certain probability. At a confidence level (1-α), the loss will not exceed the difference between the expected value of the economic measure considered, e.g. E(NPV), and its deviation over the time horizon investigated. As time progresses, the probability that the expected value deviates decreases. Hence, for a weighted volatility of the economic measure concerned, a bell-shaped distribution function can be found in which the economic loss does not exceed, say, |NPVt+T – NPVt|, if NPVt+t < NPVt, with probability (1-α). For the VaR computation, the probability distributions of the economic outcomes, considering price uncertainties on the spot and balancing markets, need to be calculated. The data from the spot and balancing markets are reported in Section 3.4. The Monte Carlo simulation is conducted with 5000 runs. The resulting histograms are reported in Appendix C (Figure A3, Figure A4, Figure A5 and Figure A6). The fitted distributions with mean, standard deviation, and confidence interval, e.g., for an NPV > 0, are listed in Table 13 (excl. flooding time) and Table 14 (inc. flooding time). The VaR is applied to NPV, NCR, PIR, and SPC—before and after tax—and for both scenarios, excluding and including flooding time.

Table 13.
Value-at-risk descriptives for Scen. 1 and 2, excl. flooding time.

Table 14.
Value-at-risk descriptives for Scen. 1 and 2, incl. flooding time.
4.3.1. Excluding Flooding Time
The results for Scen. 1 are given in Table 13 (upper part). Under the given price uncertainties, Scen. 1 will create a positive NPV AT with a probability of 18.8%. The probability of NCR AT > 0 is 66.07%. The price uncertainties induce standard deviations for NPV and NCR of up to €346.01 million, which again reflects the high sensitivity of revenues gained on the spot market. Despite the high NCR AT, the mean value of PIR AT is still <1. The SPC have a low standard deviation but are only <0.1 €/kWh, with a confidence level of 39.53%. However, regarding the sensitivity analysis, it is questionable whether this criterion set by [13] really holds. An increase in storage volume would easily outweigh an increase in specific production costs (cf. Figure 14, righ-hand side).
The values for Scen. 2 are also reported in Table 13 (lower part). The SPC (BT and AT) are low and, with a probability of almost 100%, smaller than 0.1 €/kWh. But the high standard deviation, a negative mean value for the NPV AT, and a probability of only ~35% of becoming positive make the project a risky investment without subsidies, even when flooding time is ignored.
4.3.2. Including Flooding Time
If flooding time is included, Scen. 1 yields many negative values (see Table 14, upper part). There is little chance whatsoever of the NPV (BT or AT) becoming positive. Even for the NCR, the probability of success is very low. At negative NCR, the PIR cannot turn out to be favorable either. The SPC are lower when excluding flooding because the annuity is dispersed over 20 more years. The situation for Scen. 2 is slightly better but still poor (Table 14, lower part). Although the NCR is positive and creates a PIR > 1 (BT and AT), the mean NPV turns out to be negative, with a very slim probability of becoming positive. The low SPC are again explained by the lower annuity.
5. Conclusions
This study shows that a pumped storage hydropower plant in an open pit can be constructed at relatively low investment costs and could be operated profitably and with low specific production costs, if it were not for the long flooding time.
The sensitivity analysis carried out shows that the probability of a feasible scenario increases mainly with the storage volume, output, and price spread which is also reflected by the comparison of potential PHS applications for the two scenarios (Hambach and Inden) covered in this study. However, since the head and the available area are determined by the general conditions of the open-pit mine, the fundamental parameters for the upper reservoir cannot be varied freely. Moreover, the influence of the price spread is logically congruent with that of the storage volume, so that another very important factor is outside the investor’s sphere of influence.
Furthermore, there are uncertainties of environmental risks, which bear further cost potential. However, the sensitivity analysis shows that the deviation of Capex has a minor influence on the NPV compared to other parameters such as, in addition to the above-mentioned ones, a low interest rate, which is due to the long lifetime of 70 years. For such a long-term project, it is thus all the more important that the political circumstances for fees and regulations are stable in order to reduce the investment risks. Small deviations of the specific production costs can lead to the economic infeasibility of the project.
Above all else, the duration of flooding has the biggest impact on profitability. A positive NPV is hardly possible if the PHS creates no revenues for more than a decade. A solution to this problem could be to disconnect the PHS from the pit lake. A smaller PHS plant could be realized as decentralized electricity storage. There is still an upper reservoir built on the mine dump but a lower reservoir is created in similar fashion besides the mine dump, drastically reducing the time required for flooding. The Capex would be higher because of construction of the second basin, larger area required, as well as water extraction costs (unless some exemption is granted, e.g., due to the importance of bulk energy storage as an enabler of the sustainable energy transition, water extraction costs may arise, because there is no reinjection into surface or flowing waters) but the PHS plant would still benefit from the recultivation process and the proximity to existing power lines. The environmental risks that apply to the pit lake, such as AMD, meromictic lakes, and slope failures, would no longer be relevant. The German coal mining corporation RAG AG and electric utility RWE have been discussing a similar project for the Sundern mine dump ([45]).
The results of our investigation show that open-pit mines have the potential to function as a location for electricity storage, but for doubtful economic reasons. Further investigations are required to analyze the feasibility of decentral electricity storage in an open-pit mine as an alternative option to overcome the problem of the long flooding time. Beyond that, the effects of future developments of spot prices under the influence of an increased feed-in of renewable energies could be taken into account to model the investigated scenarios more accurately.
Author Contributions
M.W. carried out the simulations. R.M. and C.H. designed and supervised the study. R.M. and M.W. wrote the manuscript in consultation with C.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
The authors would like to thank for the helpful comments received from three anonymous reviewers, Jan Martin Specht of FCN, and participants in the Annual International Conference of the German Operations Research Societies (GOR)(OR 2016) in Hamburg, Germany, 30 August–2 September 2016. Research assistance by Fynn Hackstein, Pascal Herrmann, Jonas Kuhlmann, and Christian Lange of FCN on earlier versions of the manuscript (prepublished as FCN Working Paper No. 22/2015) is also gratefully acknowledged.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| AC | Accruals | LLV | Lake level variation |
| ALR | Area lower reservoir | NC | Network charges |
| AMD | Acid mine drainage | NCR | Net cash recovery |
| AN | Annuity | NPV | Net present value |
| AT | After tax | η | Efficiency |
| ACUR | Area costs upper reservoir | ηd | Efficiency deload |
| AUR | Area upper reservoir | ηl | Efficiency load |
| α | Inclination | om | Operation & maintenance costs |
| BT | Before tax | Opex | Operational expenditures |
| Capex | Capital expenditures | PHS | Pumped hydro storage |
| cd | Capacity deload | PIR | Profit to investment ratio |
| cfix | Opex, fixed | Pl | Power load |
| cl | Capacity load | Pd | Power deload |
| cpower | Spot price per MW bought electricity | ppower | Spot price per MW sold electricity |
| PT | (Dynamic) Payback time | ||
| cvar | Opex, variable | PSR | Electric load for second. reserve market |
| δ | Depreciation rate | ρ | Density of water |
| DRneg | Demand rate secondary reserve, negative base | q | Discounting factor |
| DRpos | Demand rate secondary reserve, positive peak | Qd | Flow rate per turbine deload |
| DUR | Diameter upper reservoir | Ql | Flow rate per turbine load |
| EEG | German Renewable Energy Sources Act (Erneuerbare Energien Gesetz) | r | Inflation |
| EEX | European Energy Exchange | R | Revenues |
| EmbUR | Embankment costs | S | Number of full cycles per year |
| EnWG | German Energy Industry Act (Energiewirtschaftsgesetz) | SealUR | Sealing costs, upper reservoir |
| ERneg | Energy rate secondary reserve, negative base | SPC | Specific production costs |
| ERpos | Energy rate secondary reserve, positive peak | T | Lifetime |
| g | Gravitational constant | T# | Number of machine units |
| h | Height difference | td | Discharge time |
| hd | Full load hours deload per day | tax | Tax rate |
| hl | Full load hours load per day | TSO | Transmission system operator |
| HPFC | Hourly price forward curve | TWh | Terawatt hour |
| HUR | Height upper reservoir | V | Utilizable volume |
| i | Interest rate | vard | Var. costs of deloading per start of unit |
| IPHS | Total Capex | varl | Var. costs of loading per start of unit |
| IPHSp | Capex power-related | varo | Other variable costs |
| IUR | Capex upper reservoir | VLR | Volume lower reservoir |
Appendix A. Spot Market Contracts and Price Data, Water Extraction Fees in Germany

Table A1.
EEX power contracts.
Table A1.
EEX power contracts.
| Contract 1) | Volume of Contract |
|---|---|
| Baseload contract, Block contract for every day, Mon–Sun | 1 MW × 24 h = 24 MWh |
| Peakload contract, Block contract for Mon–Fri, 08:00–20:00 h | 1 MW × 12 h = 12 MWh |
| Weekend baseload contract Block contract Sat 00:00–Sun 24:00 h | 1 MW × 48 h = 48 MWh |
| Hourly contract for every hour of a day | 0.1 MW × 1 h = 0.1 MWh |
| Combination of hourly contracts to hourly blocks | 0.1 MW × number of h |
| EEX – night, 00:00–06:00 h | 0.1 MW × 6 h = 0.6 MWh |
| EEX – morning, 06:00–10:00 h | 0.1 MW × 4 h = 0.4 MWh |
| EEX – business, 08:00–16:00 h | 0.1 MW × 8 h = 0.8 MWh |
| 7 other combinations 2) |
1) Special contracts are traded for transition between winter- and summertime; 2) EEX—high-noon, EEX—afternoon, EEX—rush-hour, EEX—evening, base load, peak load, off-peak load. Source: [39].

Table A2.
Water extraction fees in Germany for ground- and surface waters and hydropower applications, by federal state (incl. North-Rhine Westphalia) (€/1000 m3).
Table A2.
Water extraction fees in Germany for ground- and surface waters and hydropower applications, by federal state (incl. North-Rhine Westphalia) (€/1000 m3).
| Federal State | Groundwater | Surface Water | Hydropower |
|---|---|---|---|
| Baden–Wuerttemberg | 5.1 | 1 | 1 |
| Berlin | 31 | - | - |
| Brandenburg | 10 | 2 | 2 |
| Bremen | 2.5 | 0.3 | - |
| Hamburg | 13 | - | - |
| Mecklenburg–Western Pomerania | 5 | 2 | - |
| Lower Saxony | 2.556 | 2.045 | 2.045 |
| North Rhine–Westphalia | 5 | 5 | - |
| Rhineland–Palatinate | 6 | 2.4 | - |
| Saarland | 8 | - | - |
| Saxony | 1.5 | 2 | 0.01 |
| Saxony–Anhalt | 7 | 4 | 4 |
| Schleswig–Holstein | 7 | 0.77 | 0.077 |
| Bavaria | - | - | - |
| Hesse | - | - | - |
| Thuringia | - | - | - |
Source: [37].
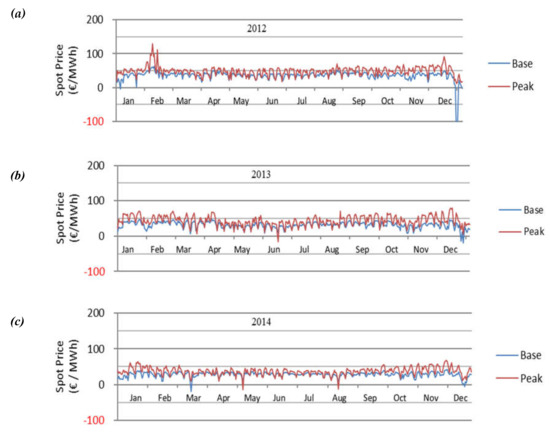
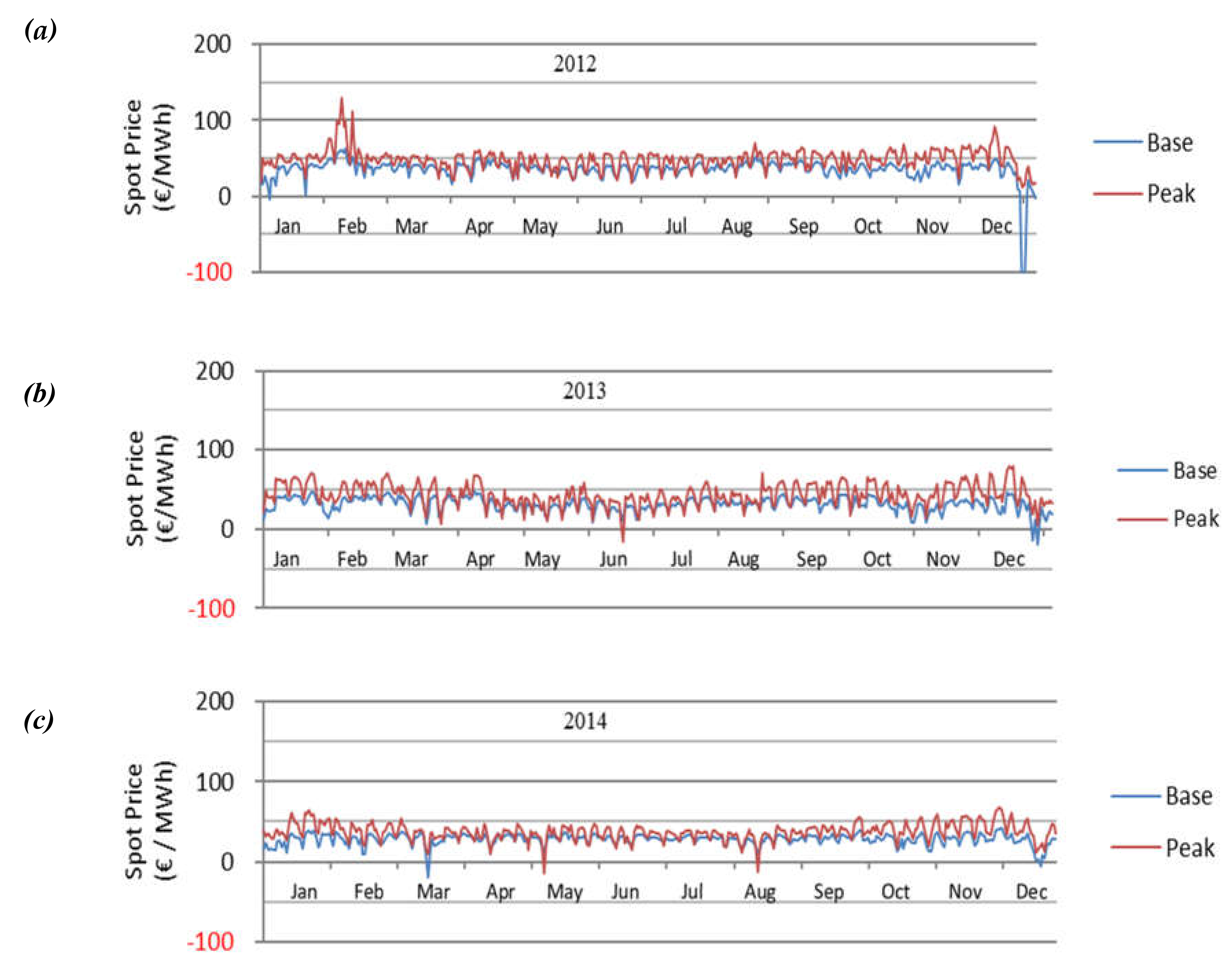
Figure A1.
(a–c) EEX spot market prices, base-load and peak-load, 2012–2014. Source: own illustration, based on weekly EEX data (1 January 2012–31 December 2014).
Figure A1.
(a–c) EEX spot market prices, base-load and peak-load, 2012–2014. Source: own illustration, based on weekly EEX data (1 January 2012–31 December 2014).
Appendix B. Statistical Testing
The most common Chi-square test is the Pearson test [46] where a data set is divided into cells. The tested hypothesis is whether values occur in each cell with equal frequency, as they do in the tested distribution. The lower the Chi-square value, the better the tested distribution fits to the data. The probability function of the Chi-square has the following density [47]:
The Kolmogorov–Smirnov test is used in the case of smaller sample sizes. The test measures the distance of two distribution functions, in this case the sample distribution (d) and the tested probability distributions (d1). The lower the measured distance, the better the goodness of fit. The greatest vertical distance is calculated by using the following equation [47]:
The Anderson–Darling test assesses whether a sample comes from a specified distribution. It is a modification of the Kolmogorov–Smirnov test. If the determined sample of data underlies a distribution, it can be transformed into the normal distribution. A variable (A) reveals the vertical distance of the transformed samples to the normal distribution. The lower the test variable, the better the goodness-of-fit. The Anderson–Darling test is specified as follows [48]:
f is the cumulative distribution function of the specified distribution and the ordered data.
Appendix C. Additional Results
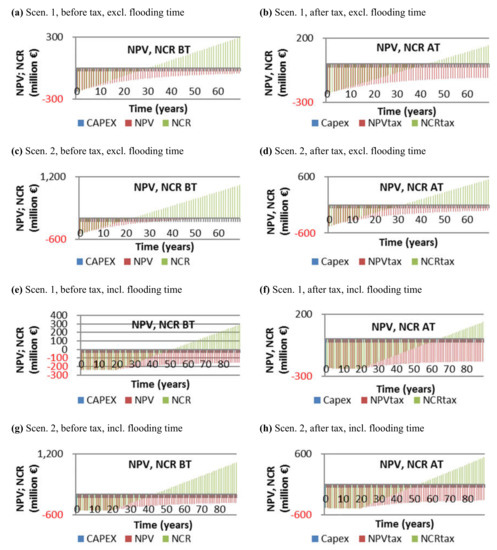
Figure A2.
Capex and net present value and net cash recovery before and after tax; excluding (plots (a–d)) and including (plots (e–h)) flooding time, Scen. 1 and 2.
Figure A2.
Capex and net present value and net cash recovery before and after tax; excluding (plots (a–d)) and including (plots (e–h)) flooding time, Scen. 1 and 2.
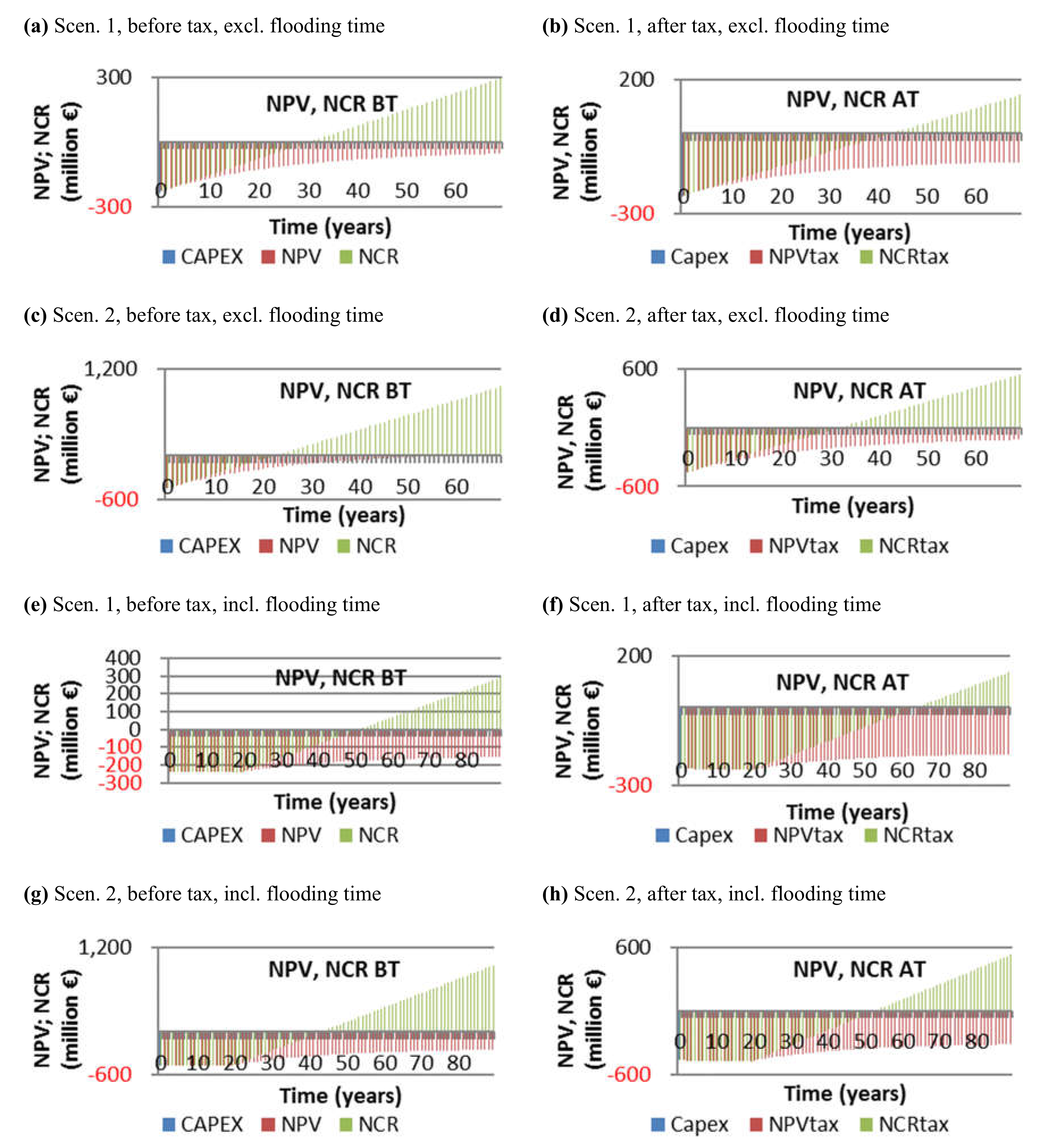
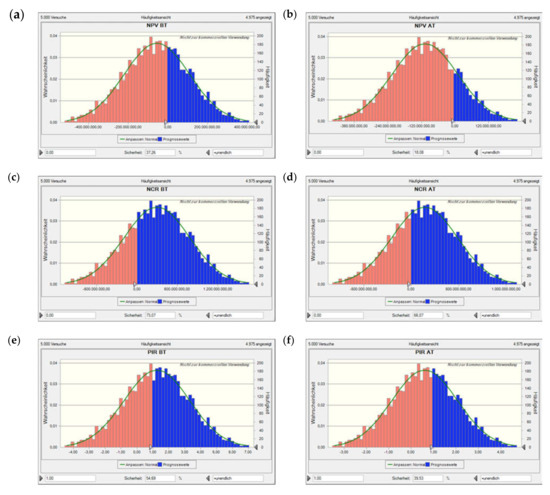
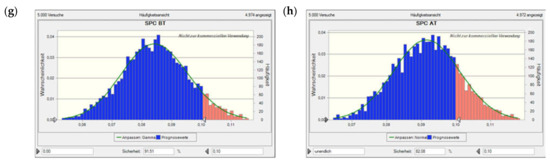
Figure A3.
Value at risk for Scen. 1, excl. flooding time, based on a Monte Carlo simulation with 5000 runs. Plots (a) and (b) show the net present value (NPV) before and after tax, plots (c) and (d) the NCR before and after tax, plots (e) and (f) the profit-to-investment ratio (PIR) before and after tax, and plots (g) and (h) the per unit (specific) production costs (SPC) before and after tax. The solid lines denote the fitted probability distribution, the red areas the confidence interval of not encountering a neg. NPV, neg. NCR, or PIR < 1 (i.e., depending on the performance indicator concerned; as the costs considered are all positive, there is only a blue histogram in those two plots).
Figure A3.
Value at risk for Scen. 1, excl. flooding time, based on a Monte Carlo simulation with 5000 runs. Plots (a) and (b) show the net present value (NPV) before and after tax, plots (c) and (d) the NCR before and after tax, plots (e) and (f) the profit-to-investment ratio (PIR) before and after tax, and plots (g) and (h) the per unit (specific) production costs (SPC) before and after tax. The solid lines denote the fitted probability distribution, the red areas the confidence interval of not encountering a neg. NPV, neg. NCR, or PIR < 1 (i.e., depending on the performance indicator concerned; as the costs considered are all positive, there is only a blue histogram in those two plots).
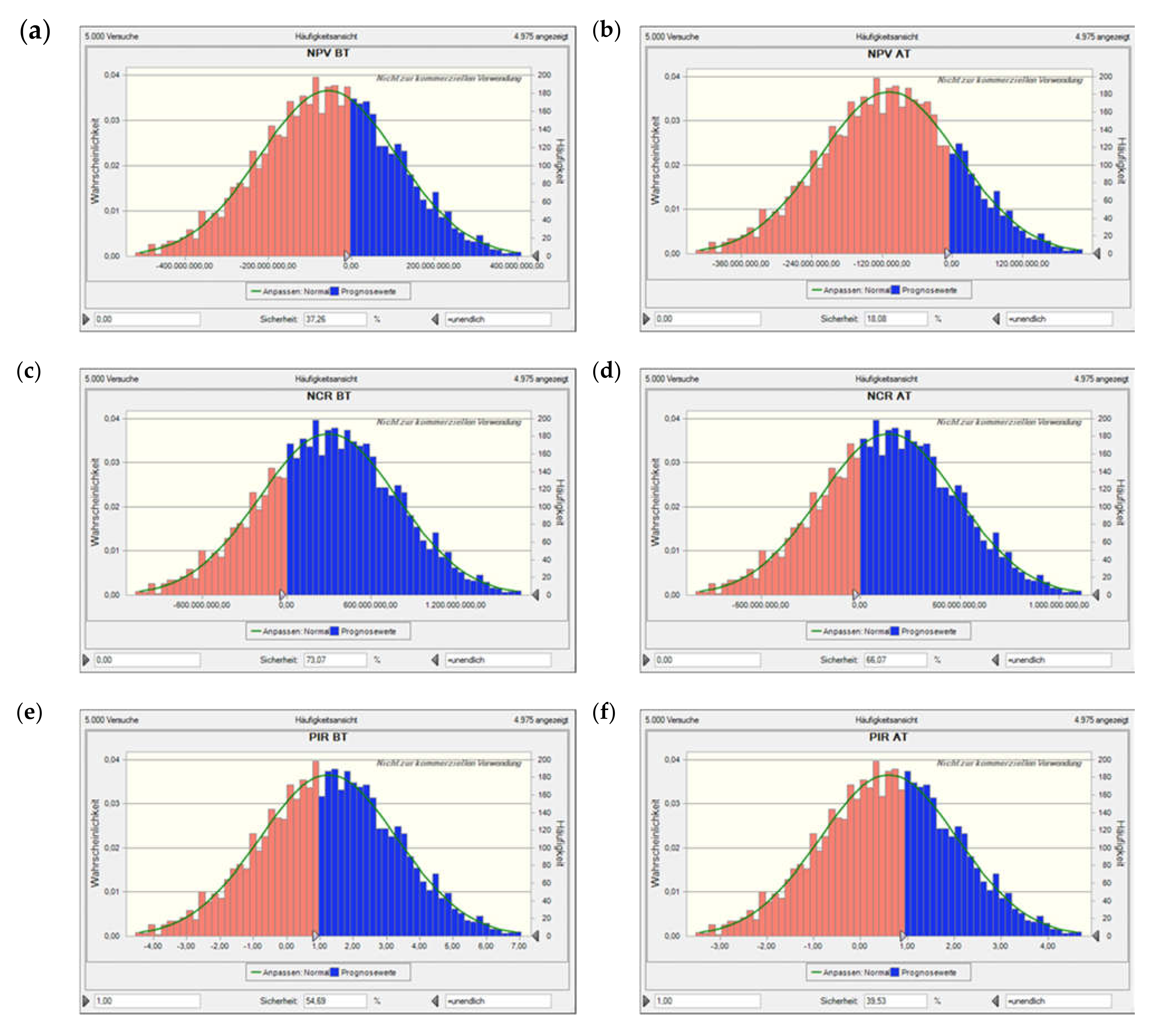
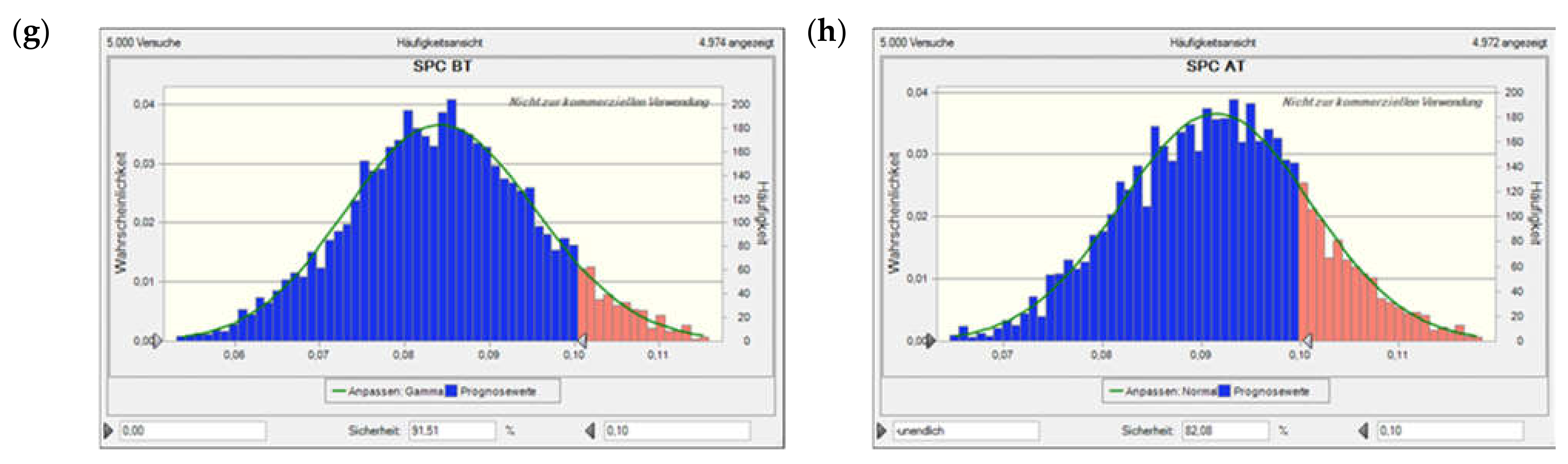
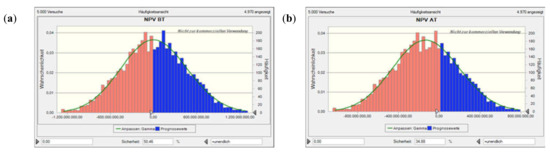
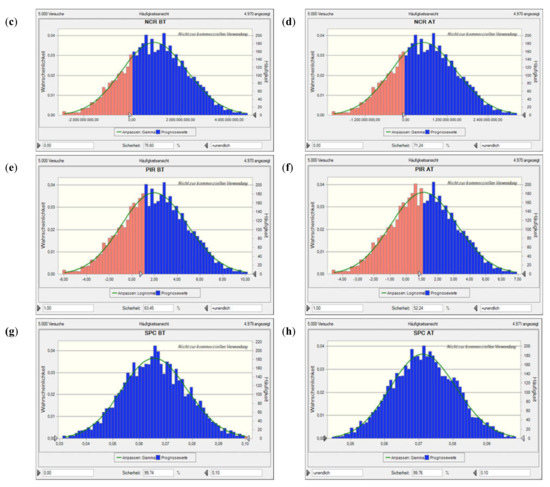
Figure A4.
Value at risk for Scen. 2, excl. flooding time, based on a Monte Carlo simulation with 5000 runs. Plots (a) and (b) show the net present value (NPV) before and after tax, plots (c) and (d) the NCR before and after tax, plots (e) and (f) the profit-to-investment ratio (PIR) before and after tax, and plots (g) and (h) the per unit (specific) production costs (SPC) before and after tax. The solid lines denote the fitted probability distribution, the red areas the confidence interval of not encountering a neg. NPV, neg. NCR, or PIR < 1 (i.e., depending on the performance indicator concerned; as the costs considered are all positive, there is only a blue histogram in those two plots).
Figure A4.
Value at risk for Scen. 2, excl. flooding time, based on a Monte Carlo simulation with 5000 runs. Plots (a) and (b) show the net present value (NPV) before and after tax, plots (c) and (d) the NCR before and after tax, plots (e) and (f) the profit-to-investment ratio (PIR) before and after tax, and plots (g) and (h) the per unit (specific) production costs (SPC) before and after tax. The solid lines denote the fitted probability distribution, the red areas the confidence interval of not encountering a neg. NPV, neg. NCR, or PIR < 1 (i.e., depending on the performance indicator concerned; as the costs considered are all positive, there is only a blue histogram in those two plots).
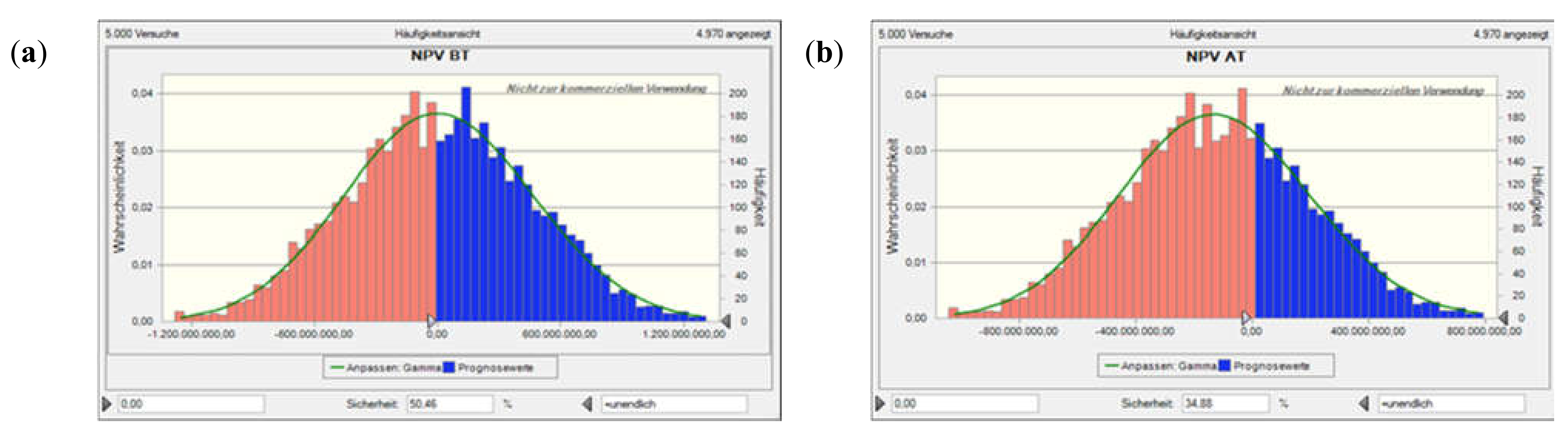
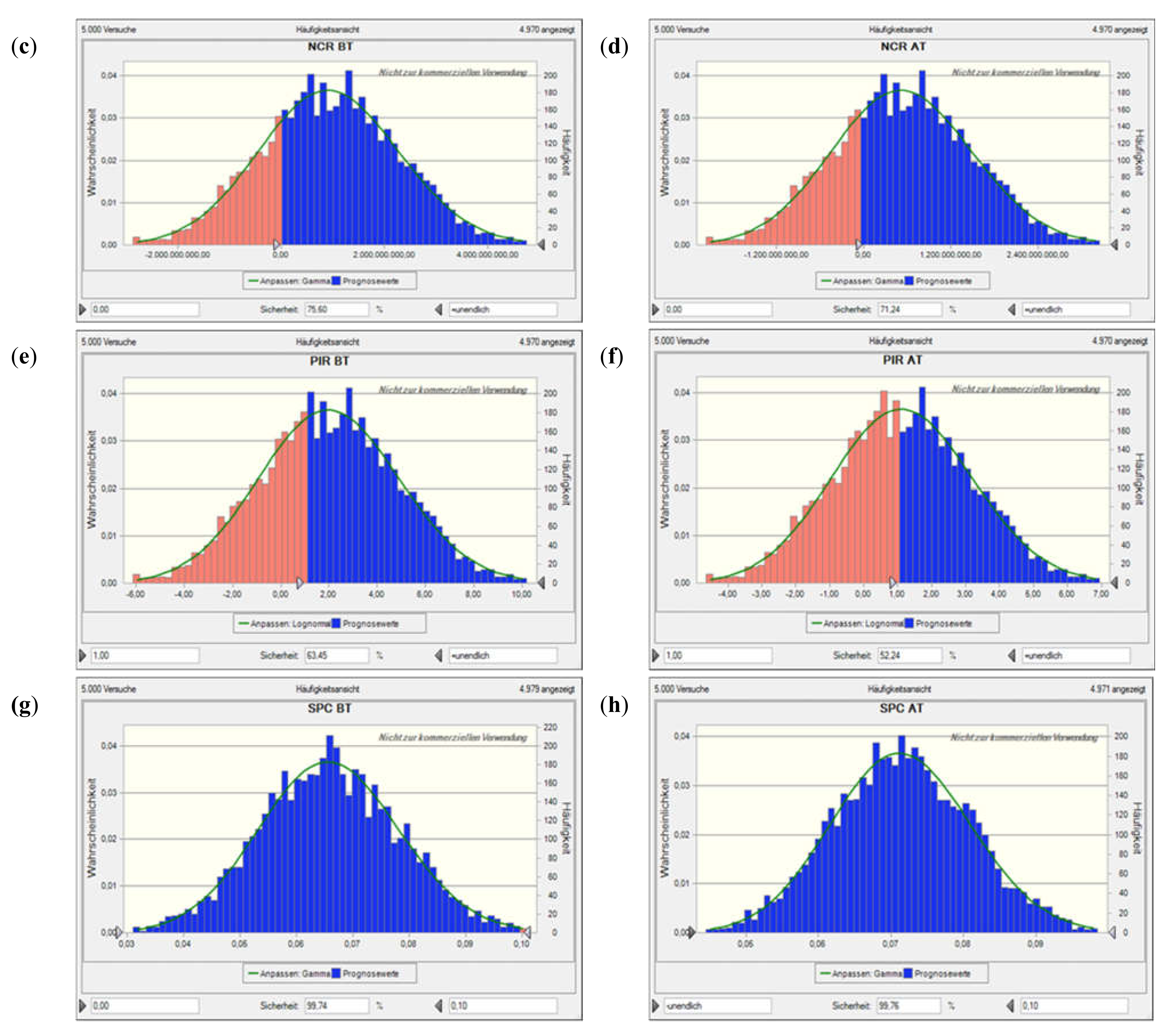
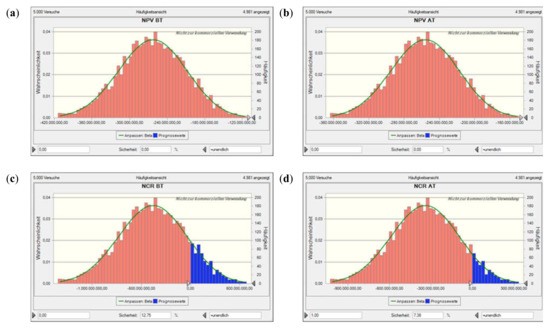
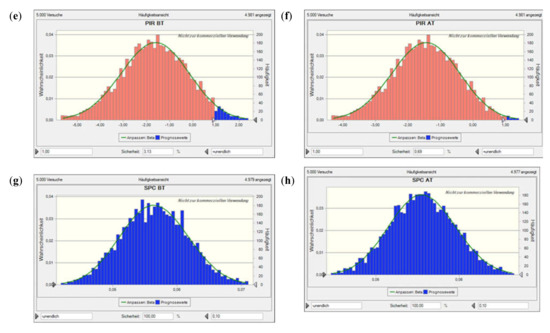
Figure A5.
Value at risk for Scen. 1, incl. flooding time, based on a Monte Carlo simulation with 5000 runs. Plots (a) and (b) show the net present value (NPV) before and after tax, plots (c) and (d) the NCR before and after tax, plots (e) and (f) the profit-to-investment ratio (PIR) before and after tax, and plots (g) and (h) the per unit (specific) production costs (SPC) before and after tax. The solid lines denote the fitted probability distribution, the red areas the confidence interval of not encountering a neg. NPV, neg. NCR, or PIR < 1 (i.e., depending on the performance indicator concerned; as the costs considered are all positive, there is only a blue histogram in those two plots).
Figure A5.
Value at risk for Scen. 1, incl. flooding time, based on a Monte Carlo simulation with 5000 runs. Plots (a) and (b) show the net present value (NPV) before and after tax, plots (c) and (d) the NCR before and after tax, plots (e) and (f) the profit-to-investment ratio (PIR) before and after tax, and plots (g) and (h) the per unit (specific) production costs (SPC) before and after tax. The solid lines denote the fitted probability distribution, the red areas the confidence interval of not encountering a neg. NPV, neg. NCR, or PIR < 1 (i.e., depending on the performance indicator concerned; as the costs considered are all positive, there is only a blue histogram in those two plots).
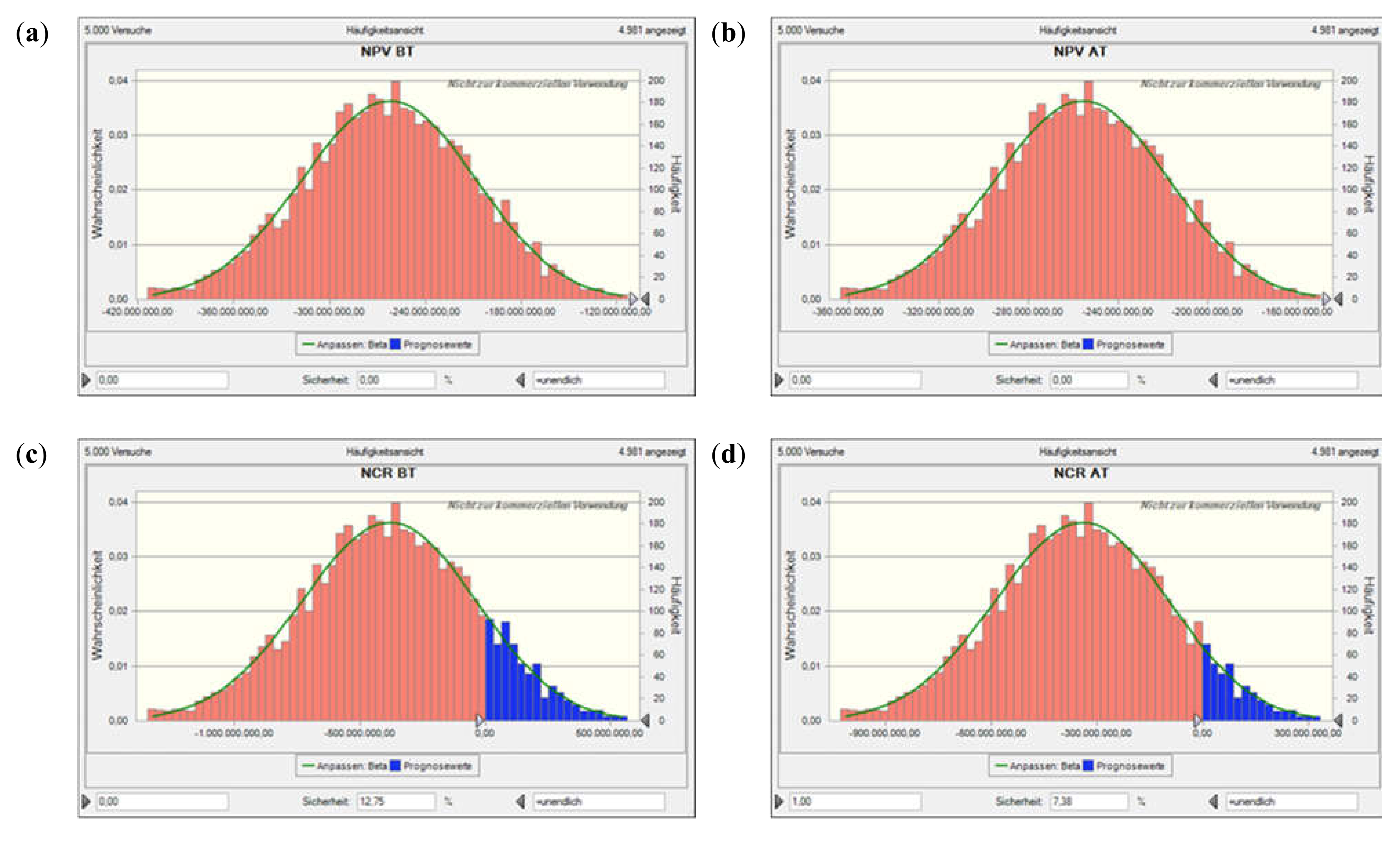
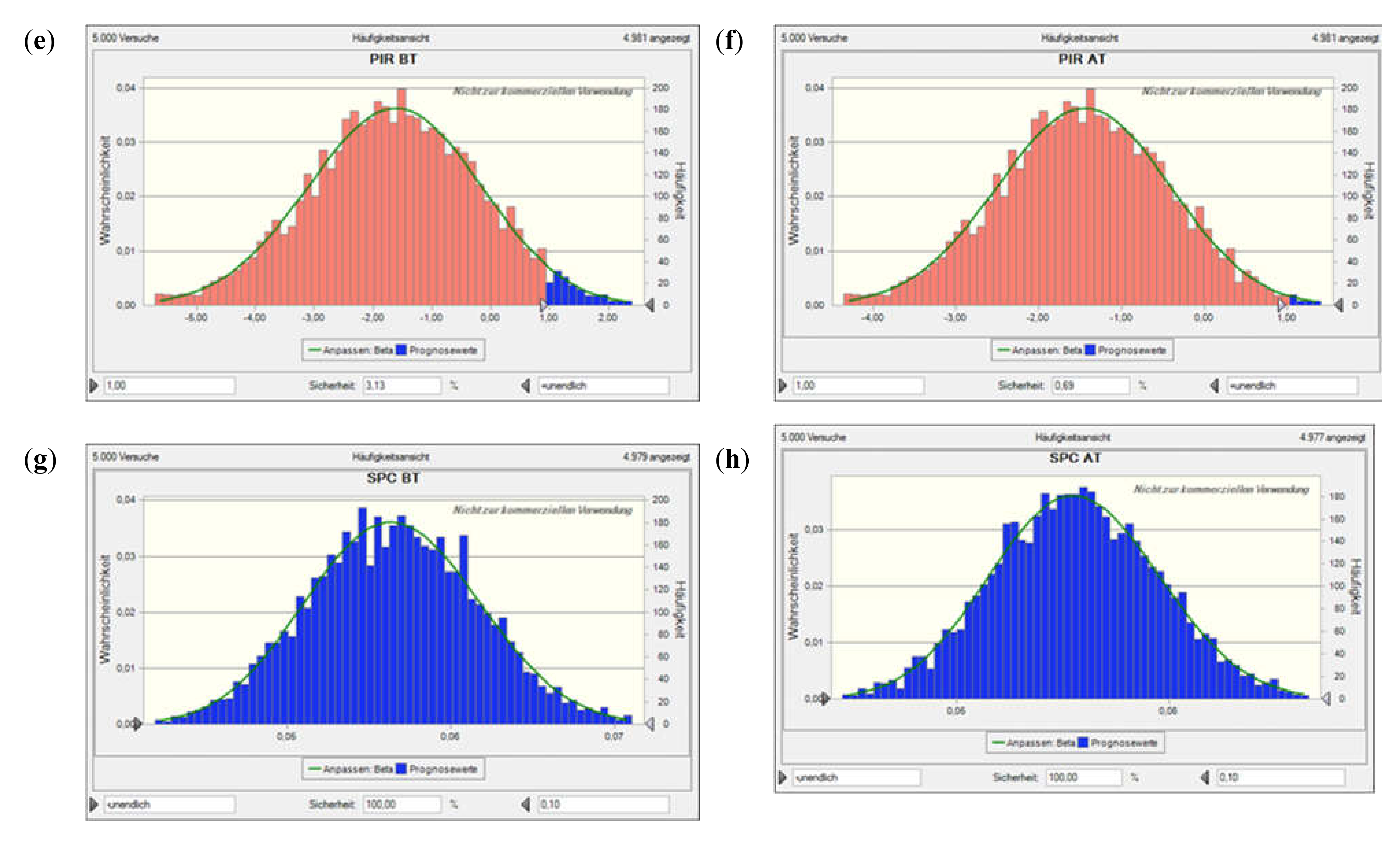
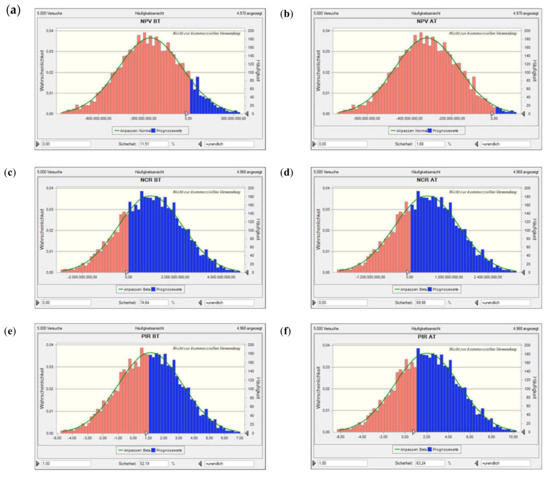
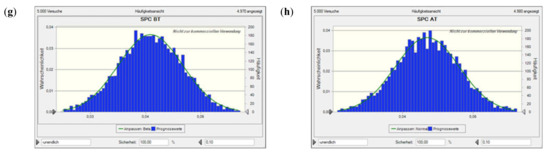
Figure A6.
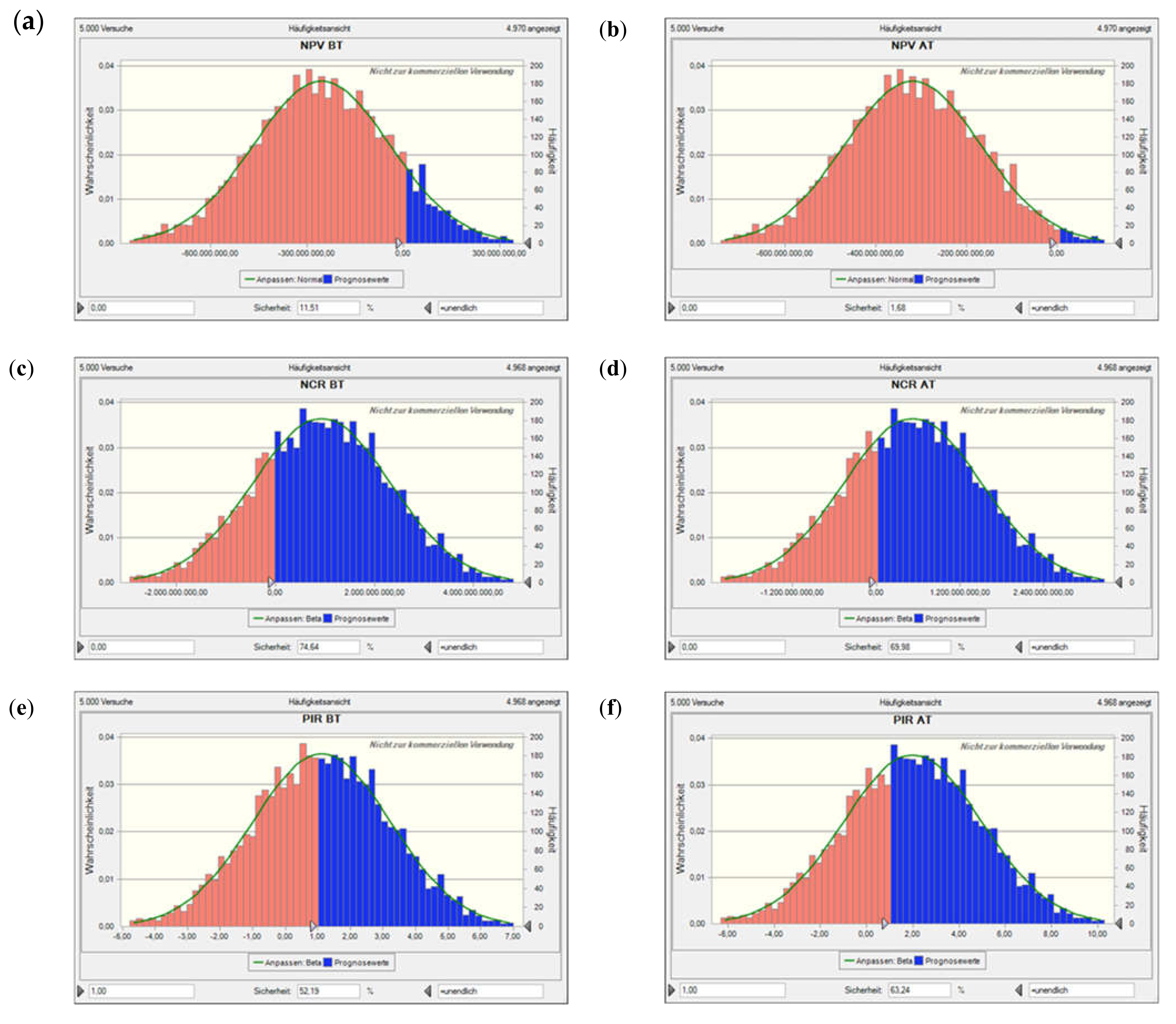
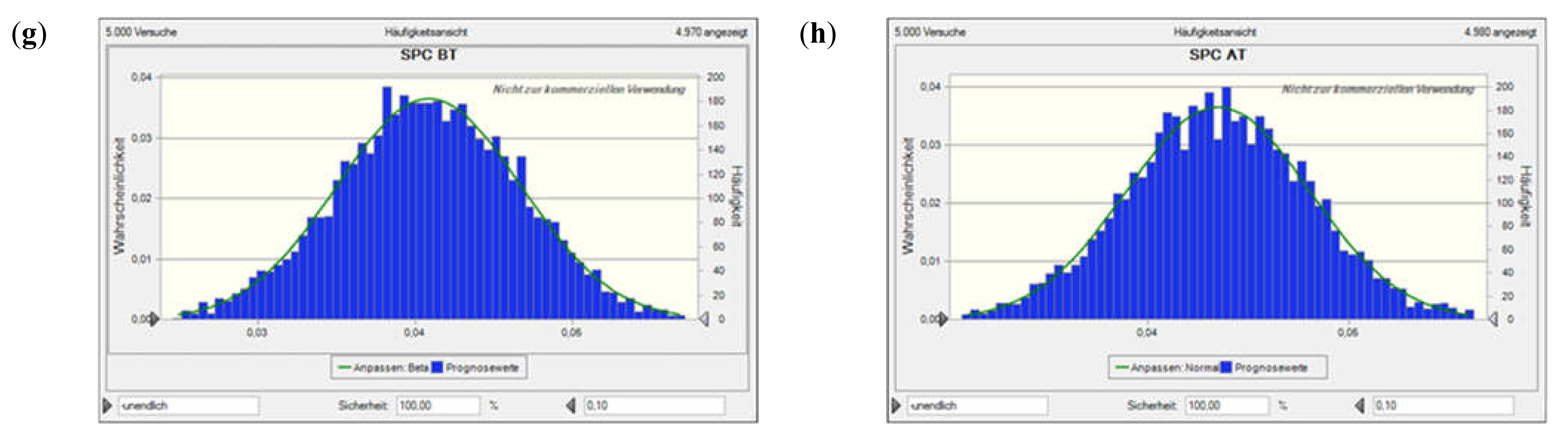
Value at risk for Scen. 2, incl. flooding time, based on a Monte Carlo simulation with 5000 runs. Plots (a) and (b) show the net present value (NPV) before and after tax, plots (c) and (d) the NCR before and after tax, plots (e) and (f) the profit-to-investment ratio (PIR) before and after tax, and plots (g) and (h) the per unit (specific) production costs (SPC) before and after tax. The solid lines denote the fitted probability distribution, the red areas the confidence interval of not encountering a neg. NPV, neg. NCR, or PIR < 1 (i.e., depending on the performance indicator concerned; as the costs considered are all positive, there is only a blue histogram in those two plots).
Figure A6.
Value at risk for Scen. 2, incl. flooding time, based on a Monte Carlo simulation with 5000 runs. Plots (a) and (b) show the net present value (NPV) before and after tax, plots (c) and (d) the NCR before and after tax, plots (e) and (f) the profit-to-investment ratio (PIR) before and after tax, and plots (g) and (h) the per unit (specific) production costs (SPC) before and after tax. The solid lines denote the fitted probability distribution, the red areas the confidence interval of not encountering a neg. NPV, neg. NCR, or PIR < 1 (i.e., depending on the performance indicator concerned; as the costs considered are all positive, there is only a blue histogram in those two plots).
References
- Hohmeyer, O.; Bohm, S. Trends toward 100% renewable electricity supply in Germany and Europe: A paradigm shift in energy policies. Wiley Interdiscip. Rev. Energy Environ. 2015, 4, 74–97. [Google Scholar] [CrossRef]
- Droste-Franke, B. Review of the Need for Storage Capacity Depending on the Share of Renewable Energies. In Electrochemical Energy Storage for Renewable Sources and Grid Balancing; Elsevier: Amsterdam, The Netherlands, 2015; pp. 61–86. [Google Scholar]
- Kapsali, M.; Kaldellis, J. Combining hydro and variable wind power generation by means of pumped-storage under economically viable terms. Appl. Energy 2010, 87, 3475–3485. [Google Scholar] [CrossRef]
- Madlener, R.; Specht, J.M. An Exploratory Economic Analysis of Underground Pumped-Storage Hydro Power Plants in Abandoned Coal Mines. In FCN Working Paper No. 2/2013; Institute for Future Energy Consumer Needs and Behavior, RWTH Aachen University: Aachen, Germany, 2013; (Revised June 2020). [Google Scholar]
- Menéndez, J.; Loredo, J. Use of closured open pit and underground coal mines for energy generation: Application to the Asturias Central Coal Basin (Spain). E3S Web Conf. 2019, 80. [Google Scholar] [CrossRef]
- Menéndez, J.; Loredo, J.; Fernandez, J.M.; Galdo, M. Underground pumped storage hydro power plants with mine water in abandoned coal mines. In Proceedings of the IMWA 2017 (Mine Water and Circular Economy), Lappenranta, Finland, 25–30 June 2017. [Google Scholar]
- Palomino, A.E.C.; Linhares Ferreira, F.C.; Barros, G.P.S.; Silva, L.; Porto, M.P. Conceptual design of a pumped hydro energy storage system for the Aguas Claras open pit mine. In Proceedings of the 23rd ABCM International Congress of Mechanical Engineering, Rio de Janeiro, Brazil, 6–11 December 2015. [Google Scholar]
- Pujades, E.; Orban, P.; Bodeux, S.; Archambeau, P.; Erpicum, S.; Dassargues, A. Underground pumped storage hydropower plants using open pit mines: How do groundwater exchanges influence the efficiency? Appl. Energy 2017, 190, 135–146. [Google Scholar] [CrossRef]
- Pujades, E.; Willems, T.; Bodeux, S.; Orban, P.; Dassargues, A. Underground pumped storage hydroelectricity using abandoned works (deep mines or open pits) and the impact on groundwater flow. Hydrogeol. J. 2016, 24, 1531–1546. [Google Scholar] [CrossRef]
- Northey, S.A.; Mudd, G.M.; Saarivuori, E.; Wessman-Jääskeläinen, H.; Haque, N. Water footprinting and mining: Where are the limitations and opportunities? J. Clean. Prod. 2016, 135, 1098–1116. [Google Scholar] [CrossRef]
- McCullough, C.D.; Marchand, G.; Unseld, J. Mine closure of pit lakes as terminal sinks: Best available practice when options are limited? Mine Water Environ. 2013, 32, 302–313. [Google Scholar] [CrossRef]
- Rehman, S.; Al-Hadhrami, L.; Alam, M. Pumped hydro energy storage system: A technological review. Renew. Sustain. Energy Rev. 2015, 44, 586–598. [Google Scholar] [CrossRef]
- Dena. NNE—Pumpspeicher. Untersuchung der elektrizitätswirtschaftlichen und energiepolitischen Auswirkungen der Erhebung von Netznutzungsentgelten für den Speicherstrombezug von Pumpspeicherwerken. In Final Report Deutsche Energie-Agentur; Deutsche Energie-Agentur: Berlin, Germany, 2008; Available online: https://www.dena.de/fileadmin/dena/Dokumente/Pdf/9112_Pumpspeicherstudie.pdf (accessed on 15 June 2020).
- BVES. Speichertechnologien—Anwendungsbeispiel Pumpspeicherwerk (PSW) Goldisthal. 2016. Available online: https://www.bves.de/wp-content/uploads/2017/04/Pumpspeicherwek.pdf (accessed on 15 June 2020).
- Levron, Y.; Shmilovitz, D. Power systems’ optimal peak-shaving applying secondary storage. Electr. Power Syst. Res. 2012, 89, 80–84. [Google Scholar] [CrossRef]
- Transnet, B.W. Grid Development Plan 2030. 2019. Available online: https://www.netzentwicklungsplan.de/sites/default/files/paragraphs-files/Standard_presentation_GDP_2030_V2019_2nd_draft.pdf (accessed on 15 June 2020).
- IWES. Energiewirtschaftliche Bewertung von Pumpspeicherwerken und anderen Speichern im zukünftigen Stromversorgungssystem. In Final Report Fraunhofer Institut für Windenergie und Energiesystemtechnik (IWES); IWES: Kassel, Germany, 2010; p. 152. [Google Scholar]
- Sensfuß, F.; Ragwitz, M.; Genoese, M. The merit-order effect: A detailed analysis of the price effect of renewable electricity generation on spot market prices in Germany. Energy Policy 2008, 36, 3086–3094. [Google Scholar] [CrossRef]
- Osanloo, M.; Gholamnejad, J.; Karimi, B. Long-term open pit mine production planning: A review of models and algorithms. Int. J. Min. Reclam. Environ. 2008, 22, 3–35. [Google Scholar] [CrossRef]
- Trettin, R.; Glässer, W.; Lerche, I.; Seelig, U.; Treutler, H.-C. Flooding of lignite mines: Isotope variations and processes in a system influenced by saline groundwater. Isot. Environ. Health Stud. 2006, 42, 159–179. [Google Scholar] [CrossRef] [PubMed]
- Höök, M.; Zittel, W.; Schindler, J.; Aleklett, K. Global coal production outlooks based on a logistic model. Fuel 2010, 89, 3546–3558. [Google Scholar] [CrossRef]
- Korbmacher, J. Residual lakes in the Rhineland lignite area. Min. Rep. 2016, 152, 233–244. [Google Scholar]
- Ma, T.; Yang, H.; Lu, L.; Peng, J. Technical feasibility study on a standalone hybrid solar-wind system with pumped hydro storage for a remote island in Hong Kong. Renew. Energy 2014, 69, 7–15. [Google Scholar] [CrossRef]
- Giesecke, J.; Mosonyi, E.; Heimerl, S. Wasserkraftanlagen. Planung, Bau und Betrieb; Springer: Berlin, Germany, 2009. [Google Scholar]
- Popp, M. Nutzung natürlicher Höhenunterschiede; Ingenieurbüro Matthias Popp: Wunsiedel, Germany, 2015; Available online: http://ringwallspeicher.de/Ringwall-Nutzung_naturlicher_Hohenunterschiede.htm (accessed on 15 June 2020).
- Weibel, S.; Madlener, R. Cost-Effective Design of Ringwall Storage Hybrid Power Plants: A Real Options Analysis. Energy Convers. Manag. 2015, 103, 871–885. [Google Scholar] [CrossRef][Green Version]
- RWE. Rahmenbetriebsplan für die Fortführung des Tagebaus Hambach im Zeitraum 2020–2030. 2012. Available online: http://www.rwe.com/web/cms/mediablob/de/1232522/data/60012/2/rwe-power-ag/energietraeger/braunkohle/standorte/tagebau-hambach/Wesentliche-Inhalte.pdf (accessed on 15 June 2020).
- Deane, J.Ó.; Gallachóir, B.; McKeogh, E. Techno-economic review of existing and new pumped hydro energy storage plant. Renew. Sustain. Energy Rev. 2010, 14, 1293–1302. [Google Scholar] [CrossRef]
- Gatzen, C. The Economics of Power Storage: Theory and Empirical Analysis for Central Europe; Oldenburg Industrieverlag: München, Germany, 2008. [Google Scholar]
- B&V Black & Veatch Holding Company. Cost Report. Cost and performance data for power generation technologies. In Report Prepared for the National Renewable Energy Laboratory; National Renewable Energy Laboratory: Golden, CO, USA, 2012; p. 105. Available online: https://refman.energytransitionmodel.com/publications/1921 (accessed on 15 June 2020).
- Steffen, B. Prospects for pumped-hydro storage in Germany. Energy Policy 2012, 45, 420–429. [Google Scholar] [CrossRef]
- Hemm, M.; Nixdorf, B.; Schlundt, A.; Kapfer, M.; Krumbeck, H. Braunkohlentagebauseen in Deutschland. Gegenwärtiger Kenntnisstand über Wasserwirtschaftliche Belange von Braunkohletagebaurestlöchern; With Assistance of Federal Environmental Agency (Umweltbundesamt); Brandenburgische Technische Universität Cottbus: Cottbus, Germany, 2000. [Google Scholar]
- BMJ Federal Office for Justice. Gesetz über die Elektrizitäts- und Gasversorgung. 2005. Available online: https://www.gesetze-im-internet.de/enwg_2005/ (accessed on 15 June 2020).
- BMWiE Federal Ministry for Economic Affairs and Energy. Das Erneuerbare-Energien-Gesetz. 2020. Available online: https://www.erneuerbare-energien.de/EE/Redaktion/DE/Dossier/eeg.html?cms_docId=401818 (accessed on 15 June 2020).
- Netztransparenz.de (2020): EEG-Umlage. Available online: https://www.netztransparenz.de/EEG/EEG-Umlagen-Uebersicht (accessed on 15 June 2020).
- Nebel, A. Energiewirtschaftsrechtliche Einordnung von PSW in Deutschland, Österreich und der Schweiz. In Proceedings of the EFZN Conference, Göttingen, Germany, 21–22 November 2014; pp. 72–91. [Google Scholar]
- European Commission. Directive 2000/60/EC of the European Parliamanet and of the Council of 23 October 2000 on establishing a framework for community action in the field of water policy. Off. J. Eur. Communities 2000, 327, 1–73. [Google Scholar]
- Becker, J.; Mikalauskas, K.; Müller, T. Wasserentnahmeentgelte der Länder—Ein Vergleich. IHK Pfalz Report. 2013. Available online: https://www.ihk-siegen.de/fileadmin/user_upload/Infrastruktur_Planung_und_Verkehr/Broschuere_WEE_Wasserentnahmeentgelte_der_Laender.pdf (accessed on 15 June 2020).
- Bhattacharyya, S.C. Energy Economics; Springer: Berlin, Germany, 2011. [Google Scholar]
- Konstantin, P. Praxisbuch Energiewirtschaft; Springer: Berlin, Germany, 2013. [Google Scholar]
- Zweifel, P.; Praktiknjo, A.; Erdmann, G. Energy Economics. Theory and Applications; Springer: Berlin, Germany, 2017. [Google Scholar]
- Charnes, J. Financial Modeling with Crystal Ball® and Excel; Wiley Sons Inc.: Hoboken, NJ, USA, 2007. [Google Scholar]
- Borchert, J.; Schemm, R.; Korth, S. Stromhandel Institutionen, Marktmodelle, Pricing und Risikomanagement; Schäffer-Poeschel: Stuttgart, Germany, 2006. [Google Scholar]
- Regelleistung.net. Available online: https://www.regelleistung.net/ext/ (accessed on 2 March 2015).
- Greenwood, P.E.; Nikulin, M.S. A Guide to Chi-Squared Testing; John Wiley & Sons, Inc.: Toronto, ON, Canada, 1996. [Google Scholar]
- Hartung, J. Statistik: Lehr- und Handbuch der Angewandten Statistik; Oldenburg Industrieverlag: München, Germany, 2009. [Google Scholar]
- NIST. Anderson-Darling Test. 2020. Available online: https://www.itl.nist.gov/div898/handbook/eda/section3/eda35e.htm (accessed on 15 June 2020).
- RWE RAG. Energiepark Sundern. Available online: http://www.rwe.com/web/cms/mediablob/de/544002/data/0/2/Flyer-Halde-Sundern.pdf (accessed on 15 June 2020).
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).