Participation of an EV Aggregator in the Reserve Market through Chance-Constrained Optimization
Abstract
1. Introduction
- To improve the strategic offering model developed in [5], by incorporating chance-constrained stochastic programming as a risk-analysis technique;
- To model the chance-constrained stochastic programming model, through the deterministic equivalent way, recurring to the Big-M and McCormick relaxation methods;
- To explore the trade-off between reliability and expected profit, assessing the level of risk assumed the aggregator.
2. Related Work
3. Chance-Constrained Participation Model
3.1. Problem Description
3.2. Bilinear Reformulation of the Chance-Constrained Problem
4. Case Study
4.1. Case Characterization
4.2. Results
4.2.1. Big-M vs. McCormick
4.2.2. Computational Effort
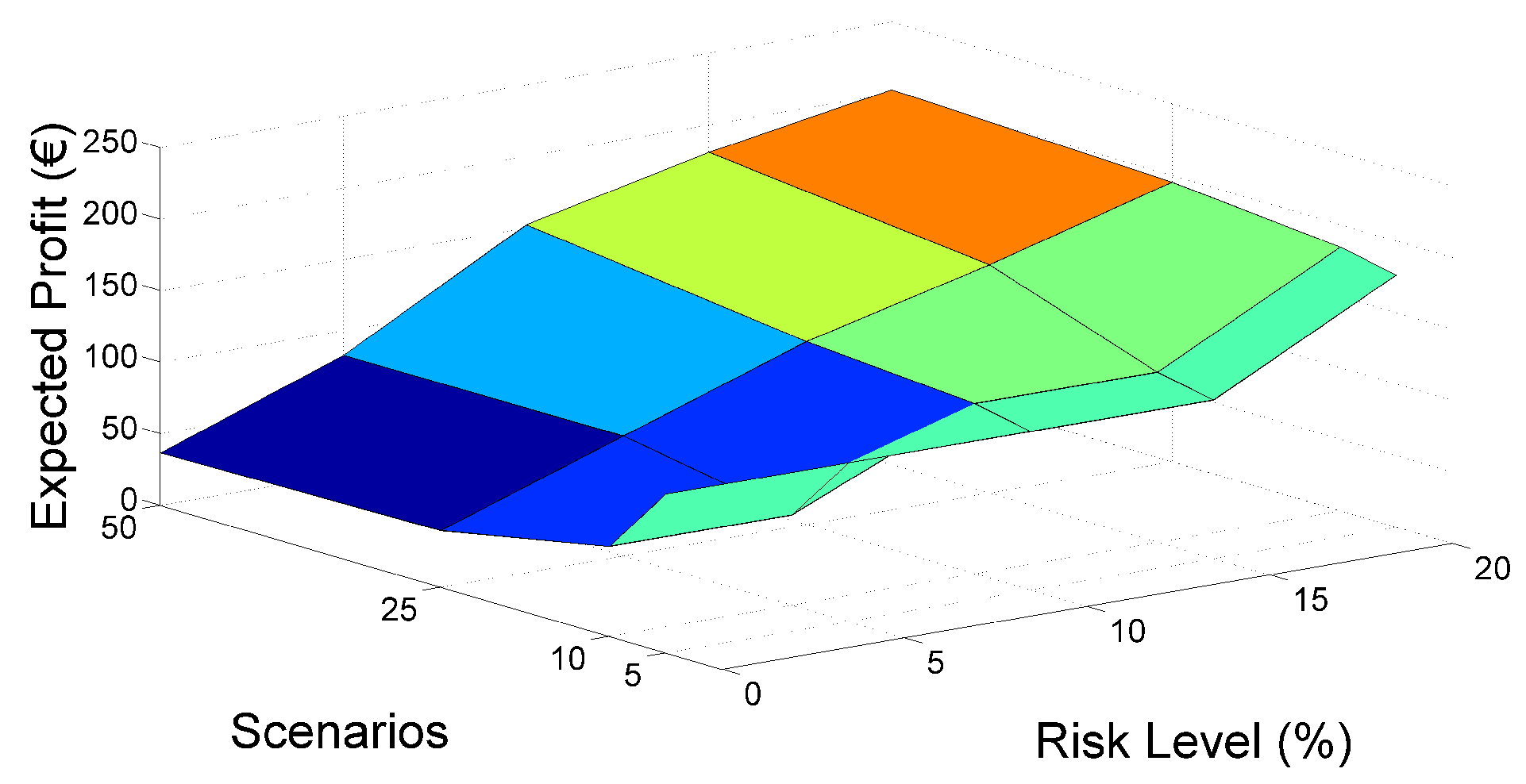
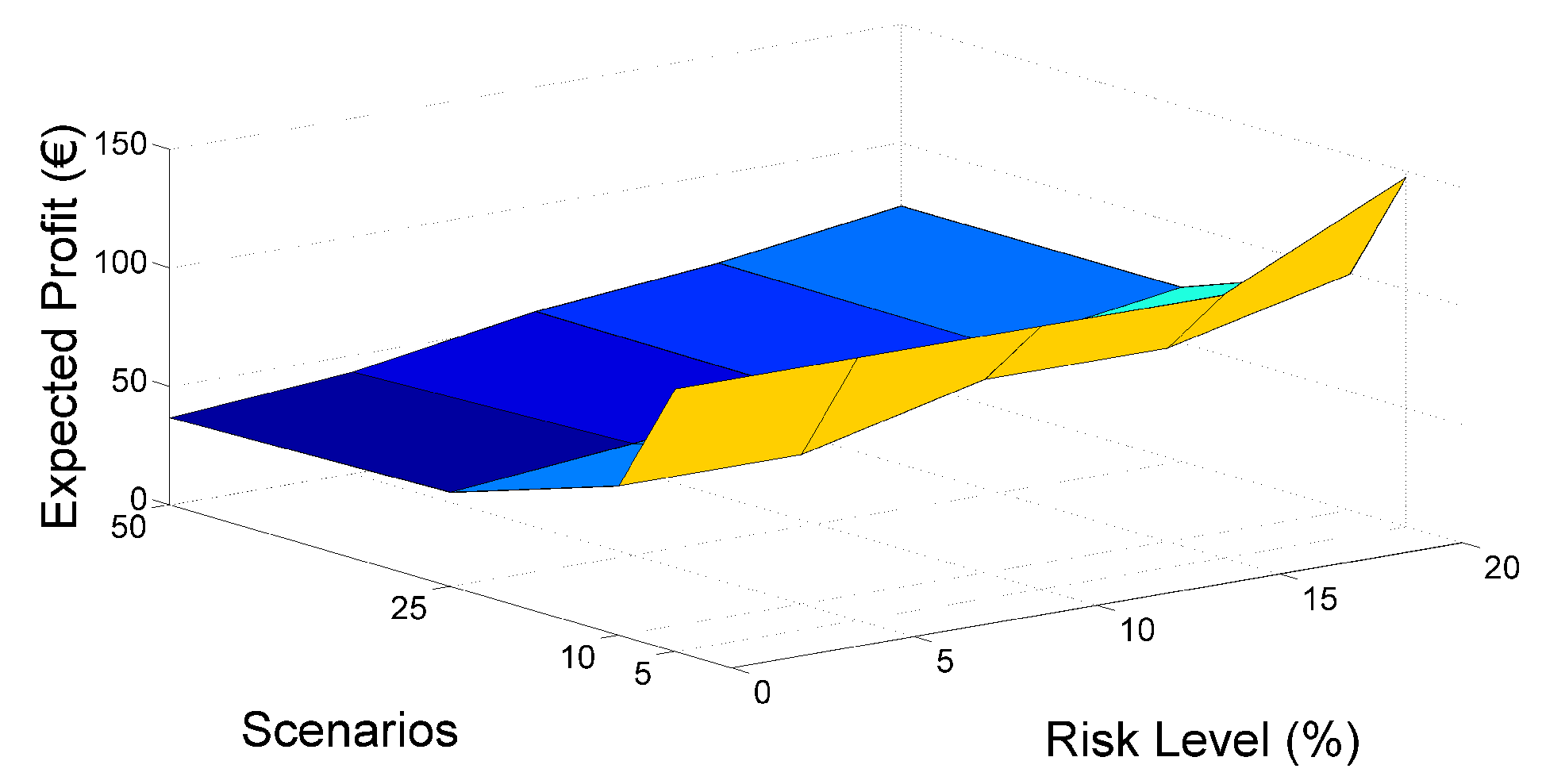
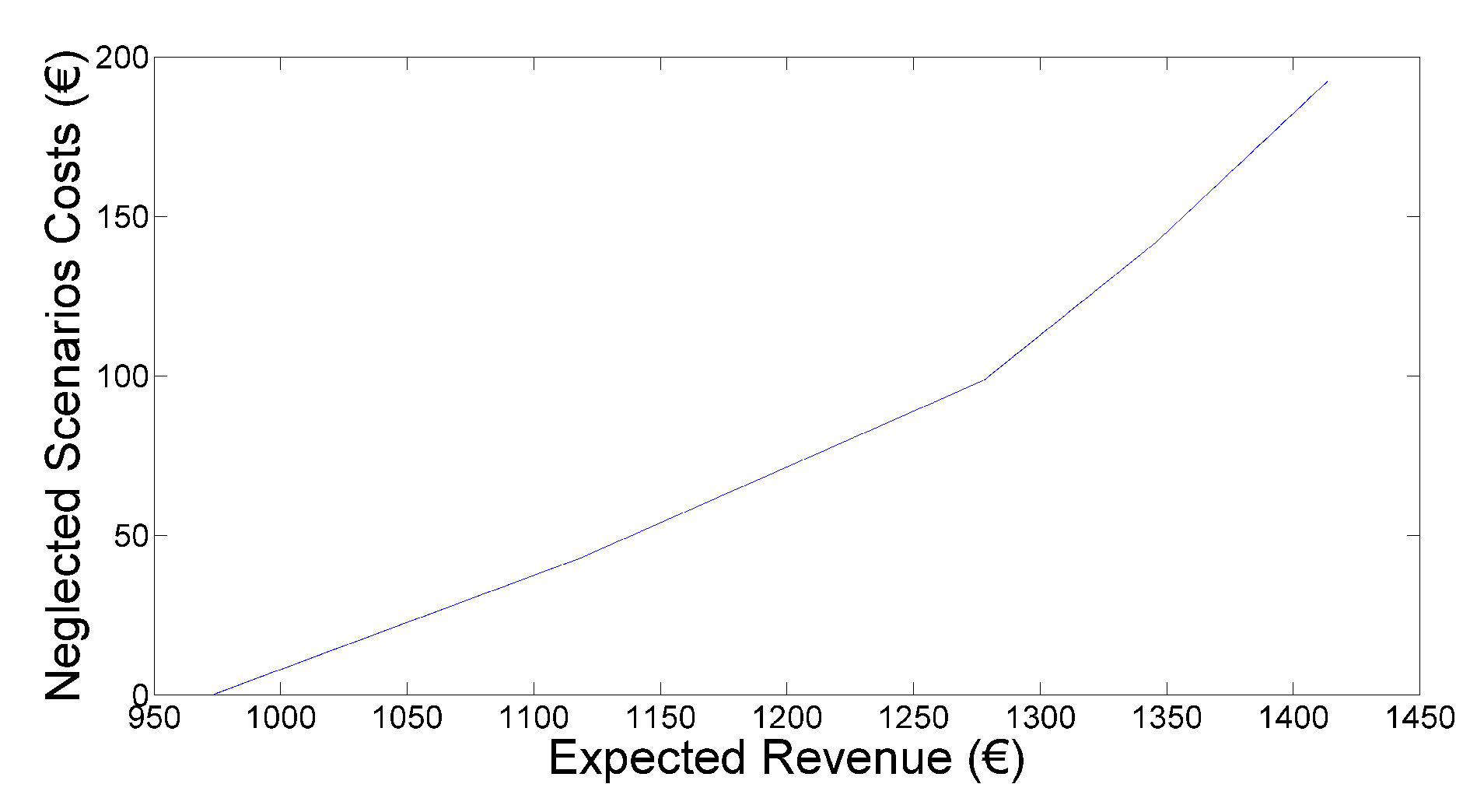
4.2.3. Risk Assessment and Related Neglected Costs
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| EV | Electric vehicle |
| FCN-R | Frequency-controlled normal operation reserve |
| SOC | State-of-charge |
| Parameters: | |
| Prices and penalties | |
| Probability of scenario | |
| Energy spot price | |
| , | Charge and discharge efficiency, respectively |
| M | Big-M parameter |
| Probability of scenario | |
| Risk Level | |
| Variables: | |
| R | Amount of offered reserve in the first-stage |
| Revenue | |
| Amount of power for missing offered upward reserve | |
| Amount of power for missing offered downward reserve | |
| P | Power |
| Y | Binary variable for offering in the market |
| r | Amount of reserve deployed in the second-stage |
| State-of-charge of the electric vehicle at the end of period t | |
| z | Binary variable |
| Subscripts: | |
| t | Period index |
| Scenario index | |
| Electric vehicle index | |
| Discharge process | |
| Charge process | |
| EV user trip | |
| Superscripts: | |
| Day-ahead - first-stage | |
| Real-time - second-stage | |
| Upward reserve | |
| R | Amount of offered reserve in the first-stage |
| Downward reserve | |
| Penalty for missing the contracted reserve | |
| E | Energy |
References
- Sarker, M.R.; Dvorkin, Y.; Ortega-Vazquez, M.A. Optimal participation of an electric vehicle aggregator in day-ahead energy and reserve markets. IEEE Trans. Power Syst. 2016, 31, 3506–3515. [Google Scholar] [CrossRef]
- Bessa, R.J.; Matos, M.A.; Soares, F.J.; Lopes, J.A. Optimized bidding of a EV aggregation agent in the electricity market. IEEE Trans. Smart Grid 2012, 3, 443–452. [Google Scholar] [CrossRef]
- Hu, J.; Morais, H.; Sousa, T.; Lind, M. Electric vehicle fleet management in smart grids: A review of services, optimization and control aspects. Renew. Sustain. Energy Rev. 2016, 56, 1207–1226. [Google Scholar] [CrossRef]
- Vagropoulos, S.I.; Bakirtzis, A.G. Optimal bidding strategy for electric vehicle aggregators in electricity markets. IEEE Trans. Power Syst. 2013, 28, 4031–4041. [Google Scholar] [CrossRef]
- Soares, T.; Sousa, T.; Andersen, P.B.; Pinson, P. Optimal offering strategy of an EV aggregator in the frequency-controlled normal operation reserve market. In Proceedings of the 15th International Conference on the European Energy Market (EEM), Lodz, Poland, 27–29 June 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Bessa, R.J.; Matos, M.A. Global against divided optimization for the participation of an EV aggregator in the day-ahead electricity market. Part I: Theory. Electr. Power Syst. Res. 2013, 95, 319–329. [Google Scholar] [CrossRef]
- Jawad, S.L. Electrical Vehicle Charging Services Planning and Operation with Interdependent Power Networks and Transportation Networks: A Review of the Current Scenario and Future Trends. Energies 2020, 13, 3371. [Google Scholar] [CrossRef]
- Faddel, S.; Al-Awami, A.T.; Mohammed, O.A. Charge control and operation of electric vehicles in power grids: A review. Energies 2018, 11, 701. [Google Scholar] [CrossRef]
- Rücker, F.; Merten, M.; Gong, J.; Villafáfila-Robles, R.; Schoeneberger, I.; Sauer, D.U. Evaluation of the Effects of Smart Charging Strategies and Frequency Restoration Reserves Market Participation of an Electric Vehicle. Energies 2020, 13, 3112. [Google Scholar] [CrossRef]
- El-Bayeh, C.Z.; Alzaareer, K.; Brahmi, B.; Zellagui, M. A Novel Algorithm for Controlling Active and Reactive Power Flows of Electric Vehicles in Buildings and Its Impact on the Distribution Network. World Electr. Veh. J. 2020, 11, 43. [Google Scholar] [CrossRef]
- Jabalameli, N.; Su, X.; Deilami, S. An online coordinated charging/discharging strategy of plug-in electric vehicles in unbalanced active distribution networks with ancillary reactive service in the energy market. Energies 2019, 12, 1350. [Google Scholar] [CrossRef]
- Sekyung, H.; Soohee, H.; Sezaki, K. Development of an Optimal Vehicle-to-Grid Aggregator for Frequency Regulation. IEEE Trans. Smart Grid 2010, 1, 65–72. [Google Scholar] [CrossRef]
- Aliasghari, P.; Mohammadi-Ivatloo, B.; Abapour, M.; Ahmadian, A.; Elkamel, A. Goal programming application for contract pricing of electric vehicle aggregator in join day-ahead market. Energies 2020, 13, 1771. [Google Scholar] [CrossRef]
- Rahmani-Andebili, M. Plug-in Electric Vehicles (PIEVs) aggregator as a renewable source in distribution network. In Proceedings of the 2012 Proceedings of 17th Conference on Electrical Power Distribution, EPDC 2012, Tehran, Iran, 2–3 May 2012; pp. 1–4. [Google Scholar]
- Sortomme, E.; El-Sharkawi, M.A. Optimal combined bidding of vehicle-to-grid ancillary services. IEEE Trans. Smart Grid 2012, 3, 70–79. [Google Scholar] [CrossRef]
- Vatandoust, B.; Ahmadian, A.; Golka, M.; Elkamel, A.; Almansoori, A.; Ghaljehei, M. Risk-Averse Optimal Bidding of Electric Vehicles and Energy Storage Aggregator in Day-ahead Frequency Regulation Market. IEEE Trans. Power Syst. 2018, 8950, 2036–2047. [Google Scholar] [CrossRef]
- Rashidizadeh-Kermani, H.; Vahedipour-Dahraie, M.; Najafi, H.R.; Anvari-Moghaddam, A.; Guerrero, J.M. A stochastic Bi-Level scheduling approach for the participation of EV aggregators in competitive electricity markets. Appl. Sci. 2017, 7, 1100. [Google Scholar] [CrossRef]
- Vardanyan, Y.; Madsen, H. Optimal coordinated bidding of a profit maximizing, risk-averse EV aggregator in three-settlement markets under uncertainty. Energies 2019, 12, 1755. [Google Scholar] [CrossRef]
- Bessa, R.J.; Matos, M.A. Optimization models for EV aggregator participation in a manual reserve market. IEEE Trans. Power Syst. 2013, 28, 3085–3095. [Google Scholar] [CrossRef]
- Goebel, C.; Jacobsen, H.A. Aggregator-Controlled EV Charging in Pay-as-Bid Reserve Markets with Strict Delivery Constraints. IEEE Trans. Power Syst. 2016, 31, 4447–4461. [Google Scholar] [CrossRef]
- Chen, D.; Jing, Z.; Tan, H. Optimal bidding/offering strategy for EV aggregators under a novel business model. Energies 2019, 12, 1384. [Google Scholar] [CrossRef]
- Liu, X.; Mancarella, P. Modelling, assessment and Sankey diagrams of integrated electricity-heat-gas networks in multi-vector district energy systems. Appl. Energy 2016, 167, 336–352. [Google Scholar] [CrossRef]
- Zhang, M.; Eliassen, F.; Taherkordi, A.; Jacobsen, H.A.; Chung, H.M.; Zhang, Y. Energy trading with demand response in a community-based P2P energy market. In Proceedings of the 2019 IEEE International Conference on Communications, Control, and Computing Technologies for Smart Grids (SmartGridComm 2019), Beijing, China, 21–23 October 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Vahedipour-Dahraie, M.; Rashidizaheh-Kermani, H.; Najafi, H.R.; Anvari-Moghaddam, A.; Guerrero, J.M. Coordination of EVs participation for load frequency control in isolated microgrids. Appl. Sci. 2017, 7, 539. [Google Scholar] [CrossRef]
- Rasouli, B.; Salehpour, M.J.; Wang, J.; Kim, G.J. Optimal day-ahead scheduling of a smart micro-grid via a probabilistic model for considering the uncertainty of electric vehicles’ load. Appl. Sci. 2019, 9, 4872. [Google Scholar] [CrossRef]
- Zhang, Q.; Hu, Y.; Tan, W.; Li, C.; Ding, Z. Dynamic time-of-use pricing strategy for electric vehicle charging considering user satisfaction degree. Appl. Sci. 2020, 10, 3247. [Google Scholar] [CrossRef]
- Clairand, J.M. Participation of electric vehicle aggregators in ancillary services considering users’ preferences. Sustainability 2020, 12, 8. [Google Scholar] [CrossRef]
- Energinet.dk. Ancillary Services to Be Delivered in Denmark Tender Conditions. 2017. Available online: https://en.energinet.dk/-/media/Energinet/El-RGD/Dokumenter/Ancillary-services-to-be-delivered-in-Denmark.pdf (accessed on 5 September 2017).
- Zeng, B.; An, Y.; Kuznia, L. Chance Constrained Mixed Integer Program: Bilinear and Linear Formulations, and Benders Decomposition. 2014. Available online: http://www.optimization-online.org/DB_FILE/2014/03/4295.pdf (accessed on 17 April 2019).
- Castro, P. Tightening Piecewise McCormick Relaxations for Bilinear Problems. Comput. Chem. Eng. 2014, 72, 253–264. [Google Scholar] [CrossRef]
- PARKER Project [Online]. Available online: https://parker-project.com/ (accessed on 5 June 2018).
| Risk Level () | TSO Constraint | |||
|---|---|---|---|---|
| Scenarios () | ||||
| 5 | 10 | 25 | 50 | |
| 0% | 0.0000% | 0.0000% | 0.0000% | 0.0000% |
| 5% | 0.0000% | 0.0000% | 0.0000% | −0.0149% |
| 10% | 0.0000% | 0.0000% | 0.0001% | 0.1143% |
| 15% | 0.0000% | 0.0000% | 0.0001% | 0.1018% |
| 20% | −0.0026% | 0.0000% | 0.0000% | −0.0293% |
| Risk Level () | TSO Constraint | |||
|---|---|---|---|---|
| Scenarios () | ||||
| 5 | 10 | 25 | 50 | |
| 0% | 6.53 | 7202.43 | 7203.06 | 7218,46 |
| 5% | 7.36 | 7201.81 | 7202.86 | 7219.88 |
| 10% | 7.15 | 7214.18 | 7202.27 | 7213.63 |
| 15% | 7.25 | 7259.65 | 7202.35 | 7209.05 |
| 20% | 30.53 | 7200.94 | 7202.23 | 7226.61 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Faria, A.S.; Soares, T.; Sousa, T.; Matos, M.A. Participation of an EV Aggregator in the Reserve Market through Chance-Constrained Optimization. Energies 2020, 13, 4071. https://doi.org/10.3390/en13164071
Faria AS, Soares T, Sousa T, Matos MA. Participation of an EV Aggregator in the Reserve Market through Chance-Constrained Optimization. Energies. 2020; 13(16):4071. https://doi.org/10.3390/en13164071
Chicago/Turabian StyleFaria, António Sérgio, Tiago Soares, Tiago Sousa, and Manuel A. Matos. 2020. "Participation of an EV Aggregator in the Reserve Market through Chance-Constrained Optimization" Energies 13, no. 16: 4071. https://doi.org/10.3390/en13164071
APA StyleFaria, A. S., Soares, T., Sousa, T., & Matos, M. A. (2020). Participation of an EV Aggregator in the Reserve Market through Chance-Constrained Optimization. Energies, 13(16), 4071. https://doi.org/10.3390/en13164071





