An Enhanced Vertical Ground Heat Exchanger Model for Whole-Building Energy Simulation
Abstract
1. Introduction
2. Literature Review
2.1. Analytical Models
2.2. Response Factor Models
2.3. Thermal Resistance-Capacitance Models
2.4. Numerical Models
3. Methodology
3.1. Enhanced Response Factor Model
- Significant effort has been expended to understand and improve the original response factor model. Since its publication, researchers have performed many studies that enhance understanding of the methods and improve on the original work. This work similarly builds on the original model, about which much is already known, and which has already been widely adopted.
- Because the formulation builds on the historical response factor model, software or other programs that already have this model implemented can more easily make modifications to incorporate the enhancements. This simplifies adoption of the model in WBES environments.
- Again because the formulation builds on the historical response factor model, methods for generating standard borehole wall temperature g-functions are still applicable (as are load aggregation procedures, which are critical to maintaining low simulation times).
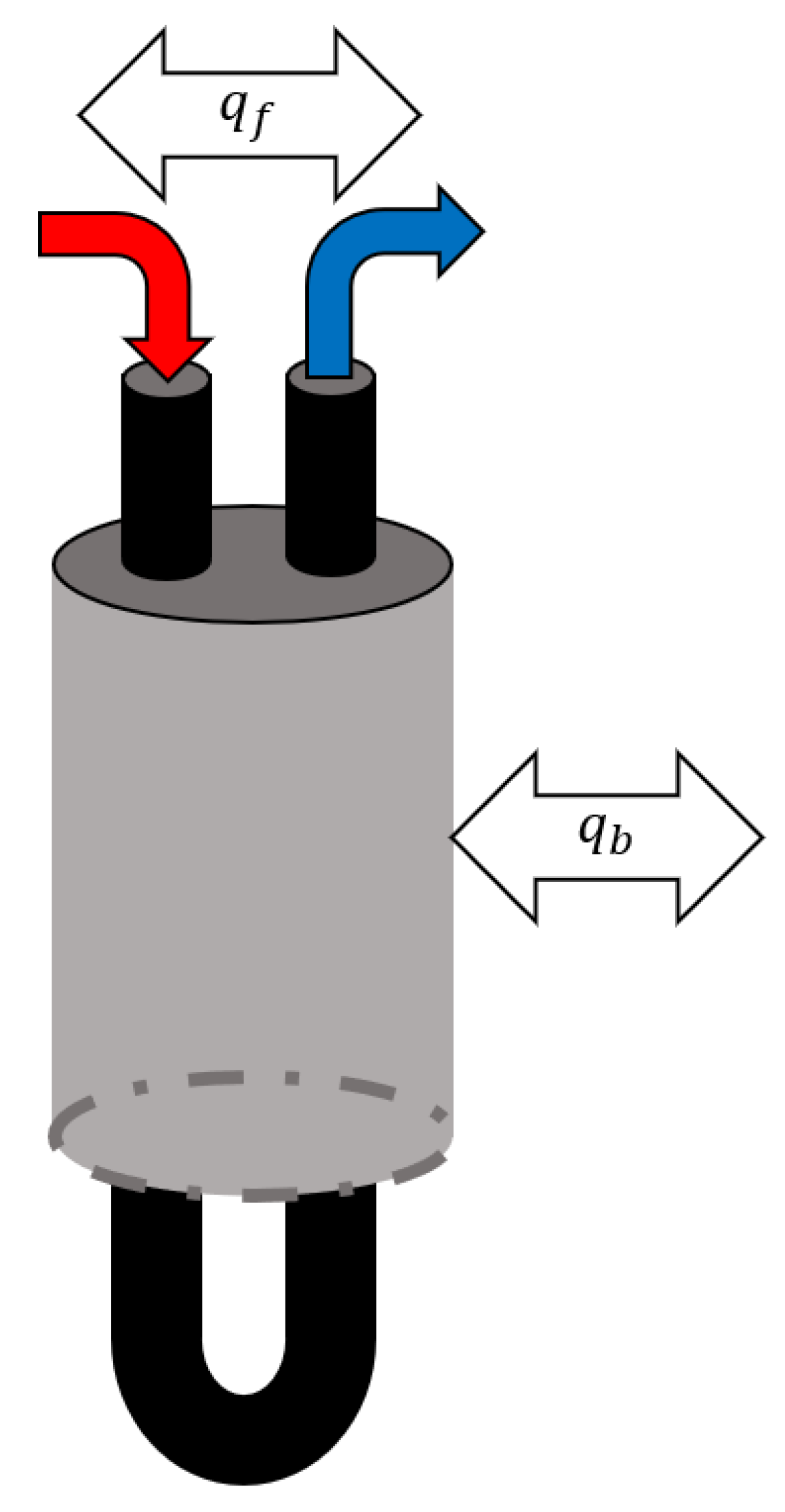
- By clearly defining the heat transfer rate applied in this model as the fluid’s heat transfer rate, the domain inside the borehole and the domain between the borehole wall and the far-field soil temperature can be coupled together easily through two separate response factor computations. This more easily allows the transient effects to be handled, even down to timesteps below the transit time of the GHE circulation fluid.
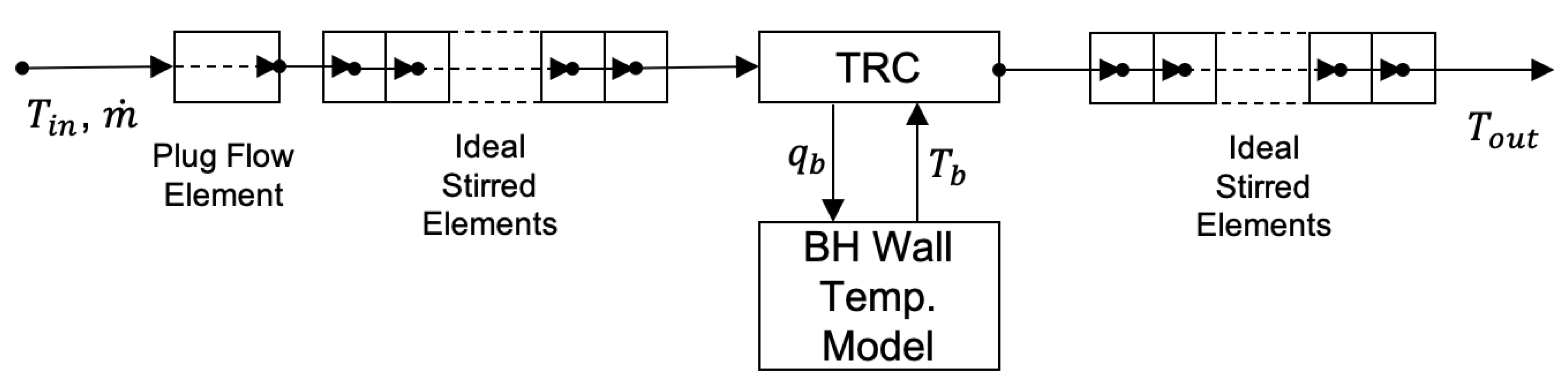
3.2. Model Reformulation for WBES Usage
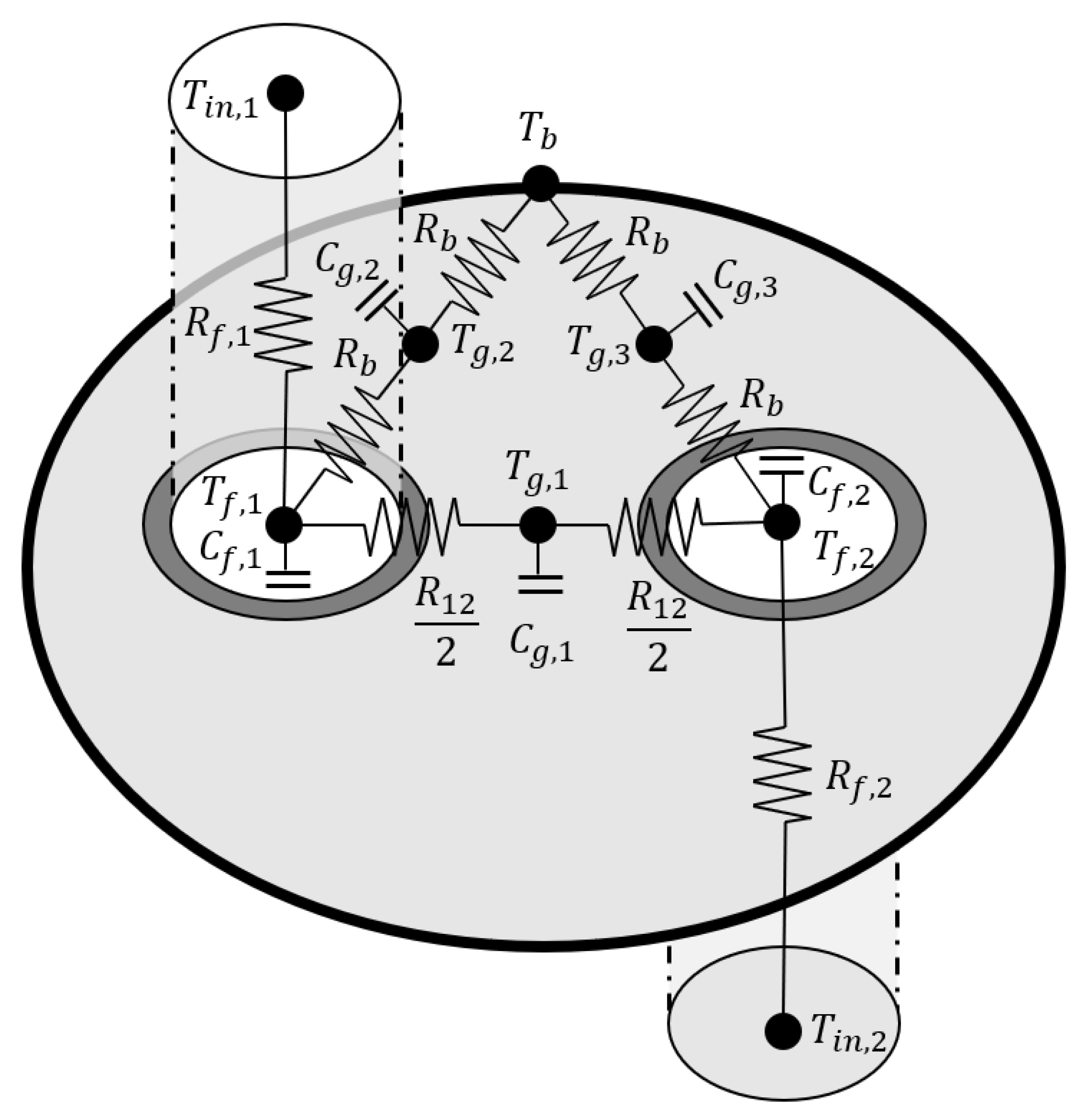
3.3. Dynamic Borehole Model
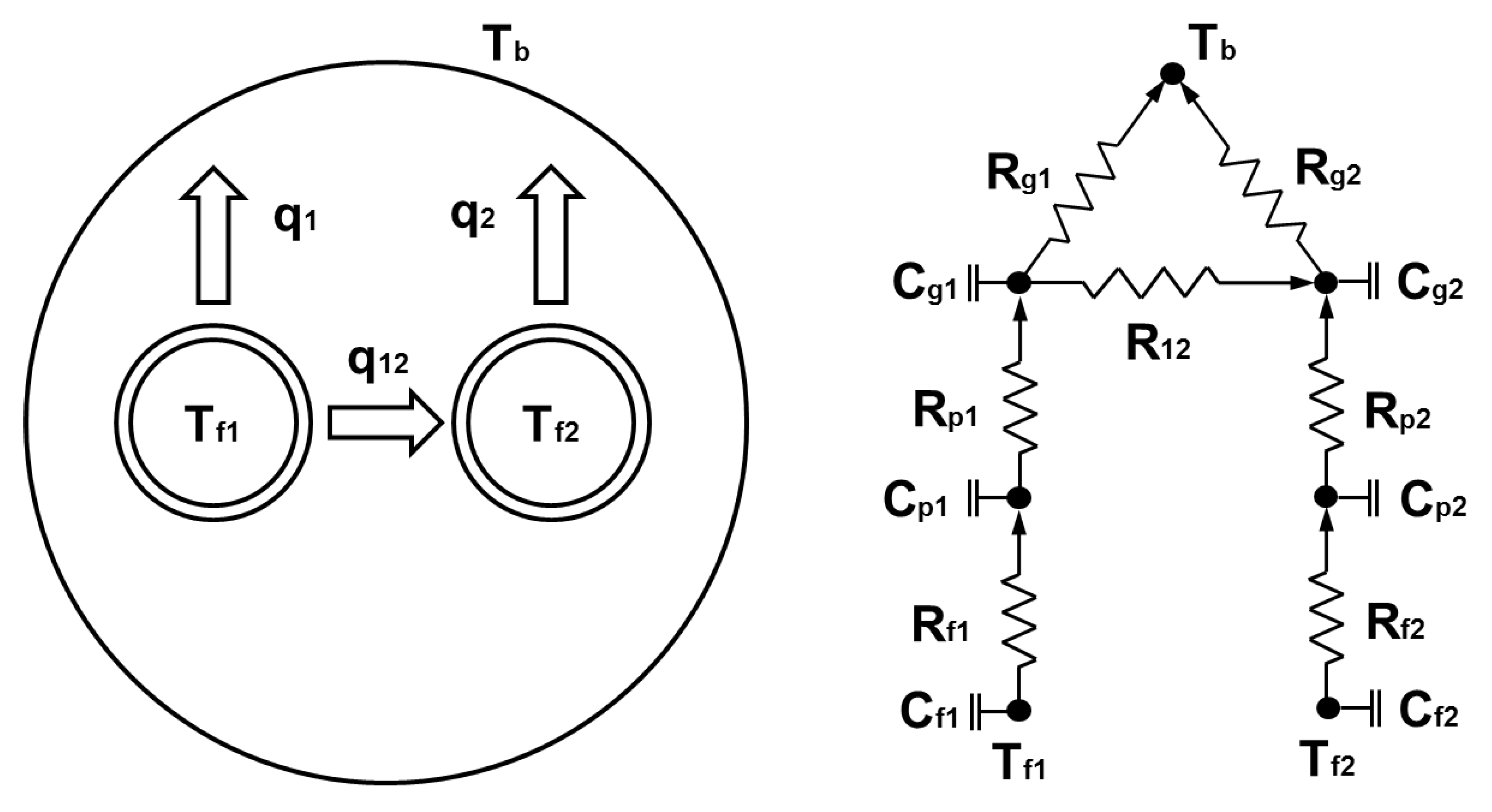
3.3.1. Simple Borehole TRC Model
3.3.2. Dynamic Pipe Model
3.3.3. Dynamic Borehole Model Validation
3.4. Exiting Fluid Temperature Response Factor Generation
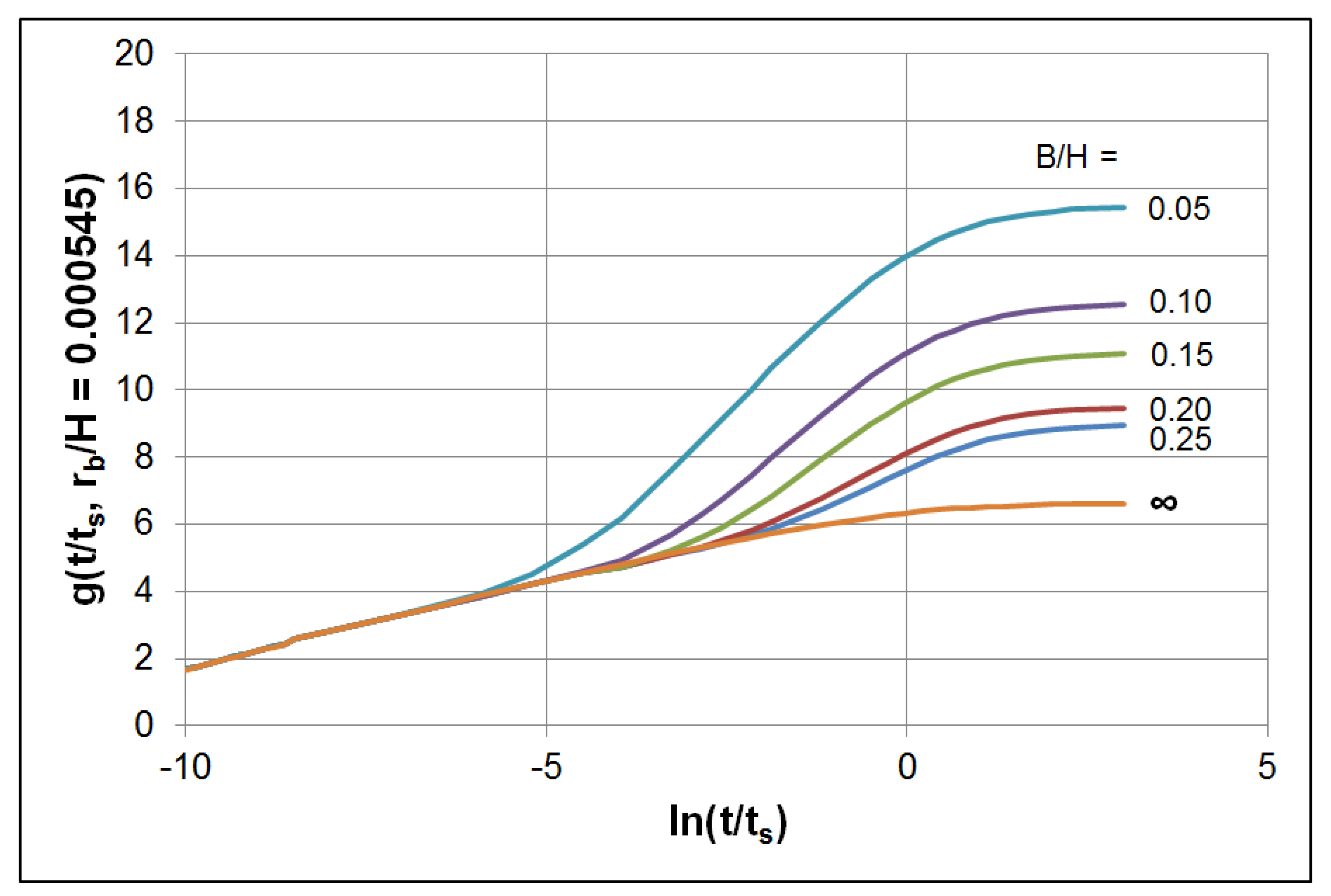
3.5. Borehole Wall Temperature Response Factor Generation
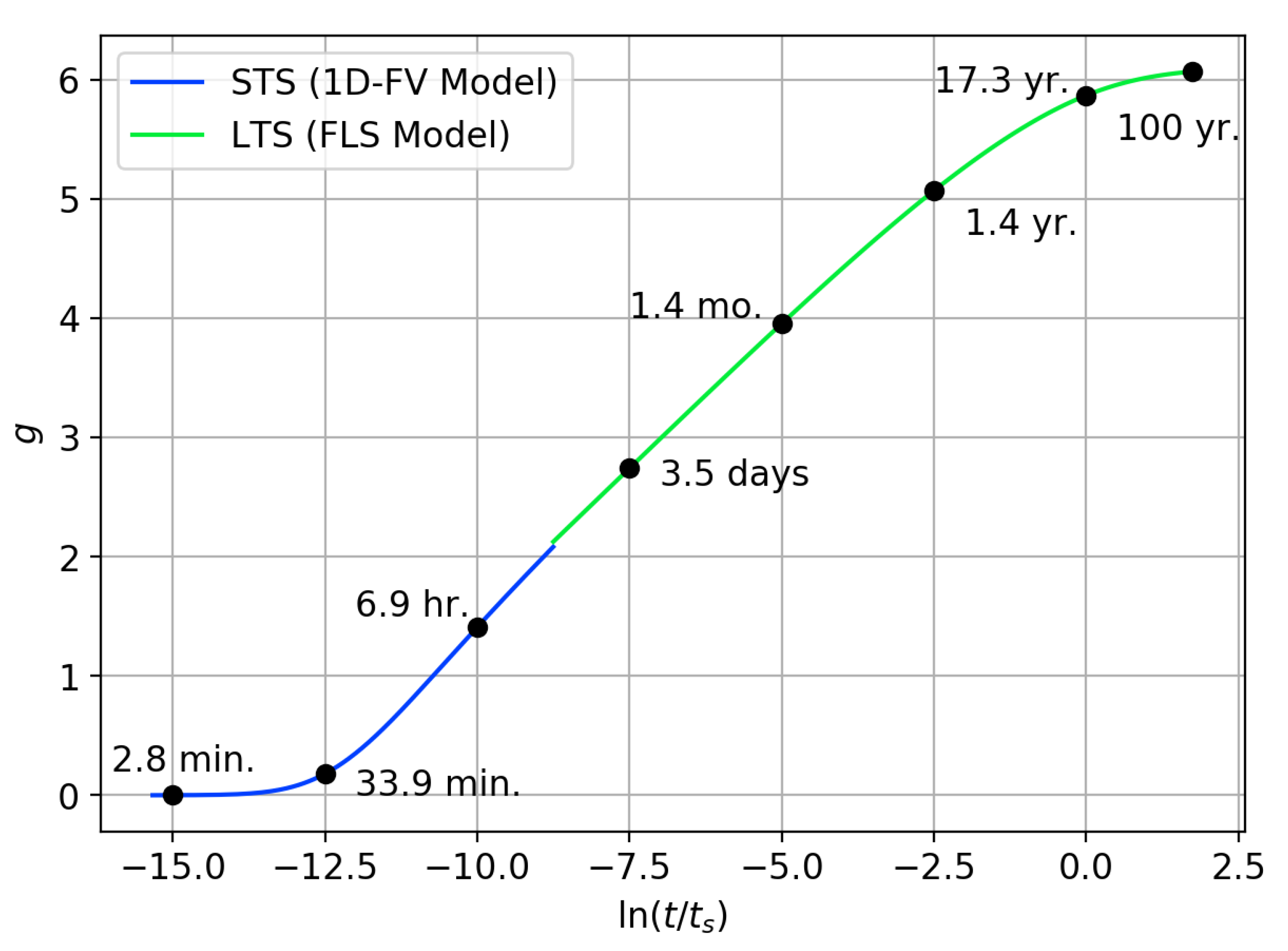
3.6. Methodology Summary and Discussion
- Long-timestep borehole wall temperature g-functions could be computed with any number of approaches outlined previously. In this work, an FLS approach was used by utilizing the pygfunction library by Cimmino [42]. No modifications are required to the methodology used to compute these g-functions. Cimmino has produced significant quantification regarding the speed of these methods [39] and has shown that for borefields with up to 64 boreholes—which is realistically expected to capture most of the WBES use cases—g-functions can be computed in times from a few seconds to a few minutes. Note that the code by Cimmino is written in Python; the computation time could likely be reduced to some extent after being implemented in a compiled programming language.
- Short-timestep borehole wall temperature g-functions could also be computed using any accurate borehole model that captures the dynamic effects of the borehole thermal capacity on the borehole wall temperature. In this work, the model by Xu & Spitler [58] was used because it uses a simplified geometry that accounts for the borehole thermal capacity. In addition, it is a 1D, radial finite-volume model that can be solved rapidly using a tri-diagonal matrix formulation. Note that the original model has to be slightly modified to compute the temperature at the borehole wall, and not at the fluid. This model is highly efficient and can compute the short-timestep g-functions in a matter of seconds.
- Exiting fluid temperatures g-functions are computed with a simplified dynamic borehole model that accounts for the transit delay of the circulation fluid via utilization of a transit delay pipe model. As before, the method presented in this paper does not rely on this specific dynamic GHE model; rather, any dynamic GHE model that accurately captures the transit delay effects of the borehole could be used, assuming that it is sufficiently fast and accurate. The borehole wall boundary temperature was updated by computing the heat flux at the borehole wall and then using that information to inform the original heat-input-formulated response factor model (Equation (4)). The borehole wall temperature resulting from that was then set as the borehole wall temperature boundary condition and updated at each timestep. Note that the short-timestep g-functions computed in the previous step are used here for determining the updated borehole wall boundary temperature. The dynamic model used here was able to compute the exiting fluid temperature g-functions for a single flow rate in , which is an acceptable time for WBES. Note that this should be repeated for different flow rates and that additional work should be done to determine how many different values are needed.
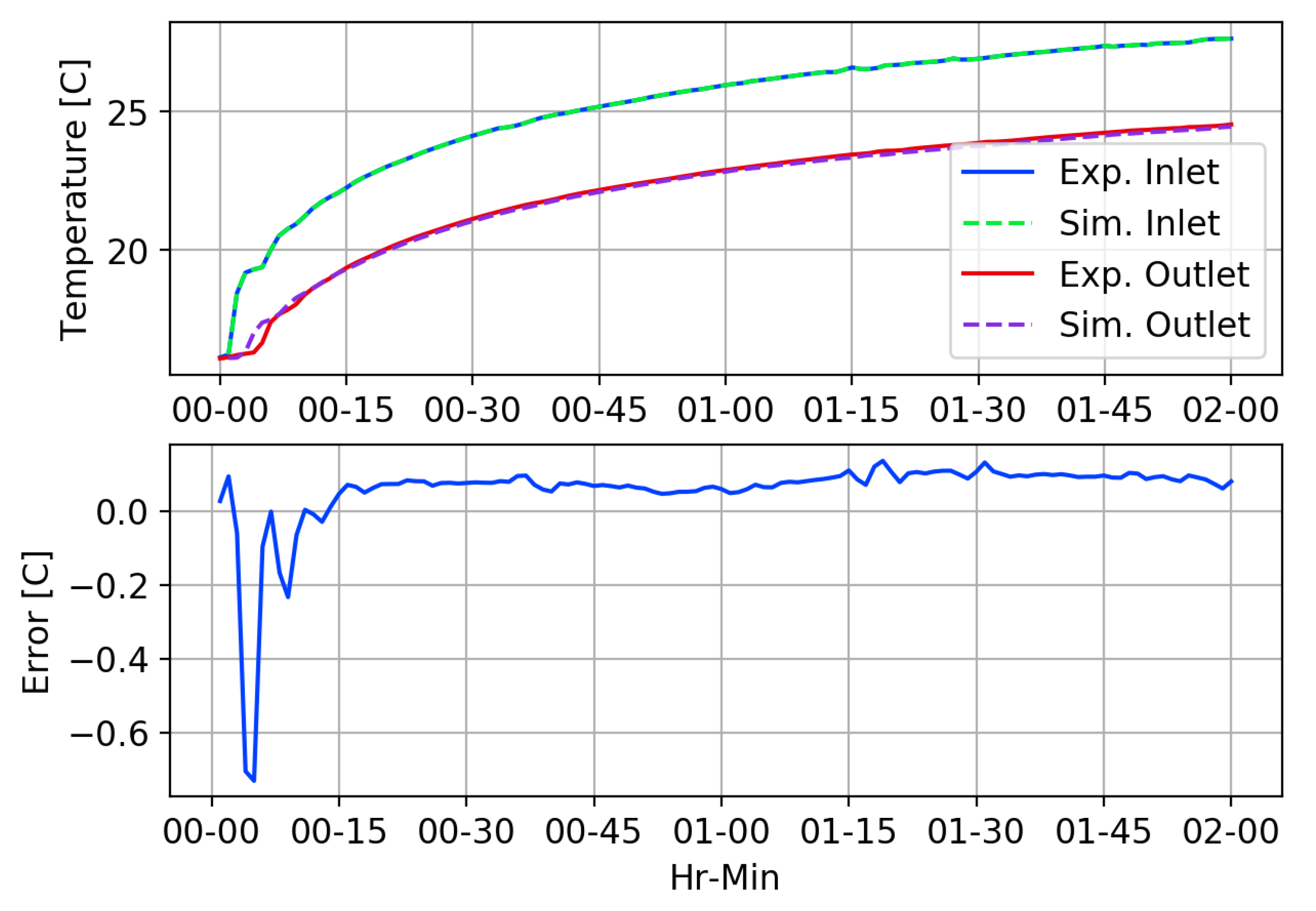
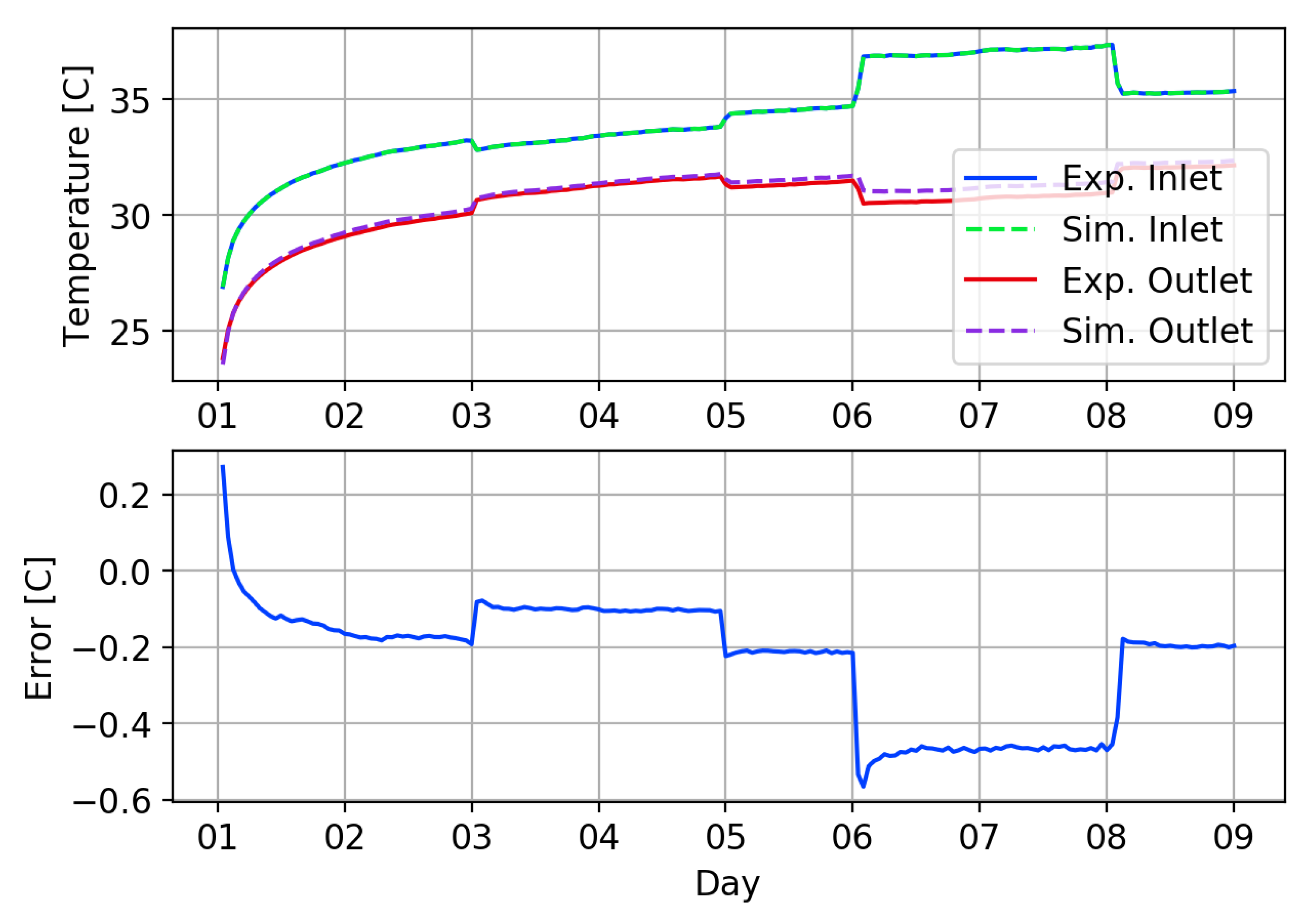
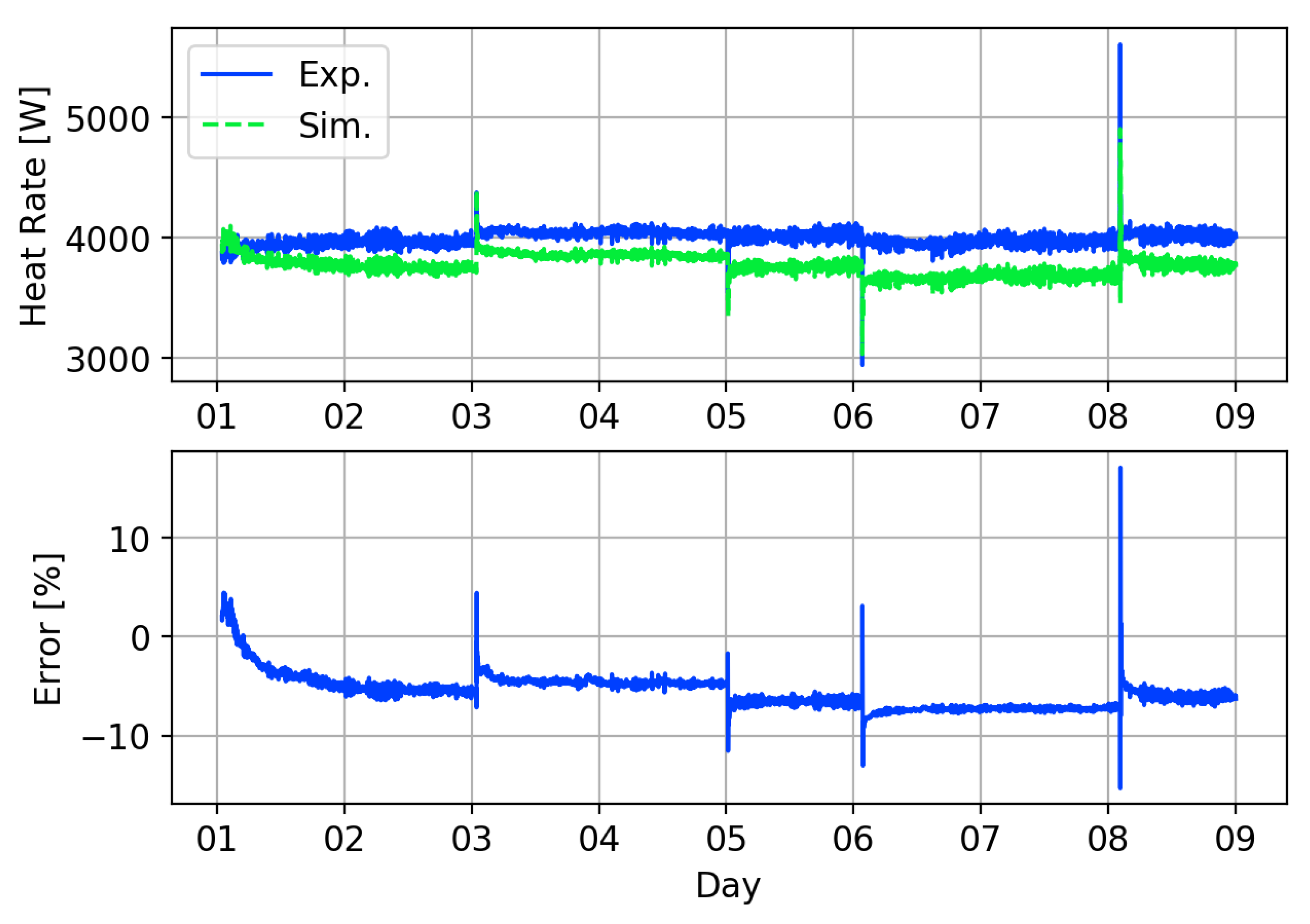
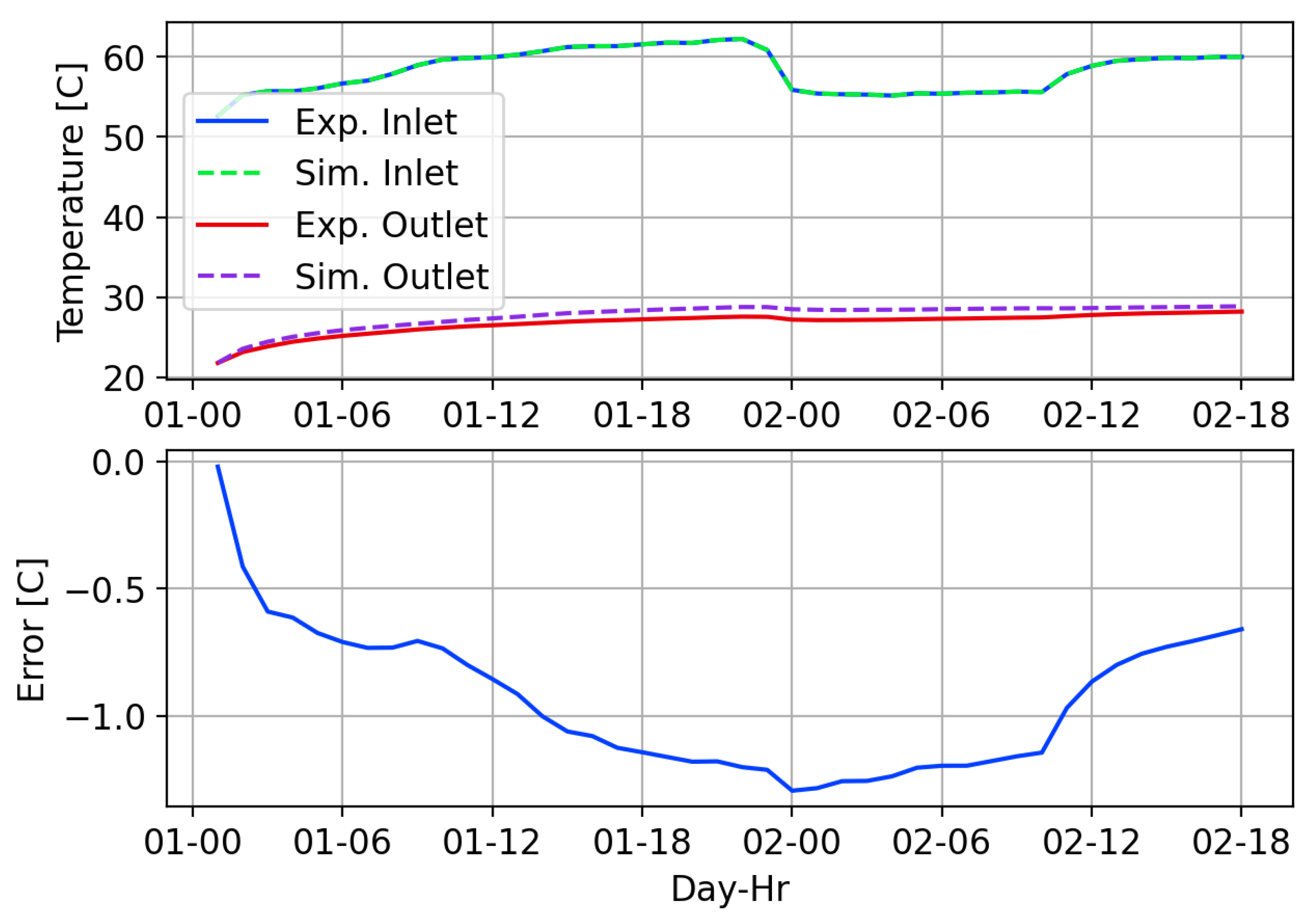
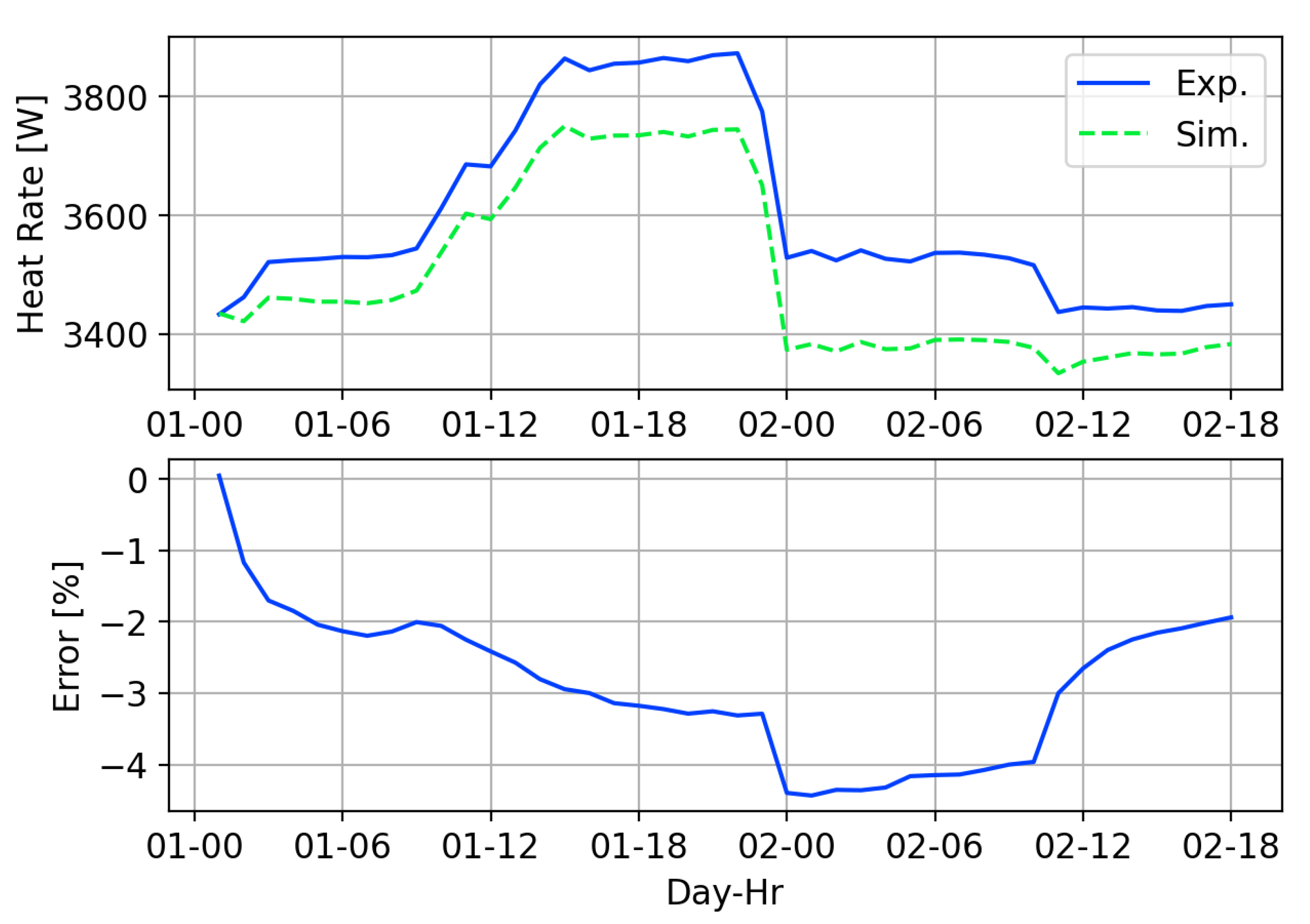
4. Validation
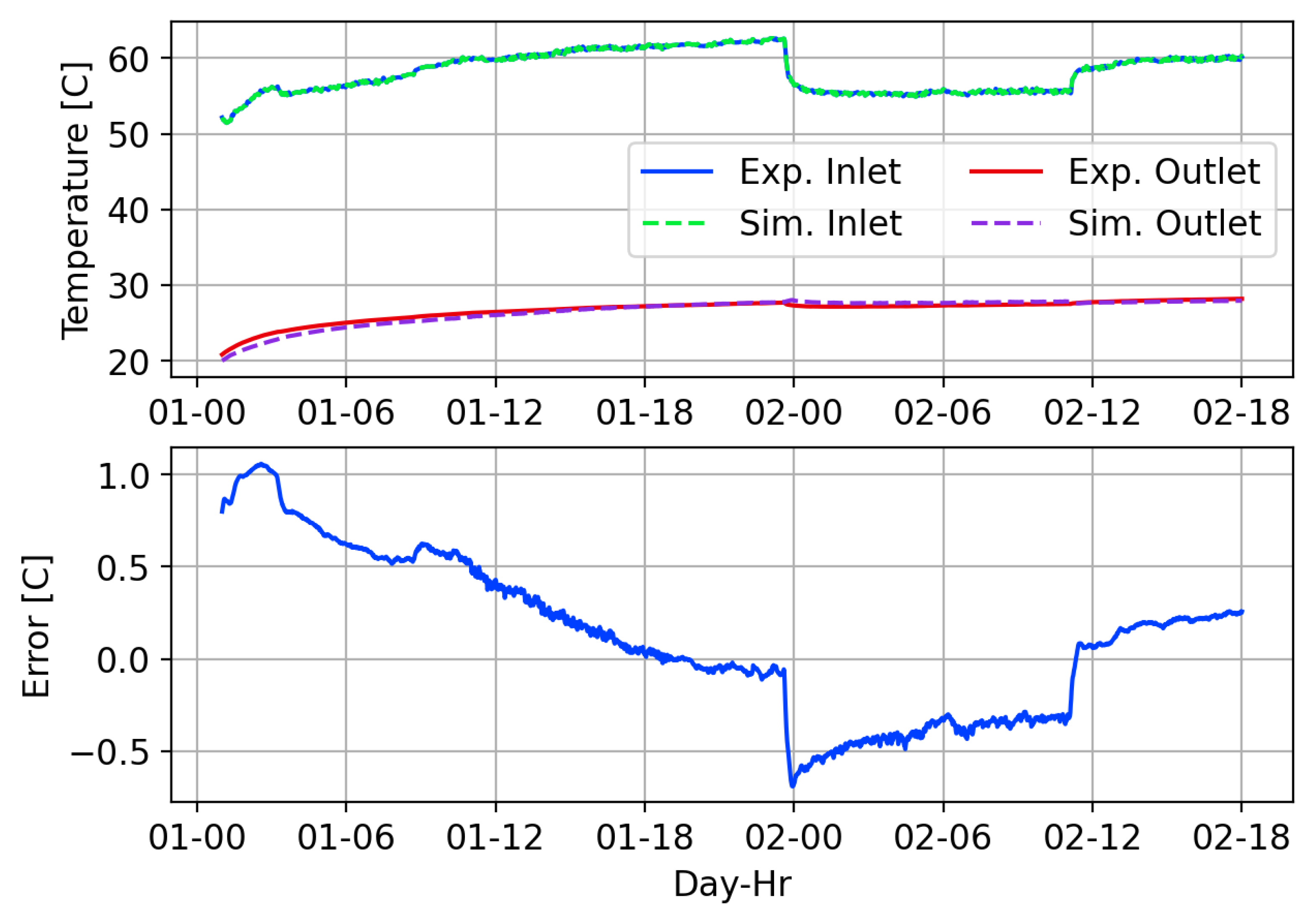
4.1. High-Flow MFRTRT
4.2. Low-Flow MFRTRT
5. Conclusions
- The pipe model currently used does not account for laminar flow; therefore, the pipe model should be enhanced to accurately account for these conditions.
- Any dynamic borehole model could be used to generate ExFT g-functions; therefore, a study should be performed to assess this model along with other existing models for accuracy and performance.
- The methods described here could also be used to model double U-tube or coaxial ground heat exchangers. Dynamic borehole models for these configurations would be needed in order to calculate the ExFT g-functions.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| ExFT | exiting fluid temperature |
| FLS | finite line source |
| GHE | ground heat exchanger |
| GSHP | ground-source heat pump |
| ICS | infinite cylinder source |
| ILS | infinite line source |
| MFRTRT | multi-flowrate thermal response test |
| TRC | thermal resistance-capacitance |
| TRT | thermal response test |
| WBES | whole-building energy simulation |
References
- Crawley, D.B.; Lawrie, L.K.; Winkelmann, F.C.; Buhl, W.F.; Huang, Y.J.; Pedersen, C.O.; Strand, R.K.; Liesen, R.J.; Fisher, D.E.; Witte, M.J.; et al. EnergyPlus: Creating a new-generation building energy simulation program. Energy Build. 2001, 33, 319–331. [Google Scholar] [CrossRef]
- Klein, S.A.; Beckman, W.A.; Mitchell, J.W.; Duffie, J.A.; Duffie, N.A.; Freeman, T.; Mitchell, J.C.; Braun, J.E.; Evans, B.L.; Kummer, J.P.; et al. TRNSYS Manual: A Transient Simulation Program; Solar Engineering Laboratory; University of Wisconsin-Madison: Madison, WI, USA, 2016. [Google Scholar]
- Li, M.; Zhu, K.; Fang, Z. Analytical methods for thermal analysis of vertical ground heat exchangers. In Advances in Ground-Source Heat Pump Systems; Woodhead Publishing: Duxford, UK, 2016; pp. 157–185. [Google Scholar]
- Spitler, J.D.; Bernier, M.A. Vertical borehole ground heat exchanger design methods. In Advances in Ground-Source Heat Pump Systems; Woodhead Publishing: Duxford, UK, 2016; pp. 29–61. [Google Scholar]
- Thomson, W. Compendium of the Fourier Mathematics for the Conduction of Heat in Solids, and the Mathematically Allied Physical Subjects of Diffusion of Fluids, and Transmission of Electrical Signals Through Submarine Cables. In Article 72. Mathematical and Physical Papers; University Press: Cambridge, UK, 1884; pp. 41–60. [Google Scholar]
- Spitler, J.D.; Gehlin, S.E.A. Thermal response testing for ground source heat pump systems—An historical review. Renew. Sustain. Energy Rev. 2015, 50, 1125–1137. [Google Scholar] [CrossRef]
- Carslaw, H.S.; Jaeger, J.C. Conduction of Heat in Solids, 2nd ed.; Clarendon Press: London, UK, 1959. [Google Scholar]
- Hellström, G. Ground Heat Storage: Thermal Analysis of Duct Storage Systems. Ph.D. Thesis, University of Lund, Lund, Sweden, 1991. [Google Scholar]
- Mogensen, P. Fluid to duct wall heat transfer in dust system heat storages. In International Conference on Subsurface Heat Storage in Theory and Practice; Swedish Council for Building Research: Stockholm, Sweden, 1983. [Google Scholar]
- Bernier, M.A. Ground-coupled heat pump system simulation. ASHRAE Trans. 2001, 107, 605–616. [Google Scholar]
- Ingersoll, L.R.; Zobel, O.J.; Ingersoll, A.C. Heat Conduction: With Engineering and Geological Applications, 2nd ed.; McGraw-Hill: New York, NY, USA, 1954. [Google Scholar]
- Diao, N.R.; Li, Q.Y.; Fang, Z. Heat transfer in ground heat exchangers with ground water advection. Int. J. Therm. Sci. 2004, 43, 1203–1211. [Google Scholar] [CrossRef]
- Man, Y.; Yang, H.; Diao, N.R.; Liu, J.; Fang, Z.H. A new model and analytical solutions for borehole and pile ground heat exchangers. Int. J. Heat Mass Transf. 2010, 53, 2593–2601. [Google Scholar] [CrossRef]
- Li, M.; Lai, L.C.K. Heat-source solutions to heat conduction in anisotropic media with applications to pile and borehole ground heat exchangers. Appl. Energy 2012, 96, 451–458. [Google Scholar] [CrossRef]
- Marcotte, D.; Pasquier, P. The effect of borehole inclination on fluid and ground temperature for GLHE systems. Geothermics 2009, 38, 392–398. [Google Scholar] [CrossRef]
- Lamarche, L.; Beauchamp, B. A new contribution to the finite line-source model for geothermal boreholes. Energy Build. 2007, 39, 188–198. [Google Scholar] [CrossRef]
- Javed, S.; Claesson, J. New analytical and numerical solutions for the short-term analysis of vertical ground heat exchangers. ASHRAE Trans. 2011, 117, 3–12. [Google Scholar]
- Grundmann, R.M. Improved Design Methods for Ground Heat Exchangers. Master’s Thesis, Oklahoma State University, Stillwater, OK, USA, 2016. [Google Scholar]
- Spitler, J.D. GLHEPro—A design tool for commercial building ground loop heat exchangers. In Proceedings of the 4th International Heat Pump in Cold Climates Conference, Alymer, QC, Canada, 17–18 August 2000. [Google Scholar]
- Duhamel, M.J.M.C. Sur les equations générales de la propagation de la chaleur dan les corps solides dont la conductiblité n’est pas la même dan tous les sens. J. L’Ecole Polytech. 1828, 21, 356–399. [Google Scholar]
- Özişik, M.N. Boundary Value Problems of Heat Conduction; Dover Publications: New York, NY, USA, 2002. [Google Scholar]
- Claesson, J.; Dunand, A. Heat Extraction from the Ground by Horizontal Pipes—A Mathematical Analysis; Technical Report; Swedish Council for Building Research: Stockholm, Sweden, 1983. [Google Scholar]
- Eskilson, P. Thermal Analysis of Heat Extraction Boreholes. Ph.D. Thesis, University of Lund, Lund, Sweden, 1987. [Google Scholar]
- Claesson, J.; Eskilson, P. Conductive heat extraction to a deep borehole—Thermal analysis and dimensioning rules. Energy 1988, 13, 509–527. [Google Scholar] [CrossRef]
- Eskilson, P.; Claesson, J. Simulation model for thermally interacting heat extraction boreholes. Numer. Heat Transf. 1988, 13, 149–165. [Google Scholar] [CrossRef]
- Mitchell, M.S.; Spitler, J.D. Characterization, testing, and optimization of load aggregation methods for ground heat exchanger response-factor models. Sci. Technol. Built Environ. 2019, 8, 1036–1051. [Google Scholar] [CrossRef]
- Brussieux, Y.; Bernier, M. Universal short time g*-functions: Generation and application. Sci. Technol. Built Environ. 2019, 8, 993–1006. [Google Scholar] [CrossRef]
- Loveridge, F.; Powrie, W. Temperature response functions (G-functions) for single pile heat exchangers. Energy 2013, 57, 554–564. [Google Scholar] [CrossRef]
- Alberdi-Pagola, M. Design and Performance of Energy Pile Foundations. Ph.D. Thesis, Aalborg University, Aalborg, Denmark, 2018. [Google Scholar]
- Alberdi-Pagola, M.; Jensen, R.L.; Poulsen, S.; Erbs, S. Method to Obtain G-Functions for Multiple Precast Quadratic Pile Heat Exchangers; Technical Report 243; Aalborg University: Aalborg Øst, Denmark, 2018. [Google Scholar]
- Dusseault, B.; Pasquier, P. Efficient g-function approximation with artificial neural networks for a varying number of boreholes on a regular or irregular layout. Sci. Technol. Built Environ. 2019, 8, 1023–1035. [Google Scholar] [CrossRef]
- Pasquier, P.; Zarrella, A.; Labib, R. Application of artificial neural networks to near-instant construction of short-term g-functions. Appl. Therm. Eng. 2018, 143, 910–921. [Google Scholar] [CrossRef]
- Pasquier, P.; Marcotte, D. Short-term simulation of ground heat exchanger with an improved TRCM. Renew. Energy 2012, 46, 92–99. [Google Scholar] [CrossRef]
- Pasquier, P.; Marcotte, D. Joint use of quasi-3D response model and spectral method to simulate borehole heat exchanger. Geothermics 2014, 51, 281–299. [Google Scholar] [CrossRef]
- Cimmino, M.; Bernier, M. A semi-analytical method to generate g-functions for geothermal bore fields. Int. J. Heat Mass Transf. 2014, 70, 641–650. [Google Scholar] [CrossRef]
- Malayappan, V.; Spitler, J.D. Limitation of using uniform heat flux assumptions in sizing vertical borehole heat exchanger fields. In Proceedings of the CLIMA 2013, Prague, Czech Republic, 16–19 June 2013. [Google Scholar]
- Marcotte, D.; Pasquier, P. Unit-response function for ground heat exchanger with parallel, series or mixed borehole arrangement. Renew. Energy 2014, 68, 14–24. [Google Scholar] [CrossRef]
- Claesson, J.; Javed, S. An analytical method to compute borehole fluid temperatures for timescales from minutes to decades. ASHRAE Trans. 2011, 117, 279–288. [Google Scholar]
- Cimmino, M. Fast calculation of the g-functions of geothermal borehole fields using similarities in the evaluation of the finite line source solution. J. Build. Perform. Simul. 2018, 11, 655–668. [Google Scholar] [CrossRef]
- Cimmino, M. g-Functions for bore fields with mixed parallel and series connections considering axial fluid temperature variations. In Proceedings of the IGSHPA Research Conference Proceedings, IGSHPA, Stockholm, Sweden, 18–19 September 2018; pp. 262–271. [Google Scholar]
- Cimmino, M. Semi-analytical method for g-function calculation of bore fields with series- and parallel-connected boreholes. Sci. Technol. Built Environ. 2019, 25, 1007–1022. [Google Scholar] [CrossRef]
- Cimmino, M. pygfunction: An open-source toolbox for the evaluation of thermal response factors for geothermal borehole fields. In Proceedings of the eSim 2018, the 10th Conference of IBPSA-Canada, International Building Performance Simulation Association, Montréal, QC, Canada, 9 March 2018; pp. 492–501. [Google Scholar] [CrossRef]
- De Carli, M.; Tonon, M.; Zarrella, A.; Zecchin, R. A computational capacity resistance model (CaRM) for vertical ground-coupled heat exchangers. Renew. Energy 2010, 35, 1537–1550. [Google Scholar] [CrossRef]
- Zarrella, A.; Scarpa, M.; De Carli, M. Short time step analysis of vertical ground-coupled heat exchangers: The approach of CaRM. Renew. Energy 2011, 36, 2357–2367. [Google Scholar] [CrossRef]
- Bauer, D.; Heidemann, W.; Müller-Steinhagen, H.; Diersch, H.J.G. Thermal resistance and capacity models for borehole heat exchangers. Int. J. Energy Res. 2011, 35, 312–320. [Google Scholar] [CrossRef]
- Ruiz-Calvo, F.; De Rosa, M.; Acuña, J.; Corberán, J.M.; Montagud, C. Experimental validation of a short-term borehole-to-ground (B2G) dynamic model. Appl. Energy 2015, 140, 210–223. [Google Scholar] [CrossRef]
- Cazorla-Marín, A.; Montagud, C.; Montero, Á.; Martos, J.; Corberán, J.M. Influence of different ground thermal properties in a borehole heat exchanger’s performance using the B2G dynamic model. In Proceedings of the IGSHPA Research Conference, IGSHPA, Denver, CO, USA, 14–16 March 2017; pp. 192–200. [Google Scholar]
- Ruiz-Calvo, F.; De Rosa, M.; Monzó, P.; Montagud, C.; Corberán, J.M. Coupling short-term (B2G model) and long-term (g-function) models for ground source heat exchanger simulation in TRNSYS. Application in a real installation. Appl. Therm. Eng. 2016, 102, 720–732. [Google Scholar] [CrossRef]
- Al-Khoury, R. Spectral framework for geothermal borehole heat exchangers. Int. J. Numer. Methods Heat Fluid Flow 2010, 20, 773–793. [Google Scholar] [CrossRef]
- Shao, H.; Hein, P.; Sachse, A.; Kolditz, O. Geoenergy Modeling II: Shallow Geothermal Systems; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Al-Khoury, R.; Bonnier, P.G.; Brinkgreve, R.B.J. Efficient finite element formulation for geothermal heating systems–Part I: Steady state. Int. J. Numer. Methods Eng. 2005, 63, 988–1013. [Google Scholar] [CrossRef]
- Al-Khoury, R.; Bonnier, P.G. Efficient finite element formulation for geothermal heating systems–Part II: Transient. Int. J. Numer. Methods Eng. 2006, 67, 725–745. [Google Scholar] [CrossRef]
- He, M.; Rees, S.; Shao, L. Simulation of a domestic ground source heat pump system using a three-dimensional numerical borehole heat exchanger model. J. Build. Perform. Simul. 2011, 4, 141–155. [Google Scholar] [CrossRef]
- Nabi, M.; Al-Khoury, R. An efficient finite volume model for shallow geothermal systems–Part I: Model formulation. Comput. Geosci. 2012, 49, 290–296. [Google Scholar] [CrossRef]
- Nabi, M.; Al-Khoury, R. An efficient finite volume model for shallow geothermal systems–Part II: Verification, validation and grid convergence. Comput. Geosci. 2012, 49, 297–307. [Google Scholar] [CrossRef]
- Fisher, D.E.; Rees, S.J.; Padhmanabhan, S.K.; Murugappan, A. Implementation and validation of ground-source heat pump system models in an integrated building and system simulation environment. HVAC&R Res. 2006, 12, 693–710. [Google Scholar] [CrossRef]
- Yavuzturk, C.; Spitler, J.D. A short time step response factor model for vertical ground loop heat exchangers. ASHRAE Trans. 1999, 105, 475–485. [Google Scholar]
- Xu, X.; Spitler, J.D. Modeling of vertical ground loop heat exchangers with variable convective resistance and thermal mass of the fluid. In Proceedings of the 10th International Conference on Thermal Energy Storage-EcoStock, Pomona, NJ, USA, 31 May–2 June 2006. [Google Scholar]
- Mitchell, M.S. An Enhanced Vertical Ground Heat Exchanger Model for Whole Building Energy Simulation. Ph.D. Thesis, Oklahoma State University, Stillwater, OK, USA, 2019. [Google Scholar]
- Loveridge, F. The Thermal Performance of Foundation Piles Used as Heat Exchangers in Ground Energy Systems. Ph.D. Thesis, University of Southampton, Southampton, UK, 2012. [Google Scholar]
- Bennet, J.; Claesson, J.; Helström, G. Multipole Method to Compute the Conductive Heat Flow to and between Pipes in a Composite Cylinder; Technical Report; University of Lund, Department of Building and Mathematical Physics: Lund, Sweden, 1987. [Google Scholar]
- Claesson, J. Multipole Method to Calculate Borehole Thermal Resistances: Mathematical Report; Technical Report 2012-06-20; Chalmers Technical University: Gothenburg, Sweden, 2011. [Google Scholar]
- Claesson, J.; Hellström, G. Multipole method to calculate borehole thermal resistances in a borehole heat exchanger. HVAC&R Res. 2011, 17, 895–911. [Google Scholar] [CrossRef]
- Javed, S.; Spitler, J.D. Accuracy of borehole thermal resistance calculation methods for grouted single u-tube ground heat exchangers. Appl. Energy 2017, 187, 790–806. [Google Scholar] [CrossRef]
- Javed, S.; Spitler, J.D. Chapter Calculation of Borehole Thermal Resistance. In Advances in Ground-Source Heat Pump Systems; Woodhead Publishing: Duxford, UK, 2016; pp. 63–95. [Google Scholar]
- Moin, P. Fundamentals of Engineering Numerical Analysis; Cambridge University Press: New York, NY, USA, 2010. [Google Scholar]
- Bischoff, K.B.; Levenspiel, O. Fluid dispersion—generalization and comparison of mathematical models—II comparison of models. Chem. Eng. Sci. 1962, 17, 257–264. [Google Scholar] [CrossRef]
- Skoglund, T.; Dejmek, P. A dynamic object-oriented model for efficient simulation of fluid dispersion in turbulent flow with varying fluid properties. Chem. Eng. Sci. 2007, 62, 2168–2178. [Google Scholar] [CrossRef]
- Rees, S.J. An extended two-dimensional borehole heat exchanger model for simulation of short and medium timescale thermal response. Renew. Energy 2015, 83, 518–526. [Google Scholar] [CrossRef]
- Beier, R.A.; Mitchell, M.S.; Spitler, J.D.; Javed, S. Validation of borehole heat exchanger models against multi-flow rate thermal response tests. Geothermics 2018, 71, 55–68. [Google Scholar] [CrossRef]
- Woodruff, M.J.; Herman, J. Pareto. 2018. Available online: https://github.com/matthewjwoodruff/pareto.py (accessed on 1 October 2018).
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Bell, I.H.; Wronski, J.; Quoilin, S.; Lemort, V. Pure and pseudo-pure fluid thermophysical property evaluation and the open-source thermophysical property library CoolProp. Ind. Eng. Chem. Res. 2014, 53, 2498–2508. [Google Scholar] [CrossRef] [PubMed]
- Patankar, S.V. Computation of Conduction and Duct Flow Heat Transfer; Innovative Research, Inc.: Maple Grove, MN, USA, 1991. [Google Scholar]
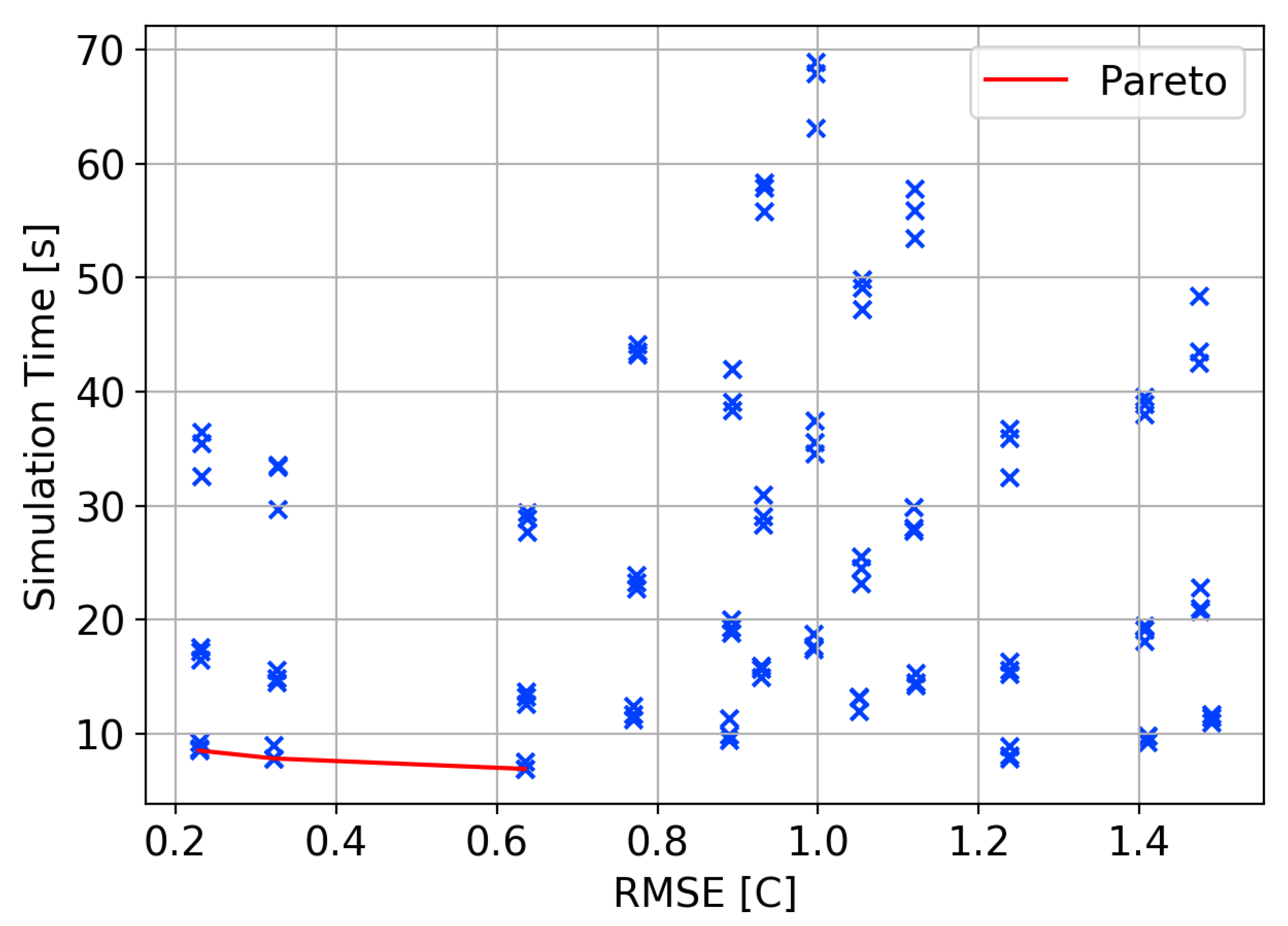





| RMSE [C] | MBE [C] | Time [s] | ||||
|---|---|---|---|---|---|---|
| 3 | 1 | 60 | 0.75 | 0.229 | −0.073 | 8.5 |
| 2 | 1 | 60 | 0.5 | 0.322 | −0.169 | 7.8 |
| 1 | 1 | 60 | 0.5 | 0.634 | −0.448 | 6.9 |
| Re | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| kg/s | - | - | - | °C | °C | (W/m) | °C/(W/m) | °C | °C |
| 0.02 | 1400 | −8.8 | 0.67 | 18.80 | 17.34 | 9.989 | 0.216 | 1.45 | 2.16 |
| 0.03 | 1967 | −8.8 | 0.71 | 18.89 | 17.35 | 9.991 | 0.217 | 1.55 | 2.16 |
| 0.04 | 2534 | −8.8 | 0.74 | 18.92 | 17.35 | 9.993 | 0.211 | 1.57 | 2.11 |
| 0.05 | 3079 | −8.8 | 0.75 | 18.62 | 17.35 | 9.994 | 0.169 | 1.27 | 1.69 |
| 0.1 | 5894 | −8.8 | 0.81 | 18.62 | 17.36 | 9.996 | 0.154 | 1.26 | 1.54 |
| 0.3 | 17,209 | −8.8 | 0.91 | 18.73 | 17.36 | 9.996 | 0.151 | 1.37 | 1.51 |
| 0.5 | 28,535 | −8.8 | 0.94 | 18.76 | 17.36 | 9.994 | 0.150 | 1.40 | 1.50 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mitchell, M.S.; Spitler, J.D. An Enhanced Vertical Ground Heat Exchanger Model for Whole-Building Energy Simulation. Energies 2020, 13, 4058. https://doi.org/10.3390/en13164058
Mitchell MS, Spitler JD. An Enhanced Vertical Ground Heat Exchanger Model for Whole-Building Energy Simulation. Energies. 2020; 13(16):4058. https://doi.org/10.3390/en13164058
Chicago/Turabian StyleMitchell, Matt S., and Jeffrey D. Spitler. 2020. "An Enhanced Vertical Ground Heat Exchanger Model for Whole-Building Energy Simulation" Energies 13, no. 16: 4058. https://doi.org/10.3390/en13164058
APA StyleMitchell, M. S., & Spitler, J. D. (2020). An Enhanced Vertical Ground Heat Exchanger Model for Whole-Building Energy Simulation. Energies, 13(16), 4058. https://doi.org/10.3390/en13164058





