Abstract
Mechatronic systems are a class of cyber-physical systems, whose increasing complexity makes their validation and verification more and more difficult, while their requirements become more challenging. This paper introduces a development method based on model-based design, co-simulation and formal verification. The objective of this paper is to show the applicability of the method in an industrial setting. An application case study comes from the field of precision servo-motors, where formal verification has been used to find acceptable intervals of values for design parameters of the motor controller, which have been further explored using co-simulation to find optimal values. The reported results show that the method has been applied successfully to the case study, augmenting the current model-driven development processes by formal verification of stability, formal identification of acceptable parameter ranges, and automatic design-space exploration.
1. Introduction
Mechatronic [1] (and, more generally, cyber-physical) systems are constantly growing in complexity and widening their fields of application, and require higher and higher levels of dependability and performance. Accordingly, system validation by simulation and testing should be complemented with rigorous analysis and verification methods, leading to a formal-verification-in-the-loop [2] development process.
This concept is the basis of the development process presented in this work. The process assumes a high-level specification, typically in natural language or some semi-formal language, from which a set of submodels is derived. The submodels may represent different structural parts (e.g., power plant and gear train of a vehicle) or different aspects (e.g., electromagnetic and mechanical physics of a motor) of the system. Each submodel can be developed by different domain experts, who use modeling languages and tools fit for each domain. Co-simulation (as opposed to traditional, monolithic simulation) is the co-ordinated simulation of heterogeneous submodels that have been developed independently.
Modeling languages are usually oriented to simulation. They may be based on different conceptual frameworks, such as e.g., signal flows for Simulink and equations for Modelica and their supporting environments provide a simulator. However, their support for verification is limited, if any. In the proposed development process, also verifiable models are built. A model is verifiable if it is written in a language oriented to verification and implemented in an environment providing tools for automatic or semiautomatic verification. In this work, we propose to use an abstract mathematical specification as the base of both the simulation-oriented and the verifiable model.
Not all submodels need be formally verified since many aspects of a system are well known and can be designed with well-proven and reliable techniques. Formal verification is needed for the more innovative components or aspects of a system, in particular for control systems. In this case, co-simulation is particularly convenient.
In this work, we present an application of formal verification, co-simulation and design-space exploration (DSE), to a case study of practical interest, a servo drive for permanent magnet synchronous motors. Servo drives are cyber-physical (more specifically, mechatronic) systems since they combine physical and algorithmic components. This case study has been chosen because servo drives are systems of particular interest as they are applied in all fields of industrial automation, industrial robotics, and automotive applications. However, the contribution of this work is not a new control algorithm for brushless motors, but rather to propose a control algorithm verification procedure in the context of mechatronic systems. The algorithm used in this case study had been previously designed by two of the authors [3] and validated with the classic software-in-the-loop (SIL) procedure.
This paper aims at showing how formal verification and co-simulation can be introduced in the design process to achieve more confidence in the system’s compliance with requirements and to assist the designer in choices that would otherwise be based on rules of thumb and trial-and-error procedures. Particular attention is paid to the tuning of parameters of the control algorithm, whose values, in a classic SIL approach, can be chosen only by making many simulations. In the approach exposed in this paper, formal methods are used to define acceptable ranges for those values, and co-simulation-based DSE is used to explore systematically the parameter space.
In the rest of this section a small collection of references to the vast literature on mechatronic [1,4,5,6] systems development is presented, grouped by their relevance to the main themes of this work, i.e., modeling and simulation, co-simulation, and formal approaches.
Concerning modeling and simulation, system models are typically built with block-based languages, which describe a system as an assembly of functional blocks, each representing a possibly complex mathematical operation, and interconnected by data flows. The blocks have a visual representation, but their semantics is defined in an underlying textual language. The models are then simulated by running test scenarios and successful runs reinforce confidence on the correctness of the design. However, exhaustive testing is not possible and high reliability of the system requires a high level of testing coverage.
The MATLAB/Simulink suite [7,8] is a prime example of an environment supporting block-based modeling. Among its large number of application-oriented toolboxes, the Stateflow toolbox, based on a state machine formalism, can be used to model hybrid systems, which are characterized by having a finite number of distinct modes of operation, and in each mode the system evolves according to time-continuous laws.
Several papers may be cited from the literature on simulation of mechatronic systems published in recent years. Dell’Amico and Krus [9] use monolithic simulation and hardware-in-the-loop (HIL) simulation to design an electrohydraulic power steering system. In the HIL simulation, both the controller and the vehicle-tire model are in software while the mechanical and hydraulic parts are assembled in a test rig comprising the steering wheel, the rack and pinion, pump and valves, and associated sensors and actuators.
An interface between Simulink and the finite elements toolkit Abaqus is presented by Orszulik and Gabbert [10], oriented to the simulation of smart structures, i.e., solid bodies whose shape can be modified through a control stimulus, such as, e.g., an electric field. As a case study, an aluminum beam controlled by piezoelectric sensors and actuators is simulated with Abaqus, while the controller is simulated in Simulink, in order to study the vibrational behavior.
Isermann et al. [11] discuss the role of HIL simulation in the development of engine-control systems and report on the simulation of a Diesel engine interacting with real injection pumps and real control units for engines and pumps.
Concerning co-simulation, an extensive survey has been recently published by Gomes et al. [12], providing definitions of the fundamental concepts and the taxonomy of the literature based on the computational model adopted in the various works: discrete events, continuous time and hybrid, i.e., a mix of the two.
Co-simulation of multibody dynamic systems in ADAMS [13] and controllers in Simulink are used by Hadas et al. [14] to analyze various types of industrial robots.
Use of the SysML language [15] is discussed in a paper by Sadovykh et al. [16], where a SysML model defines the high-level architecture of a heating, ventilation, and air conditioning system composed of various physical subsystems modeled in 20-sim and a controller modeled in VDM. The latter has a digital (event-driven) component that reacts to user inputs and temperature changes by switching between modes of operation (heating or cooling), and a continuous-time component that in each mode controls the temperature with a PID algorithm.
Foldager et al. [17] present a case study on the development of a driverless lawn mower, describing the interplay between experiment and simulation to study physical parameters, design parameters, and operating conditions. First, two physical parameters have been determined by experiment, then co-simulation has been used to choose an optimal value for a design parameter of the controller, which has been validated by field testing. Finally, co-simulation has been used again to assess system behavior for different speeds. The plant has been simulated in 20-sim and the controller in VDM.
From the literature of formal approaches, we may cite Giese et al. [18], who develop a formal extension to UML Statecharts and components enabling developers to model cyber-physical systems as hybrid automata [19] and supporting the modular composition of subsystems.
Model checking with UPPAAL is used by Lindahl et al. [20] to verify a gearbox controller, modeled as a network of timed automata, against requirements of different kinds, including performance and time bounds.
Cimatti et al. [21] developed HyComp, an SMT-based tool for the verification of networks of hybrid automata. The tool can also synthesize design parameters [22].
The KeYmaera X interactive theorem prover is introduced by Fulton et al. [23]. In this environment, continuous-time behaviors are expressed in the language of differential dynamic logic [24].
Another theorem proving environment is the Prototype Verification System which, differently from KeYmaera, uses a general-purpose higher-order logic [25]. This environment has been used in many application fields such as medical [26,27] and control systems [28,29], and it will be described more extensively in Section 2.1.
Other interesting works, which exploit formal methods for verification, are listed below. In [30], the authors propose a review of the state of the art in the field of automotive cyber-security, evaluating the best combinations of on-board HW simulation methods and formal verification methods to cover special cases. In [31], the authors present a strategy to control the power distribution system to minimize electricity bills and meeting the comfort constraints of users. They use the UPPAAL environment for modeling and verification by model checking.
This work is organized as follows: Section 2 provides background information on the theorem proving and co-simulation; Section 3 introduces the methodology presented in this paper; Section 4 reports the design of a controller for brushless motors as a case study, and the application of formal verification, Section 5 contains co-simulation, and DSE results, and Section 6 concludes the paper.
2. Background on PVS and Co-Simulation
This section introduces the two main techniques underpinning the proposed process: using higher-order logic for verification and using co-simulation for validation and design-space exploration. Verification is supported by the Prototype Verification System (PVS) [25] and co-simulation by the INTO-CPS framework [32].
2.1. The PVS Environment
The PVS is an interactive theorem prover environment based on a typed higher-order logic language and a sequent calculus deduction system [33], provided with a rich, extendable type system.
A PVS theory is a collection of definitions and formulae between a ‘name THEORY BEGIN’ and an ‘END name’ statement. A user can define types, constants, variables, and functions. A formula is a named logical statement, and it may be either an axiom (declared as such with the AXIOM keyword) or a theorem (declared with such keywords as THEOREM, LEMMA, etc.). Axioms are taken as proved, while theorems are proved using a large set of prover commands based on the sequent calculus. The PVS language has arithmetic and logic types, and structured types, including record types and predicate subtypes. For example, the specification of a particular motor may include the definition of physical magnitudes, possibly with the acceptable ranges of values:
electric_motor_th: THEORY
BEGIN
Resistance: TYPE =
{x: nonneg_real | 1.5 <= x and x <= 3.5}
Inductance: TYPE = nnreal
Flux: TYPE = nnreal
Current: TYPE = nnreal
...
electric_motor: TYPE = [#
stator_resistance: Resistance,
inductance :Inductance,
pole_pairs: nat,
flux_intensity: Flux #]
The above definitions declare that a current is a magnitude with non-negative real (nnreal) values, that a resistance takes non-negative values in the range , and so on. Type Resistance is an example of a predicate subtype, defined by adding a constraint to its supertype. The concept of electrical motor can then be modeled as a record type containing the parameters of a generic motor. A particular motor is then modeled as an instance of type electric_motor, specifying the values of its parameters:
acmePN123: electric_motor =
(# stator_resistance := 3.1, inductance := 0.5, pole_pairs := 4,
flux_intensity := 0.85 #)
The theory introduces relationships among physical magnitudes, e.g.,
power(R: Resistance, i1, i2, i3: Current): real =
R*((i1*i1) + (i2*i2) + (i3*i3))
Finally, system properties are expressed as theorems to be verified, e.g.,
power_positive: THEOREM
FORALL (R: Resistance, i1, i2, i3: Current):
power(R, i1, i2, i3) >= 0
END electric_motor_th
The PVS syntax language uses logical connectives and quantifiers, the IF ... ENDIF clause and the COND ... ENDCOND clause, which is composed of pairs and translates to a set of conditional clauses.
Any theory can use other theories by importing them. The specification of complex systems can be built incrementally importing theories defining subsystems into the theory of the overall system.
The proof for the simple power_positive theorem in the theory above is shown below:
power_positive :
|-------
{1} FORALL (R: Resistance, i1, i2, i3: Current): Power(R, i1, i2, i3) >= 0
Rule? (grind)
Power rewrites Power(R, i1, i2, i3)
to R*i1*i1 + R*i2*i2 + R*i3*i3
Trying repeated Skolemization, instantiation, and~if-lifting,
Q.E.D.
The theorem is proved with the single PVS grind command, which automatically applies simplifications, using type information. More realistic theorems are proved with longer sequences of commands.
2.2. Co-Simulation
Co-simulation is the simulation of a complex system by the co-ordinated simulation of its subsystems, each executed in a specific environment. This makes it possible to model each subsystem independently, using the preferred modeling language and simulator.
The Functional Mockup Interface (FMI) [34] is the standard for co-simulation adopted in this work. In this standard, each submodel is packaged in a Functional Mockup Unit (FMU) containing the submodel itself (e.g., in Simulink) and possibly the respective simulator, together with any resource required for simulation. The FMUs communicate with a co-simulation orchestration engine that synchronizes the FMUs and dispatches data among them.
In this work, co-simulation was supported by the INTO-CPS toolchain, developed by the INTO-CPS project [32]. With this toolchain it is possible to co-simulate models formalized in different languages, such as Modelica, MATLAB, VDM, and PVS. The user interface (the INTO-CPS Application) of the toolchain allows developers to design a co-simulation by assembling different FMUs and configuring how simulations are executed.
Figure 1 shows the standard architecture of an FMI co-simulation.
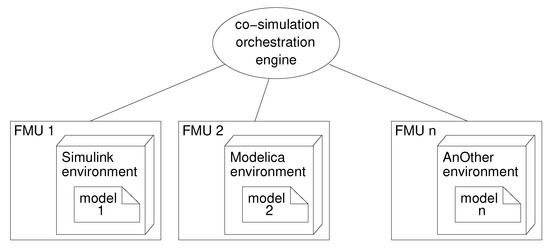
Figure 1.
FMI co-simulation architecture.
The INTO-CPS toolchain also provides DSE, which allows parametric robustness analyzes to be performed in a systematic way. This feature enables designers to specify the desired sets of parameter values, the objective functions, and the ranking criterion. The INTO-CPS application executes the co-simulations, collects the results, computes the objective functions for each tuple of parameter values, and ranks the tuples according to the specified criterion.
3. A Development Process Integrating Verification and Co-Simulation
In the development of complex, possibly safety-critical applications, it is desirable to exploit both simulation and formal verification. In this section, we present a development process that integrates co-simulation and verification by computer-assisted theorem proving. This section is the core of this paper’s contribution, as it defines the structure of the development process in its general form. An example of its application is shown in the next section, where the design of a control algorithm for a brushless motor is taken as a case study. Readers interested in the details and performance of the algorithm are referred to [3].
The process, represented in Figure 2, is based on three models of a mechatronic system (rectangular boxes), which are the inputs to the process activities (ovals). The models are the mathematical, logic, and simulation model. The latter two models are the starting points of two activity flows, simulation and verification.
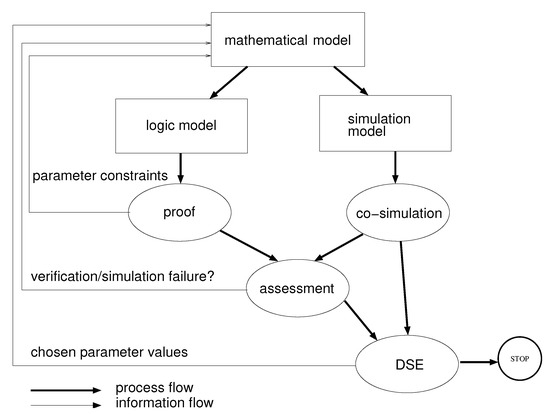
Figure 2.
Integrated workflow.
The mathematical model is a mathematical specification of the system, from which the two other models are derived. This model is composed of three parts: (i) the definition of the plant dynamics, (ii) the control algorithm, and (iii) the system requirements. Each part, in turn. may be decomposed into submodels, reflecting the system’s structure.
The simulation model is an executable specification of the plant dynamics and the control algorithm. This specification is usually built as a monolithic model using a block-based language such as Simulink, but co-simulation affords the convenience of using different languages for different submodels. This is particularly useful when a model is already available for one subsystem (e.g., the plant) and a model for another subsystem (e.g., the controller) is to be created anew.
The logic model is a translation of the mathematical model into a language suitable for verification. In the present work, the logic model has been expressed in the PVS higher-order logic language. In this language, a logic model can be structured into a set of theories, each corresponding to a different submodel of the mathematical model. The mathematical models of plant and control algorithm are translated directly into PVS axioms and definitions, while requirements become theorems to be proved against the theory.
The simulation flow uses the executable models of the plant and control parts to collect experimental results from the co-simulation activity. At this stage of development, the control part design is software design, so that its executable model is conveniently built with a software specification language, or directly in the implementation language, whereas the plant is built with physical modeling languages. Co-simulation is chosen as the simulation method to cater for the different formalisms.
The verification flow uses the logic model to prove if the requirements are satisfied. The proof activity takes place as interactive theorem proving, as anticipated in Section 2.1: The theorem prover displays the goal, i.e., the statement to be proved, and the user issues commands that simplify the goal or decompose it into subgoals. This is repeated until the initial goal is reduced to a set of subgoals simple enough to be proved automatically by the theorem prover, or else until no command can simplify some subgoal, in which case the theorem is not verified. The proof activity then results in a verdict of verified or not verified for each theorem. As a byproduct, verification may lead to the definition of constraints on design parameters, which are fed back to the mathematical model and propagated to the simulation and verification flows, as shown in Figure 2.
The two workflows merge into the assessment activity, which consists of taking action in response to the results of proof and co-simulation. In case of negative results of either proof or simulation, the logic and simulation models are reviewed and compared with each other. Comparing logic and simulation models is useful since the two models, albeit derived from the same mathematical specification, are built on different conceptual frameworks, and either one can shed light on the other one’s issues. The two models are then compared with the mathematical model, to ensure that it has been correctly translated. In the following, we assume that the three models are coherent. As a result of the assessment activity, the mathematical model is updated and the updates are propagated to the two parallel flows.
In the case of negative simulation results, tests can be designed to isolate the parts of the specifications where problems lie, and the mathematical model can be changed accordingly.
Negative verification verdicts are caused by inconsistencies in the logical specification, such as false, incomplete, or contradictory assumptions or requirements. There is no mechanical procedure to pinpoint such inconsistencies, but the interactive theorem proving process usually guides the developer in the search for inconsistencies. Typically, a failed proof gets stuck in the attempt to prove a faulty statement, whose analysis reveals a conceptual problem in the specification.
Depending on the project context, different parts of the specification can be changed. If the requirements and plant are fixed, clearly only the control part can be acted upon. Otherwise, modifications of the plant or even the requirements can be considered. For example, components with different characteristics can be chosen, or performance requirements can be loosened.
The above cycle is iterated as necessary until the results are satisfactory. In this case, the design-space exploration activity starts. DSE consists of trying out different combinations of design parameters to find those that maximize certain figures of merit or minimize certain costs. In the approach proposed in this work, the design space is made of the intervals of parameter values that have been formally and experimentally shown to satisfy the requirements.
The design parameter values chosen by DSE are used to produce the final version of all the models, ready for further stages of development, such as HIL simulation and implementation.
Many variations to the above schema are possible. In particular, a logic specification can be both verifiable and executable, and then used both for verification and simulation. Another variation is the side by side deployment of verification tools and automated mathematical tools, as shown in the following sections.
Furthermore, it may be remarked that the software-based process introduced in this paper can be included in a complete process, where a HIL phase is used to validate the simulations.
4. Design of a Controller to Reduce Cogging Torque in Brushless Motors
This section describes the application of the proposed process to the design of a control algorithm for a precision servo-motor. The control algorithm is designed to reduce the cogging effect, an adverse phenomenon causing mechanical oscillations, in a large brushless motor [3].
This case study is meant to show how the integration of co-simulation, formal verification, and design-space exploration tools can provide additional contributions to the analysis of control algorithms with respect to development processes relying only on (monolithic) simulation.

Table 1.
Parameters.

Table 2.
Variables.
4.1. Mathematical Model
The mathematical model is composed of the control and the motor model. The latter, as explained in [3,35], includes a model of the cogging effect, together with the nominal physical behavior of the motor.
The electromagnetic component of the motor model is given by the equations for the counter-electromotive force (Equation (1)) and applied voltage (Equation (2)) on each winding (a, b, c).
The resulting useful electromagnetic torque is
Cogging is caused by the magnetic interaction between the permanent magnets arranged on the surface of the rotor and the teeth of the stator cavities, as shown in Figure 3. This interaction results in an alternating mechanical torque with zero mean value that is added to the electromagnetic one, causing a vibration of the rotor axis. As described in [3,35], the value of the cogging torque can be approximated with a truncated Fourier series (Equation (4)).
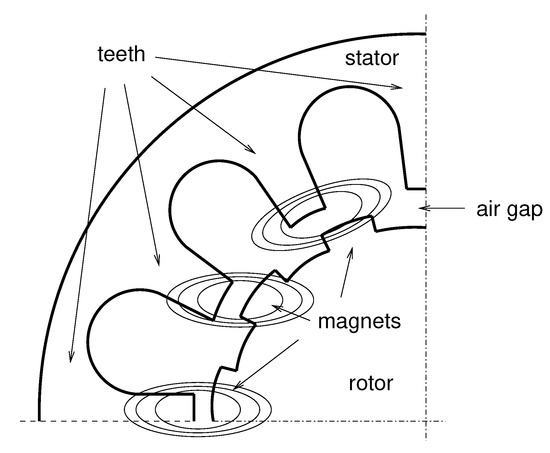
Figure 3.
Schematic representation of the magnetic interaction between stator and rotor.
The mechanical component of the motor model is then given by Equations (5):
The controller has been designed with a Feedback Linearization Control (FLC) technique [36]. For simplicity, the electromagnetic laws are expressed in terms of d-q phasors [37] and the law describing the cogging torque is truncated to its first harmonic. The controller’s inputs are the desired values of current and angular position , and the feedback values of current ( and ), angular position , and angular speed . Its characteristic parameters are the gains and , from which the intermediate control voltages and are computed according to Equation (6). The latter are fed to a compensation block that computes the controller outputs and (Figure 4).
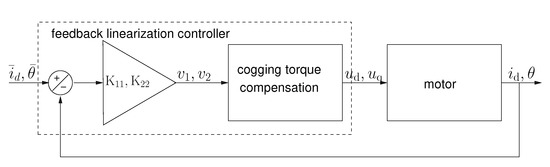
Figure 4.
Schematic representation of the control loop.
Equations (7) define the control voltages according to the resulting control law.
4.2. Simulation Model
This section shows the block diagrams of the motor and control simulation models.
As a first step, the motor model has been split into its electrical and mechanical parts (Figure 5) and modeled in Simulink. In the schema, (, , ) and (, , ) are the phasors of voltage and current, respectively, while and are the rotor’s position and speed, respectively.
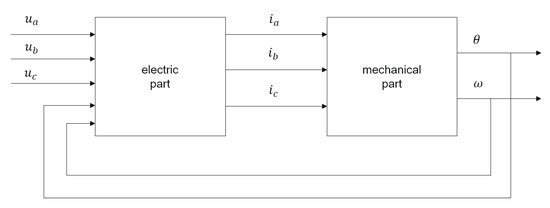
Figure 5.
Block Diagram Model of the Motor.
Figure 6 and Figure 7 show, respectively, the block diagrams for the electrical equilibrium of a single stator phase and the mechanical equilibrium of the motor.
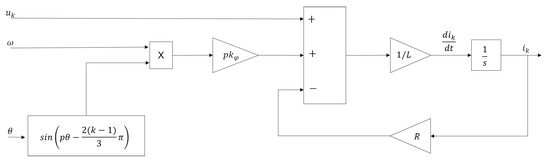
Figure 6.
Block diagram of the equation for the electromagnetic equilibrium of the k-th stator phase.
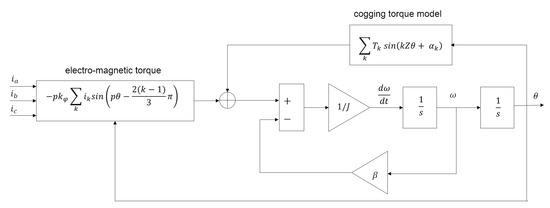
Figure 7.
Block diagram of the mechanical equilibrium.
The block diagram of the controller part is shown in Figure 8. The diagram includes the blocks for coordinate transformation from the three-phase to the two-phase frame. The FLC compensation and the feedback gain are computed by a Simulink M-function written in C.
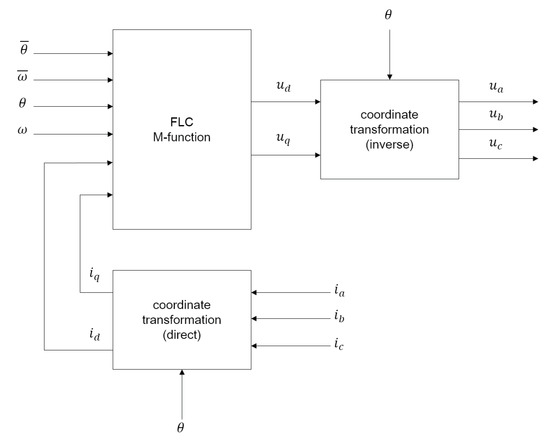
Figure 8.
Block diagram of the control law.
4.3. Logic Model
The logic model has been built to find acceptable ranges of values for the controller gains that ensure stability. To do so, a linearized mathematical model has been introduced [38]. In Equations (8), , , and are the voltage, current, and counter-electromotive force, respectively, expressed as pairs of d-q phasors, while and are the inductance and resistance matrices, respectively. From a well-known result of control theory, stability requires the eigenvalues of the system’s Jacobian to have non-positive real parts.
The eigenvalues of the Jacobian depend on the position and on the controller gains, and they have been computed symbolically with MATLAB, obtaining Equations (10), where and are auxiliary functions (Equations (9)) and are constants (Table 3).

Table 3.
Numerical coefficients.
We may notice that the real part of equals , therefore this parameter is ignored in the following discussion since any negative value is acceptable for stability.
Equations (10) were translated into the PVS language, together with the necessary definitions of variables, constants, and functions. For example, the following PVS fragment is the definition of :
re_lambda_3(K_22, theta: real): real =
Phi_1(theta)/cubicrt(K_22/2 + Phi_2(theta)
+ sqrt((K_22/2 + Phi_2(theta))^2 - Phi_1(theta)^3))
+ cubicrt(K_22/2 + Phi_2(theta)
+ sqrt((K_22/2 + Phi_2(theta))^2 - Phi_1(theta)^3)) - C_6
Auxiliary functions were introduced to rewrite (10) more compactly, for example:
a(K_22, theta: real): real = K_22/2 + Phi_2(theta)
X(K_22, theta: real): real =
cubicrt(a(K_22, theta) + sqrt(sq(a(K_22, theta)) - Phi_1(theta)^3))
re_lambda_3_rew(K_22, theta: real): real =
Phi_1(theta)/X(K_22, theta) + X(K_22, theta) - C_6
4.4. Verification
In this particular application, the verification activity might more properly be called a logic-based design since it is oriented to the synthesis of design parameters rather than the a posteriori requirements verification. The starting point; however, is the stability requirement, which constrains the eigenvectors to be non-positive. For example, the requirement for is
This inequality is first rewritten in terms of function re_lambda_3_rew above. First, this function is shown to be equivalent to the original definition of :
lem_1: LEMMA
FORALL (K_22, theta: real):
re_lambda_3_rew(K_22, theta) = re_lambda_3(K_22, theta)
Then it was shown that the inequality can be expressed with the quadratic function defined in the NASALIB library, considering the real part of as a quadratic function of X(k_22, theta)
quad3: LEMMA
FORALL (K_22, theta: real):
real_lam3(K_22, theta) <= 0
IFF quadratic(1, -C_6, Phi_1(theta))(X(K_22, theta)) <= 0
From this point on, relationships involving X(k_22, theta) are found, e.g.,
lem_3: LEMMA
FORALL (K_22, theta: real):
re_lambda_3_rew(K_22, theta) <= 0
IMPLIES X(K_22, theta) >= b_1_lam3(theta)
AND X(K_22, theta) <= b_2_lam3(theta)
where b_1_lam3(theta) and b_2_lam3 are the roots of the quadratic function. From such relationships, conditions on are derived.By proving several lemmas like the one above, it was shown that a given interval of values for guarantees asymptotic stability. This interval was computed numerically (namely ) since the actual physical characteristics of a specific motor were used.
In summary, the main points of the procedure for the design of the control algorithm was presented, starting from the mathematical model of electro-mechanical equilibrium. The mathematical model of the electric machine is derived from the unified theory of electrical machines [39] and additionally it includes the mathematical model of the cogging torque, a non-negligible source of non-linearity. The control algorithm has been designed to reduce the cogging effect, in addition to tracking the reference values of position and electric current. Moreover, combining control systems theory with formal verification, the choice of some parameters of the control algorithm was made as systematic as possible, instead of relying only on multiple simulations.
5. Co-Simulation and Design-Space Exploration
In this section, we report the results of co-simulation for trajectory tracking of the rotor position.
Three FMUs have been generated starting from a complex Simulink schema that implements the entire electric drive: the first related to the generator of the desired angular position of the rotor axis; the second related to the control laws obtained with the FLC technique described above; a third one incorporating the part of the process to be controlled, which includes the models of pulse width modulator (PWM), inverter, and synchronous motor. The plant and signal generator FMUs have been generated using the FMI export feature of Simulink, while the FLC controller and its FMU have been implemented in Misra C.
Figure 9 describes how the three FMUs are connected together. In particular, the co-simulation orchestration engine manages the communication between each FMU so that when all FMUs execute a simulation step the updated outputs are provided to the FMU that requires them as input. For example, the output values , , and of the plant FMU are connected to the input values , , and of the control FMU, so at the end of every simulation step the co-simulation orchestration engine forwards their updated values from the plant FMU to the control FMU.
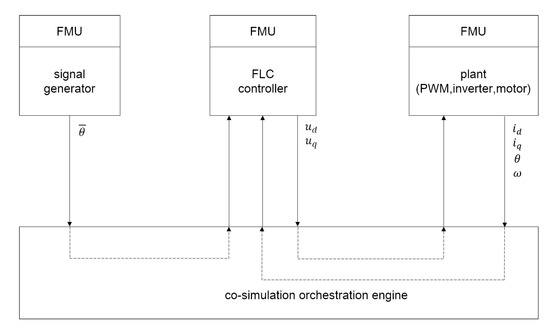
Figure 9.
Schematic representation of the FMU connections.
The chosen sampling time is 100 s. The choice is in accordance with the Nyquist sampling theorem. All the co-simulations performed in this work assume a fixed step size of 100 s and have a duration of 10 s.
In the simulations, the desired values of are sequences of rectangular pulses. The co-simulation results are shown as plots of the system response superimposed to the system positioning command . The figures are generated by the INTO-CPS interface. The ordinates are the values of and in radians and the abscissae represent time in seconds.
The line labeled Out1 in the legend represents and the line labeled Theta_m represents ; the label prefixes track.trackInstance and plant.plantInstance are the INTO-CPS names of the signal generator and plant FMUs, respectively.
Figure 10 shows the results of co-simulation for a value of outside the range identified in the proof activity. In this case, fails to reach three out of five desired values (, 10, and ).
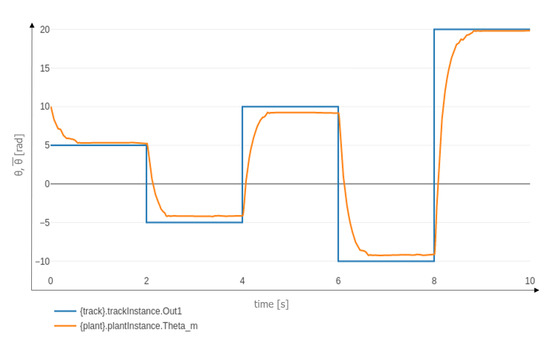
Figure 10.
Co-simulation for and .
As another example, Figure 11 shows the results of co-simulation when is further above the upper bound of the range identified by the proof activity. The value of does not follow the requested value and remains stuck near its initial value.
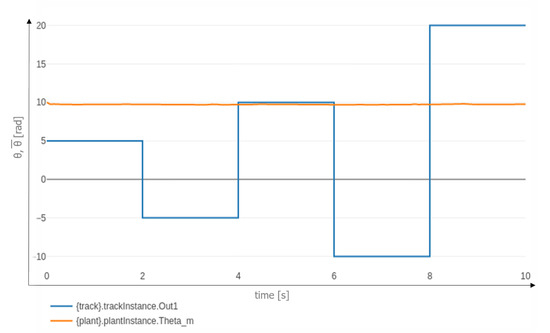
Figure 11.
Co-simulation for and .
Figure 12 shows the results of co-simulation when the value of is below the lower bound of the identified range. In this case, approaches with a damped oscillation.
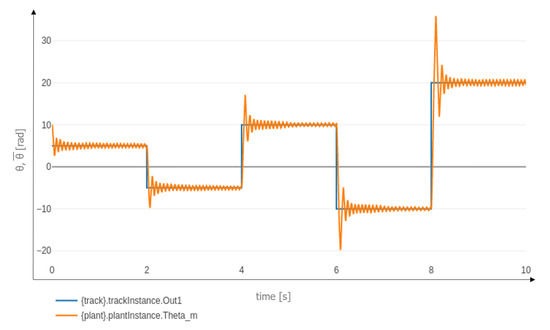
Figure 12.
Co-simulation for and .
Figure 13 shows that asymptotic stability is attained for a value of within the indicated range, as follows closely except in the transient phase where it shows an overshoot depending on the difference between and .
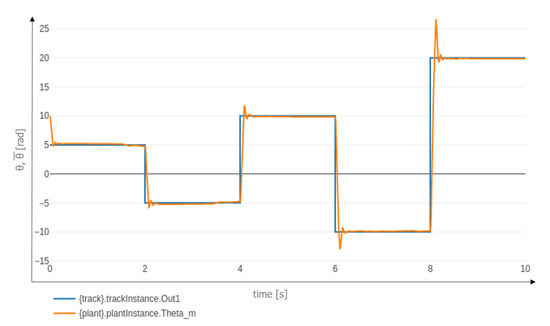
Figure 13.
Co-simulation for and .
On average, on an Intel Core i7-7700 CPU processor with 32 Gb of RAM, each co-simulation took 2 and half minutes to complete. It should be stressed that the FMI standard allows a black-box approach for co-simulation, in which each model can be expressed as a standalone FMU and different languages and tools can be easily combined together. The co-simulation presented in this section can, therefore, be easily expanded by replacing any FMU with a more refined one. Moreover, the standalone FMUs can be reused in other scenarios, reducing the time needed to assemble a new co-simulation.
5.1. Assessment
The verification work allowed the definition of sufficient conditions for system stability on the design parameters, and its assessment did not result in the need for changing the original mathematical model.
The assessment of the simulation resulted in the validation of verification results, as it showed that parameters values chosen within and outside the indicated ranges proved to be, respectively, satisfactory or unsatisfactory, as shown by the counterexamples in Figure 11 and Figure 12.
In a different scenario, the simulation activity reported in Section 5 can be seen as an example of design carried out by heuristic, or trial and error, methods. In this approach different vales of have been tried until acceptable values have been found.
5.2. Design-Space Exploration
The INTO-CPS DSE feature enables designers to specify the desired sets of parameter values to try, the objective functions, and the ranking criterion. The INTO-CPS application executes the co-simulations, collects the results, computes the objective functions for each tuple of parameter values, and ranks the tuples according to the specified criterion.
This section shows two applications of DSE, one to analyze design robustness with respect to variations of physical parameters and one to optimize design parameters.
In the first experiment, Figure 14 shows the behavior of for values of inductance L equal to the nominal value (50 mH) and to the values corresponding to the nominal value . The control gain is . The continuous line is the desired (Theta_des in the legend), and each dotted line represents for the three values of inductance. The results are qualitatively satisfactory since the differences among the curves are small. Clearly, a quantitative statement of the robustness requirements is needed for a definitive assessment.
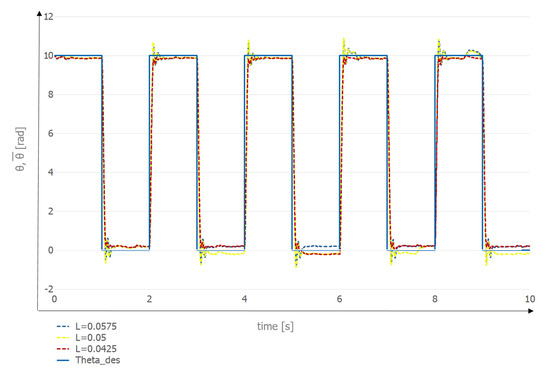
Figure 14.
Co-simulation runs for different values of inductance (in Henry).
In the second application, DSE was used to determine combinations of design parameter values that minimize the following objective functions:
- the absorbed power, :
- the mean square deviation of the tracking error on the angular position,
- the mean square deviation of the tracking error on the current’s direct component
In these equations, is the number of samples collected in a single co-simulation run, one for each co-simulation step. In Equation (12), the samples are the three-phase supply voltage () and the three-phase current vector (). In Equation (13), the samples are the values of the angular rotor position () and of its desired value (). In Equation (14), the samples are the values of current’s direct component () and of its desired value ().
The following combinations of parameters are used:
- has been fixed at because this variable has a low impact on the system behavior, as shown in a previous work [3].
- takes the values and in order to study the behavior with two values, one inside and one outside the interval found in Section 4.4.
- the angular position takes the values of 10, 20 and 30 radians.
- The inductance L takes the values , 50, and mH, i.e., the nominal value and small variations.
The Pareto front [40] method has been used to find the best parameter combinations to simultaneously minimize pairs of cost functions. The combinations are ranked so that lower rank values indicate better performance.
Since the goal of this DSE analysis is to minimize all pairs of the objective functions, in the plots shown in this section, lower rank points are closer to the origin of the axes (the green points are the closest ones). In the figures, adjacent rank groupings have different colors, points connected by a line have the same rank and the values of the angular position are reported in the figures as they are related to different clusters, shown by ovals.
Table 4 and Figure 15 show results for the power absorption of the machine () and the mean square deviation of the desired current tracking error (), respectively.

Table 4.
Pareto ranking for and .
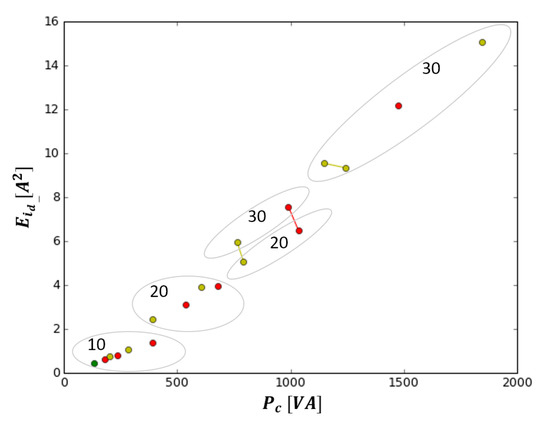
Figure 15.
Pareto front for and .
Increasing values of (the number in the oval) lead to higher values of mean square deviation and more power absorption, meaning that small movements are more controllable and need less power, as expected. Regarding the effects of and L for any fixed value of , the best performance is achieved for smaller values of L and larger values of . For any , the best combination of parameter is L , while the worst combination is L .
Table 5 and Figure 16 show the minimization of the power input () and the mean square deviation of angular position tracking error ().

Table 5.
Pareto ranking for and .
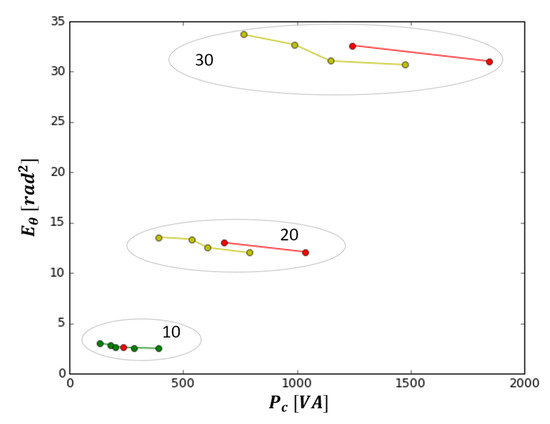
Figure 16.
Pareto front for and .
In Figure 16, changes of significantly affect the error of the tracking position, creating well separated clusters. For , the values of L and have little influence, whereas their influence increases for larger values of . The combination of parameters that minimizes the error on tracking position is L , while the combination that minimizes the power required is L . The worst cases of each cluster are correlated with a larger value of L (Table 5, rows 5 and 6 for ; rows 11 and 12 for ; rows 17 and 18 for ).
Table 6 and Figure 17 show results for the minimization of deviations both of angular position () and current (). In Figure 17, it is possible to notice that the three different values of lead to distinct clusters, well separated along the abscissae. Parameters L and affect more than . For every , the parameter combination that minimizes the error of the current is L . It is possible to identify the worst combination for all parameters which is L .

Table 6.
Pareto ranking for and .
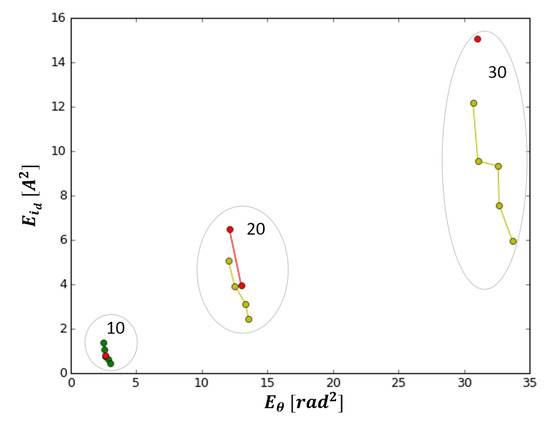
Figure 17.
Pareto front for and .
From the results of the analysis, it is possible to recognize some patterns, so as to identify recurring behaviors or some trends of the system under examination.
It is possible to notice that experiments with the lowest value of have better performance for each pair of objective functions. This result is expected, as higher values of amplitude require the motor to perform faster and longer rotations.
Finally, from the minimization of and , it is possible to notice that the value of suggested by the formal method analysis produces the best results for while lower values of L produce the best results for .
6. Conclusions
This article presents a development process integrating formal verification, co-simulation and design-space exploration. An application of this method has been shown in the design of a controller for a mechatronic system, namely a feedback linearization controller for the reduction of cogging torque in a brushless motor.
Formal verification has been used to identify ranges of values for the controller gain coefficients, satisfying the stability requirement of the non-linear dynamic system. This verification provides designers with the starting point for subsequent design refinements, which otherwise could be derived only through a trial-and-error process.
Co-simulation made it possible to build a system model by assembling different submodels simulated by heterogeneous environments. This is a relevant advantage in the design of complex systems combining subsystems of different natures, such as electrical, hydraulic, mechanical, software, etc. The results of the co-simulation have validated the results of the verification activity. Furthermore, co-simulation driven by a high-level design-space exploration environment has been used to assess the robustness of the control algorithm with respect to parameter variations and to find optimal parameter values.
This work shows the usefulness of the proposed method in the development of control in electric drive systems, but it is as well applicable to many other areas such as driving and navigation algorithms and energy management.
Synergies between verification and co-simulation lead to a development process that exploits the results of both approaches to enhance the initial model.
Summarizing, a method of verification of a control algorithm has been proposed in this work that can be considered an advanced version of the classic SIL method in which part of the physical system to be tested is replaced with a software component that simulates its outputs. The new features of the proposed verification method with respect to the classic SIL method are listed as follows:
- using the methodology described in the article, one could think of formally analyzing the global state of a mechatronic systems, with a view to safety, mapping the operating states directly with PVS and analyzing the final effects of the unpredictable variations of the parameters via DSE, as well as verify the robustness of the entire dynamic system through co-simulation
- the development of a generalized and more automatic procedure can be used to analyze and verify conditions for the safety of the dynamic system and its users, which is essential in the field of automation and industrial robotics and in the motor vehicle industry, where often the development of a safe and efficient system requires a large number of field tests, which have significant costs
- a systematic development process based on formal methods and co-simulations in the early phases of system design allows reducing risks in the physical prototyping phase.
Author Contributions
The authors contributed in equal measure to the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Italian Government under the CrossLab program, “Dipartimenti di Eccellenza” project.
Acknowledgments
The authors would like to thank the reviewers for their useful comments and suggestions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Isermann, R. Mechatronic Systems: Fundamentals; Springer: Berlin, Germany, 2005; pp. 1–624. [Google Scholar] [CrossRef]
- Bernardeschi, C.; Domenici, A.; Saponara, S. Formal Verification in the Loop to Enhance Verification of Safety-Critical Cyber-physical Systems. Electron. Commun. EASST 2019, 77. [Google Scholar] [CrossRef]
- Dini, P.; Saponara, S. Cogging Torque Reduction in Brushless Motors by a Nonlinear Control Technique. Energies 2019, 12, 2224. [Google Scholar] [CrossRef]
- Pelz, G. Mechatronic Systems: Modelling and Simulation with HDLs; Wiley: Hoboken, NJ, USA, 2003. [Google Scholar]
- Gausemeier, J.; Moehringer, S. VDI 2206—A New Guideline for the Design of Mechatronic Systems. IFAC Proc. Vol. 2002, 35, 785–790. [Google Scholar] [CrossRef]
- Entwicklungsmethodik für Mechatronische Systeme—Design Methodology for Mechatronic Systems; Technical Report VDI 2206; VDI—Verein Deutscher Ingenieure: Dusseldorf, Germany, 2004.
- Scicoslab Web Site. Available online: http://www.scicoslab.org. (accessed on 30 June 2020).
- Simulink® Web Site. Available online: http://www.mathworks.com/products/simulink (accessed on 30 June 2020).
- Dell’Amico, A.; Krus, P. Modeling, Simulation, and Experimental Investigation of an Electrohydraulic Closed-Center Power Steering System. IEEE/ASME Trans. Mechatronics 2015, 20, 2452–2462. [Google Scholar] [CrossRef]
- Orszulik, R.R.; Gabbert, U. An Interface Between Abaqus and Simulink for High-Fidelity Simulations of Smart Structures. IEEE/ASME Trans. Mechatronics 2016, 21, 879–887. [Google Scholar] [CrossRef]
- Isermann, R.; Schaffnit, J.; Sinsel, S. Hardware-in-the-loop simulation for the design and testing of engine-control systems. Control Eng. Pract. 1999, 7, 643–653. [Google Scholar] [CrossRef]
- Gomes, C.; Thule, C.; Broman, D.; Larsen, P.G.; Vangheluwe, H. Co-Simulation: A Survey. ACM Comput. Surv. 2018, 51, 49:1–49:33. [Google Scholar] [CrossRef]
- Ryan, R. ADAMS—Multibody System Analysis Software. In Multibody Systems Handbook; Schiehlen, W., Ed.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 361–402. [Google Scholar] [CrossRef]
- Hadas, Z.; Březina, T.; Andrs, O.; Vetiska, J.; Březina, L. Simulation modelling of mechatronic system with flexible parts. In Proceedings of the 15th International Power Electronics and Motion Control Conference (EPE/PEMC), Novi Sad, Serbia, 4–6 December 2012; pp. LS2e.1-1–LS2e.1-7. [Google Scholar] [CrossRef]
- Friedenthal, S.; Moore, A.; Steiner, R. A Practical Guide to SysML—The Systems Modeling Language; Morgan Kaufmann: Burlington, MA, USA, 2015. [Google Scholar] [CrossRef]
- Sadovykh, A.; Bagnato, A.; Quadri, I.; Mady, A.; Couto, L.; Basagiannis, S.; Hasanagic, M. SysML as a Common Integration Platform for CoSimulations: Example of a Cyber Physical System Design Methodology in Green Heating Ventilation and Air Conditioning Systems. In CEE-SECR 2016: Proceedings of the 12th Central & Eastern European Software Engineering Conference, Moscow, Russia, 28–29 October 2016; Association for Computing Machinery: New York, NY, USA, 2016; pp. 1:1–1:5. [Google Scholar] [CrossRef]
- Foldager, F.; Larsen, P.; Green, O. Development of a Driverless Lawn Mower using Co-Simulation. In Software Engineering and Formal Methods: Proceedings of the International Conference on Software Engineering and Formal Methods, SEFM 2017, Trento, Italy, 6–10 September 2017; Cerone, A., Roveri, M., Eds.; Springer: Cham, Switzerland; Volume 10729, pp. 330–344. [CrossRef]
- Giese, H.; Burmester, S.; Schäfer, W.; Oberschelp, O. Modular Design and Verification of Component-based Mechatronic Systems with Online-reconfiguration. SIGSOFT Softw. Eng. Notes 2004, 29, 179–188. [Google Scholar] [CrossRef]
- Agrawal, A.; Simon, G.; Karsai, G. Semantic Translation of Simulink/Stateflow Models to Hybrid Automata Using Graph Transformations. Electron. Notes Theor. Comput. Sci. 2004, 109, 43–56. [Google Scholar] [CrossRef]
- Lindahl, M.; Pettersson, P.; Yi, W. Formal Design and Analysis of a Gearbox Controller. Springer Int. J. Softw. Tools Technol. Transf. 2001, 3, 353–368. [Google Scholar] [CrossRef]
- Cimatti, A.; Griggio, A.; Mover, S.; Tonetta, S. HyComp: An SMT-Based Model Checker for Hybrid Systems. In Tools and Algorithms for the Construction and Analysis of Systems; Baier, C., Tinelli, C., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; Volume 9035, Lecture Notes in Computer Science; pp. 52–67. [Google Scholar] [CrossRef]
- Cimatti, A.; Griggio, A.; Mover, S.; Tonetta, S. Parameter synthesis with IC3. In Proceedings of the Formal Methods in Computer-Aided Design, Portland, OR, USA, 20–23 October 2013; pp. 165–168. [Google Scholar] [CrossRef]
- Fulton, N.; Mitsch, S.; Quesel, J.D.; Völp, M.; Platzer, A. KeYmaera X: An axiomatic tactical theorem prover for hybrid systems. In Proceedings of the International Conference on Automated Deduction, Berlin, Germany, 1–7 August 2015; Springer: Berlin, Germany, 2015; pp. 527–538. [Google Scholar] [CrossRef]
- Platzer, A. Logics of Dynamical Systems. In Proceedings of the 27th Annual IEEE Symposium on Logic in Computer Science, Dubrovnik, Croatia, 25–28 June 2012; pp. 13–24. [Google Scholar] [CrossRef]
- Owre, S.; Rushby, J.; Shankar, N. PVS: A prototype verification system. In Automated Deduction—CADE-11; Kapur, D., Ed.; Springer: Berlin/Heidelberg, Germany, 1992; Lecture Notes in Computer Science; Volume 607, pp. 748–752. [Google Scholar] [CrossRef]
- Bernardeschi, C.; Domenici, A.; Masci, P. A PVS-Simulink Integrated Environment for Model-Based Analysis of Cyber-Physical Systems. IEEE Trans. Softw. Eng. 2018, 44, 512–533. [Google Scholar] [CrossRef]
- Palmieri, M.; Bernardeschi, C.; Masci, P. A framework for FMI-based co-simulation of human–machine interfaces. Softw. Syst Model 2019. [Google Scholar] [CrossRef]
- Muñoz, C.; Narkawicz, A.; Hagen, G.; Upchurch, J.; Dutle, A.; Consiglio, M. DAIDALUS: Detect and Avoid Alerting Logic for Unmanned Systems. In Proceedings of the 34th Digital Avionics Systems Conference (DASC 2015), Liverpool, UK, 26–28 October 2015. [Google Scholar] [CrossRef]
- Bernardeschi, C.; Domenici, A. Verifying safety properties of a nonlinear control by interactive theorem proving with the Prototype Verification System. Inf. Process. Lett. 2016, 116, 409–415. [Google Scholar] [CrossRef]
- Grimm, T.; Lettnin, D.; Hübner, M. A survey on formal verification techniques for safety-critical systems-on-chip. Electronics 2018, 7, 81. [Google Scholar] [CrossRef]
- Jia, K.; Xiao, J.; Fan, S.; He, G. A MQTT/MQTT-SN-based user energy management system for automated residential demand response: Formal verification and cyber-physical performance evaluation. Appl. Sci. 2018, 8, 1035. [Google Scholar] [CrossRef]
- Larsen, P.G.; Fitzgerald, J.; Woodcock, J.; Fritzson, P.; Brauer, J.; Kleijn, C.; Lecomte, T.; Pfeil, M.; Green, O.; Basagiannis, S.; et al. Integrated tool chain for model-based design of Cyber-Physical Systems: The INTO-CPS project. In Proceedings of the 2nd International Workshop on Modelling, Analysis, and Control of Complex CPS (CPS Data), Pittsburgh, PA, USA, 21–23 March 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Owre, S.; Rushby, J.; Shankar, N.; Von Henke, F. Formal verification for fault-tolerant architectures: Prolegomena to the design of PVS. IEEE Trans. Softw. Eng. 1995, 21, 107–125. [Google Scholar] [CrossRef]
- Blochwitz, T.; Otter, M.; Akesson, J.; Arnold, M.; Clauß, C.; Elmqvist, H.; Friedrich, M.; Junghanns, A.; Mauss, J.; Neumerkel, D.; et al. Functional Mockup Interface 2.0: The Standard for Tool independent Exchange of Simulation Models. In Proceedings of the 9th International MODELICA Conference, Munich, Germany, 3–5 September 2012; Linköping University Electronic Press: Linkoping, Sweden, 2012. Number 76 in Linköping Electronic Conference Proceedings. pp. 173–184. [Google Scholar] [CrossRef]
- Dini, P.; Saponara, S. Design of an Observer-Based Architecture and Non-Linear Control Algorithm for Cogging Torque Reduction in Synchronous Motors. Energies 2020, 13, 2077. [Google Scholar] [CrossRef]
- Isidori, A. Nonlinear Control Systems; Communications and Control Engineering; Springer: London, UK, 1995. [Google Scholar]
- Pulle, D.; Darnell, P.; Veltman, A. Applied Control of Electrical Drives: Real Time Embedded and Sensorless Control Using VisSimTM and PLECSTM; Power Systems; Springer International Publishing: Berlin, Germany, 2015. [Google Scholar]
- Bernardeschi, C.; Dini, P.; Domenici, A.; Saponara, S. Co-simulation and Verification of a Non-linear Control System for Cogging Torque Reduction in Brushless Motors. In Proceedings of the 3rd Workshop on Formal Co-Simulation of Cyber-Physical Systems—A satellite event of SEFM2019, Oslo, Norway, 18–20 September 2019. [Google Scholar]
- Gerling, D. Electrical Machines; Springer: Berlin, Germany, 2016. [Google Scholar]
- Gamble, C. DSE in the INTO-CPS Platform; Technical Report D5.3e; INTO-CPS Deliverable: Aarhus, Denmark, 2017. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).