Forecasting Day-Ahead Hourly Photovoltaic Power Generation Using Convolutional Self-Attention Based Long Short-Term Memory
Abstract
1. Introduction
2. Related Work
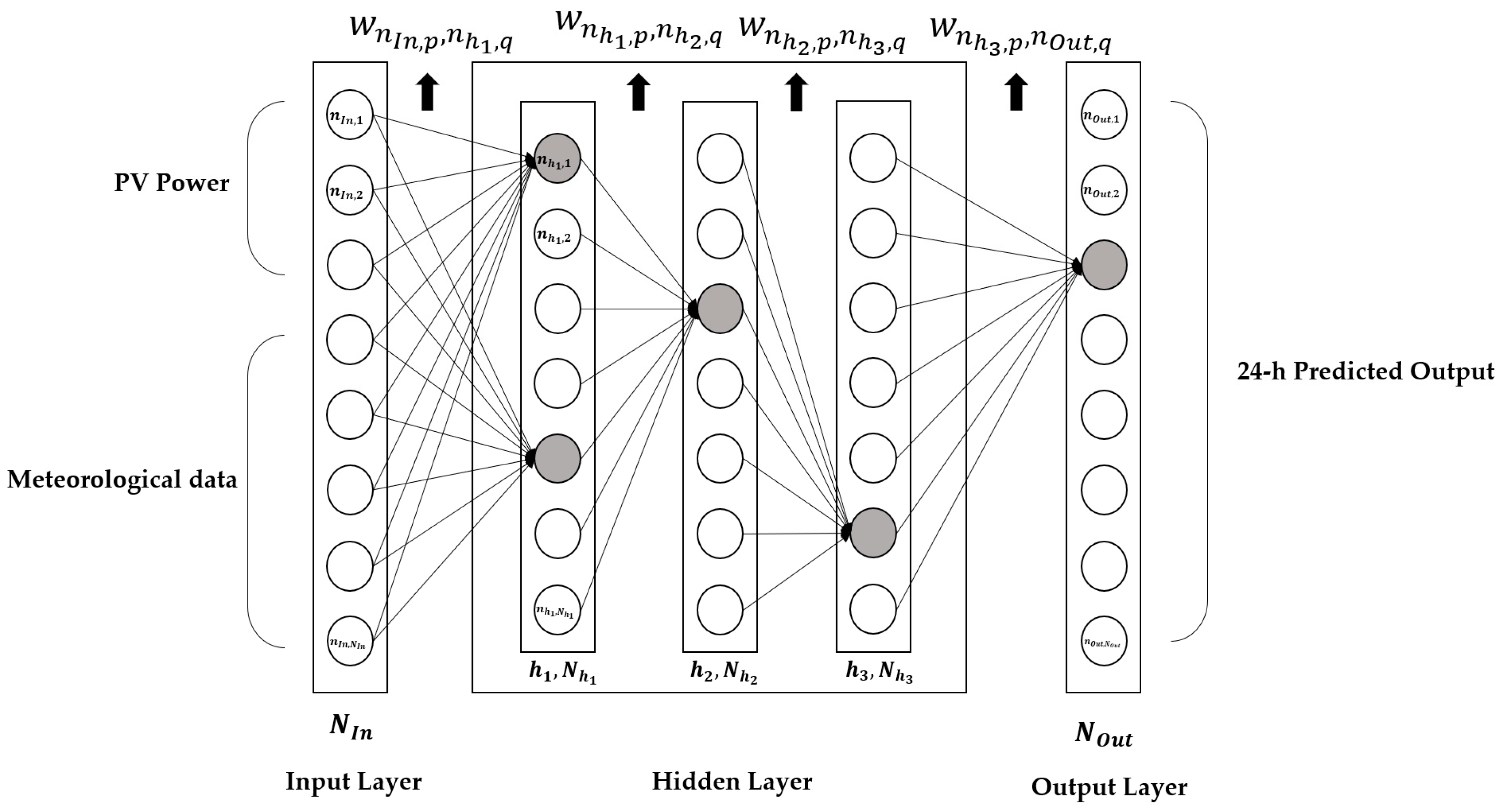
2.1. DNN Based Approach to Predict PV Power Generation
2.2. LSTM-Based Approach to Predict PV Power Generation
3. Data Processing
3.1. Features and Their Notations
3.2. Training Phase
3.3. Testing Phase
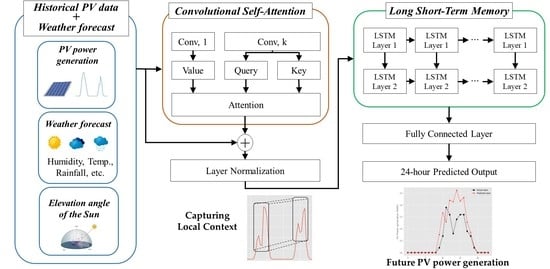
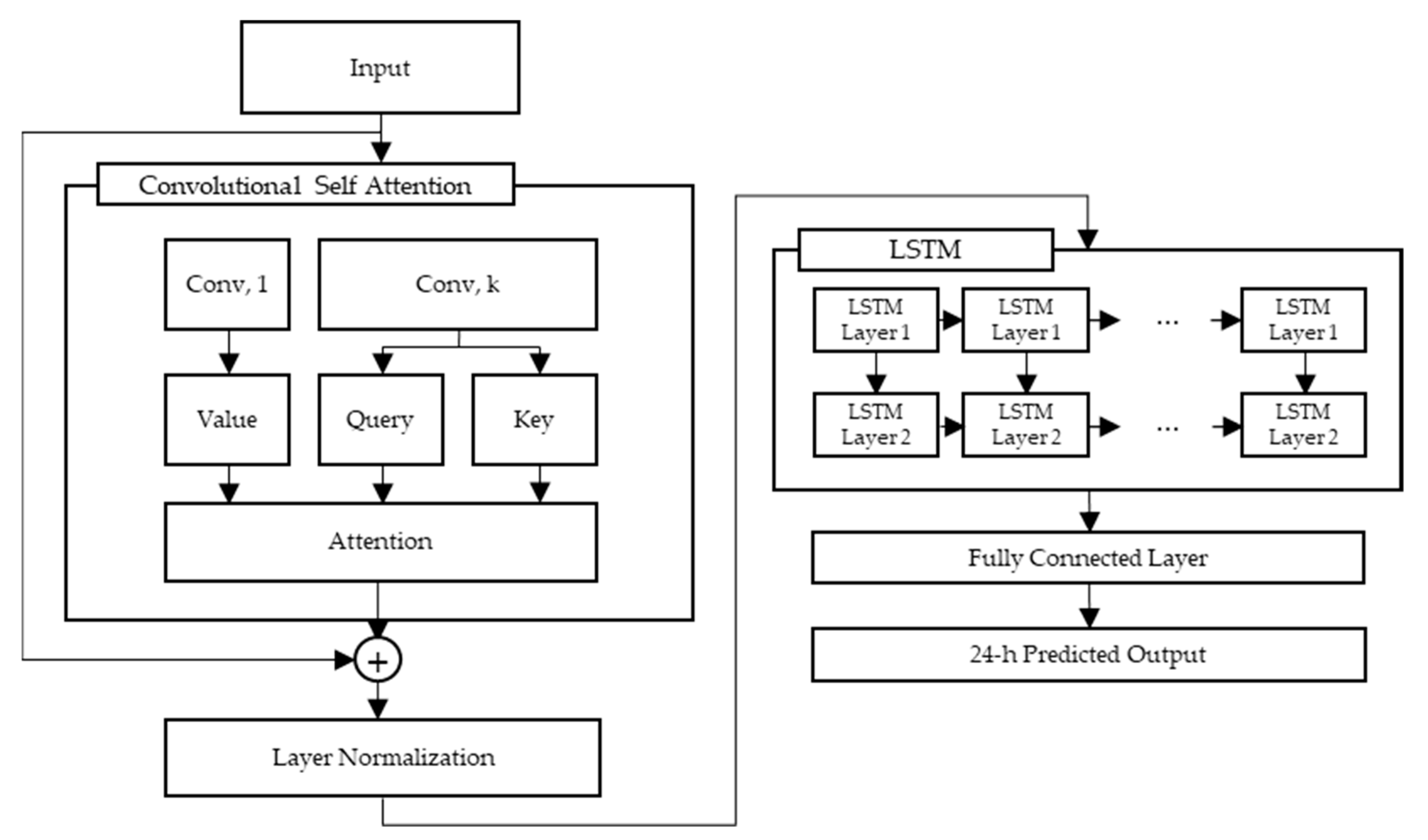
4. Proposed Method
5. Experiment
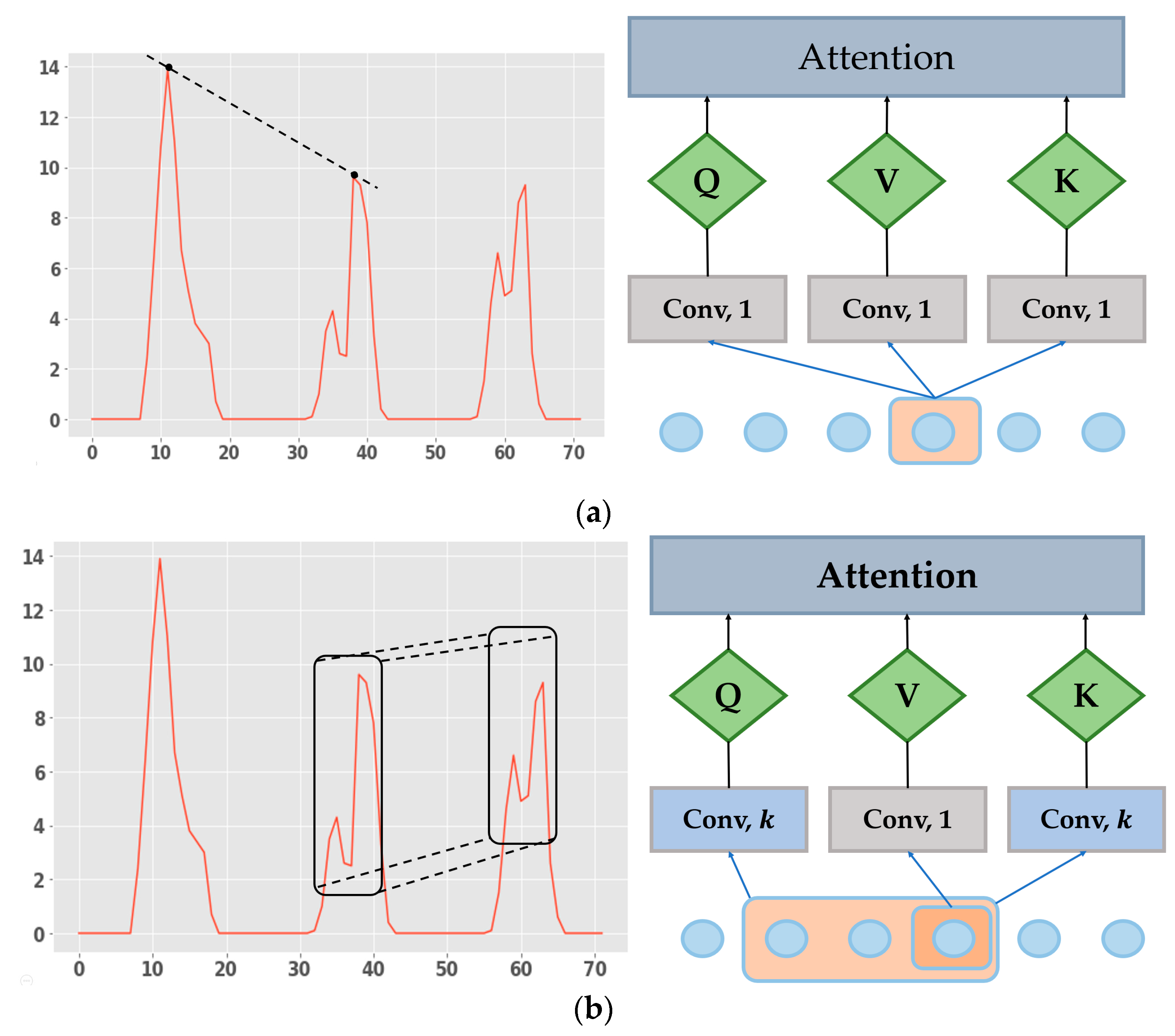
5.1. Find k of Convolutional Self-Attention
5.2. Performance Index
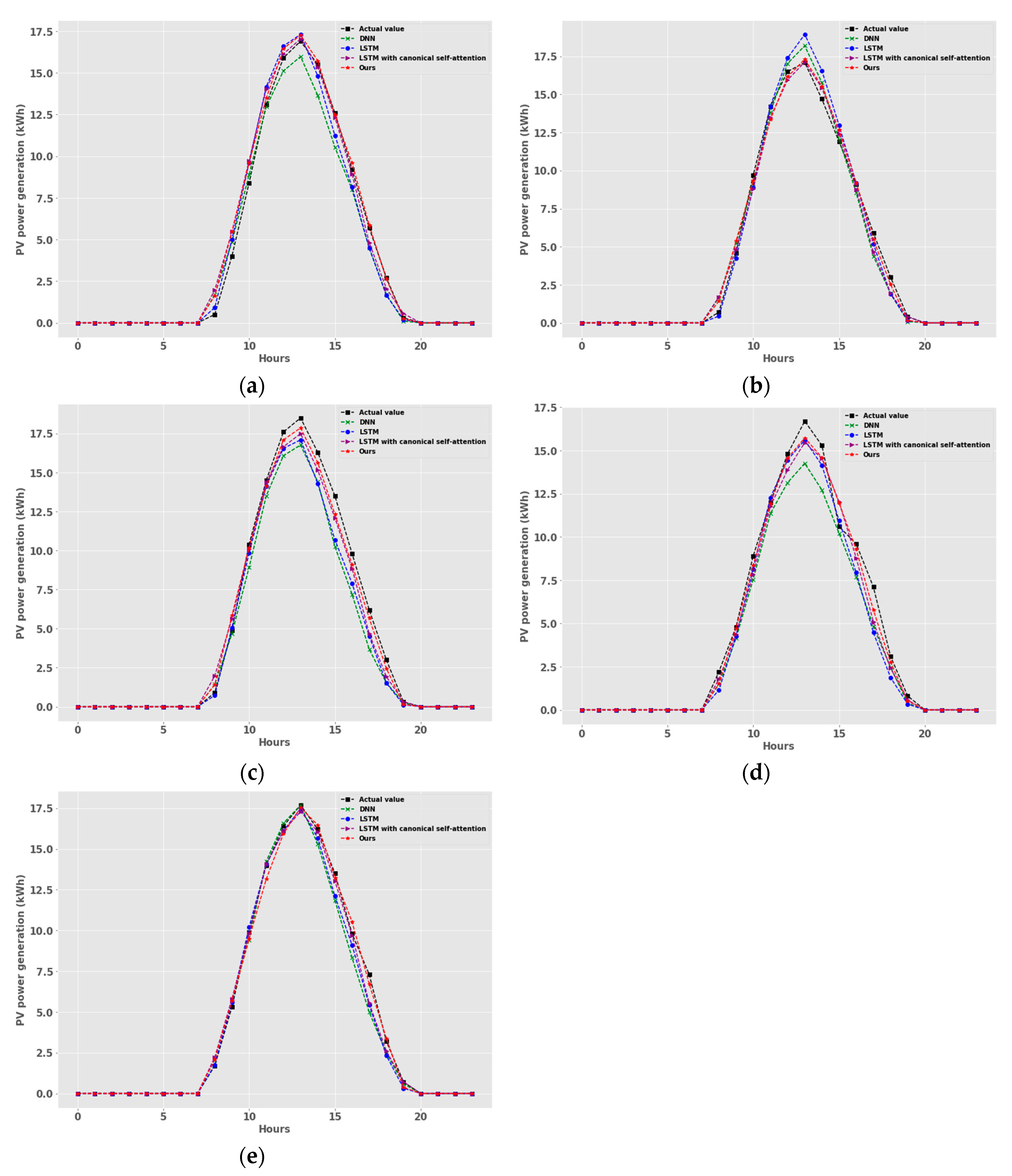
5.3. Experimental Results
5.4. Effect of Historical and Future Data
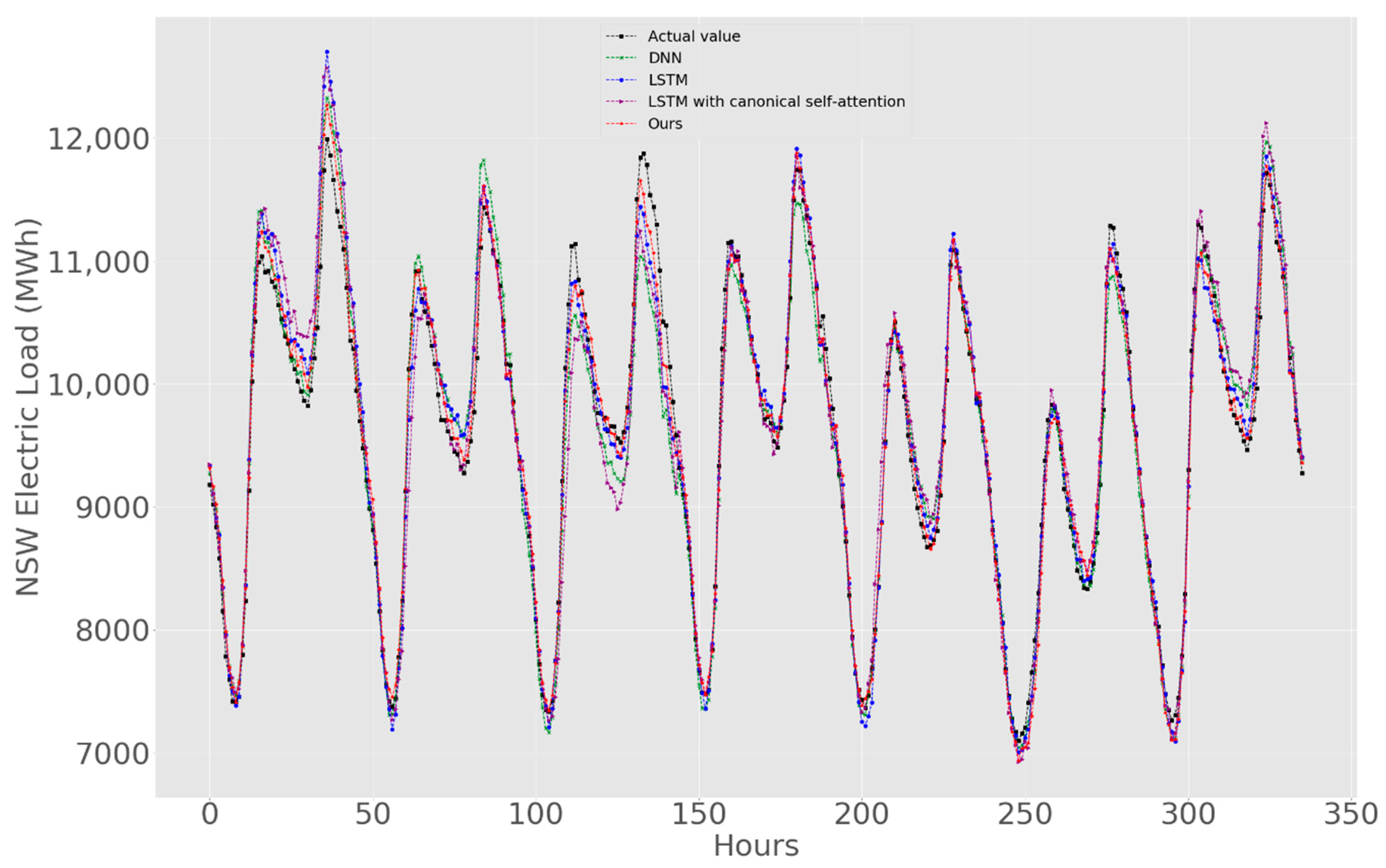
5.5. NSW Electricity Load Data
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Nosratabadi, S.M.; Hooshmand, R.-A.; Gholipour, E. A comprehensive review on microgrid and virtual power plant concepts employed for distributed energy resources scheduling in power systems. Renew. Sustain. Energy Rev. 2017, 67, 341–363. [Google Scholar] [CrossRef]
- Hatziargyriou, N.; Asano, H.; Marnay, R.I.C. Microgrids: An overview of ongoing research development and demonstration projects. IEEE Power Energy Mag. 2017, 5, 78–94. [Google Scholar] [CrossRef]
- Awerbuch, S.; Preston, A. The Virtual Utility: Accounting, Technology & Competitive Aspects of the Emerging Industry; Springer Science & Business Media: New York, NY, USA, 1997. [Google Scholar]
- Pudjianto, D.; Ramsay, C.; Strbac, G. Virtual power plant and system integration of distributed energy resources. In IET Renewable Power Generation; Institution of Engineering and Technology: London, UK, 2007; Volume 1, pp. 10–16. [Google Scholar]
- Su, W.; Wang, J. Energy management systems in micrgrid operations. Electr. J. 2012, 25, 45–60. [Google Scholar] [CrossRef]
- Moutis, P.; Hatziargyriou, N.D. Decision trees aided scheduling for firm power capacity provision by virtual power plants. Int. J. Electr. Power Energy Syst. 2014, 63, 730–739. [Google Scholar] [CrossRef]
- Sharma, N.; Sharma, P.; Irwin, D.E.; Shenoy, P.J. Predicting solar generation from weather forecasts using machine learning. In Proceedings of the 2nd IEEE International Conference on Smart Grid Communications (SmartGridComm), Brussels, Belgium, 17–20 October 2011; pp. 17–20. [Google Scholar]
- Tao, C.; Shanxu, D.; Changsong, C. Forecasting power output for grid-connected PV power system without using solar radiation measurement. In Proceedings of the 2nd IEEE International Symposium on Power Electronics for Distributed Generation Systems, Hefei, China, 16–18 June 2010. [Google Scholar]
- Das, U.K.; Tey, K.S.; Seyedmahmoudian, M.; Mekhilef, S.; Idris, M.Y.I.; Van Deventer, W.; Stojcevski, A. Forecasting of PV power generation and model optimization: A review. Renew. Sustain. Energy Rev. 2018, 81, 912–928. [Google Scholar] [CrossRef]
- Jeong, J.; Kim, H. Multi-Site Photovoltaic Forecasting Exploiting Space-Time Convolutional Neural Network. Energies 2019, 12, 4490. [Google Scholar] [CrossRef]
- Choi, S.; Hur, J. An Ensemble Learner-Based Bagging Model Using Past Output Data for Photovoltaic Forecasting. Energies 2020, 13, 1438. [Google Scholar] [CrossRef]
- Aprillia, H.; Yang, H.-T.; Huang, C.-M. Short-Term Photovoltaic Power Forecasting Using a Convolutional Neural Network–Salp Swarm Algorithm. Energies 2020, 13, 1879. [Google Scholar] [CrossRef]
- Ding, M.; Wang, L.; Bi, R. An ANN-based Approach for Forecasting the Power Output of PV System. Procedia Environ. Sci. 2011, 11, 1308–1315. [Google Scholar] [CrossRef]
- Chen, C.; Duan, S.; Cai, T.; Liu, B. Online 24-h solar power forecasting based on weather type classification using artificial neural network. Sol. Energy 2011, 85, 2856–2870. [Google Scholar] [CrossRef]
- Li, S.; Jin, X.; Xuan, Y.; Zhou, X.; Chen, W.; Wang, Y.X.; Yan, X. Enhancing the locality and breaking the memory bottleneck of transformer on time series forecasting. In Advances in Neural Information Processing Systems (NeurIPS); Association for Computing Machinery: Vancouver, BC, Canana, 2019; Volume 32, pp. 5244–5254. [Google Scholar]
- Mellit, A.; Massi Pavan, A.; Ogliari, E.; Leva, S.; Lughi, V. Advanced Methods for PV Output Power Forecasting: A Review. Appl. Sci. 2020, 10, 487. [Google Scholar] [CrossRef]
- Huang, R.; Huang, T.; Gadh, R.; Li, N. Solar generation prediction using the ARMA model in a laboratory-level micro-grid. In Proceedings of the third International Conference on Smart Grid Communications (SmartGridComm), Tainan, Taiwan, 5–8 November 2012; pp. 528–533. [Google Scholar]
- Li, Y.; Su, Y.; Shu, L. An ARMAX Model for Forecasting The Power Output of A Grid Connected PV System. Renew. Energy 2014, 66, 78–89. [Google Scholar] [CrossRef]
- Zeng, J.; Qiao, W. Short-term solar power prediction using a support vector machine. Renew. Energy 2013, 52, 118–127. [Google Scholar] [CrossRef]
- Mellit, A.; Massi Pavan, A.; Lughi, V. Short-term forecasting of power production in a large-scale PV plant. Sol. Energy 2014, 105, 401–413. [Google Scholar] [CrossRef]
- Fernandez-Jimenez, L.A.; Munoz-Jimenez, A.; Falces, A.; Mendoza-Villena, M.; Garcia-Garrido, E.; Lara-Santillan, P.M.; Zorzano-Santamaria, P.J. Short-term power forecasting system for PV plants. Renew. Energy 2012, 44, 311–317. [Google Scholar] [CrossRef]
- Son, J.; Park, Y.; Lee, J.; Kim, H. Sensorless PV power forecasting in grid-connected buildings through deep learning. Sensors 2018, 18, 2529. [Google Scholar] [CrossRef] [PubMed]
- Abdel-Nasser, M.; Mahmoud, K. Accurate PV power forecasting models using deep LSTM-RNN. Neural Comput. Appl. 2017, 31, 2727–2740. [Google Scholar] [CrossRef]
- Qing, X.; Niu, Y. Hourly day-ahead solar irradiance prediction using weather forecasts by LSTM. Energy 2018, 148, 461–468. [Google Scholar] [CrossRef]
- Huang, C.-J.; Kuo, P.-H. Multiple-input deep convolutional neural network model for short-term photovoltaic power forecasting. IEEE Access 2019, 7, 74822–74834. [Google Scholar] [CrossRef]
- Chang, G.W.; Lu, H.-J. Integrating Gray Data Preprocessor and Deep Belief Network for Day-Ahead PV Power Output Forecast. IEEE Trans. Sustain. Energy 2018, 11, 185–194. [Google Scholar] [CrossRef]
- Haneul, E.; Son, Y.; Choi, S. Feature-Selective Ensemble Learning-Based Long-Term Regional PV Generation Forecasting. IEEE Access 2020, 8, 54620–54630. [Google Scholar]
- Bouzerdoum, M.; Mellit, A.; Massi Pavan, A. A hybrid model (SARIMA-SVM) for short-term power forecasting of a small-scale grid-connected PV plant. Sol. Energy 2013, 98, 226–235. [Google Scholar] [CrossRef]
- Behera, M.K.; Majumder, I.; Nayak, N. Solar PV power forecasting using optimized modified extreme learning machine technique. Eng. Sci. Technol. Int. J. 2019, 21, 428–438. [Google Scholar]
- Dolara, A.; Grimaccia, F.; Leva, S.; Mussetta, M.; Ogliari, E. A physical hybrid artificial neural network for short term forecasting of PV plant power output. Energies 2015, 8, 1138–1153. [Google Scholar] [CrossRef]
- Maddix, D.C.; Wang, Y.; Smola, A. Deep factors with Gaussian processes for forecasting. arXiv 2018, arXiv:1812.00098. [Google Scholar]
- Lai, G.; Chang, W.-C.; Yang, Y.; Liu, H. Modeling long-and short-term temporal patterns with deep neural networks. In Proceedings of the 41st International ACM SIGIR Conference on Research & Development in Information Retrieval, Ann Arbor, MI, USA, 8–12 July 2018; pp. 95–104. [Google Scholar]
- Pascanu, R.; Mikolov, T.; Bengio, Y. On the difficulty of training recurrent neural networks. In Proceedings of the International Conference on Machine Learning, Atlanta, GA, USA, 16–21 June 2013; pp. 1310–1318. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Khandelwal, U.; He, H.; Qi, P.; Jurafsky, D. Sharp nearby, fuzzy far away: How neural language models use context. arXiv 2018, arXiv:1805.04623. [Google Scholar]
- Meeus, J. Astronomical Algorithms, 2nd ed.; William-Bell: Virginia, WV, USA, 1998. [Google Scholar]
- Zhou, H.; Zhang, Y.; Yang, L.; Liu, Q.; Yan, K.; Du, Y. Short-term PV power forecasting based on long short term memory neural network and attention mechanism. IEEE Access 2019, 7, 78063–78074. [Google Scholar] [CrossRef]
- Wang, S.; Wang, X.; Wang, S.; Wang, D. Bi-directional long short-term memory method based on attention mechanism and rolling update for short-term load forecasting. Int. J. Electr. Power Energy Syst. 2019, 109, 470–479. [Google Scholar] [CrossRef]
- Hao, S.; Lee, D.-H.; Zhao, D. Sequence to sequence learning with attention mechanism for short-term passenger flow prediction in large-scale metro system. Transp. Res. Part C Emerg. Technol. 2019, 107, 287–300. [Google Scholar] [CrossRef]
- Hollis, T.; Viscardi, A.; Yi, S.E. A comparison of LSTMs and attention mechanisms for forecasting financial time series. arXiv 2018, arXiv:1812.07699. [Google Scholar]
- Ba, J.L.; Kiros, J.R.; Hinton, G.E. Layer normalization. arXiv 2016, arXiv:1607.06450. [Google Scholar]
- Korea Meteorological Administration. Climate of Korea. Available online: https://web.kma.go.kr/eng/biz/climate_01.jsp (accessed on 3 April 2020).
- Australian Energy Market Operator (AEMO). Available online: http://www.aemo.com.au (accessed on 3 June 2020).

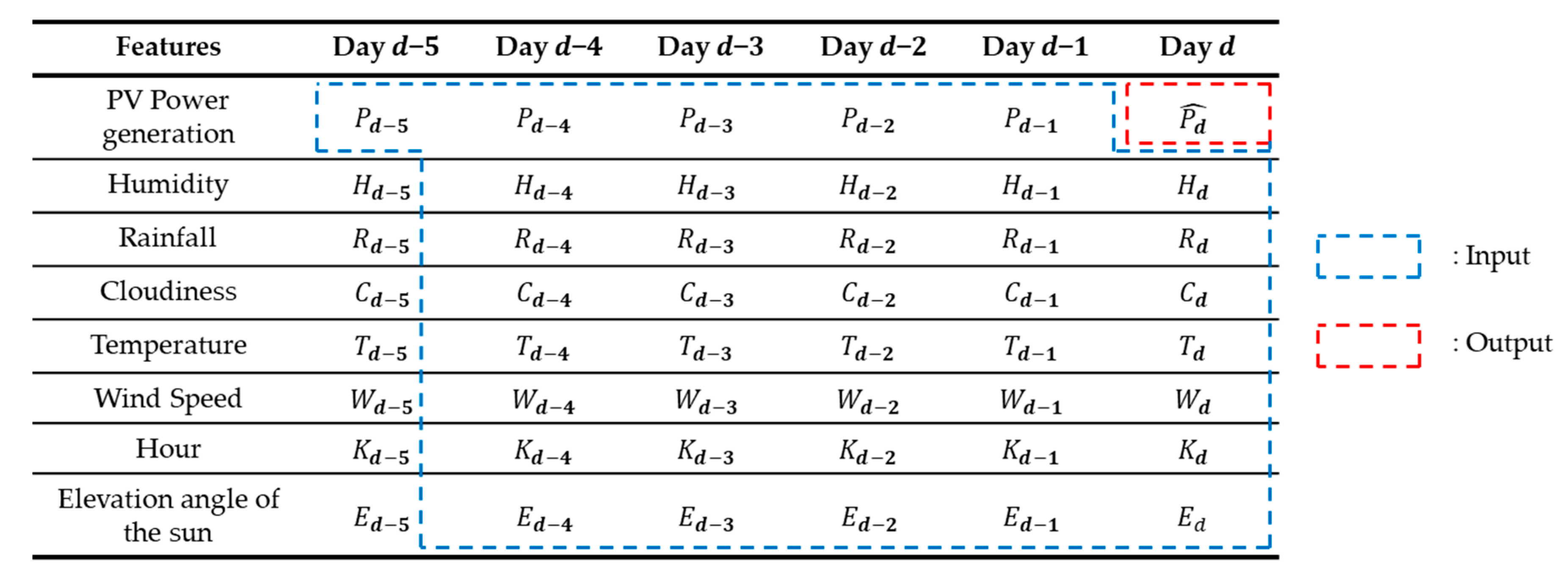
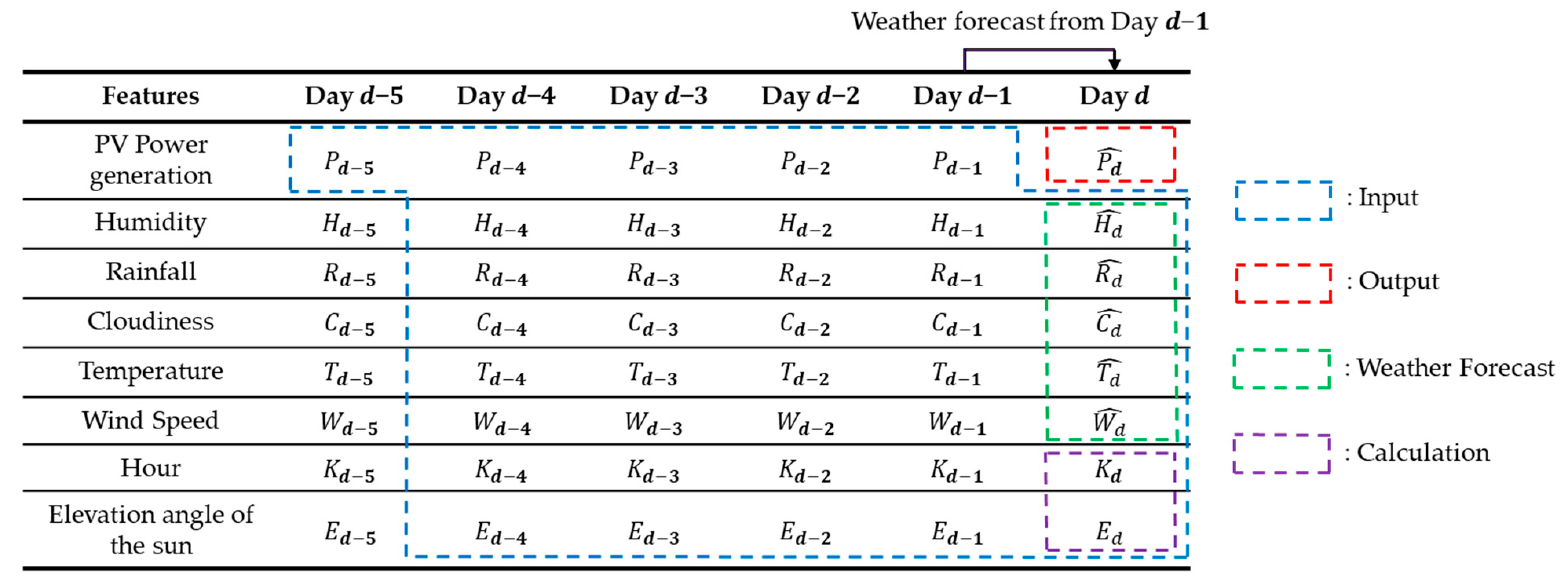
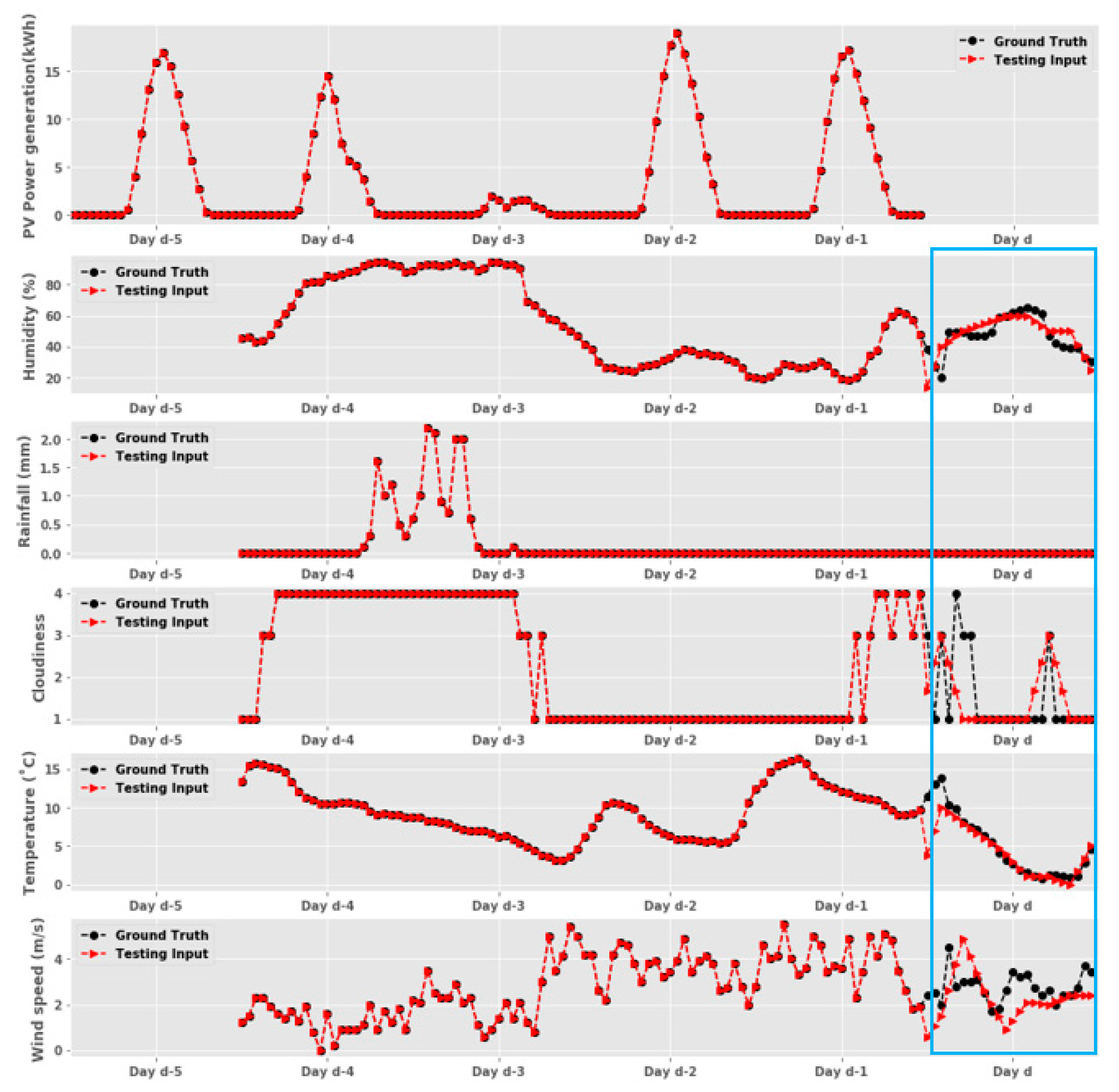
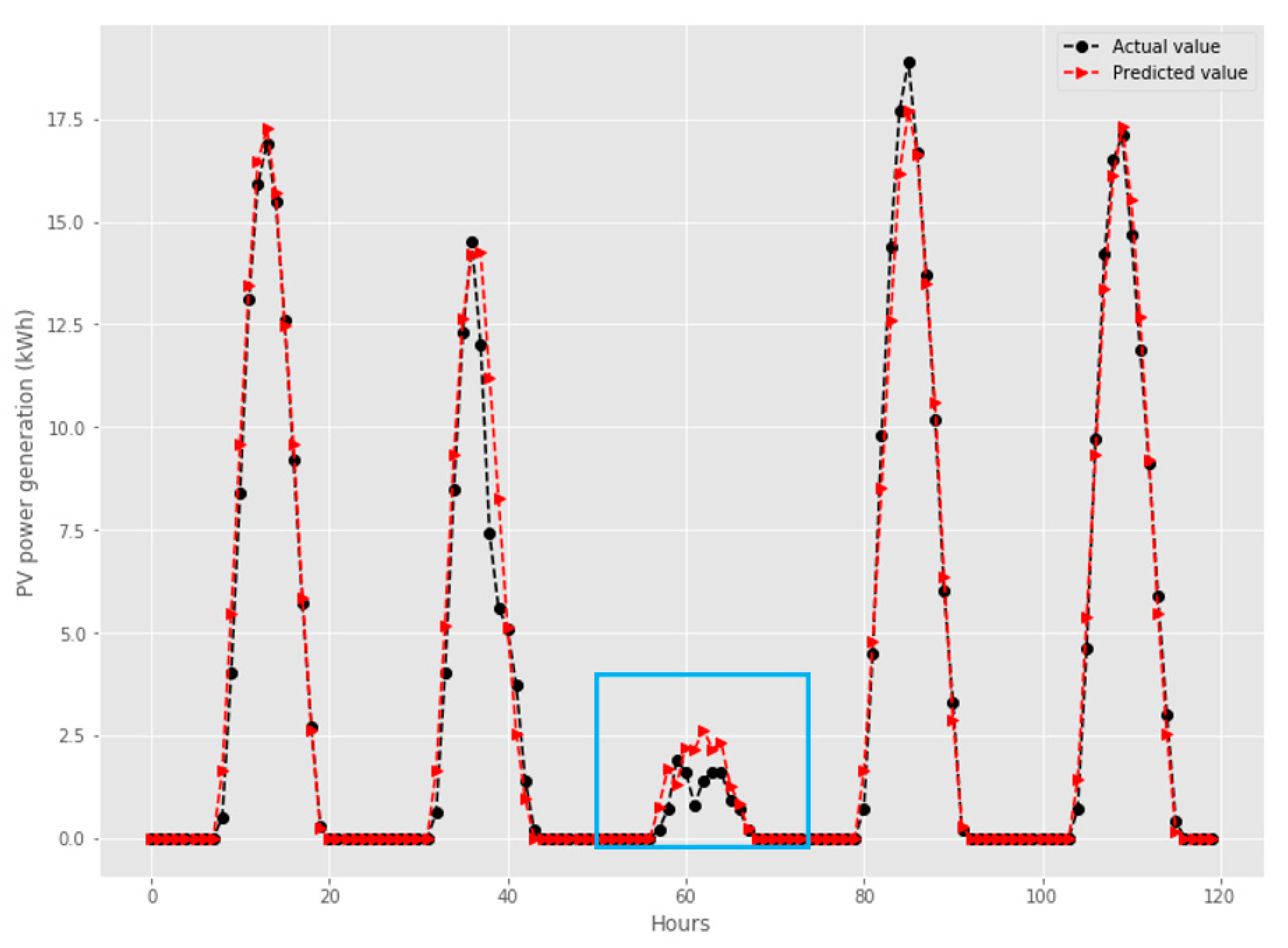
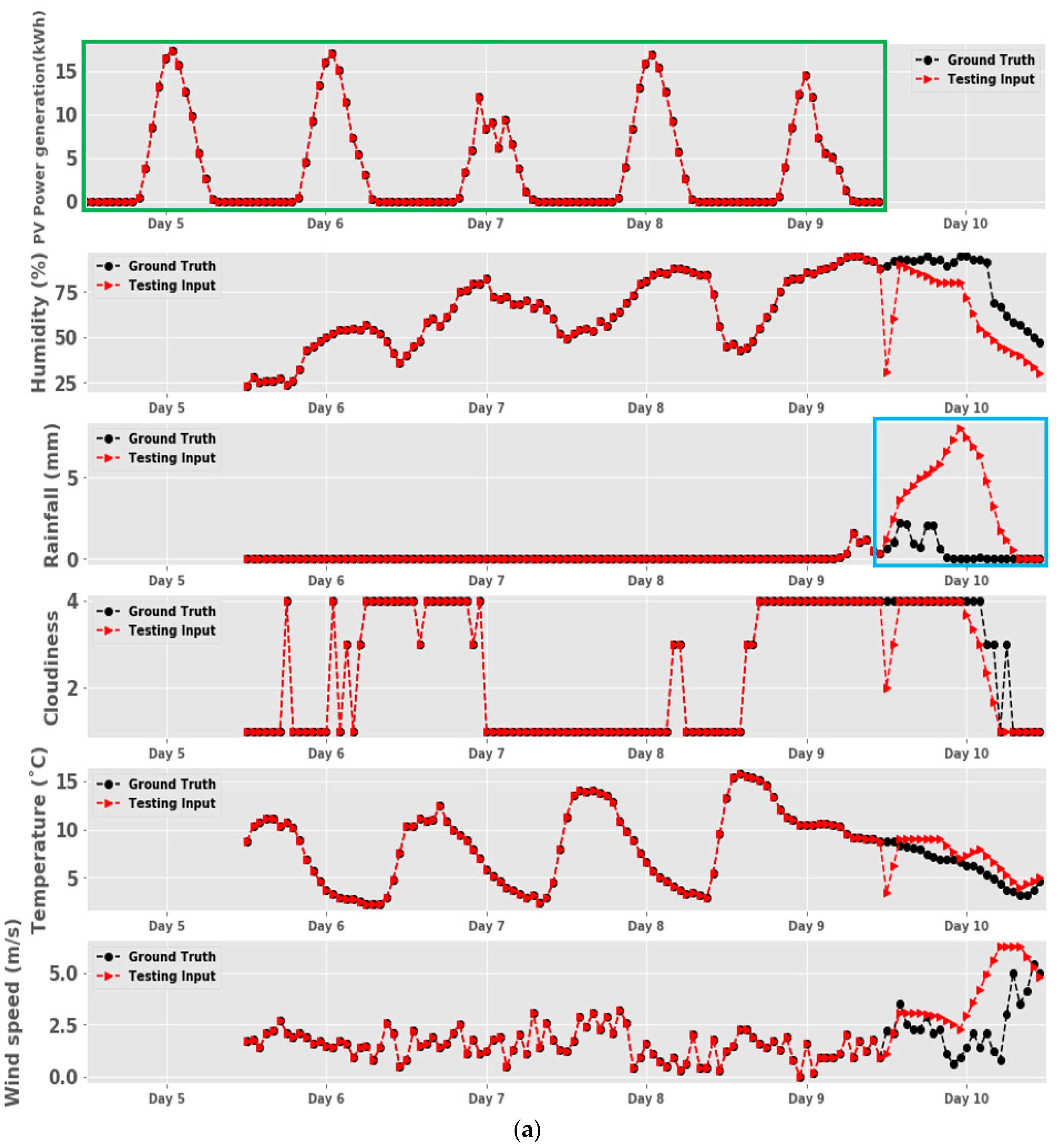
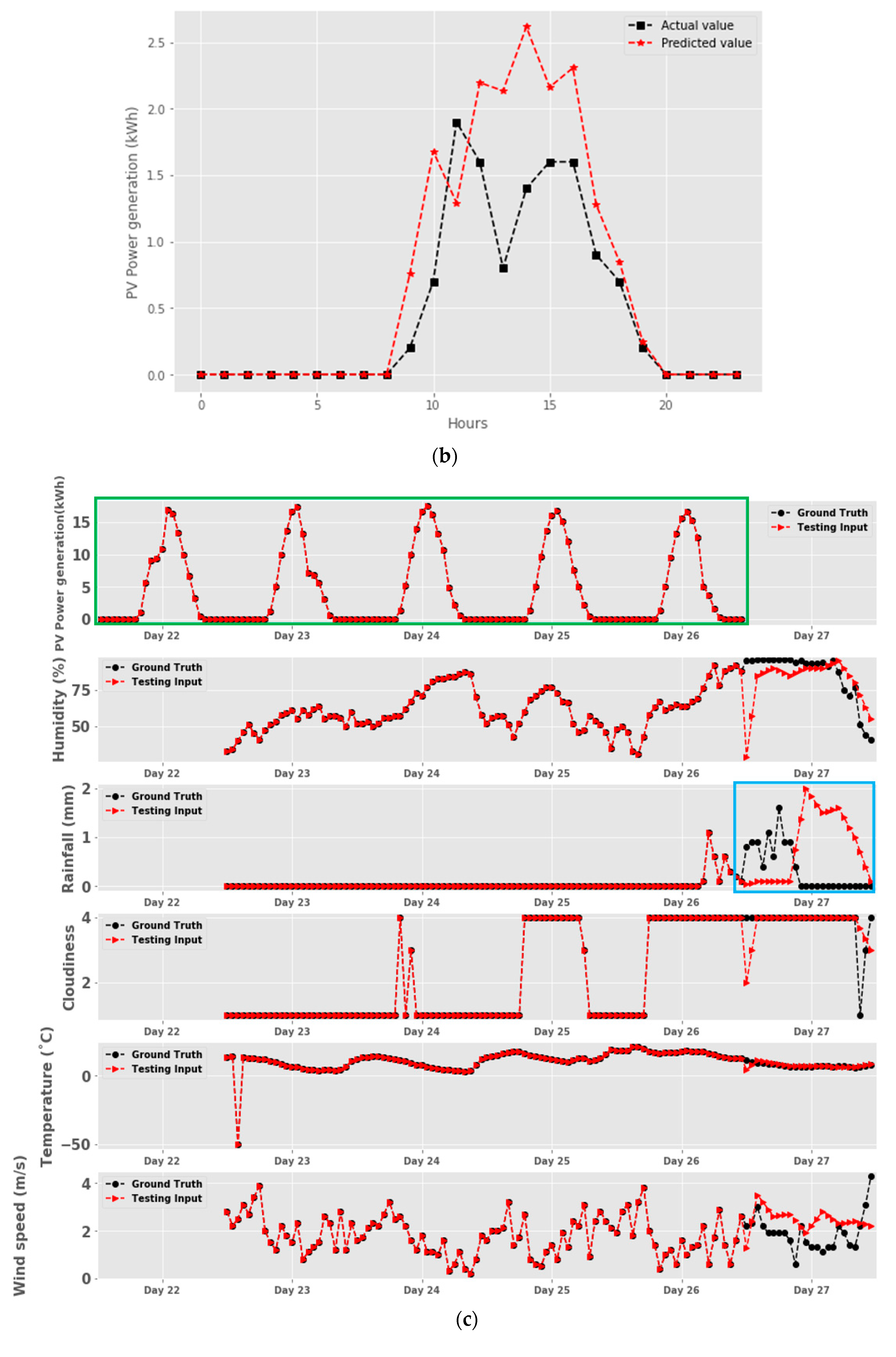
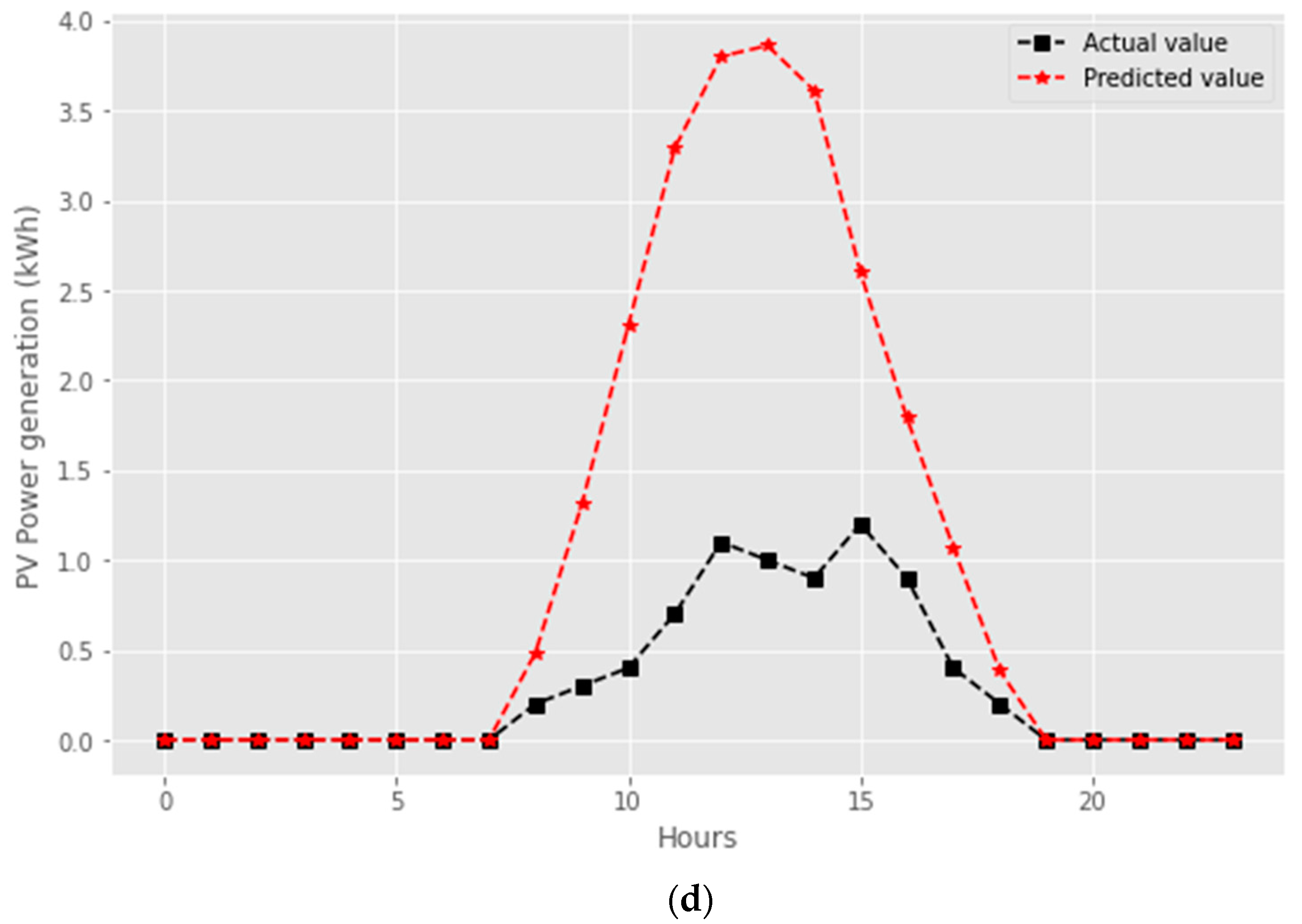
| Features | Day d-5 | Day d-4 | Day d-3 | Day d-2 | Day d-1 | Day d |
|---|---|---|---|---|---|---|
| PV Power Generation | ||||||
| Humidity | ||||||
| Rainfall | ||||||
| Cloudiness | ||||||
| Temperature | ||||||
| Wind Speed | ||||||
| Hour | ||||||
| Elevation Angle of the Sun |
| k | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| MSE | 0.0038 | 0.0036 | 0.0035 | 0.0039 | 0.0040 | 0.0037 | 0.0039 | 0.0039 | 0.0039 |
| Method | MAPE (%) | MAE (kWh) | RMSE | nMAE |
|---|---|---|---|---|
| DNN | 26.25 | 0.66 | 1.36 | 0.17 |
| LSTM | 25.77 | 0.59 | 1.32 | 0.15 |
| LSTM with canonical self-attention | 25.21 | 0.63 | 1.30 | 0.16 |
| Ours | 24.22 | 0.57 | 1.24 | 0.15 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, D.; Choi, W.; Kim, M.; Liu, L. Forecasting Day-Ahead Hourly Photovoltaic Power Generation Using Convolutional Self-Attention Based Long Short-Term Memory. Energies 2020, 13, 4017. https://doi.org/10.3390/en13154017
Yu D, Choi W, Kim M, Liu L. Forecasting Day-Ahead Hourly Photovoltaic Power Generation Using Convolutional Self-Attention Based Long Short-Term Memory. Energies. 2020; 13(15):4017. https://doi.org/10.3390/en13154017
Chicago/Turabian StyleYu, Dukhwan, Wonik Choi, Myoungsoo Kim, and Ling Liu. 2020. "Forecasting Day-Ahead Hourly Photovoltaic Power Generation Using Convolutional Self-Attention Based Long Short-Term Memory" Energies 13, no. 15: 4017. https://doi.org/10.3390/en13154017
APA StyleYu, D., Choi, W., Kim, M., & Liu, L. (2020). Forecasting Day-Ahead Hourly Photovoltaic Power Generation Using Convolutional Self-Attention Based Long Short-Term Memory. Energies, 13(15), 4017. https://doi.org/10.3390/en13154017