Optimal Sizing and Scheduling of Hybrid Energy Systems: The Cases of Morona Santiago and the Galapagos Islands
Abstract
1. Introduction
2. Problem Statement
- The hybrid energy systems are assumed to work independently and are expected to power isolated rural communities by supplying electricity in an efficient, reliable, and economical way.
- The optimization procedure is conducted over the period of one year with an hourly resolution.
- The meteorological conditions and electricity consumption values are kept constant within each one-hour time step.
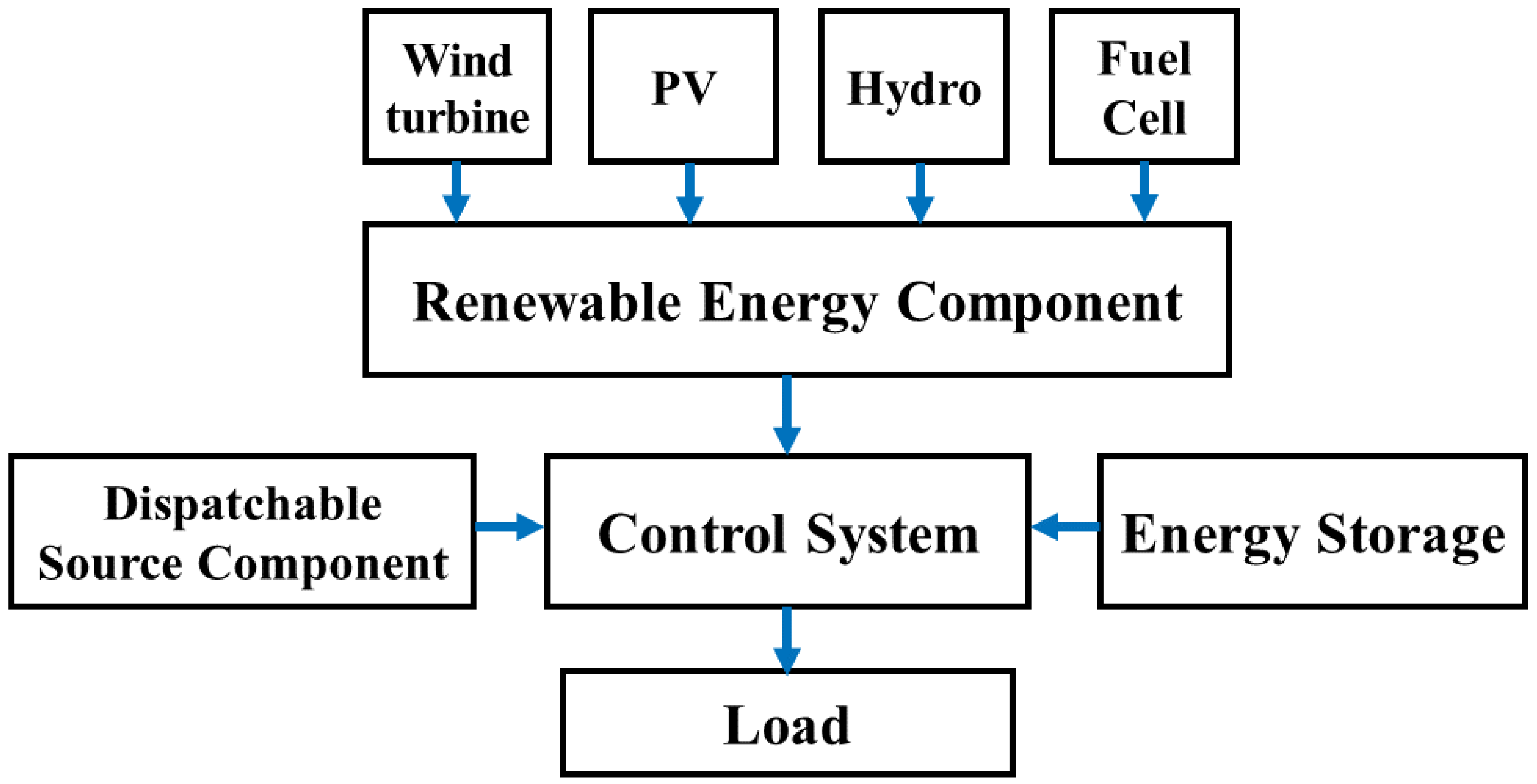
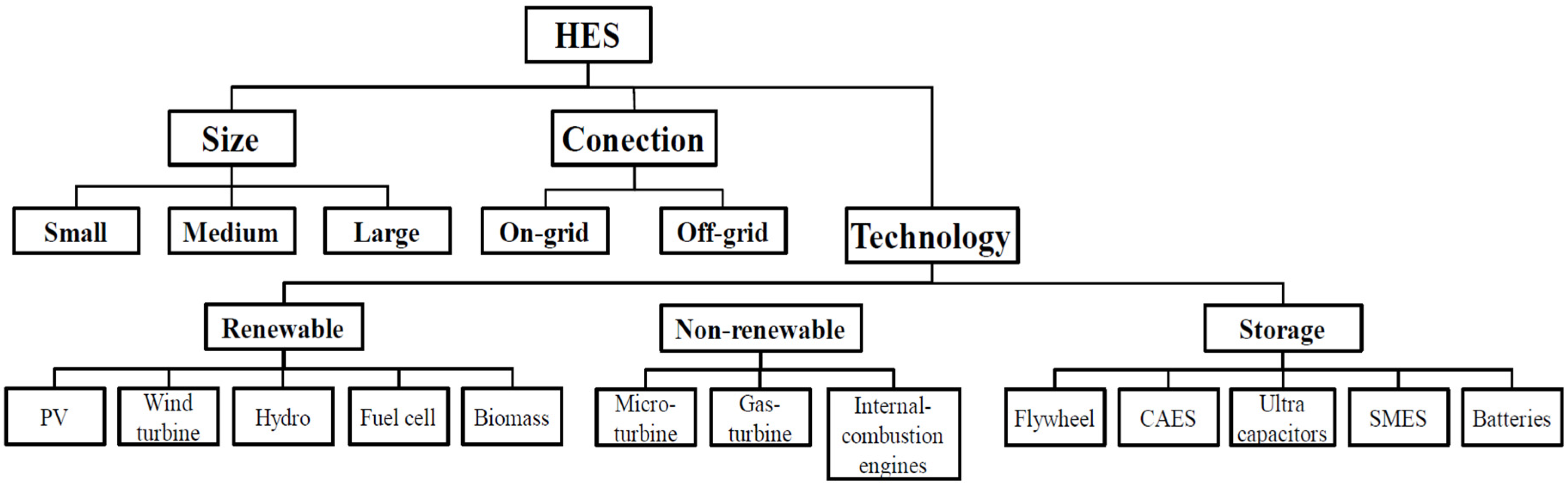
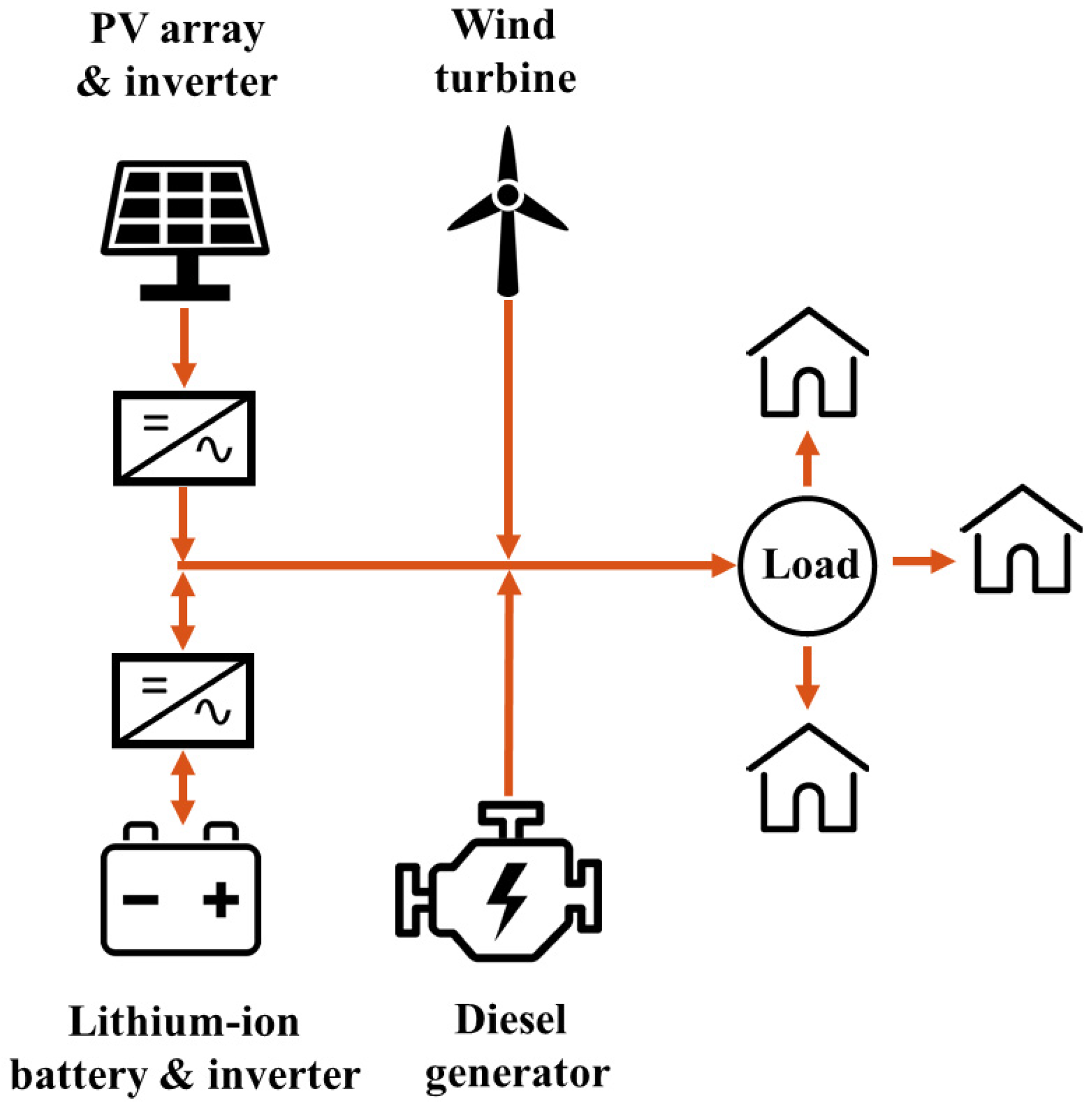
- The hybrid energy systems may be comprised of solar-, wind-, battery-, and diesel-powered subsystems. Figure 3 shows a sample layout of a potential HES configuration.
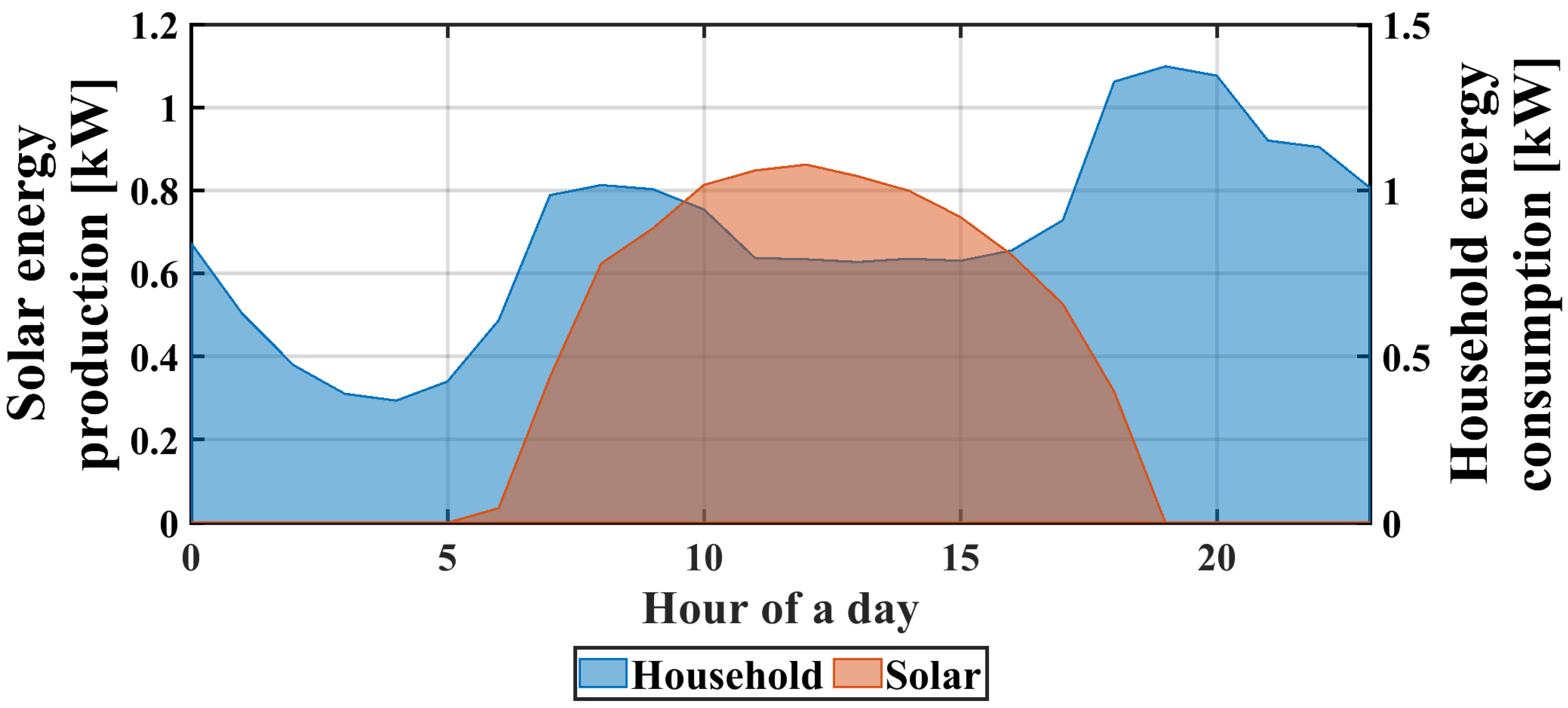
- The annual meteorological conditions, load profiles, maintenance, and capital costs are considered to be representative of each analyzed case. This allows to evaluate the economic feasibility of the project through the computation of the TLCC (total life cycle cost) of the system. A generic example of the energy usage of a typical household and a daily solar energy production profile are presented in Figure 4, illustrating the mismatch between energy supply and demand in an HES.
- The generation of renewable energy technologies is based on hourly capacity factors. This is calculated considering the specific technical properties of each technology as well as hourly meteorological conditions.
3. Model Formulation
4. Selected Sites in Ecuador
5. Results
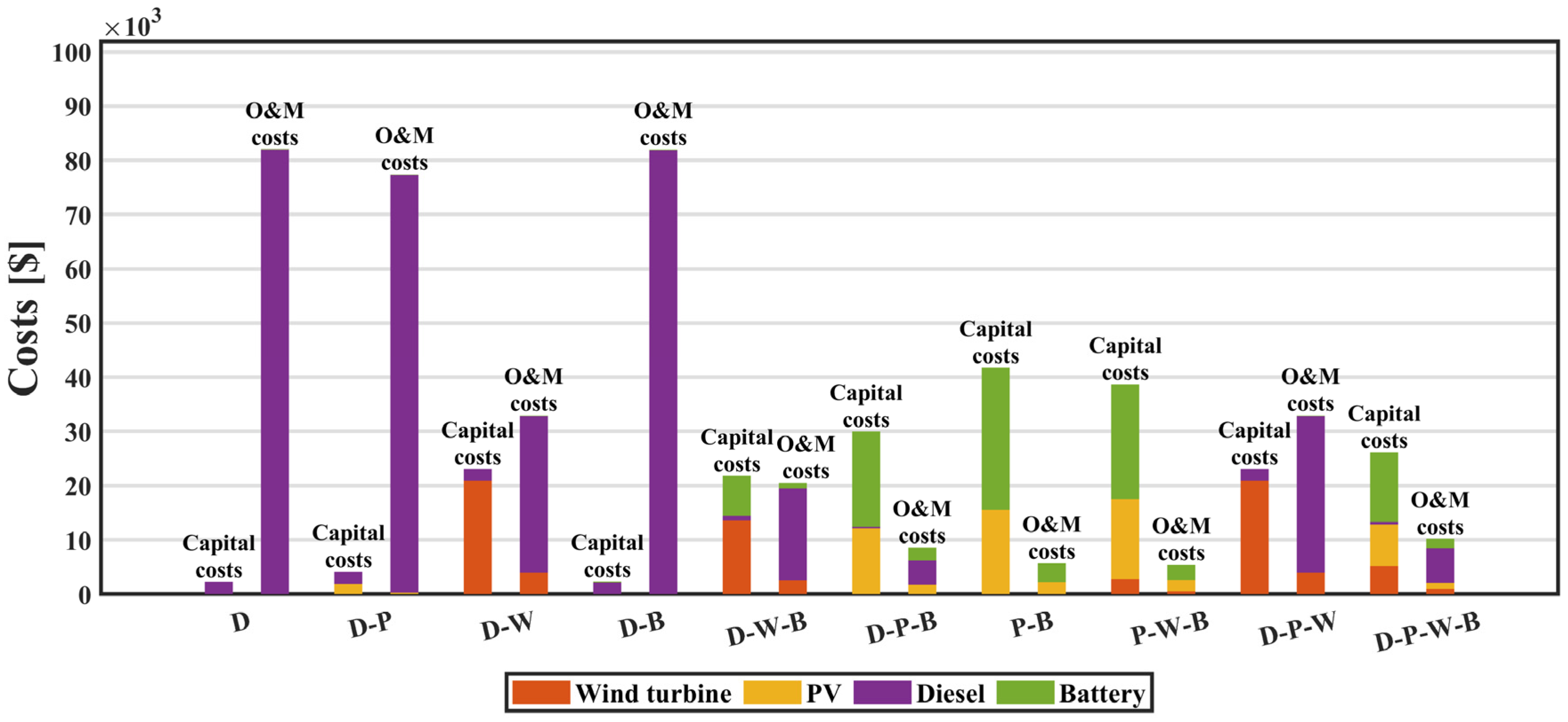
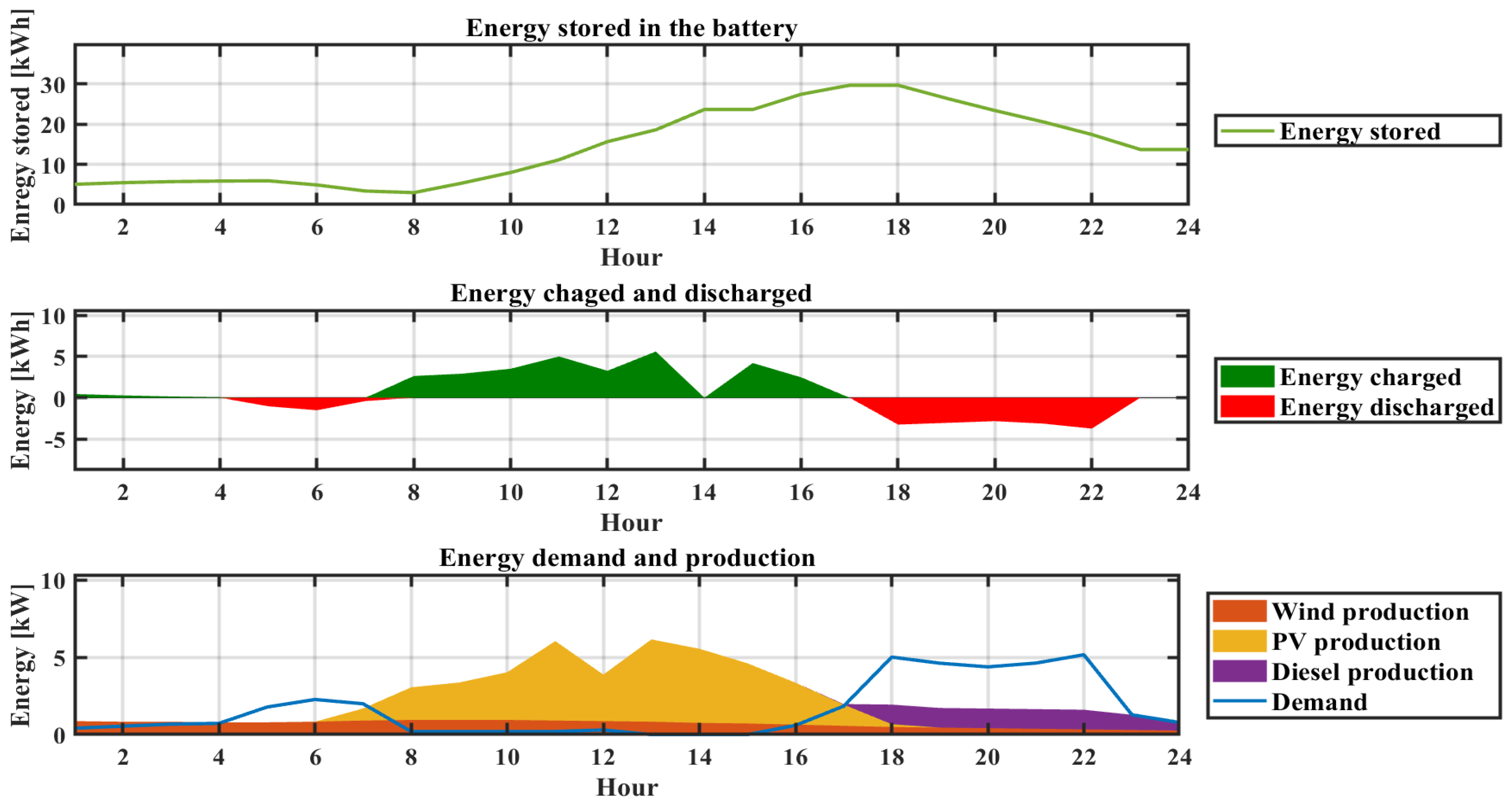
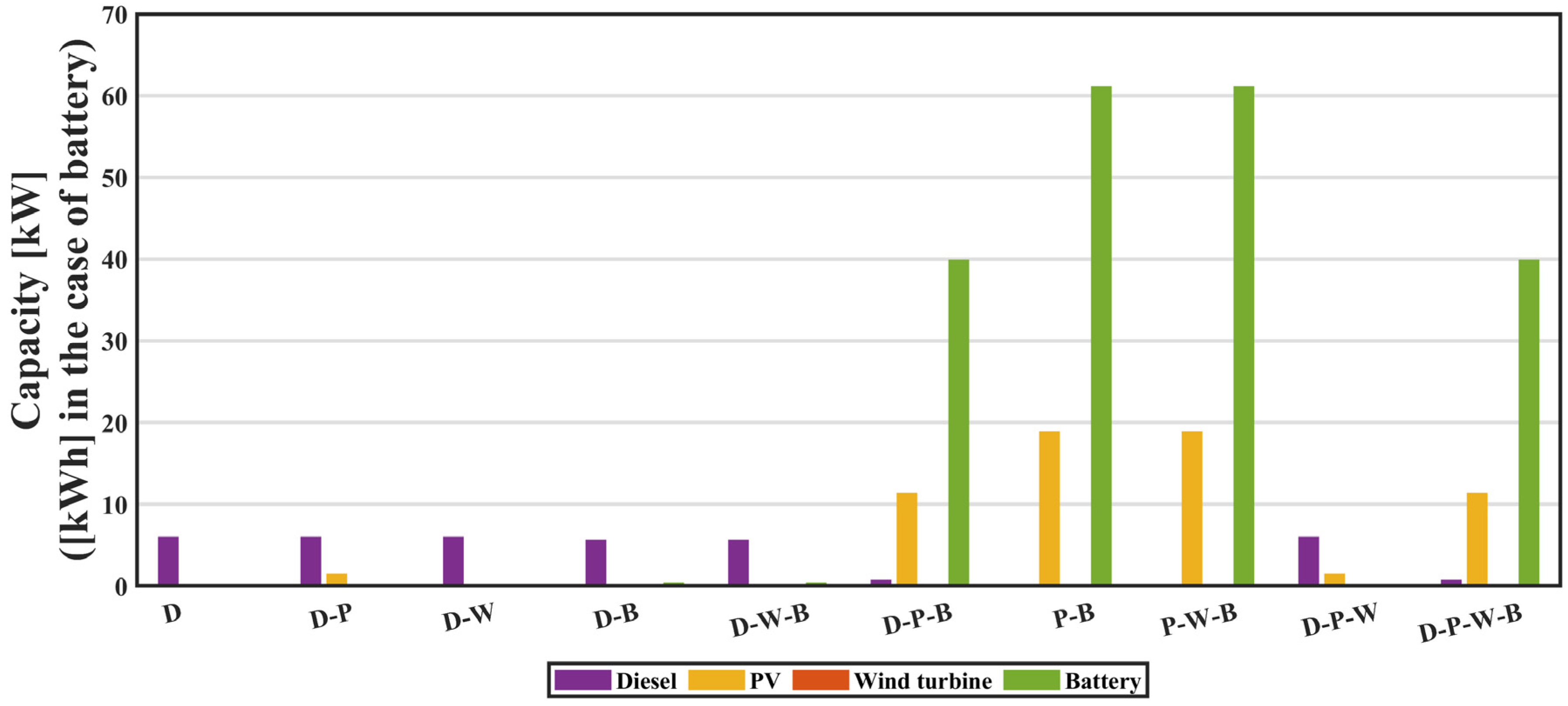
5.1. Galapagos Province
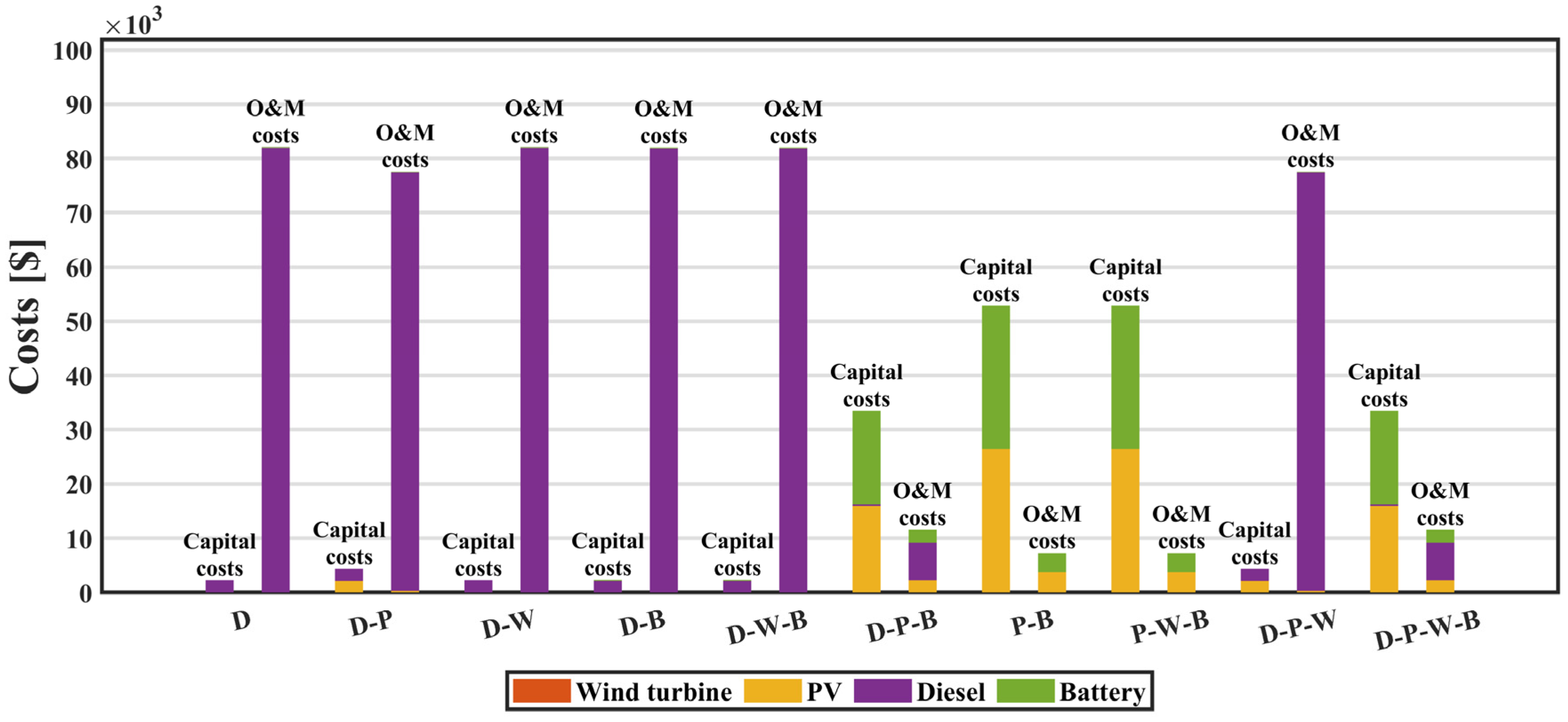
5.2. Morona Santiago Province
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Sets | |
| Photovoltaic Diesel generator Wind turbine | |
| Time step (hours) | |
| Parameters | |
| Load demand at hour (kW) | |
| Annual maintenance cost of technology given as a fixed percentage of investment cost (%) | |
| Investment cost of technology ($/kW) | |
| Battery investment cost ($/kWh) | |
| Annual maintenance cost of battery given as a fixed percentage of investment cost (%) | |
| Battery operating cost ($/kWh) | |
| Battery replacement cost ($/kWh) | |
| Efficiency of technology (%) | |
| Battery charging efficiency (%) | |
| Battery discharging efficiency (%) | |
| Capacity factor of technology at hour | |
| Global solar irradiation at hour (W/m2) | |
| Standard global solar irradiation (W/m2) | |
| Wind speed at hour (m/s) | |
| Turbine cut-in wind speed (m/s) | |
| Turbine cut-off wind speed (m/s) | |
| Turbine rated wind speed (m/s) | |
| Diesel price ($/kWh) | |
| Inverter efficiency (%) | |
| Depth of discharge (%) | |
| Capacity recovery factor | |
| Lifetime (years) | |
| Interest rate (%) | |
| Variables | |
| Installed capacity of technology (kW) | |
| Battery capacity (kWh) | |
| Power output of technology at hour (kW) | |
| Amount of energy charged at hour (kWh) | |
| Amount of energy discharged at hour (kWh) | |
| Energy stored in the battery at hour (kWh) | |
| Total life cycle costs of the technology ($) | |
| Total life cycle costs of the battery ($) | |
| Total life cycle costs of the entire system ($) | |
Abbreviations
| CAES | Compressed-air energy storage |
| CRF | Capital recovery factor |
| CS | Cuckoo search |
| GA | Genetic algorithm |
| GAMS | General Algebraic Modeling System |
| HESs | Hybrid energy systems |
| HOMER | Hybrid Optimization Model for Electric Renewables |
| HRES | Hybrid renewable energy system |
| IEA | International Energy Agency |
| LCOE | Levelized cost of energy |
| LLP | Loss of load probability |
| LP | Linear programming |
| NSRDB | National Solar Radiation Database |
| PSO | Particle swarm optimization |
| PV | Photovoltaic |
| RES | Renewable energy source |
| RHO | Receding horizon optimization approach |
| SMES | Superconducting magnetic energy storage |
References
- Davis, S.J.; Lewis, N.S.; Shaner, M.; Aggarwal, S.; Arent, D.; Azevedo, I.L.; Benson, S.M.; Bradley, T.; Brouwer, J.; Chiang, Y.-M.; et al. Net-zero emissions energy systems. Science 2018, 360, eaas9793. [Google Scholar] [CrossRef] [PubMed]
- Chu, S.; Majumdar, A. Opportunities and challenges for a sustainable energy future. Nature 2012, 488, 294–303. [Google Scholar] [CrossRef] [PubMed]
- Panwar, N.L.; Kaushik, S.C.; Kothari, S. Role of renewable energy sources in environmental protection: A review. Renew. Sustain. Energy Rev. 2011, 15, 1513–1524. [Google Scholar] [CrossRef]
- Ellabban, O.; Abu-Rub, H.; Blaabjerg, F. Renewable energy resources: Current status, future prospects and their enabling technology. Renew. Sustain. Energy Rev. 2014, 39, 748–764. [Google Scholar] [CrossRef]
- Gielen, D.; Boshell, F.; Saygin, D.; Bazilian, M.D.; Wagner, N.; Gorini, R. The role of renewable energy in the global energy transformation. Energy Strateg. Rev. 2019, 24, 38–50. [Google Scholar] [CrossRef]
- Alstone, P.; Gershenson, D.; Kammen, D.M. Decentralized energy systems for clean electricity access. Nat. Clim. Chang. 2015, 5, 305–314. [Google Scholar] [CrossRef]
- Varun; Prakash, R.; Bhat, I.K. Energy, economics and environmental impacts of renewable energy systems. Renew. Sustain. Energy Rev. 2009, 13, 2716–2721. [Google Scholar] [CrossRef]
- Goldthau, A. Rethinking the governance of energy infrastructure: Scale, decentralization and polycentrism. Energy Res. Soc. Sci. 2014, 1, 134–140. [Google Scholar] [CrossRef]
- Heussen, K.; Koch, S.; Ulbig, A.; Andersson, G. Unified system-level modeling of intermittent renewable energy sources and energy storage for power system operation. IEEE Syst. J. 2012, 6, 140–151. [Google Scholar] [CrossRef]
- Eleftheriadis, I.M.; Anagnostopoulou, E.G. Identifying barriers in the diffusion of renewable energy sources. Energy Policy 2015, 80, 153–164. [Google Scholar] [CrossRef]
- Adefarati, T.; Bansal, R.C. Reliability, economic and environmental analysis of a microgrid system in the presence of renewable energy resources. Appl. Energy 2019, 236, 1089–1114. [Google Scholar] [CrossRef]
- Zhou, W.; Lou, C.; Li, Z.; Lu, L.; Yang, H. Current status of research on optimum sizing of stand-alone hybrid solar-wind power generation systems. Appl. Energy 2010, 87, 380–389. [Google Scholar] [CrossRef]
- Fathima, A.H.; Palanisamy, K. Optimization in microgrids with hybrid energy systems—A review. Renew. Sustain. Energy Rev. 2015, 45, 431–446. [Google Scholar] [CrossRef]
- Bizon, N.; Tabatabaei, N.M.; Shayeghi, H. Analysis, Control and Optimal Operations in Hybrid Power Systems; Springer: London, UK, 2013. [Google Scholar]
- Lazarov, V.; Notton, G.; Zahari, Z.; Bochev, I. Hybrid Power Systems with Renewable Energy Sources—Types, Structures, Trends for Research and Development. In Proceedings of the Eleventh International conference on Electrical Machines, Drives and Power Systems, Sofia, Bulgaria, 15–16 September 2005; pp. 515–520. [Google Scholar]
- Faccio, M.; Gamberi, M.; Bortolini, M.; Nedaei, M. State-of-art review of the optimization methods to design the configuration of hybrid renewable energy systems (HRESs). Front. Energy 2018, 12, 591–622. [Google Scholar] [CrossRef]
- Benalcazar, P.; Suski, A.; Kaminski, J. The effects of capital and energy subsidies on the optimal design of microgrid systems. Energies 2020, 13, 955. [Google Scholar] [CrossRef]
- International Energy Agency. Energy Access Outlook 2017: From Poverty to Prosperity; International Energy Agency: Paris, France, 2017. [Google Scholar]
- Almeshqab, F.; Ustun, T.S. Lessons learned from rural electrification initiatives in developing countries: Insights for technical, social, financial and public policy aspects. Renew. Sustain. Energy Rev. 2019, 102, 35–53. [Google Scholar] [CrossRef]
- Nema, P.; Nema, R.K.; Rangnekar, S. A current and future state of art development of hybrid energy system using wind and PV–solar: A review. Renew. Sustain. Energy Rev. 2009, 13, 2096–2103. [Google Scholar] [CrossRef]
- Ashok, S. Optimised model for community-based hybrid energy system. Renew. Energy 2007, 32, 1155–1164. [Google Scholar] [CrossRef]
- Anoune, K.; Bouya, M.; Astito, A.; Abdellah, A.B. Sizing methods and optimization techniques for PV–wind based hybrid renewable energy system: A review. Renew. Sustain. Energy Rev. 2018, 93, 652–673. [Google Scholar] [CrossRef]
- Siddaiah, R.; Saini, R.P. A review on planning, configurations, modeling and optimization techniques of hybrid renewable energy systems for off grid applications. Renew. Sustain. Energy Rev. 2016, 58, 376–396. [Google Scholar] [CrossRef]
- Sinha, S.; Chandel, S.S. Review of recent trends in optimization techniques for solar photovoltaic-wind based hybrid energy systems. Renew. Sustain. Energy Rev. 2015, 50, 755–769. [Google Scholar] [CrossRef]
- Lian, J.; Zhang, Y.; Ma, C.; Yang, Y.; Chaima, E. A review on recent sizing methodologies of hybrid renewable energy systems. Energy Convers. Manag. 2019, 199, 112027. [Google Scholar] [CrossRef]
- Asrari, A.; Ghasemi, A.; Javidi, M.H. Economic evaluation of hybrid renewable energy systems for rural electrification in Iran—A case study. Renew. Sustain. Energy Rev. 2012, 16, 3123–3130. [Google Scholar] [CrossRef]
- Huneke, F.; Henkel, J.; González, J.A.B.; Erdmann, G. Optimisation of hybrid off-grid energy systems by linear programming. Energy. Sustain. Soc. 2012, 2, 7. [Google Scholar] [CrossRef]
- Zhang, W.; Maleki, A.; Rosen, M.A.; Liu, J. Optimization with a simulated annealing algorithm of a hybrid system for renewable energy including battery and hydrogen storage. Energy 2018, 163, 191–207. [Google Scholar] [CrossRef]
- Wang, X.; Palazoglu, A.; El-Farra, N.H. Operational optimization and demand response of hybrid renewable energy systems. Appl. Energy 2015, 143, 324–335. [Google Scholar] [CrossRef]
- Ismail, M.S.; Moghavvemi, M.; Mahlia, T.M.I. Genetic algorithm based optimization on modeling and design of hybrid renewable energy systems. Energy Convers. Manag. 2014, 85, 120–130. [Google Scholar] [CrossRef]
- Sanajaoba, S.; Fernandez, E. Maiden application of Cuckoo Search algorithm for optimal sizing of a remote hybrid renewable energy System. Renew. Energy 2016, 96, 1–10. [Google Scholar] [CrossRef]
- Barzola, J.; Espinoza, M.; Cabrera, F. Analysis of Hybrid Solar / Wind / Diesel Renewable Energy System for off-grid Rural Electrification. Int. J. Renew. Energy Res. 2016, 6, 1146–1152. [Google Scholar]
- Kaviani, A.K.; Riahy, G.H.; Kouhsari, S.M. Optimal design of a reliable hydrogen-based stand-alone wind/PV generating system, considering component outages. Renew. Energy 2009, 34, 2380–2390. [Google Scholar] [CrossRef]
- Chedid, R.; Saliba, Y. Optimization and control of autonomous renewable energy systems. Int. J. Energy Res. 1996, 20, 609–624. [Google Scholar] [CrossRef]
- Ekren, O.; Ekren, B.Y. Size optimization of a PV/wind hybrid energy conversion system with battery storage using simulated annealing. Appl. Energy 2010, 87, 592–598. [Google Scholar] [CrossRef]
- Bekele, G.; Tadesse, G. Feasibility study of small Hydro/PV/Wind hybrid system for off-grid rural electrification in Ethiopia. Appl. Energy 2012, 97, 5–15. [Google Scholar] [CrossRef]
- Saiprasad, N.; Kalam, A.; Zayegh, A. Triple Bottom Line Analysis and Optimum Sizing of Renewable Energy Using Improved Hybrid Optimization Employing the Genetic Algorithm: A Case Study from India. Energies 2019, 12, 349. [Google Scholar] [CrossRef]
- Panahandeh, B.; Bard, J.; Outzourhit, A.; Zejli, D. Simulation of PV–wind-hybrid systems combined with hydrogen storage for rural electrification. Int. J. Hydrog. Energy 2011, 36, 4185–4197. [Google Scholar] [CrossRef]
- Upadhyay, S.; Sharma, M.P. A review on configurations, control and sizing methodologies of hybrid energy systems. Renew. Sustain. Energy Rev. 2014, 38, 47–63. [Google Scholar] [CrossRef]
- Bajpai, P.; Dash, V. Hybrid renewable energy systems for power generation in stand-alone applications: A review. Renew. Sustain. Energy Rev. 2012, 16, 2926–2939. [Google Scholar] [CrossRef]
- Malheiro, A.; Castro, P.M.; Lima, R.M.; Estanqueiro, A. Integrated sizing and scheduling of wind/PV/diesel/battery isolated systems. Renew. Energy 2015, 83, 646–657. [Google Scholar] [CrossRef]
- Abuelrub, A.; Singh, C. Planning of a hybrid energy system connected to a distribution system. In Proceedings of the 2017 IEEE Manchester PowerTech, Manchester, UK, 18–22 June 2017. [Google Scholar]
- Hiendro, A.; Kurnianto, R.; Rajagukguk, M.; Simanjuntak, Y.M. Junaidi, Techno-economic analysis of photovoltaic/wind hybrid system for onshore/remote area in Indonesia. Energy 2013, 59, 652–657. [Google Scholar] [CrossRef]
- Dhundhara, S.; Verma, Y.P.; Williams, A. Techno-economic analysis of the lithium-ion and lead-acid battery in microgrid systems. Energy Convers. Manag. 2018, 177, 122–142. [Google Scholar] [CrossRef]
- Tezer, T.; Yaman, R.; Yaman, G. Evaluation of approaches used for optimization of stand-alone hybrid renewable energy systems. Renew. Sustain. Energy Rev. 2017, 73, 840–853. [Google Scholar] [CrossRef]
- Van den Bergh, K.; Bruninx, K.; Delarue, E.; Dhaeseleer, W. A Mixed-Integer Linear Formulation of the Unit Commitment Problem. Work. Pap. 2014. Available online: https://www.mech.kuleuven.be/en/tme/research/energy_environment/Pdf/wpen2014-07.pdf (accessed on 23 May 2019).
- Bogaraj, T.; Kanakaraj, J.; Kumar, K.M. Optimal sizing and cost analysis of hybrid power system for a stand-alone application in Coimbatore region: A case study. Arch. Electr. Eng. 2015, 64, 139–155. [Google Scholar] [CrossRef]
- King, D.L.; Kratochvil, J.A.; Boyson, W.E. Temperature coefficients for PV modules and arrays: Measurement methods, difficulties, and results. In Proceedings of the Conference Record of the Twenty Sixth IEEE Photovoltaic Specialists Conference—1997, Anaheim, CA, USA, 29 September–3 October 1997; pp. 1183–1186. [Google Scholar]
- IRENA. Electricity Storage and Renewables: Costs and Markets to 2030; IRENA: Abu Dhabi, UAE, 2017. [Google Scholar]
- Hernández-Moro, J.; Martínez-Duart, J.M. CSP electricity cost evolution and grid parities based on the IEA roadmaps. Energy Policy 2012, 41, 184–192. [Google Scholar] [CrossRef]
- Brook, A.; Kendrick, D.; Meeraus, A. GAMS, a user’s guide. ACM SIGNUM Newsl. 1988, 23, 10–11. [Google Scholar] [CrossRef]
- IRENA. Renewable Energy Market Analysis: Latin America; IRENA: Abu Dhabi, UAE, 2016. [Google Scholar]
- ARCONEL. Estadística Anual y Multianual del sector eléctrico Ecuatoriano. Annu. Rep. 2016. Available online: https://www.regulacionelectrica.gob.ec/boletines-estadisticos/ (accessed on 23 May 2019).
- Llerena-Pizarro, O.R.; Micena, R.P.; Tuna, C.E.; Silveira, J.L. Electricity sector in the Galapagos Islands: Current status, renewable sources, and hybrid power generation system proposal. Renew. Sustain. Energy Rev. 2019, 108, 65–75. [Google Scholar] [CrossRef]
- European Commission; European Union. Programa EURO-SOLAR Síntesis Final Energía renovable para un desarrollo sostenible. Ref. Ares. 2013, 2014, 2463428. [Google Scholar]
- Cevallos-Sierra, J.; Ramos-Martin, J. Spatial assessment of the potential of renewable energy: The case of Ecuador. Renew. Sustain. Energy Rev. 2018, 81, 1154–1165. [Google Scholar] [CrossRef]
- Carvajal, P.E.; Li, F.G.N.; Soria, R.; Cronin, J.; Anandarajah, G.; Mulugetta, Y. Large hydropower, decarbonisation and climate change uncertainty: Modelling power sector pathways for Ecuador. Energy Strateg. Rev. 2019, 23, 86–99. [Google Scholar] [CrossRef]
- Ponce-Jara, M.A.; Castro, M.; Pelaez-Samaniego, M.R.; Espinoza-Abad, J.L.; Ruiz, E. Electricity sector in Ecuador: An overview of the 2007–2017 decade. Energy Policy 2018, 113, 513–522. [Google Scholar] [CrossRef]
- Sengupta, M.; Xie, Y.; Lopez, A.; Habte, A.; Maclaurin, G.; Shelby, J. The National Solar Radiation Data Base (NSRDB). Renew. Sustain. Energy Rev. 2018, 89, 51–60. [Google Scholar] [CrossRef]
- ESMAP; SOLARGIS; WB; IFC. Global Solar Atlas. 2019. Available online: https://globalsolaratlas.info/map (accessed on 23 May 2019).
- DTU Wind Energy; World Bank Group. Global Wind Atlas. 2018. Available online: https://globalwindatlas.info/ (accessed on 23 May 2019).
- Razmjoo, A.; Shirmohammadi, R.; Davarpanah, A.; Pourfayaz, F.; Aslani, A. Stand-alone hybrid energy systems for remote area power generation. Energy Rep. 2019, 5, 231–241. [Google Scholar] [CrossRef]
- Meier, P.; Tuntivate, V.; Barnes, D.F.; Bogach, S.V.; Farchy, D. Peru: National Survey of Rural Household Energy Use, Energy and Poverty Special Report 007/10; World Bank: Washington, DC, USA, 2010; Available online: https://www.esmap.org/sites/esmap.org/files/ESMAP_PeruNationalSurvey_Web_0.pdf (accessed on 23 May 2019).
- Mandelli, S.; Merlo, M.; Colombo, E. Novel procedure to formulate load profiles for off-grid rural areas. Energy Sustain. Dev. 2016, 31, 130–142. [Google Scholar]
- Porras, J. Estudio de Soluciones para Integración de Microproducciones en Redes Aisladas; Instituto Politecnico de Leira: Leiria, Portugal, 2017. [Google Scholar]
- Urdiales, L. Procedimiento para la Electrificacion en Zonas Aisladas: Caso canton Taisha, Morona Santiago; Universidad de Cuenca: Cuenca, Ecuador, 2015. [Google Scholar]
- IRENA. IRENA: Renewable Power Generation Costs in 2017. Int. Renew. Energy Agency 2018. Available online: https://www.irena.org/publications/2018/Jan/Renewable-power-generation-costs-in-2017 (accessed on 23 May 2019).
- Fodhil, F.; Hamidat, A.; Nadjemi, O. Potential, optimization and sensitivity analysis of photovoltaic-diesel–battery hybrid energy system for rural electrification in Algeria. Energy 2019, 169, 613–624. [Google Scholar] [CrossRef]
- Kolhe, M.L.; Ranaweera, K.M.I.U.; Gunawardana, A.G.B.S. Techno-economic sizing of off-grid hybrid renewable energy system for rural electrification in Sri Lanka. Sustain. Energy Technol. Assess. 2015, 11, 53–64. [Google Scholar] [CrossRef]
- Trading Economics, Ecuador Interest Rate. 2019. Available online: https://tradingeconomics.com/ecuador/interest-rate (accessed on 23 May 2019).
- Walker, A. PV O&M Cost Model and Cost Reduction; NREL: Lakewood, CO, USA, 2017.
- Predescu, M. Economic evaluation of small wind turbines and hybrid systems for residential use. Renew. Energy Environ. Sustain. 2016, 1, 33. [Google Scholar] [CrossRef]
- Naumann, M.; Karl, R.C.; Truong, C.N.; Jossen, A.; Hesse, H.C. Lithium-ion battery cost analysis in PV–household application. Energy Procedia 2015, 73, 37–47. [Google Scholar] [CrossRef]
- EP PETROECUADOR. Gerencia de Comercialización Nacional, Estructura de Precios Mayo. 2019. Available online: https://www.eppetroecuador.ec/wp-content/uploads/downloads/2019/05/ESTRUCTURA-DE-PRECIOS-MAYO-2019-MENSUAL-SNI-DEL-23-AL-29-DE-MAYO-2019.pdf (accessed on 23 May 2019).
- Ghafoor, A.; Munir, A. Design and economics analysis of an off-grid PV system for household electrification. Renew. Sustain. Energy Rev. 2015, 42, 496–502. [Google Scholar] [CrossRef]
- Wheeler, R.K. Efficient Operation of Diesel Generator Sets in Remote Environments; Virginia Polytechnic Institute and State University: Blacksburg, VA, USA, 2017. [Google Scholar]
- Advances in Wind Power; InTech: London, UK, 2012.
- Altun, A.F.; Kilic, M. Design and performance evaluation based on economics and environmental impact of a PV–wind-diesel and battery standalone power system for various climates in Turkey. Renew. Energy 2020, 157, 424–443. [Google Scholar] [CrossRef]
- Agyekum, E.B.; Nutakor, C. Feasibility study and economic analysis of stand-alone hybrid energy system for southern Ghana. Sustain. Energy Technol. Assess. 2020, 39, 100695. [Google Scholar] [CrossRef]
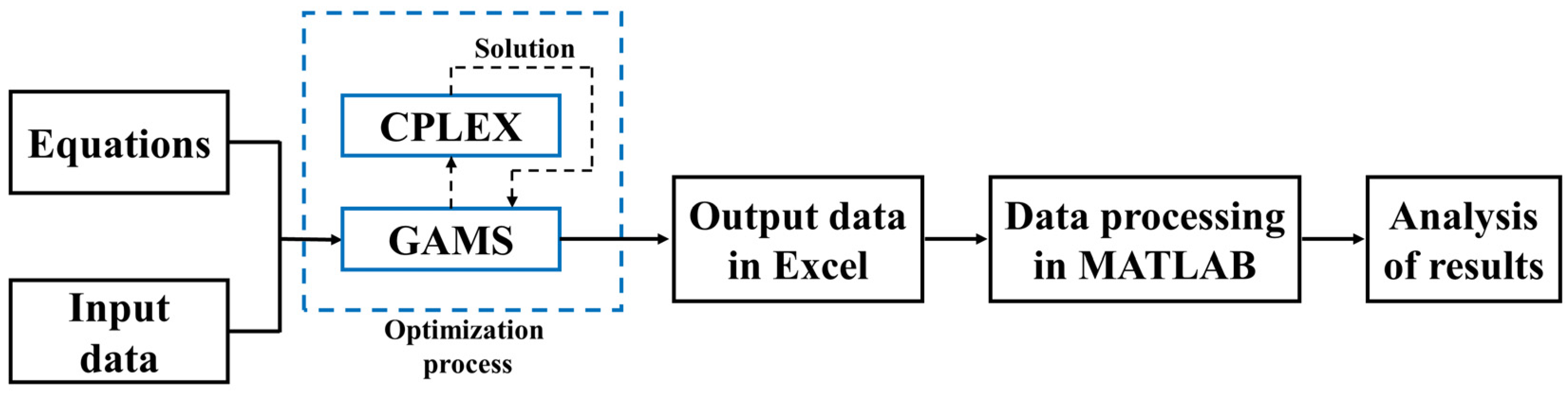
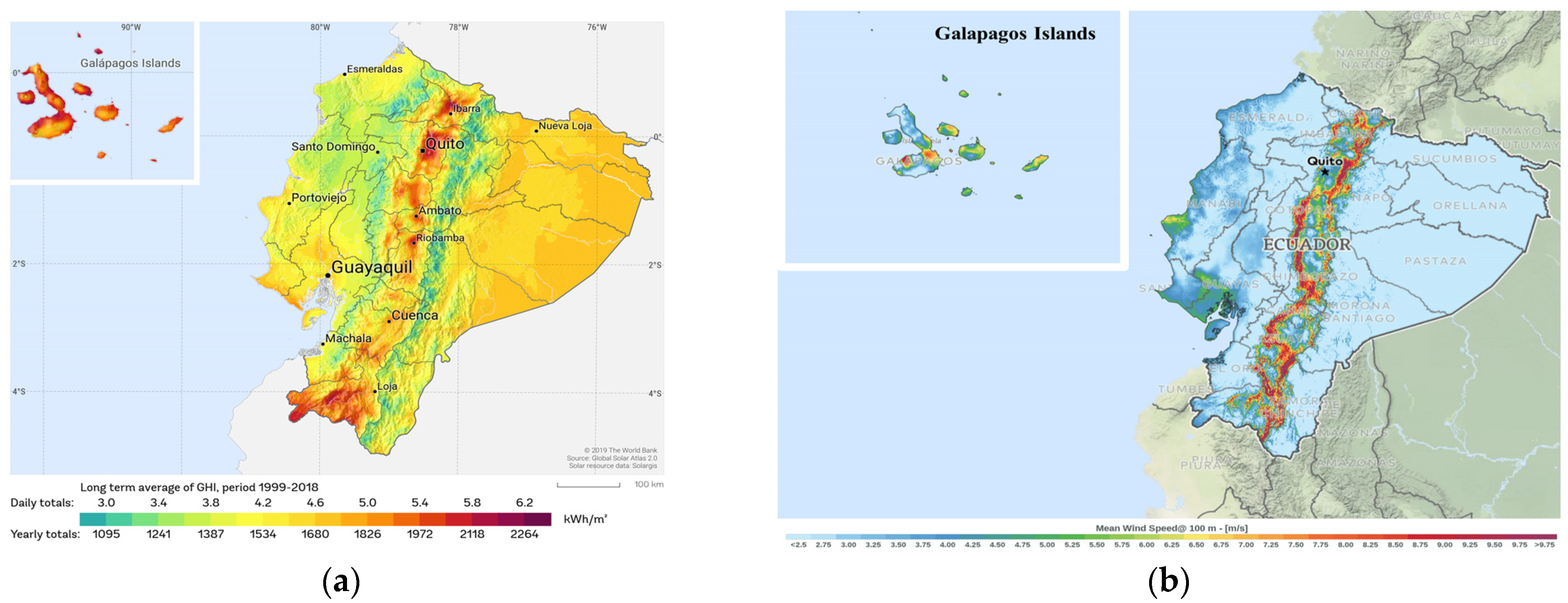
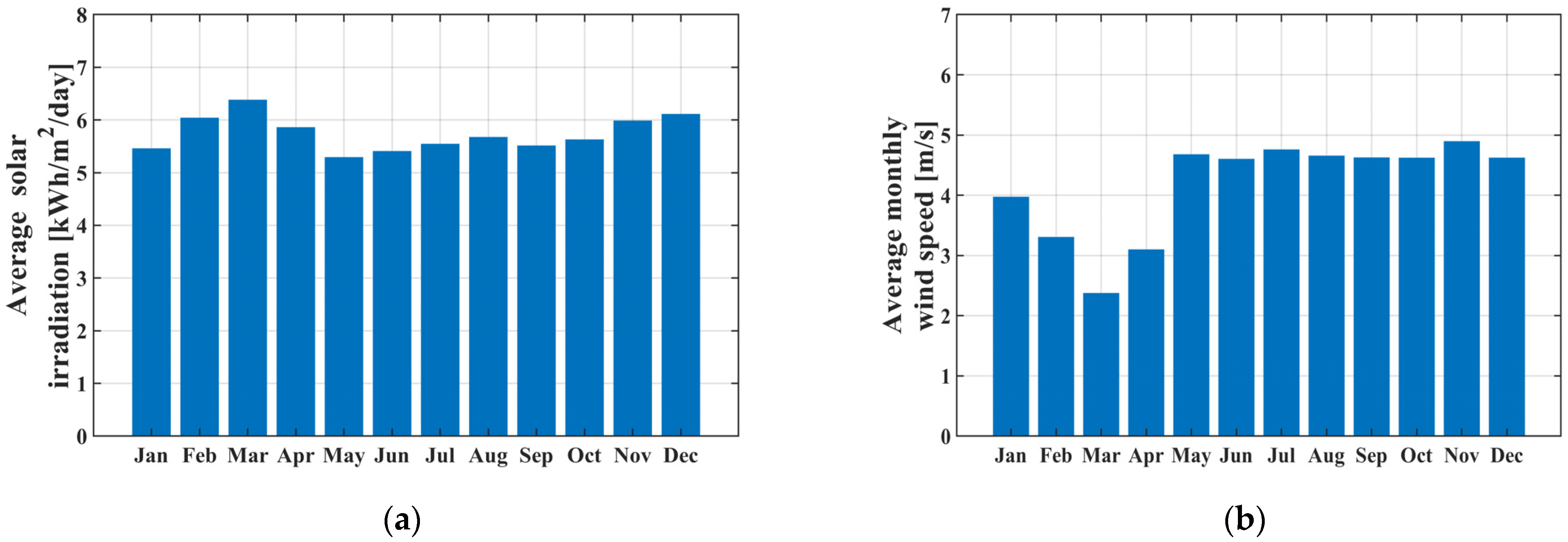
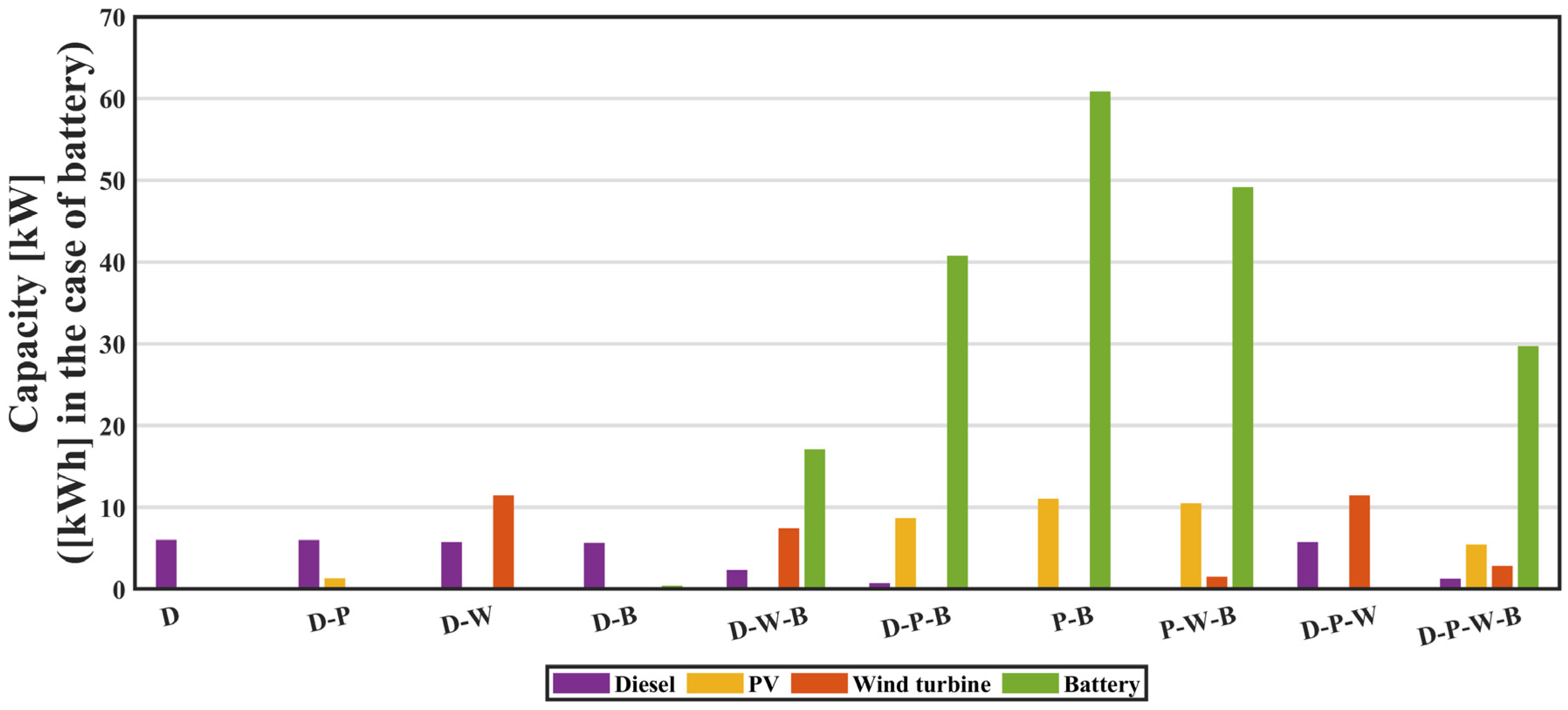
| Reference | Optimization Approach | Analyzed Technology | Objective Function(s) | Location | |||||
|---|---|---|---|---|---|---|---|---|---|
| PV | Wind Turbine | Hydro | Diesel | Fuel Cell | Storage | ||||
| [29] | GA | ● | ● | ● | ● | Minimization of total fixed capital costs and variable cost | Single-family residential home | ||
| [31] | PSO | ● | ● | ● | Minimization of total system costs | Remote area in Uttarakhand, India | |||
| [27] | LP | ● | ● | ● | ● | Minimization of annualized capital costs and O&M costs | Rural villages in India and Colombia | ||
| [28] | SA | ● | ● | ● | ● | Minimization of life cycle costs | Remote area in Kerman, Iran | ||
| [32] | HOMER | ● | ● | ● | ● | Minimization of total net present costs | Rural village in Santa Elena, Ecuador | ||
| [33] | PSO | ● | ● | ● | Minimization of annualized costs subject to reliability constraints | HES in Ardebil, Iran | |||
| [34] | LP | ● | ● | ● | ● | Minimization of production costs of electricity | Dahr-el-Baidar, Lebanon | ||
| [35] | SA | ● | ● | ● | Minimization of system total costs | Campus area in Turkey | |||
| [36] | HOMER | ● | ● | ● | ● | ● | Minimization of total net present costs | Group of nonelectrified villages in Ethiopia | |
| [37] | iHOGA | ● | ● | ● | Minimization of total net present costs | Aralvaimozhi, India | |||
| [38] | Hybrid2 | ● | ● | ● | ● | Least-cost system configuration | HES in Morocco | ||
| Appliance Name | Quantity | Nominal Power Rate | Total Power | Overall Time Each Appliance Is on | Daily Consumption |
|---|---|---|---|---|---|
| (Unit) | (-) | (W) | (kW) | (h) | (kWh/day) |
| Bulbs | 3 | 26 | 0.078 | 5 | 0.390 |
| Outdoor bulb | 1 | 26 | 0.026 | 12 | 0.312 |
| Television | 1 | 100 | 0.100 | 2 | 0.2 |
| Radio | 1 | 20 | 0.020 | 6 | 0.12 |
| Battery charger | 1 | 20 | 0.020 | 4 | 0.08 |
| Other small device | 1 | 20 | 0.02 | 4 | 0.04 |
| Subtotal | 0.244 | 1.182 | |||
| Total (30 houses) | 7.32 | 35.46 | |||
| Technology | Unit | PV | Wind Turbine | Diesel Generator | Lithium-Ion Battery |
|---|---|---|---|---|---|
| Investment cost | $/kW ($/kWh in the case of battery) | 1400 [67] | 1829 [67] | 375 [68] | 300 [49] |
| Lifespan | years | 20 [69] | 20 [69] | 20 [68] | 10 [49] |
| Interest rate | % | 8.6 [70] | 8.6 [70] | 8.6 [70] | 8.6 [70] |
| O&M | % of investment cost | 1.5 [71] | 2 [72] | 6.4 [27] | 2 [73] |
| Parameter | DP ($/kWh) | (%) | (%) | (%) | (%) | (%) | ($/kWh) | (m/s) | (m/s) | (m/s) |
| Value | 0.27 [74] | 90 [75] | 43.1 [76] | 90 [49] | 95 [49] | 90 [49] | 0.00045 [41] | 2.5 [77] | 24 [77] | 10 [77] |
| Case | Technology Capacity | Annual CO2 Emissions (kg) | LCOE ($/kWh) | TLCC ($) | |||
|---|---|---|---|---|---|---|---|
| Diesel (kW) | PV (kW) | Wind (kW) | Battery (kWh) | ||||
| Diesel (D) | 6.04 | 0.00 | 0.00 | 0.00 | 16,401 | 0.69 | 84,221 |
| Diesel–PV (D-P) | 6.02 | 1.32 | 0.00 | 0.00 | 15,398 | 0.67 | 81,386 |
| Diesel–Wind (D-W) | 5.77 | 0.00 | 11.45 | 0.00 | 5621 | 0.46 | 55,969 |
| Diesel–Battery (D-B) | 5.67 | 0.00 | 0.00 | 0.43 | 16,402 | 0.69 | 84,211 |
| Diesel–Wind–Battery (D-W-B) | 2.32 | 0.00 | 7.42 | 17.11 | 3337 | 0.35 | 42,301 |
| Diesel–PV–Battery (D-P-B) | 0.75 | 8.66 | 0.00 | 40.75 | 880 | 0.32 | 38,604 |
| PV–Battery (P-B) | 0.00 | 11.08 | 0.00 | 60.88 | 0 | 0.39 | 47,499 |
| PV–Wind–Battery (P-W-B) | 0.00 | 10.51 | 1.52 | 49.18 | 0 | 0.36 | 44,153 |
| Diesel–PV–Wind (D-P-W) | 5.77 | 0.00 | 11.45 | 0.00 | 5621 | 0.46 | 55,969 |
| Diesel–PV–Wind–Battery (D-P-W-B) | 1.27 | 5.46 | 2.84 | 29.72 | 1244 | 0.30 | 36,352 |
| Case | Technology Capacity | Annual CO2 Emissions (kg) | LCOE ($/kWh) | TLCC ($) | |||
|---|---|---|---|---|---|---|---|
| Diesel (kW) | PV (kW) | Wind (kW) | Battery (kWh) | ||||
| Diesel (D) | 6.04 | 0.00 | 0.00 | 0.00 | 16,401 | 0.69 | 84,221 |
| Diesel–PV (D-P) | 6.03 | 1.51 | 0.00 | 0.00 | 15,421 | 0.67 | 81,813 |
| Diesel–Wind (D-W) | 6.04 | 0.00 | 0.00 | 0.00 | 16,401 | 0.69 | 84,221 |
| Diesel–Battery (D-B) | 5.67 | 0.00 | 0.00 | 0.43 | 16,402 | 0.69 | 84,211 |
| Diesel–Wind–Battery (D-W-B) | 5.67 | 0.00 | 0.00 | 0.43 | 16,402 | 0.69 | 84,211 |
| Diesel–PV–Battery (D-P-B) | 0.80 | 11.38 | 0.00 | 39.95 | 1382 | 0.37 | 45,035 |
| PV–Battery (P-B) | 0.00 | 18.90 | 0.00 | 61.15 | 0 | 0.50 | 60,127 |
| PV–Wind–Battery (P-W-B) | 0.00 | 18.90 | 0.00 | 61.15 | 0 | 0.50 | 60,127 |
| Diesel–PV–Wind (D-P-W) | 6.03 | 1.51 | 0.00 | 0.00 | 15,421 | 0.67 | 81,813 |
| Diesel–PV–Wind–Battery (D-P-W-B) | 0.80 | 11.38 | 0.00 | 39.95 | 1382 | 0.37 | 45,035 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Benalcazar, P.; Suski, A.; Kamiński, J. Optimal Sizing and Scheduling of Hybrid Energy Systems: The Cases of Morona Santiago and the Galapagos Islands. Energies 2020, 13, 3933. https://doi.org/10.3390/en13153933
Benalcazar P, Suski A, Kamiński J. Optimal Sizing and Scheduling of Hybrid Energy Systems: The Cases of Morona Santiago and the Galapagos Islands. Energies. 2020; 13(15):3933. https://doi.org/10.3390/en13153933
Chicago/Turabian StyleBenalcazar, Pablo, Adam Suski, and Jacek Kamiński. 2020. "Optimal Sizing and Scheduling of Hybrid Energy Systems: The Cases of Morona Santiago and the Galapagos Islands" Energies 13, no. 15: 3933. https://doi.org/10.3390/en13153933
APA StyleBenalcazar, P., Suski, A., & Kamiński, J. (2020). Optimal Sizing and Scheduling of Hybrid Energy Systems: The Cases of Morona Santiago and the Galapagos Islands. Energies, 13(15), 3933. https://doi.org/10.3390/en13153933







