Improving Thermochemical Energy Storage Dynamics Forecast with Physics-Inspired Neural Network Architecture
Abstract
1. Introduction
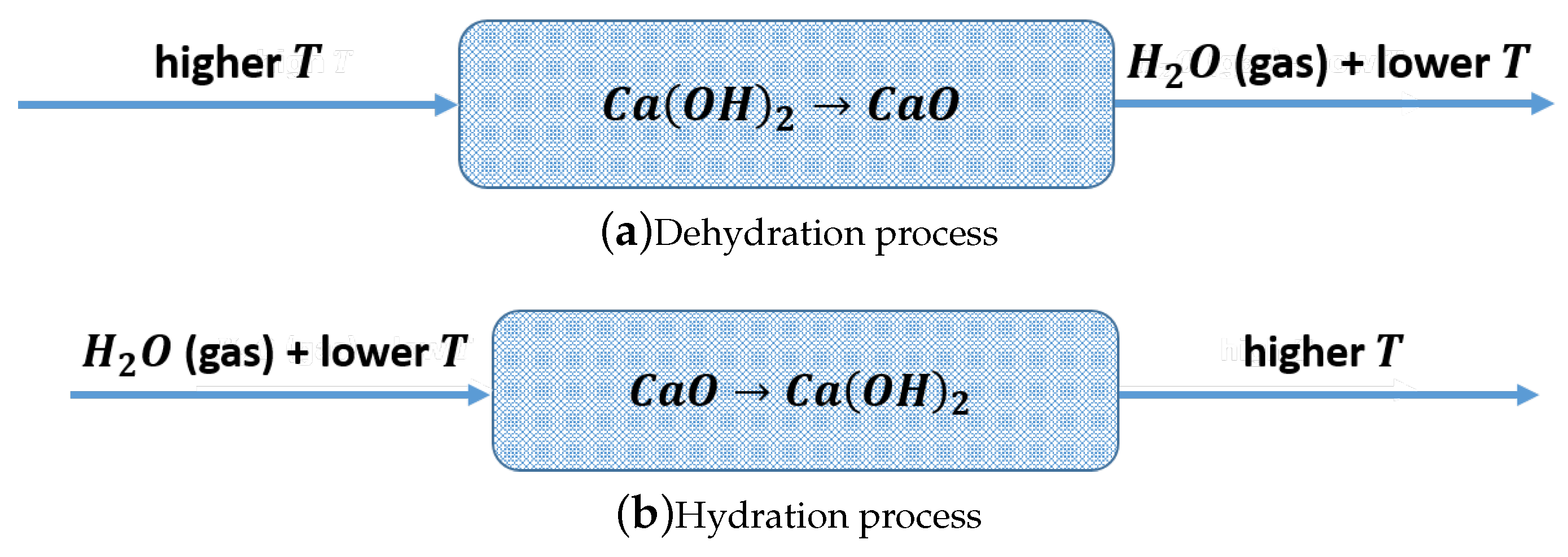
1.1. Thermochemical Energy Storage
1.2. Physics-Inspired Artificial Neural Networks
1.3. Approach and Contributions
2. Materials and Methods
2.1. Governing Equations
2.2. Input and Output Variables
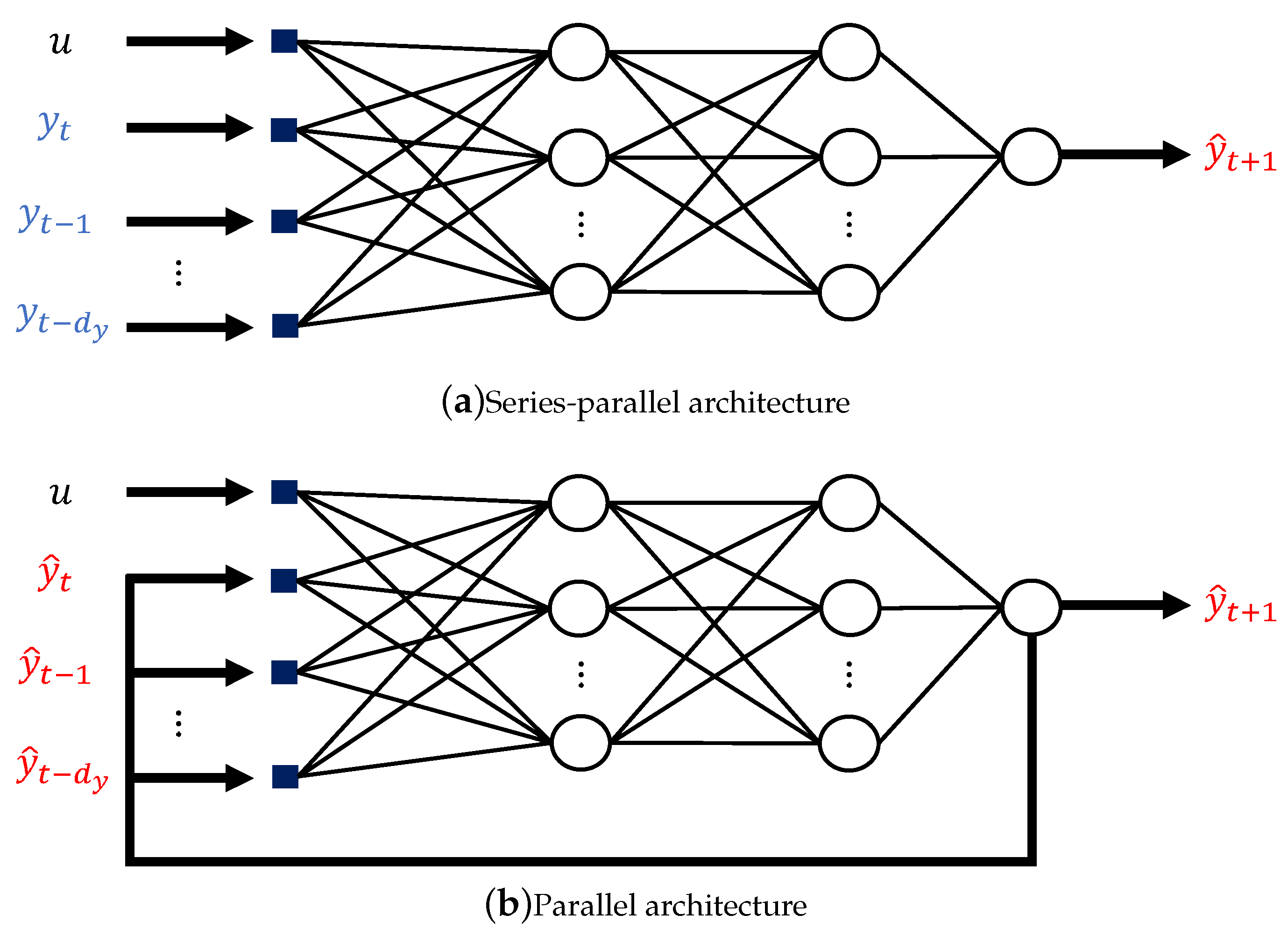
2.3. Aligning the ANN Structure with Physical Knowledge of the System
2.4. Physical Constraints in the Training Objective Function
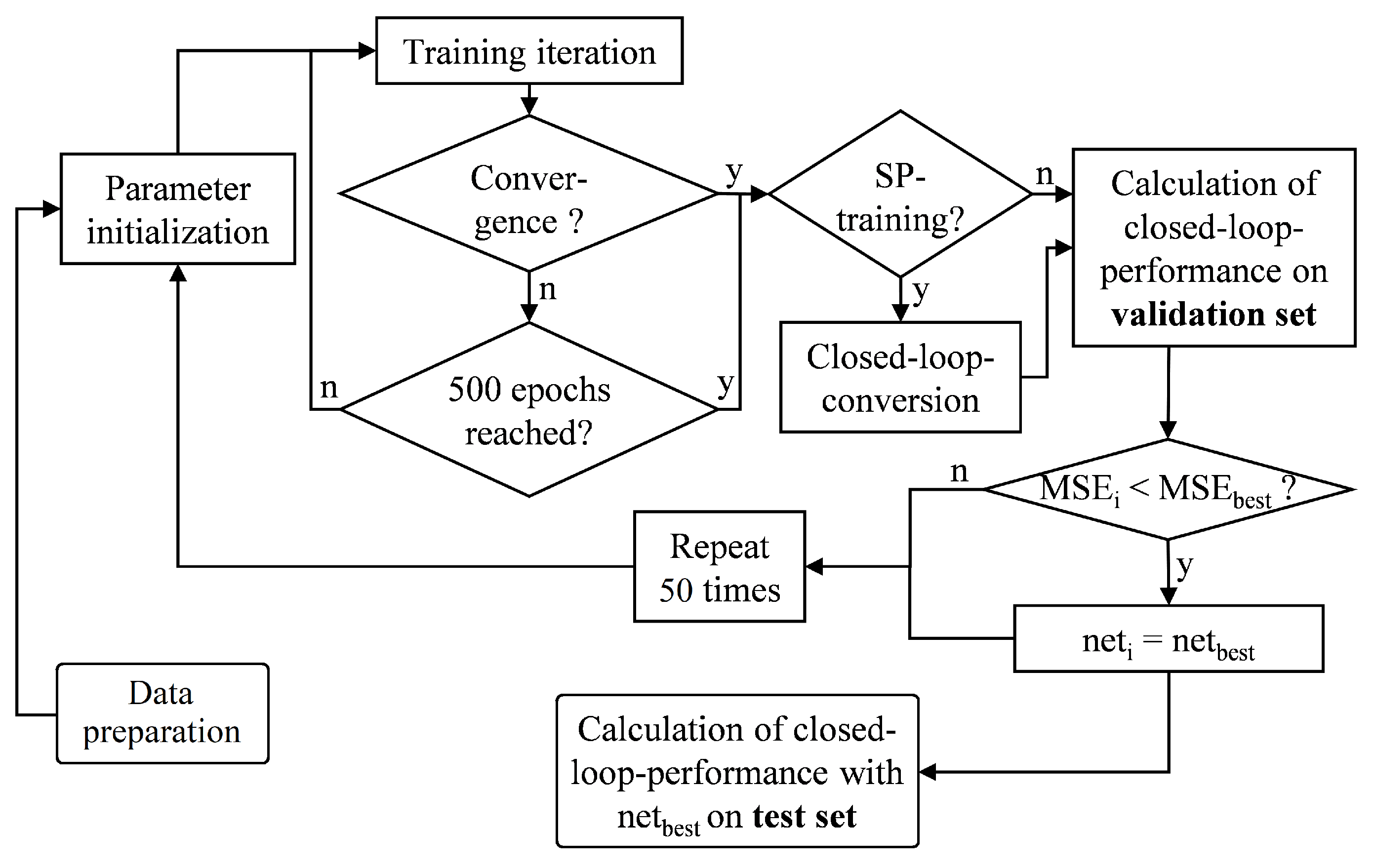
2.5. Obtaining Optimum Network Parameters
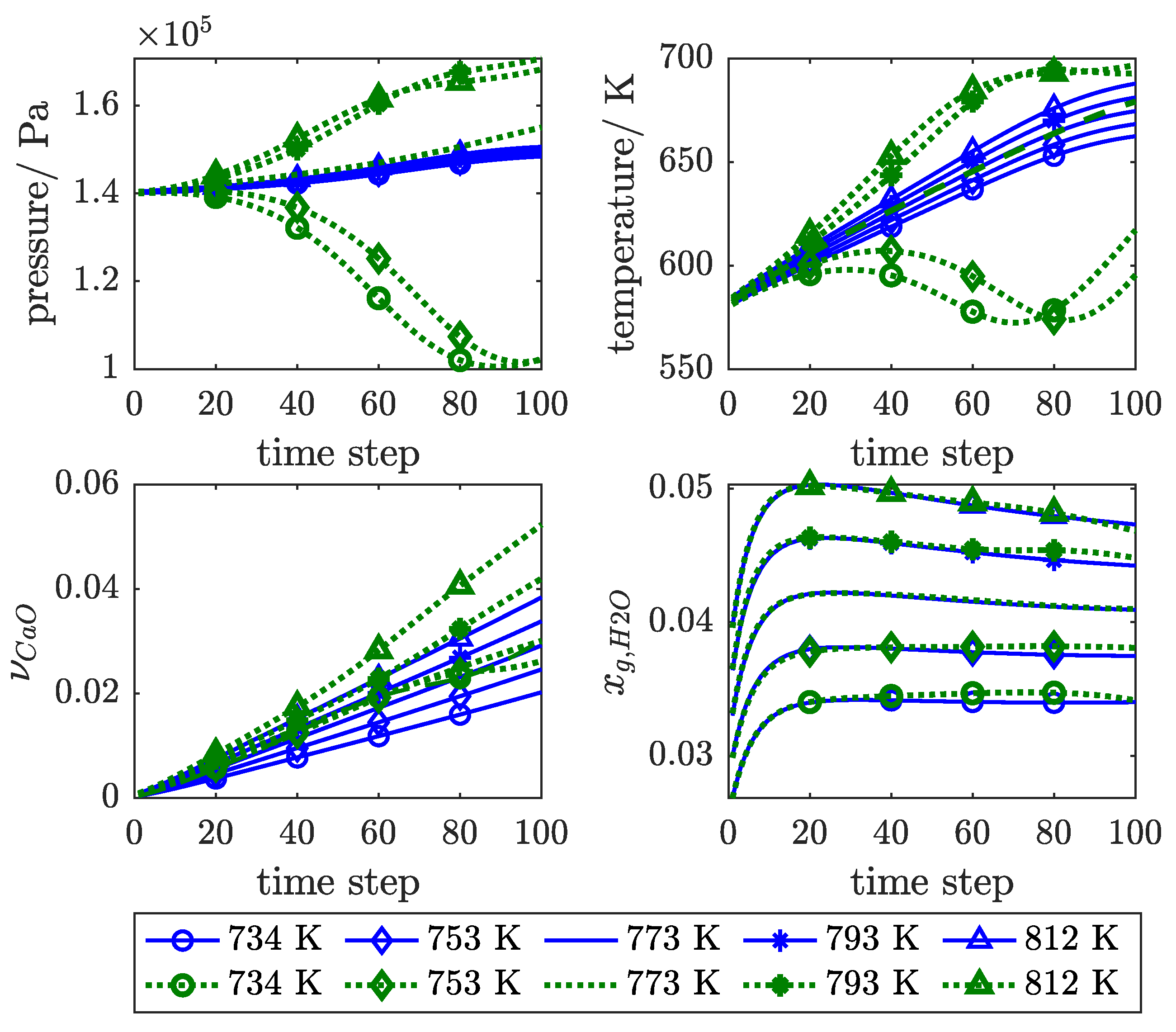
3. Results and Discussion
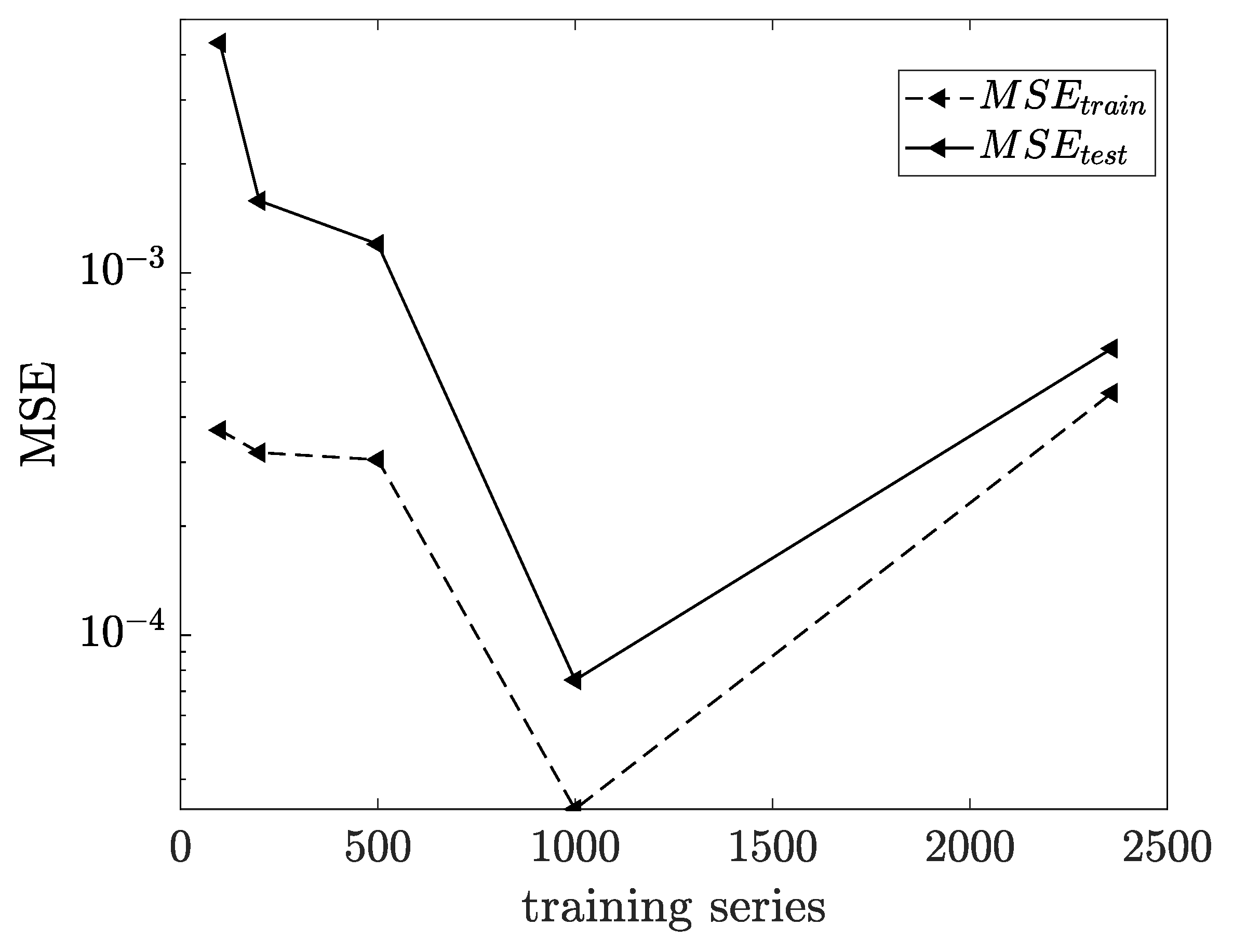
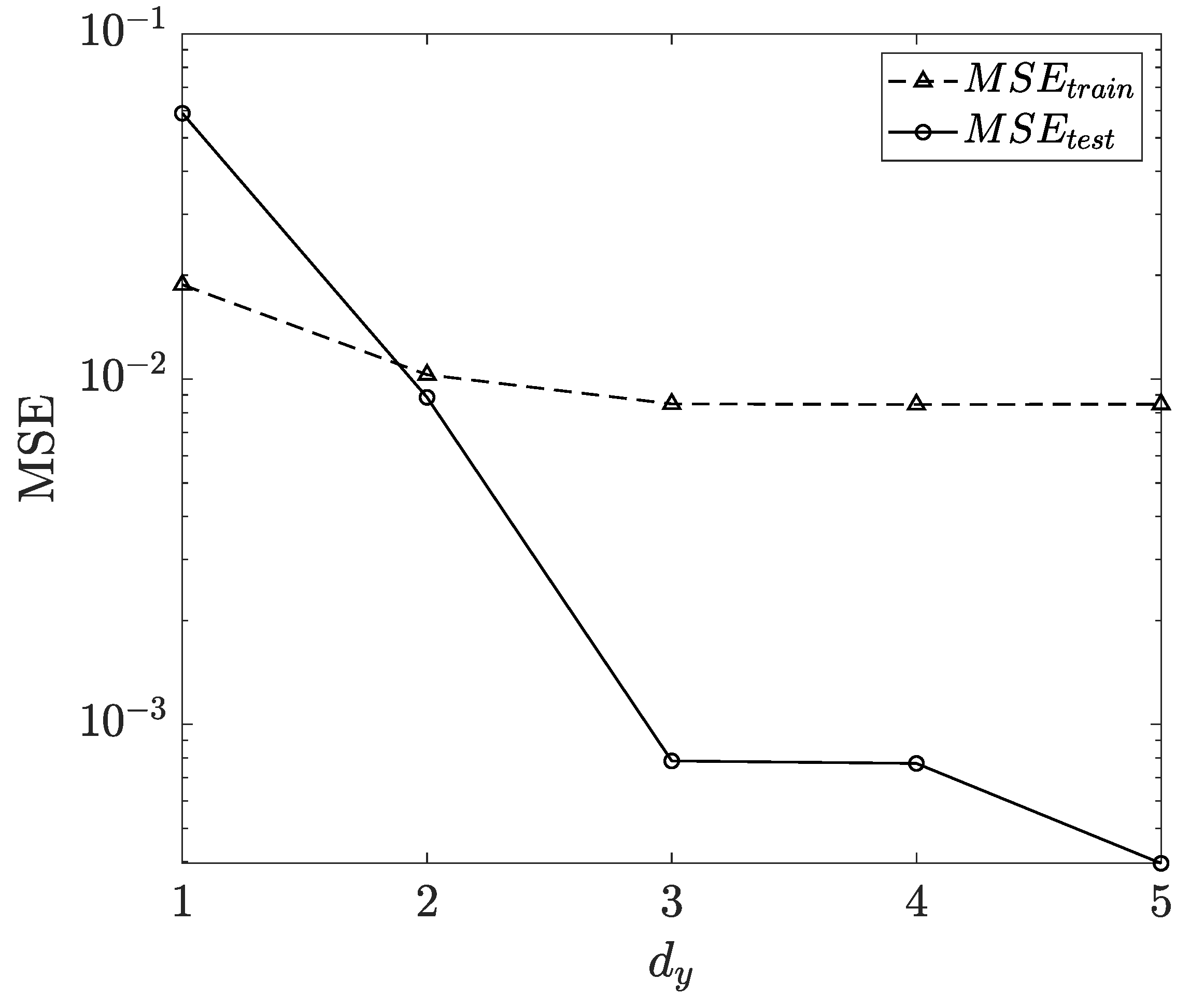
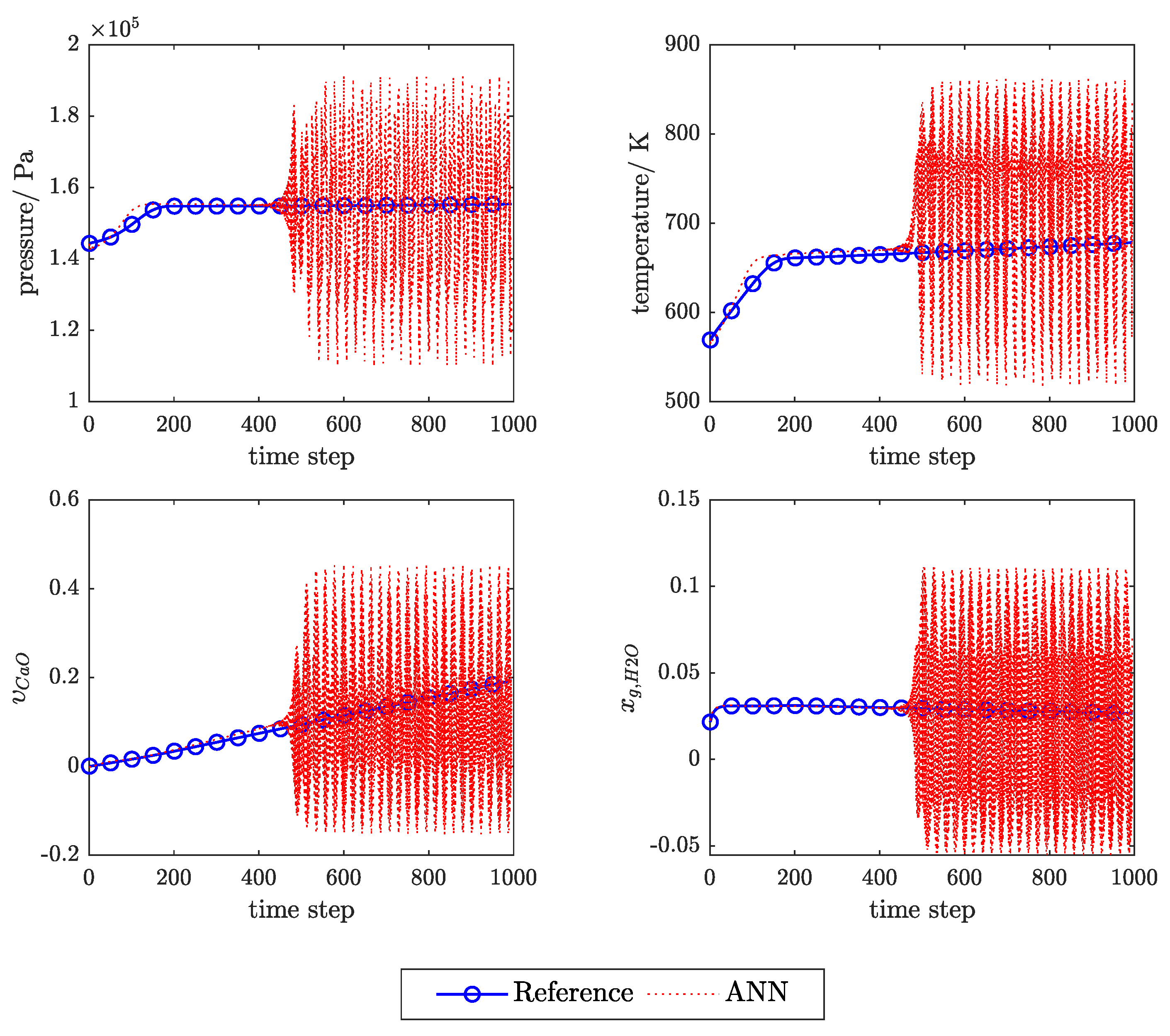
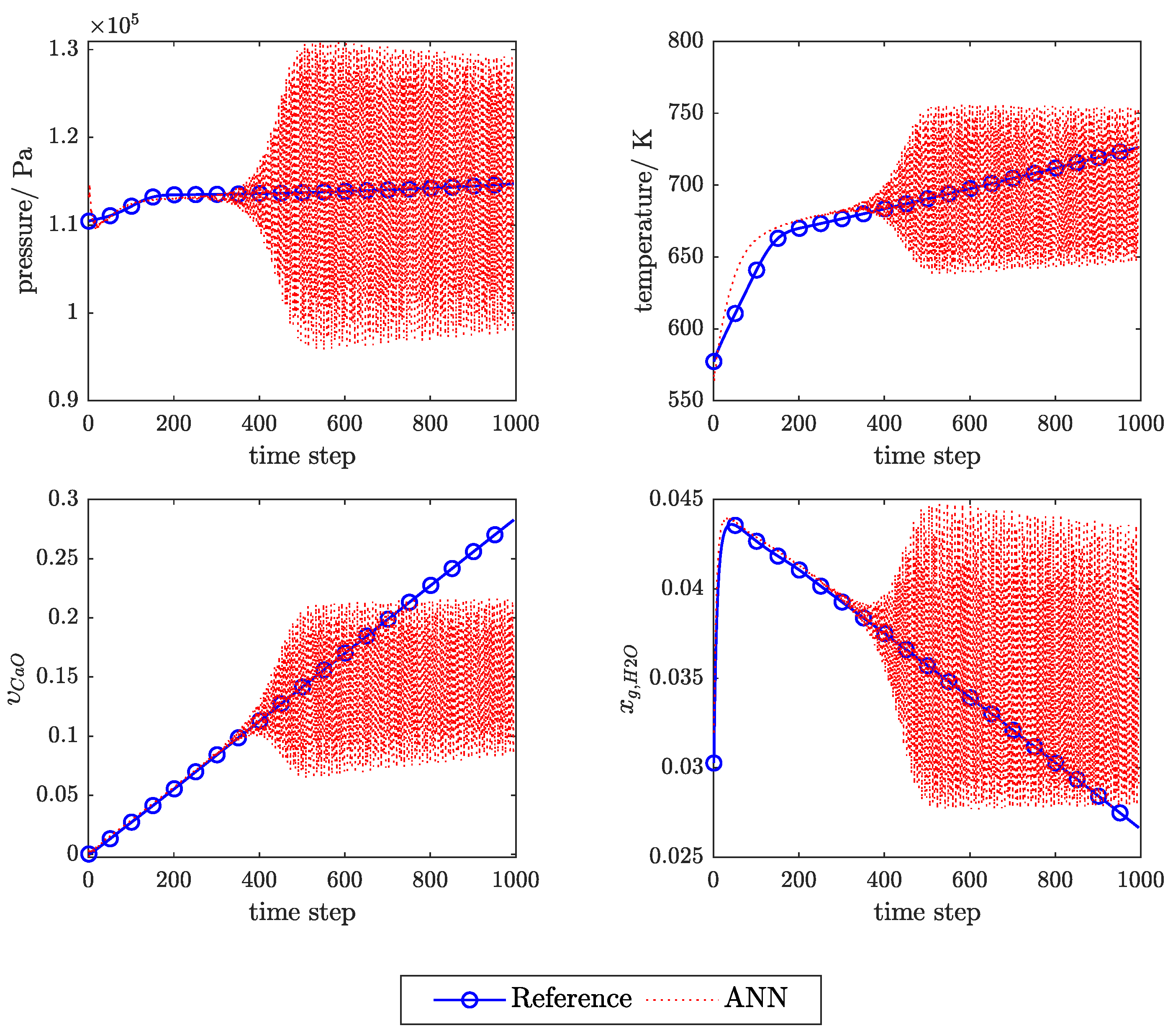
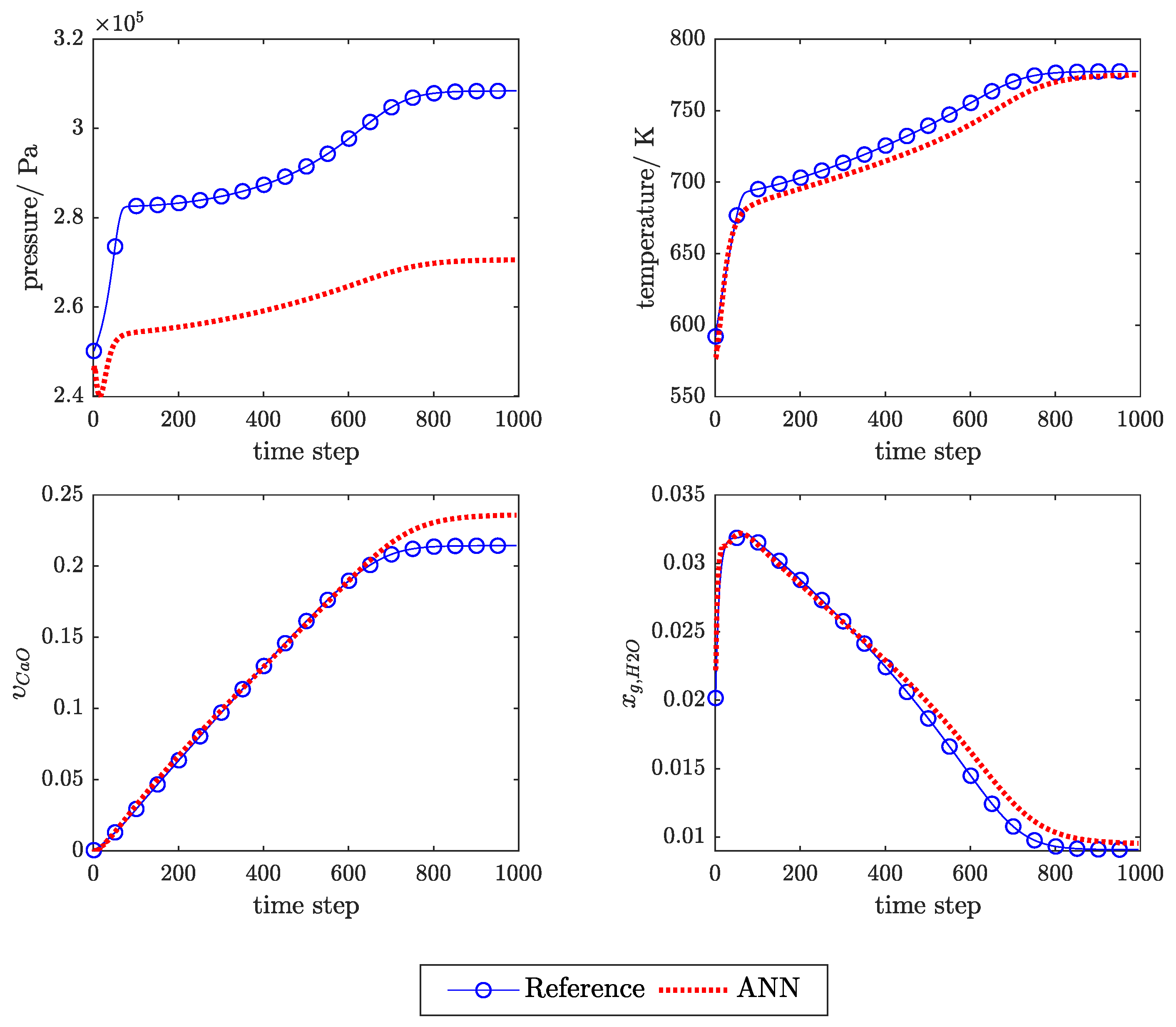
3.1. Influence of Feedback Delay
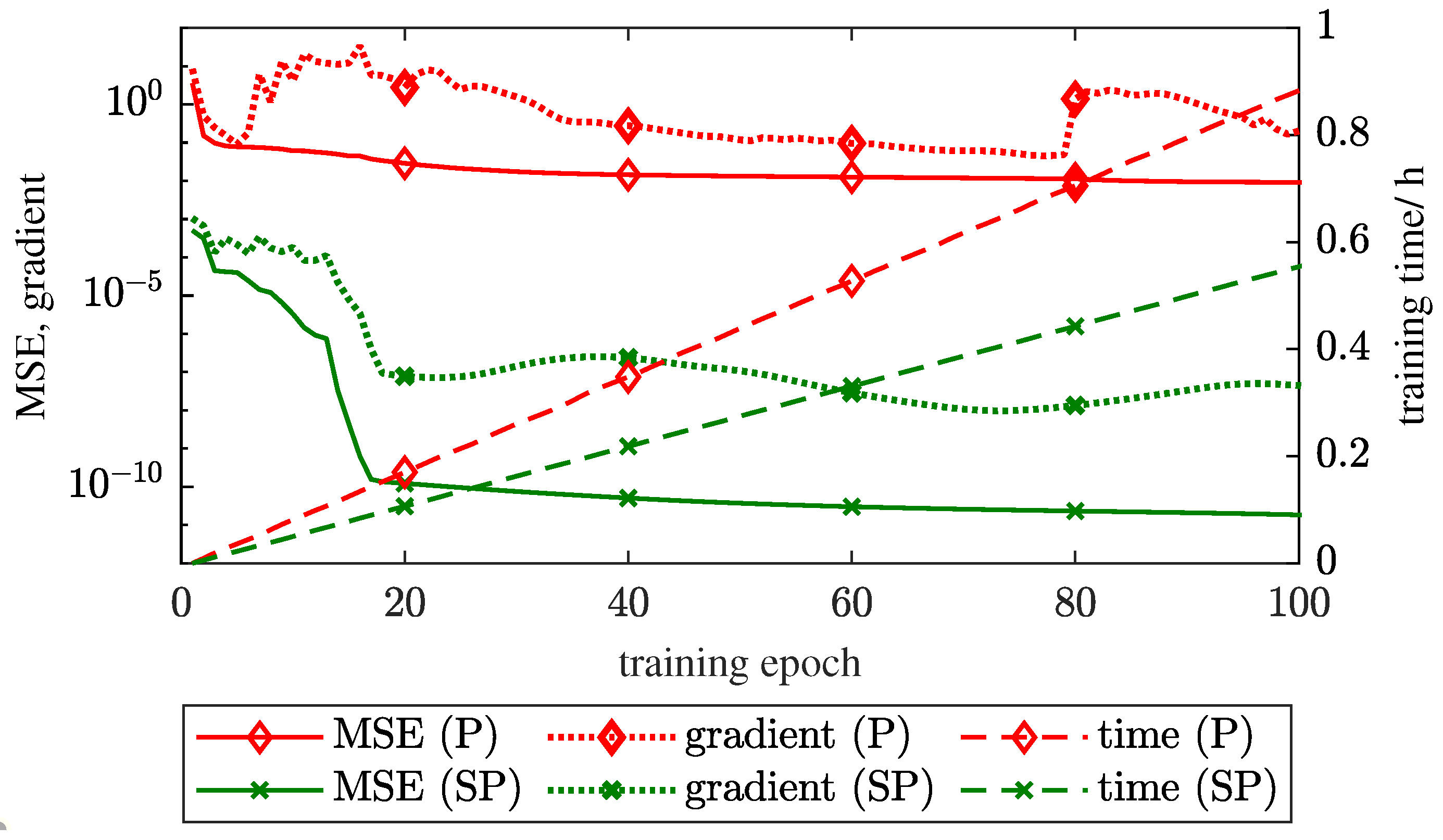
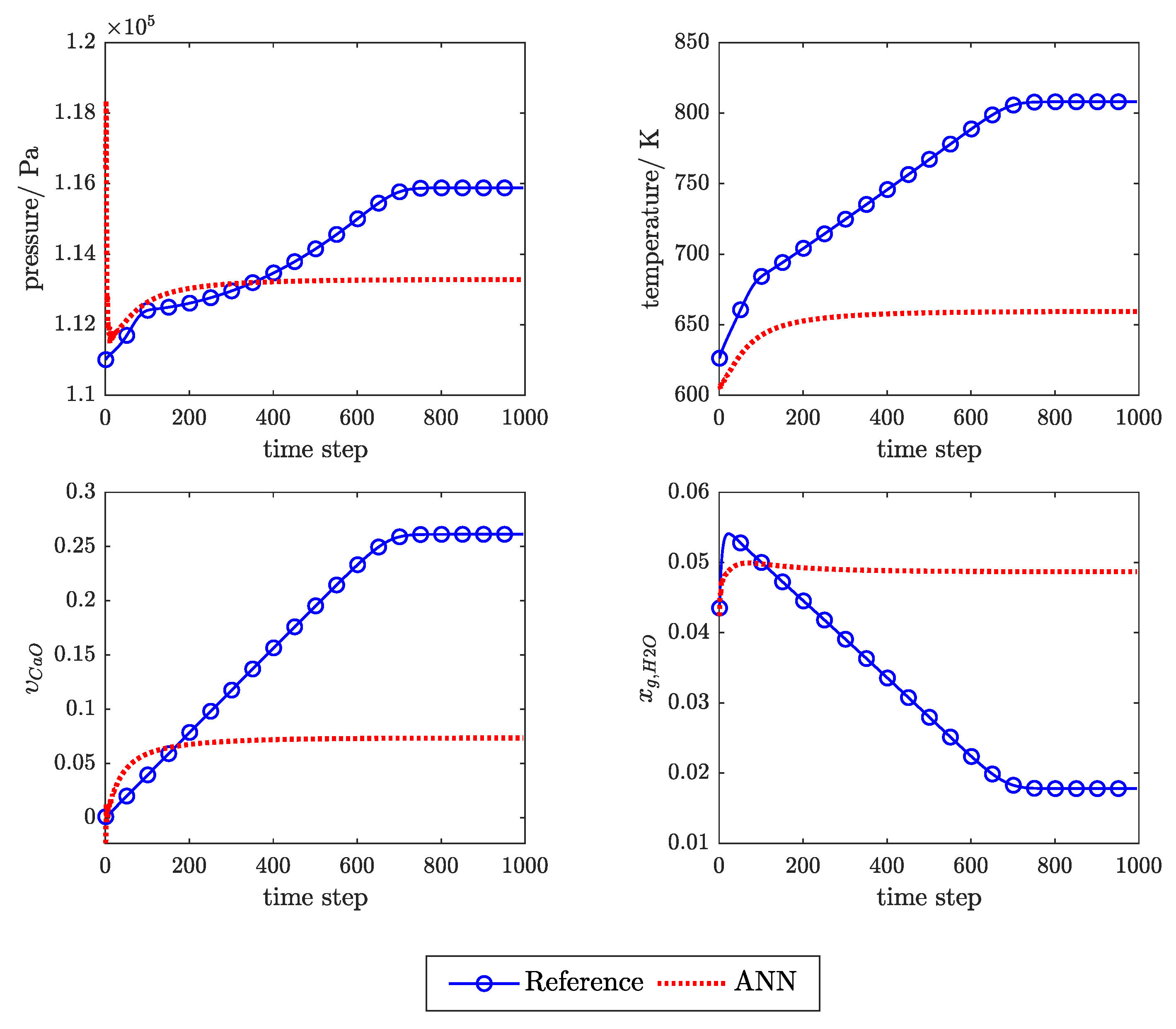
3.2. SP Versus P Training Structure
3.3. Physical Regularisation Improves Plausibility
- only MSE as the loss function (“MSE”), that is ,
- MSE combined with only L2 (“MSE + L2”), that is ,
- MSE combined with only physical regularisation (“MSE + PHY”), that is , and
- MSE combined with both L2 and physical regularisation (“MSE + L2 + PHY”), that is .
4. Conclusions
Availability of Data and Materials
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| Abbreviations: | |
| ANN | Artificial Neural Network |
| BR | Bayesian Regularisation |
| LM | Levenberg Marquardt |
| MSE | Mean Squared Error |
| NARX | Nonlinear Autoregressive Network with Exogeneous Inputs |
| ODE | Ordinary Differential Equation |
| P | Parallel (network structure) |
| PDE | Partial Differential Equation |
| PINN | Physics Inspired Neural Network |
| RNN | Recurrent Neural Network |
| SP | Series Parallel (network structure) |
| TCES | Thermochemical Energy Storage |
| TCES-related parameters: | |
| Reaction enthalpy | |
| Average thermal conductivity | |
| Viscosity | |
| Solid volume fraction | |
| Porosity | |
| Mass density | |
| Molar density | |
| t | Time |
| Specific heat capacity | |
| D | Effective diffusion coefficient |
| h | Specific enthalpy |
| K | Permeability |
| Reaction constant | |
| p | Pressure |
| q | Source/sink term |
| T | Temperature |
| u | Specific internal energy |
| Gas molar fraction | |
| ANN-related parameters: | |
| Normalising constant of L2 regularisation term | |
| Normalising constant of data-related error | |
| Hessian matrix | |
| Identity matrix | |
| Jacobian matrix | |
| Predicted value at time t | |
| Normalising constant of physical error | |
| Damping parameter for LM algorithm | |
| Network parameter | |
| b | Network bias |
| Feedback delay | |
| Data-related error | |
| Mean squared value of network parameters | |
| Physical error | |
| Loss function | |
| N | Number of network parameters |
| n | Number of training samples |
| Number of time steps | |
| u | Exogeneous input |
| w | Network weight |
| Observed value at time t | |
Appendix A. List of Exogeneous Input and Its Distribution
| Exogenous inputs with normal distribution | |||||
| u | Unit | ||||
| kg/m3 | 1656 | 25 | 1656 | 25 | |
| kg/m3 | 2200 | 25 | 2200 | 25 | |
| Pa | 1 × 10 | ||||
| K | 20 | 20 | |||
| K | 20 | 20 | |||
| mol/s.m | |||||
| mol/s.m | |||||
| Exogenous inputs with lognormal distribution | |||||
| u | Unit | ||||
| K | mD | log(5) | |||
| - | log(0.05) | ||||
| Exogenous inputs with shifted and scaled beta distribution | |||||
| u | Unit | a | b | scale | shift |
| J/kg.K | 7.1 | 2.9 | 300 | 700 | |
| J/kg.K | 7.6 | 2.4 | 350 | 1250 | |
| W/m.K | 6.5 | 3.5 | 0.6 | - | |
| W/m.K | 6.5 | 3.5 | 0.6 | - | |
| - | 8.5 | 1.5 | 0.825 | - | |
| J/mol | 4.8 | 5.2 | 3 | ||
| - | 76 | 85 | - | - | |
Appendix B. Mole and Energy Balance Error
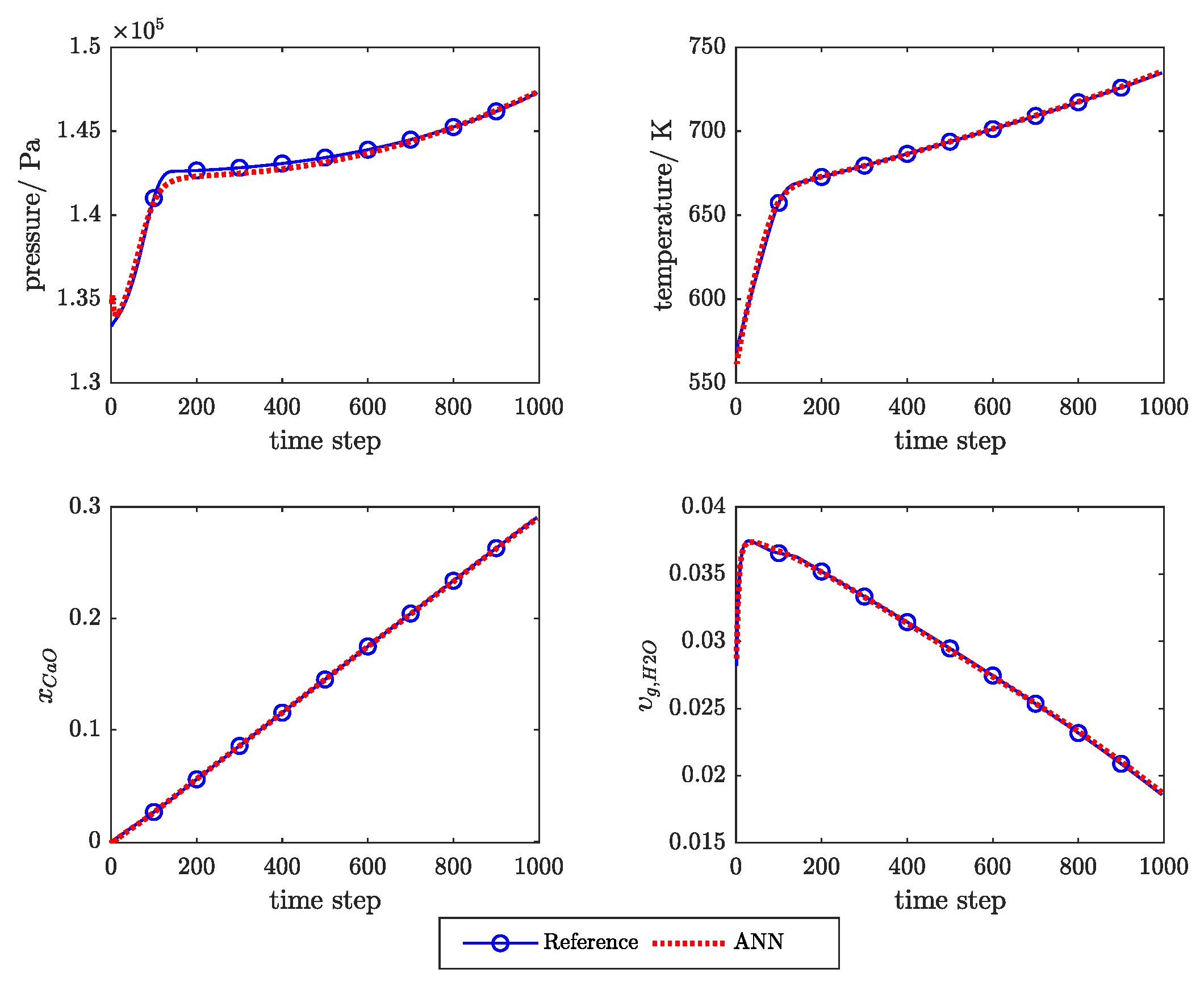
Appendix C. Example of the Ann Prediction
References
- Haas, J.; Cebulla, F.; Cao, K.; Nowak, W.; Palma-Behnke, R.; Rahmann, C.; Mancarella, P. Challenges and trends of energy storage expansion planning for flexibility provision in power systems—A review. Renew. Sustain. Energy Rev. 2017, 80, 603–619. [Google Scholar] [CrossRef]
- Møller, K.T.; Williamson, K.; Buckleyand, C.E.; Paskevicius, M. Thermochemical energy storage properties of a barium based reactive carbonate composite. J. Mater. Chem. 2020, 8, 10935–10942. [Google Scholar] [CrossRef]
- Yuan, Y.; Li, Y.; Zhao, J. Development on Thermochemical Energy Storage Based on CaO-Based Materials: A Review. Sustainability 2018, 10, 2660. [Google Scholar] [CrossRef]
- Pardo, P.; Deydier, A.; Anxionnaz-Minvielle, Z.; Rougé, S.; Cabassud, M.; Cognet, P. A review on high temperature thermochemical heat energy storage. Renew. Sustain. Energy Rev. 2014, 32, 591–610. [Google Scholar] [CrossRef]
- Scapino, L.; Zondag, H.; Van Bael, J.; Diriken, J.; Rindt, C. Energy density and storage capacity cost comparison of conceptual solid and liquid sorption seasonal heat storage systems for low-temperature space heating. Renew. Sustain. Energy Rev. 2017, 76, 1314–1331. [Google Scholar] [CrossRef]
- Schaube, F.; Wörner, A.; Tamme, R. High Temperature Thermochemical Heat Storage for Concentrated Solar Power Using Gas-Solid Reactions. J. Sol. Energy Eng. 2011, 133, 7. [Google Scholar] [CrossRef]
- Carrillo, A.; Serrano, D.; Pizarro, P.; Coronado, J. Thermochemical heat storage based on the Mn2O3/Mn3O4 redox couple: Influence of the initial particle size on the morphological evolution and cyclability. J. Mater. Chem. 2014, 2, 19435–19443. [Google Scholar] [CrossRef]
- Carrillo, A.; Moya, J.; Bayón, A.; Jana, P.; de la Peña O’Shea, V.; Romero, M.; Gonzalez-Aguilar, J.; Serrano, D.; Pizarro, P.; Coronado, J. Thermochemical energy storage at high temperature via redox cycles of Mn and Co oxides: Pure oxides versus mixed ones. Sol. Energy Mater. Sol. Cells 2014, 123, 47–57. [Google Scholar] [CrossRef]
- Carrillo, A.; Sastre, D.; Serrano, D.; Pizarro, P.; Coronado, J. Revisiting the BaO2/BaO redox cycle for solar thermochemical energy storage. Phys. Chem. Chem. Phys. 2016, 18, 8039–8048. [Google Scholar] [CrossRef]
- Muthusamy, J.P.; Calvet, N.; Shamim, T. Numerical Investigation of a Metal-oxide Reduction Reactor for Thermochemical Energy Storage and Solar Fuel Production. Energy Procedia 2014, 61, 2054–2057. [Google Scholar] [CrossRef][Green Version]
- Block, T.; Knoblauch, N.; Schmücker, M. The cobalt-oxide/iron-oxide binary system for use as high temperature thermochemical energy storage material. Thermochim. Acta 2014, 577, 25–32. [Google Scholar] [CrossRef]
- Michel, B.; Mazet, N.; Neveu, P. Experimental investigation of an innovative thermochemical process operating with a hydrate salt and moist air for thermal storage of solar energy: Global performance. Appl. Energy 2014, 129, 177–186. [Google Scholar] [CrossRef]
- Uchiyama, N.; Takasu, H.; Kato, Y. Cyclic durability of calcium carbonate materials for oxide/water thermo-chemical energy storage. Appl. Therm. Eng. 2019, 160, 113893. [Google Scholar] [CrossRef]
- Yan, T.; Wang, R.; Li, T.; Wang, L.; Fred, I. A review of promising candidate reactions for chemical heat storage. Renew. Sustain. Energy Rev. 2015, 43, 13–31. [Google Scholar] [CrossRef]
- Zhang, H.; Baeyens, J.; Cáceres, G.; Degréve, J.; Lv, Y. Thermal energy storage: Recent developments and practical aspects. Prog. Energy Combust. Sci. 2016, 53, 1–40. [Google Scholar] [CrossRef]
- André, L.; Abanades, S.; Flamant, G. Screening of thermochemical systems based on solid-gas reversible reactions for high temperature solar thermal energy storage. Renew. Sustain. Energy Rev. 2016, 64, 703–715. [Google Scholar] [CrossRef]
- Schaube, F.; Koch, L.; Wörner, A.; Müller-Steinhagen, H. A thermodynamic and kinetic study of the de- and rehydration of Ca(OH)2 at high H2O partial pressures for thermo-chemical heat storage. Thermochim. Acta 2012, 538, 9–20. [Google Scholar] [CrossRef]
- Schaube, F.; Kohzer, A.; Schütz, J.; Wörner, A.; Müller-Steinhagen, H. De- and rehydration of Ca(OH)2 in a reactor with direct heat transfer for thermo-chemical heat storage. Part A: Experimental results. Chem. Eng. Res. Des. 2013, 91, 856–864. [Google Scholar] [CrossRef]
- Schmidt, M.; Gutierrez, A.; Linder, M. Thermochemical energy storage with CaO/Ca(OH)2 - Experimental investigation of the thermal capability at low vapor pressures in a lab scale reactor. Appl. Energy 2017, 188, 672–681. [Google Scholar] [CrossRef]
- Shao, H.; Nagel, T.; Roßkopf, C.; Linder, M.; Wörner, A.; Kolditz, O. Non-equilibrium thermo-chemical heat storage in porous media: Part 2—A 1D computational model for a calcium hydroxide reaction system. Energy 2013, 60, 271–282. [Google Scholar] [CrossRef]
- Nagel, T.; Shao, H.; Roßkopf, C.; Linder, M.; Wörner, A.; Kolditz, O. The influence of gas-solid reaction kinetics in models of thermochemical heat storage under monotonic and cyclic loading. Appl. Energy 2014, 136, 289–302. [Google Scholar] [CrossRef]
- Bayon, A.; Bader, R.; Jafarian, M.; Fedunik-Hofman, L.; Sun, Y.; Hinkley, J.; Miller, S.; Lipiński, W. Techno-economic assessment of solid–gas thermochemical energy storage systems for solar thermal power applications. Energy 2018, 149, 473–484. [Google Scholar] [CrossRef]
- Rezvanizaniani, S.M.; Liu, Z.; Chen, Y.; Lee, J. Review and recent advances in battery health monitoring and prognostics technologies for electric vehicle (EV) safety and mobility. J. Power Sources 2014, 256, 110–124. [Google Scholar] [CrossRef]
- Mehne, J.; Nowak, W. Improving temperature predictions for Li-ion batteries: Data assimilation with a stochastic extension of a physically-based, thermo-electrochemical model. J. Energy Storage 2017, 12, 288–296. [Google Scholar] [CrossRef]
- Seitz, G.; Helmig, R.; Class, H. A numerical modeling study on the influence of porosity changes during thermochemical heat storage. Appl. Energy 2020, 259, 114152. [Google Scholar] [CrossRef]
- Roßkopf, C.; Haas, M.; Faik, A.; Linder, M.; Wörner, A. Improving powder bed properties for thermochemical storage by adding nanoparticles. Energy Convers. Manag. 2014, 86, 93–98. [Google Scholar] [CrossRef]
- Abiodun, O.I.; Jantan, A.; Omolara, A.E.; Dada, K.V.; Mohamed, N.A.; Arshad, H. State-of-the-art in artificial neural network applications: A survey. Heliyon 2018, 4, e00938. [Google Scholar] [CrossRef] [PubMed]
- Raissi, M.; Perdikaris, P.; Karniadakis, G. Inferring solutions of differential equations using noisy multi-fidelity data. J. Comput. Phys. 2017, 335, 736–746. [Google Scholar] [CrossRef]
- Karamizadeh, S.; Abdullah, S.M.; Halimi, M.; Shayan, J.J.; Rajabi, M. Advantage and drawback of support vector machine functionality. In Proceedings of the 2014 International Conference on Computer, Communications, and Control Technology (I4CT), Langkawi, Malaysia, 2–4 September 2014; pp. 63–65. [Google Scholar]
- Aggarwal, C. Neural Networks and Deep Learning: A Textbook, 1st ed.; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Oyebode, O.; Stretch, D. Neural network modeling of hydrological systems: A review of implementation techniques. Nat. Resour. Model. 2018, 32, e12189. [Google Scholar] [CrossRef]
- Chen, S.; Wang, Y.; Tsou, I. Using artificial neural network approach for modelling rainfall–runoff due to typhoon. J. Earth Syst. Sci. 2013, 122, 399–405. [Google Scholar] [CrossRef]
- Asadi, H.; Shahedi, K.; Jarihani, B.; Sidle, R.C. Rainfall-Runoff Modelling Using Hydrological Connectivity Index and Artificial Neural Network Approach. Water 2019, 11, 212. [Google Scholar] [CrossRef]
- Wunsch, A.; Liesch, T.; Broda, S. Forecasting groundwater levels using nonlinear autoregressive networks with exogenous input (NARX). J. Hydrol. 2018, 567, 743–758. [Google Scholar] [CrossRef]
- Taherdangkoo, R.; Tatomir, A.; Taherdangkoo, M.; Qiu, P.; Sauter, M. Nonlinear Autoregressive Neural Networks to Predict Hydraulic Fracturing Fluid Leakage into Shallow Groundwater. Water 2020, 12, 841. [Google Scholar] [CrossRef]
- Kalogirou, S. Applications of artificial neural-networks for energy systems. Appl. Energy 1995, 67, 17–35. [Google Scholar] [CrossRef]
- Bermejo, J.; Fernández, J.; Polo, F.; Márquez, A. A Review of the Use of Artificial Neural Network Models for Energy and Reliability Prediction. A Study of the Solar PV, Hydraulic and Wind Energy Sources. Appl. Sci. 2019, 9, 1844. [Google Scholar] [CrossRef]
- Yaïci, W.; Entchev, E.; Longo, M.; Brenna, M.; Foiadelli, F. Artificial neural network modelling for performance prediction of solar energy system. In Proceedings of the 2015 International Conference on Renewable Energy Research and Applications (ICRERA), Palermo, Italy, 22–25 November 2015; pp. 1147–1151. [Google Scholar]
- Kumar, A.; Zaman, M.; Goel, N.; Srivastava, V. Renewable Energy System Design by Artificial Neural Network Simulation Approach. In Proceedings of the 2014 IEEE Electrical Power and Energy Conference, Calgary, AB, Canada, 12–14 November 2014; pp. 142–147. [Google Scholar]
- Breiman, L. Statistical Modeling: The Two Cultures. Stat. Sci. 2001, 16, 199–231. [Google Scholar] [CrossRef]
- Zhang, Z.; Beck, M.W.; Winkler, D.A.; Huang, B.; Sibanda, W.; Goyal, H. Opening the black box of neural networks: Methods for interpreting neural network models in clinical applications. Ann. Transl. Med. 2018, 6, 1–11. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics Informed Deep Learning (Part I): Data-driven Solutions of Nonlinear Partial Differential Equations. arXiv 2017, arXiv:1711.10561. [Google Scholar]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics Informed Deep Learning (Part II): Data-driven Discovery of Nonlinear Partial Differential Equations. arXiv 2017, arXiv:1711.10566. [Google Scholar]
- Doshi-Velez, F.; Kim, B. Towards A Rigorous Science of Interpretable Machine Learning. arXiv 2017, arXiv:1702.08608v2. [Google Scholar]
- Miller, T. Explanation in Artificial Intelligence: Insights from the Social Sciences. arXiv 2017, arXiv:1706.07269. [Google Scholar] [CrossRef]
- Karpatne, A.; Atluri, G.; Faghmous, J.; Steinbach, M.; Banerjee, A.; Ganguly, A.; Shekhar, S.; Samatova, N.; Kumar, V. Theory-guided Data Science: A New Paradigm for Scientific Discovery from Data. arXiv 2017, arXiv:1612.08544v2. [Google Scholar] [CrossRef]
- Tartakovsky, A.; Marrero, C.; Perdikaris, P.; Tartakovsky, G.; Barajas-Solano, D. Learning Parameters and Constitutive Relationships with Physics Informed Deep Neural Networks. arXiv 2018, arXiv:1808.03398v2. [Google Scholar]
- Karpatne, A.; Watkins, W.; Read, J.; Kumar, V. Physics-guided Neural Networks (PGNN): An Application in Lake Temperature Modeling. arXiv 2018, arXiv:1710.11431v2. [Google Scholar]
- Wang, N.; Zhang, D.; Chang, H.; Li, H. Deep learning of subsurface flow via theory-guided neural network. J. Hydrol. 2020, 584, 124700. [Google Scholar] [CrossRef]
- Chen, S.; Billings, S.; Grant, P. Non-linear system identification using neural networks. Int. J. Control 1990, 51, 1191–1214. [Google Scholar] [CrossRef]
- Zhang, X. Time series analysis and prediction by neural networks. Optim. Methods Softw. 1994, 4, 151–170. [Google Scholar] [CrossRef]
- Buitrago, J.; Asfour, S. Short-Term Forecasting of Electric Loads Using Nonlinear Autoregressive Artificial Neural Networks with Exogenous Vector Inputs. Energies 2017, 10, 40. [Google Scholar] [CrossRef]
- Boussaada, Z.; Curea, O.; Remaci, A.; Camblong, H.; Bellaaj, N. A Nonlinear Autoregressive Exogenous (NARX) Neural Network Model for the Prediction of the Daily Direct Solar Radiation. Energies 2018, 11, 620. [Google Scholar] [CrossRef]
- Mellit, A.; Kalogirou, S. Artificial intelligence techniques for photovoltaic applications: A review. Prog. Energy Combust. Sci. 2008, 34, 574–632. [Google Scholar] [CrossRef]
- Jia, X.; Karpatne, A.; Willard, J.; Steinbach, M.; Read, J.; Hanson, P.; Dugan, H.; Kumar, V. Physics Guided Recurrent Neural Networks For Modeling Dynamical Systems: Application to Monitoring Water Temperature And Quality In Lakes. arXiv 2018, arXiv:1810.02880. [Google Scholar]
- Levenberg, K. A method for the solution of certain non-linear problems in least squares. Q. Appl. Math. 1944, 2, 164–168. [Google Scholar] [CrossRef]
- Marquardt, D. An Algorithm for Least-Squares Estimation of Nonlinear Parameters. J. Soc. Ind. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Yu, H.; Wilamowski, B.M. Levenberg-Marquardt Training. In The Industrial Electronics Handbook—Intelligent Systems, 2nd ed.; Wilamowski, B., Irwin, J., Eds.; CRC Press: Boca Raton, FL, USA, 2011; Volume 5, Chapter 12. [Google Scholar]
- Banerjee, I. Modeling Fractures in a CaO/Ca(OH)2 Thermo-chemical Heat Storage Reactor. Master’s Thesis, Universität Stuttgart, Stuttgart, Germany, 2018. [Google Scholar]
- Koch, T.; Gläser, D.; Weishaupt, K.; Ackermann, S.; Beck, M.; Becker, B.; Burbulla, S.; Class, H.; Coltman, E.; Fetzer, T.; et al. Release 3.0.0 of DuMux: DUNE for Multi-{Phase, Component, Scale, Physics,...} Flow and Transport in Porous Media; Zenodo: Geneva, Switzerland, 2019. [Google Scholar] [CrossRef]
- Peinado, J.; Ibáñez, J.; Arias, E.; Hernández, V. Adams-Bashforth and Adams-Moulton methods for solving differential Riccati equations. Comput. Math. Appl. 2010, 60, 3032–3045. [Google Scholar] [CrossRef]
- Tutueva, A.; Karimov, T.; Butusov, D. Semi-Implicit and Semi-Explicit Adams-Bashforth-Moulton Methods. Mathematics 2020, 8, 780. [Google Scholar] [CrossRef]
- Beale, M.; Hagan, M.; Demuth, H. Deep Learning Toolbox™ User’s Guide (R2019a); The MathWorks, Inc.: Natick, MA, USA, 2019. [Google Scholar]
- Krogh, A.; Hertz, J.A. A Simple Weight Decay Can Improve Generalization. In Advances in Neural Information Processing Systems 4; Moody, J.E., Hanson, S.J., Lippmann, R.P., Eds.; Morgan-Kaufmann: Denver, CO, USA, 1991; pp. 950–957. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016; Available online: http://www.deeplearningbook.org (accessed on 15 April 2019).
- MacKay, D. Bayesian Interpolation. Neural Comput. 1991, 4, 415–447. [Google Scholar] [CrossRef]
- Sariev, E.; Germano, G. Bayesian regularized artificial neural networks for the estimation of the probability of default. Quant. Financ. 2020, 20, 311–328. [Google Scholar] [CrossRef]
- Foresee, F.D.; Hagan, M. Gauss-Newton approximation to Bayesian learning. IEEE 1997, 3, 1930–1935. [Google Scholar] [CrossRef]
- Nguyen, D.; Widrow, B. Improving the learning speed of 2-layer neural networks by choosing initial values of the adaptive weights. IEEE 1990, 3, 21–26. [Google Scholar] [CrossRef]
- Mittal, A.; Singh, A.P.; Chandra, P. A Modification to the Nguyen–Widrow Weight Initialization Method. In Intelligent Systems, Technologies and Applications; Springer: Singapore, 2020; pp. 141–153. [Google Scholar]
- Zhang, G.; Patuwo, B.E.; Hu, M. Forecasting with artificial neural networks: The state of the art. Int. J. Forecast. 1998, 14, 35–62. [Google Scholar] [CrossRef]
- Stathakis, D. Adams-Bashforth and Adams-Moulton methods for solving differential Riccati equations. Int. J. Remote Sens. 2009, 30, 2133–2147. [Google Scholar] [CrossRef]
- Higham, D.J.; Trefethen, L.N. Stiffness of ODEs. BIT Numer. Math. 1993, 33, 285–303. [Google Scholar] [CrossRef]
- Härter, F.P.; de Campos Velho, H.F.; Rempel, E.L.; Chian, A.C.L. Neural networks in auroral data assimilation. J. Atmos. Sol.-Terr. Phys. 2008, 70, 1243–1250. [Google Scholar] [CrossRef]
- Awolusi, T.F.; Oke, O.L.; Akinkurolere, O.O.; Sojobi, A.O.; Aluko, O.G. Performance comparison of neural network training algorithms in the modeling properties of steel fiber reinforced concrete. Heliyon 2019, 5, 1–27. [Google Scholar] [CrossRef]

| k | Equation: | |
|---|---|---|
| Dehydration | Hydration | |
| 1 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | ||
| 6 | ||
| 7 | ||
| 8 | ||
| 9 | ||
| Loss Function | ||
|---|---|---|
| MSE | ||
| MSE + L2 | ||
| MSE + PHY | ||
| MSE + L2 + PHY |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Praditia, T.; Walser, T.; Oladyshkin, S.; Nowak, W. Improving Thermochemical Energy Storage Dynamics Forecast with Physics-Inspired Neural Network Architecture. Energies 2020, 13, 3873. https://doi.org/10.3390/en13153873
Praditia T, Walser T, Oladyshkin S, Nowak W. Improving Thermochemical Energy Storage Dynamics Forecast with Physics-Inspired Neural Network Architecture. Energies. 2020; 13(15):3873. https://doi.org/10.3390/en13153873
Chicago/Turabian StylePraditia, Timothy, Thilo Walser, Sergey Oladyshkin, and Wolfgang Nowak. 2020. "Improving Thermochemical Energy Storage Dynamics Forecast with Physics-Inspired Neural Network Architecture" Energies 13, no. 15: 3873. https://doi.org/10.3390/en13153873
APA StylePraditia, T., Walser, T., Oladyshkin, S., & Nowak, W. (2020). Improving Thermochemical Energy Storage Dynamics Forecast with Physics-Inspired Neural Network Architecture. Energies, 13(15), 3873. https://doi.org/10.3390/en13153873