Method for Scalable and Automatised Thermal Building Performance Documentation and Screening

Abstract

In Europe, more and more data on building energy use will be collected in the future as a result of the energy performance of buildings directive (EPBD), issued by the European Union. Moreover, both at European level and globally it became evident that the real energy performance of new buildings and the existing building stock needs to be documented better. Such documentation can, for example, be done with data-driven methods based on mathematical and statistical approaches. Even though the methods to extract energy performance characteristics of buildings are numerous, they are of varying reliability and often associated with a significant amount of human labour, making them hard to apply on a large scale. A classical approach to identify certain thermal performance parameters is the energy signature method. In this study, an automatised, nonlinear and smooth approach to the well-known energy signature is proposed, to quantify key thermal building performance parameters. The research specifically aims at describing the linear and nonlinear heat usage dependency on outdoor temperature, wind and solar irradiation. To make the model scalable, we realised it so that it only needs the daily average heat use of buildings, the outdoor temperature, the wind speed and the global solar irradiation. The results of applying the proposed method on heat consumption data from 16 different and randomly selected Danish occupied houses are analysed.

1. Introduction

Today, the building stock suffers from low energy efficiency and significant discrepancies between anticipated and actual heat consumption known as the performance gap. The performance gap has been documented in several studies, see, e.g., in [1,2]. In [3], it is stated that only 3% of the building stock in the EU has energy label A, which corresponds to the level of new buildings. Additionally, the reliability of the energy labels has been proven to be limited. In a report from 2018 by the Danish Energy Agency it was stated that 20 to 30% of the Danish building energy labels were wrong. This corresponds to between 12,000 and 18,000 energy labels that specific year.

The energy efficiency directive (EED) of the European Union (EU) [4] states that all member states are responsible for the installation of individual energy meters, including heat meters, on all buildings to the extent that it is technically possible and economically feasible. Furthermore, the new energy performance of buildings directive (EPBD) lists several requirements to boost the national renovation strategies [5]. These initiatives are established in order to increase the energy efficiency of the EU building stock. With the current data collection requirements and the new EPBD, the relevancy of data-driven methods for the screening and documentation of the thermal performance of buildings has become more relevant than ever.

Several dynamic modelling approaches used for energy performance evaluation of buildings can be mentioned. That is from pure deterministic white-box models such as TRNSYS, Modelica, IDA ICE, EnergyPlus or ESP-r models [6,7,8,9,10], to fully statistical black-box models such as artificial neural networks. The estimated energy performance of buildings based on deterministic white-box models is based on a number of assumptions which may or may not match reality. Typically, this is because the evaluations are done before the building is built and several parameters, which can affect the energy consumption, are unknown at the time. This is one of several possible reasons for the performance gap in the building stock [11]. On the other hand, the black-box models are often used for prediction, control and clustering, rather than system identification due to its lack of interpretability. Additionally, as black-box models are data-driven models, they can only be applied after the building is build and data are collected. One exception is if black-box models are applied on simulated data obtained from white-box models. A review of different black-box approaches used for building energy consumption and performance estimation can be found in [12].

A third category of models is the grey-box models. These kinds of models are a hybrid of the previously mentioned white and black-box models. Examples of grey-box models are physics-based stochastic differential equations [13,14], and autoregressive moving-average models with exogenous inputs (ARMAX models) for time series data [15]. The ARMAX model can be explained in physical terms. First, by formulating a thermal lumped resistance capacity (RC) model, and subsequently by deriving the corresponding ARMAX representation as done in, e.g., [16,17]. However, the MA term in the ARMAX model is often omitted, and the ARX models are used instead, see, for example, [18,19].

Other approaches in the literature utilise time varying parameters estimation related to the thermal building performance. For example, in [20] each parameter of interest is treated as time-varying states found by multivariate kernel estimation. This method is one of the key influences of this study.

In general, it can be said that the category of supervised machine learning techniques (such as grey-box models) can be used for building performance parameter estimation, prediction and control, whereas unsupervised techniques (such as black-box techniques) are suitable for prediction and control only, as the physical interpretability of the model parameters is lacking.

A shared commonality of most of the dynamical data-driven methods used for building performance estimation is that they require human interaction for model selection and validation as described in [17]. For large-scale assessment of building performance the before mentioned methods are therefore currently not feasible.

Alternatively, simpler quasi-stationary models have been proposed in the literature. One quasi-stationary approach to quantify thermal performance of buildings is the energy signature method, which has been studied and applied for decades. A few of the early examples can be found in [21,22,23] with the earliest known, dated all the way back to 1951 [24].

The dominating principle of the methods is to apply linear regression on, e.g., outdoor temperature measurements in order to explain the heat consumption of a building. Consequently, information on, e.g., the heat transfer coefficient can be extracted form the estimated model.

In one of the simplest energy signature models found in [25], the heat consumption is described as a linear function of the outdoor temperature during the heating period, i.e., by a slope and an intercept, where the slope represents the heat loss coefficient of the building. During the weather-independent period, the heat consumption is modelled as a constant for buildings without cooling and heat recovery. The change point for the weather dependent period (heating period) to the weather independent period is described by the base temperature. The base temperature is the outdoor temperature at which the building is in thermal balance. 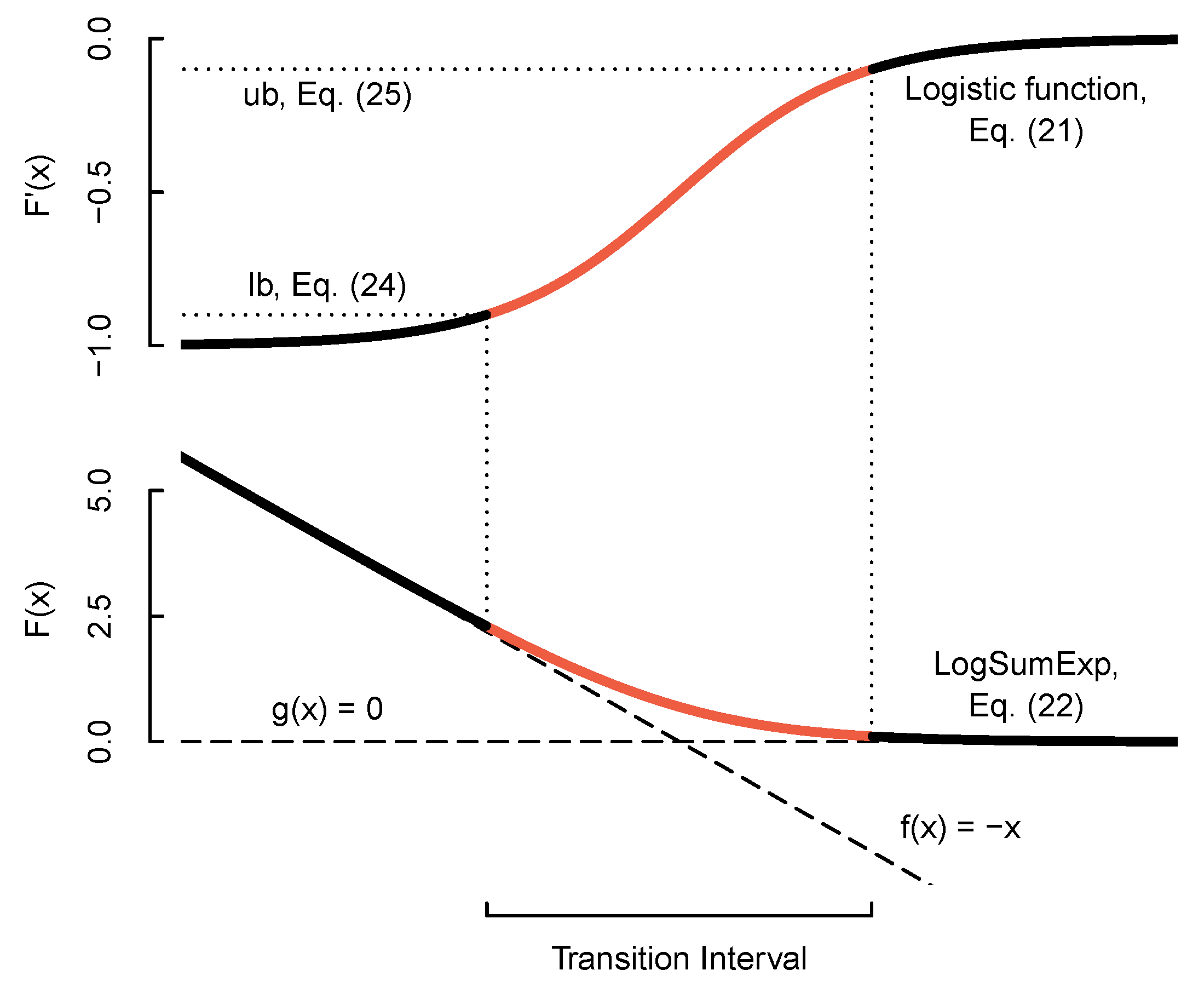For a fixed value of the base temperature, the energy signature is similar to the well-known degree-day method, see, e.g., in [26,27]. As the energy signature operates in two distinctive modes during the weather-dependent and the weather-independent periods, respectively, it is a regime model with two regimes, where $T_{{\mathrm{b}}_0}$ determines the instantaneous change between them.

In the ASHRAE Guideline 14-2002—Measurement of Energy and Demand Savings [25], seven different energy signature models are proposed depending on different factors concerning heating, cooling and heat recovery systems.

Common for all the methods in the ASHRAE Guideline is that the heat usage is a function of the outdoor temperature alone, contrary to, e.g., [22,28].

In [28], it was found that the heat loss coefficient is fairly insensitive (±5%) to solar gain and electricity use. The estimated base temperature was more sensitive to these two factors. As both electricity and solar gain are additive terms to the heat demand (i.e., a functional offset), this seems like a reasonable finding.

More recent studies, like those in [29,30], show that the energy signature method is still used in research. However, only minor advances on the technique have been reported since the earliest applications of the method. For example, in [29] a energy signature model for determining the domestic hot water production and heat loss due to hot water circulation is proposed. Additionally, only night-time data were used to reduce effects such as solar irradiation. To the best of our knowledge, the actual energy signature model in the literature is typically kept linear, which is likely to result in significant biases of the estimated building physical parameters.

Motivation

For many of the above-mentioned energy signature methods, it is assumed that the transition from a weather-dependent heat consumption to a weather-independent heat consumption is instantaneous at a specific outdoor temperature. However, this simplification does not match reality. Therefore, we propose an advancement of the traditional energy signature models by formulating it as a smooth nonlinear model, from which the transition period can be determined. Furthermore, by reformulating the traditional energy signature model as a smooth, i.e., fully differentiable, model, the estimation procedure can be made more efficient, and more advanced modelling approaches, which require full differentiability, can be applied.

As several weather phenomenons, such as wind and long-wave radiation, have nonlinear impacts on the energy consumption, new model formulations of, specifically, the heating period are proposed to get reliable building physical estimates. Five models of increasing complexity are proposed and the model accuracy is documented.

For occupied buildings, a major source of the variation in the heat consumption is related to the occupants [31]. The effects are related to personal preferences to the indoor environment and the occupants’ understanding of the building and its systems [32]. Therefore, the non-modelled effects on the heat consumption (e.g., window openings, changing temperature set points, etc.) are part of the model errors. We utilise this fact to form a method to quantify the occupants’ effect on the heat consumption, based on the model residuals.

The overall aim of this work is to establish a robust and scalable method for thermal energy performance estimation. The focus in this article is on buildings without secondary heat sources (e.g., wood stoves), cooling and heat recovery systems. However, it would be possible to extend the models to include mechanical cooling and heat recovery.

2. Method

2.1. Heat Consumption Models

The energy signature models introduced in the introduction share one common feature. Namely, that the transition from one regime to the next happens instantaneously, as seen in, for example, the ASHRAE Guideline 14 [25]. Thus, the mathematical model of the heat consumption ${\Phi }_{\mathrm{heat}}$ can be expressed as

$${\Phi }_{\mathrm{heat}}=\max [f\left(·\right),g\left(·\right)],$$

(1)

where $f\left(·\right)$ is a function describing the heat consumption during periods with heat demand, and $g\left(·\right)$ is a function describing the heat consumption during periods without heat demand. The dot notation is a placeholder for any explanatory variable use in the functions. This will typically be the outdoor temperature, but can equally well be wind speed, solar irradiation or other driving forces.

For buildings without cooling or heat recovery systems, such as those investigated in this study, a constant heat consumption model during periods without a heat demand is suggested in the ASHRAE Guideline 14. Throughout this study, the heat consumption model for periods without a heat demand, $g\left(·\right)$, is therefore defined as

$$g={\Phi }_0+e,$$

(2)

where ${\Phi }_0$ is the constant daily base heat load related to for example system heat losses, and $e\sim \mathrm{N}(0,{\sigma }^2)$ is independent and identically normal distributed noise with mean zero and variance ${\sigma }^2$.

For periods with a heating demand, i.e., a weather-dependent heat consumption, the heat consumption can be derived from the heat balance

$${\Phi }_{\mathrm{heat}}-{\Phi }_{\mathrm{tr}}+{\Phi }_{\mathrm{sol}}+{\Phi }_{\mathrm{int}}-{\Phi }_{\mathrm{vent}}+{\Phi }_{\mathrm{mass}}+{\Phi }_{\mathrm{latent}}=0,$$

(3)

where ${\Phi }_{\mathrm{heat}}$ is the heat consumption, ${\Phi }_{\mathrm{tr}}$ is the transmission loss, ${\Phi }_{\mathrm{sol}}$ is the solar gain, ${\Phi }_{\mathrm{int}}$ is the internal heat gains, ${\Phi }_{\mathrm{vent}}$ is the ventilation loss, ${\Phi }_{\mathrm{mass}}$ is the release of thermal energy stored in the thermal mass and ${\Phi }_{\mathrm{latent}}$ is the energy absorption and release due to evaporation and condensation in the thermal zone.

For daily averaged heat consumption and weather data, as used in this study, the heat exchange with the internal thermal mass (e.g., building structures and furniture) and the latent heat exchange can be neglected [22,29]. Furthermore, by lumping ${\Phi }_{\mathrm{sol}}$, ${\Phi }_{\mathrm{int}}$ and ${\Phi }_{\mathrm{vent}}$ into the new parameter ${\Phi }_{\mathrm{x}}$, and using the simplification that ${\Phi }_{\mathrm{tr}}$ only consists of transmission loss to the outdoor air, the following relation can be obtained,

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\Phi }_{\mathrm{heat}}& =\mathrm{UA}(T_{\mathrm{i}}-T_{\mathrm{a}})-{\Phi }_{\mathrm{x}}\hfill \\ \hfill & =\mathrm{UA}(T_{\mathrm{i}}-{\Phi }_{\mathrm{x}}{\left(\mathrm{UA}\right)}^{-1}-T_{\mathrm{a}})\mathrm{for}{T}_{\mathrm{a}}<T_{\mathrm{i}},\hfill \end{array}\end{array}$$

(4)

where UA is the heat loss coefficient, $T_{\mathrm{i}}$ is the indoor temperature and $T_{\mathrm{a}}$ is the ambient outdoor temperature. Furthermore, as ${\Phi }_{\mathrm{heat}}$ only can take non-negative values for buildings without cooling, the formulation is only valid during periods with a heat demand.

Due to the fact that some heat balance contributions contained in ${\Phi }_{\mathrm{x}}$, as well as the indoor temperature $T_{\mathrm{i}}$, are troublesome to measure, the base temperature $T_{{\mathrm{b}}_0}$ can be introduced and estimated directly from data. The base temperature is the outdoor temperature at which the building is in thermal balance and is defined as

$$T_{{\mathrm{b}}_0}=T_{\mathrm{i}}-\frac{{\Phi }_{\mathrm{x}}}{\mathrm{UA}},$$

(5)

for ${\Phi }_0=0$ in Equations (1) and (2).

By substituting $T_{\mathrm{i}}-{\Phi }_{\mathrm{x}}{\left(\mathrm{UA}\right)}^{-1}$ in Equation (4) with $T_{{\mathrm{b}}_0}$ from Equation (5), the energy signature in Equation (6) is obtained. This formulation will act as the basis for the model proposals in the following section.

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\Phi }_{\mathrm{heat}}& =\mathrm{UA}(T_{{\mathrm{b}}_0}-T_{\mathrm{a}})\mathrm{for}{T}_{\mathrm{a}}<T_{\mathrm{b}},\hfill \end{array}\end{array}$$

(6)

where $T_{\mathrm{b}}$ is the base temperature for an arbitrary base heat load, i.e., for ${\Phi }_0\ge 0$, which is described further in the following section.

2.1.1. Heat Consumption Models for Periods with Heat Demand

In this section, five weather-dependent heat consumption models are presented. Each of the models represents a model candidate for the function $f\left(·\right)$ in Equation (1). The five model candidates increase in complexity, and each of the model advancements builds on the previous model. The simplest model is $f_0$, and the most complex model is $f_4$.

$f_0$: Fixed Base Temperature

For daily averaged input values and a fixed value of the base temperature, Equation (6) can be directly related to the commonly known heating degree days (HDD) method as $\mathrm{HDD}=T_{\mathrm{b}}-T_{\mathrm{a}}$, and $T_{\mathrm{b}}$ is the base temperature for an arbitrary base heat load, i.e., for ${\Phi }_0\ge 0$. This is in contrast to the base temperature $T_{{\mathrm{b}}_0}$ found in Equation (5), where ${\Phi }_0$ is assumed to be zero.

Often, $T_{\mathrm{b}}$ is stated as a fixed value in building standards or conventions. Using a fixed base temperature, Equation (6) can be formulated as the first and simplest formulation of the function $f\left(·\right)$ found in Equation (1):

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill f_0& =\mathrm{UA}(T_{\mathrm{b}}-T_{\mathrm{a}})+{\Phi }_0+e,\hfill \end{array}\end{array}$$

(7)

where $T_{\mathrm{b}}$ is a fixed constant corresponding to the Danish base temperature of 17 ${}^{\circ }$C [33], and $e\sim \mathrm{N}(0,{\sigma }^2)$ is the normal distributed system and observation noise with zero mean and variance ${\sigma }^2$. The system noise can be related to multiple effects, for example, the missing description of convection and infiltration, solar gain, varying indoor temperature and thermal inertia. However, the latter has previously been stated as negligible for daily averaged data.

To obtain Equation (7), it is furthermore used that

$$T_{\mathrm{b}}=T_{{\mathrm{b}}_0}-\frac{{\Phi }_0}{\mathrm{UA}},$$

(8)

which results in the term, ${\Phi }_0$, in Equation (7).

$f_1$: Free Base Temperature

Instead of relying on an assumed base temperature as in Equation (7), it can be estimated directly from data as it is typically done for the energy signature models.

By substitution of $T_{\mathrm{b}}$ in Equation (7) with $T_{{\mathrm{b}}_0}-{\Phi }_0{\left(\mathrm{UA}\right)}^{-1}$, the second model, $f_1$, is obtained,

$$\begin{array}{cc}\hfill f_1& =\mathrm{UA}(T_{{\mathrm{b}}_0}-T_{\mathrm{a}})+e,\hfill \end{array}$$

(9)

where $T_{{\mathrm{b}}_0}$ is assumed to be constant. Furthermore, $T_{{\mathrm{b}}_0}\to T_{\mathrm{i}}$ for ${\Phi }_{\mathrm{x}}\left({\mathrm{UA}}^{-1}\right)\to 0$. Hence, $T_{{\mathrm{b}}_0}$ will approach the mean indoor temperature for poorly insulated buildings with small unmodelled heat balance contributions.

Model $f_1$ in Equation (9), as well as model $f_0$ in Equation (7), simply assumes that the heat consumption solely is a function of the temperature difference between in- and outside. The solar irradiation, the heat convection of the envelope, the air exchange between the building and the outside and the long-wave radiation heat loss are therefore not considered in the models. Therefore, the estimated UA values with this simplistic model may result in weather-biased parameters estimates. For example, for a particularly windy and cold heating season, the UA value will be overestimated by applying Equation (9). Likewise, a sunny transition period between the weather-dependent and weather-independent season results in an overestimated UA value. Therefore, the model definition is not reliable for estimating thermophysical parameters of buildings [22]. In the following, a number of model extensions are proposed to overcome this bias.

$f_2$: Convection and Infiltration

Wind has two main effects on the heat consumption. Increased wind will increase the external convection on the building facade and the infiltration rate, i.e., the unintended air exchange between inside and outside. Moreover, the infiltration depends on both wind speed and thermal stack effects. The literature provides several empirical formulas for describing the convection and infiltration, see, for example, in [22,34].

For simple quasi-stationary models like those presented in this study, we aim for a simplified formulation of the combined wind effect on the heat consumption. Therefore, we propose that the convection and infiltration due to wind speed can be treated as proportional to the temperature difference between in- and outside. Equation (9) can therefore be extended to

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill f_2& =({\mathrm{UA}}_0+W_{\mathrm{s}}{\mathrm{UA}}_{\mathrm{W}})(T_{{\mathrm{b}}_0}-T_{\mathrm{a}})+e,\hfill \end{array}\end{array}$$

(10)

where $W_{\mathrm{s}}$ is the wind speed, ${\mathrm{UA}}_0$ is the heat loss coefficient for wind speeds equal to zero and ${\mathrm{UA}}_{\mathrm{W}}$ is the additional heat loss due to the wind.

With the base temperature as defined in Equation (5), ${\Phi }_{\mathrm{x}}$ becomes

$${\Phi }_{\mathrm{x}}=({\mathrm{UA}}_0+W_{\mathrm{s}}{\mathrm{UA}}_{\mathrm{W}})(T_{\mathrm{i}}-T_{{\mathrm{b}}_0}).$$

(11)

$f_3$: Solar Gain

The solar gain can be characterised by the product of global solar irradiation $I_{\mathrm{g}}$ and a constant solar transmission coefficient gA. The previous model in Equation (10) can therefore be extended with an explicit solar gain term, such that

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill f_3& =({\mathrm{UA}}_0+W_{\mathrm{s}}{\mathrm{UA}}_{\mathrm{W}})(T_{{\mathrm{b}}_0}-T_{\mathrm{a}})-\mathrm{gA}{I}_{\mathrm{g}}+e.\hfill \end{array}\end{array}$$

(12)

If the gA value has a high dependence on, for example, time-of-year, the model can be extended further by modelling the relationship between the time-of-year and the solar gain. An approach for that can be found in [14].

$f_4$: Thermal Long Wave Radiation

Another contribution to the heat loss is the long-wave radiation between the building surfaces and its surroundings.

Assuming that the building is only exposed to two different surrounding temperatures—the temperature of the sky $T_{\mathrm{sky}}$, and the temperature of the remaining surroundings $T_{\mathrm{sur}}$ both measured in kelvin—the long-wave radiation ${\Phi }_{\mathrm{rad}}$ can be expressed as

$${\Phi }_{\mathrm{rad}}={\gamma }_1(T_{\mathrm{sky}}^4-T_{\mathrm{surf}}^4)+{\gamma }_2(T_{\mathrm{sur}}^4-T_{\mathrm{surf}}^4),$$

(13)

where $T_{\mathrm{surf}}$ is the temperature in kelvin of the outer building envelope, and the $\gamma$s are the product of the emissivities of the surfaces, the surface areas, the view factors and the Stefan–Boltzmann constant [35]. The $\gamma$s are assumed constant even though, for example, vegetation might change the view factor to the sky during the year.

In order to keep the model simple and applicable, the unknown temperatures of the outer building envelope ($T_{\mathrm{surf}}$) and the near surroundings of the building ($T_{\mathrm{sur}}$) are assumed to be equal to the ambient outdoor temperature $T_{\mathrm{a}}$. Equation (13) therefore becomes

$${\Phi }_{\mathrm{rad}}={\gamma }_1(T_{\mathrm{sky}}^4-T_{\mathrm{a}}^4).$$

(14)

The final model, $f_4$, can now be expressed as

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill f_4& =({\mathrm{UA}}_0+W_{\mathrm{s}}{\mathrm{UA}}_{\mathrm{W}})(T_{{\mathrm{b}}_0}-T_{\mathrm{a}})-\mathrm{gA}{I}_{\mathrm{g}}+{\gamma }_1(T_{\mathrm{sky}}^4-T_{\mathrm{a}}^4)+e.\hfill \end{array}\end{array}$$

(15)

In the proposed models for the function $f\left(·\right)$ in Equations (1) ($f_0$, $f_1$, $f_2$, $f_3$ and $f_4$) two different formulations of the heat transmission through the building envelope have been proposed. First as a wind independent parameter (UA) in $f_0$ and $f_1$, and since as a wind-dependent function (${\mathrm{UA}}_0+W_{\mathrm{s}}{\mathrm{UA}}_{\mathrm{W}}$) in $f_2$, $f_3$ and $f_4$. For generalisability, the heat transmission through the building envelope will in the remaining part of this article be denoted as UA, despite the fact that it might or might not be a function of the wind speed.

2.2. Smooth Maximum Approximation with LogSumExp

No matter which mathematical representations are used to model the heat consumption by Equation (1), the function is not fully differentiable as it has an instantaneous change point where $f\left(·\right)$ becomes $g\left(·\right)$. Besides potential optimisation issues with a non-differentiable function, for example, if the optimiser relies on automatic differentiation, a sudden change between the two regimes is a rough simplification for models like the energy signature, which typically use daily averaged data. Instead we propose a smooth transition between the two regimes, $f\left(·\right)$ and $g\left(·\right)$.

In this section, we explain the theory behind the smooth maximum function, LogSumExp, as an alternative to the maximum function used in Equation (1). Furthermore, we show how it can be used to quantify the transition period between two regimes, e.g., the transition from the weather-dependent heat consumption regime, $f\left(·\right)$, to the weather-independent heat consumption regime, $g\left(·\right)$.

The LogSumExp (LSE) function is a smooth maximum approximation function often used in machine learning and in artificial neural networks. It is defined as

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \mathrm{LSE}\left(y\right)& =\mathrm{LSE}(y_1,y_2,\dots ,y_n)\hfill \\ \hfill & =log\left[exp\left(y_1\right)+exp\left(y_2\right)+\dots +exp\left(y_n\right)\right],\hfill \end{array}\end{array}$$

(16)

where $y$ is a series of values from $y_1$ to $y_n$.

In essence, the inner part of the log operator in Equation (16) amplifies the differences between the individual values of $y$ exponentially. For a large value of $y$, such as $y_1\gg y_2,\dots ,y_n$, we get that ${\sum }_{i=1}^{n}exp\left(y_i\right)\approx exp\left(y_1\right)$. In order to get back to the original domain, we take the logarithm of the sum. It can therefore be said that Equation (16) approximates the maximum of the values in $y$:

$$\mathrm{LSE}(y_1,y_2,\dots ,y_n)\approx \max (y_1,y_2,\dots ,y_n).$$

(17)

By applying the chain rule for differentiation, the partial derivative of Equation (16) can be shown to be the softmax function,

$$\frac{\partial }{\partial y_i}\mathrm{LSE}(y_1,y_2,\dots ,y_n)=\frac{exp\left(y_i\right)}{{\sum }_{j=1}^{n}exp\left(y_j\right)},$$

(18)

which essentially is the multivariate version of the logistic function [36].

With $n=2$ and by differentiating Equation (16) with respect to $y_1$, we get

$$\frac{\partial }{\partial y_1}\mathrm{LSE}(y_1,y_2)=\frac{exp\left(y_1\right)}{{\sum }_{j=1}^{2}exp\left(y_j\right)}.$$

(19)

By further defining $y_1=x$ and $y_2=0$, the standard logistic function is obtained,

$$\frac{\partial }{\partial x}\mathrm{LSE}(x,0)=\underset{\begin{array}{c}\mathrm{The}\mathrm{standard}\\ \mathrm{logistic}\mathrm{function}\end{array}}{\underbrace{\frac{exp\left(x\right)}{exp\left(x\right)+1}}},$$

(20)

and the complimentary logistic function is obtained by differentiating with respect to $y_2=0$.

For $y_1$ and $y_2$ in Equation (19), being the two functions $f\left(x\right)$ and $g\left(x\right)$ of zeroth or first order, and by introducing the logistic growth rate k, Equation (19) can be rewritten as

$$\frac{\partial }{\partial f\left(x\right)}\mathrm{LSE}(f\left(x\right),g\left(x\right))=\underset{\begin{array}{c}\mathrm{The}\mathrm{logistic}\mathrm{function}\end{array}}{\underbrace{f^{\prime }\left(x\right)\frac{exp\left(f\right(x\left)k\right)}{exp\left(f\right(x\left)k\right)+exp\left(g\right(x\left)k\right)}}}.$$

(21)

Equation (21) thereby describes a smooth transition between the slope of $f\left(x\right)$ and $g\left(x\right)$, and the indefinite integral shown in Equation (22), can approximate Equation (1) with a smooth transition between the two functions. Figure 1 shows a visualisation of Equations (21) and (22).

$$\mathrm{LSE}(f\left(x\right),g\left(x\right))=\underset{\mathrm{Smooth}\mathrm{approximation}\mathrm{of}\max \left[f\right(x),g(x\left)\right]}{\underbrace{log\left[exp\left(f\right(x\left)k\right)+exp\left(g\right(x\left)k\right)\right]k^{-1}}}.$$

(22)

2.3. Transition Interval

As Equation (22) approaches $f\left(x\right)$ and $g\left(x\right)$ asymptotically, it is not possible to define a finite interval where the transition between the two functions occurs.

Instead, the transition interval can be defined and found by solving for x in Equation (23), where $f\left(x\right)<g\left(x\right)$ for $x\to \infty$.

$$\begin{array}{cc}\hfill & lb<f^{\prime }\left(x\right)\frac{exp\left(f\right(x\left)k\right)}{exp\left(f\right(x\left)k\right)+exp\left(g\right(x\left)k\right)}<ub,\hfill \end{array}$$

(23)

where $lb$ (lower bound) and $ub$ (upper bound) is

$$\begin{array}{cc}\hfill & lb=f^{\prime }\left(x\right)+p(g^{\prime }\left(x\right)-f^{\prime }\left(x\right))\mathrm{and}\hfill \end{array}$$

(24)

$$\begin{array}{cc}\hfill & ub=f^{\prime }\left(x\right)+(1-p)(g^{\prime }\left(x\right)-f^{\prime }\left(x\right))\mathrm{where}p\in [0,1].\hfill \end{array}$$

(25)

The upper plot in Figure 1 shows the logistic function from Equation (21) (i.e., the slope of the LogSumExp function), and the lower plot shows the corresponding smooth maximum function from Equation (22) (i.e., the LogSumExp function). In the specific plot, $f\left(x\right)=-x$, $g\left(x\right)=0$ and $k=1$. Furthermore, p in Equations (24) and (25) is chosen to be $0.1$, and remains so for the rest of this study. The red part of the curves shows the transition between $f^{\prime }\left(x\right)$ and $g^{\prime }\left(x\right)$ as well as $f\left(x\right)$ and $g\left(x\right)$ in the upper and lower plot, respectively.

2.4. Heat Consumption Modelling with LogSumExp

In Section 2.1, a number of model candidates for the functions $f\left(·\right)$ and $g\left(·\right)$ in the energy signature formulation in Equation (1) were proposed. In addition to that, an alternative to the max function in Equation (1), which determines if the building is in a heat demand regime or and not, is described in Section 2.2.

To estimate the heat consumption during periods with and without a heat demand, the LogSumExp function in Equation (22) is combined with one of the models for weather-dependent heat consumption $f_0$ to $f_4$ found in Section 2.1.1, and the model of the weather-independent heat consumption g in Equation (2).

In

Table 1. Overview of full models. The model names are stated in the leftmost column as M0, M1 up to M4. The bullets (•) indicate if the given inputs are included in the specific model. Model M0 distinguishes itself from the remaining models, as the base temperature $T_{\mathrm{b}}$ is fixed at 17 ${}^{\circ }$C.

Name	Functions		Input				Model Formulation
	$\mathit{f}(\mathbf{·})$	$\mathit{g}(\mathbf{·})$	${\mathit{T}}_{\mathbf{a}}$	${\mathit{W}}_{\mathbf{s}}$	${\mathit{I}}_{\mathbf{g}}$	${\mathit{T}}_{\mathbf{sky}}$	${\mathit{\Phi }}_{\mathbf{heat}}=\mathbf{LSE}[\mathit{f}\left(·\right),\mathit{g}\left(·\right)]$
M0	$f_0$	g	•	–	–	–	${\Phi }_{\mathrm{heat}}=\mathrm{LSE}[\mathrm{UA}(T_{\mathrm{b}}-T_{\mathrm{a}})+{\Phi }_0,{\Phi }_0]+e$
M1	$f_1$	g	•	–	–	–	${\Phi }_{\mathrm{heat}}=\mathrm{LSE}[\mathrm{UA}(T_{{\mathrm{b}}_0}-T_{\mathrm{a}}),{\Phi }_0]+e$
M2	$f_2$	g	•	•	–	–	${\Phi }_{\mathrm{heat}}=\mathrm{LSE}[({\mathrm{UA}}_0+W_{\mathrm{s}}{\mathrm{UA}}_{\mathrm{W}})(T_{{\mathrm{b}}_0}-T_{\mathrm{a}}),{\Phi }_0]+e$
M3	$f_3$	g	•	•	•	–	${\Phi }_{\mathrm{heat}}=\mathrm{LSE}[({\mathrm{UA}}_0+W_{\mathrm{s}}{\mathrm{UA}}_{\mathrm{W}})(T_{{\mathrm{b}}_0}-T_{\mathrm{a}})-\mathrm{gA}{I}_{\mathrm{g}},{\Phi }_0]+e$
M4	$f_4$	g	•	•	•	•	${\Phi }_{\mathrm{heat}}=\mathrm{LSE}[({\mathrm{UA}}_0+W_{\mathrm{s}}{\mathrm{UA}}_{\mathrm{W}})(T_{{\mathrm{b}}_0}-T_{\mathrm{a}})-\mathrm{gA}{I}_{\mathrm{g}}+{\gamma }_1(T_{\mathrm{sky}}^4-T_{\mathrm{a}}^4),{\Phi }_0]+e$

, all five full models candidates are stated. Each model is named correspondingly to the specific function, $f_0$, $f_1$, $f_2$, $f_3$ or $f_4$, it uses. Model M0 therefore consists of the two functions $f_0$ and g, model M1 consists of the two functions $f_1$ and g, and so on.

For any of the models in Table 1, the transition period can be obtained as described in Section 2.3. With $p=0.1$, the building is considered to operate in the transition phase between regime $f\left(·\right)$ and $g\left(·\right)$, when the slope of Equation (22) deviates more than 10% and less than 90% from the slope of $f\left(·\right)$. For deviations of more than 90%, the slope of Equation (22) starts to approach the slope of $g\left(·\right)$, which in this study is zero by definition.

2.5. Unmodelled Dynamics

Until now, the models in Table 1 have treated the base temperature $T_{{\mathrm{b}}_0}$ as constant. This is of course a crude simplification as it both describes the actual indoor temperature and the unmodelled heat balance contributions as seen in Equation (5). However, instead of including measurements of the indoor temperature and explicitly modelling all of the heat balance contributions, we propose a method where the time-varying base temperature is derived from the time ordered sequence of model residuals $\left\{e_t\right\}$.

In Section 2.1, it is argued that the heat exchange with the thermal mass as well as the latent heat exchange can be neglected, by using daily averaged heat consumption and weather data. Furthermore, heat exchange to the ground is assumed to be neglectable, and the weather’s influence on the heat consumption is assumed to be described by one of the models in Table 1. Under these assumptions, ${\Phi }_{\mathrm{x}}$ contained in $T_{{\mathrm{b}}_0}$ must be related to the building usage, which mainly is the sum of ventilation heat losses and internal heat gains, such as metabolism, electrical power and domestic hot water usage.

If the above-mentioned assumptions are not violated and the base temperature $T_{{\mathrm{b}}_0}$ is truly constant as assumed in the models in Table 1, the model errors will be identically distributed and mutually independent, i.e., the errors will not be autocorrelated.

If, on the other hand, the above-mentioned assumptions are not violated, but the base temperature $T_{{\mathrm{b}}_0}$ is varying over time, the sequences of errors will be autocorrelated (i.e., correlated over time) and reflect the unmodelled dynamics. As a consequence of the above-mentioned assumptions, the model errors contain information on the variation of $T_{{\mathrm{b}}_0}$, and therefore on $T_{\mathrm{i}}$ and ${\Phi }_{\mathrm{x}}$ in Equation (5).

To model the time-dependent base temperature, $T_{{\mathrm{b}}_0,t}$, the following model is suggested,

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill T_{{\mathrm{b}}_0,t}& =T_{{\mathrm{b}}_0}+\Delta T_{{\mathrm{b}}_0,t}+{\epsilon }_t,\hfill \end{array}\end{array}$$

(26)

where $T_{{\mathrm{b}}_0}$ is the constant base temperature estimated by one of the models in Table 1, $\Delta T_{{\mathrm{b}}_0,t}$ is the deviation from $T_{{\mathrm{b}}_0}$ at time t and ${\epsilon }_t$ is the independent and identically distributed noise with mean zero.

The model errors $e_t$ are the sum of system noise and observation noise. Following the arguments and assumptions presented in the beginning of this section, the system noise is a result of the time-varying base temperature, which in the models in Table 1 is treated as constant. The model errors, $e_t$, can therefore be described as

$$e_t=\underset{\mathrm{System} \mathrm{noise}}{\underbrace{\Delta T_{{\mathrm{b}}_0,t}\mathrm{UA}}}+{\epsilon }_t,$$

(27)

where $\Delta T_{{\mathrm{b}}_0,t}\mathrm{UA}$ is the time-varying heat gain (or heat loss for negative values) required to maintain the heat balance, and ${\epsilon }_t$ is the observation noise.

The unknown function $\Delta T_{{\mathrm{b}}_0,t}$ can be found by kernel estimation. Kernel estimation is a nonparametric technique used to determine hidden nonlinear functional relations. The kernel estimate is shown to be equal to the local weighted least squares estimate in [37]. Therefore, the time-varying model parameters ${\widehat{\beta }}_t$ are obtained by

$${\widehat{\beta }}_t=arg\underset{\beta }{min}\frac{1}{N}\sum _{i=1}^N{w}_{t_i}{(e_{t_i}-X_i\beta )}^2,$$

(28)

where N is the number of observations, i refers to the $i^{{\mathrm{th}}^{}}$ vector element or matrix row, $e_t$ is the model error, X is the design matrix of a first-order polynomial with time t as the explanatory variable, $\beta$ is the model parameters and $w_{t_i}$ is the kernel weights. The kernel weights are defined by

$$w_{t_i}=\frac{K\left[h^{-1}(t_i-t)\right]}{\frac{1}{N}{\sum }_{i=1}^{N}K\left[h^{-1}(t_i-t)\right]},$$

(29)

where K is the Epanechnikov kernel [38] with bandwidth h. The bandwidth is found by leave-one-out cross validation as described in [37].

The N-by-2 matrix ${\beta }_t$ contains a set of two parameters (slope and intercept) for each of the time steps. The time-varying term $\Delta T_{{\mathrm{b}}_0,t}$ in Equation (27) is therefore

$$\Delta T_{{\mathrm{b}}_0,t}=\frac{\mathrm{diag}\left(X{\beta }_t^{\top }\right)}{\mathrm{UA}},$$

(30)

where $\mathrm{diag}\left(X{\beta }_t^{\top }\right)$ is the diagonal of the N-by-N matrix $X{\beta }_t^{\top }$. The term $\mathrm{diag}\left(X{\beta }_t^{\top }\right)$ is the remaining time-varying heat balance contribution to obtain thermal balance, which will be named $\Delta {\Phi }_{\mathrm{x},t}$. Equation (30) therefore becomes

$$\Delta T_{{\mathrm{b}}_0,t}=\frac{\Delta {\Phi }_{\mathrm{x},t}}{\mathrm{UA}}.$$

(31)

Using the estimate from Equation (31), the corrected and time-varying estimate of $T_{{\mathrm{b}}_0,t}$ in Equation (26) is obtained.

2.6. Thermal Performance Evaluation

By substituting $T_{{\mathrm{b}}_0}$ in Equation (26) with Equation (5), the expression below is obtained.

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill T_{{\mathrm{b}}_0,t}& =T_{\mathrm{i}}-\frac{{\Phi }_{\mathrm{x}}}{\mathrm{UA}}+\Delta T_{{\mathrm{b}}_0,t}+{\epsilon }_t,\hfill \end{array}\end{array}$$

(32)

where $\Delta T_{{\mathrm{b}}_0,t}$ can be expressed by $\Delta {\Phi }_{\mathrm{x},t}/\mathrm{UA}$, such that

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill T_{{\mathrm{b}}_0,t}& =T_{\mathrm{i}}-\frac{{\Phi }_{\mathrm{x}}+\Delta {\Phi }_{\mathrm{x},t}}{\mathrm{UA}}+{\epsilon }_t\hfill \\ \hfill & =T_{\mathrm{i}}-\frac{{\Phi }_{\mathrm{x},t}}{\mathrm{UA}}+{\epsilon }_t.\hfill \end{array}\end{array}$$

(33)

The term ${\Phi }_{\mathrm{x}}$ is therefore the mean user-related heat gain needed to obtain thermal balance, $\Delta {\Phi }_{\mathrm{x},t}$ is the time-dependent variation around the mean and ${\Phi }_{\mathrm{x},t}$ is the sum of ${\Phi }_{\mathrm{x}}$ and $\Delta {\Phi }_{\mathrm{x},t}$.

The models in Table 1 can provide an estimate of UA, and Equation (26) can provide an estimate of $T_{{\mathrm{b}}_0,t}$. However, both $T_{\mathrm{i}}$ and ${\Phi }_{\mathrm{x},t}$ in Equation (33) remain unknown. Therefore, we are not able to distinguish the indoor temperature ($T_{\mathrm{i}}$ ) from the user related heat gain (${\Phi }_{\mathrm{x},t}$). However, by rearranging Equation (33) and using the actual base temperature $T_{\mathrm{b},t}$ instead of $T_{{\mathrm{b}}_0,t}$, the user related heat gain can be expressed as

$${\Phi }_{\mathrm{x},t}=\mathrm{UA}(T_{\mathrm{i}}-T_{\mathrm{b},t})+{\epsilon }_t.$$

(34)

By substituting $T_{\mathrm{i}}$ with a given design indoor temperature, the resulting heat gain related to the building use and its occupants can be estimated by Equation (34). The estimate of ${\Phi }_{\mathrm{x},t}$ can now be compared with the sum of heat gains related to metabolism, electricity consumption and ventilation losses from an energy performance calculation. It is further discussed in Section 4, how the heat consumption potentially can be separated into user-, weather- and building envelope-related heat consumption. It should, however, be noticed that the results are only valid for days with weather-dependent heat consumption.

3. Case Study

3.1. Data

Sixteen randomly selected houses in Sønderborg in Southern Denmark have been used as a demonstration case. The built year of the houses ranges from 1937 to 1996, and the heated floor area from 86 to 173 ${\mathrm{m}}^2$. All houses are heated by district heating only, i.e., there is no additional and unmeasured heat sources in the houses except from internal gains. Finally, four of the houses have night-setback on the temperature set point.

The only measurement used from the houses is the total heat consumption provided by Sønderborg Fjernvarme—a consumer-owned district heating company in Sønderborg. In addition, outdoor temperature, wind speed and global solar irradiation are measured at the district heating plant, which is within 10 $\mathrm{k}$$\mathrm{m}$ of the houses.

The sky temperature used in model M4 is obtained from the freely available reanalysis data set ERA5-Land provided by the Copernicus Climate Change Service [39]. The full documentation on the ERA5-Land can be found in [40].

The heat consumption was measured every 10th minute, and the weather data were obtained on hourly basis. In the analyses, only daily averaged values are used from a period from 2 January 2009 to 1 May 2011.

The original heat consumption data consist of both domestic hot water consumption and space heating. Before the analyses carried out in this study, the hot water consumption has been separated from the space heating by means of kernel smoothing as described and done in [41]. Therefore, the estimated space heating has been used, rather than the total heat consumption.

3.2. Software

Each of the models have been set up in Template Model Builder (TMB) (version 1.7.16) [42] and fitted with the global optimisation algorithm, Multi-Level Single-Linkage (MLSL), alongside the local optimisation algorithm Limited-memory Broyden–Fletcher–Goldfarb–Shanno Algorithm (L-BFGS). The optimisation algorithms used are implemented in the R package for nonlinear optimisation, R Interface to NLopt (nloptr) (version 1.2.1) [43]. Version 3.5.1 of R [44] has been used throughout the study.

Despite the choice of software used in this study, the models can be estimated by using a broad range of simpler optimisers and other software.

3.3. Model Validation

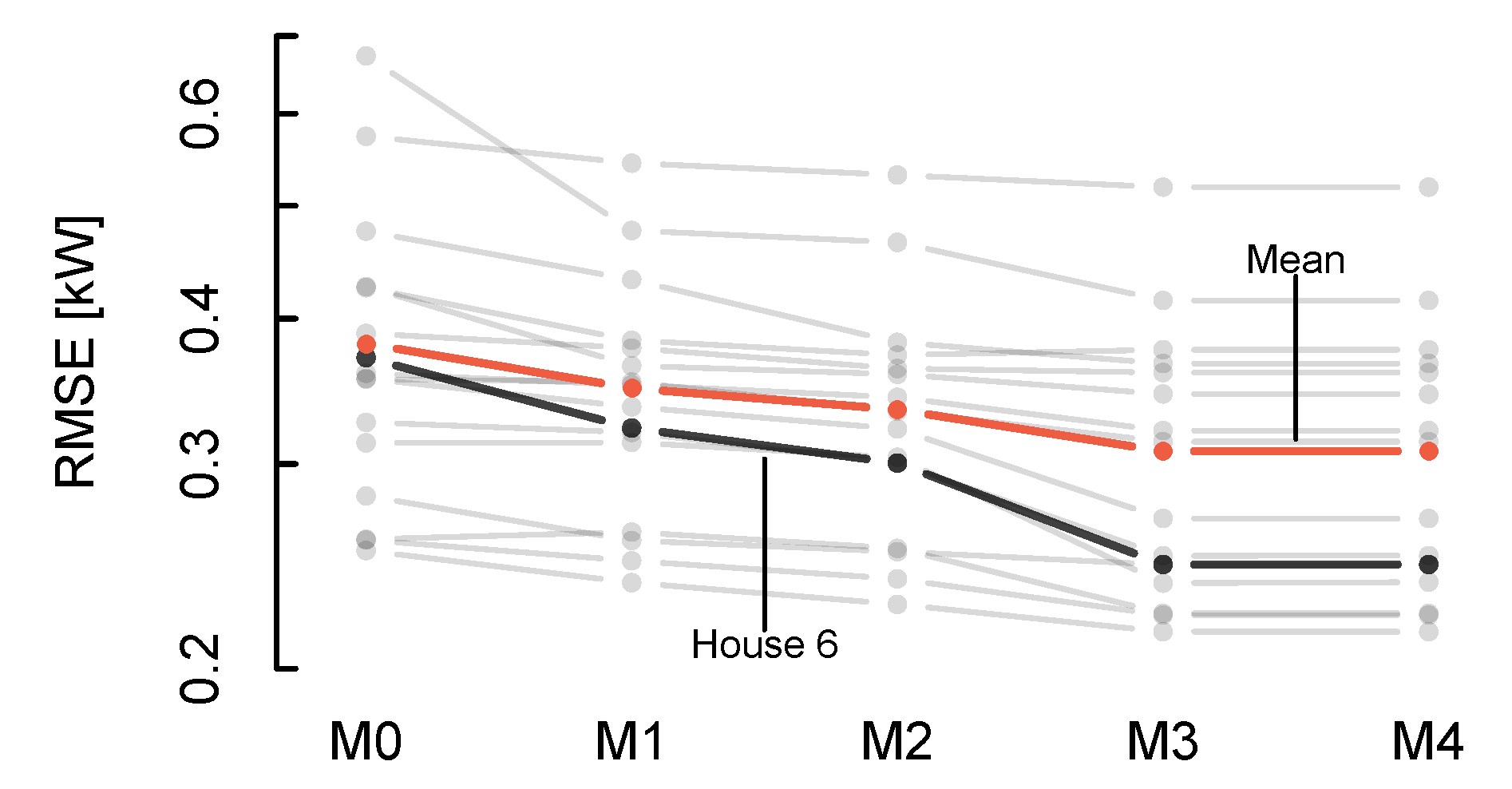
All models presented in Table 1 were fitted and validated by means of a five-fold cross-validation where the hyperparameter k in Equation (22) was tuned. The training and validation data were splitted randomly in a 80/20 ratio. The root mean squared error (RMSE) on the validation set is shown in the slope chart in Figure 2.

The corresponding RMSE for each house is indicated as a grey or black dot. The red line indicates the mean RMSE across all 16 houses and the black line indicates House 6 which we will study in details. Notice that the RMSE is plotted on a logarithmic scale, i.e., the slopes of the lines between the points express the relative change in model error.

A general model improvement is seen when the simplest model, M0, is extended by including the base temperature as a free parameter as done in model M1.

Models M2 and M3 are the model extensions, which include wind and solar irradiation, respectively. For both models we see a decrease in the RMSE, meaning that both wind and solar irradiation have a significant effect on the heat consumption. However, including solar gain has the largest positive effect on the model errors when the models are evaluated in this successive manner. This is also referred to as type I partition [45].

Finally, the heat loss related to long-wave radiation (M4) does not affect any of the model predictions. The parameter ${\gamma }_1$ in Equation (15) is simply estimated as such a low and insignificant value that it does not affect the RMSE.

3.4. Residuals

In Figure 3, the residual analysis plot for House 6 is illustrated. Each row consists of three plots: the model residuals of a given model, the fit of its extension and the residuals after the model extension.

In the top-left plot in Figure 3, the residuals are shown for model M0. From the plot, a series of systematic errors from approximately 8 to 17 ${}^{\circ }$C and a negative trend in the residuals are observed.

The negative trend in the residuals is diminished after the model M0 is extended to model M1 (top-right). However, the systematic errors are still present. The systematic error means that both models M0 and M1 are not capable of describing the heat consumption during the transition period.

Last, in the residuals for temperatures below 8.0 ${}^{\circ }$C, a slight concave trend is seen for both M0 (top-left) and M1 (top-right). These patterns indicate that the heat consumption is not only a function of the outdoor temperature.

In the second row of plots to the left, the residuals of model M1 are shown as a function of the wind speed. The red dashed line indicates that model M1 tends to underestimate the heat consumption for wind speeds above per-mode=symbol $2.5$ $\mathrm{m}$/$\mathrm{s}$ and overestimate the heat consumption for wind speeds below per-mode=symbol $2.5$ $\mathrm{m}$/$\mathrm{s}$. Modelling the wind-dependent heat loss with model M2, the tendency disappear as seen in the right-most plot in the second row.

In the third row of plots to the left, the model residuals of M2 are compared to the global solar irradiation. In this case, we see a negative linear trend in the residuals. This means that for days with high levels of solar irradiation, model M2 tends to overestimates the heat consumption, simply because the model does not include the effect of solar irradiation. After implementing the solar gain in model M3, the residuals flattens out.

It is seen that the solar irradiation explains a lot of the variance in the transition period around 5–15 ${}^{\circ }$C (third row, second column). In contrast to this, we see that the wind speed in the M2 model (second row, second column) mainly explains the variance in the lower outdoor temperature range. As the heat loss due to wind is proportional to the outdoor temperature, and due to the fact that the daily mean outdoor temperature is correlated with the solar irradiation, this is a reasonable result.

Additionally, the figure shows the residuals of model M3 as a function of the outdoor temperature in row four, column three. Compared to the residuals of the previous models, we now see that the systematic error in the transition period disappears. Only a changing variance between weather-dependent and weather-independent days is seen. Therefore, the solar gain seems to be the main reason for the heating system turning on and off in the transition period.

In the last row of plots, the effect of long-wave radiation between the building and its surroundings is shown. As expected, based on the unaffected RMSE in Figure 2, the residuals remain unaffected.

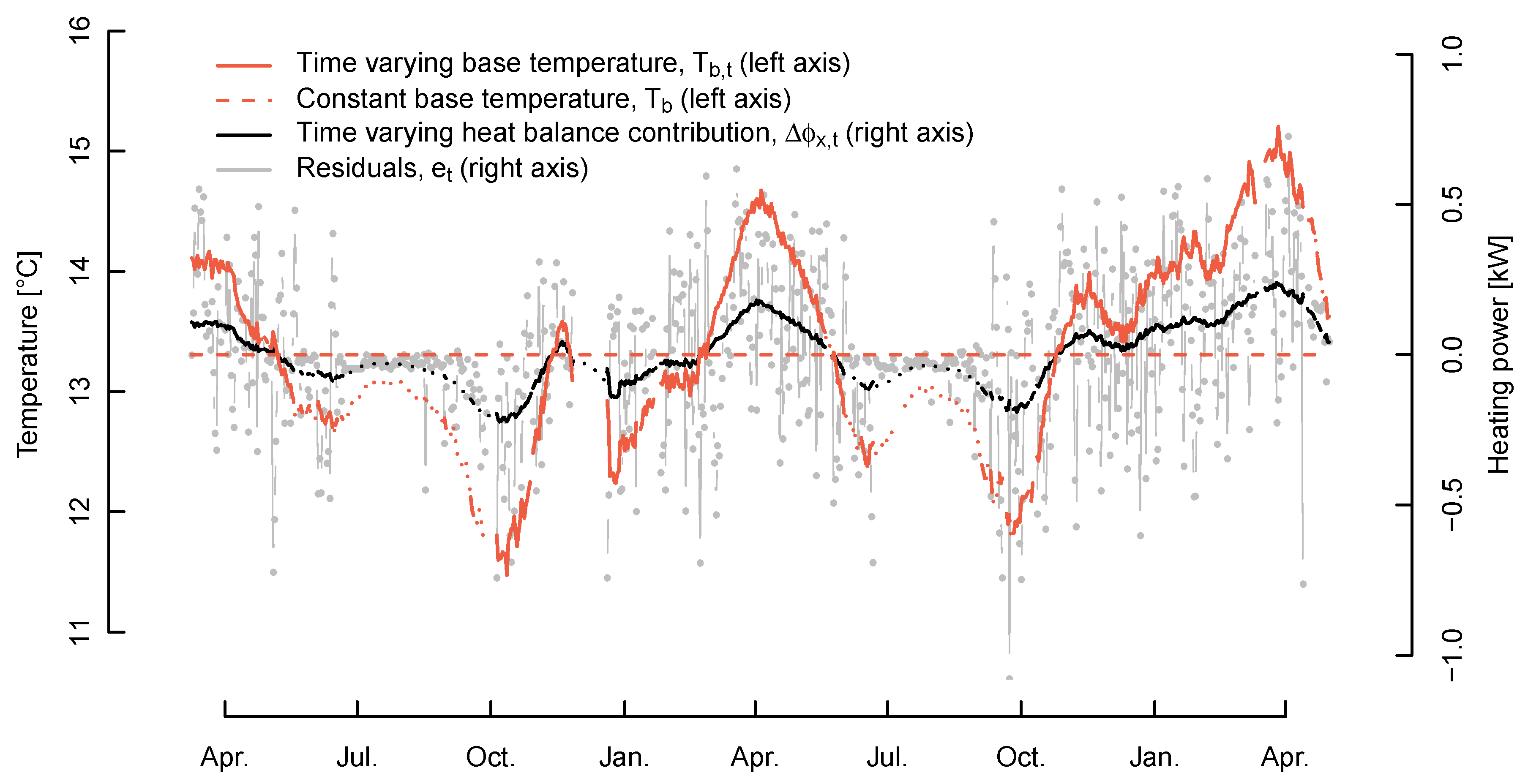
It is now shown that the model residuals of model M3 (and model M4 for that matter) are independent of the outdoor temperature, wind speed, solar irradiation and the sky temperature. However, a clear time dependence in the residuals is found in Figure 4 (grey lines). As argued for in Section 2.5, this is likely related to time-correlated occupants’ behaviour.

In Figure 4, the black line shows the time-varying heat gain needed to maintain thermal balance at all time, which is obtained as $\Delta {\Phi }_{\mathrm{x},t}=\mathrm{diag}\left(X{\beta }_t^{\top }\right)$ as described in Section 2.5. Based on the estimate of $\Delta {\Phi }_{\mathrm{x},t}$, the time-varying base temperature $T_{\mathrm{b},t}$ is found and shown as the red line. The dotted sections of the red and black lines indicate periods without a heat demand. During these periods, the estimate is not valid.

3.5. Parameter Sensitivity

It is now demonstrated how the model with outdoor temperature, global solar irradiation and wind speed as explanatory variables can describe the actual energy use of the buildings rather accurate. In this section, we will investigate how two of the common parameters across all models (UA and the base temperature $T_{\mathrm{b}}$) are affected by the different model formulations found in Table 1.

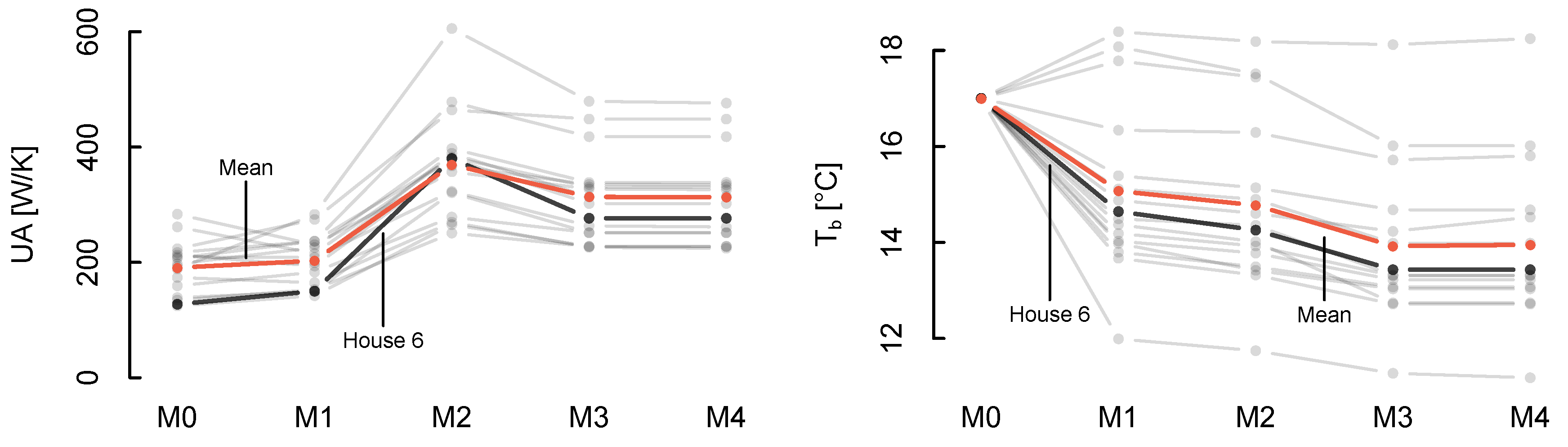
In Figure 5 (left), the estimated UA value for each house and model is shown. The UA value is the estimated heat loss coefficient under influence of the mean wind speed (per-mode=symbol $2.5$ $\mathrm{m}$/$\mathrm{s}$) observed in the measurement period. In the plot to the right, the estimated base temperatures are shown for all the houses and models.

Going from model M0 to M1 gives rise to both increments and reductions in the estimate of UA and $T_{\mathrm{b}}$. It is therefore not possible to state any general bias by fixing $T_{\mathrm{b}}$; it depends on the building and the occupants.

Including the effects of the wind speed, as done in model M2, the estimated UA values increase significantly and consistently for all houses. The effect on the base temperature $T_{\mathrm{b}}$ is more moderate and reduces slightly. On the other hand, including solar gain in model M3 creates a small decrease in the UA value, as well as in the base temperature.

The introduction of long-wave radiation does not affect UA nor $T_{\mathrm{b}}$. With the proposed implementation of long-wave radiation in model M4, it is completely irrelevant for the heat consumption.

Going from the simplest reasonable model (M1) to the best model (M3) gives an average change in the estimated UA value of +54% across all 16 buildings considered, with the smallest and largest change of +26% and +84%, respectively.

The base temperature changes from M1 to M3 in average by −8%, with the smallest and largest change of −1% and −11%, respectively.

3.6. Thermal Performance Characterisation

Based on the finding in the previous sections, model M3 has proven to be the best model. In this section, some of the results obtained from model M3 are presented in

Table 2. Estimated performance parameters for 16 houses in Denmark. The number in parentheses states the standard error of the parameters. ${\mathrm{U}}_0$ and ${\mathrm{UA}}_0$ are the heat loss coefficients under wind-free conditions, and ${\mathrm{UA}}_{\mathrm{W}}$ is the wind-dependent increment in the UA value. $T_{\mathrm{transition}}$ states the range of outdoor temperatures at which the building is in transition from heating to non-heating period, given no wind and solar irradiation. Finally, ${\overline{\Phi }}_{\mathrm{x},t}|T_{\mathrm{i}}=20{}^{\circ }\mathrm{C}$ and ${\sigma }_{{\Phi }_{\mathrm{x},t}}$ state the mean and the standard deviation, respectively, of the estimated time-varying heat balance contribution required to obtain thermal balance with an indoor temperature of 20 ${}^{\circ }\mathrm{C}$.

House	Year	Floor Area	${\mathbf{U}}_0$			${\mathbf{UA}}_0$			${\mathbf{UA}}_{\mathbf{W}}$			$\mathbf{gA}$			${\mathit{\Phi }}_0$			${\mathit{T}}_{\mathbf{b}}$			${\mathit{T}}_{\mathbf{transition}}$	${\overline{\mathit{\Phi }}}_{\mathbf{x},\mathit{t}}|{\mathit{T}}_{\mathbf{i}}=$20 ${}^{\circ }\mathbf{C}$	${\mathit{\sigma }}_{{\mathit{\Phi }}_{\mathbf{x},\mathit{t}}}$
		[${\mathbf{m}}^2$]	[$\mathbf{W}$/$(K{m}^2)$]			[$\mathbf{W}$/$\mathbf{K}$]			[$\mathbf{W}$/$\mathbf{K}$ per  $\mathbf{m}$/$\mathbf{s}$]			[${\mathbf{m}}^2$]			[$\mathbf{W}$]			[${}^{\circ }\mathbf{C}$]			[${}^{\circ }\mathbf{C}$]	[$\mathbf{W}$]	[$\mathbf{W}$]
1	1970	151	1.25	(0.03)	*	189	(4)	*	58	(7)	*	2.5	(0.3)	*	676	(84)	*	16.5	(0.5)		12.1–21.0	702	157
2	1969	163	1.25	(0.02)	*	204	(4)	*	39	(8)	*	3.7	(0.3)	*	340	(47)	*	14.2	(0.4)	*	9.5–18.9	1246	194
3	1963	140	1.28	(0.02)	*	179	(2)	*	32	(5)	*	2.5	(0.1)	*	141	(30)	*	15.7	(0.2)	*	11.9–19.5	810	103
4	1952	86	1.45	(0.03)	*	125	(2)	*	41	(5)	*	1.5	(0.2)	*	215	(19)	*	12.8	(0.3)	*	10.2–15.4	971	118
5	1966	111	1.54	(0.03)	*	171	(3)	*	61	(7)	*	1.6	(0.2)	*	110	(63)		16.6	(0.3)		9.6–23.6	643	155
6	1963	119	0.97	(0.02)	*	115	(2)	*	65	(6)	*	2.8	(0.2)	*	47	(19)	*	13.3	(0.3)	*	10.2–16.4	880	129
7	1947	119	2.17	(0.04)	*	258	(5)	*	72	(13)	*	1.2	(0.4)	*	6	(50)		13.5	(0.3)	*	6.9–20.0	1810	243
8	1965	160	1.24	(0.04)	*	199	(6)	*	57	(14)	*	2.2	(0.4)	*	376	(45)	*	12.6	(0.5)	*	8.9–16.4	1569	258
9	1965	173	1.21	(0.02)	*	210	(3)	*	42	(6)	*	1.2	(0.2)	*	523	(62)	*	18.2	(0.3)	*	15.8–20.6	389	275
10	1996	135	0.90	(0.02)	*	121	(2)	*	51	(6)	*	2.5	(0.2)	*	106	(25)	*	14.1	(0.4)	*	10.2–18.0	786	193
11	1966	122	1.09	(0.04)	*	133	(4)	*	31	(11)	*	1.2	(0.3)	*	108	(46)	*	14.7	(0.5)	*	10.5–18.9	751	96
12	1975	136	1.05	(0.02)	*	143	(2)	*	31	(4)	*	1.9	(0.1)	*	644	(17)	*	13.4	(0.3)	*	11.3–15.4	1001	94
13	1937	86	2.67	(0.06)	*	229	(5)	*	92	(14)	*	4.4	(0.4)	*	45	(31)		11.2	(0.3)	*	7.6–14.8	2227	431
14	1965	123	1.36	(0.02)	*	167	(2)	*	57	(6)	*	2.4	(0.2)	*	356	(22)	*	14.1	(0.3)	*	11.8–16.4	1068	203
15	1953	127	1.65	(0.03)	*	209	(4)	*	80	(10)	*	3.1	(0.3)	*	166	(35)	*	13.0	(0.3)	*	7.0–19.1	1593	210
16	1967	137	1.22	(0.02)	*	167	(3)	*	34	(7)	*	1.3	(0.2)	*	193	(26)	*	13.5	(0.3)	*	8.1–18.9	1137	143
$H_0:$			${\mathrm{U}}_0=0$			${\mathrm{UA}}_0=0$			${\mathrm{UA}}_{\mathrm{W}}=0$			$\mathrm{gA}=0$			${\Phi }_0=0$			$T_{\mathrm{b}}=17$
Significance code ‘*’: $p-\mathrm{value}<0.05$.

.

As an example, Table 2 shows that House 6 has a ${\mathrm{UA}}_0$ value of 115 $\mathrm{W}$/$\mathrm{K}$. The ${\mathrm{UA}}_0$ value represents the heat loss coefficient under weather conditions with a wind speed of 0 $\mathrm{m}$/$\mathrm{s}$. Even though House 6 has the smallest ${\mathrm{UA}}_0$ value estimated, the heat loss related to convection and infiltration (${\mathrm{UA}}_{\mathrm{W}}$) is the fourth highest among the 16 houses. This might indicate that House 6 potentially has air leakage issues.

Looking at the estimated ${\mathrm{UA}}_{\mathrm{W}}$ values, all houses seem to be significantly affected by the wind. Furthermore, it is reasonable to believe that a high standard error (e.g., House 8) is a result of different wind effects from different wind directions, or by the fact that people often open and close the windows. Both scenarios will result in a high standard error.

$T_{\mathrm{b}}$ in Table 2 tells us at which outdoor temperature the house is in thermal balance given the average weather conditions. The base temperature varies from $11.2$ ${}^{\circ }\mathrm{C}$ to $18.2$ ${}^{\circ }\mathrm{C}$. A low value of $T_{\mathrm{b}}$ can—as stated in the Section 2.1.1—mean different things. Either the internal gains are high, the indoor temperature low, the house is poorly insulated or some sort of combination. The opposite is true for a high value of $T_{\mathrm{b}}$.

The transition period $T_{\mathrm{transition}}$ indicates the outdoor temperature range where the building is in its transition phase. The spans indirectly indicate to which extent the heating system is affected by the weather. That is, a narrow band tells that the building or the heating system is insensitive to changing weather conditions, and visa versa.

As we do not know the indoor temperature and the heat gains related to the building use, we are not able to separate them. However, assuming that the indoor temperature is equal to the design indoor temperature (e.g., 20 ${}^{\circ }\mathrm{C}$), we can estimate the remaining unobserved heat balance contributions (${\Phi }_{\mathrm{x},t}|T_{\mathrm{i}}$) needed to obtain thermal balance as described in Section 2.5. The mean and standard deviation of the time-varying process ${\Phi }_{\mathrm{x},t}$ is stated in the two last columns of Table 2.

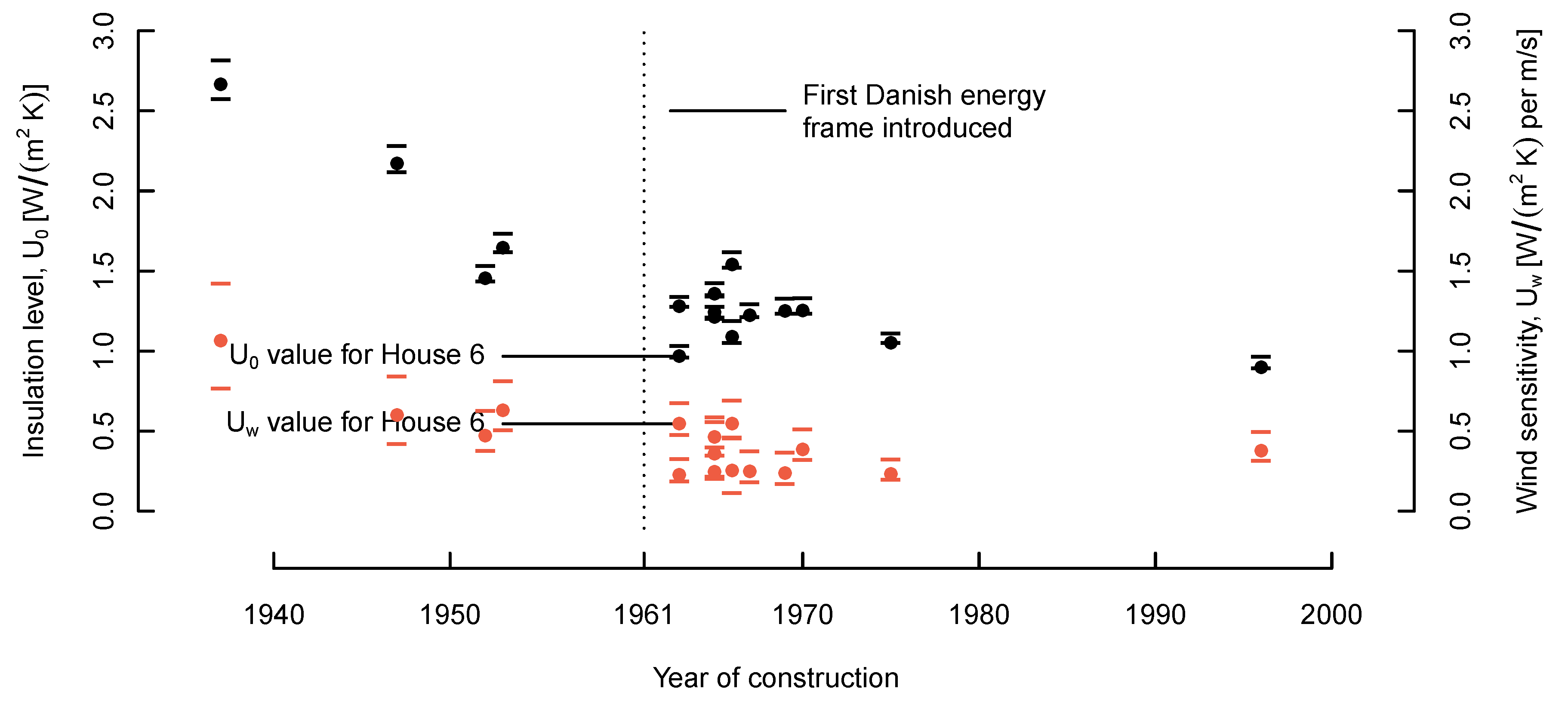
In Figure 6, the estimated ${\mathrm{U}}_0$ value and the wind-dependent increment of the U value (${\mathrm{UA}}_{\mathrm{W}}$ per ${\mathrm{m}}^2$ heated floor area) are plotted as a function of the construction year. The bars around the dots indicate a 95% confidence interval of the estimate.

Regarding both ${\mathrm{U}}_0$ and ${\mathrm{U}}_{\mathrm{W}}$, the figure shows that there is a negative trend in the estimates, which indicates that the thermal performance has increased during the years. Despite the rather small sample, it seems like there is a significant difference between houses build before 1961, which is the year where the first energy frame came in force in Denmark, and after.

Even though the negative trend is present for the ${\mathrm{U}}_0$ and the ${\mathrm{U}}_{\mathrm{W}}$ values, the reduction of ${\mathrm{U}}_0$ for the individual houses does not necessarily lead to a reduction in ${\mathrm{U}}_{\mathrm{W}}$. An example of this is shown for House 6, which has the lowest ${\mathrm{U}}_0$ value of the houses build between 1961 and 1980, but one of the highest ${\mathrm{U}}_{\mathrm{W}}$ values in the same cluster.

4. Discussion

In Section 3, it is shown how a number of building parameters, related to its thermal performance from heat consumption measurements and weather data, can be estimated. Making use of electricity consumption data and separately measured space heating is strongly believed to improve the models further.

However, for an estimation of the two most important thermal performance parameters in this paper—the ${\mathrm{UA}}_0$ and ${\mathrm{UA}}_{\mathrm{W}}$ values—the inclusion of electricity and separately measured space heating would most likely affect the estimates to a minor extent, as long as the daily average values are of approximately equal magnitude for all weather conditions. This is because such heat gains are additive terms in the model formulations. Therefore, to keep the models flexible and scalable, as few as possible measurements are preferred, as long as they do not introduce a serious bias to the estimated model parameters.

In Section 2.5, we have shown how it is possible to model the residuals and estimate the variation in the base temperature needed to maintain thermal balance. Additionally, for a given design indoor temperature, the time-varying heat balance contribution related to the building use is estimated. In Table 2, the mean and the standard deviation of the heat balance contribution required to maintain an indoor temperature of 20 ${}^{\circ }\mathrm{C}$ are given for all 16 houses; in Figure 4, the variation is shown for House 6.

From the investigation of the residuals of model M3 (Figure 3), there is no clear sign of any missing effects, that is, a function of outdoor temperature, wind speed, global solar irradiation or long-wave radiation. However, there is a correlation over time. Consequently, we have some time-dependent dynamics which are not captured by the model.

For daily averaged values or longer, the dynamics related to the heat capacities of the building should be averaged out sufficiently even though the long time constants often exceed 24 $\mathrm{h}$ [22]. Systematic errors such as those found in Figure 4 are suggested to consist of two main effects: changing temperature set-points and ventilation rates. That is, both effects which are directly related to the building use (occupant behaviour).

Besides estimating a number of important parameters that describe the thermal building performance, the methods presented in this paper are seen as a potential stepping stone towards an identification of the main reasons for the well-known performance gap in buildings. Namely, the occupants, the weather conditions and the building envelope.

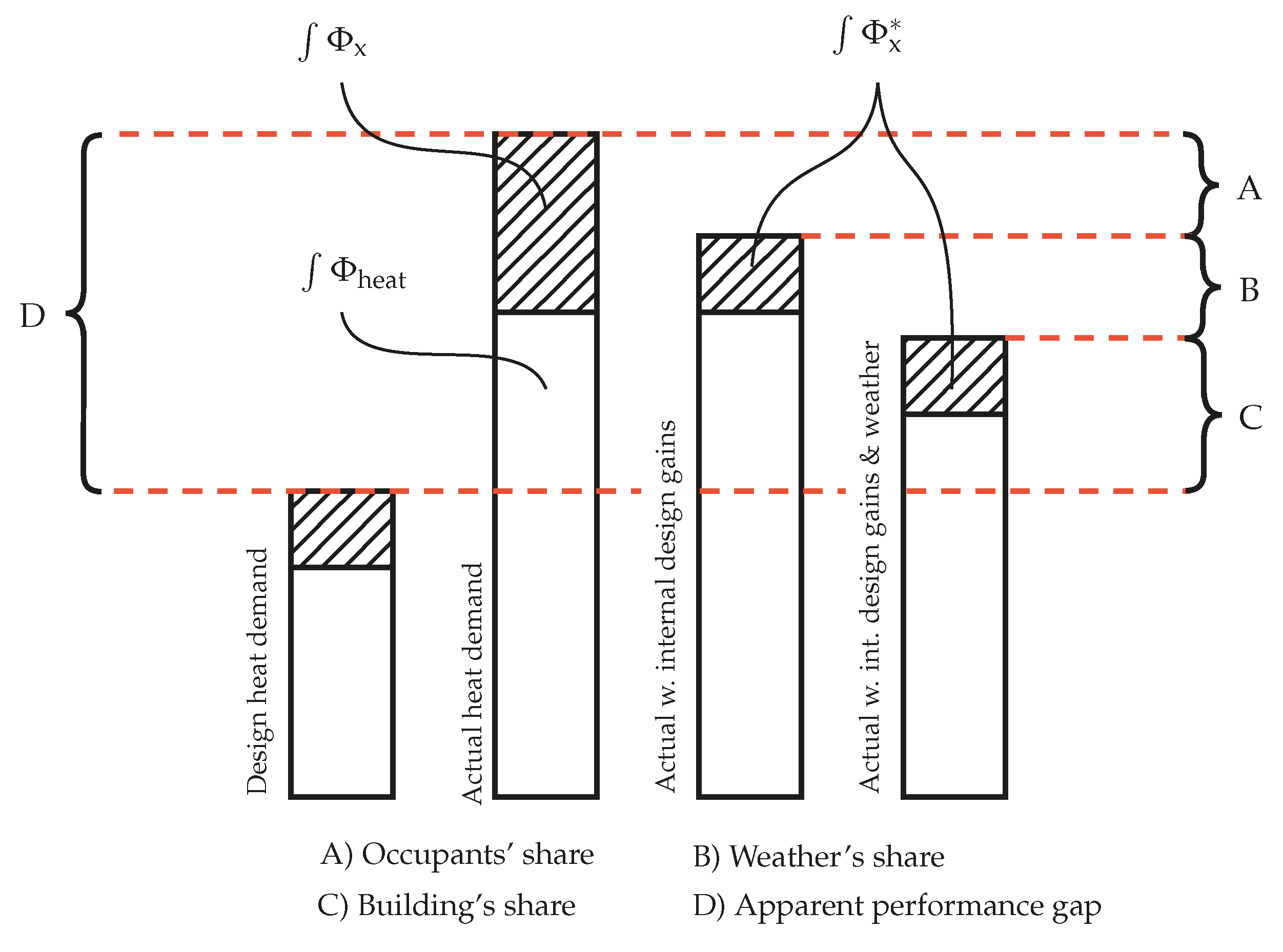
In general, to document the actual energy performance of a building under usage (including the way the occupants affect this performance), a few design parameters, used as input for the calculation of the building energy performance, are required. Those include the weather data (e.g., the design reference year (DRY) weather data), the design indoor temperature, internal heat gains and ventilation losses. The actual energy performance evaluation can then be used to illuminate the different reasons causing the discrepancy between expected and realised energy use. In Figure 7, we illustrate the apparent performance gap and the three possible causes of the discrepancy which is further described in the following.

A

Unintended occupants’ related differences in the energy consumption can be estimated as the difference between the estimated user-related heat gain ${\Phi }_{\mathrm{x},t}$ and the user-related heat gain assumed in the design phase, ${\Phi }_{\mathrm{x},t}^{*}$.

Assuming that the indoor temperature is equal to the actual temperature, the user related heat gain assumed in the design phase is

$$\begin{array}{cc}\hfill {\Phi }_{\mathrm{x},t}^{*}& ={\Phi }_{\mathrm{int}}^{*}-{\Phi }_{\mathrm{vent}}^{*},\hfill \end{array}$$

(35)

where ${\Phi }_{\mathrm{int}}^{*}$ and ${\Phi }_{\mathrm{vent}}^{*}$ are the anticipated internal heat gain (e.g., electricity and metabolism) the design ventilation loss, respectively.

Based on Equation (34), the difference between the assumed heat gain caused by the occupants and the actual heat gain (see A in Figure 7) can be estimated by

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\Phi }_{\mathrm{user}}& ={\mathrm{UA}}_0(T_{\mathrm{i}}-T_{\mathrm{b},t})-{\Phi }_{\mathrm{x},t}^{*}\hfill \\ \hfill & ={\Phi }_{\mathrm{x},t}-{\Phi }_{\mathrm{x},t}^{*},\hfill \end{array}\end{array}$$

(36)

where ${\Phi }_{\mathrm{x},t}$ is the estimated actual heat gain related to the building use given $T_{\mathrm{i}}=T_{\mathrm{i}}^{*}$ and $T_{\mathrm{i}}^{*}$ is the anticipated design indoor temperature. ${\mathrm{UA}}_0$ is the heat loss coefficient under wind-free conditions estimated by model M3 found in Table 1, and $T_{{\mathrm{b}}_0,t}$ is the time-varying estimate of the base temperature found as described in Section 2.5.

The higher ${\Phi }_{\mathrm{x},t}|T_{\mathrm{i}}=T_{\mathrm{i}}^{*}$ is, the more occupant-related heat is required to bring the building in thermal balance. This means, if ${\Phi }_{\mathrm{x},t}>{\Phi }_{\mathrm{user}}$, the internal heat gains are higher than expected in the design phase, the ventilation loss is lower than expected in the design phase, the indoor temperature is lower than the design temperature or a combination.

On the other hand, if ${\Phi }_{\mathrm{x},t}<{\Phi }_{\mathrm{user}}$ the opposite is true.

In this scenario, it is assumed that ventilation and internal gains are independent of the weather. In reality, this might be violated, and Equation (36) must by altered to account for that.

B

Weather-related differences in the energy use can be estimated by comparing the predicted energy use with the actual weather conditions, and the predicted energy use with the outdoor temperature, wind speed and global solar irradiation used in the design phase. Model M3 in Table 1 is used for prediction.

C

Building envelope-related differences in the energy use can be estimated as the difference between the predicted energy use obtained using model M3 in Table 1 and the occupants and weather corrected energy use obtained from points A and B, above.

The concept is further illustrated in Figure 7, but it still needs to be validated on either simulated or actual building data. The method for estimating the occupants’ effect on the energy use may eventually be refined as well, as this can cause significant changes in the model parameter estimates as seen, e.g., in [46]. In this study, the occupancy rate was used as proxy for different buildings operation modes. It was found that the energy signature (with only the ambient outdoor air temperature as explanatory variable) resulted in significantly different model parameter estimates if the models were estimated on occupied, unoccupied or both occupied and unoccupied data.

As the model is formulated as a fully differentiable model, contrary to the typical energy signature model, it allows for more advanced estimation techniques. One natural model extension is to estimate model M3 in Table 1 and the occupant-related heat gain ${\Phi }_{\mathrm{x},t}$, simultaneously. This can be done by formulating the model as a second-order state-space model, with the occupants’ related heat gain $\Delta {\Phi }_{\mathrm{x},t}$ seen in Figure 4 (black line), as a mean-reverting hidden state.

Alternatively, the modelling approach presented in the paper can be estimated recursively, such that the estimate of ${\Phi }_{\mathrm{x},t}$ is fed back into model M3 as an additional heat gain. A new realisation of ${\Phi }_{\mathrm{x},t}$ can then be obtained, and the routine can be repeated until convergence.

5. Conclusions

This study has shown that the typical linear energy signature methods, found in the literature, can be significantly improved by applying a nonlinear and smooth model formulation.

Only daily averaged values of heat consumption and measurements of outdoor temperature, wind speed and global solar irradiation were used as model input. From that, several measures for the thermal building performance were estimated, including heat loss coefficients, heat losses related to convection and infiltration, solar transmittance, base heat load and transition periods. The use of so few variables makes the proposed method highly scalable and easily automatised. This was demonstrated on a study on 16 random selected single family houses.

It has been illustrated how the proposed model is more accurate in describing the variance and nonlinearities in the heat consumption compared to a simple energy signature with only the outdoor temperature as the explanatory variable.

Based on the model residuals, the heat gains related to the building usage were estimated by means of nonparametric kernel estimation methods. The estimation of building usage-related heat consumption paves the way for detailed building performance documentation and screening, as outlined in the current energy performance of buildings directive (EPBD) [5]. For example, the impact on energy use related to weather, building use and the building envelope itself can be estimated separately.

The novel heat demand formulation using a smooth maximum function (LogSumExp) does not only provide a way of estimating the transition period from weather-dependent to weather-independent heat consumption. It also makes it possible to make more advanced models as they are fully differentiable contrary to the traditional energy signature model. This was further discussed in Section 4.

In the future, three main issues should be addressed:

• In the present paper, only 24 h average values were used with the argument that the effects of the heat capacities were averaged out as stated in [22]. Several tests on parameter sensitivity could be done with the input variables averaged over longer and shorter periods than 24 $\mathrm{h}$.
  Furthermore, the heat capacity could be modelled to account for potential dynamics related to the heat capacities of the building. Residuals ($e_t$) with no cross-correlation with the differentiated outdoor temperature ($\mathrm{corr}(e_t,T_{a,t}-T_{a,t-1})\approx 0$) indicate that no thermal dynamics are left unmodelled. However, autocorrelation in the residuals might still appear, which indicates time correlated building use, e.g., the building use in one time step is correlated with the next.
• In Figure 5, it was shown that the wind speed had a tremendous effect on the estimated heat loss (UA value). Even though the model predictions improved and the parameters that describe the wind sensitivity are significant for all 16 houses (see Table 2), it might be worth investigating other ways of modelling the wind’s effect on the heat consumption. As the effects are highly dependent on surroundings, building geometry and other unknown factors, it is suggested to model the wind dependence by means of nonparametric methods such as kernel or splines estimation.
• As the variance of the model residuals is highly dependent on the outdoor temperature, they are seemingly heteroskedastic, i.e., not constant. The implication of heteroskedastic residuals is that the standard errors of the model parameters are biased. To correct it, the model should be formulated as a weighted least square problem where the weights are the inverse of the error variance.