Thermal Analysis of Pure and Nanoparticle-Enhanced PCM—Application in Concentric Tube Heat Exchanger
Abstract
1. Introduction
2. Materials and Methods
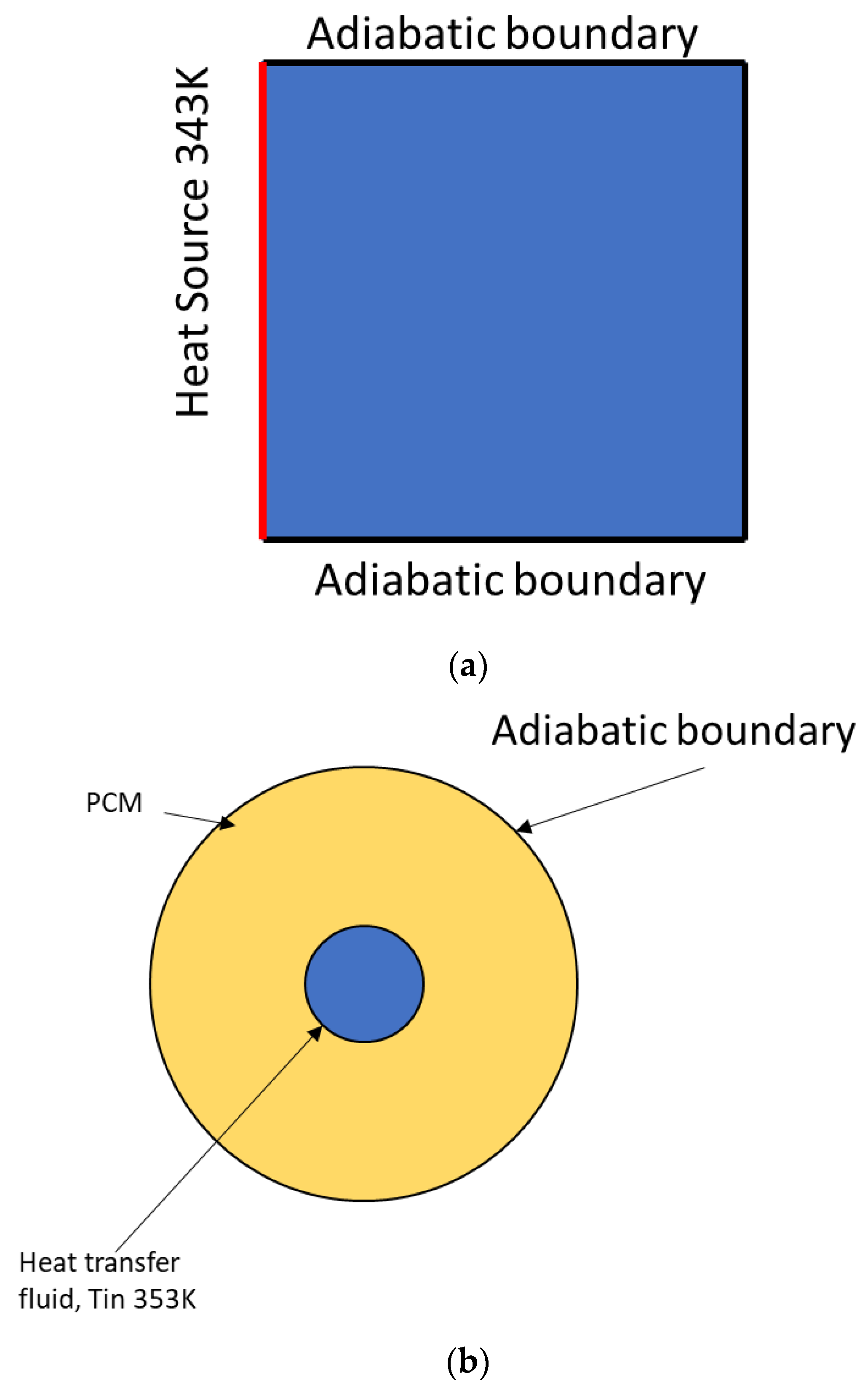
2.1. The Examined Domain
2.2. Mathematical Modeling
2.2.1. Pure PCM Mathematical Modeling
2.2.2. Effect of Nanoparticle Addition to Phase Change Material
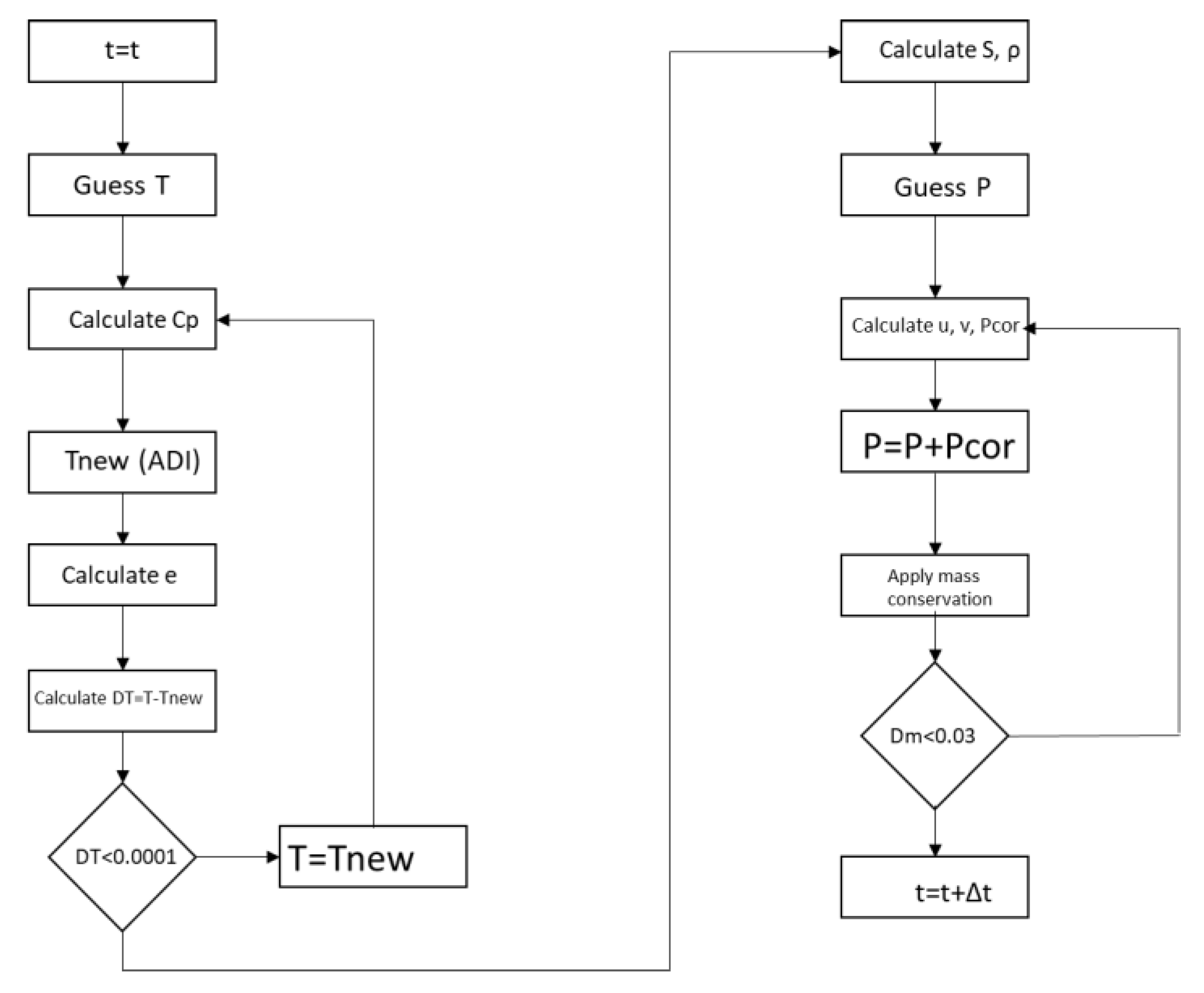
2.3. Solution Procedure of the Phase Change Problem
2.3.1. Numerical Solution Scheme
2.3.2. Computational Solution Scheme
3. Results and Discussion
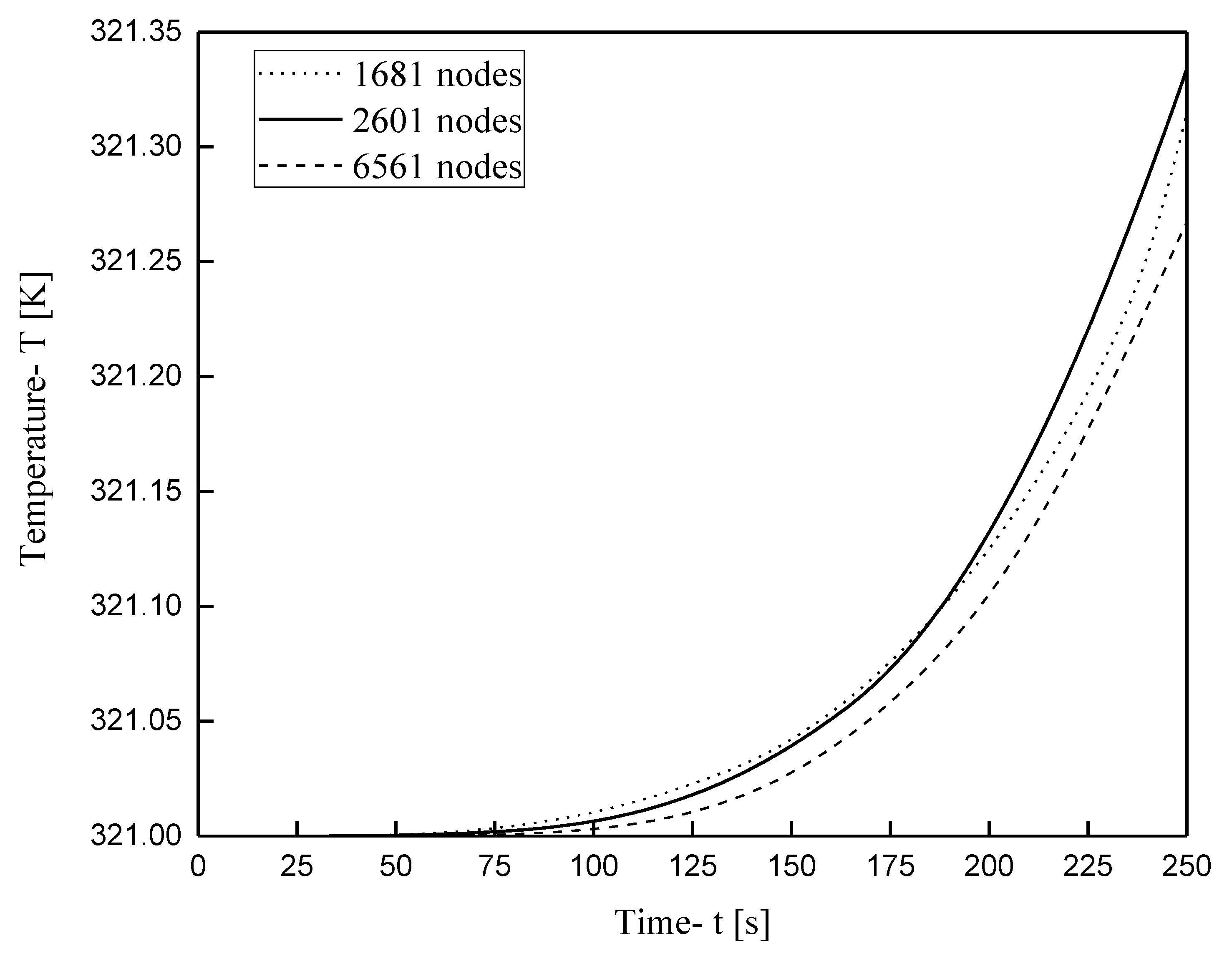
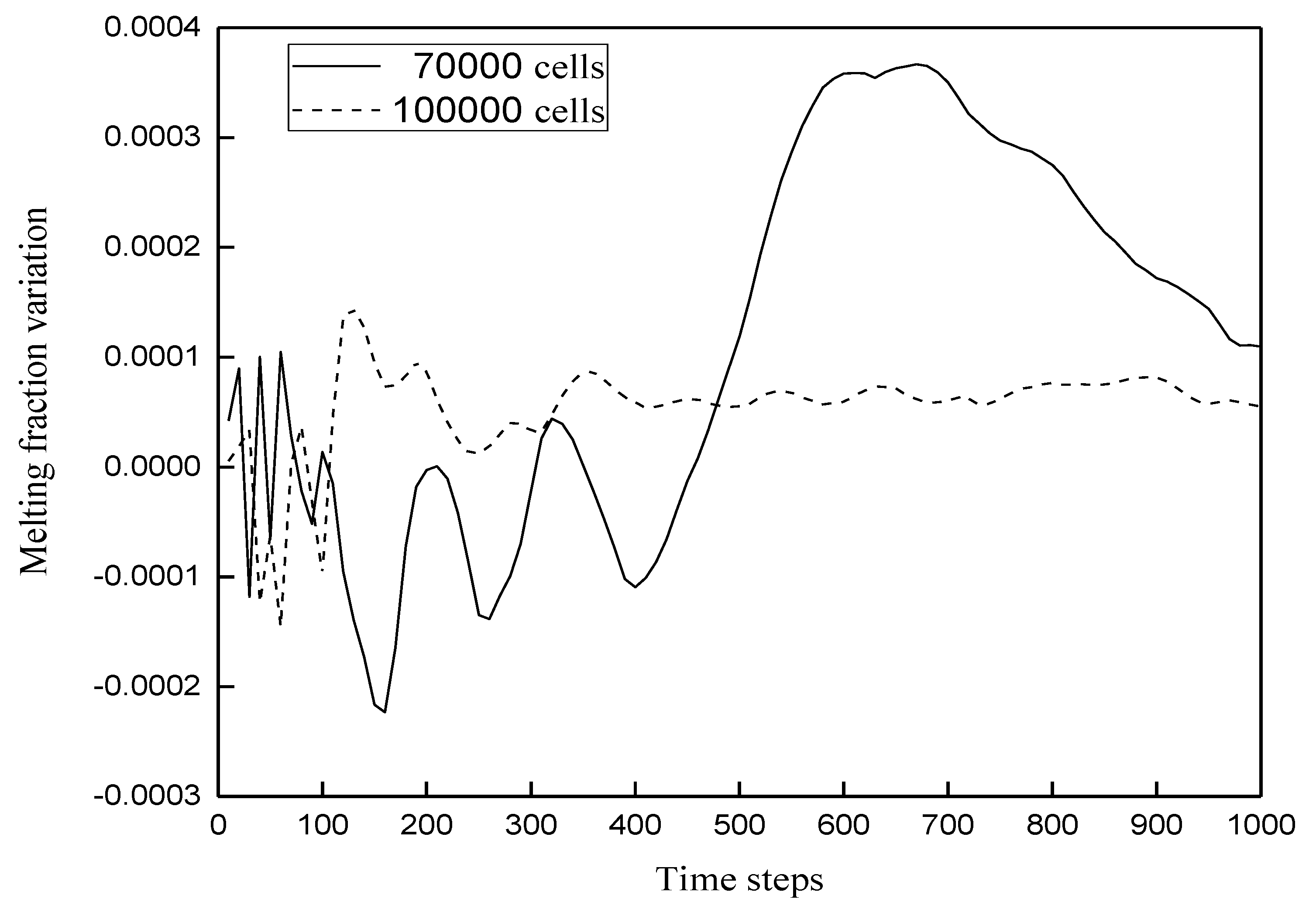
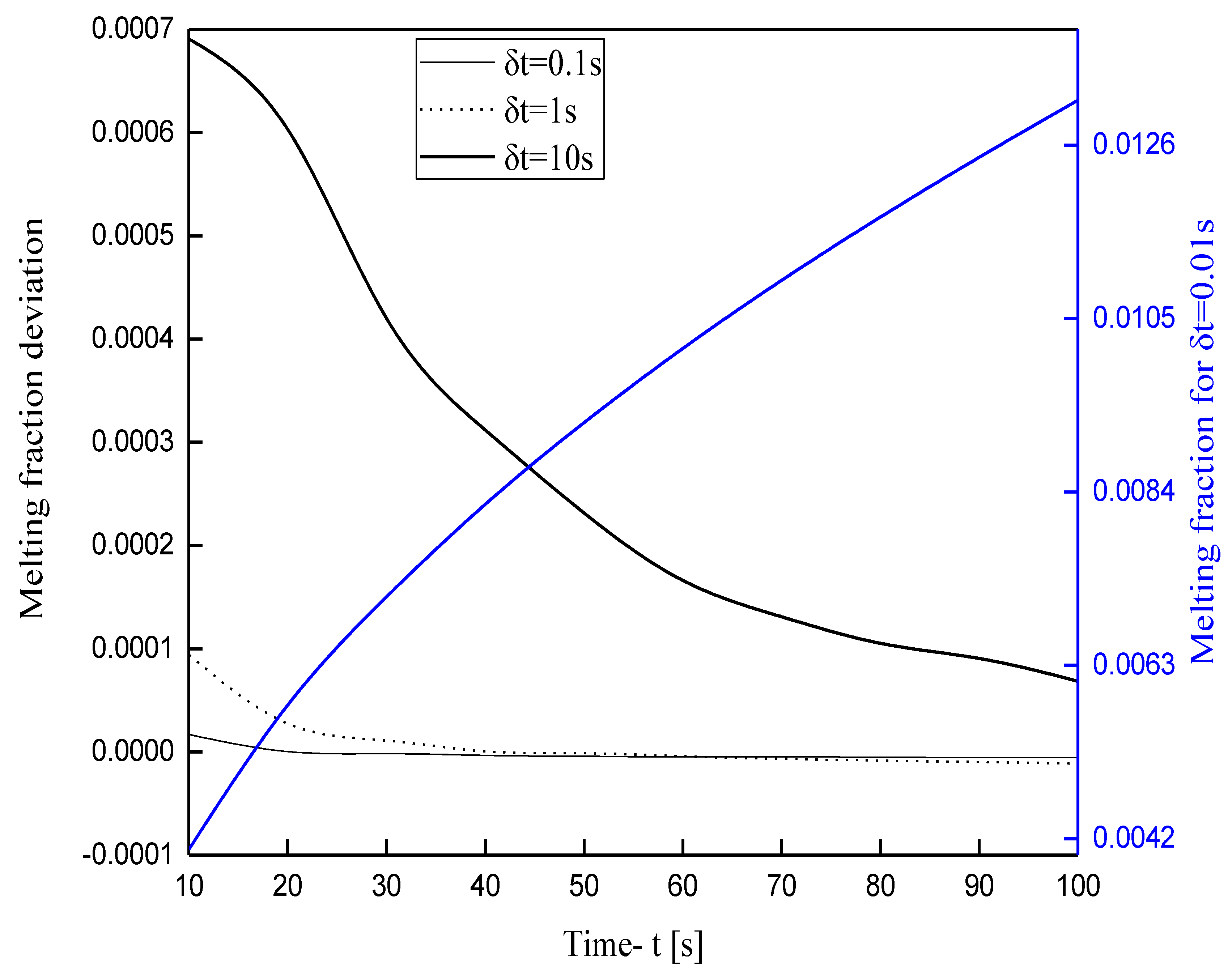
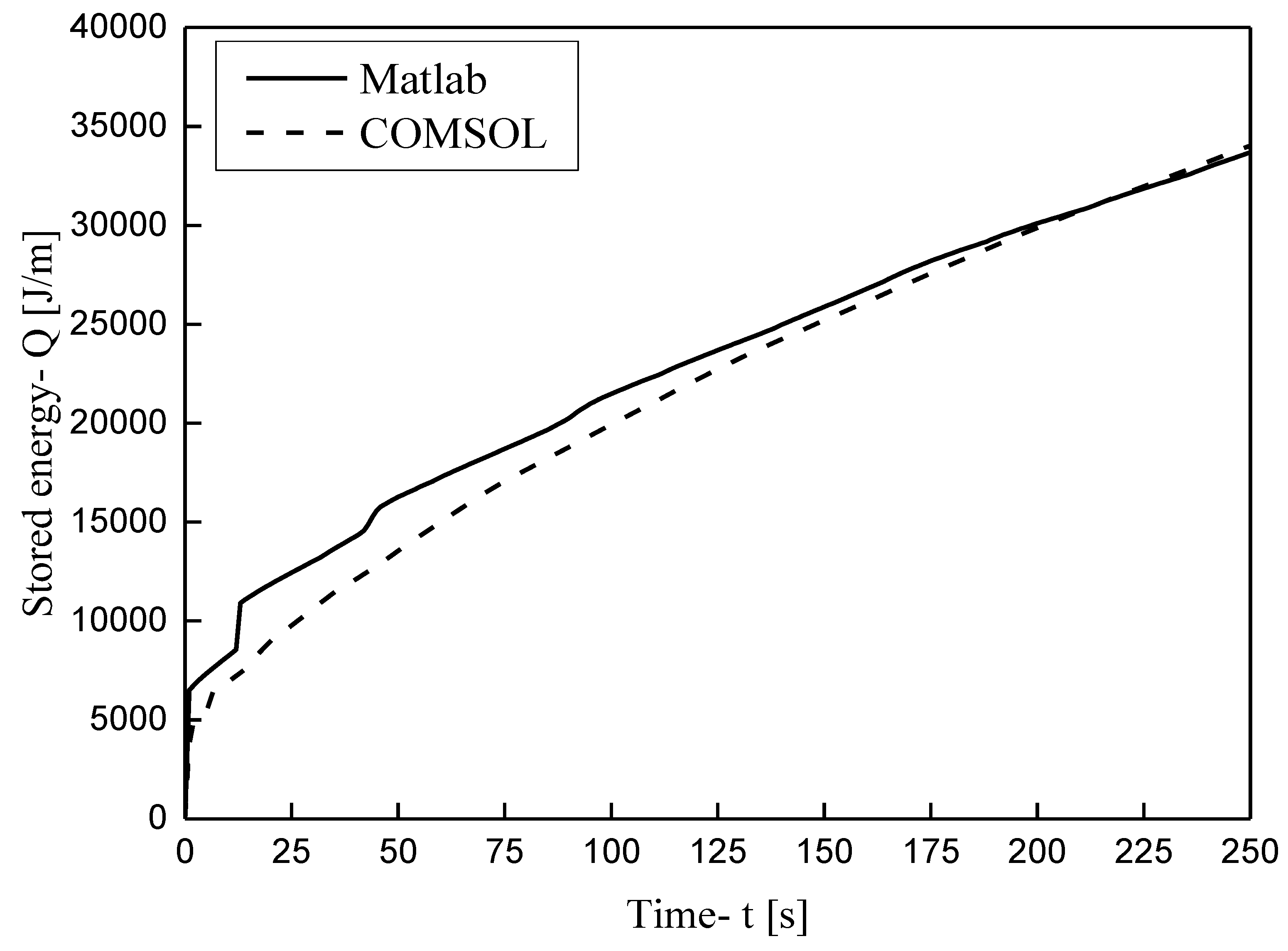
3.1. Grid Independence
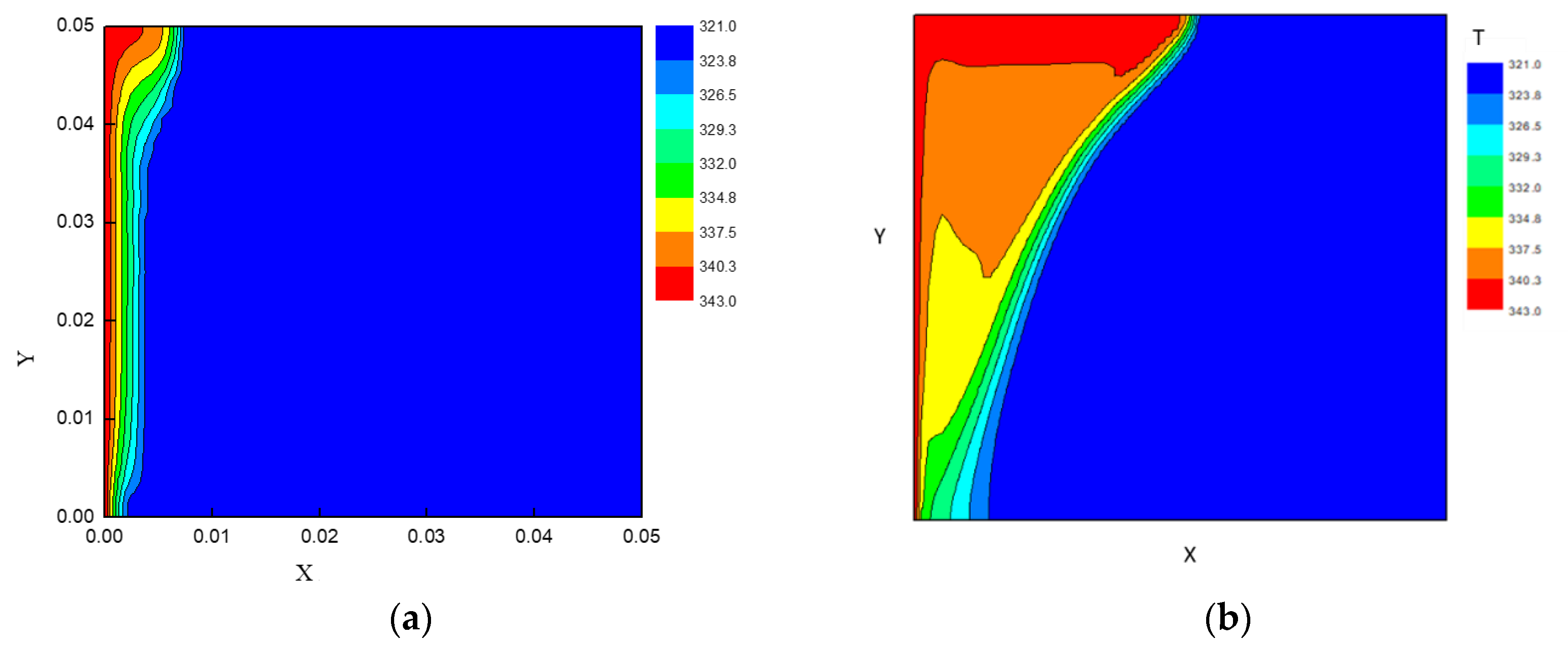
3.2. Rectangular Cross Section Analysis
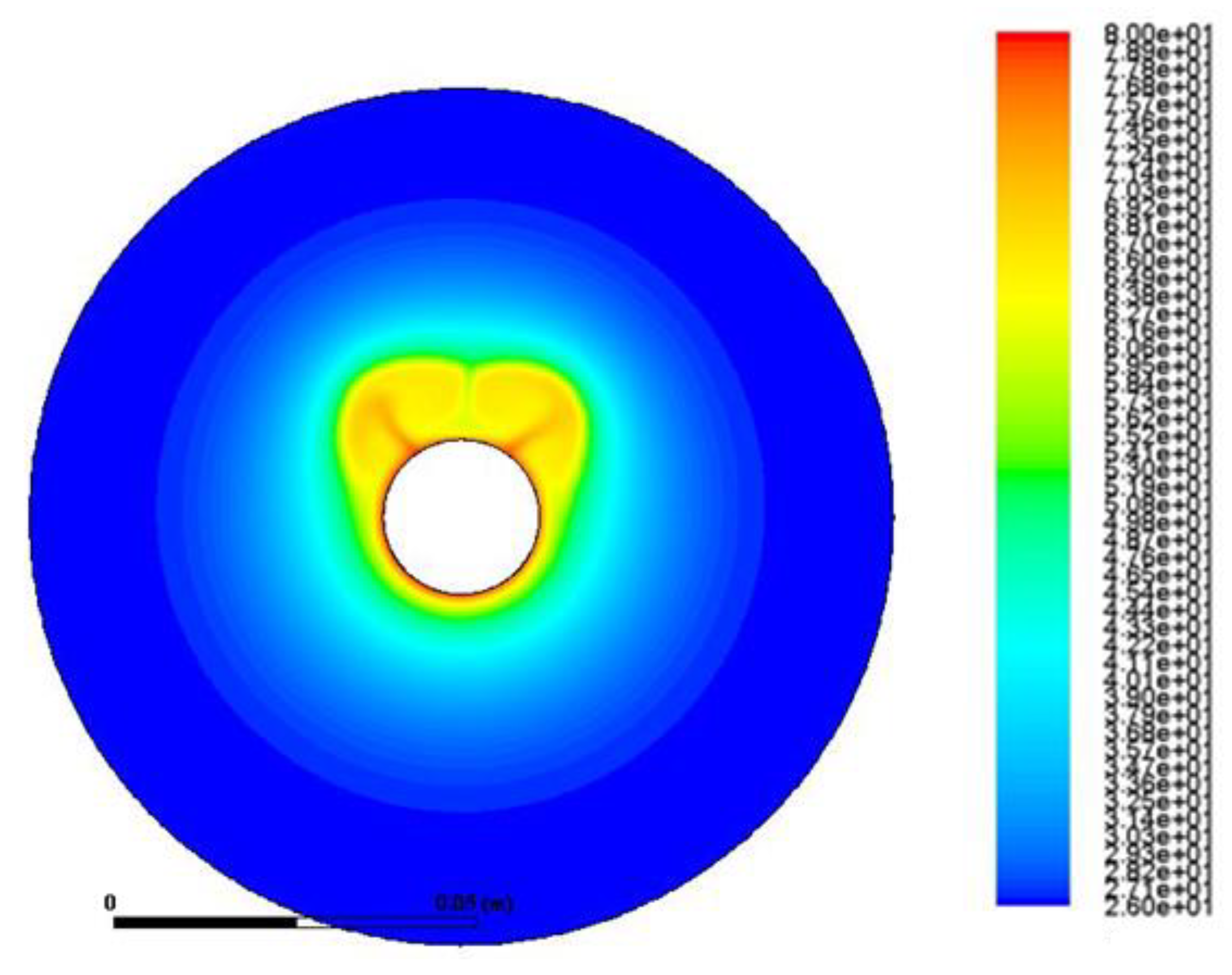
3.3. Concentric Tube Heat Exchange Analysis
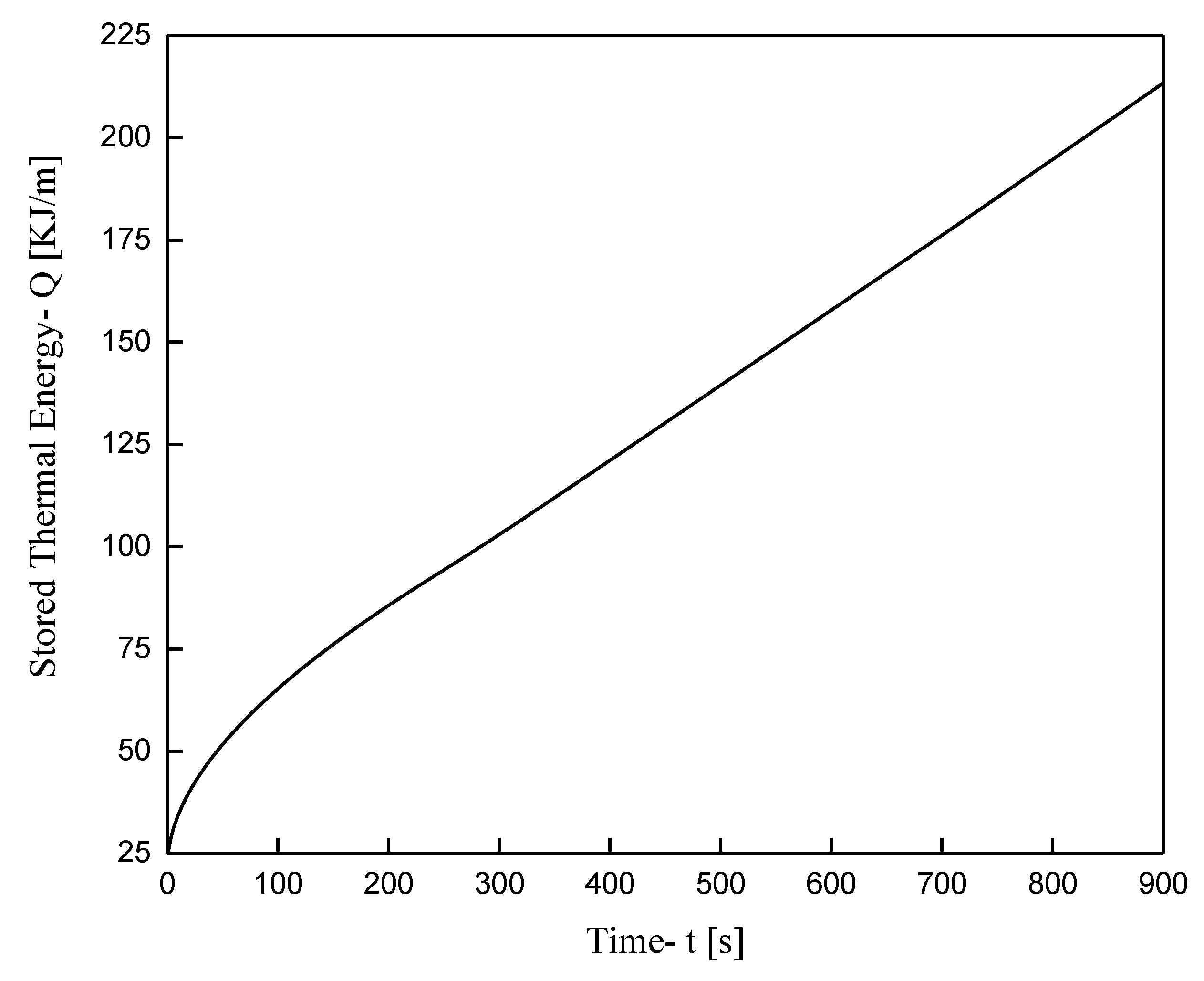
3.3.1. Pure PCM Results
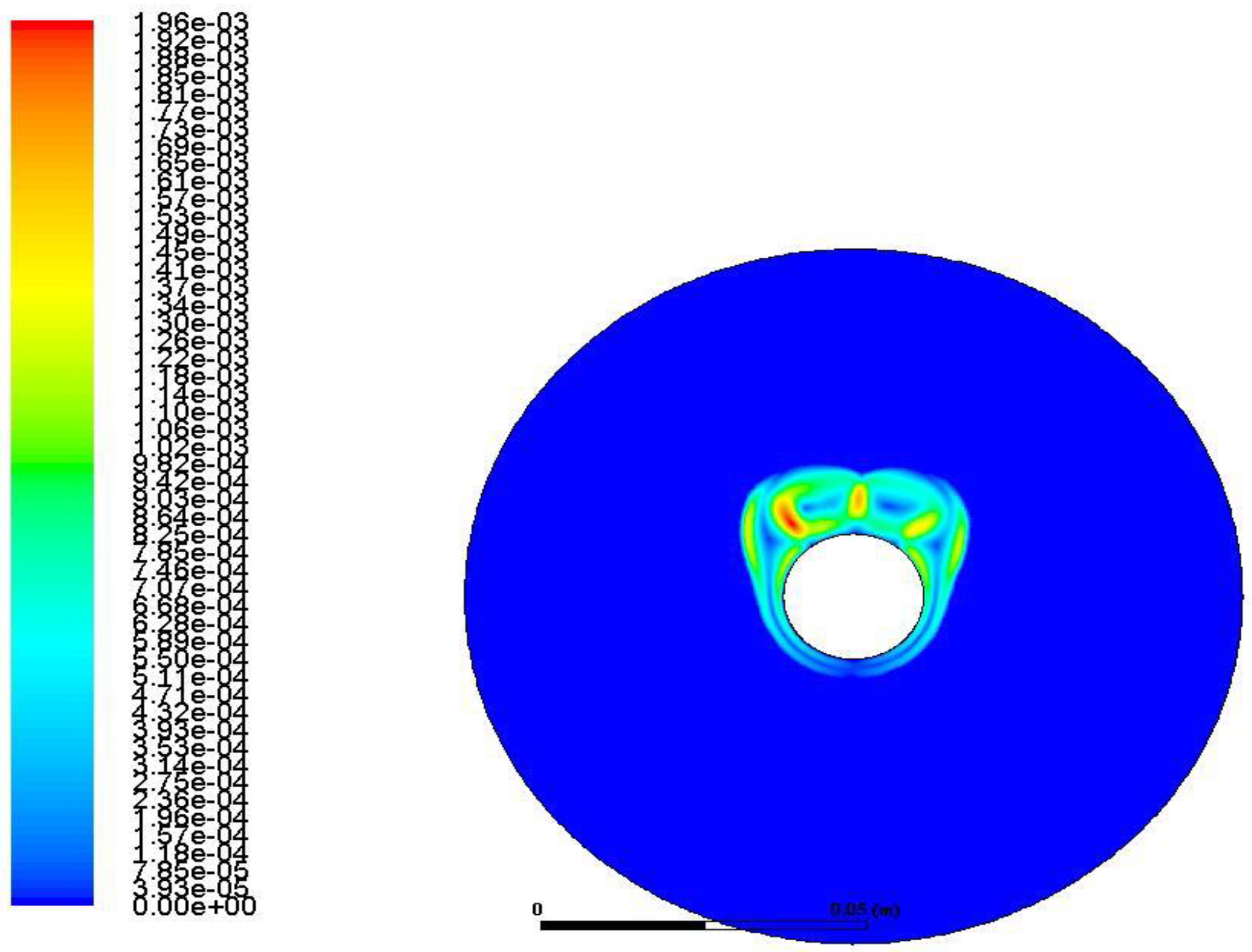
3.3.2. Nanoparticle-Enhanced PCM
4. Conclusions
- The complexity of the problem, especially in the “mushy zone” area, necessitates particularly long simulation periods and increased computing power for the solution. For example, the evolution of the phenomenon up to 7200 s requires approximately 160.6 h of simulation.
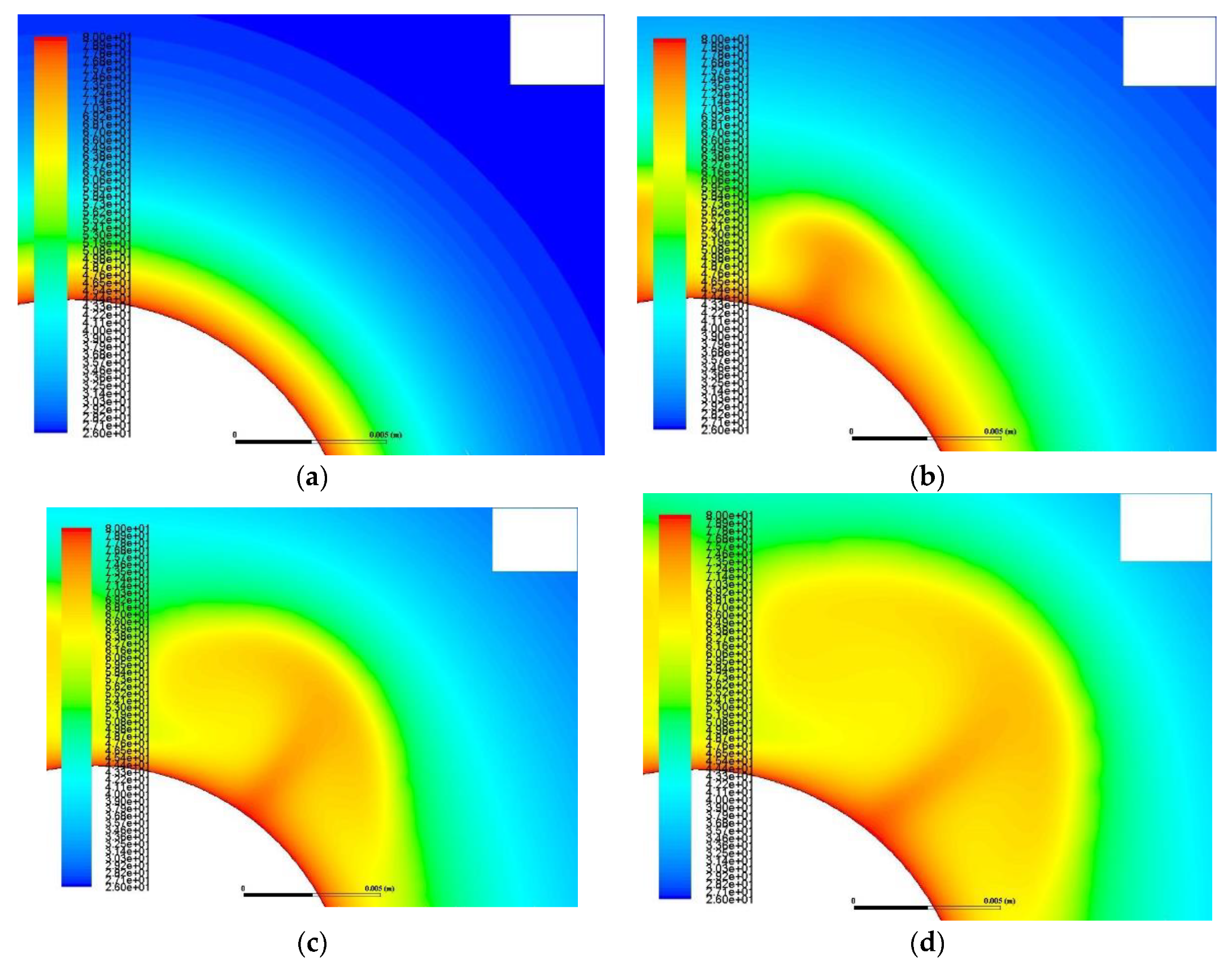
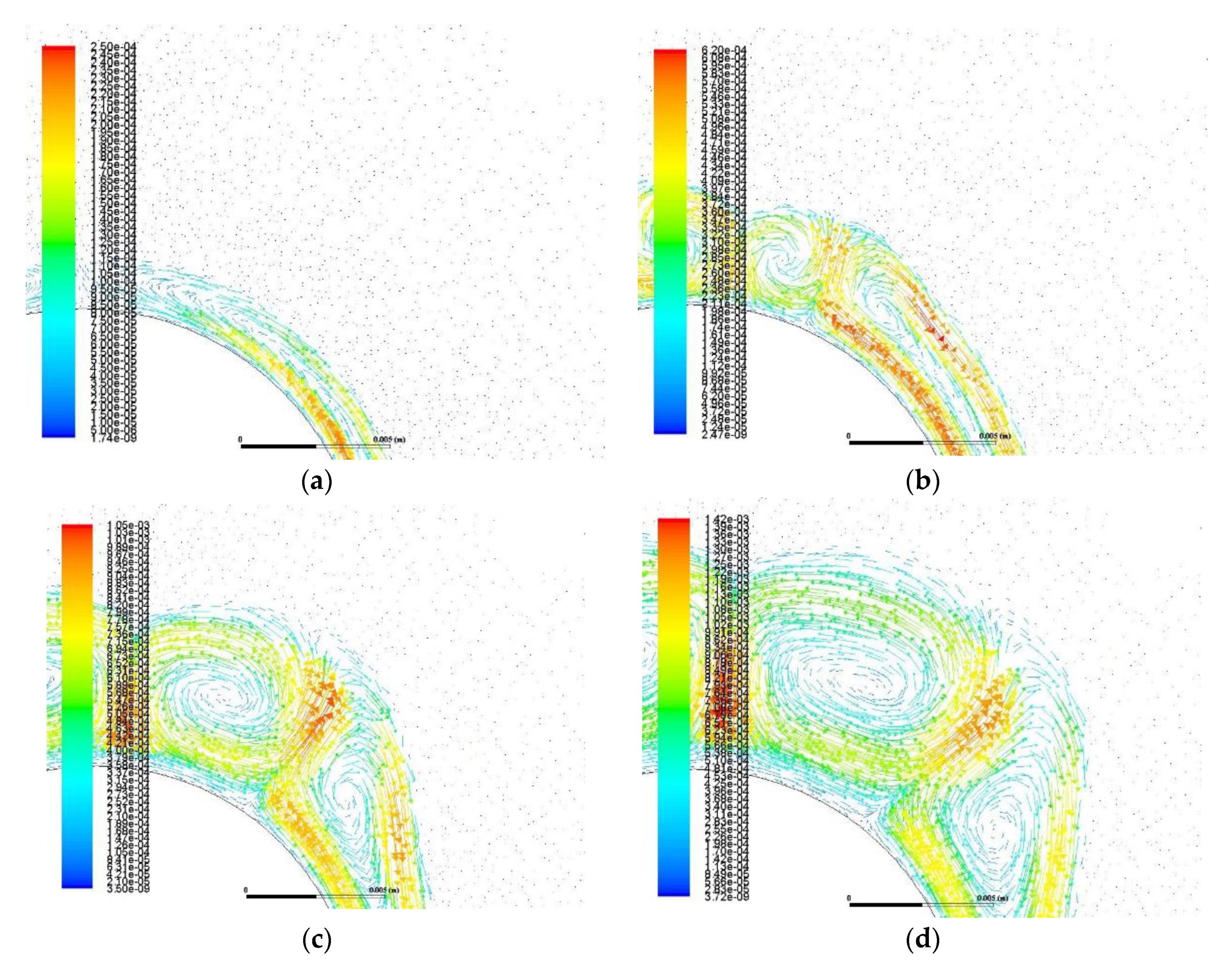
- Buoyancy induces velocity fields with measured velocity of about 10−3 m/s. This natural circulation of the melt intensifies the heat transfer and the phase change as it transfers heat from the melt to the solid by a combination of natural convection and conduction.
- The velocity field takes the form of vortex with areas of zero velocity (vortex center) and areas of maximum velocity (confluence with neighboring vortex).
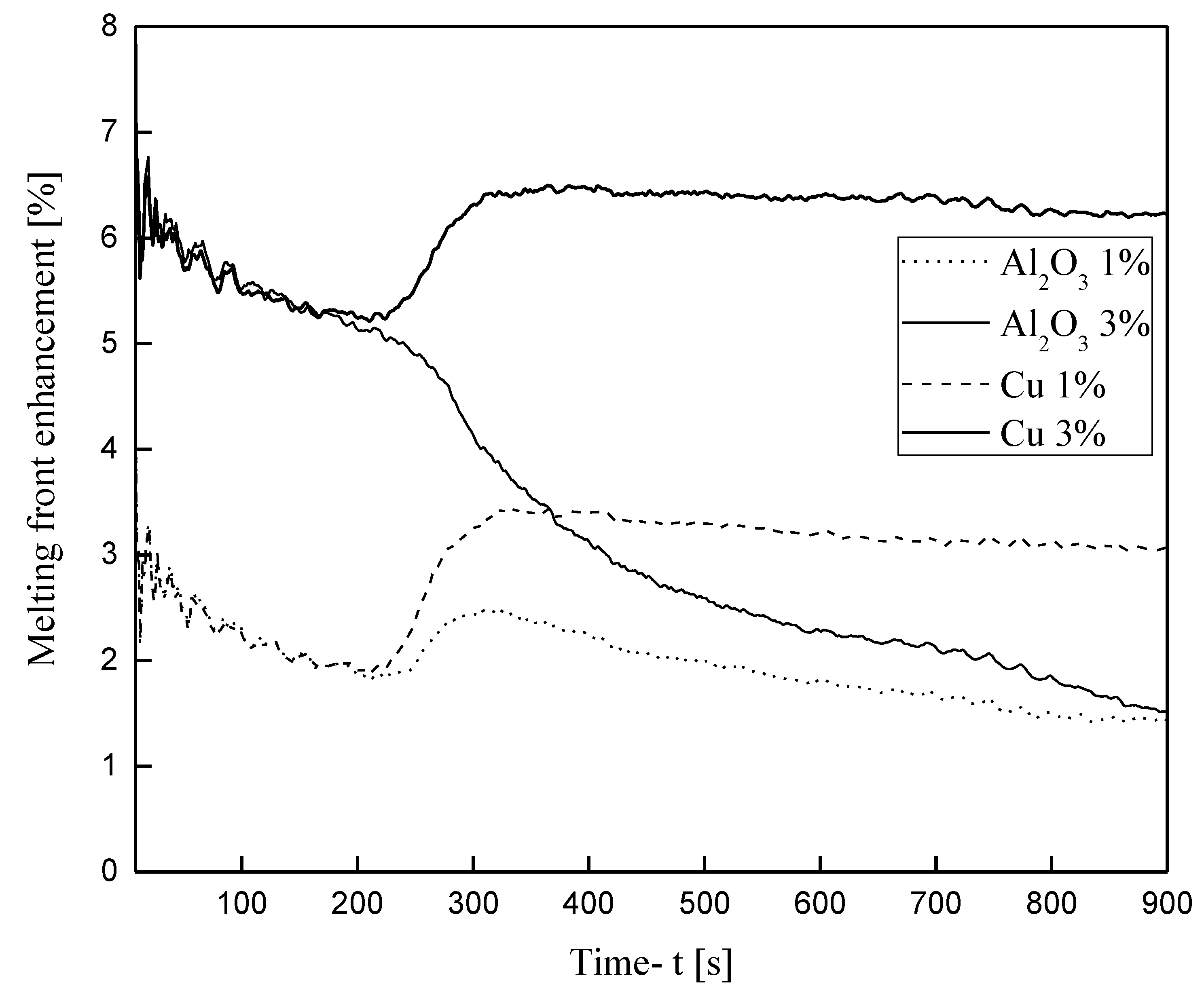
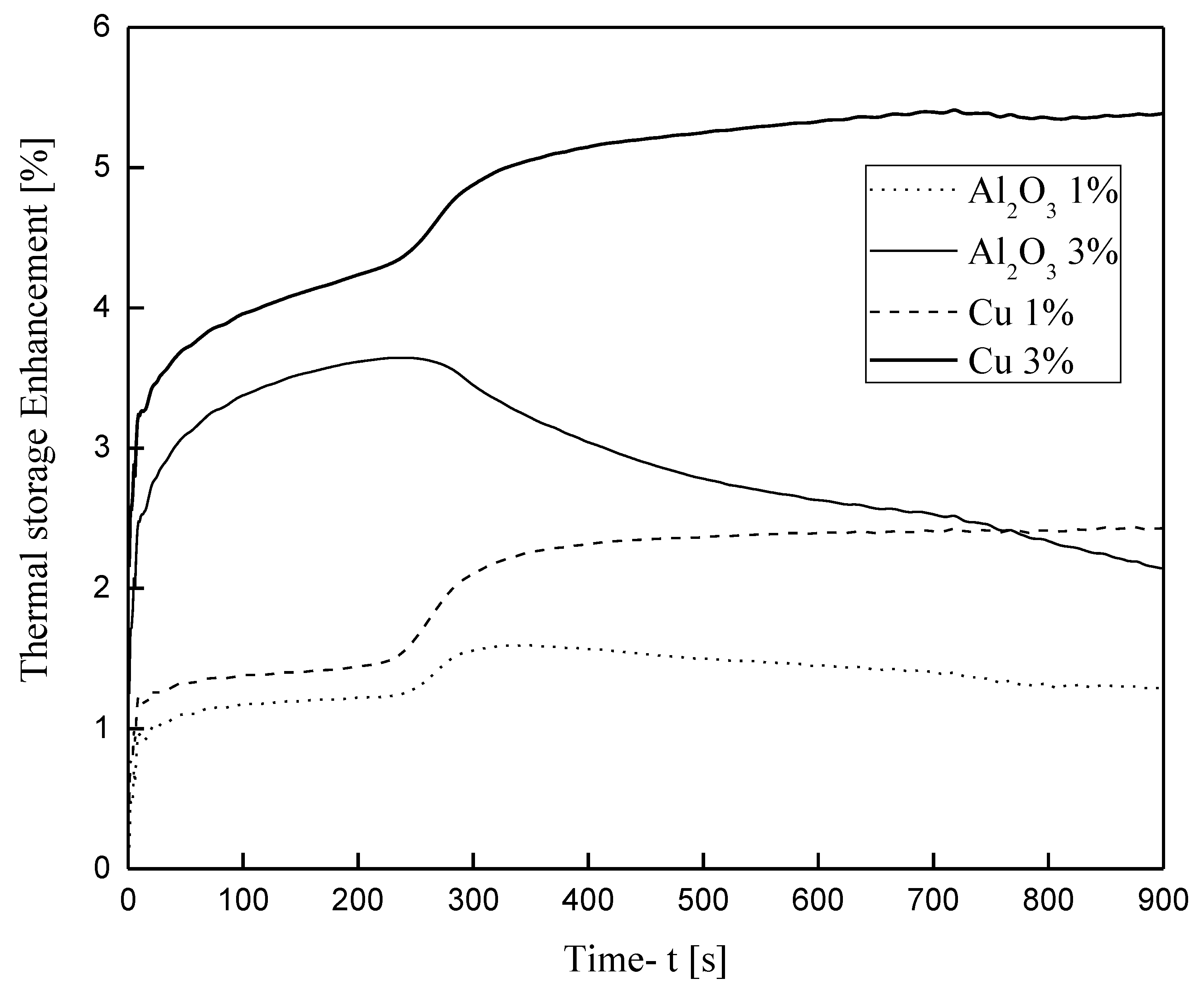
- The addition of Cu and Al2O3 nanoparticles to the compositions studied enhances both the melt percentage and the heat stored in the material. However, this effect declines over time for the case of the enhanced PCM bearing Al2O3 nanoparticles. On the other hand, for the case of copper nanoparticles, this enhancement exhibits intense and irregular fluctuations for the first seconds of the process and then maintains stable values of about 6.5% for the melt percentage and 5.5% for the heat stored.
- The quantity of the nanoparticles added cannot be increased infinitely, and the reason for this is the kinematic viscosity of the enhanced material, which increases with the addition of nanoparticles. The increase in kinematic viscosity inhibits the growth of melt circulation, thus suspending natural convection and, consequently, heat transfer from the hot wall to the enhanced PCM.
Author Contributions
Funding

Acknowledgments
Conflicts of Interest
Nomenclature
| Latin letters | ||
| u, v | [m/s] | Velocity components |
| g | [m/s2] | Gravitational acceleration |
| D, d | [m] | Diameter |
| Τ | [K], [οC] | Temperature |
| k | [W/mK] | Thermal conductivity |
| Cp | [J/kgK] | Specific heat |
| p | [Pa] | Pressure |
| A | [m2] | Surface |
| q | [W/m2] | Thermal flux |
| L | m | Length |
| h | [W/m2K] | Convection coefficient |
| X, Y | m | Coordinates |
| m | [kg/s] | Mass flow rate |
| e | [-] | Melting fraction |
| E | [-] | Enhancement |
| r | [m] | Radius |
| h | [KJ/kg] | Specific enthalpy |
| L | [KJ/kg] | Latent heat of melting |
| S | [m] | Displacement of melting front |
| Q | [J], [W] | Heat |
| Greek | ||
| [m2/s] | Kinematic viscosity, = μ/ρ | |
| βν | [1/Κ] | Volume expansion coefficient |
| ρ | [kg/m3] | Density |
| [-] | Volumetric nanoparticle concentration | |
| μ | [Pas] | Dynamic viscosity |
| Subscripts and Superscripts | ||
| p | Nanoparticles | |
| s | Solid | |
| l | Liquid | |
| tot | Total | |
| melt | Melting | |
| pcm | Phase change | |
| stored | Stored | |
| comp | Composite | |
| cPCM | composite PCM | |
| hybrid | Hybrid | |
| Abbreviations | ||
| PCM | Phase change material | |
References
- Fleischer, A.S. Thermal Energy Storage Using Phase Change Materials; Springer: New York, NY, USA, 2015; ISBN 978-3-319-20922-7. [Google Scholar]
- Chakraborty, P.R. Enthalpy porosity model for melting and solidification of pure-substances with large difference in phase specific heats. Int. Commun. Heat Mass Transf. 2017, 81, 183–189. [Google Scholar] [CrossRef]
- Voller, V.; Prakash, C. A fixed grid numerical modelling methodology for convection-diffusion mushy region phase-change problems. Int. J. Heat Mass Transf. 1987, 30, 1709–1719. [Google Scholar] [CrossRef]
- Niezgoda-Żelasko, B. The Enthalpy-porosity Method Applied to the Modelling of the Ice Slurry Melting Process During Tube Flow. Procedia Eng. 2016, 157, 114–121. [Google Scholar] [CrossRef]
- Brent, A.D.; Voller, V.R.; Reid, K.J. Enthalpy-Porosity technique for modeling convection-diffusion phase change: Application to the melting of a pure metal. Numer. Heat Transf. 1988, 13, 297–318. [Google Scholar] [CrossRef]
- Taghilou, M.; Talati, F. Numerical investigation on the natural convection effects in the melting process of PCM in a finned container using lattice Boltzmann method. Int. J. Refrig. 2016, 70, 157–170. [Google Scholar] [CrossRef]
- Talati, F.; Taghilou, M. Lattice Boltzmann application on the PCM solidification within a rectangular finned container. Appl. Therm. Eng. 2015, 83, 108–120. [Google Scholar] [CrossRef]
- Siebert, D.N.; Hegele, L.; Philippi, P. Lattice Boltzmann equation linear stability analysis: Thermal and athermal models. Phys. Rev. E 2008, 77, 026707. [Google Scholar] [CrossRef]
- Yuan, P. Thermal Lattice Boltzmann Two Phase Flow Model for Fluid Dynamics. Ph.D. Thesis, University of Pittsburgh, Pittsburgh, PA, USA, 2005. [Google Scholar]
- Bawazeer, S. Stability and Accuracy of Lattice Boltzmann Method. Master’s Thesis, University of Calgary, Calgary, AB, Canada, 2013. [Google Scholar]
- Tabares-Velasco, P.C.; Christensen, C.; Bianchi, M. Verification and validation of EnergyPlus phase change material model for opaque wall assemblies. Build. Environ. 2012, 54, 186–196. [Google Scholar] [CrossRef]
- Kuznik, F.; Virgone, J.; Johannes, K. Development and validation of a new TRNSYS type for the simulation of external building walls containing PCM. Energy Build. 2010, 42, 1004–1009. [Google Scholar] [CrossRef]
- Al-Saadi, S.N.; Zhai, Z.Q. A new validated TRNSYS module for simulating latent heat storage walls. Energy Build. 2015, 109, 274–290. [Google Scholar] [CrossRef]
- Lu, S.; Liu, S.; Huang, J.; Kong, X. Establishment and experimental verification of PCM room’s TRNSYS heat transfer model based on latent heat utilization ratio. Energy Build. 2014, 84, 287–298. [Google Scholar] [CrossRef]
- Li, L.; Yu, H.; Wang, X.; Zheng, S. Thermal analysis of melting and freezing processes of phase change materials (PCMs) based on dynamic DSC test. Energy Build. 2016, 130, 388–396. [Google Scholar] [CrossRef]
- Iten, M.; Liu, S.; Shukla, A.; Da Silva, P.D. Investigating the impact of Cp-T values determined by DSC on the PCM-CFD model. Appl. Therm. Eng. 2017, 117, 65–75. [Google Scholar] [CrossRef]
- Ferrer, G.; Barreneche, C.; Palacios, A.; Solé, A.; Fernández, A.I.; Cabeza, L.F. Empirical equations for viscosity and specific heat capacity determination of fatty acids. J. Energy Storage 2017, 10, 20–27. [Google Scholar] [CrossRef]
- Ferrer, G.; Gschwander, S.; Solé, A.; Barreneche, C.; Fernández, A.I.; Schossig, P.; Cabeza, L.F. Empirical equation to estimate viscosity of paraffin. J. Energy Storage 2017, 11, 154–161. [Google Scholar] [CrossRef]
- Lopez, J.; Marques, F.; Shen, J. An Efficient Spectral-Projection Method for the Navier–Stokes Equations in Cylindrical Geometries. J. Comput. Phys. 2002, 176, 384–401. [Google Scholar] [CrossRef][Green Version]
- Ahmad, R.A. Steady-State Numerical Solution of the Navier-Stokes and Energy Equations around a Horizontal Cylinder at Moderate Reynolds Numbers from 100 to 500. Heat Transf. Eng. 1996, 17, 31–81. [Google Scholar] [CrossRef]
- Galione, P.A.; Lehmkuhl, O.; Rigola, J.; Oliva, A. Fixed-Grid Modeling of Solid-Liquid Phase Change in Unstructured Meshes Using Explicit Time Schemes. Numer. Heat Transf. Part B Fundam. 2013, 65, 27–52. [Google Scholar] [CrossRef]
- Shmueli, H.; Ziskind, G.; Letan, R. Melting in a vertical cylindrical tube: Numerical investigation and comparison with experiments. Int. J. Heat Mass Transf. 2010, 53, 4082–4091. [Google Scholar] [CrossRef]
- Yang, L.; Xu, X. A renovated Hamilton–Crosser model for the effective thermal conductivity of CNTs nanofluids. Int. Commun. Heat Mass Transf. 2017, 81, 42–50. [Google Scholar] [CrossRef]
- Kavusi, H.; Toghraie, D. A comprehensive study of the performance of a heat pipe by using of various nanofluids. Adv. Powder Technol. 2017, 28, 3074–3084. [Google Scholar] [CrossRef]
- Lamberg, P.; Lehtiniemi, R.; Henell, A.-M. Numerical and experimental investigation of melting and freezing processes in phase change material storage. Int. J. Therm. Sci. 2004, 43, 277–287. [Google Scholar] [CrossRef]
- Murray, R.; Groulx, D. Modeling Convection during Melting of a Phase Change Material. In Proceedings of the COMSOL Conference, Boston, MA, USA, 13–15 October 2011. [Google Scholar]
- Samara, F.; Groulx, D.; Biwole, P. Natural Convection Driven Melting of Phase Change Material: Comparison of Two Methods. In Proceedings of the COMSOL Conference, Boston, MA, USA, 3–5 October 2012. [Google Scholar]
- ANSYS. Ansys Fluent 12.0 User’s Guide; ANSYS: Pittsburgh, PA, USA, 2009. [Google Scholar]
- Souayfane, F.; Biwole, P.H.; Fardoun, F. Melting of a phase change material in presence of natural convection and radiation: A simplified model. Appl. Therm. Eng. 2018, 130, 660–671. [Google Scholar] [CrossRef]
- Darzi, A.R.; Farhadi, M.; Sedighi, K. Numerical study of melting inside concentric and eccentric horizontal annulus. Appl. Math. Model. 2012, 36, 4080–4086. [Google Scholar] [CrossRef]



| Nanoparticles | |||
|---|---|---|---|
| 3600 | 36 | 765 | |
| 8933 | 400 | 385 |
| Property | RT50 |
|---|---|
| Phase change temperature | °C °C |
| Ts | 45 °C |
| Latent heat | |
| Density (solid state) | |
| Density (liquid state) | |
| Specific heat (both phases) | |
| Conductivity |
| Cartesian Coordinates | Cylindrical Coordinates |
|---|---|
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
T. Nitsas, M.; P. Koronaki, I. Thermal Analysis of Pure and Nanoparticle-Enhanced PCM—Application in Concentric Tube Heat Exchanger. Energies 2020, 13, 3841. https://doi.org/10.3390/en13153841
T. Nitsas M, P. Koronaki I. Thermal Analysis of Pure and Nanoparticle-Enhanced PCM—Application in Concentric Tube Heat Exchanger. Energies. 2020; 13(15):3841. https://doi.org/10.3390/en13153841
Chicago/Turabian StyleT. Nitsas, M., and I. P. Koronaki. 2020. "Thermal Analysis of Pure and Nanoparticle-Enhanced PCM—Application in Concentric Tube Heat Exchanger" Energies 13, no. 15: 3841. https://doi.org/10.3390/en13153841
APA StyleT. Nitsas, M., & P. Koronaki, I. (2020). Thermal Analysis of Pure and Nanoparticle-Enhanced PCM—Application in Concentric Tube Heat Exchanger. Energies, 13(15), 3841. https://doi.org/10.3390/en13153841





