Condition-Monitoring System for Identification and Representation of the Capability Diagram Limits for Multiple Synchronous Generators in a Hydro Power-Plant
Abstract
1. Introduction
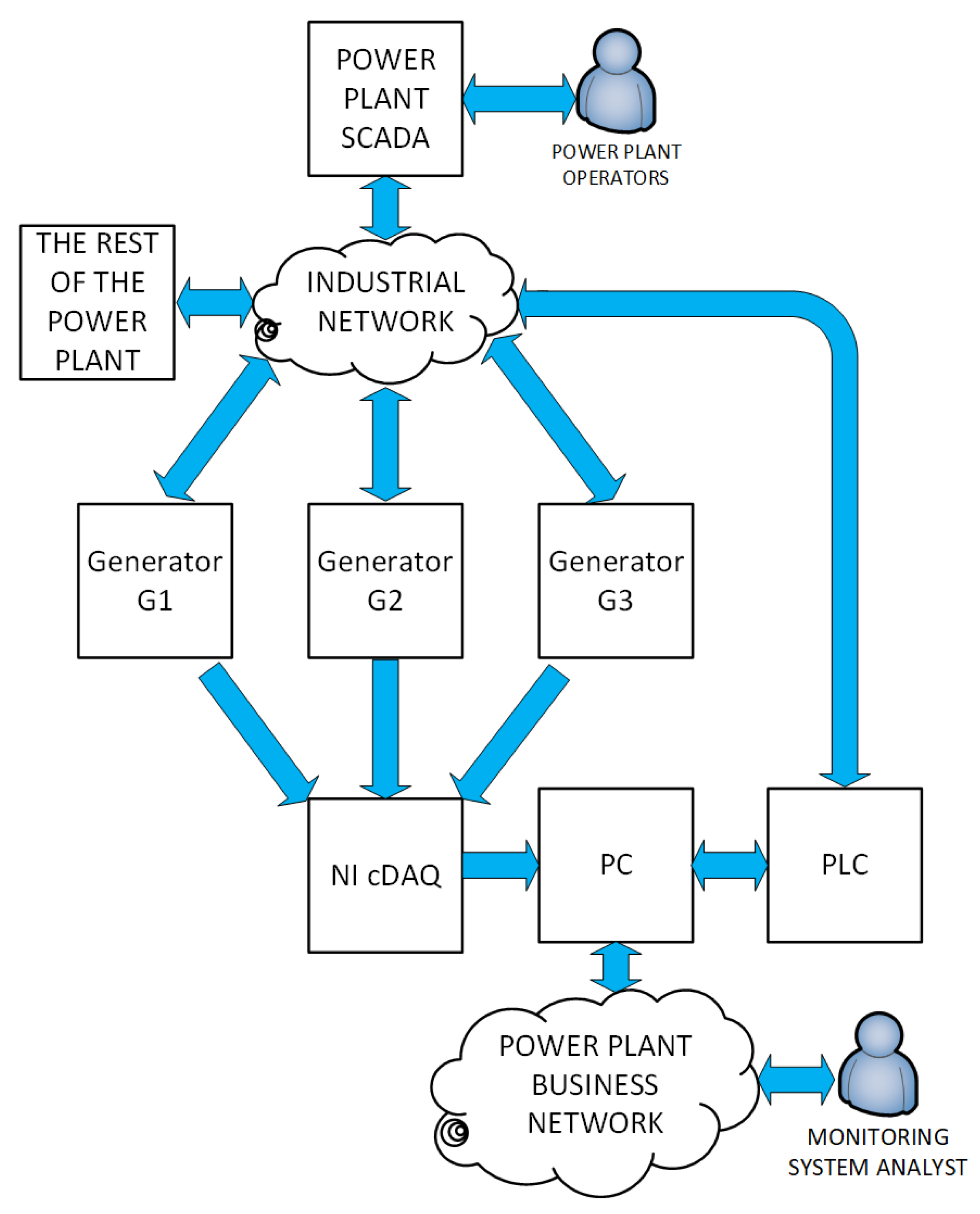
2. Condition-Monitoring System
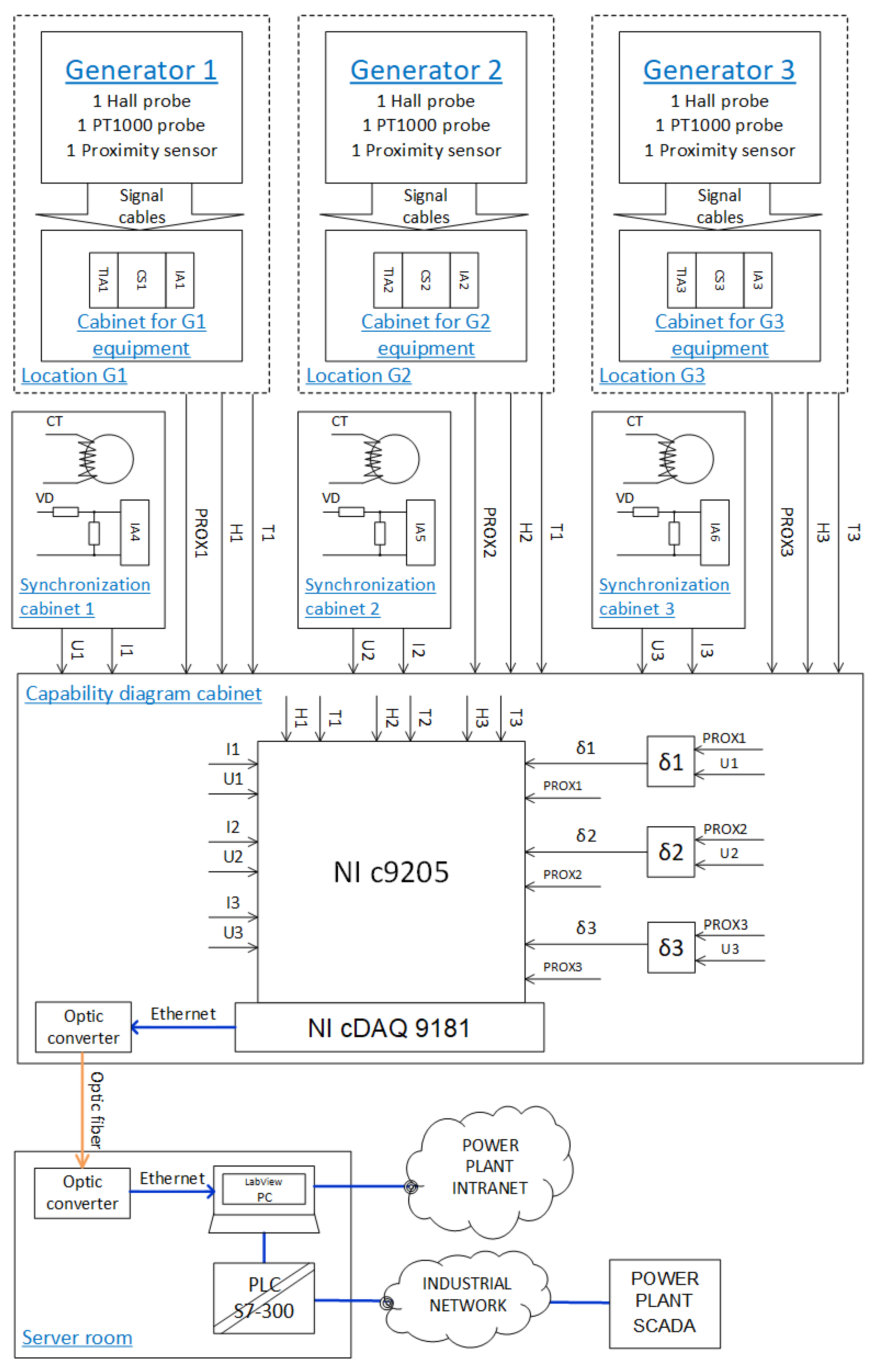
2.1. Topology of the Condition-Monitoring System
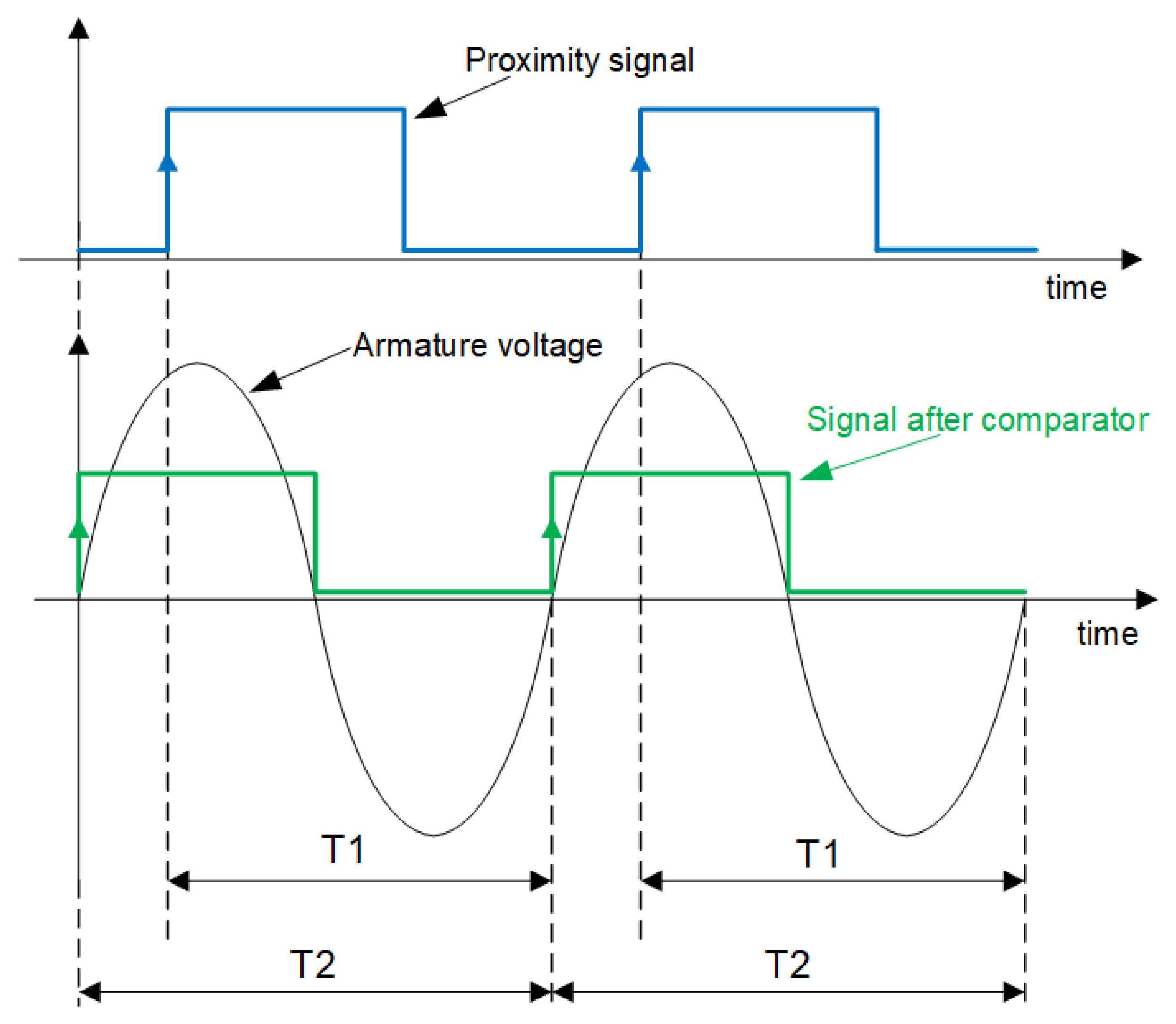
2.2. Nonstandard Measurements and Features of the Condition-Monitoring System
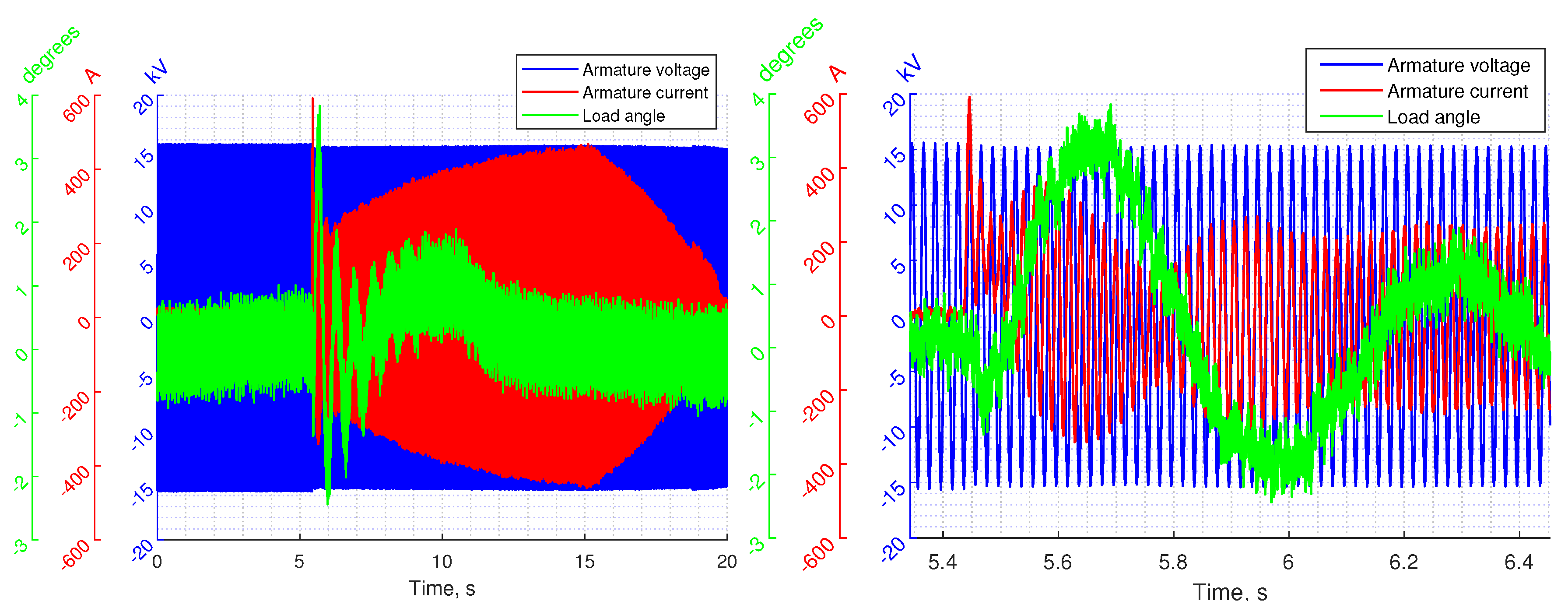
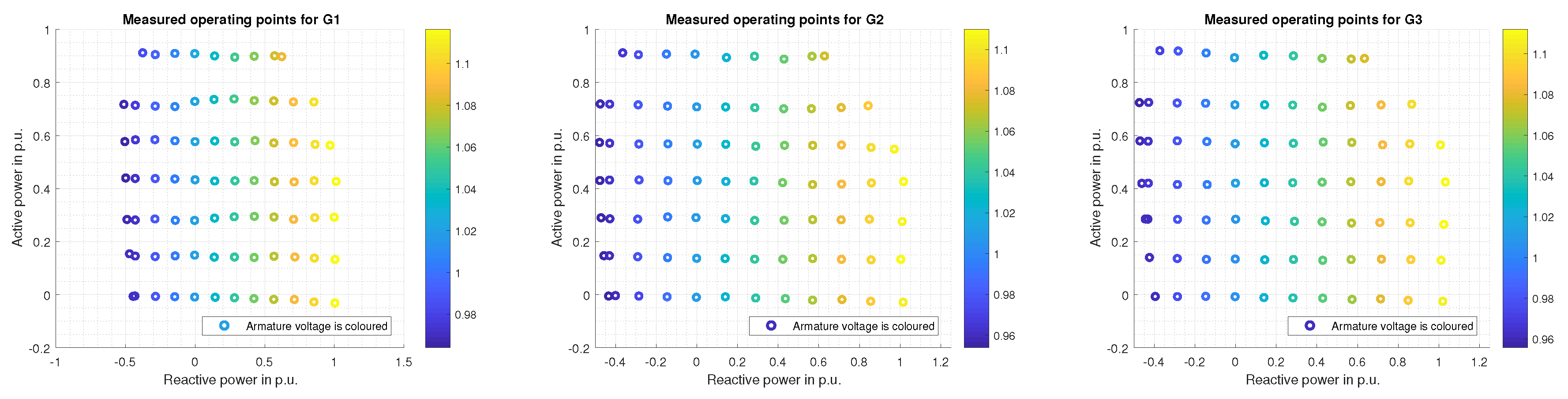
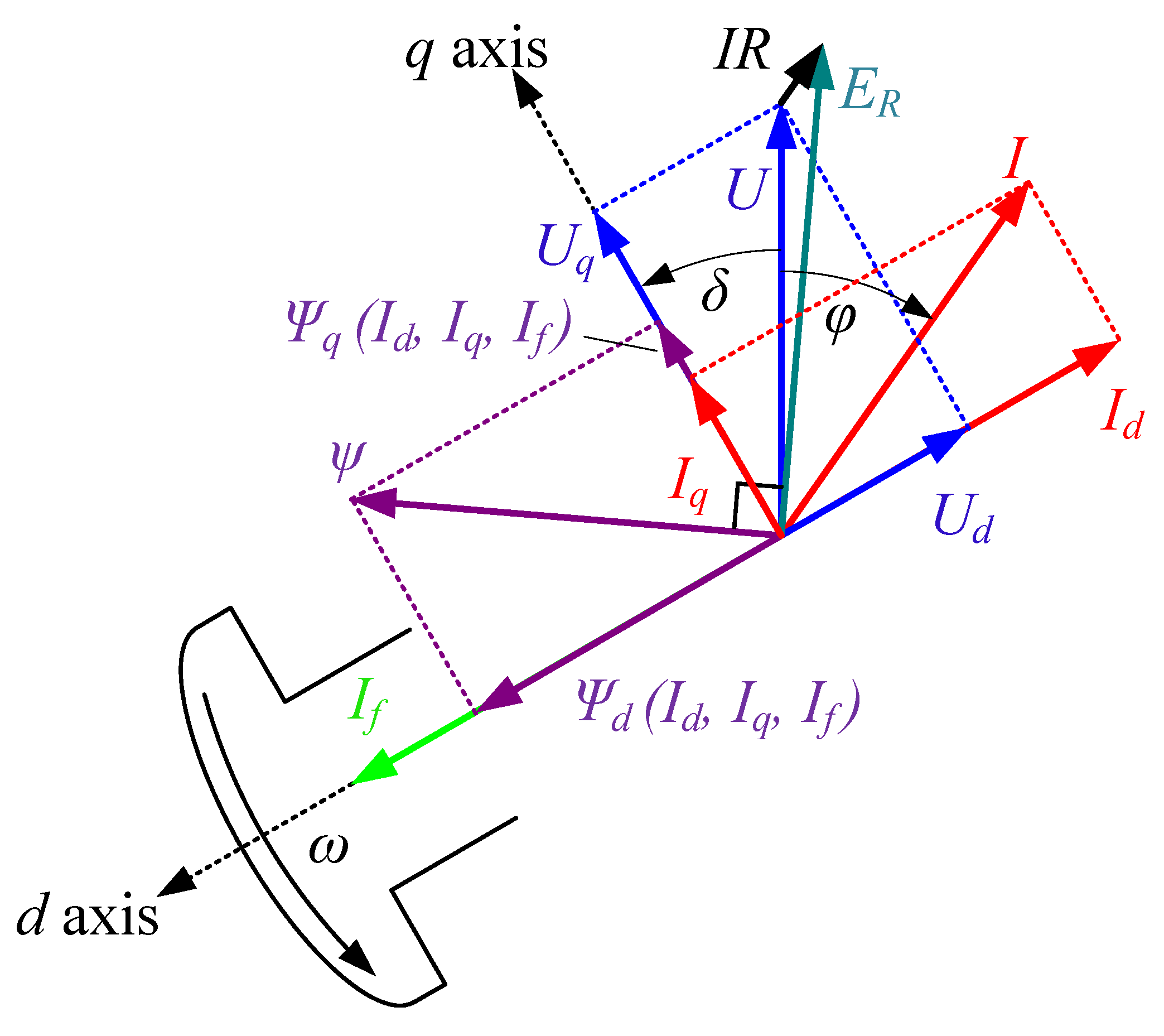
3. Measured Data and Identification of the Current Dependent Flux Linkage Models for the Generators
4. Calculation of the Operational Limits in the P–Q Diagram
4.1. Maximum Armature Current Limit
4.2. Constant Field Current Limit
4.3. Theoretical Steady-State Stability Limit
4.4. Practical Steady-State Stability Limit
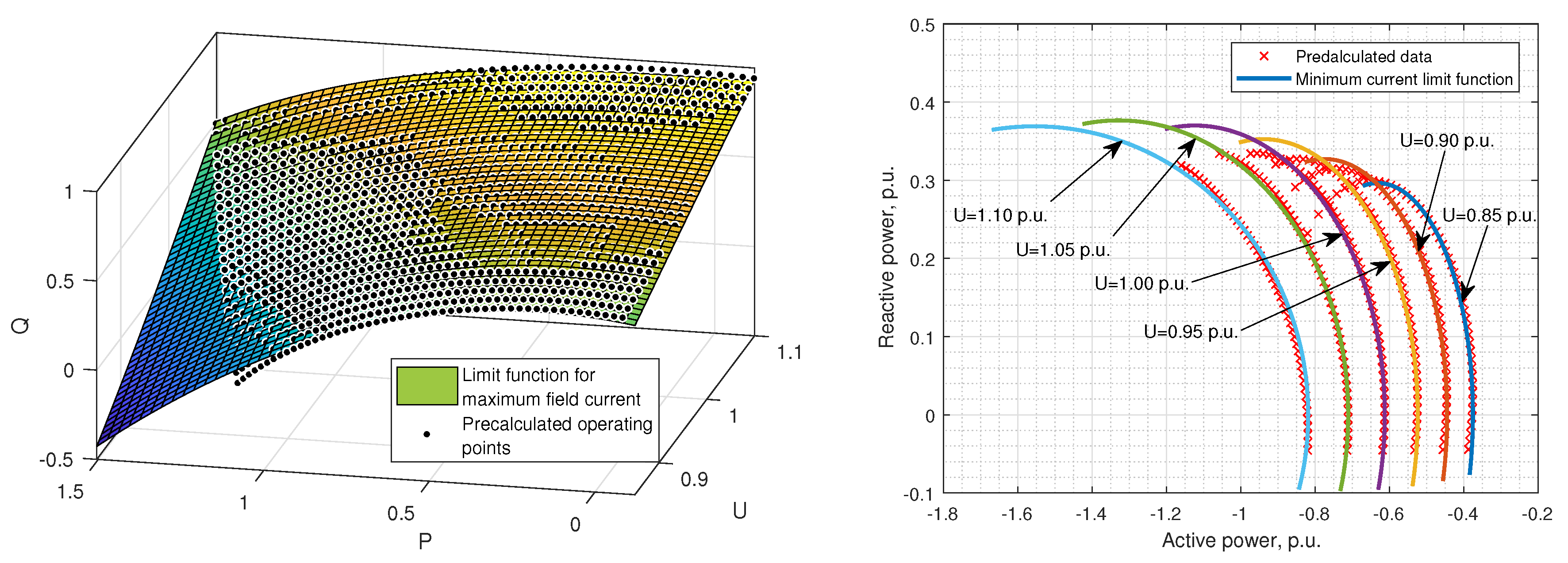
5. Computationally Efficient Calculation of the Capability Limits in the P–Q Diagram Capable for Implementation in the Power-Plant SCADA System
5.1. Maximum Field Current Limit and Practical Steady-State Stability Limit
5.2. Minimum Field Current Limit
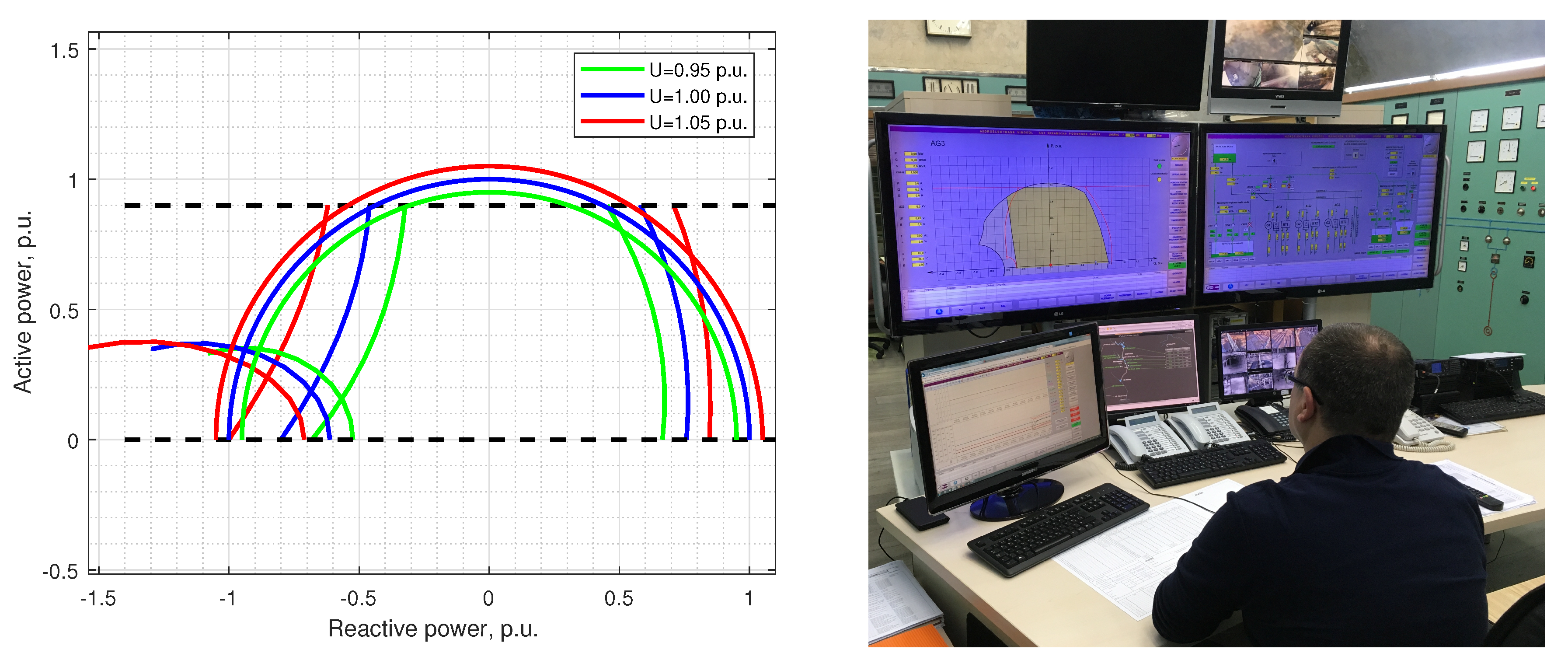
5.3. Implementation of the P–Q Diagram with the Real-Time Limits within the Power-Plant SCADA System
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| SCADA | supervisory control and data acquisition system |
| PLC | Programmable logic controller |
Appendix A. Used Equipment
| Equipment | Designation and Description |
|---|---|
| Existing voltage transformer in power-plant | 10 kV/100 V, class: 0.5 |
| Existing current transformer in power-plant | 2000 A/1A, class: 0.5 |
| Installed current transformer | Dent CT-SRS-005-U, 2.5 A/0.333 V, class 0.2 |
| Voltage divider | 2 × 22 k |
| Proximity sensor | Balluff BES M18MI-PSC50B-BV10 |
| Temperature sensor | PT1000 |
| Hall probe | HGT-2010 |
| Supply for the hall probes | 24 V, 50 mA, custom made |
| Signal conditioner for PT1000 | Weidmueller WAS5 PRO RTD 1000 |
| Signal conditioner for current and voltage measurements | Weidmueller WAS4 PRO DC/DC |
| NI chassis | NI cDAQ 9181 |
| NI voltage input module | NI 9205 |
| Optic converter | Planet, IGT-905A, SFP module |
| Device for power angle measurement | Custom made |
| PLC | Simatic S7-300 CPU 315-2 PN/DP |
References
- Hamidifar, S.; Kar, N. A Novel Approach to Saturation Characteristics Modeling and Its Impact on Synchronous Machine Transient Stability Analysis. IEEE Trans. Energy Convers. 2012, 27, 139–150. [Google Scholar] [CrossRef]
- Levi, E.; Levi, V. Impact of dynamic cross-saturation on accuracy of saturated synchronous machine models. IEEE Trans. Energy Convers. 2000, 15, 224–230. [Google Scholar] [CrossRef]
- Mirosevic, M.; Maljkovic, Z.; Miskovic, M. The effect of implementing of dynamic cross saturation on modeling of synchronous generator. In Proceedings of the 2013 Fourth International Conference on Power Engineering, Energy and Electrical Drives (POWERENG), Istanbul, Turkey, 13–17 May 2013; pp. 1477–1481. [Google Scholar] [CrossRef]
- Karayaka, H.; Keyhani, A.; Heydt, G.; Agrawal, B.; Selin, D.A. Synchronous generator model identification and parameter estimation from operating data. IEEE Trans. Energy Convers. 2003, 18, 121–126. [Google Scholar] [CrossRef]
- Karrari, M.; Malik, O. Identification of Heffron-Phillips model parameters for synchronous generators using online measurements. IEEE Proc. Gener. Transm. Distrib. 2004, 151, 313–320. [Google Scholar] [CrossRef]
- Despalatovic, M.; Jadric, M.; Terzic, B. Modeling of Saturated Synchronous Generator Based on Steady-State Operating Data. IEEE Trans. Ind. Appl. 2012, 48, 62–69. [Google Scholar] [CrossRef]
- Despalatovic, M.; Jadric, M.; Terzic, B. Modeling of saturated synchronous generator based on steady-state operating data. In Proceedings of the 2010 XIX International Conference on Electrical Machines (ICEM), Rome, Italy, 6–8 September 2010; pp. 1–6. [Google Scholar] [CrossRef]
- Jadrić, M.; Despalatović, M.; Terzić, B. Development of synchronous generator saturation model from steady-state operating data. Electr. Power Syst. Res. 2010, 80, 1323–1331. [Google Scholar] [CrossRef]
- Marti, J.; Louie, K. A phase-domain synchronous generator model including saturation effects. IEEE Trans. Power Syst. 1997, 12, 222–229. [Google Scholar] [CrossRef]
- Garcia-Dominguez, M.; Ruiz-Vega, D. An alternative synchronous machine model for Quasi-Steady-State simulations. In Proceedings of the 40th North American Power Symposium (NAPS ’08), Calgary, AB, Canada, 28–30 September 2008; pp. 1–7. [Google Scholar] [CrossRef]
- Racewicz, S.; Riu, D.; Retiere, N.; Chrzan, P. Half-Order Modeling of Saturated Synchronous Machine. IEEE Trans. Ind. Electr. 2014, 61, 5241–5248. [Google Scholar] [CrossRef]
- Wang, L.; Jatskevich, J. A Voltage-Behind-Reactance Synchronous Machine Model for the EMTP-Type Solution. IEEE Trans. Power Syst. 2006, 21, 1539–1549. [Google Scholar] [CrossRef]
- Huang, Y.; Chapariha, M.; Therrien, F.; Jatskevich, J.; Marti, J. A Constant-Parameter Voltage-Behind-Reactance Synchronous Machine Model Based on Shifted-Frequency Analysis. IEEE Trans. Energy Convers. 2015. [Google Scholar] [CrossRef]
- Cramer, A.; Loop, B.; Aliprantis, D. Synchronous Machine Model With Voltage-Behind-Reactance Formulation of Stator and Field Windings. IEEE Trans. Energy Convers. 2012, 27, 391–402. [Google Scholar] [CrossRef]
- Karaagac, U.; Mahseredjian, J.; Kocar, I.; Saad, O. An Efficient Voltage-Behind-Reactance Formulation-Based Synchronous Machine Model for Electromagnetic Transients. IEEE Trans. Power Deliv. 2013, 28, 1788–1795. [Google Scholar] [CrossRef]
- Liu, S.; Cheng, Y.; Li, L. A voltage-behind-reactance model and validation for six-phase synchronous machines. In Proceedings of the 2014 IEEE Conference and Expo Transportation Electrification Asia-Pacific (ITEC Asia-Pacific), Beijing, China, 31 August–3 September 2014; pp. 1–6. [Google Scholar] [CrossRef]
- Wang, L.; Jatskevich, J. Magnetically-Saturable Voltage-Behind-Reactance Synchronous Machine Model for EMTP-Type Solution. IEEE Trans. Power Syst. 2011, 26, 2355–2363. [Google Scholar] [CrossRef]
- Aliprantis, D.; Wasynczuk, O.; Rodriguez Valdez, C. A Voltage-Behind-Reactance Synchronous Machine Model with Saturation and Arbitrary Rotor Network Representation. IEEE Trans. Energy Convers. 2008, 23, 499–508. [Google Scholar] [CrossRef]
- Pekarek, S.; Walters, E.; Kuhn, B. An efficient and accurate method of representing magnetic saturation in physical-variable models of synchronous machines. IEEE Trans. Energy Convers. 1999, 14, 72–79. [Google Scholar] [CrossRef]
- Levi, E. Saturation modelling in d-q axis models of salient pole synchronous machines. IEEE Trans. Energy Convers. 1999, 14, 44–50. [Google Scholar] [CrossRef]
- Liang, X.; El-Serafi, A.; Faried, S. Application of the Finite-Element Method for the Determination of the Parameters Representing the Cross-Magnetizing in Saturated Synchronous Machines. IEEE Trans. Energy Convers. 2010, 25, 70–79. [Google Scholar] [CrossRef]
- Stumberger, B.; Stumberger, G.; Dolinar, D.; Hamler, A.; Trlep, M. Evaluation of Saturation and Cross-Magnetization Effects in Interior Permanent-Magnet Synchronous Motor. IEEE Trans. Ind. Appl. 2003, 39, 1264–1271. [Google Scholar] [CrossRef]
- Bianchi, N.; Bolognani, S. Magnetic Models Of Saturated Interior Permanent Magnet Motors Based on Finite Element Analysis. In Proceedings of the 33rd IAS Annual Meeting 1998 IEEE Industry Applications Conference, St. Louis, MO, USA, 12–15 October 1998; Volume 1, pp. 27–34. [Google Scholar] [CrossRef]
- Tahan, S.A.; Kamwa, I. A two-factor saturation model for synchronous machines with multiple rotor circuits. IEEE Trans. Energy Convers. 1995, 10, 609–616. [Google Scholar] [CrossRef]
- Pillutla, S.; Keyhani, A. Neural network based saturation model for round rotor synchronous generator. IEEE Trans. Energy Convers. 1999, 14, 1019–1025. [Google Scholar] [CrossRef]
- Pillutla, S.; Keyhani, A. Neural network based modeling of round rotor synchronous generator rotor body parameters from operating data. IEEE Trans. Energy Convers. 1999, 14, 321–327. [Google Scholar] [CrossRef]
- Abido, M.; Abdel-Magid, Y. On-line identification of synchronous machines using radial basis function neural networks. IEEE Trans. Power Syst. 1997, 12, 1500–1506. [Google Scholar] [CrossRef]
- Wu, X.; Fan, Y. Synchronous generator model identification using half-complex wavelet nonlinear ARX network. In Proceedings of the International Conference on Electrical Machines and Systems (ICEMS 2008), Wuhan, China, 17–20 October 2008; pp. 20–25. [Google Scholar]
- Wamkeue, R.; Jolette, C.; Mabwe, A.; Kamwa, I. Cross-Identification of Synchronous Generator Parameters From RTDR Test Time-Domain Analytical Responses. IEEE Trans. Energy Convers. 2011, 26, 776–786. [Google Scholar] [CrossRef]
- Wamkeue, R.; Baetscher, F.; Kamwa, I. Hybrid-State-Model-Based Time-Domain Identification of Synchronous Machine Parameters From Saturated Load Rejection Test Records. IEEE Trans. Energy Convers. 2008, 23, 68–77. [Google Scholar] [CrossRef]
- Fard, R.; Karrari, M.; Malik, O. Synchronous generator model identification using Volterra series. In Proceedings of the Power Engineering Society General Meeting, Denver, CO, USA, 6–10 June 2004; Volume 2, pp. 1344–1349. [Google Scholar] [CrossRef]
- Fard, R.; Karrari, M.; Malik, O. Synchronous generator model identification for control application using volterra series. IEEE Trans. Energy Convers. 2005, 20, 852–858. [Google Scholar] [CrossRef]
- Vakil, V.; Karrari, M.; Rosehart, W.; Malik, O. Synchronous generator model identification using adaptive pursuit method. IEEE Proc. Gener. Transm. Distrib. 2006, 153, 247–252. [Google Scholar] [CrossRef]
- Chaudhry, S.; Ahmed-Zaid, S.; Demerdash, N. An artificial-neural-network method for the identification of saturated turbogenerator parameters based on a coupled finite-element/state-space computational algorithm. IEEE Trans. Energy Convers. 1995, 10, 625–633. [Google Scholar] [CrossRef]
- Pillutla, S.; Keyhani, A.; Kamwa, I. Neural network observers for on-line tracking of synchronous generator parameters. IEEE Trans. Energy Convers. 1999, 14, 23–30. [Google Scholar] [CrossRef]
- Gong, R.; Huang, Y.; Wei, H.; Meng, X.; Xie, L. Design of PID excitation controllers for synchronous generators based on fuzzy RBF neural network. In Proceedings of the International Conference on Electrical Machines and Systems (ICEMS 2008), Wuhan, China, 17–20 October 2008; pp. 122–127. [Google Scholar]
- Guha, S.; Kar, N. Saturation Modeling and Stability Analysis of Synchronous Reluctance Generator. IEEE Trans. Energy Convers. 2008, 23, 814–823. [Google Scholar] [CrossRef]
- Babaei, E.; Mozaffari Niapour, S.; Tabarraie, M. Design of a non-linear power system stabiliser using the concept of the feedback linearisation based on the back-stepping technique. IET Gener. Transm. Distrib. 2011, 5, 860–868. [Google Scholar] [CrossRef]
- Dineley, J.; Mikhail, S. The dynamic stability of a steam turbine driven synchronous generator under leading power factor load conditions. IEEE Trans. Power Appar. Syst. 1975, 94, 288–298. [Google Scholar] [CrossRef]
- Wang, L.; Truong, D.N. Dynamic Stability Improvement of Four Parallel-Operated PMSG-Based Offshore Wind Turbine Generators Fed to a Power System Using a STATCOM. IEEE Trans. Power Deliv. 2013, 28, 111–119. [Google Scholar] [CrossRef]
- Sellschopp, F.; Arjona, M. Determination of Synchronous Machine Parameters Using Standstill Frequency Response Tests at Different Excitation Levels. In Proceedings of the IEEE International Electric Machines Drives Conference (IEMDC ’07), Antalya, Turkey, 3–5 May 2007; Volume 2, pp. 1014–1019. [Google Scholar] [CrossRef]
- El-Serafi, A.; Kar, N. Methods for determining the q-axis saturation characteristics of salient-pole synchronous machines from the measured d-axis characteristics. IEEE Trans. Energy Convers. 2003, 18, 80–86. [Google Scholar] [CrossRef]
- MacDonald, D.; Reece, A.; Turner, P. Turbine-generator steady-state reactances. IEEE Proc. Gener. Transm. Distrib. 1985, 132, 101–108. [Google Scholar] [CrossRef]
- Mandić, I.; Tomljenović, V.; Pužar, M. Sinkroni i Asinkroni Električni Strojevi; Polytechnic of Zagreb, Electrical Engineering Department: Zagreb, Croatia, 2012. [Google Scholar]
- Ilić, I.; Maljković, Z.; Gašparac, I.; Pavlica, M.; Ilić-Zubović, D.; Jarić, V.; Višković, A.; Belobrajić, R. An Example of Applying Algorithm to Create the Actual PQ Diagram of a Hydrogenerator. Energija 2007, 56, 456–489. [Google Scholar]
- Ilić, I.; Maljković, Z.; Gašparac, I.; Pavlica, M.; Ilić-Zubović, D.; Jarić, V.; Višković, A.; Belobrajić, R. Methodology for Determining the Actual PQ Diagram of a Hydrogwenerators. Energija 2007, 56, 144–181. [Google Scholar]
- Maljkovic, Z.; Gasparac, I.; Pavlica, M. Large turbogenerator’s synchronous reactance’s load dependence determined by measurements. In Proceedings of the 2014 International Conference on Electrical Machines (ICEM), Berlin, Germany, 2–5 September 2014; pp. 203–207. [Google Scholar] [CrossRef]
- Vrazic, M.; Viskovic, A.; Hanic, Z. User PQ Diagram as a Part of a Synchronous Generator Monitoring System. Elektronika ir Elektrotechnika 2014, 20, 33–38. [Google Scholar] [CrossRef]
- Escarela-Perez, R.; Niewierowicz, T.; Campero-Littlewood, E. A study of the variation of synchronous machine parameters due to saturation: A numerical approach. Electr. Power Syst. Res. 2004, 72, 1–11. [Google Scholar] [CrossRef]
- Sobczyk, T. Inductanceless model of salient-pole synchronous machines. In Proceedings of the International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM 2008), Ischia, Italy, 11–13 June 2008; pp. 620–625. [Google Scholar] [CrossRef]
- Hamidifar, S.; Kar, N.C. A state space synchronous machine model with multifunctional characterization of saturation using Levenberg–Marquardt optimization algorithm. Electr. Power Syst. Res. 2013, 102, 33–41. [Google Scholar] [CrossRef]
- Calvo, M.; Malik, O. Synchronous Machine steady-State parameter estimation using neural networks. IEEE Trans. Energy Convers. 2004, 19, 237–244. [Google Scholar] [CrossRef]
- Fukami, T.; Matsui, Y.; Hayamizu, T.; Shima, K.; Hanaoka, R.; Takata, S. Steady-state analysis of a permanent-magnet-assisted salient-pole synchronous generator. In Proceedings of the 18th International Conference on Electrical Machines (ICEM 2008), Vilamoura, Portugal, 6–9 September 2008; pp. 1–6. [Google Scholar] [CrossRef]
- Fukami, T.; Hayamizu, T.; Matsui, Y.; Shima, K.; Hanaoka, R.; Takata, S. Steady-State Analysis of a Permanent-Magnet-Assisted Salient-Pole Synchronous Generator. IEEE Trans. Energy Convers. 2010, 25, 388–393. [Google Scholar] [CrossRef]
- Arjona, L.; Macdonald, D. Saturation effects on the steady-state stability limit of turbine-generators. IEEE Trans. Energy Convers. 1999, 14, 133–138. [Google Scholar] [CrossRef]
- Gargiulo, G.; Mangoni, V.; Russo, M. Capability charts for combined cycle power plants. IEEE Proc. Gener. Transm. Distrib. 2002, 149, 407–415. [Google Scholar] [CrossRef]
- Walker, J. Operating characteristics of salient-pole machines. Proc. IEEE Part II Power Eng. 1953, 100, 13–24. [Google Scholar]
- Hanic, Z.; Vrazic, M.; Maljkovic, Z. Steady-state synchronous machine model which incorporates saturation and cross-magnetization effects. In Proceedings of the Fourth International Conference on Power Engineering, Energy and Electrical Drives (POWERENG), Istanbul, Turkey, 13–17 May 2013; pp. 1553–1557. [Google Scholar]
- Vražić, M.; Kovačić, M.; Hanić, Z. Design of the monitoring system for a synchronous generators in hydro power plant. In Proceedings of the 2012 International Conference on Renewable Energy Research and Applications (ICRERA), Nagasaki, Japan, 11–14 November 2012; pp. 1–5. [Google Scholar] [CrossRef]
- Ehya, H.; Sadeghi, I.; Faiz, J. Online condition monitoring of large synchronous generator under eccentricity fault. In Proceedings of the 2017 12th IEEE Conference on Industrial Electronics and Applications (ICIEA), Siem Reap, Cambodia, 18–20 June 2017; pp. 19–24. [Google Scholar] [CrossRef]
- Colak, I.; Garip, I.; Sagiroglu, S.; Bayhan, S. Remote monitoring of the load characteristics of synchronous generators. In Proceedings of the 2011 International Conference on Power Engineering, Energy and Electrical Drives, Malaga, Spain, 11–13 May 2011; pp. 1–4. [Google Scholar] [CrossRef]


| Quantity | Value | Unit |
|---|---|---|
| Apparent power | 35 | MVA |
| Armature voltage | 10,500 | V |
| Armature current | 1925 | A |
| Frequency | 50 | Hz |
| Rotor speed | 500 | rpm |
| Power factor | 0.9 | |
| Number of phases | 3 | |
| Field current | 643 | A |
| G1 | G2 | G3 | G1 | G2 | G3 | ||
|---|---|---|---|---|---|---|---|
| 2.006 | 2.071 | 1.707 | -0.157 | 0.078 | 0.388 | ||
| −0.011 | 0.104 | 0.067 | 0.887 | 0.927 | 0.789 | ||
| 1.850 | 1.791 | 1.581 | −0.016 | 0.132 | 0.472 | ||
| −1.062 | −1.156 | −0.666 | 0.192 | −0.133 | −0.661 | ||
| −0.421 | −0.423 | −0.250 | 0.033 | −0.019 | −0.369 | ||
| −0.900 | −0.836 | −0.615 | 0.029 | −0.100 | −0.526 | ||
| 0.115 | −0.089 | −0.060 | 0.004 | −0.104 | 0.212 | ||
| −1.769 | −1.774 | −1.139 | 0.218 | −0.177 | −1.021 | ||
| 0.036 | −0.075 | −0.040 | −0.136 | −0.199 | 0.002 | ||
| 0.139 | 0.099 | 0.055 | −0.047 | −0.004 | 0.220 | ||
| 0.257 | 0.225 | 0.111 | −0.059 | −0.066 | 0.221 | ||
| 0.060 | 0.048 | 0.034 | 0.003 | 0.010 | 0.059 |
| Maximum Field Current Limit | Practical Steady-State Stability Limit | |||||
|---|---|---|---|---|---|---|
| G1 | G2 | G3 | G1 | G2 | G3 | |
| −2.134 | 2.628 | −1.316 | 0.03741 | −0.8958 | −1.484 | |
| 4.731 | −7.076 | 5.875 | −0.2657 | −2.153 | 2.478 | |
| −1.839 | 4.730 | −3.894 | −0.6721 | −0.07416 | −1.909 | |
| 0.8528 | −1.555 | 0.3566 | 4.154 | 0.567 | 3.632 | |
| −2.704 | −0.665 | −0.4793 | −6.092 | −3.294 | −4.300 | |
| 0.4354 | 9.1444 | −0.3489 | 3.111 | 2.900 | 1.165 | |
| −7.742 | 2.130 | −0.3111 | −3.46 | 2.107 | −3.053 | |
| 2.450 | 0.09048 | 0.1848 | 5.792 | 0.866 | 3.987 | |
| −0.4941 | −0.7989 | 0.3871 | −3.098 | −1.788 | −1.045 | |
| G1 | G2 | G3 | |
|---|---|---|---|
| −1.6911 | 20.8262 | −0.37627 | |
| 4.4154 | 2.5768 | 8.9683 | |
| 2.0611 | −20.5271 | 0.6251 | |
| 3.7442 | 2.6596 | 3.5168 | |
| −0.27902 | 6.1522 | 0.004537 | |
| 1.0581 | 6.4281 | 0.1156 | |
| 0.79029 | −5.7361 | 0.31297 | |
| 2.9298 | 7.0448 | 2.1688 | |
| 24.1127 | −3.1951 | −0.54913 | |
| 4.5645 | 4.9298 | 4.7285 | |
| −25.2362 | 2.1303 | −0.45285 | |
| 4.5156 | 6.724 | 1.1757 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Glavan, B.; Hanić, Z.; Kovačić, M.; Vražić, M. Condition-Monitoring System for Identification and Representation of the Capability Diagram Limits for Multiple Synchronous Generators in a Hydro Power-Plant. Energies 2020, 13, 3800. https://doi.org/10.3390/en13153800
Glavan B, Hanić Z, Kovačić M, Vražić M. Condition-Monitoring System for Identification and Representation of the Capability Diagram Limits for Multiple Synchronous Generators in a Hydro Power-Plant. Energies. 2020; 13(15):3800. https://doi.org/10.3390/en13153800
Chicago/Turabian StyleGlavan, Boris, Zlatko Hanić, Marinko Kovačić, and Mario Vražić. 2020. "Condition-Monitoring System for Identification and Representation of the Capability Diagram Limits for Multiple Synchronous Generators in a Hydro Power-Plant" Energies 13, no. 15: 3800. https://doi.org/10.3390/en13153800
APA StyleGlavan, B., Hanić, Z., Kovačić, M., & Vražić, M. (2020). Condition-Monitoring System for Identification and Representation of the Capability Diagram Limits for Multiple Synchronous Generators in a Hydro Power-Plant. Energies, 13(15), 3800. https://doi.org/10.3390/en13153800





