A Novel Two-Zone Thermodynamic Model for Spark-Ignition Engines Based on an Idealized Thermodynamic Process
Abstract
1. Introduction
2. Description of Model
- Only the combustion process and the expansion process in the closed cycle of a spark-ignition engine in the steady-state operating conditions are considered in this study.
- The fuel is completely vaporized and well mixed with the incoming air before the models are applied [24].
- Two types of gas models, i.e., unburned gas and burned gas, are adopted in the thermodynamic models. The unburned gas is a mixture of fuel and air, therefore its composition keeps constant in this study. The burned gas is a mixture of combustion products, and its composition varies due to the chemical equilibrium (at the temperature of the zone and the uniform cylinder pressure) [25]. Both unburned gas and burned gas are regarded as the ideal gas, and their composition and thermodynamic properties are spatially uniform in each zone [24].
- The pressure is spatially uniform in the whole combustion chamber, while the temperature is spatially uniform in each zone [24].
- The cylinder wall temperature is assumed to be uniform and keeps constant during the simulation [26].
- All crevice effects are ignored, and the blow-by is assumed to be zero [26]. As a result, the trapped mass of gas in the cylinder is treated as constant during the simulation.
2.1. Formation of Benchmark Models
2.1.1. Formation of a Single-Zone Model
- The differential-form ideal gas law of state in the combustion chamber.
- The energy conservation equation in the combustion chamber.where is the cylinder pressure; is the cylinder volume; is the cylinder temperature; is the trapped mass of gas in cylinder; is the cylinder gas constant; is the specific internal energy of the combustion chamber; is the heat transfer from the cylinder wall to the combustion chamber; is the heat released from the combustion, and its derivative is calculated from lower heating value of the fuel , air-fuel ratio , trapped mass of gas in cylinder and burned mass rate by:
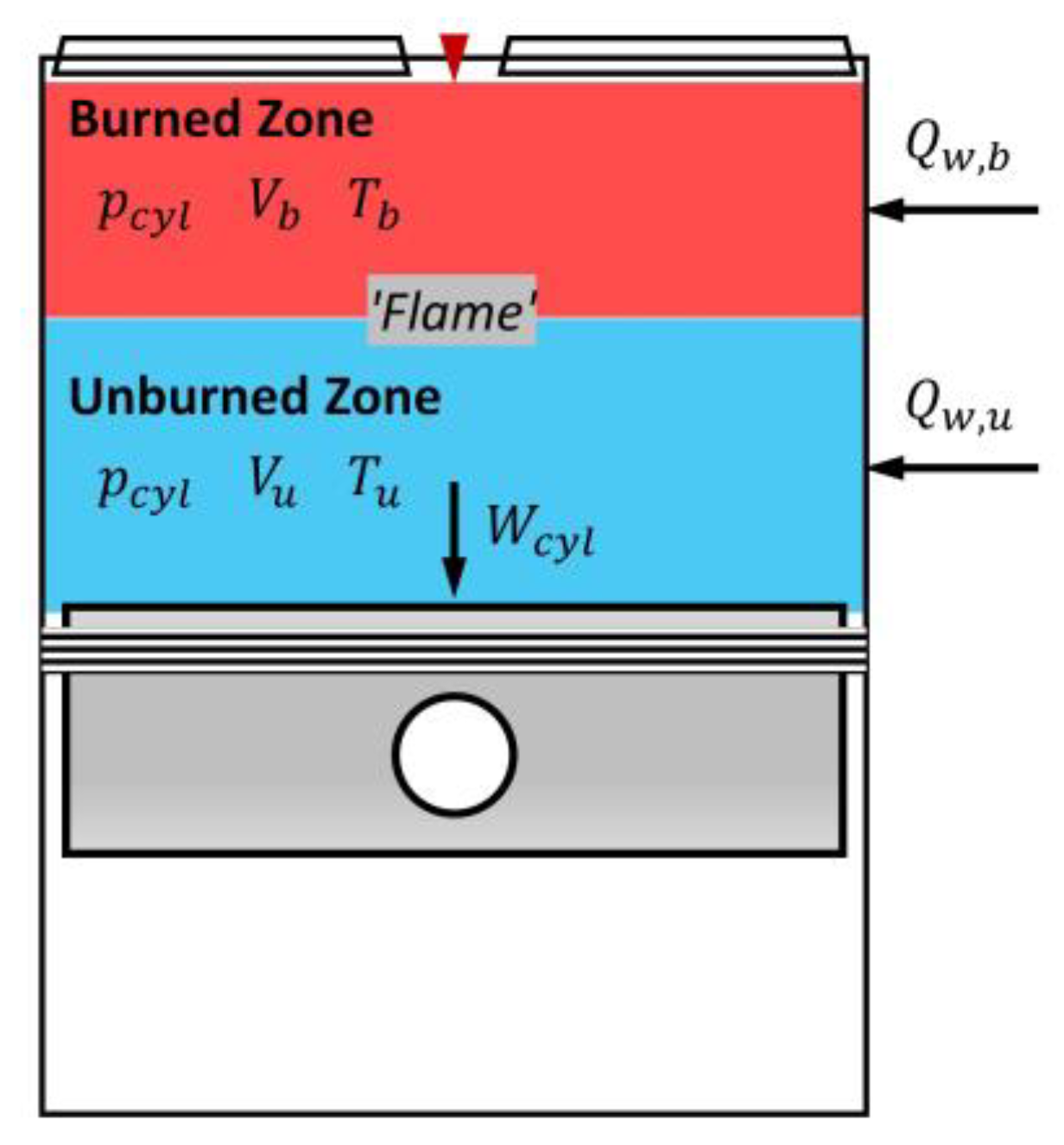
2.1.2. Formation of Conventional Two-Zone Model
- The differential-form volumetric continuity.
- The differential-form ideal gas law of state in the unburned zone.
- The energy conservation equation in the unburned zone.
- The differential-form ideal gas law of state in the burned zone
- The energy conservation equation in the burned zone.where is the specific enthalpy of the unburned zone; is the specific internal energy of the burned zone; is the heat transfer from the cylinder wall to the unburned zone, is the heat transfer from the cylinder wall to the burned zone.
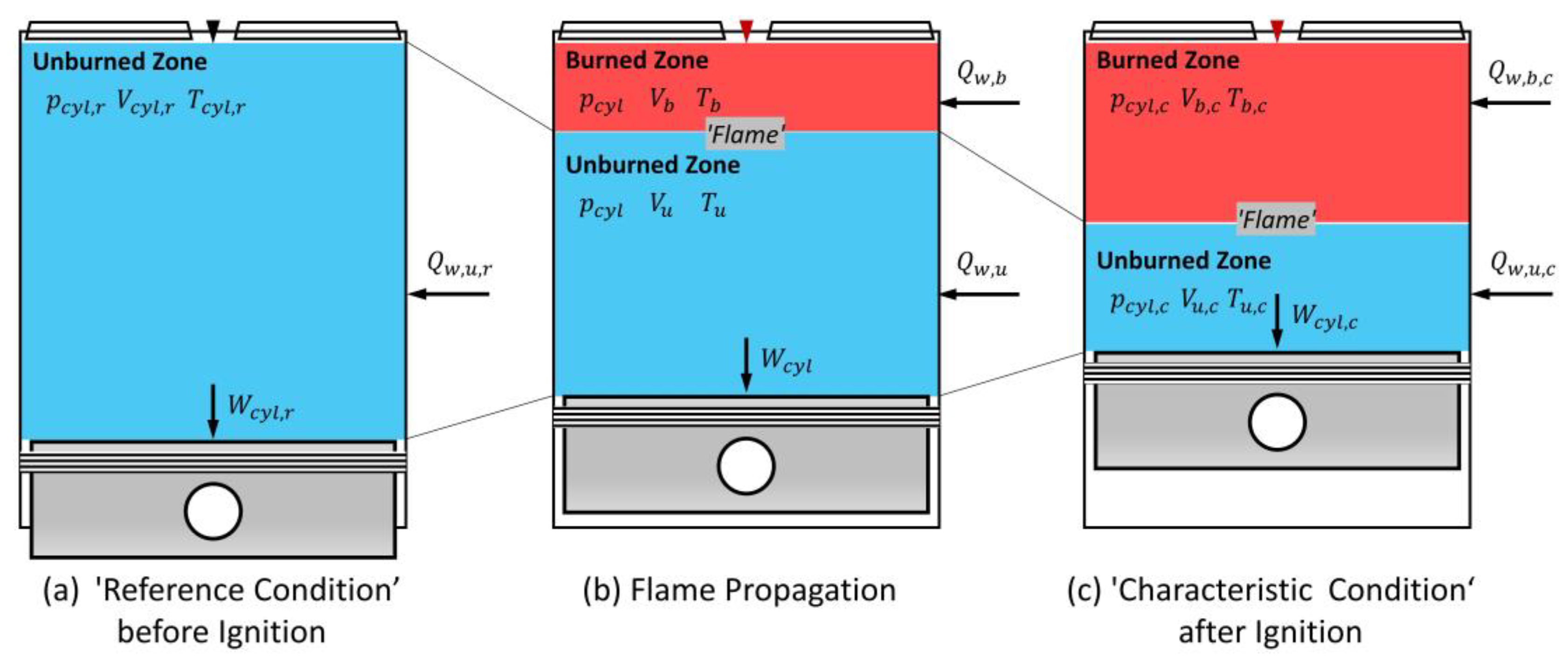
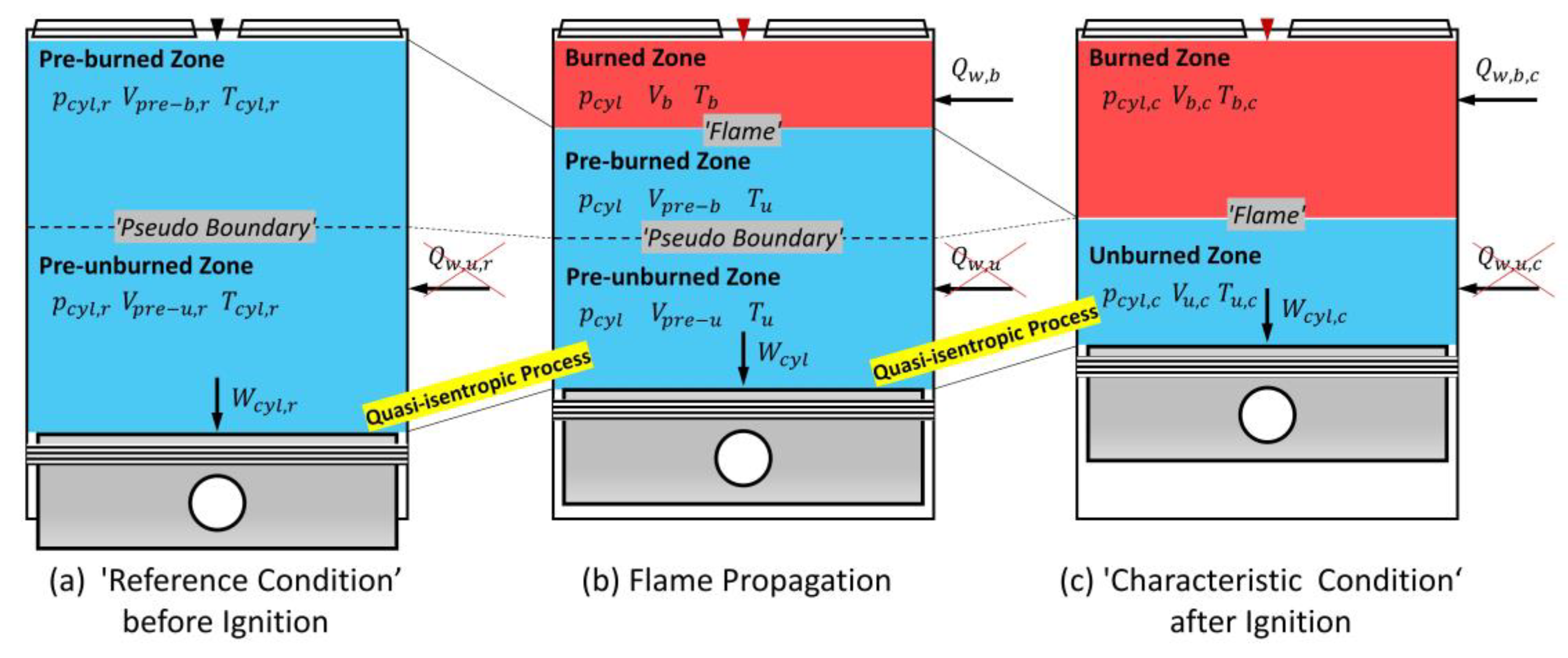
2.2. Quasi-Isentropic Process
- S1: In the unburned zone, compared to the pressure-volume work , the heat transferred from the wall to the gas is ignored, which is expressed in differential-form:
- S2: The unburned zone’s heat capacity ratio , which is the ratio of the heat capacity at constant pressure over the heat capacity at constant volume , keeps constant, i.e.,
2.3. Formation of a Novel Two-Zone Model
- Algebraizing the volumetric continuity (Equation (8)), the ideal gas law of state (Equation (9)), and the energy conservation equation (Equation (10)) in the unburned zone. As a result, the set of governing equations of the two-zone model becomes a set of differential-algebraic equations (DAEs).
- Decoupling the subset of the ODEs and the subset of the AEs in the governing equations of the two-zone model. As a result, the set of governing equations of the two-zone model is split into a set of ODEs and an accompanying set of AEs.
- The algebraic-form volumetric continuity.
- The algebraic-form ideal gas law of state in the unburned zone, Equation (32).
- The governing equation of the quasi-isentropic process, Equation (31).
- The differential-form ideal gas law of state in the burned zone, Equation (11).
- The energy conservation equation in the burned zone, Equation (12).
- The ideal gas equation of state in the burned zone, Equation (43).
- The energy conservation equation in the burned zone, Equation (44).
2.4. Numerical Methodology
- The single-zone model:
- The conventional two-zone model:
- The novel two-zone modelwhere is the cylinder pressure at ignition and obtained from the experiment; is the cylinder temperature and determined by the cylinder pressure at ignition and the trapped mass of gas in cylinder according to the ideal gas equation of state; is the cylinder volume at ignition and determined by engine kinematics; is the adiabatic flame temperature at constant pressure and calculated by the method introduced by Ferguson [25].
3. Results and Discussion
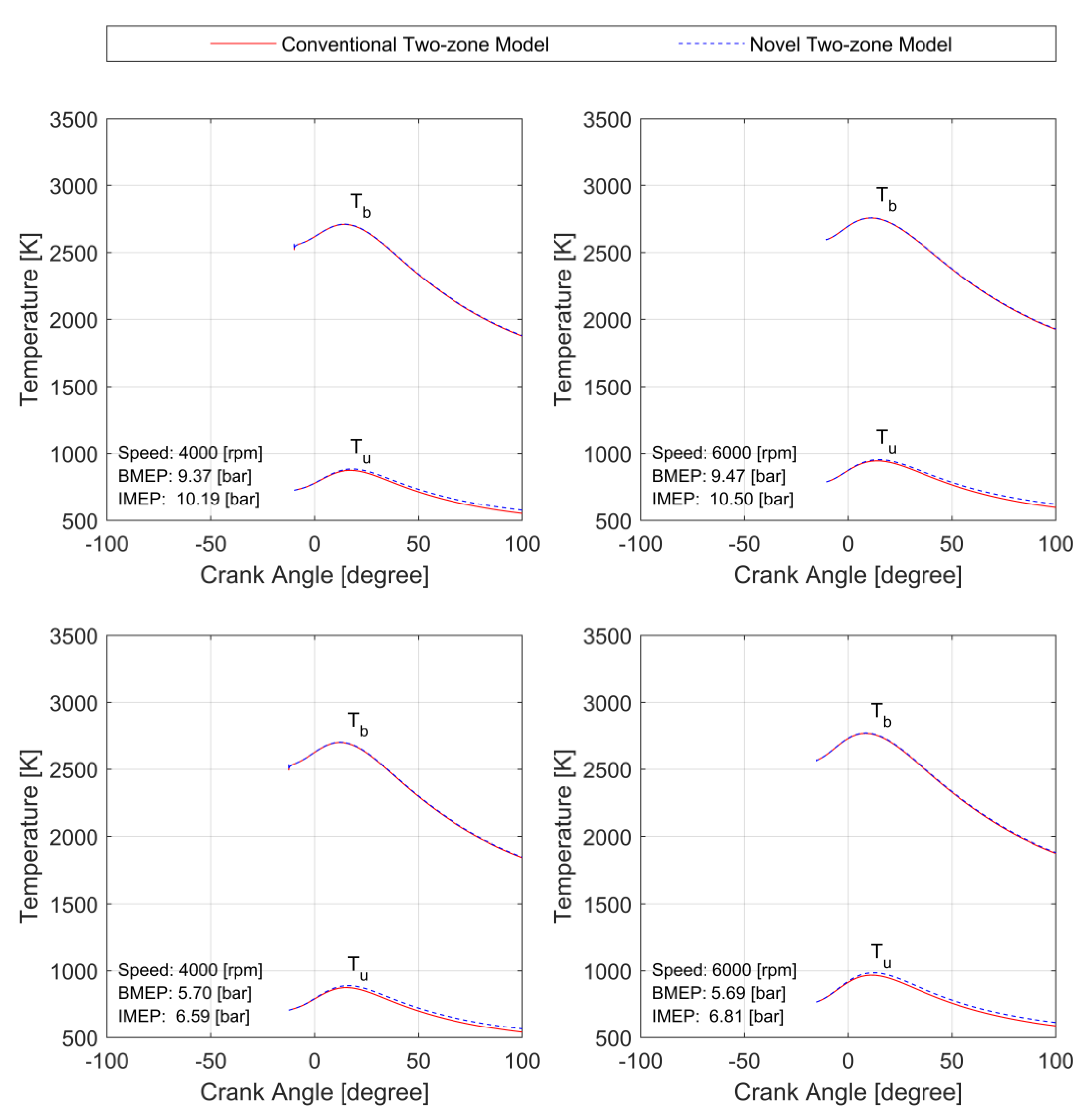
3.1. Model Validation
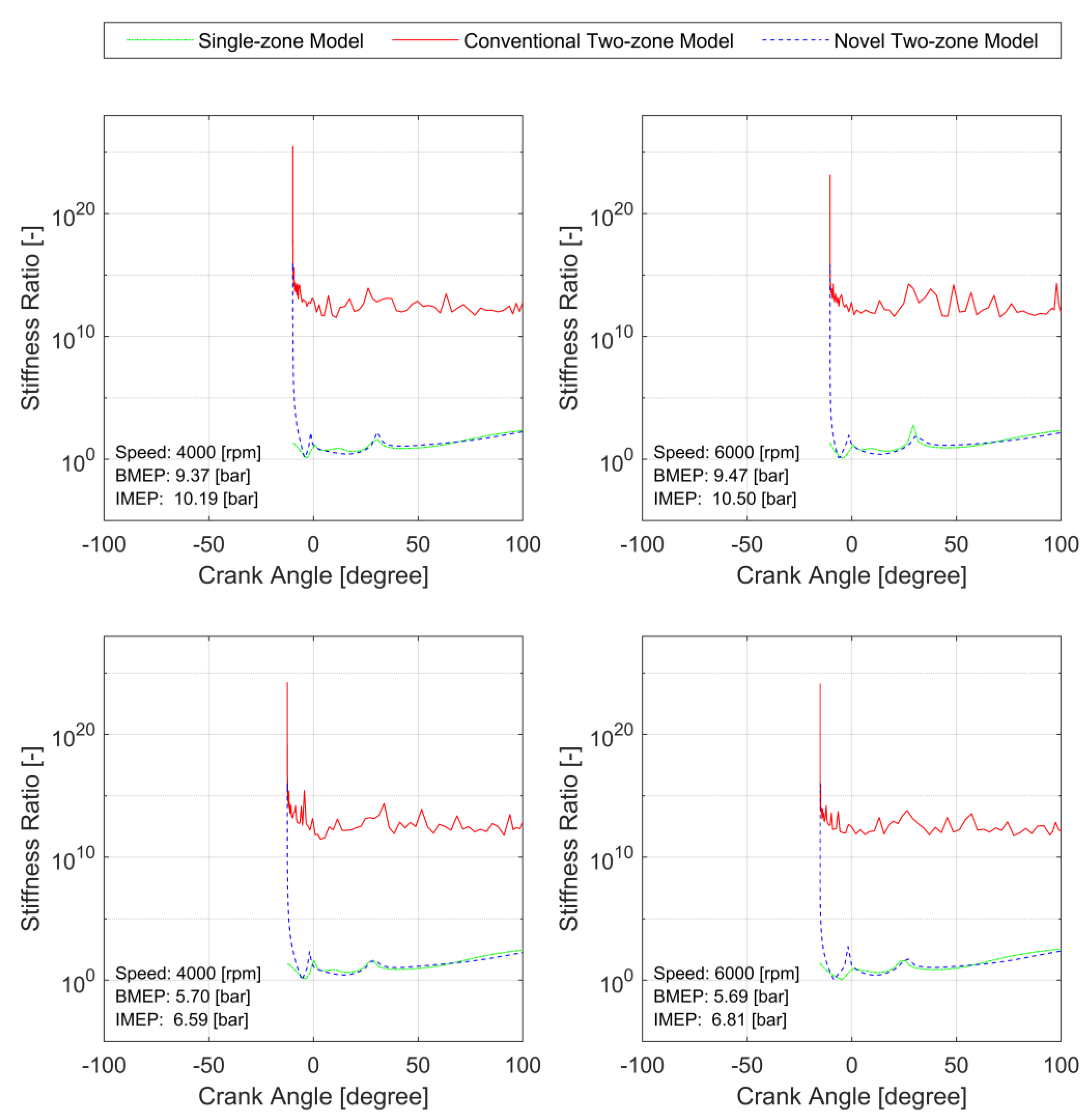
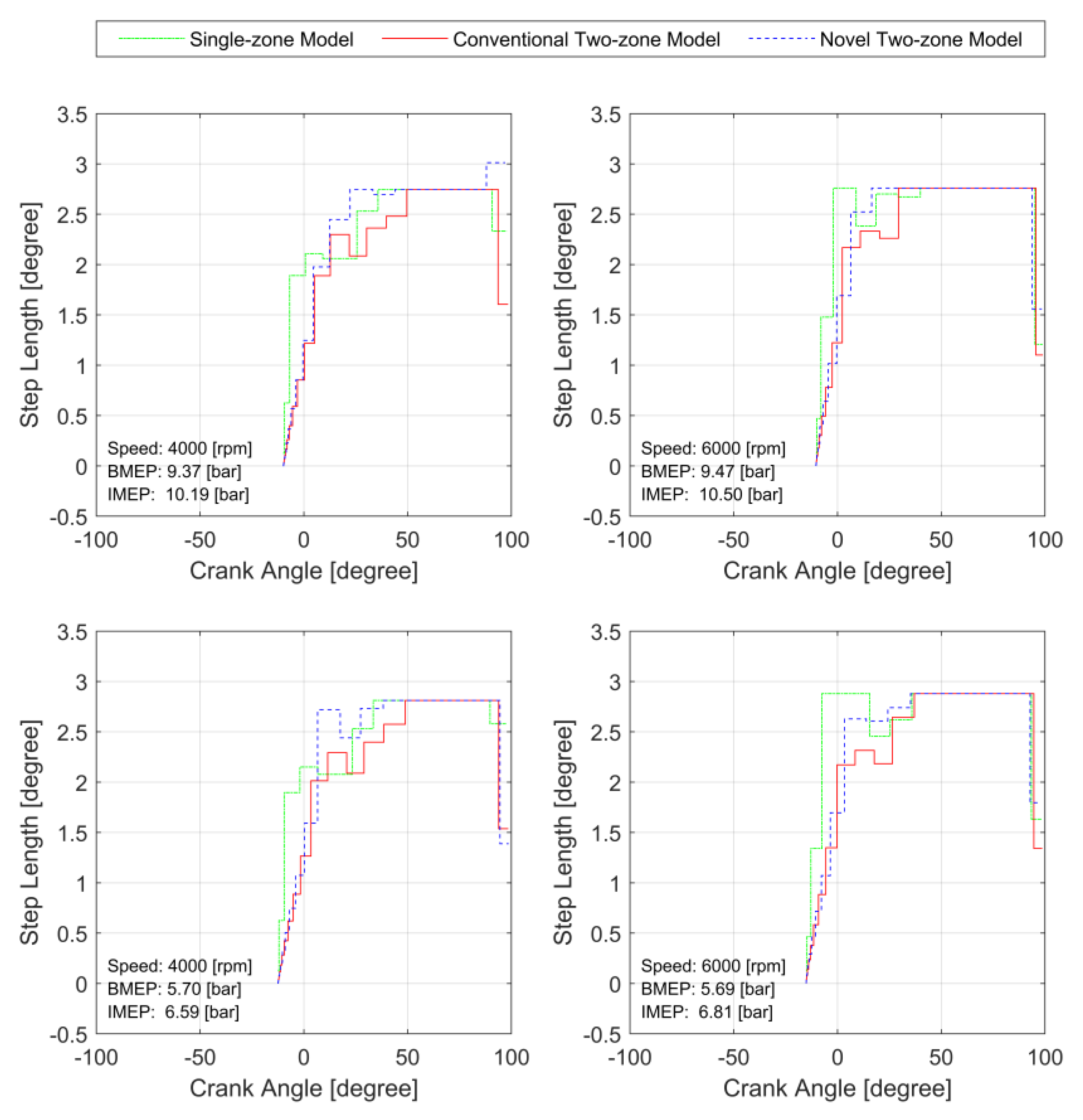
3.2. Model Stiffness
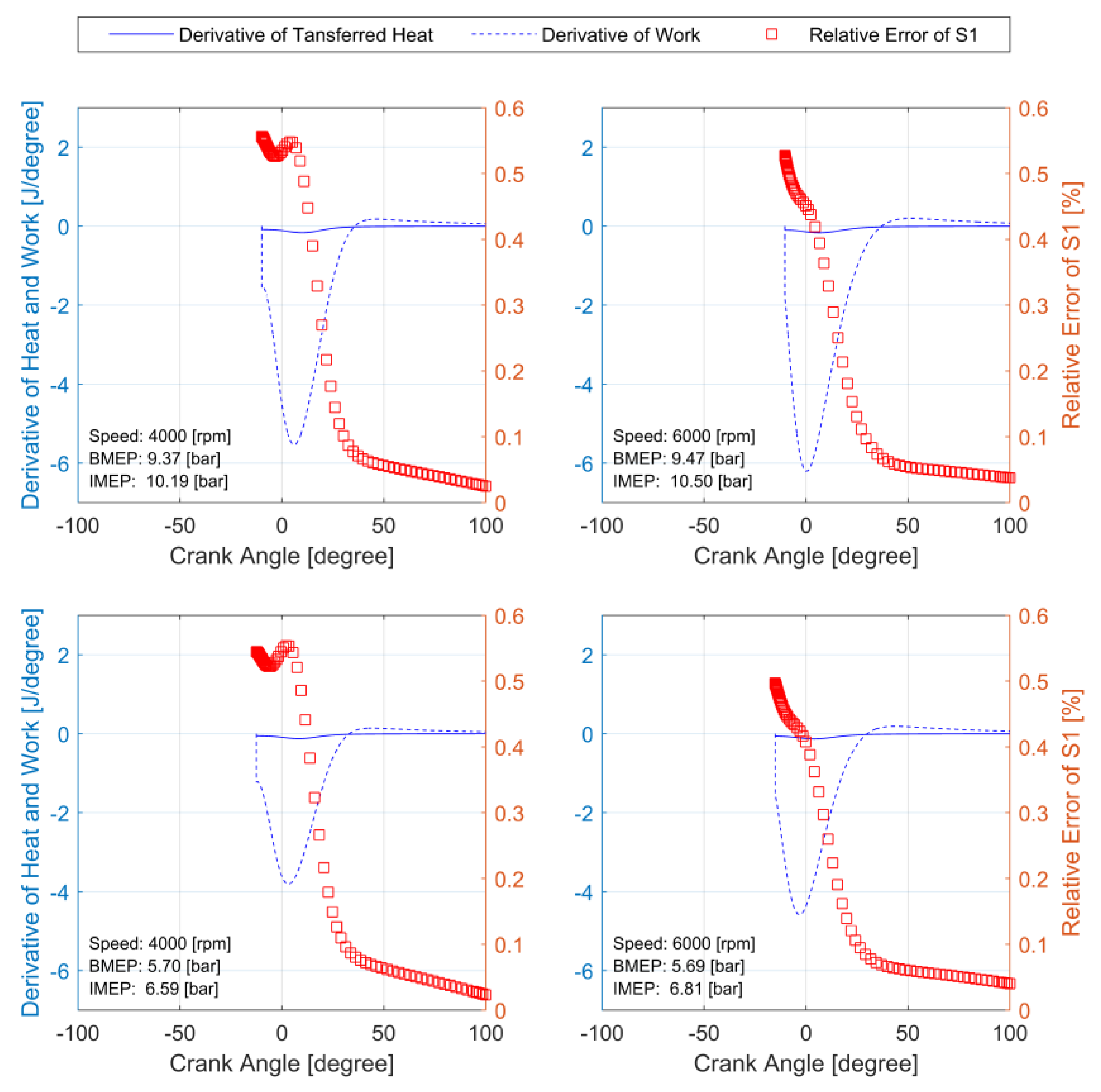
3.3. Analysis of Error Due to Simplifications
4. Conclusions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Sub-Models of the Thermodynamic Model
Appendix A.1. Engine Kinematics
Appendix A.2. Burned Mass Fraction—Wiebe Function
Appendix A.3. Heat Transfer
Appendix A.4. Chemical Composition and Thermodynamic Property
- Unburned gas, as shown at the left-hand-side of Equation (A7), is a homogeneous mixture of the fuel () and the air ( and ), and its composition is determined by the fuel-air equivalence ratio .
- Burned gas, as shown at the right-hand-side of Equation (A7), is a homogeneous mixture of 11 combustion products (, , , , , , , , , , ) at chemical equilibrium (at the temperature of the zone and the uniform cylinder pressure) [31].
Appendix B. Mathematical Derivation of the Governing Equation of the Quasi-Isentropic Process
- Multiplying Equation (9) by the heat capacity at constant volume yields Equation (A9).
- Multiplying Equation (10) by the gas constant yields Equation (A10).
- Summing Equations (A9) and (A10) side-by-side yields Equation (A11).
- Substituting Equation (A12) into Equation (A11) yields Equation (A13).
- Substituting unburned zone’s algebraic-form ideal gas law of state (Equation (A14)) into Equation (A13) yields Equation (A15).
- Substituting the expression of unburned zone’s mass (Equation (14)) and its derivative (Equation (15)) into Equation (A15) yields Equation (A16).
- Dividing Equation (A16) by yields Equation (A17).
- Rearranging Equation (A17) yields Equation (A18).
- Applying the simplification S1 (Equation (22) on Equation (A18) yields Equation (A19).
- Applying the simplification S2 (Equation (23)) on Equation (A19) converts Equation (A19) to an ODE with constant coefficients.
- Integrating Equation (A19) yields Equation (A20).
- To obtain the constant in Equation (A20), applying Equation (A20) in its initial condition (Equation (A21)), i.e., the ‘reference condition’ shown in Figure 4a, yields Equation (A22).
- Exponentiating Equation (A22) finally derives the governing equation of the quasi-isentropic process Equation (31).
Nomenclature
| area | |
| crank radius | |
| cylinder bore | |
| heat capacity at constant pressure | |
| heat capacity at constant volume | |
| enthalpy | |
| connecting rod length | |
| mass | |
| pressure | |
| heat | |
| gas constant | |
| temperature | |
| , | internal energy |
| volume | |
| clearance volume | |
| pressure-volume work | |
| burned mass fraction | |
| Subscript | |
| initial value | |
| cylinder | |
| target zone | |
| surrounding zone | |
| unburned zone | |
| burned zone | |
| pre-unburned zone | |
| pre-burned zone | |
| reference condition before ignition | |
| characteristic condition after ignition | |
| combustion | |
| compression | |
| wall | |
| single-zone model | |
| conventional two-zone model | |
| novel two zone model | |
| Wiebe function | |
| Greek symbols | |
| crank angle | |
| angular velocity of crank angle | |
| fuel-air equivalence ratio | |
| heat capacity ratio | |
| vector of dependent state variables | |
| coefficient matrix | |
| coefficient vector | |
| eigenvalue | |
| coefficient | |
| Abbreviation | |
| AE | Algebraic Equation |
| BMEP | Brake Mean Effective Pressure |
| CO | Carbon Monoxide |
| HiL | Hardware in the Loop |
| IMEP | Indicated Mean Effective Pressure |
| NOx | Nitrogen Oxides |
| ODE | Ordinary Differential Equation |
| LHV | Lower Heating Value |
| Notation | |
| derivative of with respect to crank angle/time | |
| partial derivative of | |
| magnitude of | |
| inverse of matrix |
References
- Hatami, M.; Cuijpers, M.C.M.; Boot, M.D. Experimental optimization of the vanes geometry for a variable geometry turbocharger (VGT) using a Design of Experiment (DoE) approach. Energy Convers. Manag. 2015, 106, 1057–1070. [Google Scholar] [CrossRef]
- Abd-Alla, G.H. Using exhaust gas recirculation in internal combustion engines: A review. Energy Convers. Manag. 2002, 43, 1027–1042. [Google Scholar] [CrossRef]
- Gao, J.; Wu, Y.; Shen, T. On-line statistical combustion phase optimization and control of SI gasoline engines. Appl. Therm. Eng. 2017, 112, 1396–1407. [Google Scholar] [CrossRef]
- Finesso, R.; Spessa, E. A real time zero-dimensional diagnostic model for the calculation of in-cylinder temperatures, HRR and nitrogen oxides in diesel engines. Energy Convers. Manag. 2014, 79, 498–510. [Google Scholar] [CrossRef]
- Benajes, J.; García, A.; Monsalve-Serrano, J.; Martínez-Boggio, S. Optimization of the parallel and mild hybrid vehicle platforms operating under conventional and advanced combustion modes. Energy Convers. Manag. 2019, 190, 73–90. [Google Scholar] [CrossRef]
- Ngayihi Abbe, C.V.; Nzengwa, R.; Danwe, R.; Ayissi, Z.M.; Obonou, M. A study on the 0D phenomenological model for diesel engine simulation: Application to combustion of Neem methyl esther biodiesel. Energy Convers. Manag. 2015, 89, 568–576. [Google Scholar] [CrossRef]
- Rakopoulos, C.D.; Michos, C.N. Development and validation of a multi-zone combustion model for performance and nitric oxide formation in syngas fueled spark ignition engine. Energy Convers. Manag. 2008, 49, 2924–2938. [Google Scholar] [CrossRef]
- Nilsson, Y.; Eriksson, L. A New Formulation of Multi-Zone Combustion Engine Models. IFAC Proc. Vol. 2017, 34, 357–362. [Google Scholar] [CrossRef]
- Maroteaux, F.; Saad, C.; Aubertin, F. Development and validation of double and single Wiebe function for multi-injection mode Diesel engine combustion modelling for hardware-in-the-loop applications. Energy Convers. Manag. 2015, 105, 630–641. [Google Scholar] [CrossRef]
- Verhelst, S.; Sheppard, C.G.W. Multi-zone thermodynamic modelling of spark-ignition engine combustion—An overview. Energy Convers. Manag. 2009, 50, 1326–1335. [Google Scholar] [CrossRef]
- Maroteaux, F.; Saad, C. Combined mean value engine model and crank angle resolved in-cylinder modeling with NOx emissions model for real-time Diesel engine simulations at high engine speed. Energy 2015, 88, 515–527. [Google Scholar] [CrossRef]
- Neshat, E.; Honnery, D.; Saray, R.K. Multi-zone model for diesel engine simulation based on chemical kinetics mechanism. Appl. Therm. Eng. 2017, 121, 351–360. [Google Scholar] [CrossRef]
- Song, E.; Shi, X.; Yao, C.; Li, Y. Research on real-time simulation modelling of a diesel engine based on fuel inter-zone transfer and an array calculation method. Energy Convers. Manag. 2018, 178, 1–12. [Google Scholar] [CrossRef]
- Maroteaux, F.; Saad, C. Diesel engine combustion modeling for hardware in the loop applications: Effects of ignition delay time model. Energy 2013, 57, 641–652. [Google Scholar] [CrossRef]
- Gambarotta, A.; Lucchetti lng, G. Control-Oriented “Crank-Angle” Based Modeling of Automotive Engines. SAE Tech. Pap. Ser. 2011, 1, 16. [Google Scholar] [CrossRef]
- Corti, E.; Migliore, F.; Moro, D.; Capozzella, P.; Pagano, M. Development of a control-oriented model of engine, transmission and vehicle systems for motor scooter HIL testing. SAE Tech. Pap. 2009, 4970, 12. [Google Scholar] [CrossRef]
- D’Errico, G. Prediction of the combustion process and emission formation of a bi-fuel s.i. engine. Energy Convers. Manag. 2008, 49, 3116–3128. [Google Scholar] [CrossRef]
- Rakopoulos, C.D.; Rakopoulos, D.C.; Giakoumis, E.G.; Kyritsis, D.C. Validation and sensitivity analysis of a two zone Diesel engine model for combustion and emissions prediction. Energy Convers. Manag. 2004, 45, 1471–1495. [Google Scholar] [CrossRef]
- Savva, N.; Hountalas, D. Detailed evaluation of a new semi-empirical multi-zone NOx model by application on various diesel engine configurations. SAE Tech. Pap. 2012, 1–17. [Google Scholar] [CrossRef]
- Provataris, S.A.; Savva, N.S.; Chountalas, T.D.; Hountalas, D.T. Prediction of NOx emissions for high speed DI Diesel engines using a semi-empirical, two-zone model. Energy Convers. Manag. 2017, 153, 659–670. [Google Scholar] [CrossRef]
- Chindaprasert, N.; Hassel, E.; Nocke, J.; Janssen, C.; Schultalbers, M.; Magnor, O. Prediction of co emissions from a gasoline direct injection engine using chemkin®. SAE Tech. Pap. 2006. [Google Scholar] [CrossRef]
- Soylu, S. Prediction of knock limited operating conditions of a natural gas engine. Energy Convers. Manag. 2005, 46, 121–138. [Google Scholar] [CrossRef]
- Manivel, R.; Dhandapani, S. Two Zone Combustion Modelling of Two Stroke Spark Ignited Catalytic Engine. SAE Tech. Pap. 2001, 2001-Janua, 297–302. [Google Scholar] [CrossRef]
- Caton, J. An Introduction to Thermodynamic Cycle Simulations for Internal Combustion Engines; John Wiley & Sons, Ltd Registered: Hoboken, NJ, USA, 2016; ISBN 9781119037569. [Google Scholar]
- Ferguson, C.; Kirkpatrick, A. Internal Combustion Engines: Applied Thermosciences; John Wiley & Sons, Ltd Registered: Hoboken, NJ, USA, 2015; ISBN 978-1-118-53331-4. [Google Scholar]
- Lounici, M.S.; Loubar, K.; Balistrou, M.; Tazerout, M. Investigation on heat transfer evaluation for a more efficient two-zone combustion model in the case of natural gas SI engines. Appl. Therm. Eng. 2011, 31, 319–328. [Google Scholar] [CrossRef]
- Ashino, R.; Nagase, M.; Vaillancourt, R. Behind and Beyond the MATLAB ODE Suite. Comput. Math. Appl. 2000, 40, 491–512. [Google Scholar] [CrossRef]
- Spijker, M.N. Stiffness in numerical initial-value problems. J. Comput. Appl. Math. 1996, 72, 393–406. [Google Scholar] [CrossRef]
- de Faria, M.M.N.; Vargas Machuca Bueno, J.P.; Ayad, S.M.M.E.; Belchior, C.R.P. Thermodynamic simulation model for predicting the performance of spark ignition engines using biogas as fuel. Energy Convers. Manag. 2017, 149, 1096–1108. [Google Scholar] [CrossRef]
- Nefischer, A.; Neumann, J.; Stanciu, A.; Wimmer, A. Quasi-dimensional modelling of turbulence-driven phenomena in SI engines. Int. J. Veh. Des. 2014, 66, 297. [Google Scholar] [CrossRef]
- Rakopoulos, C.D.; Michos, C.N. Quasi-dimensional, multi-zone combustion modelling of turbulent entrainment and flame stretch for a spark ignition engine fuelled with hydrogen-enriched biogas. Int. J. Veh. Des. 2009, 49, 3. [Google Scholar] [CrossRef]
- Rakopoulos, C.D.; Hountalas, D.T.; Tzanos, E.I.; Taklis, G.N. A fast algorithm for calculating the composition of diesel combustion products using 11 species chemical equilibrium scheme. Adv. Eng. Softw. 1994, 19, 109–119. [Google Scholar] [CrossRef]
- Mcbride, B.; Gordon, S.; Reno, M. Coefficients for Calculating Thermodynamic and Transport Properties of Individual Species. Nasa Tech. Memo. 1993, 4513, 98. [Google Scholar]
- Depcik, C.; Jacobs, T.; Hagena, J.; Assanis, D. Instructional use of a single-zone, premixed charge, spark-ignition engine heat release simulation. Int. J. Mech. Eng. Educ. 2007, 35, 1–31. [Google Scholar] [CrossRef]

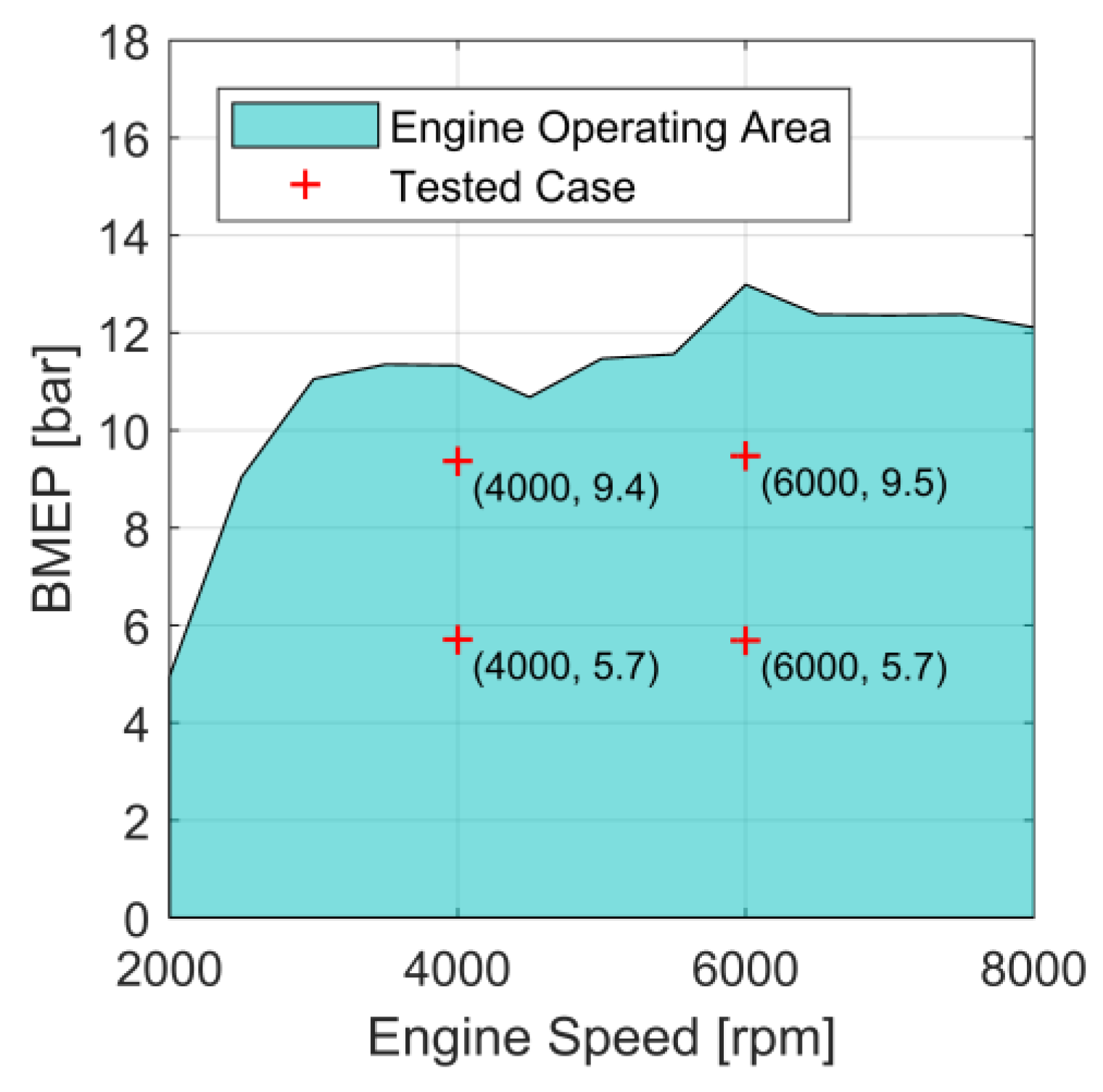



| Engine feature | Twin-cylinder 4-stroke engine, 4 valves operated by rocker arm, liquid cooling, integrated coolant pump, dry-sump lubrication |
| Displacement | 798 [cm3] |
| Cylinder bore | 82 [mm] |
| Piston stroke | 75.6 [mm] |
| Compression ratio | 12: 1 |
| Nominal output | 66 [kW], —at engine speed: 8000 [rpm] |
| Torque | 86 [Nm], —at engine speed: 5800 [rpm] |
| Maximum engine speed | 9000 [rpm] |
| Idle speed | 1250 [rpm] |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y. A Novel Two-Zone Thermodynamic Model for Spark-Ignition Engines Based on an Idealized Thermodynamic Process. Energies 2020, 13, 3801. https://doi.org/10.3390/en13153801
Wang Y. A Novel Two-Zone Thermodynamic Model for Spark-Ignition Engines Based on an Idealized Thermodynamic Process. Energies. 2020; 13(15):3801. https://doi.org/10.3390/en13153801
Chicago/Turabian StyleWang, Yuanfeng. 2020. "A Novel Two-Zone Thermodynamic Model for Spark-Ignition Engines Based on an Idealized Thermodynamic Process" Energies 13, no. 15: 3801. https://doi.org/10.3390/en13153801
APA StyleWang, Y. (2020). A Novel Two-Zone Thermodynamic Model for Spark-Ignition Engines Based on an Idealized Thermodynamic Process. Energies, 13(15), 3801. https://doi.org/10.3390/en13153801




