An Efficient Robust Predictive Control of Main Steam Temperature of Coal-Fired Power Plant
Abstract
:1. Introduction
- The excessively high MST results in serious damage of the superheater and inlet pipe of turbine;
- The excessively low MST decreases the net efficiency of power plant, and moreover, the steam in the last stage of the low pressure turbine may become wet under low MST condition, which endangers the turbine blades;
- The frequent temperature fluctuation worsens the heat exchanging in superheater and increases thermal stress of the superheater and turbine cylinder, which will bring material damage to the plant.
- Numerical optimization problem must be solved at each sampling interval; the online computational effort of these control algorithms is too heavy;
- MST system is operated under complicated working circumstance, such as aging of equipment, complicated combustion process involved in boiler and unpredictable disturbance, however, the robustness of control strategies is rarely involved in the control design.
- An improved offline RMPC approach is proposed by introducing two extra parameters for a better convergence of the recursive algorithm;
- A manipulated variable target observer is developed based on the center parameter of zonotope-type prediction model, which can help the RMPC achieve an offset-free control of the MST.
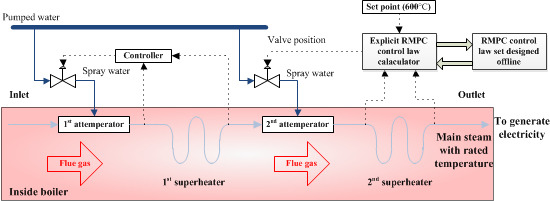
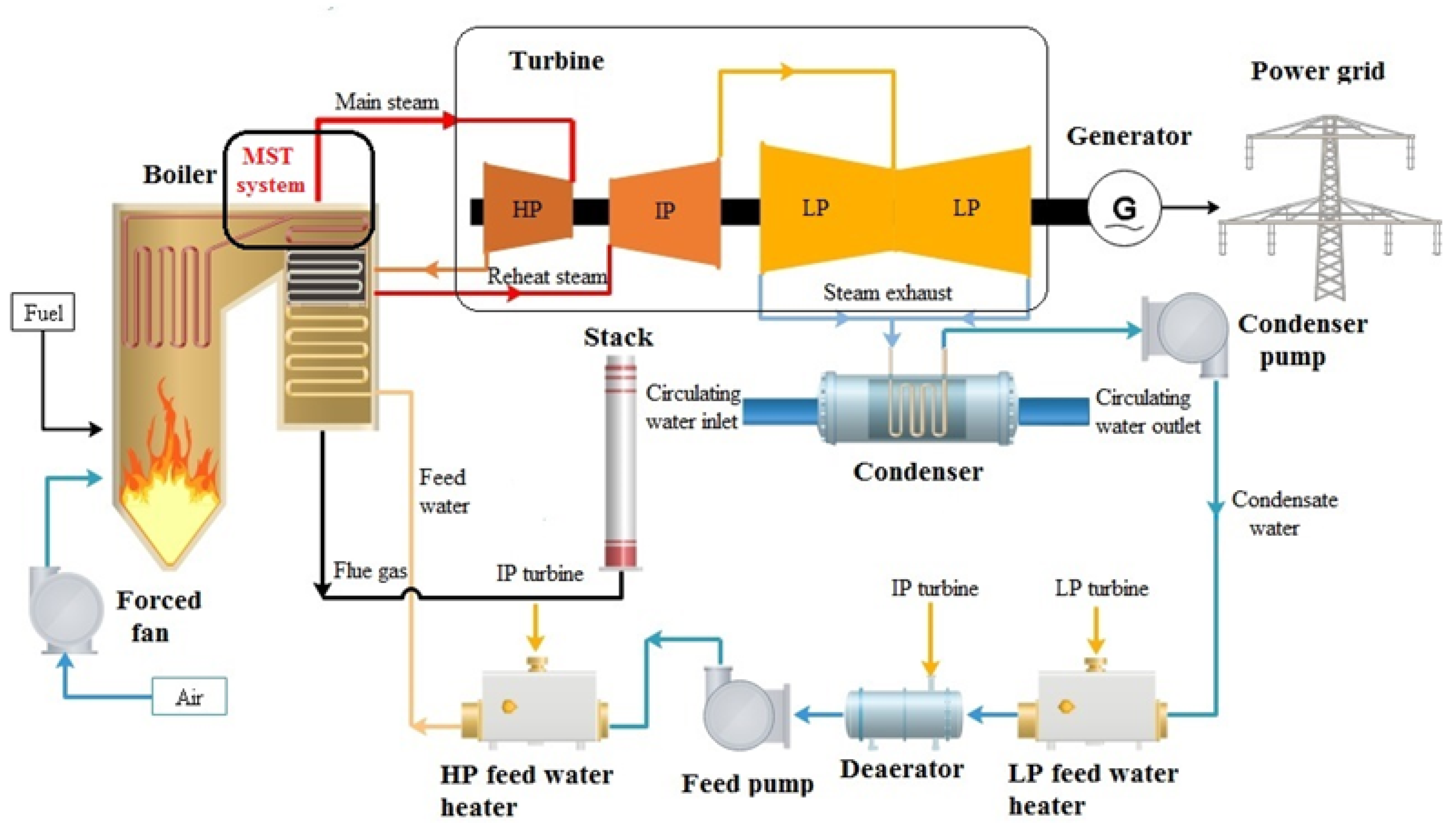
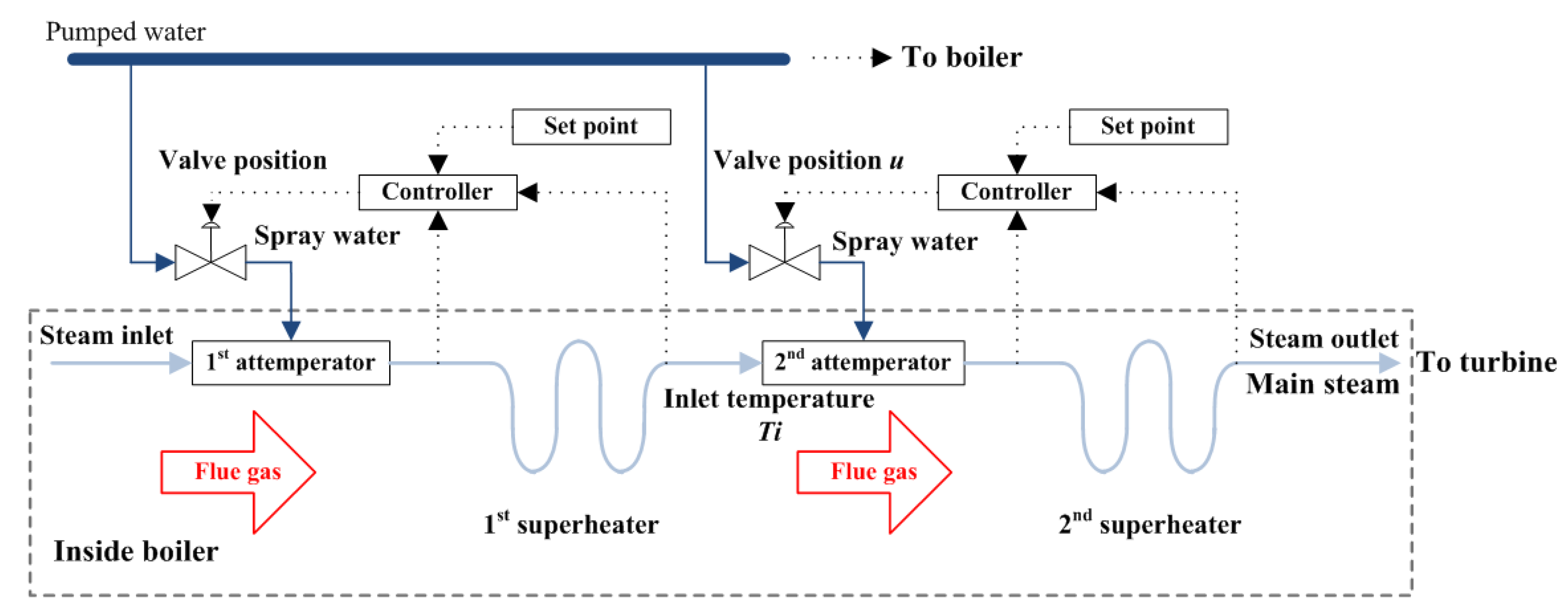
2. Main Steam Temperature System
2.1. System Description
2.2. Simulation Model
3. Problem Formulation
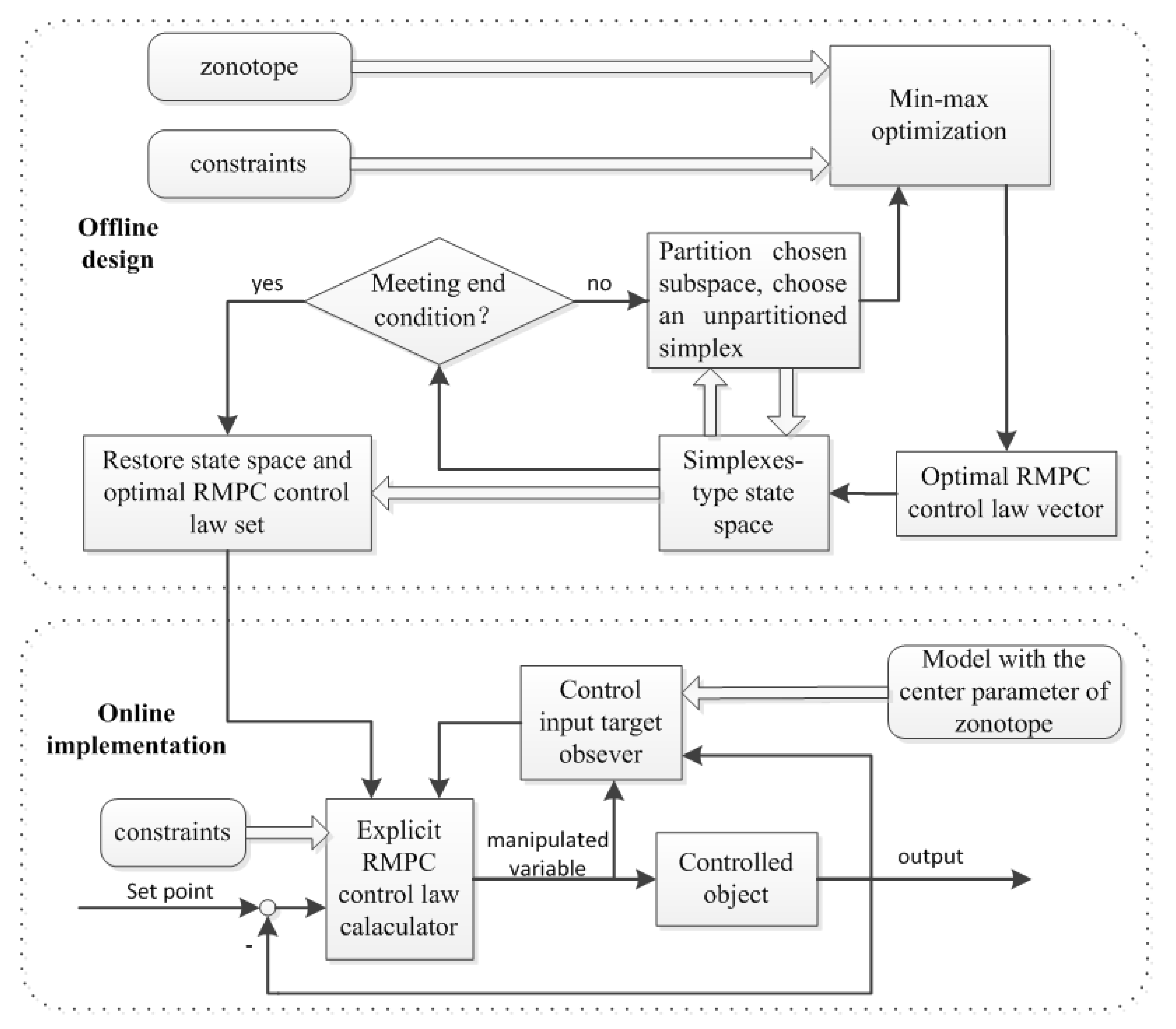
4. An Improved Offline Robust Model Predictive Control Approach for MST System
4.1. The Offline Design for RMPC Control Law
- Partition into several simplexes , applying Delaunay triangulation [37], i.e., , calculate and store respectively and at simplexes vertexes state points via (10), build , preset threshold , and , let ;
- If , select the current simplex and turn to Step 3; if , algorithm ends, return and , h is size of well-partitioned space ;
- Compare the size of and conditional number of , if , delete , , and turn to Step 2; if , turn to Step 4;
- Obtain , , and via (19), if , , and turn to Step 2; if , replace the vertexes of with in sequence yielding new simplex, add them to , and delete , , turn to Step 5;
- Determine whether the longest side is times longer than the shortest side, if not, turn to Step 2; if yes, take the midpoint of the longest side as a new point , calculate and , two end points of the longest side are replaced with in sequence, then two simplexes yield, delete , , turn to Step 2.
4.2. The Online Implementation for Offline Designed RMPC Control Law
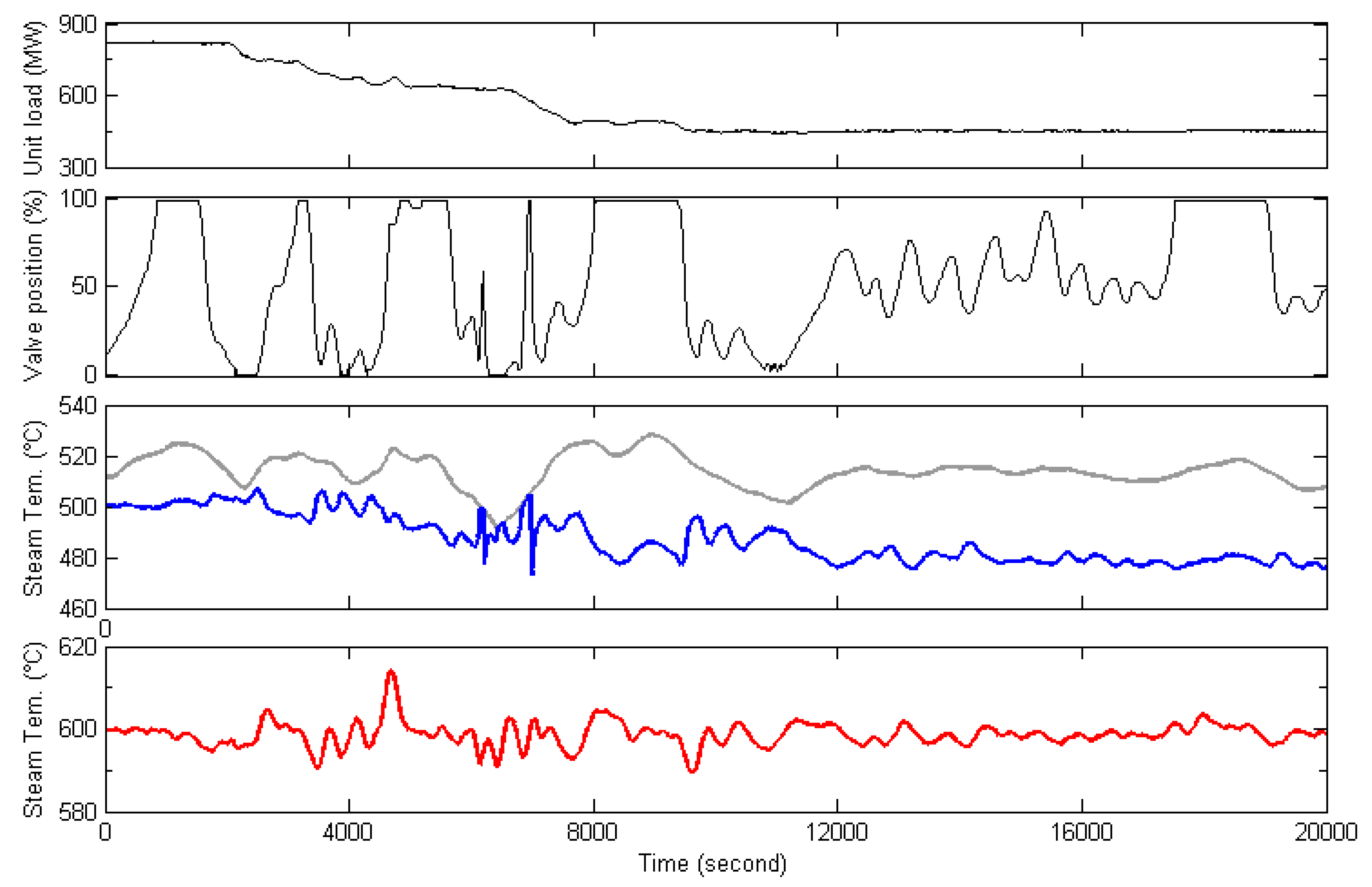
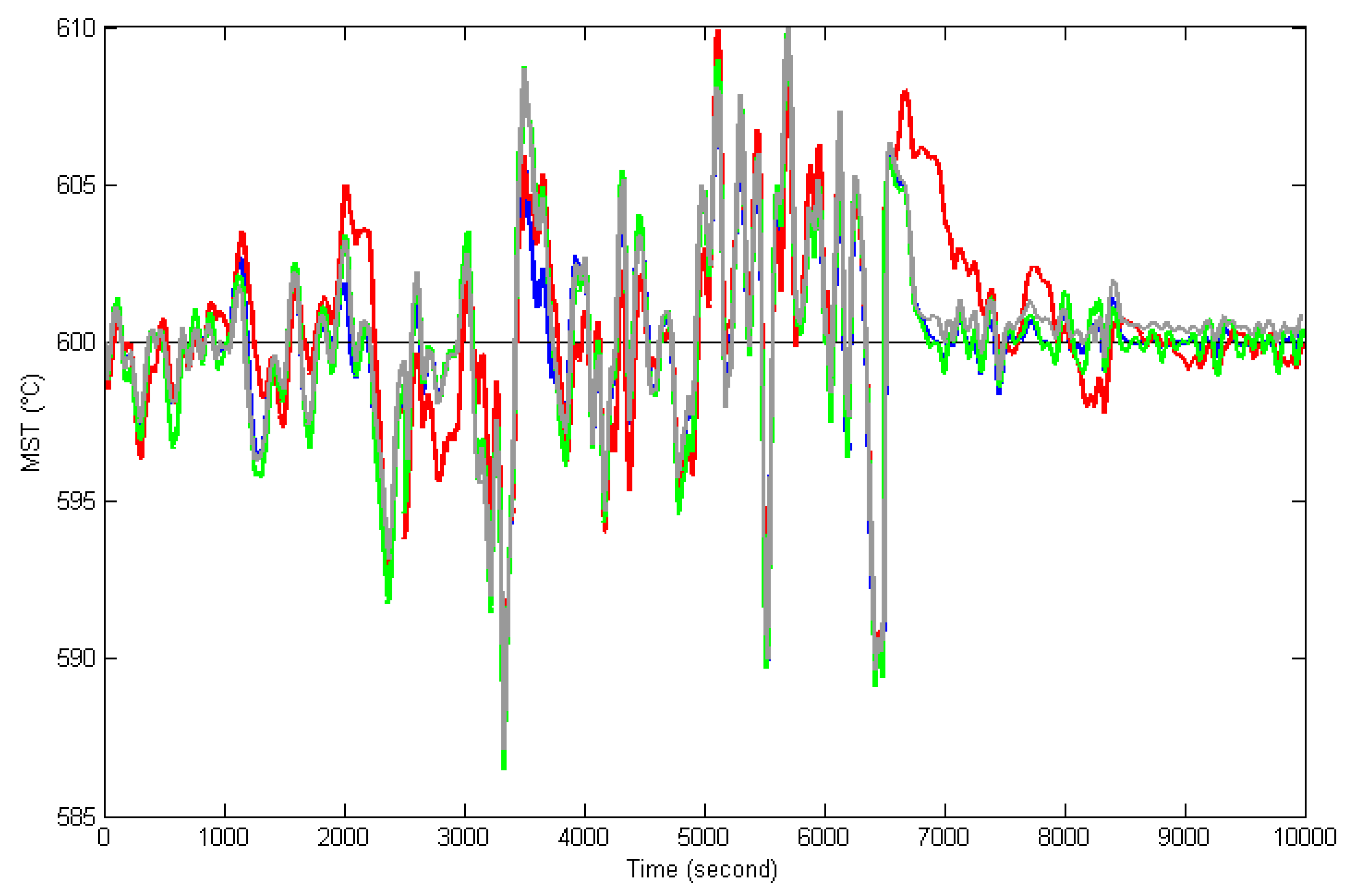
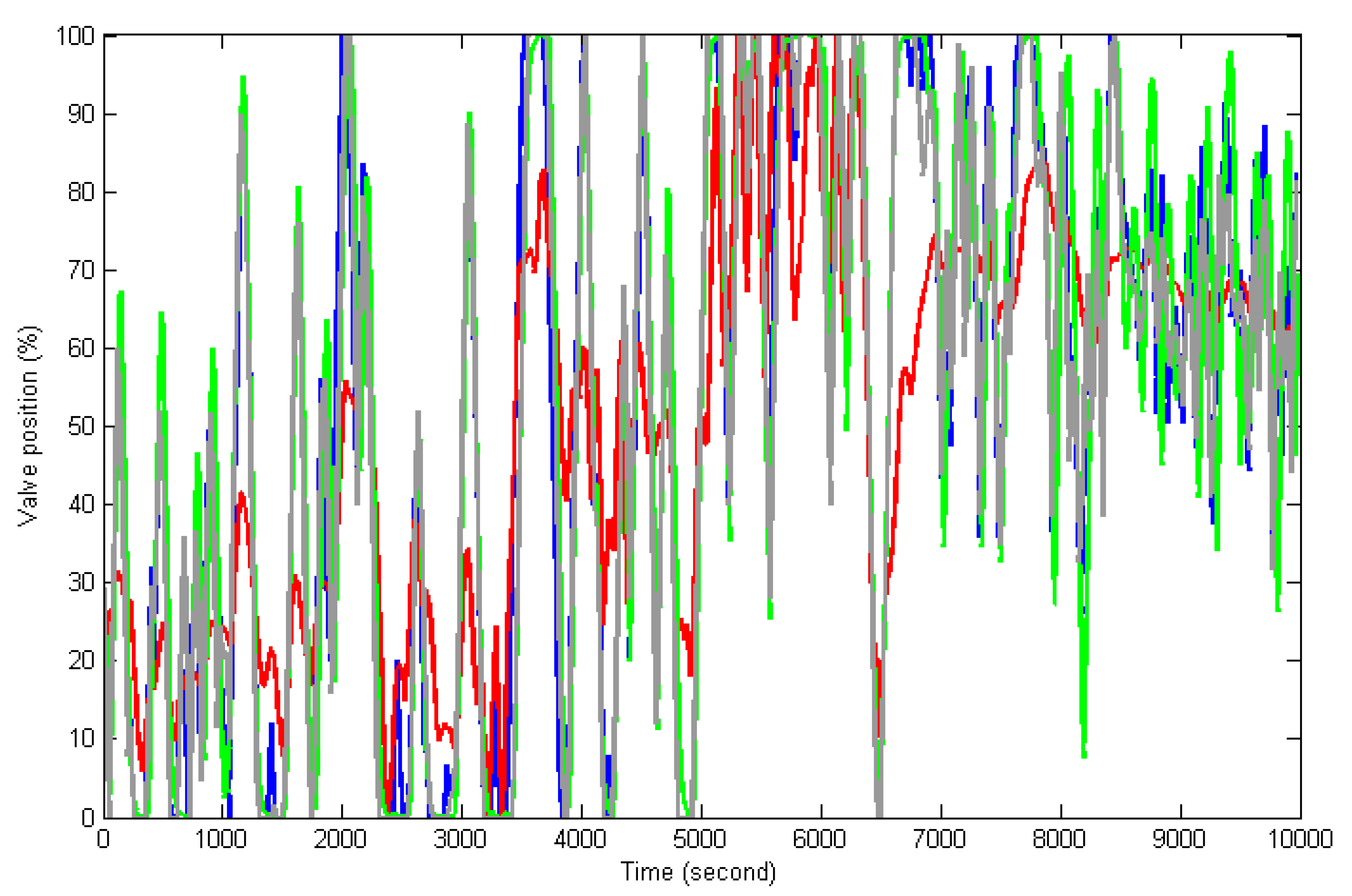
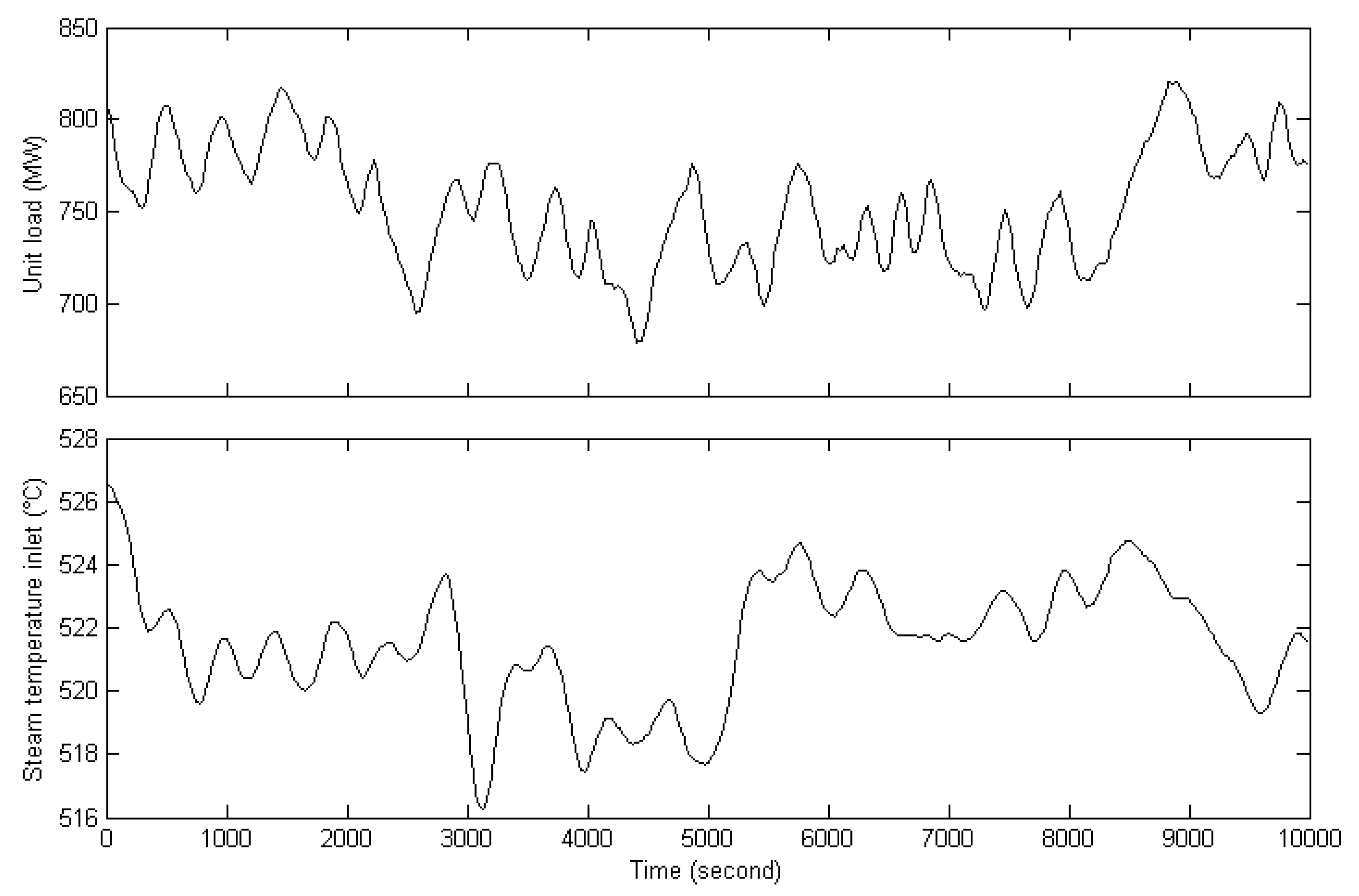
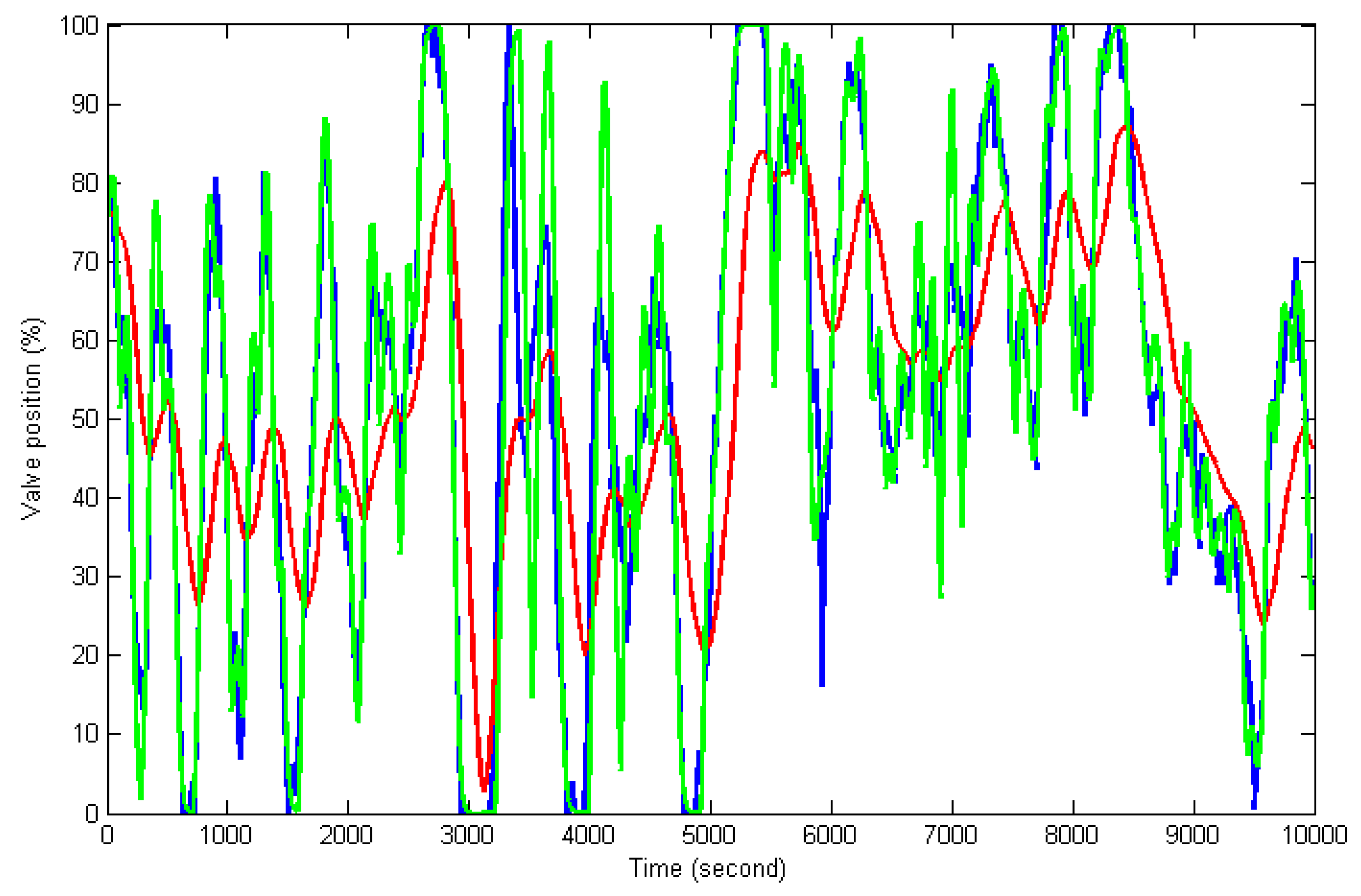
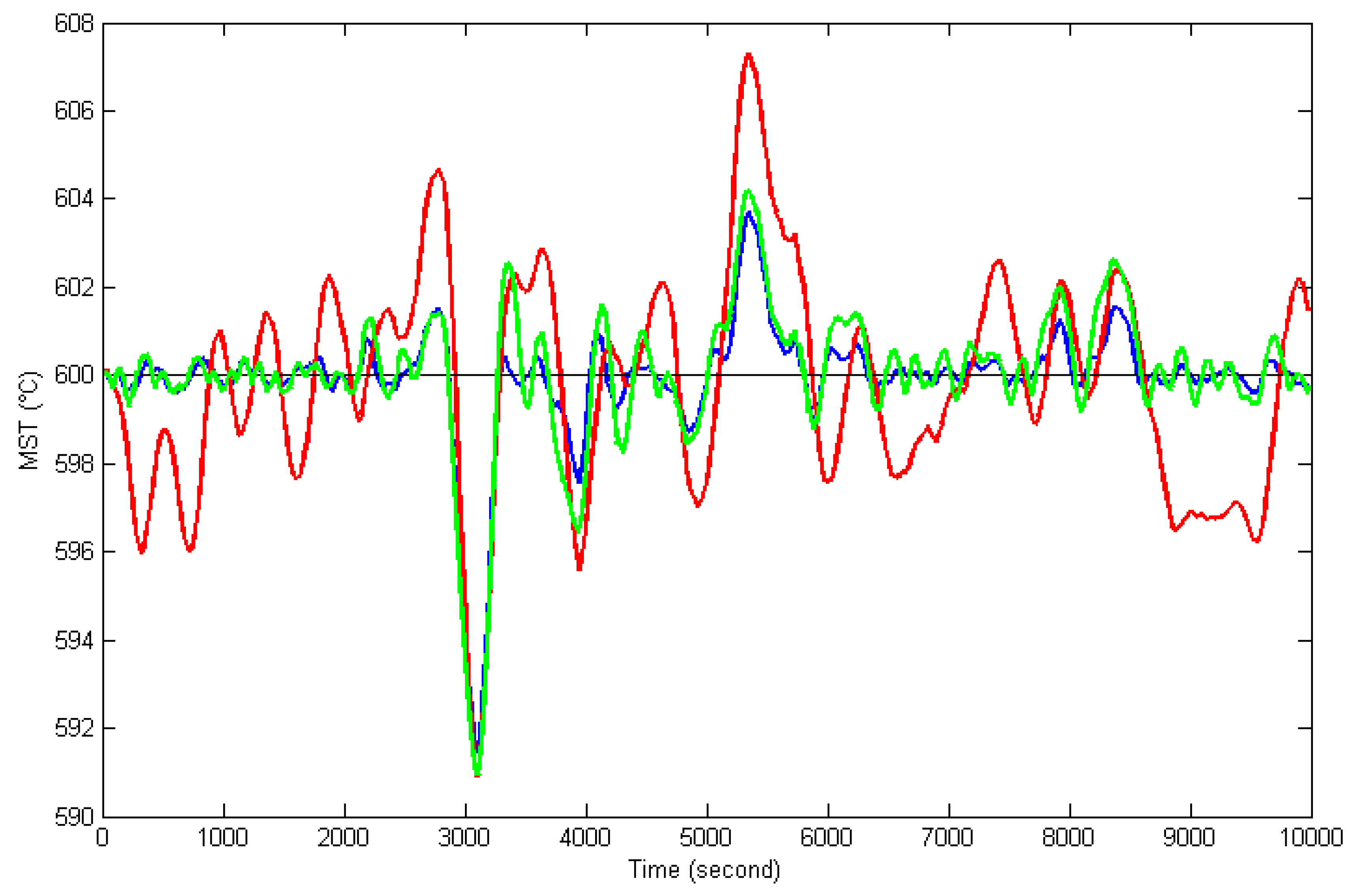
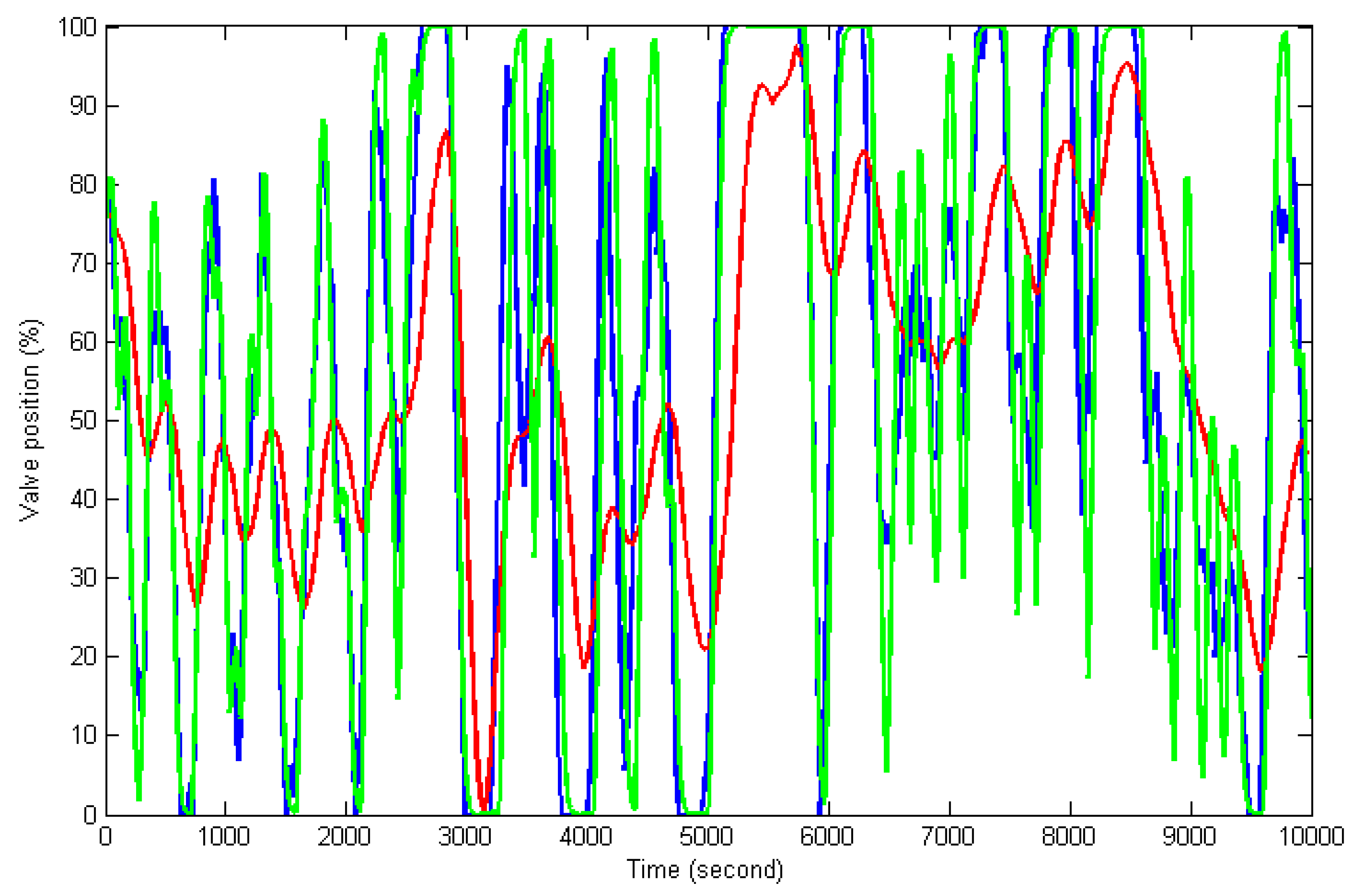
5. Simulation Results
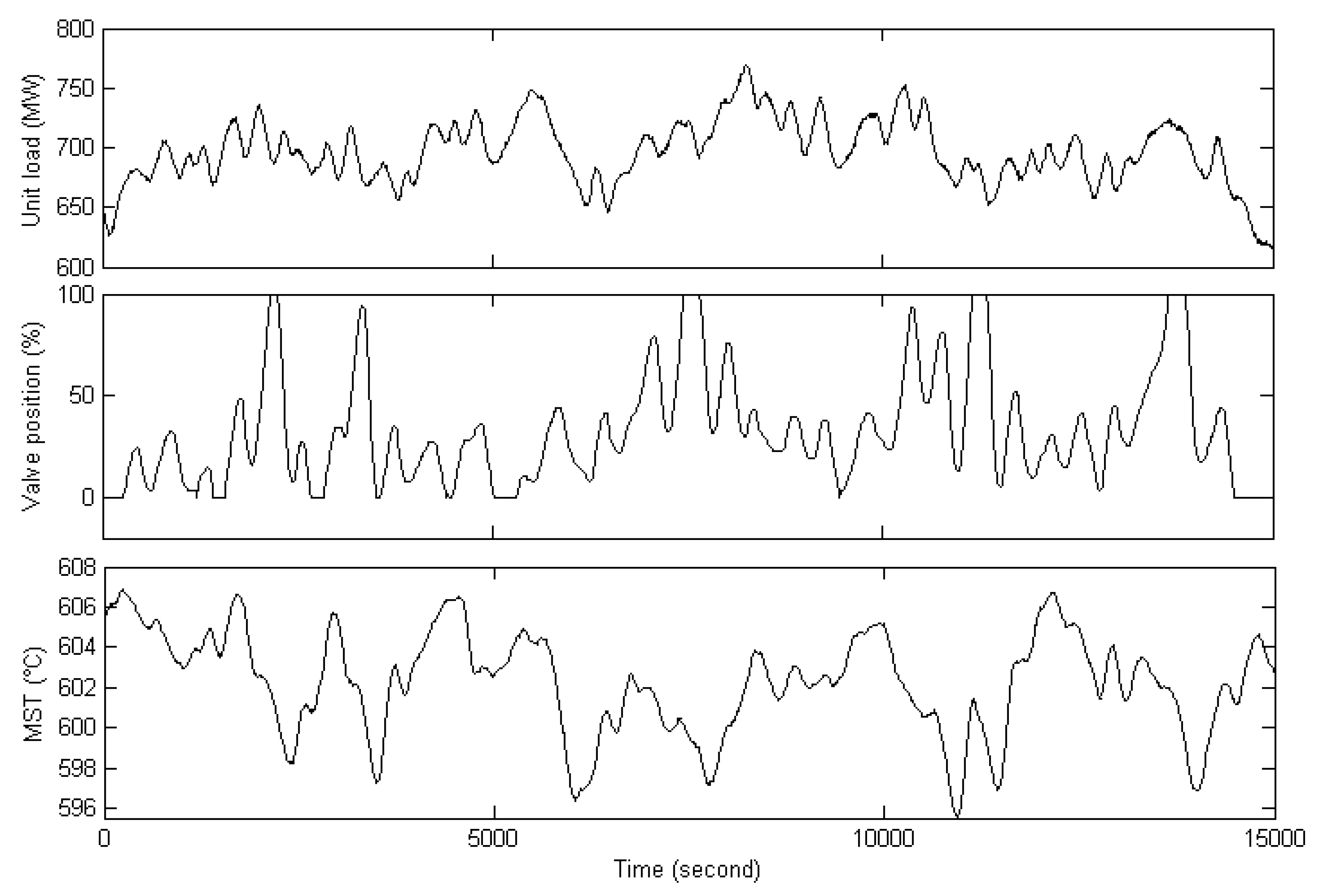
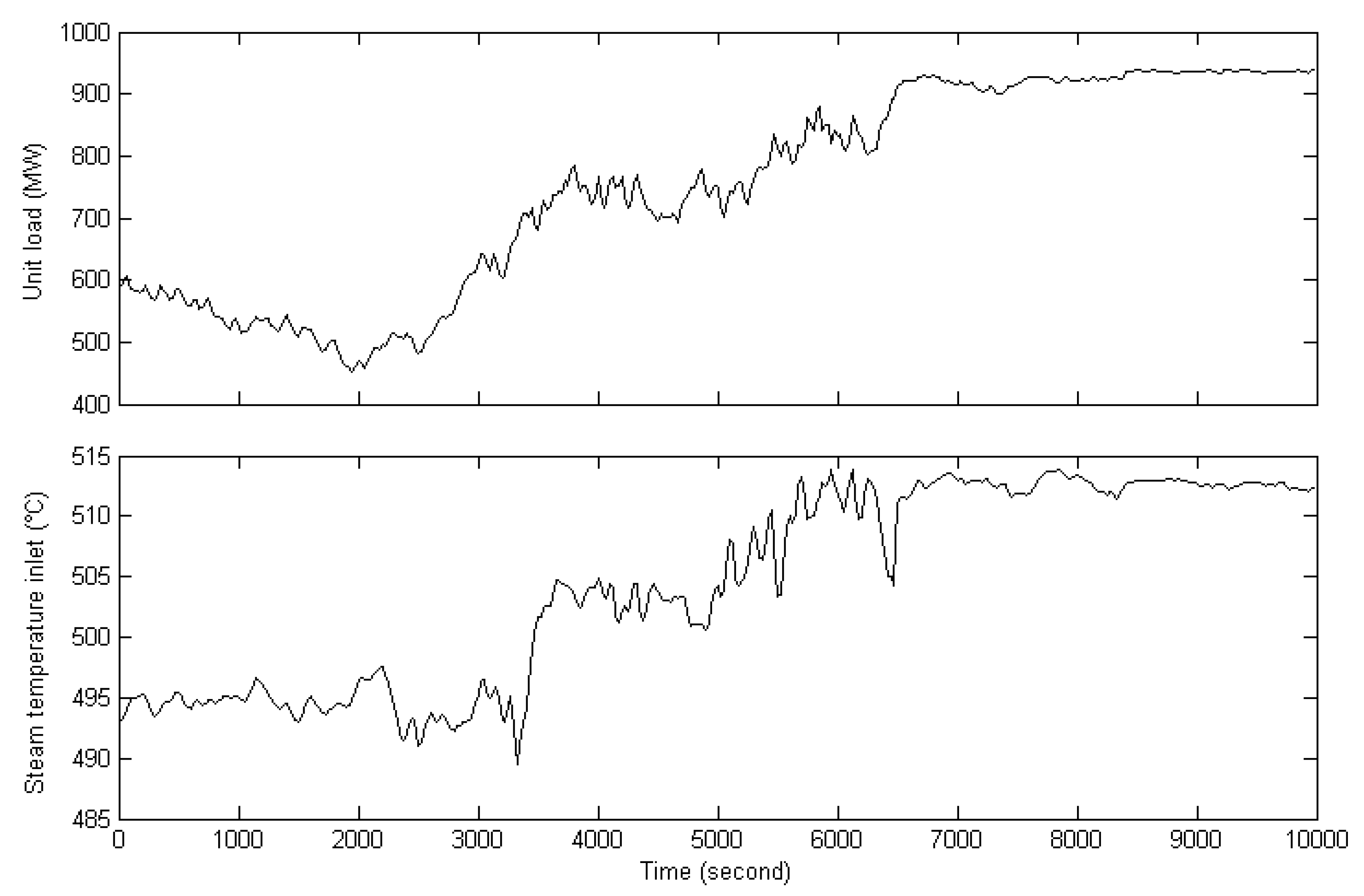
5.1. Establishment of the Zonotope-Type Uncertain Model for MST System
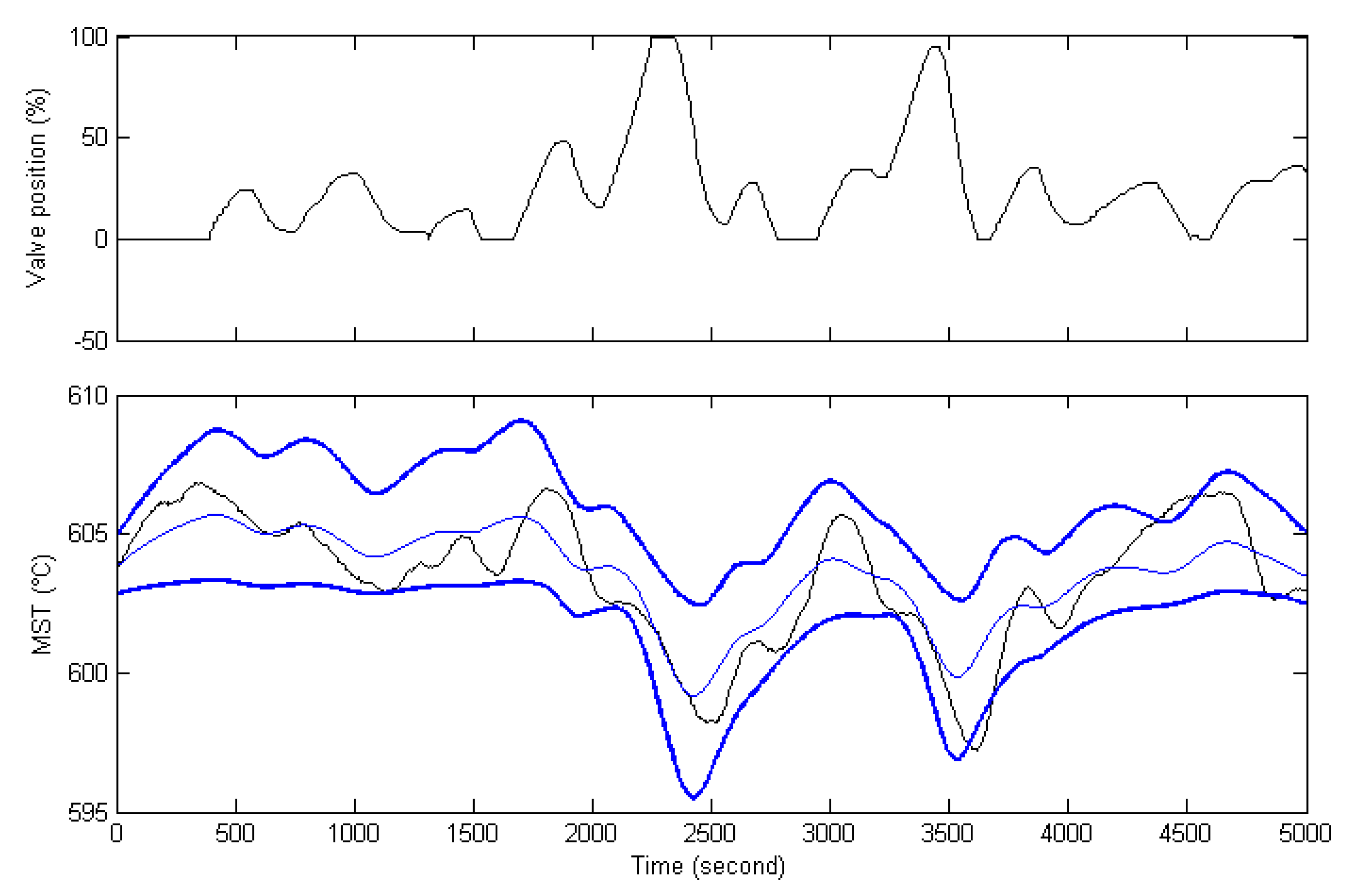
5.2. Control Simulation for MST System
- the proposed OFAERMPC;
- incremental model predictive controller (IMPC) based on the nominal model of the identified zonotope (29) with weighting coefficients and , control horizon 5, prediction horizon 500 and sampling interval = 5 s;
- digital PI controller with proportional coefficient 5.26 and integral time 292.22 (design by matlab PID controller tuning modular);
- standard AEMPC.
6. Conclusions
- In the offline design stage, an explicit RMPC control law design method with improved convergence is proposed by introducing two extra parameters;
- Based on the nominal model of zonotope, a manipulated variable target observer is developed to make control results no offset exists.
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| AEMPC | Approximated explicit model predictive control |
| CFPP | Coal-fired power plant |
| MIMO | Multiple inputs multiple outputs |
| MPC | Model predictive control |
| MST | Main steam temperature |
| NN | Neural network |
| OFAERMPC | Offset-free approximated explicit robust model predictive control |
| PWA | Piecewise affine |
| PID | Proportion integration differentiation |
| RMPC | Robust model predictive control |
| SISO | Single input single output |
| SMI | Set membership identification |
References
- China Electricity Council. Letters of Chinese Electricity Power Statistics in 2018; China National Energy Administration: Beijing, China, 2018. (In Chinese)
- Wu, X.; Shen, J.; Li, Y.; Lee, K.Y. Fuzzy modeling and predictive control of superheater steam temperature for power plant. ISA Trans. 2015, 56, 241–251. [Google Scholar] [CrossRef] [PubMed]
- Song, X.; Liu, C.; Song, Z.; Song, X. Robust PID control for Steam superheater. In Proceedings of the Third International Conference on Machine Learning and Cybernetics, Shanghai, China, 26–29 August 2004; pp. 988–991. [Google Scholar]
- Kim, H.; Kim, E.; Kim, J.; Lee, K.; Kim, S.; Han, Y. Prediction-based feedforward control of superheated steam temperature of a power plant. Electr. Power Energy Syst. 2015, 71, 351–357. [Google Scholar] [CrossRef]
- Hlava, J.; Opalka, J.; Johansen, A. Model predictive control of power plant superheater - comparison of multi model and nonlinear approaches. In Proceedings of the 2013 18th International Conference on Methods in Automation & Robotics, Miedzyzdroje, Poland, 27–29 August 2013; pp. 311–316. [Google Scholar]
- Wang, G.; Yan, W.; Chen, S.; Zhang, X.; Shao, H. Multivariable constrained predictive control of main steam temperature in ultra-supercritical coal-fired power unit. J. Energy Inst. 2015, 88, 181–187. [Google Scholar] [CrossRef]
- Liang, W.; Wang, W.; Zhang, X. Fuzzy-PID control system of main steam temperature based on intermediate point temperature feedforward. Electr. Power Sci. Eng. 2019, 35, 72–78. [Google Scholar]
- Valsalam, R.; Snish, S.; Singh, R. Boiler Modelling and Optimal Control of Steam Temperature in Power Plants. IFAC Proc. Vol. 2009, 42, 125–130. [Google Scholar] [CrossRef]
- Ma, L.; Lin, Y.; Lee, K.Y. Superheater steam temperature control for a 300 MW boiler unit with inverse dynamic process models. In Proceedings of the IEEE PES General Meeting, Providence, RI, USA, 25–29 July 2010; pp. 1–6. [Google Scholar]
- Ma, L.; Lee, K.Y.; Ge, Y. An improved predictive optimal controller with elastic search space for steam temperature control of large-scale supercritical power unit. In Proceedings of the 51st IEEE Conference on Decision and Control, Maui, HI, USA, 10–13 December 2012; pp. 2024–2029. [Google Scholar]
- Mayne, D.Q.; Rawlings, J.B.; Rao, C.V.; Scokaert, P.O. Constrained model predictive control: Stability and optimality. Automatica 2000, 36, 789–814. [Google Scholar] [CrossRef]
- Mayne, D.Q. Model predictive control: Recent developments and future promise. Automatica 2014, 50, 2967–2986. [Google Scholar] [CrossRef]
- Hu, H.; Zhang, J.; Yang, Q. Dynamic matrix control for main steam temperature control system based on optimal state estimation. Control Decis. 2019, 34, 1475–1480. [Google Scholar]
- Hlava, J. Model predictive control of the superheater temperature based on a piecewise affine model. In Proceedings of the UKACC International Conference on Control 2010, Coventry, UK, 7–10 September 2010; pp. 423–428. [Google Scholar]
- Zhao, H.; Shen, J.; Shen, D.; Li, Y. Multiple model disturbance rejection predictive control of main steam temperature. Proc. CSEE 2014, 32, 5763–5770. [Google Scholar]
- Van Overschee, P.; De Moor, B. N4SID: Subspace algorithms for the identification of combined deterministic stochastic systems. Automatica 1994, 30, 75–93. [Google Scholar] [CrossRef]
- Vuolo, F.; Ng, W.; Atzberger, C. Smoothing and gap-filling of high resolution muti-spectral time series: Example of Landsat data. Int. J. Appl. Earth Obs. Geoinf. 2017, 57, 202–213. [Google Scholar] [CrossRef]
- Kim, J.; Ryu, J. A heuristic gap filling method for daily precipition series. Water Recour Manag. 2016, 30, 2275–2294. [Google Scholar] [CrossRef]
- Shary, S. Maximum consistency method for data fitting under interval uncertainty. J. Glob. Optim. 2016, 66, 111–126. [Google Scholar] [CrossRef]
- Duan, Y.; Wang, Q.; Liao, Y.; Wei, L. Exploration on fitting function in data processing of physical chemistry experiments. J. Cap. Norm. Univ. 2019, 40, 33–36. [Google Scholar]
- Vera-Sanchez, J.; Ruiz-Morales, C.; Gonzalez-Lopez, A. Monte Carlo uncertainty analysis of dose estimates in radiochromic film dosimetry with single-channel and multichannel algorithms. Phys. Medica 2018, 47, 23–33. [Google Scholar] [CrossRef]
- Castro, E.; Ahnert, C.; Buss, O.; Garacia-Herranz, N.; Hoefer, A.; Porsch, D. Improving PWR core simulations by Monte Carlo uncertainty analysis and Bayesian inference. Ann. Nucl. Energy 2016, 95, 148–156. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Li, Y.; Huang, G.; Baetz, B.; Liu, J. Uncertainty analysis for effluent trading planning using a Bayesian estimation-based simulation modelling approach. Water Res. 2017, 116, 159–181. [Google Scholar] [CrossRef]
- Liu, J.; Zeng, X.; Wu, J.; Liang, X.; Sun, Y.; Zhan, H. Assessing titanium dioxide nanoparticles transport models by Bayesian uncertainty analysis. Stoch. Environ. Res. Risk Assess. 2018, 32, 3365–3379. [Google Scholar] [CrossRef]
- Milanese, M.; Taragna, M. H infinity set membership identification: A survey. Atomatica 2005, 41, 2019–2032. [Google Scholar] [CrossRef]
- Cerone, V.; Piga, D.; Regruto, D. Set-membership error-in-variables identification through convex relaxation techniques. IEEE Trans. Autom. Control 2012, 57, 517–522. [Google Scholar] [CrossRef]
- Zhou, B.; Qian, K.; Ma, X.; Dai, X. Ellipsoidal bounding set-membership identification approach for robust fault diagnosis with application to mobile robots. J. Syst. Eng. Electron. 2017, 28, 986–995. [Google Scholar] [CrossRef]
- Reppa, V.; Tzse, A. Fault diagnosis based on set membership identification using output-error models. Int. J. Adapt. Control Signal Process. 2016, 30, 224–255. [Google Scholar] [CrossRef]
- Scott, J.; Raimaondo, D.; Marseglia, G.; Braatz, R. Constrained zonotopes: A new tool for set-based estimation and fault detection. Automatica 2016, 69, 126–136. [Google Scholar] [CrossRef]
- Alamo, T.; Bravo, J.; Camacho, E. Guaranteed state estimation by zonotopes. Automatica 2006, 41, 1035–1043. [Google Scholar] [CrossRef]
- Wang, D.; Wu, X.; Pan, L.; Shen, J.; Lee, K.Y. A novel zonotope-based set-membership identification approach for uncertain system. In Proceedings of the 2017 IEEE Conference on Control Technology and Applications, Kohala Coast, HI, USA, 27–30 August 2017; pp. 1420–1425.
- Kothare, M.V.; Balakrishnan, V.; Morari, M. Robust constrained model predictive control using linear matrix inequalities. Automatica 1996, 32, 1361–1379. [Google Scholar] [CrossRef] [Green Version]
- Sartipizzadeh, H.; Vincent, T. A new robust MPC using an approximate convex hull. Automatica 2018, 92, 115–122. [Google Scholar] [CrossRef]
- Bemporad, A.; Filippi, C. An algorithm for approximate multiparametric convex programming. Comput. Optim. Appl. 2006, 35, 87–108. [Google Scholar] [CrossRef]
- Pluymers, B.; Suykens, J.A.; Moor, B.D. Min-max feedback MPC using a time-varying terminal constraint set and comments on “Efficient robust constrained model predictive control with a time-varying terminal constraint set”. Syst. Control Lett. 2005, 54, 1143–1148. [Google Scholar] [CrossRef]
- Wu, Q.; Xi, Y.; Nagy, Z.; Li, D. A real-time optimization framework for the time-varying economic environment. Comput. Chem. Eng. 2018, 115, 333–341. [Google Scholar] [CrossRef]
- Feng, L.; Alliez, P.; Buse, L.; Delingette, H.; Desbrun, M. Curved optimal Delaunay triangulation. Acm Trans. Graph. 2018, 37, 61.1–61.16. [Google Scholar] [CrossRef] [Green Version]
- Zhu, Y.; Butoyi, F. Case studies on closed-loop identification for MPC. Control Eng. Pract. 2002, 10, 404–417. [Google Scholar] [CrossRef]
- Soderstrom, T.; Stoica, P. System Identification; Prentice-Hall: London, UK, 1989. [Google Scholar]
- Lofberg, J. Yalmip: A toolbox for modelling and optimization in Matlab. In Proceedings of the 2004 IEEE International Conference on Robotics and Automation, New Orleans, LA, USA, 2–4 September 2004; pp. 284–289. [Google Scholar]


| Order of pre-estimation model | 8 |
| Error bound to be restrained | 1.76 |
| Weighting ratio | 50 |
| Computation Time | Number of Subspaces | |
|---|---|---|
| Standard AEMPC | 3619 s | 1914 |
| OFAERMPC | 170 s | 108 |
| PI | IMPC | OLRMPC | OFAERMPC | |
|---|---|---|---|---|
| Performance index | 10.04 | 9.32 | 8.80 | 8.10 |
| Total Simulation time | 0.24 | 11.94 | 8.74 | 0.96 |
| PI | IMPC | OFAERMPC | |
|---|---|---|---|
| Performance index | 5.05 | 0.71 | 0.55 |
| Total Simulation time | 0.22 | 0.05 | 0.98 |
| PI | IMPC | OFAERMPC | |
|---|---|---|---|
| Performance index (unchanged behavior) | 5.36 | 0.88 | 0.68 |
| Performance index (changed behavior) | 7.17 | 3.32 | 2.28 |
| Total Simulation time | 0.23 | 10.36 | 0.98 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, D.; Wu, X.; Shen, J. An Efficient Robust Predictive Control of Main Steam Temperature of Coal-Fired Power Plant. Energies 2020, 13, 3775. https://doi.org/10.3390/en13153775
Wang D, Wu X, Shen J. An Efficient Robust Predictive Control of Main Steam Temperature of Coal-Fired Power Plant. Energies. 2020; 13(15):3775. https://doi.org/10.3390/en13153775
Chicago/Turabian StyleWang, Di, Xiao Wu, and Jiong Shen. 2020. "An Efficient Robust Predictive Control of Main Steam Temperature of Coal-Fired Power Plant" Energies 13, no. 15: 3775. https://doi.org/10.3390/en13153775
APA StyleWang, D., Wu, X., & Shen, J. (2020). An Efficient Robust Predictive Control of Main Steam Temperature of Coal-Fired Power Plant. Energies, 13(15), 3775. https://doi.org/10.3390/en13153775