A Novel Probabilistic Power Flow Algorithm Based on Principal Component Analysis and High-Dimensional Model Representation Techniques
Abstract
1. Introduction
2. Methodology
2.1. Problem Formation
2.2. Principal Component Analysis
2.3. High-Dimensional Model Representation
3. Solution Procedure
4. Case Study
4.1. IEEE-30 Test System
4.2. Sensitivity to Correlations
4.3. IEEE-118 Test System
5. Discussions
5.1. Non-Linear Dependency
5.2. Probability Distribution Approximation
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Borkowska, B. Probabilistic load flow. IEEE Trans. Power Appar Syst. 1974, 93, 752–759. [Google Scholar] [CrossRef]
- Henneaux, P.; Daniel, S. Probabilistic security analysis of optimal transmission switching. IEEE Trans. Power Syst. 2015, 31, 508–517. [Google Scholar] [CrossRef]
- Wang, Z.; Shen, C.; Liu, F.; W, X.; Liu, C.; Gao, F. Chance-constrained economic dispatch with non-Gaussian correlated wind power uncertainty. IEEE Trans. Power Syst. 2017, 32, 4880–4893. [Google Scholar] [CrossRef]
- Prusty, B.R.; Jena, D. A critical review on probabilistic load flow studies in uncertainty constrained power systems with photovoltaic generation and a new approach. Renew. Sustain. Energy Rev. 2017, 69, 1286–1302. [Google Scholar] [CrossRef]
- Wu, W.; Wang, K.; Li, G.; Jiang, X.; Feng, L.; Crow, M. A multivariate dimension-reduction method for probabilistic power flow calculation. Electr. Power Syst. Res. 2016, 141, 272–280. [Google Scholar] [CrossRef]
- Cai, D.; Shi, D.; Chen, J. Probabilistic load flow with correlated input random variables using uniform design sampling. Int. J. Electr. Power Energy Syst. 2014, 63, 105–112. [Google Scholar] [CrossRef]
- Chen, Y.; Wen, J.; Cheng, S. Probabilistic load flow method based on Nataf transformation and Latin hypercube sampling. IEEE Trans. Sustain. Energy 2012, 4, 294–301. [Google Scholar] [CrossRef]
- Zhang, L.; Cheng, H.; Zhang, S.; Zeng, P.; Yao, L. Probabilistic power flow calculation using the Johnson system and Sobol’s quasi-random numbers. IET Gener. Transm. Distrib. 2016, 10, 3050–3059. [Google Scholar] [CrossRef]
- Allan, R.N.; Al-Shakarchi, M. Probabilistic a.c. load flow. Proc. IEE 1976, 123, 531–536. [Google Scholar] [CrossRef]
- Zhang, P.; Stephen, T. Probabilistic load flow computation using the method of combined cumulants and Gram-Charlier expansion. IEEE Trans. Power Syst. 2004, 19, 676–682. [Google Scholar] [CrossRef]
- Usaola, J. Probabilistic load flow with correlated wind power injections. Electr. Power Syst. Res. 2010, 80, 528–536. [Google Scholar] [CrossRef]
- Williams, T.; Curran, C. Probabilistic load flow modeling comparing maximum entropy and Gram-Charlier probability density function reconstructions. IEEE Trans. Power Syst. 2012, 28, 272–280. [Google Scholar] [CrossRef]
- Fan, M.; Vittal, V.; Heydt, G.; Ayyanar, R. Probabilistic power flow studies for transmission systems with photovoltaic generation using cumulants. IEEE Trans. Power Syst. 2012, 27, 2251–2261. [Google Scholar] [CrossRef]
- Wu, W.; Wang, K.; Li, G.; Jiang, X.; Wang, Z. Probabilistic load flow calculation using cumulants and multiple integrals. IET Gener. Transm. Distrib. 2016, 10, 1703–1709. [Google Scholar] [CrossRef]
- Rosenblueth, E. Point estimates for probability moments. Proc. Natl. Acad. Sci. 2013, 28, 3114–3125. [Google Scholar] [CrossRef]
- Zhao, Y.; Ono, T. New Point Estimates for Probability Moments. J. Eng. Mech. 2000, 126, 433–436. [Google Scholar] [CrossRef]
- Hong, H. An efficient point estimate method for probabilistic analysis. Reliab. Eng. Syst. Saf. 1998, 59, 261–267. [Google Scholar] [CrossRef]
- Su, C. Probabilistic load-flow computation using point estimate method. IEEE Trans. Power Syst. 2005, 20, 1843–1851. [Google Scholar] [CrossRef]
- Morales, J.; Perez-Ruiz, J. Point estimate schemes to solve the probabilistic power flow. IEEE Trans. Power Syst. 2007, 22, 1594–1601. [Google Scholar] [CrossRef]
- Liu, Y.; Gao, S.; Cui, H.; Yu, L. Probabilistic load flow considering correlations of input variables following arbitrary distributions. Electr. Power Syst. Res. 2010, 140, 354–362. [Google Scholar] [CrossRef]
- Chen, C.; Wu, W.; Zhang, B.; Sun, H. Correlated probabilistic load flow using a point estimate method with Nataf transformation. Int. J. Electr. Power Energy Syst. 2015, 65, 325–333. [Google Scholar] [CrossRef]
- Xiao, Q.; He, Y.; Yang, Y.; Lu, Y. Point estimate method based on univariate dimension reduction model for probabilistic power flow computation. IET Gener. Transm. Distrib. 2017, 11, 3522–3531. [Google Scholar] [CrossRef]
- Le, D.; Gross, G.; Berizzi, A. Probabilistic modeling of multisite wind farm production for scenario-based applications. IEEE Trans. Sustain. Energy 2016, 6, 748–758. [Google Scholar] [CrossRef]
- Saunders, C. Point estimate method addressing correlated wind power for probabilistic optimal power flow. IEEE Trans. Power Syst. 2013, 29, 1045–1054. [Google Scholar] [CrossRef]
- Li, H.; Lu, Z.; Yuan, X. Nataf transformation based point estimate method. Chin. Sci. Bull. 2008, 53, 2586–2592. [Google Scholar] [CrossRef]
- Xu, H.; Rahman, S. A generalized dimension-reduction method for multidimensional integration in stochastic mechanics. Int. J. Numer. Methods Eng. 2004, 61, 1992–2019. [Google Scholar] [CrossRef]
- Chowdhury, R.; Rao, B.; Prasad, A. High-dimensional model representation for structural reliability analysis. Commun. Number. Meth. Eng. 2009, 25, 301–337. [Google Scholar] [CrossRef]
- Fan, W.; Wei, J.; Ang, A.; Li, Z. Adaptive estimation of statistical moments of the responses of random systems. Probab. Eng. Eng. Mech. 2016, 43, 50–67. [Google Scholar] [CrossRef]
- Zimmerman, R.; Murillo-Sánchez, C.; Thomas, R. MATPOWER: Steady-state operations, planning, and analysis tools for power systems research and education. IEEE Trans. Power Syst. 2010, 26, 12–19. [Google Scholar] [CrossRef]
- Power System Test Case Archive. Available online: https://labs.ece.uw.edu/pstca/ (accessed on 1 March 2020).
- Bludszuweit, H.; Dominguez-Navarro, J.A.; Llombart, A. Statistical analysis of wind power forecast error. IEEE Trans. Power Syst. 2008, 23, 983–991. [Google Scholar] [CrossRef]
- Kwok, J.; Tsang, I. The Pre-Image Problem in Kernel Methods. IEEE Trans. Neural Netw. 2004, 15, 1517–1525. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Sun, Y.; Gao, D.; Lin, J.; Cheng, L. A Versatile Probability Distribution Model for Wind Power Forecast Errors and Its Application in Economic Dispatch. IEEE Trans. Power Syst. 2013, 28, 3114–3125. [Google Scholar] [CrossRef]
- Xie, X.; Schenkendorf, R. Robust optimization of a pharmaceutical freeze-drying process under non-Gaussian parameter uncertainties. Chem. Eng. Sci. 2019, 207, 805–819. [Google Scholar] [CrossRef]

| Numbers | Abscissas | Weights |
|---|---|---|
| 3 | 0 | 1.1816 |
| ±1.2247 | 2.9541 × 10−1 | |
| 5 | 0 | 9.4530 × 10−1 |
| ±0.9585 | 3.9362 × 10−1 | |
| ±2.0201 | 1.9953 × 10−2 | |
| 7 | 0 | 8.1027 × 10−1 |
| ±0.8162 | 4.2561 × 10−1 | |
| ±1.6735 | 5.4512 × 10−2 | |
| ±2.6519 | 9.7178 × 10−4 |
| WF | Bus | Distribution Parameters | Fluctuation Range (MW) |
|---|---|---|---|
| 1 | 15 | Beta (5.32, 7.34) | 0–25 |
| 2 | 16 | ||
| 3 | 26 | Beta (4.18, 1.80) | 0–18 |
| 4 | 30 |
| Method | AREI | Calculation Time (s) | ||||
|---|---|---|---|---|---|---|
| Type of ORV | ||||||
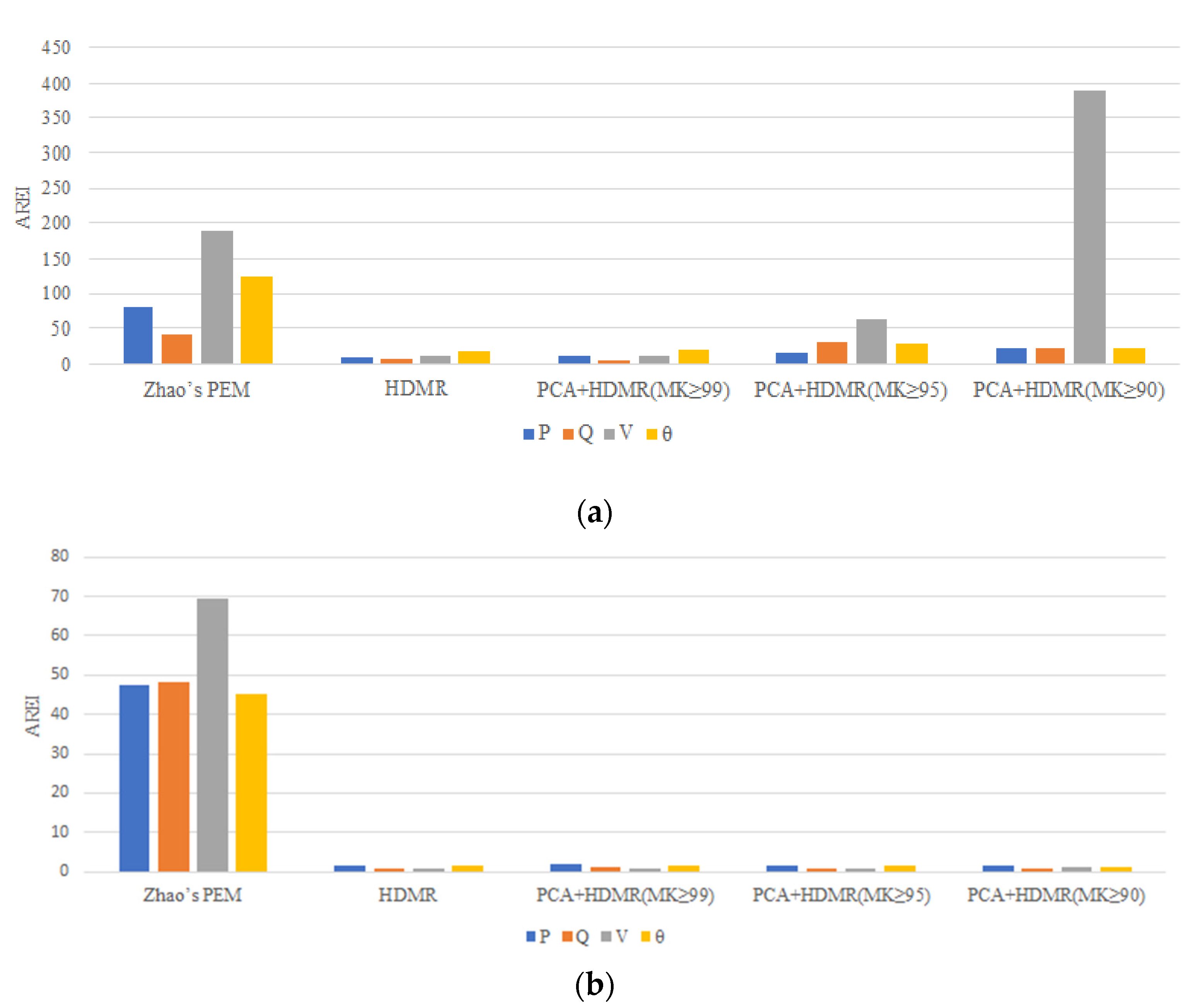
| Zhao’s PEM | P | 0.0944 | 1.3002 | 80.2243 | 47.4376 | 1.27 |
| Q | 0.1273 | 2.4155 | 43.3680 | 48.1434 | ||
| V | 4.1262 × 10−4 | 1.6993 | 189.0701 | 69.5160 | ||
| 0.1877 | 0.6081 | 125.3632 | 45.0952 | |||
| HDMR | P | 0.0564 | 0.2419 | 10.4886 | 1.6998 | 52.13 |
| Q | 0.0727 | 0.0922 | 6.8338 | 0.9072 | ||
| V | 3.6439 × 10−4 | 0.1124 | 11.4566 | 0.6689 | ||
| 0.1417 | 0.0859 | 18.4550 | 1.6844 | |||
| PCA+HDMR () | P | 0.1132 | 1.3447 | 12.7240 | 1.9275 | 4.98 |
| Q | 0.1986 | 0.4641 | 4.3147 | 1.0406 | ||
| V | 5.3721 × 10−4 | 0.4107 | 11.4707 | 0.7315 | ||
| 0.0967 | 0.4550 | 21.3574 | 1.5991 | |||
| PCA+HDMR () | P | 0.0564 | 3.8661 | 16.1810 | 1.5683 | 1.79 |
| Q | 0.1166 | 11.9587 | 31.1181 | 0.7725 | ||
| V | 4.1600 × 10−4 | 9.9708 | 61.7536 | 0.7817 | ||
| 0.1902 | 2.6245 | 30.0443 | 1.4042 | |||
| PCA+HDMR () | P | 0.0704 | 9.2014 | 22.7468 | 1.3903 | 0.89 |
| Q | 0.0544 | 20.5477 | 23.7019 | 0.9561 | ||
| V | 3.4794 × 10−4 | 19.526 | 389.3838 | 1.0878 | ||
| 0.2106 | 6.1322 | 22.4920 | 1.2454 | |||
| MCS | 164.86 | |||||
| Method | AREI | ||||
|---|---|---|---|---|---|
| Type of ORV | |||||
| Low correlation | P | 0.1011 | 1.3796 | 9.5218 | 2.6647 |
| Q | 0.0956 | 2.7176 | 7.3381 | 1.7268 | |
| V | 3.9626 × 10−4 | 1.4616 | 12.7701 | 1.9133 | |
| 0.2716 | 0.1764 | 19.1871 | 0.6482 | ||
| Medium correlation | P | 0.0310 | 1.9153 | 11.0052 | 1.5038 |
| Q | 0.0684 | 3.0162 | 8.6251 | 1.8370 | |
| V | 1.8130 × 10−4 | 2.0106 | 10.8609 | 0.9980 | |
| 0.0883 | 1.2564 | 20.1425 | 1.6366 | ||
| High correlation | P | 0.0782 | 1.8078 | 11.9801 | 1.1834 |
| Q | 0.0658 | 3.0001 | 7.5388 | 1.6983 | |
| V | 4.7408 × 10−4 | 1.8222 | 10.9358 | 0.9288 | |
| 0.2106 | 6.1322 | 22.4920 | 1.2454 | ||
| WF | Bus | Distribution Parameters | Fluctuation Range (MW) |
|---|---|---|---|
| 1–4 | 2, 3, 44, 50 | Beta (3.76, 5.82) | 0–300 |
| 5–8 | 82, 88, 98, 115 | Beta (6.82, 2.44) | 0–160 |
| Method | AREI | Calculation Time (s) | ||||
|---|---|---|---|---|---|---|
| Type of ORV | ||||||
| Zhao’s PEM | P | 0.0379 | 3.3787 | 119.7405 | 51.6410 | 3.29 |
| Q | 0.0334 | 8.2555 | 163.1540 | 52.8882 | ||
| V | 2.9447 × 10−4 | 4.4120 | 155.3896 | 37.7793 | ||
| 0.0088 | 1.2012 | 78.0240 | 66.3490 | |||
| HDMR | P | 0.0286 | 0.1707 | 9.3664 | 1.8081 | 406.33 |
| Q | 0.0219 | 0.5212 | 12.8664 | 3.1527 | ||
| V | 1.8866 × 10−4 | 0.4320 | 17.4510 | 3.1466 | ||
| 0.0058 | 0.1442 | 15.2332 | 0.5527 | |||
| PCA+HDMR () | P | 0.0379 | 2.4125 | 11.4793 | 2.0809 | 6.52 |
| Q | 0.0314 | 7.9233 | 18.9019 | 3.6851 | ||
| V | 3.3919 × 10−4 | 3.4223 | 19.6508 | 4.8801 | ||
| 0.0085 | 1.0298 | 17.0902 | 0.7055 | |||
| MCS | 391.62 | 164.86 | ||||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Zhang, Z.; Yin, X. A Novel Probabilistic Power Flow Algorithm Based on Principal Component Analysis and High-Dimensional Model Representation Techniques. Energies 2020, 13, 3520. https://doi.org/10.3390/en13143520
Li H, Zhang Z, Yin X. A Novel Probabilistic Power Flow Algorithm Based on Principal Component Analysis and High-Dimensional Model Representation Techniques. Energies. 2020; 13(14):3520. https://doi.org/10.3390/en13143520
Chicago/Turabian StyleLi, Hang, Zhe Zhang, and Xianggen Yin. 2020. "A Novel Probabilistic Power Flow Algorithm Based on Principal Component Analysis and High-Dimensional Model Representation Techniques" Energies 13, no. 14: 3520. https://doi.org/10.3390/en13143520
APA StyleLi, H., Zhang, Z., & Yin, X. (2020). A Novel Probabilistic Power Flow Algorithm Based on Principal Component Analysis and High-Dimensional Model Representation Techniques. Energies, 13(14), 3520. https://doi.org/10.3390/en13143520




