Numerical Study on the Gravity Effect on Heat Transfer of Supercritical CO2 in a Vertical Tube
Abstract
:1. Introduction
2. Methodology
2.1. Governing Equation and Turbulent Model
2.2. Turbulent Prandtl Number Modification
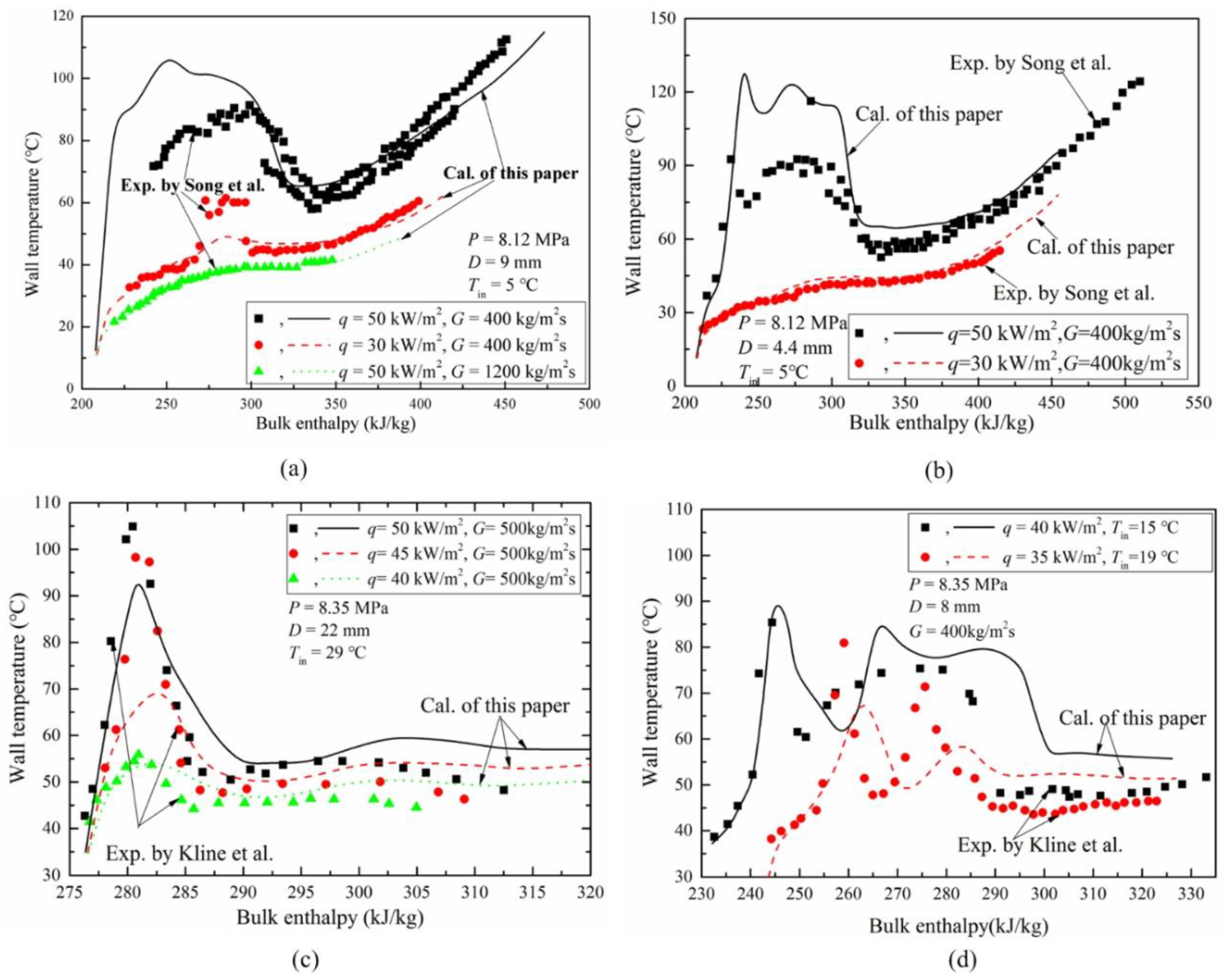
2.3. Validation of Turbulent Model
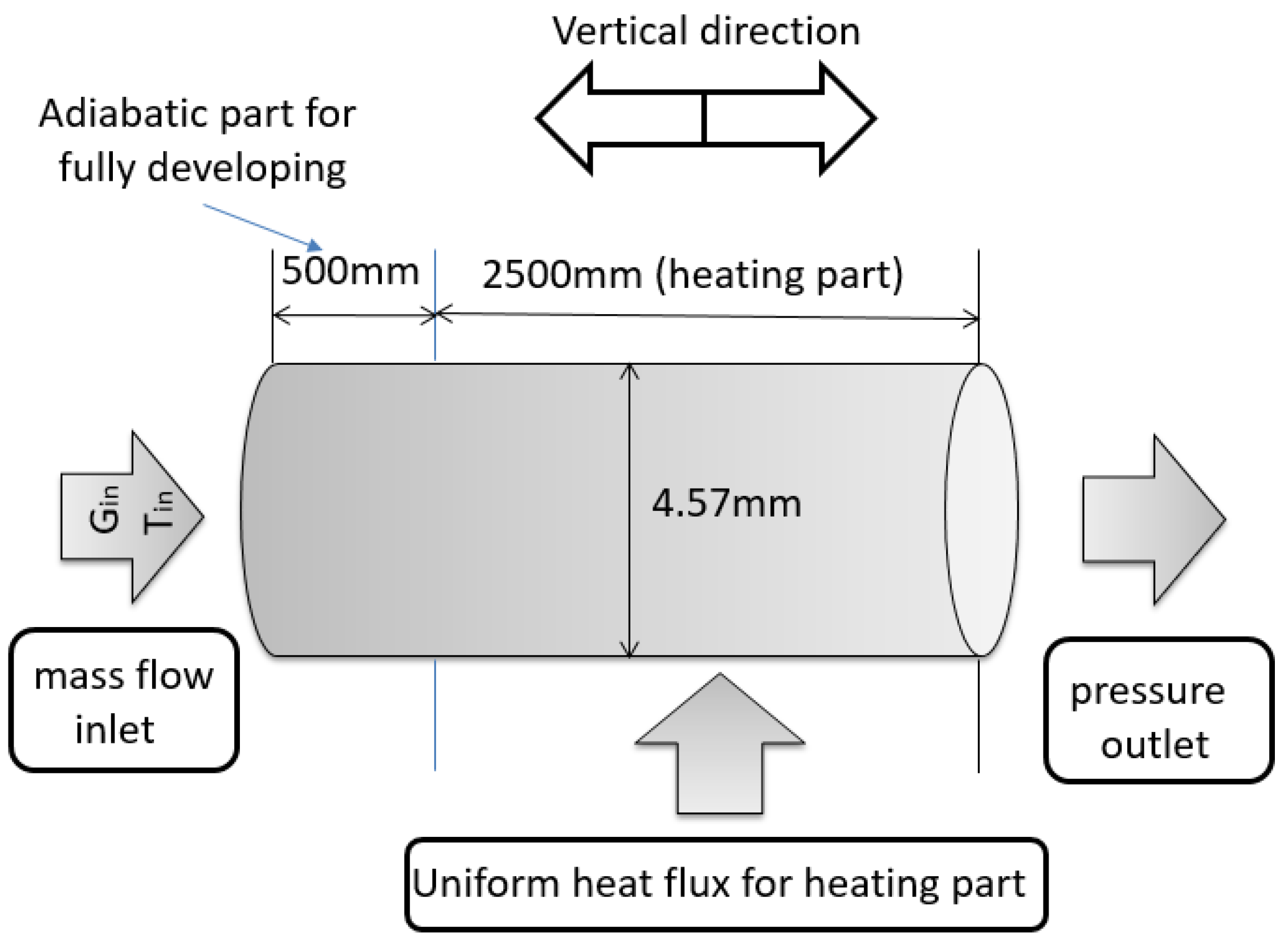
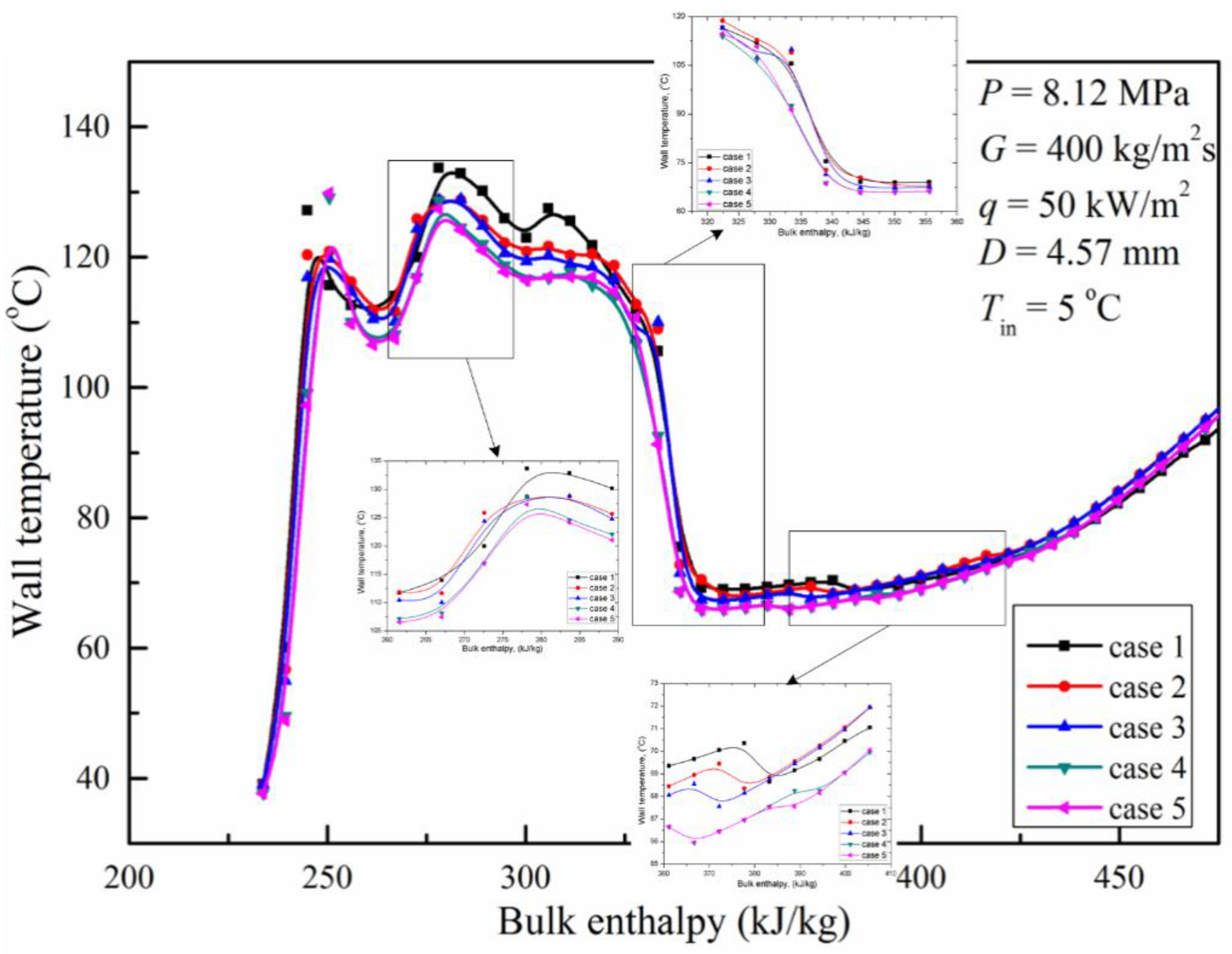
2.4. Boundary Conditions and Mesh Dependency
3. Results and Discussions
3.1. Effect of Gravity for the Upward Flow
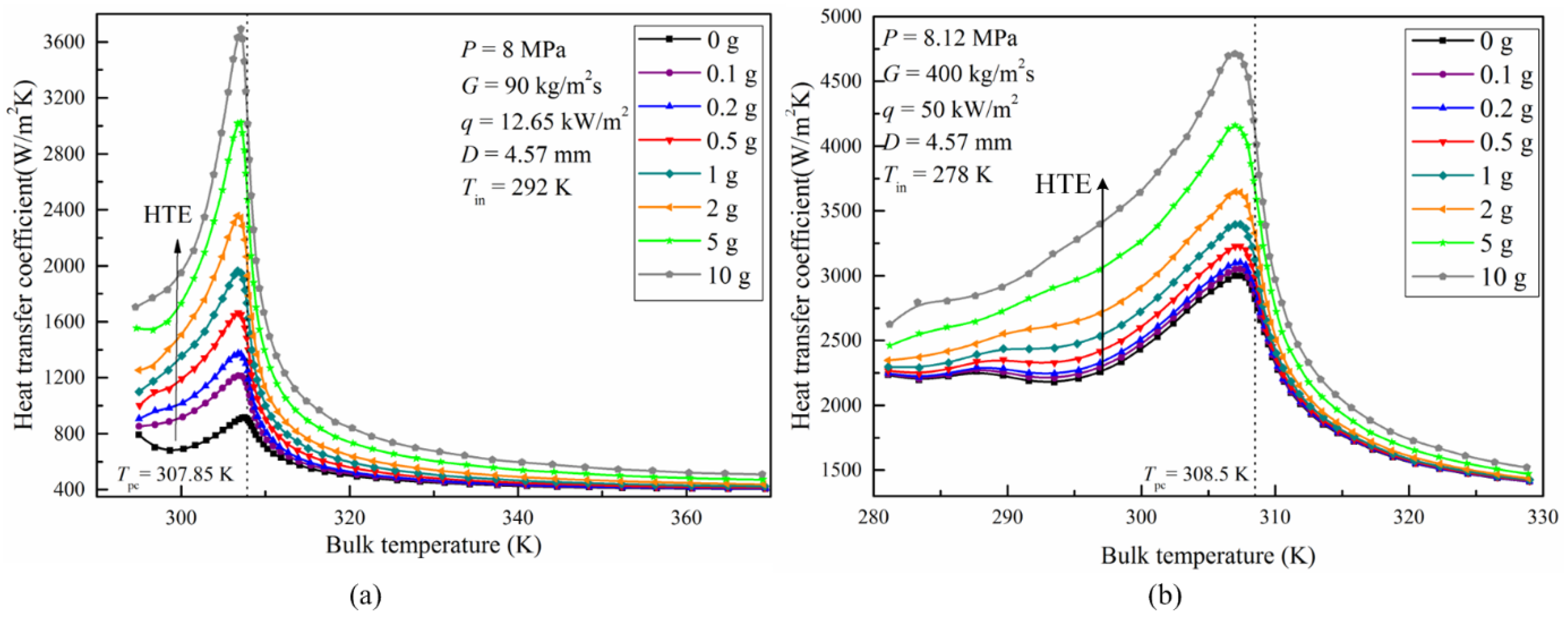
3.1.1. Variations of HTC
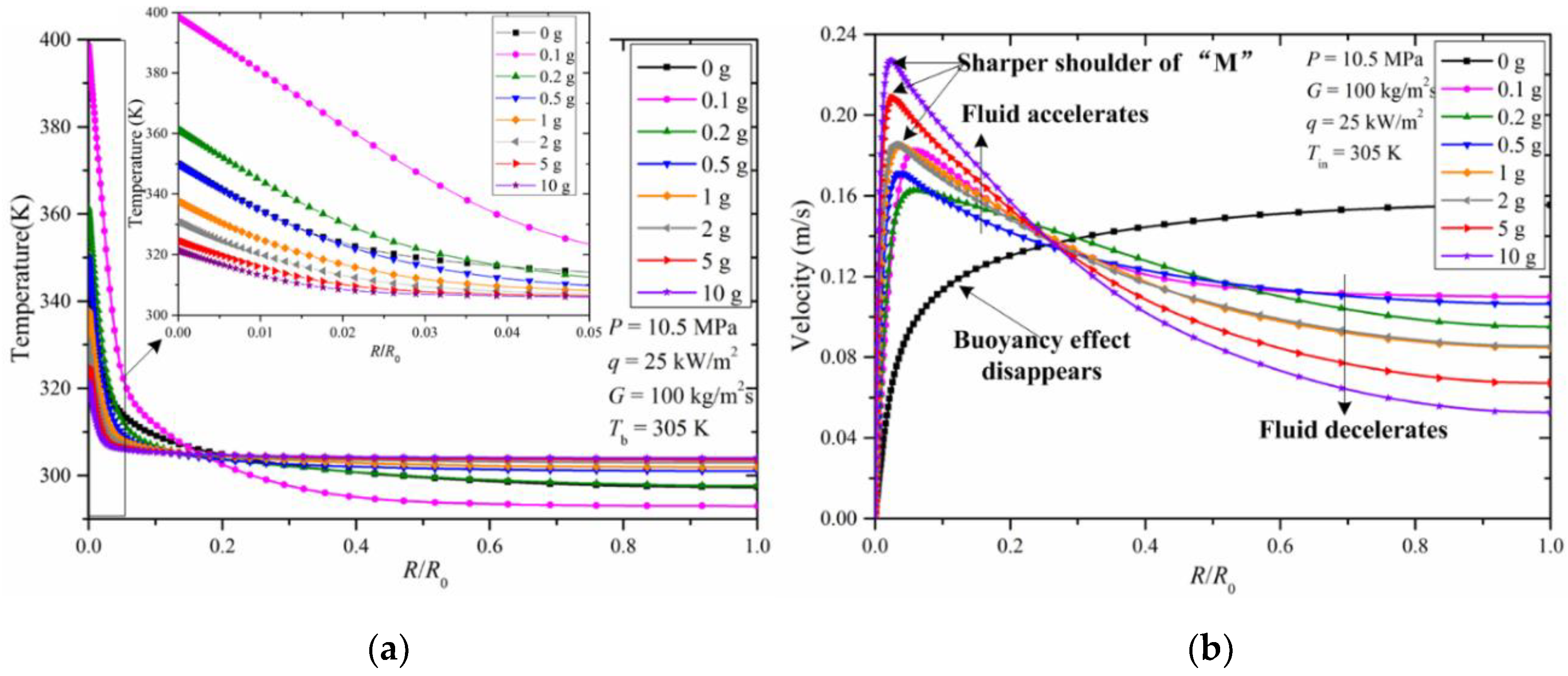
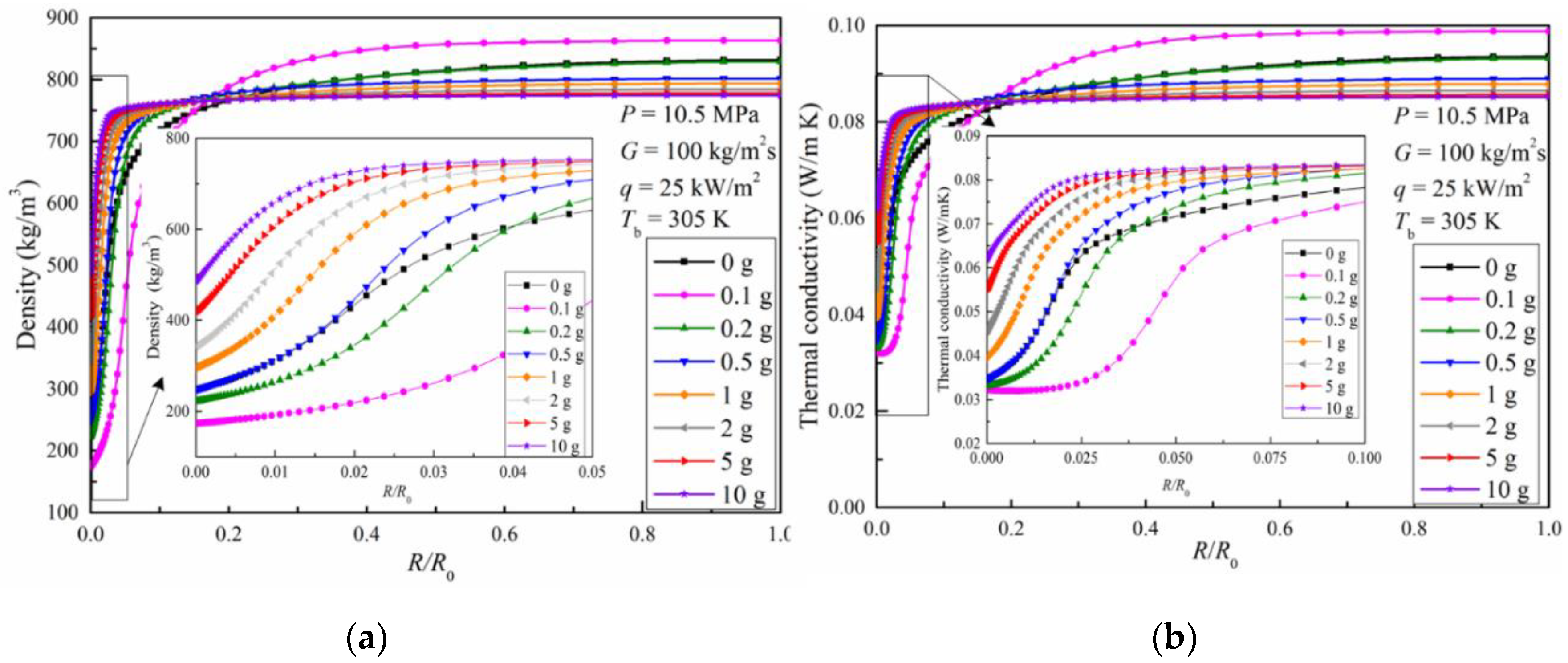
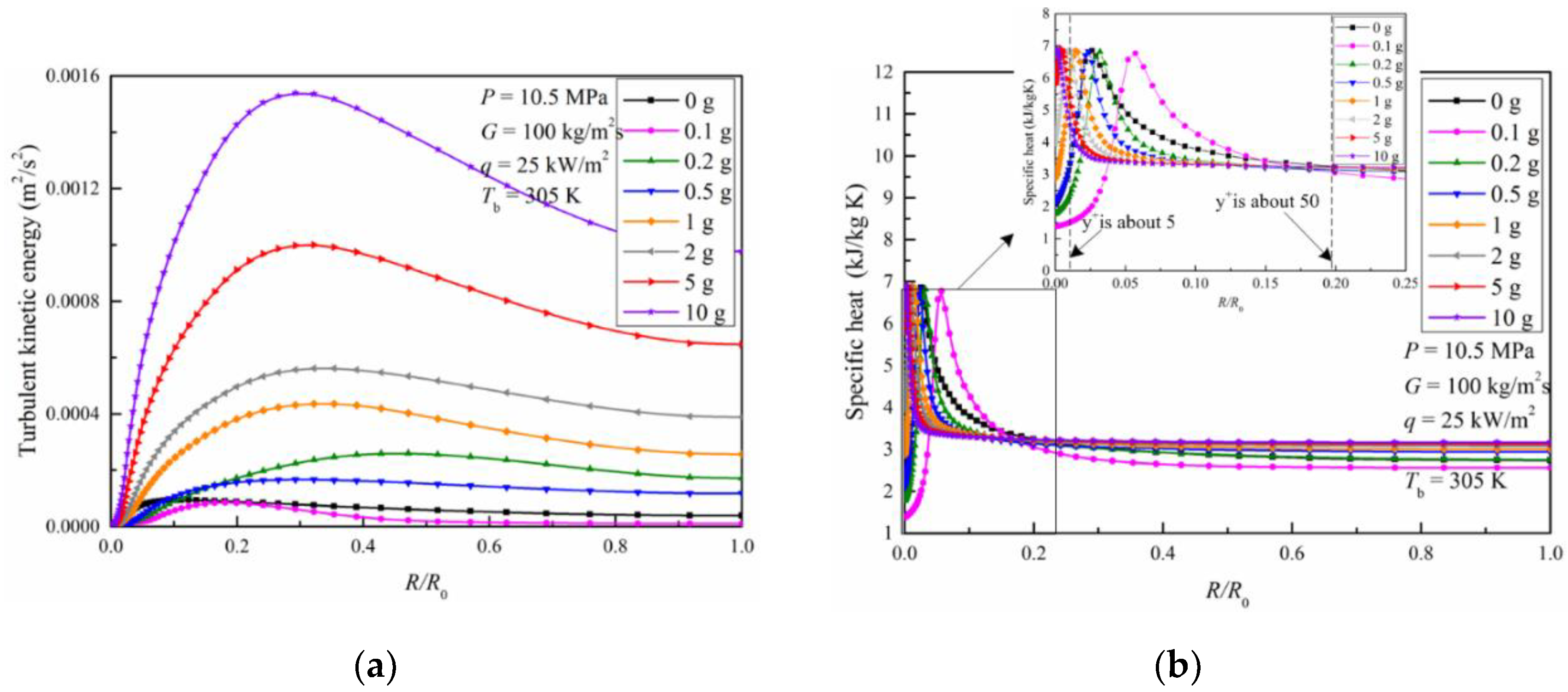
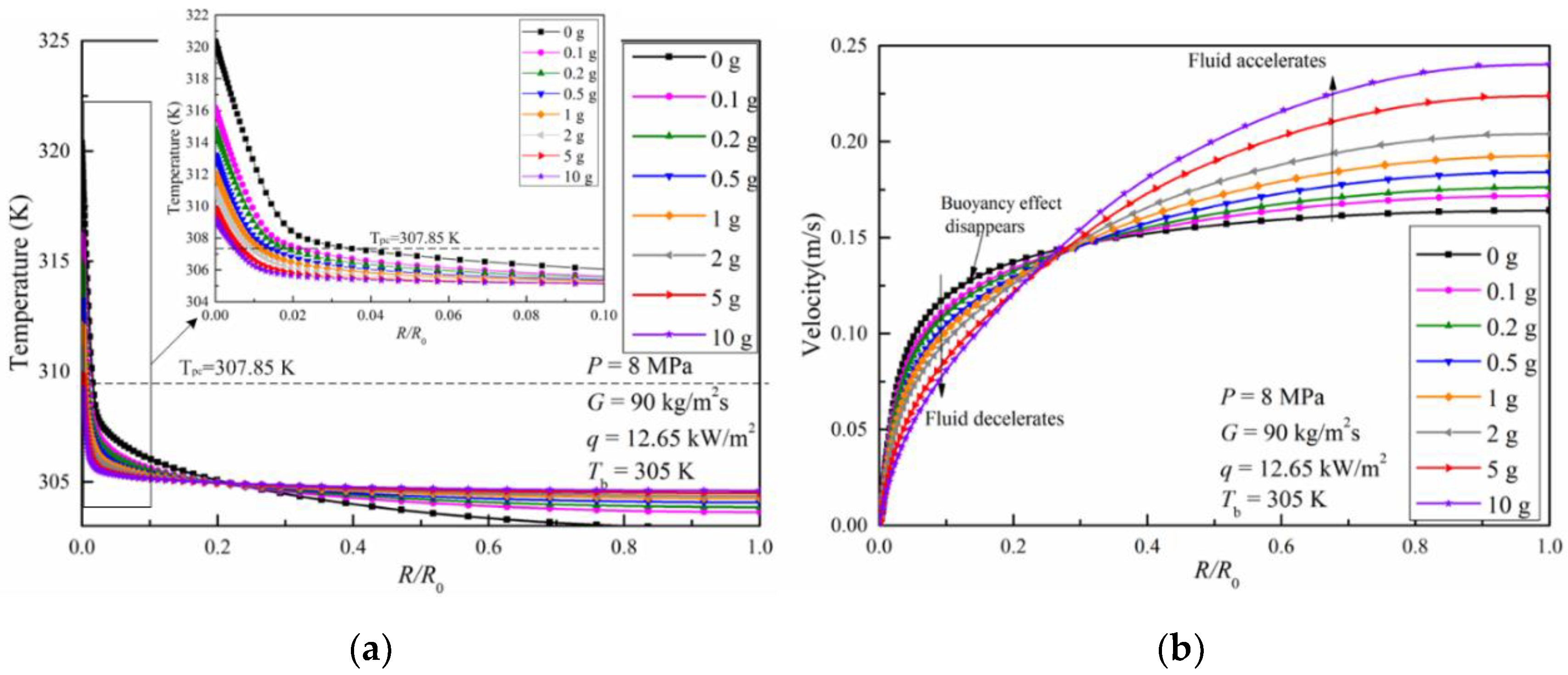
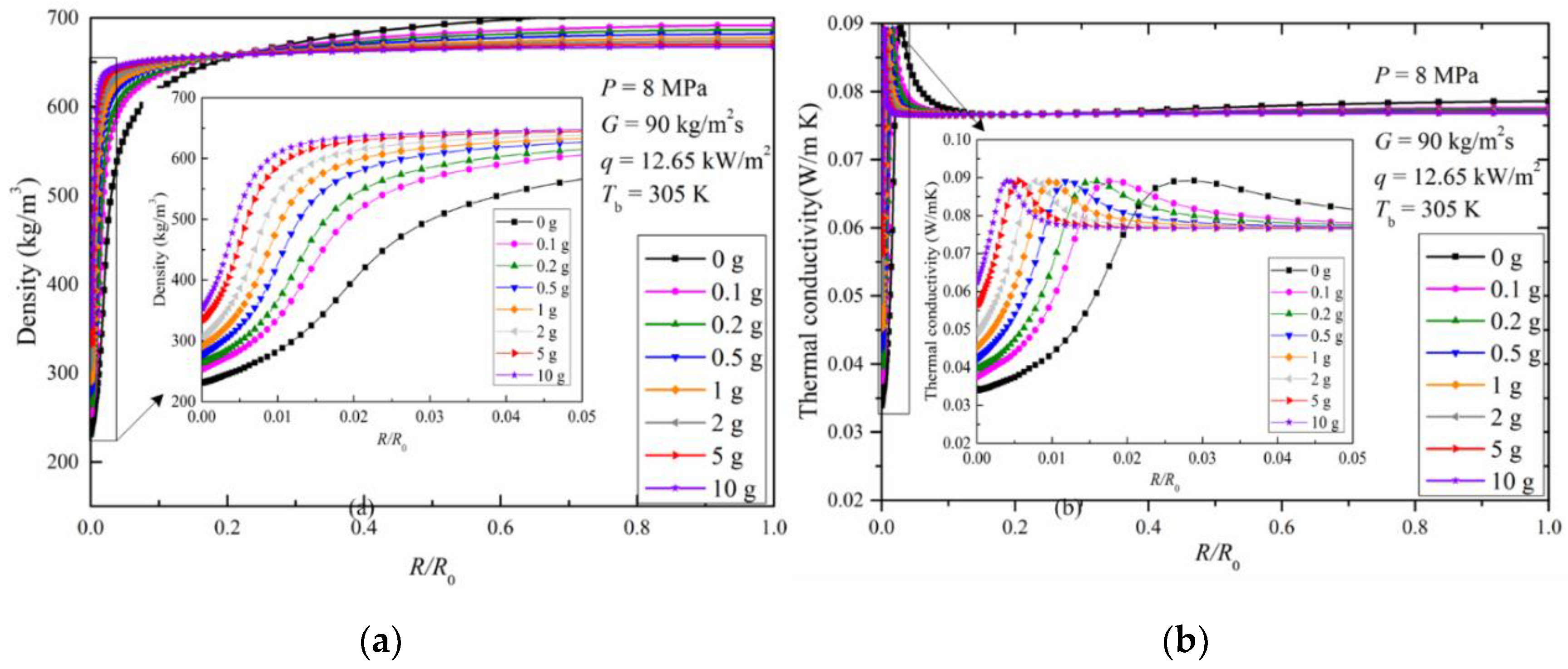
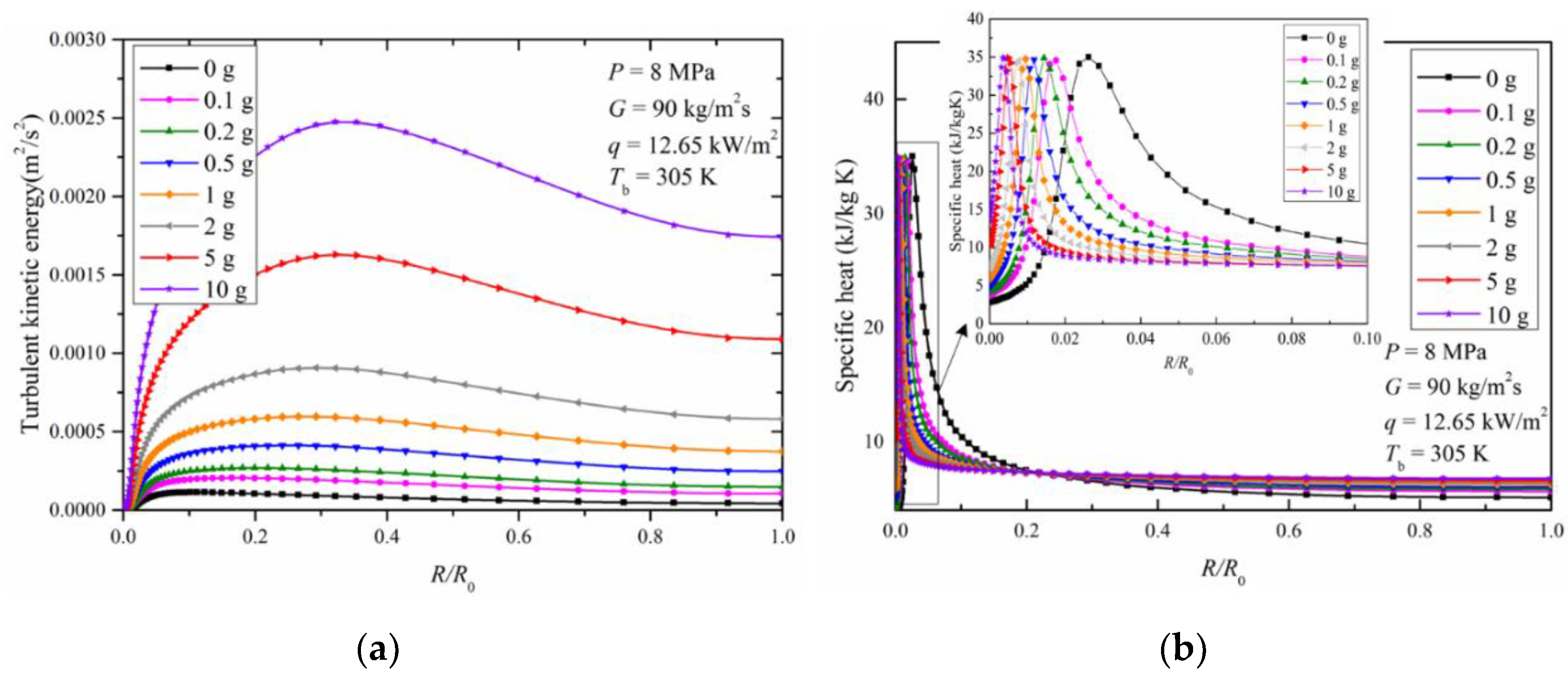
3.1.2. Radial Distribution of Thermal Properties for Upward Flow
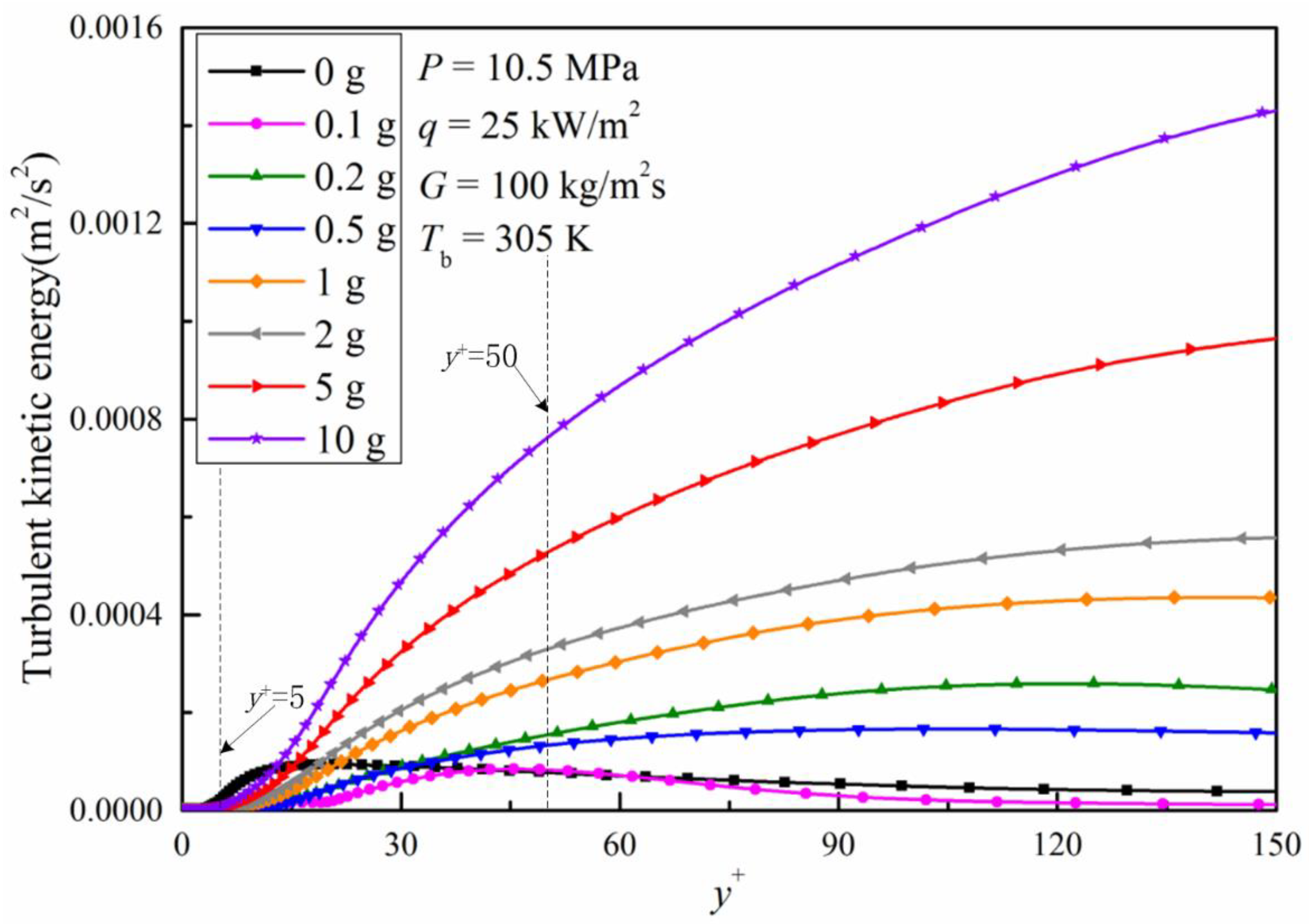
3.1.3. Heat Transfer Mechanism Analysis for Upward Flow
3.2. Effect of Gravity on Downward Flow
3.2.1. Variations of HTC
3.2.2. Radial Distribution of Thermal Properties for Downward Flow
3.2.3. Heat Transfer Mechanism Analysis for Downward Flow
4. Conclusions
- A modified SST k-ω model is recommended as a turbulence model for the prediction of heat transfer of supercritical CO2 flowing in a vertical tube. Comparison results show that the modified turbulence model is more suitable for the prediction of HTD of supercritical fluid induced by buoyancy effect.
- For both the upward and downward flows, the heat transfer of supercritical CO2 is enhanced with increased gravity magnitude. The effect of gravity on heat transfer is closely related to the variations of thermal properties and it is more pronounced under a low mass flux condition than a high mass flux condition.
- For the upward flow, increased gravity magnitude enhances the effect of buoyancy within the tube. The fluid in the near wall region accelerates and the fluid in the turbulent core decelerates. A classic M-shaped radial velocity distribution is thus created. The radial velocity difference between the near wall region and the turbulent core region is increased and the turbulent kinetic energy is greatly increased. This benefits the heat transfer dominated by turbulent eddy diffusion. Meanwhile, high density and high thermal conductivity fluid occupies the near wall region and enhances the heat transfer dominated by molecular diffusion.
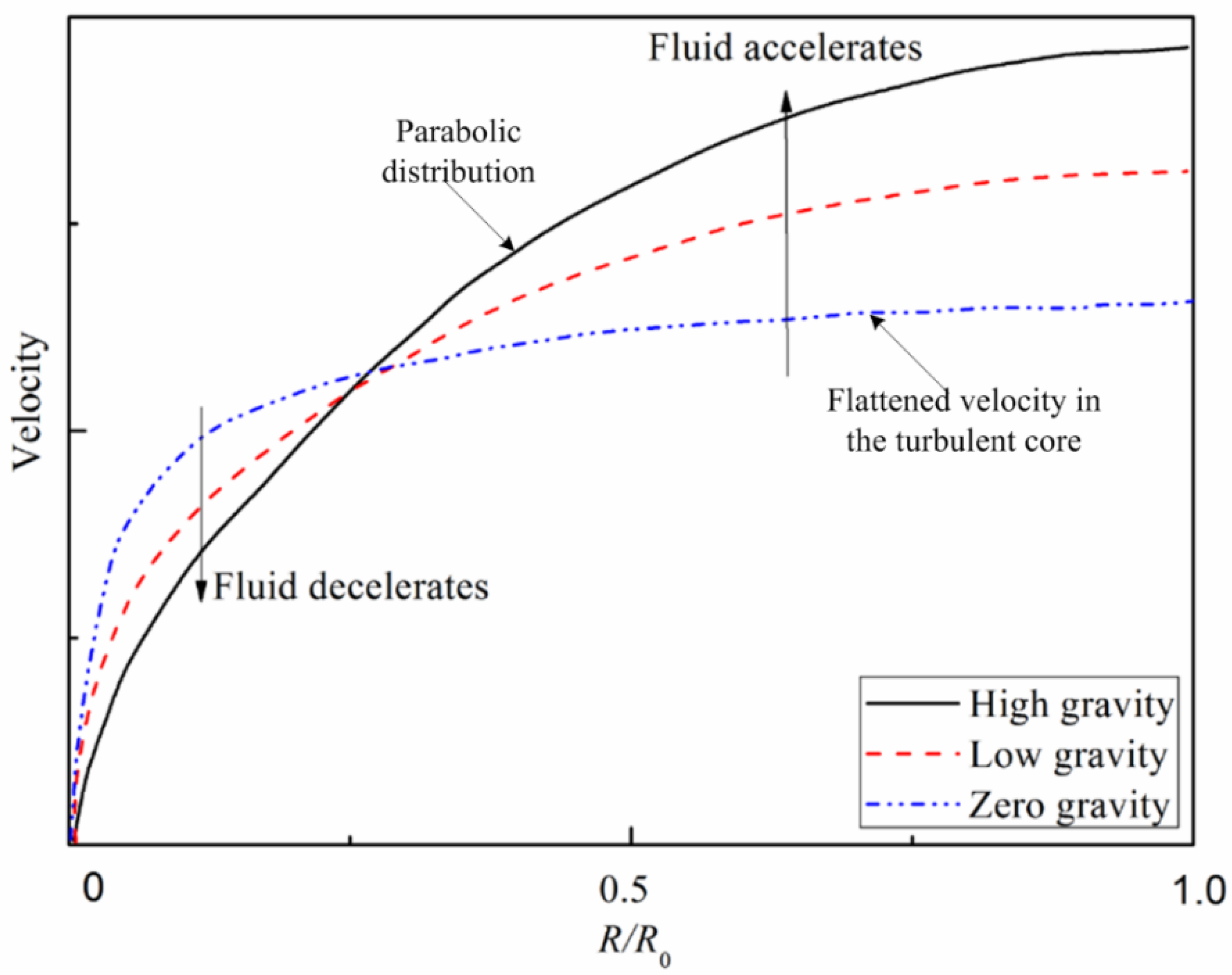
- For the downward flow, the fluid in the near wall region decelerates and the fluid in the turbulent core region accelerates with increasing gravity magnitude. A parabolic radial velocity distribution is created and this is the main qualitative difference between the upward flow and downward flow as the gravity magnitude increases. The flattened velocity distribution in the turbulent core at low or zero gravity disappears and the turbulent kinetic energy is greatly increased. Similar to the upward flow case, this benefits the turbulent convective heat transfer and improves the heat transfer efficiency from the tube wall to the turbulent core.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Bo* | buoyancy parameter, expressed as: |
| cp | specific heat (J/kgK) |
| D, d | diameter (mm) |
| g | gravitational acceleration (m/s2) |
| G | mass flux (kg/m2s) |
| Gk and Gω | generation of k and ω due to the mean velocity gradients |
| Gr | Grash of number, expressed as: |
| h | local heat transfer coefficient (W/m2K) |
| h0 | reference heat transfer coefficient (W/m2K) |
| k | turbulent kinetic energy (m2/s2) |
| Nu | Nusselt number |
| P | pressure (MPa) |
| Pr | Prandtl number |
| q | heat flux (W/m2) |
| Re | Reynolds number |
| T | temperature (K) |
| x | distance (mm) |
| y+ | non-dimensional wall distance |
| Yk and Yω | dissipation of k and ω due to the turbulence |
| Greek symbols | |
| α1 and α2 | correction factor |
| α* | damping coefficient |
| ω | turbulent frequency |
| β | thermal expansion coefficient (1/K) |
| λ | thermal conductivity (W/m K) |
| μ | molecular viscosity (kg/ms) |
| μt | turbulent viscosity (kg/ms) |
| v | kinematic viscosity (m2/s) |
| ρ | density (kg/m3) |
| Γk and Γω | the effective diffusivity of k and ω |
| Subscripts | |
| b | evaluated at bulk |
| C | critical point |
| in | inlet |
| pc | pseudo-critical |
| w | evaluated at wall |
| Abbreviation | |
| HTC | heat transfer coefficient |
| HTE | heat transfer enhancement |
| HTD | heat transfer deterioration |
| PCHE | printed circuit heat exchanger |
| SCO2 | supercritical carbon dioxide |
References
- Chen, M.; Sun, X.; Christensen, R.N.; Shi, S.; Skavdahl, I.; Utgikar, V.; Sabharwall, P. Experimental and numerical study of a printed circuit heat exchanger. Ann. Nucl. Energy 2016, 97, 221–231. [Google Scholar] [CrossRef] [Green Version]
- Khmelinskii, I.; Woodcock, L.V. Supercritical Fluid Gaseous and Liquid States: A Review of Experimental Results. Entropy 2020, 22, 437. [Google Scholar] [CrossRef] [Green Version]
- Gkountas, A.A.; Stamatelos, A.; Kalfas, A. Recuperators investigation for high temperature supercritical carbon dioxide power generation cycles. Appl. Therm. Eng. 2017, 125, 1094–1102. [Google Scholar] [CrossRef]
- Jacob, F.; Rolt, A.M.; Sebastiampillai, J.; Sethi, V.; Belmonte, M.; Cobas, P. Performance of a Supercritical CO2 Bottoming Cycle for Aero Applications. Appl. Sci. 2017, 7, 255. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Q.T. Effects of buoyancy on the heat transfer of supercritical water in vertical tube. J. Eng. Thermophys. 1983, 4, 165–172. (In Chinese) [Google Scholar]
- Jackson, J.D.; Hall, W.B.; Fewster, J.; Watson, A.; Watts, M.J. Heat Transfer to Supercritical Pressure Fluids; UKAEA, AERER 8158. Design Report 34; Intech: Rijeka, Croatia, 1975. [Google Scholar]
- Petukhov, B.S.; Polyakof, A.F.; Kuleshov, V.A.; Sheckter, Y.L. Turbulent Flow and Heat Transfer in Horizontal Tubes with Substantial Influence of Thermo-Gravitational Forces; International Heat Transfer Conference: Tokyo, Japan, 1974. [Google Scholar]
- Liao, S.; Zhao, T. An experimental investigation of convection heat transfer to supercritical carbon dioxide in miniature tubes. Int. J. Heat Mass Transf. 2002, 45, 5025–5034. [Google Scholar] [CrossRef]
- Jiang, P.-X.; Zhang, Y.; Xu, Y.-J.; Shi, R.-F. Experimental and numerical investigation of convection heat transfer of CO2 at supercritical pressures in a vertical tube at low Reynolds numbers. Int. J. Therm. Sci. 2008, 47, 998–1011. [Google Scholar] [CrossRef]
- Li, Z.; Jiang, P.; Zhao, C.-R.; Zhang, Y. Experimental investigation of convection heat transfer of CO2 at supercritical pressures in a vertical circular tube. Exp. Therm. Fluid Sci. 2010, 34, 1162–1171. [Google Scholar] [CrossRef]
- Xu, R.; Luo, F.; Jiang, P. Buoyancy effects on turbulent heat transfer of supercritical CO 2 in a vertical mini-tube based on continuous wall temperature measurements. Int. J. Heat Mass Transf. 2017, 110, 576–586. [Google Scholar] [CrossRef]
- Zhao, C.-R.; Liu, Q.; Zhang, Z.; Jiang, P.; Bo, H.-L. Investigation of buoyancy-enhanced heat transfer of supercritical CO2 in upward and downward tube flows. J. Supercrit. Fluids 2018, 138, 154–166. [Google Scholar] [CrossRef]
- Zhu, X.; Du, X.; Ding, Y.; Qiu, Q. Analysis of entropy generation behavior of supercritical water flow in a hexagon rod bundle. Int. J. Heat Mass Transf. 2017, 114, 20–30. [Google Scholar] [CrossRef]
- Qiu, Q.; Du, X.; Zhao, S.; Zhu, X.; Shen, S. Numerical study on heat transfer of SCW near the pseudo-critical temperature in a hexagon sub-channel. Nucl. Eng. Des. 2018, 331, 263–273. [Google Scholar] [CrossRef]
- Du, X.; Lv, Z.; Zhao, S.; Qiu, Q.; Zhu, X. Numerical analysis of diameter effects on convective supercritical water flow in a vertical round tube. Appl. Therm. Eng. 2019, 160, 114095. [Google Scholar] [CrossRef]
- Bazargan, M.; Mohseni, M. The significance of the buffer zone of boundary layer on convective heat transfer to a vertical turbulent flow of a supercritical fluid. J. Supercrit. Fluids 2009, 51, 221–229. [Google Scholar] [CrossRef]
- Hasan, N.; Farouk, B. Buoyancy driven convection in near-critical and supercritical fluids. Int. J. Heat Mass Transf. 2012, 55, 4207–4216. [Google Scholar] [CrossRef]
- Li, Z.; Tang, G.; Wu, Y.; Zhai, Y.; Xu, J.; Wang, H.; Lu, J. Improved gas heaters for supercritical CO2 Rankine cycles: Considerations on forced and mixed convection heat transfer enhancement. Appl. Energy 2016, 178, 126–141. [Google Scholar] [CrossRef]
- Bae, Y.-Y.; Kim, E.-S.; Kim, M. Numerical simulation of upward flowing supercritical fluids using buoyancy-influence-reflected turbulence model. Nucl. Eng. Des. 2017, 324, 231–249. [Google Scholar] [CrossRef]
- Tian, R.; Zhang, Y.; Ma, Y.; Li, H.; Shi, L. Experimental study of buoyancy effect and its criteria for heat transfer of supercritical R134a in horizontal tubes. Int. J. Heat Mass Transf. 2018, 127, 555–567. [Google Scholar] [CrossRef]
- Kim, T.H.; Kwon, J.G.; Kim, M.H.; Park, H.S. Experimental investigation on validity of buoyancy parameters to heat transfer of CO2 at supercritical pressures in a horizontal tube. Exp. Therm. Fluid Sci. 2018, 92, 222–230. [Google Scholar] [CrossRef]
- Zhang, S.; Xu, X.; Liu, C.; Liu, X.; Zhang, Y.; Dang, C. The heat transfer of supercritical CO2 in helically coiled tube: Trade-off between curvature and buoyancy effect. Energy 2019, 176, 765–777. [Google Scholar] [CrossRef]
- Kawanami, O.; Azuma, H.; Ohta, H. Effect of gravity on cryogenic boiling heat transfer during tube quenching. Int. J. Heat Mass Transf. 2007, 50, 3490–3497. [Google Scholar] [CrossRef]
- Xie, L.-Y.; Xie, Y.; Wu, H.; Yu, J. High gravity influence on boiling heat transfer in helical coils. Int. J. Heat Mass Transf. 2014, 73, 706–715. [Google Scholar] [CrossRef]
- Vlachou, M.C.; Lioumbas, J.S.; Kostoglou, M.; David, K.; Chasapis, D.; Schwarz, C.; Van Loon, J.J.W.A.; Karapantsios, T.D. Subcooled flow boiling in horizontal and vertical macro-channel under Earth-gravity and hyper-gravity conditions. Int. J. Heat Mass Transf. 2019, 133, 36–51. [Google Scholar] [CrossRef]
- Li, X.; Ma, T.; Liu, J.; Zhang, H.; Wang, Q. Pore-scale investigation of gravity effects on phase change heat transfer characteristics using lattice Boltzmann method. Appl. Energy 2018, 222, 92–103. [Google Scholar] [CrossRef]
- Lebon, M.; Hammer, C.F.; Kim, J. Gravity effects on subcooled flow boiling heat transfer. Int. J. Heat Mass Transf. 2019, 128, 700–714. [Google Scholar] [CrossRef]
- Yi, T.-H.; Lei, Z.; Zhao, J.F. Numerical investigation of bubble dynamics and heat transfer in subcooling pool boiling under low gravity. Int. J. Heat Mass Transf. 2019, 132, 1176–1186. [Google Scholar] [CrossRef] [Green Version]
- Fang, X.; Tang, D.; Zheng, L.; Li, G.; Yuan, Y. Experimental investigation of gravity and channel size effects on flow boiling heat transfer under hyper gravity. Aerosp. Sci. Technol. 2019, 94, 105372. [Google Scholar] [CrossRef]
- Fang, X.; Li, G.; Li, D.; Xu, Y. An experimental study of R134a flow boiling heat transfer in a 4.07 mm tube under Earth’s gravity and hyper gravity. Int. J. Heat Mass Transf. 2015, 87, 399–408. [Google Scholar] [CrossRef]
- ANSYS Inc. ANSYS Fluent Theory Guide Release 15.0; ANSYS: Pennsylvania, PA, USA, 2013. [Google Scholar]
- Du, X.; Lv, Z.; Yu, X.; Cao, M.; Zhou, J.; Ren, Y.; Qiu, Q.; Zhu, X. Heat transfer of supercritical CO2 in vertical round tube: A considerate turbulent Prandtl number modification. Energy 2020, 192, 116612. [Google Scholar] [CrossRef]
- Song, J.; Kim, H.; Kim, H.; Bae, Y. Heat transfer characteristics of a supercritical fluid flow in a vertical pipe. J. Supercrit. Fluids 2008, 44, 164–171. [Google Scholar] [CrossRef]
- Kline, N.; Feuerstein, F.; Tavoularis, S. Onset of heat transfer deterioration in vertical pipe flow of CO2 at supercritical pressure. Int. J. Heat Mass Transf. 2018, 118, 1056–1068. [Google Scholar] [CrossRef]

| Researcher | Geometry | Flow Direction | Working Conditions |
|---|---|---|---|
| Song et al. [33] | Round tube D = 9 mm | Verticalupward | Case1: P = 8.12 MPa, G = 400 kg/m2s, q = 50 kW/m2, Tin = 5 °C Case2: P = 8.12 MPa, G = 400 kg/m2s, q = 30 kW/m2, Tin = 5 °C Case3: P = 8.12 MPa, G = 1200 kg/m2s, q = 50 kW/m2, Tin = 5 °C |
| Song et al. [33] | Round tube D = 4.4 mm | Verticalupward | Case4: P = 8.12 MPa, G = 400 kg/m2s, q = 50 kW/m2, Tin = 5 °C Case5: P = 8.12 MPa, G = 400 kg/m2s, q = 30 kW/m2, Tin = 5 °C |
| Kline et al. [34] | Round tube D = 22 mm | Vertical upward | Case6: P = 8.35 MPa, G = 500 kg/m2s, q = 50 kW/m2, Tin = 29 °C Case7: P = 8.35 MPa, G = 500 kg/m2s, q = 45 kW/m2, Tin = 29 °C Case8: P = 8.35 MPa, G = 500 kg/m2s, q = 40 kW/m2, Tin = 29 °C |
| Kline et al. [34] | Round tube D = 8 mm | Vertical upward | Case9: P = 8.35 MPa, G = 400 kg/m2s, q = 40 kW/m2, Tin = 15 °C Case10: P = 8.35 MPa, G = 400 kg/m2s, q = 35 kW/m2, Tin = 19 °C |
| Geometry | Flow Direction | Working Pressure | Mass Flux | Heat Flux | Gravity Magnitude |
|---|---|---|---|---|---|
| P, MPa | G, kg/m2s | q, kW/m2 | |||
| Round tube D = 4.57 mm | Downward and upward | 8, 8.12, 10.5 | 90, 100, 400 | 12.65, 25, 50 | 0 g–10 g |
| Case | Number of Meshes | Minimum Near-Wall y+ |
|---|---|---|
| 1 | 35,052 | 1.18 |
| 2 | 42,567 | 0.51 |
| 3 | 45,058 | 0.17 |
| 4 | 52,580 | 0.03 |
| 5 | 62,596 | 0.01 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, X.; Zhang, R.; Yu, X.; Cao, M.; Ren, Y. Numerical Study on the Gravity Effect on Heat Transfer of Supercritical CO2 in a Vertical Tube. Energies 2020, 13, 3502. https://doi.org/10.3390/en13133502
Zhu X, Zhang R, Yu X, Cao M, Ren Y. Numerical Study on the Gravity Effect on Heat Transfer of Supercritical CO2 in a Vertical Tube. Energies. 2020; 13(13):3502. https://doi.org/10.3390/en13133502
Chicago/Turabian StyleZhu, Xiaojing, Ruizeng Zhang, Xiao Yu, Maoguo Cao, and Yongxiang Ren. 2020. "Numerical Study on the Gravity Effect on Heat Transfer of Supercritical CO2 in a Vertical Tube" Energies 13, no. 13: 3502. https://doi.org/10.3390/en13133502
APA StyleZhu, X., Zhang, R., Yu, X., Cao, M., & Ren, Y. (2020). Numerical Study on the Gravity Effect on Heat Transfer of Supercritical CO2 in a Vertical Tube. Energies, 13(13), 3502. https://doi.org/10.3390/en13133502




