Distributed Machine Learning on Dynamic Power System Data Features to Improve Resiliency for the Purpose of Self-Healing
Abstract
:1. Introduction
- Development of a feature selection based event detection algorithm for a multi-machine based grid, that can be sectionalized under duress. The proposed algorithm is prepared for the segmented power system used in this study. Despite not being a generic solution for all types of grids the algorithm introduces novelty in the decision making process.
- In larger systems, the curse of dimensionality poses a bigger threat in applying machine learning algorithms, specially for making decisions. The proposed method, by implementing feature extraction on a reduced data set, addresses those challenges and enables an effective decision making scheme.
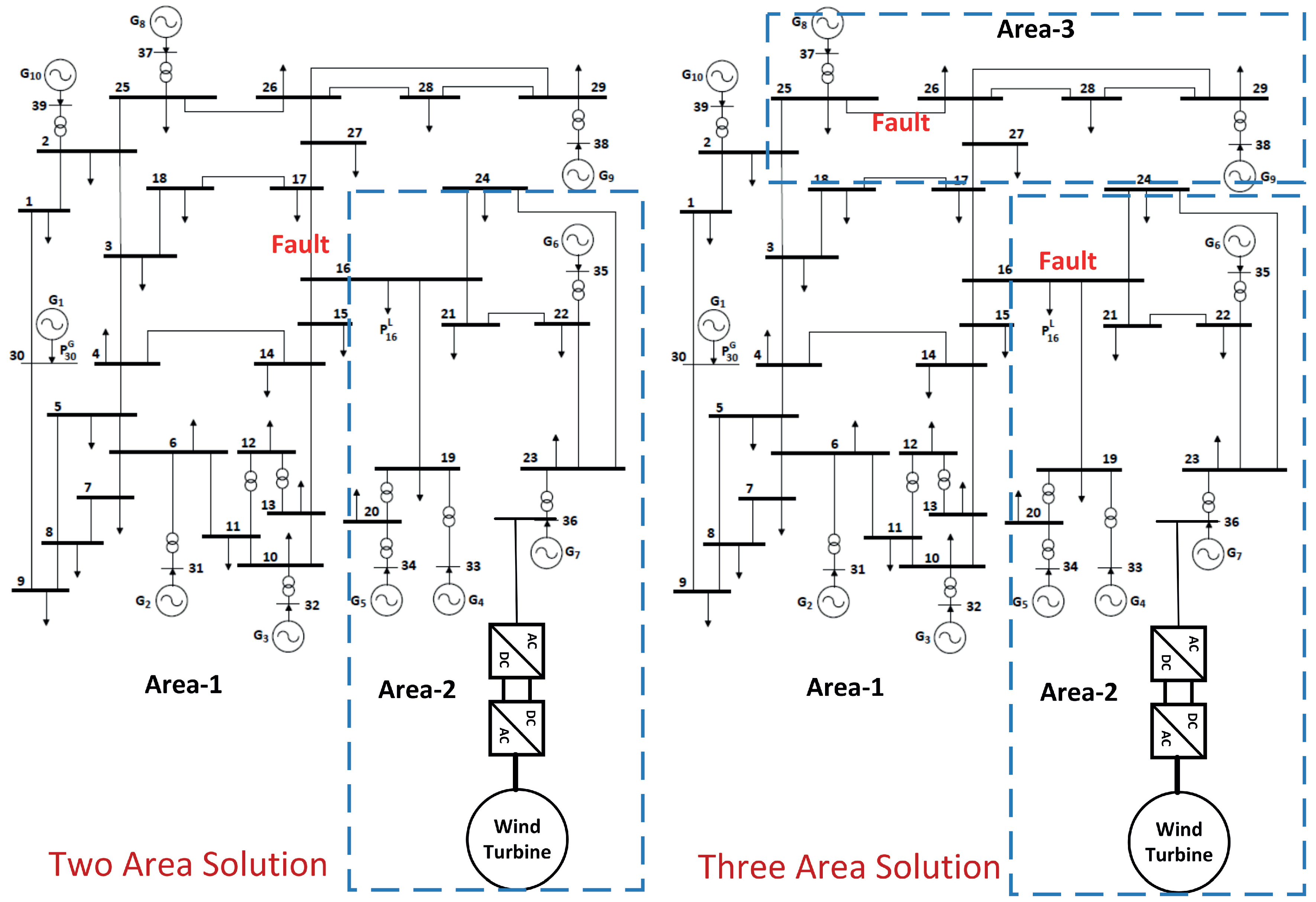
2. System Under Consideration
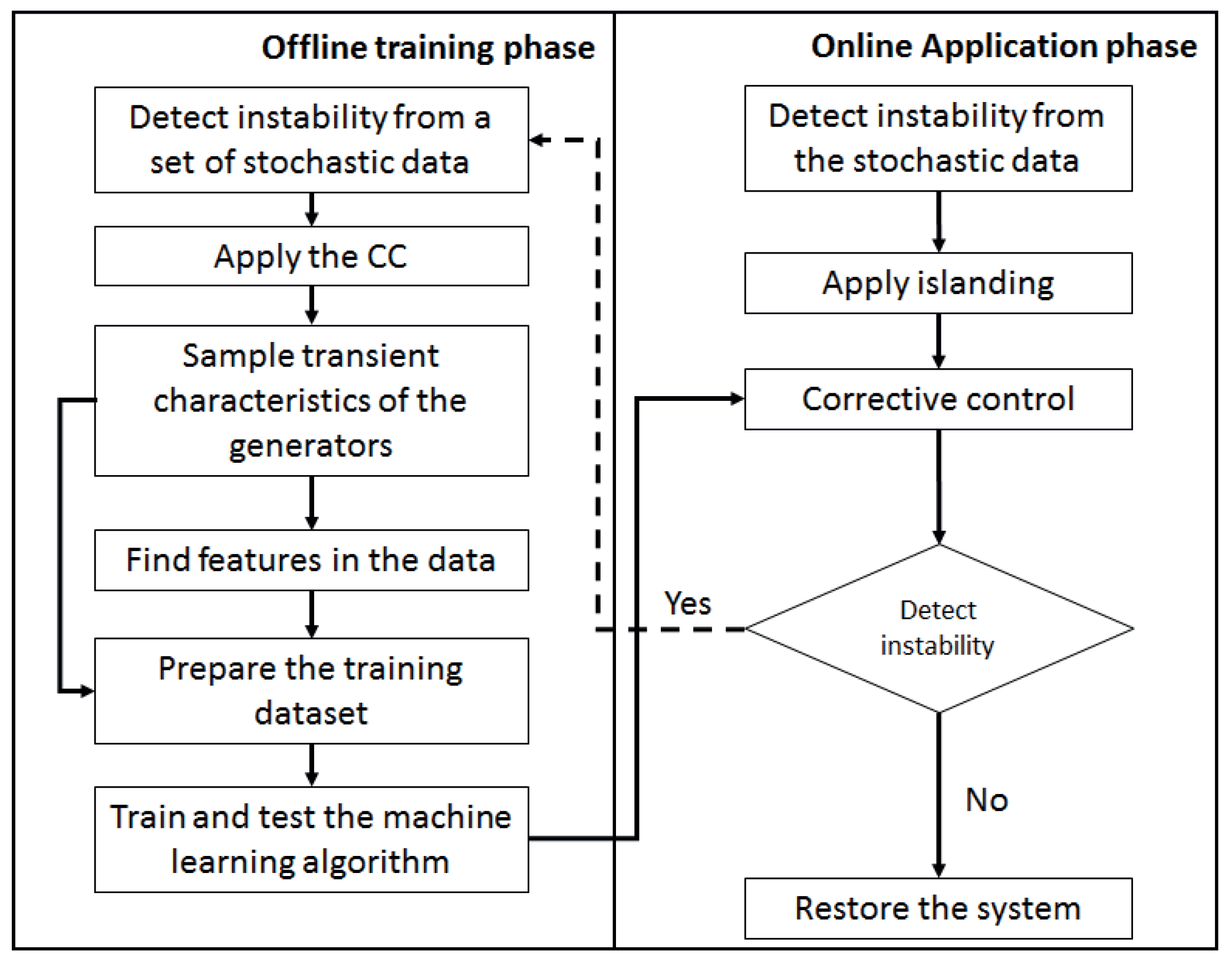
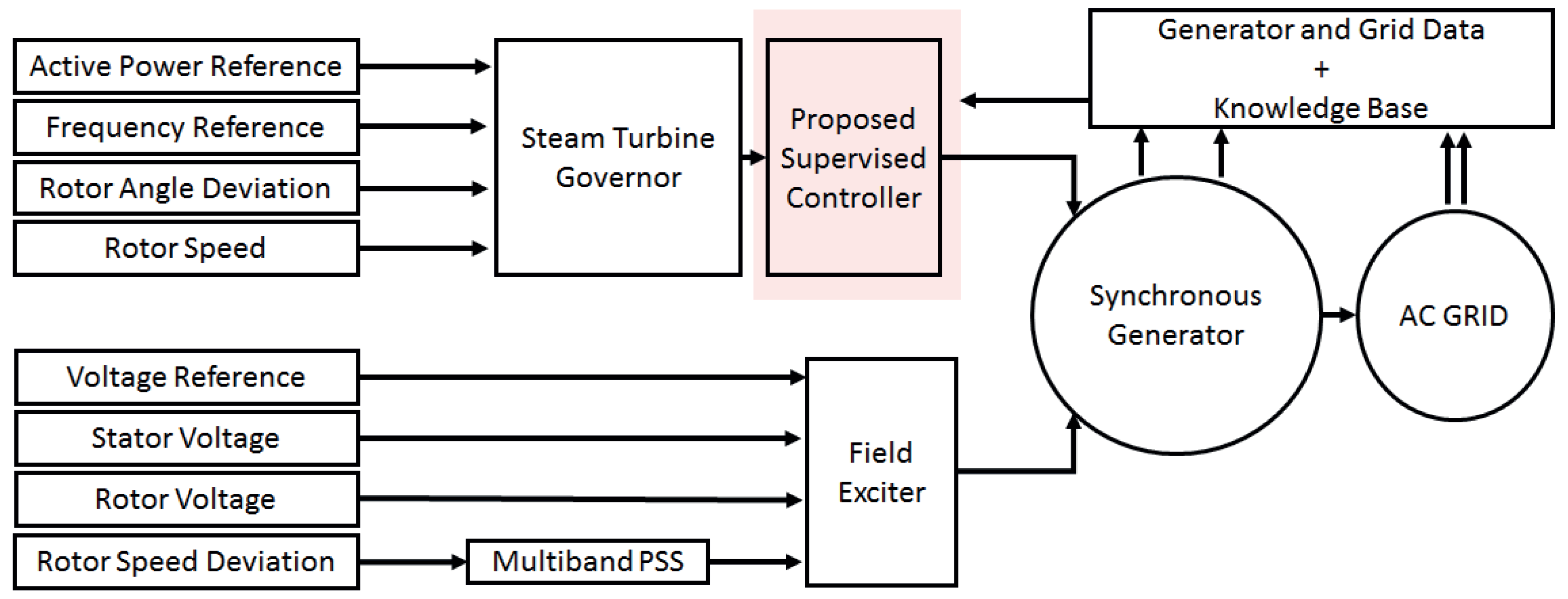
3. The Proposed Supervised Control
3.1. Controlled Islanding
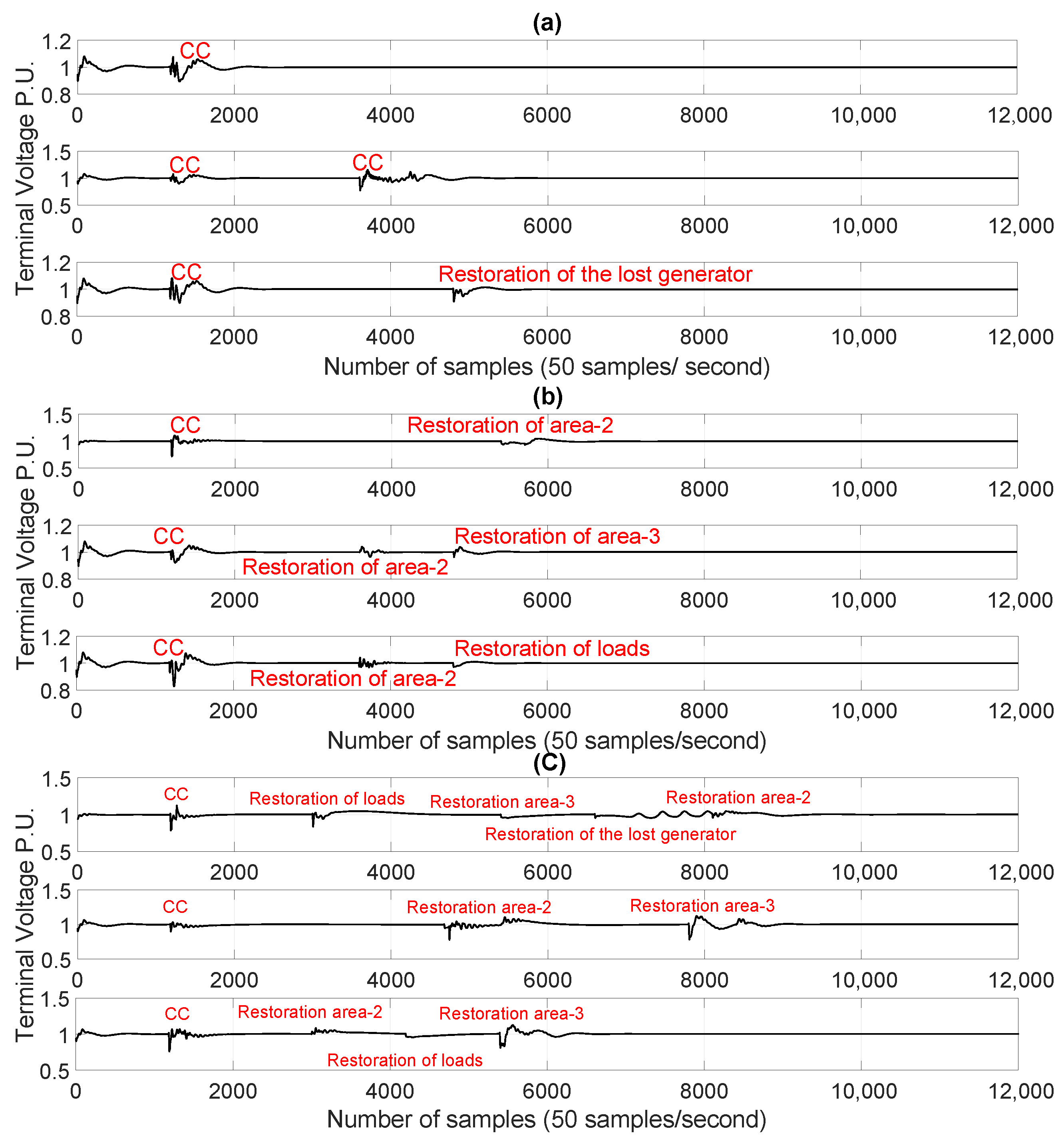
3.2. The Corrective Control
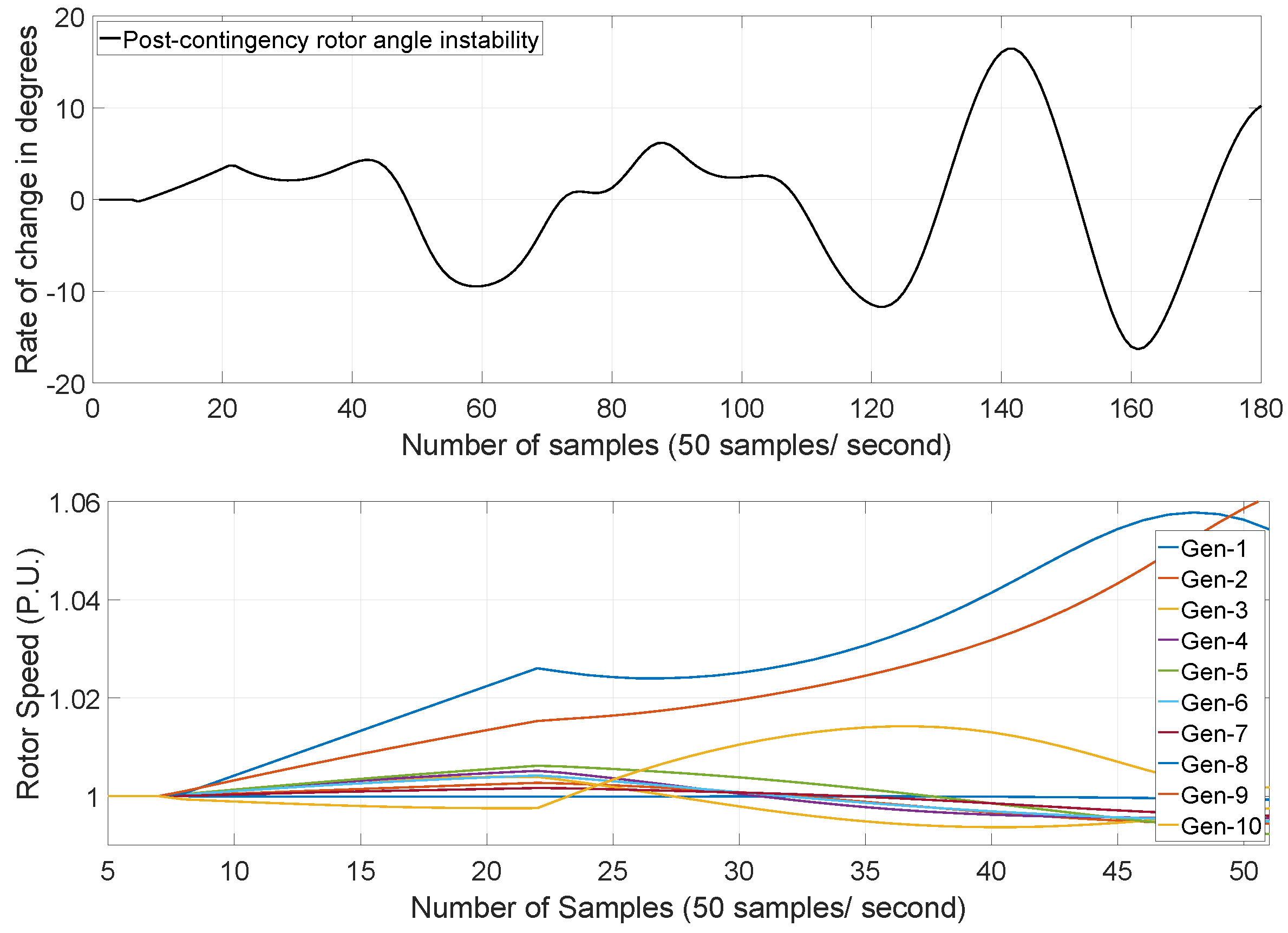
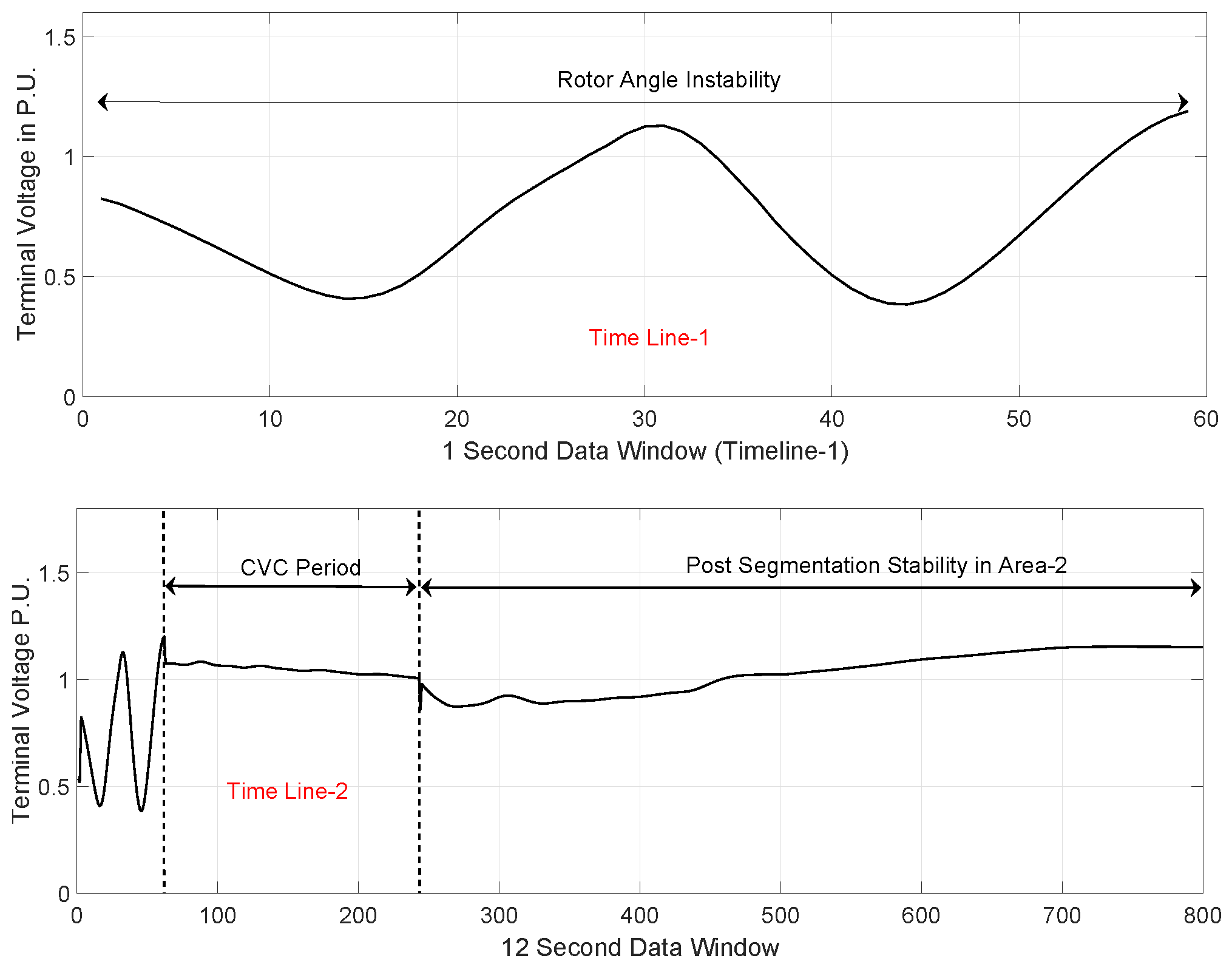
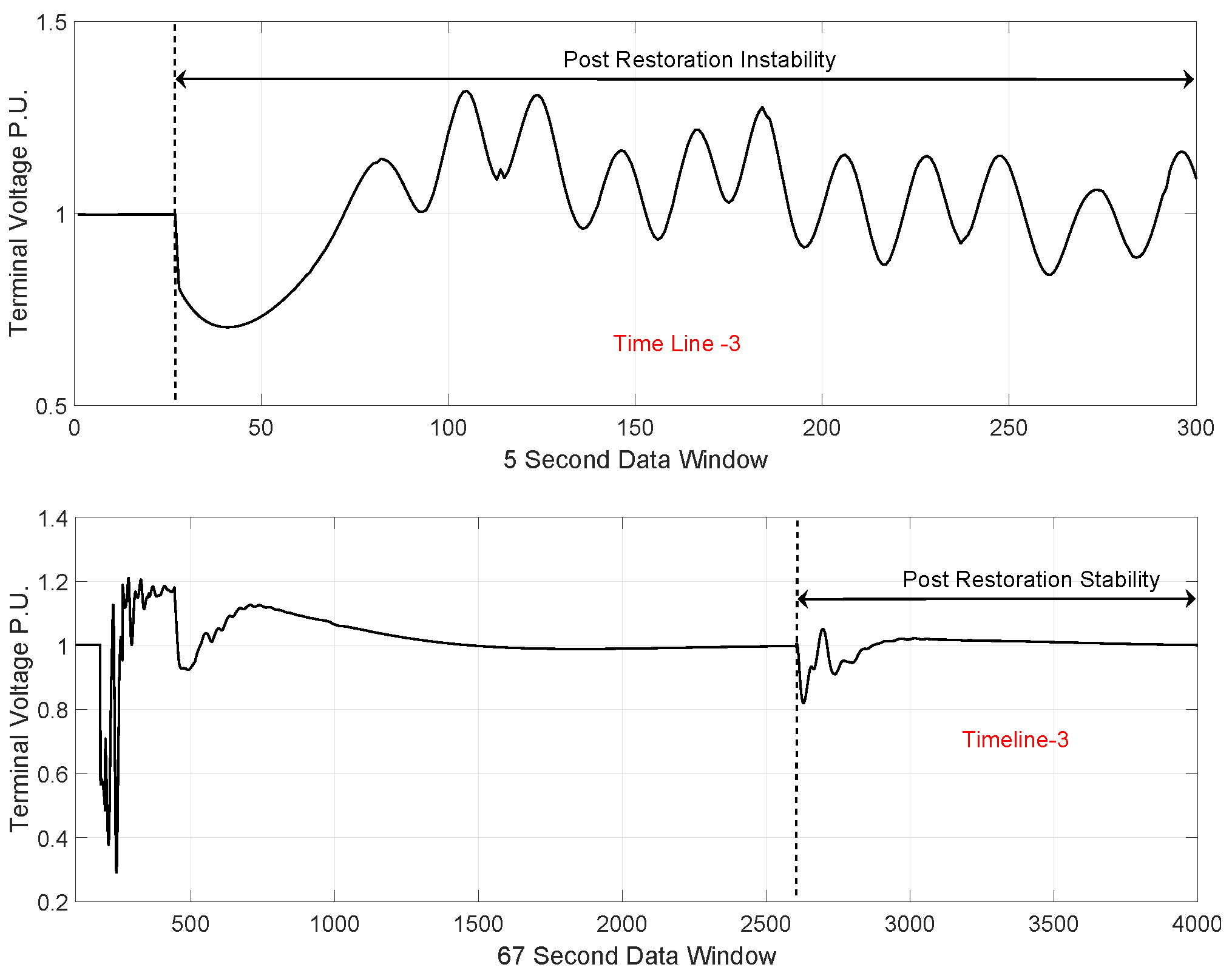
3.3. Power System Events
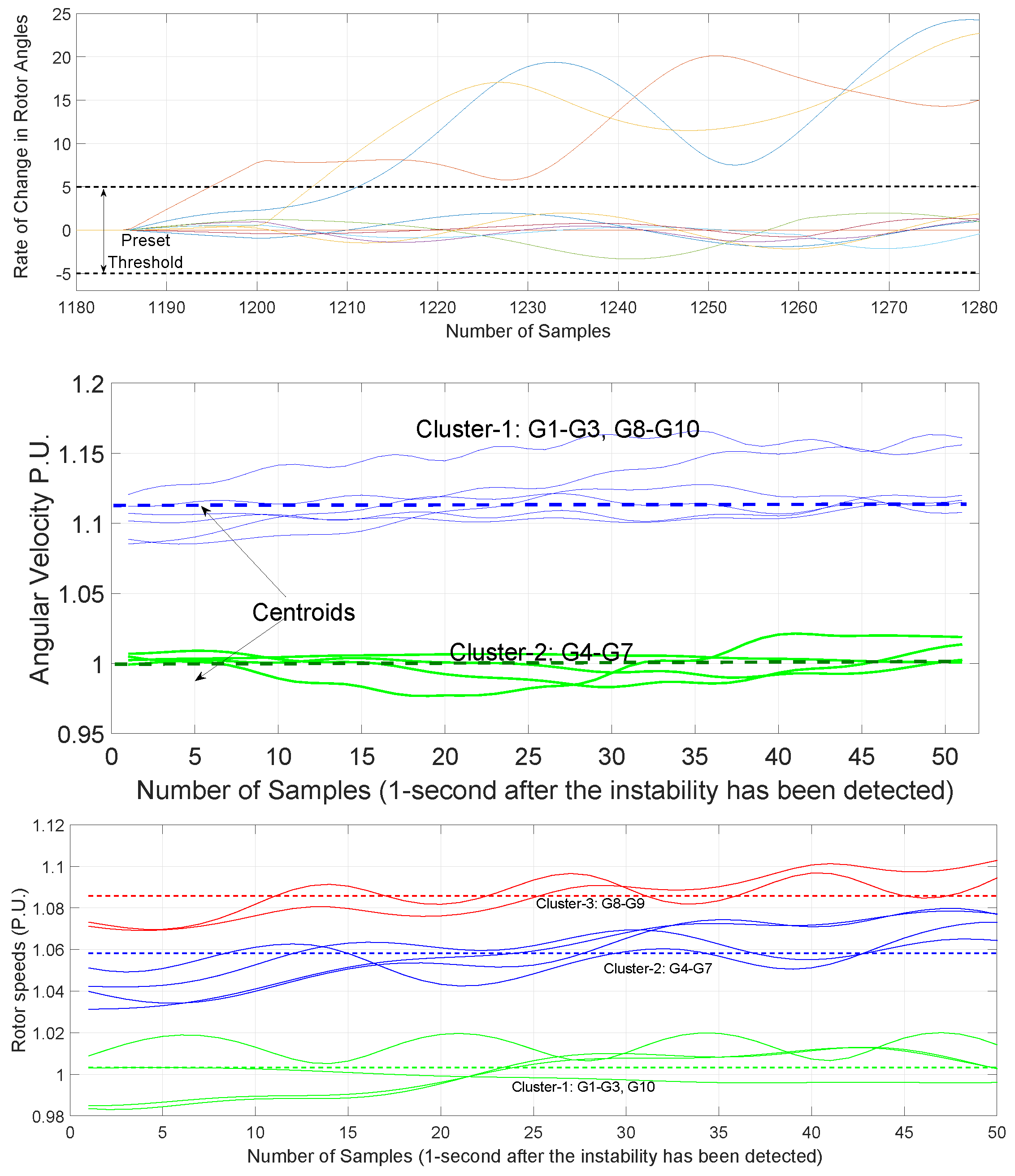
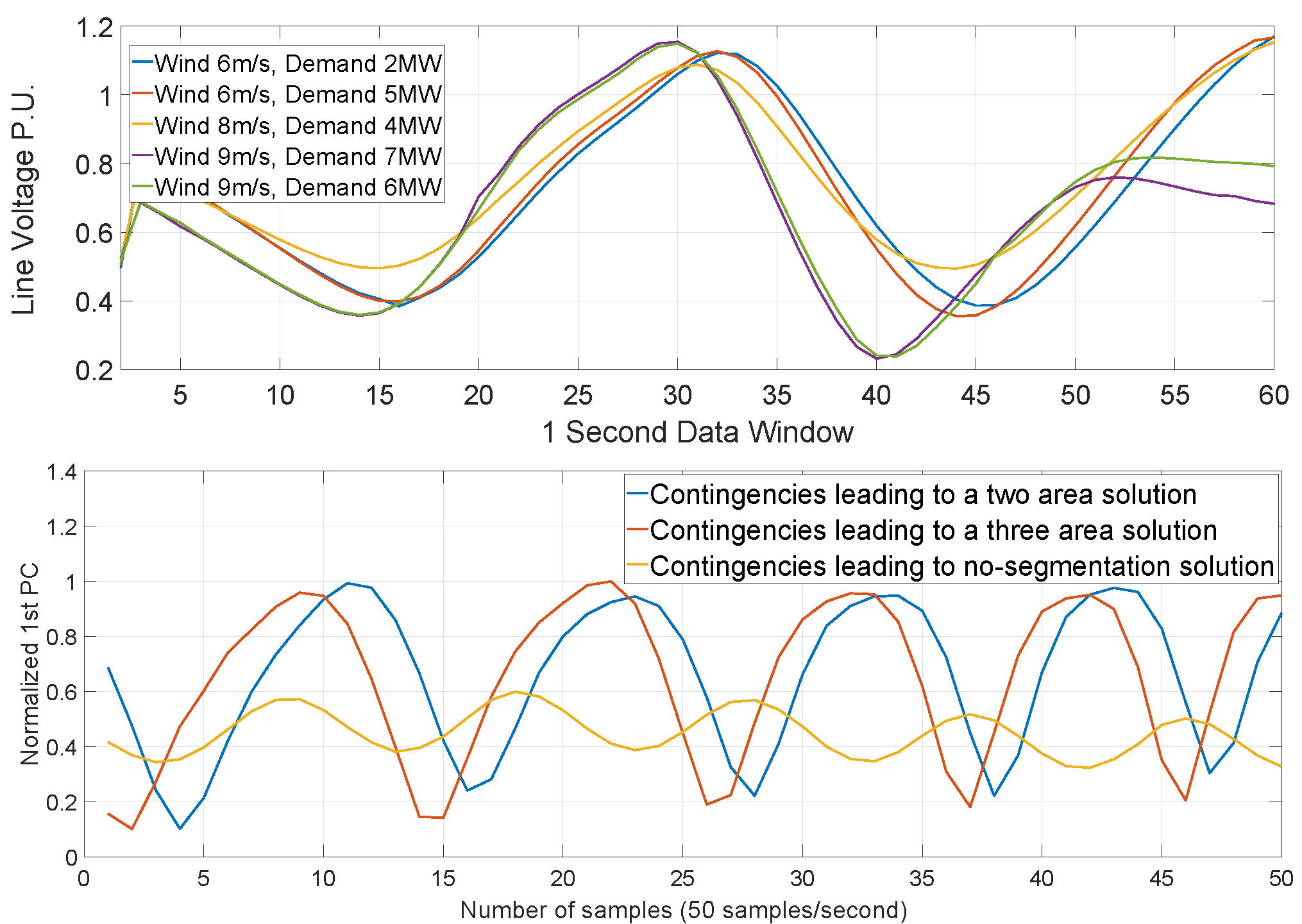
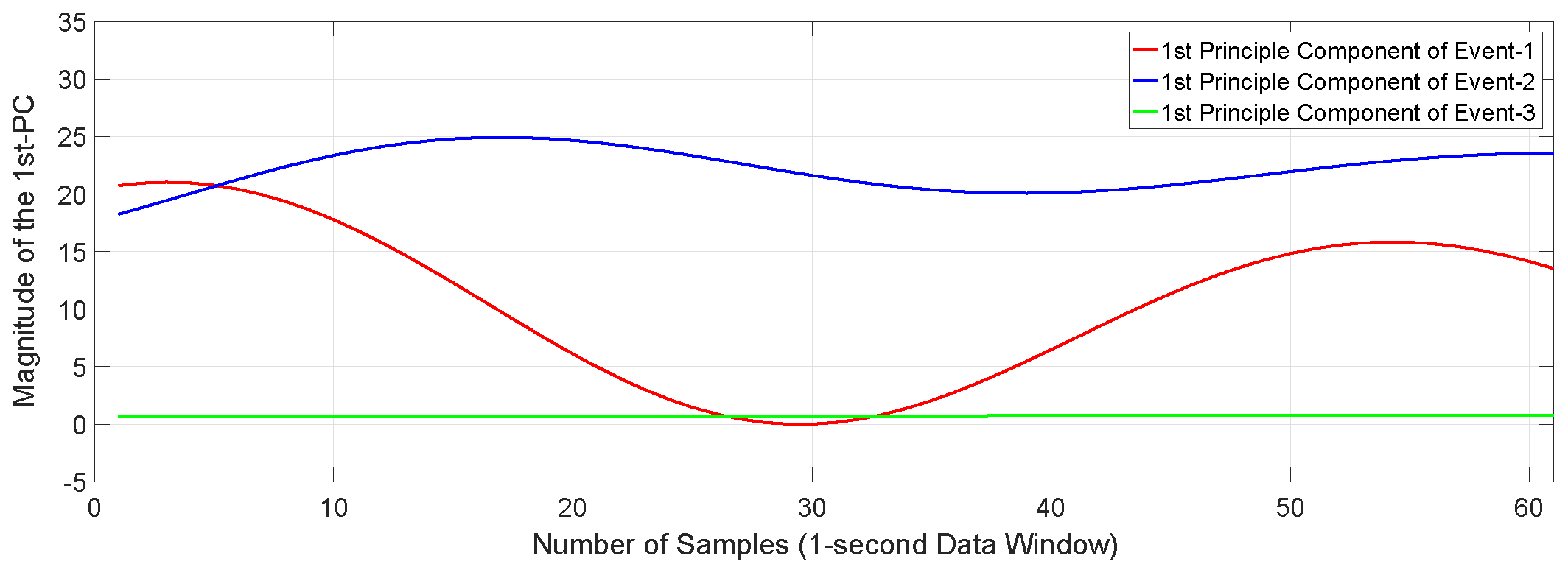
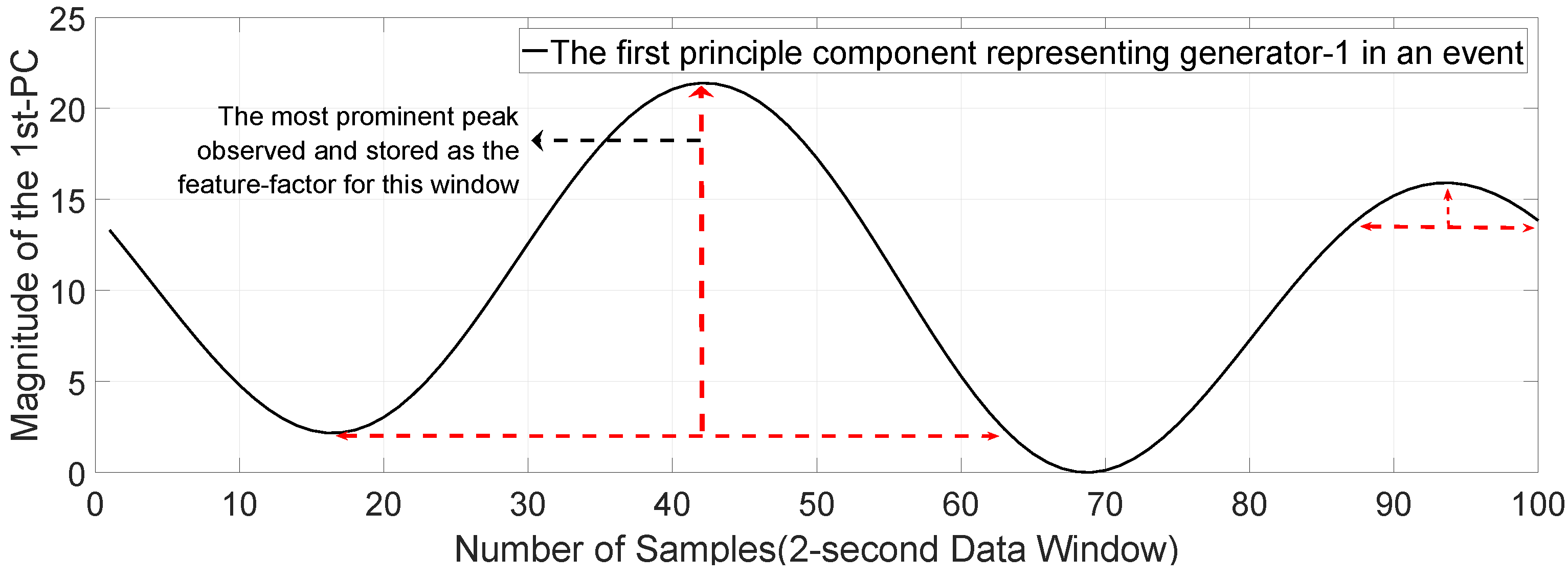
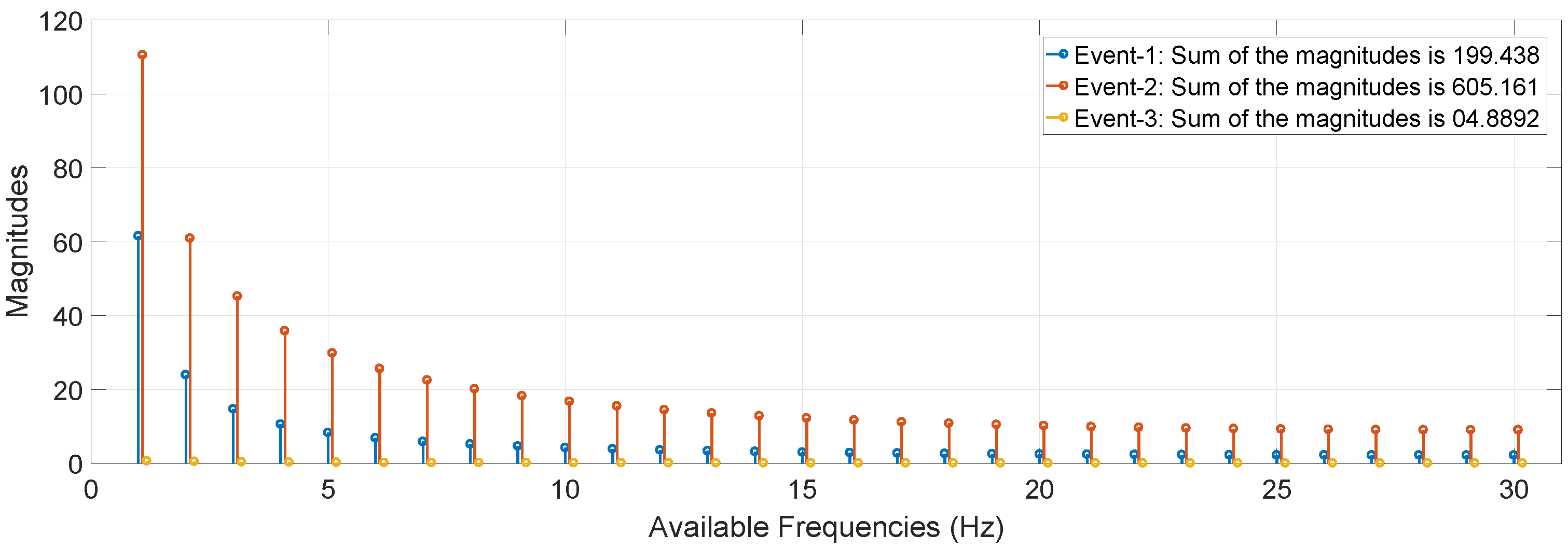
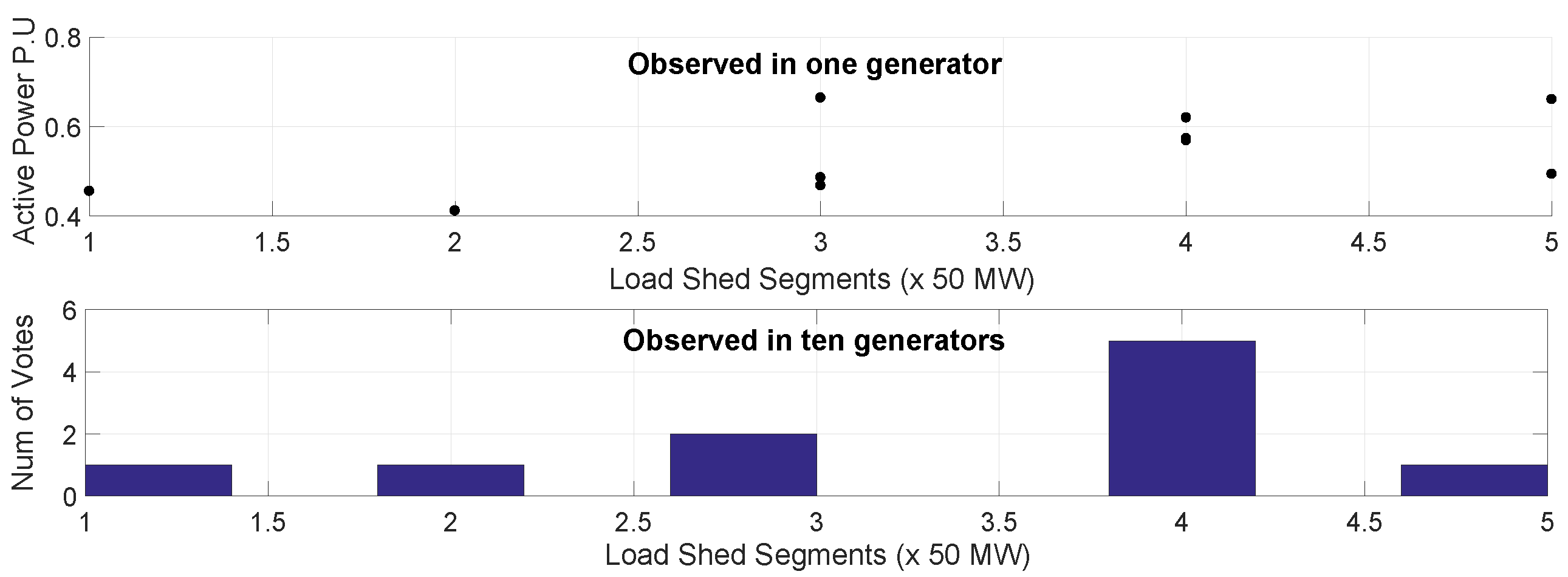
3.4. Available Observed Features
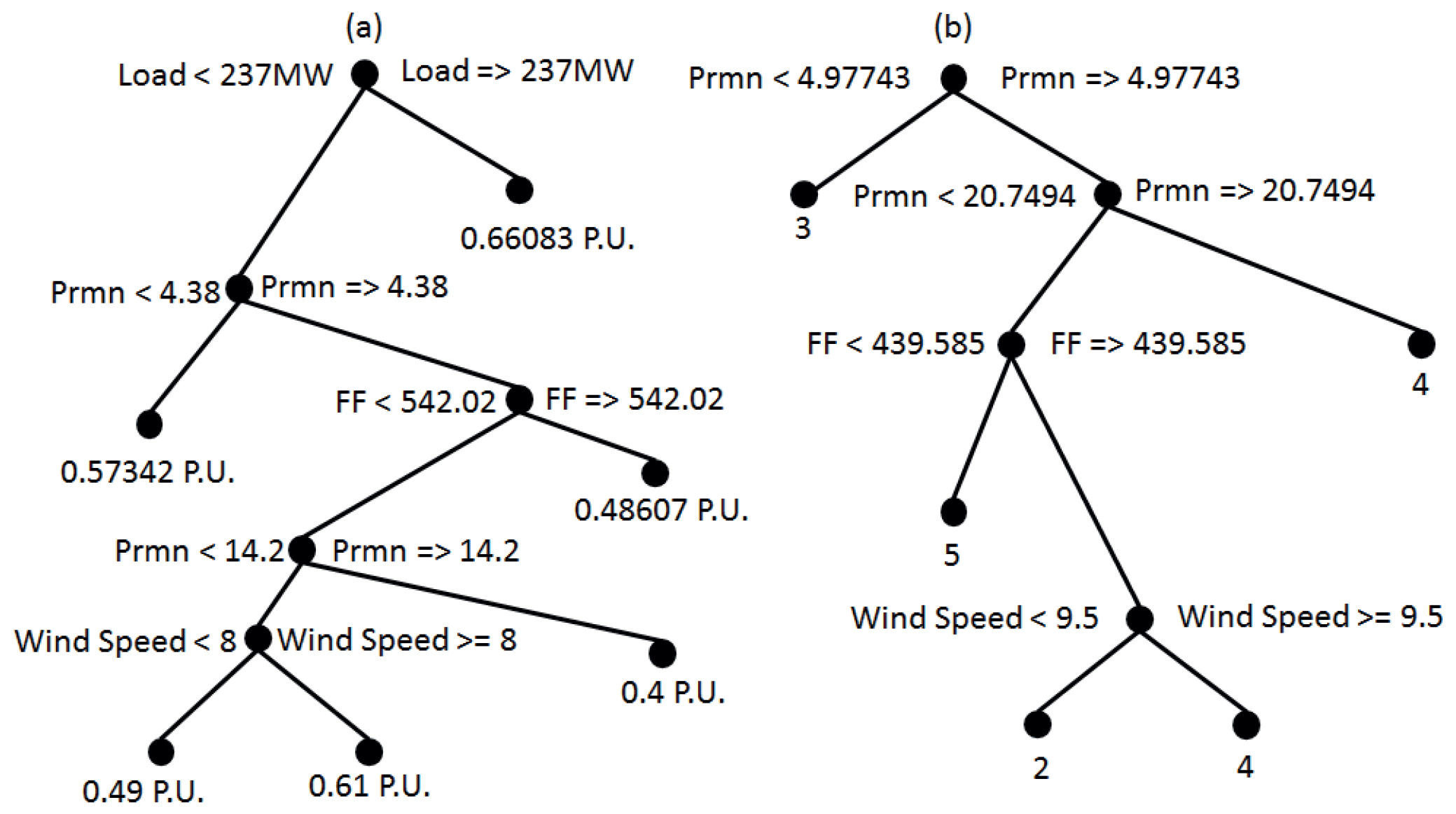
3.5. Multiclass Classifier
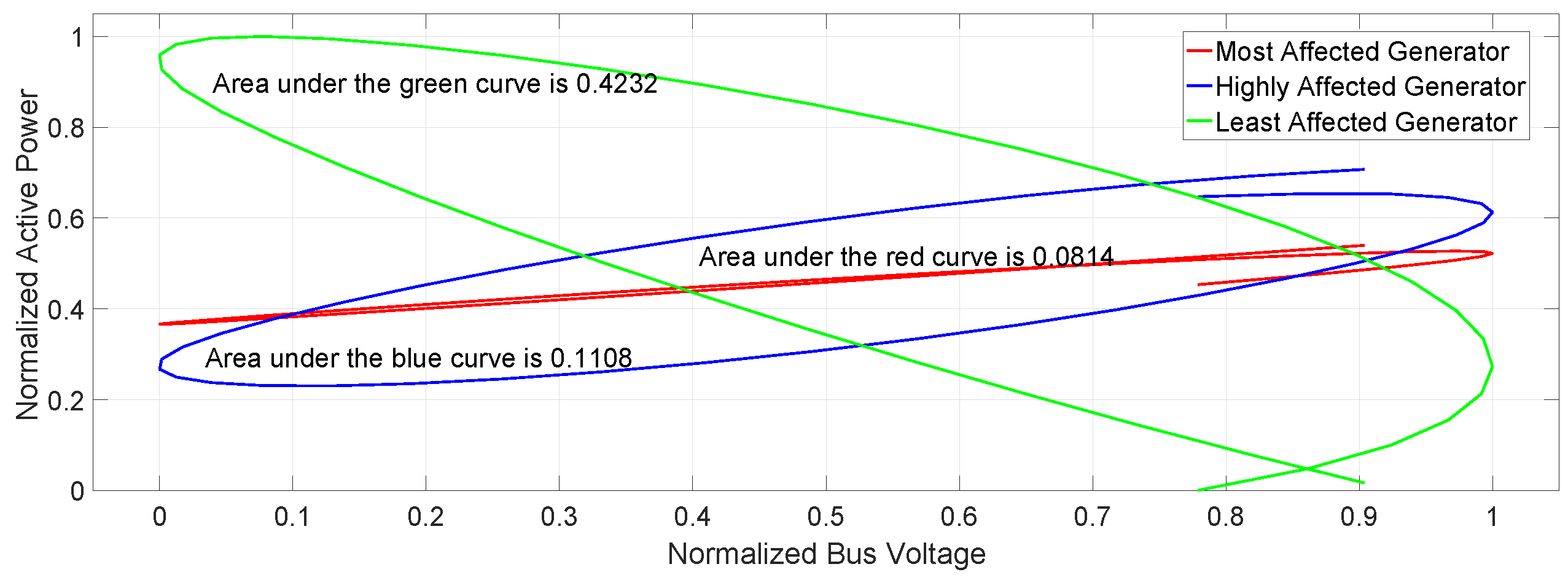
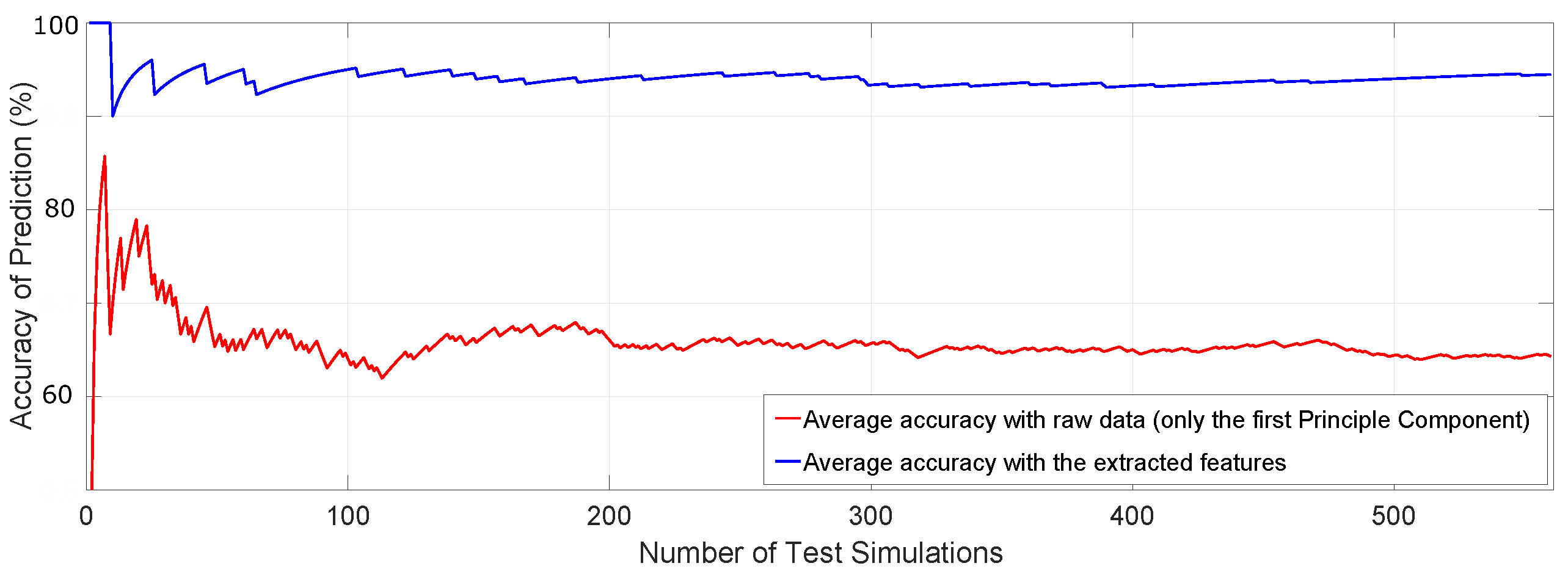
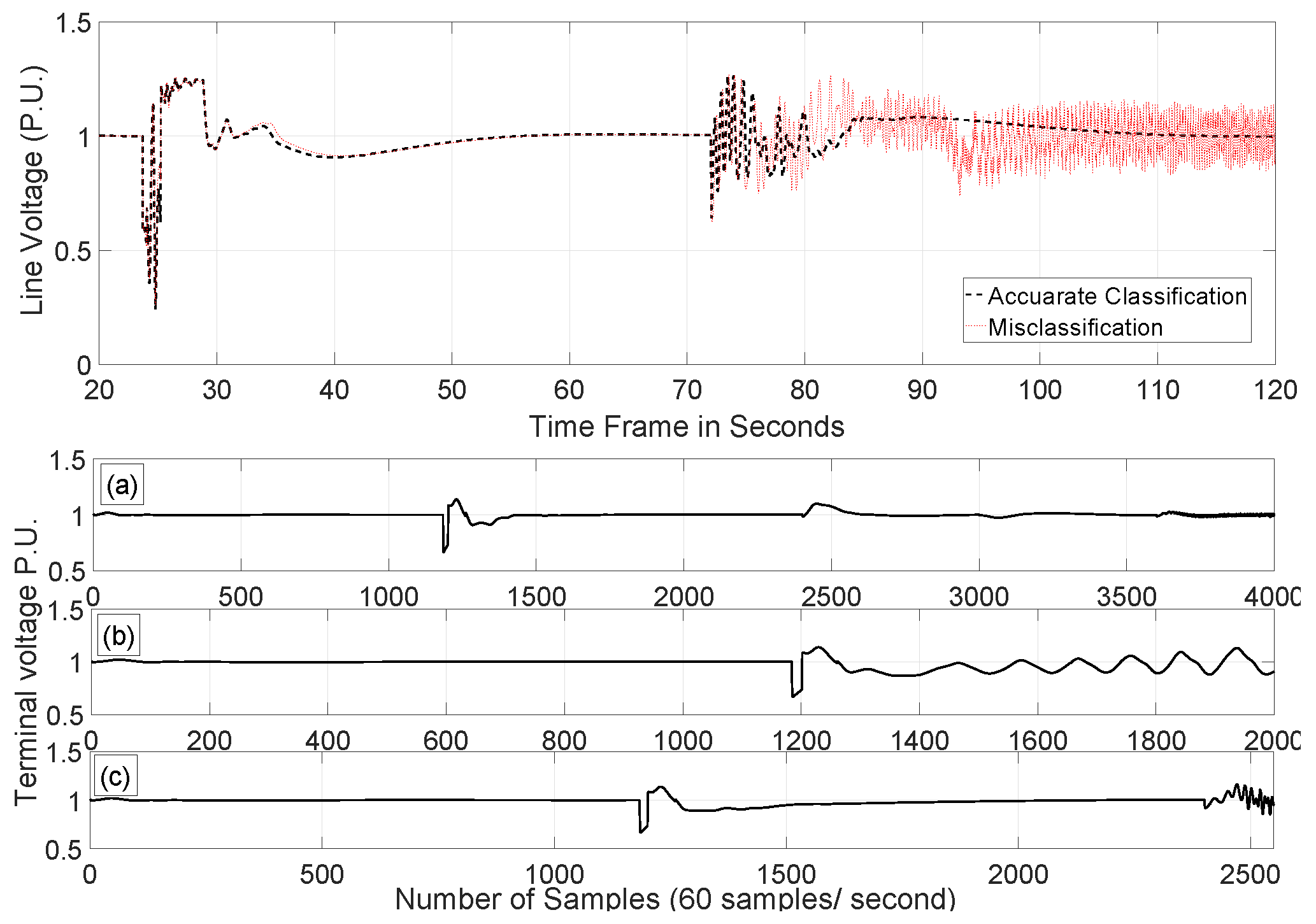
4. Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zhang, J.; Zheng, X.; Wang, Z.; Guan, L.; Chung, C.Y. Power System Sensitivity Identification 2014;Inherent System Properties and Data Quality. IEEE Trans. Power Syst. 2017, 32, 2756–2766. [Google Scholar] [CrossRef]
- Al Karim, M.; Currie, J.; Lie, T.T. A machine learning based optimized energy dispatching scheme for restoring a hybrid microgrid. Electr. Power Syst. Res. 2018, 155, 206–215. [Google Scholar] [CrossRef] [Green Version]
- Shahnia, F.; Chandrasena, R.P.S.; Rajakaruna, S.; Ghosh, A. Primary control level of parallel distributed energy resources converters in system of multiple interconnected autonomous microgrids within self-healing networks. IET Gener. Transm. Distrib. 2014, 8, 203–222. [Google Scholar] [CrossRef]
- Konstantelos, I.; Jamgotchian, G.; Tindemans, S.H.; Duchesne, P.; Cole, S.; Merckx, C.; Strbac, G.; Panciatici, P. Implementation of a Massively Parallel Dynamic Security Assessment Platform for Large-Scale Grids. IEEE Trans. Smart Grid 2017, 8, 1417–1426. [Google Scholar] [CrossRef] [Green Version]
- Zidan, A.; Khairalla, M.; Abdrabou, A.M.; Khalifa, T.; Shaban, K.; Abdrabou, A.; Shatshat, R.E.; Gaouda, A.M. Fault Detection, Isolation, and Service Restoration in Distribution Systems: State-of-the-Art and Future Trends. IEEE Trans. Smart Grid 2017, PP, 1–16. [Google Scholar] [CrossRef]
- Zhou, Y.; Arghandeh, R.; Konstantakopoulos, I.; Abdullah, S.; von Meier, A.; Spanos, C.J. Abnormal event detection with high resolution micro-PMU data. In Proceedings of the 2016 Power Systems Computation Conference (PSCC), Genoa, Italy, 20–24 June 2016; pp. 1–7. [Google Scholar] [CrossRef] [Green Version]
- Jin, S.; Huang, Z.; Diao, R.; Wu, D.; Chen, Y. Comparative Implementation of High Performance Computing for Power System Dynamic Simulations. IEEE Trans. Smart Grid 2017, 8, 1387–1395. [Google Scholar] [CrossRef]
- Khaitan, S.K. A survey of high-performance computing approaches in power systems. In Proceedings of the 2016 IEEE Power and Energy Society General Meeting (PESGM), Boston, MA, USA, 17–21 July 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Vasconcelos, M.H.; Carvalho, L.M.; Meirinhos, J.; Omont, N.; Gambier-Morel, P.; Jamgotchian, G.; Cirio, D.; Ciapessoni, E.; Pitto, A.; Konstantelos, I.; et al. Online security assessment with load and renewable generation uncertainty: The iTesla project approach. In Proceedings of the 2016 International Conference on Probabilistic Methods Applied to Power Systems (PMAPS), Beijing, China, 16–20 October 2016; pp. 1–8. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Xie, L.; Kumar, P.R. Power system event classification via dimensionality reduction of synchrophasor data. In Proceedings of the 2014 IEEE 8th Sensor Array and Multichannel Signal Processing Workshop (SAM), A Coruna, Spain, 22–25 June 2014; pp. 57–60. [Google Scholar] [CrossRef]
- Mohammadi, M.; Gharehpetian, G.B. Application of core vector machines for on-line voltage security assessment using a decisiontree-based feature selection algorithm. IET Gener. Transm. Distrib. 2009, 3, 701–712. [Google Scholar] [CrossRef]
- Jain, A.; Zongker, D. Feature selection: Evaluation, application, and small sample performance. IEEE Trans. Pattern Anal. Mach. Intell. 1997, 19, 153–158. [Google Scholar] [CrossRef] [Green Version]
- Niazi, K.; Arora, C.; Surana, S. Power system security evaluation using ANN: Feature selection using divergence. Electr. Power Syst. Res. 2004, 69, 161–167. [Google Scholar] [CrossRef]
- Geeganage, J.; Annakkage, U.D.; Weekes, T.; Archer, B.A. Application of Energy-Based Power System Features for Dynamic Security Assessment. IEEE Trans. Power Syst. 2015, 30, 1957–1965. [Google Scholar] [CrossRef] [Green Version]
- Abedinia, O.; Amjady, N.; Zareipour, H. A New Feature Selection Technique for Load and Price Forecast of Electrical Power Systems. IEEE Trans. Power Syst. 2017, 32, 62–74. [Google Scholar] [CrossRef]
- dos Santos, A.; de Barros, M.T.C. Sensitivity of voltage sags to network failure rate improvement. In Proceedings of the 2016 Power Systems Computation Conference (PSCC), Genoa, Italy, 20–24 June 2016; pp. 1–7. [Google Scholar] [CrossRef]
- Papadopoulos, P.N.; Guo, T.; Milanović, J.V. Probabilistic Framework for Online Identification of Dynamic Behavior of Power Systems With Renewable Generation. IEEE Trans. Power Syst. 2018, 33, 45–54. [Google Scholar] [CrossRef]
- Athay, T.; Podmore, R.; Virmani, S. A Practical Method for the Direct Analysis of Transient Stability. IEEE Trans. Power Appar. Syst. 1979, PAS-98, 573–584. [Google Scholar] [CrossRef]
- Bidram, A.; Davoudi, A. Hierarchical structure of microgrids control system. Smart Grid IEEE Trans. 2012, 3, 1963–1976. [Google Scholar] [CrossRef]
- Arunagirinathan, P.; Abdelsalam, H.A.; Venayagamoorthy, G.K. Remote power system stabilizer tuning using synchrophasor data. In Proceedings of the 2014 IEEE Symposium on Computational Intelligence Applications in Smart Grid (CIASG), Orlando, FL, USA, 9–12 December 2014; pp. 1–7. [Google Scholar] [CrossRef]
- Grondin, R.; Kamwa, I.; Trudel, G.; Gerin-Lajoie, L.; Taborda, J. Modeling and closed-loop validation of a new PSS concept, the multi-band PSS. In Proceedings of the 2003 IEEE Power Engineering Society General Meeting (IEEE Cat. No.03CH37491), Toronto, ON, Canada, 13–17 July 2003; Volume 3, p. 1809. [Google Scholar] [CrossRef]
- Lee, D. Ieee recommended practice for excitation system models for power system stability studies (ieee std 421.5-1992). Energy Dev. Power Gener. Comm. Power Eng. Soc. 1992, 95, 96. [Google Scholar]
- Grondin, R.; Kamwa, I.; Soulieres, L.; Potvin, J.; Champagne, R. An approach to PSS design for transient stability improvement through supplementary damping of the common low-frequency. IEEE Trans. Power Syst. 1993, 8, 954–963. [Google Scholar] [CrossRef]
- Liu, D.; Antsaklis, P.J. Stability and Control of Dynamical Systems with Applications: A Tribute to Anthony N. Michel; Springer Science & Business Media: Berlin, Germany, 2012. [Google Scholar]
- Teymouri, F.; Amraee, T.; Saberi, H.; Capitanescu, F. Towards Controlled Islanding for Enhancing Power Grid Resilience Considering Frequency Stability Constraints. IEEE Trans. Smart Grid 2017, 10, 1735–1746. [Google Scholar] [CrossRef]
- Rabiee, A.; Soroudi, A.; Keane, A. Risk-Averse Preventive Voltage Control of AC/DC Power Systems Including Wind Power Generation. IEEE Trans. Sustain. Energy 2015, 6, 1494–1505. [Google Scholar] [CrossRef]
- Babazadeh, M.; Karimi, H. Robust decentralized control for islanded operation of a microgrid. In Proceedings of the 2011 IEEE Power and Energy Society General Meeting, Detroit, MI, USA, 24–28 July 2011; pp. 1–8. [Google Scholar] [CrossRef]
- Vittal, E.; O’Malley, M.; Keane, A. Rotor angle stability with high penetrations of wind generation. IEEE Trans. Power Syst. 2012, 27, 353–362. [Google Scholar] [CrossRef]
- Hijazi, H.L.; Mak, T.W.; Van Hentenryck, P. Power System Restoration With Transient Stability. In Proceedings of the AAAI, Austin, TX, USA, 25–30 January 2015; pp. 658–664. [Google Scholar]
- Wang, Z.; Makram, E.B.; Venayagamoorthy, G.K.; Ji, C. Dynamic estimation of rotor angle deviation of a generator in multi-machine power systems. Electr. Power Syst. Res. 2013, 97, 1–9. [Google Scholar] [CrossRef]
- Rabiee, A.; Soroudi, A.; Mohammadi-ivatloo, B.; Parniani, M. Corrective Voltage Control Scheme Considering Demand Response and Stochastic Wind Power. IEEE Trans. Power Syst. 2014, 29, 2965–2973. [Google Scholar] [CrossRef] [Green Version]
- Genc, I.; Diao, R.; Vittal, V.; Kolluri, S.; Mandal, S. Decision Tree-Based Preventive and Corrective Control Applications for Dynamic Security Enhancement in Power Systems. IEEE Trans. Power Syst. 2010, 25, 1611–1619. [Google Scholar] [CrossRef]
- Karim, M.A.; Currie, J.; Lie, T.T. A distributed machine learning approach for the secondary voltage control of an Islanded micro-grid. In Proceedings of the 2016 IEEE Innovative Smart Grid Technologies—Asia (ISGT-Asia), Melbourne, Australia, 28 November–1 December 2016; pp. 611–616. [Google Scholar] [CrossRef] [Green Version]
- Guo, T.; Milanović, J.V. Online Identification of Power System Dynamic Signature Using PMU Measurements and Data Mining. IEEE Trans. Power Syst. 2016, 31, 1760–1768. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Nguyen, V.L. Power System Security Restoration by Secondary Control. In Proceedings of the 2007 IEEE Power Engineering Society General Meeting, Tampa, FL, USA, 24–28 June 2007; pp. 1–8. [Google Scholar] [CrossRef]
- Zhang, C.; Li, Y.; Yu, Z.; Tian, F. Feature selection of power system transient stability assessment based on random forest and recursive feature elimination. In Proceedings of the 2016 IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), Xi’an, China, 25–28 October 2016; pp. 1264–1268. [Google Scholar] [CrossRef]
- Jurado, S.; Nebot, À.; Mugica, F.; Avellana, N. Hybrid methodologies for electricity load forecasting: Entropy-based feature selection with machine learning and soft computing techniques. Energy 2015, 86, 276–291. [Google Scholar] [CrossRef] [Green Version]
- Honkala, I.S.; Laihonen, T.K. The probability of undetected error can have several local maxima. IEEE Trans. Inf. Theory 1999, 45, 2537–2539. [Google Scholar] [CrossRef]
- Abel, E.W.; Arkidis, N.S.; Forster, A. Inter-scale local maxima-a new technique for wavelet analysis of EMG signals. In Proceedings of the 20th Annual International Conference of the IEEE Engineering in Medicine and Biology Society. Vol.20 Biomedical Engineering Towards the Year 2000 and Beyond (Cat. No.98CH36286), Hong Kong, China, 1 November 1998; Volume 3, pp. 1471–1473. [Google Scholar] [CrossRef]
- Griffié, J.; Boelen, L.; Burn, G.; Cope, A.P.; Owen, D.M. Topographic prominence as a method for cluster identification in single-molecule localisation data. J. Biophotonics 2015, 8, 925–934. [Google Scholar] [CrossRef]
- Hu, Z.; Xiong, M.; Shang, H.; Deng, A. Anti-Interference Measurement Methods of the Coupled Transmission-Line Capacitance Parameters Based on the Harmonic Components. IEEE Trans. Power Deliv. 2016, 31, 2464–2472. [Google Scholar] [CrossRef]
- Bühlmann, P. Bagging, boosting and ensemble methods. In Handbook of Computational Statistics; Springer: Berlin/Heidelberg, Germany, 2012; pp. 985–1022. [Google Scholar]
| Decisions | Wind Speed (m/s) | Variable Demand (MW) | Contingencies |
|---|---|---|---|
| 1 | 10 | 546 | Loss of Genearator-4. No segmentation is required |
| 2 | 12 | 609 | Loss of Genearator-9. No segmentation is required |
| 3 | 8 | 405 | Three phase fault at Bus-16. Two area segmentation |
| 4 | 12 | 35 | Three phase fault at Bus-19. Two area segmentation |
| 5 | 8.2 | 662 | Three phase fault at Bus-16 and Bus-25. Three area segmentation |
| ... | ... | ... | ... |
| ... | ... | ... | ... |
| n | 11.2 | 408 | Three phase fault at Bus-25 and loss of Generator-4. Three area segmentation |
| Decisions | Wind Speed (m/s) | Variable Demand (MW) | Snsvt (Sensitivity) | Prmn (Prominence) | FF (Frequency Factor) |
|---|---|---|---|---|---|
| 1 | 12 | 35 | 0.1384 | 34.1 | 197.4 |
| 2 | 6 | 145 | 0.1333 | 0.659 | 34.48 |
| 3 | 8 | 405 | 0.1636 | 0.0566 | 7.5878 |
| .. | .. | .. | .. | .. | .. |
| .. | .. | .. | .. | .. | .. |
| n | 11 | 790 | 0.1424 | 0.593 | 25.2 |
| Decisions | Wind Speed (m/s) | Variable Demand (MW) | Snsvt (Fault-1) | Snsvt (Fault-2) | Prmn (Prominence) | FF (Frequency Factor) |
|---|---|---|---|---|---|---|
| 1 | 8.2 | 662 | 0.8770 | 1.0195 | 0.4374 | 13.7012 |
| 2 | 10 | 372 | 0.9349 | 0.9910 | 0.7647 | 178.1212 |
| .. | .. | .. | .. | .. | .. | .. |
| .. | .. | .. | .. | .. | .. | .. |
| n | 11.2 | 408 | 0.8515 | 0.2779 | 0.7099 | 32.4 |
| Decisions | Wind Speed (m/s) | Variable Demand (MW) | Snsvt (Sensitivity) | Prmn (Prominence) | FF (Frequency Factor) |
|---|---|---|---|---|---|
| 1 | 9.9965 | 252 | 0.2192 | 0.0008 | 46.7454 |
| 2 | 10 | 546 | 0.2119 | 0.2541 | 46.8115 |
| .. | .. | .. | .. | .. | .. |
| .. | .. | .. | .. | .. | .. |
| n | 12 | 609 | 0.1547 | 0.1291 | 9.56 |
| Generator | Proposed Method | Ensemble of Clusters and Decision Tree | ANN | PCA and Decision Tree |
|---|---|---|---|---|
| 4 | 96.2 | 89.4 | <40 | 83.71 |
| 5 | 96.4 | 96.4 | <40 | 82.02 |
| 6 | 94.64 | 94.56 | <40 | 84.2 |
| 7 | 95.08 | 93.33 | <40 | 65.72 |
| 8 | 94.32 | 90.17 | <40 | 67.23 |
| 9 | 95.48 | 92.8 | <40 | 66.49 |
| 10 | 93.8 | 91.1 | <40 | 89.7 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karim, M.A.; Currie, J.; Lie, T.-T. Distributed Machine Learning on Dynamic Power System Data Features to Improve Resiliency for the Purpose of Self-Healing. Energies 2020, 13, 3494. https://doi.org/10.3390/en13133494
Karim MA, Currie J, Lie T-T. Distributed Machine Learning on Dynamic Power System Data Features to Improve Resiliency for the Purpose of Self-Healing. Energies. 2020; 13(13):3494. https://doi.org/10.3390/en13133494
Chicago/Turabian StyleKarim, Miftah Al, Jonathan Currie, and Tek-Tjing Lie. 2020. "Distributed Machine Learning on Dynamic Power System Data Features to Improve Resiliency for the Purpose of Self-Healing" Energies 13, no. 13: 3494. https://doi.org/10.3390/en13133494
APA StyleKarim, M. A., Currie, J., & Lie, T.-T. (2020). Distributed Machine Learning on Dynamic Power System Data Features to Improve Resiliency for the Purpose of Self-Healing. Energies, 13(13), 3494. https://doi.org/10.3390/en13133494







