Maximum Utilization of Dynamic Rating Operated Distribution Transformer (DRoDT) with Battery Energy Storage System: Analysis on Impact from Battery Electric Vehicles Charging

Abstract

This paper investigates thermal overloading, voltage dips and insulation failure across a distribution transformer (DT), under residential and battery electric vehicle (BEV) loadings. The objective of this paper is to discuss the charging impact of BEVs on voltage across consumer-service points, as well as across the life of paper insulation under varying ambient temperatures (during winter and summer), with and without a centralized battery energy storage system (BESS). This study contributes in two ways. The first part of this study deals with coordinated and uncoordinated BEV charging scenarios. The second part of this study deals with maximum utilization of a test DT rated under dynamic thermal rating (DRoDT). The DRoDT integration with BESS is carried out to flatten the load spikes, to obtain maximum DT utilization, to achieve active power and voltage supports in addition to an enhanced DT lifespan. The obtained results indicate that, when test DT operates under the proposed hybrid technique (combining both dynamic transformer ratings and a centralized BESS), it attains maximum utilization, lower hot-spot temperature, enhanced lifespan, less degraded paper insulation and an improved voltage across each consumer service point. The proposed technique is furthermore found effective in maintaining the loading across the distribution transformer within the nominal limits. However, under excess loading during peak hours, the proposed technique provides relief to the DT to a certain extent. To achieve an optimal DT operation and an enhanced BESS lifespan, the BESS is operated under nominal charging and discharging cyclic limits. Under the proposed DRoDT integration with BESS, DT attains 25.9% more life when loaded with coordinated BEV charging, in comparison to no BESS integration under the same loading scenario. The worst loading due to uncoordinated BEV charging also brings 51% increase in DT life when loaded under the proposed technique.

1. Introduction

A rising demand in battery electric vehicles (BEVs) is becoming the major cause of both the underutilization and overutilization of distribution transformers (DTs) in low-voltage (LV) distribution networks. The BEV fleet has got the potential to underutilize DTs (loaded below the design rating) or overutilize DTs (loaded above the design rating), based on their charging and demand profiles. An uncoordinated BEV charging load integration with the base load will significantly raise the hot-spot temperature inside the windings, becoming an ultimate cause of insulation degradation through pyrolysis [1]. Additionally, due to aggregated BEV charging, distribution network operators (DNOs) are seen facing added complexity in securing and managing a reliable electricity flow in their networks [2,3]. Hence, if left unaddressed, the problem can lead to cause congestion in the distribution networks as well as can bring a non-optimal asset loading across assets like cables, feeders and distribution transformers.

BEV charging can take place under both fast and slow charging modes. Slow BEV charging can be further classified in coordinated and uncoordinated charging. An uncoordinated BEV charging is the type of charging which not only affects DT insulation but also causes phase and line voltage drops in addition to increasing the system load factor [4]. Similarly, authors in Reference [4] have also demonstrated that uncoordinated BEV charging can significantly increase peak loading in a distribution network regardless of uncontrolled or non-resilient charging patterns. Despite causing insecurity and congestion in the network, the uncoordinated BEV charging is still widely adopted in contrast to smart BEV charging, mainly due to lack of communication infrastructures to enable demand response-based BEV charging [3]. Under uncoordinated BEV charging, a vehicle is allowed to be charged when plugged. This type of charging causes load spikes which can cause DT overloading. A DT operating under maximum utilization can address uncoordinated-BEV-charging-associated problems, provided it can handle the rising hot-spot temperature under no voltage violations, particularly at the end-most residential loads. As shown in Reference [5], uncoordinated BEV charging causes severe voltage violations and DT overloading, leading to the likelihood of N-1 state.

The coordinated BEV charging method can reduce and/or eliminate congestion in the LV network, besides delaying the costly asset upgrades. Hence, by providing technical and economic benefits to DNOs, coordinated BEV charging is thus considered a better option over uncoordinated BEV charging. BEVs under coordinated BEV charging are not allowed to be charged at the plug-in time; instead, they are charged at the time defined by DNOs, usually the off-peak time. The benefits associated with delayed BEV charging are illustrated in References [4,6,7]; the authors in Reference [4] have claimed that coordinated-BEV-charging-based implementation will be able to improve asset efficiency, power quality and voltage regulation in the LV network. The coordinated BEV charging enables coordination between local and centralized control systems leading towards effective congestion management and participation in the electricity trading [6].

To obtain a reliable electricity flow and an efficient and/or optimal DT loading, increased BEV penetration trend needs to be addressed through efficient charging techniques useful for both users and the utilities. As an immediate asset to facilitate BEV charging, the DT efficiency and lifespan are heavily influenced by available battery capacity, current drawn, charger efficiency and the power limit of BEV chargers. The recent research work as published in References [8,9,10,11] has suggested various viable techniques capable of addressing the LV network issues resulting from inefficient BEV charging. For instance, an optimized BEV charging schedule enables shifting the charging load and simultaneously contributes towards shaved peak load spikes [8]. Similarly, as suggested in Reference [9], an integrated technique combining the day-ahead load planning with optimized smart charging can be effective toward minimizing the network congestion. In Reference [10], a fuzzy logic control system was implemented to bring real-time communication between LV distribution system and BEVs, to control the battery state of charge (SoC) based on electricity pricing. The implementation of incentive-based regulation, as suggested in Reference [11] will allow peak load shifting to minimize network congestion.

The BEV penetration across distribution transformers is mainly seen as an unbalanced load, causing harmonics [12], increased loss of life and reduced DT lifespan [13]. The techniques like demand response [14], demand response with dynamic rating [15], demand response in an intelligent grid [16] and the usage of battery storage in the LV network to provide active and reactive power balancing [17,18] are considered as potential means towards relieving the loading stress across distribution transformers in addition to an enhanced DT lifespan. However, when DTs are loaded, particularly under uncoordinated BEV charging, the challenges like voltage regulation and peak shaving amid improved DT life and costly asset upgrade deferral become major concerns for DNOs. To counteract these problems, the hybrid approach is thus proposed in this study with an aim to solve DNO issues and bring maximum DT-utilization-based loading operation.

The remainder of this paper is organized as follows. Section 2 describes the motivation behind the research work. Section 3 illustrates the methodology of the proposed work. Section 4 describes the test system. Section 5 presents the results and highlights the discussion. Section 6 summarizes the findings and presents the future work.

2. Motivation

Residential load aggregation with BEV charging load is carried out to obtain maximum DT utilization, which is beneficial for users, as well as for DNOs, in terms of reducing both losses and the asset upgrading costs. This work is inspired by References [13,15]. In Reference [13], the algorithm is designed to provide the maximum DT utilization under short-term emergency overloading. Similarly, the algorithm in Reference [15] is designed to make sure ${\mathit{T}}_{\mathit{H}\mathit{S}\mathit{T}}$ remains under 110 °C, based on demand response and dynamic thermal rating techniques. Regardless of optimal DT design, loading the DTs above their normal cyclic loading will likely cause the temporary weakening in the dielectric strength of insulation paper and oil, due to presence of gas bubbles when the temperature reaches 140 °C or above [13]. The model can moreover be feasible under loss of supply to make sure that the DT loading duration is within the nominal DT limits [19]. Besides, the voltage regulation in Reference [13] was investigated without considering the voltage drop due to impedance of the service cable. Similarly, the study considered phase voltage regulation without analyzing the voltage drop across each household and/or the amount of voltage drop between the households nearest and farthest to the DT. Another drawback of the proposed algorithms in References [13,15] is their load profile consideration for a single day instead of the entire seasonal-based loading.

The seasonal-load profile can provide better estimates regarding maximum peak demand and its impact on thermal loading, as well as the total loss of life (LoL) of the DT, as demonstrated in Reference [20]. Furthermore, the algorithm in Reference [15] proposes maximum DT utilization without considering the BEV charging load. Therefore, utilizing such an approach in presence of BEV charging load will cause DT utilization above the maximum limits, leading to thermal overloads for a longer duration, particularly in case of slow BEV charging. Slow BEV charging moreover causes increased thermal overload time across the DTs. References [7,13] have considered loading the DT above the nominal thermal limits. The studies, however, lack in examining the impact of DT’S thermal overloading on voltage drop across each household, i.e., the thermal load causing voltage beyond minimum nominal limits, hence compromising the network reliability.

The work presented in References [21,22] has demonstrated the BESS application in the LV network. The loading impact of BEV charging on the DT is reduced through the stored energy [21], further useful to increase hosting capacity and reduce congestion in the LV network [22]. A centralized BESS approach in Reference [21,22] is found useful to reduce congestion in the LV network and increase the hosting capacity. The work, however, did not address the BESS charging/discharging impact on DT insulation and LoL. The voltage across each load point was also ignored under DT–BESS operation. The proposed approach in this paper is therefore designed as a proof of concept to overcome shortcomings of above studies by offering following objectives:

• Minimizing the BEV-charging impact on DT life.
• BESS charging and discharging during low-price and high-price hours, respectively.
• Flattening the load factor towards obtaining the DT operation within the nominal thermal limits.
• Maintaining the voltage drop within nominal limits across each household.
• Maximizing the paper insulation life of the distribution transformer.

The hybrid DRoDT–BESS technique is therefore proposed in this paper, to achieve the said objectives. The proposed technique is designed to not exceed the test DT’s temperature beyond 120 °C (design nominal [19]) during winter with base load demand comparatively higher than during summer. In this study, the weather-dependent DT thermal loading associated with electro-thermal coordination (ETC) between electrical and thermal parameters is carried out, where electrical parameter was considered in the form of load factor as a ratio between actual and base loads and thermal parameter in the form of ambient temperature across the test DT. The relationship based on coordination between electrical and thermal parameters is moreover found as effectively determining the maximum DT capacity towards reliable transfer of excess electricity. For instance, a higher load factor under increased ambient temperature will limit the DT’s hosting and thermal capacities and will thus cause a rise in voltage dip across consumer load points. Contrary to that, a reduced load-factor coupled with low ambient temperature will increase the DT’s hosting and thermal capacities, in addition to voltage surge across the load-points. In order to ensure an optimum DT operation to avoid these extreme conditions, this study therefore introduces the hybrid technique capable of achieving the core objectives.

The constraints like insulation degradation and excessive voltage dips in result of increased DT loading can be considered as bottlenecks to optimal power flow through distribution feeders and the DTs, resulting in overutilization of DTs, higher LoL, power flow limitations, increased congestion and costly asset upgrading. Contrary to that, load-factor decrement can lead to underutilization of DTs and voltage surges. The DRoDT–BESS combination can bring DT loading within the limits by providing an optimal load sharing between DT and the BESS, DT capacity enhancement and an improved power flow. The proposed technique can also be beneficial under the circumstances when DT goes out for maintenance and the stored energy in the centralized BESS can be used to improve voltage across each phase (a centralized BESS advantage over the decentralized BESS). BESS as a grid-booster, together with DRoDT can mitigate voltage violations at each consumer service point. As mentioned in Reference [14], voltage imbalance must be monitored at each consumer service point, not just across primary distribution levels. This study addresses this very issue by monitoring the voltage across each consumer service point before and after BESS implementation, to analyze voltage deviation from the allowable range and the required voltage improvement.

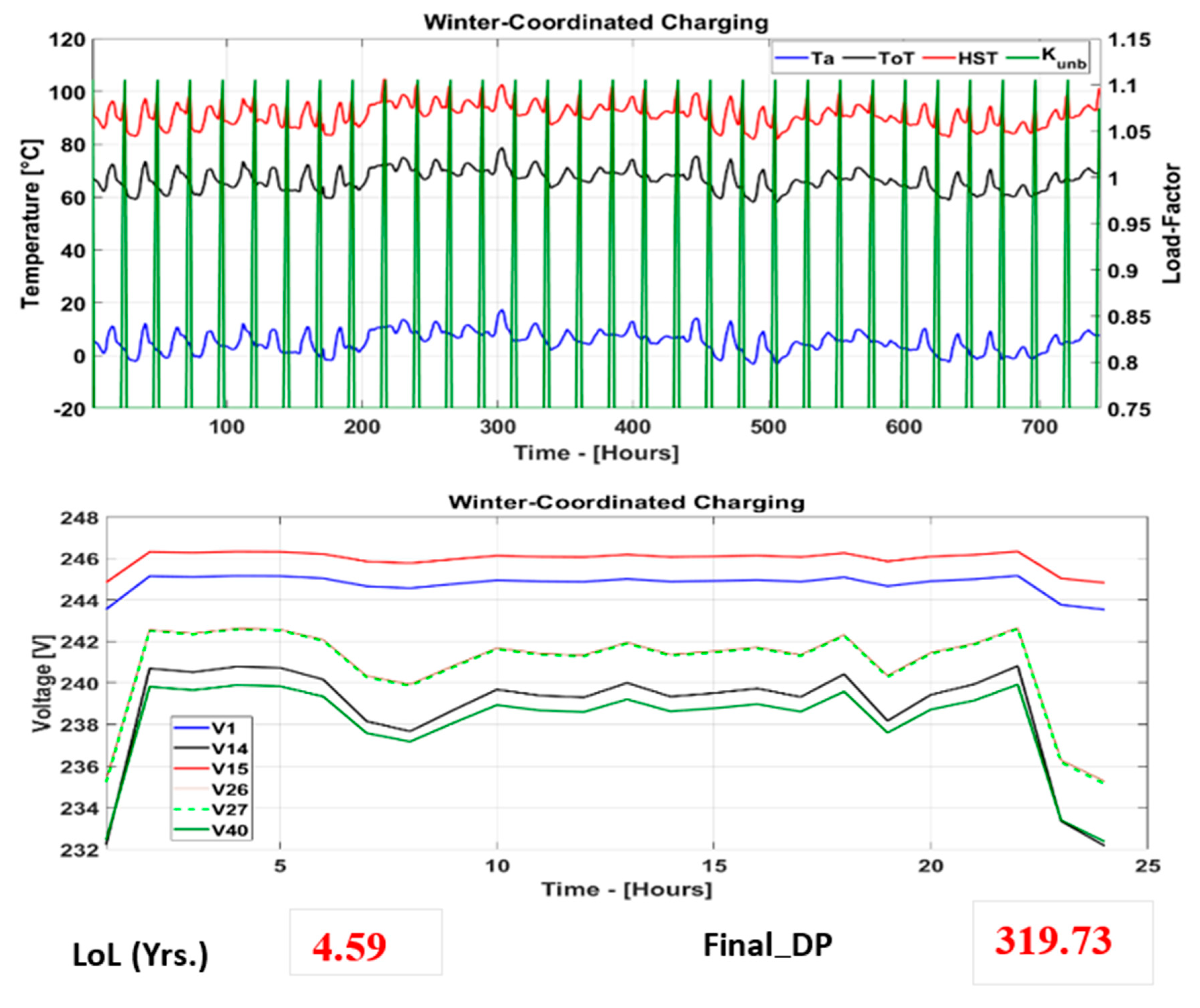
Regarding BESS feasibility, a centralized 100 kW BESS across the test LV distribution network was used in this study. The BESS was installed at the secondary side of the test DT, to provide load sharing with test DT, to obtain peak shaving and/or contribute towards valley filling. In this study, BESS provided the optimal DT loading within the maximum limits. To get a better idea about feasibility of the BESS, it is important to know the challenges and/or drawbacks that a BESS may bring, in addition to offering such benefits. The benefits associated with BESS, as per claimed in this study, may overweigh the drawbacks associated with BESS. It is because, the importance of installing BESS in the LV network, particularly in this study is substantial towards as helping the test DT in fulfilling the load demand, mainly arising from BEVs. To make a fair judgment, following points will serve as both benefits and drawbacks, associated with integration of a centralized BESS:

• Reduced electricity cost by 16.7% per house/day after centralized BESS installation [23].
• Substantial peak-load reduction in the MV/LV substation due to utility owned BESS over distributed ownership of PV-battery system [24].
• Reinforcement deferral of a 10 kV cable in the distribution network.
• Leading to high investment costs but enabling the reduced loading across the DT while offering the voltage support [25].
• BESS as a possible solution to cope with drawbacks associated to DGs, such as voltage fluctuations, reverse power flows and high capital costs [26].
• Reduced life of lead-acid batteries when operating under high temperature and reduced efficiency while operating under low temperature [27].

3. Methodology

In this study, an LV network with 40 households under base and BEV charging loads is designed. The loads are supplied electricity through a test DT and a centralized BESS. The BESS at the time of charging through the test DT works as a load, while under discharging mode, it works as a source. DT–BESS integration is considered to fulfil the active power and voltage demands such that the DT attains maximum utilization within the maximum allowable loading while BESS operates within the optimal charging and discharging range (10–90%). The BESS size selection is based on attaining the maximum DT utilization during off-peak and peak loading periods. This hybrid combination is implemented to maximize the test DT’s utilization and bring an improvement in DT’s life, in addition to obtaining the within-limits voltage across each household under BEV charging scenarios. To make this possible, the stored energy from the BESS is used at times of need. Additionally, the BESS charging and discharging range is selected carefully, to avoid any undercharging and/or overcharging situation(s).

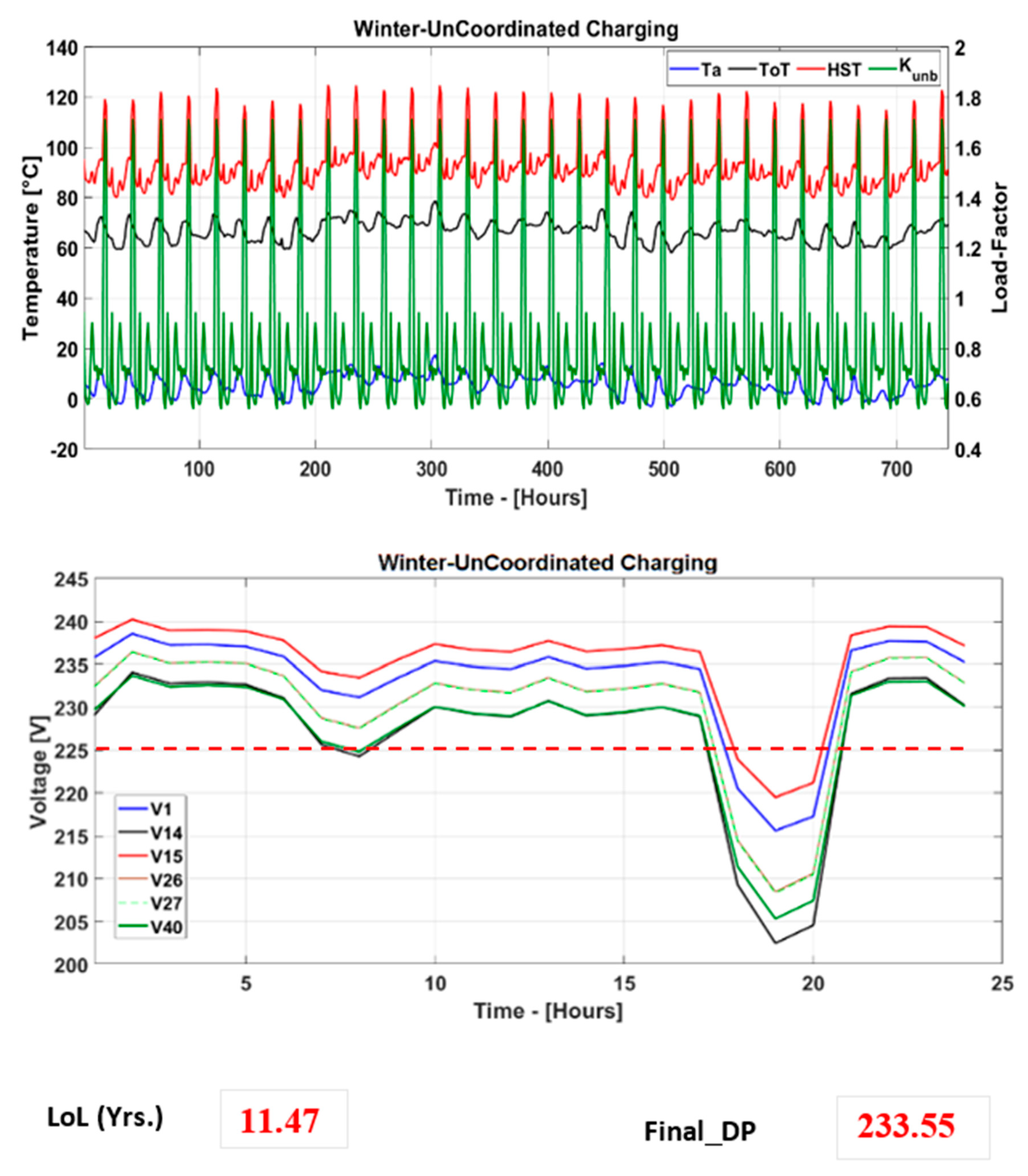
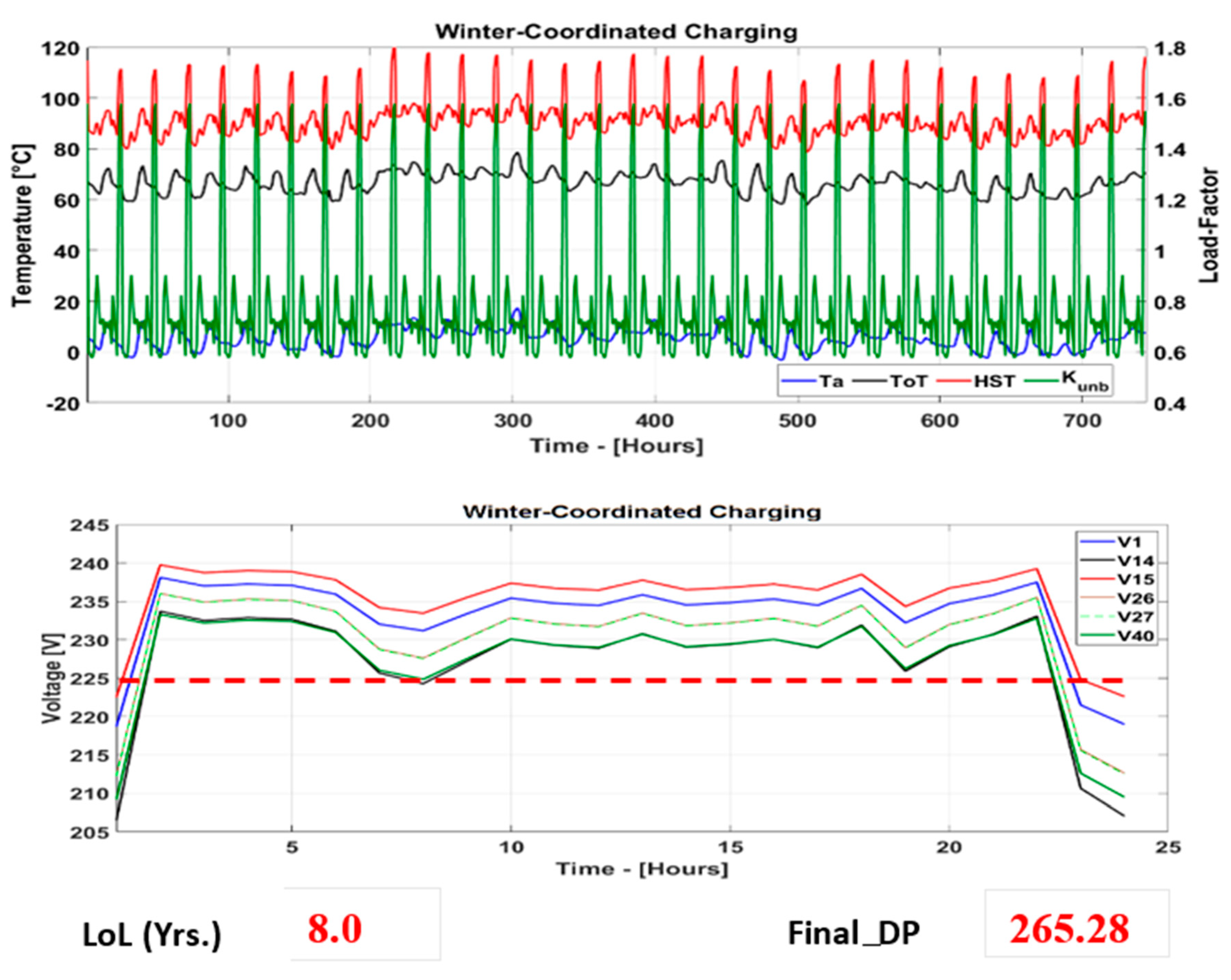
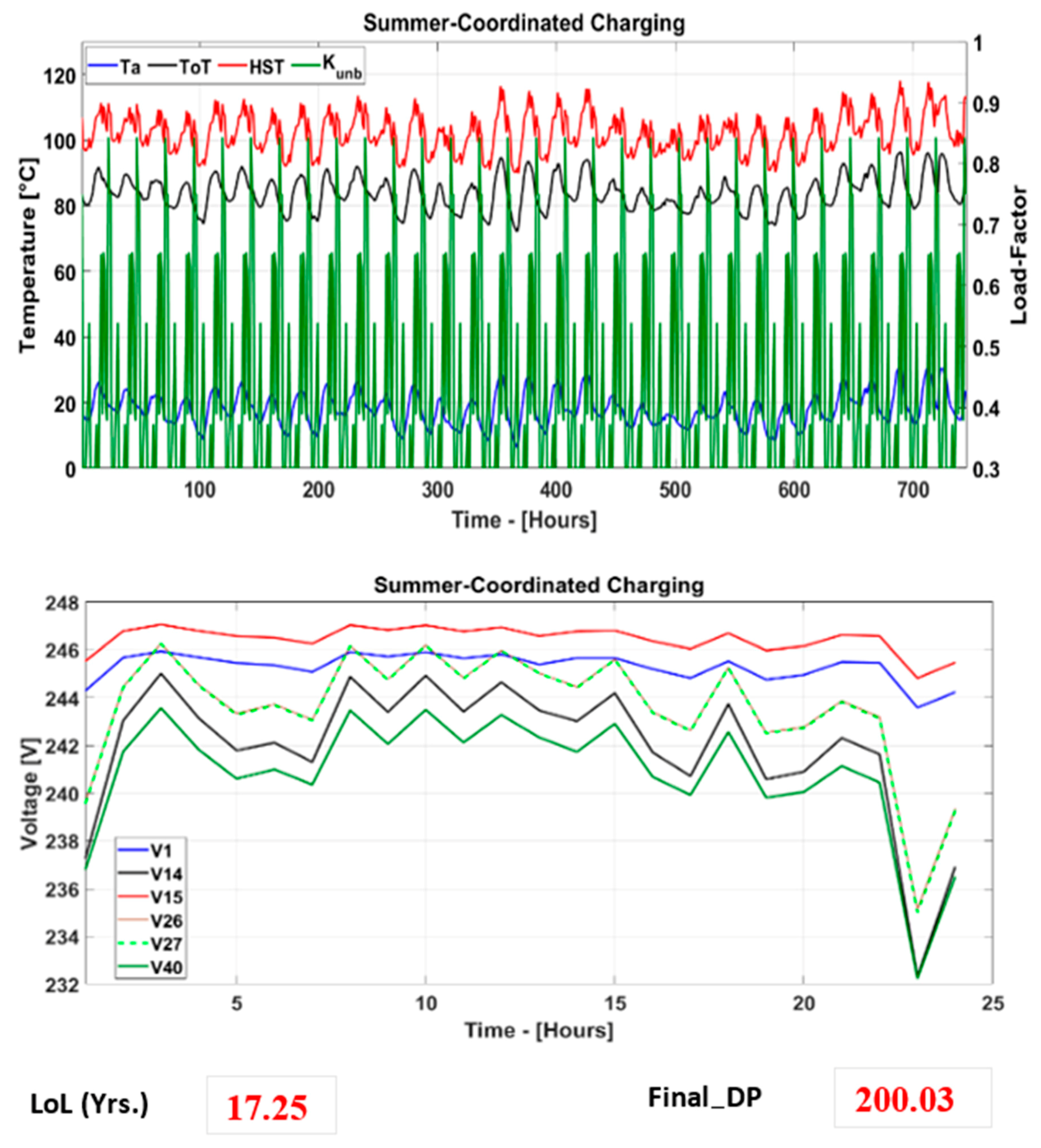
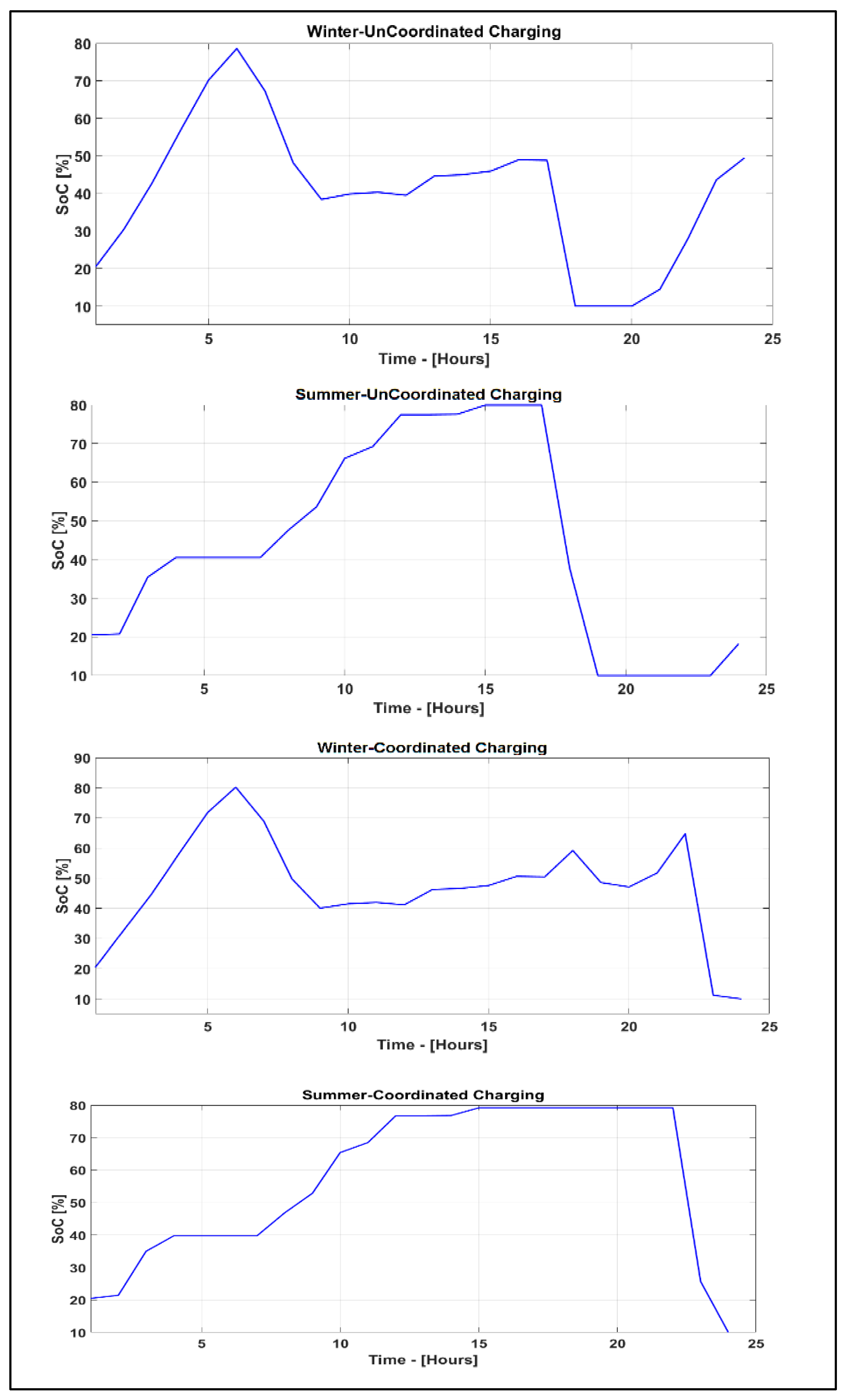
The test model is simulated under two BEV charging scenarios (coordinated and uncoordinated) to obtain respective load factor across each phase of the DT. The resulting phase load factors are used in Algorihm-1 to obtain the resultant load-factor, top-oil temperature (in °C) and winding hot-spot temperature (in °C), degree of polymerization (DP) and the life of paper insulation during winter and summer months, in the year 2018. The working principle of Algorithm-1 is moreover shown in Figure 1. The purpose of the designed Algorithm-1 is twofold, i.e., to load the test DT in such a way that it operates and attains maximum loading throughout the entire loading operation. The load factor across each phase of the test DT is calculated through the phase current ratios, as shown in Equation (1), indicating non-identical load factors across all three phases of the test DT under varying non-cyclic load currents flowing through each phase of the test DT. The phase load factors are then used to find the unbalance load factor, representing the uneven load distribution through each phase of the test DT, as shown in Equation (2) [13]. ${\mathit{T}}_{\mathit{H}\mathit{S}\mathit{T}}$ as shown in Equation (5) is calculated under the exponential equations method, as provided in Reference [19] by using ${\mathit{T}}_{\mathit{T}\mathit{o}\mathit{T}}$ from Equations (3) and (4). An increment in ${\mathit{T}}_{\mathit{T}\mathit{o}\mathit{T}}$ $({\mathit{T}}_{\mathit{T}\mathit{o}{\mathit{T}}_{\mathit{r}\mathit{i}\mathit{s}\mathit{e}}}$) is seen under increasing ${\mathit{k}}_{\mathit{u}\mathit{n}\mathit{b}}$ and rising ${\mathit{T}}_{\mathit{a}}$ as shown in Equation (3). Similarly, a decrement in ${\mathit{T}}_{\mathit{T}\mathit{o}\mathit{T}}$ $({\mathit{T}}_{\mathit{T}\mathit{o}{\mathit{T}}_{\mathit{f}\mathit{a}\mathit{l}\mathit{l}}}$) is seen under decreasing ${\mathit{k}}_{\mathit{u}\mathit{n}\mathit{b}}$ and falling ${\mathit{T}}_{\mathit{a}}$ as shown in Equation (4). Both rising and falling ${\mathit{T}}_{\mathit{T}\mathit{o}\mathit{T}}$ are then used with increasing and decreasing hot-spot to top-oil gradients to find ${\mathit{T}}_{\mathit{H}\mathit{S}\mathit{T}}$ from Equation (5).

$$k_a=\frac{I_{actual,a}}{I_{base}}, k_b=\frac{I_{actual,b}}{I_{base}}, k_c=\frac{I_{actual,c}}{I_{base}}$$

(1)

$$k_{unb}=\sqrt{\frac{\left(k_a{}^2+k_b{}^2+k_c{}^2\right)}{3}}$$

(2)

$$T_{To{T}_{rise}}=\left(T_a+\Delta T_{oi}\right)+\left\{\Delta T_{or}\times {\left[\frac{1+R\times k_{unb}{}^2}{1+R}\right]}^x-\Delta T_{oi}\right\}\times \left(1-e^{\frac{\left(-t\right)}{\left(k_{11}\ast {\tau }_0\right)}}\right)$$

(3)

$$\begin{array}{cc}{T}_{To{T}_{fall}}=& \left(T_a+\Delta T_{or}\right)\times {\left[\frac{1+R\times k_{unb}{}^2}{1+R}\right]}^x\\ & +\left\{\Delta T_{oi}-\Delta T_{or}\times {\left[\frac{1+R\times k_{unb}{}^2}{1+R}\right]}^x\right\}\times \left(e^{\frac{\left(-t\right)}{\left(k_{11}\ast {\tau }_0\right)}}\right)\end{array}$$

(4)

$$T_{HST}=\left(T_{To{T}_{rise/fall}}+\left(\Delta T_{H_{rise}}-\Delta T_{H_{fall}}\right)\right)$$

(5)

Here, $\mathit{I}$ is current in Amperes; ${\mathit{k}}_{\mathit{a}}, {\mathit{k}}_{\mathit{b}}, {\mathit{k}}_{\mathit{c}}$ represent phase load factors in p.u.; $\Delta {\mathit{T}}_{\mathit{o}\mathit{i}}$ and $\Delta {\mathit{T}}_{\mathit{o}\mathit{r}}$ are top-oil temperature rise during start and steady states in degree K, respectively; ${\mathit{k}}_{\mathbf{11}}$ is thermal model constant; $\mathit{t}$ is time variable in min; ${\mathit{\tau }}_{\mathbf{0}}$ is oil-time constant; and $\mathit{R}$ is ratio of load losses at rated current to losses at no-load current. Equation (6) (Arrhenius formula) in Reference [19] is used to find the change in degree of polymerization (DP) from initial $\mathit{D}{\mathit{P}}_{\mathit{s}\mathit{t}\mathit{a}\mathit{r}\mathit{t}}$ = 1000 (at the start of the DT loading) to the final $\mathit{D}{\mathit{P}}_{{\mathit{t}}_{\mathit{e}\mathit{n}\mathit{d}}}$ (at time ${\mathit{t}}_{\mathit{e}\mathit{n}\mathit{d}}$) as shown in Equation (6) [19].

$$\frac{1}{D{P}_{t_{end}}}=\left(A\times t_{end}\times \exp \left(\frac{E_A}{R\times T_{HST}}\right)\right)+\frac{1}{D{P}_{start}}$$

(6)

Here, $\mathit{D}{\mathit{P}}_{{\mathit{t}}_{\mathit{e}\mathit{n}\mathit{d}}}$ is found at ${\mathit{T}}_{\mathit{H}\mathit{S}\mathit{T},\mathit{e}\mathit{n}\mathit{d}}$. The other parameters considered are the environmental factor $\mathit{A}=1.6\times {10}^4$ in h⁻¹, gas constant $\mathit{R}=8.314$ in J⋅K⁻¹⋅mol⁻¹ and activation energy ${\mathit{E}}_{\mathit{A}}$ = 86 kJ·mol⁻¹ for a thermally upgraded paper. The total loss of life (LoL) based on ${\mathit{T}}_{\mathit{H}\mathit{S}\mathit{T}}$ is calculated through (7) [19].

$$Los{s}_{life}={\displaystyle \sum }_{n=1}^N\left(ex{p}^{\left(\frac{15000}{383}-\frac{15000}{\left(T_{HST}+273\right)}\right)} \right)\times t_n$$

(7)

In Equation (7), $\mathit{n}$ is number of each loading interval, $\mathit{N}$ is the total number of loading intervals and ${\mathit{t}}_{\mathit{n}}$ as the step time of each loading interval in hours. The expected DT life can then be calculated through (8) [19].

$$t_{exp}=\frac{\left(\frac{1}{D{P}_{t_{end}}}-\frac{1}{D{P}_{start}}\right)}{\left(A\times 24\times 365\right)}\times \exp \left(\frac{E_A}{R\times T_{HST,end}}\right)$$

(8)

Equation (7) from Reference [19] is used to find the total estimated DT life in years, where $\mathit{D}{\mathit{P}}_{{\mathit{t}}_{\mathit{e}\mathit{n}\mathit{d}}}$ is computed at ${\mathit{T}}_{\mathit{H}\mathit{S}\mathit{T},\mathit{e}\mathit{n}\mathit{d}}$. The proposed DRoDT–BESS technique as illustrated in Algorithm 1 and Figure 1 is based on load sharing between DT and BESS to achieve the following:

(1)

Accuracy in ${\mathit{T}}_{\mathit{T}\mathit{o}\mathit{T}}$- and ${\mathit{T}}_{\mathit{H}\mathit{S}\mathit{T}}$-based calculations for accurate estimation of DP, LoL and the expected DT lifetime.

(2)

BESS charging during low-priced hours and discharging during high-priced hours.

(3)

Optimal load sharing between DT and BESS to obtain maximum DT operation and within limits phase-rms voltage across each household.

(4)

Required load flow in the test network in order to obtain suppressed load peaks mainly during high-priced peak loading hours.

Algorithm-1 considers both peak and off-peak loading periods, where the peak period is from 17:00 to 21:00 h, and the off-peak loading period is before 17:00 and after 21:00 h. The load current in result of base and BEV loadings flowing through each phase of the test DT is obtained from the test system (see Section 4) and is converted into respective load factors that further with the help of (2), are converted into the resultant load factor. The resultant load factor under varying ambient temperatures is then used to find the hourly changes in ${\mathit{T}}_{\mathit{T}\mathit{o}\mathit{T}}$ during the winter and summer seasons. It is important to mention that the ${\mathit{T}}_{\mathit{T}\mathit{o}\mathit{T}}$ calculation in this paper is carried out by using the exponential equations method instead of the differential equation method from Reference [19]. Under the combined DT–BESS operation, ${\mathit{T}}_{\mathit{T}\mathit{o}\mathit{T}}$ is calculated by using the load factor as obtained after their load sharing. The coupling between thermal and electrical characteristics of the DT is therefore addressed in the context of electro-thermal coordination.

Based on degree of coordination between DT and BESS, an optimal DT loading can be obtained. For instance, a lower ambient temperature coupled with lower load factor will enhance DT loading and will contribute towards reduced congestion across the DTs [13]. Similarly, a higher ambient temperature under peak loading will force DT beyond the maximum allowable thermal limit [13]. A non-linear combination between ambient temperature and the load factor will also impact the optimal DT loading range.

The optimal loading across the test DT in this study is set at either DT achieving the maximum utilization or operating under the nominal electrical and thermal loading limits, as specified in Reference [19]. To meet these criteria, the stored energy in BESS is used to fulfil the load-requirement while operating with test DT. The DT loading limits under which BESS must feed into the loads via stored energy are set in accordance to the time-based load demand. For instance, during peak loading period, when DT load factor is equal to or above 0.73 p.u., and/or any load factor with corresponding ${\mathit{T}}_{\mathit{a}}$ to cause ${\mathit{T}}_{\mathit{H}\mathit{S}\mathit{T}}$ between 80–140 °C during winter and summer seasons, the stored energy from the BESS is thereafter utilized. Similarly, during off-peak loading period, energy extraction from the BESS is carried under the condition that either DT load is obtained above 0.6 p.u. or ${\mathit{T}}_{\mathit{H}\mathit{S}\mathit{T}}$ above 110 °C, further shown in Figure 1. The proposed technique, in addition to providing the active power support to flatten the load peaks is found with effectively regulating the voltage across each household within the nominal limits (±6%), as per specified in Reference [28].

Algorithm 1. Proposed Technique during BESS Discharging

for $\left(E_{BESS, stored}=\left({\eta }_{BESS}\times \left(E_{nominal}-E_{losses}\right)\right)\right)$ $\left(E_{BESS\_Max\_charge} \ge E_{BESS, stored} \ge E_{BESS,Min\_discharge}\right)$ $t=\left(1:1:24\right)$  for $\left(t \ge 17\right) \&\& \left(t \le 21\right)$   while $\left[\begin{array}{c}\left\{\left(k_{unb}\times S_{T/F,base}\right)\to S_{T/F,max}\to \left(140°<T_{HST}\right)\right\}\\ \left|\right| \left(k_{unb} \ge 0.73\right)\end{array}\right]$    do $\left(E_{BESS,extracted}\right)=\left(E_{BESS,stored}-E_{BESS,available}\right)$ ${ S_{T/F,max}|}_{T_{a,min}}^{T_{a,max}}=\left[\left(P_{load}\right)-\left(E_{BESS,extracted}\right)\right]$ $k_{unb}=\left(\frac{S_{T/F,max}}{S_{T/F,base}}\right)$ $\left(1.06\times V_{base}\right) \ge V_{a,b,c}^{actual} \ge \left(0.94\times V_{base}\right)$   end  end  for $\left(t \le 17\right) \&\& \left(t>21\right)$   while $\left[\left(k_{unb }>0.6\right)\to S_{T/F,max}\to \left(110°<T_{HST}\right)\right]$    do $\left(E_{BESS,extracted}\right)=\left(E_{BESS,stored}-E_{BESS,available}\right)$ ${ S_{T/F,max}|}_{T_{a,min}}^{T_{a,max}}=\left[\left(P_{load}\right)-\left(E_{BESS,extracted}\right)\right]$ $k_{unb}=\left(\frac{S_{T/F,max}}{S_{T/F,base}}\right)$ $\left(1.06\times V_{base}\right) \ge V_{a,b,c}^{actual} \ge \left(0.94\times V_{base}\right)$   end  end end

Figure 1 indicates that the test DT supplies electricity to both residential load (including BEVs) and the BESS. However, the loading across test DT is reduced when BESS shares the load with the test DT. Load sharing with the help of BESS is a suboptimal problem, where the test DT is required to operate under maximum utilization. The parameter responsible for ensuring the maximum utilization of test DT is $T_{HST}$. The setting of $T_{HST}$ is based on the loading time. During the peak loading period, $T_{HST}$ must be below 140 °C and during off-peak loading, it must be below 110 °C. This suboptimal criterion is set to make sure that the test DT operates under maximum utilization. When $T_{HST}$ exceeds the maximum limit of 140°/110 °C, BESS starts supplying the stored energy to the load until reaching the minimum discharge limit of 10%. Under both or any of these situations, the nominal voltage limit is also taken into account, which means after BESS sharing, the load with the test DT, the voltage across all test DT phases is required to be within the nominal limit of ±6%. Besides, as indicated in Figure 1, $T_{HST}$ at which the test DT operates in the operation mode is further used to find the degree of polymerization of the insulation paper, loss of life and the expected DT life with the help of ambient and top-oil temperatures under both winter and summer seasons in the simulation environment.

4. Test System

A test system developed in Simulink was used to carry out the design, modeling and simulation work in order to implement the proposed technique in the test LV network. A neighborhood of 40 households, where each household had segregated base and BEV loads was connected to the secondary side of the test DT through an XLPE service cable. Identical base-load data as taken from Reference [29] was used for each household in the entire neighborhood. Weather data for both winter and summer months were taken from Reference [30]. The service cable was considered a resistive-inductive type with data as shown in

Table 1. Service cable parameters.

Type	XLPE Insulated/Single Core/Copper
Area	281 mm2
Resistance (mΩ)	0.081 (at H-1), 52.71 (at H-14)
Reactance (mΩ)	0.082 (at H-1), 53.04 (at H-14)

. A 50 m distance was considered between two adjacent households. A complete model involving test DT, BESS, base and BEV loads is shown in Figure 2.

BEVs used in the test system were 24 kWh Nissan Leaf, charged through 6.6 kW single-phase Level 2 AC chargers at 240 Vrms and 32 A rated charging current with additional parameters, as shown in

Table 2. Battery electric vehicle (BEV) parameters.

Charging Load Power Factor	0.9
Battery charging status	1 (SoC—100%), 0 (SoC—0%)
Initial battery SoC	0%
Charger load type	constant impedance

under two charging scenarios, (1) coordinated and (2) uncoordinated. Under coordinated charging (controlled charging) scenario, all BEVs were charged during off-peak time, whereas under uncoordinated charging (uncontrolled charging) scenario, all BEVs were simultaneously charged during peak loading time (plug-in time). BEVs under uncoordinated charging scenario were allowed charging at the time of plugged-in, thus leading to cause voltage dips across each household, further increasing with cable length, hence higher voltage-drop across the farthest household than the household nearest to test DT. BEV state of the charge as shown in Table 2 represents an unrealistic charging and discharging status, where the aim was to focus on maximum DT loading period under the worst loading scenario and to find the amount of load, BESS can supply during maximum DT loading.

In terms of connection, primary side of test DT was connected to 11 kV LV grid (primary side with phase-factors), considered as a slack-node at fixed input voltage (|U| = 1.0 pu, δ = 0°) to restrict BESS influence on grid-side. An unbalanced phase load consisting of 14 households across Phase-A and 13 households across each Phase-B and Phase-C was connected to 415 V secondary side of the test DT. Some important data used for electrical and thermal modeling of the test DT is shown in

Table 3. Transformer parameters for 200 kVA.

Number of Phases	3
LV Voltage	415 V/50 Hz
Cooling method	ONAN
Impedance	8%
Top-oil temperature rise	55 K
Top-oil temperature rise above ambient	60.95 K
Hot-spot to top-oil	23 K
Oil time constant	180
Winding time constant	4
Loss ratio	5
k11/k21/k22	1.0/1.0/2.0

. The BESS used in the test system was considered 100 kW/200 kWh as a stationary centralized energy storage connected with the test DT.

5. Results and Discussion

The results in the following studied scenarios indicate that, in order to obtain maximum DT utilization, the DT must be operating under nominal limits through its entire loading operation. These nominal limits must consider region-specific voltage regulation to facilitate an uninterrupted and reliable supply of electricity to consumers. Two weather scenarios were considered in this study, i.e., winter and summer. Weather data for both seasons was obtained from the location of test DT that was in Henderson, New Zealand. A two-month study was carried out in a simulation environment, where the month of July 2018 represented winter season and January 2018 represented as a month in summer season.

5.1. DT Simulation Scenarios

5.1.1. Scenario 1: Uncoordinated BEV Charging during Winter

a. Without BESS

The results of this scenario, as shown in Figure 3 represent uncoordinated charging impact from BEVs on electrical and thermal loading states across the test DT without BESS installation. All 40 EVs under this scenario are charged simultaneously at the time of being plugged. Hence, under this scenario, no delay associated to BEV charging is considered. The simultaneous charging impact can therefore be seen as causing congestion across the test DT in addition to voltage drop across each residential house nearest to and farthest from the test DT. A continuous hourly loading across the test DT for the whole month of July 2018 is seen to cause paper DP to fall from 1000 to 233.5, slightly above the end-of-life threshold of 200.

b. With BESS

Load sharing through BESS is obtained to relieve congestion across the test DT in addition to reducing the voltage dips across each household nearest to and farthest from the test DT, as shown in Figure 4. After BESS installation in the modeled LV network, 31.25% improvement in DP is obtained in comparison to the non-BESS installation under the same scenario. Similarly, 54.92% decrement in DT’s LoL is obtained in BESS presence under same weather and loading conditions.

5.1.2. Scenario 2: Uncoordinated BEV Charging during Summer

a. Without BESS

Under this scenario, besides BEV charging load, the ambient temperature is found to influence DT’s thermal loading. A significant rise in the ambient temperature is observed to increase ${\mathit{T}}_{\mathit{H}\mathit{S}\mathit{T}}$ by 11.56% and decrease DP by 10.85%, in comparison to the winter season under the identical residential and BEV charging load conditions, as shown in Figure 5.

b. With BESS

This scenario represents load sharing between BESS and test DT during the summer season. The results as shown in Figure 6 indicate that the presence of BESS can effectively mitigate DT thermal overloading in comparison to the scenario carried out under the absence of BESS. The results further indicate that the hybrid technique is capable of reducing the ${\mathit{T}}_{\mathit{H}\mathit{S}\mathit{T}}$ to a certain extent throughout the entire loading duration.

5.1.3. Scenario 3: Coordinated BEV Charging during Winter

a. Without BESS

As shown in Figure 7, the delay associated with coordinated BEV charging has the capability to protect test DT from thermal overloading but at excessive voltage dip making residential voltages well below the nominal limit. For instance, the maximum voltage dip under this scenario across Household 14 is observed 16.22% below the nominal limit as set under [28].

b. With BESS

As shown in Figure 8, after BESS installation, not only load spikes are flattened but around 4.76% rise in voltage is also achieved across each residential load point during a 24 h continuous DT operation in comparison to scenario with no BESS installation during the same season.

5.1.4. Scenario 4: Coordinated BEV Charging during Summer

a. Without BESS

The results in Figure 9 indicate that during summer, test DT is found with experiencing a comparatively high congestion, resulting in a significant rise in ${\mathit{T}}_{\mathit{H}\mathit{S}\mathit{T}}$ and in voltage drop across each household. Furthermore, LoL of the test DT without BESS is observed around 24.52% higher than DT LoL with BESS.

b. With BESS

To mitigate congestion by reducing the DT thermal overloading and by improving the phase voltage across each household, BESS installation is carried out with respect to test DT. For instance, average voltage across all households during 24 h of DT loading is observed around 2.34% higher with BESS than without BESS under the same loading and weather conditions, as shown in Figure 10.

5.2. Centralized BESS Integration

The integration of a centralized BESS with test DT is carried out to fulfil the load demand mainly in result of BEVs. BESS charging and discharging can be seen under nominal optimal range during all studied scenarios, as shown in Figure 11. The figure further indicates that BESS SoC remains between 10%-80% of the charging range. BESS integration during peak-loading period (under uncoordinated BEV charging) in winter resulted in optimal DT loading equivalent to 1.24 p.u. (i.e., well below the nominal cyclic loading [19] of the DT) with maximum ${\mathit{T}}_{\mathit{H}\mathit{S}\mathit{T}}$ obtained as 108.7 °C (below 120 °C). The same scenario in summer has resulted in optimal DT loading of 1.01 p.u. with maximum ${\mathit{T}}_{\mathit{H}\mathit{S}\mathit{T}}$ obtained around 124.7 °C (below maximum permissible limit of 140 °C [19]). During winter, the test system under uncoordinated BEV charging without BESS resulted in 30% higher DT loading in comparison to coordinated BEV charging. Similarly, test DT loading in result of uncoordinated BEV charging during winter season is found around 10% higher than under uncoordinated BEV charging. The results therefore indicate that BESS integration with a DT can significantly reduce DT loading, particularly when DTs are faced with excess BEV penetration. Moreover, it may also improve DT life and provide voltage support in the LV network.

The proposed technique with BESS is further able to improve voltage across each household by a significant margin. After BESS installation, average voltage across all households under Scenario 1 is seen to be 4.64% higher than without BESS. Similarly, the average voltage dip across same households under Scenario 2 with BESS is seen to be 2.27% lower than that found without BESS. Scenario 3 and Scenario 4 are also observed with improved voltage across each household after BESS installation. For instance, before BESS installation, the average voltage drop during 24 h of DT loading between Household 1 and Household 14 under Scenario 3 and Scenario 4 is obtained around 2.61% and 1.43%, respectively; that is then reduced to 2.45% and 1.37%, respectively after the BESS installation with test DT.

6. Conclusions and Future Work

In this paper, an integrated DRoDT–BESS technique is presented, which is unique in its “designing for maximum utilization” concept. The obtained results indicate the capability of the proposed technique in reducing the congestion, DT thermal loading and voltage dips under studied BEV charging scenarios and under different weather conditions. The objectives, such as optimal DT loading, optimum DT utilization under non-cyclic loading, accuracy regarding the $T_{ToT}$ calculation, minimized DT thermal loading, reduced congestion and voltage within the nominal limits, are achieved with the help of the proposed technique. Under the proposed technique, the minimized congestion and reduced thermal loading were obtained due to optimal timing factor associated with BESS charging/discharging cycles. BESS charging was carried out during off-peak period, whereas the discharging took place during peak loading period and/or at the times of DT thermal loading going beyond the nominal thermal overloading to benefit both end-consumers and the DNOs. For the end-consumers, the benefits like (1) reliable active power flow without any risk of load-shedding (through minimized DT overloading), (2) voltage within limits and (3) reduced electricity price were obtained. For the DNOs, the benefits like (1) longer DT life and (2) deferral of costly asset upgrading were obtained. Under ambient temperature based dynamic transformer rating and BESS integration, the proposed technique is found useful in significantly reducing the test DT’s loss of life by 11.21% during winter when loaded under coordinated BEV charging in comparison to loaded under uncoordinated BEV charging during the same season. Similarly, reduction in loss of life of the test DT during summer under coordinated BEV charging was observed around 15.52% lower than that observed under uncoordinated BEV charging.

As a future work, the technical and economic challenges associated with BESS are found as posing concerns on feasibility of the BESS. It is therefore important to take into account these issues before operational usage of a BESS. Additionally, temperature variation, degradation and loss of life of the BESS are important parameters for a better evaluation of the BESS feasibility in the LV network. Their careful analysis and study will lead to decision making regarding the application of BESS in the LV network. These factors further lying out of the focus of the paper are therefore recommended as a future work.