Improved Appliance Classification in Non-Intrusive Load Monitoring Using Weighted Recurrence Graph and Convolutional Neural Networks
Abstract
:1. Introduction
- We present a recurrence graph feature representation that gives a few more values (WRG) instead of the binary output, which improves the robustness of appliance recognition. The WRG representation for activation current and voltage not only enhances appliance classification performance but also guarantees the appliance feature’s uniqueness, which is highly desirable for generalization purposes.
- We present a novel pre-processing procedure for extracting steady-state cycle activation current from current and voltage measurements. The pre-processing method ensures that the selected activation current is not a transient signal.
- We conduct evaluations on three sub-metered public datasets and comparing with the V–I image, which is its most direct competitor. We also conduct an empirical investigation on how different parameters of the proposed WRG influence classification performance.
2. Proposed Methods
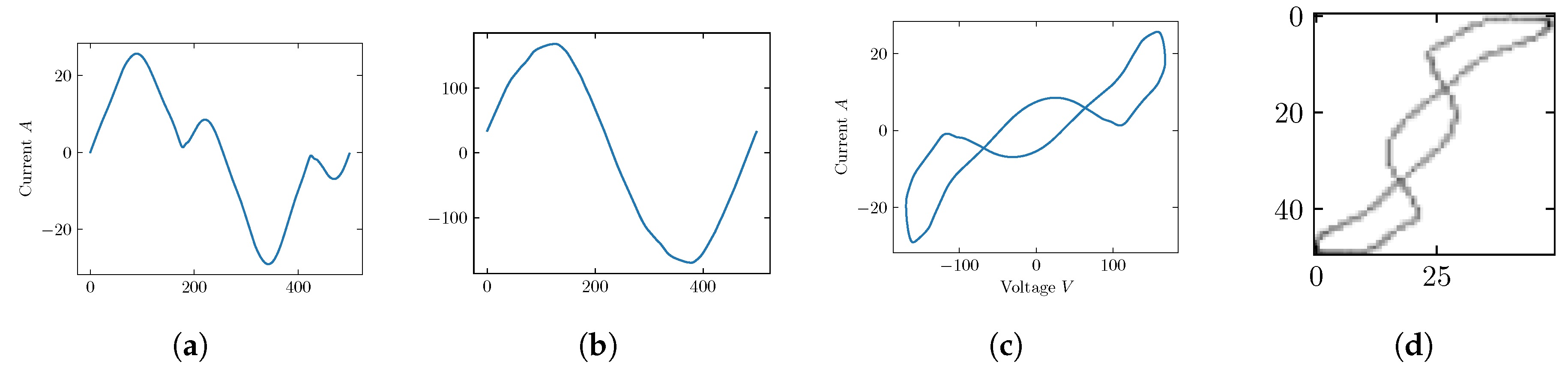
2.1. Feature Extraction and Pre-Processing
| Algorithm 1: Feature pre-processing |
| Result: Data: Get voltage zero crossings: ;  |
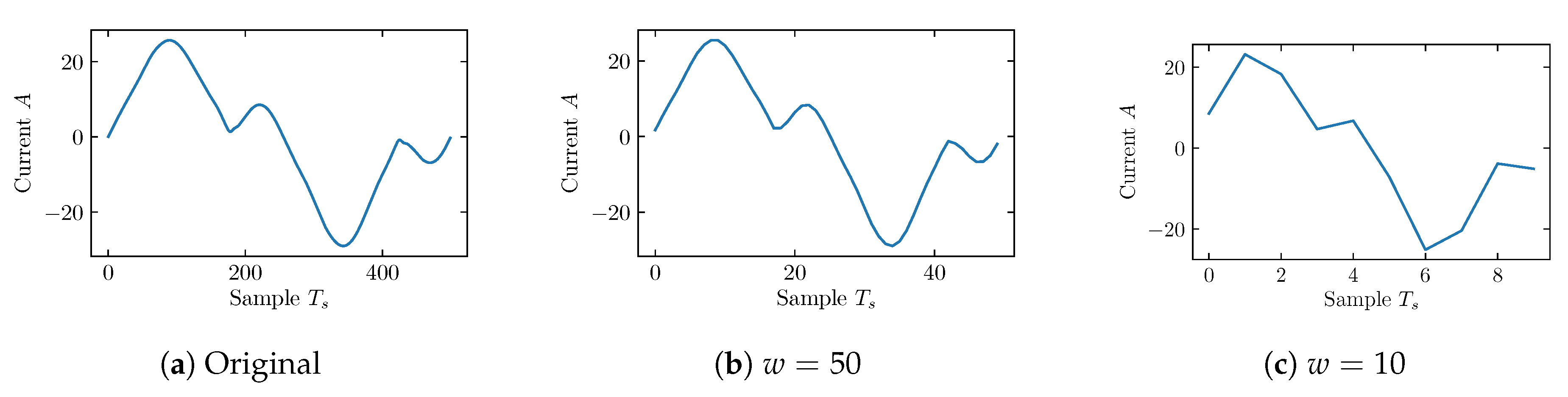
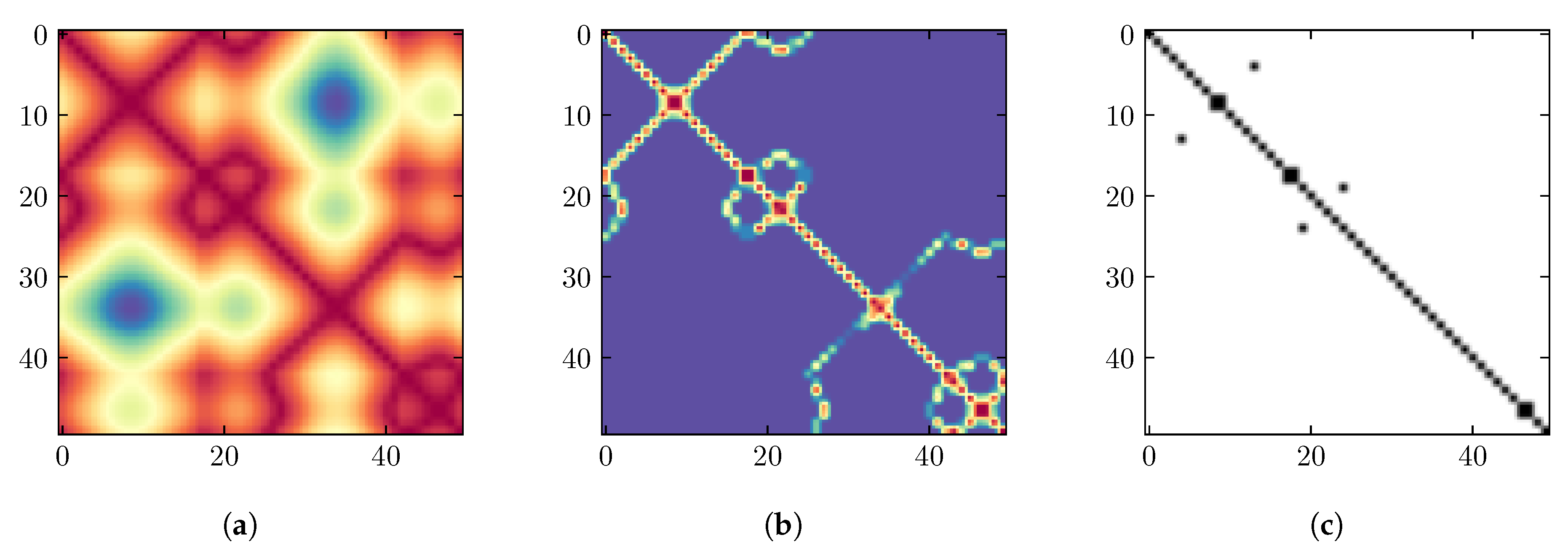
2.2. Weighted Recurrence Plot (WRG)
2.3. Classifier and Training Procedure
3. Experimental Design
3.1. Datasets
3.2. Evaluation Metrics
3.3. Experimental Description
4. Results and Discussion
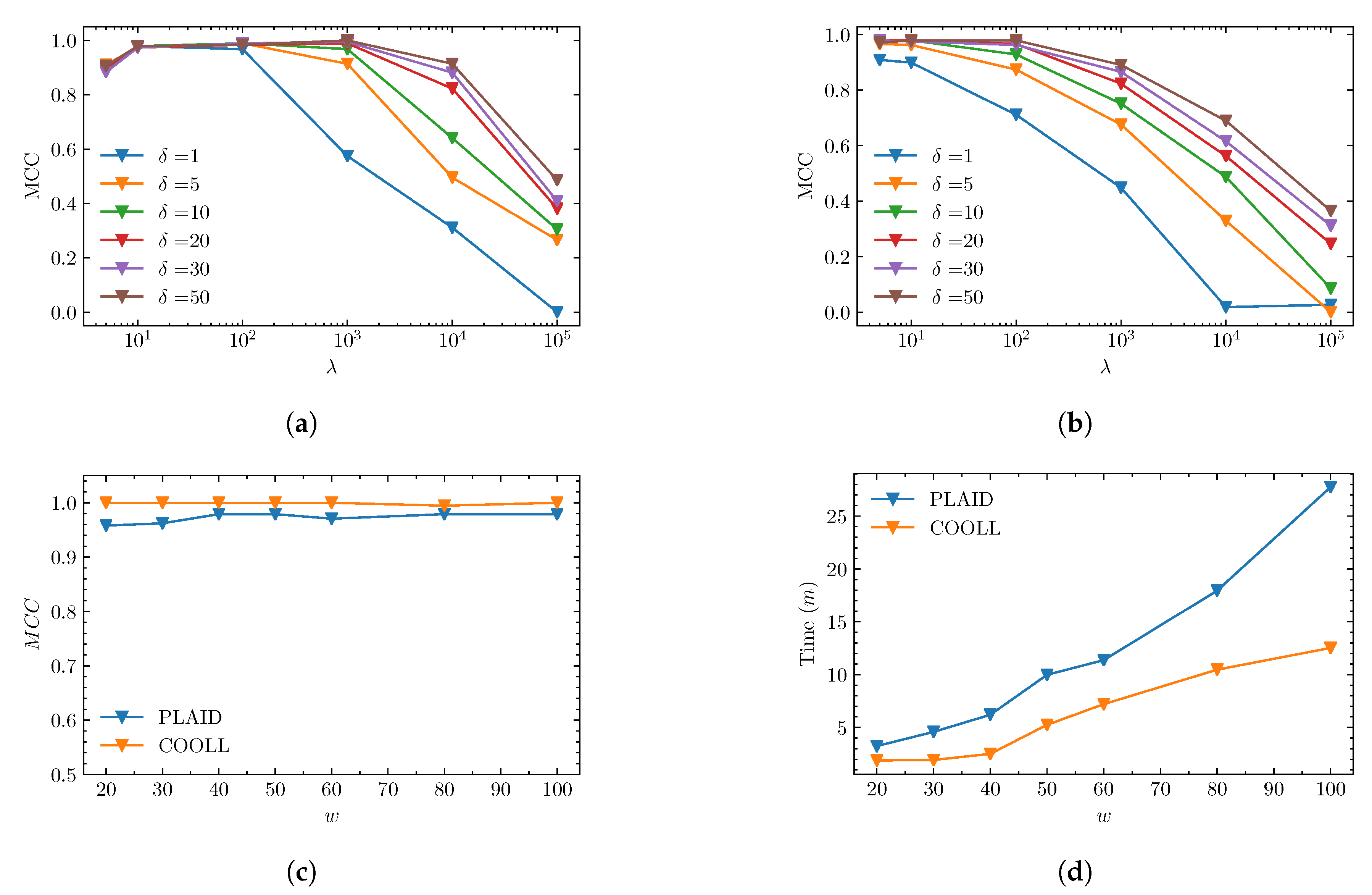
4.1. Objective 1: WRG Analysis
4.2. Objective 2: Comparison against V–I Image Method
5. Conclusions and Future Work Directions
Author Contributions
Funding
Conflicts of Interest
References
- Cominola, A.; Giuliani, M.; Piga, D.; Castelletti, A.; Rizzoli, A. A Hybrid Signature-based Iterative Disaggregation algorithm for Non-Intrusive Load Monitoring. Appl. Energy 2017, 185, 331–344. [Google Scholar] [CrossRef]
- Batra, N.; Singh, A.; Whitehouse, K. If You Measure It, Can You Improve It? Exploring The Value of Energy Disaggregation. In Proceedings of the 2nd ACM International Conference on Embedded Systems for Energy-Efficient Built Environments (BuildSys ’15), Seoul, Korea, 4–5 November 2015; pp. 191–200. [Google Scholar] [CrossRef]
- Huss, A. Hybrid Model Approach to Appliance Load Disaggregation. Ph.D. Thesis, KTH Royal Institute of Technology, Stockholm, Sweden, 2015. [Google Scholar]
- Kelly, J.; Knottenbelt, W. The UK-DALE dataset, domestic appliance-level electricity demand and whole-house demand from five UK homes. Sci. Data 2015, 2, 150007. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Makonin, S.; Popowich, F.; Bajić, I.V.; Gill, B.; Bartram, L. Exploiting HMM Sparsity to Perform Online Real-Time Nonintrusive Load Monitoring. IEEE Trans. Smart Grid 2016, 7, 2575–25857. [Google Scholar] [CrossRef]
- Kelly, J.; Knottenbelt, W. Neural nilm: Deep neural networks applied to energy disaggregation. In Proceedings of the 2nd ACM International Conference on Embedded Systems for Energy-Efficient Built Environments, Seoul, Korea, 4–5 November 2015; pp. 55–64. [Google Scholar]
- Zhang, C.; Zhong, M.; Wang, Z.; Goddard, N.; Sutton, C. Sequence-to-point learning with neural networks for non-intrusive load monitoring. In Proceedings of the Thirty-Second AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2017. [Google Scholar]
- Murray, D.; Stankovic, L.; Stankovic, V.; Lulic, S.; Sladojevic, S. Transferability of Neural Network Approaches for Low-rate Energy Disaggregation. In Proceedings of the 2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brighton, UK, 12–17 May 2019; pp. 8330–8334. [Google Scholar]
- De Baets, L.; Dhaene, T.; Deschrijver, D.; Develder, C.; Berges, M. VI-Based Appliance Classification Using Aggregated Power Consumption Data. In Proceedings of the 2018 IEEE International Conference on Smart Computing (SMARTCOMP), Taormina, Italy, 18–20 June 2018; pp. 179–186. [Google Scholar] [CrossRef] [Green Version]
- De Baets, L.; Ruyssinck, J.; Develder, C.; Dhaene, T.; Deschrijver, D. Appliance classification using VI trajectories and convolutional neural networks. Energy Build. 2018, 158, 32–36. [Google Scholar] [CrossRef] [Green Version]
- Gomes, E.; Pereira, L. PB-NILM: Pinball Guided Deep Non-Intrusive Load Monitoring. IEEE Access 2020, 8, 48386–48398. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, X.; You, W. Non-Intrusive Load Monitoring by Voltage–Current Trajectory Enabled Transfer Learning. IEEE Trans. Smart Grid 2019, 10, 5609–5619. [Google Scholar] [CrossRef]
- Pereira, L.; Nunes, N. Performance evaluation in non-intrusive load monitoring: Datasets, metrics, and tools—A review. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2018, 8, e1265. [Google Scholar] [CrossRef] [Green Version]
- Baptista, D.; Mostafa, S.; Pereira, L.; Sousa, L.; Morgado, D.F. Implementation Strategy of Convolution Neural Networks on Field Programmable Gate Arrays for Appliance Classification Using the Voltage and Current (V–I) Trajectory. Energies 2018, 11, 2460. [Google Scholar] [CrossRef] [Green Version]
- Faustine, A.; Mvungi, N.H.; Kaijage, S.; Kisangiri, M. A Survey on Non-Intrusive Load Monitoring Methodies and Techniques for Energy Disaggregation Problem. arXiv 2017, arXiv:1703.00785. [Google Scholar]
- Du, L.; He, D.; Harley, R.G.; Habetler, T.G. Electric Load Classification by Binary Voltage–Current Trajectory Mapping. IEEE Trans. Smart Grid 2016, 7, 358–365. [Google Scholar] [CrossRef]
- Sadeghianpourhamami, N.; Ruyssinck, J.; Deschrijver, D.; Dhaene, T.; Develder, C. Comprehensive feature selection for appliance classification in NILM. Energy Build. 2017, 151, 98–106. [Google Scholar] [CrossRef] [Green Version]
- Lam, H.Y.; Fung, G.S.K.; Lee, W.K. A Novel Method to Construct Taxonomy Electrical Appliances Based on Load Signaturesof. IEEE Trans. Consum. Electron. 2007, 53, 653–660. [Google Scholar] [CrossRef] [Green Version]
- Li, L.; Zhao, Y.; Jiang, D.; Zhang, Y.; Wang, F.; Gonzalez, I.; Valentin, E.; Sahli, H. Hybrid Deep Neural Network–Hidden Markov Model (DNN-HMM) Based Speech Emotion Recognition. In Proceedings of the 2013 Humaine Association Conference on Affective Computing and Intelligent Interaction, Geneva, Switzerland, 2–5 September 2013; pp. 312–317. [Google Scholar] [CrossRef]
- Wang, A.L.; Chen, B.X.; Wang, C.G.; Hua, D. Non-intrusive load monitoring algorithm based on features of V–I trajectory. Electr. Power Syst. Res. 2018, 157, 134–144. [Google Scholar] [CrossRef]
- Gao, J.; Kara, E.C.; Giri, S.; Bergés, M. A feasibility study of automated plug-load identification from high-frequency measurements. In Proceedings of the 2015 IEEE Global Conference on Signal and Information Processing (GlobalSIP), Orlando, FL, USA, 14–16 December 2015; pp. 220–224. [Google Scholar] [CrossRef]
- Hassan, T.; Javed, F.; Arshad, N. An Empirical Investigation of V–I Trajectory Based Load Signatures for Non-Intrusive Load Monitoring. IEEE Trans. Smart Grid 2014, 5, 870–878. [Google Scholar] [CrossRef] [Green Version]
- Garcia-Ceja, E.; Uddin, M.Z.; Torresen, J. Classification of Recurrence Plots’ Distance Matrices with a Convolutional Neural Network for Activity Recognition. Procedia Comput. Sci. 2018, 130, 157–163. [Google Scholar] [CrossRef]
- Hatami, N.; Gavet, Y.; Debayle, J. Classification of Time-Series Images Using Deep Convolutional Neural Networks. arXiv 2017, arXiv:1710.00886. [Google Scholar]
- Tsai, Y.; Chen, J.H.; Wang, C. Encoding Candlesticks as Images for Patterns Classification Using Convolutional Neural Networks. arXiv 2019, arXiv:1901.05237. [Google Scholar]
- Popescu, F.; Enache, F.; Vizitiu, I.; Ciotîrnae, P. Recurrence Plot Analysis for characterization of appliance load signature. In Proceedings of the 2014 10th International Conference on Communications (COMM), Bucharest, Romania, 29–31 May 2014; pp. 1–4. [Google Scholar] [CrossRef]
- Rajabi, R.; Estebsari, A. Deep Learning Based Forecasting of Individual Residential Loads Using Recurrence Plots. In Proceedings of the 2019 IEEE Milan PowerTech, Milan, Italy, 23–27 June 2019; pp. 1–5. [Google Scholar]
- Dokmanic, I.; Parhizkar, R.; Ranieri, J.; Vetterli, M. Euclidean Distance Matrices: Essential theory, algorithms, and applications. IEEE Signal Process. Mag. 2015, 32, 12–30. [Google Scholar] [CrossRef] [Green Version]
- Tamura, K.; Ichimura, T. MACD-histogram-based recurrence plot: A new representation for time series classification. In Proceedings of the 2017 IEEE 10th International Workshop on Computational Intelligence and Applications (IWCIA), Hiroshima, Japan, 11–12 November 2017; pp. 135–140. [Google Scholar] [CrossRef]
- Gao, J.; Giri, S.; Kara, E.C.; Bergés, M. PLAID: A Public Dataset of High-resolution Electrical Appliance Measurements for Load Identification Research: Demo Abstract. In Proceedings of the 1st ACM Conference on Embedded Systems for Energy-Efficient Buildings (BuildSys ’14), Memphis, TN, USA, 3–6 November 2014; ACM: New York, NY, USA, 2014; pp. 198–199. [Google Scholar] [CrossRef]
- Kahl, M.; Haq, A.U.; Kriechbaumer, T.; Jacobsen, H.A. WHITED-A Worldwide Household and Industry Transient Energy Data Set. In Proceedings of the 3rd International Workshop on Non-Intrusive Load Monitoring (NILM), Vancouver, BC, Canada, 14–15 May 2016. [Google Scholar]
- Picon, T.; Nait Meziane, M.; Ravier, P.; Lamarque, G.; Novello, C.; Le Bunetel, J.C.; Raingeaud, Y. COOLL: Controlled On/Off Loads Library, a Public Dataset of High-Sampled Electrical Signals for Appliance Identification. arXiv 2016, arXiv:1611.05803. [Google Scholar]
- Pereira, L.; Nunes, N. A comparison of performance metrics for event classification in Non-Intrusive Load Monitoring. In Proceedings of the 2017 IEEE International Conference on Smart Grid Communications (SmartGridComm), Dresden, Germany, 23–27 October 2017; pp. 159–164. [Google Scholar] [CrossRef]
- Pereira, L. Developing and evaluating a probabilistic event detector for non-intrusive load monitoring. In Proceedings of the 2017 Sustainable Internet and ICT for Sustainability (SustainIT), Funchal, Portugal, 6–7 December 2017; IEEE: Funchal, Portugal, 2017; pp. 1–10. [Google Scholar] [CrossRef]
- De Baets, L.; Ruyssinck, J.; Develder, C.; Dhaene, T.; Deschrijver, D. On the Bayesian optimization and robustness of event detection methods in NILM. Energy Build. 2017, 145, 57–66. [Google Scholar] [CrossRef] [Green Version]


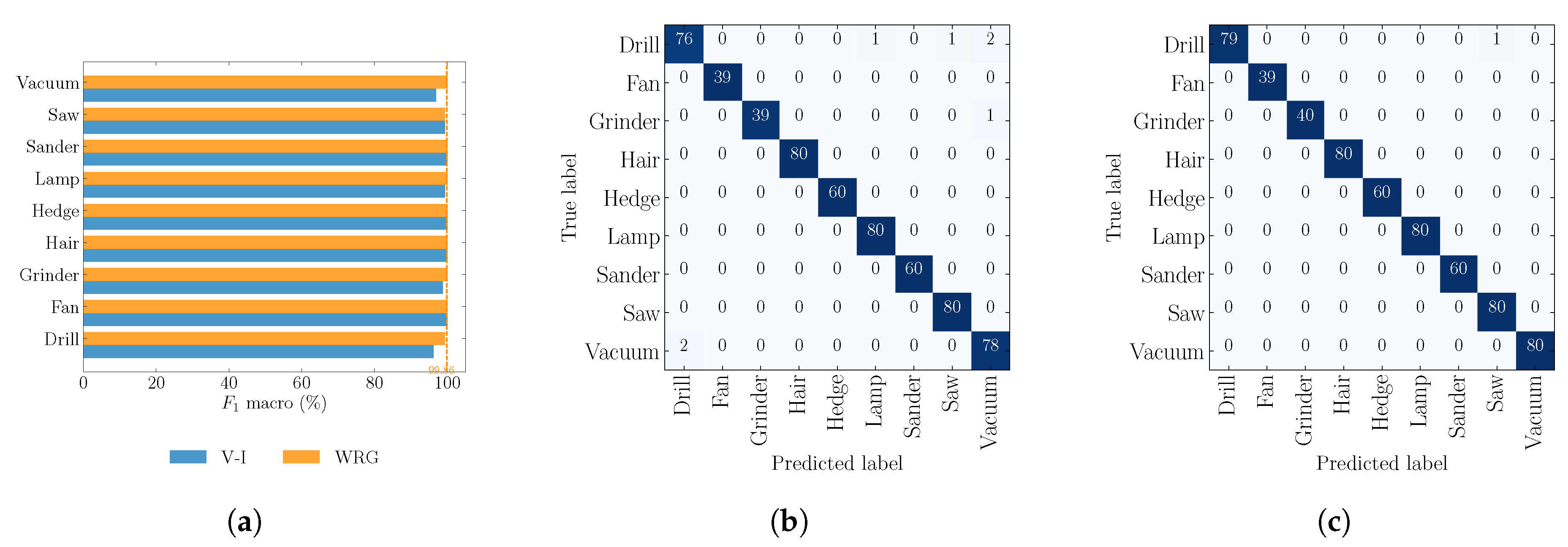
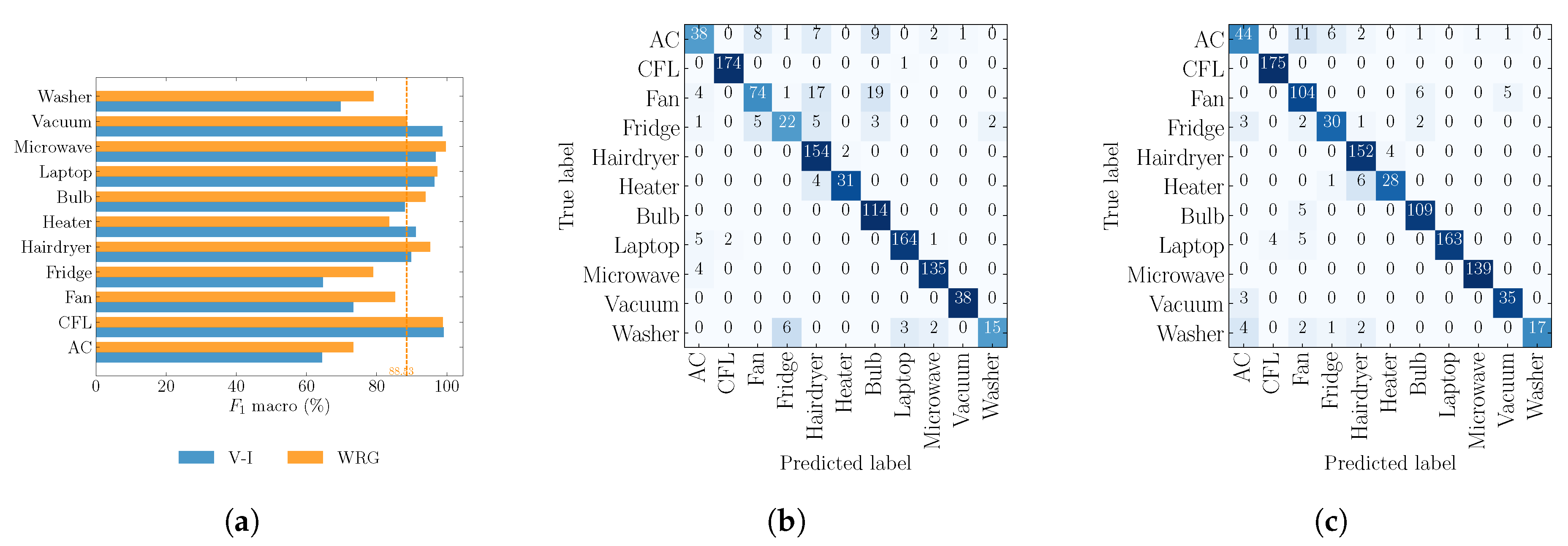
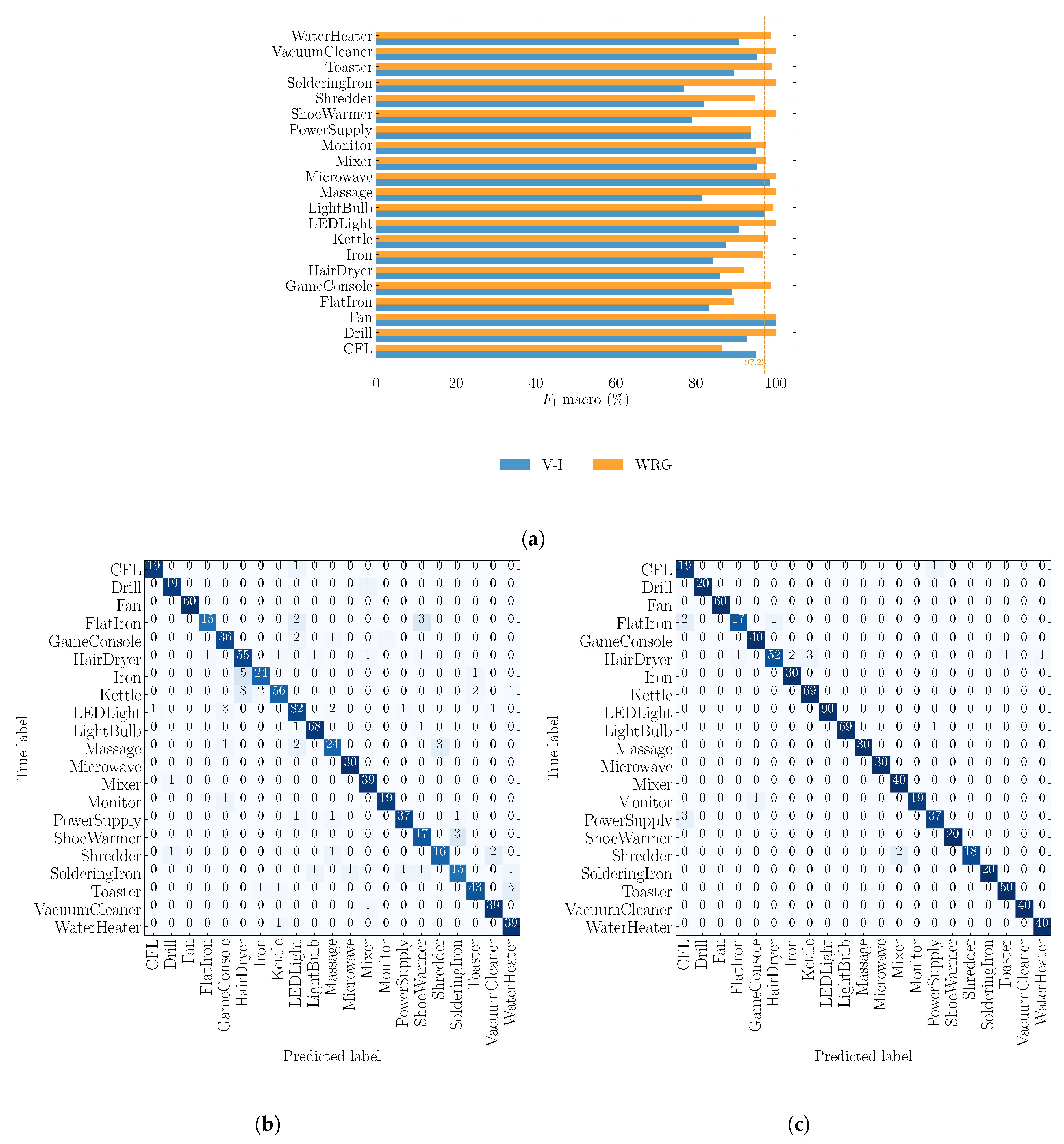
| Parameter | COOLL | WHITED | PLAID |
|---|---|---|---|
| 50 | 50 | 20 | |
| w | 50 | 50 | 50 |
| Data | Method | Metrics | ||
|---|---|---|---|---|
| MCC | F1 | ZL | ||
| COOLL | RG | |||
| WRG | ||||
| PLAID | RG | |||
| WRG | ||||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Faustine, A.; Pereira, L. Improved Appliance Classification in Non-Intrusive Load Monitoring Using Weighted Recurrence Graph and Convolutional Neural Networks. Energies 2020, 13, 3374. https://doi.org/10.3390/en13133374
Faustine A, Pereira L. Improved Appliance Classification in Non-Intrusive Load Monitoring Using Weighted Recurrence Graph and Convolutional Neural Networks. Energies. 2020; 13(13):3374. https://doi.org/10.3390/en13133374
Chicago/Turabian StyleFaustine, Anthony, and Lucas Pereira. 2020. "Improved Appliance Classification in Non-Intrusive Load Monitoring Using Weighted Recurrence Graph and Convolutional Neural Networks" Energies 13, no. 13: 3374. https://doi.org/10.3390/en13133374
APA StyleFaustine, A., & Pereira, L. (2020). Improved Appliance Classification in Non-Intrusive Load Monitoring Using Weighted Recurrence Graph and Convolutional Neural Networks. Energies, 13(13), 3374. https://doi.org/10.3390/en13133374






