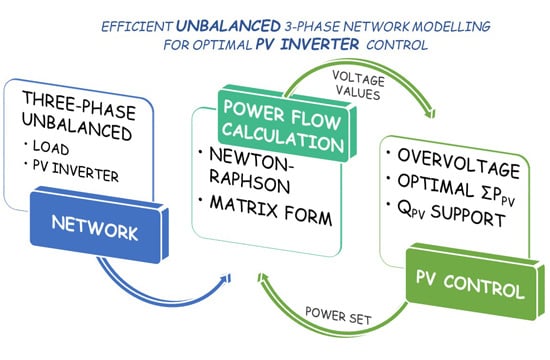
Efficient Unbalanced Three-Phase Network Modelling for Optimal PV Inverter Control
Abstract
1. Introduction
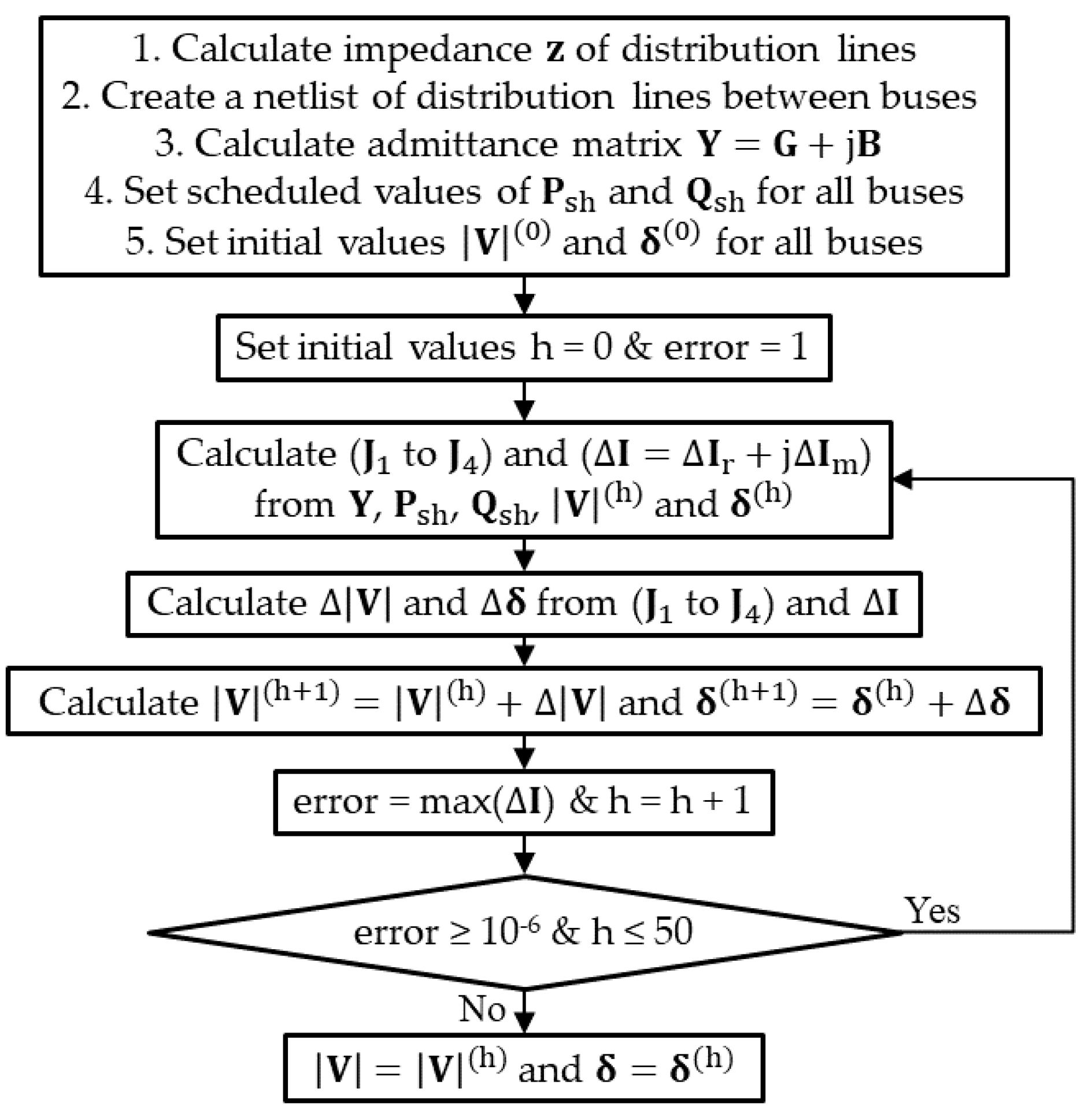
2. Power Flow Matrix Formation of an Unbalanced 3-Phase Network
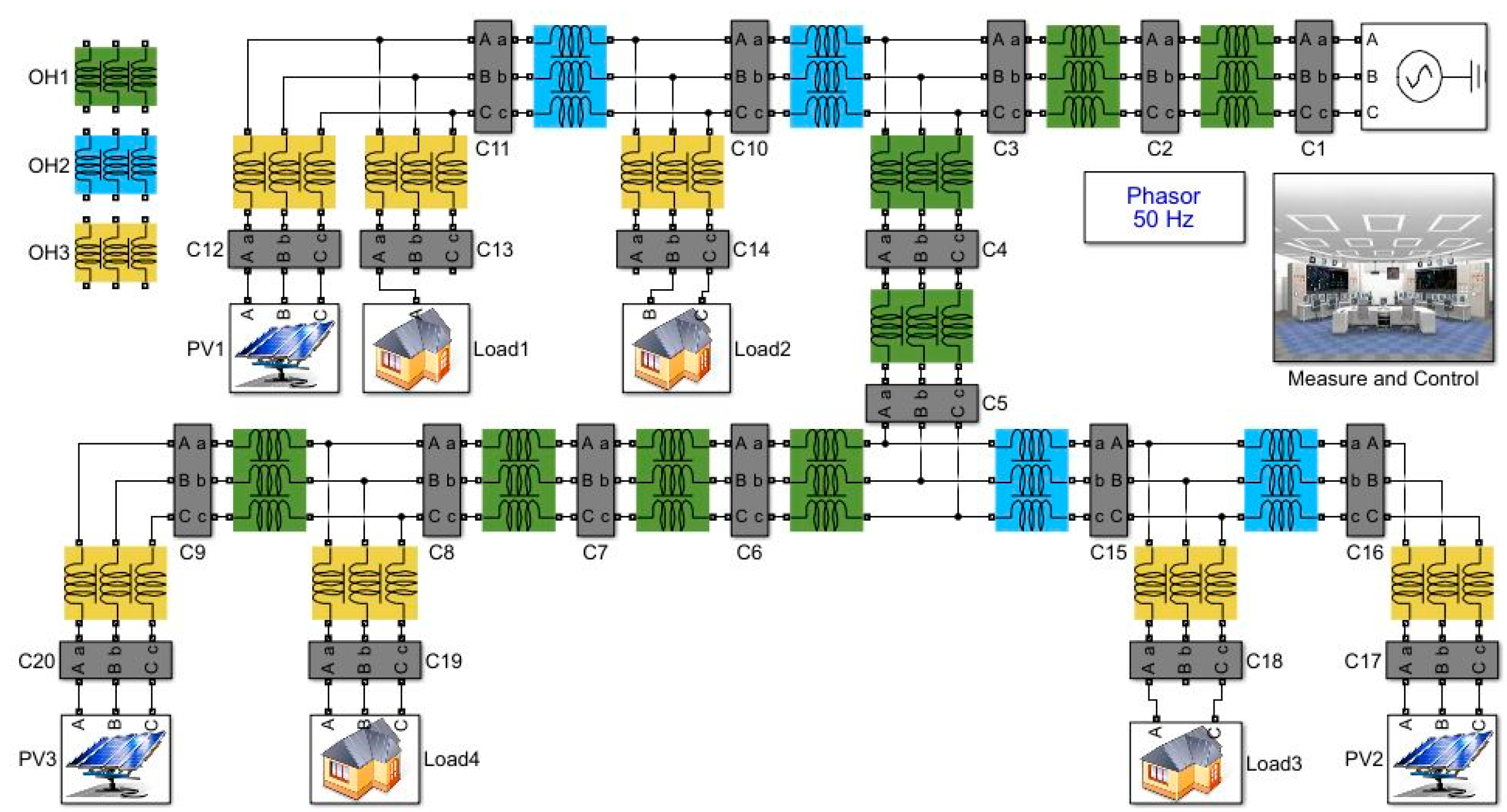
3. Network Simulation Using Matrix Formation
4. Network Control Application
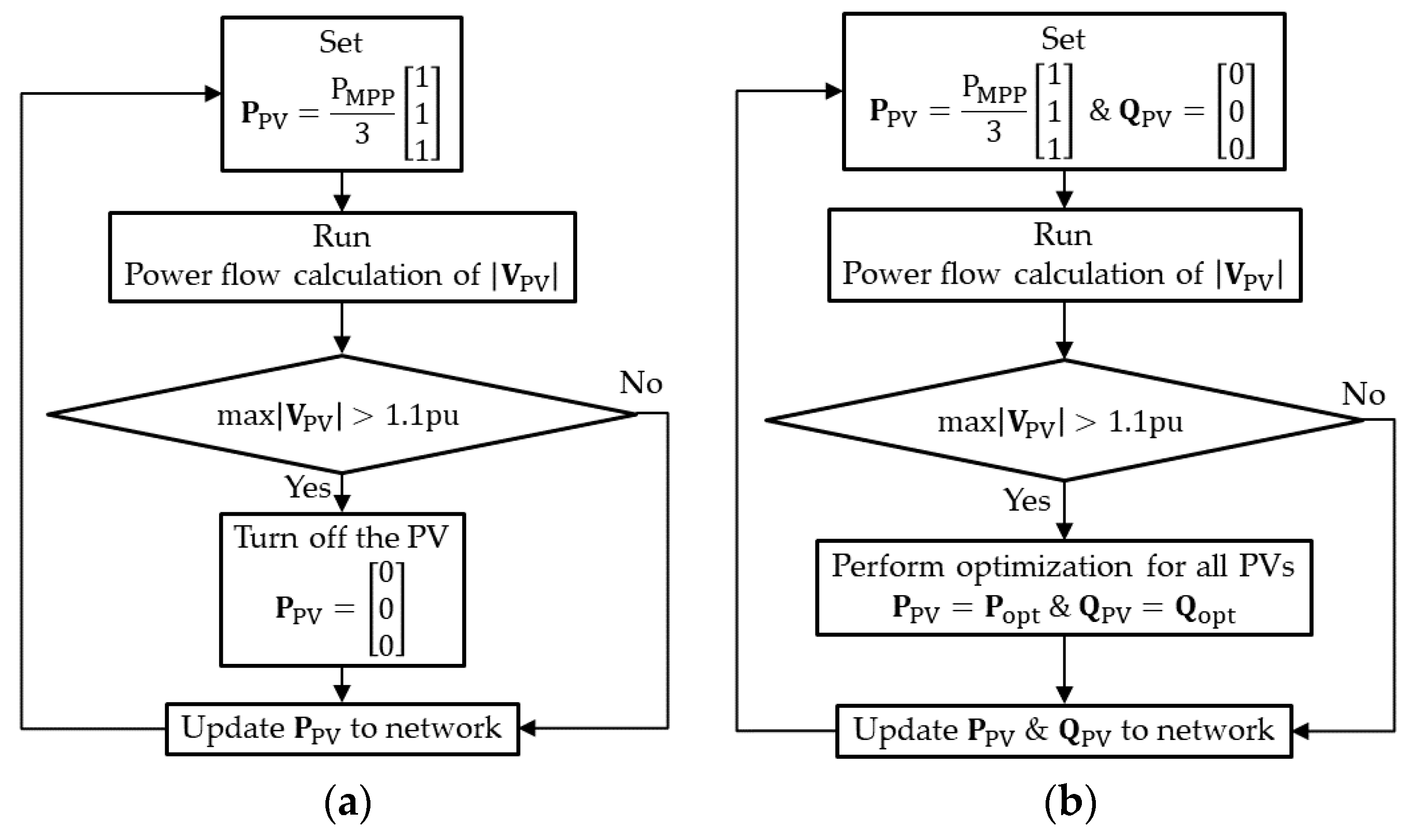
4.1. Decentralized Overvoltage Control (DOVC)
4.2. Decentralized Power Dispatch Control (DPDC)
5. Simulation Results
6. Discussion
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Shayani, R.A.; de Oliveira, M.A.G. Photovoltaic Generation Penetration Limits in Radial Distribution Systems. IEEE Trans. Power Syst. 2011, 26, 1625–1631. [Google Scholar] [CrossRef]
- Budka, K.; Deshpande, J.; Thottan, M. Communication Networks for Smart Grids: Making Smart Grid Real; Computer Communications and Networks; Springer: Berlin, Germany, 2014; ISBN 978-1-4471-6302-2. [Google Scholar]
- Thomas, M.; McDonald, J. Power System SCADA and Smart Grids; Taylor & Francis: Abingdon, UK, 2015. [Google Scholar]
- Saadat, H. Power System Analysis; WCB/McGraw Hill: New York, NY, USA, 1999; ISBN 0-07-561634-3. [Google Scholar]
- Glover, J.D.; Sarma, M.S.; Overbye, T.J. Power System Analysis and Design; Cengage Learning: Boston, MA, USA, 2017; ISBN 978-1-305-63213-4. [Google Scholar]
- Sereeter, B.; Vuik, C.; Witteveen, C. On a Comparison of Newton-Raphson Solvers for Power Flow Problems; Report 17-7; Delft Institute of Applied Mathematics, Delft University of Technology: Delft, The Netherlands, 2017. [Google Scholar]
- Sereeter, B.; Vuik, K.; Witteveen, C. Newton Power Flow Methods for Unbalanced Three-Phase Distribution Networks. Energies 2017, 10, 1658. [Google Scholar] [CrossRef]
- Rajaei, N.; Ahmed, M.H.; Salama, M.M.A. A novel Newton-Raphson algorithm for power flow analysis in the presence of constant current sources. In Proceedings of the 2016 IEEE/PES Transmission and Distribution Conference and Exposition (T&D), Dallas, TX, USA, 3–5 May 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Zhang, X.P.; Ju, P.; Handschin, E. Continuation three-phase power flow: A tool for voltage stability analysis of unbalanced three-phase power systems. IEEE Trans. Power Syst. 2005, 20, 1320–1329. [Google Scholar] [CrossRef]
- Chindris, M.; Sudria i Anderu, A.; Bud, C.; Tomoiaga, B. The load flow calculation in unbalanced radial electric networks with distributed generation. In Proceedings of the 2007 9th International Conference on Electrical Power Quality and Utilisation, Barcelona, Spain, 9–11 October 2007; pp. 1–5. [Google Scholar] [CrossRef]
- Aguirre, R.A.; Bobis, D.X.S. Improved power flow program for unbalanced radial distribution systems including voltage dependent loads. In Proceedings of the 2016 IEEE 6th International Conference on Power Systems (ICPS), New Delhi, India, 4–6 March 2016; pp. 1–6. [Google Scholar] [CrossRef]
- AlHajri, M.F.; El-Hawary, M.E. Exploiting the Radial Distribution Structure in Developing a Fast and Flexible Radial Power Flow for Unbalanced Three-Phase Networks. IEEE Trans. Power Deliv. 2010, 25, 378–389. [Google Scholar] [CrossRef]
- Garces, A. A Linear Three-Phase Load Flow for Power Distribution Systems. IEEE Trans. Power Syst. 2016, 31, 827–828. [Google Scholar] [CrossRef]
- Li, H.; Yan, X.; Yan, J.; Zhang, A.; Zhang, F. A Three-Phase Unbalanced Linear Power Flow Solution with PV Bus and ZIP Load. IEEE Access 2019, 7, 138879–138889. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, N.; Li, H.; Yang, J.; Kang, C. Linear three-phase power flow for unbalanced active distribution networks with PV nodes. CSEE J. Power Energy Syst. 2017, 3, 321–324. [Google Scholar] [CrossRef]
- Chatterjee, S.; Mandal, S. A novel comparison of Gauss-Seidel and Newton-Raphson methods for load flow analysis. In Proceedings of the 2017 International Conference on Power and Embedded Drive Control (ICPEDC), Chennai, India, 16–18 March 2017; pp. 1–7. [Google Scholar] [CrossRef]
- Muzzammel, R.; Ahsan, M.; Ahmad, W. Non-linear analytic approaches of power flow analysis and voltage profile improvement. In Proceedings of the 2015 Power Generation System and Renewable Energy Technologies (PGSRET), Islamabad, Pakistan, 10–11 June 2015; pp. 1–7. [Google Scholar] [CrossRef]
- Kamel, S.; Abdel-Akher, M.; El-Nemr, M. Hybrid power and current mismatches Newton-Raphson load-flow analysis for solving power systems with voltage controlled devices. In Proceedings of the 14th International Middle East Power Systems Conference (MEPCON), Cairo, Egypt, 19–21 December 2010; pp. 763–768. [Google Scholar]
- Sairam, S. Analysis of ZIP Load Modeling in Power Transmission System. Int. J. Control Autom. 2018, 11, 11–24. [Google Scholar] [CrossRef]
- Okyere, H.K.; Nouri, H.; Moradi, H.; Li, Z. Statcom and load tap changing transformer (LTC) in Newton Raphson Power Flow: Bus voltage constraint and losses. In Proceedings of the 42nd International Universities Power Engineering Conference, Brighton, UK, 4–6 September 2007; pp. 1013–1018. [Google Scholar] [CrossRef]
- Santos, N.M.; Dias, O.; Pires, V.F. Use of an Interline Power Flow Controller Model for Power Flow Analysis. Energy Procedia 2012, 14, 2096–2101. [Google Scholar] [CrossRef]
- Kamel, S.; Jurado, F.; Chen, Z.; Abdel-Akher, M.; Ebeed, M. Developed generalised unified power flow controller model in the Newton–Raphson power-flow analysis using combined mismatches method. Iet Gener. Transm. Distrib. 2016, 10, 2177–2184. [Google Scholar] [CrossRef]
- Ren, B.X.; Cai, H.; Du, W.J.; Wang, H.F.; Fan, L.L. Analysis of power flow control capability of a unified power flow controller to be installed in a real Chinese power network. In Proceedings of the 12th IET International Conference on AC and DC Power Transmission (ACDC 2016), Beijing, China, 28–29 May 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Yang, J.; Xu, Z.; Wang, W.; Cai, H. Implementation of a novel unified power flow controller into Newton-Raphson load flow. In Proceedings of the 2017 IEEE Power Energy Society General Meeting, Chicago, IL, USA, 16–20 July 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Schneider, K.P.; Mather, B.A.; Pal, B.C.; Ten, C.-W.; Shirek, G.J.; Zhu, H.; Fuller, J.C.; Pereira, J.L.R.; Ochoa, L.F.; de Araujo, L.R.; et al. Analytic Considerations and Design Basis for the IEEE Distribution Test Feeders. IEEE Trans. Power Syst. 2018, 33, 3181–3188. [Google Scholar] [CrossRef]
- IEEE PES AMPS DSAS Test Feeder. Available online: https://site.ieee.org/pes-testfeeders/resources/ (accessed on 6 March 2020).
- Strunz, K.; Abbasi, E.; Fletcher, R.; Hatziargyriou, N.; Iravani, R.; Joos, G. TF C6.04.02: TB 575—Benchmark Systems for Network Integration of Renewable and Distributed Energy Resources; CIGRE: Paris, France, 2014; pp. 54–62. ISBN 978-285-873-270-8. [Google Scholar]
- Clua, J.; Sainz, L.; Corcoles, F. Three-phase transformer modeling for unbalanced harmonic power flow studies. In Proceedings of the Ninth International Conference on Harmonics and Quality of Power, Orlando, FL, USA, 1–4 October 2000; Cat. No.00EX441. Volume 2, pp. 726–731. [Google Scholar] [CrossRef]
- Guggilam, S.S.; Dall’Anese, E.; Chen, Y.C.; Dhople, S.V.; Giannakis, G.B. Scalable Optimization Methods for Distribution Networks With High PV Integration. IEEE Trans. Smart Grid 2016, 7, 2061–2070. [Google Scholar] [CrossRef]
- Craciun, B.; Sera, D.; Man, E.A.; Kerekes, T.; Muresan, V.A.; Teodorescu, R. Improved voltage regulation strategies by PV inverters in LV rural networks. In Proceedings of the 2012 3rd IEEE International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Aalborg, Denmark, 25–28 June 2012; pp. 775–781. [Google Scholar] [CrossRef]
- Levis, C. Smart Inverters for Distributed PV Network Management. Ph.D. Thesis, Cork Institute of Technology, Cork, Ireland, 2019. [Google Scholar]
- Samadi, A.; Shayesteh, E.; Eriksson, R.; Rawn, B.; Soder, L. Multi-objective coordinated droop-based voltage regulation in distribution grids with PV systems. Renew. Energy 2014, 71, 315–323. [Google Scholar] [CrossRef]
- Hou, J.; Xu, Y.; Liu, J.; Xin, L.; Wei, W. A multi-objective volt-var control strategy for distribution networks with high PV penetration. In Proceedings of the 10th International Conference on Advances in Power System Control, Operation Management (APSCOM 2015), Hong Kong, China, 8–12 November 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Zhang, Y.; Lu, Y. A novel newton current equation method on power flow analysis in microgrid. In Proceedings of the 2009 IEEE Power Energy Society General Meeting, Calgary, AB, Canada, 26–30 July 2009; pp. 1–6. [Google Scholar] [CrossRef]
- Le Nguyen, H. Newton-Raphson method in complex form. IEEE Trans. Power Syst. 1997, 12, 1355–1359. [Google Scholar] [CrossRef]
- MATLAB Generalized Mutual Inductance. Available online: https://www.mathworks.com/help/physmod/sps/powersys/ref/mutualinductance.html#f3-2480259 (accessed on 6 March 2020).
- Markiewicz, H.; Klajn, A. Voltage Disturbances Standard EN 50160—Voltage Characteristics in Public Distribution Systems; Wroclaw University of Technology: Wroclaw, Poland, 2004. [Google Scholar]
- NRS 097-2-3. Grid Interconnection of Embedded Generation, Part 2: Small-Scale Embedded Generation, Section 3: Simplified Utility Connection Criteria for Low-Voltage Connected Generators; Standard, South African National Standards (SANS): Midrand, South Africa, 2014. [Google Scholar]
- MATLAB Fmincon. Available online: https://www.mathworks.com/help/optim/ug/fmincon.html (accessed on 6 March 2020).






| Diagonal | |
| Off-Diagonal | |
| The operations , , and °2 are the matrix element-wise multiplication, division and power. The diag(A3×1) creates a 3 × 3 matrix with the elements of A on the main diagonal. , , , , , | |
| Line Type | (Ω/km) |
|---|---|
| From Bus | To Bus | Impedance | Admittance | From Bus | To Bus | Impedance | Admittance |
|---|---|---|---|---|---|---|---|
| C1 | C2 | C11 | C12 | ||||
| C2 | C3 | C11 | C13 | ||||
| C3 | C4 | C10 | C14 | ||||
| C4 | C5 | C5 | C15 | ||||
| C5 | C6 | C15 | C16 | ||||
| C6 | C7 | C15 | C17 | ||||
| C7 | C8 | C16 | C18 | ||||
| C8 | C9 | C8 | C19 | ||||
| C3 | C10 | C9 | C20 | ||||
| C10 | C11 |
| Bus | PV | Load | Swing | Others | |||||
|---|---|---|---|---|---|---|---|---|---|
| C12 | C17 | C20 | C13 | C14 | C18 | C19 | C1 | C2-11,15-16 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Phan-Tan, C.-T.; Hill, M. Efficient Unbalanced Three-Phase Network Modelling for Optimal PV Inverter Control. Energies 2020, 13, 3011. https://doi.org/10.3390/en13113011
Phan-Tan C-T, Hill M. Efficient Unbalanced Three-Phase Network Modelling for Optimal PV Inverter Control. Energies. 2020; 13(11):3011. https://doi.org/10.3390/en13113011
Chicago/Turabian StylePhan-Tan, Chi-Thang, and Martin Hill. 2020. "Efficient Unbalanced Three-Phase Network Modelling for Optimal PV Inverter Control" Energies 13, no. 11: 3011. https://doi.org/10.3390/en13113011
APA StylePhan-Tan, C.-T., & Hill, M. (2020). Efficient Unbalanced Three-Phase Network Modelling for Optimal PV Inverter Control. Energies, 13(11), 3011. https://doi.org/10.3390/en13113011