Singularly Perturbed Modeling and LQR Controller Design for a Fuel Cell System
Abstract
1. Introduction
2. Preliminaries
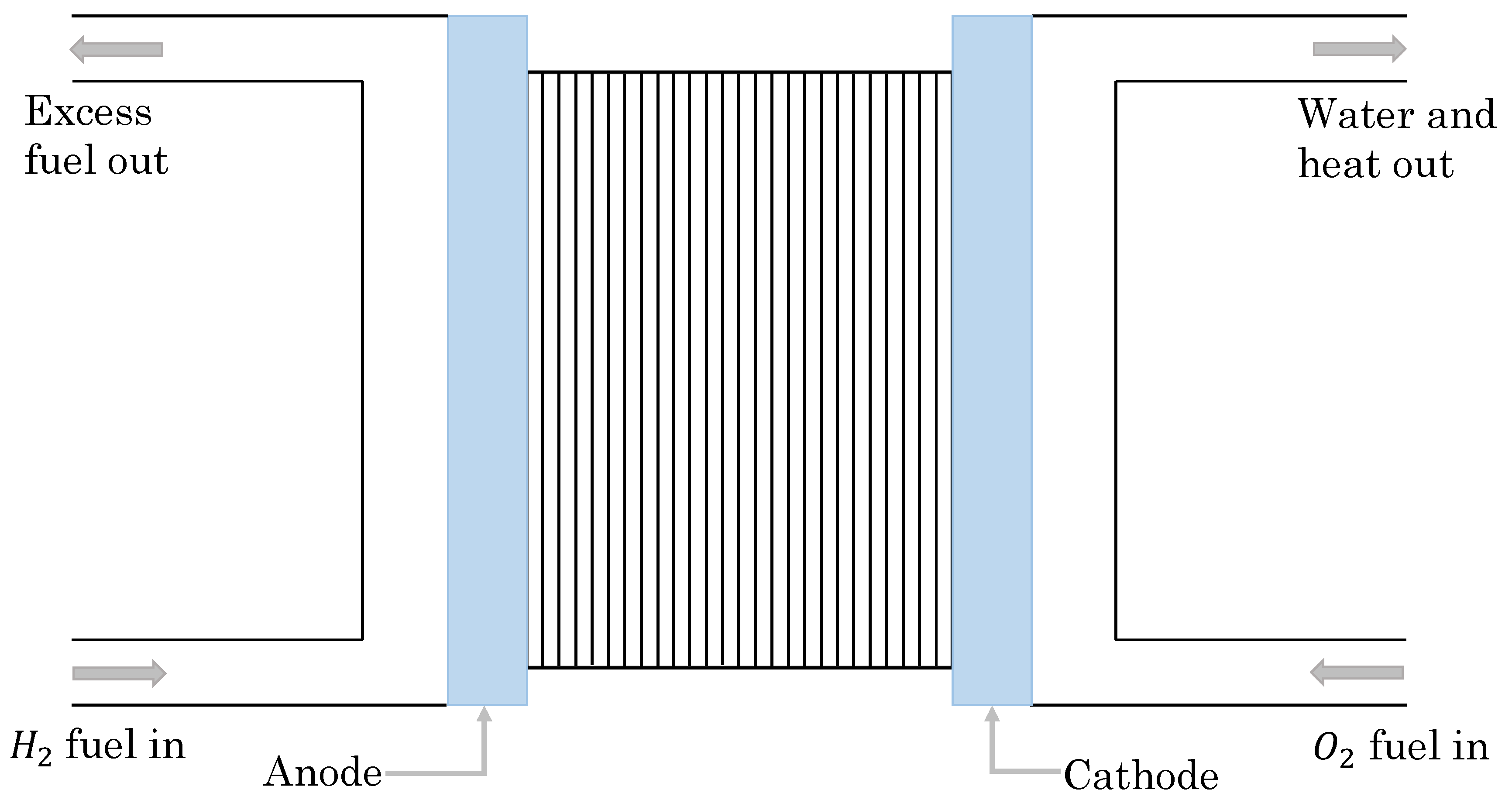
2.1. PEM Fuel Cells
2.2. Overview of Singularly Perturbed Methods in Control
3. Time-Scale Decoupling via the Ordered Schur Decomposition
3.1. Ordered Schur Transformation
3.2. Parameter Extraction and Time-Scale Decoupling
| Algorithm 1 Time-Scale Decoupling of Implicit Singularly Perturbed Systems |
|
4. Singularly Perturbed Modeling of the PEMFC-FPS
4.1. PEMFC and FPS Linear Model
4.2. Singularly Perturbed Model of the PEMFC-FPS
5. LQ Control System Design for the PEMFC-Reformer System
5.1. LQ Control Overview
5.2. Feedback Controller Design
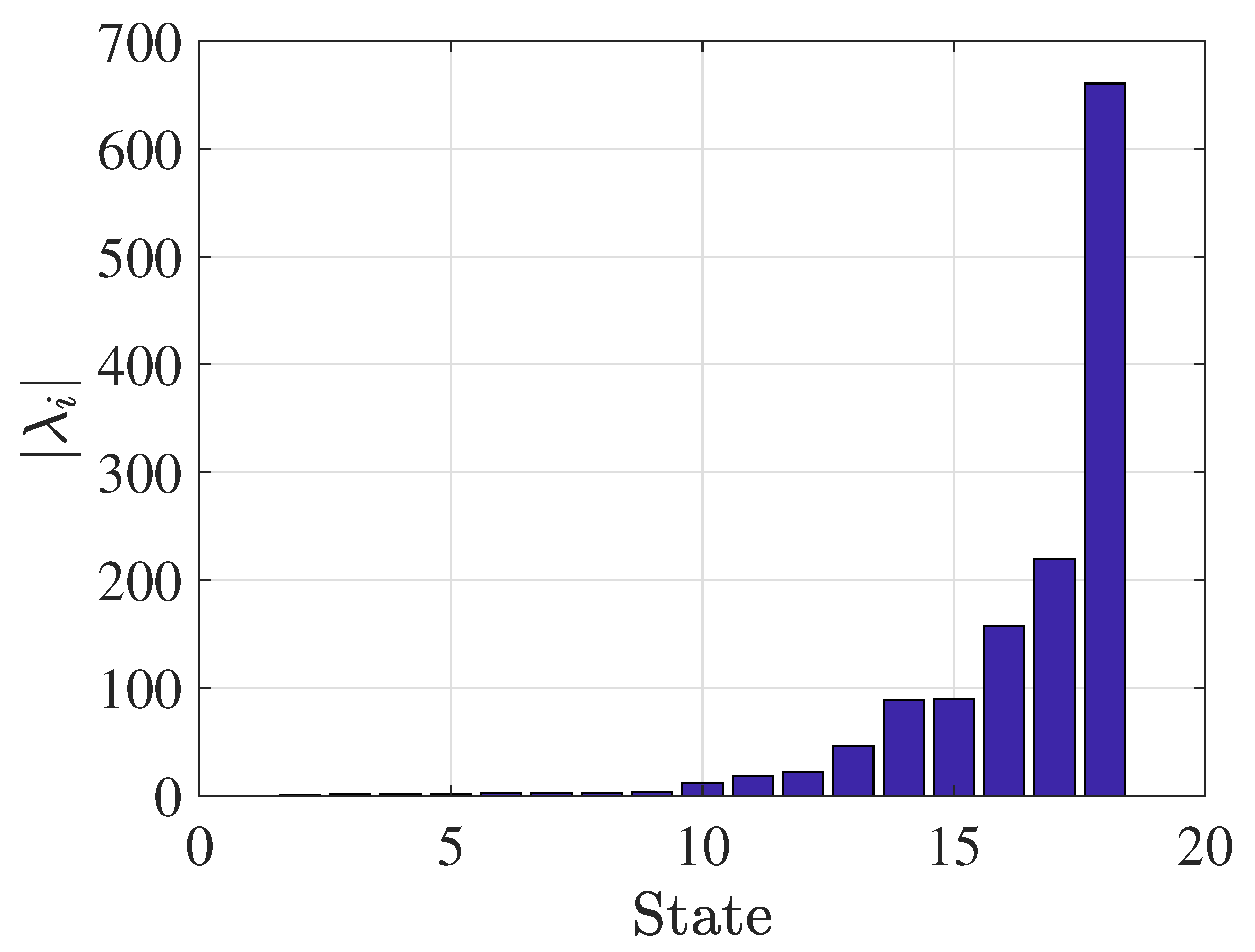
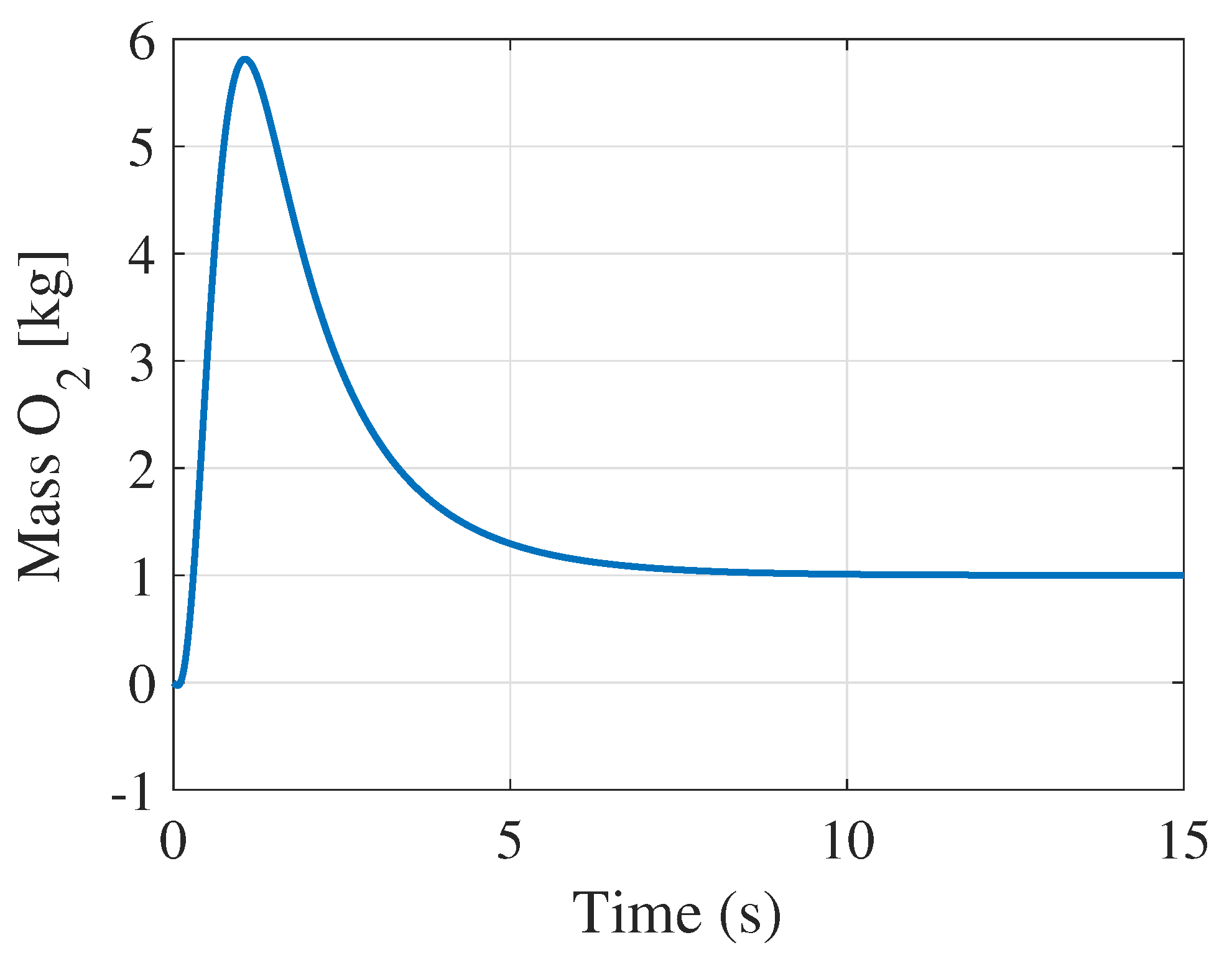
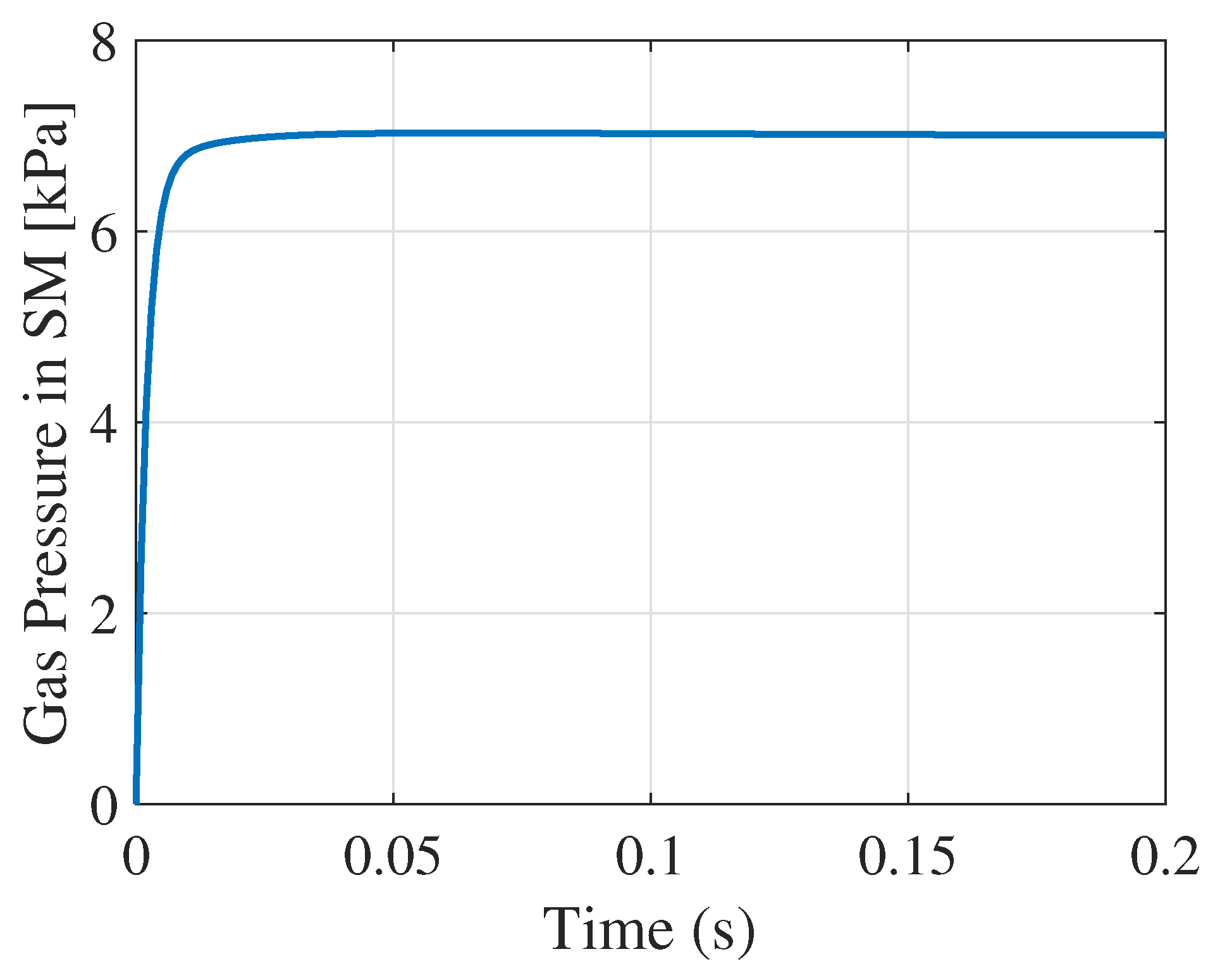
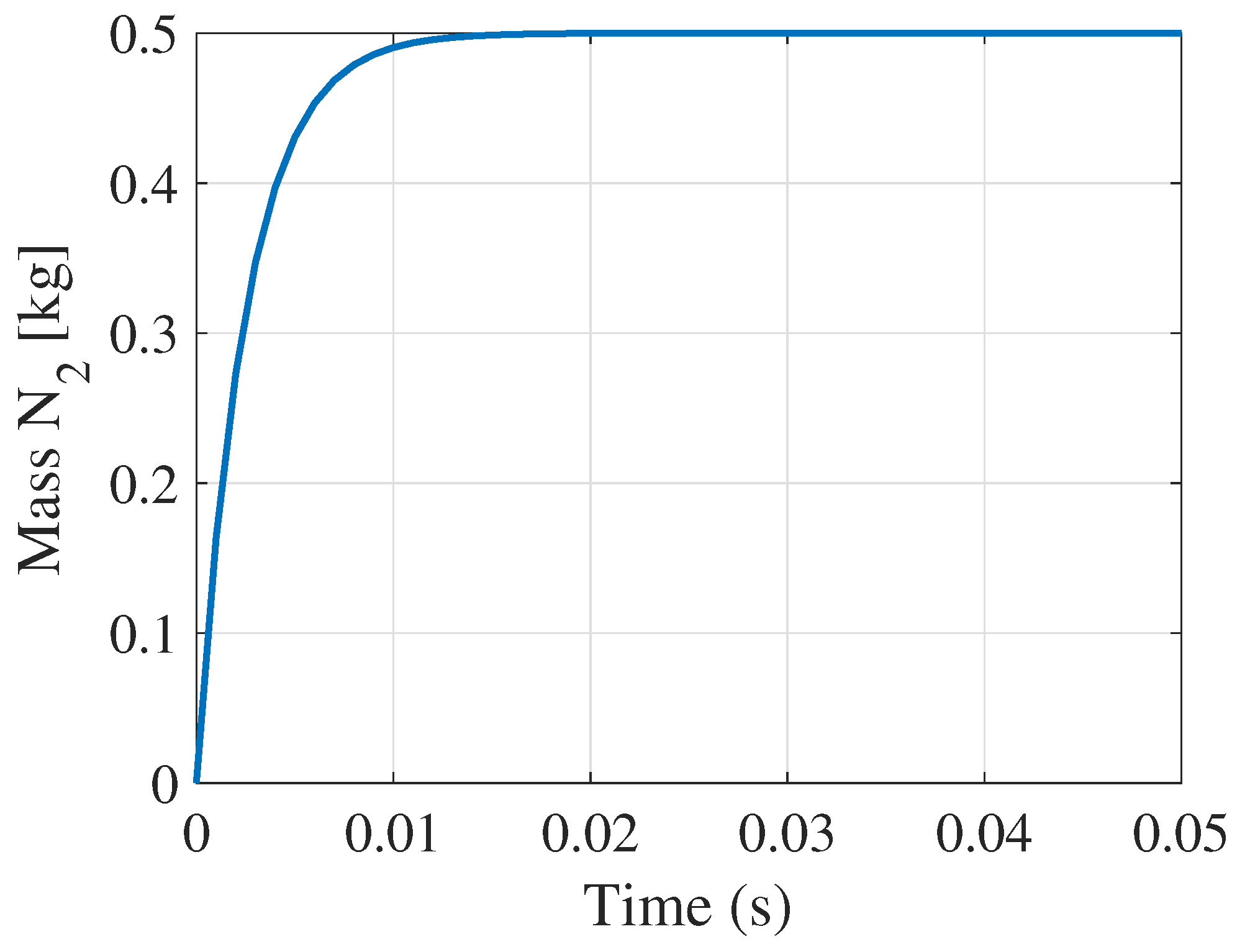
5.3. LQ Control Simulation Results
6. Discussion of Results
- Introduction of an algorithm that converts implicit singularly perturbed systems into explicit ones.
- Singularly perturbed modeling of the PEMFC-FPS augmented model followed by LQ controller design.
6.1. From Implicit to Explicit Singularly Perturbed Systems
6.2. Singularly Perturbed Modeling of the PEMFC-FPS and Controller Design
6.3. Real-World Implications
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| CB | Catalytic burner |
| FPS | Fuel processing system |
| LQ | Linear quadratic |
| PAFC | Phosphoric acid fuel cell |
| PEMFC | Proton exchange membrane fuel cell |
| SOFC | Solid oxide fuel cell |
Appendix A. Linear Model Matrices
Appendix A.1. PEMFC Model State-Space Matrices
Appendix A.2. Reformer Model State-Space Matrices
Appendix B. Singularly Perturbed Model Matrices
References
- Casas, Y.; Dewulf, J.; Arteaga-Pérez, L.E.; Morales, M.; Van Langenhove, H.; Rosa, E. Integration of Solid Oxide Fuel Cell in a sugar–ethanol factory: Analysis of the efficiency and the environmental profile of the products. J. Clean. Prod. 2011, 19, 1395–1404. [Google Scholar] [CrossRef]
- Bizon, N.; Mazare, A.G.; Ionescu, L.M.; Enescu, F.M. Optimization of the proton exchange membrane fuel cell hybrid power system for residential buildings. Energy Convers. Manag. 2018, 163, 22–37. [Google Scholar]
- Serpi, A.; Porru, M. Modelling and Design of Real-Time Energy Management Systems for Fuel Cell/Battery Electric Vehicles. Energies 2019, 12, 4260. [Google Scholar] [CrossRef]
- Lee, D.-Y.; Elgowainy, A.; Vijayagopal, R. Well-to-wheel environmental implications of fuel economy targets for hydrogen fuel cell electric buses in the United States. Energy Policy 2019, 128, 565–583. [Google Scholar]
- Qazi, S.H.; Mustafa, M.W.; Sultana, U.; Mirjat, N.H.; Soomro, S.A.; Rasheed, N. Regulation of Voltage and Frequency in Solid Oxide Fuel Cell-Based Autonomous Microgrids Using the Whales Optimisation Algorithm. Energies 2018, 11, 1318. [Google Scholar]
- Brunaccini, G.; Sergi, F.; Aloisio, D.; Randazzo, N.; Ferraro, M.; Antonucci, V. Fuel cells hybrid systems for resilient microgrids. Int. J. Hydrogen Energy 2019, 44, 21162–21173. [Google Scholar] [CrossRef]
- Viesi, D.; Crema, L.; Testi, M. The Italian hydrogen mobility scenario implementing the European directive on alternative fuels infrastructure (DAFI 2014/94/EU). Int. J. Hydrogen Energy 2017, 42, 27354–27373. [Google Scholar] [CrossRef]
- Tlili, O.; Mansila, C.; Frimat, D.; Perez, Y. Hydrogen market penetration feasibility assessment: Mobility and natural gas markets in the US, Europe, China and Japan. Int. J. Hydrogen Energy 2019, 44, 16048–16068. [Google Scholar] [CrossRef]
- Pukrushpan, J.T.; Stefanopoulou, A.G.; Peng, H. Control of Fuel Cell Power Systems: Principles, Modeling, Analysis and Feedback Design, 1st ed.; Springer: New York, NY, USA, 2010. [Google Scholar]
- Pukrushpan, J.T.; Stefanopoulou, A.G.; Peng, H. Control of fuel cell breathing. IEEE Control Syst. Mag. 2004, 24, 30–46. [Google Scholar]
- Minh, N.Q. Solid oxide fuel cell technology—Features and applications. Solid State Ion. 2004, 174, 271–277. [Google Scholar] [CrossRef]
- Fuller, T.F.; Gallagher, K.G. Phosphoric acid fuel cells. In Materials for Fuel Cells, 1st ed.; Woodhead Publishing Series in Electronic and Optical Materials; Gasik, M., Ed.; Woodhead Publishing: Cambridge, UK, 2008; pp. 209–247. [Google Scholar]
- Tsourapas, V.; Stefanopoulou, A.G.; Sun, J. Model-based control of an integrated fuel cell and fuel processor with exhaust heat recirculation. IEEE Trans. Control Syst. Technol. 2007, 15, 233–245. [Google Scholar]
- Kodra, K.; Gajic, Z. Order reduction via balancing and suboptimal control of a fuel cell-reformer system. Int. J. Hydrogen Energy 2014, 39, 2215–2223. [Google Scholar]
- Kokotovic, P.V.; O’Malley, R.E.; Sannuti, P. Singular perturbations and order reduction in control theory—An overview. Automatica 1976, 12, 123–132. [Google Scholar] [CrossRef]
- Kodra, K.; Gajic, Z. Optimal control for a new class of singularly perturbed linear systems. Automatica 2017, 81, 203–208. [Google Scholar] [CrossRef]
- Kodra, K.; Skataric, M.; Gajic, Z. Finding Hankel singular values for singularly perturbed linear continuous-time systems. IET Control Theory A 2017, 11, 1063–1069. [Google Scholar] [CrossRef]
- Meng, X.; Wang, Q.; Zhou, N.; Xiao, S.; Chi, Y. Multi-Time Scale Model Order Reduction and Stability Consistency Certification of Inverter-Interfaced DG System in AC Microgrid. Energies 2018, 11, 254. [Google Scholar] [CrossRef]
- Kokotovic, P.; Khalil, H.; O’Reilly, J. Singular Perturbation Methods in Control: Analysis and Design, 2nd ed.; SIAM Press: Philadelphia, PA, USA, 1999. [Google Scholar]
- Naidu, D.S.; Calise, A.J. Singular perturbations and time scales in guidance and control of aerospace systems: A survey. J. Guid. Control Dyn. 2001, 24, 1057–1078. [Google Scholar] [CrossRef]
- Gajic, Z.; Lelic, M. Improvement of system order reduction via balancing using the method of singular perturbations. Automatica 2001, 37, 1859–1865. [Google Scholar] [CrossRef]
- Chang, K.W. Singular perturbations of a general boundary value problem. SIAM J. Math. Anal. 1972, 3, 520–526. [Google Scholar] [CrossRef]
- Gajic, Z.; Lim, M.-T. Optimal Control of Singularly Perturbed Linear Systems and Applications: High Accuracy Techniques, 1st ed.; CRC Press: Boca Raton, MA, USA, 2001. [Google Scholar]
- Kecman, V.; Bingulac, S.; Gajic, Z. Eigenvector approach for order-reduction of singularly perturbed linear-quadratic optimal control problems. Automatica 1999, 35, 151–158. [Google Scholar] [CrossRef]
- Grodt, T.; Gajic, Z. The recursive reduced-order numerical solution of the singularly perturbed matrix differential riccati equation. IEEE Trans. Autom. Control 1988, 33, 751–754. [Google Scholar] [CrossRef]
- Kodra, K.; Zhong, N.; Gajic, Z. Multi-time-scale systems control via use of combined controllers. In Proceedings of the European Control Conference, Aalborg, Denmark, 29 June–1 July 2016; IEEE: Piscataway, NJ, USA, 2016. [Google Scholar]
- Golub, G.; Van Loan, C.F. Matrix Computations, 4th ed.; Johns Hopkins University Press: Baltimore, MD, USA, 2013. [Google Scholar]
- Stewart, G.W. Algorithm 506: HQR3 and EXCHNG: Fortran subroutines for calculating and ordering the eigenvalues of a real upper hessenberg matrix. ACM Trans. Math. Softw. 1976, 2, 275–280. [Google Scholar] [CrossRef]
- Bai, Z.; Demmel, J.W. On swapping diagonal blocks in real schur form. Linear Algebra Appl. 1993, 186, 75–95. [Google Scholar] [CrossRef]
- Kailath, T. Linear Systems, 1st ed.; Prentice Hall: Englewood Cliffs, NJ, USA, 1980. [Google Scholar]
- Prljaca, N.; Gajic, Z. General transformation for block diagonalization of multitime-scale singularly perturbed linear systems. IEEE Trans. Autom. Control 2008, 53, 1303–1305. [Google Scholar] [CrossRef]
- Athans, M.; Falb, P. Optimal Control: An Introduction to the Theory and Its Applications; Dover: New York, NY, USA, 2013. [Google Scholar]
- Radisavljevic-Gajic, V.; Milanovic, M.; Rose, P. Multi-Stage and Multi-Time Scale Feedback Control of Linear Systems with Applications to Fuel Cells, 1st ed.; Springer: New York, NY, USA, 2019. [Google Scholar]

| Symbol | Variable Definition | Units |
|---|---|---|
| Mass of oxygen | kg | |
| Mass of hydrogen | kg | |
| Mass of nitrogen | kg | |
| Compressor speed | rad/s | |
| Pressure of gas in supply manifold | kPa | |
| Mass of gas in supply manifold | kg | |
| Mass of water in anode channel | kg | |
| Pressure in return manifold | kPa |
| Symbol | Variable Definition | Units |
|---|---|---|
| Catalyst temperature | K | |
| Pressure of hydrogen in anode | kPa | |
| Anode pressure | kPa | |
| Heat-exchanger pressure | kPa | |
| Speed of the blower (rad/sec) | kPa | |
| Pressure of hydrodesulfurizer | kPa | |
| Pressure of in mixer | kPa | |
| Pressure of air in mixer | kPa | |
| Hydrogen pressure in water gas shift converter (WROX) | kPa | |
| Total pressure in WROX | kPa |
| State Variables | |
|---|---|
| Time-scale 1 | |
| Time-scale 2 | |
| Time-scale 3 |
| Process | Operating Time |
|---|---|
| Electrochemistry | s) |
| Hydrogen & air manifolds | s) |
| Flow control/supercharging devices | s) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kodra, K.; Zhong, N. Singularly Perturbed Modeling and LQR Controller Design for a Fuel Cell System. Energies 2020, 13, 2735. https://doi.org/10.3390/en13112735
Kodra K, Zhong N. Singularly Perturbed Modeling and LQR Controller Design for a Fuel Cell System. Energies. 2020; 13(11):2735. https://doi.org/10.3390/en13112735
Chicago/Turabian StyleKodra, Kliti, and Ningfan Zhong. 2020. "Singularly Perturbed Modeling and LQR Controller Design for a Fuel Cell System" Energies 13, no. 11: 2735. https://doi.org/10.3390/en13112735
APA StyleKodra, K., & Zhong, N. (2020). Singularly Perturbed Modeling and LQR Controller Design for a Fuel Cell System. Energies, 13(11), 2735. https://doi.org/10.3390/en13112735




