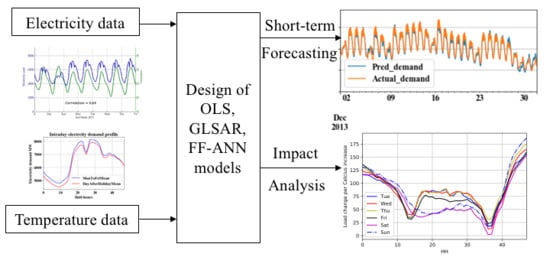
Short-Term Electricity Demand Forecasting: Impact Analysis of Temperature for Thailand
Abstract
1. Introduction
1.1. Motivation and Background
1.2. Review of Related Works
1.2.1. Temperature Effect
1.2.2. Weekend, Holiday/Special Day Effects
1.2.3. Grouping of Dataset
1.3. Model Selection
1.4. Contributions
- The marginal impact of temperature that leads to raising the demand for day hours and night hours is explored for Thailand which is quite useful for tropical countries.
- The quantitative analysis among the variables such as the impact of holidays, working days, working days after a holiday/long holiday, AR effect, special days/events such as Bangkok flood for the demand is discussed in detail.
- The unexpected Bangkok flood and lockdown situation were quite similar to the current Covid-19 in terms of electricity demand. Therefore, the researcher can extend this methodology to analyze the impact on electricity due to Covid-19.
- Construction of four different scenarios based on similar characteristics of demand which leads to achieving the best prediction capability among the existing literature of the Thai dataset.
- The strategy for the selection of variables, determination of the training length of a dataset, hidden layers and nodes are also major contributions for the improvement of the accuracy are also major contributions of this study.
2. Methods
- Scenario 1: only demand for working days.
- Scenario 2: only demand for weekends.
- Scenario 3: only holiday demand and highly fluctuated demand from December 24 to New Years eve.
- Scenario 4: all the demand dataset.
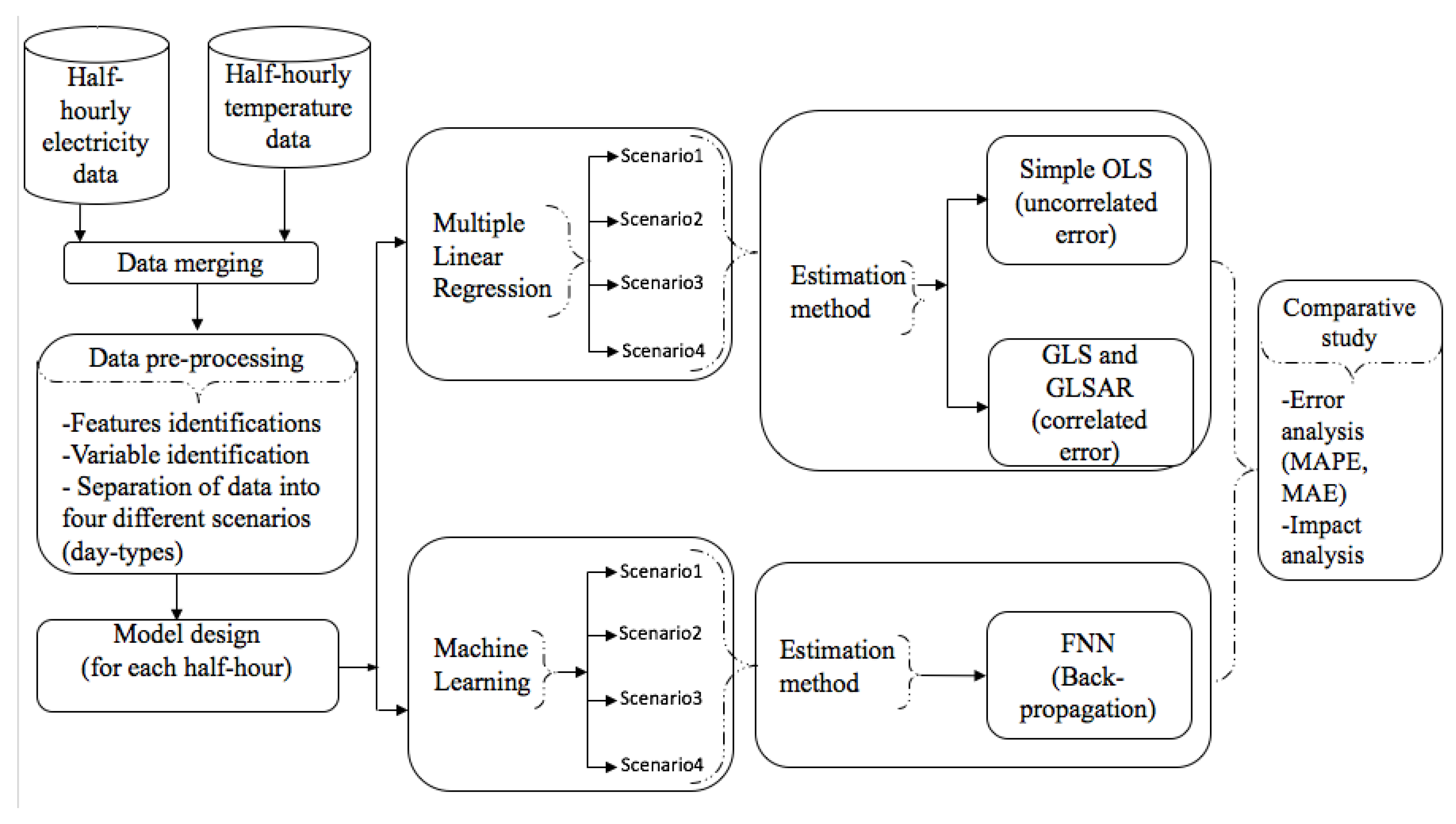
2.1. Model Design
2.1.1. MLR Model Description
- OLS: where errors
- GLS: for orbitrary covariance ∑
- GLSAR: where AR(p)
2.1.2. OLS and GLSAR Estimation
2.1.3. Performance Measurements
2.2. Artificial Neural Network Approach
2.2.1. Structure of ANNs
2.2.2. Activation Function
2.2.3. Resolving Overfitting
3. Results and Discussion
3.1. Selection of Training Length
- Case I: Training period: 911 days, test period: 239 days in the year 2013.
- Case II: Training period: 717 days, test period: 239 days in the year 2013.
- Case III: Training period: 475 days, test period: 239 days in the year 2013.
- Case IV: Training period: 236 days, test period: 239 days in the year 2013.
3.2. MLR Approach: Simple OLS Method
3.2.1. Model Selection
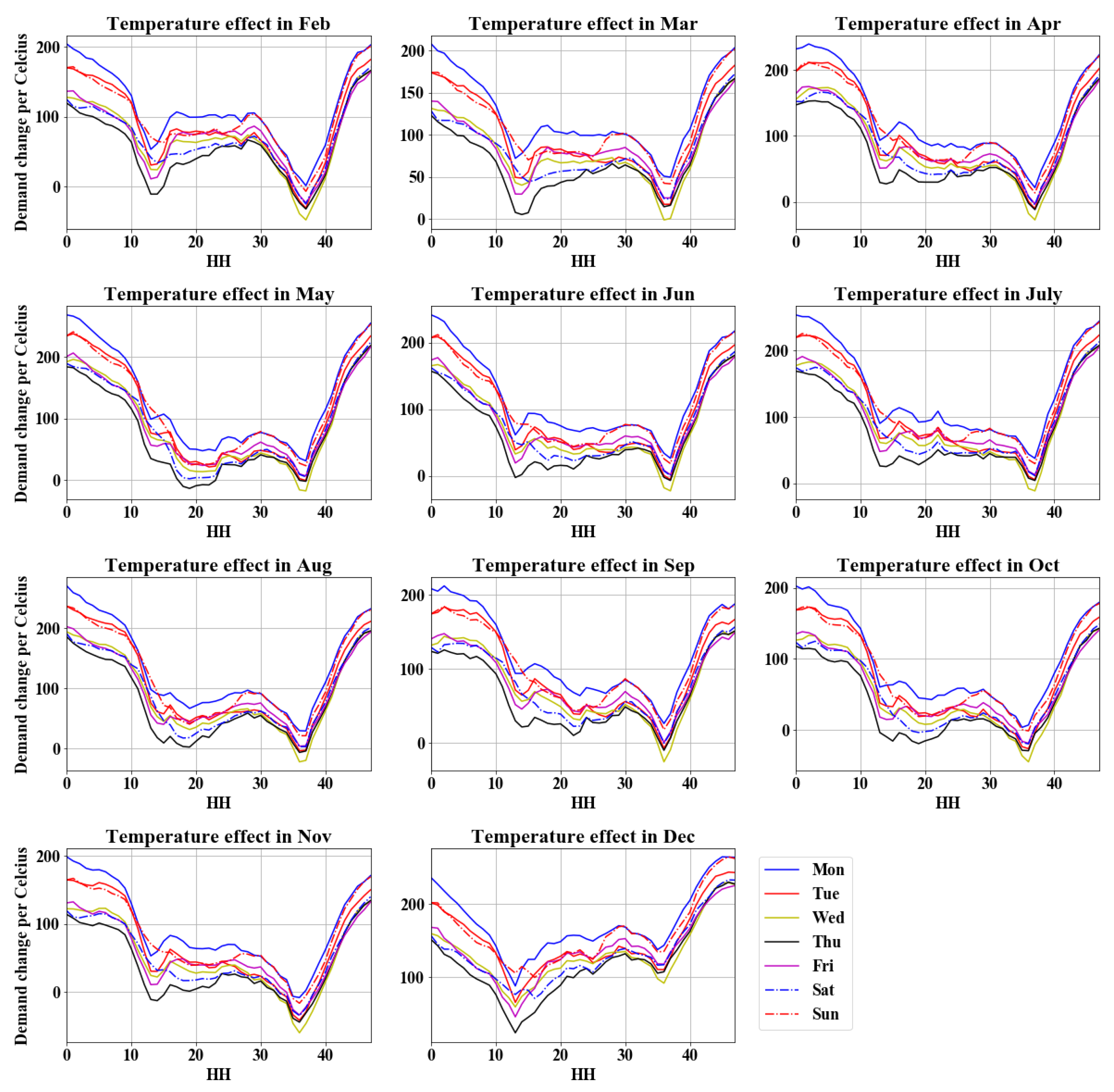
3.2.2. Temperature Effect
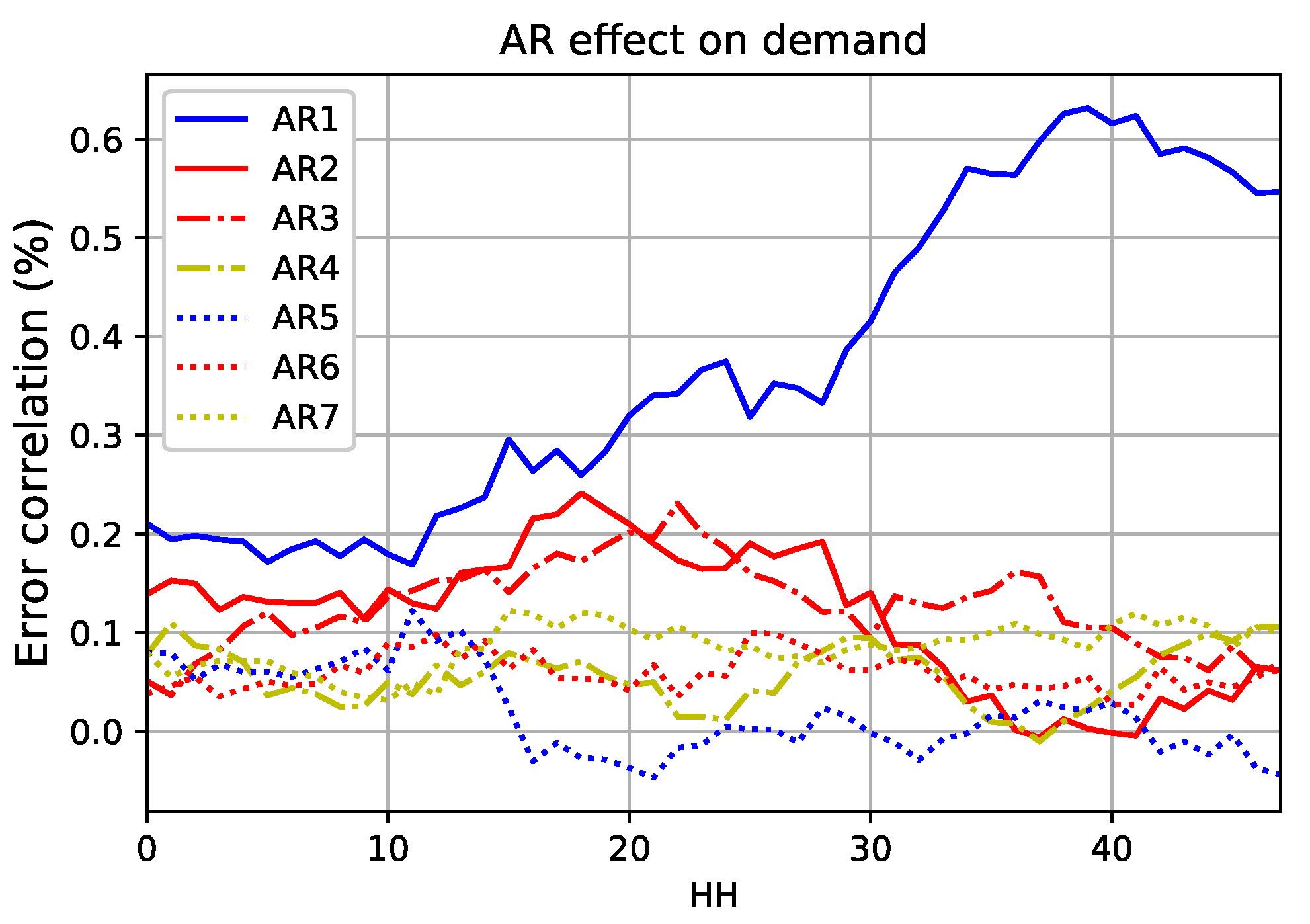
3.2.3. Special Day and AR Effect
3.3. ANN Approach: FF-ANN: A Simple DNN
3.4. Computation Time
3.5. Pro and Cons of the Methods
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| AC | Air Condition |
| AR | Auto-regression |
| ARMAX | Auto-regressive Moving Average with Exogenous Variable |
| CDD | Cooling Degree Day |
| Covid-19 | Corona Virus Disease 2019 |
| DW | Durbin–Watson |
| EGAT | Electricity Generating Authority of Thailand |
| FF-ANN | Feed Forward Artificial Neural Network |
| GA | Genetic Algorithm |
| GLSAR | Generalized Least Square Auto Regression |
| HWT | Holt Winters Triple |
| MAPE | Mean Absolute Percentage Error |
| MEA | Metropolitan Electricity Authority |
| MLR | Multiple linear regression |
| MW | Megawatt |
| OLS | Ordinary Least Square |
| PSO | Particle Swarm Optimization |
| STDF | Short-term Demand Forecasting |
| RegSARIMA | Regression Seasonal ARIMA |
| ReLU | Rectified Linear Unit |
| SVM | Support Vector Machine |
Appendix A. Data Pre-Processing
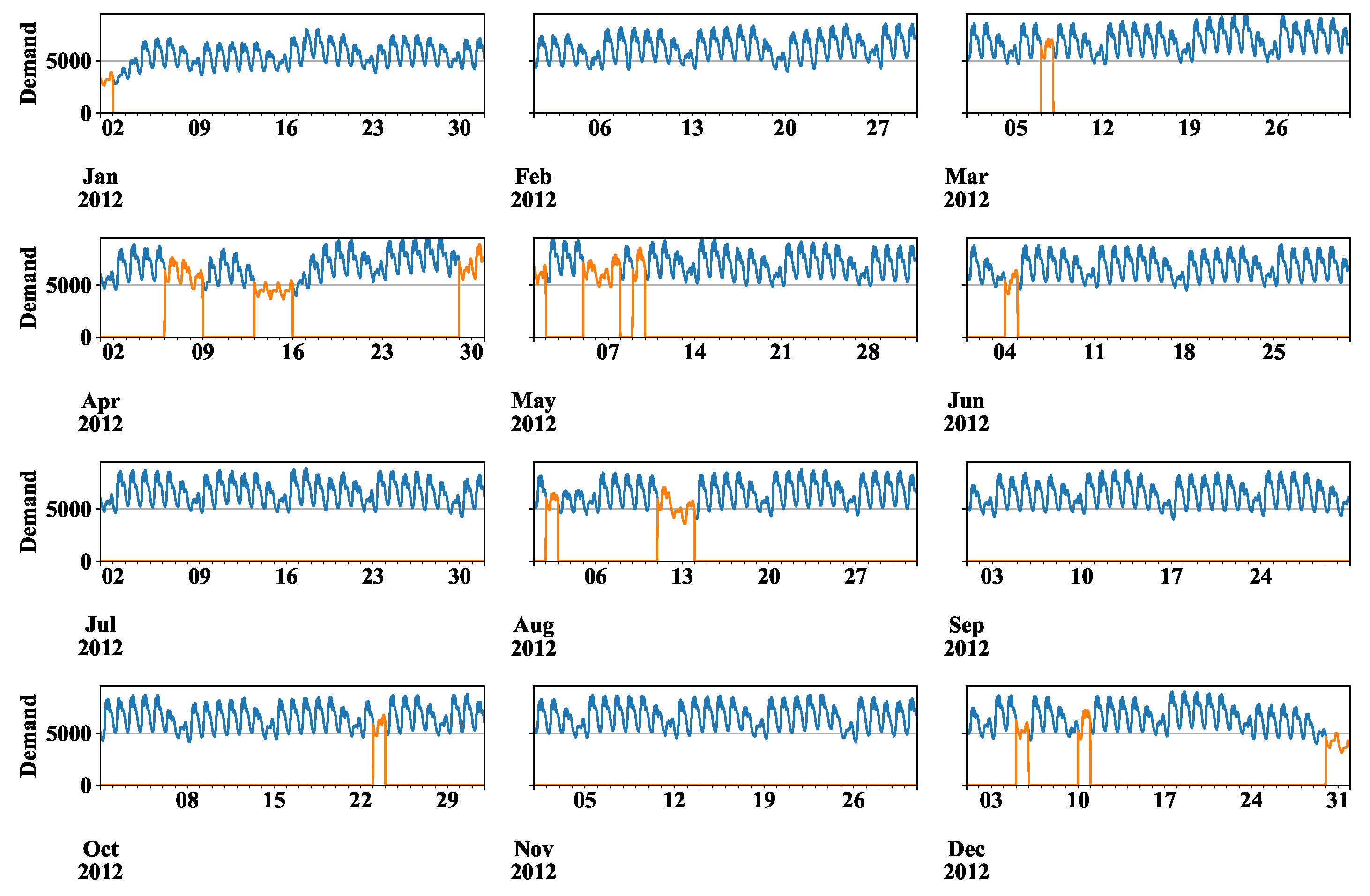
Appendix A.1. Monthly and Seasonal Pattern

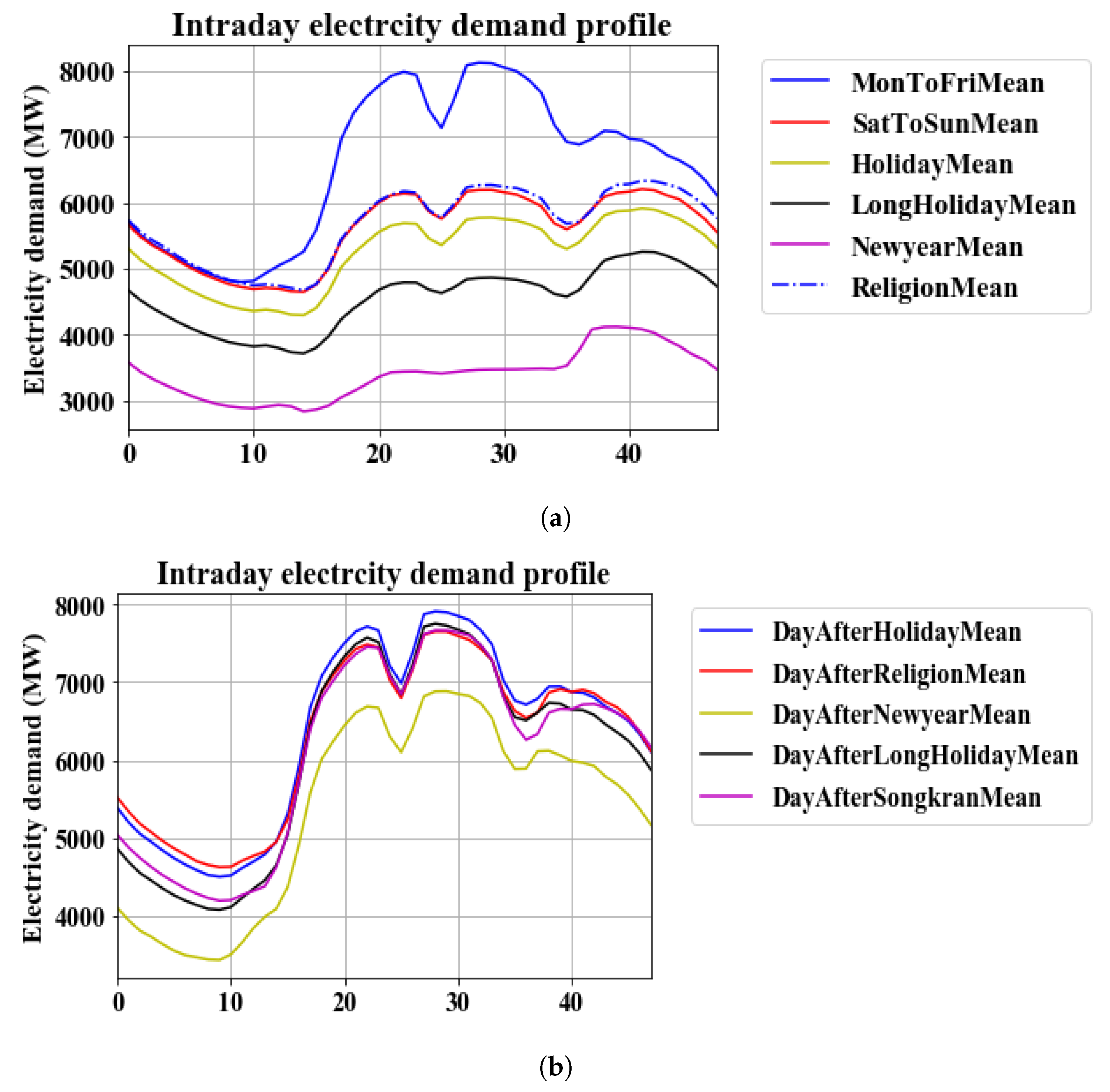
Appendix A.2. Weekly, Daily and Holiday Patterns
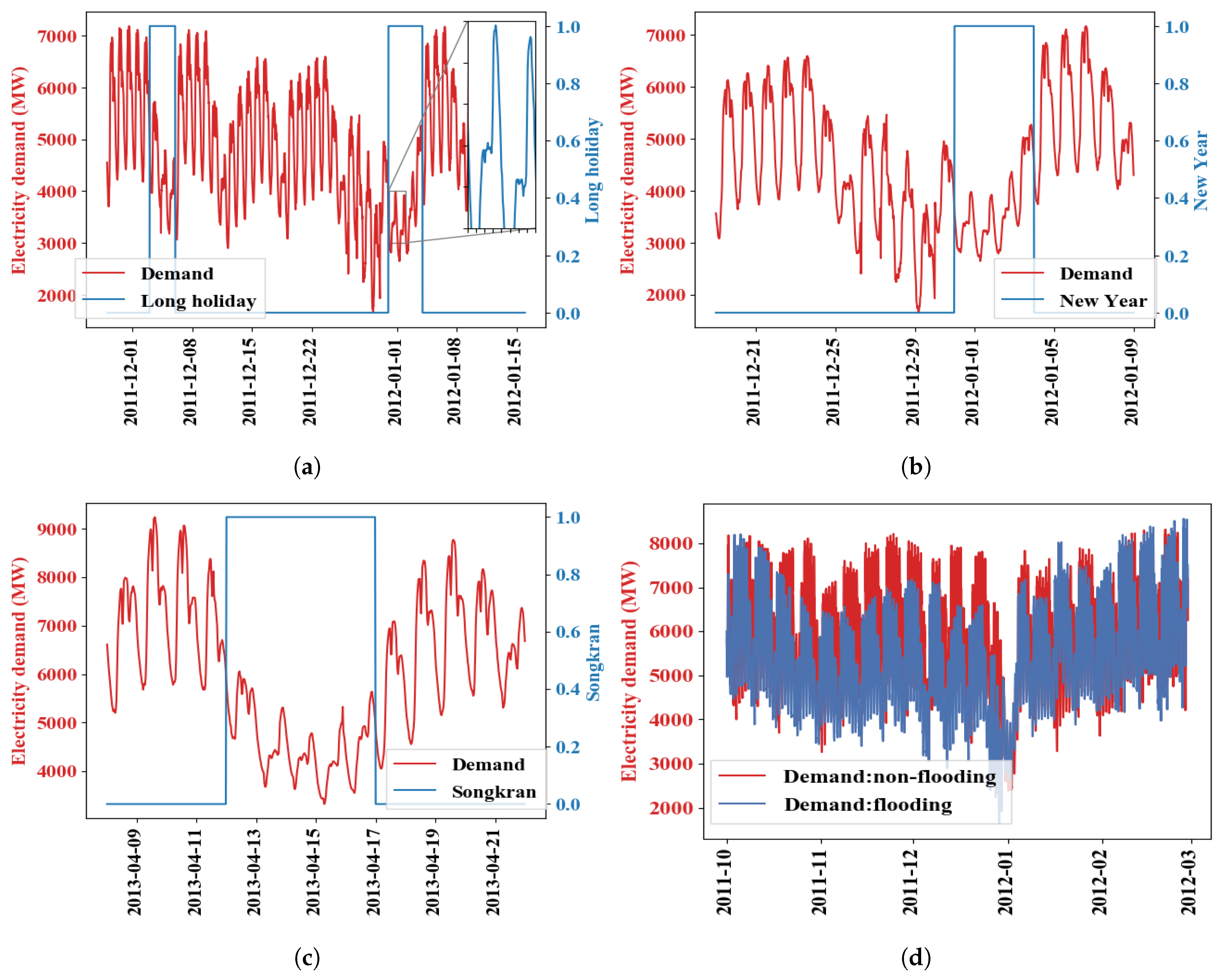
Appendix A.3. Temperature

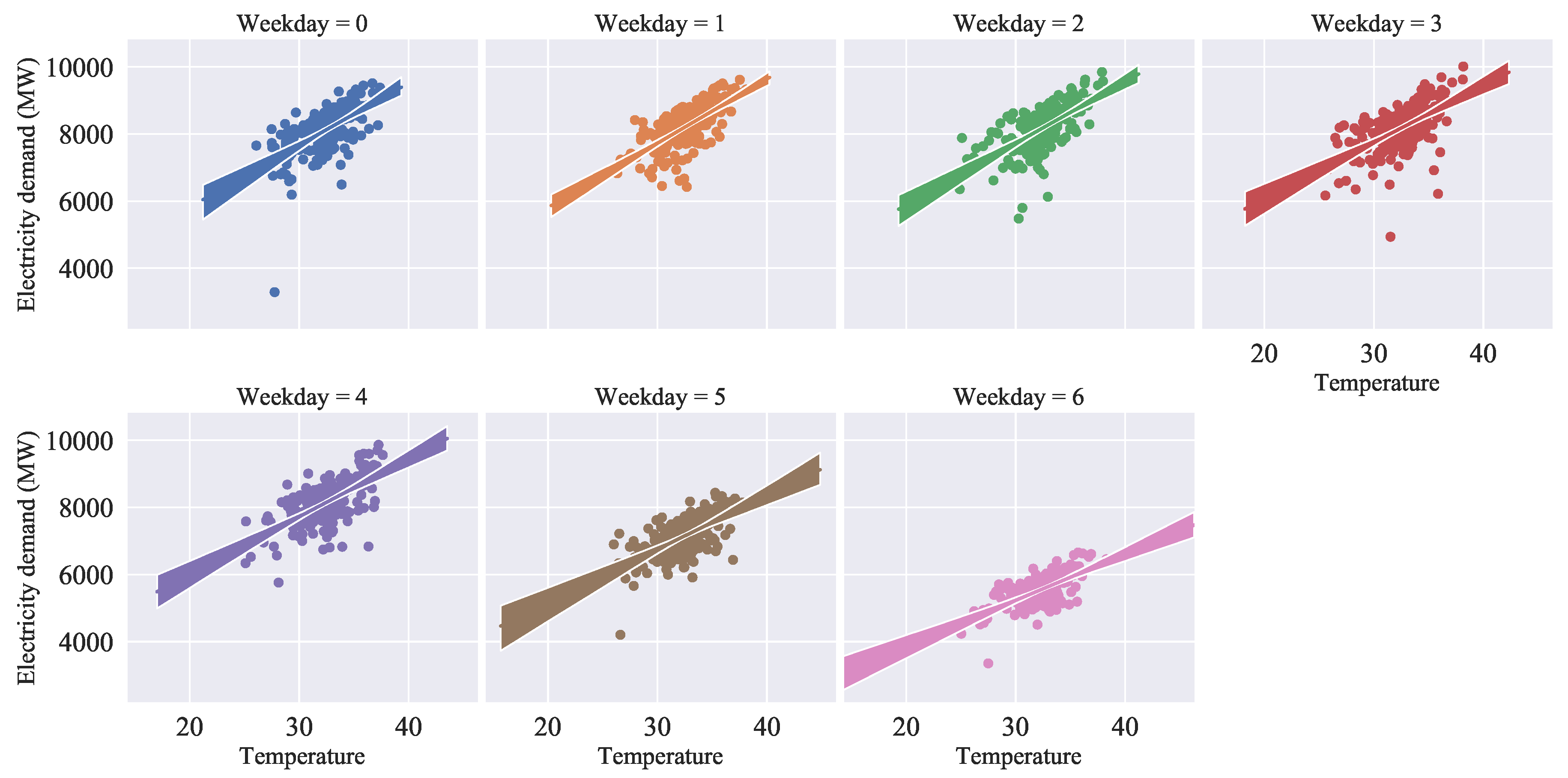
Appendix A.4. Variable Identification

| Types | Variables | Description |
|---|---|---|
| Deterministic | WD | Week dummy [Mon <Tue ...<Sat<Sun] |
| MD | Month dummy [Feb <Mar <...<Nov <Dec] | |
| DayAfterHoliday | Binary 0 or 1 | |
| DayAfterLongHoliday | Binary 0 or 1 | |
| DayAfterSongkran | Binary 0 or 1 | |
| DayAfterNewyear | Binary 0 or 1 | |
| Temperature | Temp | Forecasted temperature |
| MaxTemp | Maximum forecasted temperature | |
| Square temperature | Square of the forecasted temperature | |
| MA2pmTemp | Moving avearage of temperature at 2pm | |
| Lagged | load1d_cut2pm | 1 day ahead untill 2pm and 2 day ahead after 2pm load |
| load2d_cut2pm | 2 days ahead untill 2pm and 3 day ahead after 2pm load | |
| load3d_cut2pmR | 3 days ahead untill 2pm and 4 days ahead after 2pm load | |
| load4d_cut2pmR | 4 days ahead untill 2pm and 5 days ahead after 2pm load | |
| Interaction | WD:Temp | Interaction of week day dummy to temperature |
| MD:Temp | Interaction of month dummy to temperature | |
| WD:load1d_cut2pm | Interaction of week day dummy to load1d_cut2pm | |
| WD:load2d_cut2pm | Interaction of week day dummy to load2d_cut2pm |
Appendix B. Figures and Tables
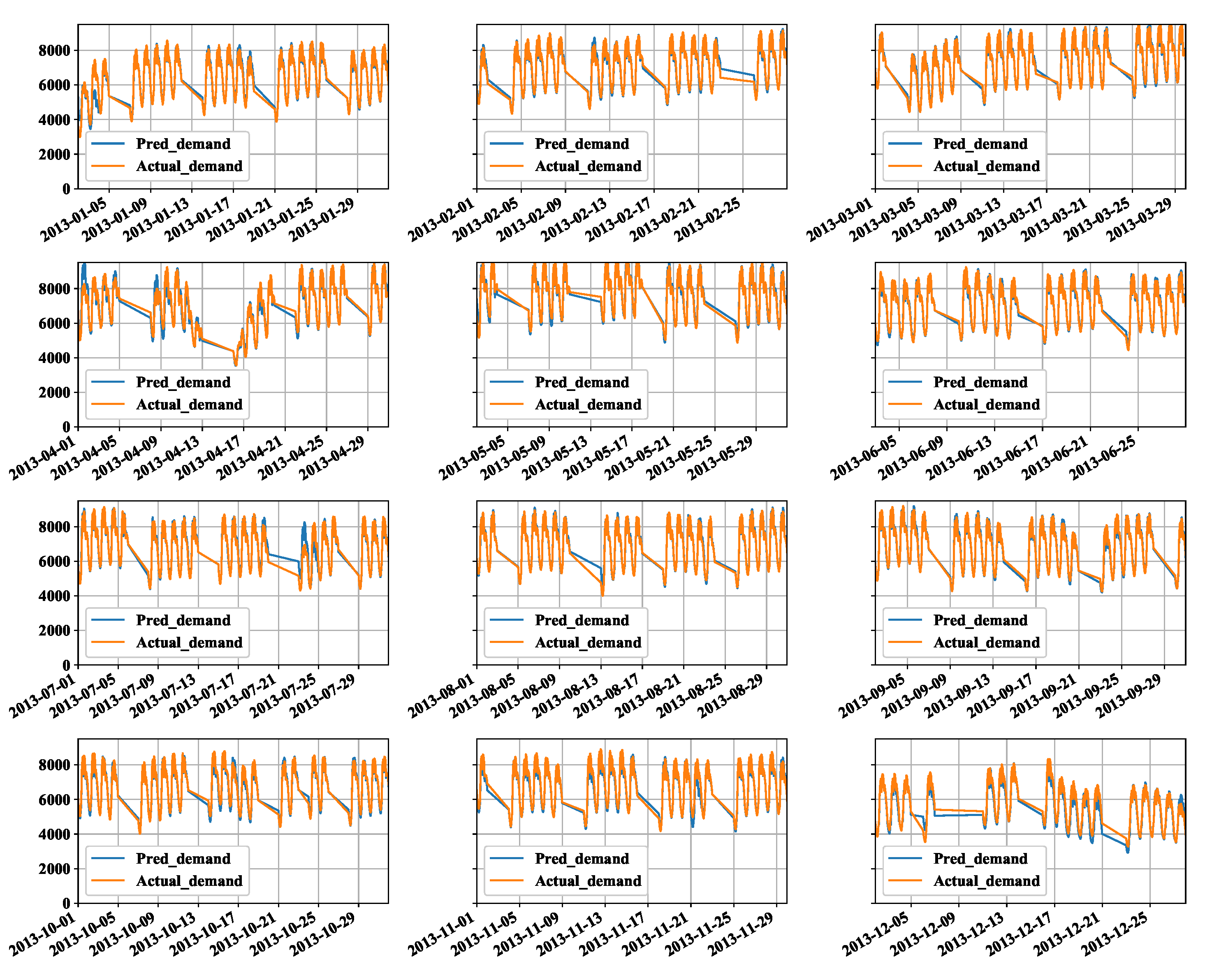
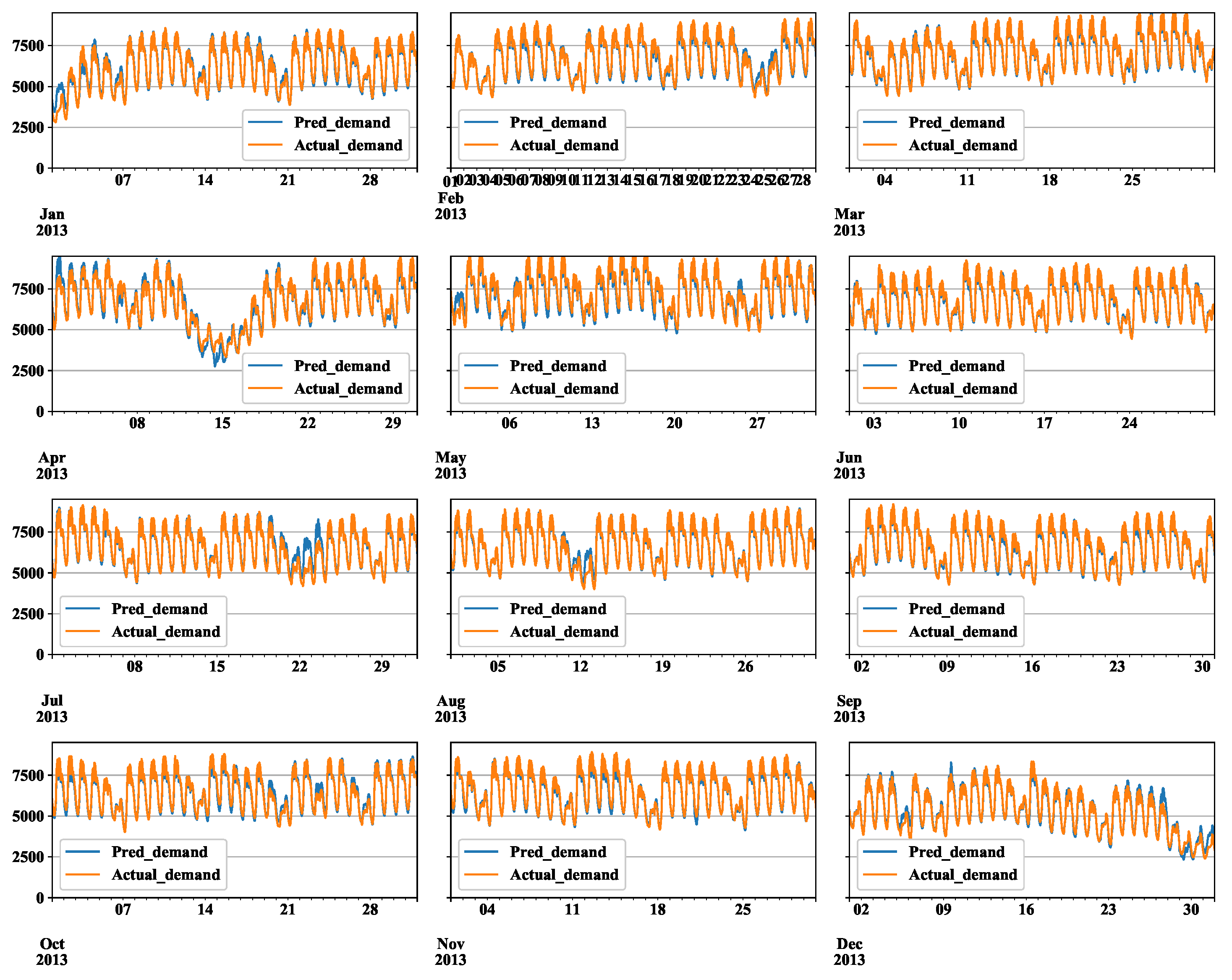
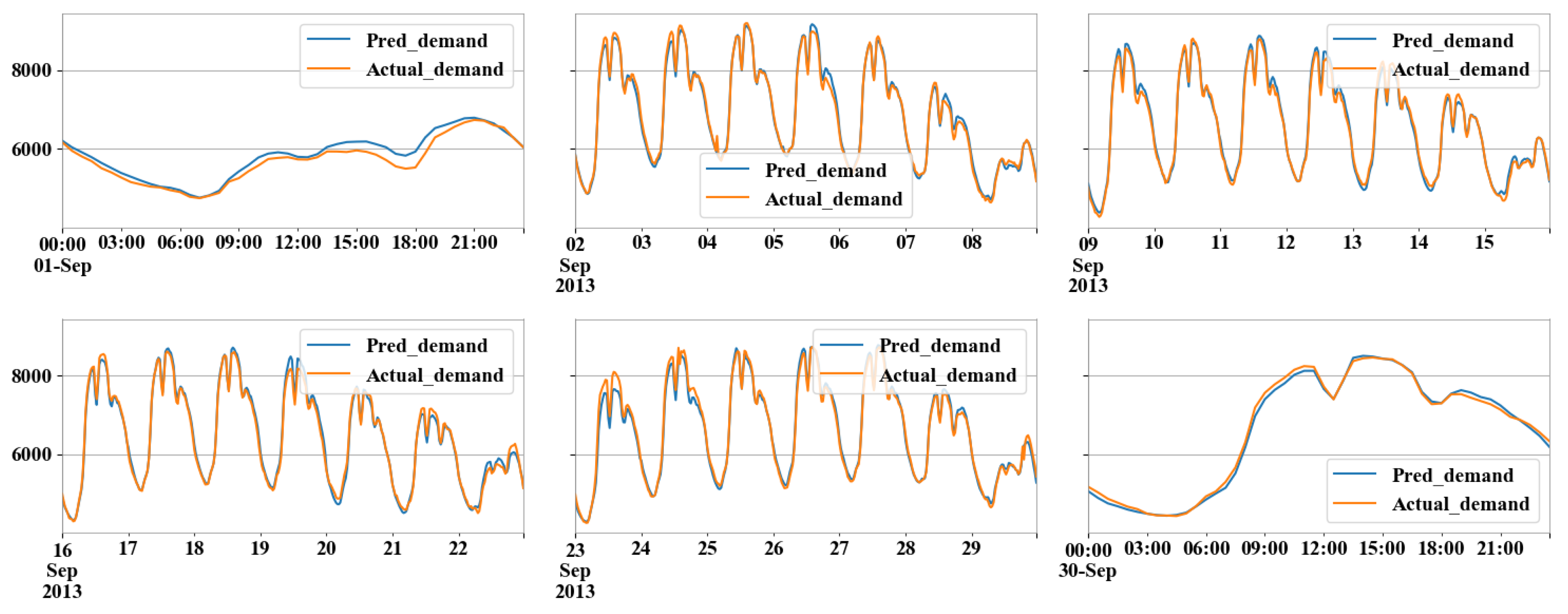
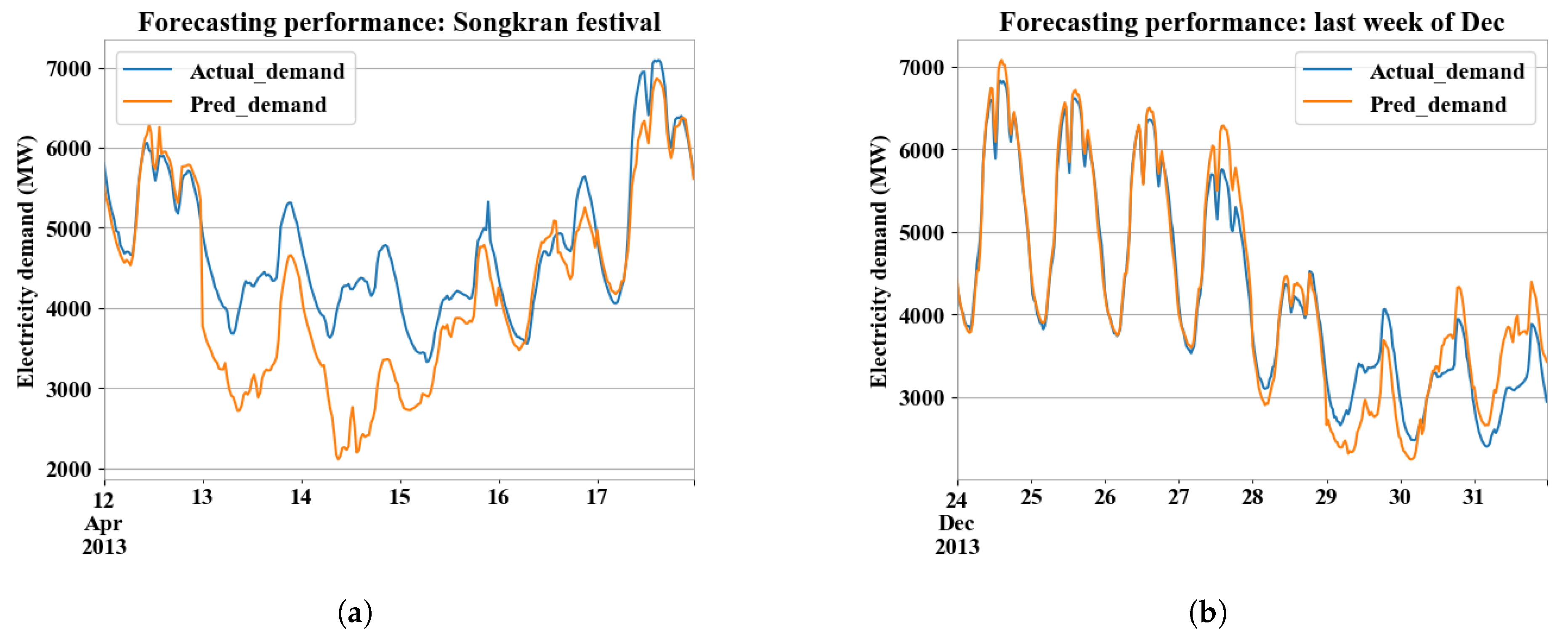
References
- Murakoshi, C.; Namagami, H.; Xuan, J.; Takayama, A.; Takayama, H. State of residential energy consumption in Southest Asia: Need to promote smart appliances because urban household consumption is higher than some develped countries. ECEEE Summer Study Proc. 2017, 1489–1499. Available online: https://www.eceee.org/library/conference_proceedings/eceee_Summer_Studies/2017/7-appliances-products-lighting-and-ict/state-of-residential-energy-consumption-in-southeast-asia-need-to-promote-smart-appliances-because-urban-household-consumption-is-higher-than-some-developed-countries/ (accessed on 4 May 2020).
- Panklib, K.; Prakasvudhisarn, C.; Khummongkol, D. Electricity Consumption Forecasting in Thailand Using an Artificial Neural Network and Multiple Linear Regression. Energy Sources Part B Econ. Plan. Policy 2015, 10, 427–434. [Google Scholar] [CrossRef]
- ADB. Key Indicators for Asia and the Pacific 2017. Online 2017. Available online: https://www.adb.org/sites/default/files/publication/357006/06-rt-energy-electricity.pdf (accessed on 1 May 2020).
- Kaur, N.; Sood, S.K. An Energy-Efficient Architecture for the Internet of Things (IoT). IEEE Syst. J. 2017, 11, 796–805. [Google Scholar] [CrossRef]
- Samson, O. Electricity and the Fourth Industrial Revolution. 2018. Available online: https://www.researchgate.net/publication/324876698_ELECTRICITY_AND_THE_FOURTH_INDUSTRIAL_REVOLUTION (accessed on 4 May 2020).
- Clarke, L.; Jiang, K.; Akimoto, K.; Babiker, M.; Blanford, G.; Fisher-Vanden, K.; Hourcade, J.C.; Krey, V.; Kriegler, E.; Löschel, A.; et al. Chapter 6—Assessing transformation pathways. In Climate Change 2014: Mitigation of Climate Change. IPCC Working Group III Contribution to AR5; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Momami, M. Factors Affecting Electricity Demand in Jordan. Energy Power Eng. 2013, 5, 50–58. [Google Scholar] [CrossRef]
- Parkpoom, S.; Harrison, G.P. Analyzing the Impact of Climate Change on Future Electricity Demand in Thailand. IEEE Trans. Power Syst. 2008, 23, 1441–1448. [Google Scholar] [CrossRef]
- Mideksa, T.; Kallbekken, S. The impact of climate change on the electricity market: A review. Energy Policy 2010, 38, 3579–3585. [Google Scholar] [CrossRef]
- McCulloch, J.; Ignatieva, K. Forecasting High Frequency Intra-Day Electricity Demand Using Temperature. SSRN Electr. J. 2017. [Google Scholar] [CrossRef]
- Julian, M.C.; Julian, P. Temperature effects on firms’ electricity demand: An analysis of sectorial differences in Spain. Appl. Energy 2015. [Google Scholar] [CrossRef]
- Hossein Motlagh, N.; Mohammadrezaei, M.; Hunt, J.; Zakeri, B. Internet of Things (IoT) and the Energy Sector. Energies 2020, 13. [Google Scholar] [CrossRef]
- Csoknyai, T.; Legardeur, J.; Akle, A.A.; Horvath, M. Analysis of energy consumption profiles in residential buildings and impact assessment of a serious game on occupants behavior. Energy Build. 2019, 196, 1–20. [Google Scholar] [CrossRef]
- Serralles, R.J. Electric energy restructuring in the European Union: Integration, subsidiarity and the challenge of harmonization. Energy Policy 2006, 34, 2542–2551. [Google Scholar] [CrossRef]
- Chapagain, K.; Kittipiyakul, S. Short-Term Electricity Demand Forecasting with Seasonal and Interactions of Variables for Thailand. In Proceedings of the 2018 Int Electrl Eng Congress (iEECON), Krabi, Thailand, 7–9 March 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Taylor, J.W.; de Menezes, L.M.; McSharry, P.E. A comparison of univariate methods for forecasting electricity demand up to a day ahead. Int. J. Forecast. 2006, 22, 1–16. [Google Scholar] [CrossRef]
- Ramanathan, R.; Engle, R.; Granger, C.W.; Vahid-Araghi, F.; Brace, C. Short-run forecasts of electricity loads and peaks. Int. J. Forecast. 1997, 13, 161–174. [Google Scholar] [CrossRef]
- Dordonnat, V.; Koopman, S.J.; Ooms, M. Dynamic factors in periodic time-varying regressions with an application to hourly electricity load modelling. Comput. Stat. Data Anal. 2012, 56, 3134–3152. [Google Scholar] [CrossRef]
- Chapagain, K.; Kittipiyakul, S. Performance Analysis of Short-Term Electricity Demand with Atmospheric Variables. Energies 2018, 11, 818. [Google Scholar] [CrossRef]
- Chapagain, K.; Kittipiyakul, S. Short-term Electricity Load Forecasting Model and Bayesian Estimation for Thailand Data. In Proceedings of the 2016 Asia Conf on Power and Electl Engg (ACPEE 2016), Bankok, Thailand, 20–22 March 2016; Volume 55, p. 06003. [Google Scholar]
- Clements, A.E.; Hurn, A.S.; Li, Z. Forecasting day-ahead electricity load using a multiple equation time series approach. Eur. J. Oper. Res. 2016, 251, 522–530. [Google Scholar] [CrossRef]
- Phyo, P.; Jeenanunta, C. Electricity Load Forecasting using a Deep Neural Network. Eng. Appl. Sci. Res. 2019, 46, 10–17. [Google Scholar]
- Su, W.H.; Jeenanunta, C. Short-term Electricity Load Forecasting in Thailand: An Analysis on Different Input Variables. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2018. [Google Scholar] [CrossRef]
- Darshana, A.K.; Chawalit, J. Hybrid Particle Swarm Optimization with Genetic Algorithm to Train Artificial Neural Networks for Short-term Load Forecasting. Int. J. Swarm Intell. Res. 2019, 10, 1–14. [Google Scholar]
- Chapagain, K.; Sato, T.; Kittipiyakul, S. Performance analysis of short-term electricity demand with meteorological parameters. In Proceedings of the 2017 14th Int Conf on Electl Eng/Elx, Computer, Telecom and IT (ECTI-CON), Phuket, Thailand, 27–30 June 2017; pp. 330–333. [Google Scholar]
- Ministry, E. Energy data visualaization for Thailand. Energy Policy Plan. Off. 2020. Available online: http://www.eppo.go.th/index.php/en/ (accessed on 2 May 2020).
- Wangpattarapong, K.; Maneewan, S.; Ketjoy, N.; Rakwichian, W. The impacts of climatic and economic factors on residential electricity consumption of Bangkok Metropolis. Energy Build. 2008, 40, 1419–1425. [Google Scholar] [CrossRef]
- Cian, D.E.; Lanzi, E.; Roberto, R. The Impacts of Temperature Change on Energy Demand: A Dynamic Panel Analysis. SSRN Electr. J. 2007. [Google Scholar] [CrossRef]
- Mirasgedis, S.; Sarafidis, Y.; Georgopoulou, E.; Kotroni, V.; Lagouvardos, K.; Lalas, D. Modeling framework for estimating impacts of climate change on electricity demand at regional level: Case of Greece. Energy Convers. Manag. 2007, 48, 1737–1750. [Google Scholar] [CrossRef]
- Masood, N.A.; Sadi, M.Z.; Deeba, S.R.; Siddique, R.H. Temperature Sensitivity Forecasting of Electrical Load. In Proceedings of the 2010 4th International Power Engineering and Optimization Conference (PEOCO), Shah Alam, Malaysia, 23–24 June 2010. [Google Scholar]
- Istiaque, A.; Khan, S.I. Impact of Ambient Temperature on Electricity Demand of Dhaka City of Bangladesh. Sci. Res. Publ. 2018, 10, 319–331. [Google Scholar] [CrossRef]
- Zhang, C.; Liao, H.; Mi, Z. Climate impacts: Temperature and electricity consumption. Nat. Hazards 2019, 99, 1259–1275. [Google Scholar] [CrossRef]
- Zhang, M.; Zhang, K.; Hu, W.; Zhu, B.; Wang, P.; Wei, Y.M. Exploring the climatic impacts on residential electricity consumption in Jiangsu, China. Energy Policy 2020, 140, 111398. [Google Scholar] [CrossRef]
- Li, B.; Lu, M.; Zhang, Y.; Huang, J. A Weekend Load Forecasting Model Based on Semi-Parametric Regression Analysis Considering Weather and Load Interaction. Energies 2019, 12, 3820. [Google Scholar] [CrossRef]
- Bessec, M.; Fouquau, J. The non-linear link between electricity consumption and temperature in Europe: A threshold panel approach. Energy Econ. 2008, 30, 2705–2721. [Google Scholar] [CrossRef]
- Asadoorian, M.O.; Eckaus, R.S.; Schlosser, C.A. Modeling climate feedbacks to electricity demand: The case of China. Energy Econ. 2008, 30, 1577–1602. [Google Scholar] [CrossRef]
- Chang, Y.; Kim, C.S.; Miller, J.I.; Park, J.Y.; Park, S. A new approach to modeling the effects of temperature fluctuations on monthly electricity demand. Energy Econ. 2016, 60, 206–216. [Google Scholar] [CrossRef]
- Ang, B.; Wang, H.; Ma, X. Climatic influence on electricity consumption: The case of Singapore and Hong Kong. Energy 2017, 127, 534–543. [Google Scholar] [CrossRef]
- Fung, W.; Lam, K.; Hung, W.; Pang, S.; Lee, Y. Impact of urban temperature on energy consumption of Hong Kong. Energy 2006, 31, 2623–2637. [Google Scholar] [CrossRef]
- Maheshwari, A.; Murari, K.K.; Jayaraman, T. Peak Electricity Demand and Global Warming in the Industrial and Residential areas of Pune: An Extreme Value Approach. arXiv 2019, arXiv:1908.08570. [Google Scholar]
- Li, Y.; Pizer, W.A.; Wu, L. Climate change and residential electricity consumption in the Yangtze River Delta, China. Proc. Natl. Acad. Sci. USA 2019, 116, 472–477. [Google Scholar] [CrossRef] [PubMed]
- Apadula, F.; Bassini, A.; Elli, A.; Scapin, S. Relationships between meteorological variables and monthly electricity demand. Appl. Energy 2012, 98, 346–356. [Google Scholar] [CrossRef]
- Sailor, D.; Pavlova, A. Air conditioning market saturation and long-term response of residential cooling energy demand to climate change. Energy 2003, 28, 941–951. [Google Scholar] [CrossRef]
- Lopez, M.; Sans, C.; Valero, S.; Senabre, C. Classification of Special Days in Short-Term Load Forecasting: The Spanish Case Study. Energies 2019, 12, 1253. [Google Scholar] [CrossRef]
- Darbellay, G.A.; Slama, M. Forecasting the short-term demand for electricity: Do neural networks stand a better chance? Int. J. Forecast. 2000, 16, 71–83. [Google Scholar] [CrossRef]
- Hippert, H.; Bunn, D.; Souza, R. Large neural networks for electricity load forecasting: Are they overfitted? Int. J. Forecast. 2005, 21, 425–434. [Google Scholar] [CrossRef]
- Chapagain, K.; Kittipiyakul, S. Short-term Electricity Load Forecasting for Thailand. In Proceedings of the 2018 15th International Conference on Electrical Engineering/Electronics, Computer, Telecommunications and Information Technology (ECTI-CON), Chiang Rai, Thailand, 18–21 July 2018; pp. 521–524. [Google Scholar] [CrossRef]
- Srinivasan, D.; Chang, C.S.; Liew, A.C. Demand forecasting using fuzzy neural computation, with special emphasis on weekend and public holiday forecasting. IEEE Trans. Power Syst. 1995, 10, 1897–1903. [Google Scholar] [CrossRef]
- Ziel, F. Modeling Public Holidays in Load Forecasting: A German Case Study. J. Mod. Power Syst. Clean Energy 2018, 6, 191–207. [Google Scholar] [CrossRef]
- Darshana, A.K.; Chawalit, J. Combine Particle Swarm Optimization with Artificial Neural Networks for Short-Term Load Forecasting. Int. Sci. J. Eng. Technol 2017, 1, 25–30. [Google Scholar]
- Cottet, R.; Smith, M. Bayesian Modeling and Forecasting of Intraday Electricity Load. J. Am. Stat. Assoc. 2003, 98, 839–849. [Google Scholar] [CrossRef]
- Soares, L.J.; Medeiros, M.C. Modeling and forecasting short-term electricity load: A comparison of methods with an application to Brazilian data. Int. J. Forecast. 2008, 24, 630–644. [Google Scholar] [CrossRef]
- Papalexopoulos, A.D.; Hesterberg, T.C. A regression-based approach to short-term system load forecasting. IEEE Trans. Power Syst. 1990, 5, 1535–1547. [Google Scholar] [CrossRef]
- Ismail, Z.; Jamaluddin, F.; Jamaludin, F. Time Series Regression Model for Forecasting Malaysian Electricity Load Demand. Asian J. Math. Stat. 2008, 1, 139–149. [Google Scholar] [CrossRef]
- Dilhani, M.H.M.R.S.; Jeenanunta, C. Daily electric load forecasting: Case of Thailand. In Proceedings of the 2016 7th Int Conf of Inf and Comm Tech for Embedded Sys (IC-ICTES), Bangkok, Thailand, 20–22 March 2016; pp. 25–29. [Google Scholar] [CrossRef]
- Hippert, H.S.; Pedreira, C.E.; Souza, R.C. Neural networks for short-term load forecasting: A review and evaluation. IEEE Trans. Power Syst. 2001, 16, 44–55. [Google Scholar] [CrossRef]
- Hong, T.; Wang, P. Fuzzy interaction regression for short term load forecasting. Fuzzy Opt. Decis. Mak. 2014, 13, 91–103. [Google Scholar] [CrossRef]
- Shi, H.; Xu, M.; Li, R. Deep Learning for Household Load Forecasting Novel Pooling Deep RNN. IEEE Trans. Smart Grid 2018, 9, 5271–5280. [Google Scholar] [CrossRef]
- Asaleye, D.A.; Breen, M.; Murphy, M.D. A Decision Support Tool for Building Integrated Renewable Energy Microgrids Connected to a Smart Grid. Energies 2017, 10, 1765. [Google Scholar] [CrossRef]
- Sigauke, C.; Chikobvu, D. Peak electricity demand forecasting using time series regression models: An application to South African data. J. Stat. Manag. Syst. 2016, 19, 567–586. [Google Scholar] [CrossRef]
- Sigauke, C. Regression-SARIMA modelling of daily peak electricity demand in South Africa. J. Energy South. Afr. 2012, 23, 23–30. [Google Scholar]
- Haben, S.; Giasemidis, G.; Ziel, F.; Arora, S. Short term load forecasting and the effect of temperature at the low voltage level. Int. J. Forecast. 2019, 35, 1469–1484. [Google Scholar] [CrossRef]
- Soares, L.J.; Souza, L.R. Forecasting electricity demand using generalized long memory. Int. J. Forecast. 2006, 22, 17–28. [Google Scholar] [CrossRef]
- Sigauke, C.; Nemukula, M.M.; Maposa, D. Probabilistic Hourly Load Forecasting Using Additive Quantile Regression Models. Energies 2018, 11, 2208. [Google Scholar] [CrossRef]
- Botoc, C.; Anton, S.G. Is Profitability Driven by Working Capital Management? Evidence for High-growth Firms from Emerging Europe. J. Bus. Econ. Manag. 2017, 18, 1135–1155. [Google Scholar] [CrossRef]
- Lusis, P.; Khalilpour, K.; Andrew, L.; Liebman, A. Short-term residential load forecasting: Impact of calendar effects and forecast granularity. Appl. Energy 2017, 205, 654–669. [Google Scholar] [CrossRef]
- Goodwin, R. Convert Irregular Time Sereis to Hourly Data in Python and Have Normal Distribution. 2018. Available online: https://stackoverflow.com/questions/51392012/convert-irregular-time-series-to-hourly-data-in-python (accessed on 10 April 2020).
- Hor, C.; Watson, S.J.; Majithia, S. Analyzing the impact of weather variables on monthly electricity demand. IEEE Trans. Power Syst. 2005, 20, 2078–2085. [Google Scholar] [CrossRef]
- Hong, T.; Wang, P.; Willis, H.L. Short Term Electric Load Forecasting. Int. J. Forecast. 2010, 74, 1–6. [Google Scholar] [CrossRef]
- Wang, Y.; Niu, D.; Ji, L. Short-term power load forecasting based on IVL-BP neural network technology. Syst. Eng. Procedia 2012, 4, 168–174. [Google Scholar] [CrossRef]

| Simple OLS | FF-ANN | |||||
|---|---|---|---|---|---|---|
| Training Length (Days) | Testing Days | MAPE (%) | Exe. Time (Sec) | MAPE (%) | Exe. Time (Sec) | |
| Case I | 911 | 239 | 1.97 | 109.2 | 2.96 | 565.97 |
| Case II | 717 | 239 | 2.33 | 87.38 | 3.41 | 516.46 |
| Case III | 475 | 239 | 2.04 | 114.26 | 6.00 | 435.32 |
| Case IV | 236 | 239 | 2.44 | 78.82 | 18.00 | 309.81 |
| Model | Deterministics and Interaction | Temp | Temp Square | Holiday | Holiday 2 | MAPE (%) |
|---|---|---|---|---|---|---|
| OLS-(Scenario 1) | Yes | Yes | Yes | Yes | Yes | 1.97 |
| Yes | Yes | No | No | No | 2.00 | |
| Yes | No | No | No | No | 3.04 | |
| OLS-(Scenario 2) | Yes | Yes | Yes | Yes | Yes | 1.78 |
| OLS-(Scenario 3) | Yes | Yes | Yes | Yes | Yes | 16.00 |
| OLS-(Scenario 4) | Yes | Yes | Yes | Yes | Yes | 2.94 |
| HH | Rsq | Adj-Rsq | DW | HH | Rsq | Adj-Rsq | DW | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| OLS | GLSAR-7 | OLS | GLSAR-7 | OLS | GLSAR-7 | OLS | GLSAR-7 | OLS | GLSAR-7 | OLS | GLSAR-7 | ||
| 0 | 0.97 | 0.96 | 0.97 | 0.95 | 1.80 | 2.00 | 24 | 0.86 | 0.62 | 0.86 | 0.59 | 1.73 | 1.99 |
| 1 | 0.97 | 0.96 | 0.97 | 0.95 | 1.86 | 2.01 | 25 | 0.88 | 0.68 | 0.88 | 0.66 | 1.79 | 1.99 |
| 2 | 0.97 | 0.96 | 0.97 | 0.95 | 1.85 | 2.00 | 26 | 0.87 | 0.67 | 0.87 | 0.65 | 1.77 | 1.98 |
| 3 | 0.97 | 0.95 | 0.97 | 0.95 | 1.85 | 2.00 | 27 | 0.86 | 0.63 | 0.86 | 0.61 | 1.74 | 1.98 |
| 4 | 0.97 | 0.95 | 0.97 | 0.94 | 1.85 | 2.00 | 28 | 0.85 | 0.62 | 0.85 | 0.60 | 1.78 | 1.97 |
| 5 | 0.97 | 0.95 | 0.97 | 0.94 | 1.87 | 2.00 | 29 | 0.86 | 0.63 | 0.86 | 0.61 | 1.67 | 1.98 |
| 6 | 0.97 | 0.94 | 0.96 | 0.94 | 1.85 | 2.00 | 30 | 0.87 | 0.64 | 0.87 | 0.61 | 1.64 | 1.98 |
| 7 | 0.96 | 0.94 | 0.96 | 0.94 | 1.86 | 2.01 | 31 | 0.87 | 0.64 | 0.87 | 0.61 | 1.59 | 1.98 |
| 8 | 0.96 | 0.94 | 0.96 | 0.93 | 1.87 | 2.01 | 32 | 0.86 | 0.64 | 0.86 | 0.60 | 1.57 | 1.98 |
| 9 | 0.96 | 0.36 | 0.96 | 0.93 | 1.88 | 2.00 | 33 | 0.86 | 0.61 | 0.86 | 0.58 | 1.51 | 1.98 |
| 10 | 0.96 | 0.93 | 0.96 | 0.93 | 1.88 | 2.01 | 34 | 0.85 | 0.59 | 0.85 | 0.57 | 1.44 | 1.99 |
| 11 | 0.95 | 0.92 | 0.95 | 0.92 | 1.84 | 1.99 | 35 | 0.84 | 0.56 | 0.84 | 0.53 | 1.40 | 1.99 |
| 12 | 0.94 | 0.92 | 0.94 | 0.91 | 1.78 | 2.00 | 36 | 0.80 | 0.52 | 0.80 | 0.49 | 1.38 | 2.00 |
| 13 | 0.93 | 0.90 | 0.93 | 0.89 | 1.80 | 2.00 | 37 | 0.80 | 0.52 | 0.80 | 0.49 | 1.35 | 2.00 |
| 14 | 0.93 | 0.88 | 0.92 | 0.97 | 1.78 | 1.99 | 38 | 0.84 | 0.60 | 0.84 | 0.58 | 1.33 | 2.00 |
| 15 | 0.92 | 0.85 | 0.92 | 0.84 | 1.65 | 1.99 | 39 | 0.86 | 0.65 | 0.86 | 0.63 | 1.33 | 2.00 |
| 16 | 0.90 | 0.78 | 0.89 | 0.76 | 1.67 | 1.98 | 40 | 0.87 | 0.68 | 0.87 | 0.66 | 1.33 | 2.00 |
| 17 | 0.88 | 0.73 | 0.88 | 0.71 | 1.69 | 1.99 | 41 | 0.88 | 0.72 | 0.88 | 0.70 | 1.17 | 1.99 |
| 18 | 0.87 | 0.69 | 0.86 | 0.67 | 1.73 | 1.99 | 42 | 0.90 | 0.74 | 0.90 | 0.73 | 1.43 | 1.99 |
| 19 | 0.86 | 0.65 | 0.85 | 0.63 | 1.74 | 2.00 | 43 | 0.91 | 0.77 | 0.91 | 0.75 | 1.45 | 1.99 |
| 20 | 0.86 | 0.64 | 0.85 | 0.61 | 1.71 | 2.00 | 44 | 0.91 | 0.77 | 0.91 | 0.76 | 1.45 | 2.00 |
| 21 | 0.85 | 0.61 | 0.84 | 0.59 | 1.69 | 2.00 | 45 | 0.91 | 0.78 | 0.91 | 0.77 | 1.48 | 2.00 |
| 22 | 0.84 | 0.59 | 0.83 | 0.56 | 1.70 | 2.00 | 46 | 0.92 | 0.79 | 0.92 | 0.78 | 1.46 | 1.99 |
| 23 | 0.84 | 0.60 | 0.83 | 0.57 | 1.74 | 1.99 | 47 | 0.92 | 0.80 | 0.92 | 0.79 | 1.46 | 2.00 |
| Methods with AR(p) | MAPE(%) | Time Elapse (Sec) |
|---|---|---|
| OLS | 1.97 | 47.00 |
| GLSAR-1 | 1.92 | 223.00 |
| GLSAR-2 | 1.94 | 247.00 |
| GLSAR-3 | 1.92 | 223.00 |
| GLSAR-4 | 1.90 | 223.00 |
| GLSAR-5 | 1.90 | 230.00 |
| GLSAR-6 | 1.90 | 232.00 |
| GLSAR-7 | 1.88 | 241.00 |
| Nos of Hidden Layers | Nos of Neurons | MAPE (%) | Epochs |
|---|---|---|---|
| 1 | 2.85 | 8000 | |
| 2.82 | 15,000 | ||
| 2.92 | 22,000 | ||
| 2 | 2.78 | 45,000 | |
| 3.18 | 55,000 | ||
| 3.06 | 75,000 | ||
| 38.79 | 100,000 | ||
| 2.78 | 3000 | ||
| 2.72 | 4000 | ||
| 2.72 | 2500 | ||
| 3 | 2.75 | 3000 | |
| 4 | 2.92 | 2500 |
| Pre_Intervals | MAPE% | Exe Time (Sec.) | ||
|---|---|---|---|---|
| Simple OLS | FF-ANN | Simple OLS | FF-ANN | |
| 1 | 2.03 | 2.89 | 2.96 | 273 |
| 2 | 2.03 | 2.69 | 3.22 | 539 |
| 3 | 2.03 | 2.70 | 3.04 | 800 |
| 4 | 2.05 | 2.65 | 3.20 | 1062 |
| 5 | 2.05 | 2.56 | 3.40 | 1585 |
| 239 | 1.97 | NA | 33.4 | NA |
| Simple OLS (MAPE%) | GLSAR (MAPE%) | |||||||
|---|---|---|---|---|---|---|---|---|
| Parameters | Scenario 1 | Scenario 2 | Scenario 3 | Scenario 4 | Scenario 1 | Scenario 2 | Scenario 3 | Scenario 4 |
| Mon | 1.99 | NaN | 19.21 | 4.37 | 2.10 | NaN | 18.47 | 4.70 |
| Tue | 1.72 | NaN | 15.49 | 2.54 | 1.84 | NaN | 22.96 | 2.89 |
| Wed | 1.96 | NaN | 12.49 | 2.44 | 1.99 | NaN | 25.85 | 2.96 |
| Thu | 1.78 | NaN | 26.01 | 2.32 | 1.9 | NaN | 30.44 | 2.86 |
| Fri | 1.59 | NaN | 11.28 | 2.18 | 1.55 | NaN | 23.97 | 2.87 |
| Sat | NaN | 1.76 | NaN | 3.17 | NaN | 1.77 | NaN | 2.69 |
| Sun | NaN | 1.77 | NaN | 3.62 | NaN | 1.69 | NaN | 2.54 |
| Holiday | NaN | NaN | 14.73 | 9.62 | NaN | NaN | 21.00 | 10.22 |
| Holiday 2 | NaN | NaN | 16.62 | 10.92 | NaN | NaN | 22.58 | 9.68 |
| Songkran | NaN | NaN | 13.54 | 11.42 | NaN | NaN | 18.48 | 14.76 |
| Newyear | NaN | NaN | 26.35 | 17.85 | NaN | NaN | 30.48 | 17.96 |
| DayAfterHoliday | 5.13 | NaN | NaN | 5.22 | 4.97 | NaN | NaN | 7.06 |
| DayAfterLongHoliday | 7.38 | NaN | NaN | 2.73 | 6.41 | NaN | NaN | 6.59 |
| DayAfterSongkran | 3.10 | NaN | NaN | 2.03 | 1.82 | NaN | NaN | 6.09 |
| DayAfterNewyear | 15.77 | NaN | NaN | 12.18 | 13.82 | NaN | NaN | 6.46 |
| DayAfterLabor | 3.39 | NaN | NaN | 5.14 | 4.85 | NaN | NaN | 9.26 |
| DayAfterReligion | 5.54 | NaN | NaN | 5.54 | 5.18 | NaN | NaN | 6.04 |
| Overall MAPE | 1.81 | 1.77 | 16.63 | 2.95 | 1.88 | 1.74 | 22.59 | 3.08 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chapagain, K.; Kittipiyakul, S.; Kulthanavit, P. Short-Term Electricity Demand Forecasting: Impact Analysis of Temperature for Thailand. Energies 2020, 13, 2498. https://doi.org/10.3390/en13102498
Chapagain K, Kittipiyakul S, Kulthanavit P. Short-Term Electricity Demand Forecasting: Impact Analysis of Temperature for Thailand. Energies. 2020; 13(10):2498. https://doi.org/10.3390/en13102498
Chicago/Turabian StyleChapagain, Kamal, Somsak Kittipiyakul, and Pisut Kulthanavit. 2020. "Short-Term Electricity Demand Forecasting: Impact Analysis of Temperature for Thailand" Energies 13, no. 10: 2498. https://doi.org/10.3390/en13102498
APA StyleChapagain, K., Kittipiyakul, S., & Kulthanavit, P. (2020). Short-Term Electricity Demand Forecasting: Impact Analysis of Temperature for Thailand. Energies, 13(10), 2498. https://doi.org/10.3390/en13102498