Abstract
The development and utilization of wind energy has alleviated the problems of energy shortage and environmental pollution; however, it caused many negative impacts due to suboptimal site selections. This study proposes an innovative method integrating Geographic Information System (GIS), fuzzy Analytic Hierarchy Process (FAHP), and fuzzy VIšekriterijumsko KOmpromisno Rangiranje (VIKOR) for site selection of wind farms in the Wafangdian region, China. The uncertainties caused by subjective judgments of the stakeholders were tackled by the FAHP method firstly, where weight values of six criteria were identified. Next, the fuzzy VIKOR method and GIS tool were used to generate the Qi value of each location for ranking their appropriate degrees for wind energy development. The results demonstrated that the middle and upper parts of the studied area are suitable for the exploitation of wind energy, while the central and eastern areas are unfavorable. The influences exerted by various weight combinations and climate change on a site suitability assessment were examined. The resulting comparison with existing wind farms reflected the practicability and reliability of the proposed method; the estimation of climate change impacts on site selection provided the suggestion and support of a long-term plan for wind power development, and even the energy structure adjustment scheme adapted to climate change.
1. Introduction
Energy is a critical driving force for the productivity growth in China. The primary statistical and analytical results released by the National Bureau of Statistics demonstrated that total energy consumption in China has been at the forefront on a worldwide scale for many years. According to the National Bureau of Statistics of China and China Energy Statistics Yearbook 2018, in 2018, China’s total energy consumption reached 4.64 billion tons of standard coal, an increase of 2.9% over 2017. Considering the total energy consumption of 3.36 billion tons of standard coal in 2009 as a baseline reference, the magnitude of energy consumption increased by 38% during the past ten years [1]. With a significant increase in energy consumption, it is more obvious that the utilization in fossil fuel brought about many problems such as global warming, smog, acid rain, sharp reduction in species diversity, the highest mortality rate of respiratory diseases, land acidification, as well as water pollution [2]. Especially, as released by the Intergovernmental Panel on Climate Change (IPCC), the carbon dioxide concentration would increase from 280 to 560 ppm, leading the global average temperature to possibly rise by 1.5 to 4 °C, while the energy consumption pattern remains unchanged [3]. Global warming not only affects the ecological environment, but also threatens human survival and development, where increased frequency of extreme weather, sharp decline in the biodiversity, and the collapse of offshore ecosystems, as well as frequent occurrence of infectious diseases, were inevitable [4]. Therefore, it is necessary to explore and utilize new energy forms with clean, pollution-free, and renewable characteristics, including wind, solar, nuclear, biomass, and tidal energy. Among them, wind power is characterized by an abundant reserve, distributed widely and a low discharge of greenhouse gases (GHGs) [5,6]. In the development of all kinds of renewable and new resources, wind energy was advantageous in some aspects. For example, it owned the short investment cycle and high security than the nuclear power; moreover, it had the great potential of scale production compared with the biomass and tidal energy. Therefore, wind energy is considered as the most mature and prospective energy form with a large potential for commercial development [7,8,9]. The vast territory and long coastline of China provides a great basis for promoting the rapid development of the wind power industry. Meanwhile, the support of relevant policies and the development of wind turbine technology also played an important role. The new installed capacity of China in 2017 was increased by 19.66 GW; correspondingly, the cumulative installed capacity reached 188 GW with the increase rate of 11.7% than 2016 [10].
However, there were still many problems in the wind power generation at this stage, which caused the gap between global expectation and reality of the wind power development. In addition to being subjected to meteorological conditions and high initial investment costs, wind power also had some negative influences in the society and eco-environment, including noise, landscape, and visual impact, as well as ecological damage. These negative impacts would lead to criticism and opposition from the local government and residents and seriously affect its large-scale development. It is clear that the above negative impacts were mainly sourced from the inappropriate location of the wind turbine, where the electricity output is the only evaluation criterion. In fact, many types of evaluation criteria should be incorporated into the site selection process, including some geological and geomorphic factors, the factors associated with the local ecosystem and residents, and the distance from the public infrastructure (including roads and power lines). Therefore, it is urgent to evaluate the potential location suitability of the wind farm by the aid of the Multi-Criteria Decision Making (MCDM) method, where a comprehensive evaluation index system including social, economic, and environmental evaluation criteria was established and the reasonable position was identified based on systematic and scientific decision-making methods. With regard to the large amount of geographic and spatial information involved in site selection, the Geographic Information System (GIS) tool was capable of analyzing and organizing the spatial data, estimating the candidate site score corresponding to each criterion through the raster calculation, and providing the visual map for the result demonstration. Therefore, the combination of GIS and MCDM was extensively explored to tackle the problem of wind farm location [11].
In recent years, many studies related to the site selection of energy power facilities have been conducted. For example, Latinopoulos and Kechagia incorporated GIS and MCDM into a general evaluation framework to support wind farm planning at the regional level [12]. Höfer et al. provided a holistic GIS-based AHP approach that incorporates techno-economic, socio-political, and environmental criteria [13]. The resulting comparison with existing wind farms validated the reliability and accuracy of the model results. Villacreses et al. developed a combined method of GIS and MCDM for determining the feasible location of wind farms in continental Ecuador [14]. Mahdy and Bahajutilized utilized the integration of GIS and AHP to provide an accurate estimate of suitable locations of wind farms in Egypt [15]. Sajid and Jang developed the GIS-MCDM method to identify ten potential sites of onshore wind farms in South Korea and provided the technical and economic assessment of an appropriate type of wind turbines at each site [16]. Wu et al. proposed a decision-making framework that combines the Triangular Intuitionistic Fuzzy N(TIFN), Analytic Network Process (ANP), and Preference Ranking Organization Method for Enrichment Evaluations (PROMETHEE), and applied it to offshore wind farms site selection [17]. Konstantinos et al. presented a MCDM methodology which was combined with GIS to spatially represent the evaluated results in order to determine the most suitable locations for wind farms installation [18]. The results studied above proved that the combination of GIS and MCDM were capable of providing an effective technical support for the site selection problems. Nevertheless, the intrinsic uncertainties involved in the evaluation process were ignored. In fact, the weight identification of evaluation criteria and their scores estimation are affected by some subjective factors, such as the background and preference of the respondents and their regulated scoring rule, which resulted in significant uncertainties in the weight determination and score estimation. In addition, as the most important evaluation criterion, the wind speed would directly affect the site selection results through adjusting the power output. Currently, many studies related to wind farm location selection mainly utilized the multi-year average wind speed as the evaluation indicator and ignored the impact of climate change. Previous studies have shown that the wind speed change markedly under climate change, probably drops by a range of 0.10 to 0.19 m/s per decade [19,20,21]. Therefore, in this research, an innovative GIS based fuzzy AHP and VIKOR method, taking into account the uncertainties of the weight coefficients of evaluation criteria and the scores related to various locations, was firstly proposed for wind farm site selection in the Wafangdian district of China and provided good demonstration for a location selection issue in the future. Moreover, the wind speed value under two climate change scenarios (RCP 4.5 and RCP 8.5, where the item RCP is the abbreviation of Representative Concentration Pathway) based on the regional climate model (i.e., Providing Regional Climate for Impacts Studies, PRECIS) was used as the evaluation index in order to investigate the possible impact of climate change on site selection results and help local managers generate a long-term plan for wind power development, even the energy structure adjustment scheme adapted to climate change [22].
The paper is organized as follows. Section 2 introduces the studied region. Section 3 provides a general theoretical and technological framework and describes how to use fuzzy AHP and VIKOR to calculate the weight values and identify the best site under the support of the GIS tool. Section 4 analyzes the solutions obtained from the proposed integrated method and discusses its potential improvements in the future. Conclusions are drawn in Section 5.
2. Study Area
2.1. Overview of Studied Region
The geographical location of the study area is shown in Figure 1. Wafangdian city is located in the west side of the central part of the Liaodong Peninsula (between 39°20′~40°07′ north latitude and 21°13′~122°17′ east longitude). As illustrated in Figure 1, it is adjacent to Pulandian City in the east, neighbors Bohai Sea in the west, faces the Jinzhou District across the sea, and closes Gaizhou City in the north. This region is dominated by mountains and hills, instead of plains and lowland; moreover, its terrain is high in the northeast and low in the southwest. The territory is located in the temperate continental monsoon climate zone in the eastern Asian of the middle latitudes of the Northern Hemisphere. At the end of 2017, the total registered population of this region was 998, 000 with a natural growth rate of 1.60%, birth rate of 8.89%, and mortality rate of 7.29%. The rapid economic development and population growth have brought a huge pressure on local energy provision. The energy requirement of Wafangdian City was satisfied by the aid of imports due to its limited primary energy. Currently, the shortage in fresh water, territory, and electricity have already become the main bottleneck of economic development. Four types of power generations were used to provide the electricity: (i) Wind power: Total installed capacity of seven wind farms reached 360–500 MW approximately and the annual power generation is 36.02 GWh; (ii) Hydropower: Total capacity provided by the Dongfeng Reservoir and Songshu Reservoir during the flood season is 640 kW; (iii) Thermoelectricity: Three power generation units involved in the Wafangdian Thermal Power Plant were characterized by a total installed capacity of 39.6 MW, annual power generation of 1.847 × 108 kWh, and on-grid power of 1.62 × 108 kWh; (iv) Thermal power: Two generator units with 3 MW were sourced from the Wazhou self-provided power plant and one generator unit with 3 MW was provided by the Washuiyuan self-provided power plant.
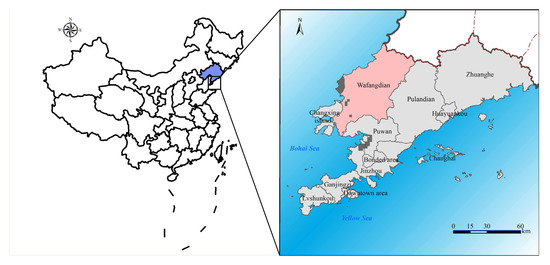
Figure 1.
Study area.
2.2. The Necessity of Wind Energy Development
In the future, the development of thermal power and thermoelectricity will no longer be encouraged due to the limited primary energy and their adverse influences on the environment; moreover, the hydropower was subjected to the unpredictability and volatility of available water resources. Compared with the above energy forms, the development of wind power is expectable and prospective. According to ‘Wind Power Density Rating Table’, the local wind power density was in the third level; the annual average wind speed is 4–5 m/s, without destructive speed. The prevailing wind direction is stable, where the dominant wind direction is South-East (SE) and North-Northwest (NNW), with the SE direction accounting for 14.1% and the NNW direction accounting for 13.2%. It is ensured that enough wind resource is available for the wind farms. At present, there are seven wind farms in this city, which are Xizhong Island, Changxing Island, Camel Mountain, Xiping Mountain, Donggang, Dongli, and Daoli, respectively. The total area is about 129–155 km2, and the installed capacity is approximately 360–500 MW. Therefore, it has a good prospect for planning and development of wind energy in the future.
3. Methodology
3.1. Methodological Framework
The wind farm site selection assessment is characterized as a complex and systematic process, which includes the establishment of a judgment criterion system, the determination of criterion’ weights, the scores estimation of all candidate sites corresponding to each criterion, and the suitability evaluation of nominated sites. The combination of fuzzy AHP and VIKOR and GIS is capable of providing technical support for the whole process. Figure 2 demonstrated a main framework of site selection, which is detailed as follows: (i) The studied region is divided into 1844 grids, where each grid represents a candidate location. The determination of grid quantity is based on the comprehensive considerations of the trade-off between the computation burden and resolution; (ii) the excluded region is identified and removed from the studied region by the means of GIS tools based on predefined restrictive criteria, such that remaining appropriate sites with different suitability degrees are determined; (iii) the fuzzy AHP method is used to characterize the ambiguity of the importance degree measure among the evaluation criteria and determine the weight coefficient of each criterion; (iv) the fuzzy VIKOR method is explored to tackle the score subjectivity provided by 125 stakeholders and evaluate the suitability degree of candidate points in a feasible region; (v) the sensitivity analysis is performed through designing three weight combination scenarios and examining the climate change impacts. The potential evaluation for a candidate region is accomplished through the above scientific, systematic, and comprehensive evaluation, which provides the decision support for a rational development of the wind energy industry in the future.
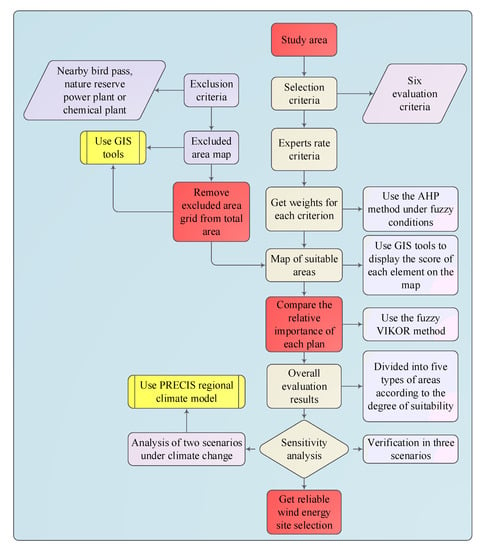
Figure 2.
General framework of wind farm site selection.
3.2. Exclusion Area
The identification of an infeasible region (i.e., exclusion zone) is the primary task of a wind farm site selection assessment in order to reduce unnecessary computation burden. The first step is to specify the restrictive criteria. Considering ecological damage and a potential accident risk that may be caused during the site selection, installation, and operation of wind power facilities, the zones that lie in the bird migration channel or close to the power plant or chemical plant are designated as exclusion areas. Figure 3 shows the grid partition of the study area and typical exclusion areas. Table 1 provided the detail of an exclusion area determination, which is delineated by the buffering tool of ArcGIS. Specifically, a buffer zone is firstly created around the region according to the restriction criteria. Next, the IS NULL and CON tools based on the Boolean logic are used to assign a true or false value to the targeted zones, where the zones meeting the restriction standards are designated as the false value, being 0. Finally, the exclusion area is determined. From Table 1, 345 grids, located in the western and central eastern parts of the region, are designated to the exclusion area, which account for 18.71% of the total candidate region. The remaining 1499 grids are identified as feasible for the facilities placement. The reason is that (i) the wintering habitat of big swans and grey cranes (national second-class protected animal) and the migration channel for the waterfowl birds (mainly gulls and geese) are located in the western side of the studied region. The placement of the wind turbines will affect their survival and reproduction. One hundred and eighteen grids were occupied this region, accounting for 34.2% of the exclusion area; (ii) the production safety is also a factor to be considered in the site selection process. The chemical plant and power plant have potential production safety hazards. Hence, two three-kilometer buffer zones with them as the center are established, where 199 grids belong to two buffer zones, being 57.7% of the exclusion area; (iii) the number of grids both at the birds’ migration passage and close to the power plant and chemical plant are 28, accounting for 8.1%. These grids have the most unfavorable factors and are the first areas to be excluded. It can be seen that the determination of the evaluation criteria has a significant impact on the site selection.
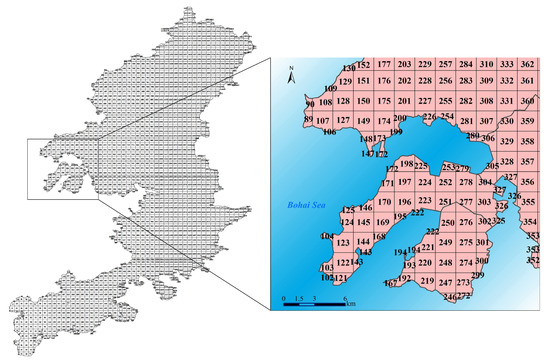
Figure 3.
Grid partition of candidate region.

Table 1.
Points and reasons for exclusion.
3.3. Evaluation Criteria
Although the preliminary feasible area of the wind farm does not need to consider the impact of restriction criteria, it is still affected by other factors. This means that some of them are still not suitable for the installation of wind energy facilities. Four types of evaluation factors for wind farm location were predetermined in order to obtain accurate evaluation results. They are geographical factors, economic factors, social factors, and ecological environment factors, respectively, where the slope represents the geographical factor, while the economic factors include the wind speed, distance from the main road, and distance from the transmission line. The social factor is determined by the building area representing disturbed people. Possibly affected bird sanctuaries are considered in the eco-environmental factor.
In detail, (i) the wind speed is the most important criterion for site selection. It directly determines the electricity output. The main principle is that, within an appropriate wind-speed range, a higher speed corresponds to a higher score; (ii) as an important geographical criterion, the slope reflects the flatness of the terrain. A steep terrain leads to more difficulties for the installation and operation of wind turbines. Therefore, the slope should be as small as possible; (iii) whether it belongs to the bird sanctuary reflects the influence of the site selection on the ecological environment, i.e., the protection of rare species. The bird habitat of Wafangdian City is a national key protection area, where big swans and grey cranes belong to the national secondary protected animal. The land occupancy, noise, and rotating blade at the installation and operation stages of the wind farm may affect birds’ normal activities. Therefore, the installation of a wind turbine should be kept away from the bird sanctuary; (iv) the building area is selected as the social factor. In fact, the site selection process needs to focus the attention on the acceptance of local residents because it will inevitably produce noise and visual impact. Hence, the locations of the wind farm should be far from residential areas, and a small population density is more favorable to establish wind farms; (v) the distance from the transmission line correlates with economic cost. The long distance between the transmission line and wind turbine means a higher investment and increased electricity-transmission losses. The closer the line is, the more suitable it is for wind farm placement; (vi) the distance from the main road also affects the economic aspect. A short distance between the main road and wind farm allows the lower transportation cost and more convenient maintenance of the wind facilities.
3.4. The Determination of Weight Coefficients Based on the FAHP Method
The AHP methodology, proposed by Saaty, has been accepted by the international scientific community as a robust and flexible MCDM tool to deal with complex decision problems [23]. The first task of the traditional Analytic Hierarchy Process (AHP) method is to convert the subjective judgments of stakeholders to the numerical information, where a selected fixed value was used to reflect the importance between various criteria. Then, a pairwise comparison matrix is established. Finally, the weight coefficients of all criteria were identified based on the eigenvector method. In fact, this quantification process mainly depends on the subjective evaluation in most cases, and the personal preferences and willingness of stakeholders will have a substantial impact on the final results. For example, the experts in the environmental protection department regard the environmental protection as a very important criterion. Hence, they will give almost the same score to both biodiversity-protection and wind-speed criteria. Conversely, the energy department pays more attention to the operation and production of wind facilities, where the wind speed is the most important criterion. The engineering design department naturally prioritizes the convenience of project construction and maintenance. They consider that the distance between the candidate location and the main road, and the distance from the transmission line is far more important than the distance from the residential area. As for the sociologists, they might focus more on the disturbance of the surrounding residents. Therefore, it is inappropriate to describe the relative importance between two criteria as the fixed value, since it is incapable of reflecting the opinions of various respondents and may lead to an inaccurate weight combination. Fortunately, the fuzzy Analytic Hierarchy Process (FAHP) realized the improvement on traditional AHP and can effectively address the above issue, where it uses triangular fuzzy numbers to comprehensively represent subjective characteristics involved in the consultation phase, instead of fixed values. The main steps of FAHP to identify the weight combination for six criteria associated with the wind farm site selection are:
Step 1: Transform stakeholders’ evaluation language into the triangular fuzzy number to reflect the importance degree between any two criteria involved in the wind farm site selection, where the 1-to-9 scale method was used;
Step 2: Construct a fuzzy evaluation matrix according to a hierarchical structure, which consists of three levels as follows: The highest layer is the target layer, i.e., the wind-farm site-selection alternative; the middle layer is the criterion layer, which contains six criteria (see Section 3.3); the lowest layer is the plan layer, which is the location of the wind farm to be selected for the studied region. The establishment of the hierarchical structure is a prerequisite for the FAHP method. In the hierarchical structure, n factors included in the criterion layer are expressed as C1, C2, ..., Cn, where Cij reflects the importance of index Ci relative to Cj. As mentioned above, it is difficult to express the relative importance among six criteria as the fixed value due to the existence of a subjective preference. The fuzzy evaluation matrix A = (aij) n × n was established as follows:
Step 3: Estimate the consistency of the fuzzy evaluation matrix. The fuzzy matrix consistency was calculated and improved according to Equations (3) and (4) as follows:
The RI value varies with the change of n, in this study, RI is 1.26 under n = 6. Moreover, the final result should satisfy the following inequality, CR < 0.1. If it is not satisfied, the evaluation matrix needs to be adjusted consistently until the calculated result satisfies the above inequality.
Step 4: Generate the weight coefficients through solving the priority vector of the triangular fuzzy comparison matrix. The degree analysis method proposed by Chang (1996) is used to calculate the priority vector of the triangular fuzzy comparison matrix (1), which is formulated as follows:
- (i)
- The comprehensive degree of the i-th evaluation target unit is expressed as follows:
- (ii)
- If , , Equation (6) is utilized to calculate the degree of possibility:
- (iii)
- In order to get and , it is necessary to calculate the corresponding values of and . The possible degree values for the remaining (n − 1) fuzzy numbers are as follows:
- (iv)
- Get the weight and express it as Equation (8); correspondingly, normalize it to Equation (9) as follows:
Step 5: Identify the weight combination for the judgment criterion system. After the single factor weight of the index is obtained, the whole ordering for each evaluation index to the target layer was calculated based on . The weight of the index with respect to the previous attribute was evaluated, where Wi(k+1) is the weight of the evaluation index i to the k + 1 layer index, Wjk is the weight value of the j index of the k layer, Wij(k) is the weight of the index i to criterion j, and m represents the number of the evaluation index. The generated weight coefficients of the evaluated criteria are introduced as follows: Where the wind speed owns the largest weight value (0.28), the second is bird estuary protection zone (0.25), the third is slope (0.22), the fourth is building area (0.16), then the distance from the transmission line (0.07), and the last one is the distance from the main road (0.02). It can be seen that the wind speed is the most important factor for wind farm site selection, and followed by whether it belongs to the bird estuary protection area, instead of some traditional engineering factors. This indicates that the site selection process emphasizes on the economical aspect but also pays attention to the eco-environmental protection and social impact.
3.5. The Suitability Evaluation of the Studied Region Based on Fuzzy VIKOR
Finding the right place for the wind farm is a complex decision-making issue that involves several conflicting standards and multiple objectives. The Multiple Criteria Decision Making (MCDM) approach provides a logical framework to investigate, analyze, and solve such problems [24]. As the one among MCDM methods, VIKOR is capable of determining the overall score of each candidate object based on a pre-allocated weight combination for the evaluation criterion system and identifying the most suitable scheme through comprehensive ordering [25,26,27]. It is advantageous in strengthening the role of group utility and reducing the interference of individual regret [28]. Considering that the traditional VIKOR method was incapable of tackling the inherent ambiguity involved in the score of a candidate site subject to the preference of the stakeholders, the triangular fuzzy number was used to reasonably represent the score of the site awaiting assessment, instead of a fixed value. The main steps of fuzzy VIKOR for realizing the suitability evaluation of the studied region are as follows:
Step 1: Convert linguistic evaluations of the stakeholders on the candidate site to triangular fuzzy numbers, where (i = 1, 2, ..., m; j = 1, 2, ..., n) is the evaluated result of the studied region A related to the criterion Cj; the term A is the set of candidate site expressed as A = {A1, A2, ..., Am}, where m is a total number of the candidate site; Cj (1, 2, ..., n) represents six evaluation criteria, where n is the total number of the evaluation criterion; W = {W1, W2, ..., Wn} is the weight coefficient of criteria Cj, which is provided in Section 3.4.
Step 2: Construct a fuzzy decision matrix based on the score provided by step 1, which is established as follows:
Step 3: Determine the ideal and worst evaluation values, where the optimal solution and the worst solution of site Ai corresponding to evaluation criterion Cj are determined by Equation (11):
Step 4: Calculate the values of Si, Ri, and Qi based on Equations (12) to (14), respectively.
where Si is the group utility value; is the optimal solution of the group utility value; is the worst solution of the group utility value; Ri is the individual regret value; is the optimal solution of the group utility value; is the optimal solution of the group utility value; Qi is the overall suitability index; v is the weight of the “majority criterion” strategy, where it reflects the degree of preference of the decision maker, and normally is equal to 0.5.
Step 5: Evaluate the suitability of candidate locations according to the order of the deblurred Qi values. The fuzzy number can be transformed into a certain number by Equation (15), where the items C1, C2, and C3 represent the minimum possible values, the most probable values, and the maximum possible values, respectively. The alternatives are sorted based on the Qi value. The site location with a smaller Qi value is the most suitable for wind farm placement.
4. Results Analysis and Discussion
4.1. Results Analysis
Figure 4a demonstrated the suitability-classified results generated by the integrated method of fuzzy AHP and VIKOR, where the GIS tool is used to provide the graphical depiction of the suitability evaluation and location corresponding to each candidate site. As shown in Figure 2, the studied region was divided into five types of areas, i.e., very suitable, suitable, commonly unsuitable, and very unsuitable, respectively. Among them, the most suitable area (Qi < 0.2) and suitable area (0.2 < Qi < 0.4) account for 7.1% and 13.6% of the total area, respectively. They are located mainly in the middle and upper part, where the large part of the evaluation criteria exhibits the high degree of satisfaction. In detail, the terrain in this region is relatively flat; meanwhile, the high wind speed with the stable direction occurs frequently. This makes the region suitable for the installation of wind power facilities. In addition, the scores of the slope, whether it belongs to the bird sanctuary and the building area within the grid are relatively high. These three criteria represent the production safety, ecological protection, and social impact, respectively. They also reflect the comprehensiveness of the evaluation criterion system design in this study, i.e., not only the wind speed and economy (distance from roads and transmission lines), but also place more attention on social and ecological impacts. Table 2 reflected the scores of some representative most suitable locations corresponding to each evaluation criterion. As shown in Table 2, these representative locations are almost advantageous in the wind speed, slope, and distance from the bird estuary protection area. Especially, FID 982 and 990 have the advantage in the distance from the main road; the sites (FID 678, 728, 982, 990, 1705, and 1737) have a short distance from the transmission line; the grids (FID 678, 679, 728, 990, 1206, 1611, and 1736) exert a small influence on the residents around the candidate region.
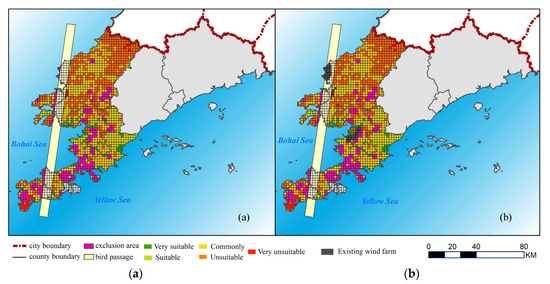
Figure 4.
Comparison of the evaluated result to the existing wind farm. (a) Suitability evaluation results obtained by fuzzy AHP and VIKOR integration method; (b) Locations of existing wind farms.

Table 2.
Index score of points in the most suitable area.
The general suitable region (0.4 < Qi < 0.6) accounts for 40.5% of the study district. Unsuitable areas (0.6 < Qi < 0.8) are those located along the central and eastern parts of the region, accounting for 36.1% of the total area. The main reason for this is that the central and eastern regions belong to the low mountainous area and are located in the area from Laomaoshan to Lugushan. The mountainous vegetation is flourishing, which results in a low overall wind speed in the region. In addition, compared with the plain area, the slope in the central and eastern districts are large; meanwhile, it is also closer to the bird-protection area, which is not beneficial for the protection of the rare animals. The very unsuitable area (0.8 < Qi < 1) accounts for 2.7% of the total area and is located in the southwest of the study area. This is due to the fact that (i) the western region is the wintering habitat of big swans and grey cranes, as well as the main passages for waterfowl birds. Wind farm location affects the bird living environment; (ii) the southwestern terrain is complex, and the area is mainly hilly. It also affects the electricity transmission and road transportation; (iii) there is a low-lying land, and twists and turns in the lower reaches of the small rivers in the southwest. Hence, the southwestern part is a very unsuitable area. Similarly, Table 3 provided the scores of selected very unsuitable locations corresponding to each evaluation criterion. The reason causing the low suitability degree of targeted sites is that they are located in the bird protection area and far away from the transmission line. For example, the sites (FID 12, 25, 38, 53, 65, and 66) have a long distance from the main road; the grids (FID 40, 53, 56, 66, 69, 71, 80, and 81) seriously affected the normal life of the residents and received the opposition from stakeholders. It is concluded that many factors exerted the influence on the evaluated results, although these candidate locations have a good wind resource.

Table 3.
Index score of points in a very unsuitable area.
Figure 4 shows the comparison situation between the evaluation results and the locations of the existing wind farms. The existing wind farms in the studied district account for 56 grids, 25 of which are located in the exclusion zone, while the remaining 31 are roughly matched with the suitable areas. Among these are eight existing wind farms in the suitable area, 18 in the general suitable area, and five in the unsuitable area. It is obvious that a large part of existing wind farms is not located in the suitable area. This is because some are located near the bird passages or petrochemical plants, with the potential risk and adverse impact on the rare birds, although these sites generally have better wind resources. For the above reasons, these areas are determined as the excluded region and are not considered in our study. It can also be seen that the existing wind farms in this region emphasize the wind power generation and the economy more, compared to ecological protection, production safety, and social impact. It may incur the opposition sourced from local residents and some departments of the ecological and environmental protection.
4.2. Discussion
The different weight combinations and the variation in wind speed under climate change would lead to various evaluation results. Therefore, the influence exerted by the variation in the above two aspects on suitability evaluation results is examined in this study. Firstly, three scenarios are predetermined, where the first scenario assumes that all factors are of equal importance and that all criteria have the same weight coefficients. For the other two scenarios, the weights were allocated to the criteria by considering two different policy biases: A policy focusing on technical and economic criteria (Scenario 2), and a policy focusing on social and eco-environmental criteria (Scenario 3). At this point, corresponding economic, eco-environmental, and social criteria were assigned the greater weight values. Table 4 shows the final results for four different scenarios, where the original results also are included for comparison purpose. It is demonstrated that the sites with Qi less than 0.4 under Scenario 1 account for 13.61% of the feasible area. Compared to the original evaluation results, the suitable area is reduced by about 7.09%, while the unsuitable area increased by 11.17%. This is because the weight value of the wind speed criterion under Scenario 1 is significantly reduced, which is beneficial to the wind farm installation through allocating the high score to the large part of candidate sites. This also reflected that the smaller the weight value of the favorable criterion, the smaller are the fewer suitable areas. The evaluation results of the other two scenarios also exhibited totally different evaluation results. For example, the northeastern part under Scenario 2 represents a very unsuitable region because of its poor performance in the economic aspect, including the low wind speed in the area, the long distance from the transmission line and main road. Conversely, the northeastern part is regarded as the suitable area under Scenario 3, mainly because the building area within this area is small, far from the bird sanctuary, and has little impact on the social and environmental aspects. Based on the above analysis, it is emphasized that, (i) different backgrounds and preferences of the stakeholders exerted a large influence on the evaluation results of the candidate sites through assigning various weight values to the evaluation criteria; (ii) the wind speed is a dominant factor for wind farm placement. However, the site selection decision should take into account all aforementioned evaluation criteria (i.e., production safety, social impact, and eco-environmental protection) because they also play the substantial role of prioritizing the potential locations of wind farms.

Table 4.
Suitable area in Wafangdian City according to the Analytic Hierarchy Process (AHP) and sensitivity analysis results.
The influence caused by the change of wind speed under climate change on the site selection also is estimated, where the evaluated results under two scenarios (i.e., RCP 4.5 and RCP 8.5) over three periods (i.e., near, medium, and longer term) were shown in Figure 4. The regional climate model PRECIS developed by the British Meteorological Office Hadley is used to generate annual wind speed values over the next 75 years under two climate change scenarios due to its flexibility and applicability, where the average wind speed at three periods were considered as the evaluation indicator, i.e., near-term (2025–2049), mid-term (2050–2074), and long-term (2075–2099), respectively [23]. Finally, site-selection results under climate change were generated. As demonstrated in Figure 5, the decrease in wind speed caused by climate change exerts the adverse effects on the wind power development. The RCP8.5 scenario is less suitable for wind power development than the RCP4.5 scenario. Compared with original evaluation results, the suitable area over three periods under the RCP 4.5 scenario reduced by 5.80%, 11.61%, and 11.61%, respectively; the unsuitable area increased by 6.87%, 20.27%, and 17.70%, respectively. Correspondingly, the suitable area under the RCP 8.5 scenario reduced by 13.87%, 26.45%, and 27.01%, respectively; the unsuitable area increased by 22.68%, 40.03%, and 41.24%, respectively. This is mainly due to the fact that the reduction of wind speed would impair its advantages in many candidate sites, leading to their degradation. For example, the upper middle part of the studied region including 304 grids, without the consideration of climate change, its total magnitudes of very suitable, suitable, general suitable, unsuitable, very unsuitable grids are 37, 31, 128, 45, and 1, respectively. Under the RCP 4.5 scenario in the long term, the suitability of 27 grids dropped by one grade, where they are 13 very suitable grids, three suitable grids, 11 general suitable grids, respectively. This variation trend was more obvious under the RCP 8.5 scenario, where the number of suitability-degraded grids reached 57, including 27 very suitable sites, four suitable sites, 25 general suitable sites, and one unsuitable site. In order to better reflect the influence exerted by the variation in wind speed on site selection results, the wind speed data in the past 25 years (1995–2019) is collected and the average wind speed in this period was considered as the evaluation indicator. Figure 6 shows the suitability evaluation results under historical wind speed. It is indicated that the grade of suitability degree was enhanced compared to the evaluated results under climate change, where the suitable area has increased by 15.81% and the unsuitable area has decreased by 13.92% over the past 25 years. This is because the available wind speed under climate change dropped significantly. Therefore, the influence exerted by the climate change on the wind speed should be incorporated into the site selection process of the wind farm in order to generate the suitable wind power development project adapted to climate change, especially the location identification of some large scale wind power bases and determination of the wind turbine quantity and type. Moreover, subjected to the reduction in wind power, relevant energy authorities should adjust the layout of renewable energy generation through exploring more renewable energy forms, as possible.
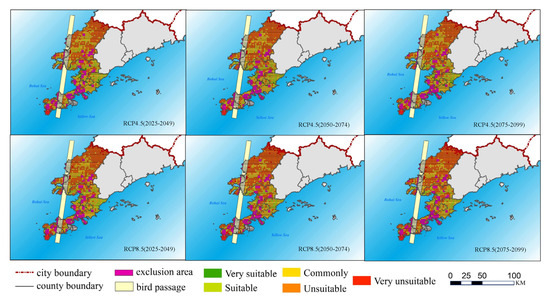
Figure 5.
Evaluation results under two climate change scenarios.
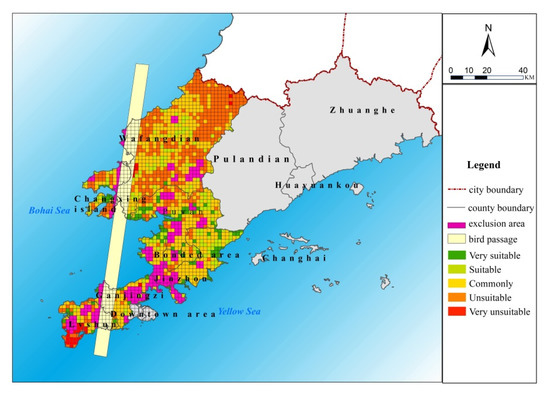
Figure 6.
Evaluation results based on historical wind speed.
Finally, this research compares the obtained results with other related studies, mainly from the following two aspects: Whether the evaluation results coincide with the location of the existing wind farm; whether the variation in weight coefficients affect the site selection of the wind farm. The comparison results demonstrated that the obtained results are generally similar, but there are still a couple of minor differences. For example, Latinopoulos and Kechagia analyzed the suitability of licensed wind farms in Greece through the site selection method [12]. The evaluation results indicated that the licensed wind farms in the Greek region rarely appear in the excluded area, while the grid quantity belonging to the excluded area in this study account for 44.64% of the total number of existing wind farms. This is mainly because the latter emphasized the wind power generation and ignored the ecological protection, production safety, and social impact. Moreover, Höfer et al. designed three weight scenarios to conduct the sensitivity analysis of evaluation results in Aachen, Germany [13]. It is found that two groups of evaluated results under various weight combinations were basically conformable. The most suitable areas under an equal-weight situation have declined due to the decrease in the weight of wind speed indicator. In the context of economic or environmental priority, the site selection results exhibit a consistent variation trend with some minor differences. This also proves that the evaluation results of this research are credible.
Regardless, there are still some problems in this study, which should be addressed in the future. Such specific issues include: (i) The evaluation criterion system needs to be improved further. Depending on local conditions, we consulted 125 local personnel with various backgrounds and preferences, including the environmental protection department, power factory, planning department, and local residents and determined six evaluation criteria for the suitability evaluation of the candidate sites. However, in practice, these six criteria were not sufficient to explain all the factors affecting the location of the wind farm. Other assessment criteria such as wind direction, land cover, and geological factors are also important criteria that affect the placement of wind power facilities, which should be incorporated into the existing criterion system in order to obtain reliable evaluation results; (ii) the division of the area grid was not precise enough. The location analysis was performed at a relatively low resolution (0.5 × 0.5 km), with an area of 0.25 km2 per grid, each grid representing a selectable location. Finally, 1844 grids were obtained as potential locations for the wind turbine. However, the actual footprint of a single grid was too large. Even if the most suitable point was obtained, it was still difficult to select the final location for wind farm installation within 0.25 km2. It is necessary to subdivide the grid and reduce the area occupied by each grid for enhancing the practicability and feasibility of the evaluated results; (iii) the observation involves both speed as well as direction that is susceptible to the environmental impact. The estimation of wind energy resource for the wind farm placement was usually based on historical data such as the weather stations, where the observation data likely deviate from the actual wind speed, which also leads to inaccurate results. Therefore, a method should be found to effectively adjust the observed data and reduce the impact of the surrounding environment on them; (iv) the appropriate degrees of candidate sites were calculated by the integrated method of fuzzy AHP, fuzzy VIKOR, and GIS tool, where their ranking results provided the decision support to the location selection of the wind farm. In fact, as mentioned in Jan et al., the final decision is still a responsibility of users based on their knowledge and experiences of the local practical situation [29]. Therefore, the decision support system with the capabilities of merging the subjective and objective evaluation results should be established for site selection of wind farms in the future.
5. Conclusions
The exploration and utilization of the renewable energy were capable of solving the energy-shortage crisis and mitigating the climate change. Wind energy is an important renewable energy source, not only in China but also in many other countries. In recent years, the wind power production in China has already increased rapidly. At the same time, due to suboptimal locations, unwanted effects to humans and the environment have increased public concern and criticism. Through the literature review and on-site survey, the stakeholders’ opinions exhibited a large difference in the determination of the weight and score due to the existence in subjective preference; meanwhile, the impact of climate change on the wind speed also was neglected. In this research, the integration of fuzzy AHP, fuzzy VIKOR, and GIS under climate change were firstly applied to analyze and estimate the wind energy potential of the Wafangdian district, China. The uncertainties involved in the estimation processes of the weight and score were reflected and tackled by both fuzzy AHP and VIKOR. The graphic depiction and demonstration of evaluation results was realized by the aid of the GIS tool. The results indicate that the suitable areas for wind power generation in the district are mainly located in the upper middle part, which accounts for more than 20% of the total area and has an acceptable Qi score (Qi < 0.4). The middle and eastern parts, however, are unsuitable (0.6 < Qi < 0.8), and the southwest is very unsuitable (Qi values between 0.8 and 1). The number of existing wind farms occupied 56 grids, of which 26 overlap with the suitable areas determined by the evaluated results, which means the coincidence degree is high enough (about 46%). This fact supports the accuracy and validity of the proposed method, where the inconsistency is mainly sourced from the difference in the evaluation criterion. Traditional site selection pays more attention to the economic and engineering factors and neglects the adverse impact on the social and biological diversity. This also exhibited in the comprehensiveness and rationality of the evaluation criterion system designed in this study. Moreover, the sensitivity analysis results exhibited the adverse impact of climate change in the suitability of candidate sites. It is necessary to incorporate the variation in the wind speed under climate change into the site selection process of a large scale wind power base and determination in the wind turbine type, in order to generate a suitable wind power development program, even the energy structure adjustment scheme. In further studies, some improvements, including the adjustment of the criterion system through introducing a more meaningful criteria, the advance of a grid-partition resolution, and the increase in the accuracy of wind speed, as well as the establishment of a complete spatial decision support system to reflect the user’s point of view, should be realized to deal with more complex problems and generate a more reliable site selection scheme.
Author Contributions
Formal analysis, M.L. and Y.X.; resources, Y.X. and W.L.; methodology, M.L., Y.X., and Y.L.; software, J.G.; data curation, Y.X. and M.L.; writing—original draft, M.L.; writing—review and editing, Y.X. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the National Key R&D Program of China CERC-WET Project (Grant No. SQ2018YFE010367).
Acknowledgments
We are very grateful to the National Key R&D Program of China CERC-WET Project (Grant No. SQ2018YFE010367).
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| A | the building area within the grid; |
| AHP | analytic hierarchy process; |
| ANP | analytic network process; |
| B | the bird estuary reserve; |
| E | the distance from the transmission line; |
| FAHP | fuzzy analytic hierarchy process; |
| FID | the number of candidate sites; |
| GHGs | greenhouse gases; |
| GIS | geographic information system; |
| IPCC | intergovernmental panel on climate change; |
| MCDM | multi-criteria decision making; |
| P | the wind speed; |
| PRECIS | providing regional climate for impacts studies; |
| PROMETHEE | preference ranking organization method for enrichment evaluations; |
| R | the distance from the main road; |
| RCP | representative concentration pathway; |
| S | the slope; |
| SE | south-east; |
| TIFN | triangular intuitionistic fuzzy number; |
| VIKOR | VIšekriterijumsko KOmpromisno Rangiranje. |
Nomenclatures for Variables and Parameters
| the fuzzy evaluation matrix for each evaluation index; | |
| the score of the index scored; | |
| Cj | evaluation criteria; |
| Cij | the importance of index Ci relative to Cj; |
| CI | consistency index; |
| CR | random consistency ratio; |
| the optimal solution; | |
| the worst solution; | |
| the minimum possible values; | |
| m | the total number of the candidate site; |
| the most probable value; | |
| n | the total number of the evaluation criterion; |
| Qi | overall suitability index; |
| Ri | the individual regret value; |
| the optimal solution of the group utility value; | |
| the optimal solution of the group utility value; | |
| RI | random consistency index; |
| Si | the group utility value; |
| the comprehensive degree of the i-th evaluation target unit; | |
| the optimal solution of the group utility value; | |
| the worst solution of the group utility value; | |
| the maximum possible values; | |
| v | the weight of the “majority criterion” strategy; |
| the weight of the indicator j; | |
| Wjk | the weight value of the j index of the k layer; |
| Wi(k+1) | the weight of the evaluation index i to the k + 1 layer index; |
| Wij(k) | the weight of the index i to criterion j; |
| the evaluated results of studied region A related to the criterion Cj; | |
| the largest characteristic root of matrix A. |
References
- National Bureau of Statistics of China. 2019. Available online: www.data.stats.gov.cn/easyquery.htm?cn=C01 (accessed on 30 April 2019).
- Ying, X.; Jie, W.; Ying, S.; Botao, Z.; Rouke, L.; Jia, W. Change in Extreme Climate Events over China Based on CMIP5. Atmos. Ocean. Sci. Lett. 2015, 8, 185–192. [Google Scholar] [CrossRef]
- The Intergovernmental Panel on Climate Change. 2016. Available online: www.ipcc.ch/sr15/chapter/summary-for-policy-makers/ (accessed on 1 April 2016).
- Rosencranz, A. The Origin and Emergence of International Environmental Norms. Hastings Int. Comp. L. Rev. 2003, 26, 309–319. [Google Scholar]
- Squalli, J. Renewable energy, coal as a baseload power source, and greenhouse gas emissions: Evidence from U.S. state-level data. Energy 2017, 127, 479–488. [Google Scholar] [CrossRef]
- Hagen, B.; Pijawka, D. Public Perceptions and Support of Renewable Energy in North America in the Context of Global Climate Change. Int. J. Disaster Risk Sci. 2015, 6, 385–398. [Google Scholar] [CrossRef]
- Wang, X.; Liu, Y.; Jiang, N.; Duan, Y. Summary of Wind Power Technology Development. Electr. Switch. 2013, 51, 16–19. [Google Scholar]
- Chaofeng, Z. Review of Wind Power Generator and Control Technology of Wind Power Generation. Low Carbon World 2015, 14, 58–59. [Google Scholar]
- Chen, Y.; Han, L.; Lin, P.; Gu, C. Review on the Development of Large-Scale Renewable Wind Power Generation Technology. Sci. Technol. Dissem. 2015, 21, 33–34. [Google Scholar]
- Chen, Z.; Dong, W.; Gao, H.; Jia, C.; Xu, X.; Zhang, G.; Zhu, L. Statistics of Wind Power installed capacity in China in 2017. Wind Energy 2018, 5, 44–57. [Google Scholar]
- Janke, J.R. Multicriteria GIS modeling of wind and solar farms in Colorado. Renew. Energy 2010, 35, 2228–2234. [Google Scholar] [CrossRef]
- Latinopoulos, D.; Kechagia, K. A GIS-based multi-criteria evaluation for wind farm site selection: A regional scale application in Greece. Renew. Energy 2015, 78, 550–560. [Google Scholar] [CrossRef]
- Höfer, T.; Sunak, Y.; Siddique, H.; Madlener, R. Wind farm siting using a spatial Analytic Hierarchy Process approach: A case study of the Städteregion Aachen. Appl. Energy 2016, 163, 222–243. [Google Scholar] [CrossRef]
- Geovanna, V.; Gabriel, G.; Javier, M.-G.; Diego, J.J. Wind farms suitability location using geographical information system(GIS), based on multi-criteria decision making (MCDM) methods: Thecase of continental Ecuador. Renew. Energy 2017, 109, 275–286. [Google Scholar]
- Mahdy, M.; Bahaj, A.S. Multi criteria decision analysis for offshore wind energy potential in Egypt. Renew. Energy 2018, 118, 278–289. [Google Scholar] [CrossRef]
- Ali, S.; Jang, C.-M. Selection of Best-Suited Wind Turbines for New Wind Farm Sites Using Techno-Economic and GIS Analysis in South Korea. Energies 2019, 12, 3140. [Google Scholar] [CrossRef]
- Wu, Y.; Tao, Y.; Zhang, B.; Wang, S.; Xu, C.; Zhou, J. A decision framework of offshore wind power station site selection using a PROMETHEE method under intuitionistic fuzzy environment: A case in China. Ocean Coast. Manag. 2019, 184, 105016. [Google Scholar] [CrossRef]
- Ioannou, K.; Tsantopoulos, G.; Arabatzis, G. A Decision Support System methodology for selecting wind farm installation locations using AHP and TOPSIS: Case study in Eastern Macedonia and Thrace region, Greece. Energy Policy 2019, 132, 232–246. [Google Scholar]
- Ding, X.; Liu, L.; Huang, G.; Xu, Y.; Guo, J. A Multi-Objective Optimization Model for a Non-Traditional Energy System in Beijing under Climate Change Conditions. Energies 2019, 12, 1692. [Google Scholar] [CrossRef]
- Guo, J.; Huang, G.; Wang, X.; Li, Y.; Lin, Q. Dynamically-downscaled projections of changes in temperature extremes over China. Clim. Dyn. 2018, 50, 1045–1066. [Google Scholar] [CrossRef]
- Zha, J.; Wu, J.; Zhao, D.; Fan, W. Future projections of the near-surface wind speed over eastern China based on CMIP5 datasets. Clim. Dyn. 2020, 54, 2361–2385. [Google Scholar] [CrossRef]
- Guo, J.; Huang, G.; Wang, X.; Xu, Y.; Li, Y. Projected changes in wind speed and its energy potential in China using a high-resolution regional climate model. Wind Energy 2020, 23, 471–485. [Google Scholar] [CrossRef]
- Sánchez-Lozano, J.M.; Lamata, M.T. GIS-based onshore wind farm site selection using Fuzzy Multi-Criteria Decision Making methods. Evaluating the case of Southeastern Spain. Appl. Energy 2016, 171, 86–102. [Google Scholar] [CrossRef]
- Sun Hongxia, L.Y. VIKOR Method with Triangular Intuitionistic Fuzzy Numbers. Oper. Res. Manag. Sci. 2015, 24, 288–294. [Google Scholar]
- Chifang, Z. VIKOR Method for Intuitionistic Fuzzy Multi-Attribute Group Decision Making. J. Xi’an Technol. Univ. 2015, 3, 182–185. [Google Scholar]
- Tavana, M.; Mavi, R.K.; Santos-Arteaga, F.J.; Doust, E.R. An extended VIKOR method using stochastic data and subjective judgments. Comput. Ind. Eng. 2016, 97, 240–247. [Google Scholar] [CrossRef]
- Azadeh, A.; Rahimi-Golkhandan, A.; Moghaddam, M. Location optimization of wind power generation–transmission systems under uncertainty using hierarchical fuzzy DEA: A case study. Renew. Sustain. Energy Rev. 2014, 30, 877–885. [Google Scholar] [CrossRef]
- Liu, P.; Jin, F. Methods for aggregating intuitionistic uncertain linguistic variables and their application to group decision making. Inf. Sci. 2012, 205, 58–71. [Google Scholar] [CrossRef]
- Jan, K.; Joost van, H.; Szymon, S. Challenges in the wind turbines location process in Central Europe—The use of spatial decision support systems. Renew. Sustain. Energy Rev. 2017, 76, 425–433. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).