Fault Detection and Classification of Shunt Compensated Transmission Line Using Discrete Wavelet Transform and Naive Bayes Classifier
Abstract
1. Introduction
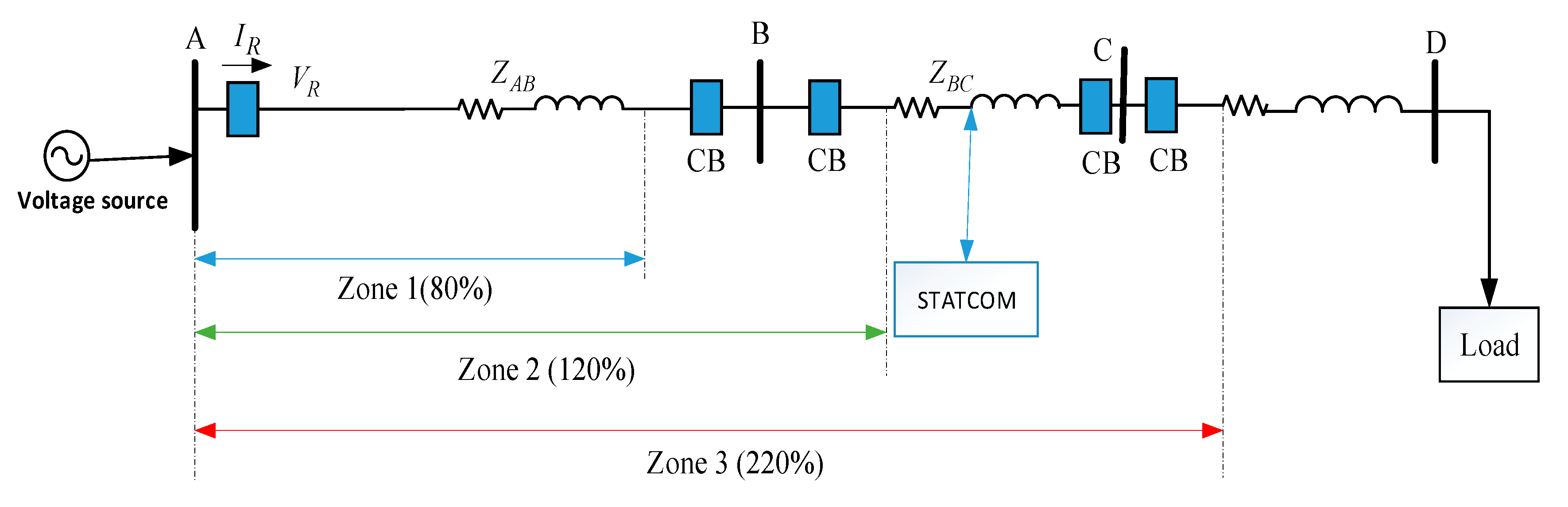
2. System Model Studied
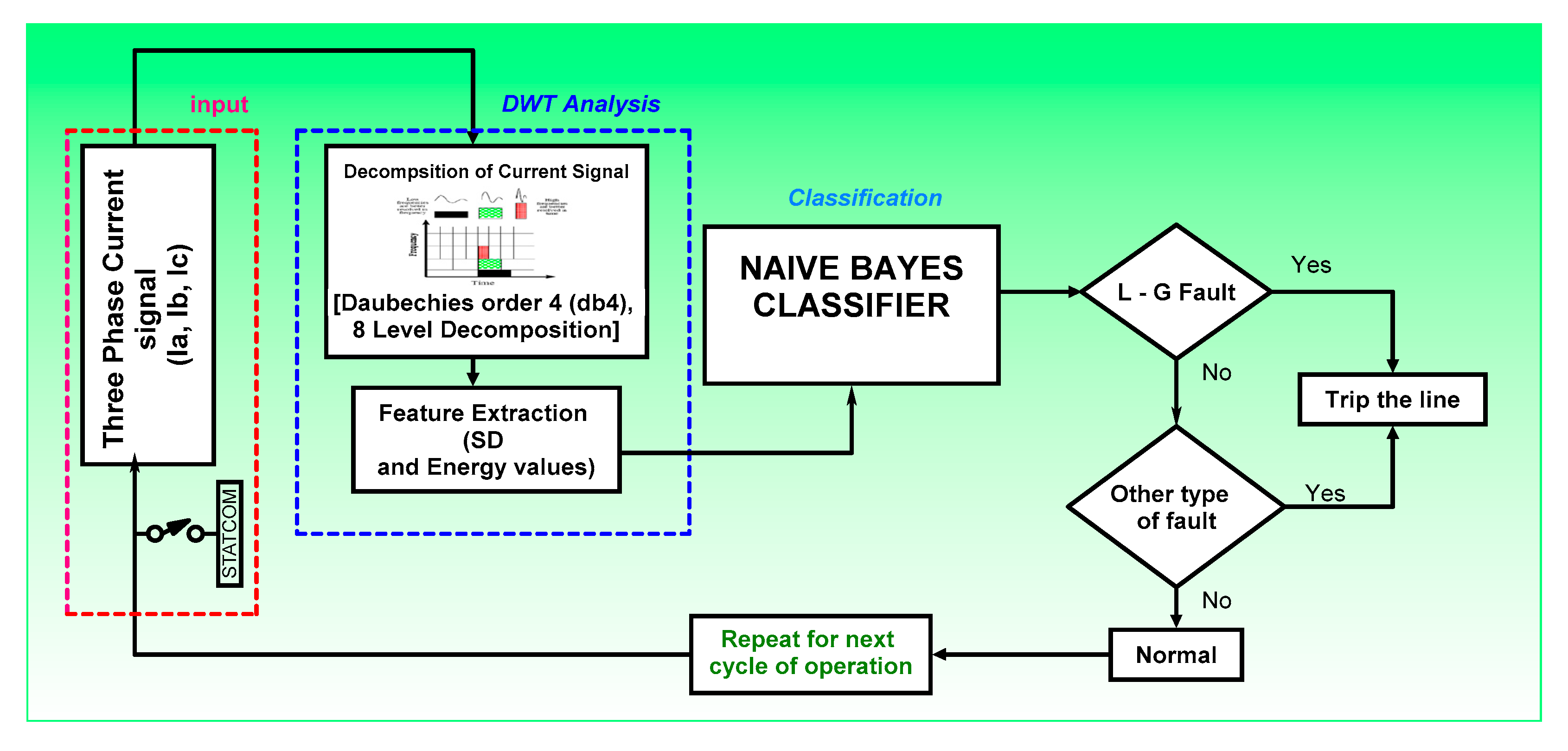
Proposed Method of Fault Detection
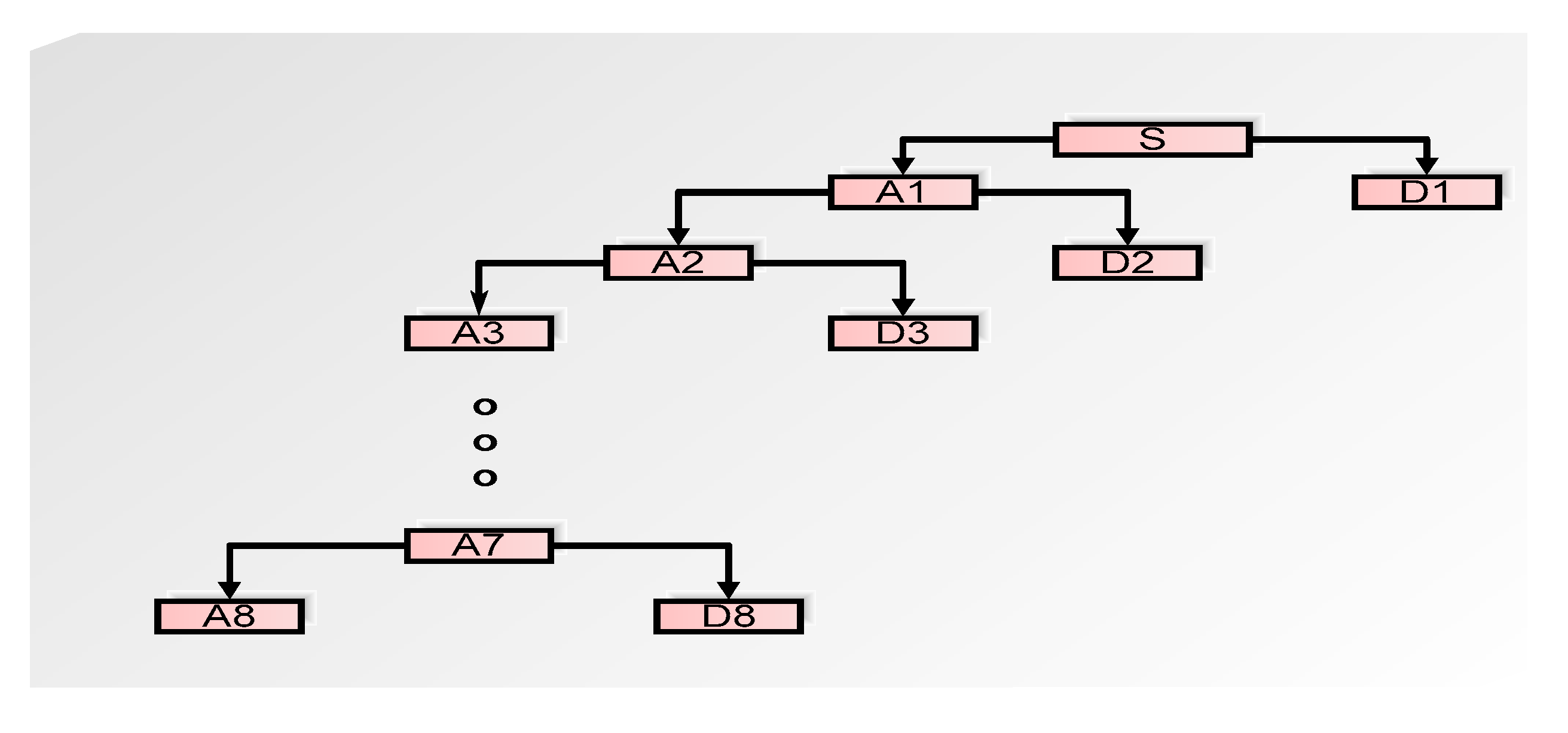
3. Feature Extraction Using Discrete Wavelet Transform
3.1. Feature Extractions
3.1.1. Standard Deviation (SD)
3.1.2. Energy Value (E)
4. Fault Classifiers
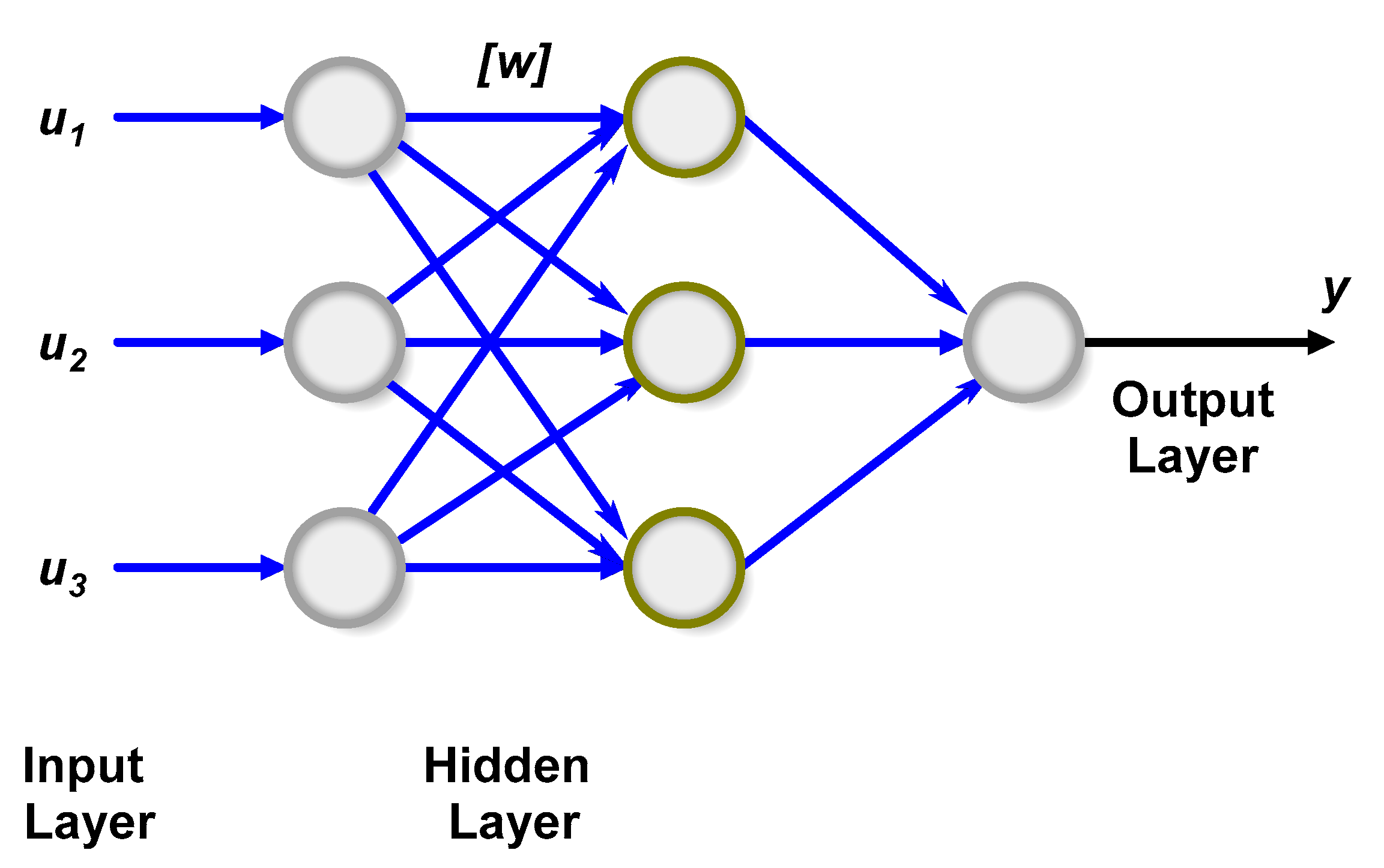
4.1. Multi-Layer Perceptron (MLP) Network
4.2. Bayes and Naive Bayes Classifiers
4.3. Performance Indices of Classifier
5. Results and Discussion
Performance Evaluation of Classifiers
6. Comparative Analysis
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Singh, A.R.; Patne, N.R.; Kale, V.S. Synchronized measurement based an adaptive distance relaying scheme for STATCOM compensated transmission line. Measurement 2018, 116, 96–105. [Google Scholar] [CrossRef]
- Mirzaei, M.; Vahidi, B.; Hosseinian, S.H. Accurate fault location and faulted section determination based on deep learning for a parallel-compensated three-terminal transmission line. IET Gener. Transm. Distrib. 2019, 13, 2770–2778. [Google Scholar] [CrossRef]
- Ghazizadeh-Ahsaee, M.; Sadeh, J. Accurate fault location algorithm for transmission lines in the presence of shunt-connected flexible AC transmission system devices. IET Gener. Transm. Distrib. 2012, 6, 247. [Google Scholar] [CrossRef]
- Mishra, S.K.; Tripathy, L.N.; Swain, S.C. DWT approach based differential relaying scheme for single circuit and double circuit transmission line protection including STATCOM. Ain Shams Eng. J. 2019, 10, 93–102. [Google Scholar] [CrossRef]
- Chen, K.; Huang, C.; He, J. Fault detection, classification and location for transmission lines and distribution systems: A review on the methods. High Volt. 2016, 1, 25–33. [Google Scholar] [CrossRef]
- Veerasamy, V.; Abdul Wahab, N.I.; Ramachandran, R.; Thirumeni, M.; Subramanian, C.; Othman, M.L.; Hizam, H. High-impedance fault detection in medium-voltage distribution network using computational intelligence-based classifiers. Neural Comput. Appl. 2019, 31, 9127–9143. [Google Scholar] [CrossRef]
- Veerasamy, V.; Abdul Wahab, N.I.; Ramachandran, R.; Mansoor, M.; Thirumeni, M.; Othman, M.L. High impedance fault detection in medium voltage distribution network using discrete wavelet transform and adaptive neuro-fuzzy inference system. Energies 2018, 11, 3330. [Google Scholar] [CrossRef]
- Gupta, O.H.; Tripathy, M. An innovative pilot relaying scheme for shunt-compensated line. IEEE Trans. Power Deliv. 2015, 30, 1439–1448. [Google Scholar] [CrossRef]
- Mehrjerdi, H.; Ghorbani, A. Adaptive algorithm for transmission line protection in the presence of UPFC. Int. J. Electr. Power Energy Syst. 2017, 91, 10–19. [Google Scholar] [CrossRef]
- Albasri, F.A.; Sidhu, T.S.; Varma, R.K. Performance comparison of distance protection schemes for shunt-FACTS compensated transmission lines. IEEE Trans. Power Deliv. 2007, 22, 2116–2125. [Google Scholar] [CrossRef]
- Aker, E.E.; Othman, M.L.; Aris, I.; Wahab, N.I.A.; Hizam, H.; Emmanuel, O. Adverse impact of STATCOM on the performance of distance relay. Indones. J. Electr. Eng. Comput. Sci. 2017, 6, 528–536. [Google Scholar] [CrossRef][Green Version]
- Othman, M.L.; Aris, I.; Wahab, N.I.A. Modeling and simulation of the industrial numerical distance relay aimed at knowledge discovery in resident event reporting. Simulation 2014, 90, 660–686. [Google Scholar] [CrossRef]
- Othman, M.L.; Aris, I.; Othman, M.R.; Osman, H. Rough-Set-and-Genetic-Algorithm based data mining and Rule Quality Measure to hypothesize distance protective relay operation characteristics from relay event report. Int. J. Electr. Power Energy Syst. 2011, 33, 1437–1456. [Google Scholar] [CrossRef]
- Othman, M.L.; Aris, I.; Othman, M.R.; Osman, H. Rough-Set-based timing characteristic analyses of distance protective relay. Appl. Soft Comput. J. 2012, 12, 2053–2062. [Google Scholar] [CrossRef]
- Hussain, S.; Osman, A.H. Fault location on series and shunt compensated lines using unsynchronized measurements. Electr. Power Syst. Res. 2014, 116, 166–173. [Google Scholar] [CrossRef]
- Kumar, B.; Yadav, A.; Pazoki, M. Impedance differential plane for fault detection and faulty phase identification of FACTS compensated transmission line. Int. Trans. Electr. Energy Syst. 2019, 29, e2804. [Google Scholar] [CrossRef]
- Megahed, A.I.; Moussa, A.M.; Bayoumy, A.E. Usage of wavelet transform in the protection of series-compensated transmission lines. IEEE Trans. Power Deliv. 2006, 21, 1213–1221. [Google Scholar] [CrossRef]
- Patel, B. A new FDOST entropy based intelligent digital relaying for detection, classification and localization of faults on the hybrid transmission line. Electr. Power Syst. Res. 2018, 157, 39–47. [Google Scholar] [CrossRef]
- Krishnanand, K.R.; Dash, P.K. A new real-time fast discrete S-transform for cross-differential protection of shunt-compensated power systems. IEEE Trans. Power Deliv. 2013, 28, 402–410. [Google Scholar]
- Dash, P.K.; Das, S.; Moirangthem, J. Distance protection of shunt compensated transmission line using a sparse S-transform. IET Gener. Transm. Distrib. 2015, 9, 1264–1274. [Google Scholar] [CrossRef]
- Wilkinson, W.A.; Cox, M.D. Discrete wavelet analysis of power system transients. IEEE Trans. Power Syst. 1996, 11, 2038–2044. [Google Scholar] [CrossRef]
- Osman, A.H.; Malik, O.P. Protection of Parallel Transmission Lines Using Wavelet Transform. IEEE Trans. Power Deliv. 2004, 19, 49–55. [Google Scholar] [CrossRef]
- Devasahayam, V.; Veluchamy, M. An enhanced ACO and PSO based fault identification and rectification approaches for FACTS devices. Int. Trans. Electr. Energy Syst. 2017, 27, e2344. [Google Scholar] [CrossRef]
- Dash, P.K.; Samantaray, S.R.; Panda, G. Fault classification and section identification of an advanced series-compensated transmission line using support vector machine. IEEE Trans. Power Deliv. 2007, 22, 67–73. [Google Scholar] [CrossRef]
- Hindarto, H.; Muntasa, A. Wavelet sub-band energy for feature extraction of electro encephalo graph (EEG) signals. J. Eng. Sci. Technol. 2019, 14, 578–588. [Google Scholar]
- Patil, K.; Jadhav, N. Multi-Layer Perceptron Classifier and Paillier Encryption Scheme for Friend Recommendation System. In Proceedings of the 2017 International Conference on Computing, Communication, Control and Automation (ICCUBEA), Pune, India, 17–18 August 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Bebarta, D.K.; Rout, A.K.; Biswal, B.; Dash, P.K. Efficient Prediction of Stack Market Indices using Adaptive Neural Network. In Proceedings of the Second International Conference on Soft Computing for Problem Solving (SocProS 2012), Jaipur, India, 28–30 December 2012; Springer: Jaipur, India, 2014; Volume 236, ISBN 978-81-322-1601-8. [Google Scholar]
- Zhang, N.; Wu, L.; Yang, J.; Guan, Y. Naive bayes bearing fault diagnosis based on enhanced independence of data. Sensors 2018, 18, 463. [Google Scholar] [CrossRef]
- Youn, E.; Jeong, M.K. Class dependent feature scaling method using naive Bayes classifier for text datamining. Pattern Recognit. Lett. 2009, 30, 477–485. [Google Scholar] [CrossRef]
- Addin, O.; Sapuan, S.M.; Mahdi, E.; Othman, M. A Naïve-Bayes classifier for damage detection in engineering materials. Mater. Des. 2007, 28, 2379–2386. [Google Scholar] [CrossRef]
- Muralidharan, V.; Sugumaran, V. A comparative study of Naïve Bayes classifier and Bayes net classifier for fault diagnosis of monoblock centrifugal pump using wavelet analysis. Appl. Soft Comput. J. 2012, 12, 2023–2029. [Google Scholar] [CrossRef]
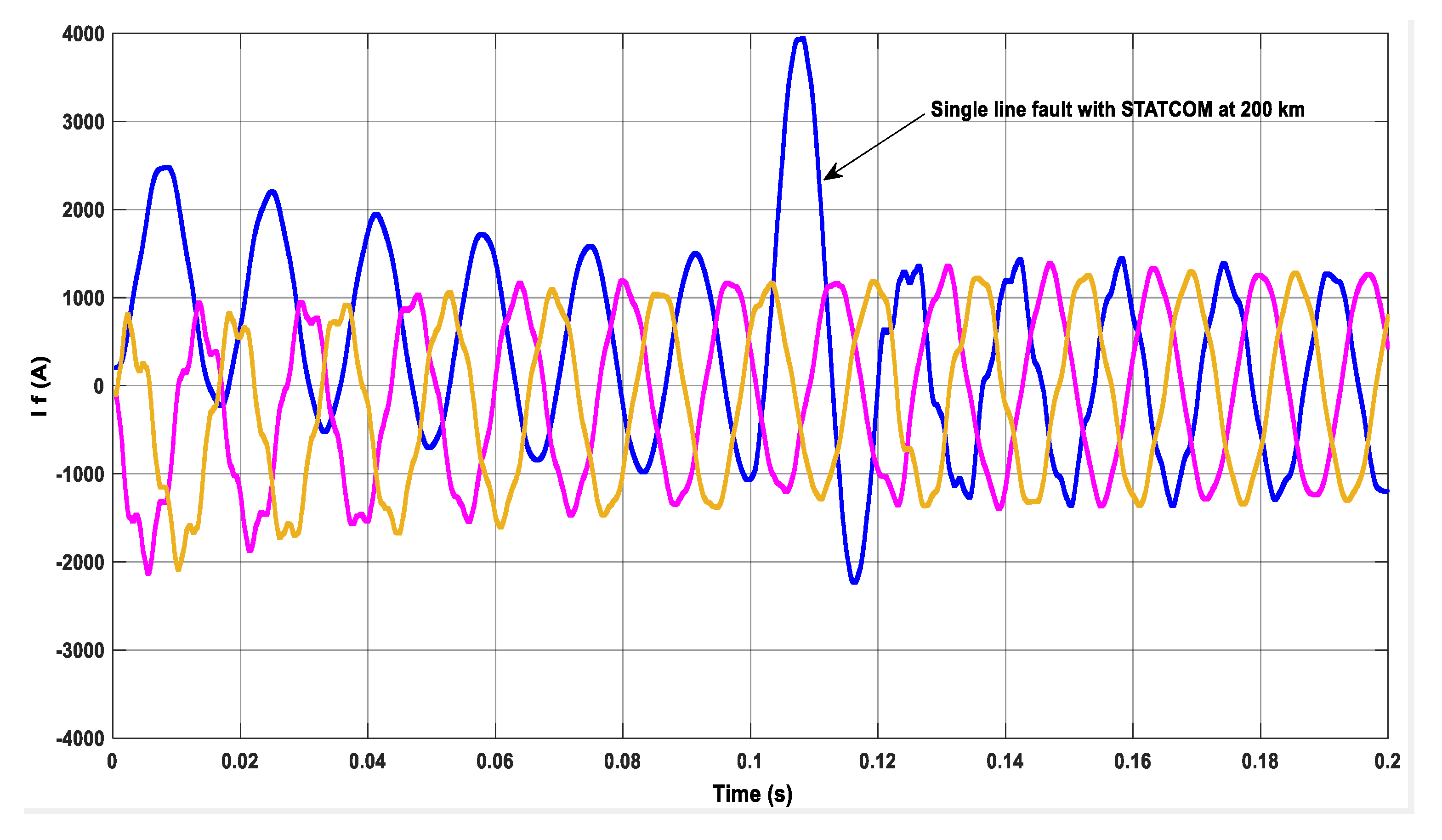
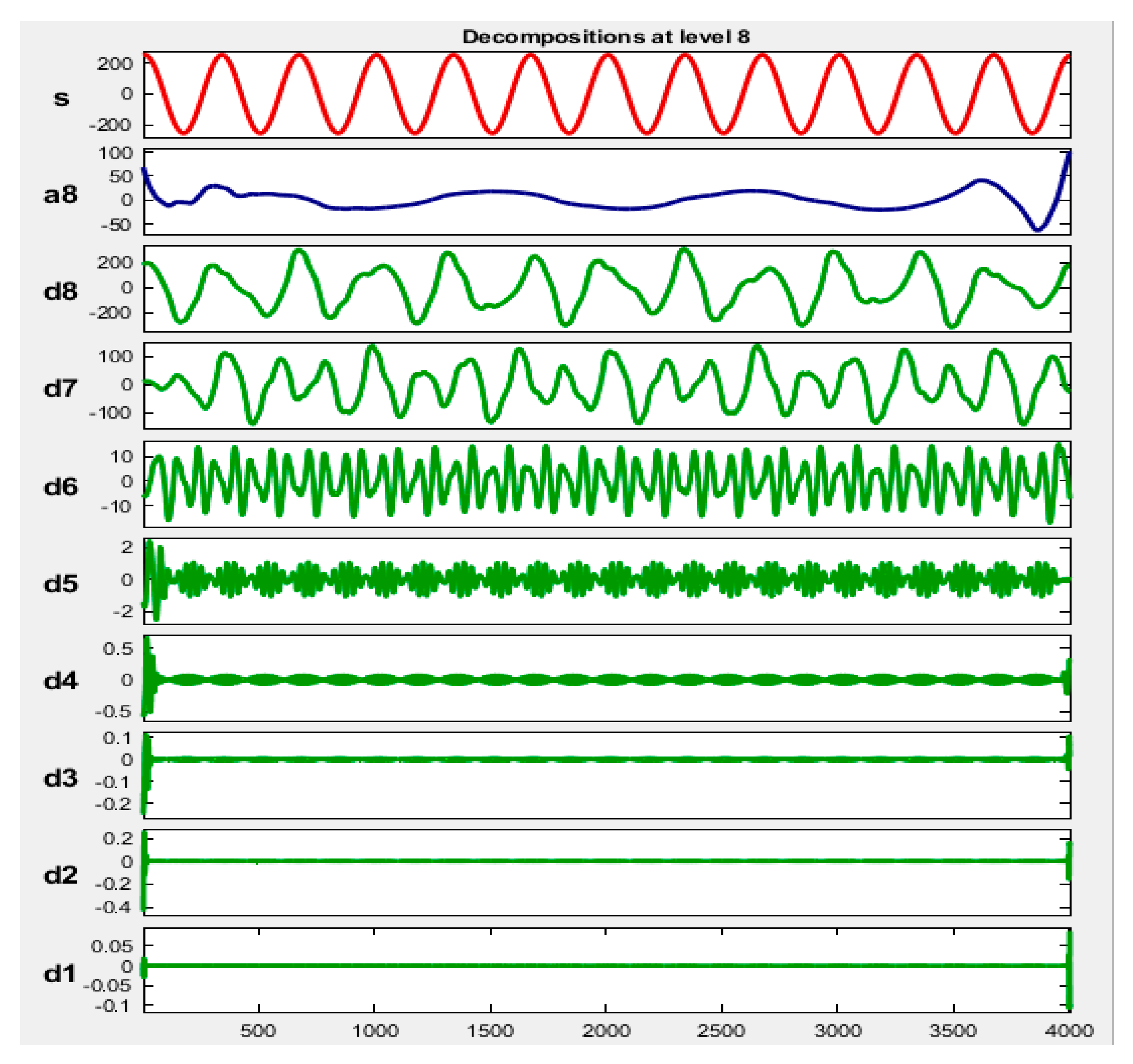
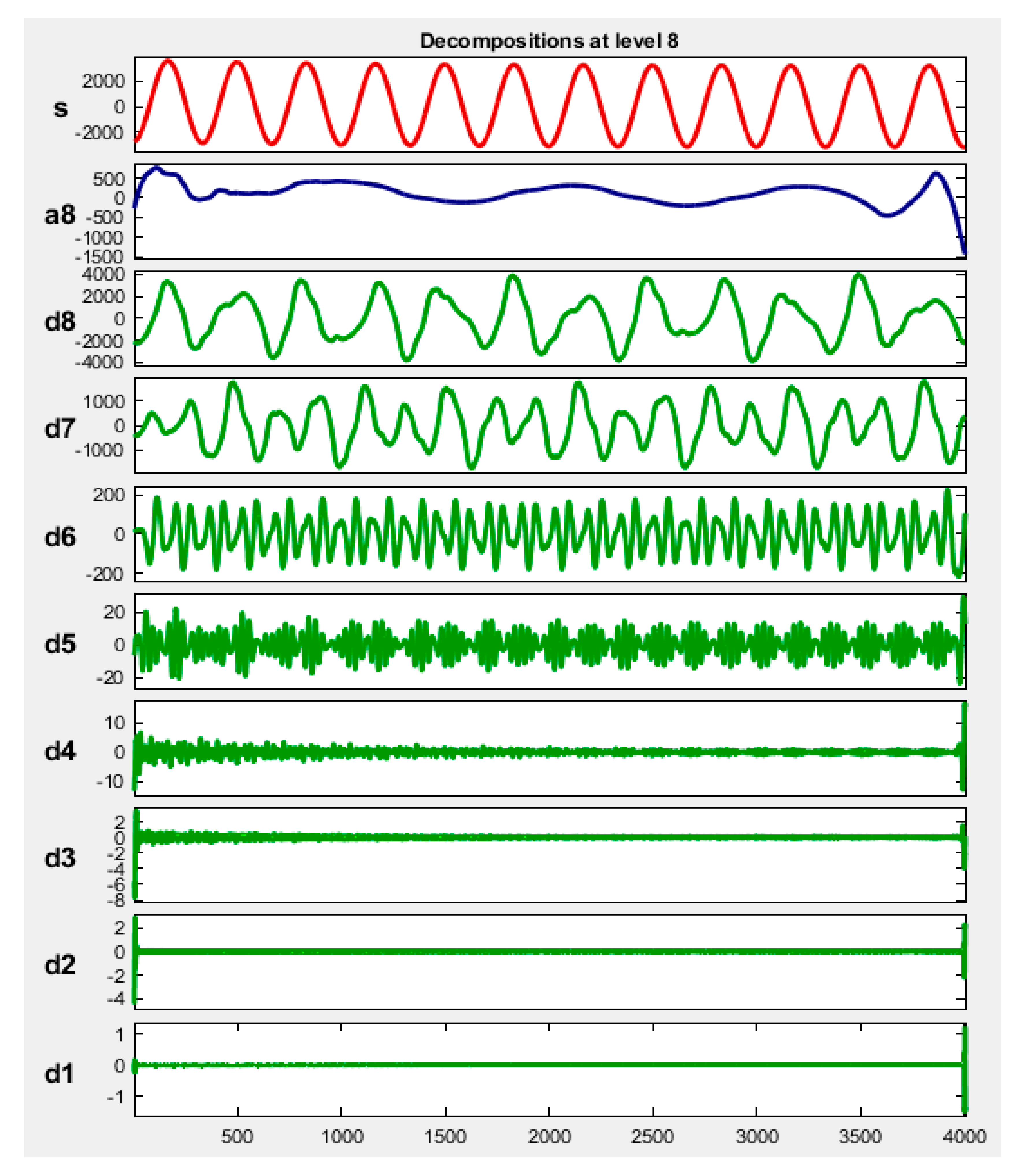
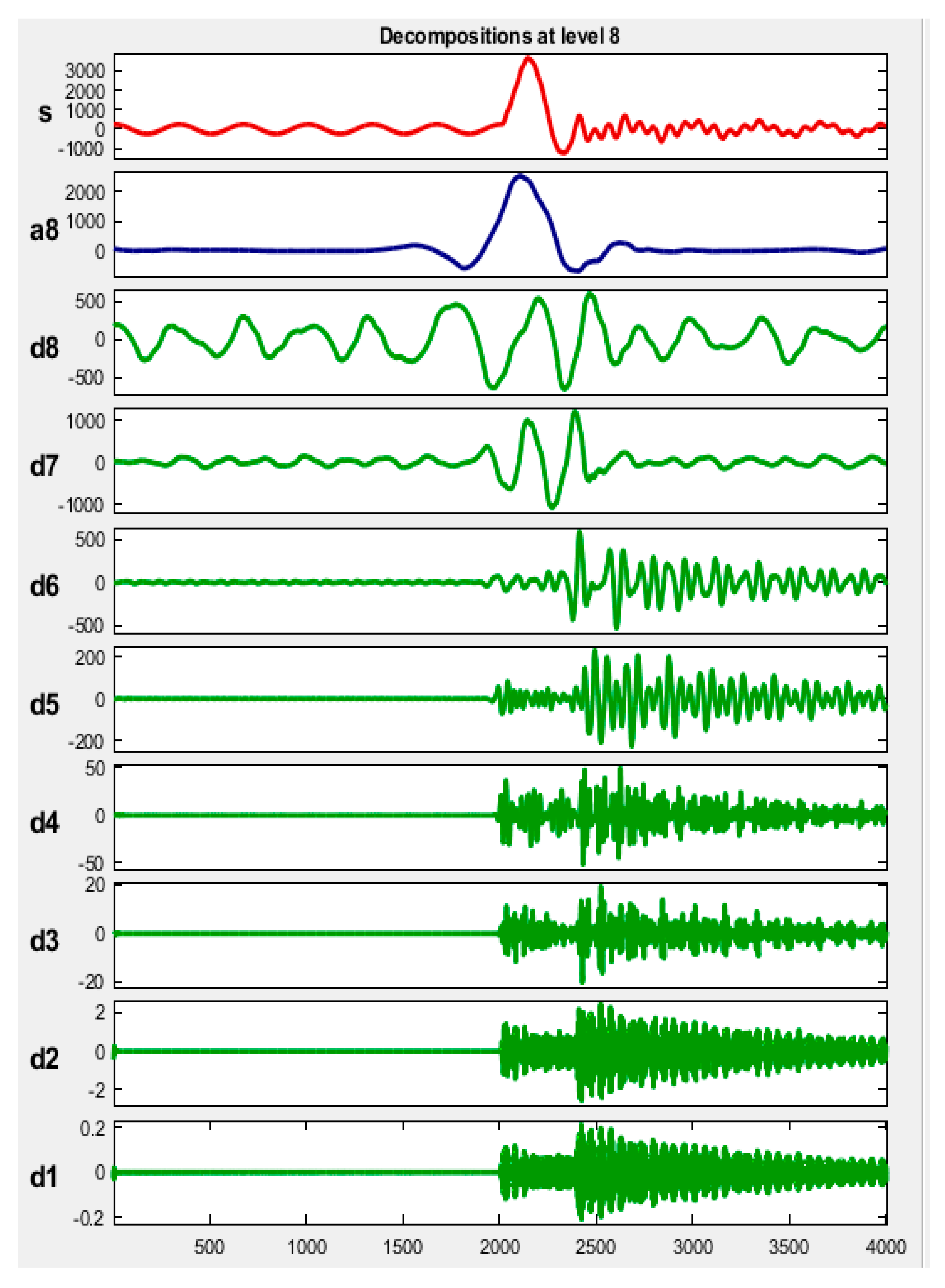
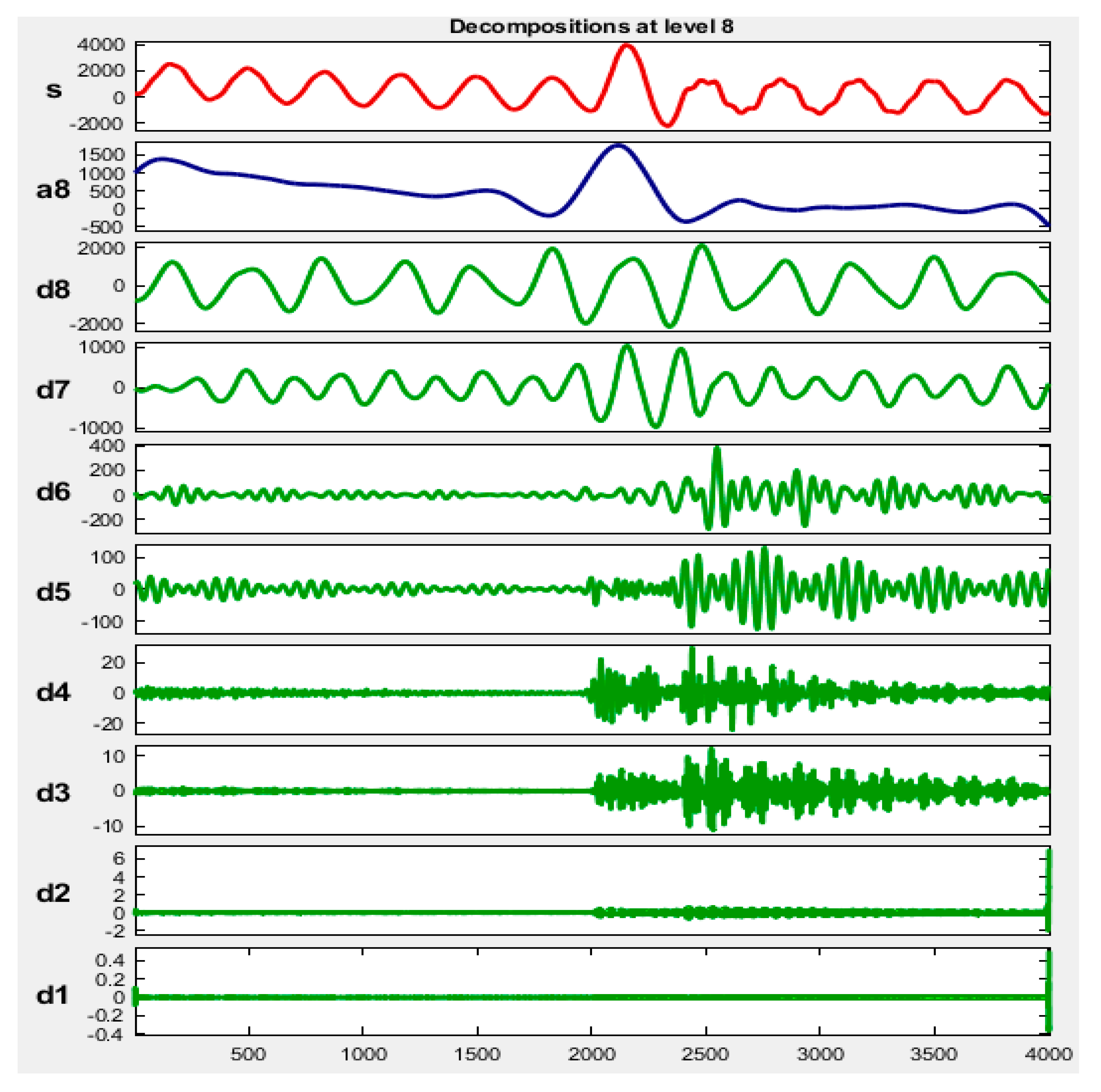
| Detailed Coefficient Levels | Frequency Band in kHz |
|---|---|
| D1 | 20 to 10 |
| D2 | 10 to 5 |
| D3 | 5 to 2.5 |
| D4 | 2.5 to 1.25 |
| D5 | 1.25 to 0.625 |
| D6 | 0.625 to 0.3125 |
| D7 | 0.3125 to 0.15625 |
| D8 | 0.15625 to 0.0781 |
| Cases | Normal | LG | LLG | LL | LLLG | |
|---|---|---|---|---|---|---|
| Without STATCOM | SDA | 0.33 | 0.89 | 0.5 | 0.49 | 0.34 |
| SDB | 0.33 | 0.05 | 0.48 | 0.49 | 0.35 | |
| SDC | 0.33 | 0.06 | 0.02 | 0.02 | 0.31 | |
| E-A | 0.58 | 0.08 | 0.01 | 0.01 | 0.43 | |
| E-B | 0.23 | 0.89 | 0.5 | 0.51 | 0.24 | |
| E-C | 0.19 | 0.02 | 0.49 | 0.48 | 0.33 | |
| With STATCOM | SDA | 0.33 | 0.22 | 0.12 | 0.13 | 0.34 |
| SDB | 0.34 | 0.56 | 0.46 | 0.44 | 0.34 | |
| SDC | 0.33 | 0.22 | 0.42 | 0.43 | 0.32 | |
| E-A | 0.54 | 0.39 | 0.03 | 0 | 0.43 | |
| E-B | 0.15 | 0.42 | 0.08 | 0.44 | 0.24 | |
| E-C | 0.31 | 0.19 | 0.89 | 0.56 | 0.32 | |
| Without STATCOM | |||||||
|---|---|---|---|---|---|---|---|
| Fault Distance | Type of Fault | Minimum Current | Maximum Current | ||||
| Ia kA | I b kA | I c kA | Ia kA | I b kA | I c kA | ||
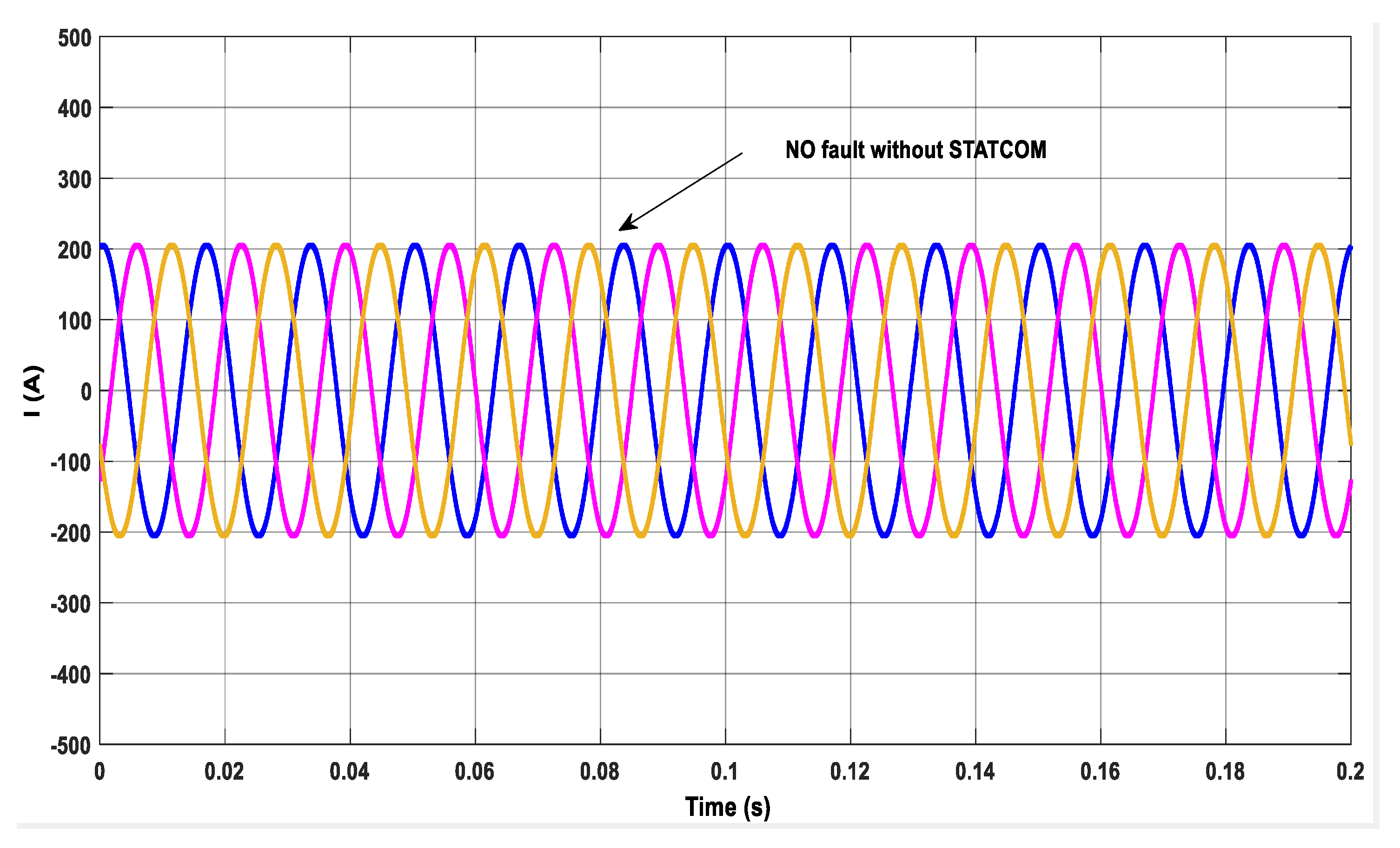
| No fault | −0.205 | −0.205 | −0.205 | 0.205 | 0.205 | 0.205 | |
| 100 km | LG | −2.57 | −0.34 | −0.46 | 6.95 | 0.28 | 0.25 |
| LL | −4.11 | −12.5 | −0.25 | 12.6 | 4.05 | 0.25 | |
| LLG | −4.19 | −12.0 | −0.71 | 1.34 | 4.3 | 0.65 | |
| LLLG | −3.88 | −12.0 | −12.4 | 1.52 | 6.76 | 4.3 | |
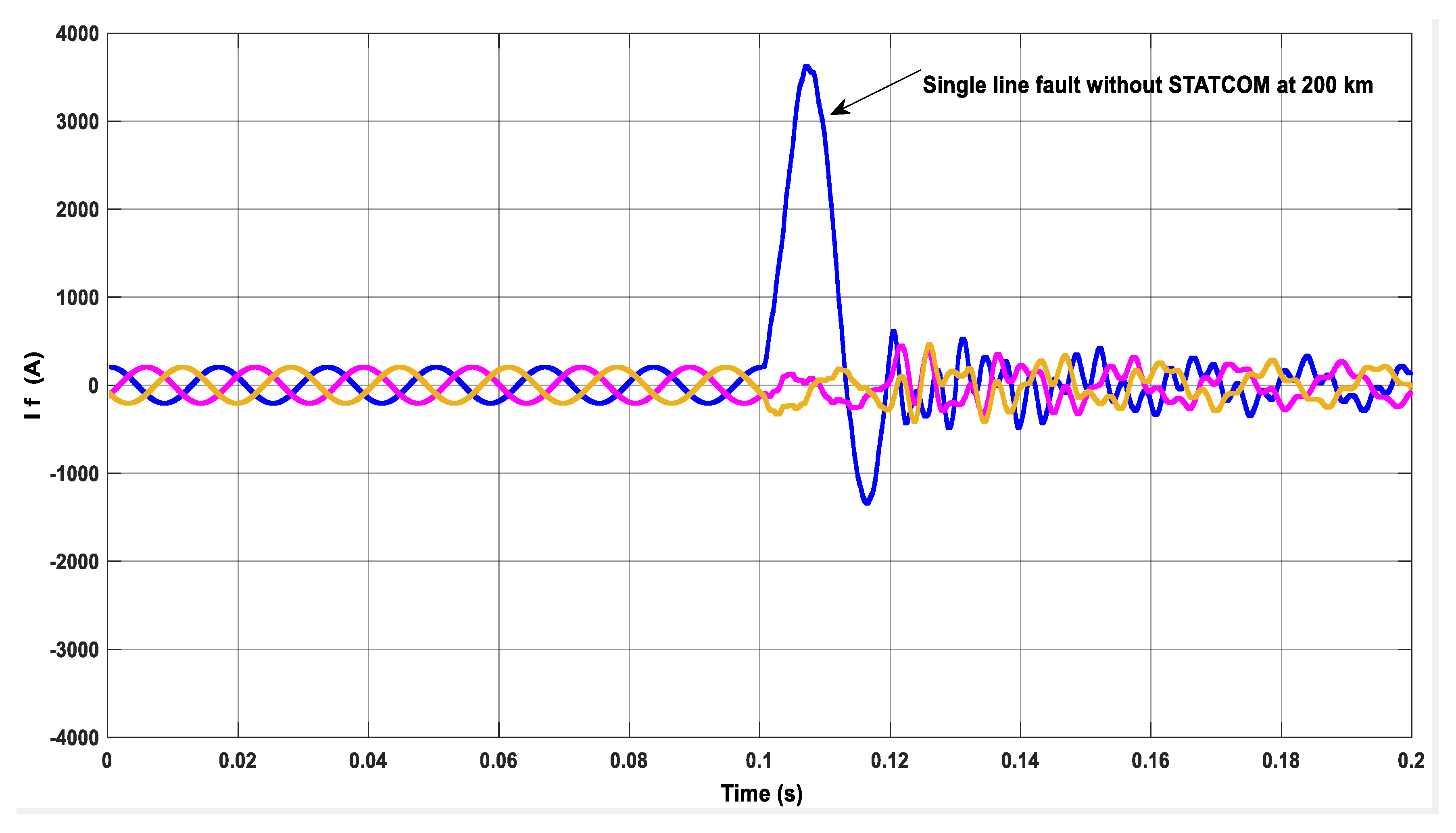
| 200 km | LG | −1.23 | −0.27 | −0.39 | 3.67 | 0.19 | 0.18 |
| LL | −2.19 | −7.01 | −0.25 | 7.06 | 2.16 | 0.25 | |
| LLG | −2.1 | −6.78 | −0.45 | 7.56 | 2.34 | 0.38 | |
| LLLG | −1.97 | −7.06 | −7.16 | 8.32 | 3.78 | 2.82 | |
| 300 km | LG | −0.78 | −0.294 | −0.37 | 2.49 | 0.185 | 0.19 |
| LL | −1.56 | −4.78 | −0.25 | 4.93 | 1.47 | 0.25 | |
| LLG | −1.51 | −4.85 | −0.51 | 5.08 | 1.62 | 0.37 | |
| LLLG | −1.31 | −5.17 | −4.97 | 5.72 | 2.62 | 2.16 | |
| Fault Distance | Type of Fault | With STATCOM | |||||
|---|---|---|---|---|---|---|---|
| Minimum Current | Maximum Current | ||||||
| I a kA | I b kA | I c kA | I a kA | I b kA | I c kA | ||
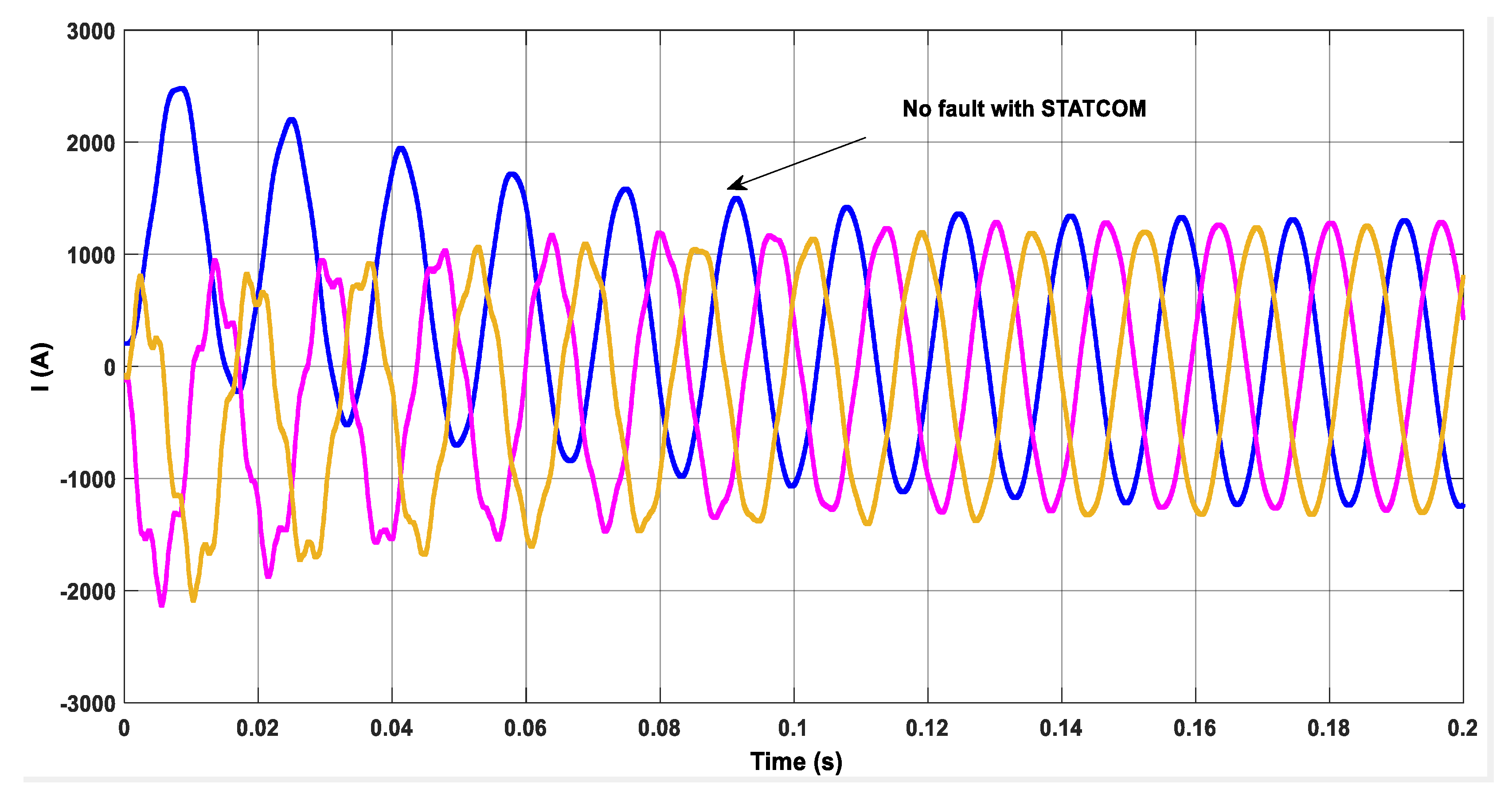
| No f | −1.22 | −2.07 | −2.08 | 2.51 | 1.26 | 1.21 | |
| 100 km | LG | −3.36 | −1.04 | 1.17 | 6.95 | 1.23 | 0.8 |
| LL | −4.57 | −11.7 | −1.24 | 11.8 | 4.58 | 1.07 | |
| LLG | −4.74 | −11.4 | −1.3 | 1.26 | 4.82 | 1.18 | |
| LLLG | −4.57 | −11.5 | −1.1.9 | 1.43 | 7.02 | 4.91 | |
| 200 km | LG | −2.20 | −1.12 | −1.23 | 3.97 | 1.23 | 1.08 |
| LL | −2.80 | −6.3 | −1.25 | 6.38 | 2.71 | 1.07 | |
| LLG | −2.85 | −6.25 | −1.36 | 6.76 | 2.99 | 1.09 | |
| LLLG | −2.72 | −6.47 | −6.46 | 4.49 | 4.06 | 3.3 | |
| 300 km | LG | −1.85 | −1.19 | −1.28 | 3.18 | 1.22 | 0.84 |
| LL | −2.22 | −4.56 | −1.27 | 4.61 | 2.22 | 1.07 | |
| LLG | −2.33 | −4.61 | −1.38 | 4.88 | 2.41 | 1.17 | |
| LLLG | −2.22 | −4.84 | −4.79 | 5.32 | 3.24 | 2.68 | |
| Without STATCOM | With STATCOM | |||||||
|---|---|---|---|---|---|---|---|---|
| Condition | Type of Fault | Location km | SD-A (×103) | SD-B (×103) | SD-C (×103) | SD-A (×103) | SD-B (×103) | SD-C (×103) |
| Normal | No fault | 100 | 0.177 | 0.177 | 0.177 | 0.875 | 0.877 | 0.866 |
| 200 | 0.177 | 0.177 | 0.177 | 0.875 | 0.877 | 0.866 | ||
| 300 | 0.177 | 0.177 | 0.0177 | 0.875 | 0.877 | 0.866 | ||
| LG | AG | 100 | 3.087 | 0.166 | 0.204 | 3.394 | 0.8 | 0.797 |
| 200 | 1.582 | 0.154 | 0.196 | 2.046 | 0.825 | 0.817 | ||
| 300 | 1.058 | 0.145 | 0.19 | 1.674 | 0.851 | 0.835 | ||
| BG | 100 | 0.3 | 3.17 | 0.267 | 0.793 | 3.49 | 0.835 | |
| 200 | 0.245 | 1.63 | 0.198 | 0.821 | 2.11 | 0.836 | ||
| 300 | 0.238 | 1.1 | 0.196 | 0.838 | 1.72 | 0.859 | ||
| CG | 100 | 0.263 | 0.299 | 2.66 | 0.854 | 0.811 | 3.305 | |
| 200 | 0.193 | 0.243 | 1.37 | 0.852 | 0.831 | 1.888 | ||
| 300 | 0.193 | 0.238 | 0.921 | 0.874 | 0.849 | 1.569 | ||
| LLG | ABG | 100 | 5.865 | 5.65 | 2.82 | 5.81 | 5.69 | 0.766 |
| 200 | 3.158 | 3.03 | 2.06 | 3.188 | 3.14 | 0.803 | ||
| 300 | 2.14 | 2.15 | 2.05 | 2.357 | 2.33 | 0.832 | ||
| BCG | 100 | 0.188 | 5.65 | 4.99 | 0.755 | 5.67 | 5.12 | |
| 200 | 0.17 | 3.06 | 2.71 | 0.799 | 3.14 | 2.87 | ||
| 300 | 0.161 | 2.09 | 1.84 | 0.834 | 2.35 | 2.16 | ||
| CAG | 100 | 5.108 | 0.287 | 5.15 | 5.247 | 0.759 | 5.21 | |
| 200 | 2.749 | 0.203 | 2.79 | 2.932 | 0.794 | 2.9 | ||
| 300 | 1.842 | 0.202 | 1.87 | 2.202 | 0.833 | 2.17 | ||
| LL | AB | 100 | 5.723 | 5.67 | 0.177 | 5.633 | 5.67 | 0.838 |
| 200 | 3.097 | 3.04 | 0.177 | 3.085 | 3.11 | 0.842 | ||
| 300 | 2.105 | 2.05 | 0.177 | 2.279 | 2.3 | 0.849 | ||
| BC | 100 | 0.177 | 5.255 | 5.691 | 0.851 | 5.281 | 5.245 | |
| 200 | 0.177 | 2.868 | 2.832 | 0.856 | 2.944 | 2.905 | ||
| 300 | 0.177 | 1.964 | 1.929 | 0.86 | 2.204 | 2.164 | ||
| CA | 100 | 4.998 | 0.177 | 5.06 | 5.112 | 0.846 | 5.04 | |
| 200 | 2.693 | 0.177 | 2.75 | 2.85 | 0.852 | 2.8 | ||
| 300 | 1.8 | 0.177 | 1.86 | 2.131 | 0.858 | 2.09 | ||
| LLLG | ABCG | 100 | 6.254 | 6.48 | 5.69 | 6.224 | 6.43 | 5.75 |
| 200 | 3.368 | 3.51 | 3.1 | 3.397 | 3.37 | 3.19 | ||
| 300 | 2.263 | 2.39 | 2.1 | 2.493 | 2.58 | 2.36 | ||
| Without STATCOM | With STATCOM | |||||||
|---|---|---|---|---|---|---|---|---|
| Condition | Type of fault | Location km | E-A (×108) | E-B (×108) | E-C (×108) | E-A (×108) | E-B (×108) | E-C (×108) |
| Normal | No fault | 100 | 1.25 | 0.49 | 0.4 | 22.7 | 6.26 | 13.1 |
| 200 | 1.25 | 0.49 | 0.4 | 22.7 | 6.26 | 13.1 | ||
| 300 | 1.25 | 0.49 | 0.4 | 22.7 | 6.26 | 13.1 | ||
| LG | AG | 100 | 96.4 | 0.56 | 0.51 | 128 | 5.36 | 11.4 |
| 200 | 25.9 | 0.56 | 0.51 | 56.5 | 5.62 | 12.1 | ||
| 300 | 12 | 0.51 | 0.46 | 42.7 | 5.85 | 12.3 | ||
| BG | 100 | 1.64 | 57.1 | 0.51 | 21.3 | 70.7 | 13.2 | |
| 200 | 1.44 | 15.3 | 0.41 | 25.8 | 27.5 | 12.3 | ||
| 300 | 1.5 | 7.08 | 0.37 | 22.3 | 18.8 | 13 | ||
| CG | 100 | 1.39 | 0.76 | 72.9 | 21.7 | 5.74 | 97.1 | |
| 200 | 1.33 | 0.6 | 18.8 | 21.2 | 6.22 | 38.6 | ||
| 300 | 1.18 | 0.63 | 8.47 | 22.1 | 6.11 | 28.8 | ||
| LLG | ABG | 100 | 301 | 223 | 0.71 | 307 | 214 | 11.3 |
| 200 | 87.1 | 65 | 0.5 | 105 | 64 | 12.8 | ||
| 300 | 41.8 | 30.4 | 0.45 | 63.8 | 34.3 | 13.6 | ||
| BCG | 100 | 1.36 | 184 | 179 | 20.8 | 185 | 200 | |
| 200 | 1.2 | 54.6 | 53.4 | 21.3 | 58.1 | 67 | ||
| 300 | 1.18 | 25 | 22.7 | 22.1 | 32.8 | 44.4 | ||
| CAG | 100 | 318 | 0.73 | 313 | 326 | 5.17 | 305 | |
| 200 | 94.6 | 0.51 | 93 | 106 | 5.09 | 94.9 | ||
| 300 | 41.6 | 0.52 | 41.2 | 66.9 | 5.53 | 56.5 | ||
| LL | AB | 100 | 255 | 254 | 4.05 | 265 | 234 | 12.8 |
| 200 | 74.7 | 73.9 | 0.4 | 92.6 | 68.3 | 12.9 | ||
| 300 | 35.6 | 35 | 0.4 | 56.8 | 35.8 | 12.9 | ||
| BC | 100 | 1.24 | 174 | 169 | 22.4 | 170 | 186 | |
| 200 | 1.24 | 53 | 50.2 | 22.4 | 49.5 | 62.4 | ||
| 300 | 1.24 | 23.5 | 22.3 | 22.4 | 30.2 | 40.8 | ||
| CA | 100 | 308 | 0.5 | 312 | 314 | 5.8 | 300 | |
| 200 | 91.5 | 0.49 | 93.4 | 103 | 5.87 | 91.7 | ||
| 300 | 40.5 | 0.49 | 41.3 | 65.5 | 5.98 | 54.3 | ||
| LLLG | ABCG | 100 | 425 | 241 | 315 | 414 | 236 | 315 |
| 200 | 125 | 70.5 | 94.7 | 130 | 71.9 | 97 | ||
| 300 | 57.5 | 33.3 | 40.7 | 76.6 | 38.6 | 59.1 | ||
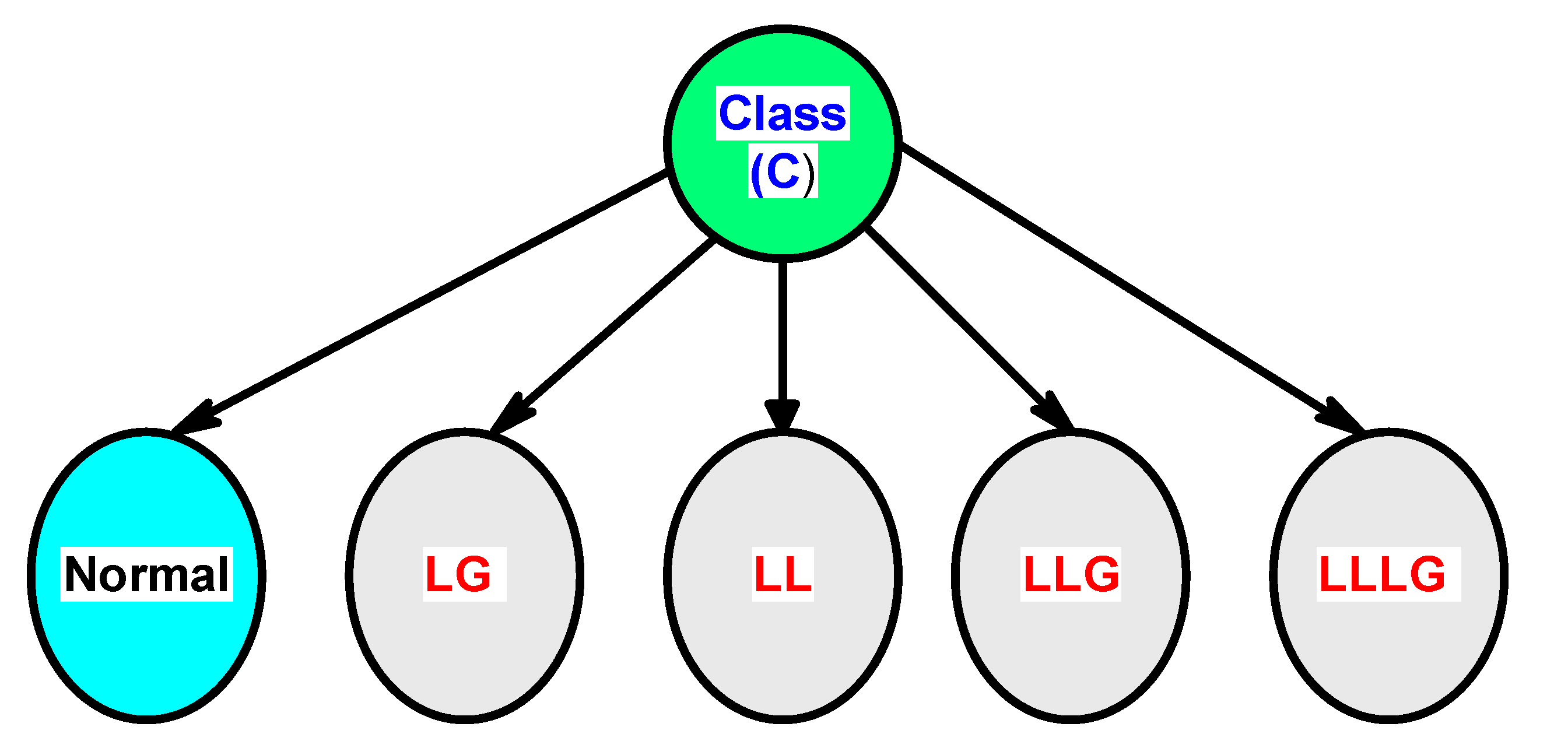
| Classes | C1 | C2 | C3 | C4 | C5 | System State |
|---|---|---|---|---|---|---|
| C1 | 1 | 0 | 0 | 0 | 0 | Normal |
| C2 | 0 | 1 | 0 | 0 | 0 | LG |
| C3 | 0 | 0 | 1 | 0 | 0 | LLG |
| C4 | 0 | 0 | 0 | 1 | 0 | LL |
| C5 | 0 | 0 | 0 | 0 | 1 | LLLG |
| Accuracy Rate | Misclassification Rate | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| MLP | Bayes | Naive Bayes | |||||||
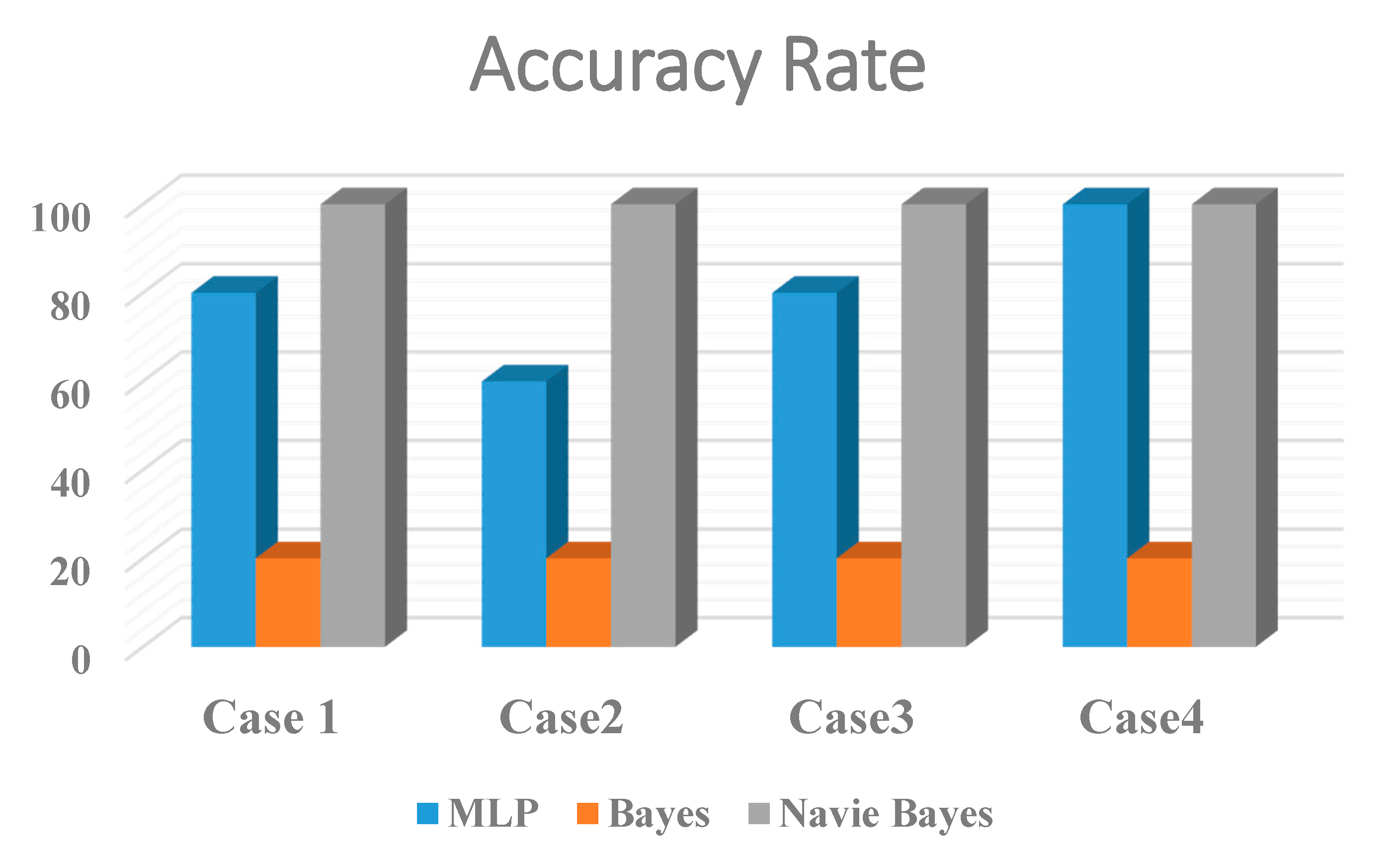
| Cases | MLP | Bayes | Naïve Bayes | % Rate | Type of Fault | Rate | Type of Fault | Rate | Type of Fault |
| Case-1 | 80 | 20 | 100 | 20 | C3 | 80 | C2-C5 | 0 | 0 |
| Case-2 | 60 | 20 | 100 | 40 | C2–C3 | 80 | C2-C5 | 0 | 0 |
| Case-3 | 80 | 20 | 100 | 20 | C3 | 80 | C2-C5 | 0 | 0 |
| Case-4 | 100 | 20 | 100 | 0 | 0 | 80 | C2-C5 | 0 | 0 |
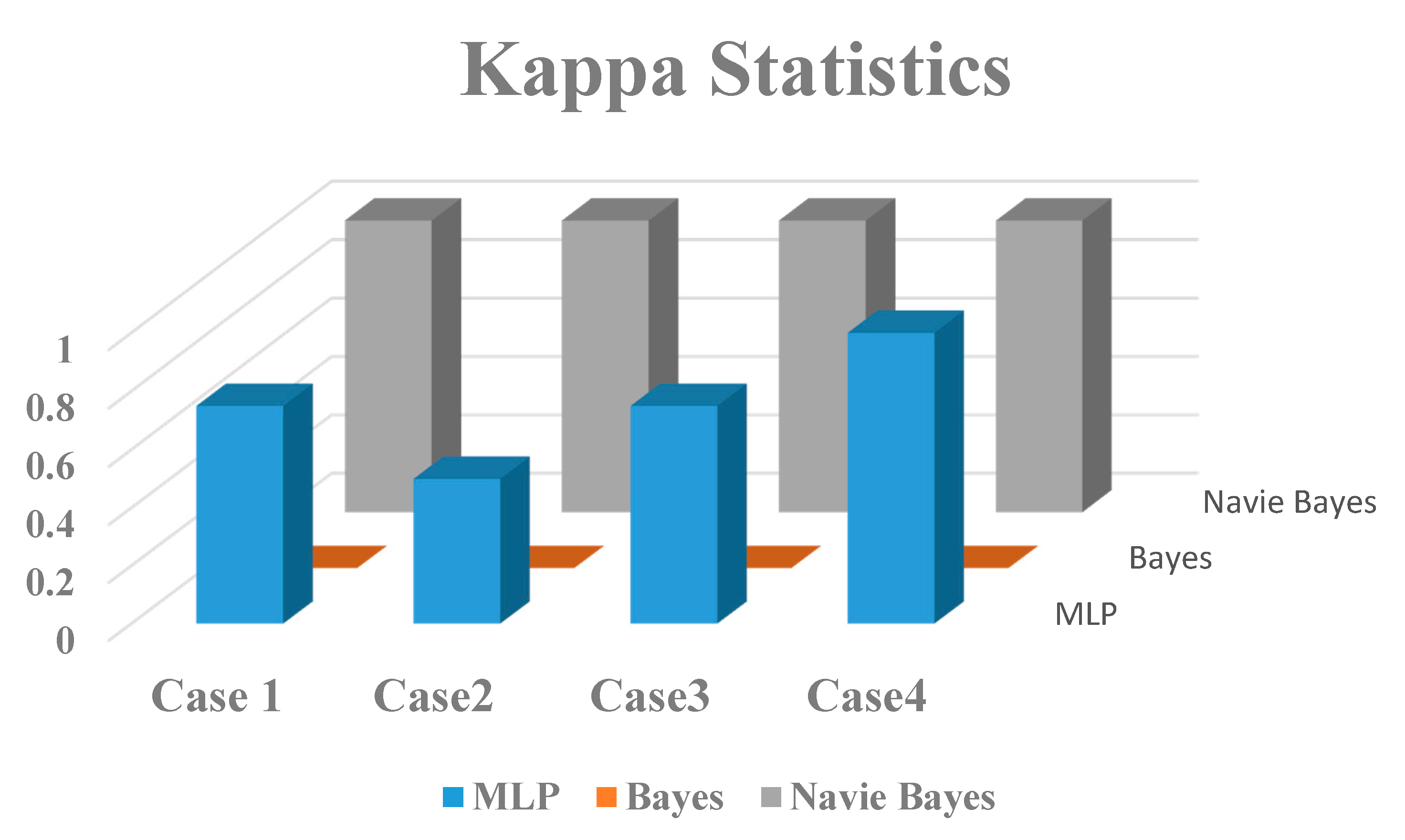
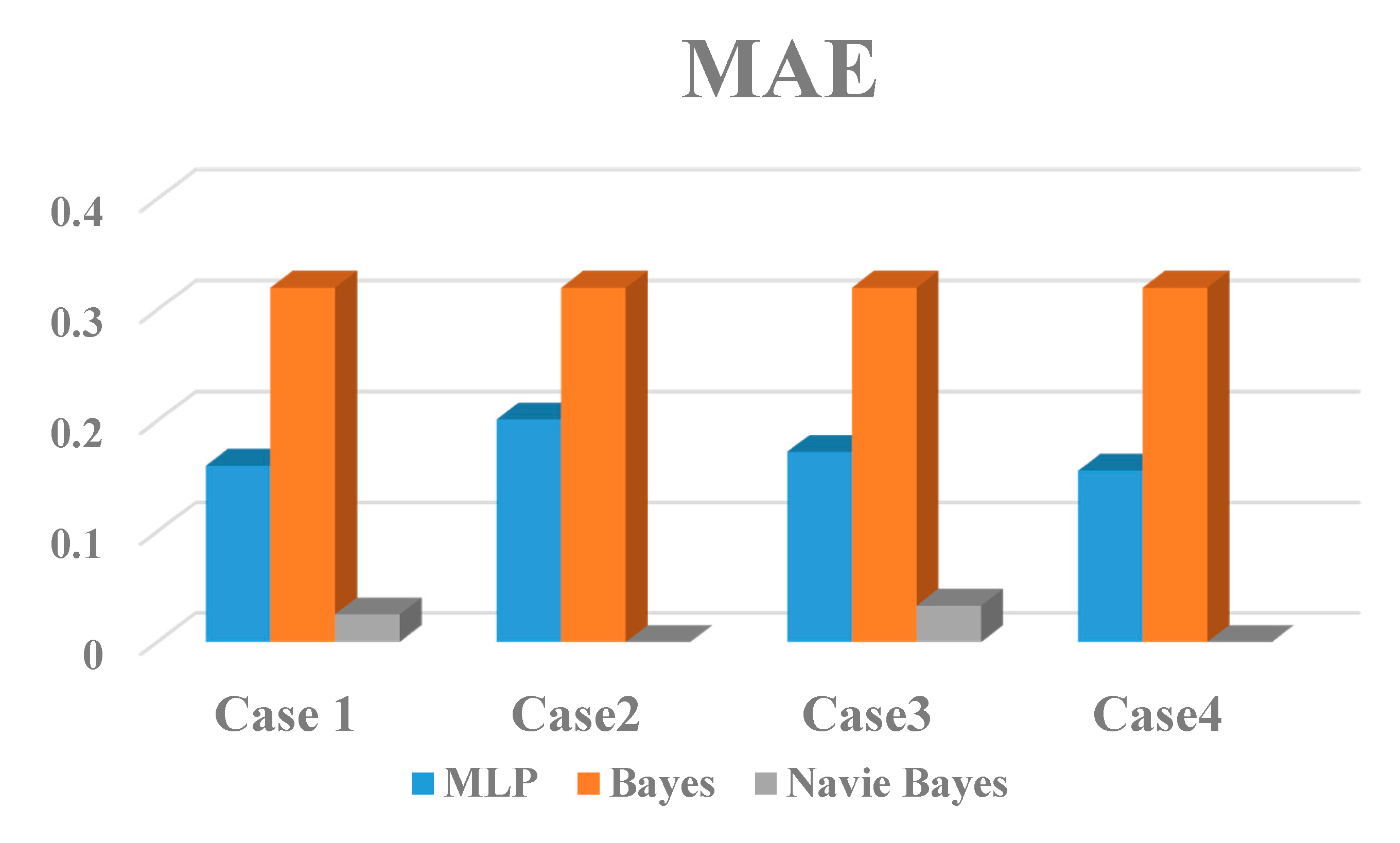
| Kappa Statistics | MAE | RMSE | |||||||
|---|---|---|---|---|---|---|---|---|---|
| MLP | Bayes | Naive Bayes | MLP | Bayes | Naive Bayes | MLP | Bayes | Naive Bayes | |
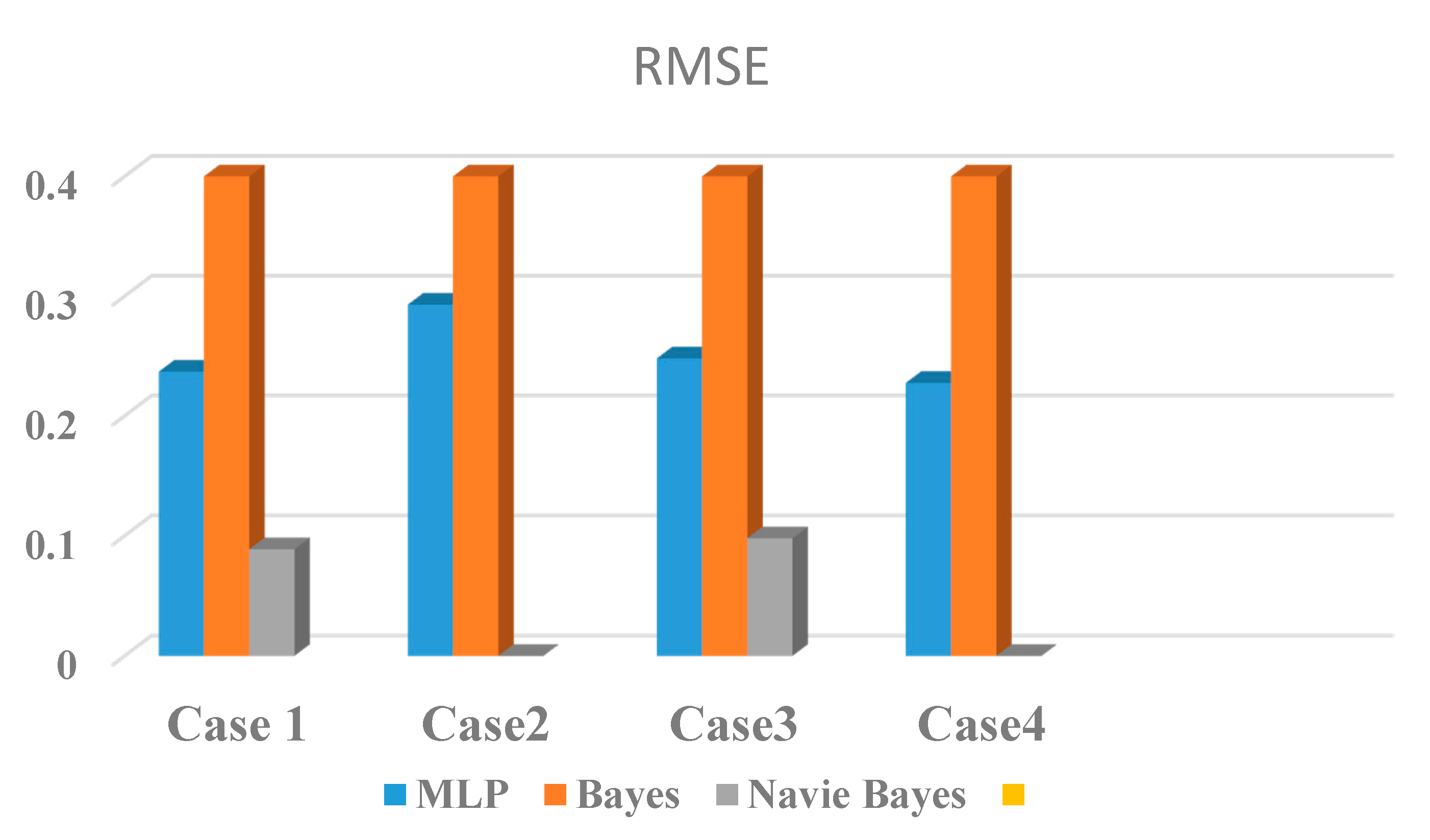
| Case-1 | 0.75 | 0 | 1 | 0.159 | 0.32 | 0.025 | 0.236 | 0.4 | 0.088 |
| Case-2 | 0.5 | 0 | 1 | 0.201 | 0.32 | 0 | 0.292 | 0.4 | 0 |
| Case-3 | 0.75 | 0 | 1 | 0.172 | 0.32 | 0.033 | 0.248 | 0.4 | 0.097 |
| Case-4 | 1 | 0 | 1 | 0.155 | 0.32 | 0 | 0.227 | 0.4 | 0 |
| Cases | %RAE | %RRSE | ||||
|---|---|---|---|---|---|---|
| MLP | Bayes | Naive Bayes | MLP | Bayes | Naive Bayes | |
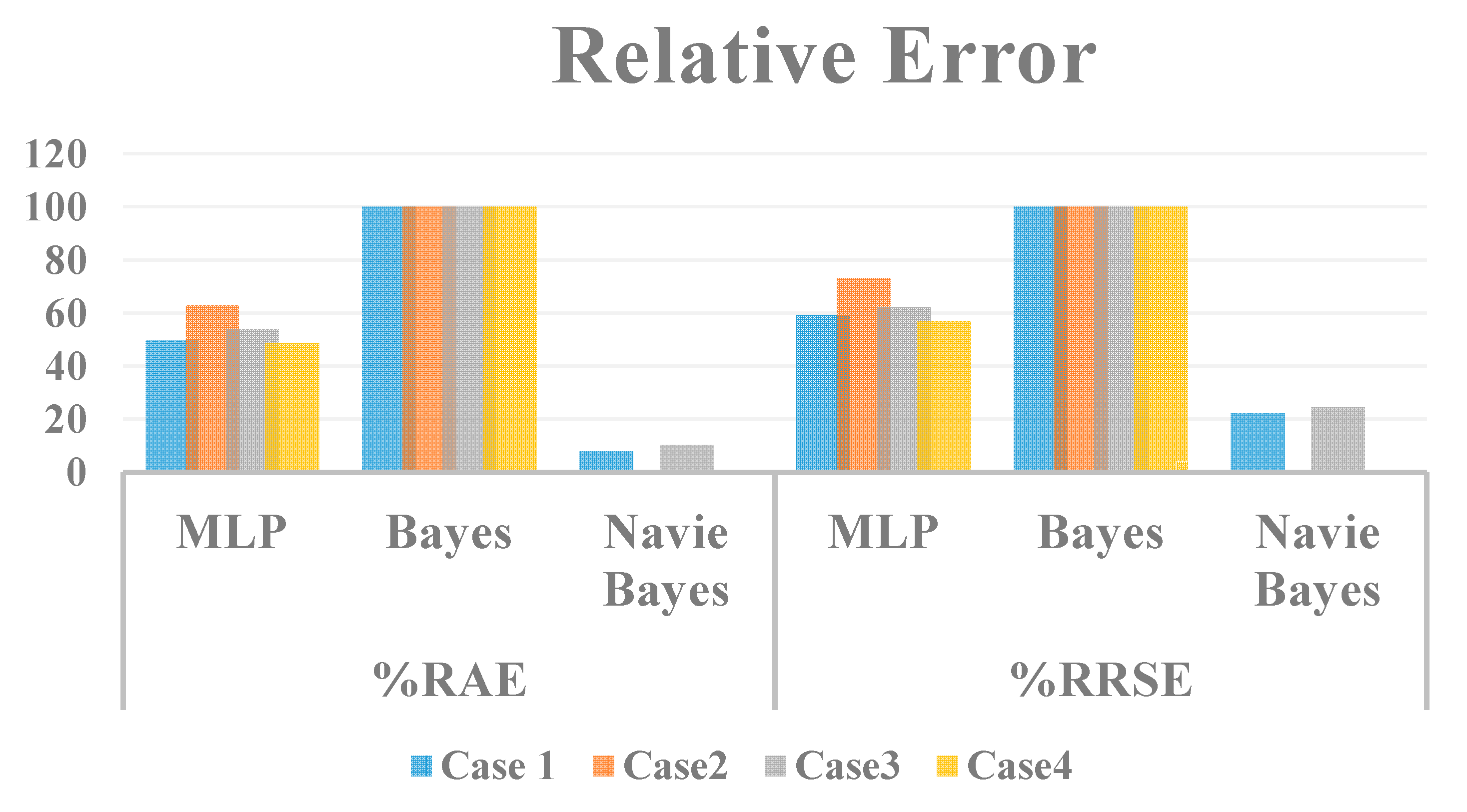
| Case-1 | 49.89 | 100 | 7.85 | 59.23 | 100 | 22.21 |
| Case-2 | 62.86 | 100 | 0 | 73.22 | 100 | 0 |
| Case-3 | 53.74 | 100 | 10.29 | 62 | 100 | 24.46 |
| Case-4 | 48.46 | 100 | 0 | 56.89 | 100 | 0 |
| Type of Fault Considered | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Authors | Methods | LG | LL | LLG | LLL | LLLG | Fault Resistance | STATCOM | %Accuracy |
| Singh. A.R [1] | Synchronized Measurements | √ | √ | √ | √ | √ | √ | √ | 99.6 |
| Ghazizadeh A. [3] | Synchronized Measurements | √ | √ | √ | × | √ | × | √ | 99.07 |
| Mishra. S.K [4] | DWT | √ | √ | √ | × | × | √ | √ | - |
| Gupta. O.H [8] | Superimposed sequence components-based integrated impedance (SSCII). | √ | √ | √ | √ | √ | √ | SVC | - |
| Albasri. F.A [10] | Impedance Measurements | √ | √ | × | √ | × | × | √ | - |
| Hussain. S [15] | Unsynchronized Measurements | √ | √ | × | √ | × | √ | √ | 99 |
| Proposed Work | DWT &NB | √ | √ | √ | × | √ | √ | √ | 100 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aker, E.; Othman, M.L.; Veerasamy, V.; Aris, I.b.; Wahab, N.I.A.; Hizam, H. Fault Detection and Classification of Shunt Compensated Transmission Line Using Discrete Wavelet Transform and Naive Bayes Classifier. Energies 2020, 13, 243. https://doi.org/10.3390/en13010243
Aker E, Othman ML, Veerasamy V, Aris Ib, Wahab NIA, Hizam H. Fault Detection and Classification of Shunt Compensated Transmission Line Using Discrete Wavelet Transform and Naive Bayes Classifier. Energies. 2020; 13(1):243. https://doi.org/10.3390/en13010243
Chicago/Turabian StyleAker, Elhadi, Mohammad Lutfi Othman, Veerapandiyan Veerasamy, Ishak bin Aris, Noor Izzri Abdul Wahab, and Hashim Hizam. 2020. "Fault Detection and Classification of Shunt Compensated Transmission Line Using Discrete Wavelet Transform and Naive Bayes Classifier" Energies 13, no. 1: 243. https://doi.org/10.3390/en13010243
APA StyleAker, E., Othman, M. L., Veerasamy, V., Aris, I. b., Wahab, N. I. A., & Hizam, H. (2020). Fault Detection and Classification of Shunt Compensated Transmission Line Using Discrete Wavelet Transform and Naive Bayes Classifier. Energies, 13(1), 243. https://doi.org/10.3390/en13010243






