New Intelligent Control Strategy Hybrid Grey–RCMAC Algorithm for Ocean Wave Power Generation Systems
Abstract
1. Introduction
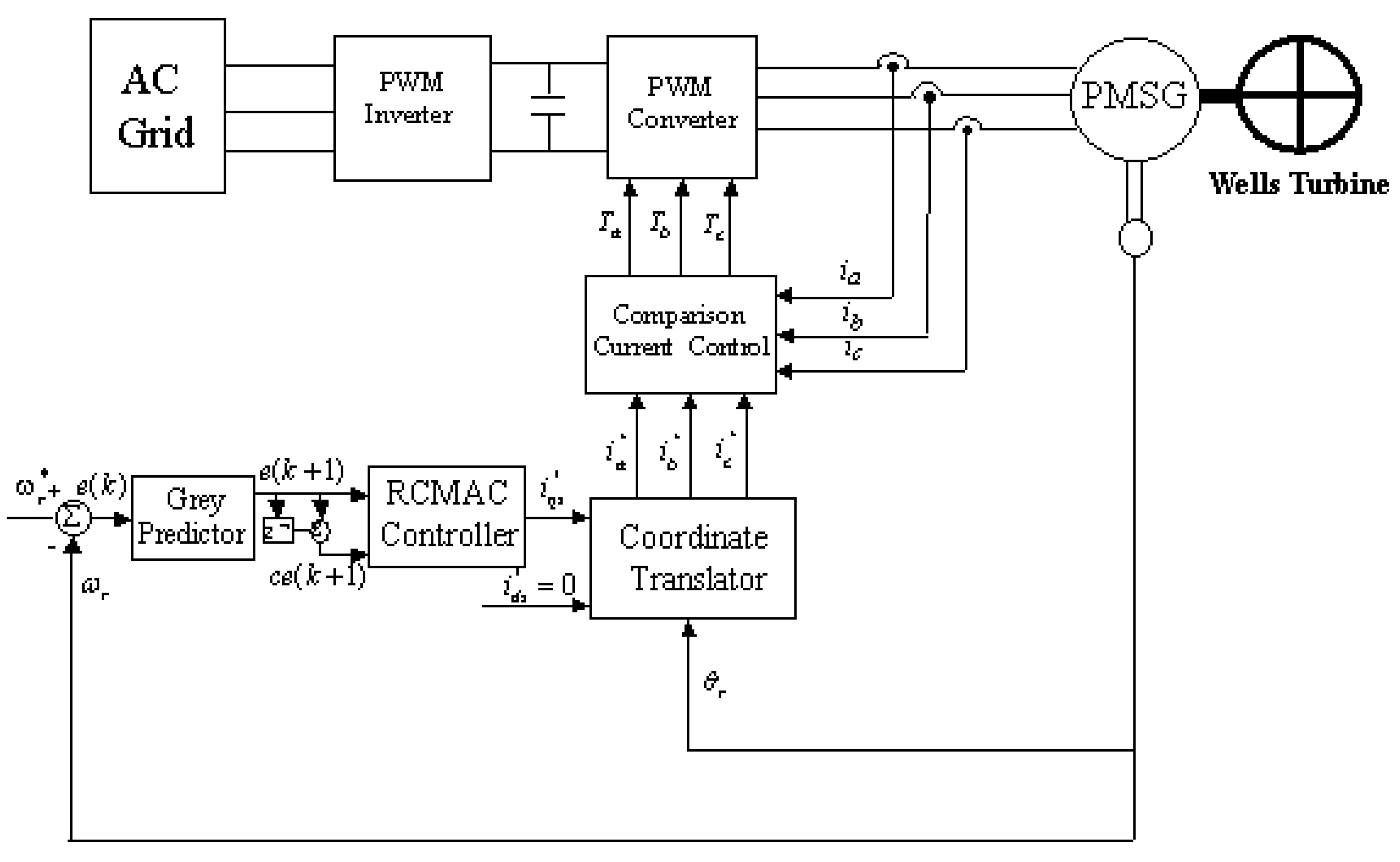
2. Modeling of the Studied System
2.1. Structure of the System
2.2. Wells Turbine Modeling
2.3. PMSG Modeling
- d, q axis stator voltages
- d, q axis stator currents
- d, q axis stator inductances
- d, q axis stator flux linkages
- stator resistance
- inverter frequency
- equivalent d-axis magnetizing current
- d-axis mutual inductance
3. Design of Maximum Power Point Tracking (MPPT) Controller Based on RCMAC with Grey Forecasting
3.1. The Online Grey Dynamic Prediction Model
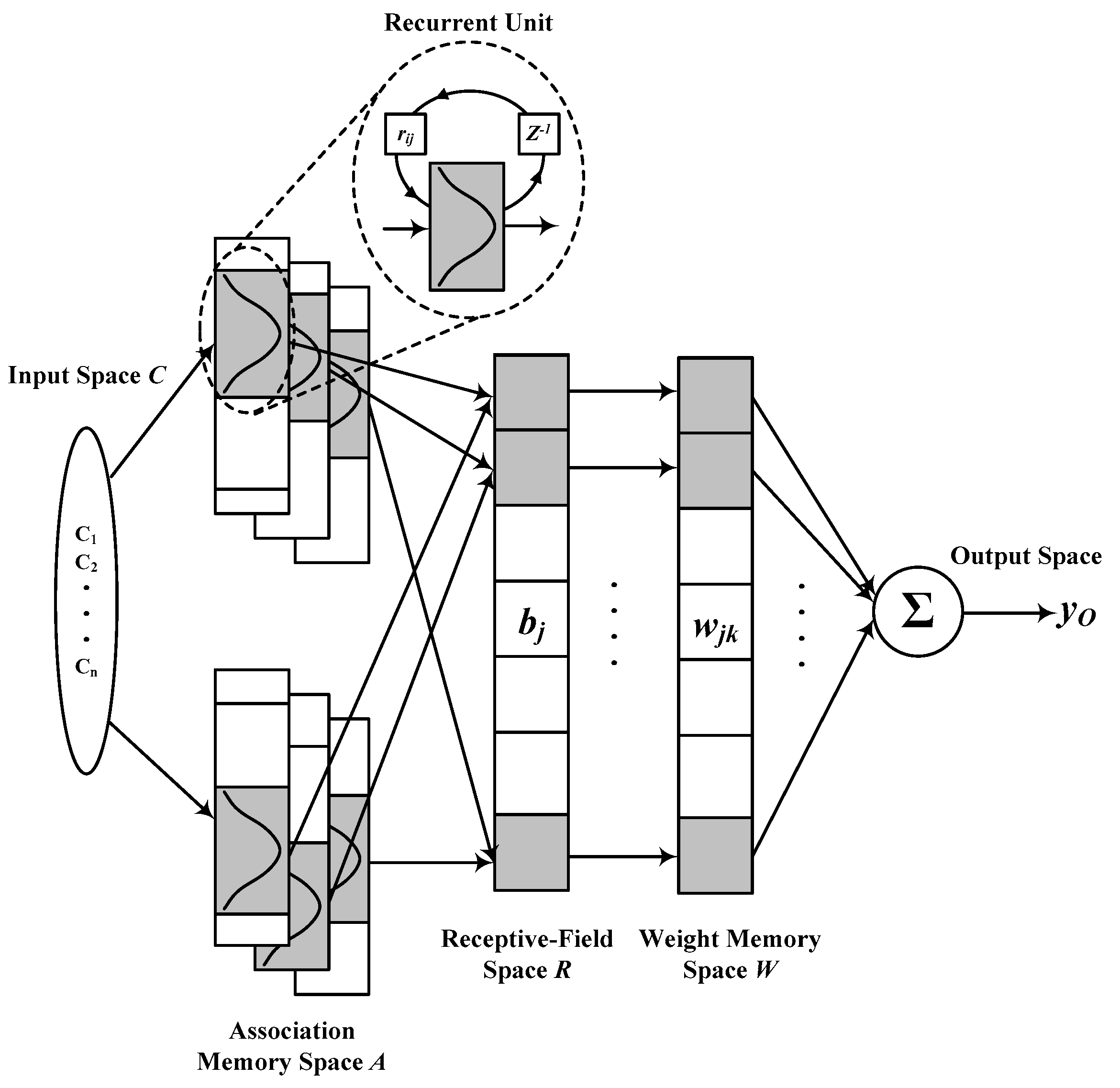
3.2. Recurrent CMAC Controller
3.2.1. RCMAC Structure
- Input Layer: For a given C = [, ], each input variable ci can be quantized into discrete reference states.
- Association Memory Layer: To effectively assign each input state in learning. Herein, the Gaussian function (receptive field basis function) is built into the hypercube block as Equation (14). In the bell-shaped manner of the Gaussian function, when the discontinuous input state is closer to the center of a certain cube, the output is more affected by the cube, and vice versa. The farther the impact is, the smaller it is.
- Receptive Field Layer: The multidimensional receptive field function is expressed as follows:
- Weight Memory Layer: This space specifies adjustable weights of the receptive field layer results as follows:
- Output Layer: The output of RCMAC mathematic form and also the control effort of the proposed controller is obtained as follows:
3.2.2. RCMAC Learning Algorithm
3.3. Adjust Learning Rates with IPSO
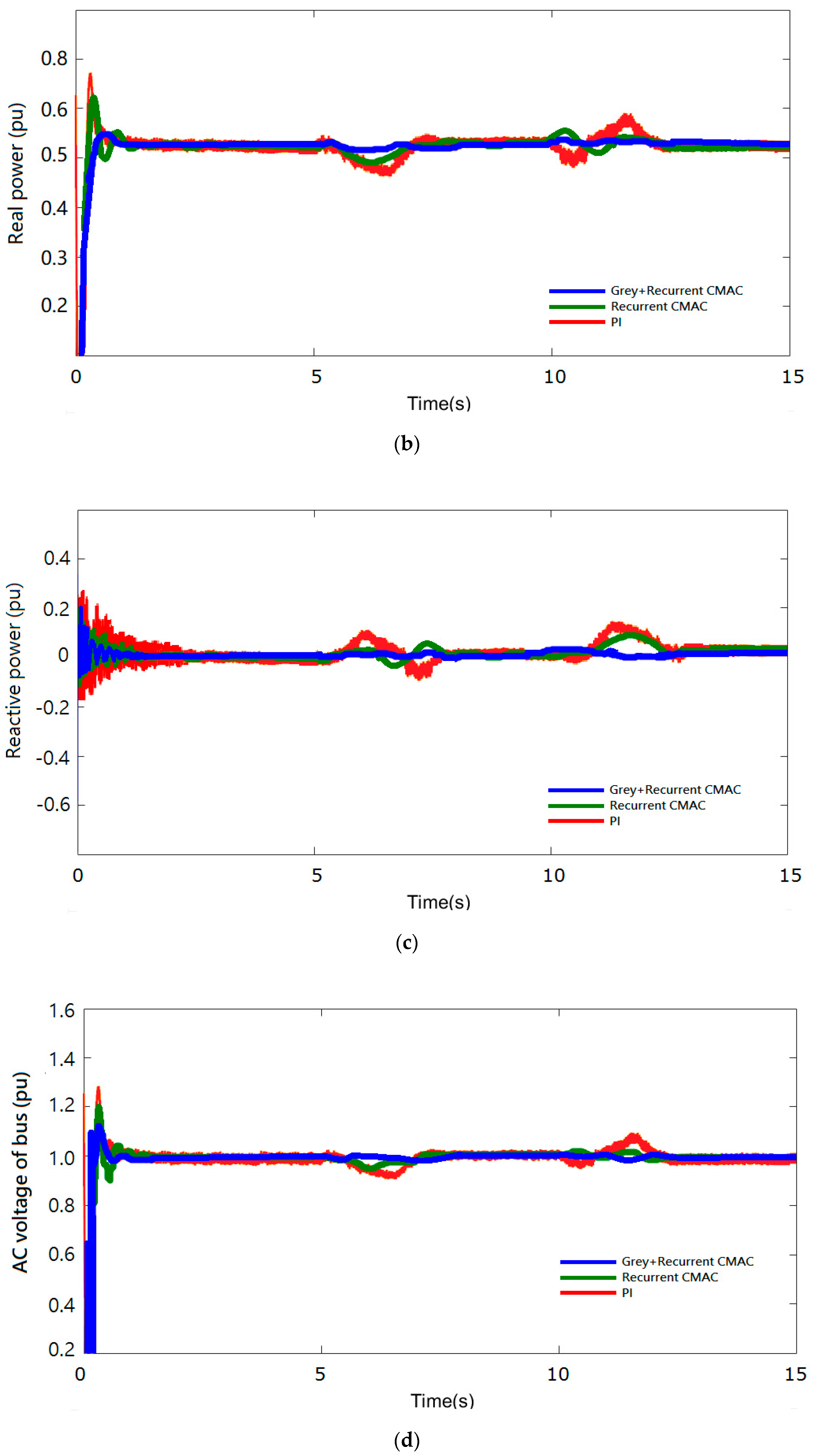
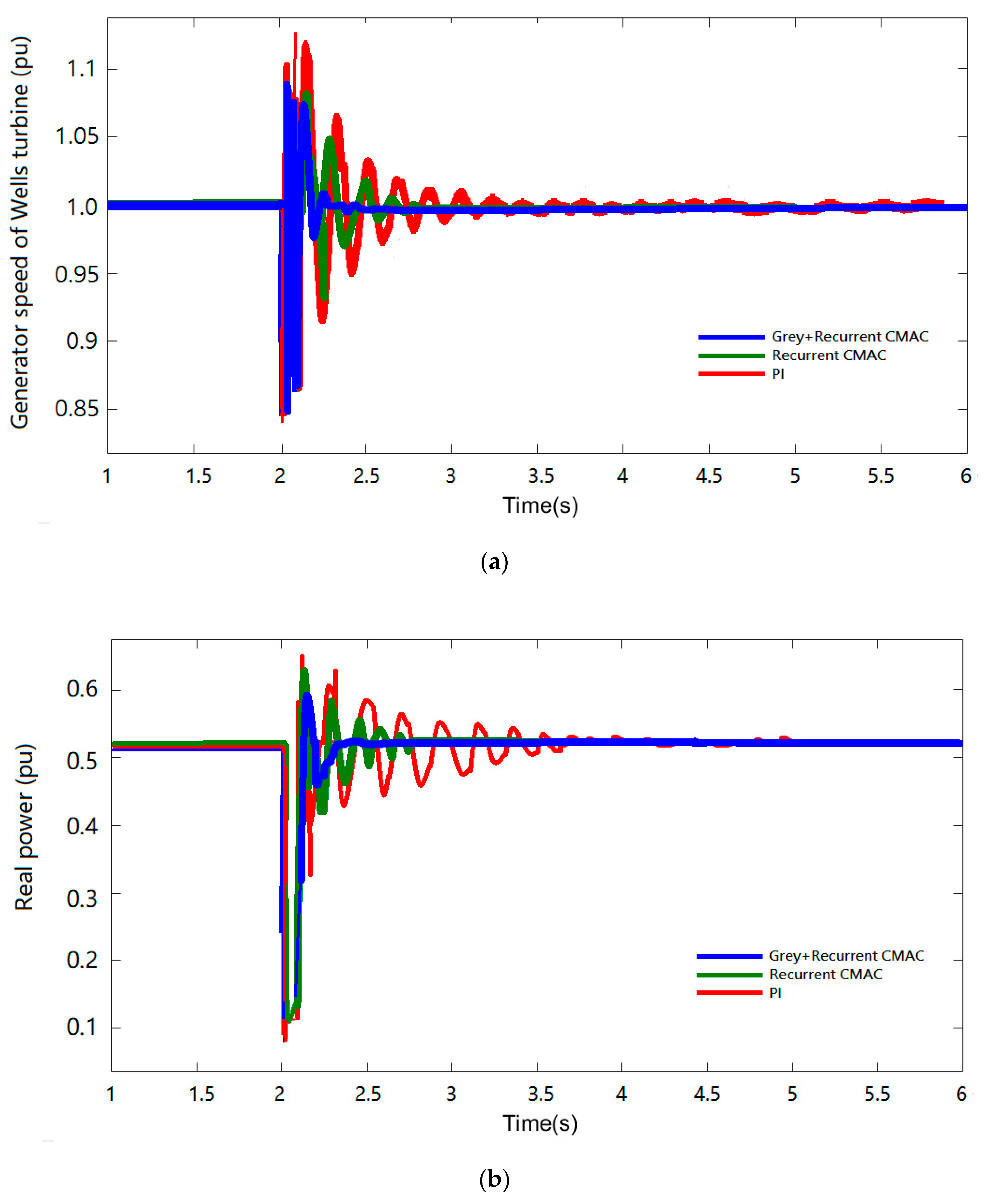
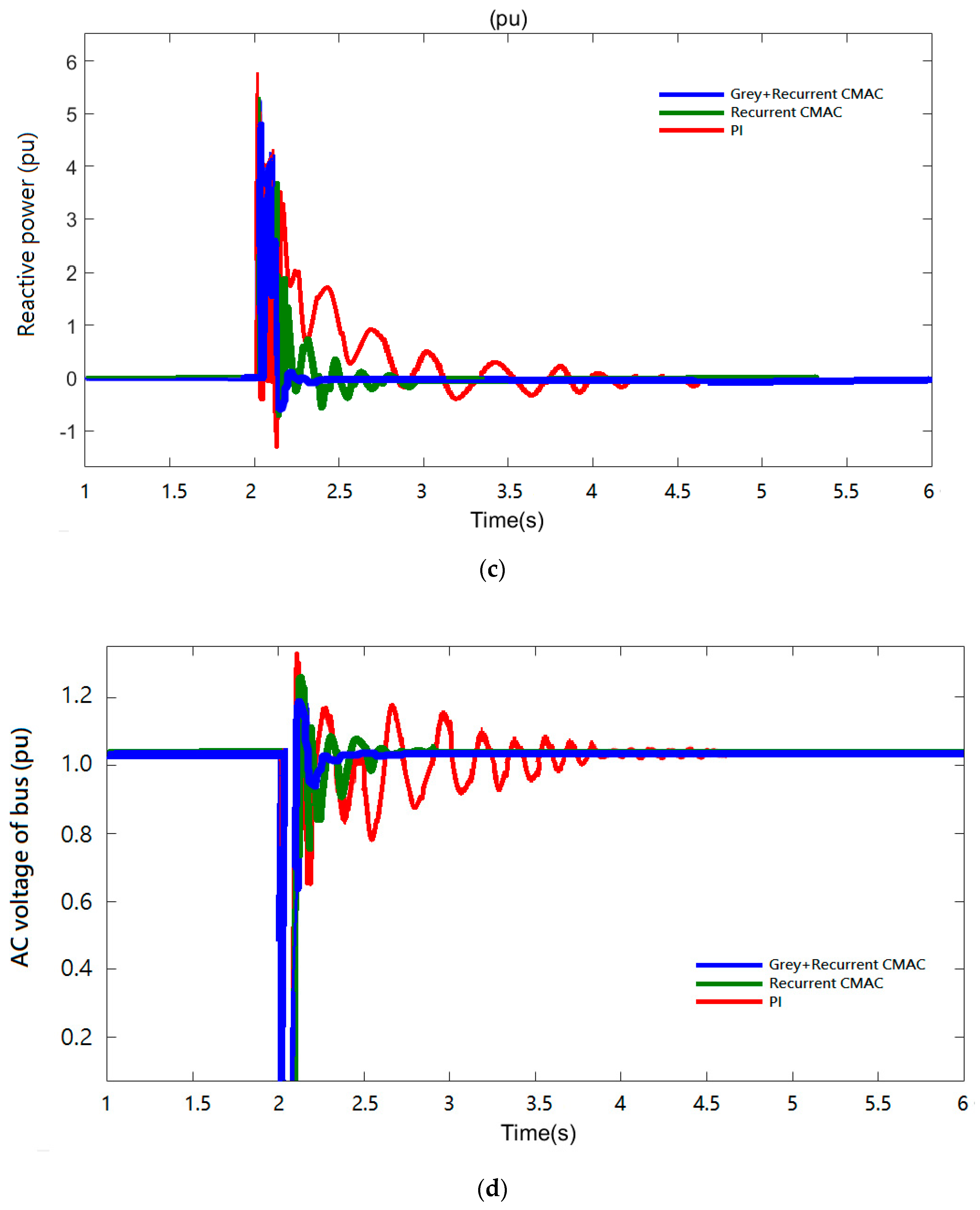
4. Simulation Results and Discussion
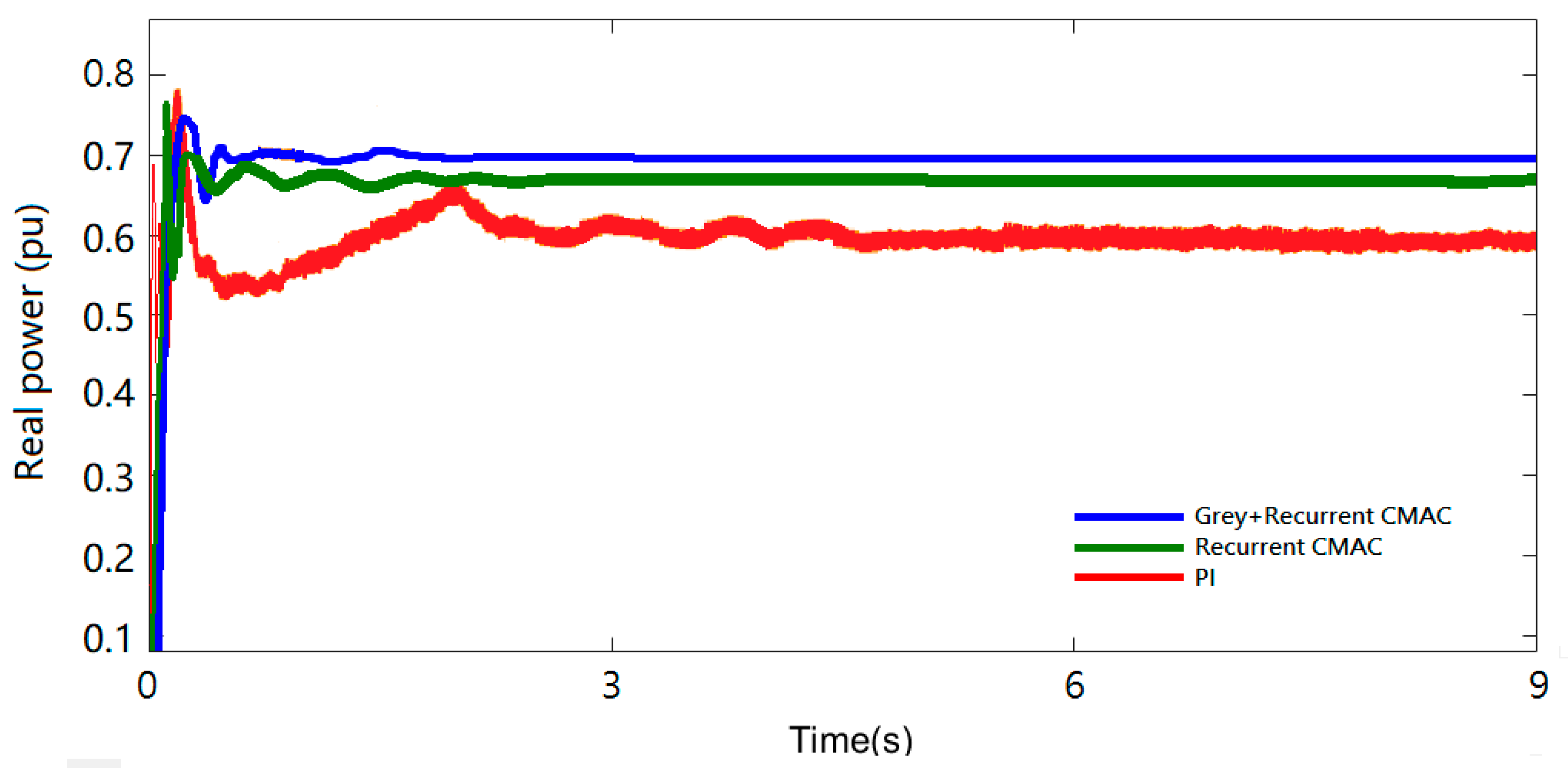
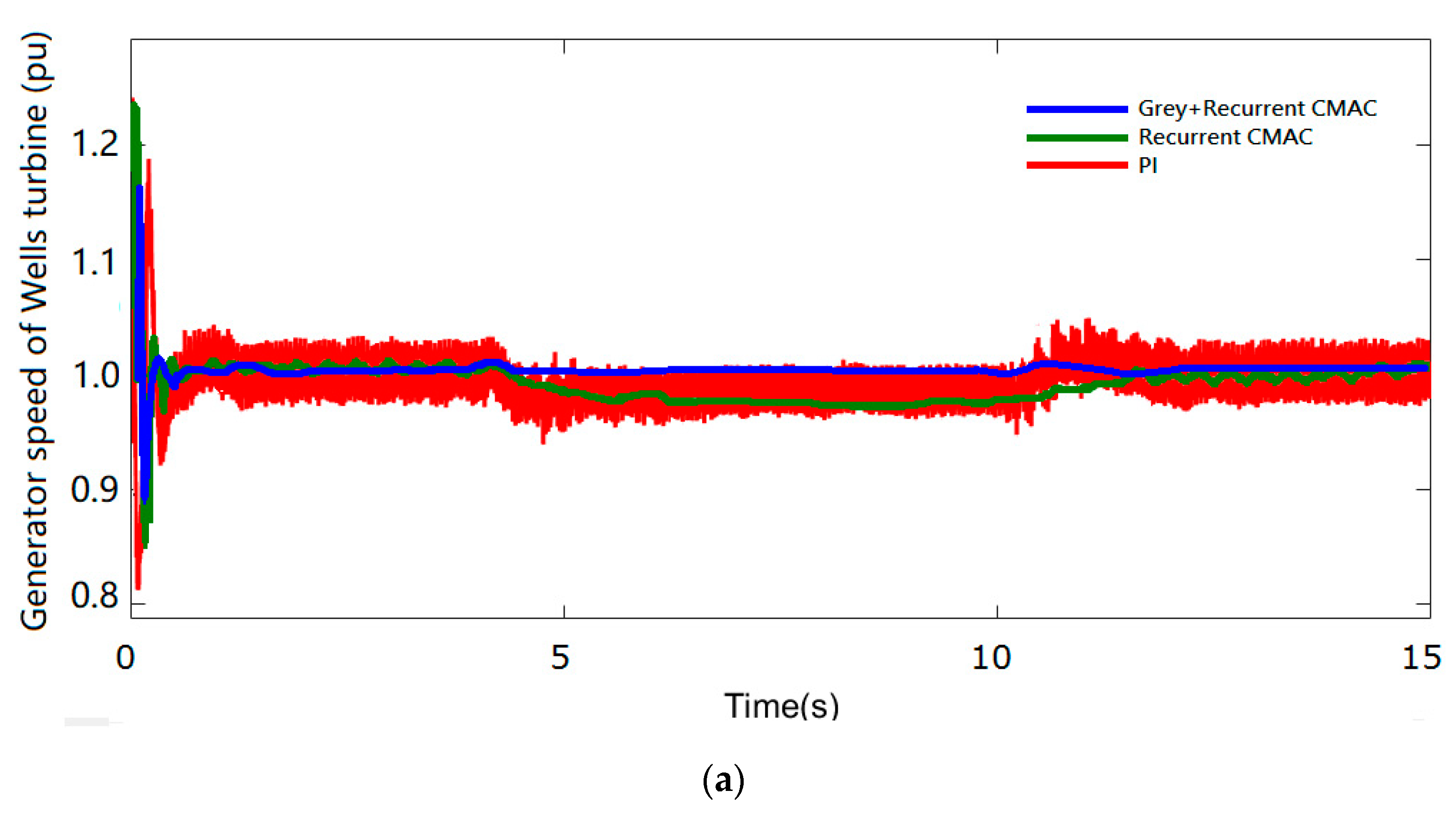
4.1. MPPT System Performance
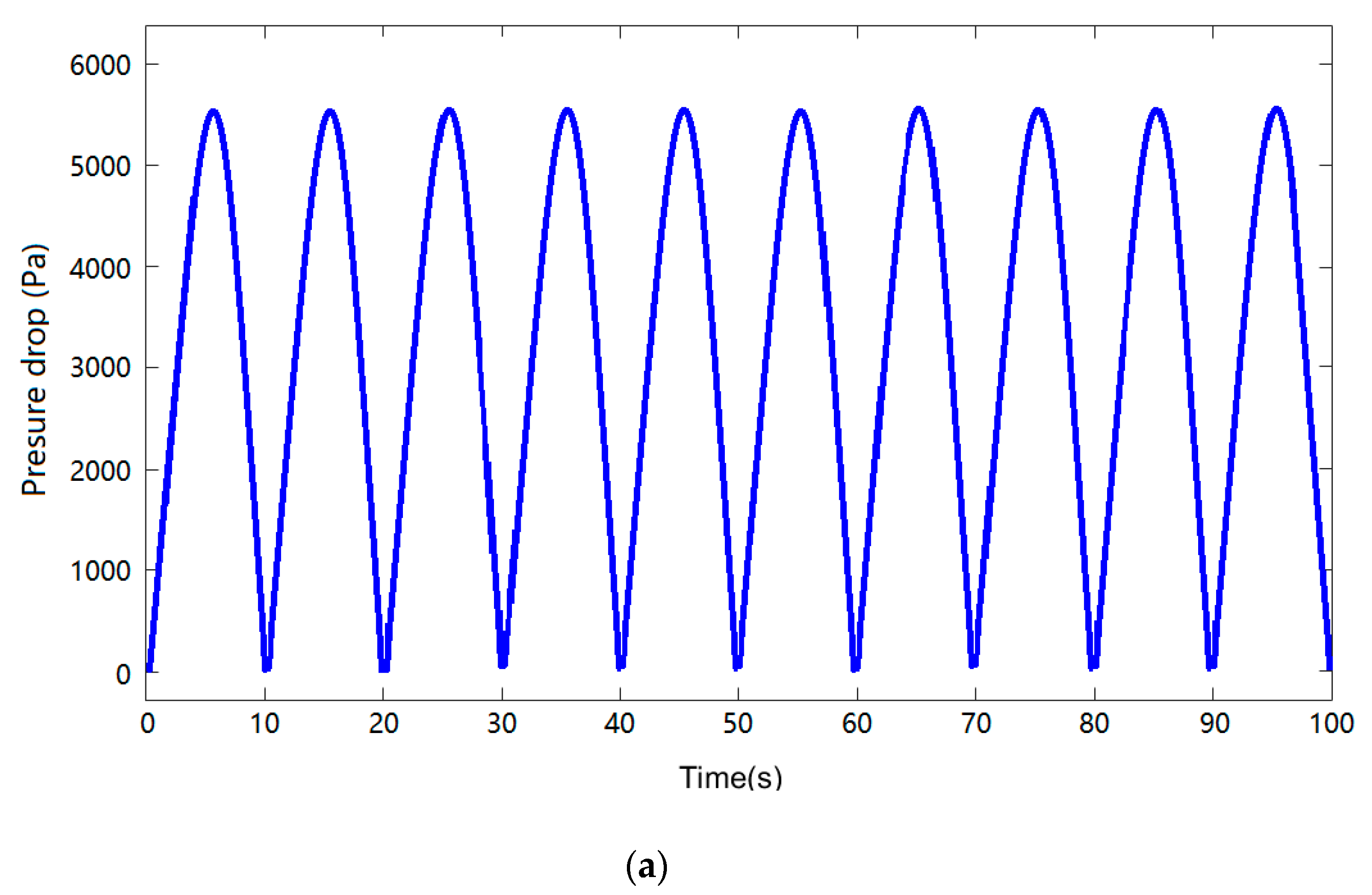
4.2. Wells Turbine Variable Axial Velocities
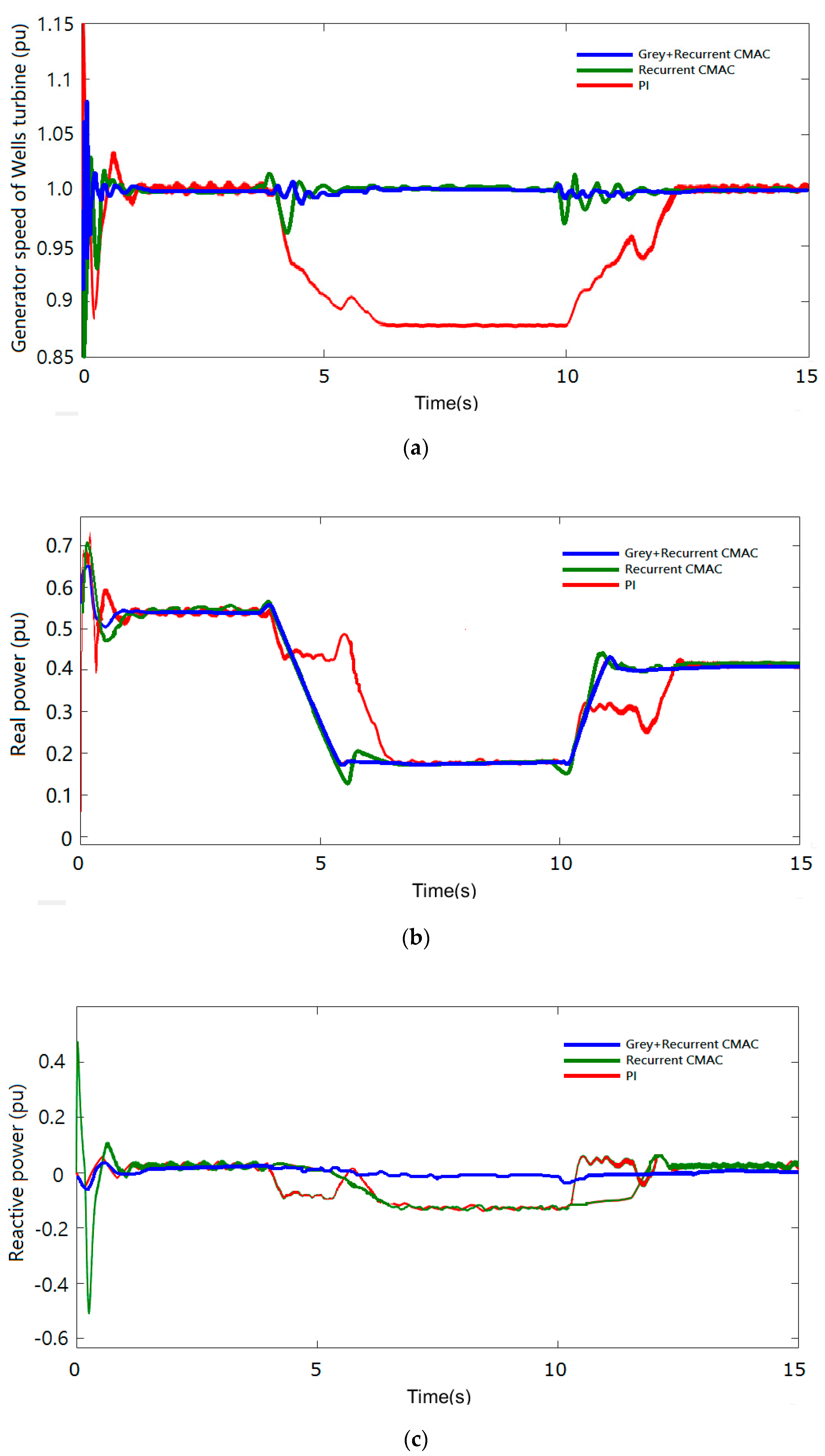
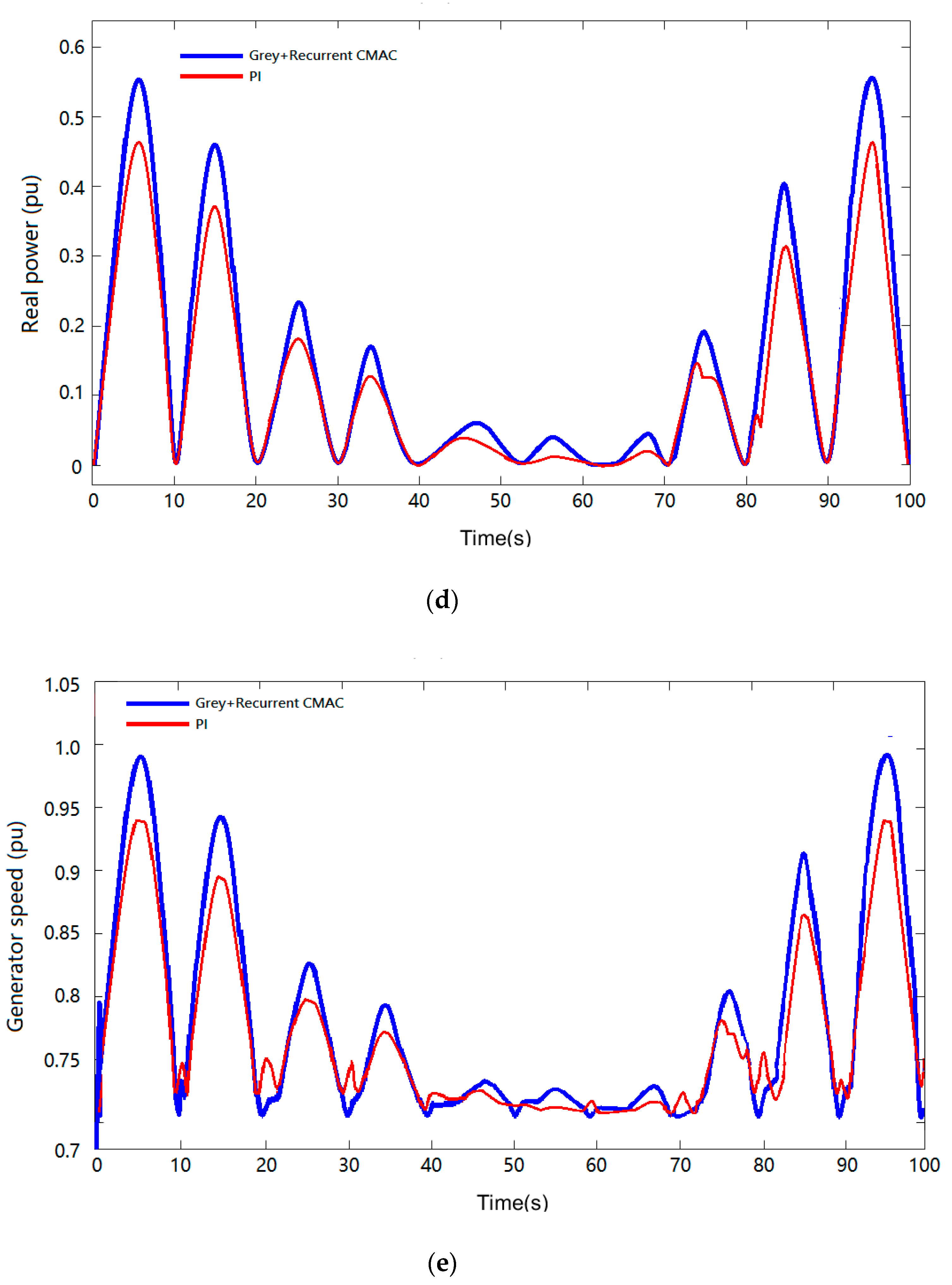
4.3. Dynamic Load Switching
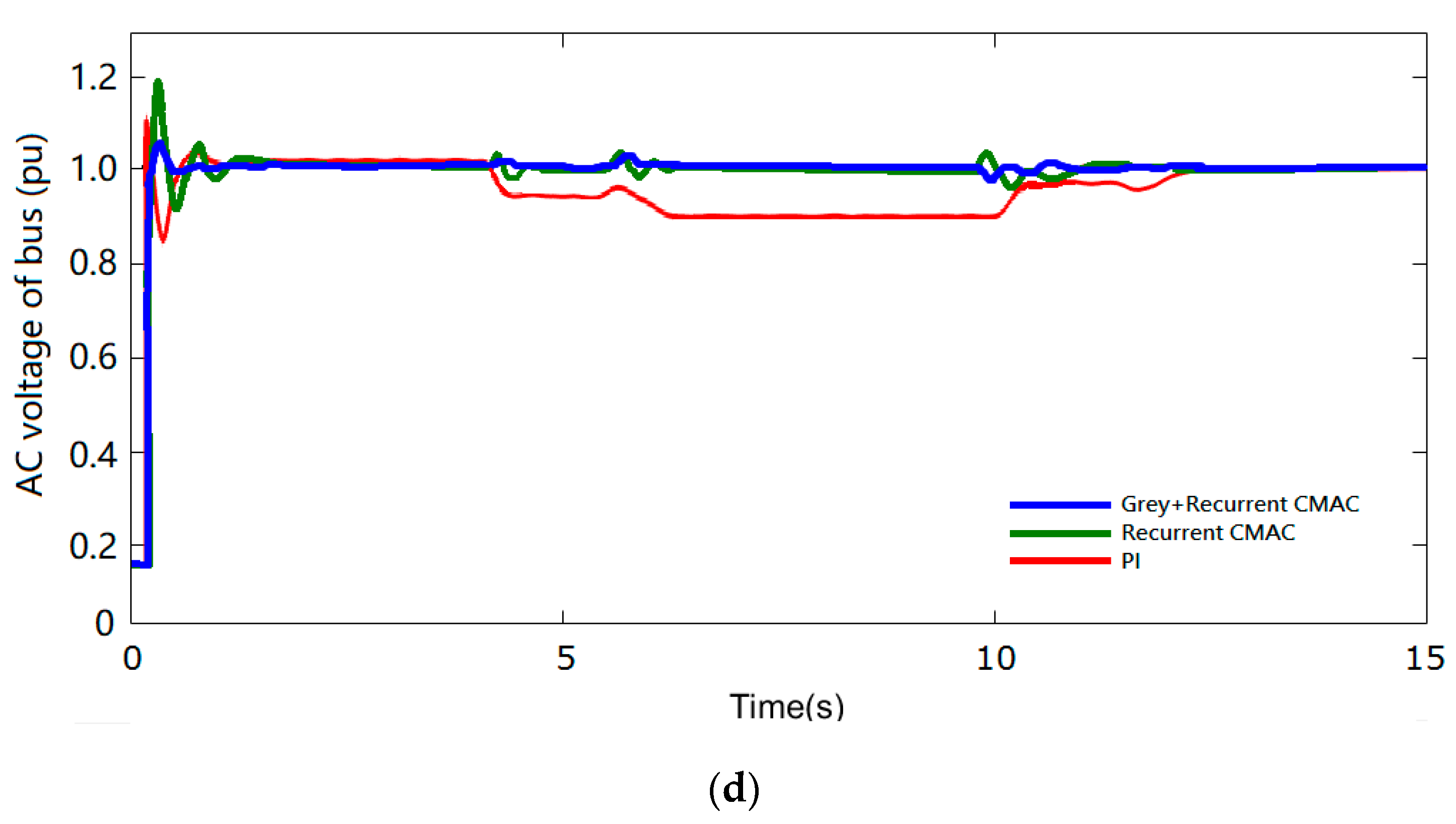
4.4. Short-Circuit Fault of Power Grid
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Halamay, D.; Brekken, T.; Simmons, A.; McArthur, S. Reserve requirement impacts of large-scale integration of wind, solar and ocean wave power generation. IEEE Trans. Sustain. Energy 2011, 2, 321–328. [Google Scholar] [CrossRef]
- Zhao, X.; Yan, Z.; Zhang, X.P. A wind-wave farm system with self-energy storage and smoothed power output. IEEE Access 2016, 4, 8634–8642. [Google Scholar] [CrossRef]
- Linda, S.; Rachel, S.; Thomas, D. What drives energy consumers: Engaging people in a sustainable energy transition. IEEE Power Energy Mag. 2018, 16, 20–28. [Google Scholar]
- Nicola, D.; Davide, B.; Francesco, G.; Paolo, C.; Giampaolo, B. Review of oscillating water column converters. IEEE Trans. Ind. Appl. 2016, 52, 1698–1710. [Google Scholar]
- Romain, G.; Josh, D.; John, V.R. Adaptive control of a wave energy converter. IEEE Trans. Sustain. Energy 2018, 9, 1588–1595. [Google Scholar]
- Murthy, B.K.; Rao, S.S. Rotor side control of Wells turbine driven variable speed constant frequency induction generator. J. Electr. Power Compon. 2005, 33, 587–596. [Google Scholar] [CrossRef]
- Oscar, B.; José, A.C.; José, M.G.d.D.; Patxi, A. A real time sliding mode control for a wave energy converter based on a Wells turbine. Ocean Eng. 2018, 163, 275–287. [Google Scholar]
- Oscar, B.; Isidro, C.; José, M.G.d.D. Adaptive sliding mode control for a control for a double fed induction generator used in an oscillating water column system. Energies 2018, 11, 1–27. [Google Scholar]
- Albus, J.S. A new approach to manipulator control: The cerebellar model articulation controller (CMAC). J. Dyn. Syst. Control. 1975, 97, 220–227. [Google Scholar] [CrossRef]
- Shiraishi, H.; Ipri, S.L.; Cho, D.D. CMAC neural network controller for fuel-injection systems. IEEE Trans. Control Syst. Technol. 1995, 3, 32–38. [Google Scholar] [CrossRef]
- Kim, Y.H.; Lewis, F.L. Optimal design of CMAC neural network controller for robot manipulators. IEEE Trans. Syst. Man Cybern. C Appl. Rev. 2000, 30, 22–31. [Google Scholar] [CrossRef]
- Chiang, C.T.; Lin, C.S. CMAC with general basis functions. J. Neural Netw. 1996, 9, 1199–1211. [Google Scholar] [CrossRef]
- Wang, S.Y.; Tseng, C.L.; Yeh, C.C. Adaptive supervisory Gaussian-cerebellar model articulation controllers for direct torque control induction motor drive. IET Electr. Power Appl. 2011, 5, 295–306. [Google Scholar] [CrossRef]
- Yeh, M.F.; Tsai, C.H. Standalone CMAC control systems with online learning ability. IEEE Trans. Syst. Man Cybern. B 2010, 40, 43–53. [Google Scholar]
- Bhattacharya, R.; Bhattacharya, T.K.; Garg, R. Position mutated hierarchical particle swarm optimization and its application in synthesis of unequally spaced antenna arrays. IEEE Trans. Antennas Propag. 2012, 60, 3174–3181. [Google Scholar] [CrossRef]
- Srivastava, L.; Dixit, S.; Agnihotri, G. Optimal location and sizing of TCSC for voltage stability enhancement using PSO-TVAC. In Proceedings of the 2014 Power and Energy Systems: Towards Sustainable Energy, Bangalore, India, 13–15 March 2014; pp. 1–6. [Google Scholar]
- Lin, W.M.; Lu, K.H.; Huang, C.H.; Ou, T.C.; Li, Y.H. Optimal location and capacity of STATCOM for voltage stability enhancement using ACO plus GA. In Proceedings of the 2009 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Singapore, 14–17 July 2009; pp. 1915–1920. [Google Scholar]
- Wang, L.; Chen, Z.J. Stability analysis of a wave-energy conversion system containing a grid-connected induction generator driven by a Wells turbine. IEEE Trans. Energy Convers. 2010, 25, 555–563. [Google Scholar] [CrossRef]
- Tomonobu, S.; Yasutaka, O.; Yasuaki, K.; Motoki, T.; Atsushi, Y.; Endusa, B.M.; Naomitsu, U.; Toshihisa, F. Sensorless maximum power point tracking control for wind generation system with squirrel cage induction generator. Renew. Energy 2009, 34, 994–999. [Google Scholar]
- Lin, W.M.; Hong, C.M.; Cheng, F.S. Design of intelligent controllers for wind generation system with sensorless maximum wind energy control. Energy Convers. Manag. 2011, 52, 1086–1096. [Google Scholar] [CrossRef]
- Krause, P.C. Analysis of Electric Machinery; McGraw-Hill: New York, NY, USA, 1986. [Google Scholar]
- Erenturk, K. Hybrid control of a mechatronic system: Fuzzy logic and grey system modeling approach. IEEE Trans. Mechatron. 2007, 12, 703–710. [Google Scholar] [CrossRef]
- Deng, J.L. Introduction to grey system theory. J. Grey Syst. 1989, 1, 1–24. [Google Scholar]
- Lin, W.M.; Hong, C.M.; Huang, C.H.; Ou, T.C. Hybrid control of a wind induction generator based on Grey–Elman neural network. IEEE Trans. Control Syst. Technol. 2013, 21, 2367–2373. [Google Scholar] [CrossRef]
- Lin, C.M.; Chen, C.H. Car-following control using RCMAC. IEEE Trans. Veh. Technol. 2007, 56, 3660–3673. [Google Scholar] [CrossRef]
- Lin, C.M.; Hsu, C.F. Neural network hybrid control for antilock braking systems. IEEE Trans. Neural Netw. 2003, 14, 351–359. [Google Scholar] [CrossRef] [PubMed]
- Lin, C.M.; Hsu, C.F. Supervisory recurrent fuzzy neural network control of wing rock for slender delta wings. IEEE Trans. Fuzzy Syst. 2004, 12, 732–742. [Google Scholar] [CrossRef]
- Jacob, R.; Yahya, R.S. Particle swarm optimization in electromagnetics. IEEE Trans. Antennas Propag. 2004, 52, 397–407. [Google Scholar]
- Varshney, S.; Srivastava, L.; Pandit, M. Optimal location and sizing of STATCOM for voltage security enhancement using PSO-TVAC. In Proceedings of the 2011 International Conference on Power and Energy Systems, Chennai, India, 22–24 December 2011; pp. 22–24. [Google Scholar]
- Oh, Y.J.; Park, J.S.; Hyon, B.J.; Lee, J. Novel control strategy of wave energy converter using linear permanent magnet synchronous generator. IEEE Trans. Appl. Supercond. 2018, 28, 1–5. [Google Scholar] [CrossRef]
- Prudell, J.; Stoddard, M.; Amon, E.; Brekken, T.K.A.; von Jouanne, A. A permanent magnet tubular linear generator for ocean wave energy conversion. IEEE Trans. Ind. Appl. 2010, 46, 2392–2400. [Google Scholar] [CrossRef]
- Lin, W.M.; Hong, C.M. A new Elman neural network-based control algorithm for adjustable-pitch variable speed wind energy conversion systems. IEEE Trans. Power Electron. 2011, 26, 473–481. [Google Scholar] [CrossRef]

| Controller | Power Efficiency (%) | Max Error of Torque Coefficient Ct (%) | MPPT Accuracy (%) | Transient Response (s) |
|---|---|---|---|---|
| Grey–RCMAC | 90.9 | 0.65 | 0.41 | 1.65 |
| RCMAC | 86.7 | 10.11 | 1.12 | 2.27 |
| CMAC | 80.1 | 15.61 | 2.29 | 3.51 |
| RFNN | 84.3 | 14.35 | 2.19 | 2.72 |
| PI | 77.5 | 22.65 | 2.82 | 4.57 |
| (a) Real Power of Wells Turbine | ||||
| Controller | Convergence Time (s) | CPU Execution Time | Mean Square Error (10−3) | Accuracy (%) |
| (102 s) | ||||
| Grey–RCMAC | 11.99 | 5.61 | 4.01 | 95.99 |
| RCMAC | 12.67 | 5.92 | 6.21 | 93.79 |
| CMAC | 9.15 | 4.30 | 10.73 | 89.27 |
| RFNN | 8.11 | 3.81 | 8.52 | 91.48 |
| PI | 13.50 | 6.34 | 21.15 | 78.85 |
| (b) Reactive Power of Wells Turbine | ||||
| Controller | Convergence Time (s) | CPU Execution Time (102 s) | Mean Square Error (10−2) | Accuracy (%) |
| Grey–RCMAC | 10.83 | 5.09 | 4.28 | 95.72 |
| RCMAC | 12.50 | 5.875 | 7.15 | 92.85 |
| CMAC | 13.93 | 6.54 | 12.11 | 87.89 |
| RFNN | 9.72 | 4.56 | 10.95 | 89.05 |
| PI | 11.67 | 5.48 | 18.59 | 81.41 |
| (c) Dynamic Voltage Amplitude Response of AC Bus on Power Grid Side | ||||
| Controller | Convergence Time (s) | CPU Execution Time (102 s) | Mean Square Error (pu) | Accuracy (%) |
| Grey–RCMAC | 4.33 | 3.313 | 0.167 | 98.33 |
| RCMAC | 4.50 | 3.443 | 0.835 | 91.65 |
| CMAC | 5.81 | 4.444 | 1.161 | 88.39 |
| RFNN | 5.87 | 4.490 | 0.677 | 93.23 |
| PI | N/A | N/A | 1.502 | 85 |
| (a) Real Power of Wells Turbine | ||||
| Controller | Convergence Time (s) | CPU Execution Time (102 s) | Mean Square Error (10−2) | Accuracy (%) |
| Grey–RCMAC | 5.66 | 4.30 | 3.080 | 96.92 |
| RCMAC | 7.50 | 5.07 | 5.390 | 94.61 |
| CMAC | 6.28 | 4.77 | 7.912 | 92.09 |
| RFNN | 8.18 | 6.21 | 6.667 | 93.33 |
| PI | 8.00 | 6.08 | 9.230 | 90.77 |
| (b) Reactive Power of Wells Turbine | ||||
| Controller | Convergence Time (s) | CPU Execution Time (102 s) | Mean Square Error (10−2) | Accuracy (%) |
| Grey–RCMAC | 5.66 | 4.07 | 5.001 | 94.99 |
| RCMAC | 7.66 | 5.51 | 13.336 | 86.66 |
| CMAC | 7.04 | 5.06 | 14.912 | 85.08 |
| RFNN | 6.15 | 4.67 | 9.730 | 90.27 |
| PI | 7.83 | 5.63 | 21.667 | 78.33 |
| (c) Dynamic Voltage Amplitude Response of AC Bus on Power Grid Side | ||||
| Controller | Convergence Time (s) | CPU Execution Time (102 s) | Mean Square Error (10−2) | Accuracy (%) |
| Grey–RCMAC | 6.00 | 4.56 | 5.001 | 94.99 |
| RCMAC | 7.66 | 5.82 | 8.335 | 91.66 |
| CMAC | 7.16 | 5.44 | 10.721 | 89.28 |
| RFNN | 6.74 | 5.12 | 7.056 | 92.94 |
| PI | 8.00 | 6.08 | 13.333 | 86.67 |
| (a) Real Power of WECS | ||||
| Controller | Convergence Time (s) | CPU Execution Time (102 s) | Mean Square Error (10−2) | Accuracy (%) |
| Grey–RCMAC | 2.40 | 1.82 | 7.50 | 92.50 |
| RCMAC | 2.65 | 2.01 | 15.00 | 85.00 |
| CMAC | 3.11 | 2.36 | 16.56 | 83.44 |
| RFNN | 2.45 | 186 | 11.91 | 88.09 |
| PI | 3.60 | 2.73 | 20.00 | 80.00 |
| (b) Reactive Power of WECS | ||||
| Controller | Convergence Time (s) | CPU Execution Time (102 s) | Mean Square Error (10−2) | Accuracy (%) |
| Grey–RCMAC | 2.25 | 1.71 | 5.01 | 94.99 |
| RCMAC | 2.75 | 2.09 | 11.25 | 88.75 |
| CMAC | 3.71 | 2.82 | 13.53 | 86.47 |
| RFNN | 3.04 | 2.31 | 8.03 | 91.97 |
| PI | 4.31 | 3.28 | 16.25 | 83.75 |
| (c) Transient Voltage Amplitude Response of AC Bus on Power Grid Side | ||||
| Controller | Convergence Time (s) | CPU Execution Time (102 s) | Mean Square Error (10−2) | Accuracy (%) |
| Grey–RCMAC | 2.55 | 1.93 | 5.00 | 95.00 |
| RCMAC | 2.90 | 2.20 | 12.50 | 87.5 |
| CMAC | 3.57 | 2.71 | 15.08 | 84.92 |
| RFNN | 2.86 | 2.17 | 8.91 | 91.09 |
| PI | 4.52 | 3.43 | 18.75 | 81.25 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, K.-H.; Hong, C.-M.; Han, Z.; Yu, L. New Intelligent Control Strategy Hybrid Grey–RCMAC Algorithm for Ocean Wave Power Generation Systems. Energies 2020, 13, 241. https://doi.org/10.3390/en13010241
Lu K-H, Hong C-M, Han Z, Yu L. New Intelligent Control Strategy Hybrid Grey–RCMAC Algorithm for Ocean Wave Power Generation Systems. Energies. 2020; 13(1):241. https://doi.org/10.3390/en13010241
Chicago/Turabian StyleLu, Kai-Hung, Chih-Ming Hong, Zhigang Han, and Lei Yu. 2020. "New Intelligent Control Strategy Hybrid Grey–RCMAC Algorithm for Ocean Wave Power Generation Systems" Energies 13, no. 1: 241. https://doi.org/10.3390/en13010241
APA StyleLu, K.-H., Hong, C.-M., Han, Z., & Yu, L. (2020). New Intelligent Control Strategy Hybrid Grey–RCMAC Algorithm for Ocean Wave Power Generation Systems. Energies, 13(1), 241. https://doi.org/10.3390/en13010241







