Harvesting Energy from Planetary Gear Using Piezoelectric Material
Abstract
1. Introduction
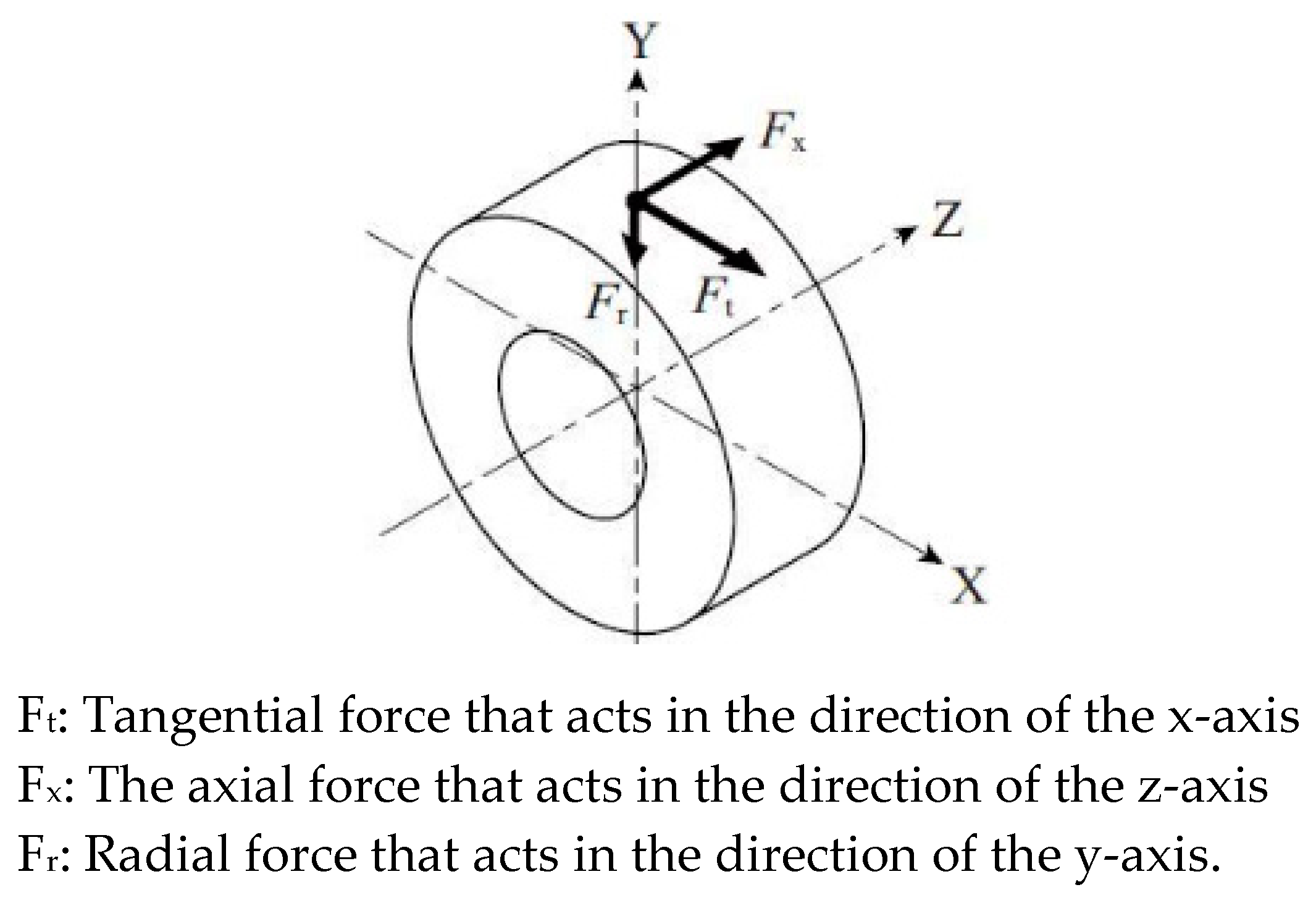
2. Theory and Analytical Equation
2.1. Planetary Gear System
2.1.1. Gear Relationship in the Planetary Gear System
2.1.2. Transmission Ratio of the Planetary Gear System
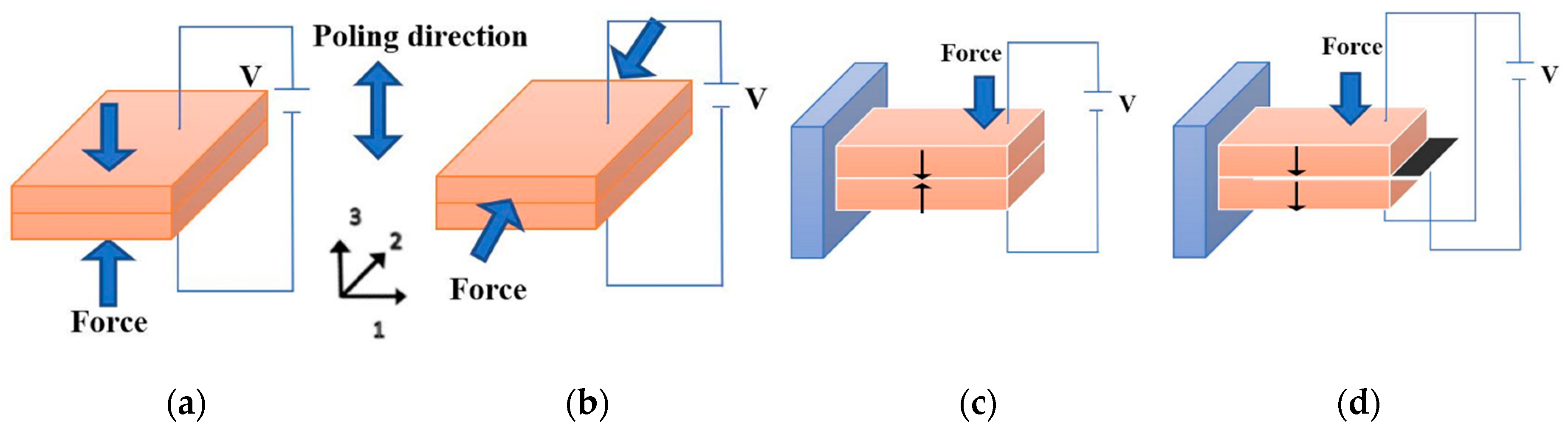
2.2. Piezoelectric Theory
3. Materials and Methods
3.1. Fabrication of the Prototype
3.2. Experimental Setup and Procedures
3.2.1. Effect of Rotational Speed
3.2.2. Effect of Planet Cover Numbers
3.2.3. Effect of Distance between PZTs
3.2.4. Effect of Increasing the PZT Number
3.2.5. Effect on the Primary System
3.3. Modeling and Simulation
4. Results and Discussion
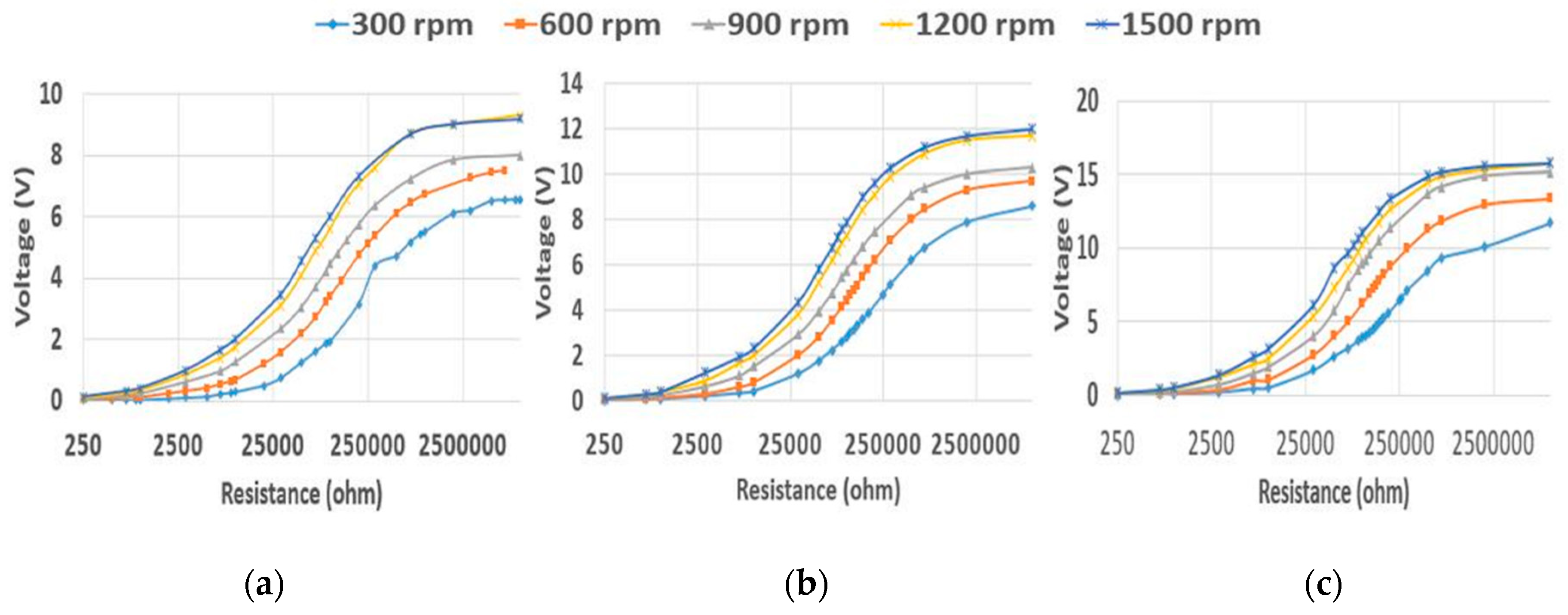
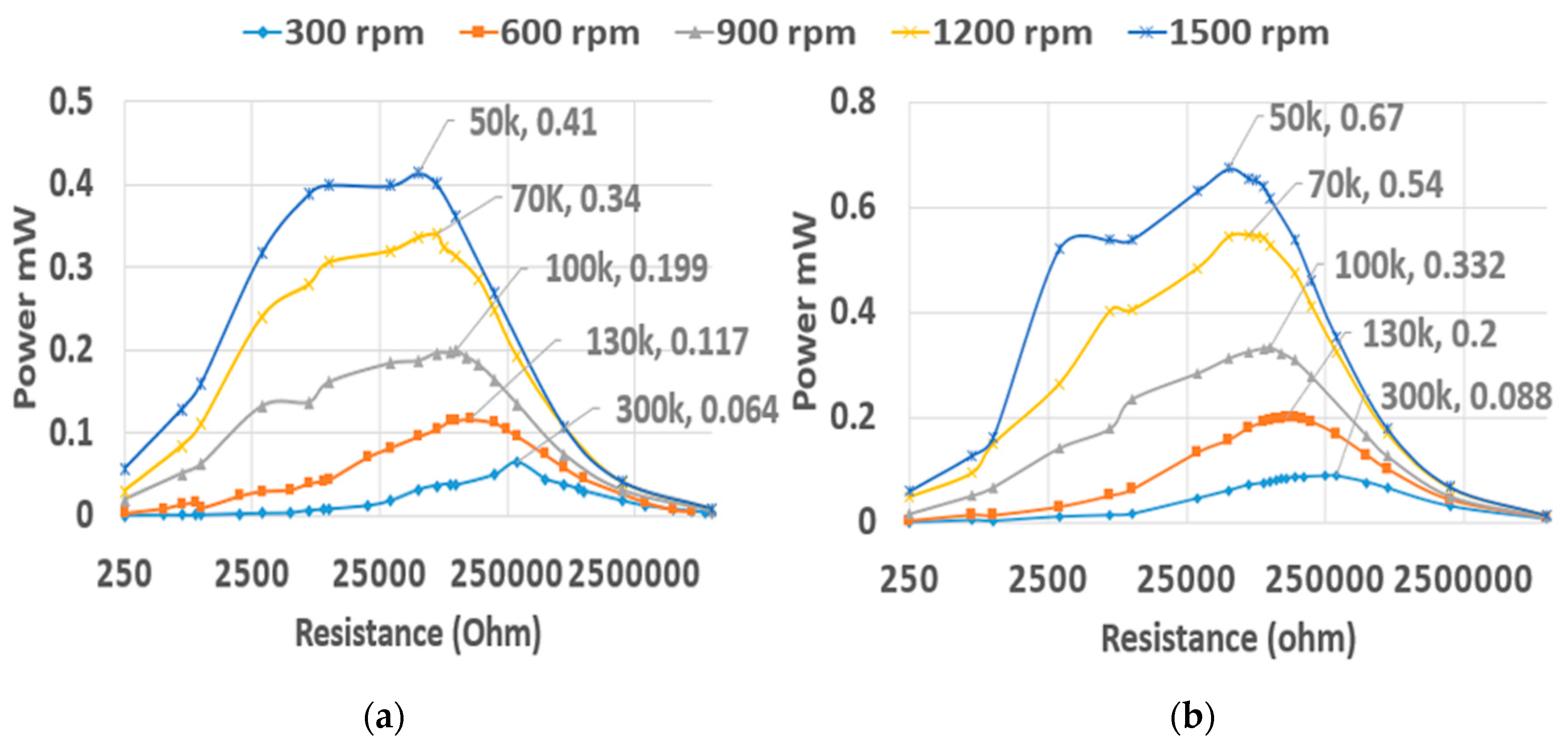
4.1. Effect of Rotational Speed
4.2. Effect of Planet Cover Numbers
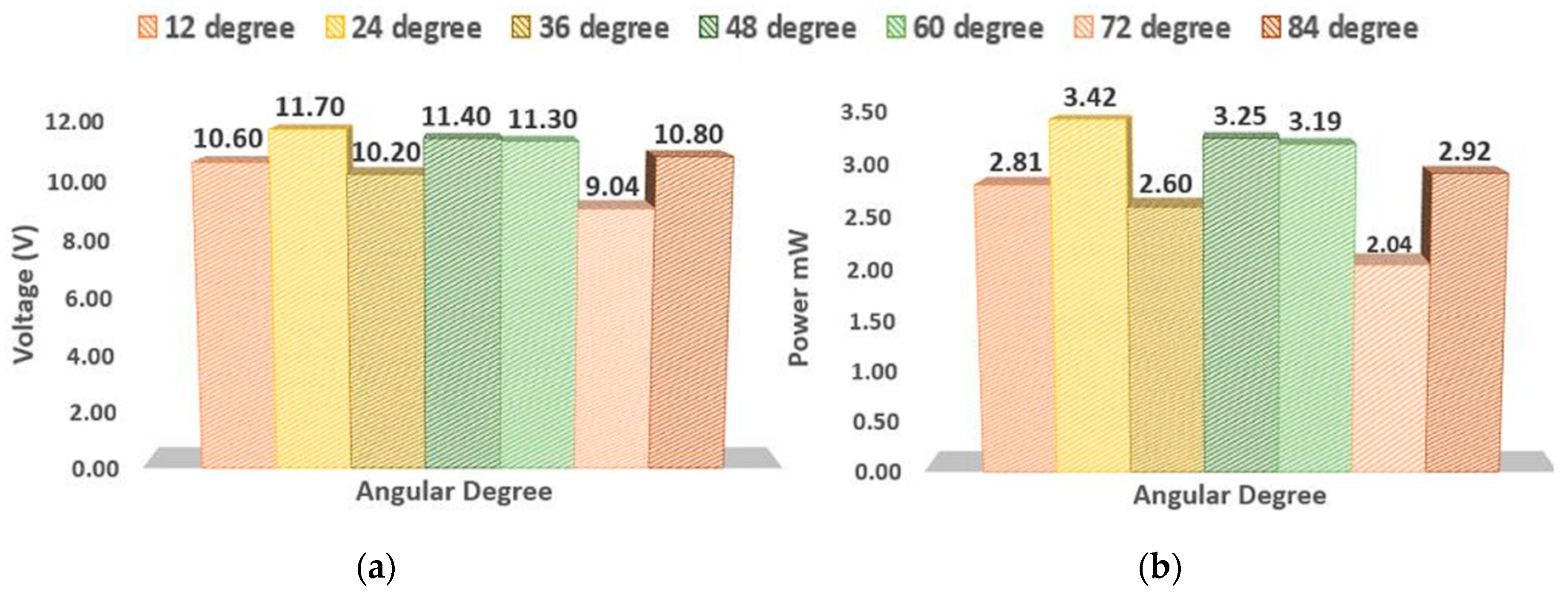
4.3. Effect of Distance between PZTs
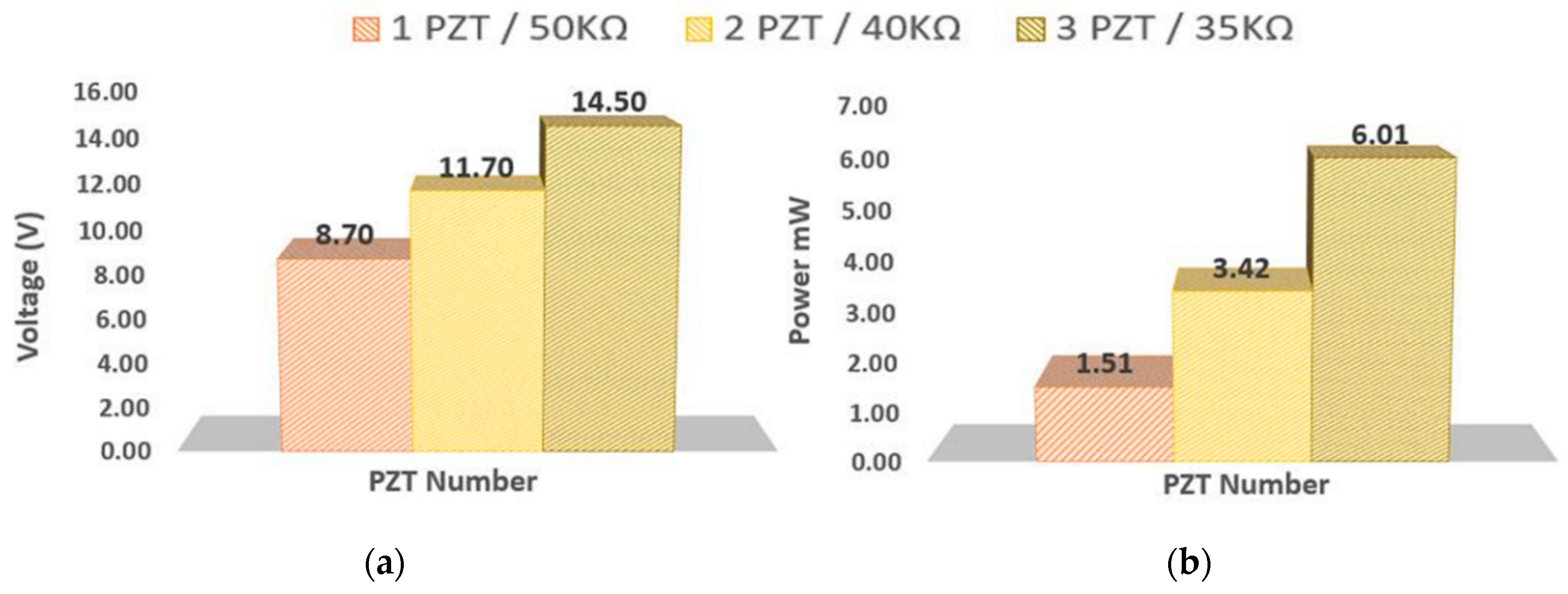
4.4. Effect of Increasing the PZT Number
4.5. Effect on the Primary System
4.6. Comparison with Previous Studies
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Yang, Z.; Zhou, S.; Zu, J.; Inman, D. High-Performance Piezoelectric Energy Harvesters and Their Applications. Joule 2018, 2, 642–697. [Google Scholar] [CrossRef]
- Wu, X.; Parmar, M.; Lee, D. A Seesaw-Structured Energy Harvester with Superwide Bandwidth for TPMS Application. IEEE/ASME Trans. Mechatron. 2014, 19, 1514–1522. [Google Scholar]
- Kherbeet, A.S.; Salleh, H.; Salman, B.H.; Salim, M. Vibration-based piezoelectric micropower generator for power plant wireless monitoring application. Sustain. Energy Technol. Assess. 2015, 11, 42–52. [Google Scholar] [CrossRef]
- Elahi, H.; Eugeni, M.; Gaudenzi, P. A Review on Mechanisms for Piezoelectric-Based Energy Harvesters. Energies 2018, 11, 1850. [Google Scholar] [CrossRef]
- Kumar, B.; Kim, S.-W. Energy harvesting based on semiconducting piezoelectric ZnO nanostructures. Nano Energy 2012, 1, 342–355. [Google Scholar] [CrossRef]
- Fu, H.; Yeatman, E.M. Rotational energy harvesting using bi-stability and frequency up-conversion for low-power sensing applications: Theoretical modelling and experimental validation. Mech. Syst. Signal Process. 2019, 125, 229–244. [Google Scholar] [CrossRef]
- Zou, H.; Zhang, W.; Li, W.; Wei, K.; Gao, Q.; Peng, Z.; Meng, G. Design and experimental investigation of a magnetically coupled vibration energy harvester using two inverted piezoelectric cantilever beams for rotational motion. Energy Convers. Manag. 2017, 148, 1391–1398. [Google Scholar] [CrossRef]
- Khameneifar, F.; Moallem, M.; Arzanpour, S. Modeling and Analysis of a Piezoelectric Energy Scavenger for Rotary Motion Applications. J. Vib. Acoust. 2011, 133, 011005. [Google Scholar] [CrossRef]
- Wu, W.; Kuo, K.; Lin, Y.; Tsai, Y. Non-contact magnetic cantilever-type piezoelectric energy harvester for rotational mechanism. Microelectron. Eng. 2018, 191, 16–19. [Google Scholar] [CrossRef]
- Dannier, A.; Brando, G.; Ruggiero, F. The Piezoelectric Phenomenon in Energy Harvesting Scenarios: A Theoretical Study of Viable Applications in Unbalanced Rotor Systems. Energies 2019, 12, 708. [Google Scholar] [CrossRef]
- Fan, K.; Wang, L.; Zhu, Y.; Liu, Z.; Yu, B. Performance of a multipurpose piezoelectric energy harvester. Int. J. Mod. Phys. B 2017, 31, 1741007. [Google Scholar] [CrossRef]
- Li, K.; He, Q.; Wang, J.; Zhou, Z.; Li, X. Wearable energy harvesters generating electricity from low-frequency human limb movement. Microsyst. Nanoeng. 2018, 4, 24. [Google Scholar] [CrossRef] [PubMed]
- Xie, Z.; Kwuimy, C.A.K.; Wang, Z.; Huang, W. A piezoelectric energy harvester for broadband rotational excitation using buckled beam. AIP Adv. 2018, 8, 015125. [Google Scholar] [CrossRef]
- Fu, H.; Yeatman, E.M. A methodology for low-speed broadband rotational energy harvesting using piezoelectric transduction and frequency up-conversion. Energy 2017, 125, 152–161. [Google Scholar] [CrossRef]
- Wang, Y.-J.; Chuang, T.-Y.; Yu, J.-H. Design and kinetic analysis of piezoelectric energy harvesters with self-adjusting resonant frequency. Smart Mater. Struct. 2017, 26, 095037. [Google Scholar]
- Wang, Y.; Chuang, T.; Lee, C. Resonant frequency self-tunable piezoelectric cantilevers for energy harvesting and disturbing torque absorbing. Sens. Actuators A Phys. 2019, 285, 25–34. [Google Scholar] [CrossRef]
- Zhang, Y.; Jin, Y. Stochastic dynamics of a piezoelectric energy harvester with correlated colored noises from rotational environment. Nonlinear Dyn. 2019, 98, 501–515. [Google Scholar] [CrossRef]
- Stamatellou, A.M.; Kalfas, A.I. Experimental investigation of energy harvesting from swirling flows using a piezoelectric film transducer. Energy Convers. Manag. 2018, 171, 1405–1415. [Google Scholar] [CrossRef]
- Yang, Y.; Shen, Q.; Jin, J.; Wang, Y.; Qian, W.; Yuan, D. Rotational piezoelectric wind energy harvesting using impact-induced resonance. Appl. Phys. Lett. 2014, 105, 053901. [Google Scholar] [CrossRef]
- Gong, Y.; Yang, Z.; Shan, X.; Sun, Y.; Xie, T.; Zi, Y. Capturing Flow Energy from Ocean and Wind. Energies 2019, 12, 2184. [Google Scholar] [CrossRef]
- An, X.; Song, B.; Tian, W.; Ma, C. Design and CFD Simulations of a Vortex-Induced Piezoelectric Energy Converter (VIPEC) for Underwater Environment. Energies 2018, 11, 330. [Google Scholar] [CrossRef]
- Kyoo, N.C.; Rho, H.H. Continuous energy harvesting method using piezoelectric element. In Proceedings of the 2015 IEEE 2nd International Future Energy Electronics Conference (IFEEC), Taipei, Taiwan, 1–4 November 2015; pp. 1–4. [Google Scholar]
- Nezami, S.; Jung, H.; Lee, S. Design of a disk-swing driven piezoelectric energy harvester for slow rotary system application. Smart Mater. Struct. 2019, 28, 074001. [Google Scholar] [CrossRef]
- Ramírez, J.M.; Gatti, C.D.; Machado, S.P.; Febbo, M. A piezoelectric energy harvester for rotating environment using a linked E-shape multi-beam. Extrem. Mech. Lett. 2019, 27, 8–19. [Google Scholar] [CrossRef]
- Li, M.; Wen, Y.; Li, P.; Yang, J.; Dai, X. A rotation energy harvester employing cantilever beam and magnetostrictive/piezoelectric laminate transducer. Sens. Actuators A Phys. 2011, 166, 102–110. [Google Scholar] [CrossRef]
- Zhang, Y.; Zheng, R.; Shimono, K.; Kaizuka, T.; Nakano, K. Effectiveness Testing of a Piezoelectric Energy Harvester for an Automobile Wheel Using Stochastic Resonance. Sensors 2016, 16, 1727. [Google Scholar] [CrossRef]
- Guan, M.; Liao, W. Design and analysis of a piezoelectric energy harvester for rotational motion system. Energy Convers. Manag. 2016, 111, 239–244. [Google Scholar] [CrossRef]
- Zhu, B.; Han, J.; Zhao, J.; Deng, W. Practical Design of an Energy Harvester Considering Wheel Rotation for Powering Intelligent Tire Systems. J. Electron. Mater. 2017, 46, 2483–2493. [Google Scholar] [CrossRef]
- Pillatsch, P.; Yeatman, E.M.; Holmes, A.S.; Wright, P.K. Wireless power transfer system for a human motion energy harvester. Sens. Actuators A Phys. 2016, 244, 77–85. [Google Scholar] [CrossRef]
- Kuang, Y.; Yang, Z.; Zhu, M. Design and characterisation of a piezoelectric knee-joint energy harvester with frequency up-conversion through magnetic plucking. Smart Mater. Struct. 2016, 25, 085029. [Google Scholar] [CrossRef]
- Hanif, N.H.H.M.; Mohaideen, A.J.; Azam, H.; Rohaimi, M.E. Rotational piezoelectric energy harvester for wearable devices. Cogent Eng. 2018, 5, 1430497. [Google Scholar]
- Choi, Y.M.; Lee, M.G.; Jeon, Y. Wearable Biomechanical Energy Harvesting Technologies. Energies 2017, 10, 1483. [Google Scholar] [CrossRef]
- Karami, M.A.; Farmer, J.R.; Inman, D.J. Parametrically excited nonlinear piezoelectric compact wind turbine. Renew. Energy 2013, 50, 977–987. [Google Scholar] [CrossRef]
- Pozzi, M. Synchronicity and pure bending of bimorphs: A new approach to piezoelectric energy harvesting. Smart Mater. Struct. 2018, 27, 085027. [Google Scholar] [CrossRef]
- Çelik, K.; Kurt, E.; Uzun, Y. Experimental and Theoretical Explorations on the Buckling Piezoelectric Layer Under Magnetic Excitation. J. Electron. Mater. 2017, 46, 4003–4016. [Google Scholar] [CrossRef]
- Gu, L.; Livermore, C. Compact passively self-tuning energy harvesting for rotating applications. Smart Mater. Struct. 2012, 21, 015002. [Google Scholar] [CrossRef]
- Gu, L.; Livermore, C. Passive self-tuning energy harvester for extracting energy from rotational motion. Appl. Phys. Lett. 2010, 97, 081904. [Google Scholar] [CrossRef]
- Febbo, M.; Machado, S.P.; Gatti, C.D.; Ramirez, J.M. An out-of-plane rotational energy harvesting system for low frequency environments. Energy Convers. Manag. 2017, 152, 166–175. [Google Scholar] [CrossRef]
- Hsu, J.; Tseng, C.; Chen, Y. Analysis and experiment of self-frequency-tuning piezoelectric energy harvesters for rotational motion. Smart Mater. Struct. 2014, 23, 075013. [Google Scholar] [CrossRef]
- Khameneifar, F.; Arzanpour, S.; Moallem, M. A Piezoelectric Energy Harvester for Rotary Motion Applications: Design and Experiments. IEEE/ASME Trans. Mechatron. 2013, 18, 1527–1534. [Google Scholar] [CrossRef]
- Park, J.; Lee, S.; Kwak, B.M. Design optimization of piezoelectric energy harvester subject to tip excitation. J. Mech. Sci. Technol. 2012, 26, 137–143. [Google Scholar] [CrossRef]
- Wei, J.; Duan, L. Piezoelectric-Based Rotary Electrical Energy Generator for Harvesting Energy from Low and Highly Variable Rotary Motion. In Proceedings of the Volume 2: Integrated System Design and Implementation; Structural Health Monitoring; Bioinspired Smart Materials and Systems; Energy Harvesting, Colorado Springs, CO, USA, 21–23 September 2015; p. V002T07A005. [Google Scholar]
- Xue, T.; Yeo, H.G.; Trolier-McKinstry, S.; Roundy, S. Wearable inertial energy harvester with sputtered bimorph lead zirconate titanate (PZT) thin-film beams. Smart Mater. Struct. 2018, 27, 085026. [Google Scholar] [CrossRef]
- Zhang, Y.; Zheng, R.; Nakano, K.; Cartmell, M.P. Stabilising high energy orbit oscillations by the utilisation of centrifugal effects for rotating-tyre-induced energy harvesting. Appl. Phys. Lett. 2018, 112, 143901. [Google Scholar] [CrossRef]
- Rezaei-Hosseinabadi, N.; Tabesh, A.; Dehghani, R. A Topology and Design Optimization Method for Wideband Piezoelectric Wind Energy Harvesters. IEEE Trans. Ind. Electron. 2016, 63, 2165–2173. [Google Scholar] [CrossRef]
- Bai, Y.; Havránek, Z.; Tofel, P.; Meggs, C.; Hughes, H.; Button, T.W. Nonlinear piezoelectric devices for broadband air-flow energy harvesting. Eur. Phys. J. Spec. Top. 2015, 224, 2675–2685. [Google Scholar] [CrossRef]
- Pillatsch, P.; Yeatman, E.M.; Holmes, A.S. A piezoelectric frequency up-converting energy harvester with rotating proof mass for human body applications. Sens. Actuators A Phys. 2014, 206, 178–185. [Google Scholar] [CrossRef]
- Larkin, M.; Tadesse, Y. HM-EH-RT: Hybrid multimodal energy harvesting from rotational and translational motions. Int. J. Smart Nano Mater. 2013, 4, 257–285. [Google Scholar] [CrossRef]
- Ramírez, J.M.; Gatti, C.D.; Machado, S.P.; Febbo, M. An experimentally validated finite element formulation for modeling 3D rotational energy harvesters. Eng. Struct. 2017, 153, 136–145. [Google Scholar] [CrossRef]
- Resali, M.S.M.; Salleh, H. Wireless condition monitoring system for rotating machinery powered by a hybrid vibration based energy harvester. J. Mech. Eng. 2017, 4, 249–267. [Google Scholar]
- Janphuang, P.; Lockhart, R.A.; Isarakorn, D.; Henein, S.; Briand, D.; de Rooij, N.F. Harvesting Energy from a Rotating Gear Using an AFM-Such as MEMS Piezoelectric Frequency Up-Converting Energy Harvester. J. Microelectromech. Syst. 2015, 24, 742–754. [Google Scholar] [CrossRef]
- Janphuang, P.; Isarakorn, D.; Briand, D.; de Rooij, N.F. Energy harvesting from a rotating gear using an impact type piezoelectric MEMS scavenger. In Proceedings of the 2011 16th International Solid-State Sensors, Actuators and Microsystems Conference, Beijing, China, 5–9 June 2011; pp. 735–738. [Google Scholar]
- Janphuang, P.; Lockhart, R.; Henein, S.; Briand, D.; de Rooij, N.F. On the experimental determination of the efficiency of piezoelectric impact-type energy harvesters using a rotational flywheel. J. Phys. Conf. Ser. 2013, 476, 012137. [Google Scholar] [CrossRef]
- Yang, B.; Yi, Z.; Tang, G.; Liu, J. A gullwing-structured piezoelectric rotational energy harvester for low frequency energy scavenging. Appl. Phys. Lett. 2019, 115, 063901. [Google Scholar] [CrossRef]
- Janphuang, P.; Lockhart, R.; Briand, D.; de Rooij, N.F. On the optimization and performances of a compact piezoelectric impact MEMS energy harvester. In Proceedings of the 2014 IEEE 27th International Conference on Micro Electro Mechanical Systems (MEMS), San Francisco, CA, USA, 26–30 January 2014; pp. 429–432. [Google Scholar]
- Khkgears. Net Planetary Gear. Available online: https://khkgears.net/new/gear_knowledge/gear_technical_reference/gear_systems.html (accessed on 5 August 2019).
- Uhl, T. Advances in Mechanism and Machine Science; Springer: Cham, Switzerland, 2019. [Google Scholar]
- Uicker, J.J.; Pennock, G.R.; Shigley, J.E. Theory of Machines and Mechanisms; Oxford University Press: New York, NY, USA, 2011. [Google Scholar]
- Damjanovic, D. Ferroelectric, dielectric and piezoelectric properties of ferroelectric thin films and ceramics. Rep. Prog. Phys. 1998, 61, 1267–1324. [Google Scholar] [CrossRef]
- Meitzler, A.H.; Tiersten, H.F.; Berlincourt, D. IEEE standard on piezoelectricity: An American National Standard; IEEE: Piscataway, NJ, USA, 1988. [Google Scholar]
- Hehn, T.; Manoli, Y. CMOS Circuits for Piezoelectric Energy Harvesters; Springer Series in Advanced Microelectronics; Springer: Dordrecht, The Netherlands, 2015; Volume 38, ISBN 978-94-017-9287-5. [Google Scholar]
- Caliò, R.; Rongala, U.; Camboni, D.; Milazzo, M.; Stefanini, C.; de Petris, G.; Oddo, C. Piezoelectric Energy Harvesting Solutions. Sensors 2014, 14, 4755–4790. [Google Scholar] [CrossRef] [PubMed]
- Thompson, S.P. Dynamo-Electric Machinery: A Manual for Students of Electrotechnics; University of California Libraries: Berkeley, CA, USA, 2009. [Google Scholar]
- Roshani, H.; Dessouky, S.; Montoya, A.; Papagiannakis, A.T. Energy harvesting from asphalt pavement roadways vehicle-induced stresses: A feasibility study. Appl. Energy 2016, 182, 210–218. [Google Scholar] [CrossRef]
- Resali, M.S.M.; Salleh, H. Development of multiple-input power management circuit for piezoelectric harvester. J. Mech. Eng. 2017, 2, 215–230. [Google Scholar]
- Jing, B.Y.; Leong, K.S. Power Optimization Configuration for Piezoelectric Cantilever Arrays. MATEC Web Conf. 2017, 108, 08007. [Google Scholar] [CrossRef]











| DC Voltage No-Load | 300 rpm | 600 rpm | 900 rpm | 1200 rpm | 1500 rpm |
|---|---|---|---|---|---|
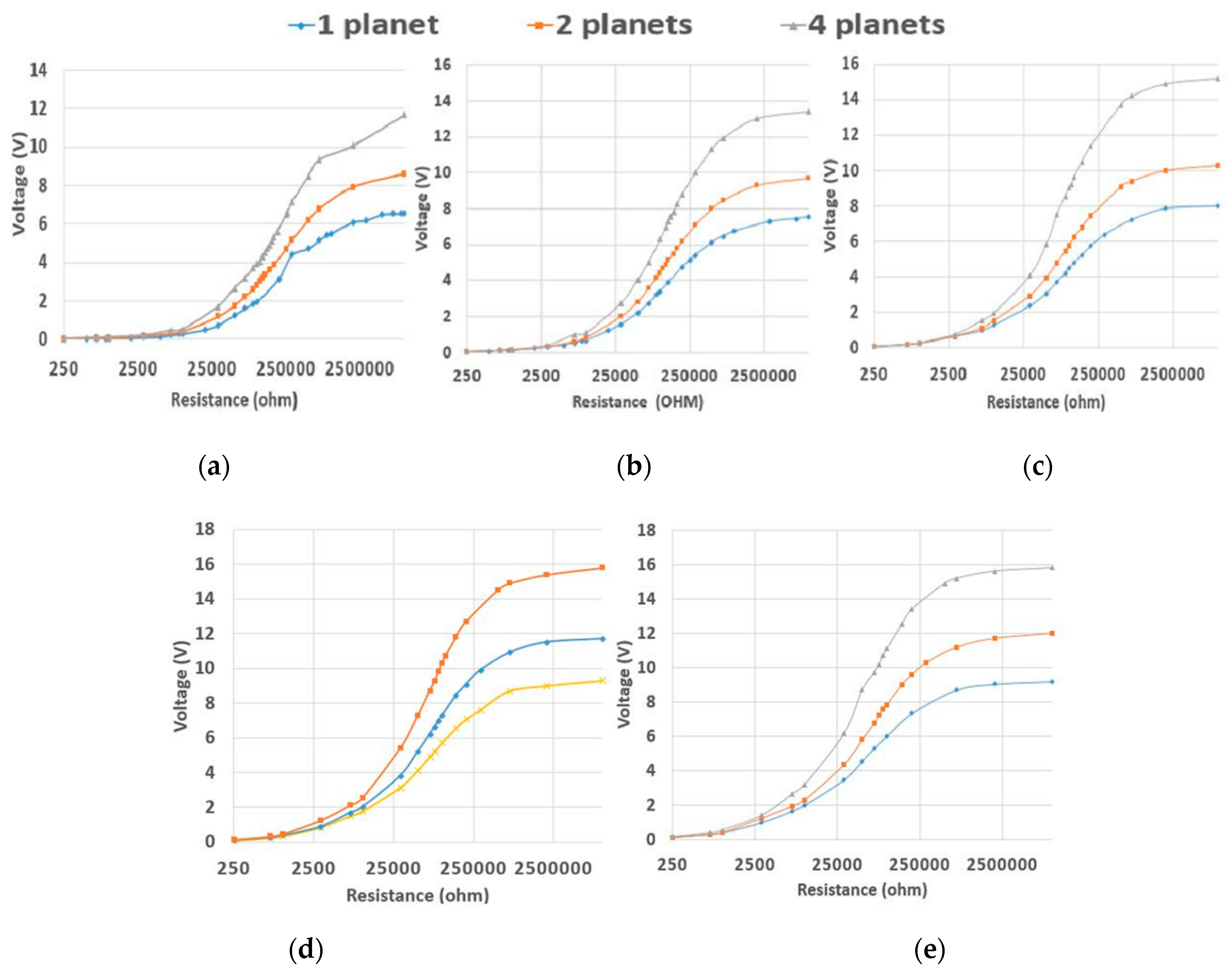
| 1 Planet | 6.9 | 7.57 | 8.27 | 9.4 | 9.3 |
| 2 planets | 8.78 | 10 | 10.3 | 11.7 | 11.9 |
| 4 Planets | 13.6 | 13.5 | 15.2 | 15.8 | 15.9 |
| Speed | 300 rpm | 600 rpm | 900 rpm | 1200 rpm | 1500 rpm | |
|---|---|---|---|---|---|---|
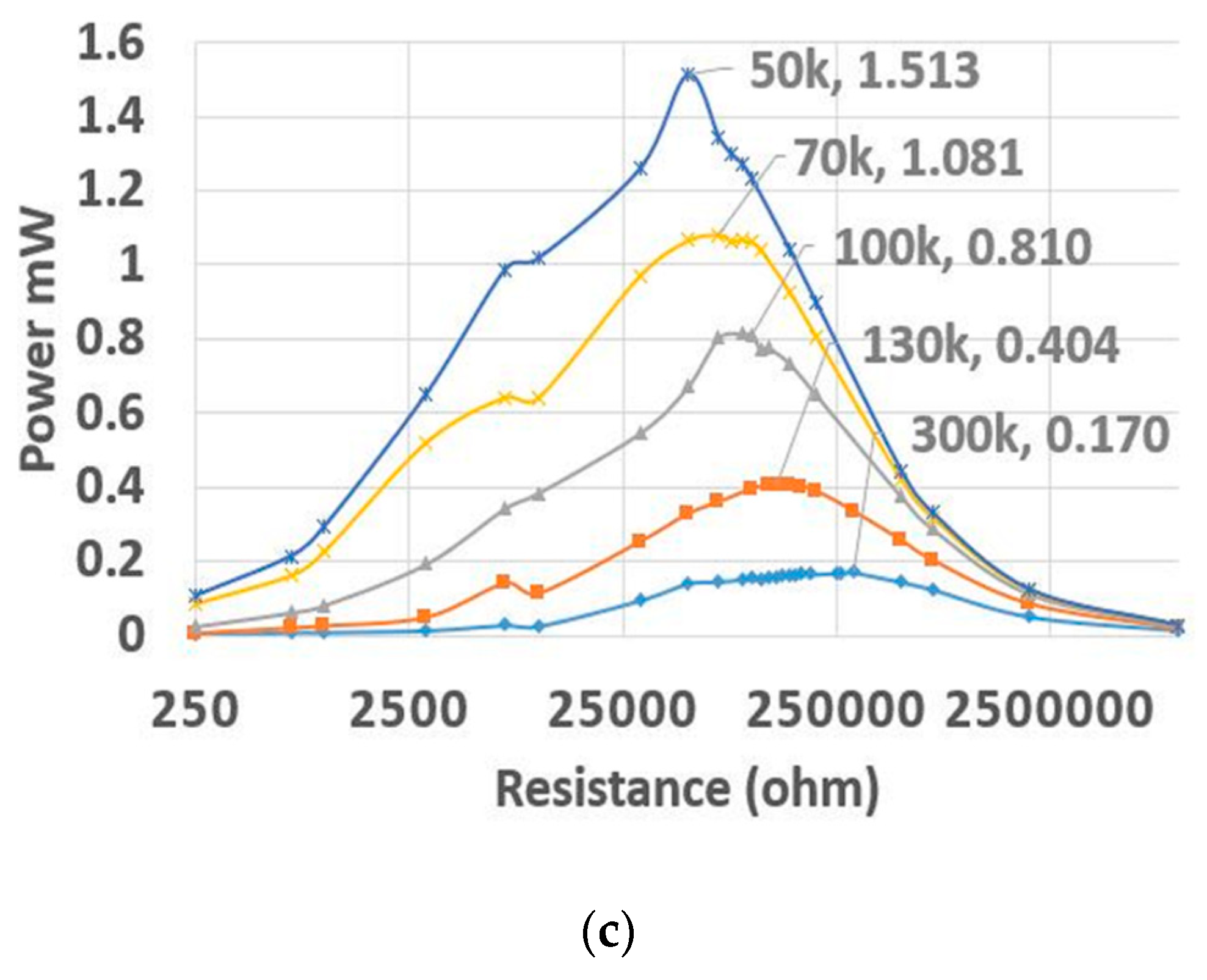
| Optimum Resistance | 300 kΩ | 130 kΩ | 100 kΩ | 70 kΩ | 50 kΩ | |
| 1 Planet | Measured Acceleration m/s2 | 0.045 | 0.19 | 0.43 | 0.87 | 1.41 |
| Simulated Voltage (V) | 3.98 | 3.64 | 4.187 | 4.451 | 4.1076 | |
| Measured Voltage (V) | 4.39 | 3.9 | 4.47 | 4.88 | 4.55 | |
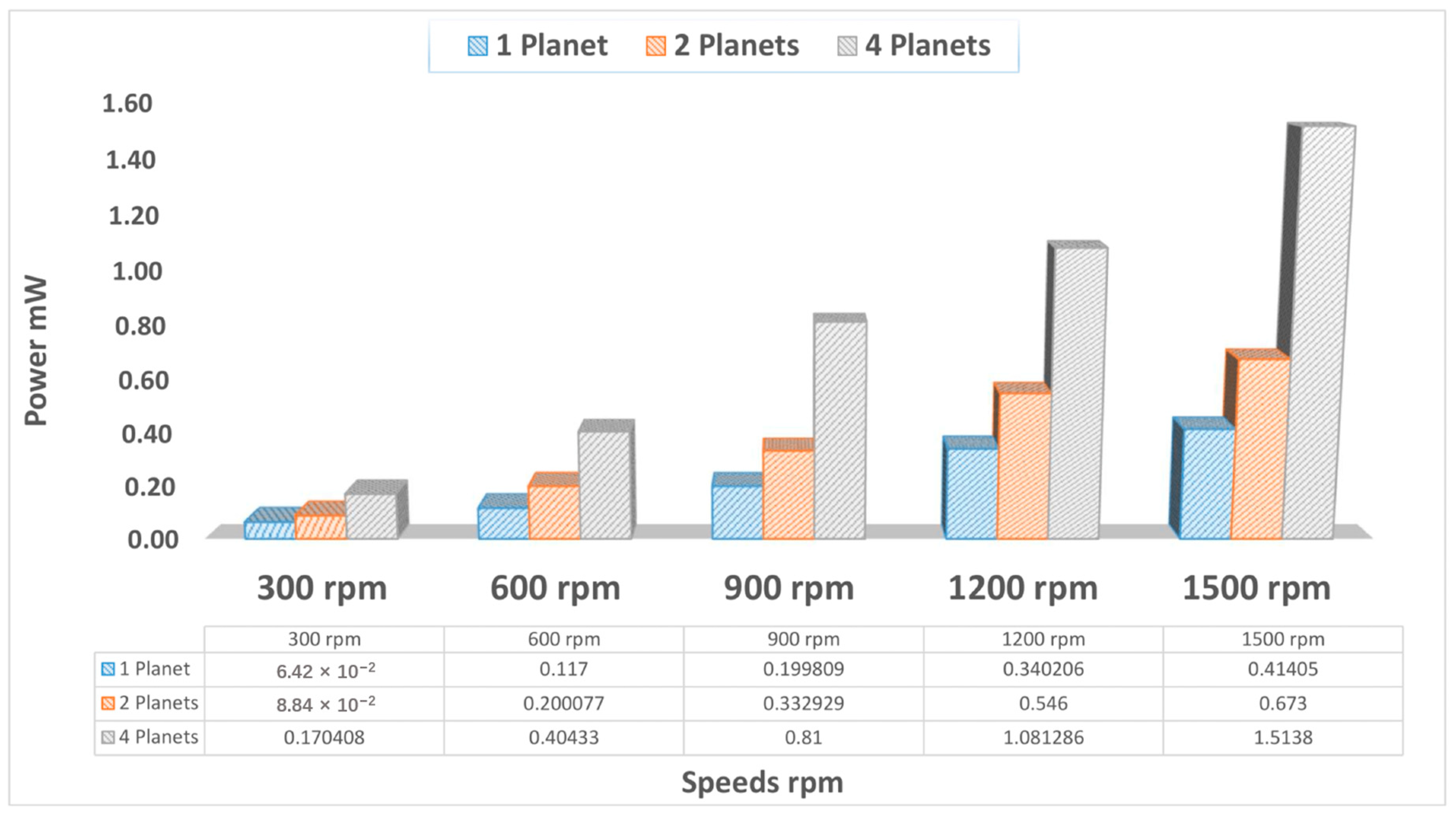
| Output Power (mW) | 0.0642 | 0.117 | 0.199 | 0.340 | 0.414 | |
| Times of increase for Output power | - | 1.821 | 3.11 | 5.295 | 6.445 | |
| 2 planets | Measured Acceleration m/s2 | 0.057 | 0.25 | 0.57 | 1.1 | 1.96 |
| Simulated Voltage (V) | 5.042 | 4.799 | 5.55 | 5.628 | 5.7099 | |
| Measured Voltage (V) | 5.15 | 5.1 | 5.77 | 6.18 | 5.8 | |
| Output Power (mW) | 0.088 | 0.2 | 0.332 | 0.546 | 0.673 | |
| Times of increase for Output power | - | 2.263 | 3.765 | 6.171 | 7.61 | |
| 4 Planets | Measured Acceleration m/s2 | 0.076 | 0.37 | 0.92 | 1.63 | 2.65 |
| Simulated Voltage (V) | 6.723 | 7.103 | 8.959 | 8.34 | 7.72 | |
| Measured Voltage (V) | 7.15 | 7.25 | 9 | 8.7 | 8.63 | |
| Output Power (mW) | 0.170 | 0.404 | 0.81 | 1.081 | 1.513 | |
| Times of increase for Output power | / | 2.372 | 4.753 | 6.345 | 8.74 | |
| DC Voltage/No Load | 1 Planet | 2 Planet | 4 Planet |
|---|---|---|---|
| 300 rpm | 6.9 | 8.78 | 13.6 |
| 600 rpm | 7.57 | 10.3 | 15.2 |
| 900 rpm | 8.27 | 10.3 | 15.2 |
| 1200 rpm | 9.4 | 11.7 | 15.8 |
| 1500 rpm | 9.3 | 11.9 | 15.9 |
| Rotational Speed | Optimum Resistance | 1 Planet | 2 Planet | 4 Planet | |
|---|---|---|---|---|---|
| 300 rpm | 300 KΩ | Measured Acceleration m/s2 | 0.045 | 0.057 | 0.076 |
| Simulated Voltage (V) | 3.98 | 5.042 | 6.723 | ||
| Measured Voltage (V) | 4.39 | 5.15 | 7.15 | ||
| Output Power (mW) | 0.0642 | 0.0884 | 0.17 | ||
| Times of increase for Output power | / | 1.376 | 2.652 | ||
| 600 rpm | 130 KΩ | Measured Acceleration m/s2 | 0.19 | 0.25 | 0.37 |
| Simulated Voltage (V) | 3.64 | 4.799 | 7.103 | ||
| Measured Voltage (V) | 3.9 | 5.1 | 7.25 | ||
| Output Power (mW) | 0.117 | 0.2 | 0.404 | ||
| Times of increase for Output power | / | 1.71 | 3.455 | ||
| 900 rpm | 100 KΩ | Measured Acceleration m/s2 | 0.43 | 0.57 | 0.92 |
| Simulated Voltage (V) | 4.187 | 5.55 | 8.959 | ||
| Measured Voltage (V) | 4.47 | 5.77 | 9 | ||
| Output Power (mW) | 0.199 | 0.333 | 0.81 | ||
| Times of increase for Output power | / | 1.666 | 4.053 | ||
| 1200 rpm | 70 KΩ | Measured Acceleration m/s2 | 0.87 | 1.1 | 1.63 |
| Simulated Voltage (V) | 4.451 | 5.628 | 8.34 | ||
| Measured Voltage (V) | 4.88 | 6.18 | 8.7 | ||
| Output Power (mW) | 0.340 | 0.546 | 1.081 | ||
| Times of increase for Output power | / | 1.603 | 3.178 | ||
| 1500 rpm | 50 KΩ | Measured Acceleration m/s2 | 1.41 | 1.96 | 2.65 |
| Simulated Voltage(V) | 4.1076 | 5.7099 | 7.72 | ||
| Measured Voltage(V) | 4.55 | 5.8 | 8.63 | ||
| Output Power (mW) | 0.414 | 0.673 | 1.513 | ||
| Times of increase for Output power | / | 1.624 | 3.654 |
| Ref. | Input | Output | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Excitation Elements | Volume | PZT Material Dimension (mm) | Polarization Mode | Material Type Use | rpm | Frequency Actually Reach the Piezo (Hz) | Resistance (Ω) | Power (µW) | Power Density (µW/mm3) | |
| [52] | G + M | 4.2 | - | - | - | 25 | 0.4 | 2.7 M | 1.26 | 0.3 (calculated) |
| [42] | G + M | 138.66 | 75.0 × 19.05 × 1.59 | - | PZT | 300 | 6 | - | 6000 | 2.55 (given) |
| [41] | G + M | 4.26 | 152 mm2 × 0.028 | bimorph with parallel connection | PZT-5A | 15 | 500 | 1000 | 3.72 | 0.87 (calculated) |
| [51] | G + M + Mg | 3.5 | - | d31 | PZT sheet, PSI-5A4E, | 1140 | 19 | 180 k | 12 | 3.43 (calculated) |
| [54] | G | 61.2 | (10 × 18 × 0.17) × 2 | - | thinned bulk lead zirconate titanate ceramic | - | 7.8 | 30 k | 400 | 6.54 (given) |
| This work | Pg | 157.76 | (46.4 × 6.8 × 0.25) × 2 | d31 | PZT- 5H | 1500 | 6.25 | 50 k | 1566 | 9.59 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chilabi, H.J.; Salleh, H.; Supeni, E.E.; As’arry, A.; Rezali, K.A.M.; Atrah, A.B. Harvesting Energy from Planetary Gear Using Piezoelectric Material. Energies 2020, 13, 223. https://doi.org/10.3390/en13010223
Chilabi HJ, Salleh H, Supeni EE, As’arry A, Rezali KAM, Atrah AB. Harvesting Energy from Planetary Gear Using Piezoelectric Material. Energies. 2020; 13(1):223. https://doi.org/10.3390/en13010223
Chicago/Turabian StyleChilabi, Haider Jaafar, Hanim Salleh, Eris E. Supeni, Azizan As’arry, Khairil Anas Md Rezali, and Ahmed B. Atrah. 2020. "Harvesting Energy from Planetary Gear Using Piezoelectric Material" Energies 13, no. 1: 223. https://doi.org/10.3390/en13010223
APA StyleChilabi, H. J., Salleh, H., Supeni, E. E., As’arry, A., Rezali, K. A. M., & Atrah, A. B. (2020). Harvesting Energy from Planetary Gear Using Piezoelectric Material. Energies, 13(1), 223. https://doi.org/10.3390/en13010223





