1. Introduction
Electric power generation from renewable, variable, and distributed resources is increasing dramatically in many countries [
1]. Other cost-effective technologies, such as all-electric vehicles, automated demand response, and customer- or community-scale energy storage, are also poised for significant growth. These distributed energy resources (DERs) introduce both challenges and opportunities at the periphery of the grid. Specific issues of concern with residential-scale solar photovoltaics (PV) include voltage rise or protection coordination problems when PV generation exceeds co-located load [
2,
3], and network congestion due to solar variability at times of peak demand [
4]. For these reasons, distribution utilities may limit the connection (or permissible levels) of PV generation, e.g., by defining feeder hosting capacities. Electric vehicle charging, if not carefully controlled, may similarly strain the limits of legacy distribution systems [
5]. Local energy storage, such as customer- or utility-owned batteries, potentially mitigate variability, but control objectives can be conflicting [
4]. Notably, resources may create local problems at the distribution level, while acting to solve system-wide problems at the transmission level: for example, causing voltage volatility, while providing frequency regulation services to the bulk grid. To support the cost-effective integration of environmentally desirable technologies and to assist grid operators in delivering reliable, high-quality power, more sophisticated approaches for controlling heterogeneous DER are needed [
6,
7,
8,
9,
10,
11].
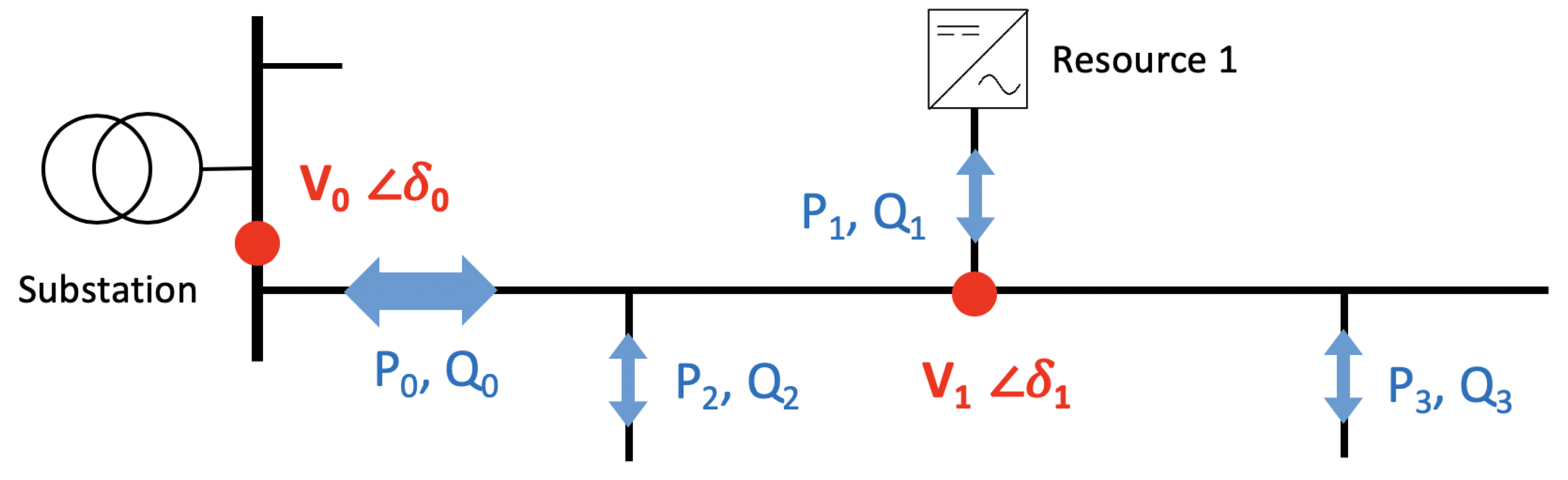
In this paper, we propose a unified framework termed phasor-based control (PBC) to facilitate dramatic increases in renewable generation levels throughout the electric grid, including the distribution network. PBC frames the contributions of generators and loads in terms of their physical effect on the network, by explicitly referring to the electrical state variables, voltage magnitude V and voltage phase angle , that constitute the voltage phasor at any given network node. (The phasor representation assumes the voltage is a sinusoid of the form , where is the (constant) angular frequency or , and . In power engineering convention, we ignore the term and write as , where is the root-mean-square magnitude.)
Our proposed PBC approach only recently became feasible with the development of ultra-precise synchronized phasor measurement units (
PMUs) that provide synchrophasor data with sufficient resolution for the power distribution context: instruments can now reliably discern angle differences as small as ten millidegrees, or about half a microsecond [
12,
13]. In controlling resources directly based on physical measurements from the grid, PBC fundamentally differs from approaches that aim to manage resources through refined economic methods, such as time-varying locational prices. To our knowledge, nowhere has a comprehensive, integrated PBC scheme been proposed to encompass real and reactive power flow control across transmission and distribution systems.
The problem of controlling large numbers of distributed resources to help rather than hinder electric grid operation is well recognized in both academic literature and industry. To date, most emphasis has been on the temporal coordination of diverse resources to satisfy overall power balance in the grid. Key innovations in this area include the refinement of time-varying price signals toward faster time steps [
14], automated demand response [
15], and eligibility of small-scale resources to participate in ancillary service markets, such as frequency regulation [
16]. The increasing participation of distributed resources in grid management, however, comes with a need to account for the spatial dimension, given the highly location-specific constraints of distribution networks that must still be satisfied while optimizing on a larger geographic scale.
The optimal recruitment of distributed energy storage resources is a case in point. Here, a single resource can allocate portions of its power and energy capacity to simultaneously provide multiple services on different time scales; for example, energy arbitrage and frequency regulation [
17]. The resource may also serve competing purposes, e.g., peak shaving for the utility versus backup power reserve for the customer in case of an outage [
18]. However, to maximize the overall benefits of the resource, it is necessary to account for its particular local impact on the network infrastructure, which can be negative or positive: namely, does the resource create or does it mitigate excessive voltage drops, thermal overload risks, or reversal of power flow direction on the distribution feeder?
One general solution strategy is to extend well-understood optimization tools from the transmission into the distribution realm. For example, Locational Marginal Pricing (LMP) could be applied to capture distribution congestion and discriminate the value of power injections with higher granularity in both time and space [
19]. Note that to properly account for differential physical impacts on distribution circuits, LMPs would have to be assigned on a small scale, potentially varying from one customer to the next (e.g., depending on distance from the substation) in a way that is not transparent to the ratepayer.
Any pricing approach will rely on the use of system models and some form of centralized optimization. Specifically, knowledge of the grid and its operating state may be converted into a suitable power or energy price at a given location and time. If that price is to reflect local as well as global conditions, it must be computed with information from both levels. The more centralized a coordination strategy, the greater a data acquisition and communications burden it imposes on grid operations, along with the need for better network model information (i.e., connectivity and line impedances). However, model data at the distribution level is often incomplete or less precise than transmission level data, and a dependence on too much information introduces an inherent vulnerability into any control scheme.
To reduce dependence on network model information, autonomous or decentralized and model-free control strategies are an attractive alternative or complement to centralized optimization where possible. For example, the highly location-sensitive voltage regulation function of distributed generators can be decoupled from power and energy provision by controlling reactive power output on a volt-VAR droop curve. Such a curve assigns a specific amount of reactive power injection as a function of, locally measured voltage magnitude [
20,
21]. In this way, while real power injection may follow some other criteria such as price-based optimization, positive or negative reactive power injection can serve to mitigate local network constraints without the need for centralized control. It has also been demonstrated that active control of generation resources based on a voltage phase angle separation constraint on a distribution line is effective at limiting real power flow [
22].
Although controlling real and reactive power separately is a practical and sensible near-term solution to feeder voltage problems [
23], this decoupled approach has fundamental limitations in the long term. Modulating real power is necessary to navigate distribution system constraints, such as capacity limits or protection coordination under reverse (real) power flow. Furthermore, at high DER penetration levels, managing voltage magnitude using only reactive power can yield unsatisfactory results with excessive losses if real and reactive power flow in opposite directions [
24]. An underlying difficulty is that distribution circuits conform poorly to the standard assumption that reactive power
Q varies mainly with the voltage magnitude
V, while real or active power
P varies mainly with voltage phase angle
. Decoupling applies when inductive reactance
X is much greater than resistance
R, as is generally true in transmission systems. Since distribution networks have smaller physical dimensions, it follows that distribution feeders tend to have significant resistive components, and
P and
Q are consequently intertwined with both
V and
. This inter-relationship is most clearly seen in a pair of equations based on the DistFlow equations [
25] adapted by [
24,
26] for the voltage magnitudes and angles at adjacent nodes 1 and 2:
where
P and
Q flow from node 1 to 2, and
is the impedance of the connecting circuit branch. The unbalanced three-phase formulation derived in [
24] expands into vector and matrix quantities but is otherwise similar. These equations can be approximated by eliminating the loss term in Equation (
1) and applying the small angle approximation to Equation (
2):
These equations can be further approximated by the linear equations:
The interdependency of
P,
Q and
V,
in distribution circuits motivates our integrated PBC framework, where real and reactive power are modulated based on the entire measured voltage phasor. Beyond yielding intuitive insight, the above linearization also yields a convex power flow equality, which is leveraged for the supervisory PBC optimization problem [
27].
4. Scalable Integration of Variable Energy Resources
4.1. Managing Variability
When a considerable proportion of electricity is supplied from renewable energy sources, such as wind turbines and solar PV, we expect higher variability of power flows and distribution supply voltages—seasonally, daily, and minute-to-minute (e.g., due to fast moving clouds or varying wind speeds). By setting explicit phasor bounds, PBC ensures the limits of the infrastructure are respected, even as power and voltage quantities vary within the permissible range. In other words, the emphasis on non-negotiable physical constraints allows PBC to flexibly accommodate evolving solutions for how the constraints are met.
The precision with which target phasors are maintained, or the deadband settings for local controllers, can be adapted to the requirements of each particular situation. A key feature of the PBC framework is that it allows for feedback at both the local and supervisory level. If, for any reason, an L-PBC controller is unable to recruit the resources needed to meet its phasor target with the desired accuracy, the discrepancy—in the form of a direct phasor measurement—is directly apparent to the S-PBC controller, which can then revise phasor targets to best manage the actual condition. PBC thus accounts for variability by design, from rejecting disturbances in real-time to adapting to changes in resource availability. We believe this makes the PBC framework ideally suited to address the fluctuations and uncertainty associated with high levels of variable energy resources.
4.2. Layered Architecture
The PBC framework, per se, is agnostic to the optimization objective, criteria, or method applied when computing phasor targets, as well as the specific means employed by local controllers to meet their targets. For example, S-PBC may run a single optimal power flow program or allow for some market-based process in determining target phasors. L-PBC enforces S-PBC target voltage phasors by measuring the actual phasor in real-time and modulating power to and from controllable energy resources—tracking the assigned target phasor. L-PBC may itself optimize locally based on information about specific resources (such as marginal cost, battery state-of-charge, etc.) in order to meet its given target phasor. Using nodal phasors as the explicit control variable allows for great diversity of implementation across controllers and zones because the only requirements for consistency are precisely the physical boundary conditions that are spelled out as phasors.
The PBC framework is also agnostic about the control time step, presuming only that L-PBC follows phasor targets faster than S-PBC updates them. At the local level, the most immediate goal is to compensate for disturbances to ensure a safe and secure operating state. Local control can be fast because it requires very limited information: a local phasor measurement, a reference phasor measurement, and any change in status among the resources under its control. The phasor measurements will instantaneously reflect changes in system conditions, which constitute disturbances to be rejected by the local resources. For example, resources under PBC might be actuated once per second to compensate for changes in load or the behavior of uncontrolled resources. (Our local controller for the simulation in [
28] used a time step of 0.1 s.) By acting to restore the phasor, the local controller will drive the system toward an operating state known to be safe and stable, without information about the nature of the disturbance. Fundamentally, this is because both power flows and physical operating constraints of the a.c. grid are directly expressible in terms of phasor differences between nodes.
With the luxury of additional information and time, supervisory control algorithms can always update phasor targets to account for additional criteria as desired or realistic under the given circumstances in order to optimize the system. The temporal disaggregation—maintaining a technically feasible operating state first, and then adjusting targets to fine-tune the system—inherently prioritizes grid stability and reliability. This agrees with the intent of traditional grid operations but reverses the standard approach: today, optimization comes first, followed by a check for possible violations that may overrule the desired solution. By starting from explicit physical constraints, PBC promises to be more robust, while avoiding costly over-corrections.
Stacked PBC layers not only offer a scalable path to implementation but also a way to integrate performance goals between distribution and transmission tiers. For example, the objective of a supervisory controller at a distribution substation might be to balance three-phase voltages while minimizing the volatility that creates unnecessary wear on legacy voltage regulation equipment. Accordingly, the S-PBC controller computes and assigns target phasors to strategically located L-PBC controllers along the feeder. The L-PBC controllers then coordinate distributed energy resources, such as loads, generators, or storage, to achieve the S-PBC objective, while rejecting disturbances on a much faster time-scale. The S-PBC controller may then additionally negotiate with a transmission-level entity to provide frequency regulation or other ancillary services. S-PBC would then re-compute and assign L-PBC phasor targets to meet the additional criteria, with the grid performance from the transmission tier incorporated. Other criteria, such as individual resource cost functions, feeder loss minimization, etc., are straightforward to include by design.
We propose that the formulation of optimal power flow objectives in terms of nodal phasors is generalizable across transmission networks. Just as large generators today modulate reactive power output to maintain a target bus voltage magnitude, we envision generators adjusting both real and reactive power output to track a complete bus voltage phasor. This logical extension was historically inconceivable without a way to empirically measure the timing of the voltage waveform (where the phase angle translates to the rotor position) with sufficient accuracy. Today, high-precision phasor measurements can serve as a feedback control input for both reactive and real power, which could effectively replace velocity with position control for rotating machines [
34].
4.3. Strategic Advantages of PBC
By assigning target phasors in terms of the grid state variables V and , the supervisory layer manages power flows at any chosen node relative to another on the grid, without articulating how to attain that prescribed condition (e.g., through a particular dispatch of resources). We believe that this approach has unique strategic value beyond the integration of variable renewable resources, particularly in helping prevent cascading failures and supporting improved restoration processes for grid resilience.
As illustrated by the above examples, a scheduled phasor profile will remain a feasible operating state in the event of contingencies—including network topology changes—whereas a scheduled power dispatch may not. This is because the phasor-based formulation of grid operating objectives focuses on the essence of what is physically required to keep the grid stable, while being agnostic to the logistics of how these objectives are met. Crucially, the use of the phasor as a network state variable enables an immediate corrective response without communication among controllers.
Suppose that all phasor targets prescribed by S-PBC are met, and the system is operating optimally. Any subsequent disturbance or change in load will render these targets suboptimal, but they will still meet system constraints and represent safe operation until new targets are computed. That is, the L-PBC controller mitigates load and generation variability by tracking the assigned S-PBC phasor. When an L-PBC controller fails to meet its target, this condition will be transparent to other controllers insofar as they will observe a change in the voltage phasor they are monitoring. Such an event can trigger the S-PBC controller to recompute the target phasor, accounting for increased variability in the network segment. To distinguish between cases where the L-PBC controller fails to meet a target as a result of (a) increased load and generation variability; (b) actuator saturation (e.g., the battery is fully charged and cannot absorb more energy); or (c) actuation failure (e.g., the PV inverter malfunctions), we may rely on (1) updated forecasts of load and generation; (2) the status of the integrator state and employ an integrator anti-wind-up scheme; and/or (3) a status report from the actuator.
The discussion on voltage stability above illustrates that control actions toward restoring assigned phasors after disturbances and contingency events will drive the system state in the direction of stability, or away from the “nose” of the curve, on P-, P-V, or Q-V curves for any node. Of course, conventional operating decisions would hope to drive the system in the same direction. The crucial difference is that the “right direction” is not obvious when the operating state of the grid is primarily expressed in terms of power injections and flows, and the state variables are computed or measured as an afterthought. Thus, in conventional practice, information about which control action at any given node would drive the system toward or away from stability is not readily available, especially to local resources. By contrast, two pieces of information—the phasor target assigned by S-PBC, and a pair of real-time phasor measurements—are sufficient to empower L-PBC controllers to “do the right thing” at their respective nodes. Actuation toward restoring phasors will further help prevent cascading sequences, where changes to P or Q inadvertently exacerbate a disturbance to the system state, as observed at a neighboring node.
Another strategic advantage of the phasor-based formulation is that it can support safe and speedy restoration processes, including “self-healing” functionality. Specifically, aligning phasor targets for interconnections or between different parts of the network enables the opening and closing of switches under load. When the main concern is the amount of arcing between electrical contacts, limiting the phasor difference between two sides of an open switch is a direct way to ascertain safe operation. The same rationale applies to high-voltage transmission switchgear, as well as sectionalizing switches in distribution systems or points of common coupling for microgrids.
The use of explicit phasors minimizes the information required for intelligent local operational decisions. For example, if the objective is to drive the phasor difference across a tie switch to within a safe value for closing that switch, the supervisory controller can simply assign the appropriate phasors on either side (or, if only one side is controllable, assign it to match the uncontrolled side) and leave the details of resource actuation to the L-PBC layer. By focusing on the most essential information about the grid operating state, PBC obviates the need for more centralized and cumbersome communication and data management structures.
Nevertheless, the possibility of communication loss must be accounted for by design. Even though a local controller requires only a single non-local piece of information (the reference phasor) to hold a target, it must have a default fail-safe mode in case the communication channel drops out. Possible strategies include minimizing departures from the most recent operating state known to be compliant and resorting to managing only voltage magnitude (which is strictly local). In addition, PBC is admittedly vulnerable to loss or spoofing of the GPS pulse-per-second signal. Because of the growing importance of PMUs in power system operations worldwide, alternative technologies to GPS timekeeping are already being considered and could plausibly meet the future needs of a control infrastructure that will depend more heavily on secure time synchronization [
35].
Arguably, the PBC paradigm could improve grid resilience with respect to cyber-attacks by virtue of its inherent simplicity and transparency. The crucial information to be transacted by controllers and participating resources—namely, the physical operating state of the grid—is both minimal in quantity and independently verifiable by any interested party. For example, phasor differences across the transmission and distribution system are easily observed with PMUs from any wall outlet, whereas current and power flows are measurable only on their particular circuit branch. While malicious cyber-intrusions can never be ruled out, the widespread use of explicit phasor measurements should make tampering with operationally relevant data more readily detectable. We look forward to further study of cyber-security implications and optimally secure design of PBC.